Estimating Displacement of Periodic Motion With Inertial Sensors

Abstract

Inertial sensors, like accelerometers and gyroscopes, are rarely used by themselves to measure displacement. Accuracy of inertial sensors is greatly handicapped by the notorious integration drift, which arises due to numerical integration of the sensors zero bias error. A solution is proposed in this paper to provide drift free estimation of displacement from inertial sensors.

I. Introduction

In broad categorization, there are two main types of motion sensing devices: externally and internally referenced sensors. Common internally referenced sensors include inertial sensors, e.g., accelerometer and rate gyroscope, which measures acceleration and angular velocity, respectively. However, accuracy of inertial sensors is hampered by the inherent integration driftwhen measurements in the inferred domains, like displacement, are desirable. The fast growing measurement drift arises from the numerical integration of zero bias error, which is almost impossible to calibrate out [1]. To make things worse, the zero bias error has been shown to be sensitive to temperature drift [2]. This drift due to numerical integration is depicted in Fig. 1. Hence, inertial sensors are seldom used alone in measurement of displacement. In most cases, at least one or more externally referenced nondrifting sensors [e.g., cameras, global positioning system (GPS), etc.] are employed to fuse with inertial-based measurements. In this paper, a method to perform drift-free displacement estimation of periodic motion with inertial sensors is proposed. An adaptive algorithm models the Fourier components of a periodic signal (acceleration or velocity) and thereafter displacement is obtained via analytical integration of the motion model. A motion tracking experiment is performed with a MEMS accelerometer to verify the proposed method.

Fig. 1.

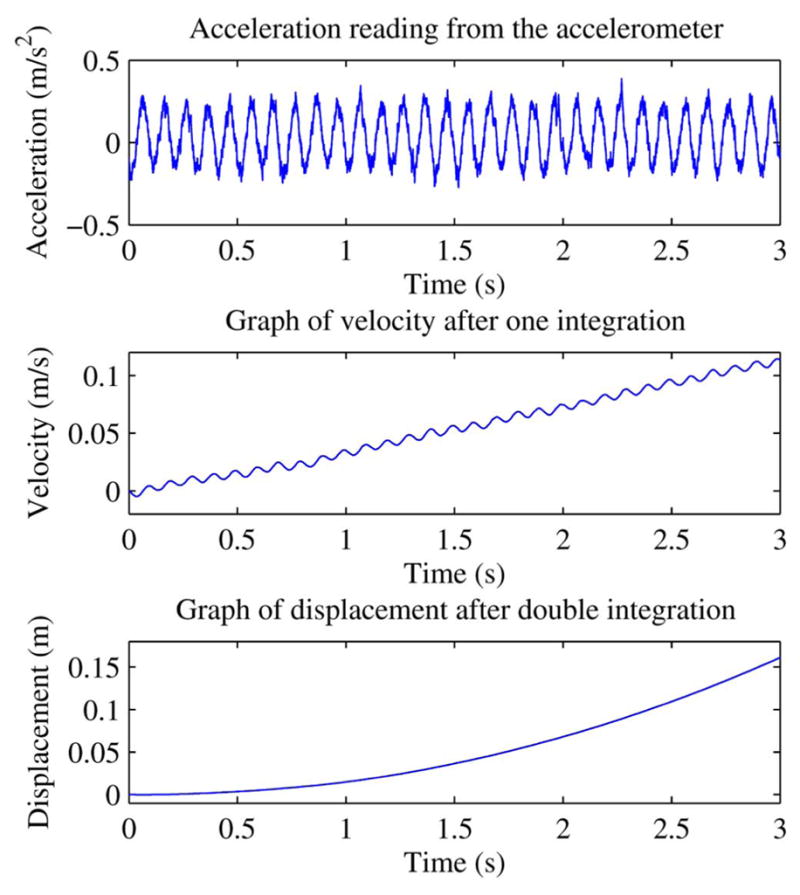
Integration drift of velocity and displacement given sinusoidal motion.

II. Methods

A. Weighted-Frequency Fourier Linear Combiner (WFLC)

Given a periodic motion with a prior known frequency, the motion may be modeled in real-time by a Fourier linear combiner (FLC) [3], which uses a least mean square algorithm to adaptively adjust a series of Fourier components. If the frequency of the motion is unknown, WFLC [4], an extension to FLC, may be used. The first portion of WFLC is the frequency estimation. The input vector x⃗_k to WFLC is

$$x_{k_r}=\{\begin{array}{l}sin\left(r\sum _{t=0}^k{w}_{o_t}\right),r=1\dots M\hfill \\ cos\left((r-M)\sum _{t=0}^k{w}_{o_t}\right),r=M+1\dots 2M\hfill \end{array}$$ (1)

Where M is the number of harmonics used. The input is the sensing domain of the inertial sensor and can be acceleration or angular velocity. The frequency can be estimated by updating every sample via

$${\epsilon }_k=s_k^{\prime }-{\overrightarrow{w}}_k^T·{\overrightarrow{x}}_k$$ (2)

$$w_{0_{k+1}}=w_0+2{\mu }_0{\epsilon }_k\sum _{i=1}^M(w_i{x}_{M+i}-w_{M+i}{x}_i)$$ (3)

$${\overrightarrow{w}}_{k+1}={\overrightarrow{w}}_k+2{\mu }_1{\overrightarrow{x}}_k{\epsilon }_k$$ (4)

where ${\overrightarrow{w}}_k^T$ is the coefficients of the input, $s_k^{\prime }$ is the signal input after the notch filter, and μ₀ and μ₁ are the adaptive gain parameters. w_o will adapt to the frequency. A second set of FLC is used to estimate the acceleration. Using the same input x⃗_k, the weights of the second FLC is updated via

$${\widehat{\epsilon }}_k=s_k-{\overrightarrow{\widehat{w}}}_k^T·{\overrightarrow{x}}_k$$ (5)

$${\overrightarrow{\widehat{w}}}_{k+1}={\overrightarrow{\widehat{w}}}_k+2\mu {\overrightarrow{x}}_k{\widehat{\epsilon }}_k$$ (6)

where ${\overrightarrow{\widehat{w}}}_k^T$ is the coefficients of the second FLC, s_k is the noisy signal input. Thus, an estimation of the acceleration/velocity can be calculated as

$$a_k={\overrightarrow{\widehat{w}}}_k^T·{\overrightarrow{x}}_k.$$ (7)

As mentioned in the previous section, a drift is usually resulted from numerical integration. Supposing the input signal is periodic with one dominant frequency, the frequency and amplitude weights can be assumed to be constant after a finite adapting time period. Thus, instead of integrating the acceleration/angular velocity sensed numerically, (7) is integrated analytically. A good estimate of displacement from acceleration reading can be obtained through double integration as

$$w_{d_{k_r}}=\{\begin{array}{ll}-{\widehat{w}}_{k_r}/{\left(\frac{r{w}_{0_k}}{T}\right)}^2,\hfill & r=1\dots M\hfill \\ -{\widehat{w}}_{k_r}/{\left(\frac{(r-M)w_{0_k}}{T}\right)}^2,\hfill & r=M+1\dots 2M\hfill \end{array}$$ (8)

$$y_k={\overrightarrow{w}}_{d_k}^T{\overrightarrow{x}}_k$$ (9)

where y_k is the estimated displacement, w⃗_dk are the weights of the FLC to estimate the displacement, and T is the sampling period. If the sensing domain of the inertial sensor is velocity, like gyroscope, estimation of displacement can be obtained as

$$w_{d_{k_r}}=\{\begin{array}{ll}-{\widehat{w}}_{k_r}/\left(\frac{r{w}_{0_k}}{T}\right),\hfill & r=1\dots M\hfill \\ {\widehat{w}}_{k_r}/\left(\frac{(r-M)w_{0_k}}{T}\right),\hfill & r=M+1\dots 2M\hfill \end{array}$$ (10)

$$y_k={\overrightarrow{w}}_{d_k}^T·{\overrightarrow{x}}_k.$$ (11)

B. Band-Limited Multiple Fourier Linear Combiner (BMFLC)

One limitation of WFLC is its inability to track more than one dominant frequency (modulated signals). To overcome that, a new algorithm BMFLC [5] was proposed recently. This approach relies on choosing a predetermined band of frequencies with spacing of frequencies chosen according to user’s requirement. The input to BMFLC is

$$x_{k_r}=\{\begin{array}{ll}sin(2\pi f_{r}kT),\hfill & r=1\dots N\hfill \\ cos(2\pi f_{r-N}kT),\hfill & r=N+1\dots 2N\hfill \end{array}$$ (12)

where f_r are the frequencies within a given band of interest and represents the number of frequencies used. The frequencies can be integer as well as rational. The weights of BMFLC can be updated via

$${\epsilon }_k=s_k-{\overrightarrow{w}}_k^T·{\overrightarrow{x}}_k$$ (13)

$${\overrightarrow{w}}_{k+1}={\overrightarrow{w}}_k+2{\mu }_1{\overrightarrow{x}}_k{\epsilon }_k.$$ (14)

An estimate of the acceleration/velocity can be given by

$$a_k={\overrightarrow{w}}_k^T·{\overrightarrow{x}}_k.$$ (15)

Thus, similar to (8)–(11), an estimate of the displacement from acceleration is

$$w_{d_{k_r}}=\{\begin{array}{ll}-w_{k_r}/{(2\pi f_r)}^2,\hfill & r=1\dots N\hfill \\ -w_{k_r}/{(2\pi f_{r-N})}^2,\hfill & r=N+1\dots 2N\hfill \end{array}$$ (16)

$$y_k={\overrightarrow{w}}_{d_k}^T·{\overrightarrow{x}}_k.$$ (17)

While the estimation of displacement from velocity is

$$w_{d_{k_r}}=\{\begin{array}{ll}-w_{k_r}/(2\pi f_r),\hfill & r=1\dots N\hfill \\ w_{k_r}/(2\pi f_{r-N}),\hfill & r=N+1\dots 2N\hfill \end{array}$$ (18)

$$y_k={\overrightarrow{w}}_{d_k}^T·{\overrightarrow{x}}_k.$$ (19)

III. Results

Accelerometer board (DE-ACCM2G) from Dimension Engineering, containing an ADXL322 accelerometer, is used in the experiment to illustrate the algorithm. Fig. 2 shows the experiment setup. The accelerometer board is placed on a nanopositioning system P-561.3CD from Physik Instrumente, which has a resolution of subnanometers for periodic motions. The nanopositioning system provides a 100 μm peak-peak sinusoidal motion. The voltage reading from the accelerometer is acquired using a DAQ card.

Fig. 2.

Experiment setup.

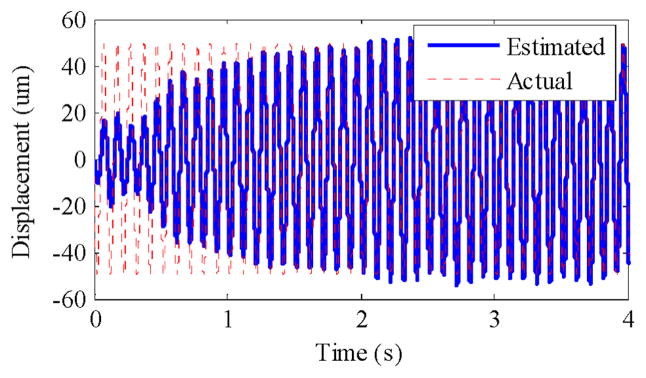
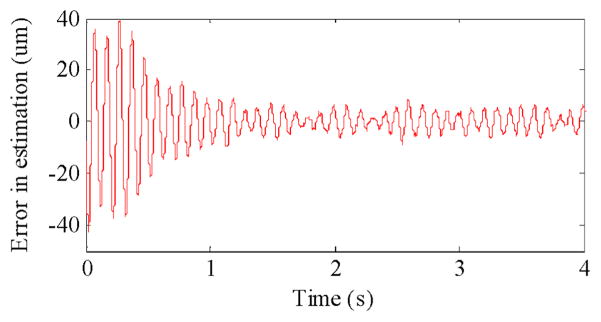
The voltage reading is then converted to acceleration domain and then passed through the algorithms, as mentioned in Section II. Fig. 1 shows the result of numerical integration. The estimated displacement using BMFLC is shown in Fig. 3 and the error between the estimated and actual displacement is shown in Fig. 4. The estimated displacement tends to the actual displacement and the root mean square error (RMSE) between the two during steady-state from 2 to 4 s is 3.498 μm. Comparing the results of BMFLC with numerical integration (third graph of Fig. 1), it is evident that the problem of drifting is eliminated.

Fig. 3.

Estimated displacement (solid) result from the accelerometer’s reading of a 100 μm peak–peak sinusoidal motion (dotted).

Fig. 4.

The error between actual displacement and estimated displacement.

IV. Discussion

The proposed algorithms provide good displacement estimation from integrated accelerometer measurement without the aid of an externally referenced sensor.

WFLC and BMFLC are proposed to be used to estimate displacement of a periodic motion from an accelerometer. The main motivation to use them is because the periodic signals in the acceleration domain can be modeled by a series of sine and cosine components. In addition, the original idea of WFLC and BMFLC is for zero phase band-pass filtering. Thus, when using the method to estimate displacement, unwanted noises from the accelerometers are also removed. However, the algorithm is limited to periodic motion. Given a nonperiodic motion, the weights of the WFLC and BMFLC will keep changing to adapt itself to the current reading. In this case, direct analytical integration will not succeed.

The algorithms are capable of handling any frequency; provided the frequency is within the bandwidth of the inertial sensors and suitable initial values are selected. However, it is also worthwhile for the readers to note that the amplitude of acceleration increases with frequency. A higher frequency will increase the signal-to-noise ratio, but it also means larger adaptive parameters μ₀ and μ₁ or appropriate initial weights are needed to ensure convergence to the global minimum.

V. Conclusion

Inertial sensors are usually not used to obtain displacement because of the drift due to numerical integration. This paper has proposed a method to estimate the displacement from inertial sensors readings, i.e., acceleration and angular velocity. Experiments are also conducted to demonstrate the effectiveness of the method.

Biographies

U-Xuan Tan (S’07) received the B.Eng. degree in mechanical and aerospace engineering from the Nanyang Technological University, Singapore, in 2005. He is currently working towards the Ph.D. degree at Nanyang Technological University, Singapore.

His research interests include mechatronics, control systems, smart materials, sensing systems, medical robotics, rehabilitative technology, mechanism design, kinematics, and signal processing.

Kalyana C. Veluvolu (S’03–M’06) was born in Ponnur, South India. He received the B.Tech. degree in electrical and electronics engineering from Nagarjuna University, Nagarjuna, India, in 2002, and the Ph.D. degree from Nanyang Technological University, Singapore, in 2007, for work on sliding mode observers and unknown input estimations for nonlinear systems.

He is currently with the Nanyang Technological University as a Research Associate before being appointed as Research Fellow. His research interests include nonlinear systems modeling, biorobotics, adaptive filtering, sliding mode observers, and signal processing.

Win Tun Latt received the B.E. degree in electronics from the Yangon Technological University, Myanmar, in 2000, and the M.Sc. degree in biomedical engineering degree from the Nanyang Technological University, Singapore, in 2004. He is currently working towards the Ph.D. degree at the Nanyang Technological University, Singapore.

His research interests include sensing systems, medical robotics, and mechatronics.

Cheng Yap Shee received the B.Eng. and M.Eng. degrees in mechanical and production engineering from the Nanyang Technological University, Singapore, in 1979 and 1999, respectively.

In 2000, he was part of the core software developer team for a startup in San Mateo, CA. Thereafter, he has worked on research projects that included code parallelization using message passing and multithreading on computer clusters for a cellular automata-based cardiac arrhythmia modeling, development of a laser-based fiber-optic polarimetric sensor instrument that measures polarization for online structural health monitoring, and the Singapore DNA Tree project, where mitochondrial and Y-DNA are sequenced and analyzed to study the genetic diversity in Singapore. He has been a research associate with the Biorobotics Group, Nanyang Technolgoical University since 2005. His research interests span the areas of cellular automata and robotics.

Cameron N. Riviere (S’94–M’96) received the B.S. degree in aerospace engineering and ocean engineering from the Virginia Polytechnic Institute and State University, Blacksburg, in 1989 and the Ph.D. degree in mechanical engineering from The Johns Hopkins University, Baltimore, MD, in 1995.

Since 1995, he has been with the Robotics Institute at Carnegie Mellon University, Pittsburgh, PA, where he is presently an Associate Research Professor and the Director of the Medical Instrumentation Laboratory. He is also an adjunct faculty member of the Department of Rehabilitation Science and Technology at the University of Pittsburgh. His research interests include medical robotics, control systems, signal processing, learning algorithms, and biomedical applications of human-machine interfaces.

Dr. Riviere served as one of the guest editors of the Special Issue on Medical Robotics of the journal Proceedings of the IEEE in September 2006.

Wei Tech Ang (S’98–M’04) received the B.Eng. and M.Eng. degrees in mechanical and production engineering from the Nanyang Technological University, Singapore, in 1997 and 1999, respectively, and the Ph.D. degree in robotics from Carnegie Mellon University, Pittsburgh, PA, in 2004.

He has been an Assistant Professor in the School of Mechanical and Aerospace Engineering, Nanyang Technological University, since 2004. His research interests include sensing and sensor, actuators, medical robotics, rehabilitative and assistive technology, mechanism design, kinematics, signal processing, and learning algorithms.