Abstract
The response of a neuron to sensory stimuli can only give correlational support for functional hypotheses. To experimentally test causal function, the neural activity needs to be manipulated in a cell-type specific, as well as spatially and temporally precise way. We review recent optogenetic experiments on parvalbumin-positive cortical interneurons that link modeling studies of synchronization to experimental studies on attentional modulation of gamma oscillations in primates.
Introduction
The receptive field (RF) of a cortical neuron, a core concept in sensory systems, is determined by recording the responses of a neuron to a wide range of sensory stimuli. In the visual cortex, for example, a neuron will respond well and with low latency to specific patterns of stimuli in a spatially restricted region of the visual field called the receptive field, reflecting information arriving primarily through feedforward pathways. Modulation of the response is studied by varying the context of the sensory stimulus, such as stimulating the visual surround (Allman et al., 1985), or the attentional state of the animal (Reynolds and Chelazzi, 2004). Although these responses are correlated with the behavior of an animal, additional experiments are needed to test for causality.
Direct causal roles can be tested by manipulating the responses of the cortical neurons. This has been done at the population level by passing current through micoelectrodes in the cortex (Salzman et al., 1990), which probably activates hundreds to thousands of neurons of different types having different functions. New optogenetic techniques that allow specific types of cortical neurons to be stimulated or silenced can be used to more precisely test predictions for the function of these neurons (Luo et al., 2008; Zhang et al., 2007). Current studies are aimed at understanding the interaction between sensory input and cortical state in rodents at the level of the local cortical circuits. Similar approaches could be used in primates to study cognitive factors that influence this interaction in vivo (Han et al., 2009).
In this review we will focus on possible mechanisms underlying spatial visual attention, and in particular on recent experimental evidence that point to fast-spiking cortical interneurons as a key circuit element in regulating the response gain of nearby pyramidal neurons. These neurons are also implicated in generating gamma oscillations (30–80 Hz) in the cortex (Cardin et al., 2009; Sohal et al., 2009). Neural models of cortical circuits provide a framework for understanding the functional significance of these results and guide new experiments that manipulate the circuit elements. In the following we refer to the excitatory cells, including pyramidal cells, as E cells and assume they correspond physiologically to regular spiking (RS) cells. We consider one class of inhibitory neurons (Markram et al., 2004), the parvalbumin-positive fast-spiking (FS) basket cells and refer to them as I cells.
Functional Forms of Response Modulation
Spatial attention has been probed in primates by presenting visual stimuli at two different locations and training an animal to detect a subtle stimulus change at one location but not the other (Fries et al., 2001). The attended location was varied between blocks of trials, and the spike trains were recorded from a single neuron that had its receptive field at one of the stimulus locations. Therefore the response R was measured when attention was directed at the location in the RF and when it was directed outside the RF, even though in both conditions exactly the same stimulus was present in the RF of the recorded neuron (Reynolds and Chelazzi, 2004).
In these attention-probing experiments, neuronal responses depended both on the properties of the presented stimulus and the focus of attention, which thus reflected the interaction between bottom-up sensory information and top-down modulation. Related attention experiments revealed a multiplicative relationship between the sensory response and attention (Figure 1A, compare green and blue curves; reviewed in (Reynolds and Heeger, 2009; Williford and Maunsell, 2006)). This is called a separable representation and is an attractive way of combining the bottom-up sensory and top-down attentional influences because it makes it easy to extract the orientation of the stimulus or the locus of attention using a population of neurons (reviewed in (Salinas and Thier, 2001)).
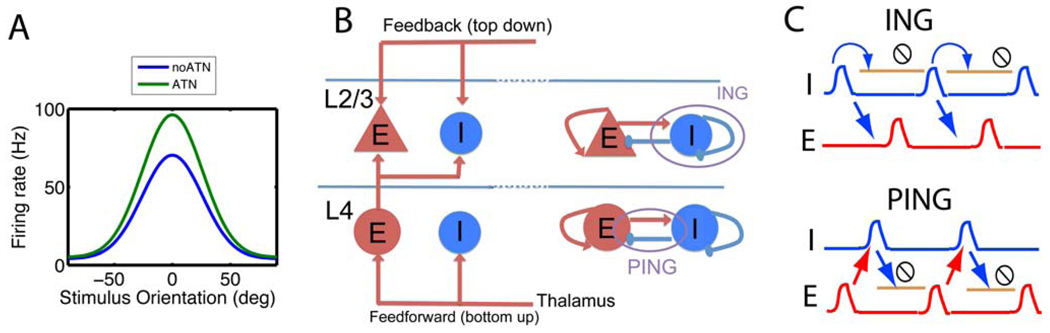
Figure 1. Response modulation is achieved by altering the voltage oscillations generated by synchronous synaptic inputs.
(A) The response of neurons in intermediate visual cortical areas reflects the interaction of multiple factors, one of which is the stimulus. We show the orientation tuning curve (firing rate as a function of the stimulus orientation) when attention is directed outside (blue -No ATN) and into the receptive field (green -- ATN). The green curve can be mathematically described as the blue curve multiplied by a gain factor (exaggerated for clarity) that is independent of the firing rate and stimulus orientation. (B, left) Simplified representation of the laminar structure of the feedforward pathway in V1. The feedforward (FF, bottom-up) pathway projects to the E and I cells in layer 4 (L4), which in turn sends an excitatory projection to L2/3 cells. The L2/3 cells also receive feedback (FB, top down) inputs from other cortical areas (such as V2). (B, right) In both layers there are reciprocally connected networks of E and I cells (‘PING’) as well as mutually connected I cells (‘ING’). The I cells and their projections are shown in blue, whereas the E cells and their projections are shown in red. For clarity, we omitted some of the inhibitory projections. (C) The synchronous network activity underlying response modulation can be generated in two different ways. For the ING mechanism, the I cells are sufficiently excited to spike in the absence of excitatory network activity. Synchrony arises because cells ready to spike shortly after the first volley will be stopped by the resulting inhibition until they can participate in the next volley. The I cells in turn synchronize the E cells. The period is determined by the recovery of the I cells, which reciprocally inhibit themselves. In the PING mechanism, a synchronous excitatory volley is necessary to elicit a synchronous volley from the I cells. The period is thus determined by the time for recovery of the E cells from the inhibition. The schematic blue and red histograms show the spike time density of the inhibitory (I) and excitatory (E) neurons, respectively. The light brown lines with the stop sign indicate the period during which the network is inactive due to the high value of the inhibitory conductance.
Gain Modulation Can Be Achieved by Modulating Inhibitory Synchrony and Phase
The fluctuation-driven spiking regime is the most relevant for studying a multiplicative gain mechanism (Tiesinga et al., 2000). For neurons in this regime, the mean of the driving current or synaptic inputs is always below spiking threshold, but there are large fluctuations, which cause the voltage to occasionally exceed threshold. In this case the neuron’s spike train is irregular, and the coefficient of variation of the interspike intervals is high, which is representative of in vivo activity. Furthermore, the firing rate can be increased either by increasing the amplitude of the fluctuations or by shifting the mean membrane potential closer to the spiking threshold.
Modeling studies have identified two potential mechanisms for multiplicative gain modulation in the fluctuation-driven regime. The first mechanism operates by changing the overall rates of excitatory and inhibitory inputs (Chance et al., 2002), while maintaining the balance between them and has been reviewed extensively (Haider and McCormick, 2009). Here we focus on the second, which works by altering the correlation structure of the synaptic inputs, such as, for example, the degree of synchrony.
A volley refers to a set of synchronous synaptic inputs that arrive at approximately the same time and can be quantified by the timing precision of the input spikes (Tiesinga et al., 2008). When the excitatory inputs arrive in volleys, they are more effective when their precision is high (Azouz and Gray, 2000; Bernander et al., 1994); that is, when the inputs arrive in the range of a few milliseconds. Modeling studies show that changes in the level of synchrony of the inhibitory inputs modulate the response gain, but only for synchrony in the gamma -frequency range (Borgers et al., 2005; Tiesinga et al., 2004; Tiesinga et al., 2008). When both the excitatory and inhibitory inputs arrive in synchronous volleys, their relative phase can modulate the gain to other inputs (Buia and Tiesinga, 2006; Mishra et al., 2006). Recent experiments have shown that the effectiveness of long-distance communication depends on the relative phase between the input spikes and the local field potential (LFP), termed the communication through coherence (CTC) hypothesis (Womelsdorf et al., 2007). Specifically, correlations of the LFP power between two recording sites was highest at one specific phase difference between them compared with other phases. Interpreted within the context of the preceding models, CTC could occur when inhibitory synchrony produces a much higher inhibitory conductance at one phase and a much lower one at another phase thereby providing a window of opportunity for excitatory inputs arriving at the latter phase to induce a spike in the neuron.
Synchrony of synaptic inputs and changes in the balance between excitation and inhibition can thus strongly affect a neuron’s firing rate via membrane potential fluctuations as long as the neuron is in the fluctuation-driven regime. Models can be used to predict how to manipulate synaptic inputs in order to achieve gain modulation.
Local Synchrony with the ING or PING Mechanisms
The cortex is a two-dimensional arrangement of minicolumns, each of which receives bottom-up input in layer 4, and feedforward (FF) projection to layer 2/3, mediated by feedback (FB) cortical projections (Figure 1B) (Douglas and Martin, 2004). Within this laminar cortical circuit, there are network motifs comprised of mutually connected I cells, recurrently connected E cells and reciprocal connections between these two groups (Figure 1B).
There are three ways of producing synchrony in a minicolumn: First, by inheritance of synchrony from upstream areas via the FF projection (Tiesinga et al., 2008); second, by activation of inhibitory networks via the interneuron gamma (ING) mechanism (Figure 1C); and third, by activation of reciprocally connected networks of excitatory and inhibitory neurons via the pyramidal-interneuron gamma (PING) mechanism (Figure 1C) as reviewed in (Whittington et al., 2000). We focus on the ING and PING mechanisms, which are common throughout the cortex. We first examine how these mechanisms function in isolation, before studying how they function together in the full network.
Intuitively, the ING mechanism can be explained in two ways. First, when all the inhibitory neurons are identical, receive identical input and there is no noise, all the neurons will fire at exactly the same rate. Recurrent inhibitory coupling can achieve synchrony by moving unsynchronized spikes towards those in the already synchronized neurons. If at a certain time a few more neurons than average fire, they will more strongly inhibit the remaining neurons, delaying their spikes and bringing them closer to the next time the first group of neurons will fire, thereby increasing synchrony. This chain of events is confirmed by mathematical analysis, which also shows that inhibition is more effective than excitation in achieving synchrony (Van Vreeswijk et al., 1994).
The ING mechanism is most robust against heterogeneity and noise when the decay constant of inhibition matches the period of the oscillation, which is also the inverse of the firing rate (Tiesinga and Jose, 2000; Wang and Buzsaki, 1996). However, during typical brain states, inhibitory neurons fire at an average rate much below 40 Hz (Fujisawa et al., 2008; Greenberg et al., 2008). Hence, in order to synchronize at gamma frequencies, their natural firing rate must be increased, which can occur when these neurons are depolarized by strong excitatory inputs or by activating their muscarinic or metabotropic glutamatergic receptors (Fisahn et al., 1998; Whittington et al., 1995).
When large numbers of I cells fire randomly, but at rates as low as 1 Hz, so that there is no synchrony, there are only small fluctuations in the population firing rate. Increasing the external drive will make the asynchronous state unstable against these fluctuations, and synchronous oscillations emerge (Brunel and Hakim, 1999).
These two approachs, one for small systems starting from synchrony, the other for large systems starting from asynchrony, show that a network of I cells can become synchronized by external activation, which leads to an increase in synchrony of the E cells they project to, yielding an overall increase in LFP power in the gamma frequency band (Tiesinga et al., 2004). The standard way to study this experimentally has been using pharmacological manipulation of slice preparations, but recent developments in optogenetic techniques now allow neurons to be selectively synchronized in vivo.
The oscillation from the ING mechanism is an emergent property from a coupled network of E and I cells, as is PING, but, in the latter, asynchronous excitatory inputs would not be effective in driving the I cells into synchrony because only when the E cells are synchronized is the drive to the I cells strong enough to elicit an inhibitory volley.
In a small, moderately connected network, the decay time constant of inhibition determines the highest oscillation frequency of the PING mechanism. When the drive to the E cells is increased, their firing rate increases, which in turn increases the firing rate of the I cells because they receive more excitatory inputs. In contrast, when the drive to the I cells is increased, their firing rate increases, but the firing rate of the E cells decreases because they receive more inhibitory inputs. This has consequences for the robustness of gamma oscillations against changes in depolarization of E or I cells, such as those caused by optogenetic activation or neuromodulation. Synchronous oscillations typically occur for a specific ratio between the mean E and I cell firing rate (Buia and Tiesinga, 2006). When both firing rates are increased at the same time, this ratio is approximately conserved, so that the oscillation is robust. But when both firing rates move in opposite directions, this ratio varies quickly and the oscillation is disrupted.
In the ING mechanism, only small effects are expected from activating the E cells, whereas activating I cells will increase the I-cell firing rate and synchrony, as mentioned previously.
Phase Differences Between E and I Cells in the Local Circuit
There is a relative phase difference between E- and I-cell activity, which is important computationally because it defines windows of opportunity in postsynaptic neurons and can change the gain of these neurons. Hence, it is important to determine how top-down projections can modulate this phase difference and whether there are differences between the PING and ING mechanism.
During the PING mechanism, an excitatory volley elicits an inhibitory volley at a delay that depends on the level of depolarization of I cells, which means that the phase between the excitatory and inhibitory volleys can be modulated by top-down inputs targeting I cells. The E cells produce a volley after the inhibitory conductance from the inhibitory volley has decayed, with a delay that depends on the depolarization of E cells. However, this mostly affects the period and thus places an upper bound on the oscillation frequency.
During the ING mechanism, the E cells fire when the inhibitory conductance has decayed sufficiently. During phase-locking, when the E cell produces a specific number of spikes per cycle, for instance one per cycle, the phase is determined by the drive to the E cells (Tiesinga et al., 2002). Outside of phase-locking, the level of drive to the E cells does not influence the phase, rather it determines the probability of firing on a cycle; that is, the overall firing rate. Even when the E cell fires at irregular interspike intervals it will nonetheless fire primarily at the troughs of the inhibitory conductance. This last scenario is more appropriate for describing the in vivo state, since the E-cell firing rate is typically low in vivo (Fujisawa et al., 2008; Greenberg et al., 2008).
Taken together, we obtain from these network mechanisms specific predictions for the effect on firing rate, synchrony and relative phase of activating either E or I cells. There are also intrinsic neural mechanisms through which neuromodulation can change the spike phase in response to oscillatory inputs, but these are outside the scope of this review.
Experimental Evidence for ING and PING in vitro and in vivo
Pharmacological manipulation of hippocampal slices targeting the metabotropic glutamate receptors has provided support for the ING mechanism (Whittington et al., 1995), whereas the cholinergically-induced oscillations in hippocampal slices are consistent with a PING mechanism (Fisahn et al., 1998). Different mechanisms could be present in the cortex (Bartos et al., 2007), but two recent in vivo optogenetic experiments reviewed here provide further support for the involvement of I cells in the generation of gamma oscillations. First, depolarization of cortical I cells by activating ChR2 channels in vivo increased gamma power in the LFP, whereas hyperpolarizing them via halorhodopsin light-activated pumps reduced gamma power (Sohal et al., 2009). Second, in the slice preparation, when I cells were indirectly depolarized by optically stimulating ChR2 in the E cells, gamma power in the LFP increased (Sohal et al., 2009). Third, when in vivo the I cells were driven by random light pulses, whose power is spread across a broad frequency range, the LFP power in the gamma range was enhanced relative to other frequency bands (Cardin et al., 2009).
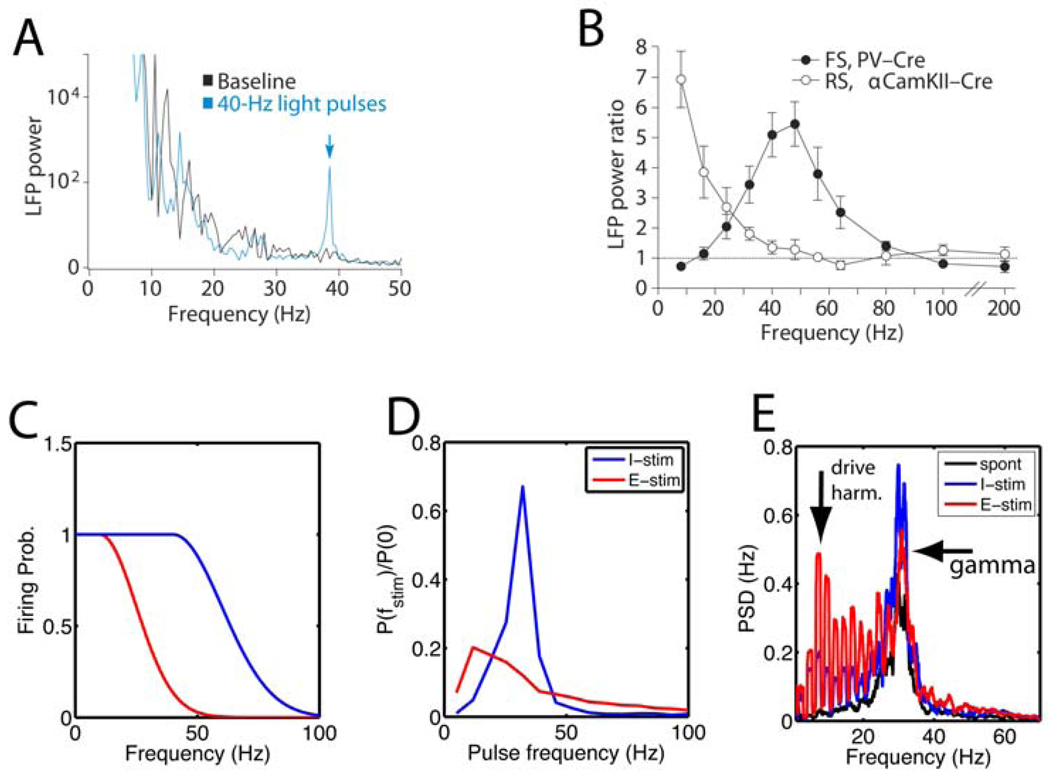
One of the key results in (Cardin et al., 2009) is that activating I cells by periodic trains of light pulses is more effective at eliciting gamma oscillations than activating E cells that way. In the former case, there was a clear peak at gamma frequencies in the LFP power at the pulse frequency as a function of the pulse frequency (Figure 2 A & B), whereas for the latter case the LFP power decreased with increasing drive frequency, without displaying a peak. At first sight, this result favors the ING mechanism. However, the models reviewed in the preceding sections predict how increasing the depolarization of the E or I cells affects the oscillations, but they do not make predictions for the response to periodic pulse trains.
Figure 2. Gamma frequency stimulation of inhibitory neurons is more effective in generating network oscillations than stimulating excitatory neurons.
(A,B) Results of in vivo experiments using periodic light pulse trains to activate cells via ChR2 channels expressed in either parvalbumin-positive cells or pyramidal cells, taken with permission from (Cardin et al., 2009). (A) The power spectrum of the recorded LFP (black line) during the baseline condition without light stimulation and (blue line) during stimulation with a 40 Hz light pulse train. The power spectrum characteristically decays as a function of frequency, but the blue curve has a peak at the stimulation frequency (indicated by the arrow). (B) The power at the stimulation frequency normalized by the power in the baseline condition is plotted as a function of stimulation frequency for light activation of (filled circles) FS cells and (open circles) RS cells, here referred to as E and I cells, respectively. There was a peak at gamma frequencies for the I cell stimulation, indicating a resonance, which was absent for E-cell stimulation. (C) The effectiveness of above threshold periodic stimulation depends on cell class because of the duration of the refractory period and other adaptation effects (Fellous et al., 2001). These data are schematically summarized by plotting the spike probability per light pulse as a function of pulse frequency. The E cell (red) firing probability drops off at lower pulse frequencies compared with the I cells (blue). This shows that the amount of spiking activity induced in the cortical circuit for a given frequency depends on the cell type that is targeted. (D–E) Results obtained from a computer model from (Buia and Tiesinga, 2006) of a reciprocally connected network of I and E cells capable of producing gamma oscillations using the PING mechanism (see Supplementary Information). (D) The network was stimulated by periodic conductance pulse trains to either the I cells (blue) or the E cells (red) and the fraction of power at the stimulated frequency is shown relative to the power at zero frequency. Stimulating the I cells led to more power at the harmonic of the drive frequency, which peaked in the gamma frequency range, whereas stimulating E cells led to less power, which peaked at a lower frequency near 12 Hz. Compare with the experimental results in (B). (E) A more critical test of the ability of the network to generate (transient) gamma oscillations is obtained by applying one pulse and determining whether and for how long there is an increase in power in the gamma frequency range. This was quantified using the power spectral density (PSD) of the E-cell spike time histograms (related to the LFP), where the highest peak at gamma frequencies is obtained in response to stimulation of I cells (blue, ‘I-stim’), less power by stimulating the E cells (red, ‘E-stim’), with the lowest power obtained when there is no stimulation (black, ‘spont’). The light pulses were presented at an average interval of about 400ms, corresponding to a frequency of 2.5 Hz. Hence, there are peaks at harmonics of the stimulation frequency which are strongest when the E cells are directly stimulated.
In Models Two Effects Could Account for E-I Asymmetry in the Response to Light Pulse Trains
In the PING mechanism an excitatory volley recruits an inhibitory volley, which inhibits the E cells for a gamma cycle, after which they recover. In this mechanism it should not matter whether the circuit is driven by a periodic sequence of excitatory volleys or by inhibitory volleys via periodic light pulses as long as the frequency of the stimuli is approximately in the gamma frequency range and cells respond with a spike to each pulse. Nevertheless, in the experiment only inhibitory stimulation was effective (Cardin et al., 2009). Models incorporating physiological data suggest two possible reasons.
First, there are differences in the intrinsic dynamics between FS cells (I cells) and RS cells (E cells), with the RS cells typically firing at lower rates and responding more slowly. As a result, subthreshold inputs in the gamma frequency range excite I cells more strongly than the E cells. For above threshold periodic currents, the E cells have a longer relative refractory period compared with I cells, which means that E cells will skip beats for fast oscillatory driving currents, whereas the I cells could still follow them (Figure 2C). The experimental results obtained using periodic light pulse trains are consistent with those of previous studies using current injection (Fellous et al., 2001). For E cells, the fraction of cycles on which a spike is obtained in response to a light pulse decreased from one for low frequencies to values less than 0.25 for gamma frequencies; whereas the I cells were able to follow the light pulses up to gamma frequencies (Cardin et al., 2009).
Second, in model simulations, strong pulses activating I cells were also more effective than those activating E cells (Figure 2D). In the PING mechanism, after the effects of the inhibitory volley have subsided the E-cells recover simultaneously in the form of a synchronous volley. During spontaneous activity, there are bouts of transient oscillations within otherwise asynchronous periods. For both synchronous and asynchronous periods, when the I cells are activated by a light pulse in model simulations, they reset the oscillation by stopping the excitatory activity, which subsequently recovers in the form of a synchronous volley, often followed by a few cycles of gamma oscillation. In the model we estimated the LFP as the spike time histogram of E-cell activity because the E-cells constitute 80% of all cortical neurons and are thought to dominate the LFP (Mitzdorf, 1985). Overall, activation of inhibitory cells will increase the strength of transient oscillations, as measured using the induced gamma power in the estimated LFP, compared with the spontaneous oscillations (Figure 2E).
The degree of activation of E cells by a light pulse depends on the level of inhibitory conductance (and thus the phase of the spontaneous oscillation). Therefore, if the pulse happens when the inhibitory conductance is high in both I and E cells, it will not elicit a transient gamma oscillation. Taken together, this makes activation of I cells more effective in inducing gamma oscillations than activation of E cells as measured in terms of the gamma power in the LFP (Figure 2E). If attention is mediated by top-down depolarizing inputs, projections onto I cells would be more effective than onto E cells in modulating and gating feedforward information flows (Tiesinga et al., 2008).
Experiments and modeling studies support the PING mechanism in the cortex but the ING mechanism may still contribute in some circumstances, such as during sleep. In the ING mechanism the E cells are followers, which can be modeled by cutting out the E to I projection. In this circuit, activation of E cells should have no effect on the gamma oscillation. The activation of inhibitory neurons would reset the oscillations, just as in the PING case, except that now it is the I cells rather than the E cells that recover in the form of a synchronous volley.
New Experiments to Distinguish ING and PING Should Be Based on Non-periodic Stimulation
The recent experiments using optogenetic techniques (Cardin et al., 2009; Sohal et al., 2009) cannot distinguish between the ING and PING mechanisms. These mechanisms do, however, make different predictions for the effects of depolarizing E and I cells. In summary, when the E cells are constantly depolarized, PING predicts an increase in oscillation frequency, whereas ING predicts a higher E-cell firing rate for the same oscillation frequency. In contrast, when I cells are constantly depolarized, PING predicts a shorter delay between inhibitory and excitatory volleys, whereas ING predicts changes in synchronization and oscillation frequency. Model simulations confirm that the experiments to check these predictions are feasible, but require light pulses to be relatively weak and applied as aperiodic sequences.
New Experiments that Manipulate Cortical Phase to Uncover Attention Mechanisms
When gamma oscillations are generated in the local circuit, there is a phase difference between the excitatory and inhibitory activity due to the network dynamics. The preceding predictions can be cast in terms of the relative phase between E and I cells, which connects to the CTC hypothesis, in which phase differences between non-local excitatory and local inhibitory inputs determine the effectiveness of the interaction between two brain areas.
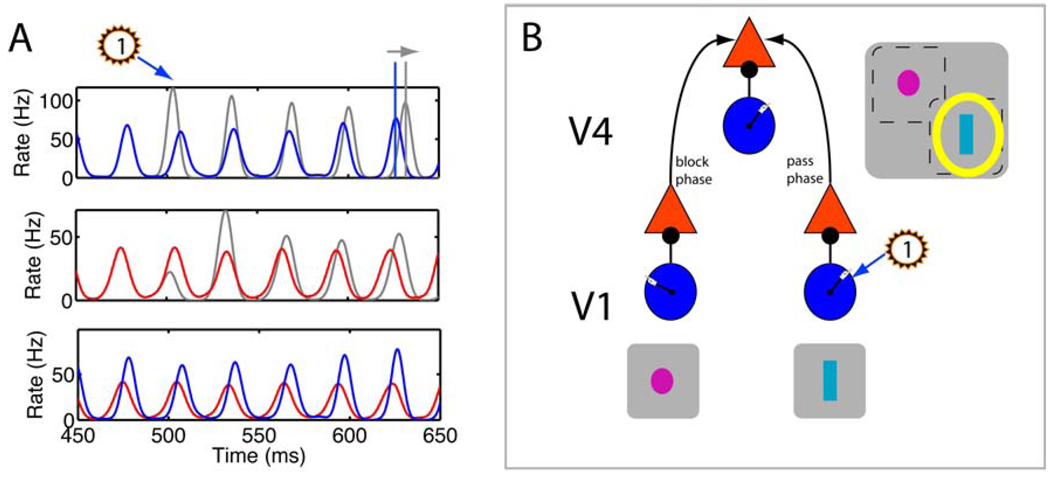
In simulations of cortical circuits, the absolute phase of the oscillation was altered via external inputs (Figure 3A). The E cells projected outside the local circuit, hence these synaptic inputs interacted at their target with the synchronized local excitation and inhibition. These outside inputs were most effective when they arrived at the postsynaptic side when the inhibition was low (the ‘pass’ phase), thereby generating a gating (or modulation) based on the phase differences between different cortical areas. This mechanism can be important at the level of V4 where the outputs from cells in VI and V2 inputs are integrated, as illustrated in Figure 3B.
Figure 3. Simulation of an experiment in which light activation of ChR2 channels can he used to study the communication through coherence (CTC) hypothesis.
In models of the E-I circuit (Buia and Tiesinga, 2006), a pulse to the I cells changed the global phase of the oscillations (see Supplementary Information). (A) The spike time histograms show: (bottom) the unperturbed oscillation, with I- and E-cell activity in blue and red, respectively; (middle) the E-cell activity (gray) was perturbed by a pulse to the I cells at 500ms (flashed “1”) and, for comparison, is shown together with the reference curve from the unperturbed oscillations in red; and (top) the perturbed I-cell activity with the reference curve. The pulse made the inhibitory volley appear earlier, and (middle) cut short the excitatory volley that was building up. After a 100 ms transient, the perturbed oscillation is delayed with respect to the reference (horizontal arrow), showing that an overall phase change occurred. (B) The schematic model V4 cell had a large RF that contained the two non-overlapping RFs of presynaptic neurons, for instance in V1. Each neuron was part of a local circuit (shown as an E cell, red triangle, receiving input from an I cell, blue circle), which when synchronized has a global phase as indicated by the hand of the clock in the blue circle. According to the CTC hypothesis, by altering the relative phase between V1 and V4 neurons (‘pass phase’, indicated by the arrow), the effectiveness of stimulus 1 (cyan bar) in driving the V4 neuron can be increased (yellow halo). Thus the CTC hypothesis can be tested in experiments where phase changes elicited by light pulses can be manipulated and linked to perception.
Several interesting questions can be addressed in experiments in the behaving primate where local circuits are stimulated by light pulses to mimic the effects of attention and where the resulting perceptual effects are quantified. For example, during attention, is the phase altered in the local circuit on the postsynaptic side (V4), or on the presynaptic side (V1, V2)? In order to achieve the shift in phase, which cell type is most effectively targeted? The experiments reviewed here and computational studies suggest the I cells would be preferred (Buia and Tiesinga, 2008), but recent experiments in V1 (Chen etal., 2008) when interpreted in the context of a large-scale V1 model (Tiesinga and Buia, 2009) provide support for attentional modulation of E cells.
Summary
We reviewed possible cortical circuit mechanisms that could give rise to the observed cortical gamma oscillations based on modeling studies and recent optogenetic experiments. The models made predictions for the effects of selectively stimulating FS neurons or RS neurons on the LFP that can distinguish between the ING and PING mechanisms. The predictions can be tested using optogenetic techniques that allow specific populations of neurons to be stimulated with high temporal precision. These effects may also depend on the state of the cortex, which can be shifted by neuromodulation.
Acknowledgment
This study was supported in part by the Human Frontier Science Program (PT), the Howard Hughes Medical Institute (TJS) and the NSF Science of Learning Center SBE 0542013 (TJS).
References
- Allman J, Miezin F, McGuiness E. Stimulus-specific responses from beyond the classical receptive field: neurophysiological mechanisms for local-global comparisons on visual neurons. Annu Rev Neurosci. 1985;8:407–430. doi: 10.1146/annurev.ne.08.030185.002203. [DOI] [PubMed] [Google Scholar]
- Azouz R, Gray CM. Dynamic spike threshold reveals a mechanism for synaptic coincidence detection in cortical neurons in vivo. Proc Natl Acad Sci U S A. 2000;97:8110–8115. doi: 10.1073/pnas.130200797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartos M, Vida I, Jonas P. Synaptic mechanisms of synchronized gamma oscillations in inhibitory interneuron networks. Nat Rev Neurosci. 2007;8:45–56. doi: 10.1038/nrn2044. [DOI] [PubMed] [Google Scholar]
- Bernander O, Koch C, Usher M. The Effect of Synchronized Inputs at the Single Neuron Level. Neural Computation. 1994;6:622–641. [Google Scholar]
- Borgers C, Epstein S, Kopell NJ. Background gamma rhythmicity and attention in cortical local circuits: A computational study. Proc Natl Acad Sci U S A. 2005;102:7002–7007. doi: 10.1073/pnas.0502366102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brunel N, Hakim V. Fast global oscillations in networks of integrate-and-fire neurons with low firing rates. Neural Comput. 1999;11:1621–1671. doi: 10.1162/089976699300016179. [DOI] [PubMed] [Google Scholar]
- Buia CI, Tiesinga PH. Attentional modulation of firing rate and synchrony in a model cortical network. Journal of Computational Neuroscience. 2006;20:247–264. doi: 10.1007/s10827-006-6358-0. [DOI] [PubMed] [Google Scholar]
- Buia CI, Tiesinga PH. Role of interneuron diversity in the cortical microcircuit for attention. J Neurophysiol. 2008;99:2158–2182. doi: 10.1152/jn.01004.2007. [DOI] [PubMed] [Google Scholar]
- Cardin JA, Carlen M, Meletis K, Knoblich U, Zhang F, Deisseroth K, Tsai LH, Moore CI. Driving fast-spiking cells induces gamma rhythm and controls sensory responses. Nature. 2009;459:663–667. doi: 10.1038/nature08002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chance FS, Abbott LF, Reyes AD. Gain modulation from background synaptic input. Neuron. 2002;35:773–782. doi: 10.1016/s0896-6273(02)00820-6. [DOI] [PubMed] [Google Scholar]
- Chen Y, Martinez-Conde S, Macknik SL, Bereshpolova Y, Swadlow HA, Alonso JM. Task difficulty modulates the activity of specific neuronal populations in primary visual cortex. Nat Neurosci. 2008;11:974–982. doi: 10.1038/nn.2147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Douglas RJ, Martin KA. Neuronal circuits of the neocortex. Annu Rev Neurosci. 2004;27:419–451. doi: 10.1146/annurev.neuro.27.070203.144152. [DOI] [PubMed] [Google Scholar]
- Fellous JM, Houweling AR, Modi RH, Rao RPN, Tiesinga PHE, Sejnowski TJ. Frequency dependence of spike timing reliability in cortical pyramidal cells and interneurons. Journal of Neurophysiology. 2001;85:1782–1787. doi: 10.1152/jn.2001.85.4.1782. [DOI] [PubMed] [Google Scholar]
- Fisahn A, Pike FG, Buhl EH, Paulsen O. Cholinergic induction of network oscillations at 40 Hz in the hippocampus in vitro. Nature. 1998;394:186–189. doi: 10.1038/28179. [DOI] [PubMed] [Google Scholar]
- Fries P, Reynolds JH, Rorie AE, Desimone R. Modulation of oscillatory neuronal synchronization by selective visual attention. Science. 2001;291:1560–1563. doi: 10.1126/science.1055465. [DOI] [PubMed] [Google Scholar]
- Fujisawa S, Amarasingham A, Harrison MT, Buzsaki G. Behavior-dependent short-term assembly dynamics in the medial prefrontal cortex. Nat Neurosci. 2008;11:823–833. doi: 10.1038/nn.2134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greenberg DS, Houweling AR, Kerr JN. Population imaging of ongoing neuronal activity in the visual cortex of awake rats. Nat Neurosci. 2008;11:749–751. doi: 10.1038/nn.2140. [DOI] [PubMed] [Google Scholar]
- Haider B, McCormick DA. Rapid neocortical dynamics: cellular and network mechanisms. Neuron. 2009;62:171–189. doi: 10.1016/j.neuron.2009.04.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han X, Qian X, Bernstein JG, Zhou H-h, Franzesi GT, Stern P, Bronson RT, Graybiel AM, Desimone R, Boyden ES. Millisecond-Timescale Optical Control of Neural Dynamics in the Nonhuman Primate Brain. Neuron. 2009;62:191–198. doi: 10.1016/j.neuron.2009.03.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo L, Callaway EM, Svoboda K. Genetic dissection of neural circuits. Neuron. 2008;57:634–660. doi: 10.1016/j.neuron.2008.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markram H, Toledo-Rodriguez M, Wang Y, Gupta A, Silberberg G, Wu C. Interneurons of the neocortical inhibitory system. Nat Rev Neurosci. 2004;5:793–807. doi: 10.1038/nrn1519. [DOI] [PubMed] [Google Scholar]
- Mishra J, Fellous JM, Sejnowski TJ. Selective attention through phase relationship of excitatory and inhibitory input synchrony in a model cortical neuron. Neural Netw. 2006;19:1329–1346. doi: 10.1016/j.neunet.2006.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitzdorf U. Current source-density method and application in cat cerebral cortex: investigation of evoked potentials and EEG phenomena. Physiol Rev. 1985;65:37–100. doi: 10.1152/physrev.1985.65.1.37. [DOI] [PubMed] [Google Scholar]
- Reynolds JH, Chelazzi L. Attentional modulation of visual processing. Annu Rev Neurosci. 2004;27:611–647. doi: 10.1146/annurev.neuro.26.041002.131039. [DOI] [PubMed] [Google Scholar]
- Reynolds JH, Heeger DJ. The normalization model of attention. Neuron. 2009;61:168–185. doi: 10.1016/j.neuron.2009.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salinas E, Thier P. Gain modulation: a major computational principle of the central nervous system. Neuron. 2001;27:15–21. doi: 10.1016/s0896-6273(00)00004-0. [DOI] [PubMed] [Google Scholar]
- Salzman CD, Britten KH, Newsome WT. Cortical microstimulation influences perceptual judgements of motion direction. Nature. 1990;346:174–177. doi: 10.1038/346174a0. [DOI] [PubMed] [Google Scholar]
- Sohal VS, Zhang F, Yizhar O, Deisseroth K. Parvalbumin neurons and gamma rhythms enhance cortical circuit performance. Nature. 2009;459:698–702. doi: 10.1038/nature07991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tiesinga P, Buia CI. Spatial attention in area V4 is mediated by circuits in primary visual cortex. Neural Networks. 2009 doi: 10.1016/j.neunet.2009.07.010. in press. [DOI] [PubMed] [Google Scholar]
- Tiesinga PH, Fellous JM, Salinas E, Jose JV, Sejnowski TJ. Inhibitory synchrony as a mechanism for attentional gain modulation. Journal of Physiology-Paris. 2004;98:296–314. doi: 10.1016/j.jphysparis.2005.09.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tiesinga PH, Fellous JM, Sejnowski TJ. Spike-time reliability of periodically driven integrate-and-fire neurons. Neurocomputing. 2002;44:195–200. [Google Scholar]
- Tiesinga PH, Fellous JM, Sejnowski TJ. Regulation of spike timing in visual cortical circuits. Nat Rev Neurosci. 2008;9:97–109. doi: 10.1038/nrn2315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tiesinga PH, Jose JV. Robust gamma oscillations in networks of inhibitory hippocampal interneurons. Network-Computation in Neural Systems. 2000;11:1–23. [PubMed] [Google Scholar]
- Tiesinga PHE, Jose JV, Sejnowski TJ. Comparison of current-driven and conductance-driven neocortical model neurons with Hodgkin-Huxley voltage-gated channels. Physical Review E. 2000;62:8413–8419. doi: 10.1103/physreve.62.8413. [DOI] [PubMed] [Google Scholar]
- Van Vreeswijk C, Abbott LF, Ermentrout GB. When inhibition not excitation synchronizes neural firing. J Comput Neurosci. 1994;1:313–321. doi: 10.1007/BF00961879. [DOI] [PubMed] [Google Scholar]
- Wang XJ, Buzsaki G. Gamma oscillation by synaptic inhibition in a hippocampal interneuronal network model. J Neurosci. 1996;16:6402–6413. doi: 10.1523/JNEUROSCI.16-20-06402.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whittington MA, Traub RD, Jefferys JG. Synchronized oscillations in interneuron networks driven by metabotropic glutamate receptor activation. Nature. 1995;373:612–615. doi: 10.1038/373612a0. [DOI] [PubMed] [Google Scholar]
- Whittington MA, Traub RD, Kopell N, Ermentrout B, Buhl EH. Inhibition-based rhythms: experimental and mathematical observations on network dynamics. Int J Psychophysiol. 2000;38:315–336. doi: 10.1016/s0167-8760(00)00173-2. [DOI] [PubMed] [Google Scholar]
- Williford T, Maunsell JH. Effects of spatial attention on contrast response functions in macaque area V4. J Neurophysiol. 2006;96:40–54. doi: 10.1152/jn.01207.2005. [DOI] [PubMed] [Google Scholar]
- Womelsdorf T, Schoffelen JM, Oostenveld R, Singer W, Desimone R, Engel AK, Fries P. Modulation of neuronal interactions through neuronal synchronization. Science. 2007;316:1609–1612. doi: 10.1126/science.1139597. [DOI] [PubMed] [Google Scholar]
- Zhang F, Aravanis AM, Adamantidis A, de Lecea L, Deisseroth K. Circuit-breakers: optical technologies for probing neural signals and systems. Nat Rev Neurosci. 2007;8:577–581. doi: 10.1038/nrn2192. [DOI] [PubMed] [Google Scholar]