The Sheltered Genetic Load Linked to the S Locus in Plants: New Insights From Theoretical and Empirical Approaches in Sporophytic Self-Incompatibility

Abstract

Inbreeding depression and mating systems evolution are closely linked, because the purging of deleterious mutations and the fitness of individuals may depend on outcrossing vs. selfing rates. Further, the accumulation of deleterious mutations may vary among genomic regions, especially for genes closely linked to loci under balancing selection. Sporophytic self-incompatibility (SSI) is a common genetic mechanism in angiosperm that enables hermaphrodite plants to avoid selfing and promote outcrossing. The SSI phenotype is determined by the S locus and may depend on dominance relationships among alleles. Since most individuals are heterozygous at the S locus and recombination is suppressed in the S-locus region, it has been suggested that deleterious mutations could accumulate at genes linked to the S locus, generating a “sheltered load.” In this article, we first theoretically investigate the conditions generating sheltered load in SSI. We show that deleterious mutations can accumulate in linkage with specific S alleles, and particularly if those S alleles are dominant. Second, we looked for the presence of sheltered load in Arabidopsis halleri using CO₂ gas treatment to overcome self-incompatibility. By examining the segregation of S alleles and measuring the relative fitness of progeny, we found significant sheltered load associated with the most dominant S allele (S15) of three S alleles tested. This sheltered load seems to be expressed at several stages of the life cycle and to have a larger effect than genomic inbreeding depression.

THE main genetic mechanism causing inbreeding depression is believed to be the expression of recessive mildly deleterious mutations in inbred individuals (Charlesworth and Charlesworth 1999). These deleterious mutations are generally supposed to be distributed throughout the genome. However, some genomic regions where loci under balancing selection are present may be more inclined than others to accumulate deleterious mutations and could lead to the formation of what is generally called a “sheltered load” (Uyenoyama 1997; van Oosterhout 2009). The sheltered load has been suggested as a potential reason why MHC genes, mating-type systems in fungi, and self-incompatibility systems in plants generally show longer terminal branches in their genealogies than expected (Richman 2000). Despite its potential importance, the extent of the sheltered load is still largely unknown.

Homomorphic self-incompatibility is widely distributed among angiosperm families (de Nettancourt 2001; Igic et al. 2008). Self-incompatibility (SI) is controlled by genes under strong balancing selection. SI prevents self-fertilization and promotes outcrossing by the presence of a gamete recognition system involving proteins expressed in both the pollen and the pistil. The proteins controlling the recognition system are generally encoded by genes located in a single genomic region, the S locus. Each plant in a self-incompatible population expresses an S specificity and is unable to mate with other plants expressing the same specificity. In species with gametophytic self-incompatibility (GSI), the S specificity is controlled by interactions between protein expressed in the pollen's haploid genome, the male gametophyte, and the pistil's diploid genome. In species with sporophytic self-incompatibility (SSI), S specificity is controlled by interactions between gene products of the diploid sporophyte expressed on the pollen coat and those on the stigmatic surface. In this mating system, three reasons may facilitate the accumulation of recessive deleterious mutations in this region, namely a sheltered load (Uyenoyama 1997). First, high heterozygote frequencies are expected in populations at the S locus but also at other linked loci in the S-locus genomic region (Kamau et al. 2007). Second, negative frequency-dependent selection, a form of balancing selection, is the main selective force acting on the S locus and on linked genes (Castric and Vekemans 2004). Third, the recombination rate is low in the S-locus region (Casselman et al. 2000; Charlesworth et al. 2003). Such a sheltered load may have important evolutionary consequences for SI evolution: it can slow down the rate of emergence of new S alleles (Uyenoyama 2003), considerably extend the conditions for the persistence of GSI (Porcher and Lande 2005), and, finally, substantially increase the inbreeding depression in a small population (Glémin et al. 2001), which can have large consequences for endangered species and the viability of their populations.

The magnitude of the sheltered load should depend on the size of the genomic region in which heterozygosity is enforced because of linkage to the S locus and also on the number of genes affecting fitness in that region. From an analysis of recombination rates in the S-locus genomic region in Arabidopsis lyrata, a species with SSI, Kawabe et al. (2006) suggested that the number of genes in the S-genomic region is probably not high enough for a large sheltered load to have an impact on fitness compared to the overall genomic load. Dowd et al. (2000) indeed found only 13 genes near the S locus in Petunia inflata. However, two studies have demonstrated the existence of transmission ratio distortion of some S alleles in A. lyrata (Bechsgaard et al. 2004; Leppala et al. 2008). The authors proposed that this could be indirect evidence of the existence of a sheltered load. To the best of our knowledge, the existence of sheltered load in SI species was specifically demonstrated so far only in Solanum carolinense, a species with GSI: Stone (2004) crossed individuals sharing alleles at the S locus, using bud pollination to overcome self-incompatibility. By looking at seed number and genotype of the progeny, a sheltered load linked to only two of seven S alleles investigated was detected. Direct evidence and estimations of the extent of the sheltered load are thus lacking.

In SSI, complex dominance interactions among S alleles are usually observed [Ipomoea trifida (Kowyama et al. 1994), Brassica campestris (Hatakeyama et al. 1998), A. lyrata (Mable et al. 2003), and A. halleri (Llaurens et al. 2008a)]. The effect of these dominance interactions on the occurrence of a sheltered genetic load has not been investigated either theoretically or empirically, but may potentially be large. Indeed, recessive S alleles are expected to be more often homozygous in natural populations than dominant alleles (Schierup et al. 1997), and so may rapidly purge strongly deleterious recessive mutations, and thus should limit the sheltering effect. The sheltered load could thus differ depending on the dominance levels of the associated S alleles.

In this study, we first investigated the theoretical conditions for the accumulation of a sheltered load in a SSI system, using stochastic simulations. Then, we empirically tested the existence and strength of an S-linked sheltered load in relation to dominance levels in SSI. We focused on A. halleri, a member of the Brassicaceae family. In this family, the S-locus region includes two major genes: SCR (also called SP-11), encoding a cysteine-rich protein of the pollen envelope, and SRK, encoding a receptor kinase located across the membrane of the papilla cells. High heterozygote frequencies at the S locus have been found in several species like B. insularis (Glémin et al. 2005) or A. lyrata (Schierup et al. 2006). The SRK and SCR genes are tightly linked, since they are located close to each other, and recombination suppression in the S-locus region has been suggested in several studies: in Brassica (Casselman et al. 2000) and in A. lyrata (Kamau and Charlesworth 2005; Kawabe et al. 2006). The conditions thus may be suitable for the existence of sheltered genetic load in A. halleri. We performed controlled pollinations in A. halleri to specifically measure the magnitude of the potential sheltered load of three S alleles with different dominance levels: a dominant, an intermediate, and a recessive allele. To evaluate the effect of the sheltered load on these crosses, we looked at the number of seeds produced, as well as at the development and the genotype at the S locus of the progeny.

MATERIALS AND METHODS

Simulations:

We aim at testing whether a sheltered genetic load could accumulate in the S-locus region and whether its strength depends on the dominance of the linked S allele. We thus studied the frequencies of deleterious mutations at loci completely linked to a sporophytic self-incompatibility locus. We simulated a panmictic population of N diploid individuals with nonoverlapping generations. Each individual is defined by its genotype in a genomic region within which there is no recombination. This region contains the S locus, as well as a locus we called the “D locus,” at which two alleles could segregate: 0 and 1. Allele 1 is deleterious and completely or partially recessive.

The life cycle in our simulations had four steps:

1. Gametogenesis: N adult individuals produced infinity of ovules and pollen.

2. Syngamy: The frequency of each S-locus genotype in seeds was deterministically computed following the general equations given in Billiard et al. (2007). Crosses between ovules and pollen were compatible when the specificities expressed in pollen and stigmas were different. We define ϕ_i as the proportion of allele S_i associated with allele 1 at the D locus. Since genotypic frequency change during syngamy depends only on the genotype at the S locus, ϕ_i is constant during syngamy. For any {i, j}, the proportions of the four possible genotypes at the D locus among genotypes S_iS_j were computed as ϕ_iϕ_j and (1 − ϕ_i)(1 − ϕ_j) for homozygotes at the D locus and as ϕ_i(1 − ϕ_i) and ϕ_j(1 − ϕ_i) for heterozygotes. During this step, the frequency of allele 1 in the whole population may have changed by hitchhiking if the frequency of allele S_i or S_j changed. The reproduction regime used was the “fecundity selection” model (Vekemans et al. 1998), which assumes that frequency-dependent selection acts through both pollen and pistil.

3. Viability selection and regulation: We assumed that the survival probability p of a zygote depends on its genotype at the D locus: for heterozygous individuals p = (1 − hs) while for homozygotes p = (1 − s), where s and h are, respectively, the selection and the dominance coefficients of allele 1 relative to allele 0. To form the next generation, we randomly drew zygotes following multinomial sampling with the genotypic frequencies after syngamy as parameters; we computed p for this zygote and randomly determined whether this individual survived. We repeated these steps until N surviving individuals were obtained.

4. Mutation: We defined the mutation rate μ from allele 0 to allele 1 at the D locus and the reverse mutation rate η from allele 1 to allele 0. We randomly drew the total number of mutations occurring in the population following a Poisson distribution. We then randomly assigned each mutation to a single chromosome, with replacement. The mutation rates were fixed to μ = 10⁻⁴ and η = 10⁻⁵ or 10⁻⁷ per chromosome per generation.

We used a simple model of SSI, with hierarchical dominance interactions, similar to those observed in A. halleri (Llaurens et al. 2008a). Three dominance classes were assumed with five S alleles (two alleles in the most dominant and the intermediate dominance classes, and one allele in the most recessive class) or eight S alleles (respectively four, three, and one alleles in the dominant, intermediate, and recessive classes). The alleles in the most dominant class were codominant relative to each other and dominant over all alleles of the intermediate and the recessive classes. The alleles in the intermediate dominance class were also codominant relative to each other and dominant over the allele in the most recessive class. The same dominance relationships were assumed in both pollen and pistil. We also assumed that no new S allele could appear by mutation during simulations. The size of the population was, however, large enough (N = 1000) to avoid S-alleles loss by drift during the simulations.

At the initial state, only allele 0 occurs at the D locus. We first ran simulations without deleterious mutations until deterministic equilibrium was reached for S-allele frequencies, defined by the time when all allelic frequency changes in one generation were <10⁻³. Mutations at the D locus were then allowed. Each simulation was performed with 100 independent replicates of 100,000 generations and the frequency of the deleterious alleles was recorded every 1000 generations. We use the term “fixation within an allelic family” when all haplotypes of a given S-allele S_i are carrying the same deleterious mutation at the D locus, in other words, when ϕ_i = 1. We estimated the frequency spectrum of the deleterious allele in the whole population as 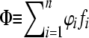, with n the total number of S alleles in the population and f_i the frequency of allele S_i in the whole population.

Plant material:

A. halleri (Brassicaceae) is a diploid species taxonomically closely related to the two model species, A. thaliana, and A. lyrata (Clauss and Koch 2006). It is a European species growing both in mountainous areas and on heavy-metal polluted areas. We used plants issued from seeds collected in a single natural population of A. halleri located in Nivelle (France) whose mating pattern has been extensively studied (Llaurens et al. 2008b). In this population, the selfing rate was estimated to be null, on the basis of progeny analyses from natural pollinations. In controlled self-pollinations performed on the plants grown in the greenhouse, fruits were formed after only ∼3% of pollinations (Llaurens et al. 2008a). These results demonstrated that the self-incompatibility system is functional in individuals from this population.

Overcoming self-incompatibility:

We used the following experimental procedure to disentangle the effect of reduced fitness caused by sheltered load of deleterious mutations, from inbreeding depression due to mildly deleterious mutations located throughout the whole genome (genomic load or background inbreeding depression). Three different categories of crosses were performed by manual transfer of pollen from different donor plants to stigmas: (1) selfing crosses (S), enforced selfing with pollen from the same plant; (2) incompatible crosses (I), enforced incompatible crosses with pollen from a different individual sharing the same genotype at the S locus; and (3) control crosses (C), outcrossing with pollen from an individual with a different genotype at the S locus, i.e., crosses are hence performed between compatible individuals. The decline in fitness, measured by the difference in the number and development of seeds, in offspring derived from selfing vs. incompatible crosses was interpreted as the effect of deleterious mutations located genomewide. We hypothesized that offspring from enforced selfing should be affected by both genomic and sheltered loads while offspring from enforced incompatible crosses should be affected by sheltered load only. Finally, offspring from outcrossing controls should experience neither the background inbreeding depression nor the sheltered load. We assumed that the phenotypic measurements of the control, incompatible, and selfed crosses were estimators of the fitness components of outbred individuals, 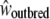, incompatible but outbred, 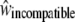, and inbred individuals, 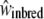. We defined the sheltered genetic load and genomic inbreeding depression as and 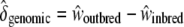, respectively. We thus inferred the contribution of the sheltered load relative to the genomic inbreeding depression by computing .

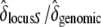Genotypes at the S locus were determined by PCR targeted for the pistil-expressed SRK gene, with S-allele-specific primers as described below. We use the abbreviation S instead of S-allele AhSRK throughout the article for simplification. We used two sets of five individuals with genotypes [S01 S15] and [S01 S02]. A previous study on this population showed that the S-allele S01 was the most recessive allele, S02 had an intermediate dominance level, and S15 had a high dominance level (Llaurens et al. 2008a). The individual used for the control crosses had genotype [S04 S20]. For each plant, we performed 20 self-pollinations, 8 incompatible crosses (2 with each of the four other plants of the same S-locus genotype), and 4 control crosses. In some cases, pollinations were not successful and we thus performed the same cross several times. In summary, we performed 469 crosses, collected 1200 seeds, and measured and genotyped 872 offspring.

All crosses were performed under CO₂ gas treatment to overcome self-incompatibility, as described in Nakanishii et al. (1969). Although this method is commonly used by seed companies to maintain inbred lines of Brassicaceae, we used this method for the first time in A. halleri. We performed controlled pollinations under a binocular magnifying glass. Anthers of pollen donors were collected with tweezers and the recipient pistil was dusted with pollen. The pollinated plants were then placed overnight in an atmosphere with 5% CO₂. Pistils were marked individually and measured 7 days after pollination. We considered a cross successful when the size of the silique after 7 days was larger than 6.1 mm and seed development was observed (Llaurens et al. 2008a). We collected seeds and grew the offspring in a greenhouse under constant temperature T = 20° and photoperiod 16 hr day/8 hr night. Offspring from the three cross categories were randomly placed on the greenhouse tables.

To check our controlled pollinations for contamination by pollen from other sources, we determined some of the offspring genotypes at seven neutral markers, to ensure that they were compatible with the genotypes of the parents. In total, 87 offspring from six self-pollinations, 55 offspring from six incompatible crosses, and 13 offspring from one control cross were tested for seven microsatellite loci (NGA112, NGA361, GC22, MDC16, ICE13, H117, and Athzfpg) following the method described in Llaurens et al. (2008b). We detected inconsistent genotype in only 3.2% of the offspring analyzed, possibly due to contaminated pollination.

Estimation of genomic inbreeding depression and sheltered load via phenotypic traits:

We assessed the reproductive success of offspring from the different categories of crosses, on the basis of several fitness measures. We expect a priori that fitness depends on the cross type in the following order: 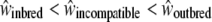; that is, the fitness measures from selfing crosses are expected to be lower than those for incompatible crosses, themselves lower than those for control crosses. Here we measured seven phenotypic traits as an estimation of the fitness, and we expect that there should be significant differences in phenotypic values in the order S < I < C (or the reverse, depending on the measured phenotypic trait). Hence, if such a trend is significant in our measure, we conclude that our hypothesis 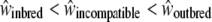is verified.

As the fitness effects associated with the overcoming of self-incompatibility may differ depending on the maternal strain, maternal effects were controlled by performing two kinds of analysis, depending on the considered fitness trait. The number of seeds per fruit and the seed germination rates were analyzed with Page's trend test (Page 1963), using the software StatXact8. Page's trend test is a nonparametric test, used for ordered correlated variables when there are more than two related samples. It was applied here since we measured the number of seeds per fruit and the germination rate for different types of cross, for five mothers only. It specifically tests the hypothesis H₀: S = I = C against the alternative H₁: S < I < C (or the reverse). If H₀ is rejected, it means that at least one of the categories of variable is significantly lower with respect to any others. When the test was significant, multiple comparisons were performed using Page's trend tests, with Bonferroni correction.

The length and width of the biggest leaf measured 2 weeks after germination, the appearance time of the first leaf, and the germination and cotyledon appearance times were compared by a two-way ANOVA, with the maternal identity and the cross type as fixed effects. The two variables “germination time” and “first leaf appearance time” were transformed in logarithm for normality. When there was a significant mother × cross interaction and no clear trend in the means was detected, our expectation S < I < C was considered invalidated. When a significant effect of the types of cross was detected without interaction between mother and cross types, a Dunnett multiple comparisons test was performed, using the incompatible cross as a reference.

Finally, the offspring fitness estimate was compared depending on their genotype at the S locus. A three-way ANOVA was performed on the genotypes of offspring from the selfing and incompatible crosses only. The three factors tested were the maternal identity, the cross type, and the genotype at the S locus. In cases where there was no interaction, a Dunnett multiple comparisons test was performed with the heterozygote genotype as a reference.

The relative effect of the sheltered load compared to the effect of background inbreeding depression was also computed. For fitness parameters with significantly different values for the three categories of crosses, we estimated the contribution of the sheltered load relative to the genomic inbreeding depression by computing 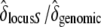(as described above).

Estimation of background inbreeding depression and sheltered load via segregation bias:

To detect early-acting inbreeding depression, we computed the segregation of S alleles in the offspring. We extracted DNA from offspring leaves collected 2 weeks after germination. Leaf samples were oven dried at 55°, and DNA was extracted using the Nucleospin Multi-96 Plant extraction kit from Macherey-Nagel. We used S-allele-specific primers to amplify only one S allele (for details see Llaurens et al. 2008a). The reaction mixture (15 μl) contained 20 ng DNA, 1× buffer (Applied Biosystems, Foster City, CA), 2 or 2.5 mm of MgCl₂ (depending on the primer pair), 200 μm of Fermentas DNTP mix, 200 μg/ml of BSA, 0.2 μm of each microsatellite primer, and 0.025 unit/μl of Taq polymerase (Amplitaq DNA polymerase, Applied Biosystems). The amplification was carried out for 5 min at 95°, followed by 35 cycles of 40 sec at 95°, 40 sec at annealing temperature (specific for each pair of primer), and 40 sec at 72° and then one cycle of 10 min at 72° and performed in an MJ Research PTC 200 thermocycler. PCR products were mixed with loading dye and then loaded into 2% agarose, subjected to 110 MV current, and visualized with ethidium bromide. The PCR products were sized by comparison with a sizing marker. We used DNA from an individual carrying the targeted S allele as a positive control for each PCR.

We looked for evidence of segregation distortion in the offspring at the S locus. As a first test, χ²-tests were used to check for discrepancy from Mendelian expectations in the genotypic frequencies in the offspring. To estimate the strength of the sheltered load, we used the observed genotypic frequency changes in incompatible crosses. We estimated S, the selection coefficient of the deleterious mutations associated with allele Sb, and their dominance level H, assuming that the sheltered load acts during the sporophytic stage only. In other words, we assumed that the initial frequencies of genotypes SaSa, SaSb, and SbSb in zygotes produced by a cross between two parents SaSb were 1/4, 1/2, 1/4, respectively. 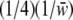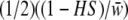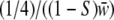We assumed that the fitnesses of these genotypes in zygotes are, respectively, 1, 1 − HS, and 1 − S such that the genotypic frequencies in offspring after selection are, respectively, , , and with 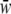the mean fitness among all genotypes. Using the observed genotypic frequencies in offspring, we computed H and S.

RESULTS

A sheltered genetic load can occur:

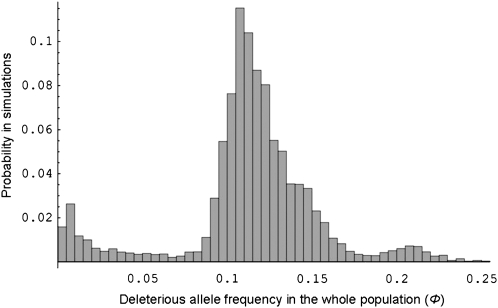
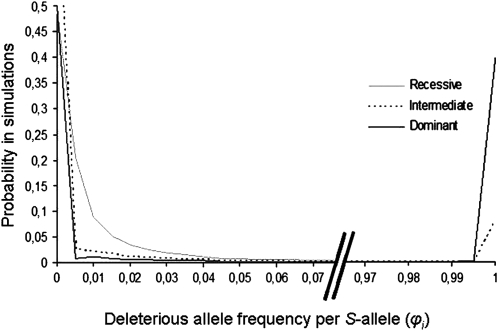
The frequency spectrum of a completely recessive (h = 0) deleterious allele linked to the S locus in our simulations, with a selection coefficient s = 0.1, is shown in Figure 1 in a finite population with N = 1000 diploid individuals, with forward and backward mutation rates set to μ = 10⁻⁴ and η = 10⁻⁵, respectively. The existence of three modes in the frequency spectrum (Figure 1) corresponds to three cases: (i) the deleterious allele is absent from the population or at very low frequency, corresponding to the mutation–selection–drift balance; (ii) the deleterious allele has a frequency of 0.11, which is the overall mode of the simulation; and (iii) the frequency of the deleterious allele reaches ∼0.2. To explain this pattern, we looked at the influence of the dominance level of the associated S allele on the probability of fixation of the linked deleterious allele within S alleles by estimating the distribution of ϕ_i in our simulations for all alleles S_i (Figure 2). Figure 2 shows that most often, a given S allele is not linked with a deleterious allele. Figure 2 also shows that S alleles with different dominance levels differed greatly in their probability of fixation of the deleterious alleles: ϕ_i = 1 in 38% of the simulations for a dominant allele, in 8% of the simulations for an intermediate dominance S allele, and in no simulations for the recessive S allele. Since we assumed two selectively equivalent S alleles in the dominant and intermediate classes, and because no simulations showed simultaneous fixation of the deleterious mutation with both S alleles of the same dominance class, this means that there is a 76% probability that all copies of one of the two dominant S alleles would be associated with the deleterious allele and a 16% probability that one of the intermediate S alleles would become fixed for a deleterious allele. The probability of fixation of the deleterious allele thus depended strongly on the dominance level of the linked S allele. We therefore predict that most of the genetic load should be associated with dominant S alleles.

Figure 1.—

Frequency distribution of the deleterious mutation in the whole population (Φ) with complete recessivity of the deleterious mutation (h = 0). The histogram shows the proportion of the 10,000 samples from simulations (y-axis) where the deleterious mutation is encountered with a given frequency (x-axis). Five S alleles and three dominance classes were assumed, with two alleles in the most dominant and the intermediate classes and one allele in the most recessive class. Other parameters values: μ = 10⁻⁴, η = 10⁻⁵, N = 1000, and s = 0.1.

Figure 2.—

Frequency distribution of deleterious mutations in linkage with S-alleles i (ϕ_i) belonging to different dominance classes (dominant, intermediate, or recessive). Five S alleles and three dominance classes were assumed, with two alleles in the most dominant and the intermediate classes and one allele in the most recessive class. Since the two alleles in a given dominance class are selectively equivalent, their frequency distributions are identical and only one frequency distribution by dominance class is shown. Parameters values: N = 1000, s = 0.1, h = 0, μ = 10⁻⁴, and η = 10⁻⁵.

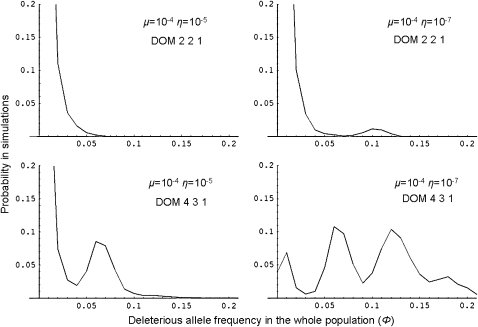
We further looked at the impact of the dominance level of the deleterious mutation at the D locus on sheltered load by performing simulations in which h = 0.2, without changing the value of the other parameters. Figure 3 (top left) shows that, contrarily to the case where h = 0, the deleterious mutation frequency remains low mainly due to the balance between mutation and selection. Decreasing the backward mutation η (Figure 3, top right) shows a similar frequency spectrum, with the exception that some simulations showed a frequency of the deleterious mutation close to 0.1. Increasing the total number of S alleles in the population from five to eight (Figure 3, bottom graphs) gave very different results. For both values of η, the sheltered load may be large (Figure 3, bottom left and right). Especially, for the lowest value of η, the frequency of the deleterious mutation is, in most cases, >0.05. In this case, the frequency distribution shows four modes. The left mode represents the mutation–selection balance in which the deleterious mutation reaches a low frequency but is not associated with a specific S haplotype. The three other modes show that the sheltered load associated to an S allele is highly variable and may be complex and difficult to interpret. Indeed, the frequency of deleterious mutations depends on the number and on the relative dominance of the S alleles that they are linked to. These results show that a large sheltered load can occur even if the deleterious mutations are not completely recessive and that it can be shared among several S alleles.

Figure 3.—

Frequency distribution of the deleterious mutation in the whole population with partial recessivity (h = 0.2). Top: Five S alleles and three dominance classes as in Figure 1. Bottom: Eight S alleles and three dominance classes with respectively four, three, and one alleles in the dominant, intermediate, and recessive classes. The mutation rates were μ = 10⁻⁴ and η = 10⁻⁵ and μ = 10⁻⁴ and η = 10⁻⁷, for left and right histograms, respectively. Other parameters values: N = 1000, s = 0.1.

We found a small discrepancy between the observed genotypic frequencies in the simulations and the expected frequencies without sheltered load. For instance, in the case with the largest sheltered load (the bottom right graph in Figure 3), the discrepancies were only ∼ −2.3, −0.004, and +1.7%, respectively, for the dominant, intermediate, and recessive S-alleles. However, other simulations showed that for small populations, the discrepancies can be much larger, with a much higher frequency than expected for the recessive allele and much lower frequencies for the dominant and the intermediate S alleles (not shown). This suggests that the sheltered load may modify the frequencies of S haplotypes and thus modified their dynamics in the populations.

Segregation of S alleles:

We compared segregation of S alleles in self and incompatible crosses for maternal plants of genotypes [S01 S15] and [S01 S02] (Table 1). S01 has been identified as the most recessive allele in A. halleri, S15 is dominant over S01 and S02, and S02 is dominant over S01 only (Llaurens et al. 2008a). The segregation of S alleles in self and incompatible crosses in the case of the maternal genotype [S01 S15] departed highly significantly from Mendelian expectations, with an excess of [S01 S01] homozygotes and a deficiency of [S15 S15] homozygotes and [S01 S15] heterozygotes (Table 1). There was thus a segregation bias against allele S15. No such significant departure from the Mendelian segregation was found for genotype [S01 S02] except for the incompatible cross category, which showed an excess of [S01 S01] homozygotes and a corresponding lack of [S01 S02] heterozygotes (Table 1).

TABLE 1.

Genotypic frequencies at the S locus in the offspring of the selfing and incompatible crosses and Mendelian segregation tests (chi-square test)

		Offspring genotype
Mother genotype	Cross type	[S01 S01]	[S01 S15]	[S15 S15]	Total no. of offspring	P-value (chi-square test)
[S01 S15]	Selfing	0.391	0.466	0.143	160	P < 0.001
	Incompatible	0.367	0.438	0.195	128	P < 0.001
	All	0.381	0.453	0.166	288	P < 0.001
		[S01 S01]	[S01 S02]	[S02 S02]
[S01 S02]	Selfing	0.208	0.528	0.264	231	P = 0.33
	Incompatible	0.350	0.390	0.260	123	P = 0.02
	All	0.257	0.480	0.262	354	P = 0.75

We checked the segregation of the studied S-alleles S01, S02, and S15 in compatible crosses by studying the control crosses. For the cross [S01 S15] × [S04 S20], we found no significant departure from Mendelian expectations (chi-square test: P = 0.085) although S15 had a slightly lower frequency than expected (58 offspring from the compatible crosses carry allele S15, while 77 carry allele S01), which departs marginally significantly from the Mendelian expectations (exact binomial cumulative probability: P = 0.061). This last result suggests that S15 may carry a partially recessive sheltered load. For the crossing [S01 S02] × [S04 S20] a negative segregation bias for S04 was detected (P = 0.02). Our results hence suggest that the S alleles used in this study, S01, S02, and S15 were apparently not associated with strong segregation distorters in genetically compatible crosses. Assuming that selection occurs during the sporophytic stage, we estimated the selection and the dominance coefficients for allele S15, respectively, as 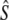= 0.468 and 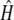= 0.864. These results suggest that the deleterious mutations linked to alleles S15 have a large effect on fitness and are not fully recessive.

Effect of the type of cross on fitness components:

We compared six fitness traits in the offspring from the three categories of crosses for the two different maternal genotypes (Table 2, A and B). Concerning the maternal genotype [S01 S15], we initially found a strong interaction effect between mother and cross categories. However, this interaction was due almost exclusively to the offspring of one mother (maternal ID 5012) from control crosses (appendix). We discarded all measures from individual 5012 and the interaction effect was not significant anymore, except for the germination time (Table 2A). Overall, results with or without mother 5012 gave the same results (appendix). In short, for the maternal genotype [S01 S15], we found that the mean number of seeds per cross and the length and width of the largest leaf were different among cross categories (Table 2A). The germination time, the cotyledon appearance time, and the appearance time of the first leaf showed no significant difference between self and incompatible crosses, but both were significantly different from the control. Finally, the germination rate showed no significant differences between all cross categories. When there was a significant difference among the three types of crosses, we computed 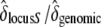. This ratio 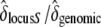indicated that the decline in fitness due to the sheltered genetic load explains ∼ ≥60% of the decline in fitness compared to the genomic load (Table 2A). For the maternal genotype [S01 S02], no clear patterns between the three categories of crosses were found, mainly because of strong interaction effects (Table 2B). However, we showed that for the appearance time of cotyledons, seed number per cross, and the germination rate, differences between selfing and control crosses were significantly different (Table 2B). In summary, concerning genotype [S01 S15], for three of seven measured traits (seed number per crossed flower, leaf length, and leaf width), we observed the expected trend S < I < C, and for three other traits (germination time, cotyledon appearance time, and first leaf time) we observed S = I < C or S = I > C. For genotype [S01 S02] such trends were absent. Altogether, these results suggest that the expectation about fitness 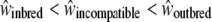is verified for the maternal genotype [S01 S15] and not for [S01 S02].

TABLE 2.

Two-way ANOVA analysis for fitness measures of mother genotype (cross types: S, selfing; I, incompatible; C, control)

Trait	Factor	Deviance (d.f., P-value)	Residual deviance	Posthoc Dunnett test difference estimate (SE, P-value)	Mean per cross type (SE)	Result summary
A. Mother genotype [S01 S15], n = 374
Width (cm)	Cross	5.2 (2, P < 0.001)	9.8	S − I = −0.08 (0.02, P < 0.001)	S: 0.57 (0.014)	S < I < C	0.68
	Maternal ID	1.06 (3, P < 0.001)		C − I = 0.17 (0.02, P < 0.001)	I: 0.67 (0.015)
	Interaction	0.07 (6, P = 0.87)			C: 0.83 (0.015)
Length (cm)	Cross	4.5 (2, P < 0.001)	12.5	S − I = −0.1 (0.02, P < 0.001)	S: 0.65 (0.02)	S < I < C	0.6
	Maternal ID	1.5 (3, P < 0.001)		C − I = 0.15 (0.02, P < 0.001)	I: 0.76 (0.02)
	Interaction	0.13 (6, P = 0.69)			C: 0.91 (0.02)
Log (germination time) (days)	Cross	1.7 (2, P < 0.001)	38.7	S − I = 0.17 (0.10, P = 0.18)	S: 8.3 (0.29)	S = I < C	.
	Maternal ID	6.4 (3, P < 0.001)		C − I = 3.89 (0.14, P = 0.03)	I: 7.89 (0.32)
	Interaction	2.9 (6, P < 0.001)			C: 9.22 (0.31)
Cotyledon time (days)	Cross	7.4 (2, P = 0.001)	205.9	S − I = 0.11 (0.09, P = 0.41)	S: 1.81 (0.06)	S = I > C	.
	Maternal ID	0.6 (3, P = 0.758)		C − I = −0.23 (0.1, P = 0.036)	I: 1.7 (0.07)
	Interaction	6.0(6, P = 0.089)			C: 1.48 (0.07)
Log (first leaf time) (days)	Cross	5.3 (2, P < 0.001)	16.7	S − I = 0.03 (0.07, P = 0.88)	S: 6.58 (0.13)	S = I > C	.
	Maternal ID	0.6 (3, P = 0.005)		C − I = −0.27 (0.09, P = 0.004)	I: 6.27 (0.12)
	Interaction	0.4 (6, P = 0.2)			C: 4.97 (0.12)
Trait	Page's statistic	One-sided P-value		Multiple comparisons	Value per cross type	Result summary
Seed no. per crossed flower	3.162	P < 0.001		S < I, P = 0.013	S: 2.25	S < I < C	0.82
				S < C, P = 0.013	I: 3.73
				I < C, P = 0.013	C: 10.3
Germination rate	0	P = 0.557		NS	S: 0.9	S = I = C	.
						I: 1
					C: 0.74
B. Mother genotype [S01 S02], n = 429
Width (cm)	Cross	0.01(2, P = 0.79)	11.0	NS	S: 0.7 (0.02)	S = I = C
	Maternal ID	3.2 (4, P < 0.001)			I: 0.71 (0.01)
	Interaction	1.5 (8, P < 0.001)			C: 0.71 (0.02)
Length (cm)	Cross	0.04 (2, P = 0.469)	11.7	NS	S: 0.76 (0.01)	S = I = C
	Maternal ID	2.8 (4, P < 0.001)			I: 0.78 (0.02)
	Interaction	1.3 (8, P < 0.001)			C: 0.76 (0.02)
Log (germination time) (days)	Cross	0.2 (2, P = 0.36)	42.7	NS	S: 8.8 (0.3)	S = I = C
	Maternal ID	22.4 (4, P < 0.001)			I: 9.39 (0.4)
	Interaction	1.5 (8, P = 0.07)			C: 9.3 (0.4)
Cotyledon time (days)	Cross	9.8 (2, P = 0.002)	205.9	S − I = 0.14 (0.1, P = 0.243)	S: 1.71 (0.05)	S = I > C
	Maternal ID	8.6 (4, P = 0.006)		C − I = −0.28 (0.1, P = 0.02)	I: 1.66 (0.08)
	Interaction	6.0 (8, P = 0.253)			C: 1.35 (0.07)
Log (first leaf time) (days)	Cross	0.5 (2, P < 0.001)	13.5	NS	S: 5.72 (0.09)	S = I = C
	Maternal ID	5.3 (4, P < 0.001)			I: 5.36 (0.11)
	Interaction	2.1 (8, P < 0.001)			C: 5.27 (0.12)
Trait	Page's statistic	One-sided P-value		Multiple comparisons	Value per cross type	Result summary
Seed no. per crossed flower	2.214	P = 0.03		S < I, NS	S: 3.39	S = I, I = C, S < C
				S < C, P =0.013	I: 3.8
				I < C, NS	C: 6.25
Germination rate	2.53	P = 0.006		S < I, NS	S: 0.7	S = I, I = C, S < C
				S < C, P = 0.013	I: 0.86
				I < C, NS	C: 0.82

APPENDIX.

Two-way ANOVA analysis for fitness measures of mother genotype [S01 S15], including mother 5012 (n = 424)

Trait	Factor	Deviance (d.f., P-value)	Residual deviance	Significant interactions (maternal ID × cross type)	Posthoc Dunnett test difference estimate (SE, P-value)	Mean per cross type (SE)	Result summary
Width (cm)	Cross	4.9 (2, P < 0.001)	10.3	5012 × C	S − I = −0.11 (0.05, P = 0.065)	S: 0.57 (0.014)	S < I < C
	Maternal ID	1.6 (4, P < 0.001)			C − I = 0.19 (0.07, P = 0.007)	I: 0.67 (0.015)
	Interaction	0.7 (8, P = 0.001)				C: 0.83 (0.015)
Length (cm)	Cross	3.8 (2, P < 0.001)	13.2	5012 × C	S − I = −0.11 (0.06, P = 0.094)	S: 0.66 (0.02)	S = I, I = C, S < C
	Maternal ID	1.6 (4, P < 0.001)			C − I = 0.08 (0.08, P = 0.459)	I: 0.77 (0.02)
	Interaction	1.05 (8, P < 0.001)				C: 0.89 (0.02)
Log (germination time) (days)	Cross	1.23 (2, P = 0.003)	41.7	5012 × C 5026 × C	S − I = 0.17 (0.1, P = 0.17)	S: 8.5 (0.27)	S = I < C
	Maternal ID	8.42 (4, P < 0.001)			C − I = 0.33 (0.1, P = 0.027)	I: 8.1 (0.3)
	Interaction	3.36 (8, P < 0.001)				C: 9.3 (0.3)
Cotyledon time (days)	Cross	6.7 (2, P = 0.001)	217.3	5037 × S	S − I = 0.10 (0.09, P = 0.399)	S: 1.8 (0.06)	S = I > C
	Maternal ID	0.8 (4, P = 0.758)			C − I = −0.2 (0.09, P = 0.051)	I: 1.7 (0.07)
	Interaction	6.9 (8, P = 0.089)				C: 1.5 (0.06)
Log (first leaf time)(days)	Cross	4.8 (2, P < 0.001)	18.3	5012 × C	S − I = 0.03 (0.07, P = 0.88)	S: 6.57 (0.11)	S = I > C
	Maternal ID	0.8 (4, P = 0.002)			C − I = −0.27 (0.09, P = 0.004)	I: 6.26 (0.12)
	Interaction	1.2 (8, P < 0.001)				C: 5.12 (0.12)

Effect of the genotype at the S locus on fitness components:

Table 3 shows the extent of the differences in fitness-related variables between selfing and incompatible crosses associated with the S-locus genotype of the offspring, for the offspring of the maternal genotype [S01 S15] (the analysis was also performed for the maternal genotype [S01 S02] but results were not significant and thus not shown). Concerning the maternal genotype [S01 S15], for all measured traits, the interactions were not significant and thus not presented here for simplicity. As shown in Table 3, homozygous [S15 S15] individuals showed significantly lower width and length of the largest leaf than heterozygotes [S01 S15] and homozygotes [S01 S01]. They also showed a slower time until the appearance of the first leaf than homozygotes [S01 S01]. No significant differences were found for the germination time and the appearance time of cotyledons. Hence, our results seem concordant to what we may expect from our theoretical results: sheltered load should be higher in the dominant allele S15 than in the recessive allele S01 or in the intermediate allele S02. Our results also suggest that the sheltered load associated with allele S15 should be mostly recessive since the fitness traits of genotype [S01 S15] were never significantly different from those of genotype [S01 S01].

TABLE 3.

Three-way ANOVA analysis for fitness measures of mother genotype [S01 S15] (n = 283; interactions not shown, see text for details)

Trait	Factor	Deviance (d.f., P-value)	Residual deviance	Posthoc Dunnett test difference estimate (SE, P-value)	Mean per genotype (SE)	Result summary
Width (cm)	Cross	0.67 (1, P < 0.001)	6.4	[S01S01] – [S15S15] = 0.06 (0.03, P = 0.052)	[S01S01]: 0.62 (0.02)	[S01 S01] = [S01 S15] > [S15 S15]
	Maternal ID	0.86 (4, P < 0.001)		[S01S15] – [S15S15] = 0.06 (0.03, P = 0.054)	[S01S15]: 0.62 (0.02)
	Genotype	0.14 (2, P = 0.067)			[S15S15]: 0.57 (0.03)
Length (cm)	Cross	0.76 (1, P < 0.001)	13.2	[S01S01] – [S15S15] = 0.07 (0.03, P = 0.038)	[S01S01]: 0.72 (0.02)	[S01 S01] = [S01 S15] > [S15 S15]
	Maternal ID	1.22 (4, P < 0.001)		[S01S15] – [S15S15] = 0.07(0.03, P = 0.034)	[S01S15]: 0.72 (0.02)
	Genotype	0.21 (2, P = 0.04)			[S15S15]: 0.65 (0.03)
Log (germination time) (days)	Cross	0.2 (1, P = 0.13)	25.6	NS	[S01S01]: 8.5 (0.03)	[S01 S01] = [S01 S15] = [S15 S15]
	Maternal ID	8.1 (4, P < 0.001)			[S01S15]: 8.1 (0.03)
	Genotype	0.3 (2, P = 0.29)			[S15S15]: 8.9 (0.05)
Cotyledon time (days)	Cross	0.76 (1, P = 0.253)	147.0	NS	[S01S01]: 1.84 (0.07)	[S01 S01] = [S01 S15] = [S15 S15]
	Maternal ID	1.2 (4, P = 0.724)			[S01S15]: 1.7 (0.07)
	Genotype	1.29 (2, P = 0.331)			[S15S15]: 1.7 (0.11)
Log (first leaf time) (days)	Cross	0.1 (1, P = 0.10)	11.7	[S01S01] – [S15S15] = −0.11 (0.04, P = 0.012)	[S01S01]: 6.2 (0.14)	[S01 S01] = [S01 S15] [S01 S01] > [S15 S15] [S01 S15] = [S15 S15]
	Maternal ID	0.4 (4, P = 0.07)		[S01S15] – [S15S15] = −0.08 (0.04, P = 0.06)	[S01S15]: 6.4 (0.13)
	Genotype	0.4 (2, P = 0.01)			[S15S15]: 6.9 (0.22)

DISCUSSION

The sheltered load hypothesis in SSI:

Few theoretical studies have investigated the extent of a sheltered load associated to the S locus in GSI (Uyenoyama 2003). Here, we have, for the first time, investigated theoretically the conditions favoring and the dynamics of the accumulation of deleterious mutations linked to the S-locus region assuming SSI. Our model showed that in SSI, deleterious recessive mutations would accumulate in a region closely linked to S alleles, particularly when (1) the deleterious mutations are recessive or partially recessive, (2) the number of S alleles in the population is large, and (3) the reverse mutation rate η is low. The probability of fixation of a deleterious mutation in a population, apart from the selection coefficient of the mutation and the backward and forward mutations rates, largely depends on the inbreeding coefficient, the dominance coefficient h, and the size of the population (Bataillon and Kirkpatrick 2000; Glémin et al. 2001). We can easily explain the observed patterns of sheltered load in simulations by considering these latter parameters. First, the purging of recessive deleterious mutations is higher when homozygotes are produced each generation. In SSI, the more recessive an allele is, the higher the expected frequency of homozygous individuals for that allele (Billiard et al. 2007). Hence, the sheltered load was never found to be linked with the recessive S alleles and was most often found to be linked with the dominant S alleles. This effect is modulated by the value of the dominance coefficient of the deleterious mutation: if h is high, then purging is effective even in heterozygotes. Second, we showed that the number of S alleles in the population has a large impact on the presence and amount of sheltered load. This can be explained in terms of the “effective size” of each S allele (Vekemans and Slatkin 1994; Bechsgaard et al. 2004). Indeed, at equilibrium and without genetic load, it is expected that all S alleles from a given dominance class will have the same frequency (isoplethy), which is a direct consequence of negative frequency-dependent selection. Hence, the higher the number of alleles is in a given dominance class, the lower the frequency of each S allele at equilibrium. This should lead to a higher sheltered load associated with S alleles, since the fixation probability of a deleterious mutation is higher for a lower effective size of each S allele. Furthermore, when the number of alleles increases in the population, the heterozygote frequency is higher, leading to an increase in the probability of fixation of a deleterious mutation within an allelic family. Third, when there is positive linkage disequilibrium between the deleterious allele and a given S allele, the hitchhiking effect mutually occurs. In particular, negative frequency-dependent selection that occurs on the S allele will tend to make the frequency of the deleterious allele increase when rare, limiting the purging and further contributing to the maintenance of the sheltered load (Glémin et al. 2001). In short, our theoretical results suggest that the sheltered load is more likely to exist in linkage with the most dominant S alleles and that no sheltered load is expected with the most recessive alleles (Figure 2). These results hold true when deleterious mutations are only partially recessive (Figure 3).

Experimental evidence of sheltered load in A. halleri:

Our results obtained with controlled pollination and forced fertilization between compatible and incompatible individuals of A. halleri first showed that there may be a significant level of background inbreeding depression. Indeed, for [S01 S15], the fitness-related variables of offspring derived from self crosses were significantly different from those from the incompatible crosses for three traits of seven (Table 2A) and significantly different from those from the compatible crosses for six traits of seven. Second, the experimental results suggest the existence of a large sheltered load associated with the S15 allele. Indeed, we showed that three fitness-related variables in the offspring from incompatible crosses had intermediate values relative to offspring from the self and control crosses (Table 2A). Furthermore, in the case of two other variables, the values for the incompatible crosses were intermediate, even if not significant. The differences observed between incompatible and control crosses may arise from a biparental inbreeding effect, since all plants used in this experiment came from the same population. However, this hypothesis could neither explain the segregation bias nor explain the genotypic effect on the phenotypic traits (Table 3).

The differences between fitness-related variables were mainly due to genotypes bearing S15 (Table 3). Furthermore, we showed segregation bias against S15 in offspring from both self and incompatible crosses (Table 1). Our study in SSI corroborates with the results obtained in GSI in S. carolinense (i) by Stone (2004), who found a sheltered load associated to two alleles at the S locus, and (ii) by Mena-Ali et al. (2009), who showed some variations in the strength of the sheltered load carried by different S alleles.

Our results further suggest, first, that the sheltered load is mainly linked to allele S15 and, second, that the sheltered load linked to allele S02 is low or nonexistent since neither a clear pattern of difference between crosses nor a clear segregation bias has been found (Table 3). These empirical results are consistent with our theoretical results since S15 is dominant while allele S02 has an intermediate dominance level.

When does the sheltered load act in the life cycle?

On the basis of the segregation bias data, while there is a clear deficiency of allele S15 in the offspring of the selfed and incompatible crosses (Table 1), it is not possible to disentangle whether the sheltered load is mainly expressed at gametic or zygotic stages. Indeed, the observed discrepancy between the observed genotypic frequencies and the expectations under Mendelian segregation can be explained by the expression of deleterious alleles in pollen and ovules only, in zygotes only, or in both. We used Bechsgaard et al.'s (2004) statistical framework to compare gametic and zygotic effects but our results did not show significant differences between the two hypotheses (see supporting information, File S1). However, our results based on phenotypic traits measurements suggest at least a zygotic effect of the sheltered load. Indeed, the largest differences among the three types of crosses in the phenotypic traits were observed for the seed number and the width and length of the largest leaf. On the one hand, the differences in seed number may be explained by a gametic effect or a sporophytic effect or both, through ovule or zygote selective abortion, respectively. On the other hand, the differences observed for all the other phenotypic traits measured suggest that the sheltered load has a sporophytic effect. However, the next stages of the plant life cycle have not been investigated here. Other stages that have a great importance for the fitness of the progeny like number of flowers and male and female fertility could also be affected by the effect of the sheltered load and require further study. Mena-Ali et al. (2009) indeed showed that sheltered load may have an effect on the number of flowers and on the seed set in S. carolinense, a species with GSI.

Genetic bases of the sheltered load:

On the basis of analysis of recombination rates in the genomic region surrounding the S locus, Kawabe et al. (2006) suggested that only a few genes are susceptible to contributing to the sheltered load. It was therefore suggested that the sheltered load is unlikely to be a major influence on fitness as compared with the genomic load. Indeed, the number of genes linked to the S locus is quite low according to estimates of the size of the region undergoing S-locus-influenced recombination suppression: based on Uyenoyama (2005), the S-locus cosegregating region in Brassica is ∼0.3 Mb and the gene density is 15 per 100 kb, suggesting that we may expect ∼45 cosegregating genes with the S locus. However, even though the total number of these genes is low, some of these genes may have important functions, such as, for example, a gene influencing seed dormancy in Papaver rhoeas as shown by Lane and Lawrence (1995). As a consequence, a single mutation in one of these genes could have a severe effect at the individual level.

Our theoretical model suggested that the fixation of deleterious mutations linked to the S locus is possible, so that even if the region cosegregating with the S locus is small, some mutations can be fixed. Moreover, our empirical results in A. halleri suggest that, at least for allele S15, the sheltered load is large enough to be detected through segregation bias and some phenotypic traits (Table 3). Hence, the deleterious mutations linked to S15 in A. halleri must have a large effect, as compared to the mildly deleterious mutations responsible of the background inbreeding depression.

The sheltered load is usually thought to be caused by recessive mutations (Stone 2004; Porcher and Lande 2005). However, the expression time and intensity of the sheltered load can be more complex. First, as shown above, we cannot exclude that the sheltered load acts at the gametic stage. Second, if the sheltered load indeed acts during sporophytic early stages of the life cycle, then the dominance level of the sheltered load may be high, as estimated by 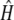, which suggests that deleterious mutations may not be totally recessive, which is corroborated by our theoretical results since a sheltered load can accumulate with partially recessive deleterious mutations (Figure 3). Finally, the genotypic effects on the leaf size and appearance time suggest that the dominance of the sheltered load is low at this stage: indeed, no significant difference was detected between the genotypes [S01 S01] and [S01 S15] while the difference between [S01 S15] and [S15 S15] was significant (Table 3).

Evolutionary consequences of the sheltered genetic load:

The sheltered load could play an important role in the maintenance of the self-incompatibility system. Porcher and Lande (2005) showed that a large sheltered load combined with high background inbreeding depression may enlarge the conditions for the maintenance of the gametophytic self-incompatibility system. It would now be interesting to estimate if the sheltered load and background inbreeding depression allow the persistence of the sporophytic self-incompatibility system. Indeed, as shown here, we expect that the sheltered load should be large only for dominant S alleles and almost absent for recessive or intermediate S alleles. Hence, we would expect there to be a smaller influence of sheltered load on the maintenance of SI in an SSI system than in a GSI system, due to the reduced or absent sheltered load associated with the most frequent S alleles in a population.

The sheltered load could also influence the dynamics of self-incompatibility alleles: since a new S allele should share deleterious alleles with its ancestor, the sheltered load is thought to slow down the appearance of new alleles (Uyenoyama 2003). Our results indicate that the sheltered genetic load depends on the level of dominance of the associated S allele. Hence, if the sheltered load is large, we can expect that the differentiation rate of the S alleles should differ among dominance classes, with a slower rate in a dominant than in a recessive S-allelic class.