Skip to main content
PMC home page
Molecular Systems Biology logoLink to Molecular Systems Biology
. 2009 Oct 13;5:316. doi: 10.1038/msb.2009.74

The switching dynamics of the bacterial flagellar motor

Siebe B van Albada 1,*, Sorin Tănase-Nicola 1,†, Pieter Rein ten Wolde 1,a
PMCID: PMC2779088  PMID: 19888211

Abstract

Many bacteria are propelled by flagellar motors that stochastically switch between the clockwise and counterclockwise rotation direction. Although the switching dynamics is one of their most important characteristics, the mechanisms that control it are poorly understood. We present a statistical–mechanical model of the bacterial flagellar motor. At its heart is the assumption that the rotor protein complex, which is connected to the flagellum, can exist in two conformational states and that switching between these states depends on the interactions with the stator proteins, which drive the rotor. This couples switching to rotation, making the switch sensitive to torque and speed. Another key element is that after a switch, it takes time for the load to build up, due to conformational transitions of the flagellum. This slow relaxation dynamics of the filament leads, in combination with the load dependence of the switching frequency, to a characteristic switching time, as recently observed. Hence, our model predicts that the switching dynamics is not only controlled by the chemotaxis-signaling network, but also by mechanical feedback of the flagellum.

Keywords: bacteria, chemotaxis, fluctuations, modeling, supramolecular assemblies

Introduction

Flagellated bacteria, such as Escherichia coli, are propelled by flagellar filaments. Each flagellar filament is under the action of a rotary motor, which can rotate either in a clockwise (CW) or a counterclockwise (CCW) direction (see Box 1; and Thomas et al, 2006). When all motors run in the CCW direction, the flagella form a helical bundle and the bacterium swims smoothly. When one motor switches direction to run in the CW direction, however, the connected flagellar filament disentangles from the bundle, and the bacterium performs a so-called tumble. These tumble events randomize the cell's trajectory, and it is the modulation of their occurrence that allows these bacteria to chemotax.

A cartoon of the bacterial flagellar motor is shown in panel A of Box 1. It consists of a protein complex called the rotor, and a number of stator proteins that are fixed in the inner membrane and the peptidoglycan layer. Interactions between the stator proteins and a ring of FliG proteins of the rotor protein complex drive the rotation of the rotor, and thereby the rotation of the flagellum, which is connected to the rotor. The rotation direction depends on the concentration of the phosphorylated form of the messenger protein CheY, which binds to the ring of FLiM proteins of the rotor protein complex. The concentration of CheYp is regulated by the intracellular chemotaxis network, which transmits the ligand signal from the receptor cluster to the motors.

Recent experiments suggest that the switching dynamics of the bacterial flagellar motor is not only under the control of the intracellular chemotaxis pathway (Korobkova et al, 2004; Tu and Grinstein, 2005), but is also sensitive to mechanical feedback. Fahrner et al (2003) showed that the average motor switching frequency depends on the torque and rotation speed of the motor. Moreover, Korobkova et al (2004, 2006) studied the motor switching statistics in mutant cells in which the switching dynamics is no longer modulated by the chemotaxis signaling network. To this end, they measured power spectra of the switching dynamics, which reflect the time scales on which the motor switches direction, by monitoring the rotation of a 0.5-μm latex bead connected to a flagellum (Korobkova et al, 2004, 2006). Interestingly, the power spectra are not consistent with a two-state Poisson process, in which the switching events are independent, and the CW and CCW intervals are uncorrelated and exponentially distributed (Korobkova et al, 2006). They show a distinct peak at around 1 s−1 (Korobkova et al, 2006), which means that there is a characteristic frequency at which the motor switches. Moreover, the peak implies that switching is coupled to a non-equilibrium process (Van Kampen, 1992; Tu, 2008; Van Albada, 2008). This is intriguing, because this observation, combined with the observation that the switch is sensitive to torque and speed (Fahrner et al, 2003), suggests that switching is coupled to the non-equilibrium process of rotation.

We argue that to explain the switching dynamics of the bacterial flagellar motor, we have to integrate a description of the switching dynamics of the rotor with a description of both the flagellum dynamics and the dynamics of the stator proteins that drive the rotation of the rotor (see Box 1). In our model, the proteins of the rotor complex collectively switch between a CW and a CCW conformational state, corresponding to the respective rotation directions of the motor. Interactions between the stator proteins and the rotor do not only drive the rotation of the rotor, but also continually change the relative stability of the two conformational states of the rotor. This couples switching to rotation, making the switch sensitive to torque and speed. Our model also predicts that the probability for the rotor to switch increases strongly with the load at low load, in agreement with recent experiments (Yuan et al, 2009). This property, in combination with the conformational dynamics of the flagellum, is key to understanding the switching dynamics of the bacterial flagellar motor.

Bacterial flagella can exist in different conformational or so-called polymorphic states (Calladine, 1975; Macnab and Ornston, 1977; Hotani, 1982; Darnton and Berg, 2007), which are either left-handed or right-handed helices. When the motor runs in the CCW direction, the flagellum adopts a left-handed, normal state, whereas if the motor runs in the CW direction, the flagellum adopts a right-handed, semi-coiled or curly state (Turner et al, 2000). By pulling on a single flagellum using optical tweezers, Darnton and Berg (2007) recently observed that transitions between these polymorphic forms occur in discrete steps, during which elastic strain energy is released. We argue that the change in the torque upon a motor reversal induces a polymorphic transition that proceeds through a similar series of discrete steps. As in each of these steps strain energy is released, the torque on the motor, and hence the switching propensity, remains low. Only when the flagellum has reached its final polymorphic form, and the strain energy can no longer be released, does the torque on the motor, and hence the switching propensity, increase. This mechanical feedback of the flagellum on the switching propensity of the rotor leads to the characteristic switching time of the motor, as observed (Korobkova et al, 2006). Our results thus show that the switching dynamics of the bacterial flagellar motor is not only controlled by the dynamics of the intracellular signaling pathway, but also by mechanical feedback of the flagellum. As the characteristic switching time due to mechanical feedback is on the same time scale as the response time of the intracellular chemotaxis network (Korobkova et al, 2004), the mechanical feedback of the flagellum on the switching frequency of the motor is expected to have an important role in modulating the run and tumble times of chemotacting bacteria.

Results

The stator–rotor interaction

We consider the switching of a single motor, consisting of eight stator proteins that drive the rotation of the rotor protein complex, which is connected to a single flagellum (see Box 1). In a given conformational state, the rotor protein complex interacts with the stator proteins according to a model that is inspired by that of Meacci and Tu (2009), and that of Xing et al (2006), which is based on the description by Kojima and Blair (2001). According to this proposal, the motor cycle of each stator protein consists of two ‘half strokes'. During the first power stroke, two protons bind the stator protein (Kojima and Blair, 2001; Xing et al, 2006). This leads to a thermally activated conformational transition of the stator protein, allowing it to exert a force on the rotor protein complex. During the second stroke, the recovery stroke, the two protons are released to the cytoplasm, triggering another conformational transition of the stator, allowing another part of the stator to exert a force on the rotor (Kojima and Blair, 2001; Xing et al, 2006).

The torque exerted by a stator protein on the rotor is modeled as a constant force along an energy surface, and the conformational transitions of the stator proteins are described as hops between the two respective surfaces (panel B of Box 1). The rotation dynamics of the rotor is modeled according to the overdamped Langevin equation, and, following Meacci and Tu (2009), the hopping rates are assumed to depend on the torque exerted by the stator (see Materials and methods). Supplementary Figure S1 shows that this model accurately describes the torque–speed relation of the flagellar motor of E. coli, with its characteristic ‘knee' (Ryu et al, 2000) and the maximum speed that is independent of the number of stators (Yuan and Berg, 2008).

The rotor switching dynamics

In E. coli, the fraction of time the motor rotates in the CW direction, the so-called CW bias, is controlled by the concentration of the intracellular messenger CheYp. This protein modulates the CW bias by binding to the ring of FliM proteins. This ring is connected to the ring of FliG proteins, which interact with the stator proteins (see Box 1).

The molecular mechanism of the switch is unknown. Yet, it is widely believed that the binding of CheYp to FliM tends to change the conformation of FliM, and thereby the direction of rotation. Following earlier work, we assume that each FliM protein can exist in either a CW or CCW conformational state and that binding of CheYp shifts the relative stability of these two conformational states (Scharf et al, 1998; Turner et al, 1999; Duke et al, 2001). Moreover, we also assume that each FliG protein can exist in either a CW or CCW conformational state. In the spirit of a Monod–Wyman–Changeux (MWC) model (Monod et al, 1965), we assume that the energetic cost of having two rotor protein molecules in two different conformational states is prohibitively large. We can then speak of the rotor being in either the CW or the CCW state.

When the rotor complex switches from one state to another, the interactions between the FliG proteins and the stator proteins change, due to the new conformational state of the FliG proteins. In our model, each stator–rotor interaction is described by four energy surfaces, corresponding to the 2 × 2 conformational states of the rotor and stator protein, respectively (see Materials and methods). We assume that the two rotor surfaces corresponding to a given state of the stator are simply each other's mirror image plus a shift, but offset by an energy difference given by the CW bias (panel C of Box 1). Importantly, the instantaneous switching rate depends on the rotation angle of the rotor, but not on the load (see Materials and methods).

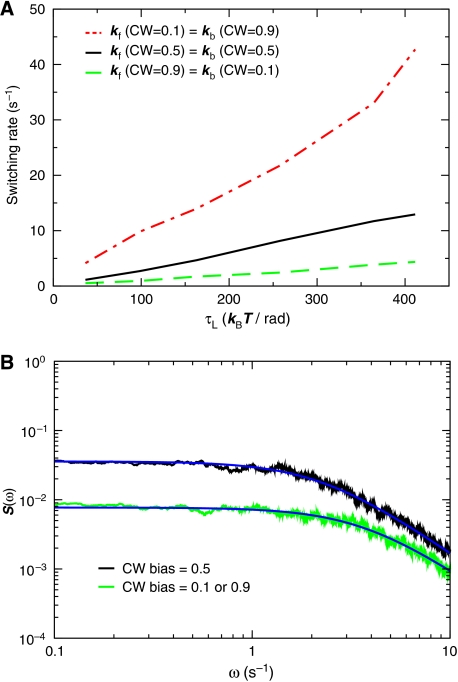
Figure 1 shows the switching dynamics of the motor in the absence of the flagellum. This corresponds to the switching of a bead connected to a filament stub (Fahrner et al, 2003) or a bead directly connected to the hook (Yuan et al, 2009). As expected, the average CCW → CW switching rate increases as the CW bias increases (Figure 1A). More interestingly, it increases with the external load. As we describe below, this is key to understanding the bump in the power spectrum. The average switching rate increases with the load, because that brings the rotor more often to positions in which its interactions with the stator proteins favor the alternative conformation of the rotor (see Supplementary Figure S2). This mechanism differs fundamentally from that commonly used to explain the force dependence of processes, such as protein unfolding and molecular dissociation (see Supplementary information; Howard, 2001). Interestingly, recent experiments by Yuan et al (2009) confirm the prediction of our model that the switching rate increases with the load in the low-load regime.

Figure 1.

Figure 1

Open in a new tab

Switching dynamics in the absence of a flagellum. The load is constant in magnitude, but instantaneously changes sign upon a rotation reversal. (A) Switching rate as a function of the load τL in the forward CW → CCW (kf) and backward (CCW → CW) direction (kb) for CW bias=0.1, 0.5, and 0.9. Note that because of the symmetry of our model, the switching dynamics in the forward (backward) direction for CW bias=x, equals the switching dynamics in the backward (forward) direction for CW bias=1−x. (B) Power spectra S(ω) for CW bias=0.1, 0.5 and 0.9.

Figure 1B shows the power spectra of the switching dynamics. It is given by a Lorentzian, which shows that the switching of the rotor without a flagellum can be modeled as a random telegraph process.

Flagellum dynamics

In the model discussed above, after a switching event the torque on the motor immediately changes sign and instantaneously reaches its steady-state value. However, in the experiments by Korobkova et al (2004, 2006), the switching of the motor was visualized through a bead that was attached to the flagellar filament. We argue that the flagellum dynamics is critical for understanding the switching dynamics of the flagellar motor.

Darnton and Berg (2007) recently studied polymorphic transitions of a single filament using optical tweezers. The following three observations were made: (1) The transitions occur in discrete, rapid steps that are stochastic in nature, suggesting that they are activated processes during which an energy barrier is crossed; (2) In between the steps, the filament behaves as a linear elastic object that accumulates elastic strain energy that is released during the next transformation; (3) During a step, it is not the whole filament but micrometer-long sections that are converted.

On the basis of these three observations, we have constructed the filament model shown in panel D of Box 1. It consists of a number of harmonic potentials as a function of the winding angle θ, corresponding to different conformational states of the filament. The left-most well corresponds to the normal state, which is the polymorphic form of the filament when the motor runs in the CCW direction. The right-most well corresponds to the curly state, which is one of the polymorphic forms that the filament adopts when the motor runs in the CW direction. The states in between correspond to an ensemble of polymorphic forms that includes not only the coiled and semi-coiled states, but, according to the third observation above, also states in which different filament sections have different polymorphic forms. According to the second observation, and by following the earlier studies (Goldstein et al, 2000; Darnton and Berg, 2007), we assume that the free energy of a filament in a given state m is quadratic in the curvature and torsion. This leads to a quadratic potential in θ under the assumption that the bead position quickly relaxes to its steady-state value (see Materials and methods). Motivated by the first observation, we assume that the transition from one conformational state to another is an activated process. The dynamics of the bead connected to the flagellum is assumed to obey overdamped Langevin dynamics (see Materials and methods).

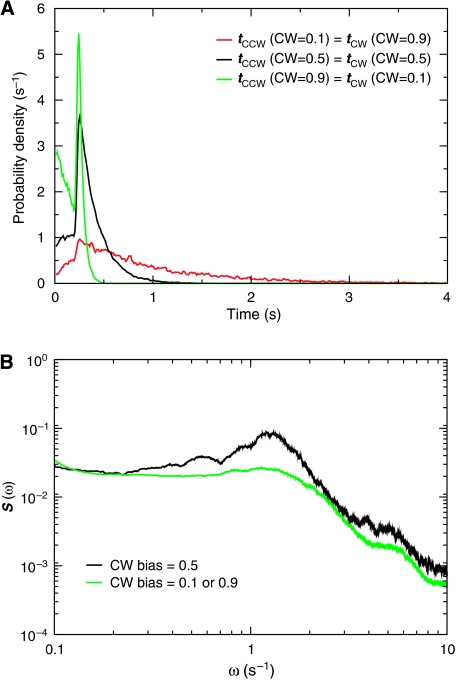
Figure 2 shows the switching characteristics of the motor in the presence of the flagellum. They agree remarkably well with those observed by (Korobkova et al, 2006). First, the waiting-time distributions (Figure 2A) are not exponential, as would be expected for a random telegraph process: they exhibit a clear peak at around 0.4 s. Second, the waiting-time distribution for the forward (CW → CCW) transition changes from a narrow distribution at CW bias=0.1 to a broad distribution at CW bias=0.9. Moreover, the power spectra show a distinct peak at ω∼1 s−1 (Figure 2B), with the peak being most pronounced when the CW bias=0.5. All these features are in near quantitative agreement with experiment (Korobkova et al, 2006). The peak in the waiting-time distributions (Tu, 2008) and power spectra (Van Kampen, 1992; Van Albada, 2008) imply that the motor shows a characteristic switching time.

Figure 2.

Figure 2

Open in a new tab

The switching dynamics of a motor to which a flagellum is connected. The dynamics of the bead instead of the motor, as that has been measured experimentally is shown (Korobkova et al, 2006); however, the switching dynamics of the two are very similar. (A) Distribution of waiting times for the forward CW → CCW transition (tCW) and backward CCW → CW transition (tCCW), for CW bias=0.1, 0.5 and 0.9. (B) The power spectra S(ω) for CW bias=0.1, 0.5 and 0.9. Our model is symmetric by construction—the CW energy surface is the mirror image of the CCW surface (see panel (C) of Box 1) and the wells of the filament potential are of equal depth (see panel (D) of Box 1). Accordingly, the distribution of the forward (backward) transition for CW bias=x overlaps with that of the backward (forward) transition for CW bias=1−x.

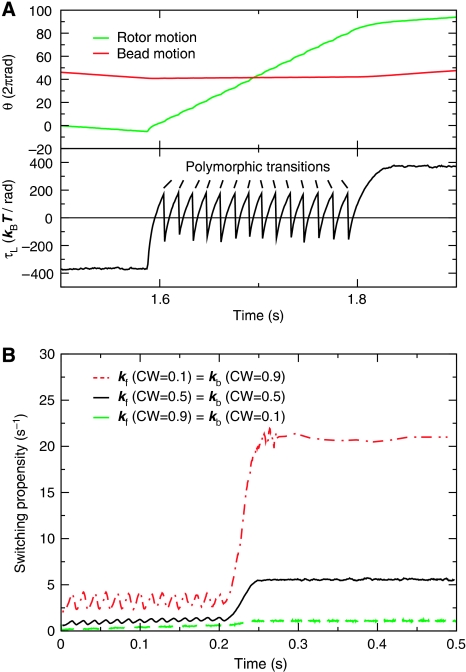
Our model predicts that the characteristic switching time arises from the interplay between the conformational dynamics of the flagellum and the dependence of the switching rate on the load (Figure 1A). The idea is illustrated in Figure 3. After a switching event of the rotor, the torque is initially in the original direction, but decreases rapidly in magnitude (Figure 3A) as the filament approaches its optimal winding angle (corresponding to the bottom of the outer potential wells, panel D of Box 1); in this regime, the load on the motor is negative, and the elastic strain energy in the filament decreases. As the rotor drives the filament beyond its optimal winding angle, the torque changes direction and increases in magnitude; the load on the motor becomes positive, and the strain energy in the filament builds up. This strain energy can, however, be released through a polymorphic transition, leading to a sudden change in the direction of the torque. This process repeats itself until the filament reaches its final polymorphic form, upon which the strain energy can no longer be released and the torque increases to reach a plateau when the viscous drag on the bead balances the motor torque. The characteristic switching time can now be understood by combining a time trace of the load (Figure 3A) with the load dependence of the switching rate (Figure 1A), yielding to a good approximation the switching propensity as a function of time (Figure 3B). After a switching event, the torque flip-flops around zero and the switching propensity is therefore low (Figure 1A). However, when the flagellum has reached its final polymorphic form, the strain can no longer be released, and the torque and hence the switching propensity increase strongly. The characteristic switching time is precisely caused by the fact that the probability to switch is not constant in time, as for a Markovian Poisson process, but is initially low and then rises strongly (Figure 3B).

Figure 3.

Figure 3

Open in a new tab

The mechanism of switching. (A) Typical time traces for the load τL, rotor and bead position during a switching event, for CW bias=0.5. The arrows mark the polymorphic transitions of the flagellum (also see panel (D) of Box 1). Upon a polymorphic transition, the load instantly changes sign; the flagellum then pulls on the rotor in the forward rotation direction until the load crosses zero when the winding angle passes the value corresponding to the bottom of the potential well of the new conformational state (see panel (D) of Box 1); the flagellum then pulls on the rotor in the backward rotation direction until the next polymorphic transition occurs or the rotor reverses direction. (B) The switching propensity as a function of time after a switching event, for CW bias=0.1, 0.5, and 0.9.

Coarse-grained model

Our calculations suggest that a useful coarse-grained model for understanding the switching dynamics is one in which the system stochastically flips between two states with time-dependent propensity functions (Figure 3B):

graphic file with name msb200974-i1.jpg

where the propensity functions are given by the following piece-wise linear functions:

graphic file with name msb200974-i2.jpg
graphic file with name msb200974-i3.jpg
graphic file with name msb200974-i4.jpg

The important parameters of this model are the lag time, Tα=(t1+t2)/2, the minimum and maximum propensity, kαmin and kαmax, respectively, and to a lesser extent the sharpness of the transition sα=(kαmax−kαmin)/(t2−t1). For this model, the waiting-time distribution and power spectrum can be obtained analytically (see Supplementary information).

The maximum propensity function kαmax is determined by the maximum load τmax and the switching rate at that load, which depends on the CW bias (Figure 1A). The maximum load is set by the balance of the drag force and the motor torque, which can be obtained from the intersection of the torque–speed curve and the drag coefficient of the load times the speed (the load line) (Xing et al, 2006). The minimum propensity function kαmin depends on the torque τmin at which the flagellum undergoes a polymorphic transition—the polymorphic transitions release the elastic strain energy before the maximum load is reached—and the switching rate at that torque τmin, which also depends on the CW bias. The emergence of a peak in the power spectrum and waiting-time distribution requires that kαmin<kαmax. Recently, Tu (2008) showed that a peak in the waiting-time distribution implies that the system is out of equilibrium. We find that the peak in the waiting-time distribution emerges for smaller values of Δkα≡(kαmax−kαmin) than the peak in the power spectrum; this supports the idea that a peak in the waiting-time distribution is a more sensitive measure for the non-equilibrium nature of the process (Tu, 2008). The position of the peak is determined by Tα, which is given by the difference in winding angle between the normal and curly state divided by the average speed at which the rotor drives the systems between these two states. Interestingly, polymorphic transitions of filaments of swimming bacteria occur on time scales of 0.1 s (Turner et al, 2000), close to the peak of the waiting-time distribution (Korobkova et al, 2006), supporting our idea that they set the characteristic switching time.

The dependence of the difference Δkα on the CW bias explains the change in the waiting-time distributions when the CW bias is varied. The plateau load τmax and the load τmin at which the flagellum undergoes a polymorphic transition are independent of the CW bias. However, the magnitude by which the switching propensity rises as the load increases from τmin to τmax does depend on the CW bias (Figure 1A), such that Δk−=k−max−k−min increases with the CW bias. When the CW bias and hence Δk− is large, the rotor typically switches to the CW state before the switching propensity can reach its plateau value. This explains the narrow distribution of CCW intervals when the CW bias is large, as observed in both the model (Figure 2A) and experiment (Korobkova et al, 2006). For the reverse transition the situation is qualitatively different. When the CW bias is large, Δk+ is small, which means that the system can enter the regime in which the switching propensity is constant before it switches to the CCW state. This constant propensity leads to an exponential tail in the distribution of CW (CCW) intervals when the CW (CCW) bias is large, as observed in both the distributions of the model (Figure 2A) and those measured experimentally (Korobkova et al, 2006).

Discussion

We have presented a statistical–mechanical model that describes the switching dynamics of the bacterial flagellar motor. Its foundation is the assumption that the rotor protein complex can exist in two conformational states corresponding to the two respective rotation directions, and that switching between these states depends on interactions with the stator proteins, which also drive the rotation of the rotor complex. This naturally couples the switching dynamics to the rotation dynamics. The load does not directly change the relative stability of the rotor's conformational states, but it does change how often the stator proteins during their motor cycle favor one conformational state of the rotor over the other. This, according to our model, is the principal mechanism that makes the switch sensitive to torque and speed. Another central element of our model is that after a switch, it takes time for the motor load to build up, due to polymorphic transitions of the filament. This time dependence of the load leads, in combination with the load dependence of the switching propensity of the rotor, to the characteristic switching time of the motor. Hence the flagellum, by providing mechanical feedback on the rotor's switching propensity, has an integral role in the switching process.

Interestingly, the torque generated by a motor of a swimming bacterium is close to the maximum motor torque (Darnton et al, 2007), which is larger than the torque needed to induce a polymorphic transition of the flagellum upon a motor reversal. Our model thus predicts that the characteristic switching time is an intrinsic property of the motor and not an artifact of the viscous drag of the bead used to monitor the motor rotation (Korobkova et al, 2006). The prediction that the characteristic switching time is due to mechanical feedback from the flagellum could have important implications for the switching of multiple motors of swimming bacteria, which mechanically interact through their flagella.

The origin of the non-equilibrium character of our model is the coupling between switching and rotation, which is driven by a proton motive force. The binding of CheYp obeys detailed balance and has been integrated out. Our model thus differs markedly from that of Tu (2008), in which the non-equilibrium nature is due to the interplay between switching and CheYp binding, creating a new, non-equilibrium mechanism for ultrasensitivity.

Several predictions emerge from our model that could be tested experimentally. One is that the change in the torque on the filament on a motor reversal leads to a series of polymorphic transitions, which could be tested by applying a torque to a single filament using magnetic tweezers. Moreover, our model predicts that the magnitude of the characteristic switching time depends upon the position at which the bead is attached to the flagellum and the maximum speed of the motor, because these factors determine the lag time Tα. As the maximum motor torque decreases with decreasing number of stators, our model also predicts that the peak may disappear when the number of stators is reduced. Finally, our model predicts that the switching dynamics of the rotor without the mechanical feedback of the flagellum is that of a two-state Poisson process, in contrast to the model proposed by Tu (2008). This prediction could be tested by measuring the rotation dynamics of a bead that is connected either directly to the stub, or to a very short filament.

Materials and methods

Stator–rotor dynamics

In our model, each stator–rotor interaction is described by four energy surfaces, UTSj, with the subscript sj=0 or 1 denoting the conformational state of stator protein j and the superscript r=0 or 1 denoting the conformational state of the rotor (CW or CCW) (Box 1). We assume that the stator proteins remain fixed due to the peptidoglycan layer and that only the rotor complex moves. The equation of motion of the rotor is then given by

graphic file with name msb200974-i5.jpg

Here, γR is the friction coefficient of the rotor; UTSj (θj) are the free energy surfaces shown in panels B and C of the Box 1, where θj=θR−θSj, with θR the rotor rotation angle and θSj the fixed angle of stator protein j; ηR(t) is a Gaussian white noise term of magnitude 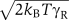Inline graphic; NS is the number of stator proteins, which, for the results presented here, is taken to be NS=8. The torque FL denotes the load with rotation angle θL (see below).

The transition (or hopping) rate for a stator protein to go from one stator energy surface to another depends on the rotation angle, in a manner that obeys detailed balance. It is given by

graphic file with name msb200974-i7.jpg

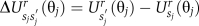Here, Inline graphic. Inspired by the observations of Meacci and Tu (2009), the prefactor is given by k0(θj)=k− for d1+mδ<θj<d2+mδ, where m is an integer and d1 and d2 are the minimum and maximum of the periodic potential with periodicity δ=2π/26 (Box 1); k0(θj)=0 for d2+mδ<θj<d3+mδ; k0(θj)=k+ for d3+mδ<θj<d1+(m=1)δd1. As shown by Meacci and Tu (2009), the maximum speed becomes independent of the number of stators when k−>k+; this allows the ‘lagging' stators, which tend to drive the rotor backwards by exerting a negative torque on it, to catch up with the other stators that drive the rotor forward.

The rotor complex is modeled as an MWC model (Monod et al, 1965), which means that all the rotor proteins switch conformation in concert. The instantaneous switching rate depends on the difference between the free energy of the initial state and that of the transition state. As the free energy of the transition state is not known, we assume it is independent of the rotor's rotation angle and that the instantaneous switching rate depends on the free-energy difference between the two conformational states of the rotor. This leads to the following expression for the instantaneous switching rate:

graphic file with name msb200974-i9.jpg

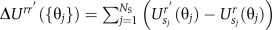where Inline graphic.

Load dynamics

The dynamics of the load is given by

graphic file with name msb200974-i11.jpg

where γL is the drag coefficient of the load and ηL is a Gaussian white noise term of magnitude 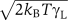Inline graphic. For the switching dynamics of a motor without a flagellum, the load dynamics has been integrated out; this corresponds to a load that is coupled to the rotor through an infinitely stiff linker (Meacci and Tu, 2009). For the switching dynamics of a motor to which a flagellum is attached, a more refined model of the flagellum is needed.

Following the earlier studies (Goldstein et al, 2000; Darnton and Berg, 2007), we assume that the free energy UF of a flagellum in a given polymorphic state m is quadratic in curvature and torsion (see Supplementary information). The curvature κ and torsion τ are functions of the height of the bead connected to the filament, z, and the winding angle θ. We assume that at each instant, the height has relaxed to its steady-state value, which means that UF becomes a quadratic function of the winding angle only:

graphic file with name msb200974-i13.jpg

where the torque constant kθ is given by the Young's and shear moduli and the contour length of the filament; the value chosen is consistent with the measurements carried out by Block et al (1989) and Darnton and Berg (2007) (see Supplementary information). For simplicity, we assume that the potentials are equally spaced, and have the same torque constant and well depth, although under neutral pH the normal state is the most stable one (Darnton and Berg, 2007). The total difference in winding angle between the normal (left-most) and curly (right-most) state is about 80 rounds, which is the correct order of magnitude determined on the basis of elastic properties of the filament (see Supplementary information). This is an important parameter, as it directly affects the characteristic switching time. The other parameters are less important; for instance, agreement with experiment (Korobkova et al, 2006) could be obtained by increasing or decreasing the number of wells (and simultaneously changing the spacing between them such that the average change in winding angle upon a switching event is unchanged) by, at least, a factor of 2 from the baseline value (see Supplementary information).

The transition from one conformational state of the flagellum to another is assumed to be an activated process, with a rate constant

graphic file with name msb200974-i14.jpg

The load dynamics is given by equation (9) with the force given by FL(θR−θL)=−kθ (θL−θR−θm).

The parameters and the algorithm to simulate our model are described in the Supplementary information.

Model of the bacterial flagellar motor.

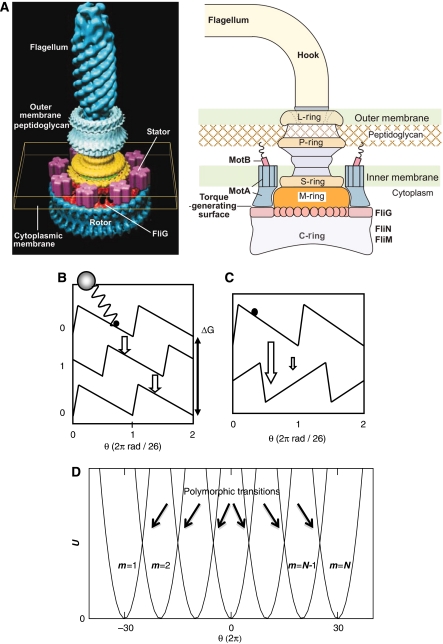
Inline graphic

The bacterial flagellar motor consists of a number of stator proteins embedded in the membrane, which drive the rotation of a protein complex called the rotor, which in turn is connected to a flagellum (see panel (A)). The interactions between the rotor and one stator protein are modeled through the energy surfaces shown in panels (B, C). Panel (B) shows the energy surfaces corresponding to two conformational states of the stator for a given conformational state of the rotor. The thermodynamic driving force is the proton motive force denoted by ΔG. Panel (C) shows the energy surfaces of the motor that correspond to the CCW and CW states of the rotor, for a given conformational state of the stator protein; the two surfaces are assumed to be each other's image plus a shift, and an energetic offset that is given by the CW bias. In total, each stator–rotor interaction is characterized by four surfaces, corresponding to the 2 × 2 conformational states of the stator and rotor proteins. Panel (D) shows the energy surfaces of the flagellum. The left-most curve (m=1) corresponds to the normal state, the right-most curve (m=N) corresponds to the curly state, whereas the intermediate states correspond not only to the semi-coiled state but also to hybrid filaments consisting of different sections of these polymorphic forms (Darnton and Berg, 2007). The polymorphic transitions are modeled as stochastic jumps between these surfaces. They are most likely to occur at the positions given by the arrows. Panel (A) is courtesy of DJ DeRosier (Thomas et al, 2006).

Supplementary Material

Supplementary information

Supplementary information, Supplementary figures S1–5

msb200974-s1.pdf (436.8KB, pdf)

Acknowledgments

We thank Howard Berg, Sanne Abeln, Tom Shimizu and Gijsje Koenderink for a critical reading of the paper. This work is part of the research program of the ‘Stichting voor Fundamenteel Onderzoek der Materie (FOM)', which is financially supported by the ‘Nederlandse organisatie voor Wetenschappelijk Onderzoek (NWO)'.

Footnotes

The authors declare that they have no conflict of interest.

References

  1. Block SM, Blair DF, Berg HC (1989) Compliance of bacterial flagella measured with optical tweezers. Nature 338: 514–518 [DOI] [PubMed] [Google Scholar]
  2. Calladine CR (1975) Construction of bacterial flagella. Nature 255: 121–124 [DOI] [PubMed] [Google Scholar]
  3. Darnton NC, Berg HC (2007) Force–extension measurements on bacterial flagella: triggering polymorphic transformations. Biophys J 92: 2230–2236 [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Darnton NC, Turner L, Rojevsky S, Berg HC (2007) On torque and tumbling in swimming Escherichia coli. J Bacteriol 189: 1756–1764 [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Duke TAJ, Le Novère NE, Bray D (2001) Conformational spread in a ring of proteins: a stochastic approach to allostery. J Mol Biol 308: 541–553 [DOI] [PubMed] [Google Scholar]
  6. Fahrner KA, Ryu WS, Berg H (2003) Bacterial flagellar switching under load. Nature 423: 938. [DOI] [PubMed] [Google Scholar]
  7. Goldstein RE, Goriely A, Huber G, Wolgemuth CW (2000) Bistable helices. Phys Rev Lett 84: 1631–1634 [DOI] [PubMed] [Google Scholar]
  8. Hotani H (1982) Micro-video study of moving bacterial flagellar filaments. III. Cyclic transformation induced by mechanical force. J Mol Biol 156: 791–806 [DOI] [PubMed] [Google Scholar]
  9. Howard J (2001) Mechanics of Motor Proteins and the Cytoskeleton. Sunderland: Sinauer Associates [Google Scholar]
  10. Kojima S, Blair DF (2001) Conformational change in the stator of the bacterial flagellar motor. Biochemistry 40: 13041–13050 [DOI] [PubMed] [Google Scholar]
  11. Korobkova EA, Emonet T, Park H, Cluzel P (2006) Hidden stochastic nature of a single bacterial motor. Phys Rev Lett 96: 058105. [DOI] [PubMed] [Google Scholar]
  12. Korobkova EA, Emonet T, Vilar JMG, Shimizu TS, Cluzel P (2004) From molecular noise to behavioural variability in a single bacterium. Nature 428: 574–578 [DOI] [PubMed] [Google Scholar]
  13. Macnab RM, Ornston MK (1977) Normal-to-curly flagellar transitions and their role in bacterial tumbling. Stabilization of an alternative quaternary structure by mechanical force. J Mol Biol 112: 1–30 [DOI] [PubMed] [Google Scholar]
  14. Meacci G, Tu Y (2009) Dynamics of the bacterial flagellar motor with multiple stators. Proc Natl Acad Sci USA 106: 3746–3751 [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Monod J, Wyman J, Changeux JP (1965) On the nature of allosteric transitions: a plausible model. J Mol Biol 12: 88–118 [DOI] [PubMed] [Google Scholar]
  16. Ryu WS, Berry RM, Berg HC (2000) Torque-generating units of the flagellar motor of Escherichia coli have a high duty ratio. Nature 403: 444–447 [DOI] [PubMed] [Google Scholar]
  17. Scharf BE, Fahrner KA, Turner L, Berg HC (1998) Control of direction of flagellar rotation in bacterial chemotaxis. Proc Natl Acad Sci USA 95: 201–206 [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Thomas DR, Francis NR, Xu C, DeRosier DJ (2006) The three-dimensional structure of the flagellar rotor from a clockwise-locked mutant of Salmonella enterica serovar Typhimurium. J Bacteriol 188: 7039–7048 [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Tu Y (2008) The nonequilibrium mechanism for ultrasensitivity in a biological switch: sensing by Maxwell's demons. Proc Natl Acad Sci USA 105: 11737–11741 [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Tu Y, Grinstein G (2005) How white noise generates power-law switching in bacterial flagellar motors. Phys Rev Lett 94: 208101. [DOI] [PubMed] [Google Scholar]
  21. Turner L, Ryu WS, Berg HC (2000) Real-time imaging of fluorescent flagellar filaments. J Bacteriol 182: 2793–2801 [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Turner L, Samuel ADT, Stern AS, Berg HC (1999) Temperature dependence of switching of the bacterial flagellar motor by the protein CheYY13DK106YW. Biophys J 77: 597–603 [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Van Albada SB (2008) A Computational Study of E. coli Chemotaxis. PhD thesis, Amsterdam: Vrije Universiteit [Google Scholar]
  24. Van Kampen NG (1992) Stochastic Processes in Physics and Chemistry. Amsterdam: North-Holland [Google Scholar]
  25. Xing J, Bai F, Berry R, Oster G (2006) Torque–speed relationship of the bacterial flagellar motor. Proc Natl Acad Sci USA 103: 1260–1265 [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Yuan J, Berg HC (2008) Resurrection of the flagellar rotary motor near zero load. Proc Natl Acad Sci USA 105: 1182–1185 [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Yuan J, Fahrner KA, Berg HC (2009) Switching of the bacterial flagellar motor near zero load. J Mol Biol 390: 394–400 [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary information

Supplementary information, Supplementary figures S1–5

msb200974-s1.pdf (436.8KB, pdf)

Articles from Molecular Systems Biology are provided here courtesy of Nature Publishing Group

RESOURCES