Time-resolved infrared spectroscopy of the lowest triplet state of thymine and thymidine

Abstract

Vibrational spectra of the lowest energy triplet states of thymine and its 2’-deoxyribonucleoside, thymidine, are reported for the first time. Time-resolved infrared (TRIR) difference spectra were recorded over seven decades of time from 300 fs – 3 µs using femtosecond and nanosecond pump-probe techniques. The carbonyl stretch bands in the triplet state are seen at 1603 and ~1700 cm⁻¹ in room-temperature acetonitrile-d₃ solution. These bands and additional ones observed between 1300 and 1450 cm⁻¹ are quenched by dissolved oxygen on a nanosecond time scale. Density-functional calculations accurately predict the difference spectrum between triplet and singlet IR absorption cross sections, confirming the peak assignments and elucidating the nature of the vibrational modes. In the triplet state, the C4=O carbonyl exhibits substantial single-bond character, explaining the large (~70 cm⁻¹) red shift in this vibration, relative to the singlet ground state. Femtosecond TRIR measurements unambiguously demonstrate that the triplet state is fully formed within the first 10 ps after excitation, ruling out a relaxed ¹nπ* state as the triplet precursor.

1. Introduction

There has been intense interest recently in excited electronic states of DNA and DNA model compounds (for recent reviews, see refs. [1,2]). In single bases, relaxation to the ground electronic state (S₀) occurs primarily via ultrafast internal conversion [1] due to the existence of accessible conical intersections [3–8]. Rapid nonradiative return to S₀ is thought to greatly reduce the probability of damaging photoreactions, and to restrict intersystem crossing to the long-lived, and therefore potentially reactive triplet states. Recent work has revealed, however, that the singlet state photophysics of hydrated pyrimidine bases (thymine, uracil, and cytosine) is considerably more complex than previously thought [9]. In free pyrimidine bases, their nucleosides and 5’-mononucleotides a second internal conversion channel provides a pathway for relaxation from the initial ¹ππ* state to an intermediate electronic state. This intermediate, which has been assigned to a ¹nπ* state, decays to S₀ with a lifetime of between 10 and 100 ps in aqueous solution to S₀ [9].

The discovery of long-lived singlet states opens a chink in the armor of the concept of DNA’s intrinsic photostability, but it has not been shown that these states are actually photoreactive. An interesting possibility is that the ¹nπ* state is a gateway to the lowest triplet state [9,10]. The quantum yields of intersystem crossing (ISC) are no greater than a few percent in aqueous solution [11], but these long-lived states are of great importance because they can react by (2+2) cycloaddition with an adjacent pyrimidine base to create a cyclobutane pyrimidine dimer (CPD). The thymine-thymine CPD is the most abundant photoproduct formed in UV-irradiated DNA [11]. In a dilute solution of monomeric pyrimidine bases that is free of aggregates, singlet excited state lifetimes are too short and diffusion is too slow to permit bimolecular encounters prior to decay of the excited singlet population. In this case, CPDs are only formed via long-lived triplet states [12,13], as shown by experiments with triplet quenchers [14].

In natural DNA, adjacent bases are held in close proximity by the phosphodiester backbone, and bimolecular encounters between adjacent bases can take place rapidly without the need for diffusion. In this case, reaction could conceivably occur via a short-lived singlet state, but there is continuing uncertainty about the multiplicity of the dimer precursor state. Triplet quenchers do not attenuate CPD formation in nucleobase multimers, but this could merely indicate an ultrafast triplet reaction, as discussed four decades ago by Lamola [15]. Thus, the recent demonstration of ultrafast thymine dimer formation [16], while most readily explained by a singlet reaction, does not completely rule out a triplet state. Singlet and triplet reaction pathways have been identified in theoretical studies [17,18], but triplet states have not been detected in base multimers in nanosecond flash photolysis measurements [19].

Ultrafast spectroscopy can in principle address these questions, but pyrimidine triplet states are difficult to study by transient electronic spectroscopy due to overlapping triplet and ¹nπ* absorption bands [10]. On the other hand, time-resolved infrared (TRIR) spectroscopy permits the recording of transient IR difference spectra of excited electronic states. TRIR spectroscopy with femtosecond pump and probe pulses has been fruitfully applied to a variety of DNA model systems recently [20,21], but vibrational spectra have never been reported for any nucleobase triplet state. Here we report transient vibrational spectra of the triplet states of thymine and thymidine in the region 1300 – 1800 cm⁻¹ recorded by time-resolved infrared spectroscopy on femtosecond to microsecond time scales. Acetonitrile was selected as the solvent because the triplet quantum yield of thymine (Φ_ISC ≈ 0.2 [22,23]) is at least an order of magnitude higher than in water. Calculated triplet frequencies are in very good agreement with experiment, allowing the strong carbonyl stretching bands to be positively assigned. By monitoring these bands as a function of time, new insights are obtained about intersystem crossing in thymine.

2. Experimental methods

Samples

Thymine (99%), thymidine (99%), D₂O (99.9% atom), and acetonitrile-d₃ (CD₃CN, > 99.998% atom purity) were purchased from Sigma-Aldrich and used as received. Spectrophotometric grade acetonitrile was obtained from VWR International. Peak positions in steady-state and transient IR spectra of thymine were essentially identical between 1600 and 1800 cm⁻¹ in acetonitrile and acetonitrile-d₃. Most measurements were therefore carried out in acetonitrile-d₃ due to this solvent’s wider IR transparency window.

Thymine-d₂ was prepared after the method of Zhang et al. [24] by dissolving several milligrams of thymine in excess D₂O. The D₂O was then removed on a vacuum line, and the sample was dissolved in acetonitrile-d₃. A spectrum of the final solution recorded with a Perkin-Elmer Spectrum 2000 FTIR spectrometer showed no N–H stretch intensity at ~3300 cm⁻¹, indicating complete exchange of the N1 and N3 hydrogens.

Nanosecond TRIR measurements

The JASCO TRIR-1000 dispersive spectrometer used to record ns TRIR difference spectra has been described previously [25]. Briefly, samples were held in a home-built flow cell composed of two 1 cm thick CaF₂ plates with a 0.5 mm Teflon spacer and excited using 266 nm pulses (~0.7 mJ / pulse, repetition rate of 97 Hz) from the fourth harmonic of an Infinity Nd:YAG laser (Coherent, Inc). The laser pulses were overlapped in the sample with the broadband output of a MoSi₂ IR source (JASCO Inc.). The IR light was then directed into a monochromator (16 cm⁻¹ resolution) equipped with an MCT photovoltaic IR detector (Kolmar Technologies model KMPV11-1-J1). The signal at each time delay was amplified with a low noise differential amplifier (NF Electronic Instruments model 5307) and digitized by a digital oscilloscope. The instrument response time was ~50 ns for these experiments. TRIR spectra in acetonitrile were recorded between 1600 and 1800 cm⁻¹ and in acetonitrile-d₃ between 1300 and 1800 cm⁻¹. Kinetic traces were recorded at select peak frequencies. Data collection and analysis was carried out using Igor Pro (Wavemetrics, Inc.).

Solutions for kinetic measurements had a solute concentration of 3 mM. They were purged with argon to avoid oxygen quenching of the triplet state and were monitored before and after pump-probe measurements by UV-vis and FTIR absorption spectroscopy to detect photodegradation. Samples were replaced as needed to minimize effects due to accumulation of photoproducts or adventitious water.

Femtosecond TRIR measurements

Mid-IR transient absorption was measured with femtosecond temporal resolution using pump-probe techniques. Femtosecond pulses at 800 nm produced by a Ti:sapphire oscillator and amplified by a 1 kHz regenerative amplifier system (Coherent, Inc.) pumped independent optical parametric amplifiers (Coherent, Inc.) to create pump and probe pulses. Pump pulses at 270 nm were generated by second harmonic generation after sum-frequency mixing of signal and idler pulses. The pump pulses were chopped at 500 Hz with a mechanical chopper (New Focus) and had pulse energies of 5 µJ at the sample. Mid-IR probe pulses centered at 1600 cm⁻¹ were generated via difference-frequency mixing of signal and idler beams. Probe pulses had spectral bandwidths of ~125 cm⁻¹ (FWHM) and pulse energies of < 1 µJ at the sample. Pump and probe polarizations were set at magic angle (54.7°). Pump and probe spot sizes were ~500 µm at the sample.

The sample was flowed through a 1 mm path length cell (Harrick Scientific) with a 2 mm thick BaF₂ front window and 2 mm thick CaF₂ back window. After the sample, probe pulses were dispersed by a spectrometer and detected on a shot-by-shot basis with a 32-element linear MCT detector array (Infrared Systems Development Corporation). A reference beam, split from the probe beam and directed through the sample was monitored on a second 32-element array and used to remove probe pulse fluctuations. At each time delay, reference-normalized spectra recorded with and without the pump pulse were averaged separately and ratioed. Induced absorbance changes (ΔA) in the transient absorption difference spectra were calculated as the negative logarithm of the ratioed spectra. The spectral resolution was ~8 cm⁻¹.

3. Computational methods

Infrared spectra of gas-phase thymine and thymidine in their singlet ground states and lowest triplet states were calculated using the B3LYP density functional [26,27] with a variety of basis sets. (The PBE0 functional [28,29] affords qualitatively similar results.) Time-resolved infrared spectra are simulated as the difference between triplet and singlet infrared absorption cross sections, which are obtained from scaled harmonic frequencies broadened by the instrument resolution, as described in the next section. The gross features of the TRIR spectrum are reproduced using B3LYP in conjunction with various basis sets (e.g., 6–311++G** and aug-cc-pVDZ). All calculations used the SG-1 quadrature grid [30]. All triplet calculations are nearly free of spin contamination, with $\langle {\widehat{S}}^2\rangle =2.01$ at the optimized geometries of both triplet thymine and triplet thymidine.

All calculations were performed using Q-Chem [31], which includes version 5.0 of the NBO program of Weinhold and co-workers [32]. The MolDen program [33] was used for visualization.

4. Results

4.1. Steady-state FTIR spectra

Steady-state FTIR spectra of thymine (see Fig. 1 for chemical structures and atom numbering of thymine and its 2’-deoxyribonucleoside thymidine) in acetonitrile-d₃ show strong peaks at 1723 and 1683 cm⁻¹ (Fig. 2 and Table 1). The vibrational modes responsible for these peaks will be referred to hereafter as the C2=O and C4=O stretching modes, respectively, even though they contain modest contributions from other nuclear motions, as will be discussed later. Smaller amplitude peaks are observed at 1484 and 1421 cm⁻¹. Upon deuteration of the N1 and N3 hydrogen atoms to give thymine-d², these bands shift to 1715 and 1672 cm⁻¹, and an additional peak appears at ~1630 cm⁻¹. In thymidine, the carbonyl stretching modes are more closely spaced, appearing at 1691 and 1709 cm⁻¹. A small shoulder is present near ~1650 cm⁻¹. In both thymine and thymidine, several low amplitude peaks are found between 1300 and 1500 cm⁻¹. Peak assignments are discussed in section 5.

Fig. 1.

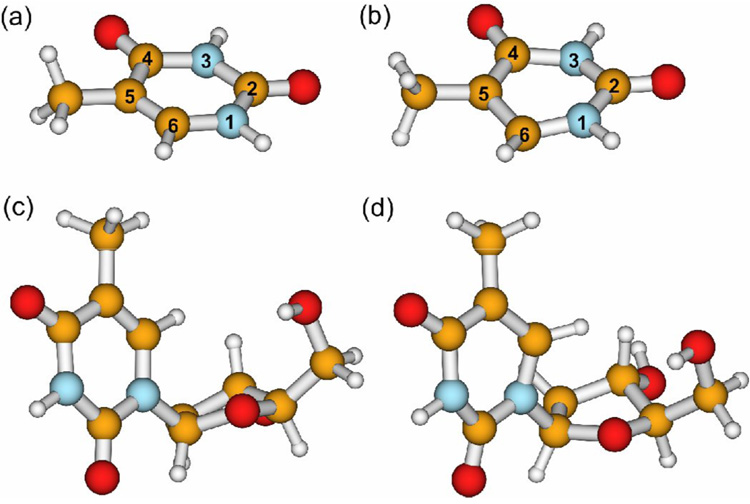
Optimized geometries for (a) the singlet ground state of thymine, (b) the lowest triplet state of thymine, (c) the singlet ground state of 2′-deoxythymidine, and (d) the lowest triplet state of 2′-deoxythymidine. Atom color scheme: nitrogen, blue; oxygen, red: carbon, orange; hydrogen, white. The conventional numbering system for the ring atoms is shown in (a) and (b); other atoms are labeled by the ring atom to which they are bonded.

Fig. 2.

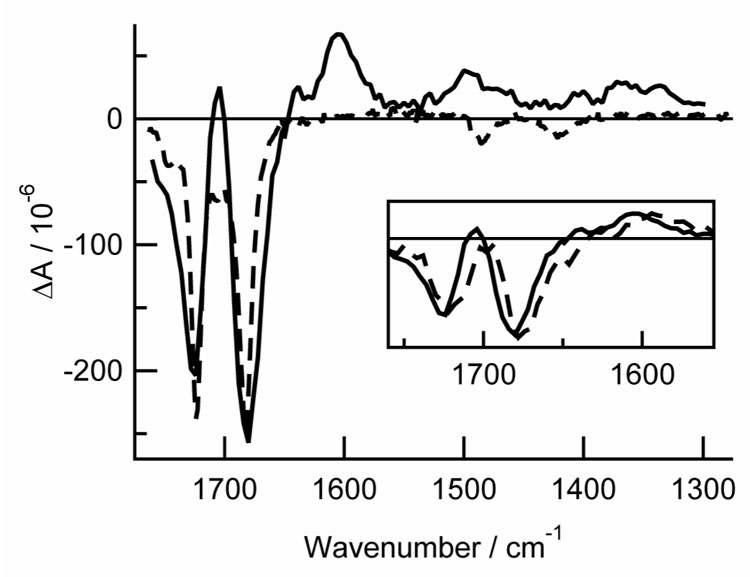
TRIR spectrum of thymine in argon-purged acetonitrile-d₃ at a delay of 0 − 1 µs (solid curve). Also shown is the inverted and scaled steady-state IR absorption spectrum (dashed curve). The inset compares the TRIR spectra of thymine (solid) and thymine-d₂ (dashed) at the same time delay.

Table 1.

Carbonyl stretch frequencies (in cm⁻¹) in the ground and lowest triplet excited states for thymine, thymine-d₂, and thymidine in various solvents

		Ground state				Triplet
		Gas phasea	H2Ob	D2O	CD3CN	CD3CN
Thymine	C2=O	1772	1704		1723	~1705
	C4=O	1725	c		1683	1603
Thymine-d2	C2=O			1673b	1715	d
	C4=O			1627b	1672	1590
Thymidine	C2=O			1661e	1709	d
	C4=O			1630e	1691	1603

^aFrom Ref. [36].

^bFrom Ref. [37].

^cObscured by solvent band.

^dObscured by ground state bleaches.

^eThymidine-d₃ in D₂O.

4.2. Nanosecond TRIR experiments

Bleaches are observed at the steady-state peak positions for thymine and thymidine in acetonitrile-d₃ immediately after UV excitation (Fig. 2 and Fig. 3). Only a single broad bleach band is observed for thymidine near 1700 cm⁻¹ (Fig. 3) because the resolution of the ns TRIR spectrometer (~16 cm⁻¹) is comparable to the separation between the two peaks seen in the FTIR spectra. A weak positive band appears at 1705 cm⁻¹ in thymine, but is not seen in thymidine due to overlap of the two ground state carbonyl bands. A broad positive band at 1603 cm⁻¹ is a prominent feature in the transient difference spectrum in both thymine and thymidine.

Fig. 3.

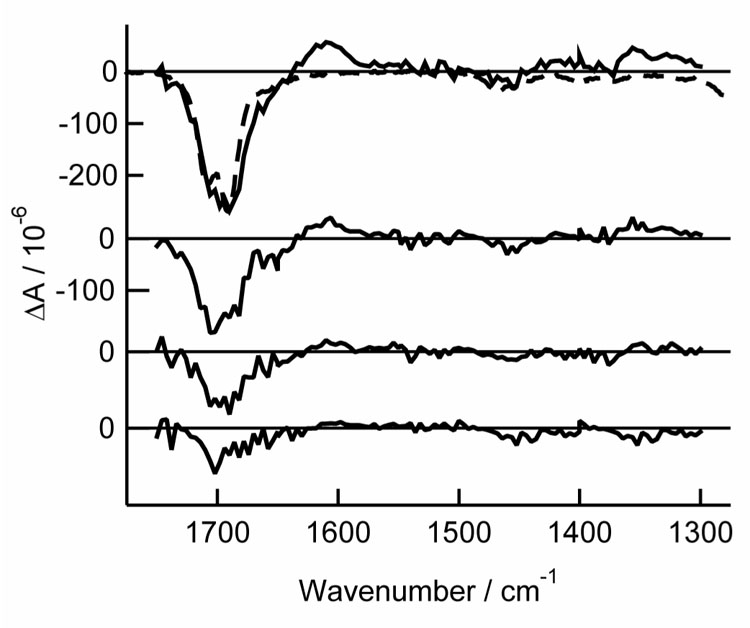
TRIR spectra of thymidine in argon-purged acetonitrile-d₃ at delays of, from top to bottom: 0 – 1 µs, 1 – 2 µs, 2 – 3 µs, and 3 – 4.5 µs. Also shown is the inverted and scaled steady state spectrum (dashed line).

A broad region of positive amplitude is present from 1300 cm⁻¹ to 1400 cm⁻¹ in both thymine and thymidine in acetonitrile-d₃ (Fig. 2 and Fig. 3). A small amplitude peak is seen at 1494 cm⁻¹ in thymine. At long delays, small residual bleaches are visible at ~1390 cm⁻¹ in thymine. The thymine-d₂ ns TRIR spectra (Fig. 4) are similar to those recorded for thymine, but the bands are slightly red shifted (see Fig. 2 inset and Table 1). A positive band appears at 1590 cm⁻¹, and bleaches are seen at 1674 and 1721 cm⁻¹.

Fig. 4.

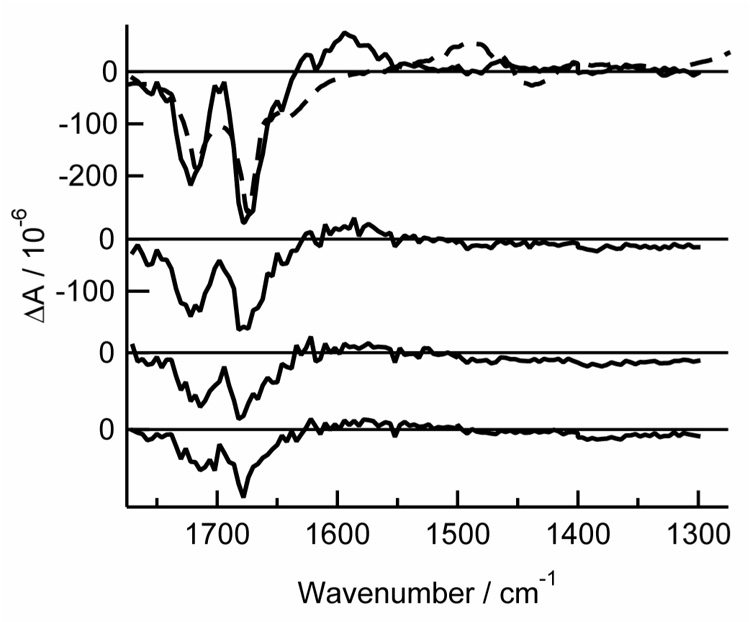
TRIR spectra of thymine-d₂ in argon-purged acetonitrile-d₃ at delays of (from top to bottom): 0 – 1 µs, 1 – 2 µs, 2 – 3 µs, and 3 – 4.5 µs. Also shown is the inverted, scaled FTIR spectrum (dashed line). The positive feature in the FTIR spectrum at ~1500 cm⁻¹ is an artifact of baseline subtraction.

Kinetic traces are shown at 1380, 1604, 1682 and 1704 cm⁻¹ for thymine in acetonitrile-d₃ in Fig. 5. These transient signals were globally fit to a single exponential decay with a lifetime of 0.56 ± 0.03 µs (2 σ) and a frequency-dependent offset to account for the residual bleaches seen at the longest delay times. Upon oxygenation, all of the transient features disappear.

Fig. 5.

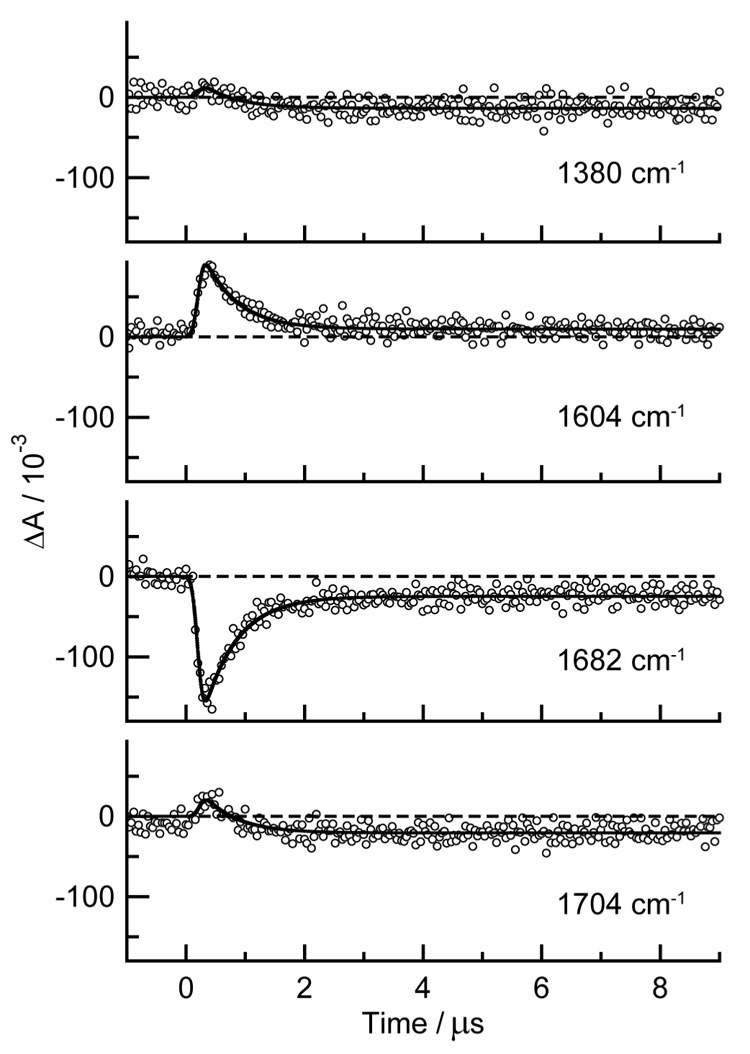
Nanosecond kinetic decays of thymine in argon-purged acentonitrile-d₃ following excitation at 266 nm and probed at the indicated frequencies. Solid lines are from a global fit to the data.

4.3. Femtosecond TRIR experiments

Femtosecond TRIR experiments were conducted at probe frequencies between 1550 and 1650 cm⁻¹ in order to observe the short-time dynamics of the 1600 cm⁻¹ band. Transient kinetic decays are shown in Fig. 6. Negative signals occurring just before time zero are due to perturbed free-induction decay [34]. A strong but short-lived positive spike occurs around zero time delay at all probe frequencies due to the optical Kerr effect in the cell windows and/or the solvent [35]. Since this signal is present only while pump and probe pulses are temporally overlapped, it provides a measure of the instrument response time, which we estimate to be ~450 fs (FWHM).

Fig. 6.

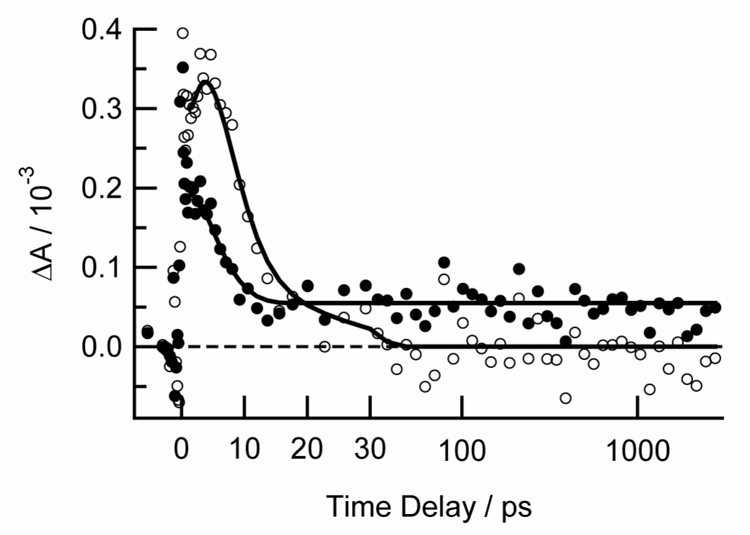
Transient kinetics of thymine following excitation with a femtosecond pump pulse at 270 nm in air-saturated acetonitrile-d₃ at 1602 cm⁻¹ (solid circles) and 1628 cm⁻¹ (open circles). Delay times after 30 ps are shown on a logarithmic scale. Sold lines are provided to guide the eye.

At delays between 0 and 10 ps, the signal is dominated by a broad positive absorption band initially centered at ~1640 cm⁻¹. This band subsequently narrows, shifts to higher frequencies and decays away by 30 ps. Due to these complex spectral dynamics, the transient absorption signal at 1628 cm⁻¹ rises to a maximum at 5 ps and decays to zero by 30 ps, while the signal measured at 1602 cm⁻¹ rapidly decays from its initial amplitude to a small offset by 10 ps. This offset it due to the presence of another much weaker band centered at 1600 cm⁻¹. This band shows no change in intensity or spectral shape from 10 to 2800 ps within signal-to-noise. As shown in Fig. 7, this band shows excellent agreement with the 1603 cm⁻¹ band observed in the ns TRIR measurements on thymine in acentonitrile-d₃.

Fig. 7.

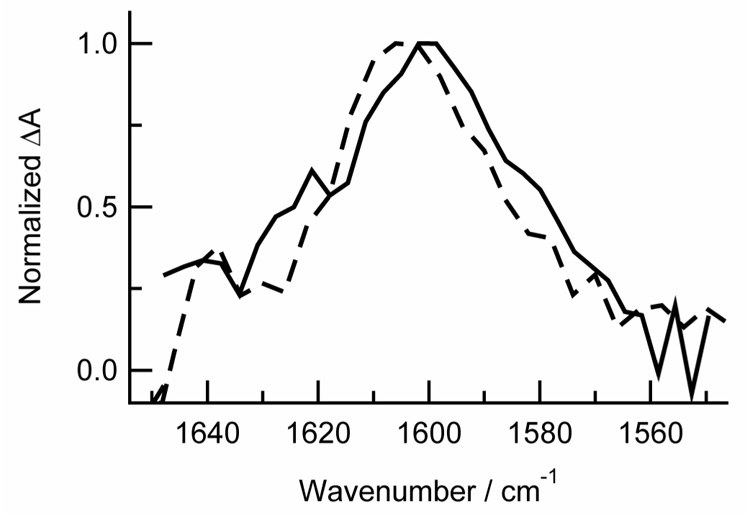
Transient spectra of thymine following excitation at 270 nm in air-saturated acetonitrile-d₃ from 30 – 2800 ps (solid line). The spectrum from Fig. 1 from 0 – 1 µs is shown for comparison (dashed line).

4.4. In silico IR spectra

TRIR spectra were simulated using density-functional calculations by taking the difference between triplet and singlet infrared absorption cross sections. These cross sections are obtained by first scaling the calculated harmonic frequencies by 0.96 (see below), then broadening the resulting stick spectra with 16 cm⁻¹ Lorentzians, corresponding to the resolution of the ns TRIR spectrometer. Both B3LYP/6-311++G** and B3LYP/aug-cc-pVDZ calculations for thymine reproduce the relative intensity pattern seen experimentally, but the latter choice of basis set is not feasible in the case of thymidine. To make a consistent comparison, we calculate TRIR spectra for both molecules at the B3LYP/6-311++G** level. (Harmonic frequencies for thymine in other basis sets are listed in Table 2.) The scaling factor of 0.96 was chosen so that the most intense bleach feature in thymine appears at 1683 cm⁻¹, its location in the experimental spectrum. The same scaling factor was used for thymidine. This scaling approximately accounts for both anharmonicity and for solvent-induced frequency shifts, permitting meaningful comparison of spectra calculated in the gas phase with ones measured in acetonitrile. Because the solvent is aprotic, we do not expect any large, mode-specific shifts upon solvation, and uniform scaling is anticipated to be a reasonable approximation.

Table 2.

Unscaled B3LYP harmonic frequencies (in cm⁻¹) and intensities (in parentheses, in km mol⁻¹) for the carbonyl stretching modes in thymine and thymidine

		Singlet ground state		Lowest triplet state
Molecule	Basis set
		C2=O	C4=O	C2=O	C4=O
thymine	aug-cc-pVDZ	1786 (772)	1741 (629)	1759 (518)	1611 (139)
thymine-d2a	aug-cc-pVDZ	1771 (604)	1730 (784)	1740 (491)	1597 (139)
thymine	aug-cc-pVTZ	1788 (748)	1744 (633)
thymine-d2a	aug-cc-pVTZ	1775 (578)	1732 (795)
thymine	6-311++G**	1798 (811)	1751 (652)	1771 (561)	1619 (167)
thymine-d2a	6-311++G**	1784 (634)	1751 (820)	1754 (531)	1604 (183)
thymidine	6-311++G**	1771 (613)	1749 (783)	1753 (470)	1633 (231)
thymidine-d3b	6-311++G**	1767 (452)	1736 (953)	1745 (447)	1619 (255)

^aIsotopomer deuterated at the N1 and N3 hydrogens

^bIsotopomer deuterated at the N3 hydrogen and both hydroxyl groups of the ribosyl moiety

Figs. 8(a) and 8(b) illustrate the absorption cross sections for singlet and triplet thymine that are obtained from scaled and broadened B3LYP/6-311++G** harmonic frequencies. The difference in these cross sections gives the TRIR spectrum shown in Fig. 8(c). A large number of bands in the 1000–1550 cm⁻¹ region, corresponding mostly to N–H and C–H in-plane bends coupled to CH₃ umbrella-type motions, are observed to shift between singlet and triplet, but since none of these modes has a large infrared intensity, the predicted TRIR signal is weak. Collectively, these modes are probably the source of the broad, low-intensity band that covers essentially the entire region below 1600 cm⁻¹ in the experimental transients. This region of the spectrum does not appear to provide useful markers that can distinguish singlet from triplet. The only high-contrast features that are useful in this respect appear in a narrow window between 1600 and 1800 cm⁻¹. Thus, these calculations suggest that the carbonyl stretches are the only significant marker bands for the triplet. Table 2 lists the calculated harmonic frequencies for the carbonyl stretches in singlet and triplet thymine and thymidine.

Fig. 8.

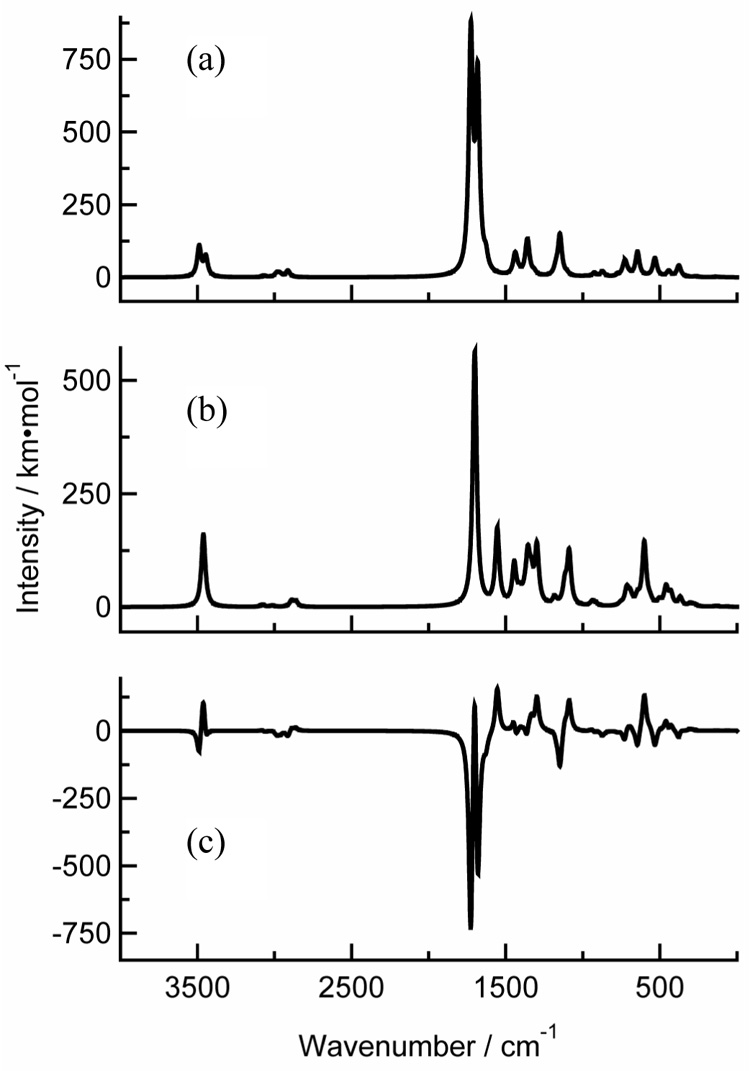
B3LYP/6-311++G** infrared spectra of gas-phase thymine: (a) the singlet ground state, (b) the lowest triplet state, and (c) triplet spectrum minus the singlet spectrum.

In Figs. 9(a) and 9(b), we plot the calculated TRIR spectra thymine and thymidine, respectively, in the carbonyl stretching region. The thymine spectra reproduce the experimental observations very well, thus validating the vibrational assignments put forth in the next section. The calculated spectrum for thymidine correctly predicts the absence of a second feature having a positive offset.

Fig. 9.

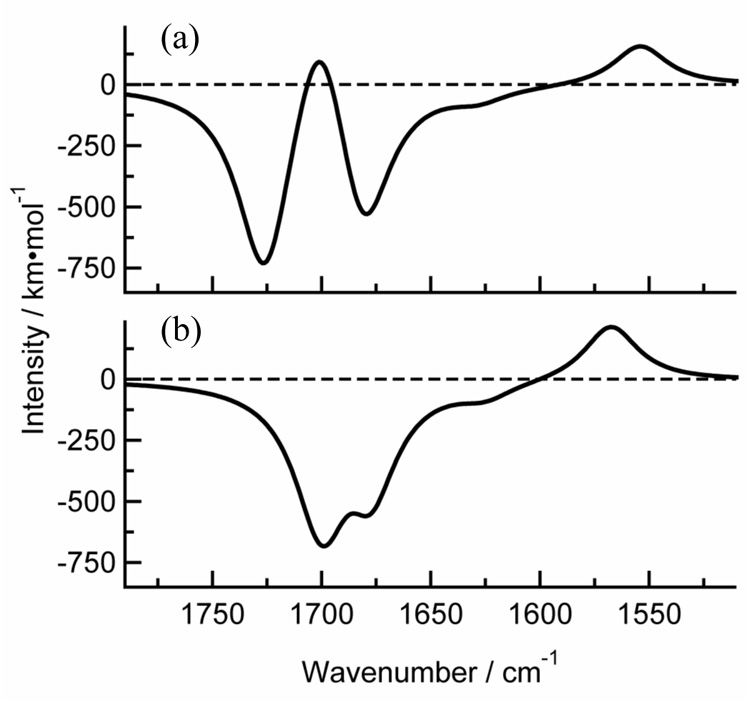
The TRIR spectrum (difference between triplet and singlet infrared absorption cross sections) calculated at the B3LYP/6-31++G** level for (a) thymine, and (b) thymidine.

5. Discussion

5.1. Mode assignments in the electronic ground state

Ground state vibrational spectra of thymine and thymidine in acetonitrile have not been published previously, to the best of our knowledge, so we discuss here the main differences with previously reported spectra. The bands at 1723 cm⁻¹ and 1683 cm⁻¹in thymine are assigned to the C2=O and C4=O carbonyl stretches, respectively. These bands appear at 1772 and 1725 cm⁻¹ in the gas phase [36], and the C2=O stretch is observed at 1704 cm⁻¹ in H₂O solution [37]. Strong bands seen at 1737 cm⁻¹ and 1673 cm⁻¹ in polycrystalline thymine at 15 K [37] are in very good agreement with the frequencies measured here in acetonitrile. Similarly, the ground state carbonyl stretch frequencies of thymine-d₂ agree best with the spectrum of a polycrystalline sample [37].

In thymine-d₂, the N1 and N3 hydrogen atoms of thymine are replaced by deuterium atoms, resulting in red shifts of 8 and 11 cm⁻¹ for the ground state C2=O and C4=O stretching fundamentals, respectively (Table 1). In thymidine, a red shift is also seen for the C2=O stretch compared to thymine, but the C4=O stretch shifts to higher frequency, bringing the two carbonyl bands close together in the deoxyribonucleoside. These observations clearly show that the C=O stretches are not strictly local modes. Indeed, they cannot be since elongation of the C=O bonds must be accompanied by some other compensatory distortion in order that the molecule’s center of mass remains fixed.

The shifts in carbonyl stretching frequencies with deuterium and ribosyl substitution can be understood on the basis of the calculations. Normal mode analysis reveals that the carbonyl stretches are strongly coupled to the N–H (or –D) bends, but basically decoupled from all other motions, as previously reported [24,38]. The C2=O motion is strongly coupled to both the N1–H and N3–H bends in the case of thymine, while for thymidine the C2=O bend is coupled to the N3–H bend and (to a lesser extent owing to the increased mass) the in-plane bend of the N1–C glycosidic bond. The increased mass of the N1–ribosyl moiety, relative to N1–H, explains why the C2=O stretch in thymidine exhibits the smallest of the deuterium-induced red shifts (see Table 1). For both thymine and thymidine, the C4=O stretch is coupled to the N3–H bend. Replacement of H by D lowers the frequency of a given in-plane bend mode, leading to a reduction in the carbonyl stretch frequencies coupled to that bend.

5.2. Assignment of bands observed in ns TRIR spectra to the lowest triplet state

The positive bands in the ns TRIR spectra are assigned to the lowest triplet state (a ³ππ* state) of the thymine derivatives studied based on their microsecond lifetimes and their complete disappearance upon exposure to oxygen. In acetonitrile solution, the lowest triplet state of thymine is quenched at a rate of 0.6 × 10⁹ M⁻¹ s⁻¹ by thymine ground state molecules [22]. When this self-quenching rate is used with our thymine concentration of 3 mM and the intrinsic triplet decay rate of 1.0 × 10⁵ s⁻¹ [22], a triplet lifetime of 0.53 µs is calculated. The excellent agreement with the observed lifetime of 0.56 ± 0.03 µs from the traces in Fig. 5 confirms assignment of the positive bands in the ns TRIR measurements to the lowest triplet electronic state.

The complete disappearance of these bands when the solution is exposed to oxygen further confirms that these are triplet bands. Assuming a diffusion-limited rate of reaction with oxygen (2 × 10¹⁰ M⁻¹ s⁻¹ [39,40]), which is present in air-saturated acetonitrile at a concentration of 2.42 mM [41], and using the previous rates for self-quenching and triplet decay, a triplet lifetime of ~20 ns is calculated. This lifetime indicates why triplet detection requires argon purging in the nanosecond, but not in the femtosecond experiments.

5.3. Assignment of carbonyl stretch frequencies in the lowest triplet state

The excellent agreement between the calculated difference spectrum in Fig. 9(a) and the experimental spectrum in Fig. 2 allows us to make vibrational mode assignments in the triplet state with confidence. The band seen at ~1603 cm⁻¹ for thymine and thymidine, which is the largest positive feature in the ns TRIR spectra, is assigned to the C4=O stretch. The small positive band at ~1705 cm⁻¹ between the strong ground state bleaches is assigned to the C2=O stretch of triplet thymine. The corresponding thymidine band is masked by bleaching of the closely spaced ground-state carbonyl bands.

The calculated harmonic frequencies for isolated thymine are systematically higher than experimental results in solution. The harmonic approximation is the primary cause of this discrepancy, though solvent effects may also contribute. Just as the ground state carbonyl stretch bands shift to lower frequency in solution (see Table 1)[42], red shifts are expected for the triplet bands. Preliminary density-functional calculations on uracil–(H₂O)₄ indicate a 20–30 cm⁻¹ red shift in both C=O stretching frequencies, for both the singlet and triplet states. Calculations by Zhang et al. for thymine solvated by explicit water molecules show a 30 cm⁻¹ red shift when one water molecule is hydrogen bonded to the oxygen of either carbonyl [43]. Calculations taking solvation by acetonitrile into account are not yet available, so we simply scaled the isolated molecule frequencies in calculating the theoretical difference spectra for comparison with experiment, as discussed above.

The triplet state C4=O stretch is seen in Table 1 to red shift by 13 cm⁻¹ on going from thymine to thymine-d₂. This change is similar to the 11 cm⁻¹ red shift seen for this mode in the electronic ground state. According to the calculations, the degree of local mode character is similar in both the singlet ground state and the triplet state. Thus, coupling to in-plane bends can explain this red shift in the triplet state as discussed earlier for the ground state.

The triplet states of both thymine and thymidine are characterized by a substantial red shift in the C4=O stretch, both in the gas-phase calculations and the experiments in acetonitrile. This substantial shift to lower frequency parallels the shift seen previously for the triplet state of an aromatic carbonyl compound [44]. Our B3LYP calculations (and also those of Zhang et al. [43]) predict a 125 cm⁻¹ shift for gas-phase thymine, based on scaled harmonic frequencies. At the PBE0/aug-cc-pVDZ level this shift is reduced to 111 cm⁻¹, which is still larger than the experimental red shift of 80 cm⁻¹ in acetonitrile. Nonetheless, calculated TRIR spectra qualitatively agree with experiment at all levels of theory explored here.

Natural bond orbital (NBO) analysis [45] clarifies the origin of this red shift. An NBO calculation (B3LYP/6-31++G**) on triplet thymine reveals substantial delocalization of the two unpaired electrons nominally associated with C5 and C6. These two atoms possess natural spin densities (differences between α and β natural populations [46]) of 0.66 and 0.74 unpaired electrons, respectively, while O2, O4, and N1 have spin densities of 0.08, 0.25, and 0.19 unpaired electrons, respectively. These five atoms account for 1.84 of the two unpaired α-spin electrons, and no other atom exhibits a spin density of more than ±0.04 electrons.

A detailed analysis of the NBOs leads to the following description of the π-electron rearrangement that accompanies relaxation of triplet thymine from the Franck-Condon geometry of the singlet state to the minimum-energy triplet geometry. First, the β electron from the N1 lone pair partially delocalizes toward C6, reducing the spin density on the latter while incurring a positive spin density on the former. Second, the unpaired α electron at C5 partially delocalizes toward C4, thus reducing the spin density at C5. This causes a significant fraction of the α electron of the C4–O4 π bond to localize into a p orbital on O4, leaving a C4–O4 single bond with partial C4=C5 double-bond character. In other words, NBO analysis predicts that the minimum-energy triplet geometry is characterized by a substantial contribution from an enol-like resonance structure with a C4=C5 double bond and a C4–O4 single bond. This does not imply that a hydrogen atom has transferred to O4; the diketo form of thymine is still the most stable tautomer in the triplet state [47]. Rather, our analysis suggests that the electronic structure of the triplet diketo tautomer is characterized by significant contribution from a Lewis structure consisting of a formal C4=C5 double bond and an O4 radical. Differences in the minimum-energy geometries of the singlet and triplet states, as summarized in Table 3, support this contention: the C4–C5 bond contracts by 0.036 Å in the triplet state, and the C4–O4 bond lengthens by 0.015 Å, explaining the substantial red shift in the C4=O stretching frequency.

Table 3.

Selected bond lengths (r, in Å) and dihedral angles (ϕ, in degrees) of thymine at the B3LYP/aug-cc-pVTZ level in the indicated electronic states

Parameter	Ground State	Triplet state
r(C2–O)	1.213	1.214
r(C4–O)	1.216	1.231
r(C4–C5)	1.464	1.428
r(C5–C6)	1.346	1.493
r(N1–C6)	1.376	1.381
ϕ(H6–C6–N1–H1)	0.0	20.6
ϕ(C4–C5–C6–H6)	180.0	163.6
ϕ(C6–N1–C2–N3)	0.0	7.9
ϕ(C5–C6–N1–C2)	0.0	−20.2

5.4. Triplet state dynamics

After the triplet state has decayed away in the ns TRIR experiments (Fig. 5), residual bleaches are still seen at the ground-state carbonyl frequencies. This could indicate photoproduct formation. Dimer marker bands reported recently in D₂O [16] are unlikely to be observed here, however, due to their weak absorption and the low photodimer yields (< 0.01) observed in acetonitrile [14,48,49].

The comparison in Fig. 7 shows that the same triplet C4=O stretch mode seen on the microsecond time scale is detected at short times in the femtosecond experiments. The transient at 1603 cm⁻¹ in Fig. 6 indicates that 1) this band is present 10 ps after UV excitation, and 2) does not grow in at later times. Both observations extend our previous conclusion about prompt triplet formation in 1-cyclohexyluracil [10] to thymine. The lifetime of the ¹nπ* state of the former compound is in the ns range in acetonitrile, and a similar lifetime is reasonable for thymine. In this case, it is very likely that the triplet state of thymine cannot be formed from the relaxed ¹nπ* state, just as in 1-cyclohexyluracil [10].

Unfortunately, it is impossible to determine precisely when the triplet is formed because the triplet band of thymine is obscured by a larger amplitude band at delay times below 10 ps. This larger amplitude band narrows, shifts to higher frequency, and completely decays by 30 ps after excitation. Such behavior is characteristic of molecules undergoing vibrational cooling [50], and we assign this band to vibrationally excited S₀ molecules, which are produced in high yield (~60% [9]) by internal conversion. Vibrational cooling by the nucleic acid base derivatives 9-methyladenine and N1-cyclohexyluracil in acetonitrile occurs with time constants of 13.1 ps [51] and 9.1 ps [10], respectively, consistent with the observed dynamics. An alternative assignment to an excited electronic state of thymine can be ruled out because the ¹ππ* state is too short-lived (τ < 1 ps [1]) and both the ¹nπ* state (τ ≈ 3 ns for the closely related pyrimidine derivative N1-cyclohexyluracil in acetonitrile [10]) and the ³ππ* state (estimated to be ~20 ns in air-saturated acetonitrile, vide supra) are too long-lived.

Exactly how the triplet state is populated in DNA and RNA bases is uncertain. Because spin-orbit coupling is largest for singlet and triplet states of different spatial symmetry [52,53] it has been suggested that ISC to the lowest energy ³ππ* state does not occur directly from the ¹ππ* state, but proceeds instead via the optically dark ¹nπ* state [9,10,23]. The ¹nπ* lifetime of N1-cyclohexyluracil varies between 30 ps in aqueous solution to ~3 ns in acetonitrile [10]. It was concluded on the basis of femtosecond transient electronic spectroscopy that the triplet state of 1-cyclohexyluracil is populated in several ps after UV excitation [10]. In order to reconcile rapid triplet formation with the long lifetime of the ¹nπ* state, it was proposed that ISC occurs mainly from the vibrationally unrelaxed ¹nπ* state [9].

A second possibility is that ISC occurs directly from the ¹ππ* state to a ³nπ* state followed by near-barrierless internal conversion within the triplet manifold to the ³ππ* state. Recent high level quantum calculations by Climent et al. on uracil have argued for the second mechanism based on the location of a singlet-triplet crossing between the ¹ππ* and ³nπ* states along the minimum energy pathway between the Franck-Condon region and a conical intersection between the ¹ππ* state and S₀ [54]. Rapid ISC is required in this model as well, in order to compete with the ultrafast nonradiative decay of the ¹ππ* state. The IR spectrum of the triplet on the microsecond time scale can only be the ³ππ* state. The fact that this same spectrum is observed ~10 ps after photoexcitation makes it less likely that the lowest triplet state is populated by way of the ³nπ* state.

6. Conclusion

We have measured the vibrational spectra of the triplet states of thymine, dideuterated thymine, and 2′-deoxythymidine from 1300 to 1800 cm⁻¹ for the first time. On the basis of density-functional calculations, two prominent peaks in the carbonyl-stretching region are assigned. On the basis of these peaks, it is possible to distinguish the singlet state from the triplet state, primarily because the C4=O stretch in the triplet state red shifts by approximately 80 cm⁻¹ in acetonitrile (~68 cm⁻¹ in the gas phase) owing to a substantial electronic-structure contribution from an enol-like Lewis structure. Importantly, our fs TRIR results show that the triplet state of thymine and thymidine is formed in ≤ 10 ps in acetonitrile solution. Our results can aid further computational efforts to fully describe the triplet states of DNA monomers. Additionally, the prominent C4=O stretch of the triplet state can be used in the future to investigate intersystem crossing in DNA base multimers.