Skip to main content
NCBI home page
RNA logoLink to RNA
. 2009 Dec;15(12):2195–2205. doi: 10.1261/rna.1747509

Do conformational biases of simple helical junctions influence RNA folding stability and specificity?

Vincent B Chu 1, Jan Lipfert 2, Yu Bai 3, Vijay S Pande 4, Sebastian Doniach 5, Daniel Herschlag 6
PMCID: PMC2779674  PMID: 19850914

Abstract

Structured RNAs must fold into their native structures and discriminate against a large number of alternative ones, an especially difficult task given the limited information content of RNA's nucleotide alphabet. The simplest motifs within structured RNAs are two helices joined by nonhelical junctions. To uncover the fundamental behavior of these motifs and to elucidate the underlying physical forces and challenges faced by structured RNAs, we computationally and experimentally studied a tethered duplex model system composed of two helices joined by flexible single- or double-stranded polyethylene glycol tethers, whose lengths correspond to those typically observed in junctions from structured RNAs. To dissect the thermodynamic properties of these simple motifs, we computationally probed how junction topology, electrostatics, and tertiary contact location influenced folding stability. Small-angle X-ray scattering was used to assess our predictions. Single- or double-stranded junctions, independent of sequence, greatly reduce the space of allowed helical conformations and influencing the preferred location and orientation of their adjoining helices. A double-stranded junction guides the helices along a hinge-like pathway. In contrast, a single-stranded junction samples a broader set of conformations and has different preferences than the double-stranded junction. In turn, these preferences determine the stability and distinct specificities of tertiary structure formation. These sequence-independent effects suggest that properties as simple as a junction's topology can generally define the accessible conformational space, thereby stabilizing desired structures and assisting in discriminating against misfolded structures. Thus, junction topology provides a fundamental strategy for transcending the limitations imposed by the low information content of RNA primary sequence.

Keywords: electrostatics, folding, junctions, thermodynamics

INTRODUCTION

The diverse biological functions of many RNAs derive from their specific, three-dimensional folds. For example, structured RNAs can excise introns from RNA transcripts (self-splicing introns), catalyze the formation of peptide bonds (ribosomes), and regulate gene function through specific binding of small metabolites (riboswitches) (Simons and Grunberg-Manago 1998; Mandal and Breaker 2004). The folding of these complex RNAs has been investigated by an array of biochemical and biophysical techniques. This extensive body of research has gradually uncovered folding behavior common to many RNAs, revealing the existence of multiple folding intermediates and distinct folding channels that suggest the existence of rugged energy landscapes for folding (Pan et al. 1999; Treiber and Williamson 1999; Thirumalai et al. 2001; Russell et al. 2002; Chu and Herschlag 2008).

Understanding RNA's diverse behavior and function—its folding, conformational motions, and interactions with proteins—will require dissecting this energy landscape in detail and comprehending the basic physical forces at play. Thankfully, features intrinsic to RNA allow us to simplify our conception of RNA structure, providing an intuitive foundation for initiating analysis. In particular, RNA structure is substantially hierarchical; the great stability of RNA helices largely decouples the formation of secondary and tertiary structures, often allowing analysis of folding as beginning from a state composed of pre-formed secondary structure (Brion and Westhof 1997). In this view, folding is the thermodynamically driven transition from a disordered ensemble of helices and junctions to a folded ensemble where the helical domains are closely packed and tertiary interactions stabilize the overall structure.

RNA folding is governed by the balance of basic physical forces that help or hinder folding (Takamoto et al. 2004; Chu and Herschlag 2008; Chu et al. 2008). Repulsive electrostatic forces between the negatively charged phosphate moieties push the helices apart, favoring the extended and collinear helical configurations of the unfolded ensemble. In sufficient concentrations, solution counterions greatly reduce this electrostatic penalty, allowing the motif to “relax” and gradually adopt more folded configurations, where the helices are arranged side by side (Russell and Herschlag 2001; Russell et al. 2002; Das et al. 2003; Koculi et al. 2004; Bai et al. 2005). Opposing electrostatic repulsion, tertiary interactions formed from the dense tangle of hydrogen bonds and stacking interactions between specific regions on the helices, loops, and junctions can act as the “molecular glue” that, in conjunction with the junction, stabilize the folded structure (Tamura et al. 2004).

Additionally, RNA folding entails the loss of a large amount of conformational entropy and the discrimination of the folded state from the astronomically large number of alternative chain configurations (Zwanzig et al. 1992). Even after formation of secondary structure, which substantially reduces the space of possible chain configurations, RNAs must pair specific helical regions to form native tertiary contacts, even when faced with multiple alternative pairings. A further complication is that RNAs must make do with only the sparse information content of their four, relatively similar constituent nucleotides (Herschlag 1995).

In the hierarchical model, helix–junction–helix (HJH) motifs, composed of two helices joined by a flexible intervening junction, are the basic and ubiquitous building blocks of RNA structure. Probing the folding behavior of these fundamental motifs, including the entangled effects of electrostatics, tertiary stabilization, and conformational entropy will be a key step in understanding the complicated folding behavior observed in higher-order RNA structures. To establish the basic behavior of a HJH motif, we investigated a tethered duplex model system composed of two 12 base-pair (bp) DNA duplexes joined by either a single-stranded polyethylene glycol (sPEG) or double-stranded (dPEG) polyethylene glycol tether of six monomers (Fig. 1).

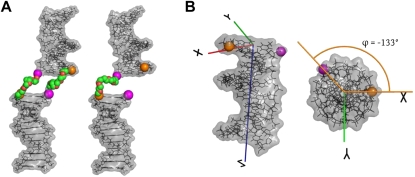
FIGURE 1.

FIGURE 1.

Open in a new tab

(A) Visualization of the dPEG (left) and sPEG (right) HJH constructs. Both constructs are composed of two 12 bp DNA duplexes (colored in gray) and double- or single-stranded PEG junctions of six ethylene–glycol monomers (green and red). The 5′ and 3′ oxygens proximal to the junction are exaggerated and highlighted in magenta and orange, respectively. (B) Angled view (left) and end-on view (right) of the standard orthonormal body frame attached to each helix. The 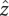Inline graphic axis was chosen to point along the helical axis, while the 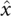Inline graphic axis was chosen to point orthogonally relative to the 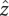Inline graphic axis in the direction of the 3′ oxygen of the terminal residue. 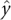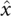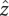The Inline graphic axis was perpendicular to the Inline graphic and Inline graphic axes and computed as Inline graphic. As noted, the polar angle φ subtended by the 5′ and 3′ oxygens is approximately −133°.

We computationally sampled its conformations over a range of solution salt concentrations using stochastic dynamics simulations and Poisson–Boltzmann (PB) calculations, validating our sampling using small-angle X-ray scattering (SAXS) experiments. To these simulations, we added a simple model of a tertiary contact, allowing us to quantitatively parse the free energy of folding into its separate components for a range of different salt concentrations, junction topologies, and tertiary contact locations.

As a model system, the tethered duplex offers instructive and pertinent insights into the behavior of RNA HJH motifs by establishing the behavior of idealized junctions. Its single- and double-stranded junction topologies are shared by a broad class of structured RNAs and its length, with 18 rotatable bonds, is roughly equivalent to a three-nucleotide linker and comparable to junction lengths found in native RNAs. Furthermore, its DNA duplexes are similar to RNA duplexes in both charge distribution and helical geometry. Such similarities enable us to build intuition into how properties like a junction's topology generally affect the conformational ensemble of a HJH motif and the rough magnitude of their effects on the thermodynamics of folding stability and specificity. Subsequent “stepwise” investigations can then assess departures from the idealized PEG junctions introduced by specific sequences, base stacking interactions, specific ion binding, and junction electrostatics (Bai et al. 2005, 2008).

RESULTS

Junction topology strongly restricts and influences the shape of the conformational ensemble

The simple polymer junctions of the dPEG and sPEG constructs allow us to investigate the effects of junction connectivity and topology apart from any idiosyncratic effects introduced by a particular choice of nucleotide sequence. Furthermore, the simple PEG junctions are reliably modeled with existing potentials and the results can be directly compared with experiment (see below) (Bai et al. 2005, 2008).

To understand how junction topologies shape the conformational ensemble of the HJH motif, we perform extensive stochastic dynamics simulations of the dPEG and sPEG constructs (see Materials and Methods). The computational efficiency attained by coarse graining the helices permit us to sample the helical configurations of the tethered duplex more extensively than all-atom simulations. The results show how simple junction topologies influence the shape of the allowed conformational ensembles at equilibrium in the absence of electrostatic effects. We then explore the effects of electrostatics and tertiary contacts by re-weighting the observed conformational ensemble with PB electrostatic calculations and a simple square-well model for the energetics of a tertiary contact.

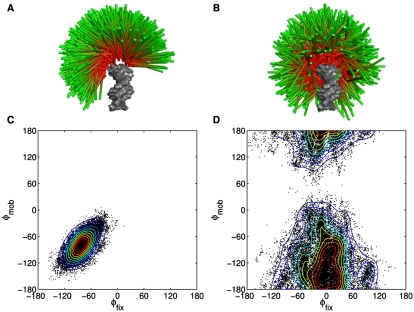
Figure 2, A and B, depicts a small fraction (∼0.33%) of the 299,900 and 290,300 observed conformers for both dPEG and sPEG junctions, respectively. In our analysis, one helix is designated as a “fixed” reference helix; the other is referred to as the “mobile” helix. The difference between the dPEG and sPEG conformational ensembles is striking. The double strands of the dPEG construct restrict the mobile helix to move in a hinge-like fashion, shaping the observed ensemble into a distinctive “Mohawk” pattern that favors bending in a particular direction. The removal of one tether in the sPEG construct allows the mobile helix to move much more freely, relative to the fixed reference helix, resulting in the broader, tilted “umbrella” shape of the observed ensemble, again favoring particular bending directions.

FIGURE 2.

FIGURE 2.

Open in a new tab

Visualization of 1000 randomly selected conformers observed in the dPEG (A) and sPEG (B) simulations. One helix, designated as a “fixed” reference helix, is colored in gray, while the other “mobile” helix is depicted as a cylinder whose radius has been reduced for clarity. The junction atoms have been hidden in this view. The differences between the ensembles induced by the different junctions are obvious; while the dPEG junction largely constrains the helices to a plane, yielding a “Mohawk”-shaped ensemble, the sPEG junction allows the helices to move with greater freedom, resulting in a broad “umbrella”-shaped ensemble. The φ–φ scatter plots reveal the tendency of the dPEG (C) and sPEG (D) junctions to bring different faces of the helices into close proximity. Each black dot represents the φ–φ measure of an individual helical configuration observed during simulation whose interhelical angle is less than 45°. Contours have been added to highlight the density of the distribution and each contour represents a 10% decrease from the maximum density. The dPEG junction tends to bring the −85° face of the fixed helix together with the −85° face of the mobile helix, consistent with a hinge-like motion. Changing the dPEG into a sPEG junction alters this hinge-like motion, makes the distribution broader and brings together the −4° and the −143° faces of the fixed and mobile helices (see also Figs. 1B, 3).

The sPEG and dPEG junctions both introduce strong geometrical constraints that greatly restrict the space of allowed helical conformations that may be explored. These constraints, and in particular, the greater constraints imposed by the double-stranded junction, will have thermodynamic consequences for folding, favoring certain folded conformers relative to a hypothetical situation, where all conformers are equally likely, a conclusion that is strongly supported by the tertiary modeling described below (see the section on junction-induced changes in conformational ensemble impact folding stability and specificity).

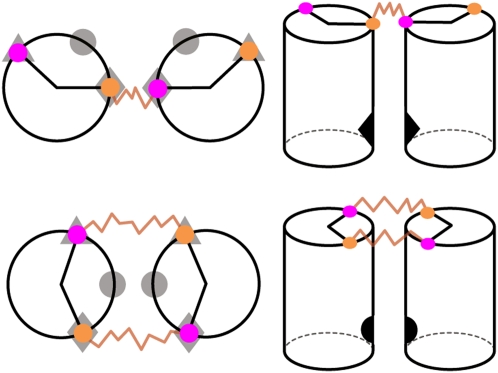
The manifest differences in the shape of the conformational ensemble for the sPEG and dPEG constructs translate into differences in how the two helices approach each other and which parts of the helices tend to be in close proximity. To assist in analysis and visualization of the data, we defined a standard body coordinate frame for each helix (Fig. 1B). In this standard frame, the “φ-face” of a helix refers to the face of the helix located at the polar angle φ; for instance, in our standardized body coordinate system, the 3′ oxygen is located on the 0° face, while the 5′ oxygen is located on −133° face (Fig. 1B). Using this definition of helical faces, we can then define the “φ–φ” measure to indicate which two helical faces are in closest proximity when the helices are in an approximately side-by-side conformation.1 For instance, in the cartoon representations of the dPEG and sPEG constructs (Fig. 3), the φ–φ measures of the sPEG and dEPG constructs are, respectively, (0°,−133°) and (−67°,−67°).

FIGURE 3.

FIGURE 3.

Open in a new tab

Schematic representation of the sPEG (top row) and dPEG (bottom row) HJH motifs in a side-by-side helical configuration. The left column is a view of the HJH motif down the helical axis and the right column is a view from the side. As in Fig. 1B, the 3′ and 5′ oxygens proximal to the junction are respectively, colored orange and magenta. To study folding specificity, tertiary contacts in three separate locations (indicated by ♦, •, and ▴ symbols) were computationally added to the ends of the helices on different helical faces (left column). In the standard body coordinate system, the diamond, circle, and triangle locations are, respectively, on the (0°,−133°), (−67°,−67°), and (−133°,0°) faces (shaded symbols, left panel). The topology of the sPEG and dPEG junctions introduces conformational biases that tend to promote the formation of different tertiary contacts; sPEG junctions promote formation of the diamond contact, while dPEG junctions promote the formation of the circle contact (solid symbols, right column).

The φ–φ distributions exhibited by the dPEG and sPEG constructs are starkly different (Fig. 2C,D). The dPEG construct tends to bring the −85° face of the fixed helix and the −85° face of the mobile helix together. The high concentration of observations in this region (reflected by the narrowness of the distribution) indicates that these two regions are brought together with high specificity, consistent with the hinge-like motion imposed by the constraints of a two-stranded junction (Fig. 2A). The observed symmetry in the distribution across the line φmob = φfix is consistent with expectations.

Changing the double-stranded junction into a single-stranded one drastically remodels the conformational preferences of the helices. In the sPEG construct, the junction has radically shifted preferences, placing the −4° face of the fixed helix and the −143° face of the mobile helix in close proximity much more frequently. In addition to changing the preferred conformations, the distribution has broadened, reflecting the greater conformational freedom afforded by the single-stranded junction. In accordance with expectations, an approximate symmetry in the distribution is noted about the φfix = 0° and φmob = −133° lines.

The conformational biases of the sPEG and dPEG constructs arise naturally from their respective molecular geometries. In retrospect, these biases could have been roughly predicted from simple cartoon depictions of the sPEG and dPEG constructs, taking into account the asymmetric connectivity enforced by the 5′–3′ linkages across the helices (Fig. 3). The sPEG construct's preference to favor one side stems from the off-center attachment of the PEG tether to the 5′- and 3′-oxygen atoms at the edges of the respective helices and is consistent with observations from a previous study (Bai et al. 2008). The dPEG construct's preference to bend in particular directions arises from the fact that its junction's 5′ and 3′ attachment points are not directly across from one another, but subtend an angle of roughly −133° (Figs. 1, 3). Because the same geometrical factors are also present in RNA helices, these conclusions will remain valid in RNA structure.

SAXS probes the electrostatically induced changes in the conformational ensemble

In the absence of electrostatics, the shape of the conformational ensemble is dictated only by the conformational preferences of the junction and the geometry of its connection to its adjoining helices. However, real nucleic acids are highly negatively charged and electrostatic interactions modify the basic shape of the conformational ensemble through electrostatic repulsion. In solution, the presence of positively charged counterions modulates these electrostatic effects. Under low-salt conditions, extended and roughly collinear helical conformations minimize repulsive electrostatic forces; the increased presence of counterions at higher salt concentrations ameliorates this repulsion, allowing the helices to sample more “relaxed conformations” (e.g., bent and side-by-side conformations) (Russell and Herschlag 2001; Russell et al. 2002; Das et al. 2003; Koculi et al. 2004; Takamoto et al. 2004; Bai et al. 2005, 2008).

To capture this salt-dependent effect in our computational model of the tethered duplex, we first computed the probability distribution P(Ω) of observing the helices in any given helical configuration Ω by smoothing the large number of discrete observations accumulated from simulation in the absence of any electrostatics (see Materials and Methods). P(Ω) encodes the conformational preferences of the HJH motif's junction. We then reweighted this distribution with a PB-derived electrostatic interaction function EM(Ω) that expresses the electrostatic cost of assembling the helices in a given configuration Ω. The combination of these two functions allowed us to model the conformational ensemble of the tethered duplex over a wide range of salt conditions and to predict how experimental observables, like its scattering profile, change with solution salt conditions.

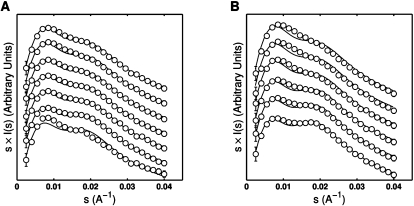
Comparisons between predictions derived from our model and experiments test whether our model has effectively captured the basic physics of the system and and its accuracy. We used SAXS to monitor the salt-induced structural relaxation of model dPEG and sPEG tethered duplex motifs. Figure 4 displays the measured and predicted SAXS profiles for the dPEG and sPEG motifs, plotted in the Holtzer representation of scattering intensity weighted by momentum transfer I ×s versus momentum transfer s (the momentum transfer s is defined as s = 2sin θ/λ, where 2sin θ is the total scattering angle and λ is the X-ray wavelength). Previous studies have shown that the Holtzer representation is sensitive to structural changes in the tethered duplex system; in this representation, the gradual disappearance of the second peak (at roughly s = 0.02 Å−1) indicates that the tethered duplex ensemble is “relaxing” away from the largely collinear configurations populated at low salt concentrations (Bai et al. 2008). The disappearance of the second peak in the sPEG construct is expected to be more pronounced than in the dPEG construct due to the presence of additional scattering density from the second PEG tether and the smaller interhelical separation in the dPEG construct (Supplemental Fig. 2).

FIGURE 4.

FIGURE 4.

Open in a new tab

Comparison between predicted (—) and experimentally measured (○) SAXS profiles for dPEG (A) and sPEG (B) tethered duplex constructs over a range of Na+ conditions (plotted as scattering intensity I(s) weighted by s). Na+ concentrations (from bottom to top) were: 0.016, 0.056, 0.116, 0.416, 0.616, and 1.016 M, with the addition of an additional profile at 0.216 M for dPEG. For clarity, profiles were vertically offset and the number of data points reduced by one-third. Error bars are smaller than symbols for some points. The disappearance of the second peak (roughly located at s = 0.02 Å−1) with increasing salt indicates that the tethered duplex is relaxing in response to the screening of the increased salt concentration.

The basic trend toward increasing structural relaxation is reproduced by the predicted SAXS profiles, including the approximate differences in scattering between the sPEG and dPEG constructs. For both the sPEG and dPEG constructs, the model predicts that the enhanced screening at higher salt concentrations allows the tethered duplex to adopt a greater variety of configurations, including the bent and side-by-side helical configurations largely precluded at low salt concentrations, in agreement with the basic behavior observed in the experimental SAXS profiles.

Nevertheless, there are systematic deviations between the predicted and measured profiles. At every single salt concentration we measured, the second peak in the predicted sPEG and dPEG profiles is more pronounced than in the experimental profiles, indicating that the predicted ensembles are less relaxed than the experimental ensembles. The absence of complicating effects in the tethered duplex beyond the simple conformational preferences of the junction and electrostatic repulsion suggests that the systematic errors likely arose from the smoothing of the stochastic dynamics simulation data and inaccuracies in our electrostatic interaction function EM(Ω).

Obtaining a smoothly varying P(Ω) representing the conformational preferences of the junction by smoothing the simulation data inherently introduces errors into P(Ω). Specifically, any smoothing algorithm will underestimate the likelihood of observing high-probability conformers and overestimate the likelihood of observing low-probability ones (Bowman and Azzalini 1997). Furthermore, the enormous cost of calculating EM(Ω), even with access to modern computer clusters, forced us to make approximations that affected the accuracy of our predictions (see Materials and Methods). The systematic deviations highlight the inherent difficulty of accurately calculating energetics in nucleic acid systems.

Such deviations were not observed in an earlier Monte Carlo study of the tethered duplex (Bai et al. 2008). However, the previous study focused only on reproducing the ensemble average of the scattering profile; this study aims to extend the analysis to the calculation of the free energy of folding, which requires the sampling of a much larger set of conformers and calculation of many more electrostatic energies. Although the agreement between prediction and experiment is not perfect, the calculations reproduce the basic salt-dependent behavior of these fundamental HJH motifs, allowing us to analyze the basic effects introduced by single- and double-stranded junction topologies on the free energy and specificity of folding.

Junction-induced changes in conformational ensemble impact folding stability and specificity

The stark differences in the distribution of helical locations and orientations induced by the junction naturally suggest that junction topology plays a role in determining folding specificity and stability. Our simulations revealed that different junction topologies—without any dependence on sequence—tend to bring different regions of the helices together as a simple consequence of their molecular geometries; such differences should affect the likelihood of interaction between tertiary contacts located on the helices and, thus, the observed stability of the HJH motif. Furthermore, the relatively narrow distribution observed for the dPEG construct (Fig. 2C) supports the notion that it will be much more sensitive to changes in tertiary contact location; i.e., it will fold more specifically. Nevertheless, the energetic scale of such effects could not have been predicted without quantitative modeling of the conformational ensemble.

Although the sPEG and dPEG motifs cannot fold as they lack tertiary contacts, we can nonetheless tackle the question of how junction topology influences folding by computationally adding tertiary contacts and studying the predicted stabilities of the different constructs as solution salt conditions are varied (see Materials and Methods). To do so, we defined three tertiary contact positions, located at the end of each helix and designated by the diamond, circle, and triangle symbols in Figure 3. The two complementary halves of the diamond contact were located on the (0°,−133°) faces of the two helices, and the circle and triangle were, respectively, located on the (−67°,−67°) and (−133°,0°) helical faces. The diamond and circle contacts were deliberately located on the helical faces that simulation (Fig. 2) and a simple visualization (Fig. 3) suggested would be in close proximity for the sPEG and dPEG junction topologies. The triangle contact was chosen to invert the location of the diamond contact.

For simplicity, each tertiary contact was modeled as a square well potential that modified the basic energy landscape defined by P(Ω) and EM(Ω). Helical configurations that placed the two halves of a contact within 7.5 Å, that kept the interhelical angle below 20°, and whose φ–φ measure was within 12° of the tertiary contact location were included in the folded ensemble and stabilized by a constant value. The strength of the contact was tuned to −14.5kBT (1kBT is ∼0.6 kcal/mol), ensuring that the sPEG or dPEG construct was ∼90% folded at 1 M salt with the most stable diamond or circle contact, respectively. Although the strength of the contact determines the extent of folding, the general conclusions of our analysis did not depend on the strength of the contact (data not shown).

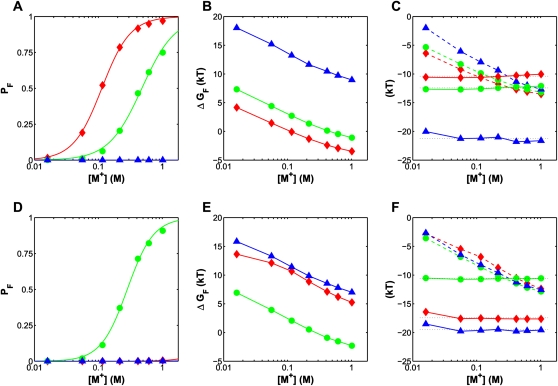
Figures 5 and 6 summarize the simulated folding curves for HJH motifs with sPEG and dPEG junctions and tertiary contacts located in the diamond, circle, and triangle positions. Focusing first on the sPEG motif (Fig. 5A), we find that it is most stable (96% folded at 1 M monovalent salt) when the tertiary contact is located in the diamond position, as predicted (see above). When the contact is rotated by 67° along the helical face to the circle position, the sPEG motif is destabilized (75% folded at 1 M). Moving the tertiary contact by an additional 67° to the triangle position virtually abolishes folding (0.01% folded at 1 M). These changes in stability have nothing to do with changes in tertiary contact strength as it was held constant. Rather, the changes in stability are due entirely to the position of the contact relative to the junction. Heuristically, as the tertiary contact location changes, it moves away from the regions that the junction prefers to bring together, leading to the observed destabilization.

FIGURE 5.

FIGURE 5.

Open in a new tab

Simulated folding of sPEG (top row) and dPEG (bottom row) motifs. Salt-induced folding progress curves, in terms of fraction folded (PF), for HJH motifs with three tertiary contact locations (♦, •, ▴) and sPEG (A) and dPEG (D) junctions. Corresponding values for ΔGfold are plotted in (B) and (E). Values for ΔUfold (- -) and TΔSfold (—) are plotted in (C) and (F). ΔUfold includes a constant contribution from the tertiary contact (−14.5kBT for both junctions). The horizontal black dotted lines in C and F denote the average value of ΔSfold over the range of salt conditions.

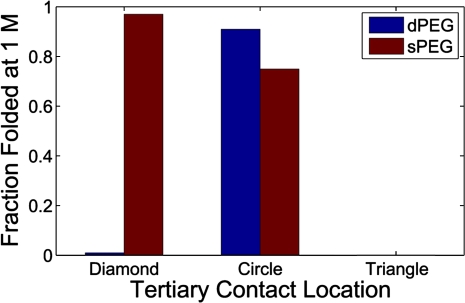
FIGURE 6.

FIGURE 6.

Open in a new tab

Comparison of the fraction folded at 1 M monovalent salt concentration for the different junction topologies and tertiary contact locations. The two junction topologies have different conformational preferences (sPEG prefers the diamond position, dPEG prefers circle) and folding specificities (sPEG is more resilient to changes in tertiary contact location). In actual motifs, the observed specificity would be somewhat reduced because the helices could fray to facilitate tertiary contact formation in regions of conformational space that would otherwise be disallowed (see the text).

The stability of the dPEG motif is even more dependent on the location of the tertiary contact (Fig. 5D). For the dPEG junction, a tertiary contact positioned on the circle location has the greatest stability (90% folded at 1 M salt) due to the enhanced likelihood that the dPEG junction will bring the two halves of the circle location together (Fig. 3). Moving the tertiary contact location by 67° to either the diamond or triangle position drastically destabilizes the dPEG motif (to 0.5% and 0.1% folded, respectively). In comparison, the equivalent 67° change in the sPEG motif (from diamond to circle) only destabilized the motif to 75% folded at 1 M salt; destabilizing the sPEG motif to the ∼0.1% folding level required displacing the tertiary contact location by approximately 133° to the triangle position.

Understanding these changes in stability requires examination of the thermodynamics underlying the free energy of folding ΔGfold:

graphic file with name 2195equ1.jpg

where ΔGfold governs the balance between folded and unfolded forms of the HJH motif and can be decomposed into separate contributions from ΔUfold, the change in internal energy, and TΔSfold, the change in conformational entropy (Equation 1). In our model, ΔUfold is the difference in mean electrostatic interaction energy (ΔUelectrostatic) and tertiary contact stabilization (ΔUtertiary), averaged over the unfolded and folded ensembles; thus, ΔUfold reflects the balance between these two opposing forces.

For each tertiary contact location, the downward slope of ΔGfold indicates that addition of salt makes folding more favorable (Fig. 5B). Parsing ΔGfold into separate contributions from ΔUfold and TΔSfold (Fig. 5C), we find that the increased stability with salt concentration originates from the downward slope of ΔUfold with salt concentration. Increasing salt concentration has no effect on the tertiary stabilization ΔUtertiary, by the assumptions of our model, but enhances the screening between helices, lowering the electrostatic penalty required to assemble the helices in any given helical configuration. In general, addition of salt lowers the electrostatic interaction energy of helical configurations in both the unfolded and folded ensembles; however, the configurations in the folded ensemble are more stabilized than those in the unfolded ensemble, due to the higher average charge density of the folded configurations, leading to an overall decrease of ΔUfold (Misra and Draper 2002; Misra et al. 2003). In contrast, TΔSfold is relatively constant over the range of salt concentrations examined in this study.

Examining the separate contributions from ΔUfold and TΔSfold, we find that the differences with tertiary contact location are due largely to changes in TΔSfold and not ΔUfold. This indicates that changes in electrostatics contribute relatively little to the observed destabilization from changing tertiary contact location. The loss in conformational entropy TΔSfold depends on the relative abundance of folded to unfolded conformers; for folding transitions, TΔSfold is negative, reflecting the greater number of unfolded configurations relative to the smaller number of folded configurations. When tertiary contacts are located in helical regions preferentially brought together by junctions, the likelihood of populating a folded configuration is enhanced, reducing the amount of conformational entropy that must be lost relative to folding with the tertiary contact placed outside of these regions.

This modulation of conformational entropy loss with tertiary contact location is evident in both sPEG and dPEG constructs. In the sPEG construct, changing the tertiary contact from the diamond location to circle and triangle gradually moves the contact out of the regions that the sPEG junction tends to bring together, increasing the amount of conformational entropy that must be lost as indicated by the drop in the average value of TΔSfold (Fig. 5C). However, the conformational flexibility of the sPEG junction still permits the contact to be formed with relative ease in the circle position, resulting in appreciable folding (∼75% folded at 1 M salt). In energetic terms, moving the tertiary contact location from diamond to circle increases this barrier by an average of 2.0kBT; moving from circle to triangle costs an additional 8.8kBT. For the dPEG junction, moving from the circle contact to triangle or diamond costs much more, an average of 8.9kBT and 6.9kBT, respectively. In reality, the energetic penalty for forming these unfavorable contacts is insurmountable and the helices would fray before incurring such a penalty.

The magnitude of change in TΔSfold with tertiary contact location is an indication of the folding specificity of the motif and is directly related to the broadness of the φ–φ distributions in Figure 2. The resilience of the sPEG motif to changes in tertiary contact location should not be surprising; the motif's single strand affords substantial conformational freedom, allowing the helices to adapt more easily to changes in tertiary contact location without sacrificing much tertiary stability; in other words, the sPEG junction allows the motif to be less selective in its choice of tertiary contact location. In contrast, the constraint of a second tether in the dPEG motif, manifested by the hinge-like motion of the helices in Figure 2B, changes the folding specificity from the diamond location to the circle and also increases the folding specificity, making the motif very sensitive to changes in tertiary contact location (see also Fig. 6).

DISCUSSION

Junctions play a large role in determining the function, stability, and overall architecture of structured RNAs (Lilley 2000; Lescoute and Westhof 2006; Bindewald et al. 2008; Lipfert et al. 2008). The four-way junction in the Hairpin ribozyme, an example of a HJH motif, positions its adjoining helices into biased configurations, specifically guiding complementary regions involved in tertiary interactions into close proximity (Walter et al. 1998; Tan et al. 2003; Hohng et al. 2004); changing the topology of its junction (e.g., changing a four-way junction to a three-way, double-stranded, or single-stranded junction) dramatically alters its stability and dynamics (Walter et al. 1999; Zhuang et al. 2002; Tan et al. 2003). Simply mutating the junction sequence in the independently folding P4–P6 subdomain of the Tetrahymena ribozyme can adversely affect its folding stability (Szewczak and Cech 1997), and altering junction length has been shown to affect the catalytic efficiency of simple self-aminoacylating ribozymes (Lehmann et al. 2007). Recently, the structure of the VS ribozyme was modeled from an analysis of the conformational biases of its isolated junctions, highlighting the major role that junctions can play in determining the overall architecture of an RNA fold (Lipfert et al. 2008).

The clear evidence that junctions strongly influence RNA folding motivates the need to understand, at a fundamental level, how junctions mediate this process. While previous theoretical analyses of RNA stability have greatly enhanced our understanding of electrostatic contributions to RNA folding thermodynamics (Misra and Draper 2000; Misra and Draper 2002; Misra et al. 2003; Draper 2004; Grilley et al. 2007), they have also typically been unable to address the contributions arising from the junction (Bai et al. 2008). In these seminal studies, neglect of the contributions of the junction to the energetics of folding made the analysis tractable, but precluded a deep understanding of folding thermodynamics.

This study explicitly considers the junction as a critical component in the energetic balance that governs RNA folding, similar in importance to the contributions arising from tertiary contacts and electrostatics. Our computational model permits us to parse the free energy of folding into distinct contributions, allowing us to analyze how different junction types, salt conditions, and tertiary contact locations modulate folding thermodynamics.

Using the tethered duplex, we found that simple polymer junction topologies strongly influenced the shape of the motif's conformational ensemble, exhibiting strikingly different folding specificities despite their inability to store information within a primary sequence (Fig. 6). The existence of such strong biases and limitations in the accessible conformational ensemble in a system as uncomplicated as the tethered duplex strongly suggests that such junction-induced behavior is a common and powerful energetic component in forming specific RNA tertiary structures. Properties as simple as the geometric constraints of a junction's topology, its location relative to a tertiary contact, and the length of its adjoining helices are capable of encoding valuable information, information which may help RNA escape the limitations of its spartan nucleotide alphabet.

The tethered duplex represents an idealized model of two helices connected by near-perfectly flexible and featureless polymer tethers; for realistic RNAs, the structural information encoded by specific junction sequences will likely perturb this idealized behavior. For instance, introducing an asymmetry in the lengths of a double stranded junction, like those found in the transactivation response element of the HIV genome, may enhance its preference to bend over in a certain direction (unpublished results). Particularly intriguing is the idea that junction sequences can modify the simple planar bending motions observed in the dPEG constructs by introducing specific interactions that stabilize and favor certain regions of the allowed conformational space.

Testing these and other ideas will require extending our analysis to native RNA junctions. Thankfully, the computational approach employed in this study is generalizable; in principle, RNA junctions could be substituted for the simple PEG junctions studied herein. However, great challenges remain in modeling RNA junctions. The application of the present methodology to RNA would likely require the development of more sophisticated molecular dynamics force fields to adequately treat base stacking and electrostatic effects within the junction, aspects that require rigorous testing. The complexity of the forces present within realistic RNAs stresses the need for experiments to validate computational modeling and prediction.

Nevertheless, we are optimistic that close cooperation between experiment and modeling will continue to advance our understanding of the physical origins of RNA structure. Particularly exciting is the prospect of dissecting the thermodynamics of increasingly complicated RNA structures; a partial analysis is now possible for the P4–P6 subdomain of the Tetrahymena ribozyme and of understanding the behavior of biological junctions, such at that of TAR RNA (data not shown). Understanding the details of RNA thermodynamics will also hopefully lead to the rational design of simple RNA folding elements or the discovery of compensatory mutations that rescue folding as tertiary contact location or junction sequence is altered.

MATERIALS AND METHODS

Folding thermodynamics

A typically sized HJH motif has on the order of a thousand individual atoms, representing thousands of coupled degrees of freedom. However, the rigidity of the helices in the motif imposes constraints that greatly reduce the number of degrees of freedom required to specify the state of the system. Formally, if we integrate over the degrees of freedom of the junction atoms and treat the junction as an “effective potential” that governs the relative placement of the helices, then the state of the system can be specified by the six generalized coordinates Ω that uniquely specify the location and orientation of one helix relative to the other. The set of all possible Ω constitutes the phase space of the HJH motif.

In this model, the thermodynamic properties of a HJH motif are determined by how the junction, electrostatic repulsion, and tertiary stabilization influence the probability of observing the helices in some configuration Ω. The conformational biases introduced by junctions make certain helical configurations more likely than others; these probabilities may be described in terms of a probability density function P(Ω). Heuristically, P(Ω) acts as a junction-dependent energy landscape for the placement of the helices in some conformation in the absence of any electrostatic effects; tertiary interactions and electrostatics reweight this landscape by energetically favoring certain conformers over others. For instance, electrostatic repulsion acts to favor extended conformers that minimize unfavorable electrostatic interactions; similarly, tertiary contacts stabilize closely packed conformations that bring specific regions of the helices into close proximity. The energetic effects arising from electrostatics and tertiary contacts may respectively be described by two functions EM(Ω) and C(Ω), where M denotes the salt dependence of the electrostatic effects. Given these three functions, we can derive the relative probability for observing any helical conformation Ω and construct a partition function for the HJH motif:

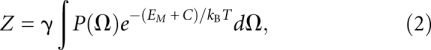graphic file with name 2195equ2.jpg

where γ is a proportionality constant, kB is Boltzmann's constant, and T is the absolute temperature.

To study HJH motif folding, we defined two disjoint ensembles of helical conformations U and F that represented the unfolded and folded states of the motif (for further details, see Reweighting by tertiary contacts and electrostatics). The union of these two sets constitutes the entire phase space of the HJH motif. The change in free energy upon folding ΔGfold is defined as

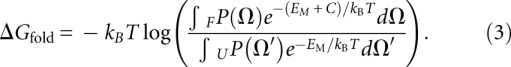graphic file with name 2195equ3.jpg

The change in internal energy ΔUfold can be computed as

graphic file with name 2195equ4.jpg

where 〈…〉X denotes the ensemble average over the ensemble X. The conformational entropy TΔSfold may be computed as the difference between the changes in free energy and internal energy:

graphic file with name 2195equ5.jpg

This framework gives us great flexibility to dissect folding energetics and thermodynamics; for example, simply recomputing P(Ω), EM(Ω), or C(Ω) allows us to study how varying junction topology, electrostatic conditions, or tertiary contacts affect folded stability.

Observation of junction biases through sampling and smoothing

P(Ω) the probability of observing the helices in a configuration Ω, for a given junction can be inferred from long stochastic dynamics (SD) simulations of a multiscale model of the HJH. Treating the helices as rigid bodies enables the replacement of most of the atoms in the helices with a few dummy atoms constrained to move rigidly; in contrast, the junction is modeled atomistically. The increase in computational efficiency afforded by coarse graining the helices greatly increases the time scales over which the junction can be practically sampled, allowing insight into the distribution of helices dictated by the junction at equilibrium. In this study, we focused on two archetype junction topologies: A single-stranded PEG (sPEG) and a double-stranded PEG (dPEG) construct of six ethylene glycol monomers (Fig. 1). We used the Gromacs software package to perform the stochastic dynamics simulation (Van Der Spoel et al. 2005). A more detailed description of the SD simulation can be found in the Supplemental Material and Supplemental Figure 1.

After the sPEG and dPEG SD simulations were completed, the dummy atoms representing the helices were replaced with atomistic helices; structures found to be sterically clashed were removed, yielding dPEG and sPEG ensembles of 299,900 and 290,300 structures, respectively (representing in excess of 90 μs of simulation time). Excluding half of the observed ensemble configurations from the smoothing procedure (see below) did not significantly affect our results.

As a particular choice of generalized coordinates, we affixed an orthonormal body frame to both helices (see Fig. 1B). Arbitrarily designating one helix as a “fixed” helix and the other as a “mobile” helix, we chose to express the six generalized degrees of freedom as Ω(r, q) where r ∈ℝ3 is the Cartesian displacement of the origin of the mobile body frame with respect to the fixed helix frame and q∈ℍ is a unit quaternion that describes the rigid-body rotation required to bring the two helices into the same orientation. Each structure was analyzed, yielding a set of rigid-body transformations 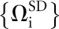Inline graphic that described the relative location and orientation of the helices observed through simulation.

To obtain the probability distribution function P(Ω) that describes the probability of finding the helices in a given conformation, the discrete 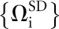Inline graphic were smoothed using a product kernel composed of a Gaussian and von Mises smoothing kernel (Fisher et al. 1987; Bowman and Azzalini 1997). The separate Gaussian and von Mises kernels, respectively, smooth over the Cartesian and orientational degrees of freedom:

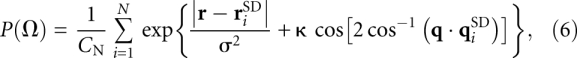graphic file with name 2195equ6.jpg

where CN = π7/2σ3N[I0 (κ)−I1 (κ)] is a normalization constant for the product kernel; N is the total number of discrete observations; I0(x) and I1(x) are the modified Bessel functions of zeroth and first order; σ and κ are the smoothing parameters for the Gaussian and von Mises kernels, respectively. The smoothing process generates a smoothly varying P(Ω) for any arbitrary helical configuration Ω. In our smoothing procedure, we set σ = 2.0 Å and κ = 2.0.

In practice, it is feasible to sample and store values of P(Ω) only for a restricted set of Ωj. Using this set {Ωj}, thermodynamic quantities derived from the partition function Z are computed by quadrature. The set of helical configurations in {Ωj} was constructed to be “evenly spaced” in both the spatial location of the mobile helix and its orientation. To construct it, we sampled P(Ω) for 8000 separate helical orientations qj at 13,754 Cartesian grid points rj spaced 2 Å apart in a box of size 52 Å ×46 Å ×46 Å (for a total of separate helical locations and orientations). The corner of the box was placed at r = (−14,−28,−28)Å and the box encompassed 98% of the observations for the mobile helix during the simulation. The orientations were selected using an algorithm that selected 8000 equally spaced points on the upper half-sphere of the unit three-sphere S3 ⊂ℝ4, yielding a set of quaternions that sampled the space of rigid body rotations SO(3) evenly (Leopardi 2006). The choice of 8000 orientations ensured that any helical configuration observed in our simulation was separated by only a 3° rotation to a sampled orientation.

Reweighting by tertiary contacts and electrostatics

We constructed the functions C(Ω) and EM(Ω) to examine how the tertiary contacts and electrostatics changed the conformational distribution imposed by the junction [encoded in P(Ω)]. We used a simple “square-well” potential as a model for the tertiary contact. To define C, two points on opposite helical surfaces were specified. Helical configurations Ω that brought these two points within 7.5 Å, whose helical axes subtended an angle less than 20°, and whose φ–φ measures were within 12° of the tertiary contact location were designated as “folded” and stabilized by a constant offset. Those helical configurations that did not satisfy this criterion were not stabilized and designated as “unfolded.” Changes in these parameters did not alter the qualitative behavior of the folding transitions.

To construct the electrostatic interaction function EM(Ω), we used the adaptive Poisson–Boltzmann solver (APBS) to solve the PB equation for atomistic representations of the two duplexes in 0.016–1.016 M monovalent salt (Baker et al. 2001). The charge on each helix was assigned using PDB2PQR (Dolinsky et al. 2004). To reduce the number of required calculations, we computed PB calculations for 100 helical configurations located at points distributed at 2 Å intervals for a total of 945,671 separate PB calculations at each salt concentration. The 100 orientations were chosen such that the helical axis of the mobile helix was isotropically distributed over the surface of a sphere (Saff and Kuijlaars 1997; Leopardi 2006). Details of the electrostatic calculations can be found in the Supplemental Material.

SAXS experiments and predictions

The tethered duplex consisted of two 12 bp DNA duplexes joined by a single- or double-stranded PEG tether of six ethylene glycol monomers. The component oligonucleotides were synthesized, purified, and annealed as described previously (Bai et al. 2005). DNA stock solution was dialyzed into 40 mM Na-MOPS buffer at pH 7.0 ([Na+] = 16 mM), with additional monovalent salt (0, 0.04, 0.1, 0.2, 0.4, 0.6, and 1 M) added. SAXS experiments were conducted at the BESSRC-CAT Beamline 12-IDC at the Advanced Photon Source and analyzed as described previously (Bai et al. 2005; Lipfert et al. 2006; Lipfert and Doniach 2007). Theoretically predicted ensembles of structures were constructed by running a Monte Carlo simulation with transition probabilities governed by P(Ω) and EM(Ω). SAXS profiles were computed for each structure in the ensemble as described previously (Svergun et al. 1995; Bai et al. 2008).

SUPPLEMENTAL MATERIAL

Supplemental material can be found at http://www.rnajournal.org.

ACKNOWLEDGMENTS

We thank Xuhui Huang, Rhiju Das, and members of the Doniach and Herschlag groups for helpful discussions and comments. V.B.C. and Y.B. were supported, respectively, in part, by a Pfizer Bio-X and Stanford Graduate Fellowship. This research was generously supported by NIH grant PO1 GM066275. Computing resources were provided by the Bio-X2 computer cluster at Stanford University (NSF award CNS-0619926). Use of the Advanced Photon Source was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under contract No. DE-AC02-06CH11357.

Footnotes

1

Operationally defined as when the angle subtended by the two helices is less than 47°. Varying this angle did not qualitatively affect the conclusions.

Article published online ahead of print. Article and publication date are at http://www.rnajournal.org/cgi/doi/10.1261/rna.1747509.

REFERENCES

  1. Bai Y, Das R, Millett IS, Herschlag D, Doniach S. Probing counterion modulated repulsion and attraction between nucleic acid duplexes in solution. Proc Natl Acad Sci. 2005;102:1035–1040. doi: 10.1073/pnas.0404448102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Bai Y, Chu V, Lipfert J, Pande V, Herschlag D, Doniach S. Critical assessment of nucleic acid electrostatics via experimental and computational investigation of an unfolded state ensemble. J Am Chem Soc. 2008;130:12334–12341. doi: 10.1021/ja800854u. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Baker N, Sept D, Joseph S, Holst MJ, McCammon JA. Electrostatics of nanosystems: Applications to microtubules and the ribosome. Proc Natl Acad Sci. 2001;98:10037–10041. doi: 10.1073/pnas.181342398. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bindewald E, Hayes R, Yingling YG, Kasprzak W, Shapiro BA. RNAJunction: A database of RNA junctions and kissing loops for three-dimensional structural analysis and nanodesign. Nucleic Acids Res. 2008;36:D392–D397. doi: 10.1093/nar/gkm842. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Bowman AW, Azzalini A. Applied smoothing techniques for data analysis: The kernel approach with S-Plus illustrations. Oxford University Press; Oxford, UK: 1997. [Google Scholar]
  6. Brion P, Westhof E. Hierarchy and dynamics of RNA folding. Annu Rev Biophys Biomol Struct. 1997;26:113–137. doi: 10.1146/annurev.biophys.26.1.113. [DOI] [PubMed] [Google Scholar]
  7. Chu VB, Herschlag D. Unwinding RNA's secrets: Advances in the biology, physics, and modeling of complex RNAs. Curr Opin Struct Biol. 2008;18:305–314. doi: 10.1016/j.sbi.2008.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Chu VB, Bai Y, Lipfert J, Herschlag D, Doniach S. A repulsive field: Advances in the electrostatics of the ion atmosphere. Curr Opin Chem Biol. 2008;12:619–625. doi: 10.1016/j.cbpa.2008.10.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Das R, Kwok LW, Millett IS, Bai Y, Mills TT, Jacob J, Maskel GS, Seifert S, Mochrie SGJ, Thiyagarajan P, et al. The fastest global events in RNA folding: electrostatic relaxation and tertiary collapse of the Tetrahymena ribozyme. J Mol Biol. 2003;332:311–319. doi: 10.1016/s0022-2836(03)00854-4. [DOI] [PubMed] [Google Scholar]
  10. Dolinsky TJ, Nielsen JE, McCammon JA, Baker NA. PDB2PQR: An automated pipeline for the setup of Poisson–Boltzmann electrostatics calculations. Nucleic Acids Res. 2004;32:W665–W667. doi: 10.1093/nar/gkh381. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Draper D. A guide to ions and RNA structure. RNA. 2004;10:335–343. doi: 10.1261/rna.5205404. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Fisher NI, Lewis T, Embleton BJ. Statistical analysis of spherical data. Cambridge University Press; Cambridge, MA: 1987. [Google Scholar]
  13. Grilley D, Misra V, Caliskan G, Draper DE. The importance of partially unfolded conformations for Mg2+-induced folding of RNA tertiary structure: Structural models and free energies of Mg2+ interactions. Biochemistry. 2007;46:10266–10278. doi: 10.1021/bi062284r. [DOI] [PubMed] [Google Scholar]
  14. Herschlag D. RNA chaperones and the RNA folding problem. J Biol Chem. 1995;270:20871–20874. doi: 10.1074/jbc.270.36.20871. [DOI] [PubMed] [Google Scholar]
  15. Hohng S, Wilson T, Tan E, Clegg R, Lilley D, Ha T. Conformational flexibility of four-way junctions in RNA. J Mol Biol. 2004;336:69–79. doi: 10.1016/j.jmb.2003.12.014. [DOI] [PubMed] [Google Scholar]
  16. Koculi E, Lee N, Thirumalai D, Woodson S. Folding of the Tetrahymena ribozyme by polyamines: Importance of counterion valence and size. J Mol Biol. 2004;341:27–36. doi: 10.1016/j.jmb.2004.06.008. [DOI] [PubMed] [Google Scholar]
  17. Lehmann J, Reichel A, Buguin A, Libchaber A. Efficiency of a self-aminoacylating ribozyme: Effect of the length and base composition of its 3′ extension. RNA. 2007;13:1191–1197. doi: 10.1261/rna.500907. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Leopardi P. A partition of the unit sphere into regions of equal area and small diameter. Electron Trans Numer Anal. 2006;25:309–327. [Google Scholar]
  19. Lescoute A, Westhof E. Topology of three-way junctions in folded RNAs. RNA. 2006;12:83–93. doi: 10.1261/rna.2208106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Lilley DM. Structures of helical junctions in nucleic acids. Q Rev Biophys. 2000;33:109–159. doi: 10.1017/s0033583500003590. [DOI] [PubMed] [Google Scholar]
  21. Lipfert J, Doniach S. Small-angle X-ray scattering from RNA, proteins, and protein complexes. Annu Rev Biophys Biomol Struct. 2007;36:307–327. doi: 10.1146/annurev.biophys.36.040306.132655. [DOI] [PubMed] [Google Scholar]
  22. Lipfert J, Millett IS, Seifert S, Doniach S. A sample holder for small-angle X-ray scattering static and flow cell measurements. Rev Sci Instrum. 2006;77:046108. doi: 10.1063/1.2194484. [DOI] [Google Scholar]
  23. Lipfert J, Ouellet J, Norman DG, Doniach S, Lilley DM. The complete VS ribozyme in solution studied by small-angle X-ray scattering. Structure. 2008;16:1357–1367. doi: 10.1016/j.str.2008.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Mandal M, Breaker RR. Gene regulation by riboswitches. Nat Rev Mol Cell Biol. 2004;5:451–463. doi: 10.1038/nrm1403. [DOI] [PubMed] [Google Scholar]
  25. Misra VK, Draper DE. Mg2+ binding to tRNA revisited: The nonlinear Poisson–Boltzmann model. J Mol Biol. 2000;299:813–825. doi: 10.1006/jmbi.2000.3769. [DOI] [PubMed] [Google Scholar]
  26. Misra V, Draper D. The linkage between magnesium binding and RNA folding. J Mol Biol. 2002;317:507–521. doi: 10.1006/jmbi.2002.5422. [DOI] [PubMed] [Google Scholar]
  27. Misra VK, Shiman R, Draper DE. A thermodynamic framework for the magnesium-dependent folding of RNA. Biopolymers. 2003;69:118–136. doi: 10.1002/bip.10353. [DOI] [PubMed] [Google Scholar]
  28. Pan T, Fang X, Sosnick T. Pathway modulation, circular permutation, and rapid RNA folding under kinetic control. J Mol Biol. 1999;286:721–731. doi: 10.1006/jmbi.1998.2516. [DOI] [PubMed] [Google Scholar]
  29. Russell R, Herschlag D. Probing the folding landscape of the Tetrahymena ribozyme: Commitment to form the native conformation is late in the folding pathway. J Mol Biol. 2001;308:839–851. doi: 10.1006/jmbi.2001.4751. [DOI] [PubMed] [Google Scholar]
  30. Russell R, Zhuang X, Babcock HP, Millett IS, Doniach S, Chu S, Herschlag D. Exploring the folding landscape of a structured RNA. Proc Natl Acad Sci. 2002;99:155–160. doi: 10.1073/pnas.221593598. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Saff EB, Kuijlaars ABJ. Distributing many points on a sphere. The Mathematical Intelligencer. 1997;19:5–11. [Google Scholar]
  32. Simons RW, Grunberg-Manago M, editors. RNA structure and function. Cold Spring Harbor Laboratory Press; Cold Spring Harbor, NY: 1998. [Google Scholar]
  33. Svergun DI, Barberato C, Koch MHJ. CRYSOL—a program to evaluate X-ray solution scattering of biological macromolecules from atomic coordinates. J Appl Crystallogr. 1995;28:768–773. [Google Scholar]
  34. Szewczak A, Cech T. An RNA internal loop acts as a hinge to facilitate ribozyme folding and catalysis. RNA. 1997;3:838–849. [PMC free article] [PubMed] [Google Scholar]
  35. Takamoto K, Das R, He Q, Doniach S, Brenowitz M, Herschlag D, Chance MR. Principles of RNA compaction: Insights from the equilibrium folding pathway of the P4–P6 RNA domain in monovalent cations. J Mol Biol. 2004;343:1195–1206. doi: 10.1016/j.jmb.2004.08.080. [DOI] [PubMed] [Google Scholar]
  36. Tamura M, Hendrix DK, Klosterman PS, Schimmelman NR, Brenner SE, Holbrook SR. SCOR: Structural classification of RNA, version 2.0. Nucleic Acids Res. 2004;32:D182–D184. doi: 10.1093/nar/gkh080. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Tan E, Wilson T, Nahas M, Clegg R, Lilley D, Ha T. A four-way junction accelerates hairpin ribozyme folding via a discrete intermediate. Proc Natl Acad Sci. 2003;100:9308–9313. doi: 10.1073/pnas.1233536100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Thirumalai D, Lee N, Woodson SA, Klimov D. Early events in RNA folding. Annu Rev Phys Chem. 2001;52:751–762. doi: 10.1146/annurev.physchem.52.1.751. [DOI] [PubMed] [Google Scholar]
  39. Treiber DK, Williamson JR. Exposing the kinetic traps in RNA folding. Curr Opin Struct Biol. 1999;9:339–345. doi: 10.1016/S0959-440X(99)80045-1. [DOI] [PubMed] [Google Scholar]
  40. Van Der Spoel D, Lindahl E, Hess B, Groenhof G, Mark A, Berendsen H. GROMACS: Fast, flexible, and free. J Comput Chem. 2005;26:1701–1718. doi: 10.1002/jcc.20291. [DOI] [PubMed] [Google Scholar]
  41. Walter F, Murchie A, Lilley D. Folding of the four-way RNA junction of the hairpin ribozyme. Biochemistry. 1998;37:17629–17636. doi: 10.1021/bi9821115. [DOI] [PubMed] [Google Scholar]
  42. Walter N, Burke J, Millar D. Stability of hairpin ribozyme tertiary structure is governed by the interdomain junction. Nat Struct Biol. 1999;6:544–549. doi: 10.1038/9316. [DOI] [PubMed] [Google Scholar]
  43. Zhuang X, Kim H, Pereira M, Babcock H, Walter N, Chu S. Correlating structural dynamics and function in single ribozyme molecules. Science. 2002;296:1473–1476. doi: 10.1126/science.1069013. [DOI] [PubMed] [Google Scholar]
  44. Zwanzig R, Szabo A, Bagchi B. Levinthal's paradox. Proc Natl Acad Sci. 1992;89:20–22. doi: 10.1073/pnas.89.1.20. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from RNA are provided here courtesy of The RNA Society

RESOURCES