Abstract
The maturation of RNAs includes site-specific post-transcriptional modifications that contribute significantly to hydrogen bond formation within RNA and between different RNAs, especially in formation of mismatch base pairs. Thus, an understanding of the geometry and strength of the base-pairing of modified ribonucleoside 5′-monophosphates, previously not defined, is applicable to investigations of RNA structure and function and of the design of novel RNAs. The geometry and free energies of base-pairings were calculated in aqueous solution under neutral conditions with AMBER force fields and molecular dynamics simulations (MDSs). For example, unmodified uridines were observed to bind to uridine and cytidine with significant stability, but the ribose C1′–C1′ distances were far short (∼8.9 Å) of distances observed for canonical A-form RNA helices. In contrast, 5-oxyacetic acid uridine, known to bind adenosine, wobble to guanosine, and form mismatch base pairs with uridine and cytidine, bound adenosine and guanosine with geometries and energies comparable to an unmodified uridine. However, the 5-oxyacetic acid uridine base paired to uridine and cytidine with a C1′–C1′ distance comparable to that of an A-form helix, ∼11 Å, when a H2O molecule migrated between and stably hydrogen bonded to both bases. Even in formation of canonical base pairs, intermediate structures with a second energy minimum consisted of transient H2O molecules forming hydrogen bonded bridges between the two bases. Thus, MDS is predictive of the effects of modifications, H2O molecule intervention in the formation of base-pair geometry, and energies that are important for native RNA structure and function.
Keywords: modified nucleosides, base pairs in water, wobble recognition, refined molecular dynamics simulation
INTRODUCTION
The hydrogen bonding and stacking interactions of the hydrophobic nucleobases are major contributors to the stable association of nucleotides within and between nucleic acid molecules. Hydrogen bonds are principally characterized by highly specific electrostatic interactions that stabilize the nucleic acid secondary structure (Saenger 1983). Watson–Crick hydrogen bonds between the bases of the nucleosides adenosine (A) and uridine (U) or thymidine, and guanosine (G) and cytidine (C), and a multitude of noncanonical hydrogen bonds play crucial roles in both the secondary and tertiary structures of nucleic acids and in their functions. Under physiological conditions where there is a competition with water molecules for the hydrogen bond donor and acceptor sites, base–base hydrogen bonding is a significant contributor to nucleic acid geometry, energy, and the specificity of base-pairing (Saenger 1983). Both DNA and RNA contain nucleotides that are modified by enzymes after replication or transcription. Yet, at the atomic level little is known concerning the effects of the many modifications on hydrogen bonding and base-pairing. Many of the more than 100 modified nucleotide chemistries of RNA are complex, involved in hydrogen bonding, and thus important to RNA folding, structure, dynamics, and function (Agris 1996; Nobles et al. 2002; Gustilo et al. 2008). Thus, a detailed understanding of the geometries and energies of hydrogen bonding by modified nucleotides is applicable to the analysis of native RNAs and to the future design of novel RNAs with new functions.
The molecular dynamics simulations (MDSs) of base-pair formation have been used to understand RNA secondary structure and tertiary folding (Auffinger and Westhof 1998; Stofer et al. 1999; Giudice and Lavery 2003; Giudice et al. 2003; McDowell et al. 2007). Though the MDS calculations for formation of the canonical base pairs in vacuo result in a high degree of similarity of the final product to that in H2O under neutral conditions, the modification chemistries add significant hydrophobic, polar, and charged elements to the problem and possible interactions with or avoidance of H2O. Rarely have computational methods been used to understand and predict modified nucleotide contributions. Here, we present models that describe the base-pairing of the modified nucleoside 5′-monophosphates to that of A, G, C, and U under aqueous and neutral conditions. In particular, we describe the geometries (ribose C1′–C1′ and hydrogen bond distances) and energies of the base pairs with modified U's. Post-transcriptional modifications of U are reflective of the extent and variety of modification chemistries (Rozenski et al. 1999). The models, derived from the general principals of the modified wobble hypothesis (Agris 1991) and empirical data, are applicable to all base-pairings that involve the chemistry, structure, and thermodynamics of RNA modification. The models take into account the pyrimidine•pyrimidine base-pairing geometry that was of concern to Francis Crick (Targanski and Cherkasova 2008) and would result in deformation of the RNA helix diameter. Today, we are able to calculate in silico the geometry, charge, energy parameters, and intervention of H2O during base-pair formation to yield reliable structural predictions that are in good agreement with the practical experimental results. In addition, we are able to observe the contribution of H2O to the formation of canonical and mismatch base pairs.
RESULTS
A thorough understanding of modified nucleotide base-pair formation, stability, and structure in RNA can be achieved at the atomistic level with MDS in H2O under neutral conditions combined with empirically derived information (Laserson et al. 2005; McDowell et al. 2007). Using molecular mechanics, we have compared the geometries and relative energies involved in the formation of modified versus unmodified base pairs of the nucleoside 5′-monophosphates in H2O under neutral conditions. Molecular mechanics employ the equations of classical mechanics in describing the potential energy surfaces and physical properties of molecules. The molecules are described as a collection of atoms that interact with each other by simple analytical functions, a force field. The force field we have selected is that of the assisted model building with energy refinement (AMBER) (Case et al. 2005). AMBER has an established use in nucleic acid modeling to determine and compare the free energies of base pairs (Arora and Jayaram 1998; Giudice and Lavery 2003; Giudice et al. 2003; Sanbonmatsu and Joseph 2003; Varnai et al. 2004; Mathews and Case 2006; Rhodes et al. 2006; Perez et al. 2008).
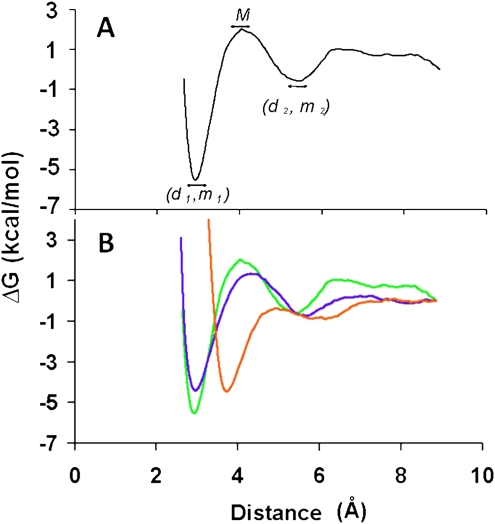
Biased molecular dynamics or umbrella sampling (Valleau and Card 1972; Torrie and Valleau 1974; Patey and Valleau 1975) was utilized to generate the potential of mean force (PMF) or free energy (Roux 1995). This method is widely applied to calculate free energy because of its accuracy and reproducibility. Indeed, the variations of free energy are faithfully reflected by the fluctuations of the PMF. The results of the free energy calculation of each base pair under study were represented by a curve displaying the variation of the PMF (kcal/mol) as a function of the hydrogen bond separation distance (Å) (Fig. 1A). Each curve featured four extremes characterized by a global maximum (M) followed by a global minimum (m1) at the hydrogen bond distance d1 (involving the imino proton of one of the bases) where the base-pairing adopted its most stable conformation. Surprisingly, a local minimum m2 at hydrogen bond distance d2 was observed where a water molecule (or water molecules in some cases) bridged and stabilized both canonical and noncanonical mismatched base-pairings through hydrogen bond formation. In certain cases, an energy barrier (EB) was detected between m1 and m2 (Table 1).
FIGURE 1.
Free energy variation as a function of hydrogen bond distance. (A) Free energy variation as a function of hydrogen bond distance for the molecular dynamics simulation (MDS) of a hypothetical base-pairing by ribonucleoside-5′-monophosphates. The global minimum of the base-pair energy, the local minimum of that energy, and energy maximum are displayed and are denoted as m1, m2, and M (kcal/mol), respectively. The hydrogen bond distances between the bases for the imino proton hydrogen bond correspond to d1 and d2 (Å). (B) Free energy for the Watson–Crick base-pairings of the ribonucleoside-5′-monophosphates U•A and C•G and for the wobble U•G base pair. The MDS of base-pairing was conducted in an aqueous environment under neutral conditions with Na+ as the counter ion to the ribonucleoside-5′-monophosphate. The Watson–Crick base pairs C•G (green), U•A (blue) exhibited comparable energy/distance relationships with the C•G pair being the more stable of the two. The wobble pair U•G (orange) exhibited a different profile, with a longer imino hydrogen bond distance. All three base-pairings exhibited a secondary interaction resulting in an intermediate stability (m2) and longer distance (d2) between bases bridged by one or two H2O molecules.
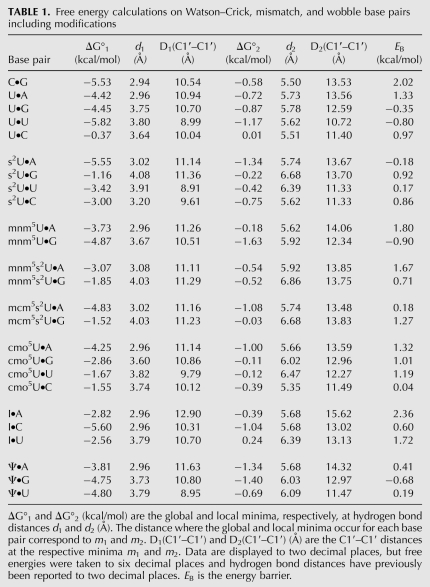
TABLE 1.
Free energy calculations on Watson–Crick, mismatch, and wobble base pairs including modifications
The canonical pairs C•G and U•A, and the wobble base-pair U•G
The appropriateness of the molecular mechanical approach was tested with its application to the Watson–Crick pairings of the mononucleoside 5′-phosphates. Using this method, we find that the geometries and free energies associated with the canonical base-pairings for unmodified mononucleotides in water, under neutral conditions and without regard to base stacking and to backbone restraints, are wholly consistent with conventional understandings (Saenger 1983). The C•G nucleotide pair was found in the Watson–Crick planar geometry and was the most stable of the unmodified base pairs with a Gibbs standard free energy (ΔG°300°K) of −5.53 kcal/mol at a hydrogen bond distance d1 = 2.94 Å (Fig. 1B). The U•A base pair was found in the canonical geometry (Fig. 2; Xin and Olson 2009) with the next lowest free energy, ΔG°300°K = −4.42 kcal/mol. The expected conformation of the U•G wobble pair (Fig. 2B) was observed with an equivalent energy, ΔG°300°K = −4.45 kcal/mol (Fig. 1B; Table 1). The ribose C1′–C1′ distances D1(C1′–C1′) of these three base pairs were determined to be 10.50, 10.90, and 10.70 Å, respectively (Table 1), and were comparable to those found at the decoding site of the 30S subunit crystallographic structure (Ogle et al. 2001; Murphy and Ramakrishnan 2004; Murphy et al. 2004; Weixlbaumer et al. 2007). The free energy curves of C•G, U•A and U•G displayed second minima at m2 = −0.58, −0.72, and −0.87 kcal/mol, respectively. These secondary points of stability corresponded to hydrogen bond distances of ∼5.5 Å and D2(C1′–C1′) of ∼13.0 Å where water molecules were observed to maintain the base-pairing conformation through hydrogen bonds.
FIGURE 2.
Base orientation at the first energy minimum of the Watson–Crick, wobble, pyrimidine•pyrimidine mismatch, modified pyrimidine, and inosine pairs. (A) C•G, U•A, and U•G and the modified U•A, and U•G. The modified uridines for the U•A and U•G pairs include 2-thiouridine [s2U; (d),(e)]; 5-methylaminomethyluridine [mnm5U; (f),(g)]; 5-methoxycarbonylmethyl-2-thiouridine [mcm5s2U; (j),(k)]; 5-oxyacetic acid uridine [cmo5U; (l),(m)]; and 5-methylaminomethyl-2-thiouridine [mnm5s2U; (h),(i)]. (B) Pyrimidine•pyrimidine base-pairing of the ribonucleoside-5′phosphates. The geometries of the unmodified U•U and U•C pairs at the global energy minimum result in short ribose C1′–C1′ distances not compatible with A-form RNA helices [(a),(b), respectively]. The modified U•U and U•C pairs including 2-thiouridine [s2U; (e),(f)], and 5-oxyacetic acid uridine [cmo5U; (g),(h)] also result in short C1′–C1′ distances. However, base-pairing of the pyrimidine to pyrimidine ribonucleoside-5′-monophosphates exhibited a second energy minimum at which a hydrogen bonding distance conformed to the diameter of an A-form RNA duplex [figures (c),(d),(i),(j)]. Stability of this interaction was achieved through a bridging by one or two H2O molecules. (C) Base-pair orientation of the pseudouridine (Ψ) and inosine (I) base pairs with A, G, C, and U at global energy minimum. Two hydrogen bonds are formed between Ψ and A [(a)], Ψ and G [(b)], and Ψ and C [(c)]. Inosine (I) binds A, C, and U with two hydrogen bonds each [(d)–(f)]. Stick models have oxygen in red, nitrogen in blue, and sulfur in yellow.
The modified U•A Watson–Crick base pair
By using molecular dynamics, we simulated the base-pairings of six differently modified U•A base pairs that include the modifications 2-thio (s2U34), 5-methylaminomethyl (mnm5U34), 5-methylaminomethyl-2-thiouridine (mnm5s2U34), 5-methoxycarbonylmethyl-2-thiouridine (mcm5s2U34), 5-oxyacetic acid (cmo5U34), and pseudouridine (Ψ) (Fig. 3). U is often found to be in its isomeric form pseudouridine (Ψ) in many RNAs and will pair with A, G, and U (Yarian et al. 1999). The Ψ•A base pair formed with the canonical U•A geometry and a similar free energy (Table 1). In transfer RNA (tRNA), the nucleotide U that is located at the wobble position (U34) is almost always modified, and this occurs especially in tRNAs with pyrimidine-rich anti-codons (Agris 2004; Agris et al. 2007). The curves of the free energy that resulted from the simulations showed similar profiles (Fig. 4A). The aforementioned six base pairs formed with the expected geometry and stability associated with the canonical U•A pair (Fig. 2A,C; Table 1). The s2U•A exhibited the most stable structure with a ΔG°300°K = −5.55 kcal/mol. In addition, s2U•A displayed no energy barrier as opposed to the rest of the five base pairs, of which mnm5U•A had the highest energy barrier of 1.80 kcal/mol (Table 1). The ribose C1′–C1′ distances of ∼11.10 ± 0.40 Å were comparable to that of the U•A pair. When the C1′–C1′ distance was ∼14.00 ± 0.30 Å, once more a water molecule was detected in the position of a hydrogen bonded bridge between the modified U and the A base pair.
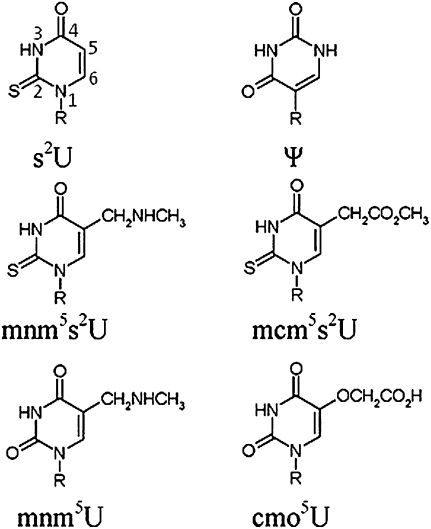
FIGURE 3.
Chemical structures of the modified nucleosides. Modified uridine chemical structures: 2-thiouridine (s2U), pseudouridine (Ψ), 5-methylaminomethyluridine (mnm5U), 5-methoxy-carbonylmethyluridine (mcm5s2U), 5-oxyacetic acid uridine (cmo5U), and 5-methylaminomethyl-2-thiouridine (mnm5s2U). R represents the ribose sugar attached to the base and 5′-phosphate. The first base demonstrates the standard uracil base numbering and can be applied throughout.
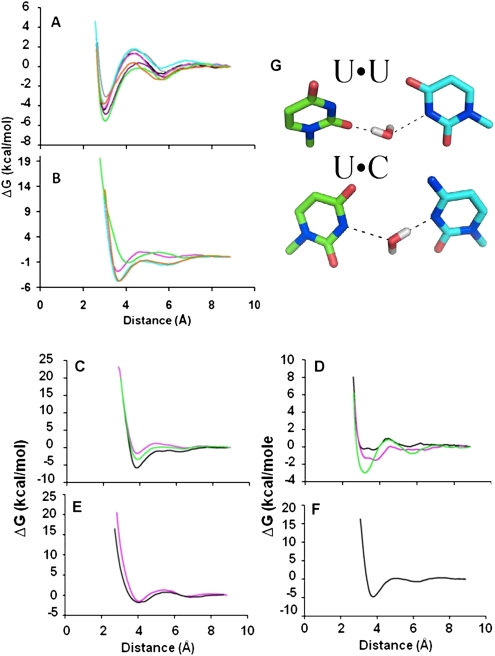
FIGURE 4.
Free energy change as a function of hydrogen bond distance for U•A, U•G and modified U base. (A) Free energy change as a function of hydrogen bond distance of the Watson–Crick and the modified U•A base pairs. Distance and energy relationships for the base-pairing of the unmodified U•A ribonucleoside-5′-monophosphates (black) and the modified uridines with A are very comparable: s2U•A (green), mnm5U•A (cyan), mnm5s2U•A (gray), mcm5s2U•A (purple), cmo5U•A (pink), Ψ•A (orange). It should be noted that the curves for cmo5U•A (pink) and U•A (black) are almost identical and obscure the lines. (B) Free energy change as a function of hydrogen bond distance of the modified wobble U•G base pairs. U•G base pairs include the modified Ψ•G (orange), cmo5U•G (pink), mnm5U•G (cyan), and s2U•G (green). (C) U•U mismatch base pairs including modified cmo5U•U (pink), s2U•U (green), and unmodified U•U (black). (D) U•C base pairs of modified cmo5U•C (pink), s2U•C (green), and unmodified U•C (black). (E) Free energy diagram of the modified mnm5s2U•G (black) and mcm5s2U•G (pink) base-pairings. (F) Free energy change as a function of hydrogen bond distance for the Ψ•U base pair. (G) Stabilization of pyrimidine•pyrimidine base-pairings by a water bridge. A water molecule bridges the pyrimidine•pyrimidine base pairs of U•U and U•C. The nonprotonated nitrogens are hydrogen bonded to the exchangeable hydrogens on the water, thus stabilizing the interaction of the bases. The resulting base-pair exhibits a ribose C1′–C1′ distance comparable to that of A-form RNA helices. Stick models have oxygen in red, nitrogen in blue, and hydrogen of the water in gray.
The modified U•G wobble base pair
G•U and U•G pairs are found within RNA structures and between RNA molecules. Though a G at tRNA's wobble position 34 will bind a U as the third base of the codon, such as that of tRNAPhe binding to the UUU codon, rarely does a cytoplasmic tRNA's unmodified U34 bind a codon ending in a G. Through MDSs, we found that the modified mnm5U•G and Ψ•G base pairs adopted the most stable conformations with an average ΔG°300°K = −4.50 ± 0.50 kcal/mol (Figs. 2, 4B; Table 1). This free energy value was comparable to that of the unmodified U•G pair. In contrast, the presence of the sulfur atom at position-2 of the U (s2U) and that of cmo- at position-5 (cmo5U) produced an increase in the free energy of base-pair formation (ΔΔG ≈ 3 and 2 kcal/mol, respectively), compared with that of unmodified U•G and the rest of the modified wobble base pairs (Fig. 4B; Table 1). As previously observed (Testa et al. 1999), the s2-moiety had a strong effect on the thermodynamic stabilization of the Watson–Crick base-pair s2U•A. However, this effect was reversed in the case of the wobble base-pairs s2U•G, mnm5s2U•G and mcm5s2U•G.
The base pairs of mnm5U•G and that of Ψ•G transitioned from the free energy of m1 to m2 in the absence of an energy barrier. In contrast, the base pairs of the variously thiolated Us and that of cmo5U•G displayed an EB between 0.71 and 1.27 kcal/mol for the same transition (Fig. 4B; Table 1). Interestingly, the s2U•G, mnm5s2U•G, and mcm5s2U•G base pairs displayed bonding distances that were greater by ∼1 Å for d1, d2, D1(C1′–C1′) and D2(C1′–C1′) than their nonthiolated counterparts (i.e., U•G, mnm5U•G3, cmo5U•G and Ψ•G) (Fig. 4B; Table 1).
The unmodified and modified U•U and U•C base pairs
The pyrimidine•pyrimidine nucleotide pairs resulting from the MDS displayed two hydrogen bonds each. In terms of the intrinsic values of their free energies at the first minimum, m1, the U•U and s2U•U and Ψ•U base pairs exhibited stabilities comparable to those of the C•G, U•A, and U•G base pairs (Fig. 4; Table 1). The cmo5U•U pair was the least stable. Surprisingly, the U•U and U•C base pairs conformed to the planarity exhibited by the canonical C•G and U•A pairs, including that of the wobble pair U•G. On the one hand, the U•C base pair appeared to be the least stable of the base pairs, with a ΔG°300°K = −0.37 kcal/mol, relative to s2U•C and cmo5U•C (Table 1). Yet, the U•U demonstrated significant thermal stability at the first minimum (ΔG°300°K = −5.82 kcal/mol).
The distance between C1s found for each type of pair is of interest. As would be expected, this distance for the unmodified or modified U•U, or the modified or unmodified U•C, nucleotide pairs (∼8.50–9.50 Å) was considerably reduced, by about 2 Å, compared to that of purine•pyrimidine pairs (Table 1). This distance was below the shortest distance (10.60 Å) detected in standard Watson–Crick (WC) base pairs that constitute A-form RNA structures (Saenger 1983). The unmodified and modified U•U and modified U•C pairs adopted the cis WC/WC conformation (Leontis and Westhof 2001). However, at the second minimum (Figs. 2, 4G; Table 1), water molecules bridged the unmodified and modified U•U and U•C pairs. The geometry of the resulting pairs was planar, and the ribose C1′–C1′ distances were 11.60 and 12.00 Å, respectively. This was accompanied by a decrease in thermodynamic stability (Fig. 4; Table 1). The H2O molecule formed hydrogen bonds bridging the 2-carbonyl of the U with the N1H imino proton of the U (or vice versa) or the N1 of C. No energy barrier was detected in the case of unmodified U•U and s2U•U, whereas the cmo5U•U, U•C, and s2U•C3 base pairs showed a relatively low energy barrier of ∼0.90 ± 0.05 kcal/mol. Though one can simulate s2U•U and s2U•C base-pairings, they have not been reported to occur in naturally-occurring RNA structures, including tRNA's ribosome-mediated decoding of mRNA. It has to be noted that at the second minimum, the anti-parallel cis WC/WC base-pairing conformation was adopted by unmodified and modified U•C, as had been previously observed (Leontis and Westhof 2001; Leontis et al. 2002).
Crick's wobble base-pairs I•A, I•U, and I•C
The base pairs that involve inosine (I) are at the origin of Francis Crick's wobble hypothesis (Crick 1966). Crick proposed that I in the first position of tRNA's anti-codon would form I•A, I•U, and I•C base pairs. Thus, we revisited the wobble hypothesis by studying the thermodynamic stability and the geometry of the above cited base pairs derived from MDSs in explicit water and under neutral conditions. As expected, the results showed that the I•C pair adopted a stability and geometry that was similar to a G•C pair (Fig. 2C; Table 1; Murphy and Ramakrishnan 2004). The I•U base pair displayed Crick's wobble pairing geometry exemplified by G•U. The ribose C1′–C1′ and hydrogen bond distances of I•U were determined to be almost identical to those of G•U (Table 1). However the free energy of the former was lower by ΔΔG ≈ 2 kcal/mol compared with that of the latter. The purine•purine base-pairing of I•A was modeled with the Ianti•Aanti conformation, as had been previously established (Crick 1966; Murphy and Ramakrishnan 2004; Watkins and SantaLucia 2005). The C1′–C1′ distance was 12.90 Å and the ΔG°300°K = 2.82 ± 0.50 kcal/mol, comparable to that of I•U. The magnitude of the energy barrier for base-pair formation with I was dependent on the partner base in the following order: I•C < I•U < I•A (Table 1).
DISCUSSION
This project was undertaken due to the lack of base-pair models that included the distinct chemical contributions and spatial dynamics of the many modifications found in RNAs. In addition, the influence of water on the base-pairing of ribonucleoside 5′-monophosphates, in general, and on modified nucleotide base-pairing as described by molecular mechanics was practically unknown. The molecular dynamics and free energy calculations of the canonical C•G, A•U, and wobble U•G base pairs in water and under neutral conditions closely simulated the stability, geometries, and ribose C1′–C1′ distances of the Watson–Crick and wobble base-pairings found in RNA helices (Saenger 1983) and in the mini-helix of the anti-codon with the codon at the decoding site of the ribosome (Ogle et al. 2001; Murphy and Ramakrishnan 2004; Murphy et al. 2004; Weixlbaumer et al. 2007).
tRNA is the most highly modified of all RNAs (Agris 1996), and its anti-codon modifications are particularly important to the correct translation of the genetic code (Saenger 1983; Targanski and Cherkasova 2008). Francis Crick surmised that “I” at the wobble position of tRNA's anti-codon would expand codon recognition by binding U, C, and A in the third position of the codon (Crick 1966). In Eschirichia coli, only seven codons are read by tRNAs without modifications at position-34 or at the conserved purine-37, 3′-adjacent to the anti-codon (Agris 2004; Sprinzl and Vassilenko 2005). The level of stability of the anti-codon to codon base-pairing, particularly at position-35 in the tRNA, considerably influences the degeneracy of the genetic code (Lehmann and Libchaber 2008). The perturbation generated throughout the ribosome by the wobble base-pair (U34•N3) formation is a major factor for the selection of the base at the third position of the codon (Lehmann and Libchaber 2008). Our results demonstrate that this could be achieved selectivity through thermodynamic stabilization of the wobble base pair by modified bases. The modified nucleotide and its base-pairing affect the stability of the adjacent nucleotide conformation and its base pairs (Smith et al. 1992; Testa et al. 1999); and, thereby, it affects the overall stability of an entire RNA, or the mini-helix of the anti-codon–codon interaction (Smith et al. 1992; Kumar and Davis 1997; Testa et al. 1999; Sipa et al. 2007).
The stability of the U•A base pair was considerably enhanced by the 2-thio-group, s2U•A, found in the wobble position-34 of specific tRNAs in all kingdoms (Agris 1996, 2004; Kumar and Davis 1997; Ashraf et al. 1999; Testa et al. 1999). The low ΔG° values of the various s2U•A base pairs, s2U•A, mnm5s2U•A, and mcm5s2U•A, confirmed that the 2-thiolation enhanced the binding affinity of U for A, no matter the nature of the five-position modification. The ribose C1′–C1′ distances for the s2U, mnm5s2U, and mcm5s2U base pairs with a G averaged greater than 11.25 Å (Table 1). This somewhat larger distance between C1s may be the result of stereochemistry. The van der Waals radius of the thio-group is ∼20% larger than that of the carbonyl oxygen.
Previous molecular dynamics modeling and NMR spectrometry experiments had indicated that lengthy modifications at position-5 of U's could freeze the conformation of the nucleotide and dictate the hydrogen bonding geometry (Murphy et al. 2004; Durant et al. 2005; McCrate et al. 2006; Weixlbaumer et al. 2007; Vendeix et al. 2008). Results from NMR studies of mononucleoside 5′-phosphates had indicated that the mnm5-modification formed a hydrogen bond to the nucleotide's 5′-phosphate and that this additional bond stabilized the ribose C3′-endo sugar pucker. The additional hydrogen bond was thought to produce a conformational “rigidity” that would contribute to accurate codon recognition (Sakamoto et al. 1996). However, in our simulations in water under neutral conditions, the mnm5-group did not approach the 5′-phosphate but was oriented away from the phosphate. The result was a base-pair geometry similar to that of the canonical U•A base pair. Also, our structure was similar to that found at the decoding site in the crystallographic structures of the 30S subunit with the mnm5U34-modified anti-codon stem and loop of tRNALys and the AAA codon (Murphy et al. 2004).
The modeling of the mnm5U•G base pair with MDS generated a ribose C1′–C1′ distance of 10.50 Å. In comparison, the mnm5U•G base pair observed in the crystal structure of the modified tRNAUUULys anti-codon stem–loop when binding to the AAG codon in the decoding site of the 30S subunit exhibited a shorter distance of 10.10 Å (Murphy et al. 2004). This slight difference in distances between the C1′ atoms could be attributed to the presence of water molecules or to the type of force field used during the simulations. There was little to no electron density for the mnm5-group in the crystallographic structure of a mnm5U•G decoding on the ribosome, indicating that a stable hydrogen bond to the 5′-phosphate was not achievable (Murphy et al. 2004). This leads one to the conclusion that tRNA's mnm5U34 and its counterpart in eukaryotes, mcm5U34, effect wobble base-pairing through stereochemistry and restrained local dynamics even though they are composed of a hydrogen donor and a hydrogen acceptor, respectively (Murphy et al. 2004; Sundaram et al. 2000).
Francis Crick believed that the geometry of the anti-codon–codon mini-helix should reflect the continuity of an RNA duplex (Crick 1966). Though he accepted that an I34 would bind A at the third position, creating a broad purine•purine base pair, he was concerned that a pyrimidine•pyrimidine base pair would deform the diameter of the helix by narrowing it. The computed C1′–C1′ distances of the unmodified U•U and U•C base pairs and their modified counterparts were ∼8.9 and ∼9.9 Å, respectively, at the first energy minimum and when hydrogen bonding occurred directly between the two nucleobases. These distances were slightly shorter than that of the shortest distance found within rRNA structures of the ribosome. However, at the second energy minimum, m2, we found that H2O molecule(s) had migrated between the two bases during the simulation, creating a stable hydrogen-bonded bridge (Fig. 4G). As a result, the H2O molecule(s) bridge stably bonded the modified U to the unmodified pyrimidine and increased the ribose C1′–C1′ distance to a length that varied between 11.30 and 12.30 Å. This wider range of base-pair geometry compared favorably to the average C1′–C1′ distances in all crystal structures, 10.60 ± 0.20 Å. Though the distances across the anti-codon–codon mini-helix on the ribosome approach the longer measured lengths, they are still short of those found for the purine•purine interaction of the I34•A3 base pair, 12.3 Å (Cochella and Green 2004; Murphy and Ramakrishnan 2004). Interestingly, the phosphate-to-phosphate distance across the helix changes little for wobble base pairs (Cochella and Green 2004; Murphy and Ramakrishnan 2004). Taken together, one can conclude that the ribosome is tolerant of the wider wobble base-pair geometries of the modified U34•N3 (with a bridging H2O) and I34•A3, but not the narrower, pyrimidine•pyrimidine base pairs found in RNA structures. Thus, Crick's concern about the deformation of the anti-codon–codon mini-helix by pyrimidine•pyrimidine base pairs was insightful, but modification of the wobble position and a bridging of the base pair by water widen the helical diameter to correspond to that of an A-form RNA helix.
The observation of a second energy minimum and the bridging of the canonical, unmodified, and modified base pairs with water may represent an intermediate step common to the formation of all base pairs. No matter the nature of the base pair, a water molecule(s) was (were) detected at the second minimum m2 bridging the bases through hydrogen bonds. Therefore, the incursion of a semistable water bridge represented an inevitable intermediate state between the directly hydrogen bonded and the completely disrupted base pairs. This intermediate state may occur systematically during base-pair formation or disruption in aqueous solution. With regard to modifications such as the free acid of the cmo5U34 modification, the hydrophobicity/hydrophilicity and polarity of modifications are expected to influence their hydration. The hydration sphere of an extensive modification could possibly effect the length of the hydrogen bonds between bases and their formation (Agris 1996). Knowing that the hydration of base pairs is important to their geometry, it may subtly or significantly alter mismatch pairs (Sundaralingam and Pan 2002). Since neutral conditions were achieved solely with Na+, our work does not exclude the possible involvement of divalent metal ion coordination, particularly Mg2+, in the formation and stabilization of modified nucleotide base pairs.
A base pair with a high energy barrier (EB), between the first and the second minimum, will require the use of a substantial force (e.g., in the order of 550 ± 35 pN for AT and 860 ± 40 pN for CG) to disrupt its hydrogen bonds formed at the most stable conformation and vice versa (Stofer et al. 1999). This could explain why the C•G pair, with three strong hydrogen bonds, has a high EB compared to a U•A that is weakly paired with only two hydrogen bonds. Thus, in the case of the modified U•A Watson–Crick base pairs, mnm5U•A has the highest energy barrier and hence the strongest hydrogen bond. In contrast, the most thermodynamically stable s2U•A base pair did not exhibit any energy barrier. Interestingly, the mcm5s2U•A pair that also contains a 2-thiouridine modification displayed an EB comparable to that of U•A and mnm5U•A base pairs. In contrast, the modification mnm5s2 strengthens the hydrogen bonding of U (mnm5s2U) with A at the expense of having a higher free energy. Similarly s2U in s2U•G, mnm5s2U•G, and mcm5s2U•G base pairs increased their respective free energies with a concurrent increase in the energy barrier compared with what was observed for the U•G pair. Thus, the same modification engaged in a base-pairing conformation with A, G, U, or C will not necessarily induce the same chemical, physical, and thermodynamic effects on each of these bases (Table 1). Our results also suggest that the s2U alone and in concert with a 5-position modification contribute to the stabilization of RNA base-pairing, such as the codon–anti-codon mini-helix, either through base stacking or base-pairing depending on the nature of the base to which it is hydrogen bound.
The melting temperature Tm and the relative thermodynamic stability (ΔGo) of the nucleic acid duplexes depend on the ionic strength and pH. More precisely, Tm and ΔGo should increase with the [Na+] concentration because cations electrostatically shield the anionic phosphates groups of the nucleotides and minimize their repulsions (SantaLucia 1998). Knowing this, it is clear that different ion concentrations will have significant effects on the base-pair thermodynamics. Our goal was to determine the ΔG of modified base pairs under neutral condition that is defined according to the AMBER 9 algorithms. Trying to compensate for absolute differences between theoretical and empirical conditions (for example, by adding extra Na+ ions) is beyond the scope of this article.
These models and their properties in water and under neutral conditions further the understanding of the thermodynamic contributions and the geometry of the wobble base-pair formation during the decoding process. They can be used in the development or improvement of computational algorithms that are designed to accurately predict the thermodynamic stability of progressively larger RNA structures and their functional interactions, especially those in which modified nucleotides are involved. Though our calculations have taken into account water and ions, it is important to include base stacking in future determinations of the effect of modifications on RNA base-pairing and structure. The full thermodynamic and conformational data of these and larger structures rendered through MDS will be made available to the scientific community through the RNA Modification Database (Rozenski et al. 1999), a web-based databank soon to be revised, with links to databanks of canonical and noncanoncal base pairs (Berman et al. 1992; Nagaswamy et al. 2000, 2002; Xin and Olson 2009).
MATERIALS AND METHODS
The MDS and the free energy calculations were conducted on the IBM Blade Center Linux Cluster (Henry2) at the High-Performance Computing center of North Carolina State University (for more details about the configuration of the system, please refer to http://www.ncsu.edu/itd/hpc/main.php). The methods used for MDS and base-pair free energy calculations were based on published protocols (Stofer et al. 1999). The force field parameters 99 (ff99) that are available in the AMBER 9 package (Case et al. 2005) were used to carry out MDSs on 25 sets of base pairs. X-ray and NMR structures were used for initial geometries when available, otherwise the nucgen module of AMBER 9 was used for building nonmodified base-pair helices from which sample pairs were used for study. All pairs were solvated and neutralized using the AMBER 9 xleap module to render the pairs. Modifications were added by replacing individual molecule designations in unmodified base Protein Data Bank (PDB) files with those from the RNA modified parameters database (Aduri et al. 2007) and were matched by comparison using Chimera (Pettersen et al. 2004) to produce new functional PDB files. Bases were initially minimized in vacuum to reach optimum geometries from which periodic restraint angles were determined. A harmonic potential restraint of 50 kcal/mol Å2 was used to restrain specified atoms in Cartesian space to keep bases from stacking, while allowing both distance fluctuation and propeller movement. After an initial minimization in vacuum, bases were neutralized with sodium and solvated with TIP3P (Jorgensen et al. 1983) water in an octahedral box. The TIP5P (Mahoney and Jorgensen 2000) water model, though an excellent tool to accurately define the geometries involving water mediated hydrogen bonds, was not included in this study because it requires at least twice the computational time that is used in the case of the TIP3P model. It has to be noted that in the case of modifications with the 2-thio group, it is likely that a substantial polarization change upon H-bonding will not be well accounted for by the fixed point charge model. Since water molecules were involved in the simulations, the SHAKE algorithm was also used to constrain bonds involving hydrogen. The particle mesh ewald (PME) algorithm with a cutoff of 12 was used (for each base-pair model) to treat the long range nonbonded and van der Waals (VdW) interactions. Solvated bases were then minimized in two steps. First, positional restraints were used on the bases while relaxing hydrogen bonds in the water molecules, and second, a relaxation of the whole solvated system was unrestrained. Subsequent to the above step, MDSs were then performed after minimization with a gradual heating step (0–300°K) with positional restraints and a force constant (50 kcal/mol Å2) for 10 psec. The Langevin thermostat was used to control the temperature with a collision frequency of 1.0 psec−1. Positional restraints were reduced progressively and stepwise (50 to 10, and 5 kcal/mol Å2). Each decrease of positional restraint constant was followed by 25 psec of equilibration, until the final step was completely unrestrained, and the total time of simulation was equal to 100 psec. The final structures were then analyzed for equilibrium achievement and then utilized in the umbrella sampling method of free energy calculation (Kumar et al. 1992, 1995; Roux 1995). A nonperiodic reaction coordinate, the hydrogen bond (hb) distance as it is the case in our study, was used to determine the PMF. A 40-psec MDS was run following the 100-psec equilibration MD, for each distance that represents a window. Within each window, the biasing of the reaction coordinate caused by the distance restraint was recorded every five steps of a 20,000-step simulation. Thus 4000 biased coordinates were obtained in each of the 65 windows.
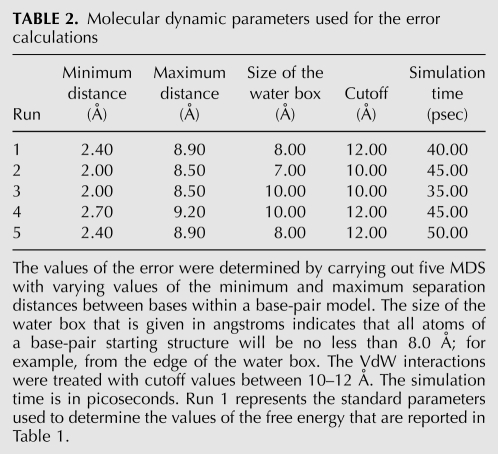
The hb distances were defined between two heteroatoms. For example in C•G and analog modified base pairs, the hbs are defined as N4–O6; N3–N1; O2–N2. The most central bond is defined by N3–N1. In the case of U•A and modified analog base pairs, the hbs are O2–N6 and N3–N1, and the most central bond is N3–N1. For unmodified and modified U•U, U•C, and U•G base pairs the most central hb was defined by N3–O2, N3–N3, and O2–N1 respectively. The hb distance for the most central bond was stretched from 2.4–8.9 Å using 0.1 Å step increments. A harmonic potential restraint with a force constant of 20 kcal/mol Å2 was used to maintain base separation; otherwise the simulation was identical to the final step of MDS. The PMF, hence the free energy, was obtained by processing the biased reaction-coordinates with the WHAM algorithm (C++ code by Dr. Alan Grossfield, University of Rochester Medical Center) (Kumar et al. 1992, 1995; Roux 1995). The WHAM iteration is considered to be converged when no Fi (potential) value for any simulation window changes by more than the convergence tolerance value (tol) on consecutive iterations. The value of our tol value, that is 0.00001, was determined by rerunning WHAM with small tolerance values and compared the resulting PMFs. The results of our WHAM calculations shows (1) no Fi values for any simulation window changed more than the convergence tolerance value on consecutive iterations, and (2) the free energy curves of each iteration stopped varying. Therefore, the fulfillment of these two conditions allowed us to conclude that sufficient sampling was generated and the free energy calculations converged. The errors on the values of free energy was determined as previously published (Stofer et al. 1999) and found to vary between ±0.30 and ±0.90 kcal/mol.
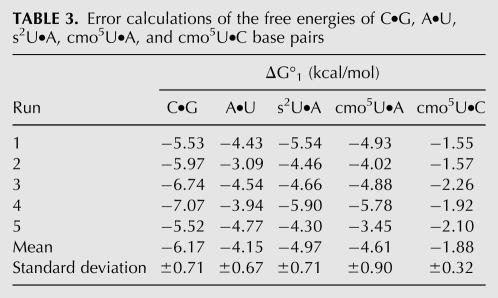
Errors are reported relative to the different simulation protocols (change in simulation time, maximum and minimum base separation distances, size of the water box and cut off) that were run to determine the ΔG of a given base pair (Tables 2, 3). The error is not related to the successive repetition of a given simulation using the same simulation protocol. The errors were determined for C•G, U•A, s2U•A, cmo5U•A and cmo5U•C base pairs. Our results are consistent with what was previously published on Watson–Crick base pairs (Stofer et al. 1999), and the errors are within the approximations inherent in the AMBER force field.
TABLE 2.
Molecular dynamic parameters used for the error calculations
TABLE 3.
Error calculations of the free energies of C•G, A•U, s2U•A, cmo5U•A, and cmo5U•C base pairs
ACKNOWLEDGMENTS
We thank Drs. Eric Sills and Gary Howell for their technical support at the High-Performance Computing Center at North Carolina State University, Dr. Alan Grossfield for his advice on the utilization of WHAM, Dr. Eric Westhof for conversations on noncanonical base-pairing, and Dr. John Santa Lucia for his suggestions for the manuscript. This work was supported by grants from the National Institutes of Health (2-RO1-GM23037) to P.F.A. and the National Science Foundation to co-investigators Carol Hall and P.F.A. (CBET-0835794) and to P.F.A. (MCB-0548602).
Footnotes
Abbreviations: cmo5U34, uridine 5-oxyacetic acid at wobble position 34; mcm5U34, 5-methoxycarbonylmethyl-uridine; mcm5s2U34, 5-methoxycarbonylmethyl-2-thiouridine; mnm5U34, 5-methylaminomethyl-uridine; mnm5s2U34, 5-methylaminomethyl-2-thiouridine; Pur37, purine ribonucleoside (A or G) at position-37; s2U34, 2-thiouridine.
Article published online ahead of print. Article and publication date are at http://www.rnajournal.org/cgi/doi/10.1261/rna.1734309.
REFERENCES
- Aduri R, Psciuk BT, Saro P, Taniga H, Schlegel HB, SantaLucia J. AMBER force field parameters for the naturally occurring modified nucleosides in RNA. J Chem Theory Comput. 2007;3:1464–1475. doi: 10.1021/ct600329w. [DOI] [PubMed] [Google Scholar]
- Agris PF. Wobble position modified nucleosides evolved to select transfer RNA codon recognition: A modified-wobble hypothesis. Biochimie. 1991;73:1345–1349. doi: 10.1016/0300-9084(91)90163-u. [DOI] [PubMed] [Google Scholar]
- Agris PF. The importance of being modified: roles of modified nucleosides and Mg2+ in RNA structure and function. Prog Nucleic Acid Res Mol Biol. 1996;53:79–129. doi: 10.1016/s0079-6603(08)60143-9. [DOI] [PubMed] [Google Scholar]
- Agris PF. Decoding the genome: A modified view. Nucleic Acids Res. 2004;32:223–238. doi: 10.1093/nar/gkh185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Agris PF, Vendeix FA, Graham WD. tRNA's wobble decoding of the genome: Forty years of modification. J Mol Biol. 2007;366:1–13. doi: 10.1016/j.jmb.2006.11.046. [DOI] [PubMed] [Google Scholar]
- Arora N, Jayaram B. Energetics of base pairs in B-DNA in solution: An appraisal of potential functions and dielectric treatments. J Phys Chem B. 1998;102:6139–6144. [Google Scholar]
- Ashraf SS, Sochacka E, Cain R, Guenther R, Malkiewicz A, Agris PF. Single atom modification (O→S) of tRNA confers ribosome binding. RNA. 1999;5:188–194. doi: 10.1017/s1355838299981529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Auffinger P, Westhof E. Simulations of the molecular dynamics of nucleic acids. Curr Opin Struct Biol. 1998;8:227–236. doi: 10.1016/s0959-440x(98)80044-4. [DOI] [PubMed] [Google Scholar]
- Berman HM, Olson WK, Beveridge DL, Westbrook J, Gelbin A, Demeny T, Hsieh SH, Srinivasan AR, Schneider B. The nucleic acid database. A comprehensive relational database of three-dimensional structures of nucleic acids. Biophys J. 1992;63:751–759. doi: 10.1016/S0006-3495(92)81649-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Case DA, Cheatham TE, III, Darden T, Gohlke H, Luo R, Merz KM, Jr, Onufriev A, Simmerling C, Wang B, Woods RJ. The AMBER biomolecular simulation programs. J Comput Chem. 2005;26:1668–1688. doi: 10.1002/jcc.20290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cochella L, Green R. Wobble during decoding: More than third-position promiscuity. Nat Struct Mol Biol. 2004;11:1160–1162. doi: 10.1038/nsmb1204-1160. [DOI] [PubMed] [Google Scholar]
- Crick FH. Codon–anticodon pairing: The wobble hypothesis. J Mol Biol. 1966;19:548–555. doi: 10.1016/s0022-2836(66)80022-0. [DOI] [PubMed] [Google Scholar]
- Durant PC, Bajji AC, Sundaram M, Kumar RK, Davis DR. Structural effects of hypermodified nucleosides in the Escherichia coli and human tRNALys anticodon loop: The effect of nucleosides s2U, mcm5U, mcm5s2U, mnm5s2U, t6A, and ms2t6A. Biochemistry. 2005;44:8078–8089. doi: 10.1021/bi050343f. [DOI] [PubMed] [Google Scholar]
- Giudice E, Lavery R. Nucleic acid base-pair dynamics: The impact of sequence and structure using free-energy calculations. J Am Chem Soc. 2003;125:4998–4999. doi: 10.1021/ja034095r. [DOI] [PubMed] [Google Scholar]
- Giudice E, Varnai P, Lavery R. Base-pair opening within B-DNA: Free energy pathways for GC and AT pairs from umbrella sampling simulations. Nucleic Acids Res. 2003;31:1434–1443. doi: 10.1093/nar/gkg239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gustilo EM, Vendeix FA, Agris PF. tRNA's modifications bring order to gene expression. Curr Opin Microbiol. 2008;11:134–140. doi: 10.1016/j.mib.2008.02.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of simple potential functions for simulating liquid water. J Chem Phys. 1983;79:926–935. [Google Scholar]
- Kumar RK, Davis DR. Synthesis and studies on the effect of 2-thiouridine and 4-thiouridine on sugar conformation and RNA duplex stability. Nucleic Acids Res. 1997;25:1272–1280. doi: 10.1093/nar/25.6.1272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar S, Bouzida D, Swendsen RH, Kollman PA, Rosenberg JM. The weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J Comput Chem. 1992;13:1011–1021. [Google Scholar]
- Kumar S, Rosenberg JM, Bouzida D, Swendsen RH, Kollman PA. Multidimensional free-energy calculations using the weighted histogram analysis method. J Comput Chem. 1995;16:1339–1350. [Google Scholar]
- Laserson U, Gan HH, Schlick T. Predicting candidate genomic sequences that correspond to synthetic functional RNA motifs. Nucleic Acids Res. 2005;33:6057–6069. doi: 10.1093/nar/gki911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lehmann J, Libchaber A. Degeneracy of the genetic code and stability of the base pair at the second position of the anticodon. RNA. 2008;14:1264–1269. doi: 10.1261/rna.1029808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leontis NB, Westhof E. Geometric nomenclature and classification of RNA base pairs. RNA. 2001;7:499–512. doi: 10.1017/s1355838201002515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leontis NB, Stombaugh J, Westhof E. The non-Watson–Crick base pairs and their associated isostericity matrices. Nucleic Acids Res. 2002;30:3497–3531. doi: 10.1093/nar/gkf481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mahoney MW, Jorgensen WL. A five-site model for liquid water and the reproduction of the density anomaly by rigid, nonpolarizable potential functions. J Chem Phys. 2000;112:8910–8922. [Google Scholar]
- Mathews DH, Case DA. Nudged elastic band calculation of minimal energy paths for the conformational change of a GG noncanonical pair. J Mol Biol. 2006;357:1683–1693. doi: 10.1016/j.jmb.2006.01.054. [DOI] [PubMed] [Google Scholar]
- McCrate NE, Varner ME, Kim KI, Nagan MC. Molecular dynamics simulations of human tRNAUUULys,3: The role of modified bases in mRNA recognition. Nucleic Acids Res. 2006;34:5361–5368. doi: 10.1093/nar/gkl580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McDowell SE, Spackova N, Sponer J, Walter NG. Molecular dynamics simulations of RNA: An in silico single molecule approach. Biopolymers. 2007;85:169–184. doi: 10.1002/bip.20620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy FV, Ramakrishnan V. Structure of a purine–purine wobble base pair in the decoding center of the ribosome. Nat Struct Mol Biol. 2004;11:1251–1252. doi: 10.1038/nsmb866. [DOI] [PubMed] [Google Scholar]
- Murphy FV, Ramakrishnan V, Malkiewicz A, Agris PF. The role of modifications in codon discrimination by tRNAUUULys,3. Nat Struct Mol Biol. 2004;11:1186–1191. doi: 10.1038/nsmb861. [DOI] [PubMed] [Google Scholar]
- Nagaswamy U, Voss N, Zhang Z, Fox GE. Database of noncanonical base pairs found in known RNA structures. Nucleic Acids Res. 2000;28:375–376. doi: 10.1093/nar/28.1.375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagaswamy U, Larios-Sanz M, Hury J, Collins S, Zhang Z, Zhao Q, Fox GE. NCIR: A database of noncanonical interactions in known RNA structures. Nucleic Acids Res. 2002;30:395–397. doi: 10.1093/nar/30.1.395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nobles KN, Yarian CS, Liu G, Guenther RH, Agris PF. Highly conserved modified nucleosides influence Mg2+-dependent tRNA folding. Nucleic Acids Res. 2002;30:4751–4760. doi: 10.1093/nar/gkf595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ogle JM, Brodersen DE, Clemons WM, Jr, Tarry MJ, Carter AP, Ramakrishnan V. Recognition of cognate transfer RNA by the 30S ribosomal subunit. Science. 2001;292:897–902. doi: 10.1126/science.1060612. [DOI] [PubMed] [Google Scholar]
- Patey GN, Valleau JP. A Monte Carlo method for obtaining the interionic potential of mean force in ionic solution. J Chem Phys. 1975;63:2334–2339. [Google Scholar]
- Perez A, Lankas F, Luque FJ, Orozco M. Toward a molecular dynamics consensus view of B-DNA flexibility. Nucleic Acids Res. 2008;36:2379–2394. doi: 10.1093/nar/gkn082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pettersen EF, Goddard TD, Huang CC, Couch GS, Greenblatt DM, Meng EC, Ferrin TE. UCSF chimera—a visualization system for exploratory research and analysis. J Comput Chem. 2004;25:1605–1612. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
- Rhodes MM, Reblova K, Sponer J, Walter NG. Trapped water molecules are essential to structural dynamics and function of a ribozyme. Proc Natl Acad Sci. 2006;103:13380–13385. doi: 10.1073/pnas.0605090103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roux B. The calculation of the potential of mean force using computer simulations. Comput Phys Commun. 1995;91:275–282. [Google Scholar]
- Rozenski J, Crain PF, McCloskey JA. The RNA Modification Database: 1999 update. Nucleic Acids Res. 1999;27:196–197. doi: 10.1093/nar/27.1.196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saenger W. Principles of nucleic acid structure. Springer; New York: 1983. [Google Scholar]
- Sakamoto K, Kawai G, Watanabe S, Niimi T, Hayashi N, Muto Y, Watanabe K, Satoh T, Sekine M, Yokoyama S. NMR studies of the effects of the 5′-phosphate group on conformational properties of 5-methylaminomethyluridine found in the first position of the anticodon of Escherichia coli tRNA4Arg. Biochemistry. 1996;35:6533–6538. doi: 10.1021/bi9526490. [DOI] [PubMed] [Google Scholar]
- Sanbonmatsu KY, Joseph S. Understanding discrimination by the ribosome: Stability testing and groove measurement of codon–anticodon pairs. J Mol Biol. 2003;328:33–47. doi: 10.1016/s0022-2836(03)00236-5. [DOI] [PubMed] [Google Scholar]
- SantaLucia J., Jr A unified view of polymer, dumbbell, and oligonucleotide DNA nearest-neighbor thermodynamics. Proc Natl Acad Sci. 1998;95:1460–1465. doi: 10.1073/pnas.95.4.1460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sipa K, Sochacka E, Kazmierczak-Baranska J, Maszewska M, Janicka M, Nowak G, Nawrot B. Effect of base modifications on structure, thermodynamic stability, and gene silencing activity of short interfering RNA. RNA. 2007;13:1301–1316. doi: 10.1261/rna.538907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith WS, Sierzputowska-Gracz H, Sochacka E, Malkiewicz A, Agris PF. Chemistry and structure of modified uridine dinucleosides are determined by thiolation. J Am Chem Soc. 1992;114:7989–7997. [Google Scholar]
- Sprinzl M, Vassilenko KS. Compilation of tRNA sequences and sequences of tRNA genes. Nucleic Acids Res. 2005;33:D139–D140. doi: 10.1093/nar/gki012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stofer E, Chipot C, Lavery R. Free energy calculations of Watson–Crick base-pairing in aqueous solution. J Am Chem Soc. 1999;121:9503–9508. [Google Scholar]
- Sundaralingam M, Pan B. Hydrogen and hydration of DNA and RNA oligonucleotides. Biophys Chem. 2002;95:273–282. doi: 10.1016/s0301-4622(01)00262-9. [DOI] [PubMed] [Google Scholar]
- Sundaram M, Durant PC, Davis DR. Hypermodified nucleosides in the anticodon of tRNALys stabilize a canonical U-turn structure. Biochemistry. 2000;39:12575–12584. doi: 10.1021/bi0014655. [DOI] [PubMed] [Google Scholar]
- Targanski I, Cherkasova V. Analysis of genomic tRNA sets from Bacteria, Archaea, and Eukarya points to anticodon–codon hydrogen bonds as a major determinant of tRNA compositional variations. RNA. 2008;14:1095–1109. doi: 10.1261/rna.896108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Testa SM, Disney MD, Turner DH, Kierzek R. Thermodynamics of RNA-RNA duplexes with 2- or 4-thiouridines: Implications for antisense design and targeting a group I intron. Biochemistry. 1999;38:16655–16662. doi: 10.1021/bi991187d. [DOI] [PubMed] [Google Scholar]
- Torrie GM, Valleau JP. Monte Carlo free energy estimates using non-Boltzmann sampling: Application to the subcritical Lennard-Jones fluid. Chem Phys Lett. 1974;28:578–581. [Google Scholar]
- Valleau JP, Card DN. Monte Carlo estimation of the free energy by multistage sampling. J Chem Phys. 1972;57:5457–5462. [Google Scholar]
- Varnai P, Canalia M, Leroy JL. Opening mechanism of G•T/U pairs in DNA and RNA duplexes: A combined study of imino proton exchange and molecular dynamics simulation. J Am Chem Soc. 2004;126:14659–14667. doi: 10.1021/ja0470721. [DOI] [PubMed] [Google Scholar]
- Vendeix FA, Dziergowska A, Gustilo EM, Graham WD, Sproat B, Malkiewicz A, Agris PF. Anticodon domain modifications contribute order to tRNA for ribosome-mediated codon binding. Biochemistry. 2008;47:6117–6129. doi: 10.1021/bi702356j. [DOI] [PubMed] [Google Scholar]
- Watkins NE, Jr, SantaLucia J., Jr Nearest-neighbor thermodynamics of deoxyinosine pairs in DNA duplexes. Nucleic Acids Res. 2005;33:6258–6267. doi: 10.1093/nar/gki918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weixlbaumer A, Murphy FV, Dziergowska A, Malkiewicz A, Vendeix FA, Agris PF, Ramakrishnan V. Mechanism for expanding the decoding capacity of transfer RNAs by modification of uridines. Nat Struct Mol Biol. 2007;14:498–502. doi: 10.1038/nsmb1242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xin Y, Olson WK. BPS: A database of RNA base-pair structures. Nucleic Acids Res. 2009;37:D83–D88. doi: 10.1093/nar/gkn676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yarian CS, Basti MM, Cain RJ, Ansari G, Guenther RH, Sochacka E, Czerwinska G, Malkiewicz A, Agris PF. Structural and functional roles of the N1- and N3-protons of ψ at tRNA's position 39. Nucleic Acids Res. 1999;27:3543–3549. doi: 10.1093/nar/27.17.3543. [DOI] [PMC free article] [PubMed] [Google Scholar]