Molecular dynamics studies of the conformation of sorbitol

Abstract

Molecular dynamics simulations of a 3 m aqueous solution of D-sorbitol (also called D-glucitol) have been performed at 300 K, as well as at two elevated temperatures to promote conformational transitions. In principle, sorbitol is more flexible than glucose since it does not contain a constraining ring. However, a conformational analysis revealed that the sorbitol chain remains extended in solution, in contrast to the bent conformation found experimentally in the crystalline form. While there are 243 staggered conformations of the backbone possible for this open-chain polyol, only a very limited number were found to be stable in the simulations. Although many conformers were briefly sampled, only eight were significantly populated in the simulation. The carbon backbones of all but two of these eight conformers were completely extended, unlike the bent crystal conformation. These extended conformers were stabilized by a quite persistent intramolecular hydrogen bond between the hydroxyl groups of carbon C-2 and C-4. The conformational populations were found to be in good agreement with the limited available NMR data except for the C-2–C-3 torsion (spanned by the O-2–O-4 hydrogen bond), where the NMR data supports a more bent structure.

I. Introduction

The sugar alcohol sorbitol, or D-glucitol (C₆H₁₄O₆), is the hexitol formed by the reduction of the free aldehyde group of D-glucose (C₆H₁₂O₆; see Figure 1)¹. Like other polyols (glycerol, mannitol), it is highly soluble in water and penetrates freely across cell membranes. Although its chemical composition is close to that of glucose, its topology differs significantly, since it is not capable of forming hemiacetal ring structures. This major difference could, in principle, lead to greater flexibility than glucose arising from additional conformational degrees of freedom. Glucose is mostly found in the ⁴C₁ pyranose ring form in aqueous solution, which locks the hydroxyl groups and aliphatic protons into specific relative positions. In sorbitol, however, the molecule could undergo conformational rotations about each of the C-C single bonds, potentially allowing significant conformational flexibility. This difference in molecular topology and its implications for molecular flexibility could have consequences for the physical properties of these two molecules, and in particular for their solvation behavior in water.

Figure 1.

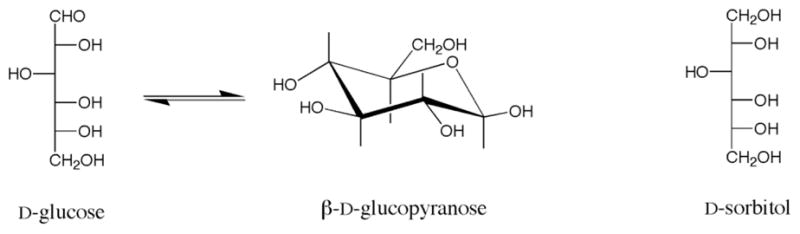
The structures of D-glucose and D-sorbitol.

Molecular dynamics (MD) simulations have proven to be quite valuable in describing the detailed molecular behavior in solutions of complex biological molecules like sorbitol. Various MD simulation studies have confirmed the stability of the pyranose ring conformation of glucose and have shown that the fixed relative positions of the functional groups of the ring impose extensive structuring on adjacent solvent water molecules, primarily through hydrogen bonding.^2–7 This solvent structuring is dependent not only on the sugar stereochemistry, but also on the ring conformation.⁴ Such structuring has been shown to have significant effects on the energetics of the conformational equilibrium.^2,3 These effects are a complex function of the molecular topology in each conformation, and may differ substantially in the case of the potentially more flexible sorbitol molecule from those seen for glucopyranose.

One important conformational difference arising from the different covalent topologies of the two solute molecules would be in their different potentials for intramolecular hydrogen bonding. For both molecules, any intramolecular hydrogen bonds would be in competition with hydrogen bonds to the solvent water. In glucose in the ⁴C₁ conformation, intramolecular hydrogen bonding between adjacent hydroxyl groups around the periphery of the rings has been observed in both simulations and NMR experiments in non-aqueous solutions.⁸ However, the ring forces such bonds into sub-optimal, non-linear geometries with energies substantially reduced relative to optimal hydrogen bonds. The much greater potential flexibility of sorbitol raises the possibility of the formation of nearly linear intramolecular hydrogen bonds for some conformations. In these cases, the competition between intramolecular hydrogen bonds and those to solvent could make a substantial contribution to the conformational equilibrium.

Sorbitol has been modeled previously using MD simulations. Grigera reported from a relatively short simulation that the conformation of sorbitol in water is bent,⁹ as observed in crystalline forms of pure sorbitol.^10–12 More recently, Sixou et al. have shown that the C-1–H bond vectors in sorbitol reorient faster than the C-4–H bond vectors at T = 400 K, in agreement with ¹³C NMR measurements.^13,14 These workers concluded that the main contribution to the C-1–H reorientation is associated with local conformational transitions. Recently, Shah and Roberts found that the excess chemical potential, μ₂^ex, of apolar solutes increases monotonically with sorbitol concentration, in line with its stabilization effect on proteins.¹⁵ None of these previous simulations studied the structuring of water around sorbitol or any possible effects that it may have on the molecular conformation.

We report here new MD simulations of sorbitol in a 3 molal (m) aqueous solution at 300 K, using a slightly modified version of the CHARMM-type CSFF force field,¹⁶ to examine the conformational structure and flexibility of the polyol compared to that of glucose in similar solutions. The conformational space of sorbitol was first investigated to determine whether its solution conformation is similar to its crystalline one. The water-sugar interactions in the sorbitol and glucose solutions were also analyzed and compared to investigate the influence of the solute’s topology on its solution properties. A secondary goal of the simulations was to determine whether the simplistic, ad hoc force field used in the simulations was sufficiently realistic to reproduce known experimental properties of sorbitol, or whether a new parameter set for polyols will be required. Several types of experimental data exist for comparison purposes. These include crystal structures for sorbitol,^{10–12,17 13}C NMR relaxation times for pure (neat) liquid sorbitol,^13,14 and additional ¹C NMR data concerning the populations of conformers in aqueous solution.^18–20

II. Computational Procedures

MD simulations of a water/sorbitol solution at 3 m were performed in the (N,V,E) ensemble, where the number of particles N, the volume V and the total energy E were constant. This relatively high concentration was simulated to facilitate future comparisons with neutron diffraction experiments. 36 sorbitol molecules in one of the reported crystallographic conformations^10–12 were first randomly placed so that the minimum distance between any atoms of two different sorbitol molecules was greater than 3.5 Å. These solute coordinates were superimposed on an equilibrated cubic box of 950 water molecules. Water molecules whose oxygen atoms were closer than 2.2 Å to any solute heavy atom were deleted. The minimal distance of the overlap criterion was chosen to achieve the desired concentration. The resulting system consisted of 36 sorbitol and 667 water molecules in a cube whose side length was 30.0388 Å, which yielded the experimentally-measured density (1.137 g.cm⁻³)²¹. The CSFF glucose force field was used to simulate sorbitol molecules,¹⁶ and water molecules were represented by the modified TIP3P model.^22,23 The CSFF force field was developed to describe pyranose sugars, and was not optimized for linear sugar alcohols. However, since no alternate CHARMM parameters for polyols were available, these parameters were used here. Thus, the torsion potential of the O-C-C-O dihedral angles was approximated by assuming it to be equal to the glucose OES-CTS-CPS-OHS potential of the CSFF force field,¹⁶ given in Table 1, which was adjusted to match the experimental equilibrium rotamer populations and rotational frequencies of the glucose primary alcohol group.

Table 1.

Parameters of the O-C-C-O dihedral potential in sorbitol (E_dih = Σ k_n(1+cos(nφ − φ₀)), n =1,2,3). The force constants of the OHS-CTS-CTS-OHS potential in glucose are also given in parentheses for comparison.

Dihedral angle	kn (kcal/mol)	Periodicity (n)	Phase angle φ0 (degrees)
O-C-C-O	−4.0193 (−4.9362)	1	0.0
	−1.2688 (+0.2907)	2	0.0
	−0.9704 (+0.4638)	3	0.0

All simulations were performed using the CHARMM program.²⁴ The lengths of covalent bonds involving hydrogen atoms were kept fixed using the SHAKE algorithm²⁵ and a time step of 1 fs was used to integrate the Newtonian equations of motion. All van der Waals and electrostatic interactions in these electrically-neutral systems were smoothly truncated on a neutral group basis using switching functions from 12.5 to 14.5 Å. Initial configurations were first minimized with the steepest descent algorithm to remove bad local contacts and then thermalized from 0 to 300 K during 5 ps, with a 5 K temperature increase every 40 steps. The simulation was then run for 4 ns. The first 200 ps were taken as equilibration and the remaining 3.8 ns were used for analysis. Two additional simulations at 500 and 600 K were performed during 2 ns to cross some high energy barriers and thus to improve the conformational sampling of sorbitol molecules. For comparison, a 500 ns simulation of one sorbitol molecule in vacuum at 300 K using Langevin dynamics with a collision frequency of 5 ps⁻¹ was also computed. Finally, a previous 2 ns simulation of a 3 m glucose solution, described in detail in reference (7) was extended to 4 ns and used here for a comparative analysis.^2–7

III. Results and Discussion

1. Conformational space of sorbitol

a. Distribution of dihedral angles

Sorbitol is likely to exhibit a rich conformational behavior because of the large degree of internal flexibility that may arise from rotations around each C-C bond of the backbone. Its conformational space can be described by a series of 5 dihedral angles which can combine to give a total of 243 (3⁵) conformations, assuming that each dihedral angle has three staggered minimum energy conformers (gauche+ (g⁺), gauche− (g⁻), and trans (t), at −60°, +60° and 180°, respectively), and neglecting the rotamers arising from the different orientations of each hydroxyl group. The φ_i dihedral angles were defined here as the angles: φ₁ = O-1–C-1–C-2–C-3, φ₂ = C-1–C-2–C-3–C-4, φ₃ = C-2–C-3–C-4–C-5, φ₄ = C-3–C-4–C-5–C-6, φ₅ = C-4–C-5–C-6–O-6. Figure 2 shows the labeling of the sorbitol heavy atoms. The carbon backbone is therefore specified by φ₂ through φ₄; when these dihedrals are all trans the conformation is denoted as “fully extended”.

Figure 2.

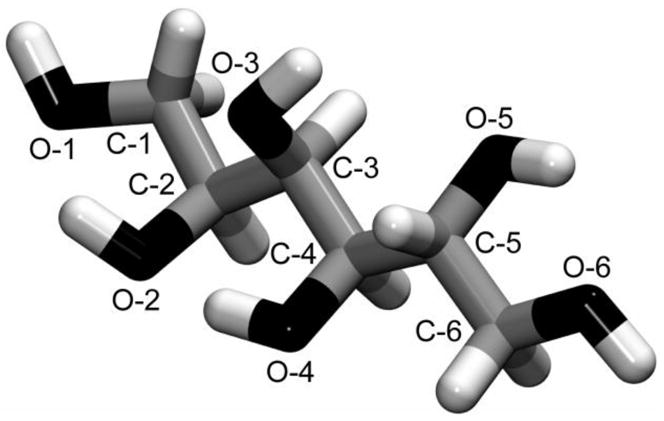
Schematic representation of D-sorbitol. Oxygen, carbon and hydrogen atoms are displayed in black, grey and white, respectively. Only heavy atoms are labeled for clarity reasons. Hydrogen atoms covalently bonded to an oxygen atom O-i are denoted here as HO-i.

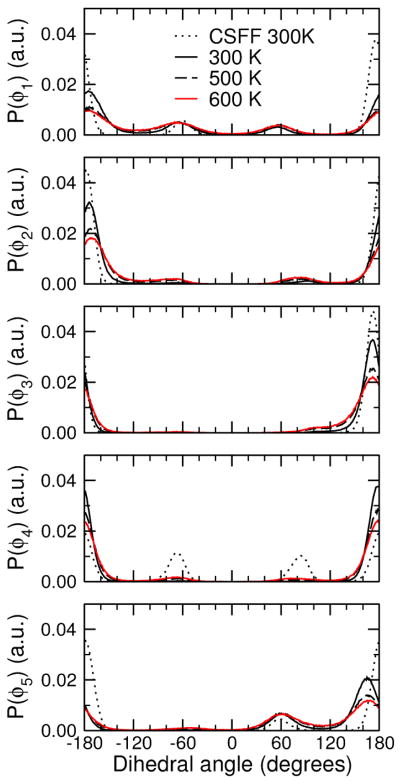
There are several known crystal polymorphs for sorbitol in different conformations.^10–12,17 Sorbitol may crystallize in two hydrated forms (called hydrates I and II) and five anhydrous forms (A, B, Γ, Δ and E). Among the reported crystal structures (hydrate I, A, E, and Γ), sorbitol is mostly found to have a bent-chain conformation: tg⁻ttt in the A form, tg⁻ttg⁺ in the Γ and hydrate I forms, and in one of the two molecules of the asymmetric unit of the E form, and finally has an almost linear carbon chain ttttg⁺ in the other molecule of the E form. The conformation of sorbitol in the starting structure for the simulations of the 3 m solution was taken from a simulation of sorbitol in vacuum and was linear (ttttt). Although all of the sorbitol molecules originally started out in this conformation, during the course of the simulation they underwent numerous transitions to other conformations, so that the reported results do not greatly depend on the initial conformation chosen for the sorbitol molecules (additional simulations, not reported in this paper, with sorbitol molecules initially in the tg⁻ttt conformation of the A crystal gave very similar results). The distributions of these dihedral angles averaged over the course of the simulations at 300, 500 and 600 K are shown in Figure 3. The change in the O-C-C-O torsion potential resulted in a significant broadening of the dihedral distributions, which was more marked for the dihedral angles at the extremities of the molecule (dihedral angles φ₁ and φ₅). This may partly arise from the fact that C-C-C-C torsion potentials also contribute to the total dihedral potential for central C-C bonds, namely C-2–C-3, C-3–C-4 and C-4–C-5, but not for the two C-C bonds at the extremities, C-1–C-2 and C-5–C-6. The effect of a temperature rise of 200 or 300 K was also a broadening of the distributions, although much less important. These results suggest that the conformations sampled by sorbitol molecules at 300 K are reasonably representative of the most stable sorbitol conformations and are not an artifact of inadequate sampling due to the starting structure or to the length of the simulation.

Figure 3.

Distributions of the dihedral angles φ₁ (O-1–C-1–C-2–C-3), φ₂ (C-1–C-2–C-3–C-4), φ₃ (C-2–C-3–C-4–C-5), φ₄ (C-3–C-4–C-5–C-6) and φ₅ (C-4–C-5–C-6–O-6) averaged over the different simulations at 300, 500 and 600 K. The distributions at 300 K with the standard CSFF force field are also represented for comparison (dotted curves).

b. Sampled conformations

The conformations sampled by the sorbitol molecules were defined using the distributions of dihedral angles φ_i shown in Figure 3. A given dihedral angle was ascribed to a gauche+, gauche−, or trans conformation if it lay within the 120° interval centered on −60°, + 60° or 180°, respectively. As pointed out above, the dihedral angles φ_i do not fully describe the entire conformational space of sorbitol since the exchangeable hydrogen atoms HO-i of the hydroxyl groups are able to rotate about the O-i–C-i bonds. However, the present analysis will be limited to the heavy atom conformational space.

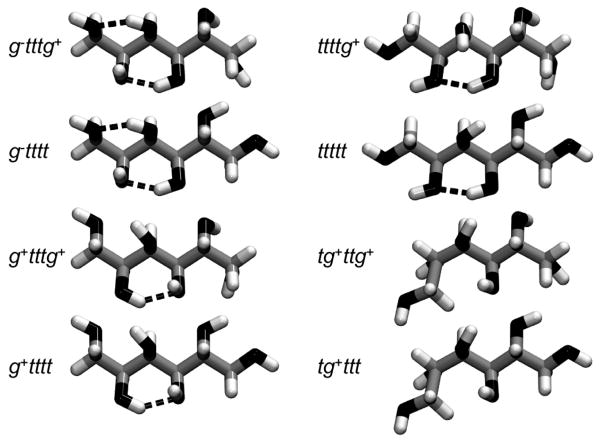
The 243 primary conformations defined by the heavy atom torsional minima were not all occupied, and those that were present were not populated equally. In fact, only a handful of these conformers occurred with significant frequencies. The relative population of the different conformers sampled at ambient temperature is likely to be dependent on such factors as the steric hindrance between groups attached to neighboring carbons i and j, as well as on the formation of intramolecular hydrogen bonds or hydrogen bonds with the solvent. The population of each of the 243 primary conformers in the different simulations was computed, and it was found that eight conformations are preferentially populated at 300 K, and represent 95 % of the minima explored (see Table 2). These different conformations are relatively close to each other in the conformational space and are shown in Figure 4. They all have in common the same trans minimum for dihedral angles φ₃ and φ₄. Furthermore, the dihedral angle φ₂ is found in the trans minimum for the six most populated conformations. In other words, these conformations have the same “central” structure (ttt for dihedrals φ_2, φ_3, and φ₄) and only differ from each other by dihedral angles φ₁ and φ₅, the angles at the extremities of the sorbitol, which are much less constrained (compare the distributions of φ₁ and φ₅ with those of φ₂, φ₃, and φ₄ in Figure 3). Thus, for these six conformations, which comprise over 90% of the trajectory time at 300 K, the carbon backbone is fully extended. This arrangement allows each of these six conformations to be stabilized by an intramolecular hydrogen bond between the hydroxyl groups on the C-2 and C-4 atoms (see Section 2 below). Conversely, one of the extremities of sorbitol is bent in conformations tg⁺ttg⁺ and tg⁺ttt, which together account for only around 5–6% of the trajectory time at all three temperatures. This result implies that the shape of the backbone of sorbitol remains essentially linear in these simulations. This is somewhat different from the results of Grigera,⁹ where the backbone was found to be bent, as is observed in the A form of crystalline sorbitol, where the conformation is tg⁻ttt.^10–12 Even at 600 K, these eight conformations still represent 65 % of the total population (see Table 2), demonstrating that the sorbitol molecules were not just trapped in these eight conformations by high barriers. The limited number of favored conformations was also not simply a solvation effect, in the sense of solvation favoring just these, since the same limited set of conformations was observed in the vacuum simulation (see Table 2). The total number of conformations sampled actually increases from sorbitol in vacuum (22 for the first 10 ns) to sorbitol in solution (78), and with a temperature increase (78, 161 and 197 conformations sampled at 300, 500 and 600 K, respectively). However, beyond the eight described conformations, the remaining conformations are not significantly populated.

Table 2.

Populations (%) of the eight most populated conformations of sorbitol in the 3 m solution at 300, 500 and 600 K and in vacuum.

Conformation	Vacuum	300 K	500 K	600 K
g−tttg+	-	5.7	6.9	6.7
g−tttt	9.8	13.8	11.9	10.1
g+tttg+	-	3.4	5.3	5.2
g+tttt	1.2	7.2	8.3	7.4
ttttg+	4.2	15.1	13.0	11.1
ttttt	75.2	46.2	24.4	17.9
tg+ttg+	1.0	0.9	1.8	2.5
tg+ttt	4.9	2.2	3.2	3.7
Total	96.3	94.5	74.8	64.5

Figure 4.

The most populated conformations of sorbitol (the orientation of molecules is similar to that in Figure 2, with C-1 and C-6 carbons on the left and right extremities of molecules, respectively). The different conformations are labeled according to which minimum each dihedral angle belongs; i.e., ijklm denotes the conformation in which the dihedral angles φ₁, φ₂, φ₃, φ₄, and φ₅ (defined in the text and in the caption of Figure 3) are found in minima i, j, k, l, and m, respectively. The conformations shown have been obtained from the minimization of a sorbitol molecule in vacuum with the steepest descent and conjugate gradient algorithms, while applying a constraint potential of 1000 kcal/mol on each dihedral angle φ. Hydrogen bonds between hydroxyl groups are represented by a dashed line (a hydrogen bond was assumed to exist if the O---O distance is less than 3.5 Å and the O–H---O bond angle is greater than 120°).

c. Comparison with experimental data

The conformational properties of sorbitol in heavy water (D₂O) have been studied previously using ¹C NMR.^18–20 Even though an accurate determination of rotamer populations is not possible from these data, it is possible to estimate the populations of trans H-C-C-H rotamers from the comparison of the measured coupling constants between two vicinal protons and those determined from a modified Karplus equation. Hoffmann et al¹⁹ used a Karplus equation proposed by Haasnoot et al., which takes into account the orientation and electronegativies of non-hydrogen substituents.²⁶ They also applied their analysis to the data of Hawkes et al.,¹⁸ obtained at room temperature (296 K instead of 354 K). Similarly, Franks et al. derived the H-H trans rotamer populations from another form of the Karplus equation.²⁰ Table 3 gives the results obtained in these NMR studies as well as the ones calculated here.

Table 3.

Percent of H-H trans rotamers for sorbitol in the simulated 3 m solution, compared to the values estimated from several NMR studies from Hawkes et al.¹⁸–²⁰, Hoffman et al.¹⁹, and Franks et al.²⁰

Vicinal H	This study	Hawkes et al.18–20/Hoffman et al.19	Franks et al.20
H-1–H-2	11	54/63	20
H-1′–H-2	66		56
H-2–H-3	2	51/43	37
H-3–H-4	1	0/3	0
H-4–H-5	99	82/74	73
H-5–H-6	1	43/47	5
H-5–H-6′	75		51

In spite of the different equations used to determine rotamer populations and the different temperatures at which the spectra were recorded, the experimental data are in qualitative agreement with one another. They are also in reasonable qualitative agreement with the present simulation results except for φ₂. The comparison between experimental and simulation data shows that the H-2–C-2–C-3–H-3 trans (i.e. the C-1–C-2–C-3–C-4 g⁻) population is underestimated in the simulations. This rotamer corresponds to the one observed in the crystalline A form of sorbitol (tg⁻ttt).^11,12 In other words, the experimental data suggest that sorbitol more frequently adopts a sickle-shaped conformation - where the backbone is bent at the C-2–C-3 bond - than in the present simulations, where sorbitol is predominantly linear.

The work of Horton et al.²⁷ on sugar derivatives and the analysis of the crystalline conformations of several polyols (including D-glucitol) of Jeffrey et al.¹⁰ suggest that acyclic carbon chains adopt extended, planar zigzag conformations provided that no parallel C-n–X and C-(n+2)–X (where X is not hydrogen) bonds exist, since they were supposed to be sterically disfavored. In the case of sorbitol, the parallel C-2–O-2 and C-4–O-4 bonds found in extended conformations (see Figure 4) can be avoided by rotation either around the C-2–C-3 bond (as in the crystal) or the C-3–C-4 bond (which requires a further rotation around the C-4–C-5 bond and is actually not observed). This rule allowed Jeffrey et al. to predict the crystalline conformations of polyols of different sizes and stereochemistries. Nevertheless, it should be pointed out that (i) the bent conformation of sorbitol in the crystal is strongly influenced by local packing effects in contrast to the solution case; (ii) the intermolecular hydrogen bond patterns formed by sorbitol in the crystal are probably significantly different from those formed with water in solution; and (iii) stabilizing intramolecular hydrogen bonds between parallel C-n–O-n and C-(n+2)–O-(n+2) bonds are observed with the force field used here, as shown in Figure 4. Therefore, it is expected that sorbitol in aqueous solution adopts conformations that differ from its crystal conformation.

d. Conformational dynamics

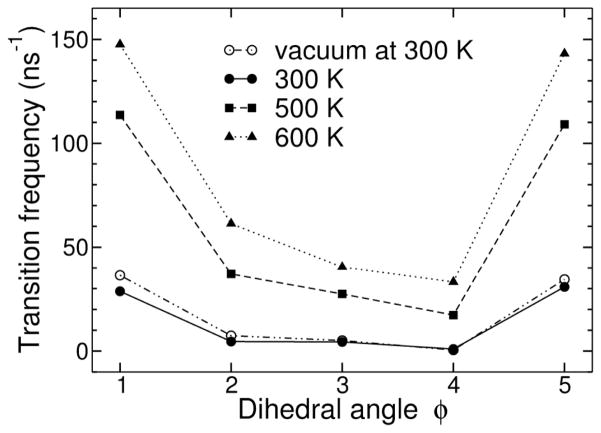
The number of transitions between minima of the dihedral angles φ_i was computed to characterize the intramolecular conformational dynamics of sorbitol. These conformational transitions were only counted if a given torsion angle did not re-cross the same boundary between two minima within 1 ps. This criterion was designed to count only true transitions.²⁸ The transition rates, defined here as the number of transitions within 1 ns, of the dihedrals φ_i of sorbitol in vacuum and in solution at 300, 500, and 600 K are shown in Figure 5. Not surprisingly, the central portion of the molecule is the most stable dynamically, while the ends undergo the most transitions, presumably due to frictional effects and the difficulties of correlated, crankshaft-like transitions. Thus, the transition rates directly reflect the distributions shown in Figure 3: those of dihedral angles φ₁ and φ₅ are much larger than those of dihedral angles φ₂, φ_3, and φ₄. The frequencies of dihedral transitions in vacuum and in solution at 300 K were found to be similar, despite the rather low collision frequency (5 ps⁻¹) used for the Langevin dynamics of sorbitol in vacuum, which should improve the conformational sampling efficiency. Given that a much larger number of conformations are sampled in solution compared to vacuum on the same time scale, it can be deduced that transitions in vacuum would be more likely to occur between neighboring conformers in the conformational space, whereas hydration may allow a wider exploration of the conformational space of sorbitol, stabilizing high-energy, transient conformations. This parallels results from simulations of ethylene glycol in water and vacuum, where the solvent stabilized the torsional barrier.²⁹

Figure 5.

Averaged number of transitions per ns of the different dihedral angles of sorbitol in the 3 m solution at 300, 500 and 600 K and in vacuum. Here a transition from one minimum to another one was counted only if it remained in the product conformation for more than 1 ps.

The reorientational correlation times of the C-H vectors in the sorbitol and glucose simulations were computed to characterize the effect of their respective topologies on their internal dynamics. These reorientational correlation times were computed from the second rank reorientational autocorrelation function C₂ (t) = 〈 P₂ (μ̂(0) · μ̂(t)〉, where P₂ is the second-order Legendre polynomial and μ̂ (t) is the unit vector along the C-H bond direction at time t. C₂(t) was averaged over each sugar molecule and over each C-H vector of a given carbon atom. The reorientational correlation times τ were then deduced from the fit of C₂(t) with a three exponential function, similar to the procedure used by Bogusz et al.³⁰

$$C_2(t)=a_1{e}^{-t/{\tau }_1}+a_2{e}^{-t/{\tau }_2}+a_3{e}^{-t/{\tau }_3}$$ (1)

where a₁ + a₂ + a₃ = 1. The correlation time τ is then defined as the integral of C₂(t), i.e.

$$\tau =\sum _{i=1}^3{a}_i{\tau }_i$$ (2)

The calculated reorientational correlation times of sorbitol and glucose in the 3 m solutions are listed in Table 4. The correlation times are longer for glucose than for sorbitol, as expected. Relaxation of the ring carbon atoms of glucose arises from molecular tumbling (the presence of the ring prohibits isomerization on the time scale of tumbling), while sorbitol can both tumble and isomerizes. The correlation times for sorbitol are not dramatically shorter than those of glucose because the isomerizations are slower than the tumbling (see Figure 5), and thereby do not dominate the relaxation. The C-H bonds of the exocyclic hydroxymethyl group of glucose reorient significantly faster than those of the ring carbons, because of the additional rotational degree of freedom along the C-5–C-6 bond. This observation is in line with the smaller reorientational correlation times of the hydroxymethyl groups of sucrose in aqueous solutions determined by Baraguey et al. by means of ¹³C NMR experiments.³¹ In sorbitol, the carbons at the ends, C-1 and C-6, which have the highest conformational transition rates, relax faster than the other carbons. This is consistent with the experimental results obtained by Sixou et al. for pure (neat) liquid sorbitol by means of ¹³C NMR and molecular dynamics simulations,^13,14 which showed that the mobilities of carbon atoms located at the ends of sorbitol are greater than those of internal carbons of the chain. It is also consistent with the broader distributions of dihedral angles. This pattern of relaxation times differs significantly from that obtained for alkanes,³² and follows from the hydrogen bond analysis described in the following subsection.

Table 4.

Reorientational correlation time τ (ps) for the C-H vectors in the simulations of sorbitol and glucose in 3 m solutions at 300 K.

Carbon	Glucose	Sorbitol
C-1	32.5	15.2
C-2	35.0	23.5
C-3	35.1	25.5
C-4	34.6	25.2
C-5	35.1	23.8
C-6	21.7	16.0

2. Hydrogen bond analysis

The presence of hydroxyl groups in sorbitol allows the formation of both intramolecular hydrogen bonds and bonds with other sorbitol molecules or with the solvent water. Hydrogen bonding was examined in the present simulations using the definition that a hydrogen bond exists between a donor-acceptor oxygen pair if the distance between them is less than 3.5 Å and the O–H---O bond angle is greater than 120°. Table 5 reports the hydrogen bond statistics for each OH group of sorbitol for the 3 m solution at 300 K. The hydroxyl groups 2 and 4 form significantly more intramolecular hydrogen bonds than the others. This result is consistent with the nearly unimodal distributions of dihedral angles φ₂ and φ₃ shown in Figure 3. It is also consistent with the most populated conformations shown before. Indeed, for the first six minimized conformations of Figure 4, a hydrogen bond exists between OH groups 2 and 4. The very similar number of intramolecular hydrogen bonds for OH groups 2 and 4 is because a hydrogen bond between these two hydroxyl groups is predominant, as will be shown below. Similarly, a hydrogen bond is formed between hydroxyl groups 1 and 3, and between OH groups 5 and 6, but with significantly lower frequencies. This reflects the much greater rotational freedom of OH groups 1 and 6, revealed in their dihedral angle distributions (see Figure 3 for the distributions of φ₁ and φ₅).

Table 5.

Statistics of the sorbitol intra- and intermolecular H bonds in the 3 m solution at 300 K.

HB center	Sorbitol		Sorbitol-water
	Intramolecular	Intermolecular
1	0.27	0.28	2.00
2	0.89	0.22	1.55
3	0.24	0.24	1.82
4	0.83	0.19	1.43
5	0.16	0.25	1.83
6	0.16	0.30	2.07
Total	1.27	1.48	10.70

Due to the high concentration of a 3 m solution, there are measurable numbers of transient intermolecular hydrogen bonds observed in these simulations. The formation of intermolecular hydrogen bonds among the different OH groups is relatively similar, although OH groups 1 and 6 tend to form slightly more hydrogen bonds and OH group 4 slightly fewer. Moreover, differences are apparent between the OH groups for sorbitol-water hydrogen bonds. Hydroxyl groups 1 and 6 form significantly more hydrogen bonds with water, due to the enhanced exposure of these hydroxyl groups to the solvent, compared to the other hydroxyl groups of sorbitol. Hydroxyl groups 2 and 4 form fewer hydrogen bonds with water, since they are involved with each other in the persistent intramolecular hydrogen bonds, and are thus less available for the formation of hydrogen bonds with water molecules.

The significant extent of intramolecular hydrogen bonding in sorbitol can be contrasted with the situation in D-glucopyranose. Table 6 presents the calculated hydrogen bond statistics for the 3 m glucose solution at 300 K. The very low number of intramolecular hydrogen bonds is due to the fact that the ⁴C₁ pyranose ring conformation of glucose, in which hydroxyl groups 2, 3 and 4 are equatorial, strongly inhibits the formation of intramolecular hydrogen bonds, unlike the case for the more linear sorbitol. However, the number of intermolecular glucose-glucose hydrogen bonds is similar to that of sorbitol-sorbitol bonds, again reflecting simple concentration effects rather than any tendency to aggregate. Finally, the number of water-solute hydrogen bonds for glucose is very close to that of sorbitol. However, these bonds are not equally distributed among the different hydroxyl groups, as has been previously observed.^2,3 Consistent with these earlier simulations, the anomeric hydroxyl group forms about 0.4 more hydrogen bonds to solvent in the β anomer than in the α, which is why the β anomer is predominant in solution in spite of the stereoelectronic anomeric effect favoring the α. In addition, the ring oxygen of glucose forms far fewer hydrogen bonds with water molecules than do oxygen atoms from the hydroxyl groups, also as has been seen before.

Table 6.

Statistics of the glucose intra- and intermolecular H bonds in the 3 m solution at 300 K. The left and right numbers are for the α and β anomers of glucose, respectively.

CSFF	Glucose		Glucose-water
HB center	Intramolecular	Intermolecular
1	0.03/0.00	0.29/0.33	2.01/2.39
2	0.03/0.01	0.28/0.29	2.14/2.05
3	0.01/0.01	0.28/0.29	1.94/1.93
4	0.01/0.01	0.28/0.28	1.79/1.75
5	0.00/0.00	0.06/0.08	0.61/0.80
6	0.01/0.01	0.30/0.29	2.21/2.22
Total	0.05/0.02	1.49/1.56	10.69/11.13

Finally, the sorbitol simulations were examined to determine whether there is any cooperativity in hydrogen bonds beyond those between groups 2 and 4, 1 and 3, and 5 and 6. Table 7 lists the different intramolecular hydrogen bond patterns observed in the 3 m sorbitol solution at 300 K. Two kinds of frequent hydrogen bonds were observed: (i) between next-nearest neighbor oxygen atoms O-i–O-(i+2) (mostly O-2–O-4 and O-1–O-3), and (ii) between vicinal oxygen atoms O-i–O-(i+1) (mostly O-5–O-6). From a purely geometrical point of view, the O-i–O-(i+2) type of hydrogen bonds should be stronger than the O-i–O-(i+1) type, for which the O–H---O angle is necessarily rather bent. Nevertheless, the analysis of the crystalline conformations of several polyols by Jeffrey et al. suggested that parallel C-i–O-i and C-(i+2)–O-(i+2) bonds are not energetically favored.¹⁰ From the present simulations it was found that the hydrogen bond between groups 2 and 4 is more likely than the one between OH groups 1 and 3 and 5 and 6. Cooperative hydrogen bonds between OH groups 1, 2 and 4 are also observed with a non negligible probability (8 %).

Table 7.

Most frequent intramolecular hydrogen bond patterns found in the 3 m sorbitol solution at 300 K.

Intramolecular HB pattern	Probability (%)
O-2–HO-2---O-4–HO-4	58
O-1–HO-1---O-3–HO-3	13
O-5–HO-5---O-6–HO-6	10
O-1–HO-1---O-2–HO-2---O-4–HO-4	8
O-3–HO-3---O-5–HO-5	3
O-2–HO-2---O-4–HO-4---O-6–HO-6	2
O-1–HO-1---O-2–HO-2	1
O-3–HO-3---O-4–HO-4	1
O-2–HO-2---O-3–HO-3	1
O-2–HO-2---O-3–HO-3---O-4–HO-4	1

III. Conclusions

The present conformational analysis found that in spite of the great potential flexibility of the sorbitol molecule, the majority of the possible conformations for this polyol do not occur to any significant extent, and that the molecule in fact restricts itself to just a handful of conformations. These results are in reasonable agreement with experimental data except for the important exception of the C-2–C-3 torsional conformation. In the present simulations, the sorbitol chain remained extended even at high temperatures (up to 600 K). This result differs from the tg⁻ttt bent conformation suggested by ¹C NMR and found in sorbitol crystalline forms. Since the C-2–C-3 torsional conformation depends on the possible intramolecular hydrogen bond between the O-2 and O-4 groups, it is particularly important to determine to what extent this hydrogen bond affects the conformational distribution. The difference with experiment may indicate that the ad hoc force field used here is inadequate to describe the conformational structure of the polyols, and that a parameter set developed specifically for this purpose is required. Such a force field is presently under development.³³ It might also indicate an incorrect assignment of this torsional conformation in the NMR studies. Further investigation of both possibilities is warranted.

Not surprisingly, the reorientational correlation times calculated from the simulations show that the extremities of the sorbitol chain are more flexible than the center, in agreement with the results for sorbitol of Sixou et al. from ¹³C NMR measurements.^13,14 The corresponding times are longer for glucose due to the greater rigidity of the glucose ring. The TIP3P water model employed in these simulations is known to be somewhat less structured than other common water models,³⁴ and to consequently have a higher mobility, reflected in its self diffusion coefficient.²² This unphysically high mobility would affect the absolute magnitudes of any dynamical properties calculated from simulations employing it, but would not affect relative trends. The most surprising thing about the present results is not that the correlation times for glucose are greater than those for sorbitol, but rather that they are only a little longer, no more than a factor of two greater. This unexpected result is due to the relative rigidity of the sorbitol, reflected in the small number of conformations observed.

The analysis of hydrogen bonds shows that sorbitol forms more intramolecular hydrogen bonds than glucose. This is again unsurprising, given the topological restrictions imposed on the glucose by the pyranose ring. However, one particular rather persistent hydrogen bond was found between the O-2 and O-4 hydroxyl groups. The persistence of this hydrogen bond and its tendency to not exchange for mixed sugar-water hydrogen bonds apparently affects the sorbitol conformational equilibrium and its preference for extended conformers. The number of intermolecular sorbitol-sorbitol hydrogen bonds was very similar to the number of glucose-glucose hydrogen bonds, which is allowed by the larger number of hydroxyl groups of sorbitol (six) compared to glucose (five). Given the rather limited number of conformations sampled by sorbitol, not only in the present study, but in both previous simulation and experimental studies, some form of stabilizing internal interactions such as the hydrogen bond observed here seems likely. Such internal hydrogen bonds should also be possible in other sugar alcohols, although their different stereochemistries would favor different sets of conformations. This possibility should be investigated in the future by both simulation and experiment.