Stage-specific cancer incidence

SUMMARY

Early detection of prostate cancer using the prostate-specific antigen test led to a sharp spike in the incidence of the disease accompanied by an equally sharp improvement in patient prognoses as evaluated at the point of advanced diagnosis. Observed outcomes represent age at diagnosis and stage, a categorical prognostic variable combining the actual stage and the grade of tumor. The picture is summarized by the stage-specific cancer incidence that represents a joint survival-multinomial response regressed on factors affecting the unobserved history of the disease before diagnosis (mixture). Fitting the complex joint mixed model to large population data is a challenge. We develop a stable and structured MLE approach to the problem allowing for the estimates to be obtained iteratively. Factorization of the likelihood achieved by our method allows us to work with only a fraction of the model dimension at a time. The approach is based on generalized self-consistency and the quasi-EM algorithm used to handle the mixed multinomial part of the response through Poisson likelihood. The model provides a causal link between the screening policy in the population and the stage-specific incidence.

1. INTRODUCTION

We based our analyses of prostate cancer on the data from Surveillance, Epidemiology and End Results database (SEER, http://seer.cancer.gov/). The data set includes 331 227 cases of prostate cancer diagnosed between 1973-2000 in the age range of 50-100 in nine states and metropolitan areas of the U.S. participating in the SEER program. Incidence data are represented by age at diagnosis, a, and year of birth, x, for each cancer case, the count of cancer cases, C(a, x), as well as the count P(a, x) representing the male population over the age of 50. The Prostate-specific antigen (PSA) test invented in the late 80s is a biomarker for the early detection of prostate cancer. Increased utilization of the test in the US male population induced a dramatic spike of the observed prostate cancer incidence

$${\lambda }_{\mathrm{obs}}(a\mid x)=\frac{C(a,x)}{P(a,x)da}$$ (1)

where da=1 year. Shown in Figure 1 is λ_obs(a|x) plotted by age a and year of diagnosis x+a. The effect gradually builds up with age and peaks at about 70. The probabilistic characteristic λ(a|x) corresponding to the empirical incidence (1) is essentially a hazard rate for the age at diagnosis of prostate cancer in the x-birth cohort. We call λ(a|x) marginal incidence to distinguish it from the joint distribution characterizing the disease presentation at diagnosis.

Figure 1.

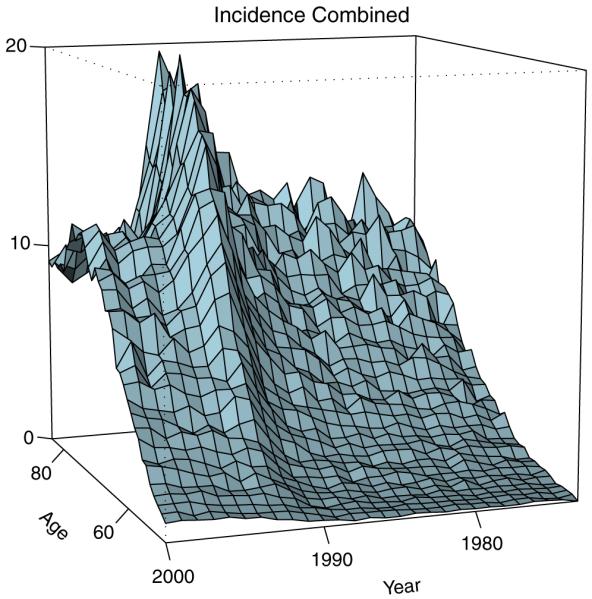
Observed marginal incidence λ_obs(a|x)×1000 of prostate cancer, λ_obs(a|x)=C(a, x)/P(a, x), by age a and year of diagnosis x+a. The empirical estimate corresponds to the ratio of the count of observed cases C to the size of the population P at risk measured in thousands. Single age-year bins are used. Figure is based on SEER data (http://seer.cancer.gov/).

Suppose, a categorical prognostic index Y is observed at diagnosis. Then we can consider the joint response represented by the random vector (A, Y). Here we treat the random age A at cancer diagnosis as a net competing risk, all other risks removed.

Here and in the sequel we will adopt the following notation rules unless noted otherwise. Capital letters are used for random variables and the corresponding lowercase letters for the values of those variables. In addition, λ will be a hazard function in its age a argument; f will be a probability density function (pdf); its discrete version will be denoted by π.

Two binary prognostic variables are considered: a stage and a grade of the disease. The stage is categorized as localized or regional (LR) vs distant (D). The grade represents a categorical assessment of the degree of differentiation of cancer cells, a measure of how different cancer cells are from the cells from which they originated. Poorer differentiation is caused by an increasing fraction of more rapidly dividing cells in a cancer tissue sample indicating a more aggressive cancer. In this paper, grade is dichotomized as well or moderately differentiated (WM) vs poor or undifferentiated (PU). While the exposition of the paper is general, in the examples Y is a multinomial response built from four possible combinations of the stage and grade of the disease as follows:

$$Y=\{\begin{array}{cc}1\text{Stage}=\mathrm{LR}\hfill & \text{Grade}=\mathrm{WM}\hfill \\ 2\text{Stage}=\mathrm{LR}\hfill & \text{Grade}=\mathrm{PU}\hfill \\ 3\text{Stage}=D\hfill & \text{Grade}=\mathrm{WM}\hfill \\ 4\text{Stage}=D\hfill & \text{Grade}=\mathrm{PU}\hfill \end{array}\phantom{\}}$$ (2)

The categories of the prognostic index Y are ordered from the best prognosis to the worst. However, it is not clear whether a similar ordering exists in age as far as the natural history of the disease prior diagnosis is concerned. For example, it is not known whether tumor growth is accompanied by a progression of the grade, or the grade is constant in time given the subject. Therefore, we prefer not to make any ordering assumptions and treat Y as a multinomial rather than ordinal variable. On the population level it is clear that PSA screening leads to a shift to better categories of Y. Much of this shift is populated by subjects who would never be detected with cancer without PSA (overdiagnosis). The shift also occurs within the subject if the incidence of an advanced disease is prevented by the early detection of cancer while in a better prognostic category.

Let C(a, x, y) be the count of cases diagnosed in year x+a at the age of a and with prognostic index y. Then it is natural to break the empirical incidence (1) by y as

$${\lambda }_{\mathrm{obs}}(a,y\mid x)=\frac{C(a,x,y)}{P(a,x)da}={\lambda }_{\mathrm{obs}}(a\mid x)\frac{C(a,x,y)}{C(a,x)}$$ (3)

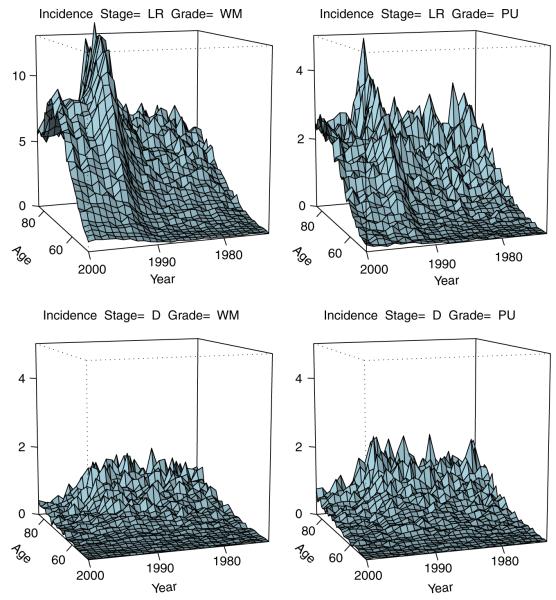
Clearly, $C(a,x)={\sum }_{y}C(a,x,y)$, and ${\lambda }_{\mathrm{obs}}(a\mid x)={\sum }_y{\lambda }_{\mathrm{obs}}(a,y\mid x)$. Plots of the empirical stage-specific incidence λ_obs(a, y|x) are shown in Figure 2. It is evident from Figure 2 that dynamics of the marginal incidence is dominated by the LR-stage-specific incidence. In addition, the incidence of the distant disease drops with the introduction of PSA indicating a favorable stage shift induced by the early detection of cancer on the population level.

Figure 2.

Observed stage- and grade-specific incidence (per 1000 men) of prostate cancer (3) by age a and calendar time x+a, where x is year of birth. Single year age and calendar time bins are used (da=1); SEER data (http://seer.cancer.gov/). Stage: LR=localized-regional, D=distant; grade: WM=well or moderate differentiation, low grade, PU=Poor or no differentiation, high grade.

The joint hazard function of the random vector (A, Y) is expressed by the y-specific incidence λ(a, y|x) defined as

$$\lambda (a,y\mid x)da=\mathrm{Pr}\{A\in [a,a+da]\&Y=y\mid A\ge a,x\}$$ (4)

The joint distribution λ(a, y|x) is a hazard function in a, and a discrete probability distribution in y. Obviously,

$$\lambda (a\mid x)=\sum _y\lambda (a,y\mid x)$$

Let π(y|a, x) be the conditional distribution of the index Y for the patient diagnosed at the age of a in year x+a. We have the following factorization for the stage-specific incidence:

$$\lambda (a,y\mid x)=\lambda (a\mid x)\pi (y\mid a,x)$$ (5)

where the conditional probability π(y|a, x) represents a multinomial regression model for a factor partitioning marginal incidence into its Y-specific components. From (3) we have an empirical estimate

$$\widehat{\pi }(y\mid a,x)=\frac{C(a,x,y)}{C(a,x)}$$ (6)

The joint modeling of (A, Y) as a function of screening processes measured on the population level is the focus of this paper.

It is evident that A and Y represent random variables with a complex pattern of dependency. This dependency is explained by the unobserved random processes W summarizing the latent history of the disease and the unobserved random screening schedule in the subject. We keep W general for now, and will specify it and reduce it to a random vector surrogate later in this paper. The subject-specific processes W are shared by A and Y, inducing dependence

$$f(a,y\mid x)=E\{f(a,y\mid x,W)\mid x\}$$ (7)

where f is the joint pdf. In this paper we will build a mechanistic model for (7). This model is intended to predict how the policy of cancer screening $\mathcal{P}$ (yet to be formalized) affects the stage-specific incidence of the disease. We will identify $\mathcal{P}$ with the distribution of the random schedule $\mathcal{T}$, a point process. $\mathcal{P}$ is defined on the population level, while the effect of screening occurs on the individual level. Screening schedules in the U.S. population are not observed on the individual level. The problem thus is about building a link between a functional parameter $\mathcal{P}$ and the multivariate response (A, Y). In the sequel, the dependence on $\mathcal{P}$ will be suppressed for brevity when $\mathcal{P}$ is not the focus of the exposition.

The estimation approach will consist of the following two stages.

Stage 1

1. First we will set up the model for [A|x] using a marginal likelihood approach

   $$\text{Data}:C(a,x),P(a,x),\text{Model}:f(a\mid x)=E\{f(a\mid x,W)\mid x\}$$ (8)

2. Second, we will determine the model for $\tilde{W}$, a suitable surrogate of W. We will use posterior prediction based on the marginal model to obtain $[\tilde{W}\mid a,x]$.

Stage 2

Assuming that the distribution $[\tilde{W}\mid a,x]$ represented by the pdf $f(\tilde{w}\mid a,x)$ to be known from the previous stage, we will build and fit the model for π(y|a, x) using $[\tilde{W}\mid a,x]$ as a subject-specific random effect

$$\text{Data}:C(a,x,y),C(a,x);\text{Model}:\pi (y\mid a,x)=E\{\pi (y\mid a,x,\tilde{W})\mid a,x\}$$ (9)

Stage 1A has already been accomplished [1], and we will review this model in Section 3. Stage 1B will be dealt with in Section 4. In Section 5 multinomial mixed model will be formulated, and interpreted as an artificial mixture model. Using this interpretation we will devise the estimation procedures based on self-consistency [2, 3] in Section 7. An application of the methodology to SEER data and a simulation study will be done in Section 8.

A number of analytic marginal [1, 4, 5] and simulation models [6, 7] have addressed overdiagnosis and marginal incidence λ(a|x). Most analytical models of cancer screening are estimated based on screening trials data where the screening schedules are known. Simulation models are informed by a broad range of studies and the literature data. In both scenarios the population predictions of cancer incidence are generated based on a simulation of screening schedules in the real population, or using hypothetical schedules. Oftentimes, the process involves an ad hoc calibration of the model predictions to the observed population incidence. Our approach is different in that it is used to build inference procedures directly using population data such as the SEER cancer registries.

2. LIKELIHOOD

Likelihood construction is essentially similar to the argument used for martingales based on counting processes [8, 9], and in the age-period-cohort models [10]. Cases C(a, x, y) originate from a population at risk of cancer detection of the size P(a, x). In practice we will assume da=1 year to be sufficiently small for Taylor first-order approximations. In addition, the disease will be considered as rare enough to identify P with the population as reported in SEER. Empirical evidence to the validity of these assumptions is the fact that C⪡P as given by SEER data.

For a subject without prior cancer diagnosis of age a observed at time t=x+a, the conditional probability to be detected with cancer, marked by a prognostic index y, is given by λ(a, y|x)da as in (4). The marginal probability of being detected with cancer of any stage is $\lambda (a\mid x)da={\sum }_y\lambda (a,y\mid x)da$. The conditional probability not to be detected is 1-λ(a|x)da. Therefore, the conditional likelihood is proportional to

$$L=\prod _{x,a}{[1-\lambda (a\mid x)da]}^{P(a,x)}\prod _y{\left[\lambda (a,y\mid x)da\right]}^{C(a,x,y)}$$ (10)

Using the product-integral representation [11]

$$\prod _a[1-\lambda (a\mid x)da]=\exp \left(-{\int }_a\lambda (a\mid x)da\right)$$

and dropping the terms that do not depend on the model parameters, the log-likelihood takes the form

$$\ell =\log L=\sum _x\sum _a\left[\left\{\sum _{y}C(a,x,y)\log \lambda (a,y\mid x)\right\}-P(a,x)\lambda (a\mid x)da\right]$$ (11)

Note that even though the likelihood (11) has Poisson form, the counts C do not represent a Poisson process. This is because P(a, x) are arbitrary, and the same subjects are contributing to multiple Ps inducing the dependence of Ps for different values of its arguments. Essentially, (11) is a consequence of the fact that any counting process behaves locally within a small interval da as a Poisson process, conditional on the prior history. In addition, (10) is a consequence of the number of events in the small interval being a Bernoulli random variable.

The factorization (5) yields a partition of the above likelihood ℓ=ℓ_I+ℓ_Y into the one for the marginal incidence model estimated at the Stage 1 (8)

$${\ell }_I=\sum _x\sum _a[C(a,x)\log \lambda (a\mid x)-P(a,x)\lambda (a\mid x)da]$$ (12)

and the one for the multinomial response Y estimated at Stage 2 (9)

$${\ell }_Y=\sum _x\sum _a\sum _{y}C(a,x,y)\log \pi (y\mid a,x)$$ (13)

As we mentioned earlier in the Introduction, our approach will be to use the marginal likelihood ℓ_I to estimate the parameters of the conditional joint distribution of [W|a, x] (or its surrogate), and then to use these estimates to specify the mixed model likelihood for Y

$${\ell }_Y=\sum _x\sum _a\sum _{y}C(a,x,y)\log E\{\pi (y\mid W,a,x)\mid a,x\}$$ (14)

based on (9). In doing so we will assume that at Stage 2 the distribution f (w|a, x) is known. This is justified by the fact that C⪡P. Note that the marginal incidence model of Stage 1 is fitted to the whole population P, while the Stage 2 model is fitted to cases C only.

3. THE MARGINAL INCIDENCE MODEL

The marginal incidence model [1] developed earlier as a mixed model for λ(a|x) will serve as a basis for the first stage (marginal modeling). The natural history of cancer is a version of the classical model [12]. A subject passes through the disease-free state and the pre-clinical state before being detected with cancer or censored without a diagnosis. The subject’s age at tumor onset A_O represents the duration of the disease-free stage. It is assumed that A_O has Weibull distribution with the hazard function of the form

$$h_{\mathrm{O}}\left(a\right)=s_{\mathrm{O}}{\left(\frac{\Gamma (1+1∕s_{\mathrm{O}})}{{\mu }_{\mathrm{O}}}\right)}^{s_{\mathrm{O}}}{a}^{s_{\mathrm{O}}-1}$$

where a is the age past 50. In the above expression, the Weibull distribution is parameterized through the mean μ_O and the shape parameter s_O.

The duration of the pre-clinical stage is given by the delay time ξ_D=A-A_O represented by the period between cancer onset at the age of A_O and its diagnosis at the age of A. We assume that cancer diagnosis is a result of two competing risks, the time to detection by screening, ξ_SDx, and the time to the clinical diagnosis due to symptoms of the disease, ξ_CDx, so that ξ_D=min(ξ_SDx, ξ_CDx). The time ξ_CDx is referred to as the sojourn time. The Weibull distribution with mean μ_CDx and shape parameter s_CDx is used to model the baseline sojourn time hazard h_CDx(ξ), where ξ is the time since tumor onset. The sojourn time is affected by changes in the practice of cancer detection other than the studied modality of screening. For example, before PSA was introduced, prostate cancer was often detected incidentally as a result of surgery for benign prostate disorders (Transurethral Resection of the Prostate) [13]. These trends in the sojourn time hazard λ_CDx(ξ|t) are modeled using a multiplicative trend function T_CDx(t) acting on the baseline sojourn time hazard h_CDx

$${\lambda }_{\mathrm{CDx}}(\xi \mid t)=h_{\mathrm{CDx}}\left(\xi \right)T_{\mathrm{CDx}}\left(t\right)$$ (15)

where ξ is the time since tumor onset (age of tumor), and t is the calendar time at this age. The trend function was assumed to be linear between the earliest year where data were available, 1973, and the last year before PSA was introduced, 1987, saturating in 1988. The trend function is set to a constant outside the observed data window, resulting in

$$T_{\mathrm{CDx}}\left(t\right)=\{\begin{array}{cc}1,\hfill & t<73\hfill \\ 1+c(t-73),\hfill & 73\le t\le 88\hfill \\ 1+c(88-73),\hfill & t>88\hfill \end{array}\phantom{\}}$$

Suppose $\mathcal{T}=\{{\tau }_1,{\tau }_2\dots \}$ are random ages when the subject is screened (a screening schedule). Given A_O, the result of a screen at the age of a=A_O+ξ is an independent Bernoulli random variable with the probability of success (detection) α(ξ), a non-decreasing function. The sensitivity of screening as a function of age is then

$$\begin{array}{cc}\hfill 0,& \hfill a<A_{\mathrm{O}}\hfill \\ \hfill \alpha (a-A_{\mathrm{O}}),& \hfill a\ge A_{\mathrm{O}}\hfill \end{array}$$ (16)

The detection by screening occurs at the age of A_Scr=τ_ν, where ν is the number of the first successful screen in a series of so-called Poisson trials (Bernoulli trials with unequal probabilities). In order to specify A_Scr=τ_ν, we also need to specify the process $\mathcal{T}$. The National Cancer Institute and collaborators have developed a generator of PSA schedules (a simulation model) for U.S. males [14]. Having experimented with the generator, we came up with the following analytical model approximating its output. Let λ_1S(a, t) be the instantaneous risk (hazard) of the first PSA test for a man of age a in year t. Then the probability that a man born in year x will not be tested by the age of a is

$$G_{1\mathrm{S}}(a\mid x)=\exp \left\{-{\int }_0^a{\lambda }_{1\mathrm{S}}(\xi ,x+\xi )\mathrm{d}\xi \right\}$$ (17)

We assume that in men who already had their first PSA tests, secondary tests {τ₂, τ₃ . . .} form a non-homogeneous Poisson process with intensity λ_2S(a, t). Both intensities of PSA testing λ_1S and λ_2S are treated as known bivariate functions of age and calendar time, and are derived by a large sampling from the schedule generator. We identify the screening policy $\mathcal{P}=({\lambda }_{1\mathrm{S}},{\lambda }_{2\mathrm{S}})$ with the set of the two screening intensities defined as functions on the age by calendar time plane.

The survival function G_SDx(ξ|x, A_O) is the probability of no screening diagnosis for a subject with the following characteristics:

• year of birth x;

• projected age at tumor onset A_O;

• age of tumor (time since onset) ξ;

• current age A_O+ξ,

is given by (see [1] for the derivation)

$$\begin{array}{cc}\hfill G_{\mathrm{SDx}}(\xi \mid x,A_{\mathrm{O}})=& G_{1\mathrm{S}}(A_{\mathrm{O}}+\xi \mid x)+[1-G_{1\mathrm{S}}(A_{\mathrm{O}}\mid x)]G_{2\mathrm{SDX}}(\xi \mid x,A_{\mathrm{O}},A_{\mathrm{O}})\hfill \\ \hfill & +{\int }_0^{\xi }[1-\alpha \left(\zeta \right)]f_{1\mathrm{S}}(A_{\mathrm{O}}+\zeta \mid x)G_{2\mathrm{SDx}}(\xi -\zeta \mid x,A_{\mathrm{O}}+\zeta ,A_{\mathrm{O}})d\zeta \hfill \end{array}$$ (18)

where

$$G_{2\mathrm{SDx}}(\xi \mid x,a,A_{\mathrm{O}})=\exp \left\{-{\int }_{\max \left(A_{\mathrm{O}-a,0}\right)}^{\xi }{\lambda }_{2\mathrm{S}}(a+\zeta ,x+a+\zeta )\alpha (\zeta +a-A_{\mathrm{O}})\mathrm{d}\zeta \right\}$$ (19)

and ${\int }_a^b=0$ for any b≤a. The above expressions are a result of averaging over $\mathcal{T}$ and ν, given A_O.

Finally, using conditional independence of the competing risks of cancer diagnosis by screening and clinically, given age at tumor onset A_O, we have

$$\lambda (a\mid x)=-\frac{d}{da}\log E\left\{G_{\mathrm{CDx}}(a-A_{\mathrm{O}}\mid x,A_{\mathrm{O}})G_{\mathrm{SDx}}(a-A_{\mathrm{O}}\mid x,A_{\mathrm{O}})\right\}$$ (20)

This model was fitted by maximizing the marginal likelihood (12) over the marginal incidence model parameters [1]. In the course of likelihood maximization, the screen sensitivity function specified as α(ξ)=1-exp(-βξ) converged to α=1(β→∞). Therefore, α was fixed at 1 for all subsequent analyses. The resultant estimates of model parameters are given in Table I.

Table I.

Estimates of model parameters and confidence intervals

Parameter	Legend	Point estimate	95 per cent CI
μCDx	Mean baseline sojourn time	18.558	(18.345, 18.775)
sCDx	Shape sojourn time	1.541	(1.5191, 1.5644)
c	Slope of trend for sojourn time	0.09354	(0.09068, 0.09641)
μO	Mean age past 50 at tumor onset	72.732	(72.498, 72.965)
sO	Shape of age past 50 at tumor onset	1.6153	(1.6067, 1.6239)
α	Screening sensitivity	1.00	—

Time and age is measured in years.

4. A SURROGATE OF THE EFFECT OF SCREENING ON THE NATURAL HISTORY OF THE DISEASE

One could consider mechanistic mixed models of various complexity based on the mixing variables

$$W=(A_{\mathrm{O}},{\xi }_{\mathrm{CDx}},\mathcal{T},\nu )$$

associated with the natural history of the disease and screening. Screening intervention $\mathcal{P}$ affects W, which determines the age at cancer diagnosis A=A_O+min(τ_ν, ξ_CDx). In addition, the stage Y is thought of as being regressed on W. With screening the distribution π(y|a, x) shifts toward values of y associated with better prognosis as a consequence of early detection.

From the point of view of computational tractability of the problem it would be unreasonable to use the mixing variable as complex as W. To simplify the modeling of π(y|a, x)=E{π(y|a, x, W)|a, x}, we replace W by a suitable surrogate $\tilde{W}$ of the unobserved processes that would allow us to reproduce the behavior of the observed response [Y|a, x]

$$E\{\pi (y\mid W,a,x)\mid a,x\}=E(\pi \{y\mid \tilde{W},a,x)\mid a,x\}$$ (21)

A stronger assumption would be that of the perfect surrogacy [15] $\pi (y\mid W,\tilde{W},a,x)=\pi (y\mid \tilde{W},a,x)$ that implies (21) as

$$E\{\pi (y\mid W,a,x)\mid a,x\}=E\{\pi (y\mid W,\tilde{W},a,x)\mid a,x\}=E\{\pi (y\mid \tilde{W},a,x)\mid a,x\}$$

where the first equality is a formula of total probability while the second one is a consequence of the perfect surrogacy.

A combination of the delay time A_D=A-A_O between tumor onset and its diagnosis and the mode of cancer detection I_scr

$$I_{\mathrm{scr}}=\{\begin{array}{cc}1\hfill & \text{detected by screening}\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$

is taken as a parsimonious surrogate of the effect of the tumor progression history, early detection and screening on the observed prognostic index Y,

$$\tilde{W}=(A_{\mathrm{D}},I_{\mathrm{scr}})$$

The resultant model has the form

$$\pi (y\mid a,x)=E\{\pi (y\mid A_{\mathrm{D}},I_{\mathrm{scr}},a,x)\mid a,x\}$$ (22)

As we will see in Section 8, predictions based on the model (22) with the complete-data part $\pi (y\mid a,x,\tilde{w}),\tilde{w}=(a_{\mathrm{D}},i_{\mathrm{scr}})$ specified according to the multinomial logit model show good agreement with the empirical estimates.

Given the age at tumor onset a_O, the time to the diagnosis is a result of competing risks of clinical and screen detection. The two crude probability densities f (a_D, i_scr|a_O, x), i_scr=0, 1

$$\begin{array}{c}\hfill f(a_{\mathrm{D}},1\mid a_{\mathrm{O}},x)=f_{\mathrm{SDx}}(a_{\mathrm{D}}\mid a_{\mathrm{O}},x)G_{\mathrm{CDx}}(a_{\mathrm{D}}\mid a_{\mathrm{O}},x)\hfill \\ \hfill f(a_{\mathrm{D}},0\mid a_{\mathrm{O}},x)=G_{\mathrm{SDx}}(a_{\mathrm{D}}\mid a_{\mathrm{O}},x)f_{\mathrm{CDx}}(a_{\mathrm{D}}\mid a_{\mathrm{O}},x)\hfill \end{array}$$ (23)

represent the joint conditional distribution of $\tilde{W}$, conditional on a_O, x. Note that we can condition on age at diagnosis a instead of a_D, since a=a_O+a_D, and a_D is a part of $\tilde{w}$

$$f(\tilde{w}\mid a_{\mathrm{O}},x)=f(\tilde{w}\mid a,x)$$ (24)

This pdf is used in the integral representing expectation (22), and in other similar expectations.

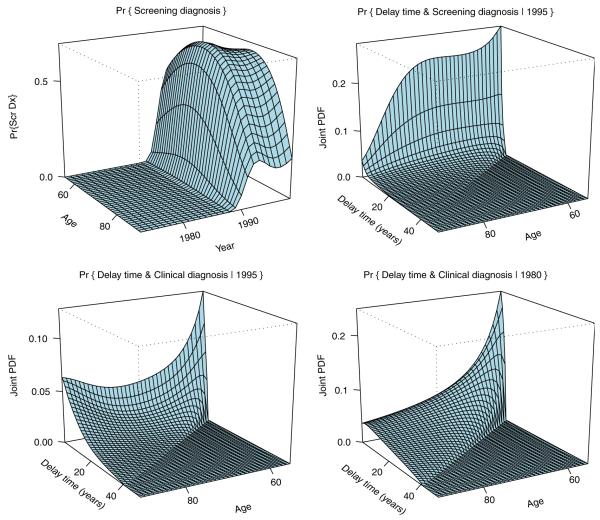
Shown in Figure 3 is the distribution (24) of the latent vector $\tilde{W}=(A_{\mathrm{D}},I_{\mathrm{scr}})$, a combination of the delay time, A_D, and an indicator of screening diagnosis, I_scr, derived from the marginal incidence model [1] as specified in Section 4.

Figure 3.

Distribution (23) of the mixing vector $\tilde{W}$ derived from the marginal incidence model. Top left: marginal distribution of the mode of detection I_scr; probability of screening diagnosis. Top right: crude distribution of delay time A_D for disease diagnosed by screening in year 1995. Bottom left: same as top right for clinical diagnoses in year 1995. Bottom right: same as bottom left in year 1980. Note the shift of probability mass toward smaller delay times with the introduction of screening, particularly for screen-detected cancers.

The marginal distribution of the mode of diagnosis shown in the top left corner of the figure indicates a rapid increase in the fraction of screen-detected prostate cancers in the late 80-ties. It is also clear that a pool of subjects around 70 years of age is most likely to be screen-detected. Lower detection rates in younger patients can be explained by lower prevalence of the latent disease in this group, while lower rates in very old men are likely a consequence of reduced screening rates in this population associated with perceived high chance of over-diagnosis and short residual lifetime expectation.

The dynamics of the joint distribution of the delay time and the mode of detection with calendar time shown in the rest of Figure 3 is quite remarkable. Note that the support for the distribution of age at onset of prostate cancer is assumed to start at the age of 50, as very few cases of prostate cancer are seen before that age. Thus, the delay time cannot be larger than age-50, which makes parts of the plots in Figure 3 corresponding to delay times exceeding the boundary equal to 0. Comparing year 1980 before PSA (bottom right) with year 1995 we see that the probability mass moves toward shorter delay times indicating early detection. We also see that a high chance of the screen detection around 70 years of age shows as a peak of probability mass for the crude density of the delay time for the screen detected cases (top right) and as the corresponding niche carved out in the crude density of the delay time for cases missed by screening (bottom left).

In what follows we will suppress the ‘∼’ accent from the surrogate $\tilde{W}$, will consider W a random variable (r.v.) conditional on a, x, and will remove this conditioning from expectations for brevity.

5. THE MULTINOMIAL MIXED MODEL

5.1. Multinomial logit model

Let Y_i∈{1, 2, . . . , K} be the ith subject’s multinomial response in one of the K possible categories. Let

$${\Delta }_{ik}=I\{Y_i=k\}=\{\begin{array}{cc}1\hfill & i\text{th subject}’\text{s response is}k\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$

a random variable, and

$${\delta }_{ik}=I(y_i=k)$$

its realization in the ith subject. Let z_i be a vector of observed covariates and W_i be a vector of unobserved (random) covariates with known joint distribution that may depend on z_i.

The marginal category-specific probabilities averaged over the unobserved covariates are given by

$${\pi }_{ik}=E\left[\mathrm{Pr}\{{\Delta }_{ik}=1\mid z_i,W_i\}\right],\begin{array}{c}\hfill k=1,2,\dots ,K\hfill \\ \hfill i=1,2,\dots ,n\hfill \end{array}$$ (25)

where n is the sample size. Connecting the various notations introduced earlier we may write

$$\begin{array}{cc}\hfill \pi (y_i\mid w_i,z_i)& =\sum _k{\delta }_{ik}\mathrm{Pr}\{{\Delta }_{ik}=1\mid z_i,w_i\}=\mathrm{Pr}\{Y_i=y_i\mid z_i,w_i\}\hfill \\ \hfill \pi (y_i\mid z_i)& =\sum _k{\delta }_{ik}{\pi }_{ik}={\pi }_{iyi}\hfill \end{array}$$

On the complete-data level the probabilities Pr{Δ_ik=1|z_i, w_i} are given by the multinomial logit model

$$\mathrm{Pr}\{{\Delta }_{ik}=1\mid z_i,w_i\}=\frac{\theta ({\beta }_k,z_i,{\alpha }_k,w_i)}{1+\sum _{c=2}^K\theta ({\beta }_c,z_i,{\alpha }_c,w_i)}$$ (26)

where the functions θ are parameterized using regression coefficients α_k and β_k associated with unobserved and observed covariates, respectively. We will use the following parameterization:

$$\theta ({\beta }_k,z_i,{\alpha }_k,w_i)=\exp \{{\beta }_k^{\mathrm{T}}{z}_i+{\alpha }_k^{\mathrm{T}}{w}_i\}$$

For identifiability, regression coefficients corresponding to the baseline first category are set to β_i1=α_i1=0, hence the summation in the denominator of (26) starts from c=2. Note that θ factors into into $\vartheta ({\beta }_k,z_i)=\exp \left\{{\beta }_k^{\mathrm{T}}{z}_i\right\}$ and $\eta ({\alpha }_k,w_i)=\exp \left\{{\alpha }_k^{\mathrm{T}}{w}_i\right\}$,

$$\theta ({\beta }_k,z_i,{\alpha }_k,w_i)=\vartheta ({\beta }_k,z_i){\eta }_{ik}({\alpha }_k,w_i)$$ (27)

6. GENERALIZED SELF-CONSISTENCY

Maximum likelihood estimation in a variety of settings can often be simplified by substituting complex multinomial likelihoods by Poisson likelihoods as an approximation [5] or augmentation of the original model [16]. Multinomial-Poisson (MP) transformation has been a popular technique simplify maximum likelihood estimation in a variety of models yielding multinomial likelihoods [16]. The approach works by substituting a Poisson likelihood for the multinomial likelihood at the cost of augmenting the model parameters by axillary ones and restricting the problem to discrete covariates. The MP transformation can be justified through the method Lagrange multipliers [17]. In this paper we use an alternative approach based on the generalized self-consistency methodology [2, 3] that allows us to use Poisson likelihood with arbitrary covariate structures. The proposed procedure is very stable numerically as it does not include matrix inverses and works with only a fraction of dimension at a time. We extend the framework of [3] to the mixed model considered in this paper.

Let us artificially represent π(y|z, w) as a marginal probability based on the mixture

$$\pi (y\mid z,w)=E\left\{\pi (y\mid z,w,U)\right\}$$ (28)

where U is a ‘missing’ variable, and π(·|·, U) are complete-data probabilities conditional on U. In other words, an artificial mixture model is considered such that one gets the original target model when the missing data are integrated out.

In the multinomial case, exponentially distributed random variable U ∝Exp(1) yields an artificial mixture formulation such that π on the left of (28) corresponds to the multinomial distribution, while π on the right of (28) gives a Poisson complete-data likelihood. The MLE procedure is an EM algorithm with the E-step solving the problem of imputation of U and W, while the M-step dealing with maximizing a log-likelihood obtained from the complete-data model π(y|z, w, u).

The multinomial probabilities (26) can be written in the artificial mixture form

$${\pi }_{ik}=E\left\{\theta ({\beta }_k,z_i,{\alpha }_k,W_i){\mathrm{e}}^{-U_i{\theta }_{\ast }(\beta ,z_i,\alpha ,W_i)}\right\}$$ (29)

where

$${\theta }_{\ast }(\beta ,z_i,\alpha ,W_i)=\sum _{c=2}^K\theta ({\beta }_c,z_i,{\alpha }_c,W_i),\alpha =\left\{{\alpha }_k\right\},\beta =\left\{{\beta }_k\right\}$$

Note that the complete-data model π⁰=π(y|z, w, u) obtained by dropping the ‘E’ symbol from (29) does not make sense as a probability. It suffices to note that the expression under E is not normalized. We call the resultant algorithm Quasi-EM to acknowledge this issue.

The multinomial logistic model (26) is constructed by linking response probabilities to positive predictors θ. Then θs are normalized to model probabilities. The alternative procedure (29) achieves normalization by means of averaging over artificial missing data.

Note that the log-complete-data ‘probabilities’ resulting from (29) give rise to a Poisson-form complete-data likelihood. Indeed, collecting the terms of the complete-data log-likelihood specific to category k, we get

$$\ell (\beta ,\alpha \mid U,W)=\sum _{i=1}^n\log \pi (y_i\mid z_i,W_i,U_i)=\sum _{k=2}^K{\ell }_k({\beta }_k,{\alpha }_k\mid U,W)$$ (30)

where ℓ_k are Poisson likelihoods parameterized using a subset of the parameter matrix β specific to the category k of the response,

$${\ell }_k({\beta }_k,{\alpha }_k\mid U,W)=\sum _i\{{\delta }_{ik}\log \theta ({\beta }_k,z_i,{\alpha }_k,W_i)-U_i\theta ({\beta }_k,z_i,{\alpha }_k,W_i)\}$$ (31)

and U={U_i}, W={W_i}. Factorization (27) of θ will ensure that the Poisson form (31) be preserved after the averaging over the random effects W. In addition, ℓ_k is linear in U. The above observations make the EM-like approach to the problem particularly attractive.

Generalized self-consistency argument replaces E in (28) by a quasi-expectation operator QE acting on π(·|·, u) as a function of u so that it would no longer be required that the complete-data model π(y|z, w, u) makes sense as a probability. An argument similar to [3] justifies the Quasi-EM algorithm to be constructed despite the fact that the complete data model is not real.

7. THE ALGORITHM

7.1. E-step

Based on [3], for any function φ(V) of a random vector V=(U, W), the imputed value φ‾ of φ(V) has the form

$$\stackrel{‒}{\phi }=E\{\phi \left(V\right)\mid L(\beta ,\alpha \mid V)\}\stackrel{\mathrm{def}}{=}\frac{E\{\phi \left(V\right)\mid L(\beta ,\alpha \mid V)\}}{E\left\{L(\beta ,\alpha \mid V)\right\}}$$ (32)

where L(β, α|V)=e^{ℓ(β, α|V)} is the complete-data likelihood given by (30). The contribution of the ith subject with the response in category y_i=k to the complete-data likelihood follows from (29) and is represented by complete-data ‘probabilities’

$${\pi }_k^0(\beta ,z_i,\alpha ,V_i)=\theta ({\beta }_k,z_i,{\alpha }_k,W_i)\exp \{-U_i{\theta }_{\ast }(\beta ,z_i,\alpha ,W_i)\}$$ (33)

We consider an iterative sequence of parameters α^(m), β^(m), m=1, 2, . . . . With the M-step of the algorithm in mind, φ in (32) is parameterized by the next-iteration (m+1)-parameters, while L in (32) is parameterized using the previous iteration (m) version. Applying the imputation operator (32) to the complete-data log-likelihood (30) φ(V)=ℓ(β^(m+1), α^(m+1)|V) we get after a little algebra

$$\begin{array}{cc}\hfill \stackrel{‒}{\ell }=& E\{\ell ({\beta }^{(m+1)},{\alpha }^{(m+1)}\mid V)\mid L({\beta }^{\left(m\right)},{\alpha }^{\left(m\right)}\mid V)\}\hfill \\ \hfill =& \sum _{k=2}^K\sum _{i=1}^n{\delta }_{ik}\log \vartheta ({\beta }_k^{(m+1)},z_i)-\vartheta ({\beta }_k^{(m+1)},z_i)E\left\{\eta ({\alpha }_k^{(m+1)},W_i){\pi }_{y_i}({\beta }^{\left(m\right)},z_i,{\alpha }^{\left(m\right)},W_i)\right\}\hfill \\ \hfill & +\frac{E\left\{\log \eta ({\alpha }_{y_i}^{(m+1)},W_i){\pi }_{y_i}({\beta }^{\left(m\right)},z_i,{\alpha }^{\left(m\right)},W_i)\right\}}{E\left\{{\pi }_{y_i}({\beta }^{\left(m\right)},z_i,{\alpha }^{\left(m\right)},W_i)\right\}}\hfill \end{array}$$ (34)

where

$${\pi }_k({\beta }^{\left(m\right)},z_i,{\alpha }^{\left(m\right)},W_i)=E\{{\pi }_k^0({\beta }^{\left(m\right)},z_i,{\alpha }^{\left(m\right)},V_i)\mid W_i\}=\frac{\theta ({\beta }_k^{\left(m\right)},z_i,{\alpha }_k^{\left(m\right)},W_i)}{1+{\theta }_{\ast }({\beta }^{\left(m\right)},z_i,{\alpha }^{\left(m\right)},W_i)}$$

In the derivation of (34) we used the fact that

$$E\left\{U{\mathrm{e}}^{-sU}\right\}=\frac{1}{{(1+s)}^2}$$

obtained by the differentiation of the Laplace transform of the exponential distribution

$$\mathcal{L}\left(s\right)=E\left\{{\mathrm{e}}^{-Us}\right\}=\frac{1}{1+s}$$ (35)

with respect to s, and a change of the order of summation with respect to subjects i and categories k.

7.2. M-step

The problem to be solved at the M-step is

$$\underset{{\beta }^{(m+1)},{\alpha }^{(m+1)}}{\max }\stackrel{‒}{\ell }({\beta }^{(m+1)},{\alpha }^{(m+1)},{\beta }^{\left(m\right)},{\alpha }^{\left(m\right)})$$ (36)

Note that the β^(m+1)-kernel of ℓ‾ represented by the second line of (34) has the form of a Poisson regression likelihood, and moreover that, given ${\alpha }_k^{(m+1)}$, the estimates of ${\beta }_k^{(m+1)}$, k=1, . . . , K, can be obtained independently using Poisson likelihoods

$${\stackrel{‒}{\ell }}_k^{\beta }\left({\beta }_k^{(m+1)}\right)=\sum _{i=1}^n[{\delta }_{ik}\log \vartheta ({\beta }_k^{(m+1)},z_i)-\vartheta ({\beta }_k^{(m+1)},z_i)E\left\{\eta ({\alpha }_k^{(m+1)},W_i){\pi }_{y_i}({\beta }^{\left(m\right)},z_i,{\alpha }^{\left(m\right)},W_i)\right\}]$$ (37)

When the Poisson likelihood is interpreted as a likelihood for rates, δ_ik plays the role of a ‘count of events’, and the expectation in the right part of (37) plays the role of ‘person years’.

Likewise, the solution for ${\alpha }_k^{(m+1)}$ can be obtained independently for each category k=2, . . . , K, given ${\beta }_k^{(m+1)}$ using the ${\alpha }_k^{(m+1)}$-likelihood kernel

$$\begin{array}{cc}\hfill {\stackrel{‒}{\ell }}_k^{\alpha }\left({\alpha }_k^{(m+1)}\right)=& \sum _{i=1}^n[\frac{E\left\{\log \eta ({\alpha }_k^{(m+1)},W_i){\pi }_{y_i}({\beta }^{\left(m\right)},z_i,{\alpha }^{\left(m\right)},W_i)\right\}}{E\left\{{\pi }_{y_i}({\beta }^{\left(m\right)},z_i,{\alpha }^{\left(m\right)},W_i)\right\}}{\delta }_{ik}\phantom{]}\hfill \\ \hfill & -\phantom{[}\vartheta ({\beta }_k^{(m+1)},z_i)E\left\{\eta ({\alpha }_k^{(m+1)},W_i){\pi }_{y_i}({\beta }^{\left(m\right)},z_i,{\alpha }^{\left(m\right)},W_i)\right\}]\hfill \end{array}$$ (38)

Therefore, it is convenient to solve the M-step problem (36) by a Gauss-Zeidel procedure alternating between

$$\underset{{\beta }_k^{(m+1)}}{\max }{\stackrel{‒}{\ell }}_k^{\beta }({\beta }_k^{(m+1)},{\beta }^{\left(m\right)},{\alpha }_k^{(m+1)},{\alpha }^{\left(m\right)})$$ (39)

given ${\alpha }_k^{(m+1)}$ and

$$\underset{{\alpha }_k^{(m+1)}}{\max }{\stackrel{‒}{\ell }}_k^{\alpha }({\alpha }_k^{(m+1)},{\beta }_k^{(m+1)},{\beta }^{\left(m\right)},{\alpha }^{\left(m\right)})$$ (40)

given ${\beta }_k^{(m+1)}$, within each category k=2, . . . , K. One could use a unidimensional line search along the vector

$$({\beta }_k^{(m+1)},{\alpha }_k^{(m+1)})-({\beta }_k^{\left(m\right)},{\alpha }_k^{\left(m\right)})$$

after each iteration of Gauss-Zeidel to speed up the convergence, which would make this procedure similar to conjugate gradient methods [18]. The category-specific M-step likelihoods (37) and (38) are maximized by a Newton-Raphson procedure with respect to the low-dimensional fixed effect coefficients ${\beta }_k^{(m+1)}$ and the random effect coefficients ${\alpha }_k^{(m+1)}$, respectively.

7.3. Standard errors

Standard error estimates are based on the inverse of the observed information matrix

$$\mathcal{I}=-\frac{{\partial }^2\ell \left(\mu \right)}{\partial \mu \partial {\mu }^{\mathrm{T}}}$$ (41)

where μ={β, α} is the combined vector of the model parameters, and

$$\ell \left(\mu \right)=\log E\left\{L(\beta ,\alpha \mid U,W)\right\}$$

is the model log-likelihood maximized as a result of the Quasi-EM algorithm. Here as in (30) we understand that U and W are collections of independent subject-specific random vectors, and that ℓ is a sum of contributions to the likelihood over subjects.

The observed information matrix is derived by an application of the missing information principle representing the observed information as the difference between expected complete-data information and the missing information, given observed data [19, 20]. Specifically, let I₁(μ|W) be the observed information matrix conditional on W (the so-called complete-data information). This matrix corresponds to the standard multinomial logit model and is derived straightforwardly by differentiation of the log of the right part of (26) with k=y_i, and summing up over subjects ${\sum }_{i=1}^n$. Let S₁(μ|W) be the corresponding complete-data score vector, the gradient of the complete-data likelihood ${\ell }_1=\log L_1={\sum }_{i=1}^n\log \pi (y_i\mid W_i,z_i)$. Then,

$$\mathcal{I}=E\{I_1(\mu \mid W)-S_1(\mu \mid W)S_1^{\mathrm{T}}(\mu \mid W)\mid L_1(\mu \mid W)\}$$ (42)

where we used notation for the conditional expectation similar to (32). Here

$$E\{\cdot \mid L_1(\mu \mid W)\}$$

is the conditional expectation of (·) given observed data,

$$E\{I_1(\mu \mid W)\mid L_1(\mu \mid W)\}$$

is the expected complete-data information, and

$$E\{S_1(\mu \mid W)S_1^{\mathrm{T}}(\mu \mid W)\mid L_1(\mu \mid W)\}$$

is the expected missing information. The above expectations are taken numerically for each subject based on the subject-specific contribution to the score vector and to the information matrix, and then summed up over subjects. Note that the observed information representation given above is only valid at the MLE point and will generally not hold true for any Hessian matrix unless the gradient of the observed likelihood is zero. Alternatively, a bootstrap estimate of standard errors could be done. In the bootstrap approach, parametric bootstrap was used. Replicates of the observed data were simulated from the fitted joint model λ(a, y|x) with the parameters set at the MLEs (Tables I and II). Empirical standard errors of the MLEs computed over a large number of replicates (1500) were used as bootstrap estimates.

Table II.

Parameter estimates for the mixed multinomial logit model fit to Prostate Cancer SEER Data. Each estimate shows MLE and the empirical mean (in brackets) of the MLEs obtained by parametric bootstrap (simulation from the fitted model). Standard errors (SE) and confidence intervals (CI) shown are based on parametric bootstrap. Upper part of the table has fixed effects, lower part shows random effects. Response categories: 1: Stage=LR, Grade=WM; 2: Stage=LR, Grade=PU; 3: Stage=D, Grade=WM; 4: Stage=D, Grade=PU

	Contrasts
Variables	2 vs 1	3 vs 1	4 vs 1
Intercept	-0.509 (-0.500)	2.301 (2.283)	2.901 (2.890)
SE	0.0125	0.0257	0.0236
CI	(-0.524, -0.475)	(2.233,2.334)	(2.844,2.936)
Age	0.0347 (0.0346)	0.0638 (0.0636)	0.0749 (0.0749)
SE	0.00108	0.00201	0.00171
CI	(0.0325,0.0368)	(0.0597,0.0676)	(0.0716,0.0783)
Year	-0.0144 (-0.0145)	-0.0560 (-0.0558)	-0.0585 (-0.0584)
SE	-0.000264	0.000488	0.000542
CI	(-0.0150, -0.0140)	(-0.0567, -0.0548)	(-0.0595, -0.0573)
DT	-0.0375 (0.0376)	-0.153 (-0.152)	-0.249 (-0.249)
SE	0.0340	0.0100	0.0128
CI	(-0.0442, -0.0309)	(-0.171, -0.132)	(-0.274, -0.224)
ScrDx	-0.108 (-0.107)	-3.394 (-3.428)	4-3.741 (-3.761)
SE	0.0270	0.415	0.466
CI	(-0.160, -0.0539)	(-4.241, -2.614)	(-4.674, -2.848)

8. DATA ANALYSIS AND SIMULATIONS

Data for C(a, x, y) come from 331 227 prostate cancer cases diagnosed in nine areas of the U.S. (San Francisco-Oakland, Connecticut, Detroit, Hawaii, Iowa, New Mexico, Seattle, Utah, Atlanta) participating in the SEER program. Population counts P(a, x) come from the SEER population files corresponding to those areas. We use the age by year box corresponding to age interval [50, 100] and calendar year interval [1973-2000]. Of the total number of cases, the vast majority, 229 726, are detected in the early localized or regional (LR) stage with low grade representing well or moderately differentiated (WM) cells. 60 272 LR cases have high grade representing predominantly poorly differentiated or undifferentiated (PU) tumors. Of the total 41 229 distant (D) stage cancers, 17 957 were low grade (WM), and 23 272 were high grade (PU).

Multinomial response probabilities are based on the following parameterization of the predictors:

$$\theta ({\beta }_k,z_i,{\alpha }_k,W_i)=\exp ({\beta }_{k0}+{\beta }_{k1}{z}_{i1}+{\beta }_{k2}{z}_{i2}+{\alpha }_{k1}{W}_{i1}+{\alpha }_{k2}{W}_{i2})$$

specific to subject i=1, . . . , n and category k∈{1, 2, 3, 4}. The response category k is coded as specified in the Introduction by (2). For the ith subject, the fixed effects z are represented by z_{i, 1}=age-50, and z_{i, 2}=calendar year-1900. Both covariates z are treated as continuous. Fixed-effects regression parameters β_kr, r=0, 1, 2 are specific to the response category k. Identifiability restriction implies θ=1 when k=1, so that β_1r=0, r=0, 1, 2. The set of intercepts β_k0 models the baseline distribution of the stage and grade combined response Y, where the baseline group of subjects represents men 50 years of age at the beginning of the 20th century. Mixed effects are represented by two random intercept terms, the delay time W_i1=ξ_D, and the indicator of screening mode of detection W_i2=I_scr. The posterior distribution of the random vector W predicted from the marginal incidence model in Section 4 is shown in Figure 3. The random effects coefficients α_kr, r=1, 2, are restricted to α_1r=0 for the baseline response category for identifiability. Note that since the distribution of the random vector W is treated as known, α_kr remain otherwise unrestricted.

The model-predicted marginal probabilities are computed by averaging over the random effects W

$${\pi }_{ik}=E\left[\frac{\theta ({\beta }_k,z_i,{\alpha }_k,W_i)}{\sum _{c=1}^4\theta ({\beta }_c,z_i,{\alpha }_c,W_i)}\right]$$ (43)

The EM algorithm of Section 7 is used to fit the model. The maximum likelihood estimates and their standard errors are shown in Table II.

To study the properties of the algorithm by simulations, we built a simulation counterpart of the model. Conditioning on the total number of cancer cases, we simulated their frequency by age, stage and grade at diagnosis from the joint model λ(a, y|x). Simulated data include 331 227 prostate cancer cases diagnosed in nine SEER areas of the U.S. The parameters of the simulation model were fixed at the MLEs given in Table II. For each of the 1500 replicates of the simulated data, the model (43) was fitted by the self-consistency algorithm of Section 7. Empirical means of the estimated regression coefficients show excellent correspondence with the original MLEs used in the place of the ‘true’ values (Table II). Table II also shows standard errors and 95 per cent confidence intervals derived from the simulation. The Q-Q plots for all 15 model parameters (not shown) suggest that MLEs are asymptotically normal.

The coefficients associated with the mode of detection (Table II) indicate that screening leads to an increase of the chance of detection in the best prognostic category of LR stage and WM grade, and a drop in the distant stage contrasts.

The negative coefficients associated with the calendar year indicate a secular trend of slightly improved prognosis over time. Age in Table II, however, has an adverse effect. Note that age has two causal paths according to the model: the direct effect as shown in the table, and the effect exerted through the age-dependent delay time distribution (Figure 3). Age effects are a result of a complex interplay of selection effects and the unobserved heterogeneity of tumor growth.

A tumor detected in an older person without screening is generally associated with a longer sojourn time because the sojourn time in this situation is bounded from above by age. If longer sojourn time is an indication that the tumor had more time for the latent growth, an advanced stage could be expected, leading to an adverse effect of age. If tumors are heterogeneous in the sense that faster growing tumors get detected earlier and present themselves in more advanced stages, age would exert a favorable selection effect on the tumor stage at diagnosis.

Screening adds another layer of complexity through the length bias effect. Length bias is a phenomenon known from point processes [12]. When a needle is thrown on the trajectory of a point process, the sojourn time between two successive events, conditional on the needle falling between them, is generally larger than the unconditional time between the events. The source of bias is the fact that the needle is more likely to catch a larger interval than a smaller one. Applied to cancer screening this means that the sojourn time for cancers detected by screening is generally larger than the unconditional duration of the pre-clinical stage in the population.

Age is clearly a surrogate of screening as the early detection generally leads to tumors detected at an earlier age. Based on the length bias phenomenon, one would therefore expect that slower growing tumors caught by screening would shift to earlier ages at diagnosis, while the more aggressive tumors missed by screening would become more pronounced in older men, a point in the direction of the adverse effect of age.

Larger sojourn and delay times may be indicative of slow tumor growth. Not surprisingly then we observe negative coefficients associated with the delay time that indicate an improved prognosis associated with slow tumor growth.

Without incorporating a mechanistic description of the tumor progression through stages, the model currently has a limited potential to measure attributions of the above mentioned effects to the dynamics of the response (A, Y). Our strategy has been to be inclusive about the possible tumor progression mechanisms, and to keep restrictions on the model to a minimum through the multinomial distribution assumption. The model was designed to construct a causal link between the screening policy in the population and the presentation of the disease at diagnosis summarized by the stage- and grade-specific incidence. This causal link would be impossible if the model simply conditioned on intermediate outcomes such as age at diagnosis, because such outcomes are affected by the policy.

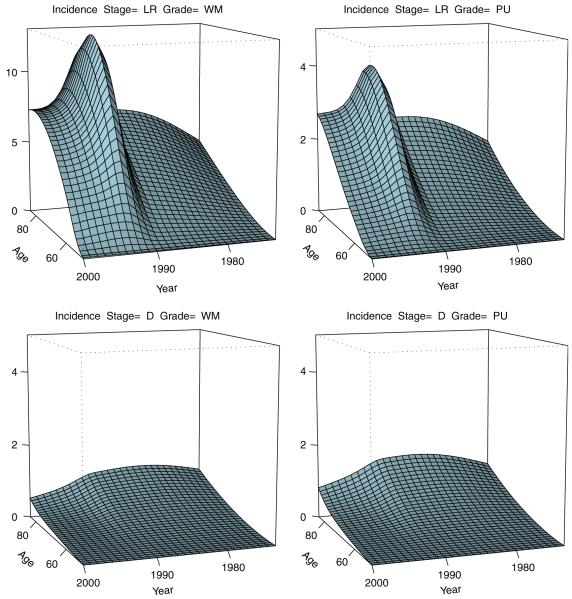
Shown in Figure 4 is the model-based prediction of the stage- and grade-specific incidence (5) of prostate cancer that shows good agreement with its empirical counterpart (Figure 2). As evident from the figure, the model reproduces the spike of the incidence of the early stage cancer induced by screening and the corresponding drop in the incidence of the distant disease associated with a fraction of distant stages being prevented by the early detection.

Figure 4.

Model-based expected stage- and grade-specific incidence of prostate cancer by age and calendar time. LR=localized-regional stage; WM=well or moderate differentiation, low grade; D=distant stage; PU=poor or no differentiation, high grade.

9. LINK FUNCTIONS

In this section we study sensitivity of the results to the link function misspecification in the multinomial logit model. In the exercise that follows we compared the multinomial logit and the generalized probit models. In doing so we noticed that the idea behind the multinomial probit model leads to a general functional form for multinomial models with arbitrary link functions. This line of thought could be quite useful in model building and sensitivity analyses. Deferring a detailed study to future research, the idea is briefly discussed in this section.

The idea of building a link function by first making multinomial probabilities proportional to individually parameterized predictors

$$\mathrm{Pr}\{\text{category}k\mid z\}~\theta ({\beta }_k,z)=\exp (-{\beta }_{k}z)$$

and then normalizing them, implies the logit link function (26). The logit link based on the normalization does not generalize to alternative link functions. Therefore, a different approach is needed. In the context of the probit models, a latent variable approach has been instrumental [21-23]. A set of linear models specific to categories k=1, 2, . . . , K

$$Y_k^{\ast }=\log \theta ({\beta }_k,z)+\epsilon$$ (44)

is the starting point. The categorical response Y is identified as the index of the first-order statistics based on $Y_k^{\ast }$

$$Y=\underset{k}{\mathrm{argmax}}{Y}_k^{\ast },{\Delta }_c=I(Y=c)$$ (45)

It is straightforward to show that if ε follows a Gumbel type I extreme value distribution

$$F\left(x\right)=\exp \{-{\mathrm{e}}^{-x}\}$$ (46)

where F is a cumulative distribution function (cdf), then (45) is equivalent to the multinomial-logistic model (26) used in this paper. Alternatively, a standard normal choice of ε, F(x)=Φ(x), gives the so-called multinomial-probit models. In the case of a binary response K=2, the two choices reduce to the logit and probit regression.

Let us derive a general expression for a multinomial model based on an arbitrary link function induced by the latent variable approach outlined above. We have

$$\mathrm{Pr}\{Y_k^{\ast }\le y\}=F(y-\log {\theta }_k),{\theta }_k=\theta ({\beta }_k,z)$$

The probability of the response falling into category c is

$$\begin{array}{cc}\hfill \mathrm{Pr}\left\{\underset{k=1,\dots ,K}{\max }{Y}_k^{\ast }=Y_c^{\ast }\right\}=& E\left[\mathrm{Pr}\left\{\underset{k=1,\dots ,K}{\max }{Y}_k^{\ast }=Y_c^{\ast }\right\}\mid Y_c^{\ast }\right]\hfill \\ \hfill =& E\left[\prod _{k=1,k\ne c}^{K}F(Y_c^{\ast }-\log {\theta }_k)\right]\hfill \end{array}$$

where the expectations are taken over $Y_c^{\ast }$. Writing the last expectation as an integral over the variable y, and changing it to the new variable u=F(y-logθ_c), we finally get

$$\mathrm{Pr}\{\text{category}c\mid z\}={\int }_0^1\prod _{k=1,k\ne c}^{K}F\left(F^{-1}\left(u\right)+\log \frac{{\theta }_c}{{\theta }_k}\right)\mathrm{d}u$$ (47)

where F^-1 is the inverse of F, and F is supposed to be an absolutely continuous cdf defined on (-∞, ∞). The general form (47) allows one to build multinomial models based on an arbitrary link function specified by any continuous cdf F defined on the real line. The general model (47) deserves a separate careful study that goes beyond the scope of the present paper.

We used (47) here to study the stability of the model fit with respect to a misspecified link function. Shown in Table III are predicted probabilities under the correct (generalized logit) link function, and their counterparts under a misspecified (generalized probit) link function. Estimates of the model parameters for both link functions are fixed at the MLEs given in Table II.

Table III.

Predictions for response probabilities based on the fitted multinomial logistic model under logit and probit link functions. The predictor is computed from the MLE estimates (Table II). Response categories 1-4 are same as in Table II

		Response probabilities
Link	Age a	Year t	y=1	y=2	y=3	y=4
Probit	60	1985	0.697	0.115	0.054	0.126
Logit			0.595	0.149	0.097	0.159
Probit	70		0.516	0.126	0.100	0.250
Logit			0.449	0.159	0.138	0.253
Probit	80		0.322	0.117	0.149	0.403
Logit			0.305	0.153	0.178	0.364
Probit	60	1992	0.769	0.116	0.032	0.077
Logit			0.661	0.150	0.073	0.117
Probit	70		0.613	0.138	0.067	0.174
Logit			0.526	0.168	0.109	0.197
Probit	80		0.423	0.141	0.113	0.314
Logit			0.379	0.172	0.149	0.300
Probit	60	2000	0.828	0.112	0.015	0.039
Logit			0.723	0.146	0.051	0.080
Probit	70		0.706	0.144	0.038	0.105
Logit			0.605	0.173	0.080	0.142
Probit	80		0.536	0.162	0.075	0.219
Logit			0.465	0.188	0.117	0.230

It is evident from Table III that the differences in the parameter estimates between the two models are small, and the basic diversity of responses and the shape of the distribution of stage and grade at diagnosis of prostate cancer are robust to the link function misspecification.

10. DISCUSSION

Cancer screening exerts complex dynamic effects in the target population. These effects are rooted in the cancer heterogeneity that largely remains unobserved, and its interaction with the screening intervention. Overdiagnosis, lead time (early detection) and length bias lead to a shift in age, stage and grade at diagnosis toward better prognosis. For the same reason post-diagnosis survival shows a profound improvement, and an increased apparent cure rate. These improvements work against an equally dramatic increase in the cancer incidence to produce a slowly changing mortality in the population. All these changes would still be happening if screening were of no benefit to mortality. In the counteraction of the many selection effects and the associated cancer treatment strategies lies the proof of the benefit of screening and treatment. Quantitative evidence of such benefits requires careful joint modeling of the latent processes and the observed outcome. In this paper we presented one such model that reproduces the complex dynamics of the disease presentation at diagnosis induced by introduction of a screening intervention.

Interaction of screening and the latent history of the disease is modeled with the help of a surrogate mixing random vector representing the delay in cancer diagnosis and the mode of detection. It should be noted that the delay time alone showed itself as a poor surrogate resulting in the distant stage predictions showing a slight bump in the cancer incidence after introduction of PSA not seen in the empirical estimates (not shown). Lack of perfect surrogacy of the delay time is likely a consequence of the heterogeneity of tumor growth rates and the length bias of cancer screening [24]. Indeed, if tumor progression was deterministic, its prognostic index at the time of diagnosis would be well explained by the delay time (age of tumor). On the other hand, with the growth rates being heterogeneous, and with screening predominantly detecting slower growing tumors (length bias), the mode of detection provides additional information essential for the goodness of fit.

The use of artificial mixtures is a technical trick that allowed us to simplify the complex estimation problems. Using this approach we achieved a transformation and factorization of the likelihood into a set of problems of reduced dimension.

Even though the Poisson complete-data likelihood does not correspond to any valid model, the algorithm is justified by invoking Quasi-Expectation and Quasi-EM techniques developed earlier.

The joint model presented in this paper is a necessary step toward providing a causal link between the policy of cancer screening defined on the population level and the dynamics of cancer mortality. Note that traditional survival models that condition on age, stage and grade as covariates measured at diagnosis, cannot be used directly to study the effect of screening on mortality, because much of this effect is expressed through changes in the covariates. The idea of the latent surrogate variables used as mixed effects to model the causal link could be extended to model mortality. Based on the model presented in this paper, a surrogate variable could be developed for use as a mixed effect in the survival model (frailty model). For the survival model, the distribution of frailty needs to be updated conditionally on age, stage and grade at diagnosis. As a result, a joint model for stage-grade-specific incidence and survival would emerge. This leads to a causal model of mortality as a function of screening policy integrating dramatic changes in incidence, disease presentation at diagnosis and survival, occurring with screening.