Assessment of Performance Improvement in Content-based Medical Image Retrieval Schemes using Fractal Dimension

Abstract

Rationale and Objectives

To investigate whether using fractal dimension as an objective index (quantitative measure) to assess and control the “visual” or “texture” similarity of reference image regions selected by a CBIR (content-based image retrieval) scheme will (or will not) affect the performance of the scheme in classification between image regions depicting suspicious breast masses.

Materials and Methods

An image dataset depicting 1500 verified mass regions and 1500 false-positive mass regions was used. We computed 14 morphological and intensity distribution based features and a fractal dimension. A CBIR scheme using a k-nearest neighbor classifier was applied and two experiments were conducted. In the first experiment, we evaluated our CBIR scheme using all 15 features. In the second experiment, we used the fractal dimension as a prescreening feature to guide the CBIR scheme to search for the most similar reference images that have similar measure in the fractal dimension.

Results

The CBIR scheme achieved classification performance with area under ROC curve (A_Z) of 0.857 with 95% confidence interval (CI) of [0.844, 0.870] using 14 features and 0.866 with 95% CI of [0.853, 0.879] after adding fractal dimension. The p-value of two classification results was 0. 005. After using fractal dimension as a prescreening feature, the CBIR scheme achieved A_Z = 0.851 with 95% CI of [0.837, 0.864] without significant difference as comparing with the previous result using the original 14 features (p = 0.120). The difference of fractal dimension values between the selected similar reference images was reduced by 56.7% indicating the improvement of image texture similarity. In addition, more than half of references were early discarded without similarity comparison indicating the improvement of searching efficiency.

Conclusions

This study demonstrated the feasibility of applying the fractal dimension as an objective (quantitative) and efficient search index to assess and maintain texture similarity of reference mass regions selected by the CBIR schemes without reducing the scheme performance in classifying between suspicious breast masses.

I. INTRODUCTION

Content-based image retrieval (CBIR) schemes have been developed to search for similar images to the queried image from the large reference image databases based on features or image content inherently contained within the images [1, 2]. In particular, CBIR method has been proposed to overcome the difficulties encountered in textual annotation or description by manual methods for large image databases [3]. Although, the use of purely visual image query is unlikely to be able to completely replace text-based searching methods, CBIR has the potential to be a very useful complement to the text-based searching methods due to the unique image characteristics [4]. In the field of computer vision, CBIR has been one of the most active research areas over the last 30 years [5].

Currently, as the advance of digital imaging technologies applied to medical imaging areas, a large number of diverse radiological and pathological images in digital format are rapidly produced in the hospitals and medical centers with sophisticated image acquisition devices and digital scanners. These digital images have been routinely used for diagnosis and therapy purpose. The management and the access to these large image repositories become increasingly complex and challenging [1]. In reading and interpreting medical images, the observers (i.e., radiologists and pathologists) often faced with new unknown and suspicious lesions depicted on medical images in daily clinical practice, which requires the observers to search for and compare the similar cases with previously verified results in their decision making of detection and diagnosis [6, 7]. This is a difficult and very time-consuming task as the rapid size or volume increase of medical image databases. Therefore, developing and applying CBIR schemes to more effectively organize and retrieve images has attracted wide research interest in medical imaging and informatics research areas [1, 4, 8]. In particular, a number of studies have been recently reported how to develop and optimize CBIR schemes to search for similar breast lesions (including masses and micro-calcification clusters) [3, 6, 9, 10, 11].

There are many factors to consider in the design of a CBIR systems based on the domains and purposes, choice of right features, similarity measurement criteria, indexing mechanism, and query formulation technique [1, 4]. One of the most important factors in the design process is the choice of suitable visual features and the methodologies to extract them from raw images [1] because the query image is formulated and represented by exclusive features [9]. Moreover, feature extraction step affects all other subsequent processes. In medical imaging applications, the performance and potential clinical utility of CBIR schemes is primarily evaluated by three factors namely (1) clinical relevance (i.e., classification performance evaluated using ROC method), (2) visual similarity between the queried image region and the selected reference regions (i.e., finding the effective visual similar indices), and (3) search efficiency (i.e., whether computation task can be done in real time). In previous studies, some focused on improving CBIR schemes in classification between positive and negative lesions (clinical relevance) [6, 10], while others investigated to assess and compare visual similarity of the selected reference images using subjective rating [11] and a two-alternative forced-choice observer preference study [12]. Although visual similarity is very important in the application of CBIR schemes, previous studies also found that it was a subjective concept with large inter-observer variability [11, 12]. Therefore, identifying and applying an objective index (a quantitative feature or feature set) to assess visual similarity of reference image regions selected by CBIR schemes is an important and technically challenging task. In addition, many of pixel value distribution related similarity indices (i.e., mutual information and Pearson’s correlation) used in previous CBIR schemes are computational expansive and cannot be used to conduct efficient (“real-time”) image search [13]. Our goal is to guarantee that all reference image regions selected by CBIR schemes have improved “visual similarity” assessed by an objective and computational efficient index (not the previously used subjective index), while without reducing the scheme performance in classification of suspicious lesions (diagnosis of medical images).

In computer vision, texture is defined by such terms as structure and randomness [5]. The fractal model (or analysis) has been introduced to describe the ruggedness of natural objects [14]. One of the advantages of fractal analysis is the ability to quantify and describe the irregularity and complexity of images with a measurable value, which is called the fractal dimension [15, 16]. Because fractal dimension shows both of self-similarity and over all roughness at multiple scales [17], it can be used to describe and interpret patterns of visual texture [18]. For example, one previous study reported because cancerous tumors exhibited a certain degree of randomness associated with their growth and were typically irregular and complex in shape, fractal analysis could provide a better measure of their complex patterns than conventional Euclidean geometry [19]. The other studies also suggested that the subjective evaluation of visual feature was highly correlated with fractal dimensions of textile design images [20] and could help in determining the inherent complexity of visual images and serve as a tool for the estimation of visual complexity [21]. In these studies, some researchers believed that visual similarity based on fractal dimension might at least partially imply or correlate with semantic similarity [22]. Therefore, fractal dimension can be used as a feature for both visually recognizable image texture and semantic similarity in searching for irregular cancerous regions.

Due to its unique advantages, fractal analysis has been widely applied to many medical imaging research areas including the detection, segmentation, and classification tasks with varied success. For example, fractal dimension has been used in detection and segmentation of microcalcifications depicted on digital mammograms [14, 23], classification between benign and malignant breast masses [24], classification and analysis of mammographic parenchyma patterns [17, 25], and analysis of trabecular bone structure [26, 27]. However, to the best of our knowledge, the fractal dimension has not been applied in any CBIR schemes to search for similar medical images (i.e., those depicted breast mass regions) from the reference database to date. In this preliminary study, we investigated and tested whether using fractal dimension as an objective index (quantitative measure) to assess and control the visual similarity of reference image regions selected by a CBIR scheme will (or will not) affect the performance of the scheme in classification between image regions depicting suspicious breast masses.

II. MATERIALS AND METHODS

A. Reference image database

We have assembled a large and diverse image database of mammograms in our laboratory. The original digitized mammograms were generated using several film digitizers with the pixel size of 50μm × 50µm and 12bit gray level resolution. To create a reference database used in CBIR based CAD studies, our computer program first sub-sampled the images by the factor of 2 (increasing pixel size to 100µm × 100µm) and then extracted all selected regions of interest (ROIs) with a fixed size of 512 × 512 pixels. The center of each suspicious mass is also located in the center of the extracted ROI. Using the ROI center pixel as a mass region growth seed, the previously developed multi-layer topographic region growth algorithm [28] used in our CAD scheme was applied to segment the mass region (define its boundary contour). For each true-positive mass, the automated segmentation result (its boundary contour) was visually examined. If the noticeable segmentation error was identified, the mass boundary contour was manually corrected (re-drawn). Unlike some of previously reported studies in which the negative ROIs were randomly selected and extracted from the negative images, each negative ROI selected in our reference database actually contains a false-positive mass that is automatically segmented and cued by CAD scheme.

The reference database used in this study includes 3000 ROIs extracted from the mammograms acquired from 1127 cases (patients). In 336 cases ROIs were extracted from two breasts and in 791 cases ROIs were only extracted from one breast. Thus, in 1463 breasts (336 + 791), 843 depict verified mass regions (true-positives), while 620 are not. Among the 843 breasts depicted positive masses, 722 depict malignant masses and 121 depict biopsy-proved benign masses. All of these masses were originally rated as BI-RADS category 4 and 5 by the radiologists. Similar to our previous study [12], the CBIR schemes compared and tested in this study is to detect suspicious mass regions (classification of whether the queried ROI depicted a suspicious breast mass). Thus, each true-positive ROI depicts one verified mass (either malignant or benign) and each false-positive ROI depicts a CAD-cued false-positive mass but it is actually negative. In summary, among these 3000 ROIs, 1500 are true-positive regions and the remaining 1500 ROIs are negative regions. The 1500 true-positive ROIs were extracted from 906 masses depicted on 843 positive breasts. Among them, 594 masses were extracted from both CC and MLO view, while 312 masses were extracted from only one view. The 1500 negative ROIs were extracted from CAD-cued false-positive mass regions depicted on 769 breasts (including 620 negative and 149 positive breasts). In addition, some of image characteristics of these selected true-positive mass regions have been reported elsewhere. Approximately one half of these masses were rated subjectively as “subtle” to “very subtle” by radiologists [12].

Based on mass segmentation results, we used a computer scheme to compute 14 morphological and intensity (pixel value) distribution features from each segmented mass region (including both true-positive and false-positive regions). These 14 features were selected from a large initial feature pool using genetic algorithm as we have reported in our previous study [12]. The detailed definitions and computing methods of these features including 3 global features computed from whole breast area segmented from the image (average pixel value in the breast area, average local pixel value fluctuation in the breast area, standard deviation of the local pixel value fluctuation in the breast area) and 11 local features computed from the segmented mass region and its surrounding background (region conspicuity, normalized mean radial length of a region, standard deviation of radial length, skew of radial length, shape factor ratio, standard deviation of pixel value inside the mass region, standard deviation of the gradient of boundary pixels, skew of the gradient of boundary pixels, standard deviation of pixel values in the surrounding background, average local pixel value fluctuation in the surround, normalized central position shift) have been previously reported [12]. These 14 computed image features have been saved in a reference feature data file that contains all extracted and selected ROIs in our reference database.

B. Fractal dimension

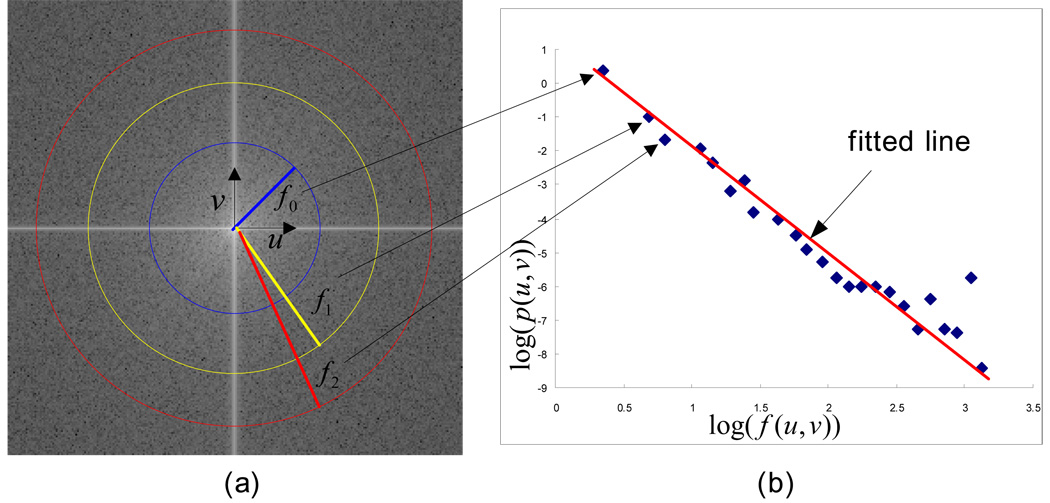
We added a new feature (fractal dimension) into the reference feature data file for each selected ROI in this study. To compute the fractal dimension, the computer scheme first applied the fast-Fourier transform (FFT) to each ROI and produced a unique two-dimensional complex array called the power spectrum [27]. The power spectrum P(u,v) is calculated.

$$\begin{array}{ll}P(u,v)\hfill & =\left|F{(u,v)}^2\right|\hfill \\ \hfill & =R{(u,v)}^2+I{(u,v)}^2\hfill \end{array}$$

where u and v represents the horizontal component and vertical component of frequencies, while R(u,v) and I (u,v) are the real and imaginary parts of Fourier transform F(u,v) , respectively. The power spectrum is displaced in polar form and shifted to locate zero frequency at the center. The scheme calculates logarithm log(f (u,v)) where $f(u,v)=\sqrt{u^2+v^2}$ and average log(P(u,v)) in the condition of $f(u,v)\text{<=}\sqrt{u^2+v^2}$. Each set of u and v is defined by every 0.1 of log(f (u,v)) [Fig. 1 (a)]. The slope of the curve on average log(P(u,v)) versus log(f (u,v)) is calculated by a least square fitting [Fig. 1 (b)]. Finally, the fractal dimension (FD) is calculated.

$$\text{FD}=\frac{(7-\mathit{\text{Slope}})}{2}$$

Figure 1.

(a) Power spectrum using Fourier transform and (b) the line fitting for the curve on average log(P(u,v)) versus log(f (u,v)) . The center of the image is the origin of the frequency coordinate system. f₀ , f₁ , and f₂ are the distance according to frequencies, u and v, from origin of the coordinate system.

Each fractal dimension computed from 3000 reference ROIs was then normalized from 0 to 1. The results were saved in the reference feature data file together with the aforementioned optimal set of 14 features. Finally, in the study, the fractal dimension was either used as an individual (prescreening) feature or combined with the other 14 features to describe each ROI.

C. CBIR scheme using a KNN classifier

In our previous study [12], we developed and tested a CBIR scheme using a multi-feature based k-nearest neighbor (KNN) classifier to search for similar breast masses depicted on the reference database. Our genetic algorithm optimized KNN based classifier which searches for and identifies 15 (K) of the most “similar” suspicious mass regions to the testing (queried) region from the pre-established reference feature data file. The similarity is measured by the Euclidean distance (d) between a testing mass region (y_T) and each of the reference regions (x_i) in a multi-dimensional space with F_N selected image features (f_r).

$$d(y_T,x_i)=\sqrt{{\displaystyle \sum _{r=1}^{F_N}{(f_r(y_T)-f_r(x_i))}^2}}$$

A smaller distance indicates a higher degree of “similarity” between two compared regions. The KNN classifier then computes a detection score to indicate the likelihood of being a true mass to the queried region:

$$P_{\mathit{\text{TP}}}=\frac{{\displaystyle \sum _{i=1}^N{w}_i^{\mathit{\text{TP}}}}}{{\displaystyle \sum _{i=1}^N{w}_i^{\mathit{\text{TP}}}}+{\displaystyle \sum _{j=1}^M{w}_j^{\mathit{\text{FP}}}}},N+M=K$$

where $w_i=\frac{1}{d{(y_T,x_i)}^2}$ (a distance weight), $w_i^{\mathit{\text{TP}}}\text{and} w_j^{\mathit{\text{FP}}}$ are the distance weights for the true-positive (i) and false-positive (j) mass regions, respectively. N is the number of verified true-positive (TP) mass regions, and M is the number of CAD-cued false-positive (FP) regions.

D. Performance evaluation

When applying the CBIR scheme, a retrieved reference image (ROI) is considered to be clinically relevant if it belongs to the same class (i.e., mass or non-mass in this study) of the query image (ROI). Since CBIR schemes use the instance-based machine learning methods that depend on nearest neighbors and/or locally weighted regression to approximate real-valued or discrete-valued target functions, no pre-training process is needed to construct a general and explicit target function [28]. In this study, we used a leave-one-case-out method to test and evaluate the performance of our CBIR scheme. In the experiment each of 3000 ROIs in our reference database was separately used once as a testing (queried) ROI. In this iterative process of performance evaluation, once a testing ROI was selected, the CBIR scheme searched for the K ROIs through the remaining reference database (excluding itself and all other ROIs extracted from the same case or patient) that are considered the most similar to this testing ROI. As a result, a set of K similar reference ROIs and a corresponding detection score is generated for the testing ROI. Based on the detection scores for both true-positive and false-positive ROIs, we applied a ROC data fitting and analysis program (ROCKIT [29]) to compute ROC curve including the area under ROC curve (A_Z value) and 95% confidence interval (CI). The A_Z value was used as an index to assess the performance of CBIR scheme in selecting clinically relevant reference ROIs. The statistically significant difference (p value) was also used to compare the performance difference between two CBIR schemes.

In this study, we conducted two experiments in evaluating CBIR schemes with the fractal dimension. In the first experiment, we tested and evaluated our KNN based CBIR scheme using 15 features (including fractal dimension and the previously selected optimal feature set with 14 features). The primary purpose of this experiment is to test whether adding fractal dimension is redundant or it can replace a number of the other existing features. We applied genetic algorithm (GA) with the same procedure as described in our previous study [12] to search for the optimal features among these 15 features (14 morphological and intensity distribution features and one fractal dimension) and the number (K) of similar reference regions. In brief, a binary coding method was applied to create GA chromosomes. Each extracted feature corresponds to one gene of a chromosome in which “1” indicates that the feature is selected and “0” indicates that the feature is discarded. Five additional genes are also appended to the chromosome to find an optimal reference K. For example, 01111 indicate that 15 neighbors are selected. Thus, each GA chromosome includes 20 genes in this experiment. GA iteratively performs cross-over and mutation operation to find the composition of genes improving the performance of the CBIR scheme. At each iteration, A_Z value of ROC curve is computed according to the combination of the features and K corresponding composition of genes selected by GA. When there is no performance improvement in the new generation or the searching generation reaches the predetermined maximum number (i.e., 100 in our studies), the GA optimization terminates in this experiment.

In the second experiment, we added the fractal dimension as a prescreening feature (condition) to our previously optimized CBIR scheme using 14 features. The purpose of this experiment is to force the CBIR scheme to only search for the reference ROIs that have similar fractal dimension values (texture similarity) to the testing ROI. In the experiment once a testing ROI was queried, fractal dimension was used as a criterion to early discard all the reference ROIs if the difference (d_FD ) of fractal dimensions between the testing ROI and these reference ROIs is larger than a predetermined threshold (α). The criterion is −α ≤ d_FD ≤ α. The reference ROIs beyond the condition are discarded in advance before the previously developed CBIR scheme [12] is applied to search for the similar ROIs from the remaining reference database. Hence, computational complexity is reduced as the amount of the reference regions removed by the condition resulting in further improvement of searching efficiency. We systematically tested and evaluated the performance of the CBIR scheme and computational complexity as the function of the threshold in fractal dimension difference (α). Finally, we compared the statistically significant difference between performances of the CBIR scheme using fractal dimension as one additional feature (experiment one) or a prescreening feature (experiment two) and the CBIR scheme using only previously optimized 14 features using CORROC program in ROCKIT package.

III. RESULTS

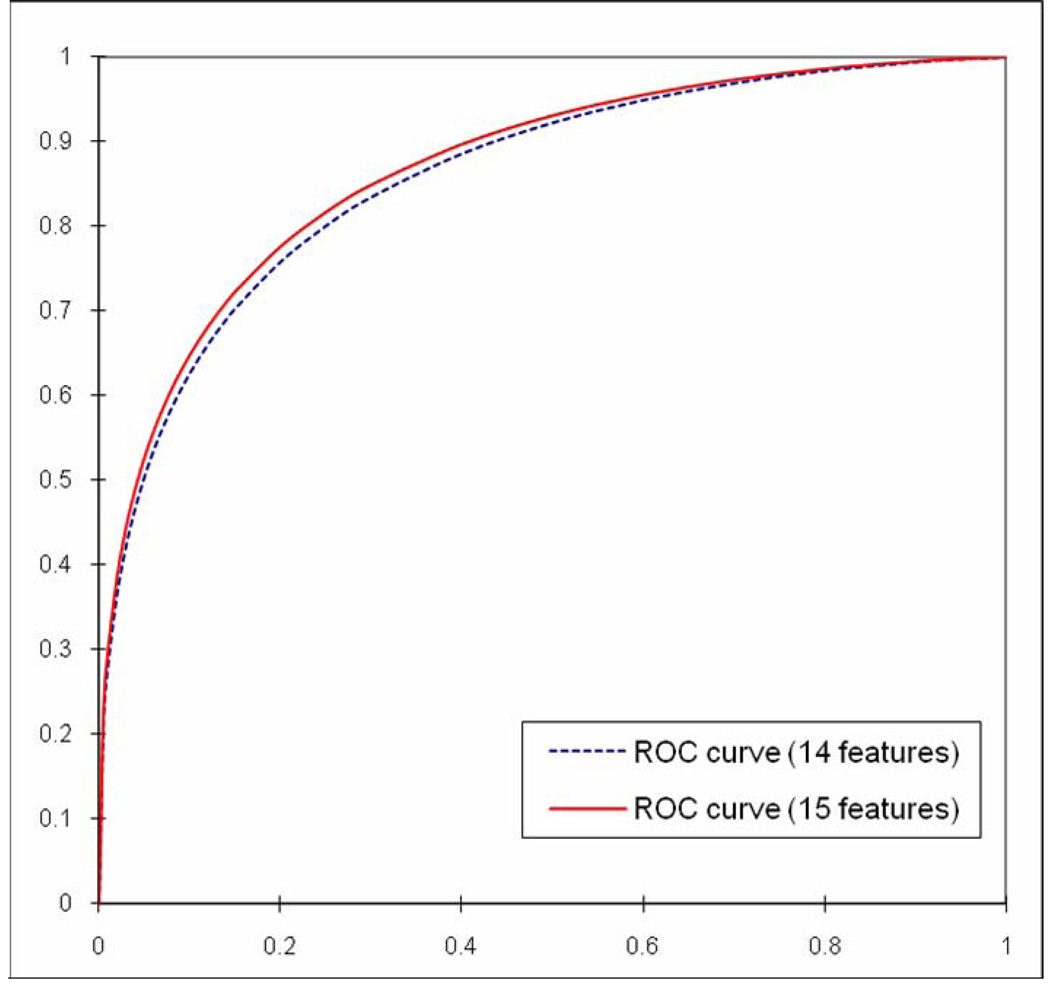
In the first experiment, the genetic algorithm generated an optimal KNN includes all 15 features and 26 neighbors (K = 26). The CBIR scheme achieved the best performance with A_Z value of 0.866 with 95% confidence interval (CI) between 0.853 and 0.879. Comparing to the previously optimized CBIR scheme that achieved A_Z value of 0.857 with 95% CI between 0.844 and 0.870 using 14 features and 15 the most nearest neighbors (K = 15), we found that fractal dimension was not a redundant feature and it could make contribution to improve CBIR scheme performance. Figure 2 shows two ROC curves plotted using classification results generated by the previous scheme using 14 features and the new scheme by adding the fractal dimension. The difference of two A_Z values was assessed with the two-tailed p-value computed by ROCKIT program (p = 0.005) with 95% CI for the difference between −0.0136 and −0.0025.

Figure 2.

Comparison of the two ROC performance curves generated using two CBIR schemes with original 14 features and adding Fourier spectrum based fractal dimension as the 15^th feature. The A_Z values are 0.857 with 95% CI [0.844, 0.870] and 0.866 with 95% CI [0.853, 0.879], respectively.

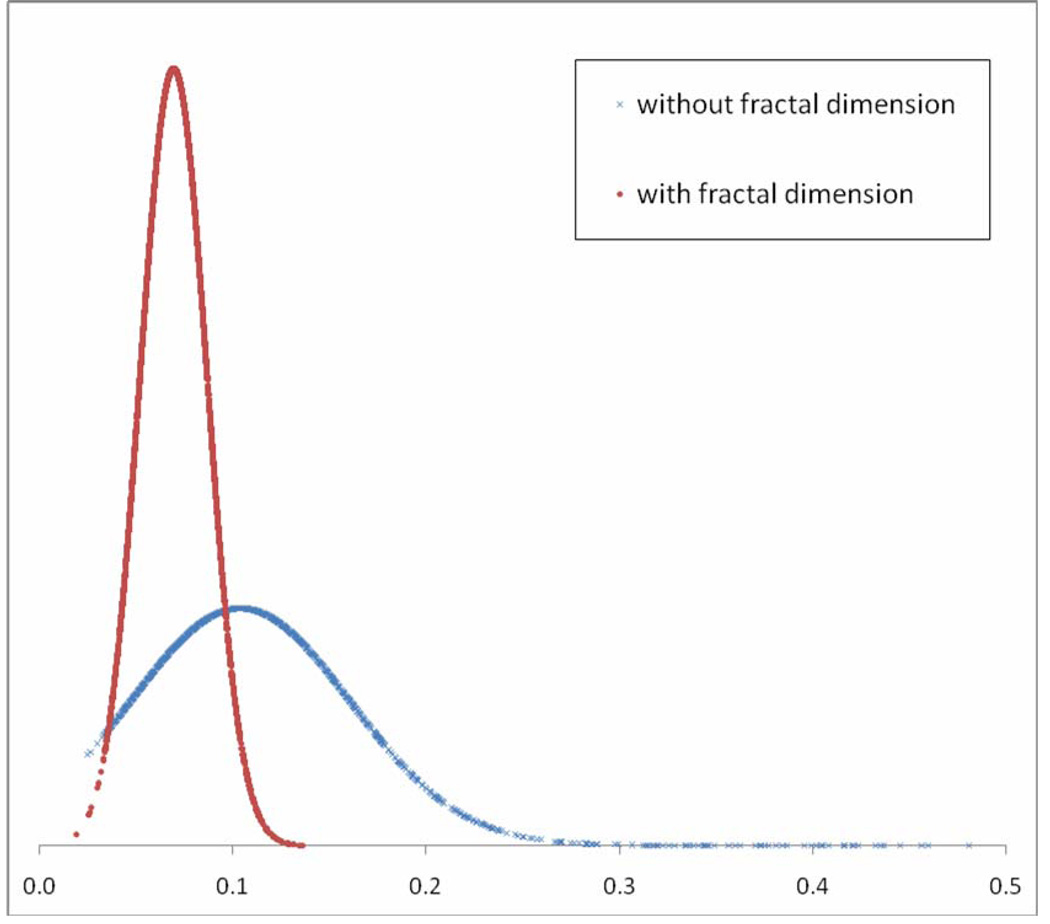
In the second experiment, table 1 shows the computed A_Z values and their 95% CI values of the CBIR scheme as the variation of the thresholds (α) on the allowed difference in fractal dimension values between the queried ROI and the selected reference ROIs. For example, the results show when α was 0.10, our CBIR scheme using 14 features and 15 nearest neighbors achieved the best performance with A_Z value of 0.851 with 95% CI of [0.837, 0.864]. There was no statistically significant difference between performances of the CBIR scheme using fractal dimension as a prescreening condition (i.e., α = 0.10) and the original CBIR scheme using only previously optimized 14 features (p =0.120). At this threshold level, 1588 (approximately 53%) reference ROIs was early discarded (Table 1). The mean and standard deviation of fractal dimension differences between one test region and each of 15 the most similar reference regions selected by the CBIR scheme using the fractal dimension as a prescreening condition was 0.045 ± 0.028. On the other hand, the mean and standard deviation of those regions selected by CBIR scheme without using fractal dimension was 0.104 ± 0.057 (Fig. 3). The results indicated that when using the new CBIR scheme, the difference of selected reference ROIs in the fractal dimension was substantially reduced by 56.7% without reducing the performance in classification between suspicious breast masses.

Table 1.

The performance of CBIR scheme and the average number of early discarded (removed) reference ROIs as the function of the comparison threshold of fractal dimension.

α (Half of Difference between two FDs )	AZ value	95% CI of AZ value	The average number of removed reference ROIs
0.06	0.843	[0.844, 0.870]	2140
0.07	0.843	[0.829, 0.857]	1967
0.08	0.845	[0.931, 0.859]	1835
0.09	0.850	[0.836, 0.862]	1709
0.10	0.851	[0.837, 0.864]	1588
0.20	0.853	[0.839, 0.866]	695
0.30	0.853	[0.839, 0.865]	272

Figure 3.

Distributions of the mean of fractal dimension differences between the testing region and each of 15 similar regions selected by two CBIR schemes with and without using fractal dimension as a prescreening condition.

IV. DISCUSSION

Although a large number of CBIR schemes have been previously developed and tested, there is no universally applicable CBIR scheme for medical imaging applications. All CBIR schemes are domain knowledge dependent because image characteristics or features vary widely in different application fields. Medical imaging will be an ideal application filed of the CBIR schemes due to the limited definition of image classes (e.g., digital mammograms) and because the meaning and interpretation of medical images is better understood and characterized [3]. Among the components of the CBIR scheme, feature selection to describe the image properties is one of the most important parts. As a “visual aid” tool, our previously pilot study has demonstrated that the low performance level of CBIR scheme in classification between lesions (clinical relevance) might mislead radiologists and reduce their diagnosis performance; while the poor visual similarity between lesions would also result in radiologists to ignore the CBIR selected reference ROIs in their decision making [30]. Therefore, finding an optimal feature set to improve performance of the CBIR schemes in both clinical relevance and visual similarity is a significant issue at present. However, the most of previous studies in developing CBIR schemes for medical images (in particular using mammograms) separately focused on improving either clinical relevance or visual similarity of CBIR schemes. The unique characteristic of this study is that we develop and assess a CBIR scheme that aims to achieve high performance in both clinical relevance and “visual” similarity.

In general, the use of multiple features leads to more accurate pattern classification than the use of a single feature because the weaknesses of one feature could be compensated by the strengths of the other features [22]. On the other hand, coarse feature set without refining for the specified purpose does not always promise the improvement of performance. Therefore, even though any feature is well known as a good feature to describe an image, in order to combine with previously well organized feature set, it needs to be evaluated again with previously developed feature set. In the first experiment, the genetic algorithm optimization resulted in a new KNN-based CBIR scheme that contained all 15 features including previously optimized 14 morphological and intensity-based features and one fractal dimension, which indicates that fractal dimension is not a redundant feature or highly correlated to any of previously selected 14 morphological and intensity distribution based features. As an additional feature used in a KNN algorithm, the fractal dimension contributes to the improvement of CBIR scheme performance.

Since there are two ways to define the relevance (or performance) in CBIR results; visual or semantic [31] in which the visual similarity means that two images "look visually similar" regardless of the image content, the selected reference image set must also be considered by the observers as actually visually “similar” and “relevant” to the case being diagnosed. Otherwise, observers will largely ignore the CBIR results [12, 30]. However, using subjective rating methods to assess the visual similarity is very difficult and often unreliable due to the large inter-observer variation. Studies have shown that the difference between the computerized selection results and the average visual selection results of a panel of radiologists was often smaller than the inter-observer selection results [11, 32]. Thus, developing an objective (or quantitative) index to assess visual similarity may be an important and practical alternative in developing and evaluating CBIR schemes. Previous studies have shown that fractal dimension could be used as a visually similar texture feature [19–22]. Thus, in this study, we selected fractal dimension as an objective index to increase visually texture similarity in the retrieved reference regions. The potentially clinical utility of using fractal dimension as an objective index to improve visual similarity depends on whether this will not significantly affect (in particular reduce) the performance of CBIR schemes in selecting the clinically relevant images. Our second experiment clearly demonstrates that the use of fractal dimension as a visually texture similarity criterion does not significantly affect the performance of the CBIR scheme in classification between suspicious breast masses depicted on digitized mammograms. However, it increases the visually texture similarity by substantially reducing the difference of the fractal dimension between the queried (testing) ROI and each of the similar reference regions selected by the CBIR scheme.

In addition, using fractal dimension as an objectively visual similarity assessment index has a number of other advantages. First, as the size increase of reference database, the computational efficiency becomes an important issue in the real-time application of CBIR schemes [5]. Using fractal dimension as prescreening tool the schemes can early discard a large fraction of ROIs and reduce searching space in the reference database before more computationally complex methods (or algorithms) are used. Second, unlike several other potentially visual similarity comparison indices (i.e., mutual information and Pearson correlation coefficient [13]), fractal dimension of all reference ROIs in the database can be pre-computed (off-line) similar to all other morphological and intensity-based features used in our KNN algorithm. Thus, fractal dimension is a unique feature suitable to be implemented in the CBIR schemes with the real-time computation and comparison capability. Third, fractal dimension or analysis is also scale independence [15]. Although shape features are the good cue to search for the same objects in an image, they rely on the accurate segmentation results and are not robust to the various scales. Therefore, fractal feature can serve as a reliable feature to search for or match the mass regions of the same patient, which depicted on images acquired during the sequential examinations.

We recognized that although the results were encouraging, this was a very preliminary study that addresses a difficult but very important technical challenge in developing and evaluating CBIR schemes applied for medical images. This study has a number of limitations. First, although fractal dimension and analysis is related to the visual similarity in image texture features, only when it is applied to an ideal fractal surface (continuous and truly self-similar), the computed fractal dimension values will be the same [16]. Therefore, in our future study, we will compare other computational methods of fractal dimension to find out the optimal solution that enables the fractal dimension having the best capability for classifying suspicious breast masses and searching for texturally similar mass regions depicted on mammography. In addition, although improving texture similarity is an important step to improve the overall visual similarity in selecting medical images using CBIR schemes, whether the use of the similarity of fractal dimension can actually produce the acceptable visual similarity required in the clinical practice by the radiologists still needs to be investigated using different observer preference studies. Second, the ultimately clinical utility of CBIR schemes depends on many factors including (1) scheme performance level, (2) observers’ confidence level to accept the CBIR scheme generated results, (3) observers’ experience in medical image diagnosis, and (4) the subtleness of the queried cases. This study only focused on improving scheme performance. Many application-related issues need to be further investigated before any CBIR schemes can be optimally used in the clinical practice.

In summary, due to the large image repositories, their complexity, and need of the reference images to compare the similar cases with the previously verified results, CBIR has recently been attracting wide research interest in medical imaging and informatics research fields. Because of the large difference between human and computer vision, developing an efficient CBIR scheme that can achieve high performance in both clinical relevance and visual similarity remains a difficultly technical challenge. In this preliminary study, we adopted and tested the fractal dimension, a well recognized texture feature that somehow correlates with the visual similarity, as a texture measure in the CBIR scheme to describe the roughness of mass regions. The results of this study indicate that (1) combining the fractal dimension with other morphological and intensity distribution features is not redundant and may increase performance of the CBIR scheme, and (2) using the fractal dimension as a prescreening tool to improve visually textural similarity of the selected reference ROIs does not significantly affect the performance of CBIR scheme in classification between suspicious breast mass regions. Therefore, fractal dimension can be selected as a “visually” and semantically promising feature used in the CBIR schemes to improve their performance and computational efficiency.