Arterial load and ventricular-arterial coupling: physiologic relations with body size and effect of obesity

Abstract

Accurate quantification of arterial function is crucial to distinguishing disease states from normal variants. However, there are little data regarding methods to scale arterial load to body size in humans. We studied 2365 adults aged 35–55 years free of overt cardiovascular disease. We assessed arterial hemodynamics and ventricular-vascular coupling with carotid tonometry and Doppler echocardiography. To define normal (physiologic) relationships between hemodynamic indices and body size, we used non-linear regression to analyze a selected reference subsample (n=612) with normal weight (body mass index 18–25 kg/m²), waist circumference and metabolic parameters. Most arterial hemodynamic indices demonstrated important relationships with body size, which were frequently allometric (non-linear). Allometric indexation using appropriate powers (but not ratiometric indexation) effectively eliminated the relationships between indices of arterial load and body size in normal subjects. In the entire sample (n=2365), the adverse effects of obesity on arterial load and end-systolic ventricular stiffening were clearly demonstrated only after appropriate indexation to account for the expected normal relationship to body size. After adjustment for age and gender, a progressive increase in indexed systemic vascular resistance, effective arterial and ventricular end-systolic elastance and a decrease in total arterial compliance were seen from normal weight to obesity (P<0.0001). Arterial load relates to body size in an allometric fashion, calling for scaling with the use of appropriate powers. Obesity exerts adverse effects on arterial load and ventricular stiffening that go beyond the normal relationship with body size. Allometric normalization should allow more accurate quantification of arterial load in future studies.

Introduction

Non-invasive assessment of arterial load provides important physiologic and prognostic information^1–3. Arterial load is not only influenced by arterial health but is also a key determinant of ventricular systolic and diastolic function, ventricular remodeling and the risk of heart disease.⁴ A comprehensive non-invasive assessment of arterial load is feasible in both clinical and epidemiologic settings using a combination of arterial tonometry and Doppler echocardiography.¹ The use of such non-invasive techniques has provided significant insights into the role of arterial hemodynamics in normal aging, hypertension and other disease states.^{1, 5, 6}

Accurate quantification of functional parameters is crucial to distinguishing disease states from normal variants. It is well recognized that the large variation in parameters of body size (such as body height) seen in adult populations strongly calls for scaling of cardiovascular parameters.⁷ However, although physiologic principles and previous empirical data strongly suggest that there should be a physiologic relationship between body size and arterial load in humans and despite the clear relationship between body size and arterial load reported in other species,^{2, 7} there are no data regarding optimal methods to scale arterial load⁸ to measures of body size in humans.

For physiologic indices that are directly related to body size, appropriate normalization is required when comparing different individuals, different groups of individuals and even changes within single individuals in situations in which body size also changes. Normalization for body size is particularly important in studies investigating the effects of obesity and gender on physiologic parameters. A key principle in establishing an optimal method of normalization for body size is that relations between body size and measures of dimensions or functions of organs are often nonlinear.^{7, 9–11} In the presence of non-linear relationships, simple ratiometric indexation or statistical adjustment for indices of body size in linear regression models can be misleading.^{7, 9} Under such circumstances, the appropriate power of the allometric relation between the physiologic measurement and body size is needed.^{7, 9, 10, 12} Allometric scaling approaches divide the cardiovascular variable of interest by a body size variable raised to a scalar exponent.^{7, 10} Such approach has proven extremely useful in examining pathologic processes such as left ventricular remodeling.^{10, 13}

Given the paucity of information regarding the metrics of the physiologic relations between arterial load and body size in human adults, we aimed to: (1) Identify the normal relationship of indices of arterial load and ventricular-arterial coupling to measures of body size in a large population-based sample of middle-aged adults; (2) To assess the impact of obesity on arterial load, beyond the normal expected relationship with body size.

Methods

We refer the reader to the online supplemental methods section available at http://hyper.ahajournals.org, for a more detailed description of our methods.

Study population

The Asklepios study recruited a cohort of 2524 apparently healthy, community-dwelling male and female volunteers aged 35 to 55 years.^{1, 14} Complete echocardiographic and tonometry data available for analyses of arterial load and ventricular-vascular coupling were available from 2368 subjects. The Ghent University Hospital Ethical Committee approved the study protocol. Subjects were sampled from the Belgian communities of Erpe-Mere and Nieuwerkerken. The sampling was by tiered direct mailing based on random samples drawn from the population lists. Further details about the study population have been previously described in detail.^{1, 14}

To provide reference standards for predicted normal (physiologic) changes in arterial parameters related to body size, we selected a reference subsample of normal-weight adults (body mass index 18–25 kg/m²) who did not meet any of the following exclusion criteria: (1) Abdominal obesity (waist circumference ≤102 cm in men and ≤88 cm in women); (2) Hypertension (systolic blood pressure ≥140 mm Hg, diastolic blood pressure ≥90 mm Hg, or drug treatment for hypertension); (3) Current smoking; (4) Diabetes mellitus (fasting blood glucose ≥126 mg/dL or pharmacologic treatment for diabetes); (5) Low-density lipoprotein cholesterol >160 mg/dL; (6) Triglycerides ≥150 mg/dL; (7) Low HDL-cholesterol (<40 mg/dL in men and <50 mg/dL in women); (8) Use of any lipid-lowering medication. The resulting reference population consisted of 612 subjects (414 women and 198 men). Of note, as part of the general selection criteria for the Asklepios study, none of the studied subjects had evidence of overt cardiovascular disease.¹⁴

Doppler echocardiography and arterial tonometry

Doppler-echocardiographic examinations were performed using a Vivid-7 ultrasound platform (Vingmed Ultrasound; Horten, Norway) as previously described and explained in more detail in the online supplemental methods section. ^{1, 14}. Arterial applanation tonometry was performed with a Millar pentype tonometer (SPT 301; Millar Instruments, Houston, Texas, USA) and a dedicated acquisition platform.^{1, 14} Arterial tonometry was first performed at the level of the left brachial artery, and the tonometric recording was calibrated with brachial systolic and diastolic blood pressure. Mean brachial arterial pressure was then computed by numerical integration of the brachial pressure wave form. Subsequently, carotid artery waveforms and left ventricular outflow tract pulsed wave Doppler flow velocities were simultaneously acquired. Carotid pressure wave forms were calibrated according to brachial mean and diastolic pressure. ^{1, 2}

Assessment of arterial load and ventricular-vascular coupling

Instantaneous flow velocities were multiplied by LV outflow tract cross-sectional area to obtain volumetric flow. After appropriate time-alignment of pressure and flow wave forms, characteristic impedance (Zc) of the proximal aorta was calculated in the time domain as the ratio of early systolic pulsatile pressure/flow as previously described ^{1, 15}. Reflection magnitude was computed using wave separation analysis.^{1, 2} Augmentation index was calculated as the amplitude of the second systolic peak divided by the amplitude of the first systolic peak (P2/P1) multiplied by 100. We chose this method as opposed to more widely used method proposed by Murgo because the latter frequently results in negative values of augmentation index, which are incompatible with the general allometric equation.

Total arterial compliance was calculated with the pulse-pressure method.^{1, 3} Total arterial elastance (Ea) was calculated as the ratio of central end-systolic pressure to stroke volume. Ea is an integrated index of arterial load that is sensitive to resistive load, pulsatile load and heart rate.¹⁶ The modified single-beat method was used to estimate end-systolic left ventricular elastance (Ees) as previously described and validated.^{6, 17, 18} The ratio of Ea/Ees ratio was computed as an index of ventricular-arterial coupling.^{8, 19, 20} Finally, because in many epidemiologic studies the ratio of pulse pressure to stroke volume is used as a crude estimate of total arterial compliance, we include data regarding this ratio as well.

Statistical Analyses

To test for allometric relations between hemodynamic indices and body size in the reference sample, the following general allometric equation was used: y = ax^b+ ε, where x is a measure of body size, a and b are parameters and ε is a random additive error term. Tested measures of body size in our study included height in meters, weight in kilograms and body surface area (BSA) estimated with the Gehan method.²¹ We first used least squares estimation after logarithmic transformation to a linear model, in order to test interactions between gender and measures of body size and establish the presence of a common exponent applicable to both genders.²² Given our large sample size, even weak relationships can prove to be statistically significant, although not important for clinical and epidemiologic purposes. Therefore, we further analyzed the metrics of only those relationships associated with an unadjusted R value of at least 0.25. Definitive estimation of allometric powers was performed using non-linear regression as detailed in the online supplemental methods section. All non-linear models also included a gender term to satisfy the group difference principle.²²

After determining the allometric powers for appropriate indexing of hemodynamic variables, comparisons of indexed variables between subjects in pre-specified body mass index (BMI) categories (<25, 25–29.9 and ≥30 kg/m²) were done with analysis of covariance, adjusting for age and gender, with post-hoc pair-wise comparisons with Bonferroni correction only when the overall test demonstrated significant differences between the groups. Similar comparisons were made between subjects with and without abdominal obesity, defined as a waist circumference >102 cm in men and >88 cm in women.²³ Statistical significance was defined as 2-tailed P<0.05. Statistical analyses were performed using SPSS for Windows v17 (SPSS Inc., Chicago, IL).

Results

Table 1 shows important demographic and clinical characteristics of subjects included in the reference population and of subjects not included in the reference population.

Table 1.

Demographic, clinical and hemodynamic characteristics of study subjects in the reference sample and those not in the reference sample (total n=2368)

Variable	In Reference Sample (n=612)	Not in Reference Sample (n=1755)
Age, Years *	44 (39–48)	46 (42–51)
Male Gender *	198 (32.4)	947 (54)
Body height, cm §	168±9	169±9
Body weight, kg †	63 (58–69)	77 (67–86)
Body Mass Index, kg/m2†	22.6 (21.1–23.7)	26.4 (24.2–28.8)
Body Surface Area, m2†	1.74±0.15	1.92±0.21
Waist Circumference, cm †	75.5 (71–81)	90 (81.5–98)
Total Cholesterol, mg/dL †	203±28	221±38
LDL–Cholesterol, mg/dL †	116 (99–131)	134 (111–160)
HDL–Cholesterol, mg/dL †	72 (62–84)	58 (49–71)
Triglycerides, mg/dL †	67 (52–88)	102 (74–147)
Diabetes Mellitus †	0 (0)	37 (2.1)
Current Smoking †	0 (0)	492 (28)
Hypertension †	0 (0)	672 (38.3)
Brachial SBP, mmHg †	125 (116–133)	134 (124–144)
Brachial DBP, mmHg †	72±9	79±11
Mean arterial pressure, mmHg †	94 (88–101)	102 (94–111)
Central SBP, mmHg †	122 (114–133)	132 (122–143)
Central PP, mmHg †	50 (44–58)	53 (46–60)
Stroke Volume, mL *	65 (57–75)	72 (61–83)
Cardiac Output, mL/min *	4190 (3625–4747)	4657 (4039–5413)
Heart Rate, bpm *	63 (57–71)	65 (59–72)
SVR, dyn·s/cm5*	1797 (1573–2088)	1727 (1487–2063)
Total Arterial Compliance, mmHg/mL §	0.95 (0.77–1.15)	0.99 (0.8–1.21)
Reflection Magnitude *	0.48 (0.42–0.53)	0.47 (0.42–0.53)
Aortic Zc, mmHg·ms/mL *	125 (105–150)	116 (96–141)
Time to Inflection Point, ms *	152 (136–176)	146 (128–171)
Time to Reflections, ms *	66±19	62±20
Central Augmentation Index, % ‡	119 (108–133)	121 (108–137)
Ea, mmHg/mL ‡	1.43 (1.24–1.65)	1.42 (1.19–1.68)
Ees, mmHg/mL ‡	1.73 (1.46–2.09)	1.73 (1.44–2.12)
Ea/Ees (coupling ratio) ‡	0.82 (0.73–0.92)	0.82 (0.72–0.92)
Left ventricular ejection fraction	60±8	60±9

Numbers represent mean ± standard deviation, median (inter-quartile range) or count (percentage).

^*P<0.01

^†Different by Design

^‡P=NS (>0.05)

^§P<0.05.

Physiologic relation of Hemodynamic Indices to Body Height

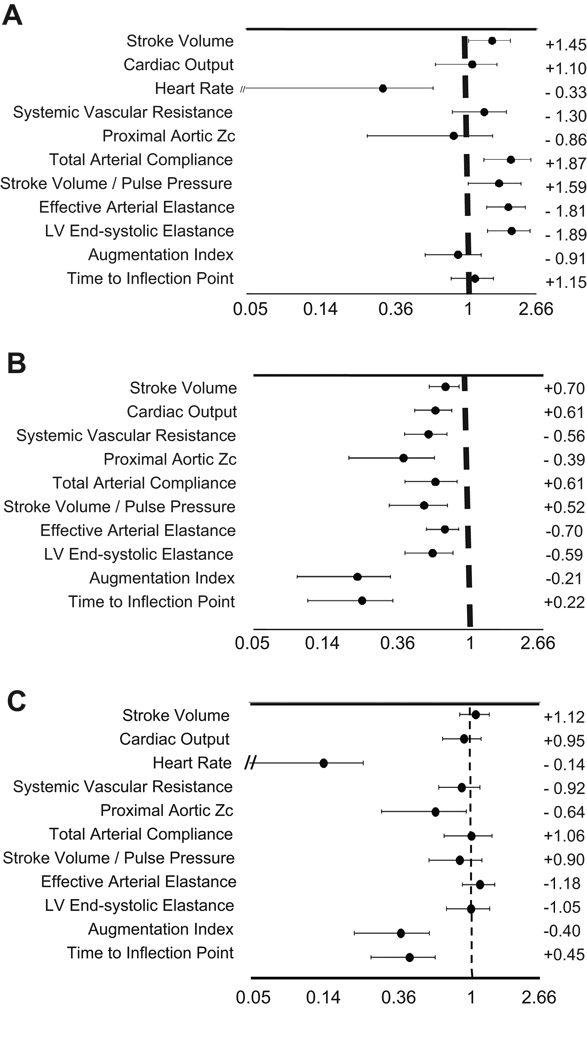
Table 2 shows relations of hemodynamic indices to body height in the reference sample. Point estimates and 95% confidence intervals of the allometric powers describing the relationships between body height and hemodynamic parameters (derived from non-linear regression) are shown in Figure 1A. If these CIs do not cross the unity, a linear relationship is rejected and an allometric relationship is demonstrated. Stroke volume and heart rate demonstrated allometric (rather than linear) relationships with body height (powers=1.45 and −0.33, respectively). Total arterial compliance, Ea and Ees demonstrated important allometric relationships with body height, with powers of +1.87, −1.81 and −1.89, respectively. The Ea/Ees coupling ratio did not demonstrate an important relationship with body height (R²<0.02). Other parameters, including cardiac output, systemic vascular resistance (SVR), proximal aortic Zc, augmentation index and time to the inflection point demonstrated important relationships with body height which were approximately linear.

Table 2.

Relations of Hemodynamic Indices to Body Height in the reference sample before and after allometric indexation and ratiometric indexation.

Hemodynamic Index	Association, Non- indexed Parameters		P value for Height*Gender	Residual Association, Allometric Indices *		Residual Association, Ratiometric Indices *
	R	P value	Interaction †	R	P value	R	P value
Stroke Volume, mL	0.51	<0.0001	0.65	−0.005	0.90	0.08	0.03
Cardiac Output, mL/min	0.32	<0.0001	0.45	−0.003	0.94	0.02	0.71
Heart Rate, bpm	0.27	<0.0001	0.66	0.002	0.96	0.17	<0.0001
SVR, dyn·s/cm5	0.34	<0.0001	0.77	−0.001	0.96	−0.05	0.18
Aortic Zc, mmHg·s/mL	0.28	<0.0001	0.48	<0.001	0.99	0.02	0.64
Total Arterial Compliance, mmHg/mL	0.49	<0.0001	0.54	0.003	0.94	0.12	0.003
Stroke Volume /Pulse Pressure, mmHg/mL	0.43	<0.0001	0.58	0.001	0.99	0.08	0.03
Ea, mmHg/mL	0.48	<0.0001	0.66	0.002	0.96	0.14	0.001
Ees, mmHg/mL	0.53	<0.0001	0.21	−0.02	0.68	0.15	<0.0001
Central Augmentation Index, %	0.43	<0.0001	0.46	−0.005	0.90	0.02	0.70
Time to Inflection Point, sec	0.55	<0.0001	0.22	−0.003	0.92	0.03	0.43

^*Gender-independent linear correlation between body height-normalized variables and body height

^†From log-log models

Figure 1. A–C. Point estimates and 95%Confidence Intervals for the allometric powers describing the relationship between various hemodynamic indices and body height (1A), body weight (1B) or body surface area (1C).

Powers are graphed in a natural logarithmic scale and the dashed line indicates the first power (1). If 95%CIs do not cross the unity, an allometric relationship (rather than a linear one) is present. Allometric powers are indicated on the left of the graph.

Residual relationships between indexed hemodynamic variables and body height are shown in Table 2. These represent the gender-independent linear correlation between body height-normalized variables (by either ratiometric or allometric indexation) and body height. Normalization of hemodynamic variables for body height to the appropriate powers essentially eliminated the gender-independent relationships of the indexed hemodynamic variables to the first-power measure of height (all R<0.01, P=NS). However, ratiometric indexation failed to eliminate this relationship for total arterial compliance, Ea, Ees and heart rate (Table 2).

Physiologic relation of Hemodynamic Indices to Body Weight

Table 3 shows relations of hemodynamic indices to body weight in the reference sample. Point estimates and 95% confidence intervals of allometric powers describing the relationships between body weight and hemodynamic parameters are shown in figure 1B. For all hemodynamic variables in which significant relationships between body weight and hemodynamic indices were found, these were allometric, rather than linear, as demonstrated by the point estimates and 95% confidence intervals shown in figure 1B. In particular, the relationships between body weight and proximal aortic Zc, augmentation index or time to inflection point were markedly non-linear (allometric powers=−0.39, −021 and +0.22, respectively).

Table 3.

Relations of Hemodynamic Indices to Body Weight in the reference sample before and after allometric indexation and ratiometric indexation.

Hemodynamic Index	Association, Non- indexed Parameters		P value for Weight*Gender	Residual Association, Allometric Indices *		Residual Association, Ratiometric Indices *
	R	P value	Interaction †	R	P value	R	P value
Stroke Volume, mL	0.57	<0.0001	0.96	0.003	0.91	0.16	<0.0001
Cardiac Output, mL/min	0.41	<0.0001	0.40	0.003	0.93	−0.19	<0.0001
SVR, dyn·s/cm5	0.36	<0.0001	0.73	0.01	0.71	0.23	<0.0001
Aortic Zc, mmHg·s/mL	0.29	<0.0001	0.32	0.005	0.86	0.23	<0.0001
Total Arterial Compliance, mmHg/mL	0.46	<0.0001	0.33	<0.0001	0.99	−0.15	<0.0001
Stroke Volume /Pulse Pressure, mmHg/mL	0.41	<0.0001	0.26	0.002	0.97	−0.19	<0.0001
Ea, mmHg/mL	0.49	<0.0001	0.78	0.007	0.85	0.15	<0.0001
Ees, mmHg/mL	0.48	<0.0001	0.88	−0.002	0.96	0.16	<0.0001
Central Augmentation Index. %	0.36	<0.0001	0.23	−0.006	0.86	0.45	<0.0001
Time to Inflection Point, sec	0.45	<0.0001	0.13	<0.001	0.98	0.47	<0.0001

^*Gender-independent linear correlation between body weight-normalized variables and body weight

^†From log-log models

Aortic characteristic impedance, SVR, Ea and Ees demonstrated inverse allometric relationships with body weight. The Ea/Ees ratio did not demonstrate a relationship with body weight (R²<0.001). Stroke volume, cardiac output, total arterial compliance and the time to the inflection point were positively (and non-linearly) related to body weight. In contrast, reflection magnitude did not demonstrate an important relationship with body weight (R²=0.02).

Table 3 shows residual linear correlations between normalized variables and body weight. These represent the gender-independent linear correlation between body weight-normalized variables (by either ratiometric or allometric indexation) and body weight. Normalization of hemodynamic variables for body weight to the appropriate allometric powers eliminated the gender-independent relations of the indexed hemodynamic variables to the first-power measure of weight (all R<0.01, P=NS). In contrast, ratiometric indexation consistently failed to eliminate these relationships (Table 3).

Physiologic relation of Hemodynamic Indices to BSA

Table 4 shows relations of hemodynamic indices to BSA in the reference sample. Point estimates and 95% confidence intervals of allometric powers describing the relationships between BSA and hemodynamic parameters are shown in figure 1C. Cardiac output, SVR, total arterial compliance, Ea and Ees demonstrated important, approximately linear relationships with BSA. The Ea/Ees ratio or reflection magnitude did not demonstrate important relationships to BSA (R²<0.02 for both). In contrast, augmentation index and the time to inflection point demonstrated highly allometric relationships with BSA (powers=−0.40 and +0.45, respectively).

Table 4.

Relations of Hemodynamic Indices to Body Surface Area in the reference sample before and after allometric indexation and ratiometric indexation.

Hemodynamic Index	Association, Non- indexed Parameters		P value for BSA*Gender	Residual Association, Allometric Indices *		Residual Association, Ratiometric Indices *
	R	P value	Interaction †	R	P value	R	P value
Stroke Volume, mL	0.57	<0.0001	0.89	0.007	0.86	0.05	0.23
Cardiac Output, mL/min	0.40	<0.0001	0.51	0.006	0.89	−0.009	0.82
Heart Rate, bpm	0.26	<0.0001	0.48	−0.002	0.94	−0.35	<0.0001
SVR, dyn·s/cm5	0.37	<0.0001	0.50	0.01	0.69	0.04	0.32
Aortic Zc, mmHg·s/mL	0.30	<0.0001	0.29	0.005	0.85	0.09	0.02
Total Arterial Compliance, mmHg/mL	0.48	<0.0001	0.28	0.002	0.95	0.02	0.70
Stroke Volume /Pulse Pressure, mmHg/mL	0.43	<0.0001	0.23	0.004	0.92	−0.02	0.61
Ea, mmHg/mL	0.51	<0.0001	0.89	0.012	0.76	−0.04	0.28
Ees, mmHg/mL	0.51	<0.0001	0.80	−0.002	0.96	−0.02	0.72
Central Augmentation Index. %	0.39	<0.0001	0.95	−0.007	0.86	0.23	<0.0001
Time to Inflection Point, sec	0.49	<0.0001	0.16	−0.005	0.89	0.24	<0.0001

^*Gender-independent linear correlation between body surface area-normalized variables and body surface area

^†From log-log models

As shown in table 4, normalization of hemodynamic variables for BSA using appropriate allometric powers eliminated the gender-independent relations of the indexed hemodynamic variables to the first-power measure of BSA (all R<.01, P=NS). Given the approximately linear relationships between BSA and SVR, cardiac output, Ea, Ees, total arterial compliance or aortic Zc, simple ratiometric indexation for BSA also eliminated these relationships. However, ratiometric indexation failed to eliminate the relationship between BSA and augmentation index, time to the inflection point or heart rate.

Sex Differences in Allometric Relations of Hemodynamic Indices to Measures of Body Size

For none of the hemodynamic indices that demonstrated important relationships with body size were there significant interactions between gender and the (logarithmically transformed) measure of body size, as predictors of the (logarithmically transformed) hemodynamic index. This indicated that the slope (which in these log models represents the allometric power) was not significantly different between men and women in any of these models (i.e., the common exponent principle was satisfied).²²

Effect of Obesity on Arterial Hemodynamics

Comparisons in hemodynamic indices between subjects with normal body weight, overweight and obesity in the entire study sample are shown in Table 5. Similar comparisons between subjects with and without abdominal obesity are shown in Table 6. Hemodynamic indices were normalized for BSA raised to the appropriate allometric powers, to account for the normal expected relationship between body size and these parameters. BSA (rather than body weight) was chosen for normalization because there were small but significant differences in body height between the groups (in addition to the expected differences in body weight). Means were age and gender-adjusted to account for differences in these variables between the groups. From normal weight to obesity, there was a progressive increase in indexed SVR, Ea and Ees and a progressive decrease in indexed total arterial compliance. Finally, there was a progressive decrease in the time of the inflection point, indicating an earlier arrival in the reflected wave with increasing degrees of overweight/obesity. Table 5 and Table 6 also show comparisons of non-indexed hemodynamic variables between the groups and comparisons of hemodynamic variables indexed for BSA with the ratiometric method. As can be seen, the adverse effects of obesity on arterial load cannot be demonstrated without appropriate normalization for body size. Indeed, although significant differences were found in non-indexed hemodynamic variables between the groups, these differences occurred in opposite directions, compared to results obtained when values are normalized for body size. In addition, it can be seen that in those cases in which allometric powers relating hemodynamic variables BSA are close to (and not significantly different from) the unity, ratiometric indexation provided similar results. Notable cases in which these allometric powers are different from the unity include aortic Zc, augmentation index and time to the inflection point. Aortic Zc was not significantly different between the groups with allometric normalization but appeared to increase with obesity when ratiometric indexation was used. Augmentation index increased and time to the inflection point decreased with obesity, regardless of whether ratiometric or allometric indexation was used. It should be noted, however, that even though differences were demonstrated in the same direction using allometric and ratiometric indexation, it cannot be assumed that the quantification of the differences is equally accurate. A clear example is provided by the comparison of augmentation index between subjects with and without abdominal obesity (Table 6) in which appropriate allometric normalization demonstrates a very small difference between obese and non-obese individuals, whereas ratiometric indexation demonstrates a large difference.

Table 5.

Comparison of key demographic, anthropometric variables and hemodynamic parameters indexed for body size (BSA) and non-indexed for body size between lean (BMI<25), overweight (BMI 25–29.9) and obese (BMI>30 kg/m²) subjects.

Variables	Lean (n=1151)	Overweight (n=901)	Obese (n=316)	P Value *
General Characteristics
Age	44.9 (44.5 to 45.2)	46.8 (46.5 to 47.2)	46.9 (46.3 to 47.6)	<0.0001 †‡
Male Gender	415 (36.0)	560 (62.2)	170 (53.8)	<0.0001 †‡₤
Body Height, m	168 (168 to 169)	170 (170 to 171)	169 (168 to 170)	<0.0001 ‡₤
Body Weight, Kg	63.7 (63.2 to 64.2)	78.9 (78.3 to 79.5)	95.2 (94 to 96.5)	---
Body Surface Area	1.76 (1.75 to 1.77)	1.92 (1.91 to 1.93)	2.12 (2.11 to 2.14)	---
Indexed Variables, allometric powers
SVR, dyn·s·cm−5m1.8 (b=−0.92)	3143 (3101 to 3185)	3255 (3207 to 3302)	3340 (3261 to 3418)	<0.0001 †‡
Aortic Zc, mmHg·ms·L−1m1.3 (b=−0.64)	183 (180 to 186)	183 (179 to 186)	186 (181 to 192)	0.56
Total Arterial Compliance, mmHg·L·m−2.1 (b=+1.06)	536 (527 to 544)	518 (509 to 528)	485 (470 to 501)	<0.0001 †‡₤
Ea, mmHg·mL−1·m2.4 (b=−1.18)	2.89 (2.85 to 2.93)	3.1 (3.06 to 3.15)	3.47 (3.4 to 3.55)	<0.0001 †‡₤
Ees, mmHg·mL−1·m2.1 (b=−1.05)	3.28 (3.22 to 3.33)	3.55 (3.49 to 3.61)	3.89 (3.79 to 3.99)	<0.0001 †‡₤
Central Augmentation Index, m0.8 (b=−0.4)	154 (153 to 155)	158 (157 to 160)	162 (159 to 165)	<0.0001 †‡
Time to Inflection Point, msec·m−0.9 (b=+0.45)	121 (119 to 122)	113 (112 to 114)	106 (104 to 108)	<0.0001 †‡₤
Indexed Variables, ratiometric method
SVR, dyn·s·cm−5m2	3280 (3236–3324)	3419 (3370–3469)	3535 (3453–3617)	<0.0001 †‡
Aortic Zc, mmHg·ms·L−1m2	224 (220–228)	230 (226–234)	243 (236–250)	<0.0001 ‡₤
Total Arterial Compliance, mmHg·L·m−2	553 (544–561)	537 (528–547)	506 (490–522)	<0.0001 ‡₤
Ea, mmHg·mL−1·m2	2.61 (2.57–2.65)	2.76 (2.71–2.8)	3.03 (2.96–3.1)	<0.0001 †‡₤
Ees, mmHg·mL−1·m2	3.19 (3.14–3.24)	3.44 (3.38–3.5)	3.76 (3.66–3.85)	<0.0001 †‡₤
Central Augmentation Index, m2	215 (213–217)	234 (231–236)	254 (250–258)	<0.0001 †‡₤
Time to Inflection Point, msec·m−2	89 (88–89)	79 (78–80)	70 (69–72)	<0.0001 †‡₤
Non-Indexed Variables
SVR, dyn·s/cm5	1880 (1855 to 1905)	1793 (1765 to 1821)	1678 (1632 to 1725)	<0.0001 †‡
Aortic Zc, mmHg·s/L	128 (126 to 130)	121 (118 to 123)	115 (111 to 119)	<0.0001 †‡
Total Arterial Compliance, mmHg/L	979 (962 to 996)	1038 (1018 to 1057)	1076 (1044 to 1108)	0.001 †‡
Ea, mmHg/mL	1.50 (1.48 to 1.52)	1.45 (1.42 to 1.47)	1.44 (1.4 to 1.48)	0.001 †‡
Ees, mmHg/mL	1.84 (1.81 to 1.87)	1.81 (1.78 to 1.84)	1.79 (1.73 to 1.84)	0.20
Central Augmentation Index	123 (122 to 124)	122 (121 to 124)	120 (118 to 122)	0.04 ‡
Time to Inflection Point, msec	156 (154 to 157)	152 (150 to 154)	149 (146 to 151)	<0.0001 †‡
Reflection Magnitude	0.48 (0.48 to 0.49)	0.47 (0.47 to 0.48)	0.47 (0.46 to 0.48)	<0.0001 †‡

Numbers represent mean (95%CI) or count (percentage). Comparisons in hemodynamic indices are adjusted for age and gender.

^*P value for overall between-groups comparison (body weight and BSA were not compared as they were different by design).

^†Significant difference between lean and overweight (post-hoc comparison with Bonferroni correction)

^‡Significant difference between lean and obese (post-hoc comparison with Bonferroni correction)

^₤Significant difference between overweight and obese (post-hoc comparison with Bonferroni correction).

Table 6.

Comparison of key demographic, anthropometric variables and hemodynamic parameters indexed for body size (BSA) and non-indexed for body size between subjects with and without abdominal obesity. Comparisons are adjusted for age and gender.

Variables	No abdominal obesity (n=1927)	Abdominal Obesity (n=438)	P Value
General Characteristics
Age	45.5 (45.2–45.8)	47.4 (46.9–48)	<0.0001
Male Gender	941 (48.8)	201 (45.9)	0.27
Body Height, m	169 (169–170)	169 (168–170)	0.95
Body Weight, Kg	69.8 (69.3–70.4)	90.6 (89.5–91.7)	<0.0001
Body Surface Area	1.82 (1.81–1.83)	2.08 (2.07–2.1)	<0.0001
Indexed Variables, allometric powers
SVR, dyn·s·cm−5m1.8 (b=−0.92)	3188 (3156–3220)	3312 (3245–3379)	0.001
Aortic Zc, mmHg·ms·L−1m1.3 (b=−0.64)	183 (181–185)	186 (181–191)	0.32
Total Arterial Compliance, mmHg·L·m−2.1 (b=+1.06)	529 (523–535)	493 (479–506)	<0.0001
Ea, mmHg·mL−1·m2.4 (b=−1.18)	2.97 (2.94–3)	3.39 (3.32–3.46)	<0.0001
Ees, mmHg·mL−1·m2.1 (b=−1.05)	3.39 (3.35–3.43)	3.79 (3.7–3.87)	<0.0001
Central Augmentation Index, m0.8 (b=−0.4)	156 (155–157)	159 (157–161)	0.03
Time to Inflection Point, msec·m−0.9 (b=+0.45)	117 (116–118)	108 (106–110)	<0.0001
Indexed Variables, ratiometric method
SVR, dyn·s·cm−5m2	3336 (3302–3369)	3502 (3432–3573)	<0.0001
Aortic Zc, mmHg·ms·L−1m2	226 (223–229)	241 (235–247)	<0.0001
Total Arterial Compliance, mmHg·L·m−2	547 (540–553)	513 (499–527)	<0.0001
Ea, mmHg·mL−1·m2	2.67 (2.64–2.7)	2.96 (2.9–3.02)	<0.0001
Ees, mmHg·mL−1·m2	3.29 (3.26–3.33)	3.66 (3.57–3.74)	<0.0001
Central Augmentation Index, m2	223 (221–225)	247 (244–251)	<0.0001
Time to Inflection Point, msec·m−2	282 (279–285)	318 (313–0.324)	<0.0001
Non-Indexed Variables
SVR, dyn·s/cm5	1851 (1832–1869)	1686 (1646–1726)	<0.0001
Aortic Zc, mmHg·s/L	125 (124–127)	116 (113–119)	<0.0001
Total Arterial Compliance, mmHg/L	1000 (987–1013)	1076 (1048–1103)	<0.0001
Ea, mmHg/mL	1.48 (1.47–1.5)	1.43 (1.39–1.46)	0.002
Ees, mmHg/mL	1.84 (1.81–1.86)	1.76 (1.72–1.81)	0.006
Central Augmentation Index	123 (123–124)	119 (117–120)	<0.0001
Time to Inflection Point, msec	154 (153–155)	151 (149–154)	0.07
Reflection Magnitude	0.48 (0.48–0.49)	0.46 (0.45–0.47)	<0.0001

Numbers represent mean (95%CI) or count (percentage). Comparisons in hemodynamic indices are adjusted for age and gender.

Discussion

In this paper, we report on the metrics of physiological relations of indices of arterial load to measures of body size in a population-based sample of middle-aged adults. We found that various measures of arterial load are physiologically related to body size and that these relationships are often markedly allometric (as opposed to linear). To our knowledge, this is the first empirical evidence for scaling of parameters of pulsatile load in humans. We also demonstrate that weight gain above the normal range exerts a deleterious effect on left ventricular afterload and end-systolic ventricular stiffening, which could be clearly demonstrated only when physiologic allometric relationships with body size were accounted for.

Various physiologic principles strongly suggest that indices of hemodynamic load should bear a non-linear relationship with body size, including: (1) The relationship between body size and arterial size; (2) The known relationship between arterial size and functional measures of wall stiffness, in particular, characteristic impedance; (3) The known relationship between body height and aortic path length, which affects the timing of wave reflections for any given pulse wave velocity; (4) The relationship between stroke volume and body size,² suggesting that a relationship between volumetric flow and body size is to be expected. Accordingly, we empirically found that in normal middle-aged adults, body size relates non-linearly to various components of arterial load and to ventricular end-systolic stiffness. In contrast, the dimensionless ventricular-arterial coupling ratio did not demonstrate relationships with body size, indicating that ventricular-arterial coupling was preserved across large variations in absolute arterial load.

Scaling approaches that use ratiometric indexation (that is, the cardiovascular parameter is simply divided or multiplied by some measure of body size) assume a linear relationship between body size and arterial function. The same can be said about methods that simply incorporate a measure of body size (such as body height) as a covariate in linear regression models. This has been common practice, given to the lack of data to guide more appropriate scaling of arterial hemodynamic indices. Our study provides such data from a large sample in which selection bias was minimized due to the population-based sampling strategy of the study and in which strict criteria were applied to select a healthy reference subsample to assess normal (physiologic) metric relationships between body size and various indices of arterial load. Appropriately accounting for the relationships between body size and arterial functional variables minimizes the confounding effects of body size. Appropriate empirical allometric corrections should eliminate the effects of body size on indices of arterial load.^{7, 10} We demonstrate that indexing hemodynamic parameters to the appropriate allometric powers indeed eliminates the relationships between body size and arterial load, making this simple indexation feasible in a variety of settings to produce body size–independent scaled cardiovascular variables.⁷ In contrast, scaling by ratiometric methods results in significant residual correlations with body size. It can be predicted that in the presence of allometric relationships, ratiometric scaling of hemodynamic indices for body size will produce systematically biased indices among small subjects versus large subjects, the direction of the bias depending on the mathematical nature of the allometric relationship between body size and the hemodynamic index.

The approach taken in this study allowed us to clearly demonstrate abnormalities in arterial load associated with obesity, beyond the expected relationship with body size, which could not be elucidated with non-indexed variables (Table 5). These abnormalities include an increase in SVR, Ea, Ees and a decrease in total arterial compliance and may play an important role in the well-known independent association between obesity and heart failure.²⁴ Interestingly, aortic Zc did not increase with increasing BMI, which may be explained by the high sensitivity of aortic Zc to aortic size, which is known to increase with body size. Increasing BMI was also associated with a higher augmentation index, which was apparent only after appropriate allometric indexation. The increased (allometrically scaled) augmentation index observed in obese individuals appears to result from an earlier arrival of the reflected wave (as indicated by a shorter time to the inflection point), since reflection magnitude did not increase with increasing BMI.

Although previous studies have addressed inter-species relationships between arterial function and body size, our study is the first to provide such data from a population-based sample of human adults. Importantly, it cannot be assumed that inter-species relationships, in which ranges of body size encompassing several orders of magnitude were examined, apply to human adults in whom the variations in body size occur over much narrower ranges. Indeed, allometric relationships found in our study differ from those seen in inter-species studies, in which allometric relationships tend to conform to quarter-power scaling.²⁵ Quarter-power scaling has been explained on the basis of theoretical models based on circulatory dynamics in fractal-like networks.²⁵ In contrast to theoretical relationships, our empirical observations do not make any assumptions about the variance and correlation between anthropomorphic parameters and arterial load and the allometric powers derived from these analyses were clearly effective to fully account for the normal relationship between body size and arterial load in our study population. There may be various reasons why these allometric relationships would differ from theoretical predictions derived from fractal models, including deviations from model theoretical assumptions, differences in the metabolic rates of different tissues (which may vary systematically with body size even within normal ranges of body weight) and the effects of various neurohormonal pathways that may exert direct distant effects on the heart and vasculature independently of local flow phenomena. For example, leptin secreted by adipocytes bears a strong relationship with body weight and is known to affect heart rate both through direct effects on the heart²⁶ and through autonomic regulation. This heart-rate increasing effect would be expected to counterbalance the strong and highly non-linear negative relationship between body mass and heart rate that would be predicted purely on the basis of from fractal-network theory.^{25, 26}

It is important to note that indexing for body size should be tailored to the research or clinical objective. Indexing that accounts for normal relationships with body size is useful to interpret changes associated with overweight or obesity, being advantageous to separate expected allometric relationships from pathologic phenomena related to the obese state. We believe that studies assessing between-subject differences should report both non-normalized and normalized values, which provide complementary information. When there is significant between-subject variability in body height and body weight (as is usual), normalization for BSA seems appropriate. When there is very little variability in body height in a specific study population, normalization for body weight could be sufficient. Normalization may or may not be needed for longitudinal studies that assess within-subject changes. In studies that examine within-subject effects of an intervention that does not change body size, unadjusted indices may be fully informative, whereas in studies that assess within-subject changes in arterial hemodynamics in response to an intervention that changes body size (such as weight loss), changes in non-normalized and normalized-values should be reported since they are likely to provide complementary information. Since such interventions in adult populations typically do not induce changes in body height, allometric indexation for body weight should be sufficient for such longitudinal studies. However, it is worth noting that the majority of allometric powers obtained with BSA were not significantly different from the unity. Therefore, BSA represents an attractive measure of body size that can be used in various situations for simple ratiometric indexation of most (but not all) hemodynamic indices presented in this study.

A relatively straightforward approach can be taken in studies in which one is not interested in the effects of obesity or the effects of body size on arterial load, but simply wants to adjust for these confounders. In order to assess whether observed relationships are independent of body size and independent of obesity, non-linear regression with adjustment for measures of body size should be adequate. This approach does not separate normal relationships with body size from pathologic effects of obesity, but does adjust for both, as long as appropriate non-linear models are used. In addition, this approach can only be applied during statistical analyses using data from groups of individuals in research studies. Allometric normalization is advantageous because not only does it allow for the comparison of groups of subjects in research studies but will also allow for: (1) Body size-independent comparisons between 2 or more individuals; (2) Comparison of measurements from individual subjects against expected ranges of values, whether these are normative values or values derived from well characterized clinical populations.

Our study has limitations. Our paper provides allometric powers derived from a large sample of Caucasian middle-aged adults. Future studies should address the validity of these allometric powers in other populations, in particular among subjects from different ethnic groups. In addition, because the cardiovascular system has evolved for efficient distribution of metabolic substrates, more appropriate scaling might be found in normalizing the circulatory supply (cardiovascular system) to the mass of metabolically active tissue (for instance, using lean body mass). Although future research should assess allometric relationships of these indices with lean body mass (versus fat mass), we provide information for appropriate indexation to the most commonly used body size indices both in clinical and epidemiologic settings.

Perspective

Assessment of arterial hemodynamics and ventricular-vascular coupling provides important physiologic information and is increasingly used in clinical and epidemiologic human research. The marked interindividual variation in body size and the marked normal (physiologic) relationships between of body size and arterial hemodynamics demonstrates the need for scaling of hemodynamic variables in simple yet mathematically accurate methods to produce size-independent parameters of arterial load and ventricular-vascular coupling. We believe that the ability to properly account for these relationships with allometric indexation is an important step forward in applying the study of arterial hemodynamics in clinical and epidemiologic settings and has important consequences for future research studies and eventually, for the clinical application of measurements of arterial load.