Avoiding Bias in Observational Studies

Abstract

Background

Many questions in human health research can only be answered with observational studies. In contrast to controlled experiments or well-planned, experimental randomized clinical trials, observational studies are subject to a number of potential problems that may bias their results.

Methods

Some of the more important problems affecting observational studies are described and illustrated by examples. Additional information is provided with reference to a selection of the literature.

Results

Factors that may bias the results of observational studies can be broadly categorized as: selection bias resulting from the way study subjects are recruited or from differing rates of study participation depending on the subjects’ cultural background, age, or socioeconomic status, information bias, measurement error, confounders, and further factors.

Conclusions

Observational studies make an important contribution to medical knowledge. The main methodological problems can be avoided by careful study planning. An understanding of the potential pitfalls is important in order to critically assess relevant publications.

The randomized clinical trial is a well established and frequently used study design and is generally accepted as the gold standard (1). Nevertheless, many questions can only be answered with epidemiological observational studies, such as the influence of cigarette consumption on the development of lung cancer (2), the effects of sport, nutrition and overweight on cardiovascular diseases (3), or the effects of UV exposure on skin diseases (4). Whereas in experimental, randomized clinical trials, randomization is intended to lead to a comparable distribution of both known and unknown factors in the two groups to be compared, this is rarely possible in observational studies (see part 3 of this series). This can lead to systematic bias and thus to erroneous results. This article will describe how possible sources of error linked to the study design can be recognized in studies in which randomization is not possible for fundamental ethical reasons and how this can be considered in the planning and evaluation.

The following sources of bias will be discussed:

• Selection mechanisms in recruitment of study participants (selection bias)

• Selective recall or inconsistent data collection (information bias), measurement errors

• Confounding, and

• Simpson’s paradox and other errors.

Once one is aware of the causes of biased results, these can either be excluded or reduced by intelligent study planning. In addition, these aspects must be properly considered during the analysis. Understanding these problems can help the critical reader to interpret study results. As this article is intended to give an introductory overview of this theme, results from a selective literature search will be presented.

Causes and effects of bias, possible countermeasures

Selection bias

Selection bias arises when the study population is not a random selection from the target population for which a statement is to be made. Individuals are then recruited in such a way that they are not representative of the target population. Even if the study is well planned, it may happen that not all selected persons take part in the study, because the voluntary character of the study must always be guaranteed.

In the following three examples, the selection of study participants evidently led to selection which can be avoided by better planning. Unfortunately, similar errors are repeatedly observed in publications.

• The health office of a large city wished to perform an empirical control of the vaccination coverage of preschool children. For this purpose, the vaccination passes of all children were to be inspected. In three kindergartens, the parents cooperated without exception, whereas the rates of participation were low in the other kindergartens. Is the result of this survey representative for all children? The answer is: probably not, as only children from specific kindergartens or neighborhoods were studied. Children from these neighborhoods may differ from children from other neighborhoods with respect to factors which influence the readiness of their families to have them vaccinated, such as social status. The population from which the study participants were recruited is probably not representative of the target population. It is known that vaccination coverage depends on social status (5).

• The US Office of Research Integrity carried out an anonymous survey of researchers, to establish what proportion of scientists whose projects were financially supported by public funds manipulated their results. The test persons were asked if they had observed lapses among their colleagues (6). As the test persons selected themselves by their participation, they are certainly not representative of the target population of all funded scientists.

• A senior physician wishes to learn more of the risk factors for a rare disease for which he is an expert. His patients travel large distances to be treated in his hospital. He gets a doctoral candidate to enquire about all patients in the last five years and takes controls (matched for age and gender) from the hospital. These controls are very probably not representative of the population from which his patients are recruited, as, in contrast to his patients, they come from the immediate vicinity of the hospital.

It is difficult to influence the participation rate of the study subjects. The aim must be a high participation rate, in order to achieve a representative cross-section of the population if possible. In any case, the publication must indicate the rate of non-participants. In most cases, a few facts are known about the non-participants, such as their age distribution. In many studies, it is at least attempted to obtain a little information from non-participants in the form of a postcard with a few questions. They are asked about their reasons for refusing to participate. These data must be considered when interpreting the results.

Self-selection of participants also takes place when linguistic or health barriers hinder participation. Cultural differences and social status can also influence readiness to participate, for example, in screening programmes. This all tends to reduce the possibility of generalizing the results.

Information bias

Information bias results from wrong or inexact recording of individual factors, either risk factors or the disease being studied. With continuous variables (such as blood pressure), this is referred to as measurement error; with categorical variables (such as tumor stage), this is known as misclassification. Measurement error or misclassification may result from lack of care by the investigator or from poor quality of measuring or survey instruments. However, they are more frequently caused by errors in the manner or time of classification. Here are some typical errors:

• Typical questions about events in the distant past: At what age did you suffer from chickenpox and measles? How much fruit did you eat last week? The answers to these questions will presumably be very imprecise.

• In a hospital, blood samples are taken in the morning from patients and in the afternoon from suitable controls. They are then analyzed at the same time by the same procedure. Unfortunately, the differences in the period of storage cause a systematic bias in the results.

• Mothers of children with congenital malformations have a better memory of potential risk factors during pregnancy than do other women (recall bias) (7).

• An interviewer treats patients during an interview with more sympathy than the controls, as their status rapidly becomes clear to him during the interview. As a result, he obtains more, and more detailed, information from the patients (interviewer bias).

These problems can partially be prevented by good planning, but cannot always be corrected by statistical evaluation. Interviewer bias can be avoided with standardized interviews; irrelevant questions can be more rapidly passed over in computer-supported interviews and inconsistent information can be recognized more quickly. Sensitive treatment of taboos or other cultural differences must be considered or possibly tested before the study.

Measurement errors

In addition, faulty or imprecise measurements can lead to problems. For example, systematic measurement errors can arise from wrongly calibrated instruments. Random, "classical" measurement errors arise from imprecision of the instrument, measurement procedure, or human investigator. Even subsequent categorization of an originally continuous variable cannot eliminate measurement errors and should be avoided (8).

If the size and direction of the measurement error are known, this can be considered in the evaluation (9). Additional and more precise measurements must be performed in a validation study in a small selection of study participants. For example, in nutritional studies, the less precise procedure—the food frequency questionnaire—is compared with a 24 hour record of consumption (9). The description of potential measurement errors is an indicator of a good quality publication.

For classical measurement errors, it is often stated that they bias the study results towards a null result. Theoretical consideration of the direction and size of the bias is only possible if major assumptions are made. However, these assumptions are often unrealistic.

Confounding

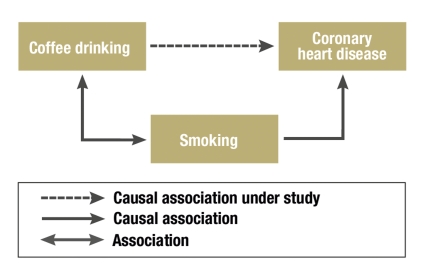
A confounder is a risk factor for the disease under study which is associated with the exposure of interest, but is not part of the causal pathway between exposure and the end point (figure). If this association is not considered in the study group during the evaluation—perhaps because the confounder was not recorded—, this leads to a biased estimate of the investigated risk factor. If the risk factor and the confounder are not associated, the effect of the risk factor will be correctly estimated.

Figure.

Confounding: Smoking is a known risk factor for coronary heart disease—the endpoint here. As smoking is also associated with coffee drinking, this gives the false impression that coffee drinking and coronary heart disease are associated (10).

Here is an example of confounding: Does drinking coffee lead to coronary heart disease? One might assume this, as a correlation has been observed (10). However, coffee drinkers are more often smokers than the average and, besides the correlation between drinking coffee and nicotine consumption, there is a strong causal correlation between smoking and the incidence of coronary heart disease. In this case, nicotine consumption is a confounder for the effect of coffee consumption on the development of heart disease.

Confounding should not be confused with interaction ("effect modification"). Two risk factors may act totally independently of each other, or the effect of one risk factor may depend on the presence of the other risk factor.

Here is an example of an interaction. It is known from studies that both smoking and alcohol consumption are risk factors for the development of carcinoma of the oral cavity. The increase in risk from alcohol consumption is greater for smokers than for non-smokers (table 1) (11).

Table 1. Example of interaction^*1.

		Smoking
		No	Yes
	No	1.00*2	1.53
Alcohol	Yes	1.23	5.71

^*1 Relative risk of alcohol consumption and smoking on the development of carcinoma of the oral cavity (taken from [11]). The effect of alcohol consumption is greater in smokers than in non-smokers.

^*2 The reference population is the group of individuals who neither smoke nor consume alcohol. Their relative risk is defined as 1.0.

Confounding can be reduced in various ways. In clinical studies, patients are randomly assigned to the treatment groups, on the assumption that all known factors (such as sex and age) and even unknown factors will have comparable frequencies in the treatment arms (see also part 2 of this series). The procedure must be different for purely observational studies.

One possibility of checking the effect of a confounder is to split the test group into subgroups (strata), defined by different levels of the confounder. In our example, the study participants could be stratified into non-smokers, individuals with moderate nicotine consumption, and heavy smokers. The analyses are first performed unstratified and then in the individual strata. The Mantel-Haenszel estimate (12, 13) is often used to combine the individual effect estimates from the stratified evaluation, correcting for the confounder. The smaller the differences between the stratified and unstratified data, the slighter is the effect of the confounder.

The attempt is often made in case control studies to achieve an equal group structure of patients and controls, so that one or several controls are selected for each patient, with the same sex, age, and known confounders as those of the reference case ("matching"). Schütz and colleagues studied risk factors for leukemia in children and assigned a child of the same sex and age from the same community to each case (14).

It is rarely possible to consider all potential confounders in matching. Observational studies are mostly evaluated with regression models. The potential confounders—aside from the risk factor under study—are incorporated in the regression model as explanatory risk factors. The effects of the individual factors are then calculated adjusted for the others. The effect of a potential confounder can be checked by comparing the results from two different models, calculated with and without the incorporation of the confounder. The adjusted and non-adjusted parameters are then published next to each other (15).

Other errors

In addition, other potential sources of error may arise: lead-time bias, ecological fallacy, and Simpson’s paradox.

After the introduction of screening programmes, the patients’ survival times are prolonged in most cases. However, this is not a proof of the success of screening programmes, as the patients are on average diagnosed earlier and live longer with their diagnosis. This phenomenon is known as lead-time bias. It can be (partially) corrected for by comparing similar regions with and without screening programmes and with stage-specific evaluation.

An apparent correlation may give the misleading impression that there is a causal relationship where none is present. One example is the association described by Höfer et al. between the increasing number of births outside hospitals and the parallel increase in the stork population (16). Errors of this sort may occur in ecological studies, which exclusively use data aggregated at the group level, for example, at the community or federal state level. However, the observed correlations do not necessarily apply to the individuals in the population considered. The plausibility of a causal relationship cannot be determined, as individual data are missing. The assumption that the observed associations can be transferred from the population to the individual level is known as ecological fallacy.

Further apparent correlations may arise when data are evaluated in groups, but there is uneven distribution of an important parameter within the groups (which does not have to be a confounder). The phenomenon is known as Simpson’s paradox. Examples are also found in medicine:

The data presented in Table 2 were observed in comparing two therapies of kidney stones (17). If the size of the kidney stones was not considered in the evaluation, therapy A appears to be less effective than therapy B (78% versus 83% success). Patients with large kidney stones have in fact a poorer prognosis. This is why treatment with therapy A seems to be poorer. The superiority of therapy A only becomes clear once the size of the kidney stones has been taken into account.

Table 2. Example of Simpson’s paradox (taken from [17]).

	Therapy A	Therapy B
	(Therapy successes/Patients)	(Therapy successes/Patients)
Small kidney stones Large kidney stones	93% (81/87) 73% (192/263)	87% (234/270) 69% (55/80)
Together	78% (273/350)	83% (289/350)

Conclusion

Observational studies make important contributions to the knowledge of the distribution and causes of diseases. We have mentioned some of the pitfalls which can lead to biased results. However, observational studies are often the best approach, particularly for long periods of observation, for rare effects, or when experimental studies would be unethical. The most important questions in the planning and evaluation of observational studies are summarized in the Box.

Box. Important questions when planning and evaluating observational studies.

• Are the study subjects representative for the target population?

• Are the subjects in the study arms comparable?

• Was the information collected in a comparable manner?

• Are potential measurement errors described?

• Does the study design allow for potential sources of error?

• How (good) is the quality of the collected data?

• Are correction procedures used?

Possible sources of error can often be recognized and corrected in good time if pilot studies or pretests are performed before the actual study, where a pilot study is a preliminary investigation used to field test the methods of the main study with a smaller test group. The performance of a pilot study can therefore be seen as a quality criterion for a study.

The amount of thought a scientist has invested in a study is apparent in how well the possible weaknesses are described, the methods to avoid or to correct predictable problems, and how unpredicted problems have been tackled.

For readers wishing more information, we recommend the German guidelines on Good Epidemiological Practice (18) (soon to be published in English) and the paperbacks of Crombie and Greenhalgh, extracts of which have been published in the British Medical Journal (19, 20). The German Radiation Protection Committee has written a short practical checklist on the evaluation of studies on the epidemiology of radiation. This has been published online (21).

Key Messages.

• Many research questions on human health can only be answered with observational studies. Like any type of study, these are prone to error.

• Many factors can lead to biased study results. These may be roughly classified as selection mechanisms, measurement errors, confounding factors, and methodical errors.

• Due to the design of observational studies (for example, the lack of randomization), specific types of bias are more common in observational studies. We present different types of interference and illustrate these with examples.

• If the investigator is aware of potential sources of bias, these can either be avoided or adequately considered by intelligent study planning.

• Understanding these problems is helpful to the critical reader to interpret study results.