Multiple-Echo Proton Spectroscopic Imaging Using Time Domain Parametric Spectral Analysis

Abstract

A multiple-echo MR spectroscopic imaging (MRSI) method is presented that enables improved metabolite imaging in the presence of local field inhomogeneities and measurement of transverse relaxation parameters. Short echo spacing is used to maximize signal energy from inhomogeneously line-broadened resonances, and time domain parametric spectral analysis of the entire echo train is used to obtain sufficient spectral resolution from the shortened sampling periods. Optimal sequence parameters for ¹H MRSI are determined by computer simulation, and performance is compared with conventional single-echo acquisition using phantom studies at a field strength of 4.7 T. A preliminary example for use at 1.5 T is also presented using phantom and human brain MRSI studies. This technique is shown to offer improved performance relative to single-echo MRSI for imaging of metabolites with shortened T₂^* values due to the presence of local field inhomogeneities. Additional advantages are the intrinsic measurement of metabolite T₂ values and determination of metabolite integrals without T₂ weighting, thereby facilitating quantitative metabolite imaging.

INTRODUCTION

A common concern for in vivo spectroscopic measurements is local magnetic-field inhomogeneity that results in shortened metabolite T₂^* values, lineshape distortions, and spectral overlap. Spatially localized field inhomogeneities may be particularly severe at regions of rapidly changing susceptibility, such as at the interfaces between air, tissue, and bone (1–4), that generally cannot be corrected using conventional shimming methods. Although it may be possible to perform localized MRS measurements in these regions by optimizing the B₀ field over a single small selected volume, this approach cannot be used for MR spectroscopic imaging (MRSI) studies where spectra are acquired over a wide field of view and a wide range of T₂^* values may be present over the imaged region.

Spectra obtained in the presence of field inhomogeneity have increased spectral overlap and decreased signal-to-noise ratio (SNR) in the frequency domain, also seen as a reduction in the total signal energy in the time domain. It is well known that when T₂^* ≪ T₂, the transverse magnetization may be repeatedly recalled with RF refocusing pulses (5, 6) and that SNR can be increased by signal averaging multiple spin-echo acquisitions. With this approach, the total acquired signal energy increases as TE is reduced (neglecting the effects of pulse imperfections and pulse length); however, the ability to analyze the resultant spectra becomes limited as each interecho sampling interval is shortened.

The limitations of Fourier analysis of truncated data sets are well known, and several alternative spectral analysis methods have been proposed to increase the effective spectral resolution (7). One such approach is to use parametric modeling, whereby a model of the signal function is optimally fit to the data. The ability to determine the best fit becomes a complex function of many variables, but in general, for a given sampling period as the signal energy increases, so does the ability to resolve closely separated frequencies. For analysis of MR spectra, additional benefit is gained from the application of prior knowledge of resonance positions (8, 9).

In this report, we describe the combination of time-domain parametric spectral analysis with a multiple-echo spectroscopic acquisition. It is shown that this provides increased sensitivity for measurement of tissue metabolites in vivo and provides a more robust measurement of metabolite distributions in regions subject to moderate B₀ field inhomogeneity. An additional advantage is the intrinsic measurement of T₂ values, leading to improved quantitation of metabolite measurements. In this initial report, this method is evaluated in three studies: first, a Monte Carlo computer simulation is used to determine the optimal acquisition parameters; second, the relative sensitivity in comparison with conventional single-echo methods is analyzed using phantom data acquired at 4.7 T; and finally, we present a preliminary demonstration of the multiecho ¹H MRSI method carried out at 1.5 T, using a phantom measurement and a study of human brain.

Multiple RF echo-acquisition methods have been used for MRI to obtain increased SNR, T₂ discrimination, or multiple k-space points for faster image acquisition (10, 11). For spectroscopic measurements, acquisition of multiple echoes has also been described for rapid water and lipid imaging (12), for metabolite T₂ measurement (13, 14), and for rapid MRSI measurement using different spatial encodings applied for each echo (15). In all cases, spectral reconstruction was obtained by Fourier transformation (FT) of each echo data set, with a corresponding reduction in spectral resolution compared with single-echo spectroscopic measurements. At higher field strengths, it has been demonstrated that because of the increased chemical shift dispersion, this loss of spectral resolution can be tolerated for in vivo ¹H MRSI, permitting a significant increase in signal or T₂ measurement to be obtained (14). In this report, we demonstrate that by using a time-domain spectral analysis, these advantages can be extended to lower field strengths.

THEORY

When T₂^* ≪ T₂, a multiple RF echo sequence enables transverse magnetization to be recalled multiple times, with each echo contributing to the total acquired signal energy. However, as the number of echoes is increased, the interecho sample period may become inadequate to resolve closely separated spectral components after FT. The increased signal energy implies that for a single resonance, or several well-separated resonances, an improvement in the performance of a spectral analysis method can be expected from the increased SNR; however, the ability to distinguish closely separated resonances is unclear.

In the following discussion, we consider two MRSI pulse sequences: a single spin-echo acquisition and a multiple spin-echo acquisition. Experimental parameters relevant for in vivo ¹H MRSI of longer T₂ metabolites at 1.5 T are used. For the single-echo acquisition, we assume that only the second half of the echo is sampled, as is commonly carried out for ¹H MRSI studies at shorter TEs. The data acquisition period is chosen to be sufficiently long to enable an accurate description of the narrowest resonance after FT. For the multiple-echo acquisition method, we assume a relatively short acquisition time per echo and that the acquisition period is now insufficient to clearly distinguish closely spaced spectral components by Fourier analysis; however, as shown below, analysis is possible using time-domain modeling procedures.

To demonstrate the reason for the improvement in performance expected with parametric-modeling spectral analysis of a multiple-echo acquisition, we examine a simple example for a parametric fit of a single resonance line. We calculate the value of the residual, χ², i.e., the sum of the squared difference between the “data” and the “model” function, a commonly used criteria that is minimized in the fit procedure. This is calculated as a function of the T₂/T₂^* ratio and frequency separation, Δf. Although the performance of a multiparametric fit will be subject to more variables than are considered in this example, the ability for the optimization algorithm to determine the necessary parameters can, nevertheless, be expected to improve given greater residual for a given difference between the model parameters and the data.

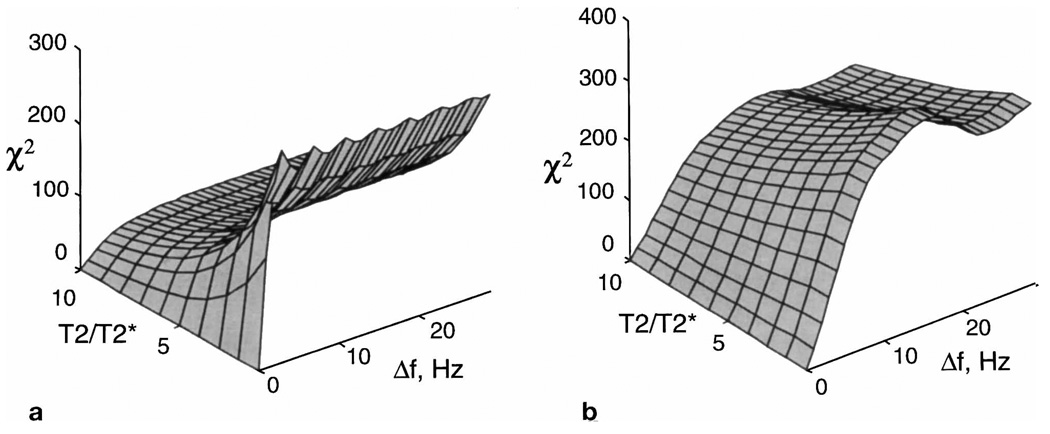
In Figs. 1a and 1b are shown the residuals for the single- and multiple-echo acquisitions, respectively. Parameters used in this simulation include the start of sampling for both cases at TE = 50 ms, a sweep width of 1000 Hz, and a transverse relaxation time, T₂, of 390 ms, which represents an average value for N-acetyl aspartate (NAA) from several studies (16). A narrowest linewidth of 4 Hz was assumed, sampled using 512 points. For the multiple-echo example, eight echoes were used with refocusing pulses of 10 ms and a total sequence length of 600 ms.

FIG. 1.

Examples of the residual, χ², for the parametric fit of a single resonance for a range of line broadening, T₂/T₂^*, plotted against the frequency difference between the model function and the data, Δf. Results are shown for (a) a single-echo acquisition and (b) a multiple-echo acquisition with eight echoes.

From Fig. 1 we note the following: i) For a single-echo acquisition, the ability of the parametric fit to resolve neighboring resonances can be expected to degrade with increasing T₂/T₂^*, whereas the multiple-echo acquisition maintains performance to a much greater degree. For a larger number of echoes, the slope of the residual remains flatter as a function of increasing T₂/T₂^* while also showing a shallower increase in value for increasing Δf, i.e., the ability to determine broad lines is increased at the expense of discrimination between closely separated resonances. ii) When T₂^* ≅ T₂, or Δf is small, the single-echo acquisition is better able to distinguish closely separated resonances. However, for in vivo studies at field strengths of 1.5 T or higher, these conditions do not apply. Even in regions of the best-achievable field homogeneity, the T₂/T₂^* ratio may be greater than 4 (corresponding to 3.3 Hz linewidth for NAA, assuming Lorentzian lineshape), and for measurement of the closely spaced resonances of creatine and choline, a spectral discrimination of only 12 Hz is required. iii) For multiple-echo acquisition in regions of good homogeneity, there is no loss of sensitivity relative to the single-echo case except in discrimination of very closely separated resonances (Δf < 4Hz).

The result of Fig. 1 applies to singlet resonances only. For closely spaced multiplet resonances, acquisitions with both single- and multiple-echo methods will incur some signal cancellation as phase shifts occur due to spin evolution of coupled spins. However, in the multiple-echo acquisition, spin evolution will continue over the echo sequence, potentially resulting in partial recovery of signals at later echoes (17, 18), from which some increase in detection sensitivity may be observed.

METHODS

Three studies to examine the performance of multiple-echo MRSI with parametric-modeling analysis are described: i) to determine the optimal TE period for in vivo MRSI of brain at 1.5 T, a Monte Carlo simulation was carried out using computer-simulated data; ii) to compare the relative performance of the multiple-echo acquisition with single-echo methods, a Monte Carlo simulation was carried out using experimental data acquired from a phantom at 4.7 T; and iii) to demonstrate feasibility for ¹H MRSI acquisition in human brain, multiple-echo acquisitions were obtained at 1.5 T.

Data Analysis Methods

MRSI data reconstruction consisted of FT in the spatial dimensions, with zero filling and mild smoothing applied, followed by parametric spectral analysis of the multiple-echo time data sequence at each image voxel. To save processing time, only voxels within a region outlining the edge of the object were analyzed by the automated spectral analysis procedure. For the phantom and human studies carried out at 1.5 T, the data were zero filled to 64 × 64 points, and Gaussian spatial smoothing equivalent to exp(−0.5) at the edges of the acquired k-space region was applied. For the 4.7 T phantom data, as phase encoding was applied once only after the initial excitation, it was necessary to take the complex conjugate of alternate echoes to account for the spatial rotation caused by the 180° pulses. For the human brain study, a lipid extrapolation procedure (19) was applied before spectral analysis to reduce ringing from subcutaneous lipid regions.

Parametric modeling in the time domain was used to determine relative integrals of all metabolite resonances for both single-echo and multiple-echo acquisitions. A constrained Levenberg-Marquardt optimization algorithm was used, applied to both parts of the unweighted complex time data. The model assumed a single linewidth applied to all resonances. Both Lorentzian and Gaussian lineshapes were evaluated, with a Lorentzian lineshape being found to result in smaller residuals for the solution spectra obtained at 4.7 T, and a Gaussian lineshape for all data obtained at 1.5 T. Additional parameters were independent amplitude for each metabolite, a common frequency shift for all resonances, and zero- and first-order phase terms. For the multiple-echo data, independent phase terms were applied to all even-and odd-numbered echoes, and a T₂ value was determined for each metabolite.

Prior knowledge was used for the metabolite chemical-shift values, lactate J coupling, and equal amplitude of each line of the doublet. The automated fit procedure was applied to all time data sets of the MRSI data; the fit results were saved in a multiparametric image format and were viewed using in-house spectroscopic imaging display software (20). Using a simple intensity threshold procedure, voxels outside the brain were excluded from spectral fitting to reduce computation time.

For the multiple-echo analysis, the whole echo train was modeled as the sum of exponentially decaying signals for all metabolite resonances, i.e.,

$$S(t)={\displaystyle \sum }_m{I}_m\mathit{\text{Exp}}(-i·{\omega }_m·t/T_2)·\mathit{\text{Exp}}(-i·t\prime /T_2^{**})$$ [1]

where the sum over m indicates all metabolite resonances, with amplitude I_m and frequency ω_m. The time variable, t′, runs over each echo, i.e., t′ = −Δt/2 to Δt/2, where Δt is the sampling interval, and the time variable, t, runs over the whole echo sequence, i.e., t = n · TE + t′, where n runs over all echoes, and TE is the interecho period. A single value was obtained for the additional line broadening due to the field inhomogeneity, which we refer to as T₂^**, where T₂^** = 2/γ · ΔB₀. The decay constant of the echo time data, or 1/T₂^*, was then calculated to account for variable T₂ of each metabolite, i.e., 1/T₂^* = 1/T₂ + 1/T₂^**. The signal integral value returned by the fit therefore corresponds to the value at t = 0, i.e., unweighted by transverse relaxation.

The same parametric spectral analysis procedure was applied to the single-echo MRSI data. Differences in this model were that T₂ was not included in the model so that the signal integral value obtained corresponds to the time at the center of the spin echo, and the T₂^* value represents the combined contributions of T₂ and field inhomogeneity.

All data processing was performed using IDL (Research Systems Inc., Boulder, CO). Typical processing times for automated spectral analysis of the 64 × 64 MRSI voxels, for three resonances, was 2 h (200 MHz PC).

Simulation Methods–Determination of the Optimal TE Period

The optimal TE period for the multiple-echo acquisition sequence represents a compromise between i) a short TE period, resulting in minimal T₂^* decay over each sampling period and maximal signal energy; ii) a long TE period, giving maximal phase evolution between closely spaced resonances (i.e., best spectral discrimination); and iii) the number of refocusing pulses, which decreases the available sampling time. The optimal TE, and hence the number of echoes, will vary depending on the SNR, T₂, T₂^*, and Δf, which we define as the smallest frequency difference between neighboring resonances. To estimate the optimal number of echoes, we performed a Monte Carlo simulation with parametric analysis of computer-simulated spectra. Time data were first generated using spectral parameters typically encountered for in vivo MRSI at 1.5 T, simulating acquisitions with different numbers of echoes from 3 to 15, and for 15 different values of the additional field-inhomogeneity contribution to the linewidth, corresponding to T₂^** values in linear steps from 22 to 440 ms. Random noise was then added to this data, and the data were analyzed using the multiecho parametric spectral analysis procedure. This procedure was repeated 320 times for each echo number and linewidth. For each fit, the initial parameter estimates passed to the spectral fit procedure were randomly varied within ±20% of the actual value for the amplitudes, T₂ and T₂^*, and with the B₀ shift varied ±20 Hz. The means and standard deviation of the fitted integral results for each resonance were then calculated, and the optimal number of echoes assumed to result in the minimal standard deviation.

Time data corresponding to a multiple-echo acquisition sequence were simulated for the singlet resonances of water, choline (Cho), creatine (Cr), and NAA using a Lorentzian lineshape. Gaussian distributed noise was added at a level equivalent to an SNR for creatine of 1.5:1 in the time domain, which represents typical values for in vivo MRSI studies at 1.5 T. The simulation assumed T₂ values of 440, 400, 210 and 440 ms for the four resonances respectively and a refocusing pulse length of 15 ms. For this simulation study, we chose a total echo-train length of 800 ms. One factor to be considered when determining this total time is the requirement that the integral of the time-domain metabolite signal at the last echo is greater than the noise. Experimentally we have observed that at 1.5 T, metabolite signals can still be observed at echo times up to approximately 600 ms at the SNR values observed with in vivo ¹H MRSI of brain. Signal acquisition for longer periods does not affect the performance of the time-domain parametric analysis fit procedure, with the only penalty being the additional processing time. An additional factor to be considered in the choice of the total echo length is T₁ relaxation. Since spin-lattice relaxation effectively starts after the last refocusing pulse, this may begin several hundred ms later than for the single-echo sequence. As an example, assuming a T₁ for NAA of 1.3 s (21), then for a six-echo sequence with TE = 130 ms and TR = 2 s, the signal amplitude relative to a single-echo acquisition (TE = 130 ms) would be reduced by 19%.

Experimental Methods–Phantom Studies at 4.7 T

To compare the relative performance of the parametric spectral analysis procedures for multiple-echo and single-echo acquisitions, ¹H MRSI studies using both methods were carried out of a phantom at a field strength of 4.7 T (Nalorac, Martinez CA). Data were acquired with high SNR, permitting single-voxel data sets to be extracted and subsequently analyzed in a Monte Carlo study after the addition of varying noise levels. A test tube (2.8-cm diameter) was filled with a solution containing Cr, Cho, NAA, and lactate (Lac) at concentrations of 54, 21, 175, and 175 mM, respectively. In one section of the tube, a piece of nylon sponge was inserted that resulted in a decrease in T₂^* due to local susceptibility variations caused by the sponge. Two, single-slice MRSI data sets were obtained, one using a conventional single-echo MRSI acquisition (TE = 141 ms) and the other using a 20-echo acquisition (TE = 68 ms). Note that the number of echoes was larger than that indicated in the previous study since this measurement was performed at higher field strength and with a sample with long T₂ values. The number of sample points was 1024 for the single-echo and 2040 for the multiple-echo acquisition. Additional parameters were identical for both data sets, including 24 × 24 phase encodings over a 6.0-cm field of view, 1.923 kHz sweep width, and 5-mm thick slice selection carried out by the 90° excitation pulse. To minimize B₁ field inhomogeneity and off-resonance effects, a 75₀–270₁₁₀−75₀ composite 180° refocusing pulse was used (22), as well as 0/90° phase alternation of the refocusing pulses (23). Water suppression was achieved using a three-pulse chemical shift selective (CHESS) sequence.

Images for all compounds were reconstructed from the fit results. For comparison of the parametric spectral analysis procedures, the time data corresponding to four individual voxels were obtained from the same spatial regions of both the single- and multiple-echo acquisitions. This was done by first performing the spatial FT only, followed by selection of data at voxel locations previously identified from the reconstructed image data. The four locations were chosen to provide a range of T₂^* values. For each of these experimentally acquired data sets, a Monte Carlo simulation was then carried out by repeating the fit procedure for increasing levels of added Gaussian white noise, with 320 repetitions of the analysis carried out at each noise level and with randomized starting values for the fit procedure. For each metabolite, the mean and standard deviations of the fitted signal integrals were then obtained.

Experimental Methods–¹H MRSI at 1.5 T

The multiple-echo MRSI sequence was implemented on a 1.5 T clinical MRI system (Siemens Magnetom Vision). Acquisition parameters included a slice thickness of 1.5 cm, circular k-space encoding of 36-points diameter (24) for a 260-mm field of view, slice-selective lipid inversion, and CHESS water suppression. Optimized pulse shapes (25) were used with 5 mT/m crusher gradients surrounding each refocusing pulse, requiring a total of 17.7 ms. The sequence used six echoes with TE = 130 ms, sampling period for each echo of 110.08 ms, and TR = 2.5 s, giving a total acquisition time of 42 min. A TR longer than that used in our conventional single-echo MRSI acquisitions was chosen to allow sufficient relaxation after the multiple-echo sequence. Due to pulse programming limitations, the data were oversampled using a sweep width of 4.64 kHz that was then digitally filtered to 1.16 kHz before further processing. Phase-encode gradients were applied and were rewound within each TE period (12). Image reconstruction was carried out as described below, using the multiple-echo parametric analysis procedure.

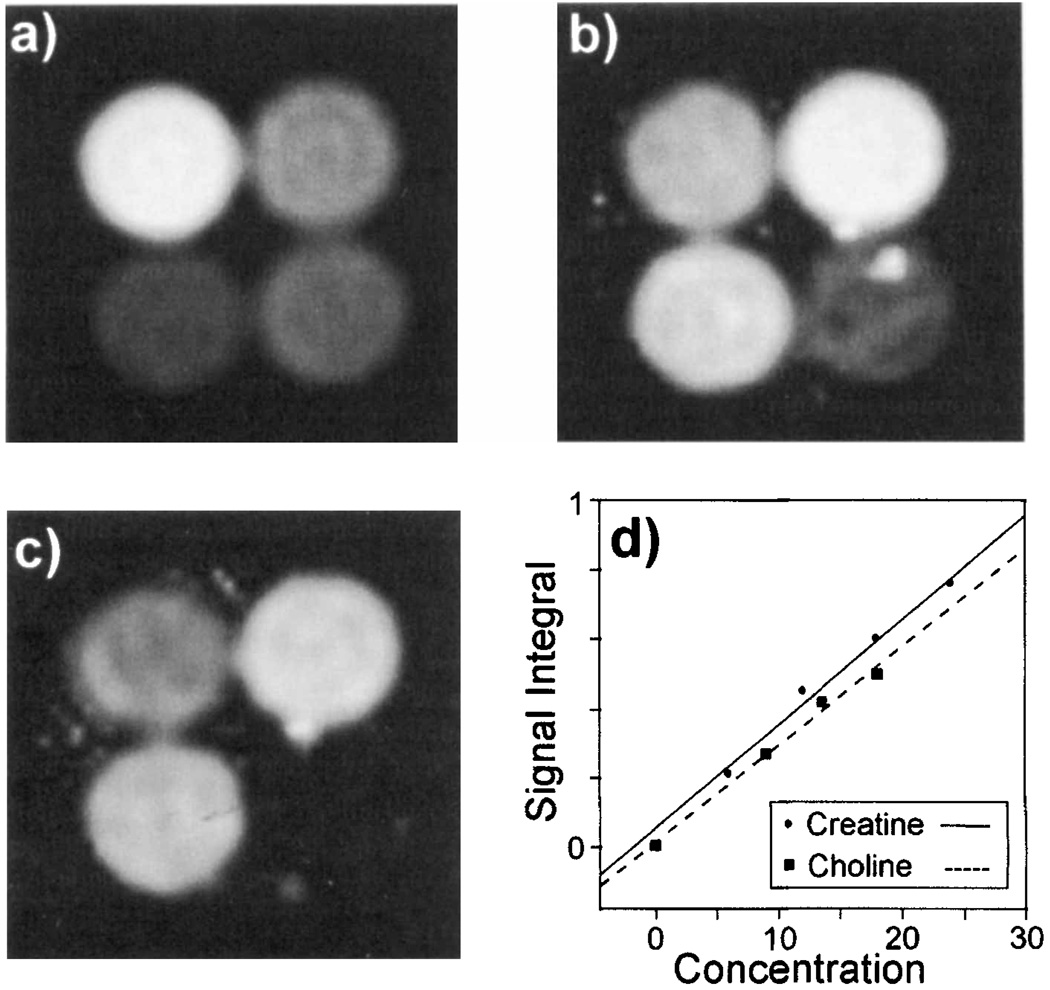
To evaluate the accuracy for measurement of individual metabolite signal intensities, a multiple-echo study was carried out of a phantom made up of four compartments, each containing different concentrations of NAA, Cr, and Cho, with the respective concentrations of these metabolites in each compartment being the following: Compartment 1: 24, 4, and 1 mM; Compartment 2: 12, 8, and 2 mM; Compartment 3: 6, 6, and 1.5 mM; and Compartment 4: 9, 2, and 0 mM. These concentration values covered a range from less than the smallest typical in vivo metabolite concentration to twice the largest. After image reconstruction, the fitted image intensity values in the center of each compartment were obtained and compared with the known concentrations.

Single-echo and multiple-echo MRSI studies were also carried out of human brain at 1.5 T. Acquisition parameters for the single-echo MRSI acquisition were the same as those described for the multiple-echo study, with the exception of a sampling period of 384 ms, sweep width of 1.33 kHz, and TR = 1.84 s, for a total acquisition time of 32 min. Both studies were performed on the same subject with the identical slice position and shim settings. An angulated slice was selected that represents a difficult area to image by MRSI methods, since it commonly includes significant susceptibility-induced field distortions in frontal brain regions that cannot be corrected for, even with the high-order shim system available on this instrument. Metabolite image formation was then carried out using similar parametric-modeling spectral analysis in both cases to fit resonances of Cr, Cho, and NAA.

RESULTS AND DISCUSSION

Optimal TE Period

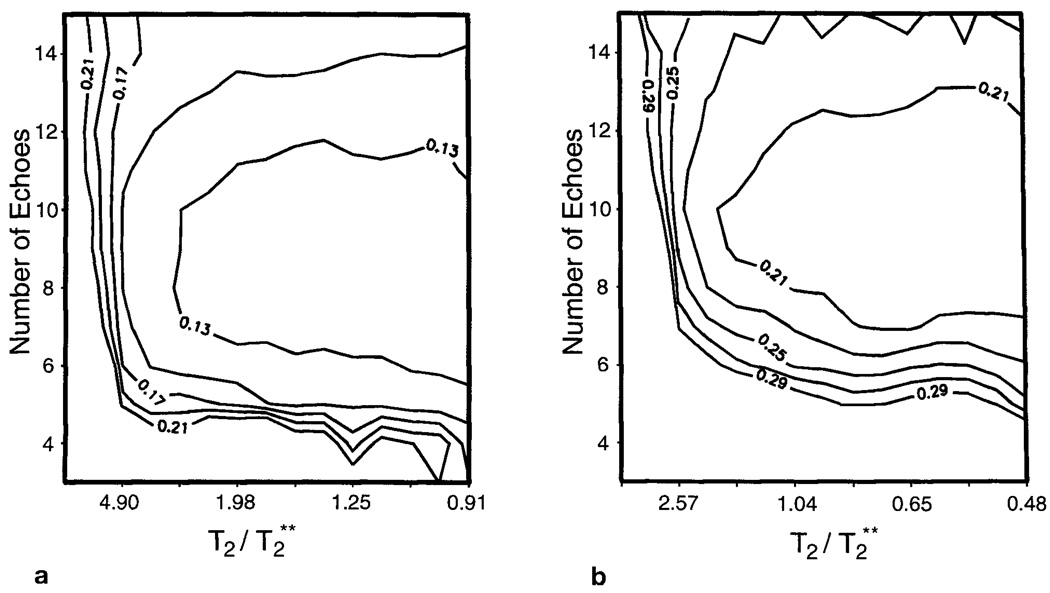
In Fig. 2 are shown the results of the Monte Carlo simulation to determine the optimal number of echoes. The standard deviations of the fitted signal integrals are plotted against the number of echoes and the relative T₂/T₂^** ratio for the Cho and Cr resonances in Figs. 2a and 2b, respectively. Lower values indicate improved performance of the parametric fit. The result for the NAA resonance shows the same general characteristics but for higher echo numbers. This occurs as the resonance is well separated in frequency, enabling spectral analysis to be readily achieved at shorter TEs.

FIG. 2.

Standard deviations of the fitted signal integrals for resonances representing (a) choline and (b) creatine, obtained by a Monte Carlo study using computer-simulated spectra, plotted for varying T₂/T₂^** value and number of echoes acquired within an 800-ms total sampling period. Data are plotted for linear steps of the field inhomogeneity line-broadening contribution, T₂^**, from 22 to 440 ms, and assuming T₂s of 400 and 210 ms, respectively.

From Fig. 2, it can be seen that the optimal number of echoes varies for each resonance and T₂/T₂^* value. For the parameters selected in this study, the discrimination of creatine requires the longest TE period, which indicates optimal performance in the range of six to 10 echoes over an 800-ms total sampling period. These results also show that the standard deviations do not change rapidly with T₂/T₂^* value or with the number of echoes, indicating that the performance of the multiple-echo analysis is suitable for a broad range of field inhomogeneity and that the choice of the number of echoes is not critical to obtain optimal performance. Based on these results, for the MRSI study of human brain, we chose to use the lower value of six echoes to allow for additional spectral discrimination in the presence of incomplete water suppression and additional resonances not included in this simulation.

Phantom Studies at 4.7 T

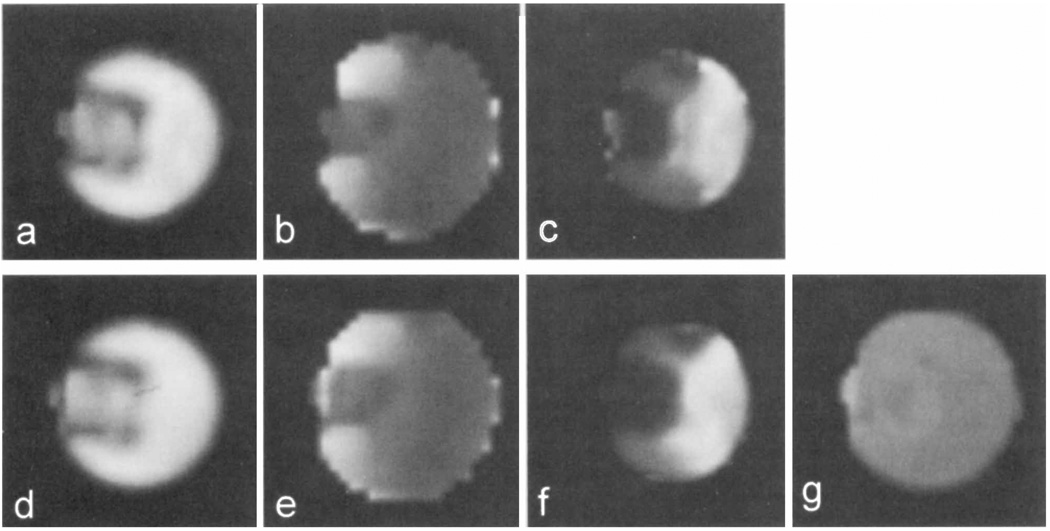
Examples of images from the phantom study are shown in Fig. 3, with the Cr images, B₀ maps, and T₂^* images reconstructed from the fit results for both the single- and multiple-echo studies. The quality of the spectroscopic images from this study are essentially identical for the single- and multiple-echo acquisitions, indicating correct performance of the multiple-echo spectral analysis procedure and that the parametric modeling analysis is indeed able to accurately separate frequencies that cannot be clearly distinguished using FT methods. The location of the sponge can be clearly identified as the lower intensity region on the metabolite images (Figs. 3a and 3d).

FIG. 3.

Comparison of metabolite images generated from automated fit results for single- and multiple-echo MRSI methods for the phantom at 4.7 T. Data for single-echo measurement are (a) creatine signal integral, (b) B₀, and (c) T₂^*. The corresponding results for multiple-echo acquisition are (d) creatine signal integral, (e) B₀, and (f) T₂^*. In (g) is shown the creatine T₂ image generated from the multiple-echo analysis.

Minor differences between the single- and multiple-echo images can be seen as a small relative decrease in image intensity in the sponge region for the single-echo case. This difference is attributed to the fact that the images from the multiple-echo fit represent signal integrals at TE = 0, whereas the single-echo fit determines the signal integrals at TE = 141 ms, and a reduced transverse relaxation time is present in the sponge region. This reduction in T₂ is believed to be due to an increased contribution to the transverse relaxation from diffusion in the presence of local field gradients in the sponge region. This is also indicated in the T₂ image for Cr, obtained from the multiple-echo study and shown in Fig. 3g, where a small reduction in the sponge region can be seen. Both T₂^* images (Figs. 3c and 3f) demonstrate reduced values in the region containing the sponge; however, some differences are again apparent. One reason for this is that the T₂^* value determined from the single-echo measurement represents the combined contributions of T₂ and field inhomogeneity, whereas the value determined by the multiple-echo method indicates T₂^**, the additional line broadening due to the field inhomogeneity contribution only. It should be noted that the B₀ and T₂ images appear slightly larger than the Cr integral images, since these calculated parameters are obtained at every voxel that has data over some small threshold value. These images therefore include valid data for voxels at the edge of the object that have only low signal amplitude due to the relatively broad point-spread function of this image. However, this low-signal amplitude region is not visible on the integral image with the windowing level used.

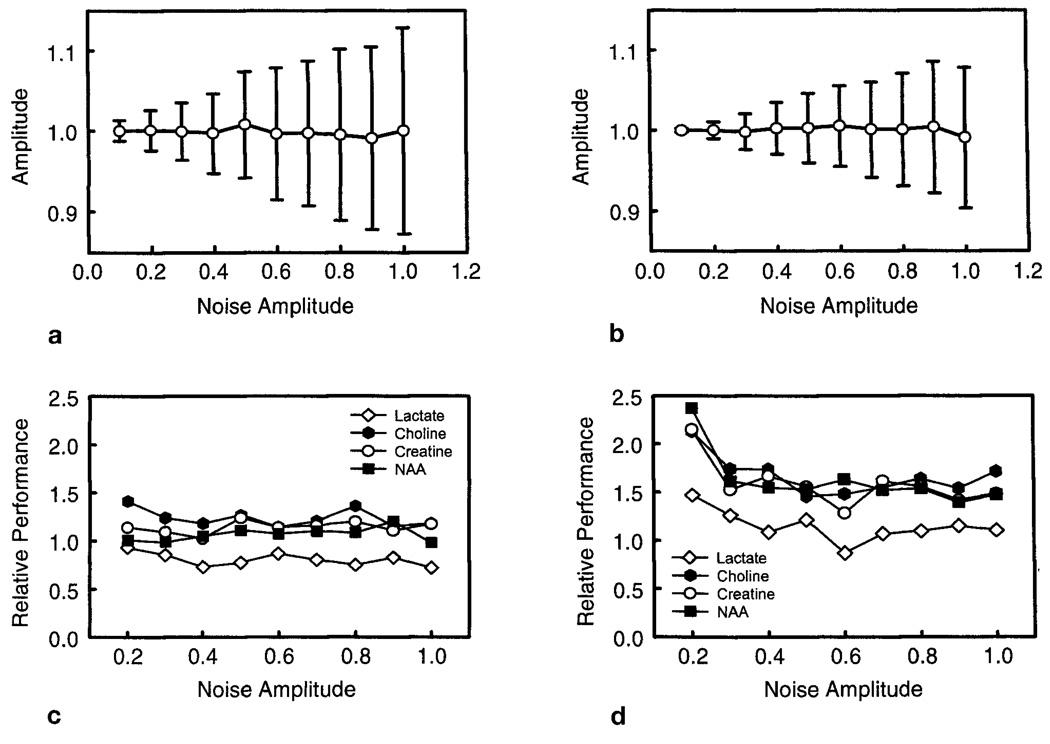
Examples of the Monte Carlo simulation results for analysis of spectra selected from the phantom data are shown in Fig. 4, and the complete results are summarized in Table 1. In Figs. 4a and 4b are shown the mean and standard deviation values of the fit result for NAA from a region with T₂^** = 74 ms, for the single- and multiple-echo data, respectively. Values are normalized by the mean fit result values obtained at low noise amplitude. Similar findings were obtained for the Cr, Cho, and Lac fit results. The standard deviations of the fit increase with the noise level for both the single- and multiple-echo analyses, as expected. From the multiple-echo analysis, we obtained T₂ values for NAA, Cr, Cho, and Lac of 753 ± 11, 752 ± 21, 1010 ± 20, and 717 ± 40 ms, respectively. For the spectra selected for the Monte Carlo analysis, the most homogeneous region was determined to have a T₂^** value of 220 ms, indicating that substantial field inhomogeneity still existed over the extent of a single MRSI voxel in this study.

FIG. 4.

Examples of results from the Monte Carlo study using spectra selected from the phantom data shown in Fig. 3. (a) and (b) show the mean normalized NAA signal integral and standard deviation for increasing levels of added noise for the single- and multiple-echo studies, respectively. (c) and (d) show the relative performance for analysis of each metabolite, defined as the ratio of the normalized standard deviation of the fitted integral values, for single-echo acquisition relative to the multiple-echo acquisition. Results are shown for T₂^* values of 220 and 74 ms, respectively.

Table 1.

Metabolite	Mean relative standard deviation, Single-echo/Multiple-echo [%]
	T2** = 220 ms	T2** = 151 ms	T2** = 74 ms	T2** = 10 ms
Choline	116 ± 9	137 ± 13	166 ± 20	193 ± 25
Creatine	114 ± 6	129 ± 14	157 ± 23	201 ± 15
NAA	106 ± 7	135 ± 17	163 ± 29	198 ± 20
Lactate	80 ± 7	103 ± 12	115 ± 16	136 ± 16

In Figs. 4c and 4d are shown the relative performance of the fitted signal integral results obtained from single-and multi-echo methods. This parameter is calculated as the ratio of the single-echo standard deviation to the multiple-echo standard deviation value, normalized by the mean for each metabolite in each case. This factor is plotted against the added noise value used. Larger values indicate that the multiple-echo method results in improved relative performance, indicated by a smaller standard deviation of the fit results. Data are shown for T₂^** values of 220 and 74 ms, and results are summarized for all T₂^** values in Table 1. For this summary, data were averaged over a range of noise values from 0.2 to 1.0. From Fig. 4 and Table 1, we conclude that the relative performance of the multiple-echo method is i) constant over a wide range of noise levels, ii) different for each resonance depending on T₂ values, and iii) greater for decreasing T₂^** values. Better performance of the multiple-echo acquisition is apparent for all compounds except Lac, for both short and long T₂^* cases, with greater relative improvement for the shorter T₂^*.

The poorer performance for Lac is due to J-coupling effects for the Lac doublet. First, the first TE period occurred at 68 ms, which coincides with the value of 1/2J, as measured for the Lac doublet in this sample, resulting in signal cancellation at the first echo due to opposing phases of each resonance of the doublet. Having a non-zero data value at this point would greatly benefit the fit procedure for determination of the T₂ value. Second, all odd echoes would also result in signal cancellation of the Lac doublet, effectively reducing the total signal energy by approximately one half. Use of a slightly different TE value can be expected to improve performance of the fit of the Lac doublet, and further studies remain to be carried out to evaluate the optimal TE periods for J-coupled spin systems.

Phantom Studies at 1.5 T

In Fig. 5 are shown metabolite images of the multicompartment phantom, obtained at 1.5 T using the automated multiple-echo spectral analysis procedure. Clear separation between the closely separated signals of Cr and Cho is obtained, indicating that the analysis procedure was able to separate these spectral components correctly for concentrations equivalent to, or lower than, that found in vivo. A bright region visible in the lower right tube for the Cho image (Fig. 5b) is attributed to inadequate water suppression in a region subject to large field shifts due to the presence of an air bubble. From the center of each of the four phantom compartments, several noncontiguous voxels were selected and the average fitted metabolite signal values obtained. In Fig. 5d is shown the relationship between the fitted image integral values and the calculated signals for Cr and Cho. The fit results are plotted against the known metabolite concentrations (in mM) multiplied by the number of protons contributing to the signal at each resonance. Good correlation between the fitted signal and the known concentration values was found (r > 0.99), indicating that the multiecho parametric analysis procedure is able to clearly separate the most closely spaced resonances of Cho and Cr even at low SNR values. The results for NAA showed the same excellent correlation as would be expected given its better SNR and spectral separation.

FIG. 5.

Images obtained by parametric fitting of multiple-echo MRSI data for the multicompartment phantom described in the text, showing (a) NAA, (b) creatine, and (c) choline. (d) Comparison of fit result for the metabolite signal integral plotted against the concentration of protons, calculated by multiplying the known metabolite concentration, in mM, by the number of protons contributing to the fitted resonance.

Human Studies at 1.5 T

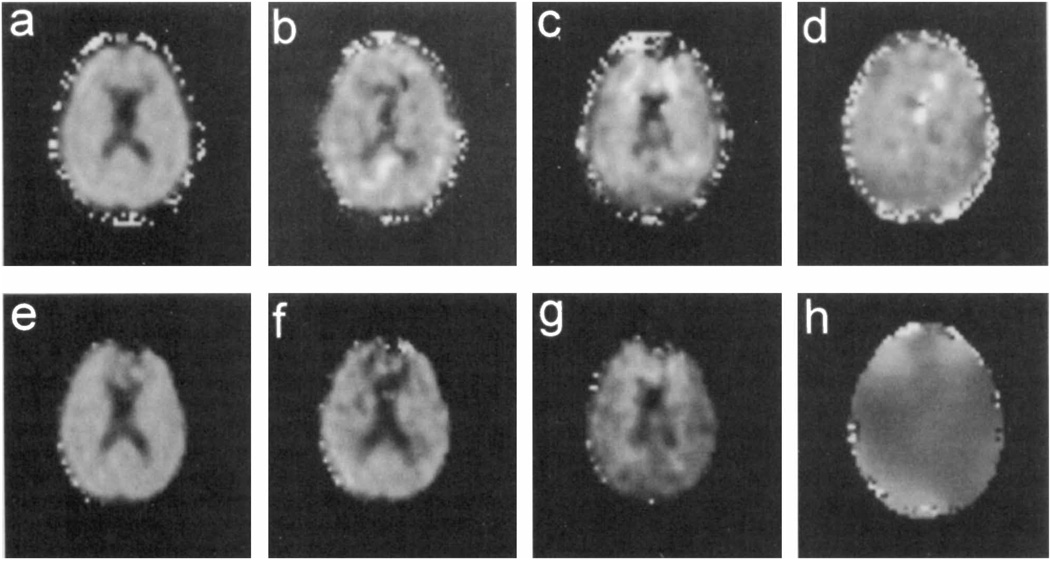
In Fig. 6 are shown metabolite images obtained after parametric spectral analysis of a multiple-echo and a single-echo MRSI acquisition of the same section through a human brain. Images show signal integrals for NAA, Cr, and Cho, as well as the NAA T₂ and the B₀ distribution obtained from the multiple-echo study. The presence of rapid field variations in the frontal region can be seen from the B₀ map of Fig. 6h. A breakdown of the fit in this area can be seen by the absence of fit results, indicated by black regions, on all metabolite images for the single-echo acquisition (Figs. 6e–6g). A comparison of the image quality indicates a similar appearance over regions having good field homogeneity, as expected, whereas a modest improvement in performance for the NAA image is apparent for the multiple-echo acquisition in the frontal regions. Difficulties still remain, notably in the Cho image (Fig. 6c), that we attribute largely to the presence of inadequately suppressed water signal. Further improvement of postprocessing water suppression is required to address this remaining problem. In addition, some areas in the Cho and Cr images indicate that these two signals have been incorrectly assigned, indicating that for this SNR a longer sampling period and fewer echoes should be used. We note that differences in the appearance of the region outside the brain arise from different masks used and are not due to differences in the performance of the parametric fit procedures used.

FIG. 6.

Images obtained by automated spectral fitting of ¹H MRSI data of human brain at 1.5 T. Results shown for the multiple-echo study are (a) the NAA integral, (b) creatine integral, (c) choline integral, and (d) the NAA T₂ value. Results from the single-echo study are signal integrals for (e) NAA, (f) creatine, and (g) choline. In (h) is shown the B₀ map obtained from the multiple-echo study.

Measured T₂ values, as determined by averaging fitted values from several noncontiguous voxels over the whole brain, were 378 ± 54 ms for Cho, 215 ± 47 ms for Cr, and 398 ± 40 ms for NAA. Although these values can be expected to contain errors in the T₂ measurement, for example due to the effect of pulse imperfections and diffusion, the calculated exponential decay functions nevertheless enable the metabolite intensity values to be extrapolated to TE = 0. We note that the NAA T₂ image (Fig. 6d) includes values in the ventricular region, although the NAA image (Fig. 6a) indicates zero signal in those areas, since T₂ values will always be returned by the fit procedure, even for zero signal integral values.

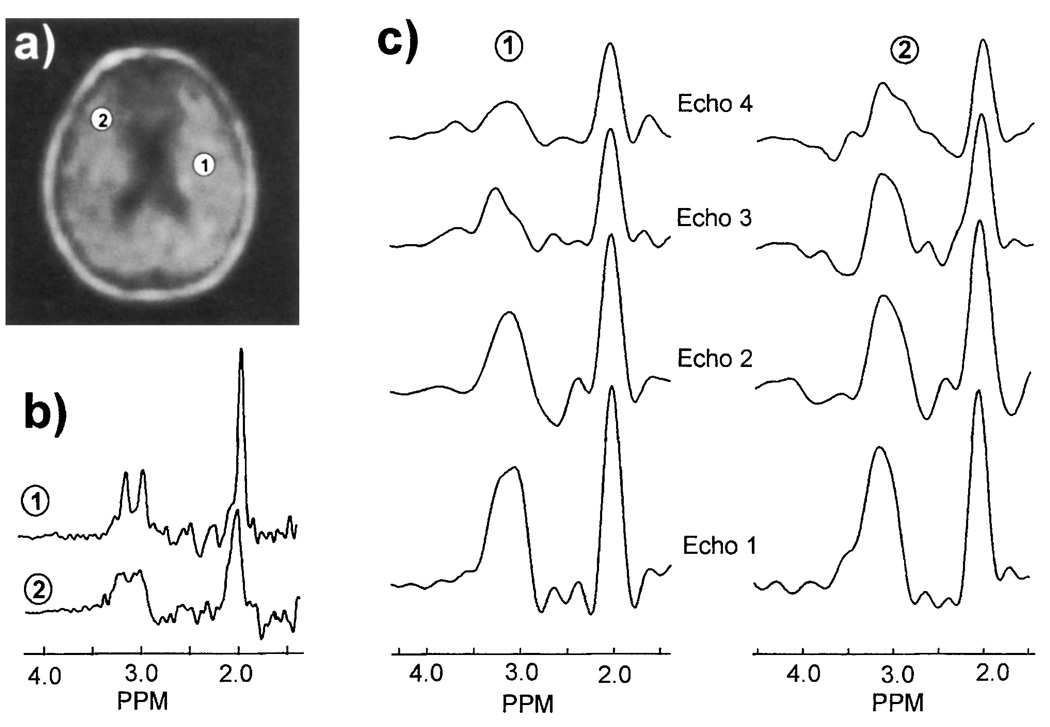
Figure 7 compares spectra obtained from brain for single- and multiple-echo acquisitions. Spectra were selected from the same two locations in both data sets, as indicated in Fig. 7a that shows the NAA image obtained by simple spectral integration from the single-echo study. The spectra obtained from the single-echo study are shown in Fig. 7b, where it can be seen that the quality of the second selected spectrum is degraded by local susceptibility variations, resulting in line broadening such that the resonances of Cr and Cho cannot be clearly resolved. For comparison, the FT of the first four echoes from the multiple-echo MRSI at the same locations are shown in Fig. 7c. For this figure, a Gaussian line broadening of 12 Hz was applied to reduce ringing. From these plots it can be seen that for the sampling period used, the Cr and Cho resonances, centered at 3.1 ppm, cannot be resolved, though there is some indication that more than one resonance is present. However, for this data set, the spectral quality from both locations is similar despite the poorer homogeneity in the second selected region. Therefore, the ability to distinguish Cr and Cho will be similar in Regions 1 and 2, in contrast with the expectation for the single-echo data. An additional observation of the data shown in Fig. 7c is that in the second echo a broad negative signal centered at 2.6 ppm is apparent. Using computer simulation (26), we have confirmed that this is due to refocusing of the CH2 multiplet group of NAA. This signal was not included in the parametric model used in this study; however, this addition would potentially improve the spectral analysis procedure.

FIG. 7.

Comparison of spectra obtained by single- and multiple-echo MRSI of human brain. (a) NAA metabolite image obtained by single-echo MRSI with image formation by spectral integration, indicating two locations from which sample spectra were selected, (b) single-echo MRSI spectra selected from the two locations indicated in (a), and (c) the corresponding multiple-echo MRSI spectra obtained by FT of the first four echoes at TEs of 130, 260, 390, and 520 ms.

CONCLUSION

In this study, we have presented a ¹H MRSI method based on multiple-echo acquisition with time-domain parametric spectral analysis. By performing parametric modeling of the whole echo train, combined with a priori spectral information, we have shown that it is possible to analyze closely separated resonances that cannot be readily distinguished using Fourier analysis of the shortened sample periods of each echo. This procedure then enables additional spin echoes to be acquired to obtain improved performance in the presence of moderate field inhomogeneity and measurement of metabolite T₂ values. To achieve this aim, it was necessary to select a compromise between the interecho period and the number of echoes to balance the loss of spectral resolution with the gains in signal energy obtained with additional echoes.

From computer simulation and phantom studies, we have demonstrated that at a field strength of 4.7 T, this technique offers improved performance for measurement of longer T₂ metabolites in the presence of field inhomogeneities, as well as measurement of metabolite integrals that are corrected for transverse relaxation. The sensitivity of the multiple-echo acquisition is relatively constant over a range of moderate field inhomogeneities and comparable to that obtained from homogeneous regions using conventional single-echo methods. These characteristics make it suitable for ¹H MRSI studies in human brain where a range of T₂^* values may be observed over the imaged region, though significant improvement in regions of good field homogeneity is not anticipated. The application of multiple-echo MRSI will improve quantitative metabolite imaging and lessen the strict homogeneity requirements normally required for clinical ¹H MRSI studies.

Although this present study has included a preliminary example of multiple-echo metabolite imaging at a field strength of 1.5 T, evaluation of the potential advantages for clinical studies remains to be carried out. However, the advantages of the multiple-echo acquisition are potentially of greater interest for higher-field spectrometers where susceptibility effects are more severe and chemical-shift dispersion is greater, permitting echo times to be reduced over the values used in this study. Detailed evaluation of the performance limitations of the fit procedure also remain to be carried out, including effect of uncharacterized baseline signals, lineshape, and the presence of resonances not included in the a priori information. Since the multiple-echo method favors observation of singlet resonances with longer T₂, the limitations are anticipated to be similar to parametric analysis of single-echo data at medium-to-long TE values. Additional limitations of the multiple-echo measurement include additional spin-lattice relaxation losses and increased dependence on B₁ homogeneity.

Our initial implementation for human brain studies indicates that by combining multiple-echo acquisition with lipid extrapolation methods, the ability to image cortical surface regions is improved. The additional tolerance to field inhomogeneities provided by the multiple-echo acquisitions should also simplify set-up procedures for clinical MRSI procedures by enabling automated global shimming methods to be routinely used. Further studies are required to evaluate performance for clinical applications of ¹H MRSI and for analysis of multiplet resonance structures.