Referenceless MR Thermometry for Monitoring Thermal Ablation in the Prostate

Abstract

Referenceless proton resonance frequency (PRF) shift thermometry provides a means to measure temperature changes during minimally invasive thermotherapy that is inherently robust to motion and tissue displacement. However, if the referenceless method is used to determine temperature changes during prostate ablation, phase gaps between water and fat in image regions used to determine the background phase can confound the phase estimation. We demonstrate an extension to referenceless thermometry which eliminates this problem by allowing background phase estimation in the presence of phase discontinuities between aqueous and fatty tissue. In this method, images are acquired with a multi-echo sequence and binary water and fat maps are generated from a Dixon reconstruction. For the background phase estimation, water and fat regions are treated separately and the phase offset between the two tissue types is determined. The method is demonstrated feasibile in phantoms and during in vivo thermal ablation of canine prostate.

I. Introduction

High temperature thermal treatments are increasingly adopted for benign prostatic hyperplasia (BPH) and localized prostatic carcinoma (CaP), due to their minimal invasiveness and low associated morbidities [1], [2], [3]. Spatial and temporal control of the tissue temperature is vital during high temperature thermal therapy to ensure destruction of the targeted tissue and to avoid damage to surrounding normal structures. This necessity requires temperature monitoring of the treatment.

Magnetic resonance proton resonance frequency (PRF) shift thermometry [4], [5] is suitable to monitor the treatment, because it provides quantitative temperature measurements in near real time. This method uses changes in the phase of gradient-recalled echo (GRE) images to estimate the relative temperature change between images. In conventional PRF shift thermometry, phase images acquired prior to heating (i.e. baseline images) are subtracted from phase images acquired during heating. In the presence of tissue motion, however, images acquired during heating are not registered to the baseline images, resulting in erroneous baseline phase subtraction and inaccurate temperature measurements.

Several mechanisms can cause motion and tissue displacement during thermotherapy of the prostate. Thermal coagulation leads to structural changes and deformation of the tissue [6]. Swelling caused by formation of edema can also contribute to tissue displacement [7] as can changes in the state of muscles and changes in bowel filling. Recent studies have focused on the correction of repetitive motion caused by respiration using motion detection [8], [9] and movement registration with navigator echoes [10], [11], [12]. These methods are not helpful for prostate ablation, due to the different nature of motion encountered during prostate treatment.

We described a method called referenceless PRF shift thermometry [13], which is inherently robust to tissue motion because the subtraction of a baseline phase image acquired prior to heating is not necessary. Instead, the background phase is estimated in every individual image from a frame region of interest (ROI) surrounding the heating region. This method has been used to monitor in vivo laser ablation in a pig model and evaluated for focused ultrasound surgery of uterine fibroids in patients [14]. In addition, others have investigated estimation strategies that fit to real and imaginary image components instead of the image phase [15] and optimal ROI size and shape [16].

In many tissues, only aqueous tissue is present in the frame and inner ROI. For thermal ablation in the prostate, however, the frame ROI is located in the periprostatic tissue which contains both adipose and aqueous tissues. In this case, the previous referenceless algorithm requires image acquisition at an echo time TE, where water and fat are exactly in phase in order to prevent phase discontinuities between the two tissue types which would distort the phase estimation. However, finding the exact in-phase echo time is difficult in practice, since it is dependent on the spectral components of the fat and the body temperature of the subject which may change during anesthesia.

We propose an extension to referenceless thermometry where the background phase is estimated from water and fat, allowing for a constant phase offset between the two tissues and thereby eliminating the constraint of an in-phase echo time TE. The method is evaluated in phantoms and during in vivo canine prostate ablation experiments.

II. Review of Conventional and Referenceless Thermometry

PRF shift thermometry uses changes in the phase of gradient-recalled echo (GRE) images to estimate the relative temperature change ΔT, as given by

$$\mathrm{\Delta }T=\frac{\mathrm{\Delta }\phi }{\gamma \alpha B_{0}TE},$$ (1)

where α = −0.01 ppm/°C is the PRF change coefficient for aqueous tissue, γ is the gyromagnetic ratio, B₀ is the main magnetic field, TE is the echo time, and Δφ is the phase difference before and during heating. In conventional thermometry, the phase difference is determined by subtracting a baseline phase image, acquired prior to heating, from the current phase image, Δφ = φ −φ_baseline. In referenceless thermometry [13] the background phase of the image is estimated from the current image itself. The background phase estimate is determined by fitting a low order polynomial in a region of interest (ROI) to the image phase outside the treatment area, which remains at body temperature. To eliminate potential phase wraps, the phase in the ROI is unwrapped before polynomial fitting using Goldstein, Zebker, and Werner’s algorithm [17]. Depending on the geometry of the lesion and surrounding tissue, the ROI partially or completely surrounds the heating area, as seen in Fig. 1. The appropriate size and location of the ROI as well as the optimal polynomial order for the phase fit are determined before heating [13], [16]. The phase difference is then calculated by subtracting the estimated phase from the image phase, Δφ = φ − φ_estimated.

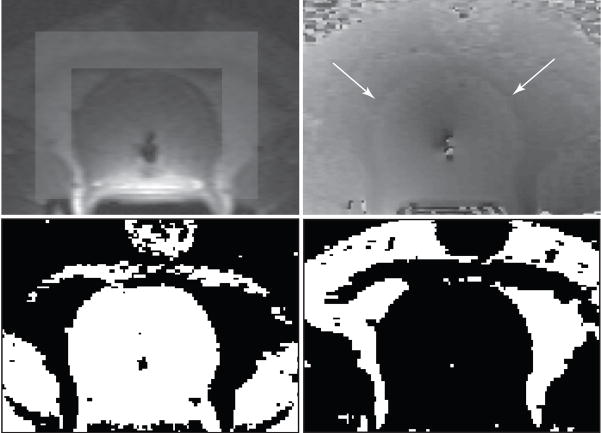
Fig. 1.

Magnitude image (upper left) showing the frame region around the prostate and unwrapped phase image (upper right). Note the small phase discontinuities between the water and fat regions in the unwrapped phase image (arrows) to which the proposed modified referenceless method is more robust. Binary maps of water (lower left) and fat (lower right) regions.

III. Modified Referenceless Reconstruction with Dixon Decomposition

A. Reconstruction Algorithm

In the modified referenceless reconstruction, a 3pt-Dixon decomposition automatically identifies water and fat regions in the periprostatic tissue. Both water and fat regions are used to estimate the background phase. The mechanisms that make the water proton resonance frequency shift with temperature do not apply to lipid protons, since there is no hydrogen bonding among the methylene protons that supply the bulk of fat signal [18]. The fact that fat has a PRF-thermal coefficient that is negligible compared to water [19] allows fatty regions inside the heating area to also be used for background phase estimation. Since fatty regions virtually maintain the same background phase at all temperatures, they do not have to be excluded from the inner ROI but add additional information for a better polynomial fit.

In the new sequence, images are acquired at three different echo times, which correspond to phase angles between water and fat of approximately 2π, 3π and 4π. Water and fat images are reconstructed from the three echoes using a 3pt-Dixon decomposition [20]. From these images, binary masking regions that contain either water or fat are created. Pixels that contain more than 90% water are considered water pixels and pixels that contain more than 90% fat are considered fat pixels. Pixels with other mixtures of water and fat are excluded from the binary maps. Depending on the SNR of the images, the threshold can be changed such that the resulting binary maps contain enough pixels for adequate polynomial fitting. Figure 1 (lower row) show typical binary maps of the prostate region.

As in the previous referenceless reconstruction, a frame region of interest is selected around the heating area in one of the acquired magnitude images prior to heating, as seen in Fig. 1 (upper left). This frame region is used for fitting a low order polynomial to the background phase. Figure 1 (upper right) shows the corresponding phase image after phase unwrapping with small phase discontinuities between water and fat (arrows). The background phase in water and fat regions has the same spatial variation, but displays a different constant term, which is dependent on the echo time TE. The unwrapped phase in aqueous tissue in this selected region can be approximated by a polynomial, φ_w:

$${\mathit{\phi }}_{\mathit{w}}\approx a_0{\mathbf{p}}_{\mathbf{0}}+a_1{\mathbf{p}}_{\mathbf{1}}+\cdots ,$$ (2)

where the p_i’s are one dimensional vectors that contain the values of the two dimensional matrices for constant, linear, and higher order phase variations in x and y direction and their cross-terms. The matrices are defined over the selected frame region. The phase in adipose tissue is then described by the same polynomial as water, but has an additional constant phase offset a_0f:

$${\mathit{\phi }}_{\mathit{f}}\approx a_0{\mathbf{p}}_{\mathbf{0}}+a_1{\mathbf{p}}_{\mathbf{1}}+\cdots +a_{0f}{\mathbf{p}}_{\mathbf{0}},$$ (3)

where a_0f is the phase offset between water and fat. It is important that the frame ROI contains a region of aqueous tissue; otherwise a_0f cannot be determined. Both equations can be combined into a single linear equation,

$$\left[\begin{array}{l}{\mathit{\phi }}_{\mathbf{w}}\hfill \\ {\mathit{\phi }}_{\mathbf{f}}\hfill \end{array}\right]=\left[\begin{array}{l}{\mathbf{p}}_{\mathbf{0}}{\mathbf{p}}_{\mathbf{1}}{\mathbf{p}}_{\mathbf{2}}\cdots \mathbf{0}\hfill \\ {\mathbf{p}}_{\mathbf{0}}{\mathbf{p}}_{\mathbf{1}}{\mathbf{p}}_{\mathbf{2}}\cdots {\mathbf{p}}_{\mathbf{0}}\hfill \end{array}\right]{[a_o{a}_1{a}_2\cdots a_{0f}]}^T$$ (4)

or φ = P · a, which can be solved for the polynomial coefficients a_i. With the binary fat/water maps, the polynomial coefficients including the offset a_0f between water and fat are determined in the least squares sense:

$$\mathbf{a}={({\mathbf{P}}^{\ast }\mathbf{WP})}^{-1}{\mathbf{P}}^{\ast }\mathbf{W}\mathit{\phi },$$ (5)

where W is a diagonal matrix containing weights (e.g. for magnitude squared weighting [21]) for each pixel multiplied by the corresponding binary mask. The extrapolation of the fitted polynomial φ_w to locations within the prostate serves as an estimation of the baseline phase.

The temperature change in the prostate is then calculated by subtracting the phase estimate φ_w from the current phase image as in the previous referenceless method, but in this case the temperature is only calculated for regions containing aqueous tissue.

B. Phase Unwrapping

All images that are reconstructed with the referenceless method have to be phase unwrapped before the polynomial fit is performed. Phase unwrapping of the out-of-phase images often does not give the desired result, because the π-phase gaps between water and fat are problematic for phase unwrapping algorithms, especially if water and fat regions are not contiguous. Therefore, we used the information of the fat location from the binary maps to subtract π from the phase of all fat regions before performing the phase unwrapping. This eliminates the problematic phase gaps so that conventional phase unwrapping algorithms [22], [17], [23] can be used.

IV. MR Imaging and Data Analysis

First, we investigated the effects of a temperature change on the Dixon decomposition in a computer simulation. Then we tested the referenceless reconstruction algorithm in two phantom experiments, one during a zero degree temperature rise and one during ultrasound heating. Finally, the new method was evaluated during in vivo thermal ablations in five canine prostates.

A. Temperature Effect on Dixon Decomposition

Decomposition of water and fat with the 3pt-Dixon method uses the chemical shift difference between water and fat of approximately 3.5 ppm or 71 Hz at 0.5 T. However, with a change in temperature, water will experience a change in resonance frequency of −0.01 ppm/°C, whereas the resonance frequency change of fat is negligible. The modified reference-less method depends on the Dixon decomposition remaining consistent when the tissue is heated. Therefore, we investigated whether the Dixon decomposition is affected by a temperature change in computer simulations.

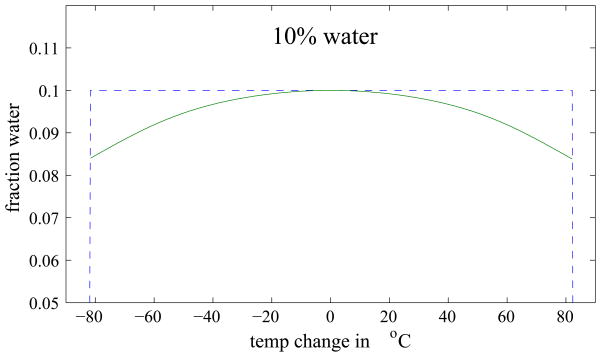
A phantom was simulated that contained different fractions of water and fat ranging from pure water to pure fat, while maintaining unity magnitude in each voxel. Figure 2 shows the water and fat distribution in the phantom and the corresponding magnitude image. We then added a temperature gradient ranging from −80 to +80°C to each line of constant water/fat ratio in the image. Phantom images at echo times 2π, 3π, and 4π were simulated and decomposed into water and fat images using a 3pt-Dixon reconstruction. The resulting images were compared to the correct water and fat ratio, and the error as a function of water/fat ratio and temperature was determined.

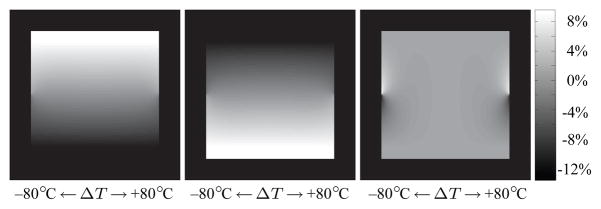
Fig. 2.

Water image (left), fat image (middle), and combined image (right) of the simulated water/fat phantom when there is no temperature rise.

B. Phantom Experiment with Zero Degree Temperature Rise

The first phantom experiment was designed to compare the accuracy of measuring a zero degree temperature rise in images reconstructed with baseline subtraction, the previous referenceless reconstruction and the here proposed, modified referenceless reconstruction. For this purpose, sets of three images of a phantom containing vials with water and oil were acquired at three different echo times in three separate acquisitions. Imaging parameters of the gradient echo sequence were TR = 100 ms, flip angle = 60°, FOV = 16 cm, matrix size = 256 × 128, slice thickness = 5 mm, BW = 6.91 kHz. With the assumption of a chemical shift between water and fat of 3.5 ppm or 71 Hz at 0.5 T, the echo times of the two in-phase and the out-of-phase images were calculated to be TE₁ = 14.3 ms, TE₂ = 21.4 ms, and TE₃ = 28.6 ms. A second and a third set of images were acquired, with echo times slightly higher and lower than the calculated echo times to investigate the effect of small phase gaps between the water and fat regions (set 2: TE₁ = 14.0 ms, TE₂ = 21.0 ms, TE₃ = 28.0 ms and set 3: TE₁ = 14.6 ms, TE₂ = 21.9 ms, and TE₃ = 29.2 ms). In addition, all three image sets were acquired twice in order to obtain appropriate baseline images for the baseline subtraction method.

Binary maps were created from each image set and temperature maps of the three individual echoes were reconstructed with the different methods. For both referenceless reconstruction methods, a rectangular frame and inner ROI were chosen in water (2.5 cm × 3.5 cm inner region surrounded by a 1.5 cm frame region). Mean and standard deviation in the temperature maps resulting from the three reconstruction methods were calculated in a region of water and compared.

C. Phantom Experiment with Ultrasound Heating

In a second phantom experiment, a bovine tissue sample consisting of muscle tissue and fat was heated with an internally-cooled interstitial ultrasound applicator [24], [25] consisting of a small diameter (1.8 mm) tubular ultrasound transducer. The tissue was imaged as the sample returned to room temperature after heating. Images were acquired with a double echo GRE sequence with gradient “fly-back” such that both echoes have the same readout polarity. In the first acquisition, in-phase echoes were collected at TE₁ = 14.3 ms and TE₃ = 28.6 ms. In the following acquisition, an out-of-phase image was collected at TE₂ = 21.4 ms (the second echo at TE₄ = 35.8 ms was collected but not used for reconstruction). Additional imaging parameters were TR = 120 ms, flip angle = 60°, FOV = 20 cm, matrix size = 256 × 128, slice thickness = 5 mm, sampling bandwidth = 12.5 kHz, resulting in a scan time of approximately 30 s to acquire all three echoes for a Dixon decomposition. Temperature maps of all three echoes were reconstructed with modified referenceless reconstruction and conventional baseline subtraction and compared.

D. In Vivo Prostate Ablation

The method was evaluated in five in vivo thermal ablations of the canine prostate using different types of transurethral ultrasound applicators [26], [27], [28]. MR imaging was performed using an endorectal coil. Two or three slices were acquired with imaging parameters TR = 150–180 ms, flip angle = 60°, FOV = 20×16 cm, slice thickness = 5 mm. In the first four experiments, images at three different echo times (TE₁ = 14.3 ms, TE₂ = 21.4 ms, and TE₃ = 28.6 ms) were acquired in two acquisitions (see section IV-C) with matrix size = 256×96 and BW = 12.5 kHz for all echoes, resulting in a scan time of approximately 30 s for each Dixon set. In this case, new binary maps were generated after two acquisitions.

In the fifth experiment, all three echoes were acquired in a single acquisition with gradient fly-back. To accommodate all echoes in one acquisition, the matrix size was decreased to 128×96 and the bandwidth increased to 15.6 kHz. This sequence allows reconstruction of binary maps with every acquisition in a scan time of 15 s for three slices. Temperature maps of all three echoes were reconstructed with modified referenceless reconstruction and compared to those obtained with baseline subtraction. In addition, the in-phase echoes were reconstructed with the unmodified referenceless method. To evaluate the performance of both reconstruction methods in the presence of tissue motion, pressure was manually applied to the animal’s abdomen. No heating was applied in this experiment and the deviation to the expected zero degree temperature rise was measured.

The transurethral ultrasound applicators used in these experiments can cause a local magnetic field change near the device. The US applicators are located inside a catheter with a water-circulated, thin walled balloon of 10 mm diameter to remove excess heat from the transducers, cool the urethra, and acoustically couple the transducer to the tissue. Only magnetic field perturbations that extend to regions outside the cooling balloon need to be corrected. A pre-heating image is used to determine if field perturbations outside the balloon exist, in which case a reference map is generated by averaging the phase variations of three preheating images. The reference map is then used to correct for the applicator artifact during heating [29].

V. Results

A. Temperature Effect on Dixon Decomposition

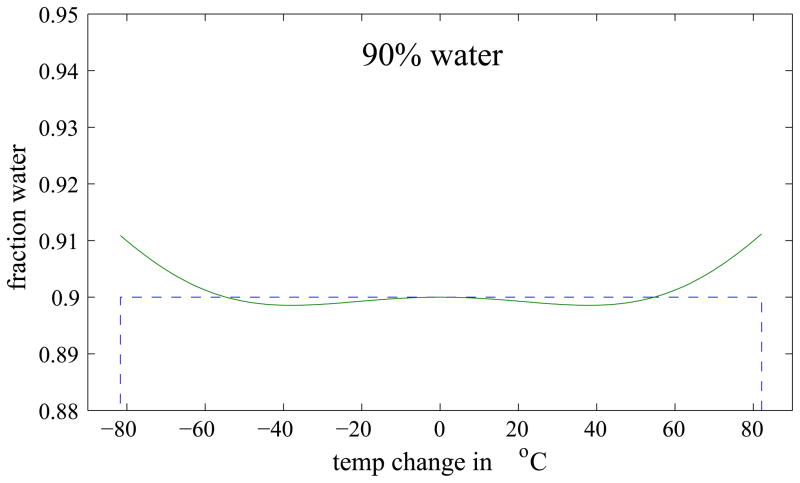
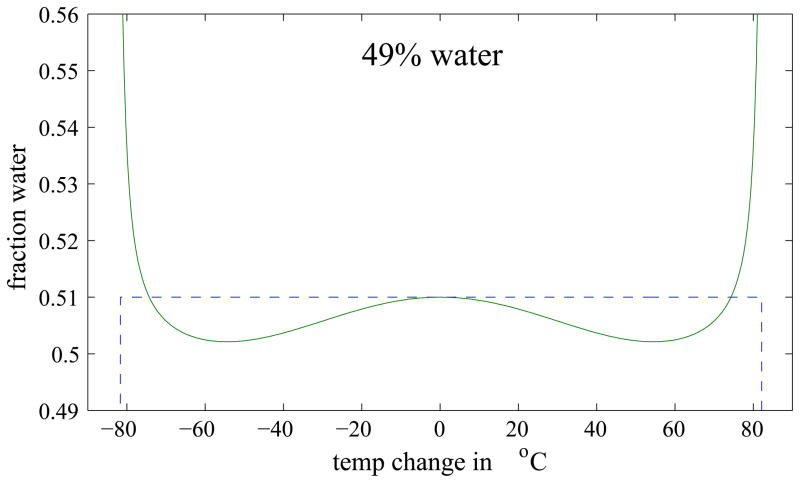
Figure 3 shows the Dixon reconstructed water and fat images of the simulated phantom and a map of the absolute error in the water decomposition. Errors can be seen at the sides of the phantom, i.e. in regions of a large temperature change. To better visualize the error, Fig. 4 compares the ideal and actual decomposition of three different water fractions as a function of temperature. For small temperature changes, the error is small, but it increases with increasing temperature. The maximum error in the decomposition was found to be 13.6% and occurred at a temperature change of 80°C in a voxel containing 49% water (see Fig. 4, middle). However, in thermal ablation therapies, the expected temperature change is usually below 50°C and rarely higher than 60°C. For these two cases, the maximum absolute error is 1.2% and 2.1%, respectively. In addition, only pixels with more than 90% water or fat, respectively, are used for the binary maps, in which case the errors are even smaller. These results suggest that errors in the Dixon decomposition caused by temperature changes during thermal ablation are minor and a Dixon decomposition can indeed be used to generate the binary maps used in modified referenceless reconstruction.

Fig. 3.

Dixon reconstructed water image (left) and fat image (middle) of the simulated phantom. Error in the water/fat decomposition are caused by the temperature change. The error map (right) shows the error of the real compared to the ideal water decomposition.

Fig. 4.

Plot of the ideal (dotted line) and actual (solid line) water decomposition as a function of temperature for different water fractions (as labeled).

B. Phantom Experiment with Zero Degree Temperature Rise

The results of the first phantom experiment are summarized in Table I. The table shows mean and standard deviation of temperature maps reconstructed with conventional baseline subtraction, referenceless reconstruction, and modified referenceless reconstruction for different echo times. No results are given for the out-of-phase echo time with the unmodified referenceless reconstruction, because this method requires an in-phase echo time. Both the subtraction method and modified referenceless method measure the zero degree temperature rise for all echo times consistently. The unmodified referenceless method, however, underestimates the temperature by several degrees. In addition, the computed temperature varies for small changes in echo time. This shows the sensitivity of the unmodified referenceless method to deviations of the exact in-phase condition which create phase gaps between water and fat that hamper the phase estimation. Comparing the standard deviation of the modified referenceless reconstruction with the subtraction methods shows similar values for all echo times.

TABLE I.

Comparison of accuracy of temperature reconstruction with baseline subtraction, previous referenceless reconstruction and modified referenceless reconstruction. The table shows mean and standard deviation of the temperature change measured with the three different methods for various echo times. No results are given for the out-of-phase echo time with unmodified referenceless reconstruction, because this method requires an in-phase echo time. The results show that even small deviation from the exact in-phase echo time cause temperature measurement errors in the unmodified referenceless method.

Echo Time (ms)	Baseline Subtraction		Referenceless Reconstruction		Mod. Referenceless Reconstruction
	mean	std	mean	std	mean	std
TE1 = 14.0	0.6	2.1	−4.7	3.1	−0.4	2.1
TE1 = 14.3	0.1	2.0	−3.2	2.5	0.0	2.0
TE1 = 14.6	0.2	2.0	−2.5	2.1	−0.8	1.9
TE2 = 21.0	−0.2	2.0	—	—	1.2	3.7
TE2 = 21.4	−0.5	2.2	—	—	1.3	4.3
TE2 = 21.9	1.2	1.8	—	—	0.7	3.6
TE3 = 28.0	0.7	1.5	−3.1	2.3	−0.2	2.0
TE3 = 28.6	−0.3	1.8	−1.5	1.9	−0.1	1.9
TE3 = 29.2	−0.1	1.5	0.4	2.1	0.3	2.1

C. Phantom Experiment with Ultrasound Heating

For our second phantom experiment, we used a lower threshold to generate the binary maps, because we found that the bovine muscle tissue contained a relative large fraction of fat (10–20%). The threshold was lowered such that all pixels in the muscle tissue appeared in the binary water image. The presence of fat in pixels used for temperature measurement causes errors that are dependent on the echo time and the fraction of fat in the pixel. Because this problem of fat contamination is fundamental to the PRF method and not to the individual reconstruction methods, it is not further discussed in this paper. Moreover, in the targeted application for modified referenceless reconstruction, the thermal ablation of prostate tissue, the problem of fat contamination does not occur because the prostate gland is lipid free.

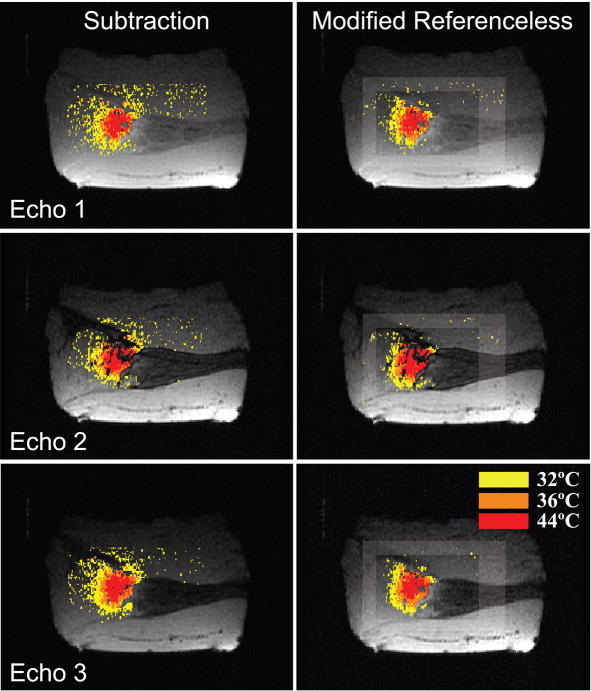
Therefore, we limit our investigation to comparing the modified referenceless method and the conventional baseline subtraction method in this experiment. Temperature maps acquired during heating are shown in Fig. 5. The images reconstructed with conventional baseline subtraction and modified referenceless reconstruction are very similar for all three echoes. The results show that temperature measurements with the modified referenceless reconstruction are indeed comparable to the subtraction method in cases without tissue motion.

Fig. 5.

Temperature maps measured in a meat phantom during heating with an ultrasound applicator (color images in the online edition). The images on the left are reconstructed with baseline subtraction, images on the right are reconstructed with the modified referenceless method. The temperature maps show the same time frame, but are reconstructed from the first, second, and third echo; the frame ROIs used for modified referenceless reconstruction are shown on the right. The images show that subtraction and modified referenceless method provide very similar results in a stationary phantom. Note that no temperature change is detected in the fat layer (dark band running horizontally), because the PRF in lipids does not change with temperature.

D. Canine Prostate Ablation

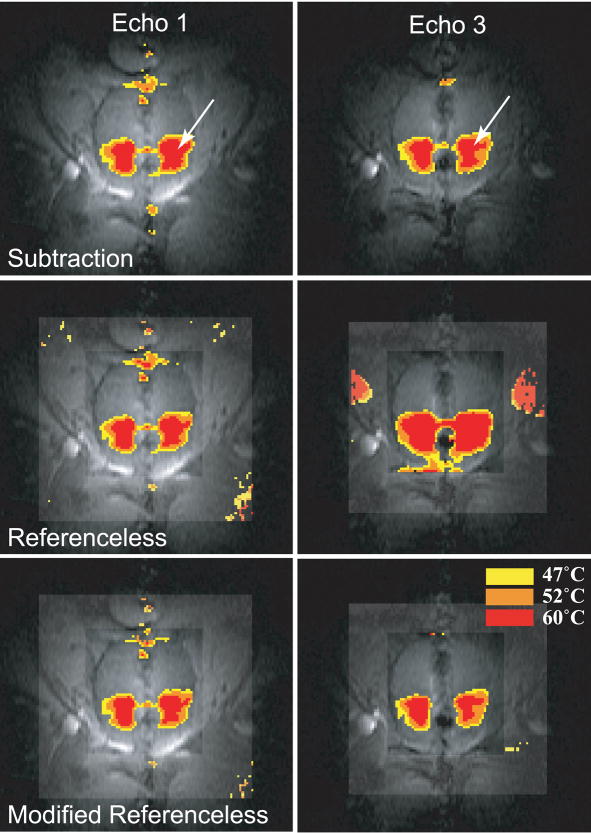
Images of five in vivo ablation experiments were acquired and reconstructed using baseline subtraction, conventional and modified referenceless reconstruction. In all experiments, the optimal polynomial order, which minimizes the temperature uncertainty in the inner region, was determined before heating started and found to be four or five (a detailed description on the process of determining the optimal polynomial order is given elsewhere [13]). Figures 6 and 7 display temperature distributions created by a transurethral ultrasound applicator consisting of two multi-sectored, tubular transducers [28], [30]. Figure 6 shows temperature maps reconstructed from a coronal slice through the prostate. The left column shows images from TE₁, the right column from TE₃. Because both echoes are acquired in the same acquisition, their temperature maps should be very similar. This is true for the subtraction method and the modified referenceless reconstruction, but clearly not the case for the unmodified referenceless method. For the short echo time TE₁, the unmodified method gives reasonable temperature maps, but at the longer echo time TE₃, larger phase gaps between water and fat result in a poor temperature estimation. Temperature measurements with baseline subtraction and modified referenceless reconstruction give similar results. There are some artifacts in the phase encode direction (superior/inferior) due to flow in the transurethral US applicator.

Fig. 6.

Temperature maps reconstructed from the first (left column) and third echo (right column). The unmodified referenceless method (middle row) suffers from phase gaps between water and fat in the third echo, whereas the modified referenceless method is not affected. Comparing baseline subtraction and modified referenceless reconstruction shows that both methods measure very similar temperatures and heating patterns in this experiment where no tissue motion was observed. Both methods display some artifacts from cooling water flow in the transurethral US applicator.

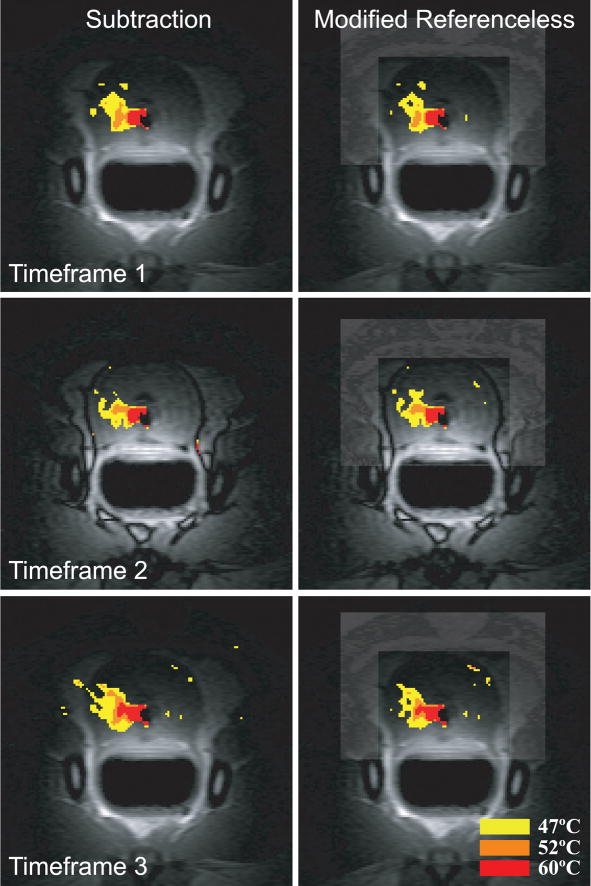
Fig. 7.

Temperature maps acquired during canine prostate ablation with a transurethral ultrasound applicator. No tissue motion was observed in this experiment. The images are reconstructed from three consecutive time frames using baseline subtraction (left column) and modified referenceless reconstruction (right column). The first and third time frame use the in-phase echoes, the second time frame uses the out-of-phase echo for temperature reconstruction. The modified referenceless reconstruction provides accurate temperature measurements in both in-phase and out-of-phase images, very similar to those measured with baseline subtraction.

Temperature maps in Fig. 7 are constructed from three consecutive time frames during heating. Because TE₁ and TE₃ are acquired in the same acquisition, their temperature maps can be combined in a single map, increasing the image SNR and reducing the temperature uncertainty. The first and third time frame are reconstructed from TE₁ and TE₃, the second time frame shows the temperature map from TE₂. Because no tissue motion was present in this experiment, temperature maps reconstructed with baseline subtraction and modified referenceless reconstruction are very similar.

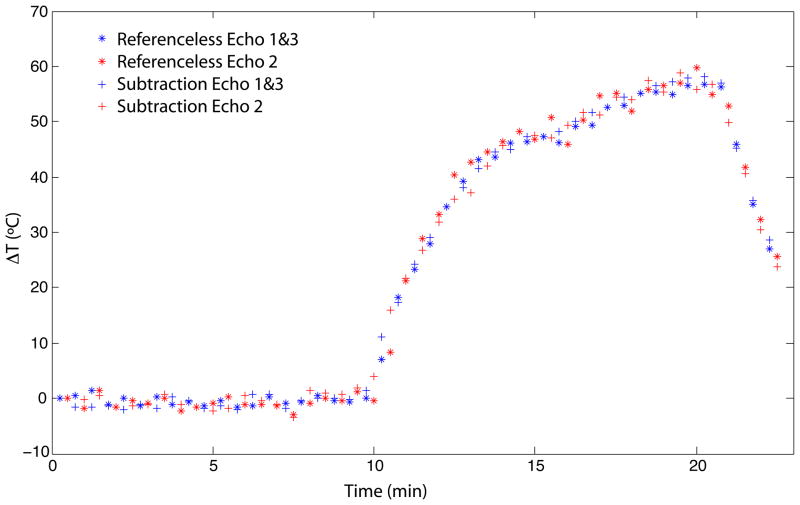
Figure 8 shows the temperature time course of a pixel near the center of the heating area, shown by the white arrow in Fig. 6, reconstructed with the modified referenceless reconstruction and with baseline subtraction. No heat was applied during the first ten minutes of the experiment. This data was used to calculate the temperature uncertainty of the methods in the different echoes. The temperature uncertainty in TE₁ and TE₃ (combined) was approximately 1.0°C for both methods and in TE₂ 1.3°C for baseline subtraction and 1.4°C for modified referenceless reconstruction.

Fig. 8.

Temperature time course of a pixel near the center of the heating area (shown by the white arrow in Fig. 6) comparing modified referenceless reconstruction and baseline subtraction. Heating started after ten minutes and was applied for ten minutes. Measurements in in-phase and out-of-phase echoes and with both methods correlate well.

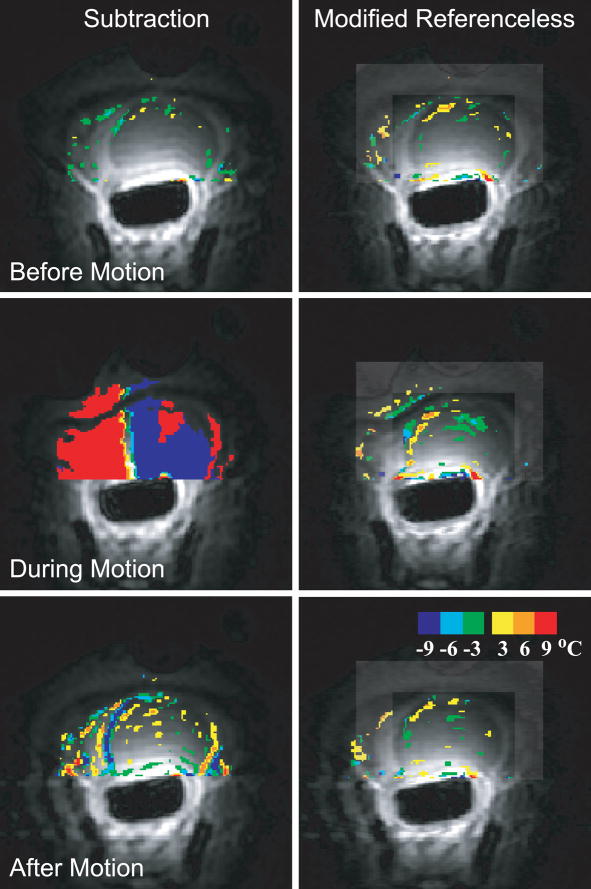
Figure 9 shows images of the canine prostate acquired before heating in the presence of tissue motion, comparing modified referenceless reconstruction and baseline subtraction. Without tissue motion (upper row), both temperature images are similar. When motion occurred (middle row), images reconstructed with baseline subtraction did not provide any useful temperature information, whereas images reconstructed with modified referenceless reconstruction have little artifact. After the motion (bottom row), an artifact remains in the baseline subtraction images, because the prostate did not return to its original position.

Fig. 9.

Temperature images acquired during preheating comparing modified referenceless reconstruction and baseline subtraction. Before motion, the temperature maps are similar (upper row). When tissue motion occurs (middle row), severe errors render baseline subtraction useless. After motion (bottom row), artifacts remain with baseline subtraction but are not as prevalent in the modified referenceless method.

VI. Discussion

The modified referenceless algorithm presented in this paper allows for temperature estimation in the presence of phase discontinuities between water and fat and takes advantage of both aqueous and adipose tissues present in the frame ROI. The results have shown that in cases without tissue motion temperature measurements with baseline subtraction and modified referenceless reconstructions give similar results that are better than the unmodified referenceless method which performs poorly when phase gaps are present. In situations where tissue motion is present causing temperature measurements with baseline subtraction to fail, the modified referenceless method can still provide reliable temperature measurements.

In the current implementation of the referenceless algorithm, images are reconstructed and displayed off-line in MatLab (MathWorks, MA). Reconstruction times vary with the polynomial order for the phase fit, but are in the order of several seconds, e.g., approximately 3 s for a 5th order polynomial, including the Dixon decomposition, generation of binary maps, phase unwrapping and phase fit for all three echoes. Implementing the referenceless algorithm in C will allow for a decrease in reconstruction time to that required for real-time temperature monitoring.

In the modified referenceless method Dixon decomposed water and fat images are used to create binary maps. For this application, $T_2^{\ast }$ decay between the echoes was not taken into account for the Dixon decomposition, since it did not affect the binary masks, even in regions of with higher susceptibility changes close to the US applicator. For the binary masks only pixels that exceed a certain water/fat ratio are used; all other pixels are excluded. We used a threshold ratio of 90% in the prostate experiments. This ratio resulted in binary maps that included all pixels in the prostate and most pixels in the frame ROI with the exception of pixels at the water/fat interfaces. Depending on the SNR of the images, the threshold ratio can be adjusted to include a sufficient number of pixels for the polynomial fit. Using a binary map works well in the prostate because the prostate gland and the surrounding fatty and aqueous periprostatic tissue form discrete regions, where the majority of pixels contain only water or fat and little heterogeneity is observed. On the other hand, use of this method in more heterogeneous tissues, where the majority of pixels contain varying amounts of water and fat (e.g. breast tissue) will require further development of the reconstruction algorithm.

For the 3pt-Dixon decomposition used in this work, images are acquired at echo times where the phase angle between water and fat are 2π, 3π, and 4π, respectively. This means, that although the modified referenceless algorithm can reconstruct images acquired at all echo times, the Dixon decomposition still restricts the choice of TEs. However, another promising water/fat decomposition algorithm allows for a variable choice of echo times [31]. A more flexible choice of echo times could be used to minimize the uncertainty in the temperature maps by choosing the echo time $TE=T_2^{\ast }$ or to avoid an echo time where water and fat are out-of-phase, such that the phase unwrapping algorithm does not have to be modified to be able to handle the π-phase gaps between water and fat.

Since fat and water areas are handled separately in the reconstruction, it is also possible to correct the phase in fatty regions for spatial shift due to chemical frequency shift before the polynomial fit [29]. With a bandwidth of 12.5 kHz or higher and a maximum of 256 readout samples in our experiments, the chemical shift of fat is less than 0.7 pixels and a correction was not found to be necessary. However, at higher field strength or lower bandwidth, a correction might be useful.

In the in vivo ablation experiments, the three different echoes were acquired in one or two acquisitions. In both cases, all echoes acquired in the same acquisition are combined into a single temperature map. Measuring the temperature uncertainty of the combined temperature map showed that averaging the echoes compensates for most of the SNR decrease due to the higher bandwidth in the individual echoes. In other words, the temperature uncertainty was comparable with that of a single echo sequence with longer readout time. If two image acquisitions are used to acquire the three echoes necessary for the 3pt-Dixon decomposition, the binary masks are updated every second image. However, since motion experienced during prostate ablation is small from image to image, the same binary mask can be used for the reconstruction of two consecutive temperature maps. Errors introduced by the delayed update of the binary maps are small compared to baseline subtraction errors and do not propagate through the image set. Because temperature measurements can be made from each acquisition, the temporal resolution of the thermal measurements is not compromised. If all three echoes are acquired in a single acquisition as in the fifth in vivo ablation experiment, the binary maps are updated constantly, but a decrease in readout resolution is necessary due to the limited gradient performance on our system. However, it has been shown that due to the relatively low spatial resolution of the heating distribution it is sufficient to acquire a low resolution image for temperature monitoring (1.7–1.9 mm in plane) [32], which can easily accomplished with the proposed pulse sequence.

Since the echoes are acquired at different echo times, the temperature uncertainty in images acquired at the three echo times is different. Temperature uncertainty decreases with increasing TE, reaches a minimum at $\text{TE}=T_2^{\ast }$, then increases again due to decreasing SNR. Depending on the uncertainty in the three echoes, a weighted average results in the lowest uncertainty in the combined image. We currently combine with equal weights, but the weights could be calculated by measuring $T_2^{\ast }$ or by measuring the temperature uncertainty directly in the pre-heating images.

As described in the reconstruction algorithm section, the frame ROI needs to contain at least a small region of aqueous tissue to determine the phase offset between water and fat. This region of aqueous tissue remains at body temperature and the temperature change is estimated with respect to body temperature. This has to be taken into account when the body temperature changes during anesthesia (which is usually monitored) and corrected to avoid overestimation or underestimation of the temperature change.

The presence of a heating applicator in the treatment area may cause a local magnetic field change and thus a phase variation near the device that results in artifacts in the temperature map. Whereas laser and extra-corporeal focused ultrasound ablation cause little or no artifact in the temperature images, interstitial or transurethral ultrasound applicators and RF-ablation probes may cause artifacts [33] that could substantially interfere with the temperature estimation. Artifacts created by the presence of the transurethral ultrasound applicators in these experiments made it necessary to correct temperature measurements obtained with referenceless reconstruction. The acquisition of an artifact map from pre-heating images and subsequent subtraction of the artifact during thermal treatment eliminates distortions from the applicator in the temperature maps and recovers the measured temperatures [29]. Shifting the applicator changes the position of the artifact, but its spatial distribution with respect to the center of the applicator remains identical. Therefore, if motion of the applicator occurs during treatment, tracking of the applicator is needed to correctly subtract the artifact. This might appear to introduce the same problem with motion that the subtraction method suffers from, which could also be corrected for shifts of the image with respect to the baseline image. However, tissue motion not only causes a mis-registration to the pre-heating image, but also changes the background magnetic field non-uniformly. These changes in magnetic field cannot be corrected using the conventional baseline subtraction method, but are detected by the referenceless reconstruction. The phase variation caused by the applicator does not change with translational motion and can, therefore, be eliminated from the images.

The temperature reconstruction method presented in this paper is an extension to the original referenceless method to allow US thermal ablation in the prostate. A limitation of the method is the required user interaction to select the appropriate ROIs before the ablation procedure starts, which is not the case for the baseline subtraction method. Compared to the original referenceless method, the reconstruction proposed here requires the acquisition of additional images to get information about the water and fat composition and needs the temperature reconstruction of three images (including the phase unwrapping of the images); the method is, therefore, computationally more intensive. However, when baseline subtraction fails in the presence of tissue motion, the referenceless method still provides accurate temperature measurements, justifying the more demanding reconstruction algorithm. Although the number of in vivo experiments performed was limited, we believe that the method has advantages in the presence of tissue motion. Additional experiments will be necessary to evaluate if the new method can reliably measure temperature changes in all situations in the prostate.

VII. Summary and Conclusion

We have presented an extension to referenceless PRF shift thermometry that allows background phase estimation in the presence of phase discontinuities between aqueous and adipose tissue. The reconstruction algorithm automatically determines aqueous and fatty regions using a Dixon decomposition, making this method applicable to real-time temperature monitoring. In this modified referenceless reconstruction, the background phase is estimated from both water and fat, allowing for a constant phase offset between the two tissues. In addition, data from adipose regions inside the inner ROI can now automatically be included in the polynomial fit, because the PRF of fat is constant with temperature. Temperature estimation with the extended referenceless algorithms was demonstrated during in vivo canine prostate ablation. The results show that the new method can reliably detect temperature changes and is more accurate in the presence of tissue motion than the subtraction of baseline images.