A diffusional bimolecular propensity function

Abstract

We derive an explicit formula for the propensity function (stochastic reaction rate) of a generic bimolecular chemical reaction in which the reactant molecules move about by diffusion, as solute molecules in a bath of much smaller and more numerous solvent molecules. Our derivation assumes that the solution is macroscopically well stirred and dilute in the solute molecules. It effectively extends the physical rationale for the chemical master equation and the stochastic simulation algorithm from well-stirred dilute gases to well-stirred dilute solutions, with the former becoming a limiting case of the latter. This extension is important for cellular systems, where the solvent molecules are typically water and the solute (reactant) molecules are much larger organic structures, whose relatively low populations often require a discrete-stochastic formalism. In the course of our derivation, we illuminate some limitations on the ability of the classical diffusion equation to accurately describe how a diffusing molecule moves on spatial and temporal scales that are relevant to collision-induced chemical reactions.

INTRODUCTION

In order to evolve a chemically reacting system in time in a “memoryless” way using as state variables only the molecular populations (or concentrations) of the reactant species, the system must remain, at least to a good approximation, spatially homogeneous, either through the natural motions of the molecules or by some exogenous means. That is because deviations from spatial homogeneity will alter the firing rates of the reactions in deviation-specific ways, and the population changes that result from the reactions may in turn alter the spatial inhomogeneities. So for chemical systems that are not kept spatially homogeneous, it will be necessary to (i) augment the molecular population variables with additional state variables that accurately characterize the spatial inhomogeneities, (ii) deduce from the underlying microphysics the equations that govern the joint evolution of all those variables, and (iii) solve those equations. This is a very challenging task. In extreme cases, it will require meticulously tracing the trajectories of the reactant molecules as they move, collide, and chemically react, somewhat in the manner of a “molecular dynamics” simulation.

Avoiding all that is, of course, why theorists and modelers like to work with spatially homogeneous systems. For such systems, stochastic chemical kinetics, as embodied in the chemical master equation (CME) and the stochastic simulation algorithm (SSA), provides a rigorous mathematical framework¹ for evolving the molecular populations in a memoryless way, provided the following is true: With x_i denoting the molecular population of species S_i, if the system is given to be in state x={x_i} at the current time t, then the probability that reaction channel R_j will fire somewhere inside the system in the next infinitesimal time interval [t,t+dt) has the mathematical form a_j(x)dt. When that is true, the function a_j is called the propensity function of reaction channel R_j. Only if all reaction channels have propensity functions will the CME and the SSA be valid. This caveat also applies to the deterministic reaction rate equation (RRE)—the set of coupled ordinary differential equations traditionally used to describe how the species concentrations evolve in time—because the RRE finds its rigorous justification at the large-population limit of the CME and the SSA.² Therefore, whether a given reaction channel in a given physical setting has a propensity function, and if so what the mathematical form of that propensity function is, are important questions for chemical kinetics. These questions cannot be answered by mathematical hypothesizing; they must be answered by looking to the physics of molecular behavior.

Unimolecular reactions are of course insensitive to the spatial distribution of the reactant molecules. The problem is with bimolecular reactions such as

$$S_1+S_2\to \text{products},$$ (1)

since their two reactant molecules must find and collide with each other before they can react. In this paper, we will be concerned with reaction (1) only when the system is macroscopically well stirred and dilute. By macroscopically well stirred, we mean that on the scale of the system volume Ω, the molecules of each reactant species appear to have a randomly uniform spatial distribution, but on the much smaller scale of the average distance between those molecules, spatial inhomogeneities are allowed. By dilute, we mean that we can find a neighborhood around each reactant molecule which is large compared to the molecule itself but small compared to Ω, and which is only rarely occupied by a second molecule of the same species.

We will also assume that our system is “at temperature T.” This means that each rectilinear component of the velocity of a randomly chosen molecule of species S_i can mathematically be regarded as a normal (Gaussian) random variable with mean 0 and variance k_BT∕m_i, where k_B is Boltzmann’s constant and m_i is the molecule’s mass. This implies that each rectilinear component of the velocity of a randomly chosen S₁ molecule relative to a randomly chosen S₂ molecule is normally distributed with mean 0 and variance k_BT∕m₁₂, where m₁₂≡m₁m₂∕(m₁+m₂).³ That in turn can be shown to imply that the average speed of an S₁ molecule relative to an S₂ molecule is⁴

$${\overline{v}}_{12}=\sqrt{\frac{8k_{\text{B}}T}{\pi m_{12}}}.$$ (2)

With respect to reaction 1, we suppose that an S₁ molecule and an S₂ molecule can be said to “collide” whenever their center-to-center distance decreases to some value σ₁₂>0. (If the molecules were hard spheres, σ₁₂ would be the sum of their radii.) We further suppose that, if a collision does occur, then with probability $q=q\left({\overline{v}}_{12}\right)$ reaction (1) will immediately follow. Notice that q as thus defined is the probability that a randomly chosen pair of S₁ and S₂ molecules will react according to Eq. 1given that they have just collided and were selected from a population of pairs that have average relative speed ${\overline{v}}_{12}$. The latter condition is, by Eq. 2, a consequence of the molecules being at temperature T. For example, in the circumstance that a colliding S₁-S₂ pair will react if and only if their “collisional kinetic energy” (the kinetic energy associated with the “head-on component” of their relative velocity, the component along their line of centers at contact) exceeds a certain threshold value E_t, it can be proved^{4, 1} that q=exp(−E_t∕k_BT), which is the famous Arrhenius factor. However, for our purposes here we will make no assumptions about the form of q, except to acknowledge that it usually depends on ${\overline{v}}_{12}$ (or T).

If the S₁ and S₂ molecules were moving about inside Ω “ballistically” as in a dilute gas, so that their trajectories are straight lines broken only by collisions with the container walls and (much less frequently) with each other, then as detailed in Appendix A, the well-stirred assumption allows a simple but rigorous derivation of a propensity function for reaction 1. The result is

$$a\left(x_1,x_2\right)=\left(\frac{\pi {\sigma }_{12}^2{\overline{v}}_{21}q}{\Omega }\right)x_1{x}_2\left(\text{ballistic}\right).$$ (3)

The “rigor” of the derivation of this result in Appendix A stems from the facts that (i) it does not approximate averages of products by products of averages, (ii) its mathematical inferences invoke only the laws of probability, (iii) it never has to imagine that any one molecule reacts more than once, and (iv) it never has to imagine that reactions occur in noninteger (e.g., infinitesimally small) numbers. An inspection of this derivation will reveal that it ultimately hinges on the fact that, in any infinitesimal time dt, a molecule will move a distance that is proportional to dt. That is what leads to the result that the probability for the reaction to fire in the next dt is proportional to dt, as is required by the definition of the propensity function.

In this paper, we will focus on a situation that is much more typical of cellular systems, which of course are practically never dilute gases. We will assume that the S₁ and S₂ molecules are solute molecules that diffuse, with respective diffusion coefficients D₁ and D₂, in a common bath of chemically inert solvent molecules (see Fig. 1). We will also assume that the solvent molecules are much smaller, lighter, and more numerous than the solute molecules, a situation that characterizes many cellular systems where the solvent molecules are water molecules and the solute molecules of interest are much larger. In such a solvent bath, a solute molecule will experience very many collisions with solvent molecules between successive collisions with other solute molecules, but the effect on the solute molecule of any one of those solvent molecule collisions will be very small. This type of “Brownian” diffusion is to be distinguished from “self-diffusion,” where the solvent molecules are physically identical to the solute molecules.

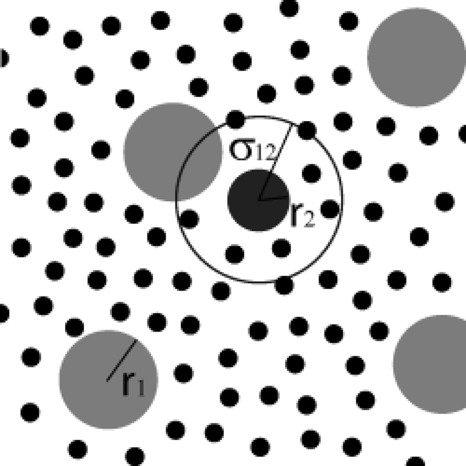
Figure 1.

An S₂ molecule (the dark gray disk) surrounded by its “action sphere” relative to the S₁ molecules (the light gray disks). Both species are “solute” molecules that move about by diffusion in a sea of very many much smaller “solvent” molecules (the small dark disks). Of interest are collisions of the S₂ molecule with any S₁ molecule, an event that happens when the center of some S₁ molecule touches the surface of the action sphere.

The traditional way of mathematically describing diffusional molecular motion is based on the classical diffusion equation. A well known consequence of that equation is that the root-mean-squared displacement in any time Δt of a molecule with diffusion coefficient D will be of the order of $\sqrt{D\Delta t}$. This result has long been thought to pose a problem for deriving a diffusional propensity function, since an analysis along the lines of the ballistic derivation in Appendix A would seem to lead to the conclusion that the firing probability of reaction 1 in time dt is proportional to $\sqrt{dt}$ instead of dt. If that were true, then the mathematical assumptions made in deriving the CME and the SSA would indeed be compromised.

In Sec. 2, we will explain why the $\sqrt{D\Delta t}$ prediction of the diffusion equation does not preclude the existence of a diffusional propensity function for reaction 1. In Secs. 3, 4, 5 we will derive, using a line of reasoning that is very different from that employed in Appendix A, an explicit formula for the diffusional propensity function. Our derivation owes much to the pioneering analysis of diffusion-controlled reaction rates of Collins and Kimball (CK).⁵ But, as we elaborate in Sec. 6, our analysis takes a different approach which yields a more specific result, and which in the end is more rigorous because it takes proper account of the intrinsic discreteness and stochasticity of what transpires at the molecular level. Our result shares with the Collins–Kimball result the satisfying feature that it smoothly segues to the dilute gas result, in our case Eq. 3, in an appropriate limit of the physical parameters.

SOME RELEVANT FACTS ABOUT THE DIFFUSION EQUATION

The traditional centerpiece of diffusion theory is the diffusion equation:

$$\frac{\partial \rho \left(\mathbf{r},t\right)}{\partial t}=D{\nabla }_{\mathbf{r}}^2\rho \left(\mathbf{r},t\right).$$ (4)

Here, ρ(r,t) is the average number of diffusing (solute) molecules per unit volume at point r at time t, and D is the diffusion coefficient of those molecules relative to the solvent molecules. The traditional “macroscopic” derivation of this equation starts with the continuity equation

$$\frac{\partial \rho \left(\mathbf{r},t\right)}{\partial t}=-{\nabla }_{\mathbf{r}}•\mathbf{J}\left(\mathbf{r},t\right),$$ (5)

which expresses the fact that matter is neither created nor destroyed by diffusion. Here, the net fluxJ(r,t) is defined so that its component $\hat{\mathbf{n}}•\mathbf{J}\left(\mathbf{r},t\right)$ in the direction of the unit vector $\hat{\mathbf{n}}$ gives the average net number of molecules per unit time crossing a unit area normal to $\hat{\mathbf{n}}$, and in the direction of $\hat{\mathbf{n}}$, at point r at time t; by “net” we mean the average number passing in the direction $\hat{\mathbf{n}}$minus the average number passing in the direction $-\hat{\mathbf{n}}$. The next step in the derivation is to assume the validity of Fick’s Law,

$$\mathbf{J}\left(\mathbf{r},t\right)=-D{\nabla }_{\mathbf{r}}\rho \left(\mathbf{r},t\right),$$ (6)

an empirical relation that effectively defines the diffusion coefficient D. Substituting Eq. 6 into Eq. 5 immediately yields the diffusion Eq. 4.

Before it was widely accepted that a fluid consists of many moving molecules, Eqs. 4, 5, 6 were regarded as statements in continuum mechanics. The kinetic molecular hypothesis was elevated to general acceptance by Einstein’s famous analysis of Brownian motion in 1905 (Ref. ⁶) and its subsequent experimental confirmation by Perrin and others. Einstein essentially rederived the diffusion Eq. 4 from a model of random molecular motion instead of from Eqs. 5, 6. In so doing, he shifted the focus from the behavior of a collection of many solute molecules to the behavior of an individual solute molecule. From a modern perspective, the key result of Einstein’s analysis was that ρ(r,t) in the diffusion equation, if renormalized to unity, can be regarded as the probability density function (pdf) of the position of an individual solute molecule at time t. That leads immediately to the conclusion that, if the x-component of the solute molecule at time 0 is known to be x₀, then, assuming that the motion of the molecule is unrestricted, its x-component at any time t>0 will be the normal random variable with mean x₀ and variance 2Dt. In symbols,

$$X\left(t\right)=\mathcal{N}\left(x_0,2Dt\right)\left(t>0\right).$$ (7)

Similar formulas hold for the y- and z-components of the solute molecule’s position, with those three components being statistically independent of each other.

The result 7 implies that, in any time t, each rectilinear component of the solute molecule’s position will suffer a mean-squared displacement of 2Dt. That in turn implies a root-mean-squared total displacement of $\sqrt{4Dt}$ in two dimensions and $\sqrt{6Dt}$ in three dimensions. Equation 7 also implies, because of the mathematical fact that N(m,σ²)≡m+σN(0,1), that if the diffusing molecule is at point (x_t,y_t,z_t) at time t, then its coordinates at any later time t+Δt can be computed as

$$x_{t+\Delta t}=x_t+\sqrt{2D\Delta t}{n}_x,$$ (8a)

$$y_{t+\Delta t}=y_t+\sqrt{2D\Delta t}{n}_y,$$ (8b)

$$z_{t+\Delta t}=z_t+\sqrt{2D\Delta t}{n}_z,$$ (8c)

where n_x, n_y, and n_z are independent samples of N(0,1), the normal random variable with mean 0 and variance 1. Formulae 8, or some mathematically equivalent version thereof, are routinely used by modelers to numerically generate Δt-separated points along the trajectory of a diffusing molecule.

Einstein’s analysis contained, however, a caveat, which he duly noted but which is not always accorded the full measure of attention that it deserves. Einstein’s derivation of the diffusion equation, and hence also of formulae 8, makes the assumption that any considered time increment must be large enough that the solute molecule will experience in that time very many collisions with solvent molecules.⁶ For many purposes this restriction is not a problem, since even time increments that are very small from a macroscopic point of view will usually be large enough to satisfy that condition. But the fact that Eq. 8 lacks a physical justification for Δtarbitrarily small, even though those equations are mathematically exact consequences of the diffusion Eq. 4 for all Δt, gives rise to two significant limitations. First, we cannot use Eq. 8 to compute a physically reliable velocity of a diffusing molecule, because that would require taking the limit Δt→0. Second, we have no physical license to use Eq. 8 to construct a finely resolved trajectory of a diffusing molecule, because that too would require taking Δt arbitrarily small.

That these two limitations in fact have serious consequences is made clear by the following result, which is proved in Appendix B. If we use Eq. 8 to construct an “n-point trajectory” of a diffusing molecule over a finite time interval [0,τ], by taking Δt=τ∕n and then computing the positions of the molecule at the n−1 intermediate times Δt,2Δt,…,(n−1)Δt, we will find that the length of the resulting trajectory increases without bound as n is increased. More precisely, each doubling of n increases the average length of the trajectory by a factor of 2. Therefore, the average length of the “true” trajectory, namely, the “fully resolved” trajectory that is obtained in the limit n→∞ is infinite. So according to Eq. 8, a diffusing molecule traverses an infinitely long path in a finite time. That of course would imply that the molecule travels with infinite speed, a conclusion that can also be seen from Eq. 8:

$$\frac{dx}{dt}\equiv \underset{\Delta t\to 0}{\text{lim}}\frac{x_{t+\Delta t}-x_t}{\Delta t}=\underset{\Delta t\to 0}{\text{lim}}\frac{\sqrt{2D\Delta t}{n}_x}{\Delta t}=n_x\underset{\Delta t\to 0}{\text{lim}}\sqrt{\frac{2D}{\Delta t}}=\pm \infty .$$ (9)

This picture of a diffusing molecule moving with infinite velocities, and hence infinite energies, and experiencing infinite accelerations as its velocity components switch infinitely rapidly between +∞ and −∞, is of course totally incompatible with any accepted physical theory of motion for a mass particle. It is important to understand that this bizarre behavior cannot be dismissed as an unimportant side effect of the “infinite tails” of the Maxwell–Boltzmann distribution for the velocity of a molecule at temperature T: The Maxwell–Boltzmann distribution implies an average speed that is finite (of the order of $\sqrt{k_{\mathrm{B}}T∕m}$ where m is the molecule’s mass), whereas the result obtained in Appendix B for Eq. 8 implies an average speed that is infinite.

We are accustomed in science and engineering to numerically solving ordinary differential equations of the form dx(t)∕dt=A(x(t)) by using the Euler formula, x(t+Δt)=x(t)+A(x(t))Δt, or some refinement thereof, always with the assurance that we can get as accurate a solution as we require simply by taking Δt “small enough.” It is therefore tempting to look at formulae 8 in the same way. But the situation with formulae 8 is fundamentally different. Even though those formulas represent the diffusion Eq. 4 exactly for all Δt, they provide a physically accurate description of the motion of a diffusing molecule only if Δt is “sufficiently large.” As we take Δt smaller and smaller in Eqs. 8, the resulting more finely resolved representation of the trajectory of the diffusing molecule becomes less and less physically accurate, and eventually it becomes physically absurd. Making matters worse, there is nothing in the Einstein derivation of Eq. 8, nor in the earlier macroscopic derivation of the diffusion Eq. 4, that tells us quantitatively when Δt has been chosen “sufficiently large.”

These difficulties with Einstein’s approach to diffusion were effectively resolved by Langevin’s analysis of Brownian motion in 1908,⁷ although that fact was not fully appreciated at the time. By making some insightful assumptions about the nature of the forces exerted on a solute molecule by the surrounding solvent molecules, Langevin used Newton’s second law and some thermodynamic reasoning to obtain a time-evolution equation for the velocity of the solute molecule (in contrast with Einstein’s focus on the molecule’s position). A modern version of that analysis⁸ leads to two results that are especially pertinent to our work here:

First, the Langevin approach reveals that formulae 7, 8 are physically accurate only when

$$t,\Delta t⪢\frac{mD}{k_{\text{B}}T},$$ (10)

where T is the absolute temperature of the system. Formulae 7, 8 therefore do have a wide range of validity, since the right side of Eq. 10 is typically small from a macroscopic point of view. But the fact that the right side of Eq. 10 is not zero means that formulae 8 indeed cannot provide us with physically reliable information about either the velocity or the true trajectory of a diffusing molecule. In particular, the popular notion that ever smaller choices for Δt in formulae 8 will produce ever more accurate representations of the trajectory of the diffusing molecule is wrong.

Second, in Langevin’s improved theory, a diffusing molecule always has a finite mean speed, roughly of the order of $\sqrt{k_{\mathrm{B}}T∕m}$, where m is the molecule’s mass. It follows that in a truly infinitesimal time dt, a diffusing molecule will travel a total distance that is proportional to dt. This does not contradict Einstein’s result that the net displacement of the molecule over a sufficiently large time Δt is proportional to $\sqrt{\Delta t}$, because the net displacement of the molecule and the total distance traveled by the molecule in realizing that net displacement are not the same thing. The latter will usually be much larger than the former, because the trajectory of the molecule over that time will be highly irregular and folded.

However, in chemical kinetics we usually do want to work on timescales where “dt” is large enough to encompass many collisions of a solute molecule with solvent molecules. In that case, as we have just seen, even though the net displacement of a solute molecule in time dt will indeed be proportional to $\sqrt{dt}$, that net displacement will not be the total distance traveled by the molecule; therefore, the concern mentioned in Sec. 1 is groundless. But even if we could use the improved Langevin theory to estimate the true distance traveled by the molecule in such a macroscopic dt, it is not clear how that information could be used by an argument along the lines of the ballistic derivation in Appendix A. For, whereas in the ballistic case the effective “collision volume” swept out by the S₂ molecule relative to the S₁ molecule in time dt is easily related to the relative distance traveled in that time, that relation will be much more complicated for irregular, highly folded diffusional trajectories because of the many rapid partial retracings of the same volume.

The bottom line here for our purposes is this: The long-standing concern that the classical $\sqrt{D\Delta t}$ result in diffusion theory might preclude the existence of a diffusional propensity function is baseless, but there seems to be no way to construct a simple derivation of the diffusional propensity function that parallels the ballistic derivation in Appendix A. For that reason, we will take a completely different approach in the diffusional case.

THE AVERAGE DIFFUSIONAL REACTION RATE

We begin by picking at random one of the x₂S₂ molecules inside Ω, and imagining it to be surrounded by two concentric spheres. The smaller sphere has radius σ₁₂; it is called the “action sphere,” because if the center of any S₁ molecule lies on the surface of that sphere the two molecules will be colliding. The larger sphere has a radius Σ₁₂ which, though very large compared to σ₁₂, is very small compared to the dimensions of Ω, and also small enough that the sphere only rarely contains a second S₂ molecule. The possibility of constructing the larger sphere follows from our assumption that the solute molecules are “dilute” inside Ω. Taking the common center of these two spheres as the origin of coordinates, we assume the S₁ molecules to be distributed isotropically in the region between the surfaces of the two spheres, and we let ρ₁(r,t) denote the average number of S₁ molecules per unit volume at distance r (σ₁₂≤r≤Σ₁₂) from the origin at time t. Since the Σ₁₂-sphere is very small compared to Ω, then ρ₁(r,t) may show a dependence on r≤Σ₁₂ without violating our hypothesis that the system is “macroscopically” well stirred.

Relative to the S₂ molecule and its two attached spheres, the x₁S₁ molecules move about with an effective diffusion coefficient,⁹

$$D=D_1+D_2,$$ (11)

at least in the present circumstance where the system is dilute in the solute molecules. So Fick’s law tells us that in the rest frame of the S₂ molecule, the instantaneous net radially outward flux of S₁ molecules at any r∊[σ₁₂,Σ₁₂] is

$$J_1\left(r,t\right)=-D\frac{\partial {\rho }_1\left(r,t\right)}{\partial t},{\sigma }_{12}\le r\le {\Sigma }_{12}.$$ (12)

This implies that the net inward flow of S₁ molecules to the surface of the action sphere is

$${\Phi }_2\left(t\right)=4\pi {\sigma }_{12}^2\times {\phantom{\mid }D\frac{\partial {\rho }_1\left(r,t\right)}{\partial r}\mid }_{r={\sigma }_{12}},$$ (13)

where the subscript 2 is to remind us that this flow pertains to a single S₂ molecule. Since Φ₂(t) is the difference {the average number of S₁ molecules that strike the action sphere in unit time} minus {the average number of S₁ molecules that are reflected by the action sphere in unit time}, then it must be equal to {the average number of S₁ molecules that are absorbed by the action sphere in unit time}. And since absorption by the action sphere is tantamount to a chemical reaction, then Φ₂(t) is the instantaneous average rate at which S₁ molecules are chemically reacting with the chosen S₂ molecule. The logically awkward fact that the S₂ molecule might very well disappear at the first such reaction will be dealt with in Sec. 5.

In order to evaluate the right side of Eq. 13, we evidently need to know the derivative of ρ₁(r,t) with respect to r at r=σ₁₂. Finding ρ₁(r,t) requires solving the diffusion Eq. 4, which in this spherically symmetric case reads

$$\frac{\partial {\rho }_1\left(r,t\right)}{\partial t}=D\frac{1}{r}\frac{{\partial }^2}{\partial r^2}\left(r{\rho }_1\left(r,t\right)\right),\left({\sigma }_{12}\le r\le {\Sigma }_{12}\right).$$ (14)

To solve this equation, we must specify one initial condition and two boundary conditions, and we must do that in a way that is physically appropriate. The initial condition is of course the function ρ₁(r,t=0), and the need to specify it raises the question of what physically defines the instantt=0. For the propensity function of reaction 1, which is our concern here, t=0 should be the instant immediately after the most recent reaction event. But because of the relative isolation of the S₂ molecules inside their individual Σ₁₂-spheres, the average distribution of S₁ molecules inside the Σ₁₂-sphere of the chosen S₂ molecule just after the last reaction event is not likely to be very different from what it was just after the reaction event before that, or the one before that. This observation suggests that a physically reasonable choice for the function ρ₁(r,0) in our case would be the time-stationary solution ρ₁(r) of the diffusion Eq. 14. That choice would in turn imply that

$${\rho }_1\left(r,t\right)\equiv {\rho }_1\left(r\right)\left({\sigma }_{12}\le r\le {\Sigma }_{12};\forall t\right),$$ (15)

where ρ₁(r) is the solution of

$$\frac{{\partial }^2}{\partial r^2}\left(r{\rho }_1\left(r\right)\right)=0\left({\sigma }_{12}\le r\le {\Sigma }_{12}\right).$$ (16)

This is of course an approximation. But it seems a reasonable one in the biochemical context that we are mainly interested in, where the pace of chemical reaction events is usually slow. Situations will undoubtedly arise where this is not an acceptable approximation, and for those the results obtained below will not apply.

Two successive integrations of Eq. 16 yield

$$r{\rho }_1\left(r\right)=\alpha r+\beta ,$$ (17)

where α and β are integration constants. They must be determined by imposing two boundary conditions. An obvious choice for one boundary condition is to require the S₁ concentration “far away” from the surface of the action sphere to be the current “well-stirred” value, x₁∕Ω. Remembering that Σ₁₂⪢σ₁₂, we thus take

$${\rho }_1\left({\Sigma }_{12}\right)=x_1∕\Omega \equiv c_1.$$ (18)

For the second boundary condition, we shall require the S₁ concentration at the surface of the action sphere, ρ₁(σ₁₂), to be some value between 0 and c₁, but we will leave that value unspecified for now. Upon substituting r=σ₁₂ and r=Σ₁₂ into Eq. 17, and using Eq. 18, we get the two equations

$${\sigma }_{12}{\rho }_1\left({\sigma }_{12}\right)=\alpha {\sigma }_{12}+\beta ,$$

$${\Sigma }_{12}{c}_1=\alpha {\Sigma }_{12}+\beta .$$

Upon subtracting the first equation from the second, an then invoking the facts that ρ₁(σ₁₂)≤c₁ and σ₁₂⪡Σ₁₂, we obtain α=c₁. Substituting that result into the first equation then yields β=−σ₁₂(c₁−ρ₁(σ₁₂)). Equation 17 thus becomes

$${\rho }_1\left(r\right)=c_1-\frac{{\sigma }_{12}\left(c_1-{\rho }_1\left({\sigma }_{12}\right)\right)}{r}\left({\sigma }_{12}\le r\le {\Sigma }_{12};{\sigma }_{12}⪡{\Sigma }_{12}\right).$$ (19)

From Eq. 19, it follows that the derivative on the right side of Eq. 13 is

$${\phantom{\mid }\frac{\partial {\rho }_1\left(r\right)}{\partial r}\mid }_{r={\sigma }_{12}}=\frac{c_1-{\rho }_1\left({\sigma }_{12}\right)}{{\sigma }_{12}}.$$ (20)

Notice that Eq. 20 implies that, given the boundary condition 18, if we specify either the value of ρ₁ at r=σ₁₂or the value of ∂ρ₁∕∂r at r=σ₁₂, the other will be uniquely determined; therefore, it really makes no difference which of those two values we specify for the second boundary condition. Substituting Eq. 20 into Eq. 13 gives for the average rate at which S₁ molecules are reacting with the chosen S₂ molecule,

$${\Phi }_2=4\pi {\sigma }_{12}D\left(c_1-{\rho }_1\left({\sigma }_{12}\right)\right).$$ (21)

Here, D is given by Eq. 11 and c₁ is given by Eq. 18; however, the value of ρ₁(σ₁₂), apart from being between 0 and c₁, remains unspecified.

At this point, Smoluchowski’s¹⁰ pioneering approach to this problem simply assumes that ρ₁(σ₁₂)=0, so that the average rate 21 becomes

$${\Phi }_2=4\pi {\sigma }_{12}D{c}_1\equiv {\Phi }_2^{\text{Smol}}.$$ (22)

But taking ρ₁(σ₁₂)=0 implies that every S₁ molecule that strikes the action sphere is immediately absorbed, meaning that reaction 1 ensues, and that should happen only in the case that q=1. Sveshnikoff¹¹ later sought to correct this deficiency by simply multiplying Smoluchowski’s result by q:

$${\Phi }_2=4\pi {\sigma }_{12}D{c}_{1}q\equiv {\Phi }_2^{\text{Sves}}.$$ (23)

But CK (Ref. ⁵) later pointed out that this formula cannot be correct either, because it is self-contradictory: The assumption ρ₁(σ₁₂)=0 that underlies the Smoluchowski result assumes that every S₁ molecule that collides with the action sphere is absorbed, whereas the circumstance q<1 says otherwise. CK (Ref. ⁵) went on to develop a new approach to this problem, and they obtained a result that has many attractive features. Our analysis below is strongly inspired by the CK analysis, and we will obtain a result that is almost the same as theirs; however we will use a very different line of reasoning which, arguably, has a more rigorous physical justification.

We start by noting that the Fick’s Law result 21 only tells what the net inward flow Φ₂ of S₁ molecules at the surface of the action sphere would be if, given an S₁ molecular concentration of c₁=x₁∕Ω far from the action sphere, the S₁ concentration at the surface of the action sphere were ρ₁(σ₁₂). Equation 21 is correct so far as it goes, but it is incomplete in that it does not tell us what the value of either Φ₂ or ρ₁(σ₁₂) is. We will adopt the unorthodox view that this incompleteness of Eq. 21 is an inevitable consequence of the fact that any theory of diffusion based solely on the classical diffusion equation cannot provide a physically accurate description of the behavior of the S₁ molecules on the small space-time scale of the immediate neighborhood of the surface of the action sphere, where the collision and reaction must take place. That’s because (see Sec. 2) the classical diffusion formulas 8 give only net displacements over sufficiently large times Δt, and hence do not describe either the velocity or the trajectory of the S₁ molecule in the final moments before its collision with the action sphere. Clearly the terminal relative velocity and trajectory of the two colliding molecules will be important in determining whether a reaction ensues.

Physical considerations suggest that, in the short span of time immediately preceding the collision of an S₁ molecule with the action sphere, and more specifically when the center of the S₁ molecule is closer to the surface of the action sphere than the mean-free-path of an S₁ molecule with respect to the solvent molecules, the S₁ molecule will be moving freely with a finite velocity. In other words, sufficiently close to the surface of the action sphere, the S₁ molecule will be moving ballistically in the manner of a dilute gas molecule. Embracing this premise, we next recall a well known result from elementary kinetic theory:⁴ In a dilute gas that is in thermal equilibrium with a constant average molecular density ρ, the average number of molecules striking the walls of the containing volume per unit area and per unit time is equal to $\left(1∕4\right)\rho \overline{v}$, where $\overline{v}$ is the average speed of the molecules. In Appendix C, we derive the following extended version of that result for our problem here:

$$4\pi {\sigma }_{12}^2\times \frac{1}{4}{\rho }_1\left({\sigma }_{12}\right){\overline{v}}_{12}=\text{the\hspace{0.5em}average\hspace{0.5em}rate\hspace{0.5em}at\hspace{0.5em}which\hspace{0.5em}}{S}_1\text{\hspace{0.5em}molecules\hspace{0.5em}are}\text{colliding\hspace{0.5em}with\hspace{0.5em}the\hspace{0.5em}surface\hspace{0.5em}of\hspace{0.5em}the}\text{action}\text{sphere}.$$ (24)

Since the average fraction of these collisions that result in a reaction 1 is $q=q\left({\overline{v}}_{12}\right)$, then the average rate at which S₁ molecules are reacting with the chosen S₂ molecule can be obtained simply by multiplying the average collision rate 24 by q. And since the resulting average reaction rate is what we have previously called Φ₂, we conclude that

$${\Phi }_2=\pi {\sigma }_{12}^2{\rho }_1\left({\sigma }_{12}\right){\overline{v}}_{12}q.$$ (25)

Notice that our last step, multiplying the collision rate 24 by the fraction q of the collisions that result in a reaction to get the reaction rate 25, is reminiscent of Sveshnikoff’s tactic of multiplying the Smoluchowski rate 22 by q to obtain his result 23. But a careful comparison reveals an important difference, and at the same time exposes the flaw in Sveshnikoff’s logic: The Smoluchowski rate 22 is itself a reaction rate, not a collision rate; therefore, its multiplication by the collision-conditioned reaction probability is unwarranted.

Equations 25, 21 are two equations in the two unknowns Φ₂ and ρ₁(σ₁₂). Solving those two equations simultaneously is straightforward. The result is

$${\rho }_1\left({\sigma }_{12}\right)=\frac{4D{c}_1}{4D+{\sigma }_{12}{\overline{v}}_{12}q},$$ (26)

$${\Phi }_2=\frac{4\pi {\sigma }_{12}^{2}D{\overline{v}}_{12}q{c}_1}{4D+{\sigma }_{12}{\overline{v}}_{12}q}.$$ (27)

Since Φ₂ is the average reaction rate per S₂ molecule, then the average rate Φ at which reactions 1 are taking place throughout the entire system can be obtained simply by multiplying Φ₂ by the number x₂ of S₂ molecules in the system. Upon doing that, and then replacing c₁ by x₁∕Ω, we conclude that the average rate at which reactions 1 are taking place inside Ω is

$$\Phi =\left(\frac{4\pi {\sigma }_{12}^{2}D{\overline{v}}_{12}q{\Omega }^{-1}}{4D+{\sigma }_{12}{\overline{v}}_{12}q}\right)x_1{x}_2.$$ (28)

TWO LIMITING REGIMES

There are two noteworthy limiting regimes of the diffusional reaction rate formula 28. These are defined by the relative magnitudes of the two terms in its denominator. The first regime is characterized by the condition

$$\eta \equiv \frac{{\sigma }_{12}{\overline{v}}_{12}q}{4D}⪡1\left(\text{ballistic}\text{regime}\right).$$ (29)

In this circumstance, it is convenient to write the denominator in Eq. 28 as

$$4D+{\sigma }_{12}{\overline{v}}_{12}q=4D\left(1+\eta \right).$$

Equation 28 then takes the form

$$\Phi =\left(\frac{\pi {\sigma }_{12}^2{\overline{v}}_{12}q{\Omega }^{-1}}{1+\eta }\right)x_1{x}_2.$$ (30)

For η→0, this reduces exactly to the ballistic, dilute gas reaction rate corresponding to the propensity function 3, which is why we call condition 29 the ballistic regime of Eq. 28. Notice that Eq. 26 can now be written ρ₁(σ₁₂)=c₁∕(1+η), and this, for η⪡1, is only slightly less than the value ρ₁(Σ₁₂)=c₁. The physical situation here is this: Fickian diffusion is capable of bringing S₁ molecules to the vicinity of the action sphere at a much faster rate than the ballistic kinetics at the surface of the action sphere can cause those molecules to have reactive collisions. This would happen, for instance, if q were very close to zero.

The other regime of interest is the opposite extreme,

$${\eta }^{-1}\equiv \frac{4D}{{\sigma }_{12}{\overline{v}}_{12}q}⪡1\left(\text{diffusional}\text{regime}\right).$$ (31)

For this circumstance, we write

$$4D+{\sigma }_{12}{\overline{v}}_{12}q={\sigma }_{12}{\overline{v}}_{12}q\left(1+{\eta }^{-1}\right),$$

so that Eq. 28 becomes

$$\Phi =\left(\frac{4\pi {\sigma }_{12}D{\Omega }^{-1}}{1+{\eta }^{-1}}\right)x_1{x}_2.$$ (32)

For η⁻¹→0, this is the Smoluchowski diffusional reaction rate that follows from Eq. 22, which is why we call this the diffusional regime of Eq. 28. Notice that Eq. 26 can now be written ρ₁(σ₁₂)=c₁η⁻¹∕(1+η⁻¹), and this, for η⁻¹⪡1, is very nearly zero. So the physical situation in this case is this: The ballistic motion of the S₁ molecules near the surface of the action sphere is capable of removing those molecules through reactive collisions at a much faster rate than Fickian diffusion can bring those molecules to the immediate vicinity of the action sphere.

In considering the limiting cases 29, 31, we should not suppose that all the variables in Eq. 28 can be varied independently of each other. For example, D≡D₁+D₂ will generally depend on both σ₁₂ and ${\overline{v}}_{12}$ (the latter via the system temperature T).

FROM AVERAGE REACTION RATE TO PROPENSITY FUNCTION

Two important issues remain to be addressed. First, we need to understand how Φ₂ in Eqs. 21, 25 can be the average rate at which a singleS₂ molecule reacts with the x₁S₁ molecules, in light of the fact that the very first such reaction might annihilate that S₂ molecule. And second, our real goal in this paper is to derive not a reaction rate, but a propensity functiona(x₁,x₂), for reaction 1. That function will exist if and only if the probability that a reaction 1 event will occur somewhere inside Ω in the next infinitesimal time dt can be written in the form a(x₁,x₂)dt. As we shall now show, these two issues can neatly be resolved together.

The assertion that Φ₂ in Eqs. 21, 25 is the average rate at which a particular S₂ molecule reacts via Eq. 1 with the x₁S₁ molecules must mean, by the very definition of rate, that if dt is an infinitesimally small interval of time, then

$${\Phi }_{2}dt=\text{the\hspace{0.5em}}\mathit{average}\mathit{number}\text{\hspace{0.5em}of\hspace{0.5em}reactions\hspace{0.5em}}\left(1\right)\text{\hspace{0.5em}that\hspace{0.5em}}\text{a\hspace{0.5em}particular\hspace{0.5em}}{S}_2\text{\hspace{0.5em}molecule\hspace{0.5em}will\hspace{0.5em}undergo}\text{in\hspace{0.5em}the\hspace{0.5em}next\hspace{0.5em}}dt.$$ (33)

Since this average number is proportional to dt, it is itself infinitesimally small, and in particular is ⪡1. But the smallest nonzero number of reactions that can actually occur during dt is 1. The only way that these two facts can be compatible with each other is for the S₂ molecule to react in the next dt either once or not at all, with the latter being much more likely than the former. It is obvious physically that this is what really happens. And from a logical standpoint, this view avoids the awkwardness of pretending that the S₂ molecule somehow survives its first reaction to have other reactions.

So, let p denote the probability that the chosen S₂ molecule will react according to (1) in the next dt. Then (1−p) is the probability that it will not react in dt. Therefore, the average number of reactions that the S₂ molecule will experience in the next dt is

$$p\cdot 1+\left(1-p\right)\cdot 0=p.$$

Since this average number is also given by Eq. 33, it follows that p=Φ₂dt. Thus we proved that

$${\Phi }_{2}dt=\text{the\hspace{0.5em}}\mathit{probability}\text{\hspace{0.5em}that\hspace{0.5em}a\hspace{0.5em}particular\hspace{0.5em}}{S}_2\text{\hspace{0.5em}molecule\hspace{0.5em}will\hspace{0.5em}undergo\hspace{0.5em}reaction\hspace{0.5em}}\left(1\right)\text{in\hspace{0.5em}the\hspace{0.5em}next\hspace{0.5em}}dt.$$ (34)

The difference between the view of Φ₂dt expressed in Eq. 34 and the view expressed in Eq. 33 might seem academic, but it is very significant from a logical standpoint: Eq. 34 allows our analysis to proceed rigorously, using the laws of probability. Thus, by the addition law of probability, we can compute the probability that any of the S₂ molecules inside Ω will react according to (1) in the next dt simply by adding up the reaction probabilities 34 of all x₂S₂ molecules.¹² Since that sum yields a simple factor of x₂, we have

$${\Phi }_2{x}_{2}dt=\text{the\hspace{0.5em}probability\hspace{0.5em}that\hspace{0.5em}}\mathit{any}{S}_2\text{\hspace{0.5em}molecule}\text{in\hspace{0.5em}}\Omega \text{\hspace{0.5em}will\hspace{0.5em}undergo\hspace{0.5em}reaction\hspace{0.5em}}\left(1\right)\text{in\hspace{0.5em}the\hspace{0.5em}next\hspace{0.5em}}dt.$$ (35)

But the probability on the right side of Eq. 35 is by definition a(x₁,x₂)dt, where a is the propensity function. And Eqs. 27, 28 show that Φ₂x₂=Φ. Thus we conclude that a(x₁,x₂)=Φ, or, by Eq. 28,

$$a\left(x_1,x_2\right)=\left(\frac{4\pi {\sigma }_{12}^{2}D{\overline{v}}_{12}q{\Omega }^{-1}}{4D+{\sigma }_{12}{\overline{v}}_{12}q}\right)x_1{x}_2.$$ (36)

Equation 36 is the central result of this paper.

COMPARISON TO COLLINS–KIMBALL

As mentioned earlier, our analysis owes much to the work of Collins and Kimball.⁵ In this section we will clarify the connection of our work to theirs, using our notation.

In Ref. 5, CK begin by solving the diffusion equation for the S₁ molecular concentration ρ₁(r,t) exterior to the action sphere around a chosen S₂ molecule. In doing that, they use the initial condition ρ₁(r,0)=x₁∕Ω, whereas we use the initial condition ρ₁(r,0)=ρ₁(r), the latter being the time-stationary solution of the diffusion equation. The choice of CK leads to an initial time-dependent spike in the net flux to the surface of the action sphere, as some of the S₁ molecules infinitesimally close to that surface are immediately absorbed. Our view is that an exact spatially homogeneous initial condition would be very difficult to establish in a real laboratory setting, and in any case it would not keep re-establishing itself after each reaction event for the next reaction event. Our choice of initial condition seems a physically more reasonable approximation for the “successive reaction” scenario that applies to the propensity function problem. And this choice has the added practical benefit of removing time from the resulting formulas.

Except for this different choice of initial condition, we followed CK’s overall strategy of deriving two equations– our Eqs. 21, 25, CK’s Eqs. (25) and (27)–and then solving those equations simultaneously for ρ₁(σ₁₂) and Φ₂, the latter being the net flow of S₁ molecules to the action sphere around the chosen S₂ molecule. But there are some noteworthy differences in our equations and equations of CK, not only in their forms but also in how they are derived.

With regard to the Fick’s law equation, which is our Eq. 21, CK go through a lengthy preliminary argument aimed at justifying the “reaction rate” interpretation of that equation in light of the fact that the chosen S₂ molecule cannot react more than once. We achieve a simpler and arguably more convincing resolution of that problem in Sec. 5 by taking explicit account of the intrinsically discrete-stochastic nature of molecular reactions. Also, the analysis of CK seems to suggest that, because Fick’s law in its usual form expresses the net flux to the surface of the action sphere as being directly proportional to the value of ∂ρ₁∕∂r there [as in our Eq. 13], we are consequently obliged to make that value one of our boundary conditions. But having chosen for one boundary condition the value of ρ₁ far from the action sphere [see our Eq. 18], we can in fact choose for the other boundary condition either a value for ∂ρ₁∕∂r at r=σ₁₂or a value for ρ₁(σ₁₂); because, as can be seen from our Eq. 20, specifying either of those two values will uniquely determine the other. Therefore, it is permissible to use as the second boundary condition a value for ρ₁(σ₁₂), as we have done in our Eq. 21.

But our Eq. 21 also shows that, if we reason from the diffusion equation alone, we will not obtain a formula for Φ₂ that is directly proportional to ρ₁(σ₁₂). This poses a problem for CK in deriving their second equation, which corresponds to our Eq. 25, as is evidenced by the way in which they present that equation (adapted to our notation):

“An obvious modification is to assume that the probability that [an S₁ molecule] reacts with [an S₂ molecule] is proportional to the probability that the [S₁ molecule] lies between [r=σ₁₂ and r=σ₁₂+ΔR], where ΔR is a small distance. This is equivalent to the assumption $\left[{\Phi }_2=k4\pi {\sigma }_{12}^2{\rho }_1\left({\sigma }_{12}\right)\right]$, where k is in the nature of a specific reaction rate.”⁵

In contrast, our derivation of Eq. 25 proceeds from the premise that, in the final stage of the collision-reaction process, the two molecules are not moving diffusionally, but ballistically, as in a dilute gas. That approach allows us to see that what CK have called k is in fact the quantity $\left(1∕4\right){\overline{v}}_{12}q$. CK subsequently attempt to justify their second equation with a lengthy analysis that models the position of the S₁ molecule as a jump Markov process. But that argument is quite complicated, and it establishes the proportionality of the rate to ρ₁(σ₁₂) only at the expense of a physically implausible limiting assumption: the frequency of collisions must go to infinity while the probability of a reaction given a collision must go to zero in such a way that their product remains finite. These same assumptions were embraced by Andrews and Bray¹³ in more recent adaptation of the result of CK. But in fact, no modeling of the position of a diffusing particle as a Markov process, whether it be of the “jump” kind as CK did⁵ or the “continuous” kind as Einstein did,⁶ will be able to describe the velocity and the true trajectory of the molecule in a physically accurate way, for reasons explained in Sec. 2. Furthermore, our Eq. 21, which is derived directly from the diffusion equation, makes it clear that the diffusion equation by itself does not imply that the net flux of S₁ molecules to the surface of the action sphere is directly proportional to ρ₁(σ₁₂). None of these difficulties arise, however, if one derives the second equation from dilute gas kinetic theory, as we have done here. And as we have shown in Appendix C, there is a plausible physical rationale for using dilute gas kinetic theory in the immediate vicinity of the surface of the action sphere.

If we make allowance for the facts that the result of CK has a transient time dependence arising from their choice of a strictly uniform initial condition, and also that what CK call k is not a reaction constant but simply $\left(1∕4\right){\overline{v}}_{12}q$, our formula 28 for the diffusional reaction rate is equivalent to the result of CK. But our analysis here has gone farther: It extended that reaction rate result to a stochastic context (in Sec. 5) to obtain the propensity function 36. A serendipitous bonus of that stochastic extension is that it makes the entire derivation more rigorous, because we no longer have to imagine that a molecule can react more than once, or that reactions can occur in noninteger numbers.

SUMMARY AND CONCLUSIONS

We have derived in Eq. 36 a formula for the propensity function of the bimolecular reaction 1 when the reactant molecules move about diffusionally in a common bath of smaller, more numerous, chemically inert solvent molecules. Our derivation assumes that the system is kept macroscopically well-stirred and dilute. The former means that, on the scale of the containing volume Ω, the spatial distributions of the S₁ and S₂ molecules appear to be randomly uniform, in that persistent spatial nonuniformities on the scale of Ω beyond what would be expected from ordinary random fluctuations do not develop. The dilute assumption means that the reactant molecules are, on average, well enough separated that they move about practically independently of each other. These conditions will not be satisfied in some cellular systems, specifically those in which the solute (reactant) molecules crowd each other severely, and for those systems our results here will not hold. The dilute scenario we focused on, in which each solute molecule typically collides many times with solvent molecules before it collides with another solute molecule, does tend to stir the system to some degree; however, some form of exogenous stirring might still be needed. In a cell, such exogenous stirring might be produced by the natural flexing of the cell’s membrane, together with the general “jostling about” that cells within living organisms typically experience.

In Eq. 36, D is the sum 11 of the diffusion coefficients of the two reactant molecules, σ₁₂ is the average distance between their centers when they collide, ${\overline{v}}_{12}$ is their average relative speed 2 at temperature T, and $q=q\left({\overline{v}}_{12}\right)$ is the probability of a reaction given a collision at that temperature. When diffusion is fast in the sense that $4D⪢{\sigma }_{12}{\overline{v}}_{12}q$, formula 36 limits to the dilute gas propensity function 3. In that case, the diffusion process is able to bring two reactant molecules close together more easily than the collision process can initiate a reaction between them; a circumstance that will arise for instance if q⪡1. When diffusion is slow in the sense that $4D⪡{\sigma }_{12}{\overline{v}}_{12}q$, formula 36 limits to (4πσ₁₂DΩ⁻¹)x₁x₂, a form that was anticipated by Smoluchowski.¹⁰ In this limit, the collision process can initiate a reaction between two reactant molecules more readily than the diffusion process can bring those molecules into close proximity. The virtue of Eq. 36, of course, is that it holds for values of the physical parameters anywhere in between these extreme limits. And even if one is unable to determine the values of such parameters as σ₁₂ or D or q in Eq. 36, the proof given here that a propensity function does exist in the form cx₁x₂ will provide a license to estimate the numerical value of c from kinetic rate experiments.

The constant c in the formula a(x₁,x₂)=cx₁x₂ is called the reaction probability rate constant. The physical interpretation of c is that cdt is the probability that a randomly chosen S₁-S₂ molecular pair will react according to 1 in the next dt. Comparing with Eq. 36, we see that c is given by

$$c=\frac{4\pi {\sigma }_{12}^{2}D{\overline{v}}_{12}q{\Omega }^{-1}}{4D+{\sigma }_{12}{\overline{v}}_{12}q}.$$ (37)

In deterministic chemical kinetics, the average reaction rate per unit volume, namely, the average reaction rate Φ divided by Ω, is usually written Φ∕Ω=kc₁c₂, where c_i is the average concentration of species S_i, and k is called the reaction rate constant. If we substitute into this expression the formula for Φ in Eq. 28, and note that c_i=x_i∕Ω, we find that the deterministic reaction rate constant k is given by

$$k=\frac{4\pi {\sigma }_{12}^{2}D{\overline{v}}_{12}q}{4D+{\sigma }_{12}{\overline{v}}_{12}q}=\Omega c.$$ (38)

Notice that k is independent of Ω. This relation between k and c gets altered slightly if species S₁ and S₂ are the same. In that case, the number of distinct reactant pairs x₁x₂ in Eqs. 28, 36 gets replaced by (1∕2)x₁(x₁−1). The propensity function is then written c(1∕2)x₁(x₁−1) with c still being given by Eq. 37. But the average reaction rate per unit volume is by convention written $k{c}_1^2$. So, since deterministic chemical kinetics assumes that x₁⪢1, the relation between the deterministic and stochastic rate constants when species S₁ and S₂ are the same is k=Ωc∕2.

Simple algebra allows us to write Eq. 38 in the form

$$\frac{1}{k}=\frac{1}{k_{\text{d}}}+\frac{1}{k_{\text{b}}},$$ (39)

where

$$k_{\text{d}}\equiv 4\pi {\sigma }_{12}D,k_{\text{b}}\equiv \pi {\sigma }_{12}^2{\overline{v}}_{12}q.$$ (40)

Note that k_d is the diffusional reaction rate constant of Smoluchowski, which holds when D is “small” in the sense of condition 31, while k_b is the ballistic reaction rate constant that follows from the dilute gas propensity function 3 derived in Appendix A. This result has an interesting heuristic interpretation: If we think of the reaction rate constant k as a kind of “conductance” for the overall reaction process, then 1∕k takes the character of a “resistance” for that process. In expressing that resistance as a sum of two other resistances, Eq. 39 suggests that the reaction process resistor actually consists of two resistors in series, one with conductance k_d and the other with conductance k_b. The resulting physical picture is that diffusion first brings two reactant molecules close to each other via a diffusional resistor, and then ballistic dynamics causes them to react via a ballistic resistor. This “pipeline” picture of the overall reaction process supports the view advanced in Sec. 3, that diffusional dynamics gives way to ballistic dynamics when the reactant molecules get sufficiently close together.

There has long been a concern that a propensity function might not exist in the diffusional case. This concern stemmed from the prediction of the classical diffusion equation that a diffusing molecule will, in a time Δt, move an average distance proportional to $\sqrt{\Delta t}$. That result would seem to suggest, by the reasoning used to derive the dilute gas propensity function in Appendix A, that the probability that a reaction will occur in the next infinitesimal time dt would be proportional to $\sqrt{dt}$. But we have shown here that this concern is unfounded for two reasons. First, the diffusion equation does not give a physically valid description of either the velocity of a diffusing molecule or the finely resolved trajectory of a diffusing molecule—features that are required to decide whether a collision will lead to a reaction. And second, even when we allow dt to be microscopically large, so that the average net displacement in time dtis proportional to $\sqrt{dt}$, that net displacement will not be a measure of the distance actually traveled by the molecule during that time.

The inverse dependence of the propensity function 36 on the system volume Ω stems from the fact that two reactant molecules will have a harder time finding each other when Ω is large than when Ω is small. An important consequence of this inverse-Ω dependence is that the propensity function diverges linearly with the size of the system in the thermodynamic limit, wherein the molecular populations x_i and the system volume Ω are imagined to approach infinity in such a way that all the concentrations x_i∕Ω remain constant. This limiting behavior of propensity functions turns out to be crucial for proving that when the system is sufficiently large, its behavior is accurately described by the set of coupled ordinary differential equations that are used in traditional deterministic chemical kinetics.²

Finally, we emphasize again that when the “macroscopically well-stirred” condition is not maintained, the system will not be accurately described by the theory developed here. In particular, if diffusion is slow, then in the absence of some form of exogenous stirring, reaction 1 might gradually “unstir” an initially well-stirred system. The nature of that unstirring would depend on what appears on the right side of reaction 1; e.g., the spatial inhomogeneities that would develop if reaction 1 destroyed S₁ molecules would be different from the spatial inhomogeneities that would develop if reaction 1 created S₁ molecules. The situation would be further complicated if, as nearly always happens in biochemical systems, other reaction channels are present that can also affect the spatial distribution of the reactant molecules. As discussed briefly in Sec. 1, the most reliable way of dealing with spatially inhomogeneous systems is to first find some set of state variables that describe not only the types but also the locations of the reactant molecules, and then evolve all those variables in time in a physically correct way. But that is not an easy thing to do, as it leads us closer to a “molecular dynamics” analysis. Some detailed studies have been made of a few simple isolated reactions under the condition that the solvent molecules are physically identical to the solute molecules, i.e., the diffusion is of the “self-diffusion” kind rather than the “Brownian motion” kind that we have been concerned with here. These studies show that if one wishes to maintain the view that the rate at which reaction 1 occurs is proportional to the product of the S₁ and S₂ molecular populations (or concentrations), then the proportionality “constant” will depend explicitly on time. The seminal papers of Zhou and Szabo¹⁴ provide a window into those studies.

APPENDIX A: A RIGOROUS DERIVATION OF THE BALLISTIC (DILUTE GAS) PROPENSITY FUNCTION

From the x₁x₂ pairs of S₁ and S₂ molecules inside Ω, randomly pick one, say the jth pair. By “randomly” we mean that we do not know the positions of the chosen molecules; we know only that they will be distributed over Ω in a randomly uniform way. Go to the rest frame of the S₁ molecule, and observe the S₂ molecule moving with some relative speed $v_{21}^{\left(j\right)}$. Ascribe about the center of molecule 2 a sphere of radius σ₁₂; this is called the “action sphere,” because if the center of the S₁ molecule lies on the surface of that sphere then the two molecules will be colliding. See Fig. 2.

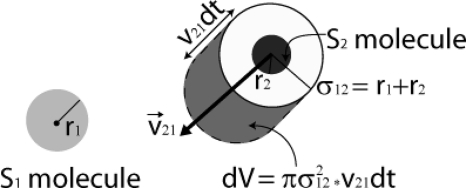
Figure 2.

In a dilute gas, and from the point of view of a randomly chosen S₁ molecule (light gray), a randomly chosen S₂ molecule (dark gray) moves with speed v₂₁. In the next infinitesimal time dt, the S₂ molecule will drag the action sphere of radius σ₁₂ a distance v₂₁dt, and in so doing will sweep out the shaded “collision volume” dV. If the center of the S₁ molecule lies inside dV, the two molecules will collide in the next dt. The figure shows how the radius σ₁₂ of the action sphere would be related to the radii of the two molecules if those molecules were hard spheres. More generally, σ₁₂ is the average or effective distance between two of these molecules at the instant of their collision.

In the next infinitesimal time dt, the action sphere, moving with the S₂ molecule, will sweep out relative to the S₁ molecule an infinitesimal region of volume $\pi {\sigma }_{12}^2\times v_{21}^{\left(j\right)}dt$, as shown in Fig. 2. The probability that a collision will occur between these two molecules during that time will be equal to the probability that the center of the S₁ molecule lies inside that region.¹⁵ By the well-stirred assumption, together with the assumption that the molecules occupy a negligibly small fraction of the system volume Ω, this probability will be the volume ratio $\left(\pi {\sigma }_{12}^2{v}_{21}^{\left(j\right)}dt\right)∕\Omega$. This ratio, then, is the probability that the jth S₁-S₂ pair of molecules will collide in the next infinitesimal time dt. Multiplying this by q gives, by the multiplication law of probability, the probability that the jth S₁-S₂ pair of molecules will react according to Eq. 1 in the next dt. And then summing that over all x₁x₂S₁-S₂ pairs in Ω gives, by the addition law of probability, the probability that any of those pairs will react according to (1) in the next dt:¹⁶

$$\sum _{j=1}^{x_1{x}_2}\left(\frac{\pi {\sigma }_{12}^2{v}_{21}^{\left(j\right)}dt}{\Omega }q\right)=\frac{\pi {\sigma }_{12}^{2}qdt}{\Omega }\left(x_1{x}_2\frac{1}{x_1{x}_2}\right)\sum _{j=1}^{x_1{x}_2}{v}_{21}^{\left(j\right)}=\frac{\pi {\sigma }_{12}^{2}qdt}{\Omega }{x}_1{x}_2{\overline{v}}_{21}=\left(\frac{\pi {\sigma }_{12}^2{\overline{v}}_{21}q}{\Omega }{x}_1{x}_2\right)dt.$$

Since this is the probability that reaction 1 will fire somewhere inside Ω in the next dt, the coefficient of dt is, by definition, the propensity function of reaction 1; hence the result 3.

APPENDIX B: DIFFUSIONAL TRAJECTORY LENGTH VIA THE DIFFUSION EQUATION

For a solute molecule at the origin O at time 0, suppose we use Eq. 8 with Δt=τ∕n to compute the successive locations P_i of the solute molecule at the n equally spaced times t_i=i(τ∕n) (i=1,…,n) between time 0 and some fixed time τ. Let L(n,τ) be the total length of the broken line $\overline{P_0{P}_1\cdots P_n}$, where P₀=O, and let R_τ be the length of the net displacement $\overline{P_0{P}_n}$ in time [0,τ]. We will prove here that, with ⟨⋯⟩ denoting an average over infinitely many repeated such n-point constructions,¹⁷

$$⟨L\left(n,\tau \right)⟩=\sqrt{n}⟨R_{\tau }⟩,$$ (B1)

where

$$⟨R_{\tau }⟩=\{\begin{array}{ll}\sqrt{\pi D\tau }\hfill & \left(\text{in}\text{two}\text{dim}\text{.}\right),\hfill \\ 4\sqrt{D\tau ∕\pi }\hfill & \left(\text{in}\text{three}\text{dim}\text{.}\right).\hfill \end{array}\phantom{\}}$$ (B2)

Since it follows from this result that L(n,τ)→∞ as n→∞, we conclude that the average “true” length of any finite-time trajectory constructed from Eq. 8 is infinite.

The proof of Eqs. B1, B2 in two dimensions goes as follows. With R_τ=(X_τ,Y_τ) denoting the diffusing molecule’s position at time τ, Einstein’s result 7, from which formulas 8 were derived, tells us that X_τ and Y_τ are statistically independent normal random variables with means 0 and variances 2Dτ. Their joint pdf is therefore

$$P_{XY}\left(x,y;\tau \right)={\left(4\pi D\tau \right)}^{-1}\text{\hspace{0.17em}exp}\left(-\frac{x^2}{4D\tau }\right)\text{exp}\left(-\frac{y^2}{4D\tau }\right)\left(-\infty <x,y<\infty \right).$$ (B3)

Define the polar coordinates R_τ and Θ_τ of R_τ in the usual way:

$$X_{\tau }=R_{\tau }\text{\hspace{0.17em}cos}{\Theta }_{\tau },Y_{\tau }=R_{\tau }\text{\hspace{0.17em}sin}{\Theta }_{\tau }.$$

The joint pdf of the two random variables R_τ and Θ_τ is related to that of X_τ and Y_τ by

$$P_{R\Theta }\left(r,\theta ;\tau \right)=P_{XY}\left(x,y;\tau \right)\mid \frac{\partial \left(x,y\right)}{\partial \left(r,\theta \right)}\mid ,$$

where the Jacobean is for the transformation x=r cos θ,y=r sin θ. That Jacobean is easily found to be equal to r, so

$$P_{R\Theta }\left(r,\theta ;\tau \right)={\left(4\pi D\tau \right)}^{-1}r\text{\hspace{0.17em}exp}\left(-\frac{r^2}{4D\tau }\right)\left(0\le r<\infty ;0\le \theta <2\pi \right).$$ (B4)

Integrating P_RΘ over θ then gives the pdf of the net displacement R_τ:

$$P_R\left(r;\tau \right)={\left(2D\tau \right)}^{-1}r\text{\hspace{0.17em}exp}\left(-\frac{r^2}{4D\tau }\right)\left(0\le r<\infty \right).$$ (B5)

From Eq. B5, it is straightforward to show that the mean net displacement of the molecule in time [0,τ] is

$$⟨R_{\tau }⟩\equiv {\int }_0^{\infty }r{P}_R\left(r;\tau \right)dr=\sqrt{\pi D\tau }.$$ (B6)

Equation B6 not only establishes the two-dimensional version of Eq. B2, it also tells us that the mean distance between any two successive points in an n-point representation of the trajectory is

$$⟨\mid \overline{P_{i-1}{P}_i}\mid ⟩=\sqrt{\pi D\Delta t}=\sqrt{\pi D\left(\tau ∕n\right)}.$$ (B7)

Therefore,

$$⟨L\left(n,\tau \right)⟩\equiv ⟨\sum _{i=1}^n\mid \overline{P_{i-1}{P}_i}\mid ⟩=\sum _{i=1}^n⟨\mid \overline{P_{i-1}{P}_i}\mid ⟩=n\sqrt{\pi D\left(\tau ∕n\right)}=\sqrt{n\pi D\tau }.$$ (B8)

This, together with Eq. B6, establishes Eq. B1 for the two dimensional case. The proof of Eqs. B1, B2 for the three dimensional case proceeds analogously.

APPENDIX C: DERIVATION OF EQUATION 24

According to Eq. 19, the average concentration ρ₁(r) of S₁ molecules at a distance r from the center of the action sphere rises from the value ρ₁(σ₁₂) at the surface of the action sphere to the value c₁ at distances ⪢σ₁₂ from that surface. Since that rise is smooth, we can find a Δr>0 that is small enough that the approximation

$${\rho }_1\left(r\right)\approx {\rho }_1\left({\sigma }_{12}\right)\text{for}\text{all}r∊\left[{\sigma }_{12},{\sigma }_{12}+\Delta r\right]$$ (C1)

holds to any desired degree of accuracy. And if the Δr that satisfies that requirement is not already smaller than the mean-free-path for collisions of an S₁ molecule with the solvent molecules, we reduce Δr until that condition too is satisfied. Then, everywhere inside the spherical shell around the action sphere of outer radius σ₁₂+Δr, we have, to a good approximation, ballistically moving S₁ molecules with a constant average concentration ρ₁(σ₁₂).

Now let δA be an infinitesimally small area element at some point Q on the surface of the action sphere. Since our system has a finite total energy, there must be some finite upper bound v_max on the speed of any S₁ molecule relative to the chosen S₂ molecule. Let

$$\delta t=\Delta r∕v_{\text{max}}.$$ (C2)

Then all S₁ molecules that can possibly strike the area element δA within the next time δt must lie inside the hemispherical volume Ω^′ of radius Δr whose flat side is tangent to the action sphere at Q, and which is otherwise external to the action sphere. See Fig. 3. Let dω^′ be an infinitesimal volume element of Ω^′ with polar coordinates (r^′,θ^′,ϕ^′) relative to a coordinate frame whose origin is at Q and whose polar axis is in the direction of $\overrightarrow{OQ}$.

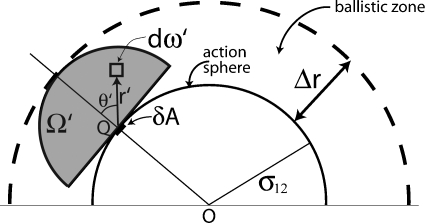
Figure 3.

Showing the region around the action sphere where the S₁ molecules move ballistically relative to the chosen S₂ molecule, and the subvolume Ω^′ of that region which contains all the S₁ molecules that can possibly strike the infinitesimal area element δA at point Q within the next time δt.

We now make the following three observations: First, the average number of S₁ molecules inside dω^′ is ρ₁(σ₁₂)dω^′. Second, since the infinitesimal area element δA subtends at dω^′ a solid angle δA cos θ^′∕r^′2, then the average fraction of the molecules in dω that will be traveling in a direction that intersects δA is δA cos θ^′∕4πr^′2. And third, letting f(v) denote the pdf of the speed of an S₁ molecule relative to the S₂ molecule, the average fraction of the molecules in dω traveling toward δA that are going fast enough to reach δA within the next δt is ${\int }_{r^{\prime }∕\delta t}^{v_{\max }}f\left(v\right)dv$. It follows from these facts that the average number of S₁ molecules that will collide with the area element δA in the next δt is

$$N_2^{\text{coll}}\left(\delta t\right)=\int \int {\int }_{{\Omega }^{\prime }}\left[{\rho }_1\left({\sigma }_{12}\right)d{\omega }^{\prime }\right]\left[\frac{\delta A\text{\hspace{0.17em}cos}{\theta }^{\prime }}{4\pi r^{\prime 2}}\right]{\int }_{v=r^{\prime }∕\delta t}^{v_{\text{max}}}f\left(v\right)dv.$$ (C3)

Since

$$d{\omega }^{\prime }=\left(d{r}^{\prime }\right)\left(r^{\prime }d{\theta }^{\prime }\right)\left(r^{\prime }\text{\hspace{0.17em}sin}{\theta }^{\prime }d{\varphi }^{\prime }\right)=r^{\prime 2}d{r}^{\prime }d{u}^{\prime }d{\varphi }^{\prime },$$

where we have put cos θ^′=u^′, then the integrals in Eq. C3 can be written more explicitly as

$$N_2^{\text{coll}}\left(\delta t\right)={\int }_{r^{\prime }=0}^{\Delta r}d{r}^{\prime }{r}^{\prime 2}{\rho }_1\left({\sigma }_{12}\right){\int }_{u^{\prime }=0}^{1}d{u}^{\prime }\left(\frac{\delta A{u}^{\prime }}{4\pi r^{\prime 2}}\right){\int }_{{\varphi }^{\prime }=0}^{2\pi }d{\varphi }^{\prime }{\int }_{v=r^{\prime }∕\delta t}^{v_{\text{max}}}dvf\left(v\right)=\frac{{\rho }_1\left({\sigma }_{12}\right)\delta A}{4\pi }{\int }_0^{\Delta r}d{r}^{\prime }{\int }_0^{1}d{u}^{\prime }{u}^{\prime }{\int }_0^{2\pi }d{\varphi }^{\prime }{\int }_{r^{\prime }∕\delta t}^{v_{\text{max}}}dvf\left(v\right).$$

The ϕ^′ and u^′ integrals are easily performed, yielding factors of 2π and 1∕2 respectively, so this expression reduces to the double integral

$$N_2^{\text{coll}}\left(\delta t\right)=\frac{{\rho }_1\left({\sigma }_{12}\right)\delta A}{4}{\int }_0^{\Delta r}d{r}^{\prime }{\int }_{r^{\prime }∕\delta t}^{v_{\text{max}}}dvf\left(v\right).$$ (C4)

Switching the order of integration over r^′ and v transforms Eq. C4 to

$$N_2^{\text{coll}}\left(\delta t\right)=\frac{{\rho }_1\left({\sigma }_{12}\right)\delta A}{4}{\int }_0^{v_{\text{max}}}dv{\int }_0^{v\delta t}d{r}^{\prime }f\left(v\right)=\frac{{\rho }_1\left({\sigma }_{12}\right)\delta A}{4}{\int }_0^{v_{\text{max}}}dv\left(v\delta t\right)f\left(v\right)=\frac{{\rho }_1\left({\sigma }_{12}\right)\delta t\delta A}{4}{\int }_0^{v_{\text{max}}}vf\left(v\right)dv$$ (C5)

$$N_2^{\text{coll}}\left(\delta t\right)=\frac{{\rho }_1\left({\sigma }_{12}\right){\overline{v}}_{12}\delta t\delta A}{4}.$$ (C6)

Dividing Eq. C6 by δt gives the average rate at which S₁ molecules are colliding with δA. Then summing that over all the infinitesimal surface elements on the action sphere replaces δA with $4\pi {\sigma }_{12}^2$, and yields formula 24 for the average rate at which S₁ molecules are colliding with the action sphere.