Kirkwood–Buff theory of molecular and protein association, aggregation, and cellular crowding

Abstract

An analysis of the effect of a cosolvent on the association of a solute in solution using the Kirkwood–Buff theory of solutions is presented. The approach builds on the previous results of Ben-Naim by extending the range of applicability to include any number of components at finite concentrations in both closed and semiopen systems. The derived expressions, which are exact, provide a foundation for the analysis and rationalization of cosolvent effects on molecular and biomolecular equilibria including protein association, aggregation, and cellular crowding. A slightly different view of cellular crowding is subsequently obtained. In particular, it is observed that the addition of large cosolvents still favors the associated form even when traditional excluded volume effects are absent.

INTRODUCTION

Protein association, protein unfolding, protein aggregation, and cellular crowding are known to affect the normal function of cellular systems.^{1, 2, 3, 4, 5, 6, 7} In many cases, the resulting small changes in normal protein-protein intra- and intermolecular interactions are thought to lead to a variety of human diseases.^{8, 9} Consequently, it is important to study these processes, at both the thermodynamic and atomic levels, in an effort to understand and eventually manipulate the behavior of such systems. One way to affect and help understand peptide and protein association is through the use of additives or cosolvents.¹⁰ A general theory describing these types of effects which relates their thermodynamic properties to the interactions between species in solution is therefore desired. This is a major aim of the present work.

The basic thermodynamic effects of additives on chemical equilibria were outlined some time ago using the concepts of binding and linkage.^{11, 12, 13} Binding polynomials are then typically used to help illustrate the resulting thermodynamic relationships. While binding polynomials can be used to provide an accurate representation of real experimental data, the physical interpretation of the binding constants requires some care for systems involving only weakly binding cosolvents.¹⁴ This is immediately apparent when attempting to define corresponding binding sites, occupation numbers, and equilibrium constants using coordinate data provided by computer simulations. The transient nature of the interactions between the cosolvent and biomolecule render such a comparison of the experimental and simulation data essentially impossible. Other thermodynamic approaches have been outlined,^{15, 16, 17, 18, 19, 20, 21} but it remains difficult to relate these to realistic distributions between the various species in solution.

The most common approach used to understand the effects of an additive on protein folding, association, and aggregation involved scaled particle theory (SPT).^{6, 19, 22, 23} Here, the change in free energy for association, denaturation, etc., is determined from the change in the free energy for insertion of the initial and final states into a system of hard spheres as a function of the additive volume fraction. These calculations generally suggest that the native and any associated states are favored on increasing the additive concentration. These are exactly the trends observed experimentally,⁶ and for simulations using simple excluded volume crowders.^{3, 24} As SPT is dominated by repulsive excluded volume effects, the above trends are usually interpreted in terms of a decrease in the free volume, or increase in the excluded volume, within the solution. Unfortunately, it is difficult to extend SPT to include attractive interactions which undoubtedly occur between proteins in real systems.⁶ Hence, other models are still required which complement existing approaches.

The application of the Kirkwood–Buff (KB) theory of solutions to biological systems recently attracted some interest.¹⁴ KB theory provides a rigorous link between intermolecular distributions in solution and the thermodynamic characteristics of that solution.^{25, 26} In particular, it has been used to understand the preferential interactions of cosolvents with proteins and small molecules,^{27, 28, 29, 30, 31, 32, 33, 34} to study changes in the hydration of solutes,^{35, 36, 37, 38} to investigate a variety of solution properties,^{39, 40, 41} and for hard sphere models of cellular crowding.⁴² Previously, Ben-Naim used KB theory to understand the effects of cosolvents on the association equilibrium of a solute in solution.⁴³ The current approach is based on the previous work of Ben-Naim and is similar to the approach of Hall for studying micelles.⁴⁴ Here, we extend the Ben-Naim approach to describe the effects of a cosolvent on the equilibrium constant for association to include semiopen and not just closed systems, and for systems with any number of components all of which can appear at finite concentrations. To achieve this we adopt a recent approach which avoids the usual matrices used for closed systems.⁴⁵ The resulting expressions are then used to illustrate some of the differences between open and closed systems, and between real and ideal solutions.

KIRKWOOD–BUFF THEORY

Kirkwood–Buff theory is an exact theory of solutions.⁴⁶ The principle quantities of interest are the Kirkwood–Buff integrals (KBIs) defined by

$$G_{ij}=G_{ji}=4\pi {\int }_0^{\infty }\left[g_{ij}^{\mu VT}\left(r\right)-1\right]r^{2}dr,$$ (1)

where g_ij is the radial distribution function (rdf) between the center of mass of species i and j. These integrals can be used to relate thermodynamic properties of a solution to the molecular distributions in that solution. This is achieved by starting with the grand canonical ensemble expression,²⁵

$$RT{\left(\frac{\partial \text{\hspace{0.17em}ln}{\rho }_i}{\partial {\mu }_j}\right)}_{T,{\mu }_{k\ne j}}={\delta }_{ij}+N_{ij},$$ (2)

where R is the gas constant, T is the absolute temperature, ρ_i=N_i∕V is the number density of species i, μ is the chemical potential, and δ_ij is the Kroenecker delta function. The N_ij=ρ_jG_ij values describe the change in the number of j particles on introduction of a central i particle, from the number of j particles found in an equivalent volume of bulk solution at the same composition. More details concerning the application of KB theory to understand a variety of solution properties can be found elsewhere.^{14, 26, 39}

The major aim of this work is to develop expressions for cosolvent effects on biomolecular equilibria in both closed and semiopen ensembles. Traditionally, KB theory starts from Eq. 2 and uses a series of thermodynamic transformations to provide expressions for similar derivatives in closed ensembles.^{25, 46} A general matrix formulation is available for chemical potential derivatives in closed systems—the most common system of interest.⁴⁶ However, we will avoid this approach as the corresponding expressions are difficult to manipulate for large numbers of components. Furthermore, it is also difficult to transform from the closed ensemble results back to expressions valid for semiopen systems.²⁹

CHEMICAL EQUILIBRIA

Let us consider a formal n_c component system containing a primary solvent (1), a biomolecule (2), and a series of cosolvents (3,4,⋯). The cosolvents can be small molecules such as urea, a salt, a proton, or larger molecules such as different proteins. We will refer to species 2 as a biomolecule, but it can easily refer to any associating species. Furthermore, the biomolecule can exist in two forms, one being a monomer (M) and the other an aggregate (A) of any shape formed from n monomers. Any counterion associated with the biomolecule will be assumed to have no effect on the equilibrium and to be different from any of the cosolvent if the latter are salts (no Donnan effect). Hence, we have the equilibrium process,

$$nM\to A,$$ (3)

which can be described by an equilibrium constant K. Formally, the equilibrium constant involves the activities of the various species. In the majority of thermodynamic approaches it is then assumed that the activities of the biomolecule species can be replaced by their concentrations as the biomolecules usually appear at low concentrations, and concentrations are relatively easy to determine experimentally. Here, we do not assume ideal behavior of any species, but simply define our equilibrium constant in terms of concentrations to match the usual experimental representation of the data. Consequently, the equilibrium constant can be defined in several ways using a variety of concentration scales. We chose

$$K=\frac{{\rho }_A}{{\rho }_M^n}$$ (4)

in terms of number densities or molarities. Other choices will be discussed later. The number of each form of the biomolecule present in solution are related by

$$N_M+n{N}_A=N_2,d{N}_M+nd{N}_A=d{N}_2,$$ (5)

and,

$$f_M=\frac{N_M}{N_2},f_A=\frac{n{N}_A}{N_2},f_M+f_A=1,$$ (6)

where f_i is the fraction of either A or M at equilibrium. The material equilibrium condition indicates that

$${\mu }_A=n{\mu }_M,d{\mu }_A=nd{\mu }_M=nd{\mu }_2,$$ (7)

as long as we remain at equilibrium. From Eq. 4 a general change in the equilibrium constant can be written as

$$d\text{\hspace{0.17em}ln}K=d\text{\hspace{0.17em}ln}{\rho }_A-nd\text{\hspace{0.17em}ln}{\rho }_M.$$ (8)

We note that all the above expressions can be applied to any chemical equilibrium that follows Eq. 3 in any thermodynamically reasonable ensemble. Our main aim is to express the changes in the number densities of A and M in terms of the KB integrals and thereby provide a simple physical picture of the effect of a cosolvent on the equilibrium constant.

GENERAL KIRKWOOD–BUFF THEORY OF CHEMICAL EQUILIBRIA

Our system corresponds to a pseudo-n_c+1 component system with thermodynamic constraints between two of the components (M and A). Before proceeding we note that the application of KB theory to this type of problem involves some subtle issues. First, N₂ is a true independent thermodynamic variable. However, N_M and N_A are not as they are related through Eq. 5. Hence, we will avoid taking derivatives with respect to the chemical potentials or concentrations of M and A, although derivatives involving either one (M or A) can be used in place of the chemical potential or concentration of 2. The application of KB theory implies that the KB integrals used here for semiopen or closed systems correspond to an equivalent system at the same composition but open to all species (including M and A). This issue has been discussed by Ben-Naim.²⁶ One can apply KB theory to understand such a system as long as one does not treat M and A as independent thermodynamic variables.⁴⁷

The traditional approach to this type of problem starts with the matrix formulation of KB theory for closed systems. However, the evaluation of the matrix determinants for a large number of components where all components are present at finite concentrations is rather cumbersome. In addition, transforming back to an open or semi-open system from the closed system results is also difficult. Hence, we use a different approach which avoids the direct evaluation of any matrices for small n_c values; thereby greatly simplifying the problem.⁴⁵ Let us consider the number density of each species to be functions of T and all the chemical potentials. The differential of the number densities at constant T is then provided by

$$d\text{\hspace{0.17em}ln}{\rho }_i=\sum _j{\left(\frac{\partial \text{\hspace{0.17em}ln}{\rho }_i}{\partial {\mu }_j}\right)}_{T,{\mu }_{k\ne j}}d{\mu }_j,$$ (9)

for any i, and where the summation is over all j components. The partial derivatives can be expressed in terms of KBIs through Eq. 2 to give

$$RTd\text{\hspace{0.17em}ln}{\rho }_i=\sum _j\left({\delta }_{ij}+N_{ij}\right)d{\mu }_j$$ (10)

for any constant T ensemble. To our knowledge the above equation was first derived by Hall,⁴⁸ but using a different route. The general Gibbs–Duhem (GD) relation at constant temperature can be written as

$$dP=\sum _j{\rho }_{j}d{\mu }_j,$$ (11)

where P is the pressure. Equations 10, 11 can be applied to any number of components in any ensemble with T constant.

Hence, for our n_c+1 component system of species 1,M,A,3,4,⋯, one can use Eq. 7 to eliminate dμ_A from the relationships provided in Eq. 10 for i=A and M to give

$$RTd\text{\hspace{0.17em}ln}{\rho }_A=\left(n+n{N}_{AA}+N_{AM}\right)d{\mu }_M+\sum _{j\ne A,M}^{n_c+1}{N}_{Aj}d{\mu }_j,$$ (12)

$$RTd\text{\hspace{0.17em}ln}{\rho }_M=\left(1+N_{MM}+n{N}_{MA}\right)d{\mu }_M+\sum _{j\ne A,M}^{n_c+1}{N}_{Mj}d{\mu }_j.$$

One could have focused on species A instead of M, but the results will be the same. However, we cannot retain bothdμ_M and dμ_A terms for the remainder of the analysis as this implies they are thermodynamically independent. To generate a relationship for changes in the equilibrium constant we use Eq. 8 and the relationships in Eq. 12 to provide

$$RTd\text{\hspace{0.17em}ln}K=\left(n{N}_{AA}+N_{AM}-n{N}_{MM}-n^2{N}_{MA}\right)d{\mu }_M+\sum _{j\ne A,M}^{n_c+1}\left(N_{Aj}-n{N}_{Mj}\right)d{\mu }_j.$$ (13)

However, the above expressions can be simplified further.

A series of relationships between KBIs involving the biomolecule can be established. These can be written as

$$N_{i2}=N_{iM}+n{N}_{iA},$$ (14)

$$N_{2i}=f_M{N}_{Mi}+f_A{N}_{Ai},$$

for i≠A, M, or 2, and

$$N_{M2}=1+N_{MM}+n{N}_{MA},$$ (15)

$$N_{A2}=n+n{N}_{AA}+N_{AM},$$

$$1+N_{22}=f_M\left(1+N_{MM}+n{N}_{MA}\right)+f_A\left(n+n{N}_{AA}+N_{AM}\right)=f_M{N}_{M2}+f_A{N}_{A2}.$$

The above expressions were obtained from the general fluctuation formula in the grand canonical (μVT) ensemble,

$${\delta }_{ij}+N_{ij}=\frac{⟨N_i{N}_j⟩-⟨N_i⟩⟨N_j⟩}{⟨N_i⟩},$$ (16)

by suitable substitutions of N₂=N_M+nN_A. We note that the above relationships do not assume that N₂ is constant. They merely reflect a change in index for the M, A, and 2 species as illustrated in Fig. 1. Their meaning will be discussed later. Application of the above relationships to Eqs. 10, 11, 12, 13 provides

$$RTd\text{\hspace{0.17em}ln}K=\sum _j^{n_c}\left(N_{Aj}-n{N}_{Mj}\right)d{\mu }_j,$$ (17)

$$RTd\text{\hspace{0.17em}ln}{\rho }_i=\sum _j^{n_c}\left({\delta }_{ij}+N_{ij}\right)d{\mu }_j,$$ (18)

$$RTd\text{\hspace{0.17em}ln}{m}_i=\sum _j^{n_c}\left({\delta }_{ij}+N_{ij}-N_{1j}-{\delta }_{1j}\right)d{\mu }_j,$$ (19)

$$dP=\sum _j^{n_c}{\rho }_{j}d{\mu }_j,$$ (20)

where d ln m_i=d ln ρ_i−d ln ρ₁, and m_i is the dimensionless molality (ρ_i∕ρ₁). The above equations represent the basic expressions required for this study. The summations over the formal n_c components only involve indices 1, 2, 3, etc., and not M or A. They can be applied to any constant T ensemble and are valid for any concentration of solvent, biomolecule, and cosolvents. We note that Eqs. 18, 19, 20 could have been written directly for n_c component systems. However, Eq. 17 is not so obvious.

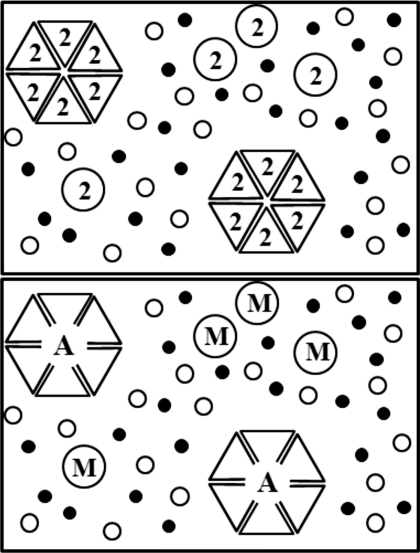
Figure 1.

The two representations of the same system used in this study. The system contains a solvent (1, shaded spheres), a solute (2), and a cosolvent (3, open spheres). In this case the solute can exist in two forms: One being the monomer (M) and the other being an aggregate (A) of n=6 monomers. The monomer can adopt different shapes in the associated and free forms.

RESULTS

We will apply Eqs. 17, 18, 19, 20 to a variety of thermodynamic ensembles to develop expressions for the effect of a cosolvent on the chemical equilibrium in terms of KB integrals. During the following analysis several combinations of KBIs appear repeatedly. Hence, in an effort to simplify the results we will define the following:

$$P_{jk}^i=N_{ij}-\frac{{\rho }_j}{{\rho }_k}{N}_{ik}={\rho }_j\left(G_{ij}-G_{ik}\right)=-\frac{{\rho }_j}{{\rho }_k}{P}_{kj}^i,$$ (21)

which should be read as the preference or affinity of j over k for species i. For example, $P_{31}^A$ quantifies the preference of 3 over 1 for the biomolecule in form A. This notation will only be used when it applies to specific differences between affinities of the various components for the two biomolecule forms. A simple physical interpretation of the sign associated with the above expression is that when $P_{jk}^i>0$ the local ratio of j to k molecules around a central i molecule is larger than the bulk ratio of j to k molecules, and vice versa. We will also make use of the notation,

$$N_{ij}^{+}=N_{ij}+m_j\left(1+N_{11}-N_{i1}-N_{j1}\right),$$ (22)

originally introduced by Hall,⁴⁸ to help simplify many of the results.

GENERAL EXPRESSIONS FOR ANY NUMBER OF COMPONENTS IN A CLOSED SYSTEM

Our initial focus will be on fully closed systems at constant pressure. Eliminating dμ₁ from Eq. 17 using Eq. 20 and then taking derivatives with respect to one of the cosolvent molalities, one obtains the expression

$${\left(\frac{\partial \text{\hspace{0.17em}ln}K}{\partial \text{\hspace{0.17em}ln}{m}_j}\right)}_{T,P,m_{k\ne j}}=\sum _{i>1}\left(P_{i1}^A-n{P}_{i1}^M\right){\mu }_{ij},$$ (23)

or alternatively,

$$RT{\left(\frac{\partial \text{\hspace{0.17em}ln}K}{\partial {\mu }_j}\right)}_{T,P,m_{k\ne j}}={\left(\frac{\partial \text{\hspace{0.17em}ln}K}{\partial \text{\hspace{0.17em}ln}{a}_j}\right)}_{T,P,m_{k\ne j}}={\mu }_{jj}^{-1}\sum _{i>1}\left(P_{i1}^A-n{P}_{i1}^M\right){\mu }_{ij},$$ (24)

where the sum involves species 2 (not M and A), a_j is the activity of j, and we defined

$${\mu }_{ij}=\frac{1}{RT}{\left(\frac{\partial {\mu }_i}{\partial \text{\hspace{0.17em}ln}{m}_j}\right)}_{T,P,m_{k\ne j}}=\frac{1}{RT}{\left(\frac{\partial {\mu }_i}{\partial \text{\hspace{0.17em}ln}{N}_j}\right)}_{T,P,N_{k\ne j}}.$$ (25)

The molality derivative has been chosen here as there is a general recursion relationship for these derivatives in any closed multicomponent solution.⁴⁵ Reference to the stability requirements for solutions indicates that μ_ii≥0 and μ_ij<0.⁴⁹ Consequently, on increasing the concentration of j the association process is favored when $P_{i1}^A-n{P}_{i1}^M$ is positive for i=j and negative for i≠j. A change in concentration scales can be performed using the following thermodynamic relationships:

$${\left(\frac{\partial \text{\hspace{0.17em}ln}{\rho }_i}{\partial \text{\hspace{0.17em}ln}{m}_i}\right)}_{T,P,m_{j\ne i}}=1-{\varphi }_i{\left(\frac{\partial \text{\hspace{0.17em}ln}{x}_i}{\partial \text{\hspace{0.17em}ln}{m}_i}\right)}_{T,P,m_{j\ne i}}=1-x_i,$$ (26)

where φ_i is the volume fraction and x_i the mole fraction. It should be noticed that these derivatives are positive and so a change in cosolvent concentration variable does not affect the sign of the previous effects.

In a closed system the affinity of all species for the M and A forms contribute to the overall effect. These contributions are expressed relative to species 1 (usually taken as the primary solvent). This is a direct consequence of our choice to eliminate dμ₁ from Eq. 17 using the GD equation, and not due to the use of molality based derivatives. Clearly, one could eliminate any dμ_i to obtain a set of equivalent expressions. Finally, one could obtain an expression for a closed system at constant volume (T, ρ_j≠i) from Eqs. 17, 18, 19, 20. However, we have not pursued this further as the resulting expressions are rather complicated and this ensemble is not relevant for most biological systems, although it is the ensemble adopted in SPT.

CONSTANT T, P, and m₂ Ensemble

The most common situation involves a closed system with n_c=3 at constant T and P, where one is interested in the effect of a single cosolvent (3) on the biomolecular equilibrium when the biomolecule (2) and primary solvent (1) concentrations are constant. To develop expressions for the effect of a cosolvent on the equilibrium in this situation, we eliminate dμ₁ from Eqs. 17, 18, 19 using Eq. 20. Then, noting that m₂ is constant we have from Eq. 19 with i=2 that

$$0=\left(1+N_{22}^{+}\right)d{\mu }_2+N_{23}^{+}d{\mu }_3.$$ (27)

This can then be used to eliminate dμ₂ from Eq. 17 to give

$$RT{\left(\frac{\partial \text{\hspace{0.17em}ln}K}{\partial {\mu }_3}\right)}_{T,P,m_2}=P_{31}^A-n{P}_{31}^M-\frac{\left(P_{21}^A-n{P}_{21}^M\right)N_{23}^{+}}{1+N_{22}^{+}}.$$ (28)

To relate this to the cosolvent concentration one can eliminate dμ₁ from Eq. 18 with i=3 using Eq. 20, and then combine with Eq. 27 to provide

$$RT{\left(\frac{\partial \text{\hspace{0.17em}ln}{\rho }_3}{\partial {\mu }_3}\right)}_{T,P,m_2}=1+N_{33}-N_{13}-\frac{\left(N_{32}-m_2{N}_{31}\right)N_{23}^{+}}{1+N_{22}^{+}}.$$ (29)

Alternatively, if one is interested in the effect of cosolvent molality one can eliminate dμ₁ from Eq. 19 using Eq. 20 with i=3, and then combine with Eq. 27 to generate

$$RT{\left(\frac{\partial \text{\hspace{0.17em}ln}{m}_3}{\partial {\mu }_3}\right)}_{T,P,m_2}=1+N_{33}^{+}-\frac{N_{32}^{+}{N}_{23}^{+}}{1+N_{22}^{+}},$$ (30)

which can then be combined with Eq. 28 if desired. Equation 30 is in agreement with previous results.⁴⁵ We note that the final terms in Eqs. 28, 29, 30 all disappear as the biomolecule concentration tends to zero, a common situation, and are then consistent with previous published expressions.^{27, 29, 47}

In some cases the cosolvent concentration might be constant and the biomolecule concentration may vary. The correct expressions for this situation can be obtained from Eqs. 28, 29, 30 via a simple 2↔3 index change, or by the same approach that led to Eqs. 28, 29, 30 but where m₃ is constant. In principle, Eq. 18 can be used to obtain expressions for d ln x_i and thereby chemical potential derivatives with respect to mole fractions. These expressions are rather cumbersome and, as mole fractions are rarely the concentration scale of choice for biological systems, we have not pursued this further here.

GENERAL EXPRESSIONS FOR ANY NUMBER OF COMPONENTS IN SEMIOPEN SYSTEMS

If the system corresponds to that of a real cell, or some approximation to a real cell, then it may be open to one or more components. Furthermore, the addition of the cosolvent can occur with volume or pressure held constant. Let us consider a system which contains a set of species at fixed concentrations (ρ), together with a set of species with fixed chemical potentials (μ). Taking derivatives of Eq. 17 with respect to one of the cosolvent molarities with volume fixed one obtains the expression

$${\left(\frac{\partial \text{\hspace{0.17em}ln}K}{\partial \text{\hspace{0.17em}ln}{\rho }_j}\right)}_{T,{\rho }_{k\ne j},\mu }=\sum _i^{n_c^{\prime }}\left(N_{Ai}-n{N}_{Mi}\right){\mu }_{ij}^{\prime },$$ (31)

where the sum is over the restricted set of components for which the system is closed $\left(n_c^{\prime }\right)$. Alternatively, with pressure constant one finds

$${\left(\frac{\partial \text{\hspace{0.17em}ln}K}{\partial \text{\hspace{0.17em}ln}{\rho }_j}\right)}_{T,P,N_{k\ne j},\mu }=\sum _i^{n_c^{\prime }}\left(N_{Ai}-n{N}_{Mi}\right){\mu }_{ij}^{″}.$$ (32)

The corresponding chemical potential derivatives are defined

$${\mu }_{ij}^{\prime }=\frac{1}{RT}{\left(\frac{\partial {\mu }_i}{\partial \text{\hspace{0.17em}ln}{\rho }_j}\right)}_{T,{\rho }_{k\ne j},\mu }=\frac{1}{RT}{\left(\frac{\partial {\mu }_i}{\partial \text{\hspace{0.17em}ln}{N}_j}\right)}_{T,V,N_{k\ne j},\mu },$$ (33)

$${\mu }_{ij}^{″}=\frac{1}{RT}{\left(\frac{\partial {\mu }_i}{\partial \text{\hspace{0.17em}ln}{\rho }_j}\right)}_{T,P,N_{k\ne j},\mu }.$$

Expressions for the required derivatives can be obtained after solving the set of simultaneous equations provided by Eqs. 18, 19, 20. This is illustrated in the following two sections.

CONSTANT T, μ₁, and ρ₂ Ensemble

A common osmotic system involves a semiopen system with n_c=3 at constant T, V, and μ₁, where one is interested in the effect of a single cosolvent (3) on a biomolecular equilibrium when the biomolecule concentration is constant and the system is closed to the cosolvent. To develop expressions for the effect of a cosolvent on the equilibrium in this situation, we note that ρ₂ is constant and hence from Eq. 18 with i=2 one has

$$0=\left(1+N_{22}\right)d{\mu }_2+N_{23}d{\mu }_3.$$ (34)

This can then be used to eliminate dμ₂ from Eq. 17 to give

$$RT{\left(\frac{\partial \text{\hspace{0.17em}ln}K}{\partial {\mu }_3}\right)}_{T,{\mu }_1,{\rho }_2}=N_{A3}-n{N}_{M3}-\frac{\left(N_{A2}-n{N}_{M2}\right)N_{23}}{1+N_{22}}.$$ (35)

To relate this to the cosolvent concentration one can eliminate dμ₂ from Eq. 18 with i=3, and then use Eq. 34 to provide

$$RT{\left(\frac{\partial \text{\hspace{0.17em}ln}{\rho }_3}{\partial {\mu }_3}\right)}_{T,{\mu }_1,{\rho }_2}=1+N_{33}-\frac{N_{32}{N}_{23}}{1+N_{22}}.$$ (36)

Alternatively, if one is interested in the effect of cosolvent molality one can eliminate dμ₂ from Eq. 19 with i=3, and then use Eq. 34 to generate

$$RT{\left(\frac{\partial \text{\hspace{0.17em}ln}{m}_3}{\partial {\mu }_3}\right)}_{T,{\mu }_1,{\rho }_2}=1+N_{33}-N_{13}-\frac{\left(N_{32}-N_{12}\right)N_{23}}{1+N_{22}},$$ (37)

which can then be combined with Eq. 35 if desired. We note that the final terms in Eqs. 35, 36, 37 all disappear as the biomolecule concentration tends to zero.

CONSTANT T, P, μ₁, and N₂ Ensemble

A second common semiopen ensemble involves a system with n_c=3 at constant T, P, and μ₁, where one is interested in the effect of a single cosolvent (3) on a biomolecular equilibrium when the number of biomolecules is constant, and the system is also closed with respect to the cosolvent. To develop expressions for the effect of a cosolvent on the equilibrium in this situation we note that P is constant and hence from Eq. 20 one has

$$0={\rho }_{2}d{\mu }_2+{\rho }_{3}d{\mu }_3.$$ (38)

This can then be used to eliminate dμ₂ from Eq. 17 to give

$$RT{\left(\frac{\partial \text{\hspace{0.17em}ln}K}{\partial {\mu }_3}\right)}_{T,P,{\mu }_1,N_2}=N_{A3}-n{N}_{M3}-\frac{{\rho }_3}{{\rho }_2}\left(N_{A2}-n{N}_{M2}\right).$$ (39)

To relate this to the cosolvent concentration one can eliminate dμ₂ from Eq. 18 with i=3, and then use Eq. 38 to provide

$$RT{\left(\frac{\partial \text{\hspace{0.17em}ln}{\rho }_3}{\partial {\mu }_3}\right)}_{T,P,{\mu }_1,N_2}=1+N_{33}-N_{23}.$$ (40)

Alternatively, if one is interested in the effect of cosolvent molality one can eliminate dμ₂ from Eq. 19 with i=3, and then use Eq. 38 to generate

$$RT{\left(\frac{\partial \text{\hspace{0.17em}ln}{m}_3}{\partial {\mu }_3}\right)}_{T,P,{\mu }_1,N_2}=1+N_{33}-N_{13}-N_{23}+m_3{N}_{21},$$ (41)

which can then be combined with Eq. 39 if desired.

SYMMETRIC IDEAL SOLUTIONS

Ideal behavior occurs when the right hand side of Eqs. 29, 30, 36, 37, etc., is unity. Clearly, the corresponding relationships between the KBIs depend on the concentration scale and the ensemble. Symmetric ideal (SI) solutions provide a useful reference point for understanding the properties of real solution mixtures in closed ensembles at constant temperature and pressure.²⁶ SI solutions are defined by the fact that the mole fraction scale activity coefficients are unity for all components over all compositions, i.e., dμ_i=RTd ln x_i. In terms of the KBIs this requirement is fulfilled when ΔG_ij=G_ii+G_jj−2G_ij=0 for all i,j pairs.²⁶ Recently, we provided a general expression for the KB integrals in SI solutions of any number of components,⁵⁰

$$G_{ij}=RT{\kappa }_T-V_i-V_j+S_{n_c}{S}_{n_c}=\sum _{k=1}^{n_c}{\rho }_k{V}_k^2,$$ (42)

where the sum is over all n_c components of the mixture, κ_T is the isothermal compressibility, and V_i is the molar volume of pure component i at the same T and P. For our pseudo-n_c+1 component system, one can write

$$S_{n_c+1}={\varphi }_2⟨V_2⟩+\sum _{k\ne M,A}^{n_c+1}{\rho }_k{V}_k^2,$$ (43)

$$⟨V_2⟩=f_M{V}_M+f_A{V}_A=V_2\left(f_M+n{f}_A\right),$$

$${\varphi }_2={\rho }_M{V}_M+{\rho }_A{V}_A=\left({\rho }_M+n{\rho }_A\right)V_2={\rho }_2{V}_2.$$

In developing the above expressions we made the very reasonable assumption that

$$V_A=n{V}_M=n{V}_2.$$ (44)

For instance, estimated differences in volume between native and denatured proteins are typically small compared to their total volumes.^{27, 51, 52} The value of ⟨V₂⟩ is the average molar volume of the biomolecule at that particular composition and varies between V_M=V₂ for f_M=1 and V_A=nV₂ for f_A=1.

Using Eq. 42 one can develop expressions for the various combinations of KB integrals that appeared in the previous sections. Hence, one finds

$$N_{ij}-N_{kj}={\rho }_j\left(V_k-V_i\right),$$ (45)

$$N_{ij}-m_j{N}_{i1}={\rho }_j\left(V_1-V_j\right),$$

$$N_{ij}^{+}=m_j,$$

for any i and j=1,2, etc. For KB integrals involving specific forms of the biomolecule we have

$$N_{Ai}-n{N}_{Mi}=\left(n-1\right){\rho }_i\left(V_i-RT{\kappa }_T-S_{n_c+1}\right),$$ (46)

$$P_{ij}^A-n{P}_{ij}^M=\left(n-1\right){\rho }_i\left(V_i-V_j\right),$$

for any i and j=1,2, etc., after using Eq. 44. In both cases the mean value of the molar volume ⟨V₂⟩ should be used when i or j=2.

For SI solutions one finds that μ_ij=δ_ij−x_j and therefore insertion of the SI expressions into Eq. 23 and performing the summation leads to a general result for SI solutions,

$${\left(\frac{\partial \text{\hspace{0.17em}ln}K}{\partial \text{\hspace{0.17em}ln}{m}_j}\right)}_{T,P,m_{k\ne j}}^{\text{SI}}=\left(n-1\right){\rho }_j\left(V_j-V_m\right)=\left(n-1\right)\left({\varphi }_j-x_j\right),$$ (47)

valid for any number of components. Here, V_m=V∕(N₁+N₂+⋯) is the molar volume, or the average volume per molecule of the solution, and φ_i=ρ_iV_i is the volume fraction. Hence, an increase in the concentration of the biomolecule or an additive has no affect on the equilibrium in SI solutions when n=1, while they increase the equilibrium constant for n>1 when their molar volume is larger than the average volume of the solution components. This appears to follow the result expected for a simple excluded volume effect where the excluded volume is smaller for the aggregate compared to an equivalent number of monomers. However, this is incorrect as we have not assumed anything concerning the character (size or shape) of either the M or A species. The real origin of the result is discussed later. SI solution results for other concentration scales are given by

$${\left(\frac{\partial \text{\hspace{0.17em}ln}K}{\partial \text{\hspace{0.17em}ln}{\rho }_j}\right)}_{T,P,m_{k\ne j}}^{\text{SI}}=\left(n-1\right){\rho }_j\frac{V_j-V_m}{1-{\varphi }_j},$$ (48)

$$RT{\left(\frac{\partial \text{\hspace{0.17em}ln}K}{\partial {\mu }_j}\right)}_{T,P,m_{k\ne j}}^{\text{SI}}={\left(\frac{\partial \text{\hspace{0.17em}ln}K}{\partial \text{\hspace{0.17em}ln}{x}_j}\right)}_{T,P,m_{k\ne j}}^{\text{SI}}=\left(n-1\right){\rho }_j\frac{V_j-V_m}{1-x_j},$$

where we used the previous relationships between the concentration derivatives.

ALTERNATIVE DEFINITIONS OF THE EQUILIBRIUM CONSTANT

Our choice of an equilibrium constant utilizing number densities was motivated by the pseudochemical potential (pcp) approach pioneered by Ben-Naim.⁴⁶ The pcp (μ^*) is related to the total chemical potential by the equation

$${\mu }_i={\mu }_i^{\ast }+RT\text{\hspace{0.17em}ln}\left({\Lambda }_i^3{\rho }_i\right),$$ (49)

where Λ is the thermal de Broglie wavelength. The equilibrium condition then provides

$$RTd\text{\hspace{0.17em}ln}K=-\left(d{\mu }_A^{\ast }-nd{\mu }_M^{\ast }\right).$$ (50)

The pcp approach helps to simplify the resulting expressions for the same reasons as outlined previously.²⁶ Other definitions of the equilibrium constant are possible, but typically generate extra terms which complicate the analysis. This can be seen from the following expressions which relate various definitions of the equilibrium constant to the one used here. For instance,

$$d\text{\hspace{0.17em}ln}{K}_m=d\text{\hspace{0.17em}ln}K+\left(n-1\right)d\text{\hspace{0.17em}ln}{\rho }_1,K_m=\left(\frac{m_A}{m_M^n}\right),$$ (51a)

$$d\text{\hspace{0.17em}ln}{K}_x=d\text{\hspace{0.17em}ln}K+\left(n-1\right)d\text{\hspace{0.17em}ln}\rho ,K_x=\left(\frac{x_A}{x_M^n}\right),$$ (51b)

$$d\text{\hspace{0.17em}ln}{K}_f=d\text{\hspace{0.17em}ln}K+\left(n-1\right)d\text{\hspace{0.17em}ln}{\rho }_2,K_f=\left(\frac{f_A}{f_M^n}\right),$$ (51c)

$$d\text{\hspace{0.17em}ln}{K}_{\rho }=d\text{\hspace{0.17em}ln}K+\left(n-1\right)d\text{\hspace{0.17em}ln}{\rho }_M,K_{\rho }=\left(\frac{{\rho }_A}{{\rho }_M}\right),$$ (51d)

where ρ is the total number density. The final terms in Eqs. 51a, 51b, 51c, 51d represent additional contributions which depend on the ensemble. They are properties of the solution mixture itself, and not directly related to the affinity of any of the species to the different forms of the biomolecule (see later). Also, we note that defining an equilibrium constant by K^′=nρ_A∕ρ_Mⁿ does not affect any of the results presented here as d ln K^′=d ln K. The final expression [Eq. 51d] does not include the factor of n for the equilibrium constant. Hence, this does not correctly reflect the stoichiometry of the association reaction. However, it may relate more meaningfully to the experimental data which are typically indirect measures of biomolecular concentrations obtained through spectroscopic or activity measurements, or for solutions where a unique value of n might not be known. Clearly, different results are obtained with different definitions of the equilibrium constant, and therefore comparisons with experimental data should be performed with care.

APPROXIMATE FREE ENERGY CURVES

KB theory provides expressions for derivatives of the equilibrium constant (or free energy) for a particular process in terms of the intermolecular distributions observed in solution. To obtain changes in the equilibrium constant one has to then integrate. Unfortunately, the general dependence of the N_ij on composition is unknown. However, one can make some reasonable approximations and investigate the results. First, most studies involve the solute (2) at low concentrations. Second, if the G_ij are assumed to be relatively constant then one can obtain approximate free energy curves. Therefore, for two of the main ternary systems [Eqs. 28, 29, and Eqs. 35, 36] one finds

$$-\beta \Delta \Delta G=\text{ln}{\left(\frac{K}{K_0}\right)}_{T,P,m_2\to 0}=\frac{P_{31}^A-n{P}_{31}^M}{N_{33}-N_{13}}\text{ln}\left(1+N_{33}-N_{13}\right),$$ (52)

$$-\beta \Delta \Delta G^{\prime }=\text{ln}{\left(\frac{K}{K_0}\right)}_{T,{\mu }_1,{\rho }_2\to 0}=\frac{N_{A3}-n{N}_{M3}}{N_{33}}\text{ln}\left(1+N_{33}\right),$$ (53)

which may be compared to the corresponding exact SI result,

$$-\beta \Delta \Delta G^{\text{SI}}=\text{ln}{\left(\frac{K}{K_0}\right)}_{T,P,m_2\to 0}^{\text{SI}}=-\left(n-1\right)\text{ln}\left[1+{\rho }_3\left(V_1-V_3\right)\right],$$ (54)

where ΔΔG=ΔG(ρ₃)−ΔG(0), β=1∕RT, and K₀ is the equilibrium constant in the absence of cosolvent. A similarity to denaturation binding models is clearly apparent.^{53, 54, 55} For small ρ₃ the right hand side reduces to $P_{31}^A-n{P}_{31}^M$ and N_A3−nN_M3 for the closed and open systems, respectively. Hence, using these approximations the cosolvent effect is predicted to be linear in cosolvent molarity for low cosolvent concentrations—a result observed experimentally.⁵⁶ We note that the infinitely dilute biomolecule limit applied to Eq. 38 results in dμ₃=0 for the T, P, and μ₁ ensemble.

There are additional relationships relating the various KBIs which can be related to the properties of solution mixtures. For instance, taking derivatives of Eq. 17 with respect to P and keeping T and all N_i constant provides,

$$\left(1-n\right)RT{\kappa }_T=\sum _i^{n_c}\left(N_{Ai}-n{N}_{Mi}\right)\overline{V_i},$$ (55)

where $\overline{V_i}$ is the partial molar volume (pmv). The above expression assumes that N_A and N_M are reasonably independent of pressure. Equation 55 can be developed further for the case of n_c=3 and an infinitely dilute biomolecule, by assuming that the left hand side of Eq. 55 is small and may be neglected. This is true for n=1 and should be reasonable for n<10 for all but small cosolvent concentrations. In this case one can relate the preference of 3 over 1 for the biomolecule to just the affinity of 3 for both forms,

$$P_{31}^A-n{P}_{31}^M\approx \frac{N_{A3}-n{N}_{M3}}{{\varphi }_1}.$$ (56)

This is a generalization of a previous result.^{27, 57} The relationship exists because, under these approximations, an increase in the local density of one species around the biomolecule should be accompanied by some degree of depletion of another species in the same region. Using Eq. 56 in Eq. 52 and comparing with Eq. 53 one can predict the relative effects of the addition of a cosolvent in both open and closed systems. The result is

$${\varphi }_1\Delta \Delta G\approx \Delta \Delta G^{\prime }$$ (57)

for low biomolecule and cosolvent concentrations. This also assumes that the KBIs are reasonably independent of the osmotic pressure, i.e., G_ij(T,N,P)≈G_ij(T,N,P+Π). Therefore, the cosolvent effect should be larger in magnitude in a closed system compared to a similar corresponding semiopen system.

RELATIONSHIP TO THE BEN-NAIM RESULT FOR CLOSED SYSTEMS

Previously, Ben-Naim studied the effects of cosolvents on molecular association using KB theory.⁴³ In particular, the effect of a cosolvent on an equilibrium involving an infinitely dilute solute expressed in terms of the quantity (∂N_A∕∂N₃)_T,P,m2→0 in closed systems. The results presented here are different from the Ben-Naim expression for several reasons. First, we used an equilibrium constant in terms of numbers densities instead of just N_A. Second, the cosolvent concentration has been expressed in terms of molarity or molality rather than N₃. This does not change the general conclusions obtained from the respective expressions, although it does change the expressions themselves. To illustrate further we will transform our result [Eqs. 28, 30] into the corresponding Ben-Naim expression. To do this we note that one can define an equilibrium constant using the molecule numbers (K_N). This is related to the equilibrium constant used here by

$$d\text{\hspace{0.17em}ln}K=d\text{\hspace{0.17em}ln}\left(\frac{N_A}{N_M^n}\right)-d\text{\hspace{0.17em}ln}\left(\frac{V}{V^n}\right)=d\text{\hspace{0.17em}ln}{K}_N+\left(n-1\right)d\text{\hspace{0.17em}ln}V.$$ (58)

Taking the appropriate derivative in the required ensemble one obtains

$${\left(\frac{\partial \text{\hspace{0.17em}ln}K}{\partial \text{\hspace{0.17em}ln}{N}_3}\right)}_{T,P,m_2}={\left(\frac{\partial \text{\hspace{0.17em}ln}{K}_N}{\partial \text{\hspace{0.17em}ln}{N}_3}\right)}_{T,P,m_2}+\left(n-1\right){\rho }_3\overline{V_3}.$$ (59)

Finally, the relationship between changes in the equilibrium constant and changes in N_A can be obtained from Eq. 5 with N₂ constant,

$$d\text{\hspace{0.17em}ln}{K}_N=\frac{N_M+n^2{N}_A}{N_A{N}_M}d{N}_A.$$ (60)

Combining these relationships with Eqs. 28, 30 one obtains the Ben-Naim result in our notation,

$${\left(\frac{\partial N_A}{\partial N_3}\right)}_{T,P,m_2\to 0}=\frac{N_A{N}_M}{N_3\left(N_M+n^2{N}_A\right)}\frac{P_{31}^A-n{P}_{31}^M-\left(n-1\right)m_3\left(1+N_{11}-N_{31}\right)}{1+N_{33}^{+}},$$ (61)

where we used the KB expression for the pmv of 3 in a binary solution of 1 and 3.⁴⁶ Clearly, the expression presented here is simpler and easier to interpret. This is a direct consequence of investigating the changes in an equilibrium constant defined using number densities, i.e., the pcp approach.

DISCUSSION

In the above sections we provided an analysis, using KB theory, of the effects of increasing biomolecule and cosolvent concentrations on molecular association in solution. KBIs involving species 2, M, and A appear in these expressions, even though they are different representations of the same species. This was done deliberately. The use of N₂₂ in the above expressions serves to indicate that this corresponds to a KBI between all forms of the biomolecule where one does not distinguish between monomer and aggregate. Alternatively, the use of N_M3 (or N_A3) indicates a correlation between M and 3 (or A and 3) which is specific for one particular form of the biomolecule. In addition, the use of N_M2 (or N_A2) signifies a correlation between the monomer (or aggregate) form and any other form of the biomolecule, both monomer and aggregate. Hence, we have nonspecific effects involving the KBIs for species 2, together with specific effects involving the KBIs for species M or A.

The resulting expressions for closed systems involve terms of the form $P_{i1}^A-n{P}_{i1}^M$. These terms quantify the excess (or depletion) of i over 1 in the vicinity of an aggregate over the same excess (or depletion) of i in the vicinity of n monomers. Therefore, if a species i displays a higher affinity for the aggregate than n individual monomers, then $P_{i1}^A-n{P}_{i1}^M>0$ and an increase in the concentration of i leads to an increase in equilibrium constant and a shift in the equilibrium toward the associated form. The cosolvent urea serves as a reasonable example. Urea is well known to denature proteins.⁵⁶ Hence, when n=1 the preference of urea (over water) for the denatured state must be larger, on average, than that for the native state. Assuming this is related to the corresponding increase in exposed surface area upon denaturation,⁵⁸ this suggests that urea should stabilize the monomer over the aggregate as an aggregate typically possesses less surface area than n monomers. Hence, urea is a denaturant of proteins but should help prevent protein aggregation. This behavior has been observed experimentally.^{59, 60} The opposite effects will be observed for classic osmolytes.

Some general trends are observed in the results. From Eq. 17 it is clear that the effect on the equilibrium does not involve any KBIs between the biomolecule and any species that is kept at a constant chemical potential. Any species at constant N will contribute to changes in the equilibrium as quantified through the KBIs. Hence, all the species contribute in closed systems [see Eq. 23]. The main reason for this is quite simple. When a cosolvent displaces a solvent molecule in the vicinity of the biomolecule both the addition of cosolvent and the removal of a solvent (or other) molecule from the biomolecule affect the Gibbs free energy of the system. On the other hand, when a cosolvent displaces a solvent molecule in a system open to the solvent, only the addition of the cosolvent affects the free energy of the system. A change in concentration scale (μ→m→ρ) typically results in a scaling effect [Eq. 26], but this does not alter the sign of the effects contributing to the change in equilibrium constant.

The expression provided in Eq. 47 for closed SI solutions indicates that the association equilibrium is increased by the addition of additives with a larger molar volume than the average molecular volume of the solution at that composition. The same expression can be obtained from Eq. 51b noting that d ln K_x=0 for SI solutions [see Eq. 7]. Hence, we have two contributions to changes in the equilibrium constant for SI solutions. First, on addition of a cosolvent the volume of the solution increases. This affects the number densities of M and A, and directly increases the equilibrium constant when n>1. Second, the addition of another particle to the system changes the total number of species present and therefore the mole fraction of each species. This causes an increase in the monomer form to maintain the equilibrium condition. Finally, we note that dilution, i.e., the addition of solvent, will favor dissociation as long as the solvent has a low molar volume. These effects dominate in the absence of a particular affinity between any of the pairs of species in solution. There is no effect on a simple denaturation equilibrium in SI solutions.

It is well known that cellular crowding, as described by the addition of rather large cosolvents, will tend to favor association.⁶ The usual explanation for this observation is that aggregates display less surface area, and therefore less excluded volume, compared to a collection of their monomers. Excluded volume effects also favor the native state over the denatured state for the n=1 case. In contrast, the SI result discussed above indicates that any excluded volume contributions are balanced by other (favorable) contributions so that ΔG_ij=0 for all i,j pairs. In a hard sphere fluid model, as adopted in SPT, the SI condition does not hold and excluded volume contributions are dominant. These also favor the associated or native forms. However, we emphasize that even for ideal (mole fraction scale) solutions the addition of a large cosolvent favors association when the equilibrium constant is defined using molarities, and this effect is not related to any change in excluded volume.

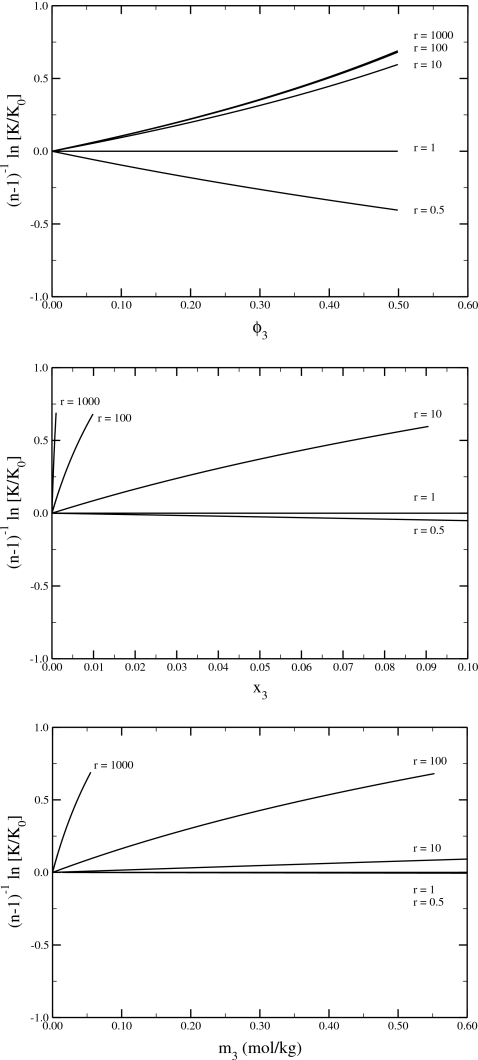
The results predicted by Eq. 54 for closed ternary SI solutions are illustrated in Fig. 2. A variety of cosolvents are considered with different molar volumes relative to the primary solvent. The effects are linear in volume fraction at low cosolvent concentrations but display deviation from linear behavior at higher concentrations. All the results scale with n−1 and are independent of the size or shape of the monomer or aggregate, although Eq. 44 was used during the derivation. The magnitude of the effects obtained from Eq. 54 for closed SI solutions is similar to that predicted by SPT depending on the biomolecule shapes used (see Fig. 3 from Ref. 6, for instance). Clearly, we have two solution models that display similar results in qualitative agreement with experiment. Both are approximations to real solution conditions of biological interest. The SI approach represents a thermodynamic model, while SPT presents a physical model for solutions. It is unclear at present which, if any, is more reasonable.

Figure 2.

SI results for the effects of a single crowder (3) on the association equilibrium (nM→A) of an infinitely dilute solute (2) in a primary solvent (1) in a closed system. The data were obtained using Eq. 54 for different molar volume ratios (r) of the crowder and solvent such that V₃=rV₁. The results are plotted as a function of cosolvent volume fraction (φ₃=ρ₃V₃), cosolvent mole fraction (x₃), and cosolvent molality (m₃) with water as the solvent. In this case x₃=φ₃∕[φ₃+r(1−φ₃)] and m₃=1000φ₃∕r(1−φ₃)∕18.015. For reference, the molar volume of pure water is V₁=18 cm³∕mol and so r=1000 would correspond to a 25 kDa protein of approximately 225 residues. All curves are truncated at a cosolvent volume fraction of 0.5.

The analysis of cosolvent effects on a chemical equilibrium using KB theory is exact. The KBIs quantify the local composition of the solution surrounding the various species corresponding to a four component system for the case of a single cosolvent. There is no problem extracting all the required KBIs from computer simulations as long as one can define the aggregate in a consistent manner. From a thermodynamic point of view, however, this is formally a three component system. Consequently, it is difficult to extract the individual KBIs from an analysis of the thermodynamic data alone. For instance, a general n_c component system has n_c(n_c+1)∕2 unique G_ij integrals. To determine the integrals from experimental data using the KB inversion approach requires 1 compressibility, n_c−1 independent pmvs, and therefore n_c(n_c−1)∕2 independent chemical potential derivatives (μ_ij) as a function of composition. However, for our pseudo-four component system one can use the relationships in Eqs. 28, 29, 30 as long as one knows K and n for a particular system as a function of composition. Hence, one still has only six (n_c=3) unique KBIs as many of the ten (n_c=4) KBIs are related through Eqs. 14, 15 and therefore are not unique.

CONCLUSIONS

In this study we applied KB theory to investigate the effects of cosolvents on molecular equilibria in solution. This is an extension of the previous approach of Ben-Naim to include any number of components at finite concentrations in both closed and semiopen systems. No assumption concerning the character, specifically the size and∕or shape, of the molecules has been made. Hence, the results are totally general and can be applied to a variety of processes such as protein denaturation, protein aggregation, and cellular crowding, where the cosolvent can be either small (H⁺, urea) or large (another protein). In addition, the extension to include semiopen systems also allows one to consider systems under typical biological (cellular) conditions. Here, the effect of a cosolvent appears to be reduced compared to closed systems.

The results obtained here depend on the definition of the equilibrium constant. We advocate the use of molarities in accord with the pcp approach of Ben-Naim. In this case, even SI solutions, where significant excluded volume effects are absent, indicate an increase in association on the addition of a cosolvent crowder. This does not mean that excluded volume effects are not important in these systems. Merely that at least some of the typical effects can be explained without invoking excluded volume. Significant deviations from SI behavior will be observed when the cosolvent displays a preference for either form of the biomolecule.

A particular advantage of the KB approach is that one has exact expressions for the cosolvent effects in terms of KBIs which are directly related to molecular distributions. Hence, one can develop a series of models, each providing different approximations to the real KBIs, and thereby determine the resulting thermodynamic effects of various approaches. We are currently using this type of approach to compare in more detail the KB based results for hard sphere crowders to those obtained from the traditional SPT approach.