Error and efficiency of replica exchange molecular dynamics simulations

Abstract

We derive simple analytical expressions for the error and computational efficiency of replica exchange molecular dynamics (REMD) simulations (and by analogy replica exchange Monte Carlo simulations). The theory applies to the important case of systems whose dynamics at long times is dominated by the slow interconversion between two metastable states. As a specific example, we consider the folding and unfolding of a protein. The efficiency is defined as the rate with which the error in an estimated equilibrium property, as measured by the variance of the estimator over repeated simulations, decreases with simulation time. For two-state systems, this rate is in general independent of the particular property. Our main result is that, with comparable computational resources used, the relative efficiency of REMD and molecular dynamics (MD) simulations is given by the ratio of the number of transitions between the two states averaged over all replicas at the different temperatures, and the number of transitions at the single temperature of the MD run. This formula applies if replica exchange is frequent, as compared to the transition times. High efficiency of REMD is thus achieved by including replica temperatures in which the frequency of transitions is higher than that at the temperature of interest. In tests of the expressions for the error in the estimator, computational efficiency, and the rate of equilibration we find quantitative agreement with the results both from kinetic models of REMD and from actual all-atom simulations of the folding of a peptide in water.

INTRODUCTION

Molecular dynamics (MD) allows us to explore the structure, energetics, and dynamics of molecular systems with atomistic resolution, including those of large biomolecular systems. However, the maximum time step permitted in the numerical integration of the equations of motion is of the order of a femtosecond, limited by the fast time scales associated with molecular vibrations and collisions. As a result of this short time step, simulations are currently limited to the nanosecond to microsecond regime. Therefore, many important (bio)molecular processes remain out of reach, such as the folding of all but the smallest proteins.

Replica exchange molecular dynamics (REMD)^{1, 2} has become an increasingly popular technique for accelerating MD simulations, including those of biological processes such as protein folding. Replica exchange (also named parallel tempering) was introduced originally^{3, 4} in combination with Monte Carlo sampling, but the central idea of establishing an equilibrium between canonical systems with different Hamiltonians (here, rescaled by temperature) can be traced back at least to the seminal papers by Bennett⁵ and Swendsen and Wang.⁶ In standard REMD, MD simulations of N identical molecular systems are run in parallel, but each replica is thermostatted at a different temperature T_i (where the thermostat has to maintain a canonical distribution⁷). At regular intervals, attempts are made to exchange the structures of pairs of replicas, i↔j, accepting the exchanges with a probability that conserves the canonical distributions at the two temperatures, T_i and T_j. In this way, one aims to transfer the improved sampling efficiency at the higher temperature, where activation barriers are more easily crossed, to the lower temperature of interest, where the system would otherwise be stuck in deep local potential energy minima.

Assessing the computational efficiency of REMD, or the analogous replica exchange Monte Carlo (REMC), is important because the primary purpose of these methods is to accelerate standard molecular simulations. Remarkably, though, the advantages of REMD are far from being clear. Despite the widespread use, there has been no general theory addressing the efficiency of the REMD protocol as a function of the system properties and simulation parameters, including the number and temperatures of the replicas and the frequency of exchange attempts.

Several recent studies addressed the problem of the replica exchange efficiency.^{8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19} An important result obtained by Sindhikara et al.⁸ is that exchange attempts are best chosen as frequently as possible. Similar conclusions were obtained by Abraham and Gready¹⁷ based on analyzing the autocorrelation function of the potential energy.

Here, we develop a general quantitative theory of the statistical error and the computational efficiency of REMD. The theory applies to systems whose relaxation behavior at long times can be described by transitions between two states with finite rates of interconversion. Moreover, our results are derived in the fully equilibrated asymptotic limit, where the variance in the estimators decreases as the reciprocal of the simulation time. For systems with true first-order transitions (instead of the quasi-first-order transitions of, say, protein folding), this would require progressively longer simulation times as the system size is increased in approaching the thermodynamic limit.

We define the efficiency as the rate with which the error in an estimated equilibrium property (as measured by the variance of the estimator over repeated simulations of the same length) decreases with simulation time. For both regular MD and REMD simulations, we then determine analytical expressions for this rate of decrease in the error that is, in general, independent of the particular property of interest. These error expressions are derived for systems in which the dynamics at long times is dominated by a single slow and exponential relaxation process, such as the folding and unfolding of a protein.

Our theory is based on a kinetic model of two-state systems at multiple temperatures coupled by replica exchange. In our model, REMD is described by a rate matrix for 2^N states, where N is the number of replicas. This kinetic framework is similar to the one presented recently by Zheng et al.,⁹ but is simplified by not keeping track of the temperature at which a certain replica started (which substantially reduces the number of states from N!2^N to 2^N). Our kinetic framework is also related to the master-equation description of replica exchange introduced by Nadler and Hansmann.^{13, 14, 15} However, these authors focused on the rate with which individual replicas sample the different temperatures and derived formulas for this rate under the assumption that at each replica the energy relaxes fast between replica exchange attempts.¹³ Here, we are concerned with the sampling of observables of interest (say, the fraction folded of a protein) at a given temperature, not the sampling of temperature space by individual replicas. These observables relax slowly at each temperature, whereas replica exchange is assumed to be fast. Indeed, in agreement with Refs. ^{13, 14, 15}, we find that efficient sampling at a low temperature, in general, requires fast replica exchange with higher temperatures, which can be assessed with the “replica round-trip time.”¹⁵ We note, however, that for our systems of interest we assume ergodicity in the regular MD such that at long times properties of interest will be properly sampled even without replica exchange (i.e., with infinite round-trip times).

Addressing the REMD efficiency requires the solution of the eigenproblem of the 2^N×2^N rate matrix, which in the general case can be obtained only numerically. However, we derive a theoretical formula for the efficiency and the slowest relaxation rate of the overall dynamics of the replica exchange protocol in the important limit of fast replica exchange and for a large number of replicas that span the temperature range densely. We show that this formula provides an excellent approximation in practical applications.

The main result is a simple expression for the relative efficiency of REMD and MD simulations. We consider REMD simulations of duration t_sim with N replicas at temperatures T_i (i=1,2,…,N). The temperatures and exchange attempt frequency are chosen such that exchanges are accepted frequently in comparison to the rate of the slow two-state transition. For the sake of concreteness, we use the specific example of folding and unfolding of a protein. In MD, a single simulation run is performed at the sole temperature of interest, T_k (which will typically be the lowest temperature, k=1), of length Nt_sim. MD and REMD runs thus require the same computational effort if one ignores overheads from replica exchange and issues of serial versus parallel runs. In this case, the relative efficiency of sampling an observable A at temperature T_k in a REMD simulation versus sampling the same property in a MD simulation using the same net resources is

$${\eta }_k\equiv \frac{{\text{var}}_{\text{MD}}\left(\overline{A}\right)}{N{\text{var}}_{\text{REMD}}\left(\overline{A}\right)}=\frac{1}{N}\sum _{i=1}^N\frac{{\tau }_k^{+}+{\tau }_k^{-}}{{\tau }_i^{+}+{\tau }_i^{-}},$$ (1)

where ${\mathrm{var}}_{\mathrm{MD}}\left(\overline{A}\right)∕N$ and ${\mathrm{var}}_{\mathrm{REMD}}\left(\overline{A}\right)$ are the variances of the estimated means of any typical observable A in MD and REMD simulations of the same length t_sim, respectively, and ${\tau }_i^{+}\equiv 1∕k_i^{+}$ and ${\tau }_i^{-}\equiv 1∕k_i^{-}$ are the lifetimes of the system in its two long-lived (unfolded and folded) states at temperature T_i; $k_i^{+}\equiv k_F\left(T_i\right)$ and $k_i^{-}\equiv k_U\left(T_i\right)$ are the corresponding (folding and unfolding) rates. If η_k>1, it is more efficient to run REMD with N replicas to sample properties at temperature T_k than to run a single MD simulation N-times as long as T_k. In practice, the REMD efficiency is further enhanced by using results from the other temperatures, for instance through histogram reweighting.

Equation 1 for the relative efficiency of REMD simulations has a physical interpretation. η_k is the ratio of the number of folding and unfolding transitions per unit time in the REMD runs averaged over the N replicas and in the N-times longer MD simulation at the temperature of interest. Equivalently, η_k is the ratio of the reactive flux in REMD and MD, with the flux averaged over all temperatures in REMD. As a consequence, it is advantageous in REMD to include replica temperatures in which the frequency of transitions is higher than that at the temperature of interest. In contrast, including temperatures with lower fluxes (typically at lower temperatures) reduces the efficiency.

By analogy, Eq. 1 for the sampling efficiency also applies to REMC simulations. Assuming that the same Monte Carlo move sets are used in regular Monte Carlo and in REMC (except for replica exchange), the relaxation times can be measured in units of the number of attempted moves. The times ${\tau }_i^{+}$ and ${\tau }_i^{-}$ are then simply the lifetimes in the two-state (folded and unfolded) measured in units of Monte Carlo moves.

In Sec. 3, we test the validity of Eq. 1 and related expressions for the absolute error and the rates of relaxation and show that their predictions are in quantitative agreement with the results from both simulated REMD and actual all-atom simulations of an alanine pentapeptide in water. We conclude with a discussion of the practical relevance of our theoretical analysis of the error and efficiency of REMD.

THEORY

Rate model of REMD

We will analyze the statistical error and efficiency of REMD simulations for the important case of systems whose dynamics at long times is governed by a single slow exponential relaxation process. In general, complex molecular systems have multiple states and, correspondingly, a broad spectrum of relaxation processes. Nevertheless, in many of these systems, the relaxation to equilibrium is dominated by a single-exponential process at sufficiently long times, resulting from the slow and practically memoryless interconversion between the two longest-lived metastable states. A specific example is the folding of small proteins, where the populations of folded and unfolded states relax on time scales that range from microseconds to seconds.

In such systems, a reduced two-state description captures the long-time dynamics. For the sake of concreteness, we will refer to the slow processes as protein folding and unfolding. In the absence of replica exchange, we assume that the interconversion between the folded and unfolded states F_i and U_i, respectively, at temperature T_i of replica i can be described by first-order kinetics,

$$U_i\underset{k_i^{-}}{\overset{k_i^{+}}{\rightleftharpoons }}{F}_i\left(i=1,2,\dots ,N\right).$$ (2)

In replica i, the folded and unfolded populations will relax to the respective equilibrium folded populations $p_i=k_i^{+}∕\left(k_i^{+}+k_i^{-}\right)$ and unfolded populations q_i=1−p_i with a rate given by the sum of the folding and unfolding rates,

$${\lambda }_i=k_i^{+}+k_i^{-},$$ (3)

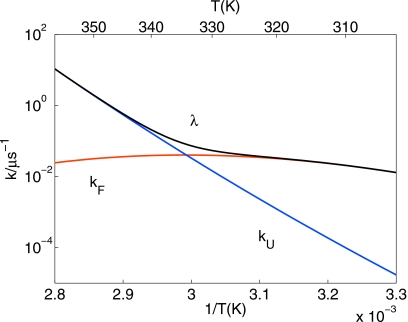
where τ_i=1∕λ_i is the corresponding relaxation time. As an illustration, Fig. 1 shows the temperature dependence of the folding and unfolding rates and the corresponding relaxation rate for the λ-repressor fragment λ_6–85.²⁰

Figure 1.

Temperature dependence of folding (k_F, red) and unfolding (k_U, blue) rates and of the relaxation rates (λ, black) of the λ-repressor fragment λ_6–85 (Ref. ²⁰). The temperature dependent rate constants were calculated based on Table II of Ref. 20 and the temperature dependence of the water viscosity.

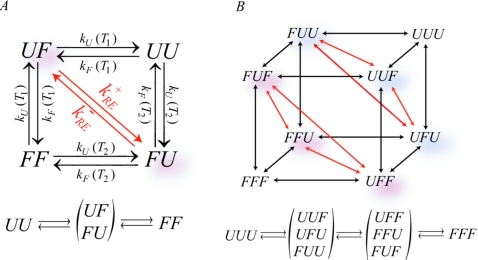
Replica exchange couples the dynamics of the systems at the different temperatures. To extend the kinetic description [Eq. 2] to REMD, we describe the overall state of the system by a vector s_i, where s_i is 1 if replica i is folded and 0 if it is unfolded. Accordingly, the number of states of the entire system is 2^N. In REMD simulations, short regular MD simulations alternate with replica exchange attempts. Typically, the lifetimes in the folded and unfolded states will be long compared to the times between attempted exchanges. Therefore, instead of alternatingly propagating the kinetic equations [Eq. 2] and applying a Markov transition matrix to perform the replica exchange, we describe replica exchange simply as an additional kinetic process occurring in parallel with the folding∕unfolding processes. The dynamics can then be described by 2^N coupled rate equations instead of the N uncoupled ones of Eq. 2 without replica exchange. In typical implementations, exchanges occur between neighboring replicas, ordered according to temperature, as illustrated in Fig. 2. To describe the kinetics of this coupling, we consider exchanges F_iU_j→U_iF_j, where the subscripts i and j=i±1 are for neighboring replicas. Exchanges between identical folding states, F_iF_j→F_jF_i=F_iF_j or U_iU_j→U_jU_i=U_iU_j, do not need to be considered since they do not change the overall state of the system.

Figure 2.

Kinetic model of replica exchange. Connectivity of all states is illustrated for (a) N=2 and (b) N=3 replicas. Black arrows represent folding and unfolding processes, while red arrows show replica exchange processes. The corresponding reduced linear kinetic schemes, obtained in the limit of fast replica exchange, are shown below the full kinetic diagrams.

Here, we implicitly assume that the two states dominating the relaxation at low and high temperatures are the same. This may not be the case always, with folding and unfolding dominating the dynamics of a protein at low temperature, for instance, and compact to extended transitions at high temperature. In such cases, the approach can be extended by expanding the number of states for each replica to, say, M. However, the overall number of possible states in a simulation with N replicas will then increase from 2^N to M^N. We note further that one could in addition keep track of the temperature from which each replica started at the beginning of the simulations. For a two-state model, this leads to the state space with N!2^N distinct states considered by Zheng et al.⁹

The change in the population in states with, say, replica i folded and replica j unfolded by replica exchange i↔j, is described by the following kinetic equation:

$$F_i{U}_j\underset{k_{\text{xc}}\left(F_i{U}_j\right)}{\overset{k_{\text{xc}}\left(U_i{F}_j\right)}{\rightleftharpoons }}{U}_i{F}_j,$$ (4)

where we use the notation k_xc(U_iF_j)=k(F_iU_j→U_iF_j) for the rate of exchange. In such an exchange, the state of the N−2 other replicas remains unchanged. The exchange rates in Eq. 4 are defined such that the equilibrium populations p_i and q_i of the uncoupled system are preserved. In REMD, this conservation of the equilibrium distribution is guaranteed by choosing an acceptance criterion that satisfies detailed balance. Accordingly, the exchange rates must satisfy

$$\frac{k_{\text{xc}}\left(U_i{F}_j\right)}{k_{\text{xc}}\left(F_i{U}_j\right)}=\frac{q_i{p}_j}{p_i{q}_j}.$$ (5)

We can determine the exchange rates from the simulations by considering the number of exchange events per unit time, i.e., by equating the flux associated with exchanges in the kinetic model and the simulations,

$$j_{\text{RE}}\left(F_i{U}_j\to U_i{F}_j\right)=p_i{q}_j{k}_{\text{xc}}\left(U_i{F}_j\right)=\frac{p_i{q}_j{p}_{\text{acc}}\left(U_i{F}_j\right)}{\delta t_{\text{xc}}},$$ (6)

where δt_xc is the time interval between exchange attempts of replicas at temperatures T_i and T_j, and p_acc(U_iF_j) is the probability of accepting a replica exchange between states F_i and U_j.

Error and efficiency of MD and REMD simulations

The calculation of equilibrium properties is one of the main objectives in both MD and REMD simulations. The computational efficiency of the simulations can then be defined as the rate with which the statistical error in the estimation of the property of interest decreases with the simulation time. In practice, this rate should be given in units of wall-clock time for given computational resources; but for simplicity, we here assume that there are no computational overheads for, say, replica exchange, such that we can instead give the rate in units of the simulation times t_sim. For times t_sim long compared to the overall longest simulation time of the system, we expect from the central limit theorem that the error in the estimate $\overline{A}$ of the exact mean ⟨A⟩ of a property A decreases as $\mathrm{var}\left(\overline{A}\right)=c∕t_{\mathrm{sim}}$, where $\mathrm{var}\left(\overline{A}\right)$ indicates the variance about the true mean in multiple simulations of the same duration t_sim and c is a constant that depends on the simulation method (MD versus REMD) and thermodynamic state (temperature, pressure, etc.). Note that we do not consider the systematic error resulting from the choice of a particular initial condition (say, all replicas folded or all unfolded). For a given initial condition, the estimate $\overline{A}$ will approach the true mean ⟨A⟩ asymptotically as 1∕t_sim, faster than the decrease in the statistical error (which decays as $t_{\mathrm{sim}}^{-1∕2}$ asymptotically).

To compare the efficiencies of MD and REMD simulations, we will calculate the constants c for each of the methods for systems with a single dominant slow relaxation process. While we consider explicitly the case of two-state protein folding, the results apply generally to systems with two metastable states that interconvert slowly compared to the relaxation processes within each state. In the two-state case the relative computational efficiencies will in general not depend on the particular property A. The reason is that in such systems, A will quickly relax to the average values ⟨A⟩_F and ⟨A⟩_U of the system in folded and unfolded states F and U, respectively, which will, in general, be different. As a consequence, the variance in the estimated mean can be expressed in terms of the variance of the relative fraction s of the folded (or, equivalently, the unfolded) state: $\mathrm{var}\left(\overline{A}\right)={\left({⟨A⟩}_F-{⟨A⟩}_U\right)}^2\mathrm{var}\left(\overline{s}\right)$, where s=1 if the system is folded, and s=0 if it is unfolded such that ⟨s⟩=p. The rate of decrease in the error of $\overline{s}$ (the fraction of folded states) is thus sufficient to compare different simulation methods, such as MD and REMD.

We define the relative efficiency of REMD simulations as compared to MD based on the asymptotic error of measuring the mean equilibrium populations. If we are interested only in the equilibrium properties at a single temperature (T_k), then we define the efficiency gain from REMD as the ratio of the variance ${\sigma }_{\mathrm{MD}}^2\left(N{t}_{\mathrm{sim}}\right)={\sigma }_{\mathrm{MD}}^2\left(t_{\mathrm{sim}}\right)∕N={\mathrm{var}}_{\mathrm{MD}}\left(\overline{s}\right)$ in the folded populations for N regular MD simulations of duration t_sim to the variance ${\sigma }_{\mathrm{REMD}}^2\left(t_{\mathrm{sim}}\right)$ for one REMD simulation of duration t_sim with N replicas,

$${\eta }_k=\frac{{\sigma }_{\text{MD}}^2\left(t_{\text{sim}}\right)}{N{\sigma }_{\text{REMD}}^2\left(t_{\text{sim}}\right)}.$$ (7)

With this definition, REMD converges more rapidly than MD if η_k>1.

For both MD and REMD simulations, we can express the variance in the estimated fraction folded as the time integral over the autocorrelation function of the folding state s(t) at the temperature of interest. The estimate of the fraction folded p=⟨s⟩ is

$$\overline{s}=\frac{1}{t_{\text{sim}}}{\int }_0^{t_{\text{sim}}}s\left(t\right)dt.$$ (8)

The corresponding variance in the estimator $\overline{s}$ can be expressed in terms of the autocorrelation function of s,²¹

$$\text{var}\left(\overline{s}\right)=\frac{2}{t_{\text{sim}}^2}{\int }_0^{t_{\text{sim}}}\left(t_{\text{sim}}-t\right)⟨\Delta s\left(t\right)\Delta s\left(0\right)⟩dt,$$ (9)

where Δs(t)=s(t)−p.

MD simulations

The analysis of the statistical error in regular MD simulations is analogous to that in single-molecule experiments.^{22, 23} For two-state kinetics, the autocorrelation function is single exponential, ⟨Δs(t)Δs(0)⟩=pq exp(−λt) with a relaxation rate λ=k_F+k_U, a folded fraction p=k_F∕(k_F+k_U), and an unfolded fraction q=1−p. For this exponential relaxation, the integral in Eq. 9 can be evaluated analytically. If the duration t_sim of the MD simulations is long compared to the folding and unfolding times 1∕k_F and 1∕k_U, respectively, then the variance in the estimator will decrease asymptotically as 1∕t_sim,

$${\sigma }_{\text{MD}}^2\left(t_{\text{sim}}\right)=\frac{2}{t_{\text{sim}}}\frac{pq}{\lambda },$$ (10)

irrespective of the initial state of the system.

REMD simulations

To estimate the error in replica exchange simulations, we again use Eq. 9. Here the autocorrelation function ⟨Δs(t)Δs(0)⟩ is for the state (folded and unfolded) of the replica at the temperature of interest, which is typically the lowest temperature. In contrast to regular MD, ⟨Δs(t)Δs(0)⟩ will, in general, not be single exponential. For REMD with N replicas, there are 2^N distinct states overall, and the correlation function will be multiexponential, requiring for its calculation either the diagonalization of the 2^N×2^N rate matrix or numerical integration. However, in the limit of fast replica exchange, one can obtain an accurate approximation to ⟨Δs(t)Δs(0)⟩ as explained in the following.

Limit of fast replica exchange

The dynamics of the folded and unfolded populations in a replica exchange simulation are described by the kinetic equations 2, 4 for the folding and exchange processes, respectively. For N>2 replicas, only numerical solutions are available in general. However, we will derive approximate but accurate analytical solutions in the limiting case when the replica exchange rates are much faster than the relaxation rates λ_i at the individual temperatures T_i.

In the limit of fast replica exchange, we can coarse grain the full problem by coupling states together that rapidly equilibrate with each other. For these collective states we can then construct a new rate matrix of greatly reduced dimension by using the local-equilibrium approximation.²⁴ This process of defining macrostates composed of the original states (microstates), coupled by fast replica exchange, is illustrated in Fig. 2. For N=2, we can couple U₁F₂ and F₁U₂ states together in a collective “U₁F₂+F₁U₂” state and decrease the total number of states from 4 to 3,

$$U_1{U}_2\rightleftharpoons “U_1{F}_2+F_1{U}_2”\rightleftharpoons F_1{F}_2.$$ (11)

Replica exchange couples two microstates of the overall system only if they have equal number of folded (or unfolded) replicas. This means that the 2^N-dimensional problem is reduced to N+1 dimensions, with macrostates n=0,1,…,N obtained by grouping together the microstates with exactly n folded replicas.

In the limit of fast exchange, the populations of states n are kinetically connected in a linear chain,

$$0\rightleftharpoons 1\rightleftharpoons \cdots \rightleftharpoons n\rightleftharpoons n+1\rightleftharpoons \cdots \rightleftharpoons N.$$ (12)

To estimate the relaxation dynamics of n, we consider the limit of a large number of replicas N. In this limit, n will fluctuate about its mean

$$⟨n⟩=\sum _{i=1}^N{p}_i$$ (13)

with variance

$$\text{var}\left(n\right)=⟨\Delta n^2⟩=\sum _{i=1}^N{q}_i{p}_i,$$ (14)

where Δn=n−⟨n⟩. These relations follow immediately from the independence of the N replicas at equilibrium. In the limit of large N, the problem can be further simplified by considering the continuum limit. Equation 12 can then be approximated as one-dimensional diffusion of a continuous variable n in a harmonic potential centered at ⟨n⟩ with a spring constant 1∕var(n). The slowest relaxation rate κ for such a diffusive harmonic oscillator description of the dynamics of n(t) is then given by

$$\kappa =D∕⟨\Delta n^2⟩,$$ (15)

where D is the diffusion coefficient in the continuous problem near n=⟨n⟩.

To estimate the effective diffusion coefficient D along n, we match the fluxes n→n+1 of the kinetic model [Eq. 12] and the harmonic oscillator diffusion model for n=n_max≈⟨n⟩, where n_max is the most probable n. In the kinetic model, the forward and backward rates of our model system are

$$K_{n\to n+1}\equiv K_{n+1,n}=\sum _{i=1}^N{k}_i^{+}p\left(U_i\mid n\right),$$ (16)

$$K_{n\to n-1}\equiv K_{n-1,n}=\sum _{i=1}^N{k}_i^{-}p\left(F_i\mid n\right),$$

where we used the local-equilibrium approximation²⁴ appropriate for fast replica exchange. p(F_i∣n) and p(U_i∣n) are the conditional probabilities of replica i at T_i being folded and unfolded, respectively, with the total number of folded replicas being exactly n. In the limit of large N, the properties of an individual replica will be the same in the restrained system with n fixed to n_max as in the unrestrained system with n fluctuating about n_max, analogous to the near equivalence of the microcanonical and canonical distributions for small components of a large system. The conditional probabilities can thus be replaced by the average probabilities p(U_i∣n_max)≈q_i and p(F_i∣n_max)≈p_i. In the discrete system [Eq. 12], the rate coefficients in Eq. 16 thus become $K_{n\to n+1}={\sum }_{i=1}^N{k}_i^{+}{q}_i$ and $K_{n\to n-1}={\sum }_{i=1}^N{k}_i^{-}{p}_i$. For the continuum diffusive harmonic oscillator, spatially discretized at steps of Δn=1,²⁵ the diffusion coefficient is directly related to these rates through D=K_{nmax−1,nmax}=K_nmax+1,nmax, where we used the fact that the potential surface is flat near the minimum. We thus arrive at the approximation

$$D\approx \sum _{i=1}^N{k}_i^{+}{q}_i=\sum _{i=1}^N{k}_i^{-}{p}_i.$$ (17)

By combining this relation with Eq. 15, we obtain an approximation for the overall slowest relaxation rate in an REMD simulation of a two-state system,

$$\kappa =\frac{1}{{\tau }_{\text{relax}}}=\frac{{\sum }_{i=1}^N{k}_i^{-}{p}_i}{{\sum }_{i=1}^N{q}_i{p}_i}=\frac{{\sum }_{i=1}^N{\lambda }_i{q}_i{p}_i}{{\sum }_{i=1}^N{q}_i{p}_i}.$$ (18)

The relaxation rate is expressed here as the weighted sum of the relaxation rates of the independent replicas at the different temperatures, where the weighting factor is the normalized product of folding and unfolding probabilities. The overall replica exchange relaxation rate falls between the fastest and the slowest relaxation rates among all the temperatures, λ_min≤κ≤λ_max. As shown in the Appendix0, Eq. 18 for κ can also be obtained from the exact short-time expansion of the correlation function ⟨Δn(t)Δn(0)⟩=⟨Δn²⟩exp(−κt) in the full system with 2^N states.

Error of REMD in the limit of fast exchange

As discussed above, if the rate of replica exchange is fast compared to actual folding and unfolding, we can coarse grain the full 2^N representation and reduce it to N+1 states of having exactly n=0,1,…,N replicas folded. At short times, the REMD dynamics is therefore governed by fast exchange between different replicas that quickly establishes an equilibrium for the given fixed number n of folded replicas. Over longer times, the dynamics will be dominated by the slow fluctuations of n(t). We thus separate our state function s(t) into two components,

$$s\left(t\right)=p\left(F_k\mid n\left(t\right)\right)+\delta s\left(t\right),$$ (19)

where p(F_k∣n(t)) is the equilibrium average of s(t) over trajectories with a fixed number of folded replicas, defined as the conditional probability of being folded in the replica at the target temperature, T_k, given that n out of N replicas are folded; and δs(t) describes the remaining fast fluctuations in the state of the replica at T_k associated with replica exchange. With this separation, the correlation function at times long compared to those associated with replica exchange becomes

$$⟨s\left(t\right)s\left(0\right)⟩\approx ⟨p\left(F_k\mid n\left(t\right)\right)p\left(F_k\mid n\left(0\right)\right)⟩.$$ (20)

This separation into a fast and a slow process is equivalent to that used in the model-free formalism of Lipari and Szabo for the orientational relaxation.²⁶ To evaluate the correlation function in Eq. 20, we again assume that we are in the limit of large N and expand p(F_k∣n(t)) about the mean number ⟨n⟩≈n_max of folded replicas, p(F_k∣n)≈p(F_k∣⟨n⟩)+B(n−⟨n⟩). To estimate the linear expansion coefficient B, we use that in the limit of large N and n≈⟨n⟩ individual replicas fluctuate independently, such that p(F_k∣⟨n⟩)≈p_k is the probability of being folded at T_k. The difference p(F_k∣⟨n⟩+1)−p(F_k∣⟨n⟩) can then be estimated from the probability that folding at T_k accounted for the increase from ⟨n⟩ to ⟨n⟩+1, among all possible folding events. This relative probability is given by the product of the replica at T_k being unfolded at ⟨n⟩ and folded at ⟨n⟩+1, normalized by the corresponding product of probabilities for all other replicas. We thus obtain

$$p\left(F_k\mid n\right)\approx p_k+\frac{p_k{q}_k}{{\sum }_{i=1}^N{p}_i{q}_i}\left(n-⟨n⟩\right).$$ (21)

With this approximation, the correlation function in Eq. 20 at long times becomes

$$⟨\Delta s\left(t\right)\Delta s\left(0\right)⟩\approx {\left(\frac{p_k{q}_k}{{\sum }_{i=1}^N{p}_i{q}_i}\right)}^2⟨\Delta n\left(t\right)\Delta n\left(0\right)⟩.$$ (22)

We have already determined an approximation for the correlation function of n(t) above in the analysis of the kinetics with fast replica exchange, ⟨Δn(t)Δn(0)⟩≈⟨Δn²⟩exp(−κt), where $⟨\Delta n^2⟩={\sum }_{i=1}^N{p}_i{q}_i$ and κ is given in Eq. 18. For the normalized folding state autocorrelation function, we obtain

$$c\left(t\right)\equiv \frac{⟨\Delta s\left(t\right)\Delta s\left(0\right)⟩}{⟨\Delta s^2⟩}\approx \frac{p_k{q}_k{e}^{-\kappa t}}{{\sum }_{i=1}^N{p}_i{q}_i}$$ (23)

at long times and in the limit of fast replica exchange, with κ given in Eq. 18.

After substituting Eq. 22 into Eq. 9, using Eq. 18 for κ, integrating over time, and taking the limit of long simulation time t_sim, we obtain

$${\sigma }_{\text{REMD}}^2\left(t_{\text{sim}}\right)\equiv \text{var}\left(\overline{s}\right)=\frac{2}{t_{\text{sim}}}\frac{p_k^2{q}_k^2}{{\sum }_{i=1}^N{p}_i{q}_i{\lambda }_i}$$ (24)

for the variance in the estimated fraction folded at temperature T_k.

By combining Eqs. 10, 24, we can now compare the relative computational efficiencies of MD versus REMD simulation,

$${\eta }_k=\frac{{\sigma }_{\text{MD}}^2\left(t_{\text{sim}}\right)}{N{\sigma }_{\text{REMD}}^2\left(t_{\text{sim}}\right)}=\frac{{\sum }_{i=1}^N{p}_i{q}_i{\lambda }_i}{N{p}_k{q}_k{\lambda }_1}.$$ (25)

By substituting $p_i=k_i^{+}∕\left(k_i^{+}+k_i^{-}\right)$ and q_i=1−p_i, this relation for the relative efficiency can be rewritten as Eq. 1. The efficiency in REMD can thus be interpreted as the ratio of the sum of unfolded and folded lifetimes at the target temperature and the average of the reciprocal lifetime sums calculated over all temperatures. Equivalently, the relative efficiency of REMD is given by the ratio of the number of folding and unfolding transitions per unit time averaged over the N replicas and in the N-times longer MD simulation at the temperature of interest. η_k also corresponds to the ratio of the reactive flux in REMD and MD to the flux averaged over all temperatures in REMD.

The relative efficiency η_k of REMD approaches a constant as the number N of replicas increases. If the replicas are spaced at equal intervals in temperature, the limiting value is given by the integral,

$${\eta }_k=\frac{1}{T_N-T_1}{\int }_{T_1}^{T_N}\frac{{\tau }^{+}\left(T_k\right)+{\tau }^{-}\left(T_k\right)}{{\tau }^{+}\left(T\right)+{\tau }^{-}\left(T\right)}dT.$$ (26)

This independence of N may seem surprising at first glance. However, it can be understood by realizing that all folding or unfolding events at any replica temperature speed up the equilibration also at the temperature T_k of interest because of the fast replica exchange.

It is instructive to compare our results for the relative efficiencies of REMD and MD to the efficiency analysis of Zheng et al.⁹ Here, we have defined the efficiency as the rate with which the variance of the estimator of an essentially arbitrary observable decreases with simulation time. Specifically, we have calculated the relative efficiencies of MD and REMD simulations as the ratio of the variances in the fraction folded for given total simulation times, $\eta ={\sigma }_{\mathrm{MD}}^2\left(N{t}_{\mathrm{sim}}\right)∕{\sigma }_{\mathrm{REMD}}^2\left(t_{\mathrm{sim}}\right)$. This ratio tells us how much longer one has to simulate in MD to achieve the same statistical error in the estimator as in a REMD simulation, correcting for the fact that only one of the N REMD runs is actually used for the analysis. In contrast, Zheng et al.⁹ introduced as a measure of the efficiency of REMD simulations the number N_TE(t_sim∣T_k) of “round-trip” transitions of particular replicas between the U and F states at the temperature of interest T_k during the observation time t_sim. For two replicas in the limit of fast exchange, they empirically found an approximation in terms of harmonic means, $N_{\mathrm{TE}}(t_{\mathrm{sim}}\mid T_1)\approx t_{\mathrm{sim}}\left[{\left(1∕k_1^{+}+1∕k_1^{-}\right)}^{-1}+{\left(1∕k_2^{+}+1∕k_2^{-}\right)}^{-1}\right]$. Remarkably, despite the seemingly unrelated definitions, their measure of efficiency combined with their empirical approximation produces a formula essentially identical to ours for the specific case of a two-replica system, with the only difference being the normalizing factor $1∕\left({\tau }_1^{+}+{\tau }_1^{-}\right)∕2$ for the MD reference simulation. Our analysis thus justifies both the choice of efficiency in Ref. 9, and the empirical approximation in terms of harmonic means. Specifically, we can now interpret the formula in Ref. 9 as the expected number of folding and unfolding events observed at all temperatures during the simulation time t_sim, which in the fast-exchange limit all contribute to the relaxation at the temperature of interest.

Optimizing the number and temperature range of replicas

For optimal efficiency the lowest replica temperature should be chosen as T₁=T_k if at temperatures below T_k the fraction in the integral of Eq. 26 is <1. To reach the fast replica exchange limit, as many replicas should be used as one can afford. The best choice of the upper temperature, T_N, however can depend on the temperature dependence of the rates. In case of Arrhenius temperature dependence, with both folding and unfolding rates increasing with T, it is best to choose T_N as high as possible given that replica exchange is still fast (to ensure fast and uniform replica exchange currents, one can employ different criteria^{11, 13, 14, 15, 27}). However, for typical proteins, the relaxation rate exhibits “chevronlike” behavior (see Fig. 1). If one of the rates actually decreases with increasing temperature, and 1∕[τ⁺(T)+τ⁻(T)] has a maximum, the best choice is to use an upper temperature T_N at a somewhat higher value than this maximum. More precisely, one should use a T_N for which η_k in Eq. 26 itself becomes maximum. By differentiating Eq. 26 for equally spaced temperatures with respect to T_N, one obtains an implicit equation for the optimal T_N,

$$\frac{T_N-T_1}{{\tau }^{+}\left(T_N\right)+{\tau }^{-}\left(T_N\right)}={\int }_{T_1}^{T_N}\frac{dT}{{\tau }^{+}\left(T\right)+{\tau }^{-}\left(T\right)}.$$ (27)

With the help of Eq. 26, we find that the maximum efficiency is

$${\eta }_{\text{max}}=\frac{{\tau }^{+}\left(T_1\right)+{\tau }^{-}\left(T_1\right)}{{\tau }^{+}\left(T_N\right)+{\tau }^{-}\left(T_N\right)}$$ (28)

for systems with chevronlike rates and using the optimal T₁=T_k and T_N of Eq. 27.

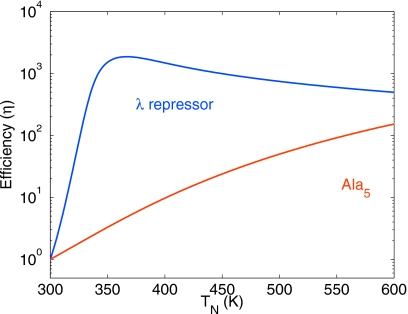
Figure 3 shows the relative efficiency of REMD as a function of temperature T_N for fixed T₁=300 K for the folding of the λ_6–85 protein²⁰ and the Ala₅ peptide in water.^{28, 29} Assuming that the rates fitted near ambient conditions hold to high temperatures (see Fig. 1 and the following section for rates), we find that for the λ_6–85 protein, the optimal upper temperature is T_N≈366 K, whereas for Ala₅ it is best to go to temperatures as high as possible, as long as replica exchange is still fast.

Figure 3.

Efficiency gain η of REMD over MD as a function of the highest replica temperature T_N. The reference temperature is T_k=T₁=300 K. Plotted is the efficiency in the limit of a large number N of replicas, which is independent of N, as obtained from Eq. 26. Note that for temperatures above 350 K, we used extrapolated rates.

RESULTS AND DISCUSSION

Convergence of the exact and approximate relaxation times

To test the range of validity of the theory, we first compare the analytical formulas for the error and efficiency of REMD to the exact values obtained by matrix diagonalization. Two systems are considered: (1) the folding of a λ repressor fragment,²⁰ in which the unfolding rate exhibits an Arrhenius-like temperature dependence, but the folding rate is highly non-Arrhenius (Fig. 1); and (2) the folding of a small helical peptide Ala₅ in water with Arrhenius-like folding and unfolding rates obtained from REMD simulations of Ala₅.²⁸ These rates were adjusted slightly for more accurate equilibrium populations from longer simulations according to the Langevin protocol in Ref. 7: k_U(T)=A_Ue^−E_U∕T and k_F(T)=A_Fe^−E_F∕T with A_U=1047.7 ns⁻¹, A_F=2.9745×10⁶ ns⁻¹, E_U=2656.3 K, and E_F=5589.5 K.

In both cases, we used a total of N=12 replicas, resulting in 2¹²=4096 states, spread uniformly over a range from 283 to 353 K for the λ repressor and from 295 to 350 K for Ala₅. For each of the two systems, we set up a 4096×4096 rate matrix corresponding to Eqs. 2, 4 and varied the rates k_xc of replica exchange (while maintaining detailed balance) to explore the convergence to the limit of fast replica exchange. We calculate both the rate κ of the slowest overall relaxation, defined as the nonzero eigenvalue of the rate matrix with the smallest magnitude, and the relative efficiency η₁ at the lowest temperature.

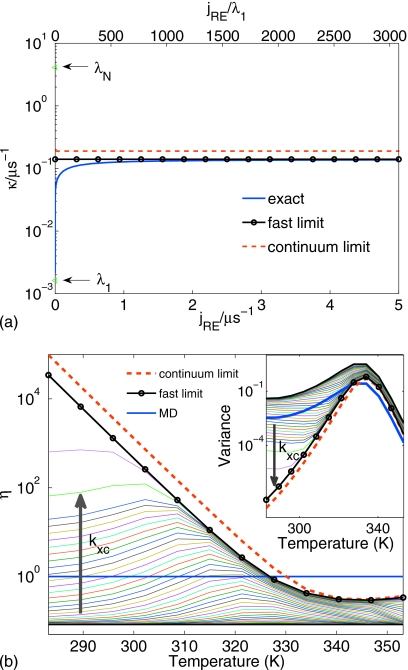
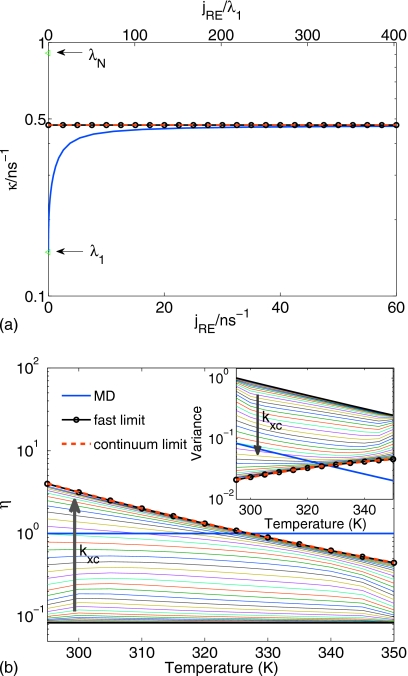
Figure 4a shows the relaxation rate κ for the λ repressor as a function of the replica exchange flux j_RE. The replica exchange rates were calculated from the flux according to Eq. 6, with j_RE varied from 0 to 5 μs⁻¹. As replica exchange is turned on (j_RE>0), the slowest relaxation rate κ [blue line in Fig. 4a] rapidly rises from the limit λ₁ without replica exchange. We conclude from these results that even infrequently accepted replica exchange can speed up the overall relaxation by a factor of 20 or more. The limit of infinitely fast replica exchange [black horizontal line in Fig. 4a] is approached already at j_RE<1 μs, less than λ_N. We also find that the analytical formula [Eq. 18] for the fast-exchange limit (red horizontal line) is a good approximation of the exact rate κ. Finally, we note that for fast exchange κ is about two orders of magnitude faster than the relaxation rate at the lowest temperature (λ₁ at 283 K) and two orders slower than that at the highest temperature (λ_N at 353 K).

Figure 4.

Convergence of the relaxation rate and the efficiency of REMD for the λ-repressor fragment λ_6–85 (Ref. ²⁰). (a) The exchange rate dependence of the rate limiting eigenvalue (κ) is shown for the full kinetic problem (blue line), for the exact fast replica exchange limit (black line), and for the approximate Eq. 18 (red line). The eigenvalues corresponding to MD (no replica exchange coupling), λ₁ (T₁=283.15 K) and λ₁₂ (T₁₂=353.15 K) are marked with arrows. (b) REMD efficiency [Eq. 7] vs the target temperature. The fast-exchange limit is shown as black line with circles, the results using Eq. 25 are shown as red dashed line, the MD simulations correspond to efficiency of 1, shown in blue. The arrow indicates the variation in the efficiency for increasing replica exchange rate. The inset shows the REMD variance for different target temperatures.

For Ala₅, the results are similar to those for the λ repressor, as shown in Fig. 5a. The main differences are that the rise in κ with increased replica exchange is not as dramatic. Also, notably, the analytical formula [Eq. 18] for κ in the fast-exchange limit (red horizontal line) is a near-perfect approximation of the exact relaxation rate.

Figure 5.

Convergence of the relaxation rate and the efficiency of REMD for the Arrhenius folding∕unfolding rates of Ala₅. (a) The exchange rate dependence of the rate limiting eigenvalue (κ) is shown for the full kinetic problem (blue line), for the exact fast replica exchange limit (black line), and for the approximate Eq. 18 (red line). The eigenvalues corresponding to MD (no replica exchange coupling), λ₁ (T₁=295 K) and λ₁₂ (T₁₂=350 K) are marked with arrows. (b) REMD efficiency [Eq. 7] vs the target temperature. The fast-exchange limit is shown as black line with circles, the results using Eq. 25 are shown as red dashed line, the MD simulations correspond to an efficiency of 1, shown in blue. The arrow indicates the variation in the efficiency for increasing replica exchange rate. The inset shows the variance σ²(t_sim) of the fraction folded as a function of the target temperature, scaled for reference and readability to a simulation length of t_sim=2 ns.

Figure 4b plots the relative efficiency gain η_k of REMD over MD for the λ repressor at each of the 12 temperatures T_k. In the limit of infinitely fast replica exchange (black line with circles), the analytical formula [Eq. 1] is an excellent approximation to the actual efficiency gain, exceeding the exact value only slightly. We also note that an efficiency gain of more than 10⁴ at the lowest temperature is dramatic. However, our model also shows that this fast-exchange limit is approached only very slowly as the exchange rate is increased. The thin lines show the efficiency for different values of the replica exchange rate [here we included very high replica exchange fluxes j_RE=10 ns⁻¹ (green) and j_RE=100 ns⁻¹ (magenta)]. An efficiency of η_k=1 is indicated as a horizontal blue line, whereas the bottom black line corresponds to no exchange with an efficiency of η_k=1∕N. We find that for finite exchange rates, the efficiency at the lower temperatures remains well below the fast-exchange limit. The inset in Fig. 4b shows the variance in the folded fraction (scaled to a simulation time t_sim=2 μs) on a log scale as a function of the target temperature. Consistent with the efficiency gains, at low temperatures and with fast exchange the variance is dramatically lower with REMD than with MD simulations even if the latter are N=12 times longer.

We again find qualitatively similar behavior for Ala₅, as shown in Fig. 5b. Here, the analytical formula [Eq. 1] for η₁ is nearly exact. However, the overall efficiency gain from replica exchange is much smaller, about a factor of 4 at the lowest temperature. Nevertheless, this means that the error in the folded fraction decreases about four times faster in the REMD simulations compared to MD simulations of N=12 times the length.

We conclude from this analysis that the analytical expressions for both the overall relaxation rate and the relative efficiency of REMD in the limit of fast replica exchange are accurate and useful in realistic systems. The data in Fig. 4 predict large possible gains in efficiency from replica exchange. Practically, there are a number of limitations. For one, our formulas are derived for the asymptotic limit of long simulations. Most current REMD simulations of, say, protein folding are far from that limit: at times of 10–100 ns∕replica, a REMD simulation system with replicas starting unfolded cannot be expected to have reached equilibrium because typical folding times are at least microseconds over the entire range of temperatures. In addition, we assumed that replica exchange was fast. In practice, this may not be the case, in particular, for large systems requiring a narrow temperature spacing. Our kinetic model shows that to reach the maximum gains at low temperature would require unrealistically high rates of replica exchange [thin lines in Fig. 4b]. For more realistic rates of exchange, we find efficiency gains limited to factors of 10–100.

Simulations of penta-alanine

As a test against actual molecular simulations, we have analyzed the relaxation in long MD and REMD simulations of Ala₅ in explicit water. The REMD simulations were run according to the Langevin protocol in Ref. 7. The MD simulation trajectories are those of Ref. 29. The folding state of the peptide was extracted from the simulation trajectories according to the transition-path based assignment described in Refs. ^{28, 29}.

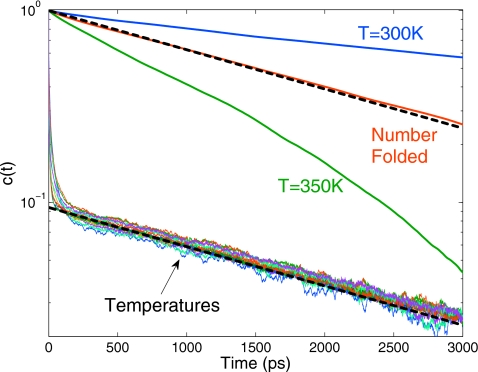
Figure 6 shows the normalized autocorrelation functions of the folding state c(t)=⟨Δs(t)Δs(0)⟩∕⟨Δs²⟩ at the 12 different temperatures of the REMD simulations, spanning the range from 295 to 350 K in intervals of 5 K. As predicted by the theory, after an initial sharp drop in c(t) because of replica exchange without actual folding or unfolding (see following paragraph), the c(t) at the different temperatures decay with the same relaxation rate κ. The amplitude of the c(t) at different temperatures is different, consistent with the predictions of the theory, but because of the narrow range in temperature with a relatively small change in the equilibrium fraction folded, the amplitudes of the slow relaxation phase vary by less than a factor of 1.5. The identical relaxation rate κ at the different temperatures is in sharp contrast to the large differences in the autocorrelation functions c(t) from regular MD simulations, as shown for 300 and 350 K. c(t) decays rapidly at 350 K and slowly at 300 K, both without an initial sharp drop.

Figure 6.

Autocorrelation function of the folding state s(t) at different temperatures obtained from REMD simulations of Ala₅. Also shown are the corresponding c(t) for regular MD simulations at T=300 K (blue) and T=350 K (green), and the autocorrelation function of the number n(t) of folded states (red). The dashed black lines show exponential decays with the slowest relaxation rate κ obtained from Eq. 18.

Figure 6 also shows the normalized autocorrelation of the total number n(t) of folded states among all replicas. As predicted by the theory for fast replica exchange, this autocorrelation function exhibits single-exponential decay with the rate κ given in Eq. 18 and is consistent with the long-time decay of the c(t) curves.

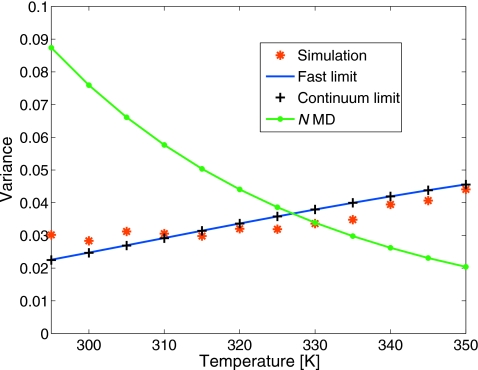
In Fig. 7, we compare the variance in the folded population obtained from 11 independent REMD runs, each with 12 replicas and run for 150 ns, to that predicted by the theory [Eq. 24]. All variances have been scaled to correspond to a simulation time of t_sim=2 ns for better readability. We find that the analytical formula provides a fully quantitative estimate of the actual variance over the entire range of temperatures. Also shown is the variance as a function of simulation temperature expected for MD simulations 12 times longer. We find that the latter is about four times larger at low temperatures than the REMD variance, but decreases with temperature; in contrast, the REMD variance increases with temperature. As predicted by the kinetic model [Fig. 5b], REMD results in an efficiency gain for temperatures below 325 K and an efficiency loss above.

Figure 7.

Variance in the fraction folded p calculated from REMD simulations of Ala₅ for different target temperatures. For reference and readability, all results have been scaled to a simulation time of t_sim=2 ns. The red symbols show data obtained from 11 independent 150-ns-long REMD simulations. The solid lines are obtained for the reduced kinetic model (blue) in the fast-exchange limit from the exact solution of the coarse grained kinetic model and in the continuum limit (black symbols) using the formula of Eq. 24. The green line corresponds to the variance for N=12 times longer MD simulations.

CONCLUDING REMARKS

We have built a kinetic model of REMD simulations to assess their error and efficiency for systems described by two-state relaxation at long times. This kinetic framework allows us to determine the slowest relaxation rate of the overall system and the error of measuring folded∕unfolded equilibrium populations and other observables.

While the general kinetic model using actual replica exchange rates can be solved either by diagonalization or by kinetic simulation, we also provide an analytic solution for obtaining the relaxation rate and the statistical error of measuring equilibrium populations in the limit of fast exchange and densely spaced replicas within the temperature range of the simulation.

We show that the analytical formulas provide a practically useful approximation for the folding of the lambda repressor fragment and the Ala₅ peptide solvated in explicit water. In particular, we obtained quantitative agreement between our formulas and the results from actual REMD simulations of Ala₅. This agreement of the errors predicted from theory and obtained from Ala₅ REMD simulations is encouraging because an earlier study of the same system²⁹ had shown that the folding kinetics was significantly better described by a four-state system than the simpler two-state system assumed in the present formalism.

We note, however, that there are a number of practical issues that may limit the efficiency gains. Most importantly, our formulas apply to the asymptotic limit of long simulations, whereas many current simulations of, say, protein folding may be too short to see any significant number of genuine folding events. In addition, replica exchange has to be fast, which may require too many replicas for large molecular systems. If the two species U and F differ significantly in their internal energy compared to the potential energy fluctuations, then one may not have the relevant fast exchange of unfolded and folded species (UF↔FU) even if the rate of accepted replica exchanges appears to be large (dominated by exchanges FF↔FF and UU↔UU). This lack of energy overlap in UF↔FU exchanges is a particular concern in implicit-solvent simulations with large energy gaps between F and U states.

Although the implementation of the kinetic models as well as the theoretical formulas require some a priori knowledge of the temperature dependence of the rates, which may not be available, a number of general recommendations can be made without detailed rate information. In particular, our theoretical analyses and numerical studies have identified a number of factors relevant for the efficiency of REMD.

Exchange frequency and number of replicas

To achieve high efficiency gains from REMD, it is important that replica exchange is fast compared to folding and unfolding at the temperature of interest. This result is consistent with the conclusions of Sindhikara et al.⁸ There are a number of factors that affect the effective exchange rate, including the frequency of exchange attempts, the temperature spacing of the replicas, and the relaxation rate of the total potential energy differences between neighboring replicas as the main factor controlling the acceptance rate. Up to a certain point, one can increase the replica exchange rate simply by decreasing the time interval δt_xc between exchange attempts. However, we expect that at short times δt_xc the relaxation of degrees of freedom other than the folding state (U and F) will become important, resulting in a breakdown of the Markovian assumption underlying the kinetic description.¹⁰ As an alternative, to enhance the exchange acceptance probability and establish fast exchange, the temperature spacing can be decreased without penalty in efficiency. The reason is that according to Eq. 1 an increase in the number of replicas within a fixed temperature range will not reduce the efficiency as long as replica exchange is fast. Finally, alternative implementations of replica exchange may also help overcome the limitations arising from low acceptance probabilities in larger systems, such as “replica exchange with solute tempering” by Liu et al.³⁰

Temperature range

Typically, τ⁺(T)+τ⁻(T) decreases as temperature T increases. Then, the target temperature T_k should be the lowest temperature in the REMD simulations (k=1). The upper limit of T_N of the temperature range should be chosen by keeping two factors in mind. Most importantly, for a fixed number N of replicas, the temperature range should be small enough such that the replica exchange rates are fast compared to folding and unfolding. Once near the fast limit, the optimal T_N depends on the temperature dependence of the folding and unfolding rates. For Arrhenius rates, τ⁺(T)+τ⁻(T) monotonically decreases with T, and T_N should be chosen as high and possible, while staying in the fast limit. If τ⁺(T)+τ⁻(T) has a minimum, then the upper temperature will also have an optimal value, as defined in Eq. 27.

Other variables that can be optimized are the precise temperatures T_i of the replicas. Here, we have implicitly assumed an even temperature spacing of the replicas. However, it follows from Eq. 1 that the highest efficiency can be achieved by having relatively more replicas where τ⁺(T)+τ⁻(T) has a minimum, while still maintaining fast replica exchange. Such optimization would result in an uneven temperature spacing of the replicas.

Equilibration

Plotting autocorrelation functions of the properties of interest, as in Fig. 6, should help in assessing the degree of equilibration. The theory predicts that at long times, the autocorrelation functions for any property coupled to folding in a two-state system should decay with a single-exponential relaxation, with a rate irrespective of the temperature of the replica and the property of interest. Moreover, in the limit of fast exchange, the autocorrelation function for the number n(t) of folded replicas should exhibit a single-exponential decay with the same time constant as the state autocorrelation functions at fixed temperatures.

In addition to the formal results of this paper, one can directly use the kinetic frameworks [Eqs. 2, 4] to explore and optimize REMD parameters. Such an approach has been pursued by Hritz and Oostenbrink.¹² Replica exchange rates can be obtained from the attempt frequencies and acceptance rates. The latter can be estimated from the energy distributions in the folded and unfolded states at the different temperatures (from simulation at some temperatures and interpolation at others). Combined with estimates of the folding and unfolding rates, the kinetic matrix can be constructed and solved either by diagonalization or by kinetic simulations. In this way, a numerically optimized protocol can be determined for an actual simulation system by minimizing the error at the temperature of interest.

In summary, we have shown that replica exchange can substantially enhance the computational efficiency, as measured by the decrease in the simulation time required to achieve a particular statistical accuracy. However, to achieve high efficiency requires a careful choice of the simulation parameters.

APPENDIX: SHORT-TIME APPROXIMATION OF THE CORRELATION FUNCTION

In this appendix, an approximation for the relaxation rate κ of the number n of folded replicas will be derived from the short-time expansion of the correlation function ⟨Δn(t)Δn⟩ for the kinetic system [Eq. 12]. We show that the κ derived from this approximation is identical to Eq. 18 derived in the main text under the assumption of diffusive dynamics on a quadratic surface for a continuous n.

The autocorrelation function of n can be written as

$$⟨n\left(t\right)n\left(0\right)⟩=\sum _{n=0}^N\sum _{m=0}^{N}np\left(n,t\mid m,0\right)m{p}_{\text{eq}}\left(m\right),$$ (A1)

where the propagator p(n,t∣m,0) is the conditional probability that exactly n replicas are folded at time t, given that m replicas were folded at time 0, and p_eq(m) is the equilibrium probability of having exactly m folded replicas. At short times, the propagator can be approximated as p(n,t∣m,0)=δ_nm+K_nmt+O(t²), where δ_nm is the Kronecker symbol and the K_nm are the rate coefficients in the kinetic scheme of Eq. 12. At short times, we can thus approximate ⟨Δn(t)Δn(0)⟩∕⟨Δn²⟩≈exp(−κt)≈1−κt with

$$\kappa =-\sum _{n=0}^N\sum _{m=0}^{N}n{K}_{nm}m{p}_{\text{eq}}\left(m\right)∕⟨\Delta n^2⟩.$$ (A2)

To simplify this expression for κ, we first use that only neighboring states are connected in the kinetic system [Eq. 12],

$$\sum _{n=0}^N\sum _{m=0}^{N}n{K}_{nm}m{p}_{\text{eq}}\left(m\right)=\sum _{n=0}^N\left[\left(n+1\right)K_{n+1,n}+n{K}_{nn}+\left(n-1\right)K_{n-1,n}\right]n{p}_{\text{eq}}\left(n\right),$$ (A3)

with K_N+1,N=K_−1,0=0. To further simplify the above expression, we use that the columns of the rate matrix sum to zero, such that K_nn=−K_n+1,n−K_n−1,n,

$$\kappa =-\sum _{n=0}^{N}n\left(K_{n+1,n}-K_{n-1,n}\right)p_{\text{eq}}\left(n\right)∕⟨\Delta n^2⟩.$$ (A4)

Substituting the detailed balance relation, K_n+1,np_eq(n)=K_n,n+1p_eq(n+1), into Eq. A4 and regrouping of the terms results in

$$\kappa =\sum _{n=0}^N{K}_{n+1,n}{p}_{\text{eq}}\left(n\right)∕⟨\Delta n^2⟩.$$ (A5)

In the final step, we assume that replica exchange is fast, such that we can use the local-equilibrium approximations [Eq. 16] for K_n±1,n. Substituting Eq. 16 into Eq. A5, we obtain

$$\kappa =\sum _{n=0}^N\sum _{i=1}^N{k}_i^{+}p\left(U_i\mid n\right)p_{\text{eq}}\left(n\right)∕⟨\Delta n^2⟩.$$ (A6)

By exchanging the order of summation, the condition on n can be eliminated, ∑_np(U_i∣n)p_eq(n)=q_i, which results in

$$\kappa =\frac{{\sum }_{i=1}^N{k}_i^{+}{q}_i}{⟨\Delta n^2⟩}.$$ (A7)

Substituting ⟨Δn²⟩ from Eq. 14, we find that κ in Eq. A7 is identical to that in Eq. 18.