Asynchronous Decoding of Dexterous Finger Movements using M1 Neurons

Abstract

While previous efforts in Brain-Machine Interfaces (BMI) have looked at decoding movement intent or hand and arm trajectory, current neural control strategies have not focused on the decoding of dexterous actions such as finger movements. The present work demonstrates the asynchronous deciphering of the neural coding associated with the movement of individual and combined fingers. Single-unit activities were recorded sequentially from a population of neurons in the M1 hand area of trained rhesus monkeys during flexion and extension movements of each finger and the wrist. Non-linear filters were used to decode both movement intent and movement type from randomly selected neuronal ensembles. Average asynchronous decoding accuracies as high as 99.8% ± 0.1%, 96.2% ± 1.8%, and 90.5% ± 2.1%, were achieved for individuated finger and wrist movements with three monkeys. Average decoding accuracy was still 92.5% ± 1.1% when combined movements of two fingers were included. These results demonstrate that it is possible to asynchronously decode dexterous finger movements from a neuronal ensemble with high accuracy. This is an important step towards the development of a BMI for direct neural control of a state-of-the-art, multi-fingered hand prosthesis.

I. INTRODUCTION

Brain-Machine Interface (BMI) uses electrophysiological measures of brain function to enable communication between the brain and external devices, such as computers or mechanical actuators. Previous studies using intracortical BMI’s have demonstrated the decoding of neuronal ensemble activity in the dorsal pre-motor cortex (PMd) [1, 2] primary motor cortex (M1) [3–6], and posterior parietal cortex (PPC) [7, 8] for the purposes of deriving a variety of cortical control signals.

Previous work using signals from the rat motor cortex has shown 1-D control of a robotic arm using a population of 32 M1 neurons to predict hand trajectory [3, 4]. Later work shows how simultaneous activity from the PMd, M1, and PPC areas of non-human primates could accurately predict 3-D arm movement trajectories [9]. Additional research in non-human primates has shown that activity from even relatively few neurons in M1 can reliably decode movement of a cursor on a computer screen [5, 6]. These results have led to breakthroughs in the translation of direct cortical control strategies from animal trials to humans. Just recently, a tetraplegic human was able to control a computer cursor to open e-mail, operate a television, and open and close a prosthetic hand using neuronal ensemble activity from a microelectrode array [5].

In general, these experiments have demonstrated the robust coding capacity of neural populations and have opened up the possibility of a BMI for direct neural control of a prosthetic limb and the restoration of motor control for amputees, paralyzed individuals, and those with degenerative muscular diseases. These efforts have focused largely on controlling a computer cursor [5, 6], predicting movement intent [1, 8], and decoding hand and arm trajectory [2–4, 9, 10], however, and current neural control strategies do not allow for dexterous neuroprosthetic control of actions such as individuated and combined finger movements.

Prior studies of motor cortical activities in primates by Schieber et al [11–14] and Georgopoulos et al [15, 16] have shown that there are indeed neurons in the primary motor cortex that code for specific finger movements, and which discharge during movements of several fingers. Their results also suggest that neuronal populations active with movements of different fingers overlap extensively in their spatial locations in the motor cortex [13, 14]. Although there are neurons that fire maximally for a specific movement type these neurons are not localized to a specific anatomic region, but rather are distributed throughout the hand region [14]. More recent MRI studies with humans [17, 18] also show that while there are regions of the primary motor cortex active with different finger movements, there is also an overlap of finger representation in the motor homunculus. The lack of A strict somatotopic organization of the M1 hand area suggests that a given subpopulation of neurons in this region should contain sufficient information to encode for individuated and combined movements of the fingers and wrist.

Original work using population vectors [15, 16], which combine the weighted contributions from each neuron along a preferred direction, found that 75% of motor cortical neurons related to finger movements were tuned to specific directions in a 3D instructed hand movement space. Although population vectors were fairly good predictors of the direction of instructed finger movements, this approach only yielded 60–70% decoding accuracy in recent work by Pouget et al [19] on decoding finger movements. However, using non-linear classification schemes such as logistic regression and softmax, they demonstrated close to 100% decoding accuracy of individuated finger movements using only 20–30 neurons. Extended to combined finger movements, they obtained approximately 90% decoding accuracy, albeit using a substantially larger neuronal population.

Although it has been shown that dexterous movements can indeed be decoded, earlier work in this field has relied on a priori knowledge of the movement events [15, 19]. BMI control of a neuroprosthesis, on the other hand, requires streaming of neuronal data in real-time where cues indicating the onset of movement are not known. The goal of this study was to demonstrate, for the first time, the feasibility of a BMI for dexterous control of individual fingers and the wrist of a multi-fingered prosthetic hand by decoding both movement intent and movement type. The final decoded output then was used to actuate a multi-fingered robotic hand in real-time for a pre-planned task.

II. METHODS

A. Experimental Setup

Three male rhesus (Macaca mulatta) monkeys – C, G, K – were trained to perform visually-cued individuated finger and wrist movements. Each monkey placed its right hand in a pistol-grip manipulandum, which separated each finger into a different slot. Each fingertip lay between two micro-switches at the end of the slot and, by flexing or extending a digit a few millimeters, the monkey closed the ventral or dorsal switches respectively. The manipulandum also was mounted on an axis that allowed for flexion and extension of the wrist. A detailed description of the experimental protocol can be found in [12].

All the monkeys performed 12 distinct individuated movements: flexion and extension of each of the fingers and of the wrist of the right hand. Each instructed movement is abbreviated with the first letter of the instructed direction (f=flexion and e=extension), and the number of the instructed digit (1=thumb…5=little finger, w=wrist; e.g. 'e4' indicates extension of ring finger). Monkey K performed an additional 6 combined finger movements involving two digits: f1+2, f2+3, f4+5, e1+2, e2+3, e4+5.

Single-unit activities were recorded from 312 task-related neurons in M1 for monkey C, 125 neurons for monkey G, and 115 neurons for monkey K. The duration of each trial was approximately 2 s, and for data analysis all trials were aligned such that switch closure occurred at 1 s. For monkey C and monkey G, data from each neuron for up to 7 trials per movement type was used, while for monkey K data from each neuron for up to 15 trials per movement type was used.

B. Analyzing the Input Space

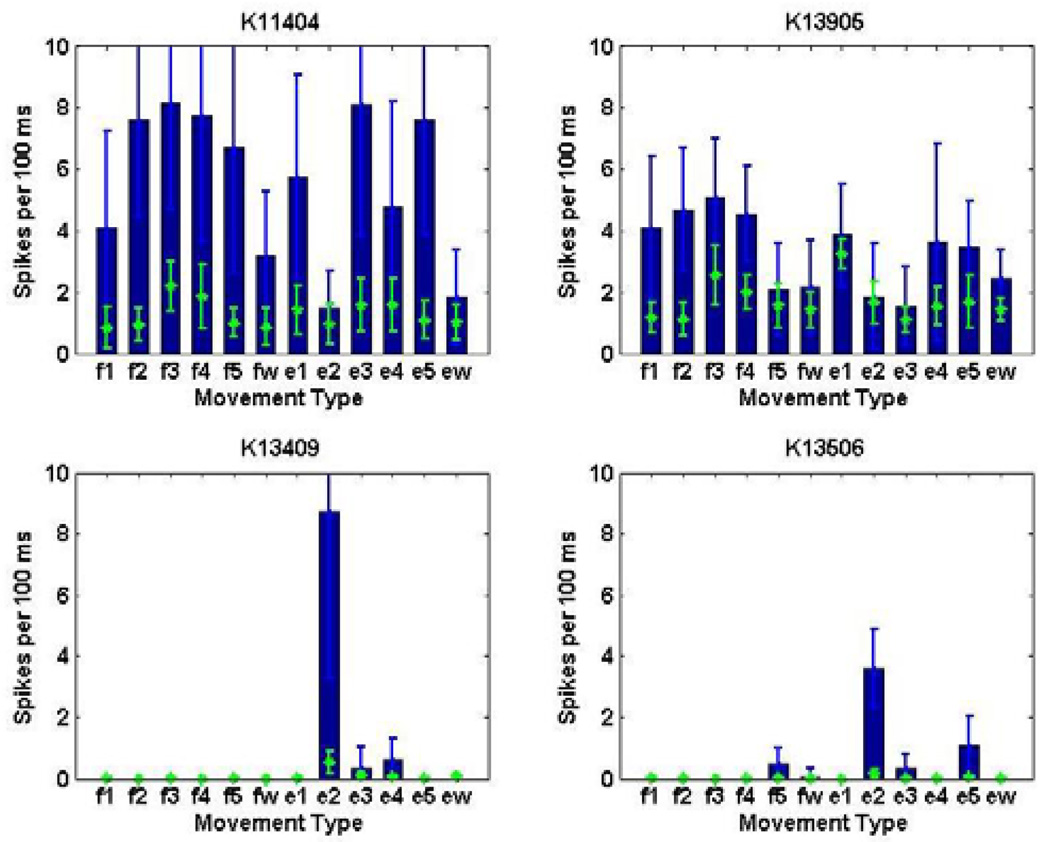
Different neurons showed different types of tuning to the set of movements. For example, certain neurons may be broadly-tuned and responsive to multiple movement types, whereas other neurons may be highly-tuned to specific movement types. Four examples of neurons from monkey K are illustrated in Fig. 1. The spike histograms show the number of spikes discharged in the 100 ms preceding switch closure for different movement types. Neurons K11404 and K13905 show a broad response to all twelve movement types, while neurons K13409 and K13506 are responsive only to extension of the index finger. Since the input space will not include dedicated neurons responsive to each movement type, an appropriate mathematical model describing the neuronal firing patterns is needed to unmask the input-output relationship of this complex multidimensional space.

Fig. 1.

Histograms of spike counts from sample neurons in monkey K show that the neuronal population contains both broadly-tuned neurons active during multiple finger movements (e.g K11404, K13905), and highly-tuned neurons active during only specific finger movements (e.g K13409, K13506). The histograms (blue) represent spiking activity during the 100 ms movement period directly preceding switch closure, while the scatter points (green) represent background spiking activity during non-movement periods.

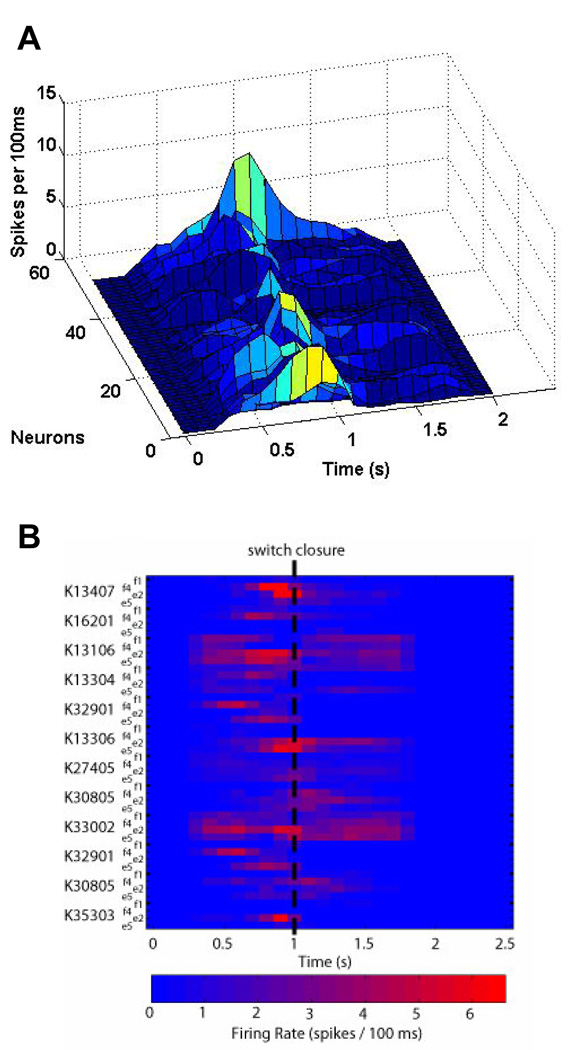
Fig. 2A further demonstrates the complexity of the input space by looking at the temporal evolution of spiking activity of a neuronal ensemble in monkey K. As seen in Fig. 2B, there was an increase in neuronal activity in the period directly preceding the switch closure at 1 s (shown for 12 neurons and 4 movement types). Since the neuronal activity is dynamic, any model describing the input space must account for changes in the neuronal activity during periods of rest and during periods of movement. Therefore, to make the problem tractable, the input space was divided into hierarchical subspaces corresponding to either rest or finger movement. The first subspace resolved movement intent from baseline activity, while the second subspace decoded each movement type from the period of activity directly preceding switch closure.

Fig. 2.

A) The timecourse of neuronal activity from monkey K shows a gradual evolution of spiking activity in and around the time of switch closure (1 s). B) Although a clear increase in activity is evident, the effect varies across neurons and movement types (shown for 12 sample neurons from monkey K and 4 movement types), which adds to the complexity of the problem at hand.

C. Choosing a Mathematical Model

Given the complex nature of neuronal firing patterns, deciphering the neural coding associated with dexterous tasks such as individual finger movements is not trivial. Many neural decoding algorithms have been developed, the simplest of which is a linear estimator. Linear classifiers have demonstrated effective neural control of a cursor [6] or arm trajectory [2, 10, 20], but require data over a long time window. Kalman filter-based methods have also been exploited for neural control of a 2D cursor [21, 22], while more recently probabilistic approaches such as maximum likelihood (ML) methods have provided promising results in decoding reaching movements [1, 23, 24]. These models, however, assume that each neuron can be treated as an independent unit, but given the spatial distribution of activity across various finger movement types it is unclear whether this assumption holds true for finger movements.

Therefore, non-linear decoding filters were designed using multilayer, feedforward Artificial Neural Networks (ANNs), which have been widely used in non-linear regression, function approximation, and classification [25], and have become a popular approach for neural decoding of movements [2–4]. In order to decode individual and combined finger movements in real-time, a hierarchical classification scheme was developed. First, a Gating Classifier was trained to distinguish baseline activity from movement intent. Second, a Movement Classifier was trained to distinguish amongst the individual or combined movement types.

D. Decoding Movement Intent: Gating Classifier

The Gating Classifier was designed as committee of N gating neural networks (where N was odd), and trained to distinguish baseline activity from movement. Each ANN in the committee, g(t_k), was trained using the neuronal firing rate over a sliding temporal window of duration T_W that was shifting every T_S (chosen to be 100 ms and 20 ms, respectively). ANNs were designed with n input neurons (where n is the number of sampled neurons), and a single output neuron. The output layer had a log sigmoidal activation function, which normalized the output to between 0 and 1.

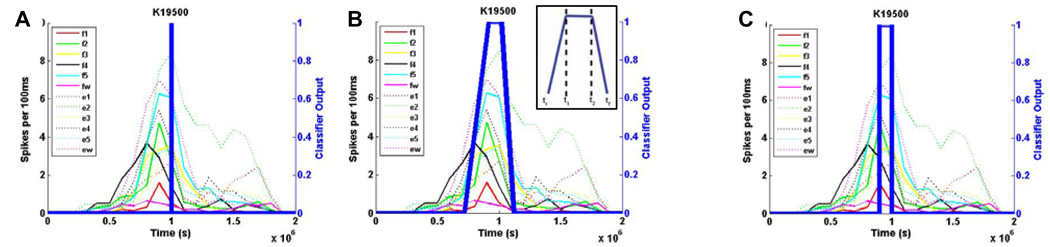
In order to train the gating networks appropriately, however, it was important to first look at the temporal evolution of spiking activity. Fig. 3 shows example timecourses of spike activity for a single neuron from monkey K. The plot overlays single trial data for each of the twelve individual finger movement types. A reasonable approach would have been to simply assign the point of switch closure as having an output of 1 and all other time points to have an output of 0 (Fig. 3A). However, due to the fact that a) this would result in limited training points, and b) the neuronal activity gradually evolved and reached a peak even prior to switch closure, the networks were trained instead with a trapezoidal membership function (Fig. 3B) and assigned a fuzzy output label, P{I(t_k)} at discrete times t_k. The membership function parameters, t_r, t_f, t₁, t₂, were determined empirically and shown in Fig 3B (inset).

$$P\{I(t_k)\}=\{\begin{array}{cc}\frac{T_s}{t_1-t_r}\hfill & \mathit{\text{if}}{t}_r\le t_k<t_1\hfill \\ \hfill 1\hfill & \mathit{\text{if}}{t}_1\le t_k<t_2\hfill \\ \frac{T_s}{t_f-t_2}\hfill & \mathit{\text{if}}{t}_2\le t_k<t_f\hfill \\ \hfill 0\hfill & \hfill \mathit{\text{else}}\hfill \end{array}$$ (1)

Fig. 3.

The timecourse of a sample neuron in monkey K during movement of individual fingers shows that the neuronal firing rate gradually increased and reached a peak at (or slightly before) the time of switch closure. A) Rather than training the Gating Classifier at only the time of switch closure, a B) “soft” trapezoidal membership function was used to train the classifier over a broad time period. The sensitivity of the Gating Classifier was improved by applying fuzzy decision boundaries and thresholding the output of the classifier. C) To train the Movement Classifier, however, only the neuronal firing rate during the 100ms period of activity directly preceding switch closure was used. This helped ensure that the Movement Classifier only captured neuronal activity associated with a specific finger movement, and not gross movements.

Since the output values ranged between 0 and 1, they could be interpreted as a probability for movement intent. The output of each individual gating network was then thresholded at a value T₁ to produce a discrete binary variable,

$$g(t_k)=\{\begin{array}{cc}1\hfill & \mathit{\text{if}}P\{I(t_k)\}>T_1\hfill \\ 0\hfill & \hfill \mathit{\text{else}}\hfill \end{array}$$ (2)

where an output of 0 corresponded to rest and 1 corresponded to movement intent. A majority voting rule was then used to determine the final committee output, G(t_k),

$$G(t_k)={\displaystyle \sum _{n=1}^N\left(g_n(t_k)\right)>\frac{N}{2}}$$ (3)

In order to eliminate spurious gating classifications, the committee output was tracked continuously. The Gating Classifier, G_track(t_k), would only fire if the committee output indicated movement intent at least T₂ times over the previous t_j time points,

$$G_{\mathit{\text{track}}}(t_k)=\{\begin{array}{cc}1\hfill & \mathit{\text{if}}{\displaystyle \sum _{t=t_k-t_j}^{t_k}(G(t_k))>T_2}\hfill \\ 0\hfill & \hfill \mathit{\text{else}}\hfill \end{array}$$ (4)

T₁, T₂, and t_j were optimized to maximize classifier accuracy.

E. Decoding Movement Type: Movement Classifier

The Movement Classifier also was designed as committee of N movement neural networks (where N was odd), but was trained to distinguish only amongst each movement type. Each ANN in the committee, s(t_k), was trained using the neuronal firing rate during only the 100 ms window preceding switch closure (T_switch). ANNs were designed with n input neurons (where n is the number of sampled neurons), and m output neurons (where m is the number of movement types). The output layer had a log sigmoidal activation function, which normalized the output to between 0 and 1.

The networks were trained with a binary membership function (Fig. 3C) and assigned an output label for each movement type, P{M_i(t_k)} at discrete times t_k (where i = 1,…,12 corresponding to the 12 individuated movement types and i = 13,…,18 corresponding to the 6 combined movement types). For the i^th movement type, the i^th output neuron was assigned an output of 1 during this window and all other neurons were assigned an output of 0.

$$\begin{array}{cc}P\{M_1(t_k)\}=0\hfill & \mathit{\text{if}}(T_{\mathit{\text{switch}}}-0.1)\le t_k<T_{\mathit{\text{switch}}}\hfill \\ \hfill & ⋮\hfill \\ P\{M_i(t_k)\}=1\hfill & \mathit{\text{if}}(T_{\mathit{\text{switch}}}-0.1)\le t_k<T_{\mathit{\text{switch}}}\hfill \\ \hfill & ⋮\hfill \\ P\{M_m(t_k)\}=0\hfill & \mathit{\text{if}}(T_{\mathit{\text{switch}}}-0.1)\le t_k<T_{\mathit{\text{switch}}}\hfill \end{array}$$ (5)

Once again, since the output values ranged between 0 and 1, they could be interpreted as probabilities for a specific movement type. The output of each of the individual movement networks was selected based on the output neuron that had the greatest output activity (or probability),

$$s(t_k)=\text{arg}\text{max}P\{M_i(t_k)\}$$ (6)

A majority voting rule was then used to determine the final committee output of the movement classifier, S(t_k),

$$S(t_k)=\text{mode}\{S_n(t_k)\}$$ (7)

F. Combining the Classifiers

Committee neural networks are commonly used for classification of biological signals and known to improve decoding accuracy [26]. We trained a total of five gating networks and five movement networks for any given subpopulation of neurons. The networks were ranked based on decoding accuracy of a virgin validation set, and the top three networks were selected to form the gating and movement classifier committees, respectively.

After applying a majority voting rule to get the final Gating Classifier output, G_track(t_k), and Movement Classifier output, S(t_k), the final decoded output, F(t_k), was obtained from the product of the two classifiers.

$$F(t_k)=G_{\mathit{\text{track}}}(t_k)\times S(t_k)$$ (8)

Individual 2 s trials were concatenated to form neuronal spike trains with activity from all the neurons selected. A classification decision was made every 20 ms using the previous 100 ms of spike activity. A decoded output of 0 yielded no action; 1–6 led to flexion of each digit and wrist (f1…fw); and 7–12 led to extension of each digit and wrist (e1…ew). For combined finger movements, an output of 13–15 led to flexion of multiple digits (f1+f2, f2+f3, f4+5) and an output of 16–18 led to extension of multiple digits (e1+e2, e2+e3, e4+e5).

G. ANN Training

All ANNs were designed with one hidden layer containing 0.5–2.5 times the number of input neurons, tan sigmoidal transfer functions for the hidden layer, and log sigmoidal transfer functions for the output layer. Dimensionality of the input space was reduced using Principle Component Analysis (PCA). After rank-ordering the components by variance, only those principle components that cumulatively contributed to >95% of the total variance were retained. The networks were trained using the steepest conjugate gradient (SCG) descent algorithm, and early validation to prevent overfitting. Training, validation, and testing data were selected from mutually exclusive trials – with ½ used for training, ¼ used for validation, and ¼ used for testing. Each training, validation, or testing set is formed through a random combination of trials for each neuron. The neural networks were trained offline using MATLAB 7.4 (Mathworks Inc.) Separate decoding filters were designed for each neuronal subpopulation selected.

H. Real-Time Actuation of Multi-Fingered Prosthetic Hand

The final decoded output was used to drive a multi-fingered robotic hand, which permitted independent flexion/extension of each finger. Each joint was controlled by a separate servo motor using pulse-width modulation (PWM) to determine the final joint angle. The real-time decoded output stream was transmitted wirelessly from a standalone PC running the signal processing algorithms to a custom 16-bit PIC microcontroller (Microchip Technology, Inc.) that interfaced with the individual servo motors. Commands from the microcontroller then were used to actuate the hand to play a sequence of musical tunes on a piano keyboard in real-time.

III. RESULTS

Asynchronous decoding of complex movements requires simultaneous recordings from an ensemble of neurons. Therefore, simultaneous multi-unit activity was re-created from the single-unit activities, event-locked to time of switch closure. Subpopulations of neurons were randomly selected from the total population of recorded task-related neurons (312 neurons for monkey C; 125 neurons for monkey G; 115 neurons for monkey K). Results were calculated for 100 trials per movement type, and the decoding accuracy was averaged across six samples for a given number of neurons.

A. Classifier Output

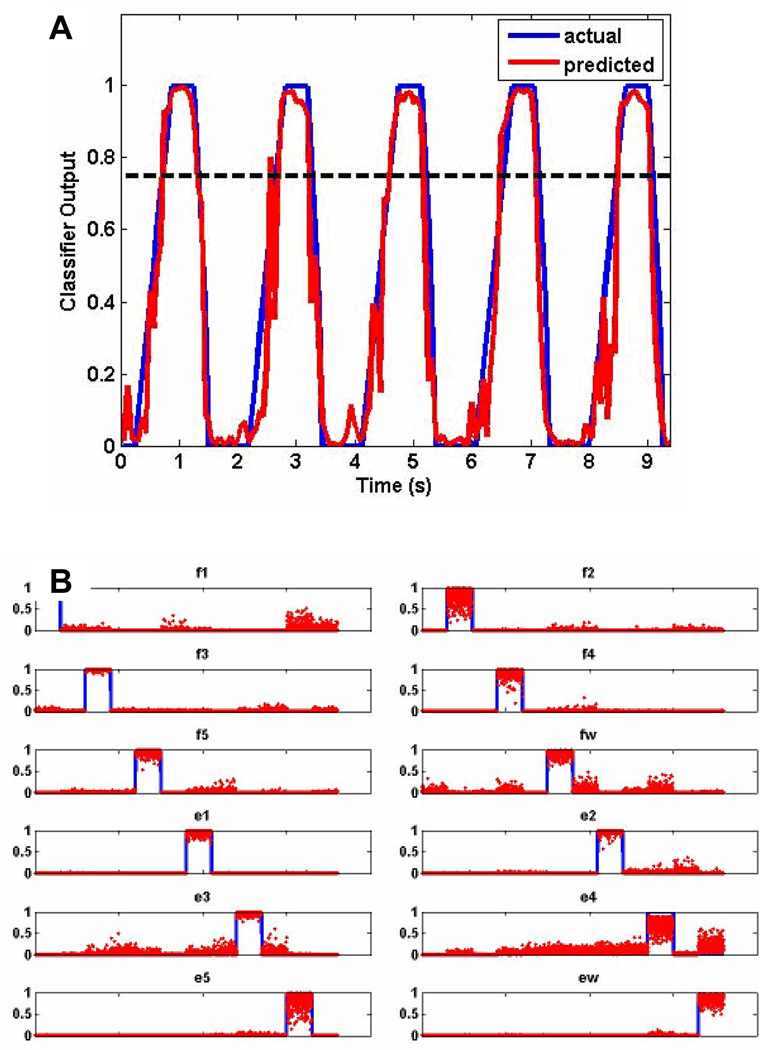
Fig. 4A shows a sample raw output of a single gating network, g(t_k), with the predicted output in red and actual output in blue. As can be seen, the predicted output closely tracked the actual output, meaning the classifier detected the occurrence of a movement well. From Eq. 2, a binary output was created by thresholding the output of the gating network at T₁ (dotted line), which was empirically determined to be 0.75.

Fig. 4.

A) The raw output from a single gating network shows that the predicted output (red) tracked the actual output (blue) very closely. Therefore, the gating classifier did a good job of decoding movement intent. B) The raw output from a single movement network shows that the predicted output neuron activity (red) was specific to the movement type to be decoded (blue). Therefore, the movement classifier did a good job of decoding the movement type.

Fig. 4B shows sample output of a single movement network (in this case trained for only 12 individual movements), s(t_k), with the predicted output in blue and actual output in red. Each subplot shows the output for the 12 output neurons corresponding to 100 trials for each movement type. As can be seen, for the most part each of the output neurons was only active for the specific movement type that it was trained to recognize. From Eq. 6, the final output was selected based on the output neuron that had the greatest output activity.

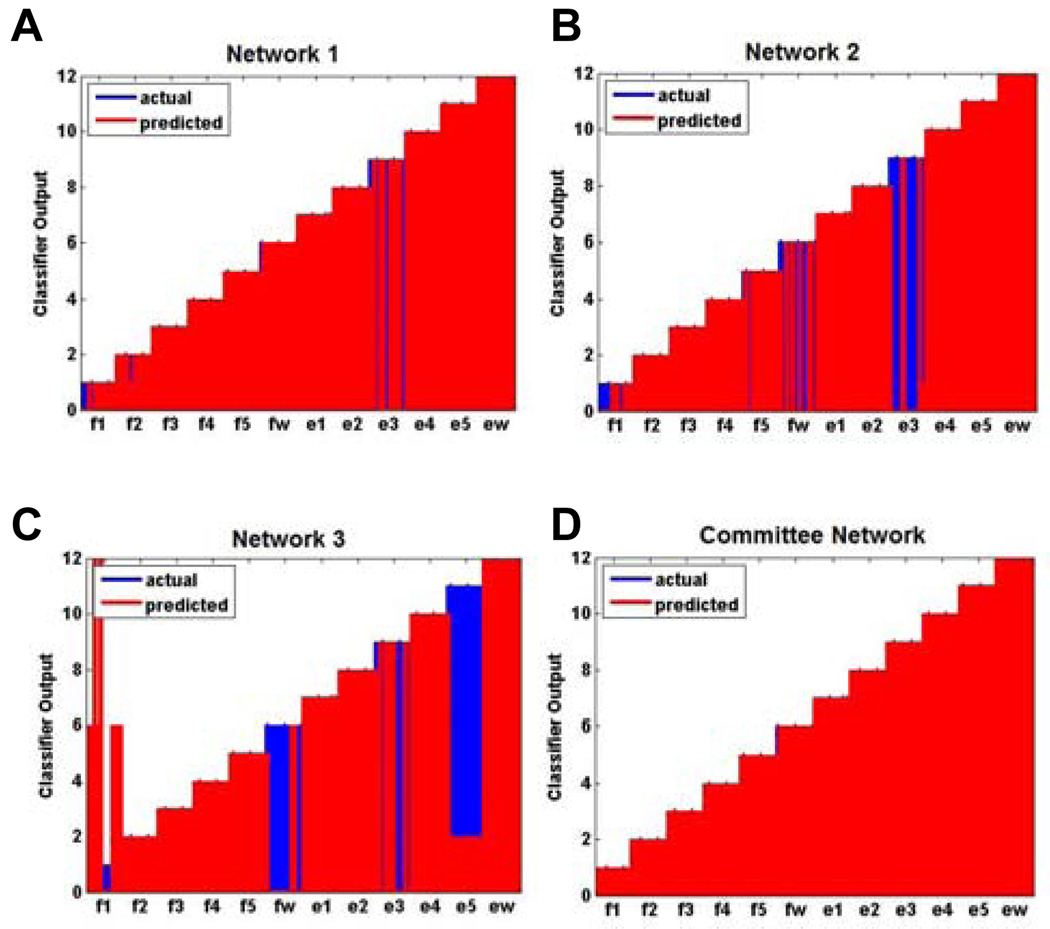
To illustrate the benefits of a committee network, Fig. 5A–C shows the final decoded output for three different classifiers where only a single gating network and movement network were used. Fig. 5D shows the final decoded output when a committee network was employed instead. As can be seen, the committee improved decoding accuracy markedly.

Fig. 5.

A–C) shows the final decoded output for 3 different classifiers where only a single gating and movement network were used (shown for monkey K using 20 neurons for decoding). Each classifier fared poorly individually, but when D) a committee network is employed the overall final decoded output showed a marked improvement.

B. Asynchronous Decoding Accuracy

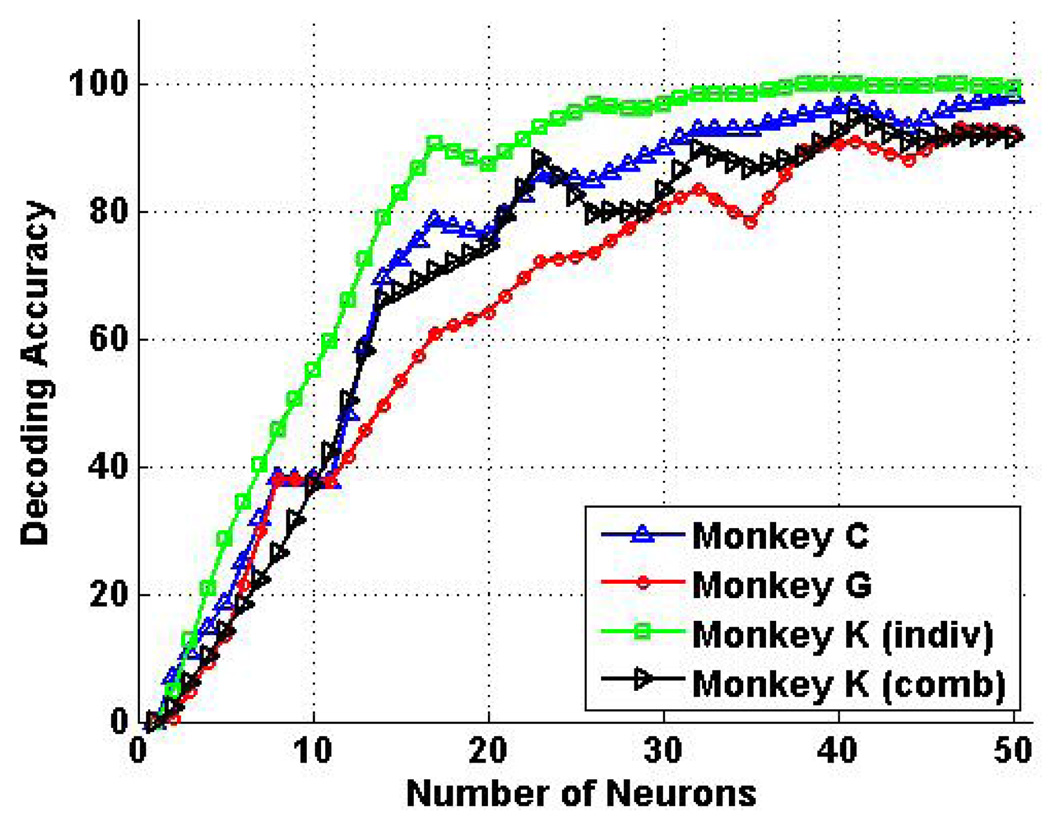
Fig. 6 shows the average asynchronous decoding accuracy for the 12 individuated finger movements for monkey C (black), monkey G (blue), and monkey K (red), as well as the 18 individuated and combined finger movements for monkey K (green). For individuated movements, the average decoding accuracy was 99.8% ± 0.1% for monkey K using 40 neurons, and 95.4% ± 1.0% with as few as 25 neurons. For monkey C, the average decoding accuracy was 96.2% ± 1.8% for monkey C using 40 neurons, and still 85.0% ± 3.0% using only 25 neurons. For monkey G, the average decoding accuracy was 90.5% ± 2.1% using 40 neurons, and dropped to 72.9% ± 2.1% using 25 neurons. When combined finger movements of two fingers were included, the average decoding accuracy was still as high as 92.5% ± 1.1% with as few as 40 neurons for monkey K. These results are summarized in Table 1.

Fig. 6.

Asynchronous decoding results for individuated and combined finger movements. For individuated movements, decoding accuracy was as high as 99.8% ± 0.1% for monkey K using 40 neurons, and 95.4% ± 1.0% using only 25 neurons. Although lower, decoding accuracy was still 96.2% ± 1.8% for monkey C and 90.5% ± 2.1% for monkey G using 40 neurons. When combined movements were included, average decoding accuracy was 92.5% ± 1.1% for all 18 movement types using 40 neurons for monkey K.

TABLE I.

Summary Of Asynchronous Decoding Results

Monkey	25 Neurons	35 Neurons	40 Neurons
C	85.0% ± 3.0%	92.9% ± 1.3%	96.2% ± 1.8%
G	72.9% ± 2.1%	78.3% ± 3.3%	90.5% ± 2.1%
K (indiv)	95.4% ± 1.0%	98.3% ± 1.5%	99.8% ± 0.1%
K (comb)	82.4% ± 2.1%	86.7% ± 1.6%	92.5% ± 1.1%

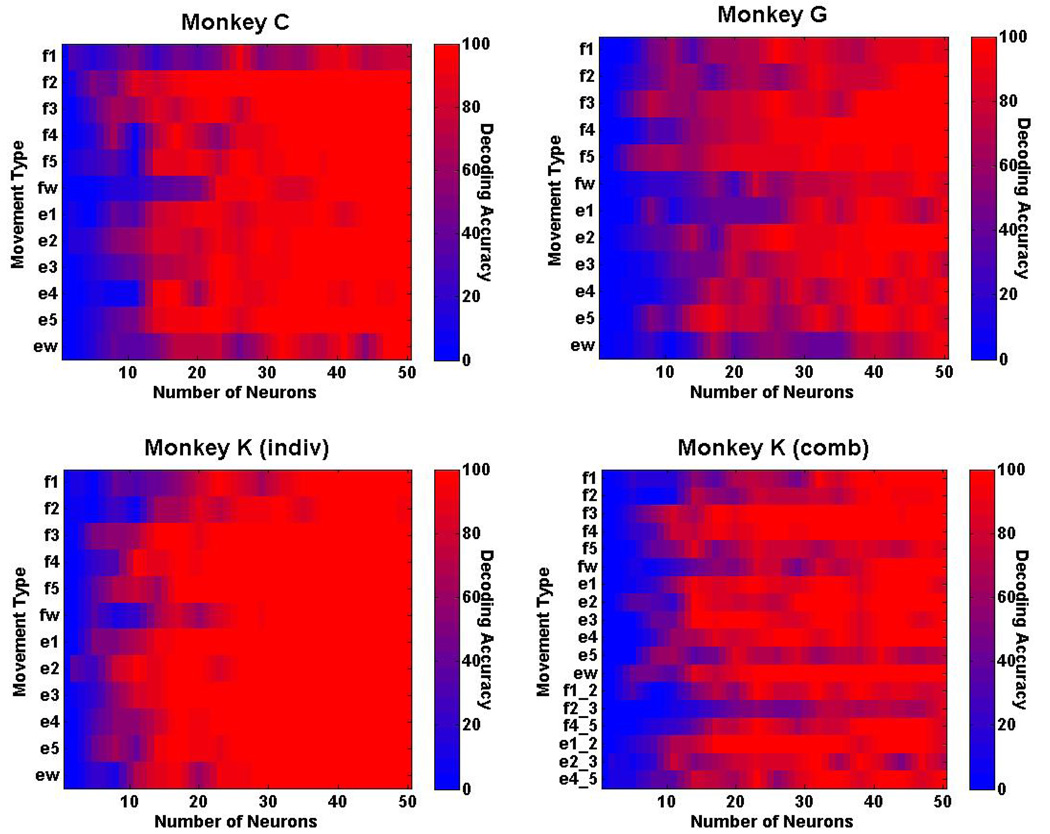
Real-time decoding accuracy also was examined separately for each movement type to determine whether accuracy varied for different movements. Fig. 7 shows the decoding accuracy for the 12 individuated finger movements for monkey C, monkey G, and monkey K, as well as the 18 individuated and combined finger movements for monkey K. The results show that 10 out of 12 movement types are decoded with greater than 95% accuracy using 50 neurons for monkey C, with flexion and extension of the wrist being two of the movements that were decoded poorly. Twelve out of 12 movement types, however, are decoded with greater than 99% accuracy using 50 neurons for monkey K. When the 6 additional combined movements are included, 13 out of 18 movement types are decoded with greater than 99% accuracy using 50 neurons for monkey K.

Fig. 7.

Real-time decoding results for each movement type. Ten out of 12 individuated movement types are decoded with >95% accuracy for monkey C, and all 12 individuated movement types are decoded with >99% accuracy for monkey K. When combined movement movements are included, 13 out 18 movement types are decoded with >99% for monkey K.

IV. DISCUSSION

The results demonstrate that activity from ensembles of randomly-selected, task-related neurons in the M1 hand area contains sufficient information to allow for the asynchronous decoding of individuated movements of the fingers and the wrist. Average asynchronous decoding accuracies for individuated movements approached 100% for two of the three monkeys with 40 neurons, and were still greater than 90% for the remaining monkey or when including combined finger movements. In particular, monkeys C and K achieved average decoding accuracies of greater than 90% with as few as 28 neurons for monkey C and 17 neurons for monkey K. Monkey G was a relatively poor performer of the individuated movement task (Schieber, unpublished observations), which may explain why overall decoding accuracies were lower for monkey G than the other monkeys.

The consistently high overall decoding accuracies across multiple monkeys, each with a different distribution of neural recordings in the M1 hand area, illustrate the robustness of the decoding algorithm to successfully decode this complex multi-dimensional input space irrespective of the specific neuronal population. However, it is apparent that there are biases in decoding accuracies when looking at specific movement types. Although flexion of the thumb and flexion/extension of the wrist are typically the easiest movements for monkeys to perform, these movement types (f1, fw, ew) had the poorest decoding performance (see Fig. 7). Previous reports show less neural activity during f1, fw, and ew, than during other movements [14]. Movements that are simpler for the monkey to perform thus may entail less M1 neural activity, making such movements paradoxically more difficult to decode.

A. Novelty of Decoding Algorithm

Unlike previous studies [15, 19] that have focused on decoding finger movements, our results are the first to demonstrate asynchronous decoding where both the movement intent and movement type are decoded. This novel hierarchical classification scheme is well-suited for BMI applications where cues indicating the onset of movement are not known. Although the training of neural networks is computationally intensive, the decoding filters are trained offline and the algorithm can still be applied to real-time applications with little latency.

Furthermore, our results show decoding accuracies on par or better than previous synchronous decoding approaches [15, 19]. In addition to ANNs that are capable of resolving this highly complex input space, a committee neural network approach was used to increase the decoding accuracy and reduce the associated measure of uncertainty. It has been shown that a committee of classifiers, each of which performs better than random chance, can result in remarkably higher classification accuracies than the individual classifiers themselves [26]. Even though one network may have decoded a movement incorrectly, on any given trial the remaining networks in the committee may have decoded the movement correctly. Therefore, based on a majority rule, the resulting final decoded output would still be correct. Further increases in decoding accuracy can be expected if the committee size were to be increased.

B. Towards a BMI for Dexterous Control

The present work is an important step towards the development of a BMI for dexterous control of finger and wrist movements. These results show that it is indeed possible to asynchronously decode individuated and combined movements of the fingers and wrist using randomly selected neuronal ensembles in the M1 hand area. It is important to note, however, that we used sequentially recorded single-unit activities from task-related neurons, and not simultaneously recorded neuronal activity as would be obtained using implanted microelectrode arrays such as the Utah Array [27].

In such an implanted array, all electrodes would not record exclusively from task-related neurons. Therefore, it is possible that activity from non-task-related neurons would hinder the ability of our algorithms to decode the correct movement type. On the other hand there may also be additional encoded information, due to coherence or phase synchrony within neuron ensembles [28] active during a single task, which could be used to improve the decoding accuracy of complex tasks.

Recordings from a microelectrode array also would be constrained geographically to the recording volume of the array. The lack of somatotopic organization in the M1 hand area, however, offers the possibility of successful decoding irrespective of the precise geographic location selected. Our preliminary work [29] using constrained virtual neuronal ensembles that mimic the reality of recording from actual electrode arrays placed in the target area, show comparable decoding accuracy to the results in this paper. Current work [30] also investigates how decoding performance is affected by constraining these virtual neuronal ensembles to volumes that correspond to actual electrode array architecture dimensions. This will be invaluable in determining both the optimal location for implantation in the M1 hand area, and optimal electrode array sizes for chronic recording.

While actual closed-loop use of a BMI will involve some degree of operant conditioning, the native decoding achieved here suggests that such retraining might be minimal, providing relatively intuitive control of the individual fingers in a prosthetic hand. Although closed-loop experiments with additional monkeys utilizing implanted arrays can extend the present findings, this work opens the door for developing a direct neural interface to provide real-time, dexterous control of a next-generation multi-fingered hand neuroprosthesis.

Biography

Vikram Aggarwal (M’05) received the B.ASc. degree in computer engineering from the University of Waterloo, Waterloo, ON, Canada in 2005. He is currently working towards an M.S.E. degree in biomedical engineering at Johns Hopkins University, Baltimore, MD, USA.

He has industry experience in research, software consulting, and device engineering. Previous employers include Sun Microsystems Laboratories and ATI Technologies. His primary research interests include neuroprostheses, brain-computer interfaces, and biomedical instrumentation.

Mr. Aggarwal is a student member of the Biomedical Engineering Society. His achievements include IEEE Student Paper Night winner (‘05), Student Design Competition finalist at the IEEE Engineering in Medicine and Biology Society Conference (EMBS ’06), and student fellowship awardee at the IEEE Engineering in Medicine and Biology Society on Neural Engineering Conference (NER ‘07).