Abstract
For a moving animal, optic flow is an important source of information about its ego-motion. In flies, the processing of optic flow is performed by motion sensitive tangential cells in the lobula plate. Amongst them, cells of the vertical system (VS cells) have receptive fields with similarities to optic flows generated during rotations around different body axes. Their output signals are further processed by pre-motor descending neurons. Here, we investigate the local motion preferences of two descending neurons called descending neurons of the ocellar and vertical system (DNOVS1 and DNOVS2). Using an LED arena subtending 240° × 95° of visual space, we mapped the receptive fields of DNOVS1 and DNOVS2 as well as those of their presynaptic elements, i.e. VS cells 1–10 and V2. The receptive field of DNOVS1 can be predicted in detail from the receptive fields of those VS cells that are most strongly coupled to the cell. The receptive field of DNOVS2 is a combination of V2 and VS cells receptive fields. Predicting the global motion preferences from the receptive field revealed a linear spatial integration in DNOVS1 and a superlinear spatial integration in DNOVS2. In addition, the superlinear integration of V2 output is necessary for DNOVS2 to differentiate between a roll rotation and a lift translation of the fly.
Keywords: Receptive field, Spatial integration, Descending neurons, Optic flow, Vision
Introduction
A moving animal causes, by its own movement, the images of the environment to shift across its retina. This motion pattern is called optic flow and can be described as a vector field representing the distribution of motion vectors on the retina at one given instance (Gibson 1974; Koenderink and van Doorn 1987). Since the optic flow is determined by the movement of the animal, it provides the animal with feedback on its actual maneuver: An expanding flow-field with the pole of expansion in front can signal forward motion of the animal with an impending collision (Borst and Bahde 1988a, b; Rind and Simmons 1992; Hatsopoulos et al. 1995), a rotational flow-field with the center above and below the animal is indicative for a rotation of the animal around its vertical body axis (Götz 1964; Reichardt 1969; Reichardt and Poggio 1976; Hengstenberg et al. 1986).
Motion sensitive neurons analyzing these optic flow patterns often have large receptive fields and are selective for specific flow fields as occurring during certain flight maneuvers. Well studied examples of such neurons having complex receptive fields are the tangential cells in the third neuropile of the fly optic lobe, the lobula plate (Srinivasan et al. 1993; Krapp and Hengstenberg 1996; Krapp et al. 1998, 2001; Nordström et al. 2008). In blowflies, the lobula plate comprises a set of about 60 lobula plate tangential cells which all can be identified due to their invariant anatomy and characteristic visual response properties (Hausen 1982; Hengstenberg et al. 1982; Borst and Haag 2002). One subgroup, the ten vertical system (VS) cells have large and complex receptive fields with different preferred directions in different parts of their receptive fields, matching the optic flow that occurs during rotations of the fly around different body axes (Krapp et al. 1998). The directionally selective input from an array of local motion detectors (Haag et al. 1992, 1999, 2004; Single and Borst 1998) as well as their coupling amongst them (Haag and Borst 2004, 2005), are responsible for the VS cells’ tuning to specific flow fields (Farrow et al. 2005; Elyada et al. 2009). The ten VS cells are major output elements of the brain and synapse onto descending neurons (Fig. 1a) which convey visual motion information to the thoracic ganglion (Strausfeld and Seyan 1984). Two descending neurons of the ocellar and vertical system (DNOVS1 and DNOVS2, Strausfeld and Bassemir 1985) turned out to be electrically coupled to different subsets of VS cells (Strausfeld and Bassemir 1985; Haag et al. 2007; Wertz et al. 2008). DNOVS1 is most strongly coupled to VS6 and VS7 and DNOVS2 to VS5 and VS6 (Haag et al. 2007; Wertz et al. 2008). Neighboring VS cells are weaker coupled to the descending neurons. In addition, DNOVS2 integrates motion information from the contralateral eye, probably via the V2 cell (Wertz et al. 2008). Whereas DNOVS1 responds with a graded shift of the membrane potential, DNOVS2 responds with action potentials to motion stimuli. Like VS cells, DNOVS cells are tuned globally to rotations of the fly around different body axes (Wertz et al. 2009). However, a precise comparison of the local motion preferences of pre- (VS and V2 cells) and postsynaptic elements (DNOVS1 and 2) was not possible due to limitations of the stimulus device used previously.
Fig. 1.
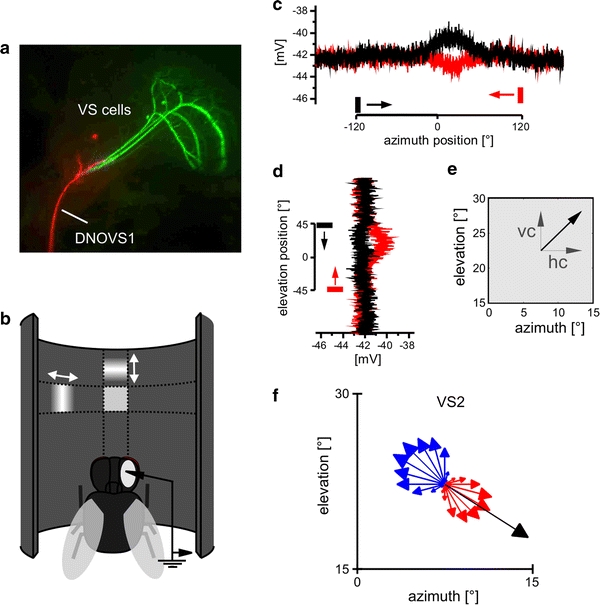
Determination of the local motion properties. a Cells of interest: three VS cells (green) and one DNOVS1 cell (red) were recorded and filled with fluorescent dyes. b Schematic of the procedure used for mapping the receptive field of a cell: a small bar (15° width) was moved first horizontally and then vertically while recording from the cell. c Example response of DNOVS1 to left- and rightward motion (black and red, respectively) at 22.5° elevation. d Example responses of DNOVS1 to a downward (black) and upward (red) moving bar at 7.5° azimuth. e From the horizontal and vertical component (hc and vc, respectively), a vector (black arrow) was calculated. The orientation of the arrow indicates the local preferred direction, the length of the arrow the local motion sensitivity at this point. f Local motion properties of VS2 to a sine grating moving in 24 directions as indicated by the arrows at 22.5° azimuth position and 22.5° elevation position. The length of the arrow represents the response strength, red represents a depolarization of the cell and blue a hyperpolarization of the cell. The black arrow is the vector summation of the vertical and horizontal component (color figure online)
Stimulating the cells by means of a custom built LED arena subtending 240° × 95° of the visual field of a fly, we determine the receptive field of DNOVS cells as well as their presynaptic cells using local motion stimuli (Fig. 1). To analyze the integration properties in DNOVS cells in more detail we ask two major questions: To what extend can the receptive fields of DNOVS cells be predicted from the receptive fields of their presynaptic neurons most strongly coupled to the cells? Can we predict the global motion sensitivity of DNOVS cells from their local motion sensitivities?
Materials and methods
Preparation and setup
Three to ten days old female blowflies (Calliphora vicina) were briefly anesthetized with CO2 and mounted ventral side up with wax on a small preparation platform. The head capsule was opened from behind; the trachea and air sacs that cover the lobula plate were removed. To eliminate movements of the brain caused by peristaltic contractions of the esophagus, the proboscis of the animal was cut away and the gut was pulled out. This allowed stable intracellular recordings of up to 45 min. After alignment of the fly with reference to its deep pseudopupil (Franceschini and Kirschfeld 1971), it was mounted on a heavy recording table facing the LED-arena (Fig. 1b). For recordings of DNOVS2, the following additional dissection steps were taken. First, the thorax was opened from dorsal to get access to the connective. Then, the large direct flight muscles and intestinal organs were pulled out. To minimize movements of the connective, the legs were cut away and the abdominal region was waxed. To stabilize the recordings, the connective was lifted up by a hook. The brain and the connective were viewed from behind through a fluorescence stereo microscope (MZ FLIII; Leica, Bensheim, Germany).
Electrical recordings
For intracellular recordings, glass electrodes were pulled on a Flaming/Brown micropipette puller (model P-97; Sutter Instrument, Novato, CA, USA), using glass capillaries with an outer diameter of 1 mm (GC100F-10; Science Products GMBH, Hofheim, Germany). The tip of the electrode was filled with either 10 mM Alexa Fluor 488 hydrazide (Alexa 488) or 10 mM Alexa Fluor 594 hydrazide (Alexa 594, both Invitrogen, Carlsbad, CA, USA). Alexa 488 and Alexa 594 fluoresce as green and red, respectively, allowing us to identify more than one cell at a time. The shaft of the electrode was filled with 2 M KAc plus 0.5 M KCl. The electrodes had resistances between 25 and 50 MΩ. Recorded signals were amplified using an SEL10 amplifier (NPI Electronic, Tamm, Germany). The output signals of the amplifier were fed to a personal computer (PC) via an analog to digital converter (PCI-DAS6025, Measurement Computing, MA, USA) with Matlab (MathWorks, Natick, MA, USA) at a sampling rate of 10 kHz. VS cells were filled with Alexa and visualized under fluorescence light. After the recording, several images of each Alexa-filled VS cell were taken (Fig. 1a) by a CCD camera (Leica DC 320). These images allowed anatomical identification of the recorded cell on the basis of their characteristic branching patterns and the relative position of their ventral dendrite within the lobula plate (Farrow 2005). The VS cell then served as a landmark for finding the DNOVS1 neuron (Haag et al. 2007). DNOVS1 was recorded intracellularly and stained with a fluorescent dye (Fig. 1a). The V2 cell was recorded intra- and extracellularly from its axonal arborization and could be identified due to its invariant anatomy (Hausen and Egelhaaf 1989) and its sensitivity for vertical motion along the azimuth (Wertz et al. 2008). Extracellular recordings of DNOVS2 were made in the connective near the thoracic ganglion. Standard tungsten electrodes with an impedance of 1 MΩ were used. DNOVS2 was identified based on the position of the tungsten electrode within the connective together with the cell’s strong response to downward motion and the specific sensitivity profile along the azimuth (Wertz et al. 2008). Extracellular signals were amplified, band-pass filtered and subsequently processed by a threshold device delivering a 100-mV pulse of 1 ms duration each time a spike was detected (workshop of Max-Planck-Institute for Biological Cybernetics, Tübingen, Germany). The output signals of the threshold device were fed to the same PC that was also used to control the stimulus. Data were acquired and analyzed with the data acquisition and analysis toolboxes of Matlab.
Visual stimulation
For visual stimulation an LED arena was custom built based on the open-source information of the Dickinson Laboratory (http://www.dickinson.caltech.edu/PanelsPage). Our arena consists of 30 × 16 TA08-81GWA dot matrix displays (Kingbright, CA, USA), each harboring 8 × 8 individual green (568 nm) LEDs. The arena is built as a cylinder with 240 LEDs arranged around two-thirds of a circle and 128 LEDs in heights covering 240° in azimuth and 95° in elevation of the fly’s visual field. This result in an angular resolution of 1° in azimuth and from 1.0° to 0.5° at elevation positions from 0° to 45° between adjacent LEDs. This angular resolution was deemed to be sufficient since the typical spatial resolution in Calliphora is approximately 2° (Petrowitz et al. 2000), although, in the frontal visual field, it can be as high as 1.2°. The luminance range of the stimuli was 0–80 cd/m2.
The arena is capable to run at frame rates above 600 fps producing 16 levels of light intensity. Each dot matrix display is controlled by an ATmega644 microcontroller (Atmel, CA, USA) that obtains pattern information from one central ATmega128 based main controller board. This board in turn reads in pattern information from a compact flash (CF) memory card. For achieving high frame rates with a system of this size each panel controller was equipped with an external AT45DB041B flash memory chip for local pattern buffering. Matlab was used for programming and generating the patterns as well as for sending the serial command sequences via RS-232 to the main controller board and local buffering.
Mapping the receptive field of a cell
To determine the spatial response characteristics of a cell, we used a similar stimulus as described by Nordström et al. (2008). A bar of 15° length and a Gaussian cross-section of σ = 2° was moved at 120°/s and a frame rate of 450 fps horizontally leftwards across the arena and then rightwards at six different elevation positions from −37.5° to 37.5° in steps of 15° (Fig. 1b). At each position the bar was presented 500 ms before and after it moved (see example traces in Fig. 1c, d). The response of the cell at each point in time was used as an indication for its sensitivity to horizontal motion at each particular position of the bar (Fig. 1c). In the example response of a DNOVS1 cell (Fig. 1c), the cell depolarized for the rightward moving bar (black) at frontal positions (~0°) and hyperpolarized for the leftward motion (red). In the same way, the cell’s sensitivity for vertical motion was probed using vertical moving bars at 16 different azimuth positions from −112.5° to 112.5° in steps of 15°. As an example response DNOVS1 depolarized for upward motion at an azimuth position of 7.5° (red trace in Fig. 1d).
We calculated the horizontal and vertical sensitivities by averaging 100 ms of the response of a cell at the given time point minus the resting potential (or spike frequency in rest) before stimulus onset at this position. From both these measurements, a vector field was calculated for the resulting 96 positions, using the horizontal and vertical sensitivities as x- and y-components of the respective vector (Fig. 1e). In this vector field the angle of an arrow indicates the local preferred direction, while the length of an arrow indicates the cell’s local motion sensitivity. All sensitivities were normalized to the maximal local motion sensitivity of the vector field. In the following this vector field is called the receptive field of a cell. The receptive fields of all cells were measured from −120° to 120° along the azimuth and from −45° to 45° in elevation. In control experiments, the cell’s local preferred direction was determined using gratings which moved in various directions at one given location. The control experiments were performed at different positions and with different cells. In the example of a VS2 cell (Fig. 1f) at 7.5° azimuth and 22.5° elevation, the cell depolarized (red arrows) for rightward and downward motion with strongest depolarization to oblique motion in between and hyperpolarized to the opposite motion (blue arrows). To investigate whether the x- and y-components are sufficient to determine the local motion properties, we calculated a response vector (black arrow) by a vector summation of only the vertical and horizontal motion sensitivities. Both types of measurements lead to the same result (Fig. 1f).
To compare two receptive fields (a, b) with each other, we defined a difference index (DI) by calculating the average vector length of the difference between the two vector fields (a, b):
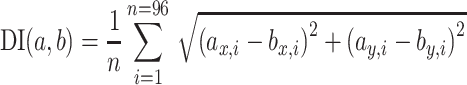 |
with each of the vector fields being normalized to maximum vector length = 1, the DI can range between 0 (identical vector fields) and 2 (two homogenous and opposite vector fields).
Mapping the superlinear receptive field of DNOVS2
To account for DNOVS2 nonlinear sensitivity for contralateral motion (Wertz et al. 2008), we measured the receptive field of DNOVS2 while depolarizing the cell with ipsilateral downward motion. A sinusoidal grating with 18° spatial wavelength was moved downwards at a speed of 120°/s. The pattern extended from 30° to 120° in azimuth and −45° to 45° in elevation. To map the contralateral local motion sensitivities (Fig. 5d), the gaussian bar was moved horizontally and vertically as described previously in the remaining part of the arena. The superlinear receptive field (Fig. 5g) was then calculated by combining the contralateral receptive field from −120° to 0° in azimuth to the receptive field from DNOVS2 from 0° to 120° azimuth.
Fig. 5.

Linear and superlinear receptive field maps of DNOVS2. a Receptive field of DNOVS2. b Expected receptive field for DNOVS1, calculated by a summation of the receptive fields of VS5 and VS6 (Fig. 2). c DIs between the average receptive field (RF mean) and each measured receptive field (RF n) of DNOVS1 (gray dots) and the DI between the average receptive field (RF mean) and the expected receptive field (RF exp) marked with a black square. d Contralateral LMS and LPD were recorded while DNOVS2 was depolarized by ipsilateral downward motion. e Receptive field of V2. f “Superlinear receptive field of DNOVS2”, calculated by adding the contralateral local motion sensitivity of DNOVS2 (d) to its receptive field (a). Data represent the mean responses recorded from n flies (DNOVS2 = 3, depolarized DNOVS2 = 3, V2 = 4)
Predicting the global motion preferences from local motion preferences
In order to predict the global motion preferences from the measured receptive field, we compared the receptive field of a cell with optic flow fields generated by various kinds of ego-motion. To do so, we used the movies to measure the preferred ego-motion of a cell (Wertz et al. 2009) as an input to our optic flow algorithm. The algorithm was written in IDL (RSI, Boulder, CO, USA) and uses region-based matching (Barron et al. 1994) to determine the vector field at each time point. Such approaches define the velocity V as the shift d = (dx, dy) that yields the best fit between image regions at subsequent times. The best fit is the one which minimizes the difference measure, defined as the sum of squared differences (SSD):
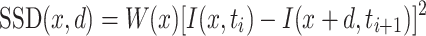 |
where W denotes a 2-d window function and x the position within the image.
The resulting time-dependent vector fields (Fig. 6a) were time averaged over the stimulus period. To quantify the match between the receptive field of the cell and the flow fields resulting from a particular flight maneuver, each of the two vector fields were first normalized with respect to the maximum vector length. The match between both vector fields was then determined by projecting the flow-field onto the receptive field of the neuron, i.e. by filtering the flow-field by the receptive field of the cell. Accordingly, the matching index (MI) was determined by averaging the scalar products between all the vectors of the flow-field (a) and the receptive field (b) at any given spot.
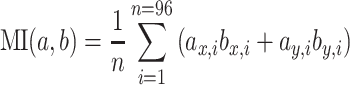 |
Fig. 6.
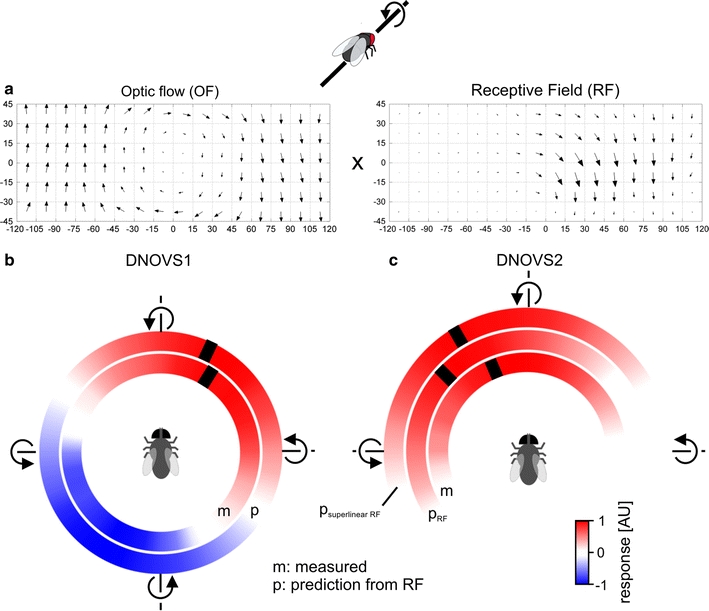
Global motion preferences from the receptive field. a Schematic of the procedure used to calculate the linear ego-motion prediction: for each movement (e.g. a counterclockwise roll movement) the optic flow (OF) was calculated and multiplied with the receptive field (RF) of a cell (see “Materials and methods”). b Measured response of DNOVS1 to 36 axis of rotation (inner circle) and the predicted sensitivity from the receptive field of DNOVS1 to 36 axes of rotations (outer circle) are shown color-coded. Red represents a depolarization or a strong similarity between the receptive field and the optic flow and blue a hyperpolarization or a contradiction for the predicted sensitivities. c Measured and predicted sensitivities of DNOVS2. For the measured responses, red represents an increase of the spike frequency of DNOVS2. Predicted sensitivities were calculated from the receptive field of DNOVS2 (p RF) and from the superlinear receptive field of DNOVS2 (p superlinearRF). p superlinearRF yields a better match to the measured response of DNOVS2 than p RF (color figure online)
Results
Mapping the receptive field of a cell
In the first set of experiments we determined the receptive field of VS or DNOVS cells by measuring the local motion sensitivities and local preferred direction at 96 positions within the visual field (Fig. 1). To do so, we applied a fast stimulus as it was used recently to describe the receptive field of motion sensitive neurons of the hoverfly (Nordström et al. 2008). With this method, we determined first the receptive fields of all VS cells (Fig. 2) and compared our results with the receptive fields measured previously (Krapp et al. 1998). All VS cells were sensitive for downward motion and the sensitivity shifts along the azimuth according to the location of the cell’s dendrite in the lobula plate (Krapp et al. 1998; Haag et al. 2007). In addition, VS7–VS10 responded to upward motion in the frontal visual field. All VS cells responded to horizontal motion, too. Whereas VS1 responded dorsally to back to front motion, VS2–VS10 responded to front to back motion. Moreover, VS7–VS10 responded ventrally slightly to back to front motion. The receptive fields described here are quite similar to the receptive fields measured by Krapp et al. (1998) using a locally rotating dot. Both stimuli, the locally rotating dot and our vertically and horizontally moving bar, produced, in general, similar receptive fields that seemed to be tailored to sense rotational optic flow. There were, however, differences between the receptive fields as determined in the two studies for VS4 and VS8–VS10.
Fig. 2.
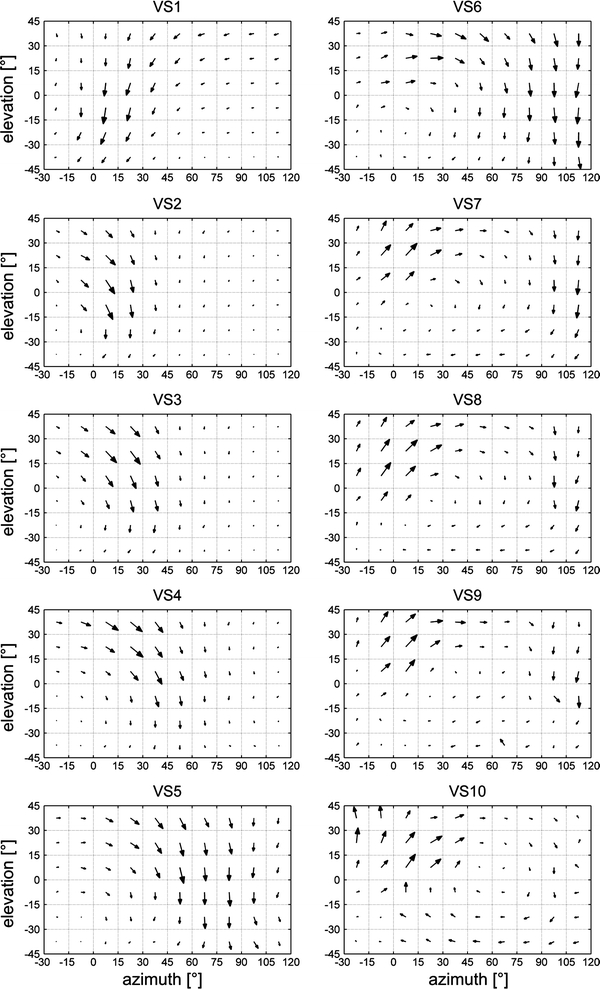
Receptive fields of VS cells. The receptive fields of VS1–VS10. All VS cells have receptive fields with similarities to optic flows generated during rotations around different body axes. Data represent the mean responses recorded from n number of flies for VS1 (n = 7), VS2 (n = 8), VS3 (n = 10), VS4 (n = 8), VS5 (n = 5), VS6 (n = 5), VS7 (n = 10), VS8 (n = 6), VS9 (n = 3), VS10 (n = 2)
To quantify the similarity between the receptive fields measured by Krapp et al. (1998) and the receptive fields determined in this study we defined a DI which calculates the average vector length of the difference between the two vector fields (see “Materials and methods”). The DI is zero for identical vector fields and two for homogenous, opposite vector fields. First, we calculated the DIs for our measurements between the average receptive field (RFmean) of a cell and each receptive fields of the same cell in different flies (RFn). For each VS cells, the distribution of the resulting DIs represents the variability of our receptive field measurements for this cell (Fig. 3, gray dots). In the same way, we calculated the DIs between our average receptive fields (RFmean) and the receptive field measured by Krapp and colleagues (RFKrapp et al. 1998) of the same cell (Fig. 3, black diamond). For most VS cells, the DIs between our RFmean and RFKrapp et al. 1998 are in the range of the variability indicating the similarity between the receptive fields. A higher DI compared to the variability was found for VS4 and VS8–VS10. Thus, consistent with the visual comparison of the receptive fields, the differences between the published receptive fields and our measured receptive fields turned out to be rather small for many VS cells.
Fig. 3.

Differences between receptive field measurements of VS cells. Difference indices (DIs) for each VS cell were calculated between the average receptive field (RF mean) of a cell and each receptive fields of the same cell for different flies (RF n). The DIs are shown with gray dots and the distribution represents the variability of our receptive field measurements a cell. The black diamond represents the DI between the average receptive field (RF mean) of a cell and the receptive field (RF Krapp et al. 1998) of the same cell determined previously by Krapp et al. (1998). Data are the same as in Fig. 2
Measured and predicted receptive field maps of DNOVS cells
The receptive field of DNOVS1 (Fig. 4a) reveals a rotational structure with a mix of upward and front to back motion in the dorso-frontal part and downward motion in the lateral part. In agreement with the previously measured vertical sensitivity along the azimuth (Haag et al. 2007) no contralateral motion sensitivity was found for DNOVS1. Current injections into VS cells revealed that DNOVS1 is most strongly coupled to VS6 and VS7 (Haag et al. 2007). To estimate whether the receptive field of DNOVS1 could be predicted from the electrical coupling of DNOVS1 with presynaptic VS cells, we calculated an expected receptive field for DNOVS1. An expected receptive field was either calculated by a linear summation of the receptive fields of all VS cells weighted by their coupling strengths or by a linear summation of the receptive fields of VS6 and VS7. The expectation from VS6 and VS7 (Fig. 4b) is quite similar to the receptive field of DNOVS1, and the subtraction (Fig. 4c) shows that, to a large extent, the receptive field of DNOVS1 can be explained by VS6 and VS7 output. Here again, we calculated the DI between the average measured receptive field (RFmean) and the expected receptive field (RFexp) and compared the value with the DIs for the different measurements of DNOVS1 (Fig. 4d). The DI between the expectation and measurement (black square) is close to the DIs representing the variability of our measurements (gray dots). We calculated also the DIs for an expectation including all VS cells. However, adding neighboring VS cells to VS6 and VS7 did not lead to a smaller DI (data not shown) and therefore to a better estimation of the receptive field of DNOVS1. Thus, the receptive field of DNOVS1 results almost exclusively from the integration of VS6 and VS7 cell receptive fields.
Fig. 4.
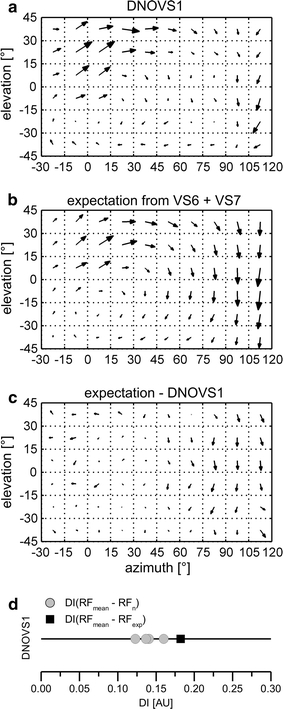
Receptive field map of DNOVS1. a Receptive field of DNOVS1. b Expected receptive field for DNOVS1, calculated by a summation of the receptive fields of VS6 and VS7 (Fig. 2), strongest coupled to DNOVS1 (Haag et al. 2007). c Difference between the receptive field of DNOVS1 and the expected receptive field. d DIs between the average receptive field (RF mean) and each measured receptive field (RF n) of DNOVS1 (gray dots) and the DI between the average receptive field (RF mean) and the expected receptive field (RF exp) marked with a black square. Data represent the mean responses recorded from n = 4 DNOVS1 cells
DNOVS2 responds broadly to downward motion and to front to back motion in the frontal part of the visual field (Fig. 5a). The receptive field of DNOVS2 has similarities to an optic flow-field generated during a lift translation as well as to an optic flow-field generated during a roll rotation of the fly. DNOVS2 is most strongly coupled to VS5 and VS6 (Wertz et al. 2008). By a summation of the receptive fields of VS5 and VS6 (Fig. 2) we calculated the expectation for DNOVS2 (Fig. 5b) and the difference between the expectation and measured receptive field (Fig. 5c). The expectation and the measured receptive field differ in the frontal part, where DNOVS2 is more sensitive for downward motion than expected from VS5 and VS6. Some differences are also observable in the lateral part, where one would expect a stronger sensitivity for downward motion for DNOVS2. The DI between the expected receptive field and the average measured receptive field is much higher than the DIs representing the variability (Fig. 5d, compare black square with gray dots). Here again, adding neighboring VS cells of VS5 and VS6 to DNOVS2 did not lead to a better estimation for the receptive field of DNOVS2. This indicates that the electrical coupling with VS cells is not sufficient to explain the receptive field of DNOVS2. As shown in a previous study (Wertz et al. 2008), DNOVS2 integrates motion in front of the contralateral eye in a superlinear way. In the presence of ipsilateral downward motion, DNOVS2 is sensitive for contralateral upward motion and increases its spike rate in a superlinear way (Wertz et al. 2008). This means that the contralateral local motion preferences of DNOVS2 can only be determined when DNOVS2 is depolarized. Thus, we depolarized DNOVS2 with ipsilateral downward motion, while measuring the receptive field on the contralateral side (Fig. 5e). In this case, the cell became sensitive for contralateral upward motion and back to front motion in more frontal regions. The heterolateral, spiking neuron V2 is thought to convey motion information from the contralateral eye onto DNOVS2 (Wertz et al. 2008). The receptive field of V2 (Fig. 5f) can explain the sensitivity for contralateral upward motion as well as the missing frontal sensitivity for downward motion which cannot be explained by the connectivity to VS cells alone. By summing up the receptive field of DNOVS2 (Fig. 5a) plus the contralateral motion sensitivities (Fig. 5e) we calculated the superlinear receptive field of DNOVS2. In contrast to the receptive field of DNOVS2 (Fig. 5a), the superlinear receptive field of DNOVS2 has a stronger rotational component than its linear receptive field.
Estimating global motion preferences
For VS cells, the preferred axes of rotation estimated from their receptive fields (Krapp et al. 1998) are in agreement with the ones obtained from global wide-field stimulation of the same neurons (Karmeier et al. 2003, 2005). This suggests a linear spatial summation in VS cells. To analyze whether a linear or nonlinear spatial summation occurs in DNOVS cells, we estimated the preferred global motion preferences from the receptive field of a cell and compared the results with the previously measured ego-motion tuning of the cells. Both DNOVS cells as well as their presynaptic cells (VS and V2) are tuned to rotations of the fly around particular body axes in the horizontal plane (Wertz et al. 2009). This ego-motion tuning was determined by presenting different stimulus movies showing a rotation in an artificial room. In short: a virtual fly was rotated around 36 axes of rotation in a virtual room which was wallpapered with checkerboard patterns on the floor, walls and ceiling. These movies were then presented to the real fly while recording from the cells of interest (Wertz et al. 2009). To estimate the ego-motion tuning of a cell from its receptive field, we determined the optic flow generated by rotating the virtual fly in the virtual room. To do so, we used the image sequences of the movies generated in the way described above as an input to our optic flow algorithm (see “Materials and methods”). We defined a MI as a measure of similarity between the respective optic flow generated by a movement of the virtual fly and the receptive field of a cell (Fig. 6a). The MI is the average dot product between the two vector fields at all 96 locations. In Fig. 6b, c the ego-motion tuning of DNOVS1 and DNOVS2 (from Wertz et al. 2009) as well as the prediction from the receptive fields are shown color-coded. DNOVS1 is tuned to a counterclockwise rotation of the fly around a pole at 32° azimuth and DNOVS2 around a pole at −23° azimuth (Fig. 6 b, c, inner circle). Counterclockwise roll movement around the longitudinal body axis was defined as a rotation with a pole at 0°, nose-down pitch with a pole at +90° and nose-up pitch with a pole at −90°. In these color-coded illustrations, red represents a depolarization of DNOVS1 (Fig. 6b, inner circle) or an increase of the firing frequency of DNOVS2 (Fig. 6c, inner circle) and blue a hyperpolarization of DNOVS1. The MIs for the 36 axes of rotation of DNOVS1 (Fig. 6b, outer circle) and DNOVS2 (Fig. 6c, central circle) are also shown color-coded. Positive MI values are shown in red and represent a match between the vector fields whereas negative MI values, indicated in blue, represent a mismatch. The preferred axes of rotation (indicated by a black stripe) were calculated by fitting a sine function either to the measured responses or to the calculated MI values. For DNOVS1, the prediction fits the measurements rather well (Fig. 6b). For DNOVS2, however, the preferred axis of rotation predicted from the receptive field is slightly shifted compared to the measured one (Fig. 6c). In contrast, the tuning curve expected from the superlinear receptive field matched the measured tuning curve quite well. Thus, taking the contralateral sensitivity into account, one can predict the tuning of DNOVS2 to global motion patterns from its local motion preferences.
From the receptive field of DNOVS2 (Fig. 5a), one would expect similarly strong responses of the cell to lift and roll movements of the fly. Predicting the preferences of DNOVS2 to counterclockwise roll and upward lift movements, no differences are observable (Fig. 7, blank bars). However, the measurements to these movements revealed that DNOVS2 responded much stronger to counterclockwise roll than lift movements (Fig. 7, black bars). Here again, the prediction from the superlinear receptive field (striped bars) matched better the measured responses. Thus, the global motion preferences of DNOVS1 can be explained by its receptive field indicating a linear spatial integration, whereas in DNOVS2 a superlinear response component is apparent.
Fig. 7.
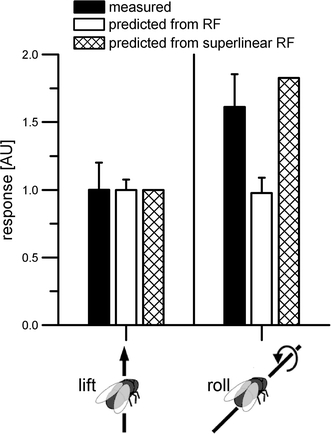
Preference of DNOVS2 to roll over lift movements. Measured and predicted sensitivities of DNOVS2 to lift and roll movements (normalized to lift movements). The linear receptive field of DNOVS2 does not reveal a higher sensitivity for rotation than translation, the superlinear receptive field does. All measured responses are from Wertz et al. (2009)
To investigate whether a linear or nonlinear spatial integration occurs in the presynaptic cells (VS and V2), we predicted the global motion preferences for these cells from their receptive fields. We calculated the MIs for each cell to the different rotations and compared the results with the previously measured responses to the different rotations in the horizontal plane (Fig. 8). In Fig. 8a, c, the previously measured ego-motion tuning for VS cells and V2 is shown, respectively (Wertz et al. 2009). The results for the VS cells are shown color-coded with VS1 plotted in the innermost circle and VS10 in the outermost one. Again, red represents a depolarization and blue a hyperpolarization of the cell. The preferred axis of rotation was again calculated by fitting a sine function to the tuning curve. In Fig. 8b, d the predicted global motion preferences for VS cells and V2 are shown. Like for DNOVS1, the predictions from local motion preferences are quite similar to the measured tuning curves.
Fig. 8.
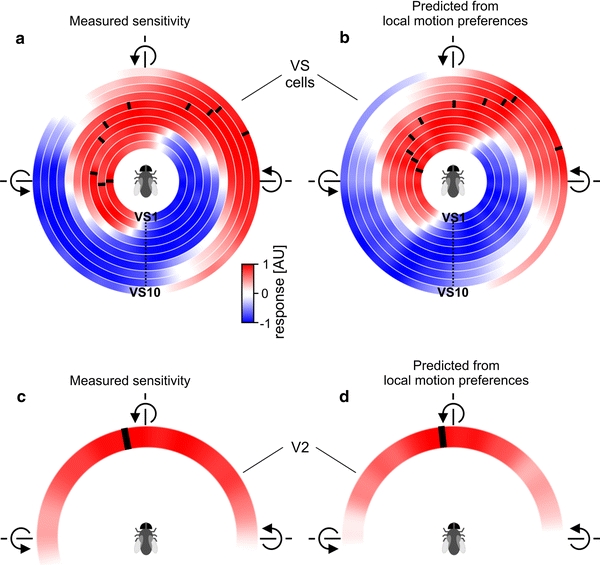
Prediction of global motion preferences for VS cells and V2. Mean responses of ten VS cells (a) and V2 (b) to 36 axes of rotation shown in a color-coded way. Red represents a depolarization or an increase of the firing frequency for V2 and blue a hyperpolarization. The preferred axis of rotation (black ticks) shifts along the azimuth with increasing VS cell number. Data are from Wertz et al. (2009). c, d Sensitivities as predicted from the receptive fields of VS cells and the V2 cell. The predictions fit the measured responses rather well for most VS cells and V2 (color figure online)
Discussion
In this study, we mapped the receptive field of DNOVS cells as well as their presynaptic cells with a custom built LED-arena covering 240° × 95° of the visual space. DNOVS1 has a receptive field reminiscent of an optic flow fields generated during a rotation of a fly (Fig. 4a). DNOVS2 has a receptive field, which is similar to both an optic flow-field generated during a rotation and an optic flow-field during a lift movement of the fly (Fig. 5a). After considering potential limitations, including the stimulus device, the receptive field measurements and multisensory integration, we discuss in the following the integration of lobula plate output in DNOVS cells, the global motion estimation and the optic flow processing from lobula plate tangential cells to neck motor neurons via DNOVS cells.
Potential limitations
The main difference between our stimulus device and previously described LED-based stimulators for investigating fly visual motion processing (Lindemann et al. 2003; Joesch et al. 2008; Reiser and Dickinson 2008) is the better spatial resolution, combined with a high temporal resolution and a fairly large coverage of the fly’s visual field. With <1° spatial resolution and refresh rates of over 600 fps, the new panel-based display system described here has been designed as a stimulus source matching the requirements for experiments on Calliphora vision. However, covering only 95° in elevation, the extension in elevation is one limitation of the arena. The LED-based stimulator FliMax (Lindemann et al. 2003) extends over a broader range, especially in ventral parts of the visual field. The locally rotating dot used by Krapp and Hengstenberg (1997) allows measurement of interpolated receptive field extending from −75° to +75° in elevation. However, our arena combines the possibility of presenting both local as well as global stimuli with a spatial and temporal resolution sufficient for Calliphora.
The receptive fields of VS cells determined here were in general similar to those published earlier (Krapp et al. 1998) corroborating the calculation of local motion preferences from the vertical and horizontal components. However, we found some differences in the receptive fields of VS4 and VS8–VS10. In contrast to Krapp et al. (1998), we found the sensitivity for vertical motion of VS4 to be shifted toward frontal parts of the visual field and no response to dorso-lateral back to front motion. These differences might be attributable to some uncertainties in assigning a cell’s morphology to a unique cell type. In fact, the receptive field structure of VS4 measured by Krapp et al. (1998) has a large resemblance to the receptive field structure of VS5 as determined in both studies. To quantify the similarity between the receptive fields measured by Krapp et al. (1998) and receptive field determined in this study, we calculated a DI for each VS cell and compared those with the variability of one cell between flies (Fig. 3). In agreement with the visual comparison of the receptive fields, the difference turned out to be rather small for many VS cells. However, larger DI’s were found for VS4 and VS8–VS10. Recordings of VS7–VS10 revealed stronger sensitivities to upward motion in frontal parts of the receptive field than described by Krapp et al. (1998). A reason for this difference might be that Krapp et al. (1998) restricted the visual input to the ipsilateral eye by occluding the contralateral eye. Thus, the stronger response to upward motion might be due to motion information from the contralateral eye via Vi, a heterolateral neuron described recently (Haag and Borst 2007).
DNOVS1 and DNOVS2 cells receive synaptic input from lobula plate tangential cells as well as from the ocelli via ocellar interneurons (Haag et al. 2007; Wertz et al. 2008). The three ocelli form a triangle on the dorsal surface of the head (for an overview see Krapp 2009). Stimulating the ocelli with an LED elicited a short on and off response in DNOVS1 (Haag et al. 2007) as well as in DNOVS2 (Wertz et al. 2008). However, no on or off components were found in the responses of both DNOVS cells to the local moving bar (see Fig. 1). Directionally selective responses to UV gratings were recently described in ocellar interneurons of dragonflies (van Kleef et al. 2008). In dragonflies (Stange 1981) as well as in locusts (Taylor 1981), the ocelli are very effective rotation detectors, crucial to proper gaze and flight stabilization. Recently it was found for blowflies that the ocellar component of V1’s response appears to be tuned to rotation (Parsons et al. 2006). Whether these rotation-specific ocellar signals are transmitted to DNOVS cells or the ocellar component of DNOVS responses itself is tuned to rotation is not yet clear. In addition to visual motion and stimulation of the ocelli, DNOVS cells respond also to antennal air currents (Gronenberg and Strausfeld 1992). Thus, at the level of descending neurons like DNOVS cells, at least three sensory modalities are integrated.
Integration of lobula plate output
The determination of the receptive fields of VS cells as well as of V2 allowed us to estimate the receptive fields of DNOVS cells and thus to study the integration of VS cell output in DNOVS cells. The receptive field of DNOVS1 can be almost completely explained by its connectivity to VS6 and VS7 most strongly coupled to the cell (Haag et al. 2007). Including more neighboring VS cells like VS4, VS5, VS8 or VS9 did not lead to a better estimation of the receptive field of DNOVS1. Although current injection experiments revealed a connectivity between those VS cells (VS4, VS5, VS8 and VS9) and DNOVS1 (Haag et al. 2007), the receptive field estimations suggest that they are not directly coupled. Since VS cells are electrically coupled amongst themselves in a chain-like manner (Haag and Borst 2004), current injection into VS5 leads to a response in VS6, which is then transmitted to DNOVS1, and consequently would not indicate a direct coupling between VS5 and DNOVS1. Thus, from our receptive field estimations, we conclude that DNOVS1 is electrically coupled to VS6 and VS7 only. Other VS cells are indirectly coupled via VS6 and VS7. A final analysis of this circuitry will have to wait until the description will be available from serial block face scanning electron microscopy (Denk and Horstmann 2004).
In contrast to DNOVS1, the receptive field of DNOVS2 cannot be explained completely by the cell’s connectivity to VS cells, neither by the input from VS5 and VS6 most strongly coupled to DNOVS2 nor by the input from all VS cells. Here again, adding neighboring VS cells to VS5 and VS6 to calculate an expectation did not lead to a better estimation. In analogy to DNOVS1, we conclude that DNOVS2 is electrically coupled to VS5 and VS6 and neighboring VS cells influence indirectly DNOVS2 via VS5 or VS6. The superlinear integration of motion information from V2 and VS5 and VS6 led to a more accurate estimation. Thus, our results are in agreement with the previously described binocular, nonlinear integration of DNOVS2 (Wertz et al. 2008) in contrast to the monocular, linear integration of motion signals in DNOVS1 (Haag et al. 2007).
Global motion preferences predicted from the receptive field
From the integration properties of both descending neurons, one would expect that a linear spatial summation occurs in DNOVS1 whereas a superlinear spatial summation occurs in DNOVS2. To analyze this, we compared the global motion preferences predicted from the receptive field of a cell with the ego-motion tuning of the cell (Wertz et al. 2009). In a previous study, we measured the responses of DNOVS cells to global motion stimuli, comprising all principal patterns according to the 6 degrees of freedom as well as 36 patterns arising from rotations around different axes within the horizontal plane of the fly (Wertz et al. 2009). From the same set of global motion stimuli, we calculated the optic flow for the different movements (see “Materials and methods”). When comparing the measured responses with the optic flow of the stimulus pattern filtered through the receptive field, we found a surprisingly good match between the measured responses and the prediction from local motion preferences for all cells besides DNOVS2 (Figs. 6b, 8). This conforms to a linear spatial integration. Apart from some sublinear saturation characteristics (Haag et al. 1992), spatial integration of VS cells has been found to be fairly linear (Haag and Borst 2007). However, this has never been observed with stimuli covering large parts of the receptive field of these cells. Thus, VS cells can indeed be regarded as matched filters for the fly’s rotation around different axes within the horizontal plane, as proposed by Franz and Krapp (2000).
In contrast to DNOVS1, the global motion preferences of DNOVS2 (Wertz et al. 2009) could not be predicted from its receptive field. The prediction from the linear receptive field of DNOVS2 revealed no difference between an upward lift and a counterclockwise roll movement (Fig. 7). In addition the tuning to rotation within the horizontal plane is slightly shifted toward a nose-up pitch movement (Fig. 6c). However, by predicting the global motion preferences from the superlinear receptive field of DNOVS2, which incorporates the contralateral motion sensitivity, we found a good match between the prediction and the measured responses (Figs. 6c, 7).
Optic flow processing from the lobula plate to neck motor neurons
Both descending neurons send their axons down the ventral nerve cord into the thoracic ganglion to branch segmentally into motor neuropils (Gronenberg et al. 1995). DNOVS1 as well as DNOVS2 are biocytin coupled to frontal nerve-neck motor neurons (FN-NMN) (Strausfeld and Bassemir 1985; Gronenberg et al. 1995). 21 pairs of neck motor neurons were identified, which are organized on each side into four neck muscle nerves innervating 21 neck muscles (Strausfeld and Seyan 1984; Strausfeld et al. 1987) involved in the fly gaze stabilization system. FN-NMNs innervate a variety of different neck muscles that, based on their anatomy (Strausfeld et al. 1987) could potentially be involved in nose-up pitch, nose-down pitch, yaw and roll of the head. In addition, FN-NMNs are motion sensitive (Milde et al. 1987), and have receptive fields reminiscent of specific optic flow fields generated during pitch, a combination of pitch and roll and almost pure roll rotation (Huston and Krapp 2008). Neck motor neurons are sensitive to local visual motion presented on either eye and are therefore more selective to rotation over translation than lobula plate tangential cells (Huston and Krapp 2008). Although DNOVS2 is sensitive to contralateral local motion in the presence of ipsilateral downward motion (Fig. 5), contralateral local motion alone elicited no response, neither in DNOVS2 nor in DNOVS1. Thus, to achieve binocular receptive fields found for FN-NMNs (Huston and Krapp 2008), different descending neurons should converge onto FN-NMNs. Strausfeld et al. (1995) proposed a heterolateral connection in the thoracic ganglion. Lesion experiments (Strausfeld et al. 1995) revealed that motion information from the contralateral DNOVS1 projects via a heterolateral neuron in the prothoracic ganglion onto the ipsilateral FNMN-8. Whether this is also the case for the contralateral DNOVS2 is not yet clear. However, the integration of motion information from the ipsi- and contralateral DNOVS1 in the prothoracic ganglion would lead to binocular receptive field like it was found for “FN-NMN A” (Huston and Krapp 2008). Thus, the binocular integration at the level of descending neurons, like it was found for DNOVS2 (Wertz et al. 2008) or at the level of the prothoracic ganglion (Strausfeld et al. 1995) are at least two pathways to achieve a higher binocularity and thus a higher selectivity in FN-NMNs.
Acknowledgments
We are grateful to Renate Gleich for excellent technical assistance, Johannes Plett for designing the stimulus device and Maximilian Joesch and Franz Weber for help on stimulus generation. This work was supported by the Max-Planck-Society, a Grant of the DFG (GRK 1091) and by a Grant of the BMBF to the Bernstein Center for Computational Neuroscience (BCCN) Munich.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
References
- Barron JL, Fleet DJ, Beauchemin SS. Systems and experiment. Performance of optical flow techniques. Int J Comput Vis. 1994;12(1):43–76. doi: 10.1007/BF01420984. [DOI] [Google Scholar]
- Borst A, Bahde S. Spatio-temporal integration of motion—a simple strategy for safe landing in flies. Naturwissenschaften. 1988;75:265–267. doi: 10.1007/BF00378023. [DOI] [Google Scholar]
- Borst A, Bahde S. Visual information processing in the fly’s landing system. J Comp Physiol A. 1988;163:167–173. doi: 10.1007/BF00612426. [DOI] [Google Scholar]
- Borst A, Haag J. Neural networks in the cockpit of the fly. J Comp Physiol A. 2002;188:419–437. doi: 10.1007/s00359-002-0316-8. [DOI] [PubMed] [Google Scholar]
- Denk W, Horstmann H. Serial block-face scanning electron microscopy to reconstruct three-dimensional tissue nanostructure. PLoS Biol. 2004;2:1900–1909. doi: 10.1371/journal.pbio.0020329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elyada YM, Haag J, Borst A. Different receptive fields in axons and dendrites underlie robust coding in motion-sensitive neurons. Nat Neurosci. 2009;12:327–332. doi: 10.1038/nn.2269. [DOI] [PubMed] [Google Scholar]
- Farrow K (2005) Lateral interactions and receptive field structure of lobula plate tangential cells in the blowfly. Doctoral thesis, Munich
- Farrow K, Borst A, Haag J. Sharing receptive fields with your neighbors: tuning the vertical system cells to wide field motion. J Neurosci. 2005;25:3985–3993. doi: 10.1523/JNEUROSCI.0168-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franceschini N, Kirschfeld K. Phenomena of pseudopupil in compound eye of Drosophila. Kybernetik. 1971;9:159–182. doi: 10.1007/BF02215177. [DOI] [PubMed] [Google Scholar]
- Franz MO, Krapp HG. Wide-field, motion-sensitive neurons and matched filters for optic flow fields. Biol Cybern. 2000;83:185–197. doi: 10.1007/s004220000163. [DOI] [PubMed] [Google Scholar]
- Gibson JJ. Perception of the visual world. Westport (Conn.): Greenwood Press; 1974. [Google Scholar]
- Götz KG. Optomotor studies of the visual system of several eye mutants of the fruit fly Drosophila. Kybernetik. 1964;2:77–92. doi: 10.1007/BF00288561. [DOI] [PubMed] [Google Scholar]
- Gronenberg W, Strausfeld NJ. Premotor descending neurons responding selectively to local visual-stimuli in flies. J Comp Neurol. 1992;316:87–103. doi: 10.1002/cne.903160108. [DOI] [PubMed] [Google Scholar]
- Gronenberg W, Milde JJ, Strausfeld NJ. Oculomotor control in calliphorid flies—organization of descending neurons to neck motor-neurons responding to visual-stimuli. J Comp Neurol. 1995;361:267–284. doi: 10.1002/cne.903610206. [DOI] [PubMed] [Google Scholar]
- Haag J, Borst A. Neural mechanism underlying complex receptive field properties of motion-sensitive interneurons. Nat Neurosci. 2004;7:628–634. doi: 10.1038/nn1245. [DOI] [PubMed] [Google Scholar]
- Haag J, Borst A. Dye-coupling visualizes networks of large-field motion-sensitive neurons in the fly. J Comp Physiol A. 2005;191:445–454. doi: 10.1007/s00359-005-0605-0. [DOI] [PubMed] [Google Scholar]
- Haag J, Borst A. Reciprocal inhibitory connections within a neural network for rotational optic-flow processing. Front Neurosci. 2007;1:111–121. doi: 10.3389/neuro.01.1.1.008.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haag J, Egelhaaf M, Borst A. Dendritic integration of motion information in visual interneurons of the blowfly. Neurosci Lett. 1992;140:173–176. doi: 10.1016/0304-3940(92)90095-O. [DOI] [PubMed] [Google Scholar]
- Haag J, Vermeulen A, Borst A. The intrinsic electrophysiological characteristics of fly lobula plate tangential cells: III. Visual response properties. J Comput Neurosci. 1999;7:213–234. doi: 10.1023/A:1008950515719. [DOI] [PubMed] [Google Scholar]
- Haag J, Denk W, Borst A. Fly motion vision is based on Reichardt detectors regardless of the signal-to-noise ratio. Proc Natl Acad Sci USA. 2004;101:16333–16338. doi: 10.1073/pnas.0407368101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haag J, Wertz A, Borst A. Integration of lobula plate output signals by DNOVS1, an identified premotor descending neuron. J Neurosci. 2007;27:1992–2000. doi: 10.1523/JNEUROSCI.4393-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hatsopoulos N, Gabbiani F, Laurent G. Elementary computation of object approach by a wide-field visual neuron. Science. 1995;270:1000–1003. doi: 10.1126/science.270.5238.1000. [DOI] [PubMed] [Google Scholar]
- Hausen K. Motion sensitive interneurons in the optomotor system of the fly. I. The horizontal cells: structure and signals. Biol Cybern. 1982;45:143–156. doi: 10.1007/BF00335241. [DOI] [Google Scholar]
- Hausen K, Egelhaaf M. Neural mechanisms of visual course control in insects. In: Stavenga DG, Hardie RC, editors. Facets of vision. Berlin: Springer; 1989. pp. 391–424. [Google Scholar]
- Hengstenberg R, Hausen K, Hengstenberg B. The number and structure of giant vertical cells (VS) in the lobula plate of the blowfly Calliphora erytrocephala. J Comp Physiol A. 1982;149:163–177. doi: 10.1007/BF00619211. [DOI] [Google Scholar]
- Hengstenberg R, Sandeman DC, Hengstenberg B. Compensatory head roll in the blowfly Calliphora during flight. Proc R Soc Lond B. 1986;227:455–482. doi: 10.1098/rspb.1986.0034. [DOI] [Google Scholar]
- Huston SJ, Krapp HG. Visuomotor transformation in the fly gaze stabilization system. PLoS Biol. 2008;6:e173. doi: 10.1371/journal.pbio.0060173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joesch M, Plett J, Borst A, Reiff DF. Response properties of motion-sensitive visual interneurons in the lobula plate of Drosophila melanogaster. Curr Biol. 2008;18:368–374. doi: 10.1016/j.cub.2008.02.022. [DOI] [PubMed] [Google Scholar]
- Karmeier K, Krapp HG, Egelhaaf M. Robustness of the tuning of fly visual interneurons to rotatory optic flow. J Neurophysiol. 2003;90:1626–1634. doi: 10.1152/jn.00234.2003. [DOI] [PubMed] [Google Scholar]
- Karmeier K, Krapp HG, Egelhaaf M. Population coding of self-motion: applying bayesian analysis to a population of visual interneurons in the fly. J Neurophysiol. 2005;94:2182–2194. doi: 10.1152/jn.00278.2005. [DOI] [PubMed] [Google Scholar]
- Koenderink JJ, van Doorn AJ. Facts on optic flow. Biol Cybern. 1987;56:247–254. doi: 10.1007/BF00365219. [DOI] [PubMed] [Google Scholar]
- Krapp HG. Ocelli. Curr Biol. 2009;19:R435–R437. doi: 10.1016/j.cub.2009.03.034. [DOI] [PubMed] [Google Scholar]
- Krapp HG, Hengstenberg R. Estimation of self-motion by optic flow processing in single visual interneurons. Nature. 1996;384:463–466. doi: 10.1038/384463a0. [DOI] [PubMed] [Google Scholar]
- Krapp HG, Hengstenberg R. A fast stimulus procedure to determine local receptive field properties of motion-sensitive visual interneurons. Vis Res. 1997;37:225–234. doi: 10.1016/S0042-6989(96)00114-9. [DOI] [PubMed] [Google Scholar]
- Krapp HG, Hengstenberg B, Hengstenberg R. Dendritic structure and receptive-field organization of optic flow processing interneurons in the fly. J Neurophysiol. 1998;79:1902–1917. doi: 10.1152/jn.1998.79.4.1902. [DOI] [PubMed] [Google Scholar]
- Krapp HG, Hengstenberg R, Egelhaaf M. Binocular contributions to optic flow processing in the fly visual system. J Neurophysiol. 2001;85:724–734. doi: 10.1152/jn.2001.85.2.724. [DOI] [PubMed] [Google Scholar]
- Lindemann JP, Kern R, Michaelis C, Meyer P, van Hateren JH, Egelhaaf M. FliMax, a novel stimulus device for panoramic and highspeed presentation of behaviourally generated optic flow. Vis Res. 2003;43:779–791. doi: 10.1016/S0042-6989(03)00039-7. [DOI] [PubMed] [Google Scholar]
- Milde JJ, Seyan HS, Strausfeld NJ. The neck motor system of the fly Calliphora erythrocephala. 2. Sensory organization. J Comp Physiol A. 1987;160:225–238. doi: 10.1007/BF00609728. [DOI] [Google Scholar]
- Nordström K, Barnett PD, Moyer de Miguel IM, Brinkworth RSA, O’Carroll DC. Sexual dimorphism in the hoverfly motion vision pathway. Curr Biol. 2008;18:661–667. doi: 10.1016/j.cub.2008.03.061. [DOI] [PubMed] [Google Scholar]
- Parsons MM, Krapp HG, Laughlin SB. A motion-sensitive neuron responds to signals from the two visual systems of the blowfly, the compound eyes and ocelli. J Exp Biol. 2006;209:4464–4474. doi: 10.1242/jeb.02560. [DOI] [PubMed] [Google Scholar]
- Petrowitz R, Dahmen H, Egelhaaf M, Krapp HG. Arrangement of optical axes and spatial resolution in the compound eye of the female blowfly Calliphora. J Comp Physiol A. 2000;168:737–746. doi: 10.1007/s003590000127. [DOI] [PubMed] [Google Scholar]
- Reichardt W (1969) Movement perception in insects. In: Processing of optical data by organisms and machines, Academic, New York, pp 465–493
- Reichardt W, Poggio T. Visual control of orientation behaviour in the fly I. A quantitative analysis. Q Rev Biophys. 1976;9:311–375. doi: 10.1017/S0033583500002523. [DOI] [PubMed] [Google Scholar]
- Reiser MB, Dickinson MH. A modular display system for insect behavioral neuroscience. J Neurosci Methods. 2008;167:127–139. doi: 10.1016/j.jneumeth.2007.07.019. [DOI] [PubMed] [Google Scholar]
- Rind FC, Simmons PJ. Orthopteran DCMD neuron: a reevaluation of responses to moving objects. I. Selective responses to approaching objects. J Neurophysiol. 1992;68:1654–1666. doi: 10.1152/jn.1992.68.5.1654. [DOI] [PubMed] [Google Scholar]
- Single S, Borst A. Dendritic integration and its role in computing image velocity. Science. 1998;281:1848–1850. doi: 10.1126/science.281.5384.1848. [DOI] [PubMed] [Google Scholar]
- Srinivasan MV, Jin ZF, Stange G, Ibbotson MR. ‘Vector white noise’: a technique for mapping the motion receptive fields of direction-selective visual neurons. Biol Cybern. 1993;68:199–207. doi: 10.1007/BF00224852. [DOI] [PubMed] [Google Scholar]
- Stange G. The ocellar component of flight equilibrium control in dragonflies. J Comp Physiol A. 1981;141:335–347. doi: 10.1007/BF00609936. [DOI] [Google Scholar]
- Strausfeld NJ, Bassemir UK. Lobula plate and ocellar interneurons converge onto a cluster of descending neurons leading to neck and leg motor neuropil in Calliphora erythrocephala. Cell Tissue Res. 1985;240:617–640. doi: 10.1007/BF00216351. [DOI] [Google Scholar]
- Strausfeld NJ, Seyan HS. Convergence of visual, haltere, and prosternal inputs at neck motor neurons of Calliphora erythrocephala. Cell Tissue Res. 1984;240:601–615. doi: 10.1007/BF00216350. [DOI] [Google Scholar]
- Strausfeld NJ, Seyan HS, Milde JJ. The neck motor system of the fly Calliphora erythrocephala. 1. Muscles and motor neurons. J Comp Physiol A. 1987;160:205–224. doi: 10.1007/BF00609727. [DOI] [Google Scholar]
- Strausfeld NJ, Kong A, Milde JJ, Gilbert C, Ramaiah L. Oculomotor control in calliphorid flies: GABAergic organization in heterolateral inhibitory pathways. J Comp Neurol. 1995;361:298–320. doi: 10.1002/cne.903610208. [DOI] [PubMed] [Google Scholar]
- Taylor CP. Contribution of compound eyes and ocelli to steering of locusts in flight: I. Behavioural analysis. J Exp Biol. 1981;93:1–18. [Google Scholar]
- van Kleef J, Berry R, Stange G. Directional selectivity in the simple eye of an insect. J Neurosci. 2008;28:2845–2855. doi: 10.1523/JNEUROSCI.5556-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wertz A, Borst A, Haag J. Nonlinear integration of binocular optic flow by DNOVS2, a descending neuron of the fly. J Neurosci. 2008;28:3131–3140. doi: 10.1523/JNEUROSCI.5460-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wertz A, Gaub B, Plett J, Haag J, Borst A (2009) Robust coding of ego-motion parameters in two descending neurons of the fly (submitted) [DOI] [PMC free article] [PubMed]


