Conservatism and diversification of plant functional traits: Evolutionary rates versus phylogenetic signal

Abstract

The concepts of niche conservatism and adaptive radiation have played central roles in the study of evolution and ecological diversification. With respect to phenotypic evolution, the two processes may be seen as opposite ends of a spectrum; however, there is no straightforward method for the comparative analysis of trait evolution that will identify these contrasting scenarios. Analysis of the rate of phenotypic evolution plays an important role in this context and merits increased attention. In this article, independent contrasts are used to estimate rates of evolution for continuous traits under a Brownian motion model of evolution. A unit for the rate of phenotypic diversification is introduced: the felsen, in honor of J. Felsenstein, is defined as an increase of one unit per million years in the variance among sister taxa of ln-transformed trait values. The use of a standardized unit of measurement facilitates comparisons among clades and traits. Rates of diversification of three functional traits (plant height, leaf size, and seed size) were estimated for four to six woody plant clades (Acer, Aesculus, Ceanothus, Arbutoideae, Hawaiian lobeliads, and the silversword alliance) for which calibrated phylogenies were available. For height and leaf size, rates were two to ≈300 times greater in the Hawaiian silversword alliance than in the other clades considered. These results highlight the value of direct estimates of rates of trait evolution for comparative analysis of adaptive radiation, niche conservatism, and trait diversification.

One of the central goals at the intersection of ecology and phylogenetics is to understand the tempo and mode of evolution for traits related to coexistence, niche, and ecological strategies. How fast do ecological differences between species evolve? Under what conditions is rapid versus slow evolution observed? What is the relative influence of climate change, isolation, and biotic interactions on ecological diversification? What is the sequence of ecological changes during speciation and adaptive radiation? These questions lie at the core of two closely related research areas: the study of adaptive radiations and the study of niche conservatism. In many ways, adaptive radiation and niche conservatism represent two ends of one spectrum, describing patterns (and underlying processes) of rapid divergence and convergent evolution versus slow divergence and phylogenetic conservatism, respectively. The two phenomena may also be seen as outcomes of the same underlying factors, albeit acting in opposite directions. Adaptive radiations are promoted by ecological opportunities that may arise after release from biotic pressures (especially competition), transition into novel adaptive zones, or colonization of island and island-like environments (1). (In this article I focus on the adaptive component of adaptive radiation- the diversification of ecological traits- and not on the rates of lineage diversification.) Niche conservatism, in contrast, was originally proposed by Harvey and Pagel (2) as an ecological and evolutionary process that can explain the observation that closely related species often retain a high degree of ecological similarity. They argued that novel habitats, and other ecological opportunities, will generally be occupied by species that are already well adapted to similar conditions. As a result, adaptive evolutionary change is minimized, and closely related species will retain similar ecological characteristics (see refs. 3 and 4). Importantly, this process is adaptive, in the sense that it reflects the outcome of selection in heterogeneous environments where species are able to track environments to which they are well adapted. Other processes may also lead to evolutionary stasis or slow evolution, including the absence of genetic variation (5), antagonistic genetic correlations (6), homogenizing gene flow (7), etc. Although niche conservatism is sometimes viewed as a process, and at other times as the resulting pattern, the important point is that conservative evolutionary change may arise from a range of processes, including the action of natural selection (see refs. 4 and 8).

The mechanisms underlying adaptive diversification and niche conservatism are rooted in population biology and the ecological context for natural selection. The outcomes of these processes are best studied by using comparative approaches, examining ecological diversity in the context of phylogenetic relatedness. This approach may involve focused studies of ecological divergence (or conservatism) of sister taxa or broader studies of ecological diversification in entire clades. A key challenge that has arisen in this regard is a conceptual and operational problem related to comparative methods. Given data on niche or trait variation, and an associated species phylogeny, how would niche conservatism be detected? Is there a distinctive pattern or signature arising from the process of niche conservatism that can be seen in comparative data on patterns of ecological diversity? Three main approaches are currently available to address this question (focusing on continuous traits). The first is the measurement of phylogenetic signal, which may be defined as the tendency for related species to resemble each other more than they resemble species drawn at random from the tree (8, 9). Blomberg et al. (9) have introduced the K statistic to measure phylogenetic signal in continuous traits, which has proven very useful for comparing patterns of trait evolution in different traits and clades and to relate these patterns to underlying evolutionary models. The second approach is to use model-fitting methods to find the best evolutionary model that is consistent with the observed distribution of trait values on the phylogeny (10). The Brownian motion model of a random walk provides the foundation for a family of alternative models that may incorporate stabilizing selection on one or multiple optima, time-dependent changes in model parameters, and more (9–13). Individual-based simulations, or analytic approximations, may also be used to develop models from first principles of population genetics, incorporating mutation, selection, and drift (14–17). The third approach is to focus on measurement or estimation of rates of phenotypic evolution, measured as the rate of evolutionary change in individual populations or lineages, or the rate of phenotypic divergence among related species (18, 19). Measurements of evolutionary rates are closely tied to the choice of underlying evolutionary models, as discussed below. The important difference is the focus on the parameter values themselves (in relative or absolute units) rather than on the identification of the best model.

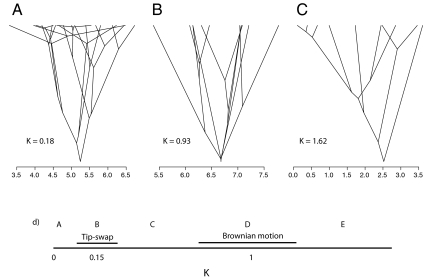
In recent years, discussions of niche conservatism have focused on the first approach, the measurement and interpretation of phylogenetic signal. Blomberg et al.'s (9) K statistic, which is in wide use, takes on values from 0 to infinity, where higher values mean a greater degree of phylogenetic signal. It is derived from an underlying Brownian motion model that describes trait evolution as a random walk along each lineage, where the change that occurs in each unit of time is drawn from a normal distribution with mean = 0 and variance = β (or s²). The variance term is often referred to as the rate parameter of the Brownian process, because it describes the rate at which the trait values of related species will diverge from each other. The K statistic reflects the observed degree of similarity among relatives, compared with expectations derived from the Brownian model and the topology and branch lengths of the species phylogeny. For traits that match the Brownian model expectation, K ≈ 1. K < 1 is a low phylogenetic signal, meaning that closely related species are more different from each other than expected (compared with the differences that have accumulated among distant relatives), and K > 1 is a high degree of phylogenetic signal, indicating that closely related species are more similar than expected. “Traitgrams,” with species arranged along a continuous trait axis, and connected by the underlying phylogeny, help provide an intuition for the meaning and interpretation of K (Fig. 1). Other approaches, such as disparity through time plots (20), can also capture patterns of phylogenetic signal and often rely on Brownian motion as a standard or null model for comparison.

Fig. 1.

Illustration of phylogenetic signal. (A–C) Phylogenetic traitgrams illustrating low, medium, and high values of the K statistic for phylogenetic signal. Tips of the phylogenies are arrayed along the x axis showing the species trait values, and internal node positions correspond to ancestral states obtained by maximum likelihood. Node depths reflect phylogenetic branch lengths. Traitgrams with more branches crossing (A) indicate greater convergent evolution. Examples illustrated are for evolution of leaf size in Hawaiian lobeliads (A), Aesculus (B), and Arbutoideae (C). (D) Axis of K values, indicating five different regions relative to alternative null models. Zones B and D illustrate the range of values obtained under a tip-swap null model for no phylogenetic signal, and under a Brownian motion model, respectively; the exact ranges of values under each model will depend on sample size, phylogenetic topology, and, for zone B, the distribution of trait values (see ref. 9). Zone A has less signal than expected under the tip-swap null model. Zones C–E all correspond to a significant degree of signal, relative to the tip-swap null model. Only zone E exhibits significantly greater signal than expected under Brownian motion.

Harvey and Pagel (2), when they introduced the concept of niche conservatism, explicitly proposed it as a process that can explain the observation that related species are ecologically similar. This has led to the idea that evidence of niche conservatism will be detected in the strength of phylogenetic signal. In a recent article, Losos (21) extended this idea and specifically proposed that niche conservatism should be identified by values of K ≫ 1. Brownian motion essentially serves as a null model, and niche conservatism should be defined as a significantly greater degree of similarity among related species than that arising from a Brownian-like process. Although Losos' article is a valuable contribution to the discussion of niche conservatism and adaptive evolution, I believe that the focus on phylogenetic signal is incomplete at best and in some cases may be misleading for the questions at hand.

I propose that a renewed attention to rates of trait diversification is important for the analysis of niche conservatism and adaptive radiation. Specifically, I propose that low rates of trait evolution, for ecologically relevant traits, will provide the best evidence of niche conservatism in comparative data. To address this proposition, I first discuss a simple method for calculating rates of trait evolution and introduce a unit of measurement, the felsen. I then address two questions: (i) What is the relationship between rates of evolution and phylogenetic signal for continuous traits, under several alternative evolutionary models, and what are the consequences for estimating evolutionary rates in empirical data? (ii) What are the observed evolutionary rates and patterns of phylogenetic signal for several plant functional traits in clades from different biogeographic regions? Comparison of evolutionary rates for exemplary cases of adaptive radiations (e.g., silverswords in Hawai'i; ref. 22) versus more ecologically conserved groups (e.g., north temperate Acer) illustrates the utility of this approach to quantify differences in phenotypic diversification across lineages.

Estimating Evolutionary Rates from Comparative Data

Rates of morphological evolution have long interested evolutionists. Haldane (23) introduced the darwin as a unit of evolutionary change. The darwin is defined as a change of one unit in the natural log of the trait value per million years (equivalently as a proportional change by a factor of e, in untransformed units, per million years). In a large metaanalysis of experimental, observational and fossil studies, Gingerich (18) reported that evolutionary rates may be as high as 200,000 darwins in short-term selection experiments, whereas rates estimated over longer time spans from the fossil record ranged from 0 to 32 darwins.

Several studies have considered the question of how to estimate rates of phenotypic evolution from comparative data, i.e., trait values measured for taxa at the tips of a phylogeny (usually extant), together with a time-calibrated phylogenetic hypothesis for the taxa. The simplest approach would be to reconstruct a hypothesis of ancestral states, using one of the available algorithms (e.g., maximum likelihood under a Brownian motion model; ref. 24). If ancestral slates are estimated using ln-transformed traits, the difference between values from ancestor to daughter node on each branch, divided by the length of the branch in millions of years, would provide a rate estimate in darwins (see ref. 19). The rates calculated over an entire tree could be averaged to provide a global estimate for the clade or could be used to identify branches where particularly high or low rates have occurred. One limitation of this approach is that the estimates obtained for sister branches on the tree are not independent, because they rely on a shared ancestral value; as a result, an original dataset with N observations at the tips ends up artificially expanded to 2N-2 rate estimates (one for each branch of a bifurcating tree). Also note that methods based on ancestral states (as well as independent contrasts) generally cannot detect trends in trait evolution across related lineages or entire clades (10), so rate estimates will represent lower bounds on rates of trait evolution (e.g., ref. 25).

As noted above, the variance β of the Brownian motion model may also be viewed as a rate parameter for the diversification of a continuous trait. However, as a rate measure β cannot be measured in units of darwins, for two reasons. First, estimates of β from comparative data are based on the diversification of trait values observed among lineages, rather than on the changes that occur within individual lineages. The term disparification (26, 27) is useful in this context, because it refers to the diversification of trait values in a clade, as distinct from diversification in the number of lineages. Second, variances are measured in terms of squared changes, not absolute changes (whether measured on ln-transformed or untransformed trait values). One can use the square root of β (i.e., the standard deviation of the Brownian process) as an absolute measure of change, but the variance has the important property of additivity: if a trait diverges by one unit of variance in one time step, it will diverge by two units in two time steps.

Several methods have been proposed to estimate β, based on a Brownian motion model of trait evolution. Garland (28) and Martins (29) adapted the method of phylogenetic independent contrasts (30) to estimate evolutionary rates. Garland's method uses the absolute value of standardized contrasts, which allows for nonparametric tests for differences in rates between groups, but does not provide a direct estimate of β itself. Martins' method is based on the slope of squared unstandardized contrasts versus the variance of the contrasts (the summed branch lengths), which does estimate β. However, there are problems related to the homogeneity of variances that must be addressed, making the method somewhat cumbersome. Maximum-likelihood methods can also be used to fit a Brownian motion model to a trait, given a phylogeny (24). Maximum-likelihood methods have been introduced to ask whether rates differ between subclades of a phylogeny (31) and to test for homogeneity of variance–covariance matrices for two or more traits evolving on a phylogeny (32). Maximum-likelihood methods provide a powerful framework for hypothesis testing and can incorporate sampling error and phylogenetic uncertainty (17, 33). Comparisons of trait variance between sister clades can also be used to test for differences in trait diversification (34, 35), although the exact linkage between trait variance and underlying models of trait evolution depends on the internal topology and branch lengths of the phylogeny.

In this article, I offer two proposals. First, returning to first principles of the independent contrasts method, it is evident that the standardized contrasts for a trait evolving under Brownian motion will be drawn from a normal distribution with variance equal to β (30). Because the sign of the contrasts is arbitrary, the true mean of this distribution is known to be 0, and one does not lose a degree of freedom estimating the mean from the data. Thus, the variance of a set of standardized contrasts (c_i) is simply Σc_i²/C, where C = N − 1 is the number of contrasts calculated for N taxa on a bifurcating tree (see maximum-likelihood derivation in ref. 31). Simulations indicate that this direct calculation of the variance provides an accurate and unbiased estimate of the true value of β (results not shown). Confidence limits can be calculated from the χ² distribution and the standard error of the variance or the curvature of a maximum-likelihood surface. F tests can also be applied to test for differences in rates between clades, based on variance ratios and appropriate degrees of freedom.

Second, I propose the term felsen as a unit for the measure of trait evolution from comparative data, in honor of J. Felsenstein's contributions to comparative methods generally and the independent contrasts method in particular. A felsen is defined as an increase of one unit per million years in the variance among sister taxa of ln-transformed trait values, or more generally as a β value = 1 for ln-transformed trait values on a phylogeny with branch lengths estimated in millions of years. Examples are provided below to illustrate the utility of this measure. The relationship between measures of trait diversification (in felsens) and estimates of evolutionary change (in darwins) depends on the amount of trait divergence. For two taxa with ln-transformed trait values of x₁ and x₂, and divergence time of t million years, the evolutionary rate in felsens will be (x₁ − x₂) ²/2t, whereas the mean rate over the two branches in darwins will be |x₁ − x₂|/2t. Over large clades the relationship between rates measured in felsens and darwins will be less straightforward and will depend on the distribution of evolutionary divergences over the entire tree. Rate estimates from maximum-likelihood methods will also be measured in felsens, if trait data are ln-transformed and branch lengths are in millions of years. Calculation of absolute rates allows comparisons between different groups and traits, as shown here, and will facilitate metaanalysis and comparison of results across studies.

Evolutionary Rates Versus Phylogenetic Signal

At first glance, it would appear that there will be a direct relationship between evolutionary rates and phylogenetic signal. For a discrete, binary trait, there is a simple relationship between the rate of evolution and the frequency of reversals: after a change from 0 to 1, another change will necessarily return the trait to state 0. The more rapid the rate of change, the more frequent are the reversals, and therefore across lineages there will be more convergent evolution and lower phylogenetic signal (36). However, as the number of states increases, more and more of the changes that occur will represent transitions to novel states, and thus reversals and convergence will become less frequent (37); as a result, increasing the rate of change will not immediately cause an increase in convergence, until the rate is high enough to saturate the range of possible states.

For continuous traits, the relationship between rate and signal also varies depending on the mode of evolution. Revell et al. (17) explored a variety of evolutionary processes, using individual-based models of drift, mutation, and selection within populations evolving along a phylogeny; for each simulation they examined the relationships between rates of evolution (based on variation in mutation rates, population size, or strength of selection) and resulting phylogenetic signal in a continuous trait (measured using Blomberg's K). Their simulations provide several important results. First, for unbounded Brownian motion (UBM), the expectation of K = 1 is maintained regardless of evolutionary rates. In other words, as the rate of trait change increases, the populations diverge more rapidly in trait space, but the degree of phylogenetic signal (the relative similarity of closely versus distantly related species) does not change (see ref. 34). In contrast, for bounded Brownian motion (BBM), increasing rates do lead to greater convergence (and lower K values), similar to the binary and multistate cases where higher rates of evolution will more quickly saturate the trait space. Stabilizing selection on a single optimum [represented by an Ornstein-Uhlenbeck (OU) process] also leads to lower K values as the stabilizing force becomes stronger. The latter result is somewhat counterintuitive, because stabilizing selection will promote evolutionary stasis, and therefore, one would think, greater phylogenetic signal. However, stabilizing selection on a single optimum pulls all species back toward the central point, erasing the signal of their prior history, and thus reducing phylogenetic signal. Few processes lead to K > 1. One example is random drift where the rate of drift is decreasing through time, so clades “lock in” to certain ranges of trait values early on and exhibit a high degree of among-clade disparity (9). Similarly, stabilizing selection models with different optima for subclades within the tree may produce values of K > 1, under certain parameter combinations. An important conclusion of these simulations is that the K value alone cannot discriminate the underlying evolutionary process, because many models can generate similar results (17).

I have conducted additional simulations for a subset of the models discussed above to further explore some of these relationships and specifically to examine the consequences of departures from Brownian motion for the estimation of evolutionary rates from empirical data (SI Text and Fig. S2). Although model-fitting approaches may prove valuable for determining the “correct” (or at least, the best fit) evolutionary model for a given trait, I would argue that estimates of β based on a simple Brownian motion model will still be useful as a measure of the “effective rate” of trait evolution. Given uncertainties caused by the evolutionary model, tree topologies, branch lengths, and trait values, these β estimates are probably most useful to distinguish traits with markedly different evolutionary rates (i.e., ≫ 2-fold).

Rates of Evolution for Plant Ecological Traits: Case Studies

Methods.

I illustrate the measurement of the rate of trait disparification with case studies of several woody plant clades and a large global trait database. For each clade, quantitative data for one or more ecological traits were available from the literature or previous comparative studies. Three traits were selected based on availability of data and ecological significance: mature height, seed size, and leaf size. These traits have been the subject of numerous recent studies examining axes of variation in plant ecological strategies (38). Height offers a measure of body size and represents a major axis of life history variation; within communities, height is the dominant factor influencing access to light, the primary energy source for plants (39). Leaf size is an important influence on energy balance (40) and is also associated with the allometry of branching and reproductive morphology (41). At the community level, leaf size tends to increase along precipitation gradients (42), although there is extensive variation observed among co-occurring species as well (43). Seed size is also an important aspect of plant life history, reflecting the tradeoff between fewer, larger offspring vs. more, smaller offspring, usually with greater dispersal potential; seed size varies with plant stature, mode of dispersal, and seedling establishment conditions (44, 45).

Six woody plant clades from three regions were chosen for study: Aesculus and Acer (north temperate), Ceanothus and Arbutoideae (mostly California), and the Hawaiian lobeliads and the silversword alliance (Hawai'i) (Table 1). All have been the subject of recent phylogenetic analysis, including chronological calibration of branch lengths. In Aesculus, the root node was an unresolved trichotomy (47) and I analyzed trait evolution over two alternative resolutions; rates of diversification were essentially identical, but values of K were more variable (results not shown). For Ceanothus, results were averaged over a set of 100 equally parsimonious trees (57), and variation among trees was negligible for the results presented here. None of the trait data were obtained from the specimens used for molecular analysis, so trait data for species were matched to corresponding species names at the tips. Methods for obtaining ultrametric trees varied among studies (see Table 1 and original citations). Calibration of absolute ages was based on interpretation of fossils or paleoclimatic events, establishing a minimum age for one or more ancestral nodes (for Ceanothus, it was based on independently estimated rates of rbcL divergence, providing a range of ages for the basal node) (58). In the absence of maximum age constraints (61), most studies assign the ancestral nodes directly to the age of the corresponding fossil, and thus all branch lengths represent minimum durations. Establishing both relative (internal) and absolute branch lengths for molecular phylogenies remains a difficult task (62). Errors in relative branch lengths will add noise to the independent contrasts, and thus inflate the variance (= rate) estimate. In contrast, errors in absolute age calibration will affect all branch lengths; if ages are too young, rates will be overestimated and vice versa. Given these uncertainties, I focus on broad patterns observed across clades and traits and do not try to resolve the significance of small differences.

Table 1.

Clades used and information on phylogenetic sources and methods used to obtain ultrametric branch lengths and chronological calibration

Clade	No. taxa	Markers	Ultrametric calibration	Chronological calibration	Crown age (95% interval), million years	Phylogeny reference	Refs. of trait data
Acer	53	7 chloroplast genes	Relaxed clock, penalized likelihood, BEAST	Multiple fossil constraints	45.3 (33.5–57.1)	Ref. 46, Fig. 3	41
Aesculus	20 (including fossils)	5 genes + morphology	Multidiv-time	Multiple fossil constraints	62.4 (58–72)	Ref. 47, Fig. 5	48–51
Arbutoideae	11	ITS	Molecular clock	Fossil	32.2	Ref. 52, Fig. 1	53–55
Ceanothus	39	ITS	Molecular clock	Fossils and rbcL divergence time analysis	28.5 (midpoint of 18–29 million-year range)	Ref. 56, Fig 1; Ref. 57, Fig. 3; Ref. 58	53–55
Hawaiian lobeliads	23	7 chloroplast genes	Penalized likelihood	Multiple fossil constraints	13.3 (7.9–18.6)	Ref. 59, Fig. 4	60
Silversword alliance	25	ITS	Molecular clock	Paleoclimate	5.23 (3.6–6.8)	Ref. 22, Fig. 1	60

Number of taxa refers to the number sampled in the original source study (Table S1 shows number of taxa for which trait data were available). The 95% intervals for crown age, where available, refer to either Bayesian credible intervals (Acer and Aesculus) or parametric confidence limits based on 1.96 standard errors (Hawaiian lobeliads and silverswords); refer to original studies for details.

For a global dataset of seed size for >12,000 taxa (51), a species-level phylogeny was constructed using Phylomatic (63), by pasting genera and species onto a backbone family level tree for the seed plants. Further resolution of intrafamilial relationships was available for some families in phylomatic or had been obtained from literature sources (51). Branch lengths for the composite tree were set by assigning stem ages of families following Wikstrom et al. (64) and adjusting the remaining branches using the bladj smoothing algorithm of Phylomatic (63).

Results.

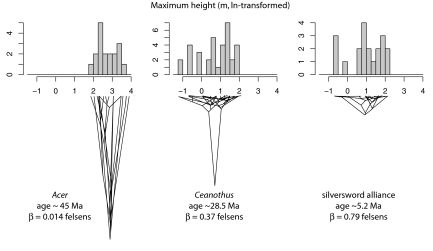
Comparative rates of trait diversification (i.e., disparification) can be visualized by plotting phylogenies with the tree depth proportional to crown age of the clade and the width proportional to the range of trait values in the extant taxa. Fig. 2 shows examples for diversification of maximum height in three clades, Acer, Ceanothus and the silverswords. Acer exhibits the narrowest range of height values among extant taxa (all ln-transformed), despite being the oldest of the three groups. Ceanothus and the silverswords have greater trait disparity than Acer and are similar to each other, but the silverswords are much younger. As a result, rates of disparification for height vary widely, from 0.014 felsens for Acer to 0.79 felsens for the silverswords.

Fig. 2.

Traitgrams for height evolution in Acer (Left), Ceanothus (Center), and the Hawaiian silversword alliance (Right). Horizontal breadth of each phylogeny corresponds to range of ln-transformed height values among terminal taxa, and vertical height is scaled to crown age of clade. Evolutionary rates (in felsens) are shown for each tree, analyzing the data with an UBM model.

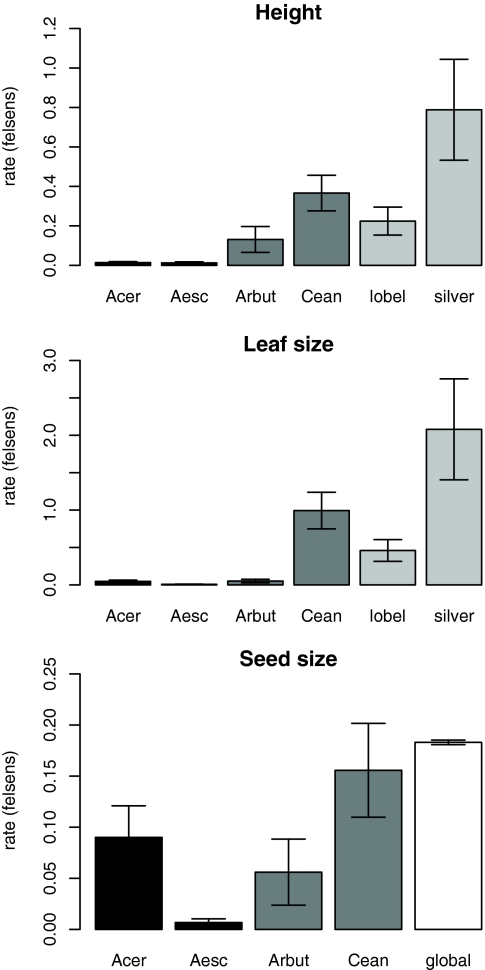
Across all traits and clades, rates of diversification exhibited >300-fold range of variation, from 0.0067 to 2.08 felsens (Table S1 and Fig. 3). Average rates (from these limited samples) increased in the order seed size < height < leaf size. The highest and second-to-lowest rates were observed for evolution of leaf size in silverswords and Aesculus, respectively. Height and leaf size data were available for all of the focal clades from different biogeographic regions. Rates of diversification for height were greatest for the silverswords, intermediate for the lobeliads and the Californian clades (Ceanothus and Arbutoideae), and lowest for the temperate deciduous clades (Acer and Aesculus) (Fig. 3). The patterns were similar for leaf size, except that rates were quite low for Arbutoideae. Aesculus, in particular, exhibited extremely low rates for leaf size and seed size, reflecting the overall similarity of these traits across the clade and its relatively old crown age. For seed size, it is noteworthy that the rate estimated from the global dataset of seed plants was actually higher than the rates for the smaller and much younger clades studied here (Fig. 3C). With improved calibration, the rates estimated for global datasets may provide the benchmark to identify smaller clades with unusually low or high rates of trait evolution, similar to the approach used for lineage diversification (65).

Fig. 3.

Rates of trait evolution in felsens (± 95% C.I.) for plant height (Top), leaf size (Middle), and seed size (Bottom). Columns, left to right, are Northern Hemisphere Acer and Aesculus (dark gray), Californian Arbutoideae and Ceanothus (medium gray), Hawaiian lobeliads and silversword alliance (light gray), and (for seed size) a large global dataset (white).

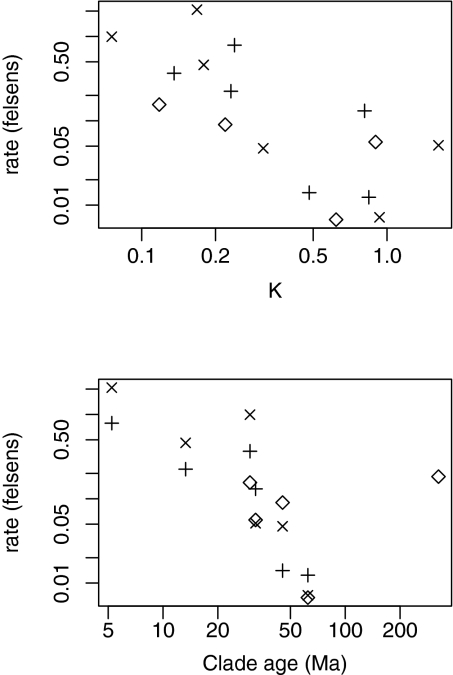
Values of K, measuring phylogenetic signal, ranged from 0.076 to 1.621, and the lowest and highest values were again observed for leaf size (in Ceanothus and Arbutoideae, respectively) (Table 1). Overall, there was a negative relationship between K and evolutionary rates (Fig. 4A, note log–log axes). β also declined in relation to the crown age of the clades (Fig. 4B). There was one distinctive outlier: the relatively high rate for seed size in the global dataset, with a seed plant crown age of 325 million years.

Fig. 4.

Observed relationships between K and β (Upper) and clade age and β (Lower) for the empirical datasets analyzed here (see Table S1). Symbols: +, height; ×, leaf size; ◇, seed size.

Discussion

The primary goal of this article is to consider the direct quantification of evolutionary rates, as opposed to calculation of phylogenetic signal, in relation to the concepts of niche conservatism and adaptive radiation. Estimates of β, the Brownian motion rate parameter, provide a simple and informative measure of phenotypic diversification rates, and I introduce the felsen as a unit for β, based on ln-transformed trait values and phylogenies calibrated in millions of years. Phylogenetic signal may be measured in several ways, and here I have focused on the K statistic (9), for reasons discussed above.

Rates of disparification (β) measured in the six focal clades considered here mirror expectations for the ecology and history of the clades. Very high rates were obtained for the Hawaiian silverswords, which may provide the most spectacular example of adaptive radiation in plants (22). The silverswords exhibit exceptionally high diversity of growth form and vegetative morphology that has evolved in a very short time since colonizing the Hawaiian archipelago. In contrast, for height evolution, the Hawaiian lobeliads and the (mostly) Californian radiations of Ceanothus and Arbutoideae exhibit intermediate rates of diversification, and the older temperate deciduous clades, Acer and Aesculus, exhibit the lowest rates. For leaf size and seed size, Acer is comparable with the Californian groups, whereas Aesculus exhibits very low trait diversification rates. These results are consistent with the impression that Acer and Aesculus comprise morphologically and ecologically coherent groups of species, while being quite old and geographically widespread, characteristics that fit the idea of niche conservatism.

Overall, there was a negative relationship between β and K and a negative relationship between crown age and β. The magnitude of β will presumably scale with the overall range of variation for a trait, so comparisons of β among traits are of limited value. In this respect, the K statistic is very useful, because it is scaled relative to expectations under Brownian motion, and values can be compared among clades and among traits. Moreover, given the significant relationship between β and K, one could argue that they provide similar insights into questions of trait evolution. I do not believe that this is the case, and I would argue that a high value of K may be a poor and even misleading measure of niche conservatism (as opposed to ref. 21). Measures of phylogenetic signal can only assess the relative similarity of close versus distant relatives and are not sensitive to the rate or total amount of trait diversification or the time span over which the clade has evolved. For example, in Fig. 1C, the three species on the left represent a conserved subclade, with respect to this trait axis; however, this is only apparent compared with the trait values for the entire clade, and the high K value is associated with the entire group. Thus, a high K value for a clade will indicate that subclades within it are highly conserved, but it does not point to the identity, age, or size of the conserved subclades. The K statistic provides an excellent and simple measure of the pattern of trait evolution, relative to Brownian motion, and will be valuable as part of an overall evaluation of phenotypic evolution. However, interpretation of K with regard to the concept of niche conservatism or adaptive radiation should be done with care.

The negative relationship between β and K is interesting in relation to the simulations discussed above. Clearly, no such relationship is expected if evolution occurs in an unbounded Brownian-like fashion. Furthermore, the K values themselves are consistently <1, again rejecting a Brownian motion pattern; similar results were reported by Blomberg et al. (9) in their initial analysis of the K statistic. K < 1 can arise from quite a few evolutionary models (17), so this result in and of itself is of limited value. As a pattern, it reveals that there is more divergence and convergence than expected under a random walk model, which could be caused by strong adaptive evolution, combined with frequent shifts between selective environments in related lineages. It could also be caused by a random walk pattern within limited bounds, and the existence of these limits can be explained based on biomechanical and physiological constraints on performance in different conditions. One prediction of bounded evolution, which is not observed in the data, is that trait values would converge toward a flat uniform distribution; in contrast, quasi-normal or log-normal distributions are commonly observed (51, 66). Interestingly, K < 1 can also arise under a model of stabilizing selection toward a single optimum for the entire clade, represented by the OU process. This model is somewhat nonintuitive because stabilizing selection is usually thought of in terms of different trait optima in different environments). Stabilizing selection on a single optimum may represent a model of soft bounds on trait evolution in which there are very few ecological settings where species with the most extreme values will thrive. The occasional lineage will reach these extreme values (e.g., the height of redwoods in the mild foggy conditions of California), but most will be pulled back toward trait values favored in more widespread environments. In the case of mammal body size, Brown (67) has postulated that there is an overall optimum body size of ≈100 g, and that lineages evolving in isolation (as on islands) will converge toward that size. Estes and Arnold (16), in a reanalysis of Gingerich's evolutionary rates dataset, assert that stabilizing selection models are uniquely capable of reproducing the observed variation in evolutionary rates across time scales.

The negative relationship between β and clade age is intriguing and seems to mirror Gingerich's (18) results in relation to rates of change vs. the time span of measurement. It does seem reasonable, or even necessary, that high rates of evolution cannot be sustained over long time periods. So high average rates of change will not be observed when rates are assessed on older clades or over longer intervals. However, low rates of change may be observed over short or long time scales, when directional selection pressures are weak, stabilizing selection is strong, or heritable variation is lacking for a trait. Thus, the relationship between evolutionary rates and temporal duration should be viewed as a triangular relationship, with an upper border representing the highest mean rates observed over a given time frame, but the lower boundary at zero across all time scales. Because of the traditional statistical focus on detection of significant effects (i.e., departure from zero or other null models), low rates of evolution are presumably underrepresented in the literature. I believe that this is caused by both reporting bias and clade selection bias. Reporting bias arises because rapid evolution is what attracts the most interest in short-term studies, whether on experimental time scales or in comparisons of recently diverged taxa, as evidence of the efficacy and potential importance of natural selection shaping phenotypic diversity. Observing a lack of response, in contrast, is not as important a result, unless it is stands in contrast to an a priori expectation of rapid evolution (e.g., refs. 5 and 54). Clade selection bias refers to a different problem, which is the factors leading researchers to choose certain clades and traits for study and the phylogenetic extent of the clades. Most studies of adaptive radiations are presumably initiated because natural history observations have already demonstrated that a set of closely related species exhibits a remarkable degree of ecological variation. Additionally, there is a clear tendency to select named clades as foci of analysis (e.g., Acer or Ceanothus). This habit raises the question of whether those clades that have traditionally been recognized and named represent a random sample of all possible clades, with respect to a given evolutionary question.

The generation of large, well-resolved phylogenies, together with methods for traversing clades and conducting comparative analyses over all nodes (e.g., ref. 51), will allow us to address the problem of clade selection bias. To illustrate this approach with regard to the question of evolutionary rates, I have traversed the Acer phylogeny and analyzed the β value for the rate of leaf size evolution for the clades defined by each of the internal nodes, and then examined the results against the node age. As expected, young clades exhibit a range of evolutionary rates, but the maximum values decline in older clades, leading to a half-triangle distribution (SI Text and Fig. S3). It will be interesting to conduct such analyses on very large and old clades (e.g., seed plants), but this should await improved resolution of the internal branch lengths as many of the clade ages are highly uncertain.

Conclusions

Evolutionary diversification comprises two interacting and equally important processes: the diversification of lineages and the disparification of phenotypes. The study of adaptive radiations has explicitly addressed both components, seeking to understand the ecological context and evolutionary mechanisms that can enhance rates of diversification and disparification. The study of niche conservatism, however, has focused on the phenotypic component, specifically addressing the ecological settings that will lead to low rates of divergence in traits that are associated with the ecological niche. As outlined above, comparative methods to study niche conservatism have increasingly focused on patterns of trait evolution, specifically the idea of phylogenetic signal. This focus likely caused in part by the belief that patterns and rates of evolution will be generally coupled, and also by the lack of absolute calibrations for phylogenetic branch lengths that are needed to calculate evolutionary rates. For continuous traits undergoing evolution by UBM, evolutionary rate and phylogenetic signal are completely decoupled. For other models, such as BBM and stabilizing selection, the two become increasingly related to each other, with higher rates generating a lower degree of phylogenetic signal. With the increasing availability of calibrated phylogenies, notwithstanding the high uncertainty that may exist in the calibrated branch lengths, it will be possible to shift toward a greater focus on absolute rates of disparification for phenotypic traits. The case studies presented here suggest that such estimates will be highly informative for contrasting trait evolution across clades and identifying cases of strong niche conservatism or the phenotypic component of adaptive radiations. Developments in eco- and phylo-informatics will facilitate widespread application of such methods, as trait data and phylogenetic hypotheses become available for more clades and can be rapidly combined for analysis. These developments promise great advances for evolutionary biology as long-standing concepts are increasingly grounded in quantitative methods and broadly based empirical comparisons.