Extraction of morphometry and branching angles of porcine coronary arterial tree from CT images

Abstract

The morphometry (diameters, length, and angles) of coronary arteries is related to their function. A simple, easy, and accurate image-based method to seamlessly extract the morphometry for coronary arteries is of significant value for understanding the structure-function relation. Here, the morphometry of large (≥1 mm in diameter) coronary arteries was extracted from computed tomography (CT) images using a recently validated segmentation algorithm. The coronary arteries of seven pigs were filled with Microfil, and the cast hearts were imaged with CT. The centerlines of the extracted vessels, the vessel radii, and the vessel lengths were identified for over 700 vessel segments. The extraction algorithm was based on a topological analysis of a vector field generated by normal vectors of the extracted vessel wall. The diameters, lengths, and angles of the right coronary artery, left anterior descending coronary artery, and left circumflex artery of all vessels ≥1 mm in diameter were tabulated for the respective orders. It was found that bifurcations at orders 9–11 are planar (∼90%). The relations between volume and length and area and length were also examined and found to scale as power laws. Furthermore, the bifurcation angles follow the minimum energy hypothesis but with significant scatter. Some of the applications of the semiautomated extraction of morphometric data in applications to coronary physiology and pathophysiology are highlighted.

the local flow patterns in large epicardial coronary arteries have significant clinical relevance because of their predilection to atherosclerosis in regions of bifurcations and curvature (4). A detailed understanding of local flow patterns must be based on an accurate reconstruction of the anatomy of the coronary vasculature (6, 7). Accordingly, a three-dimensional (3-D) reconstruction of the epicardial coronary arteries with accurate measurements of diameters, lengths, and branching angles is necessary for the accurate simulation of the local flow field. To date, we are unaware of any validated method or algorithm that addresses this need.

Recent studies that segment and reconstruct the geometric structure of vascular trees from volumetric imagery focus on vessel radii but do not extract other quantitive morphological data (e.g., lengths, volumes, and angles). A study by Nordsletten et al. (17) analyzed the renal vasculature in microcomputed tomography (micro-CT) scans, confirming Murray's law, which describes the relation between the radii of parent and daughter vessels. In a related study, Lee et al. (14) segmented a coronary micro-CT scan from a rat to determine vessel radii based on a seeded active countour algorithm. The methodology was validated using an artificial data set with an error of 0.5 voxels. There is clearly a need for a more diverse algorithm that can generate not only the diameters but also other morphological parameters necessary for hemodynamics analysis. Furthermore, there is a need for a higher-resolution extraction method with a lower voxel error. The significance of accuracy for the determination of vessel diameter is apparent based on Poiseuille's relation, which relates the fourth power of diameter to flow resistance (11), i.e., a 10% error in diameter can result in a 44% error in resistance to flow.

A recently validated software tool by our group (22) was used for measurements of radii and lengths of trunks of major coronary arteries from volumetric imagery of porcine coronary CT images (15). The method was validated on a series of CT scans with a resolution of 0.6 × 0.6 × 1.0 mm³, providing a root mean square (RMS) error of 0.27 voxels (22). The method identifies the vessels and determines the centerlines of those vessels, i.e., it reduces the entire vasculature to a curve skeleton. The major focus was on the validation of diameter and length measurements for the trunks of the major coronary arteries.

The objective of this study was to extend the previous algorithm to the entire coronary arterial tree visible under CT (vessels ≥ 1 mm in diameter). Specifically, we intended to incorporate the following new features: 1) an algorithm for 3-D angle measurements (four angles) to completely characterize the bifurcation angles, 2) an ordering scheme for classifying various vessels and hence determining the relation between order number and diameters and lengths, and 3) an algorithm to determine tree properties (area, lengths, and volume). These novel elements will further validate the algorithm in the following ways: 1) the relation between order number and diameters and lengths, 2) the relation between diameter ratios and branching angles, and 3) the scaling laws between crown length-volume and length-area. These further validations will provide greater confidence in this algorithm to be used as a standard labor-saving tool for the reconstruction of the large coronary arterial tree to test various scientific hypotheses and for potential clinical utility.

METHODS

Existing data.

We have recently validated a segmentation algorithm for CTs of porcine coronary arteries (22), which analyzed five hearts with a focus on the main trunks of the right coronary artery (RCA), left anterior descending coronary artery (LAD), and left circumflex artery (LCx). For this publication, two additional hearts were prepared and analyzed for the entire arterial tree under CT resolution.

Animal and heart preparations.

The two hearts from normal Yorkshire swine of either sex were in the size range of the previous five animals (34.3–42.1 kg). Animal and heart preparations were identical to the previous five animals (15). Briefly, animals were fasted overnight, and ketamine (20 mg/kg) and atropine (0.05 mg/kg) were administered intramuscularly before an endotracheal intubation. Animals were ventilated using a mechanical respirator, and general anesthesia was maintained with 1–2% isoflurane and oxygen. The chest was opened through a midsternal thoracotomy, and animals were then deeply anesthetized followed by an injection of a saturated KCl solution through the jugular vein to relax the heart. The aorta was clamped to keep air bubbles from entering the coronary arteries, and the heart was excised and placed in a saline solution. This study was conducted in accordance with national and local ethical guidelines, including the Institute of Laboratory Animal Research Guide, the Public Health Service policy, and the Animal Welfare Act, and was approved by the Institutional Animal Care and Use Committee of the Indiana University-Purdue University (Indianapolis, IN).

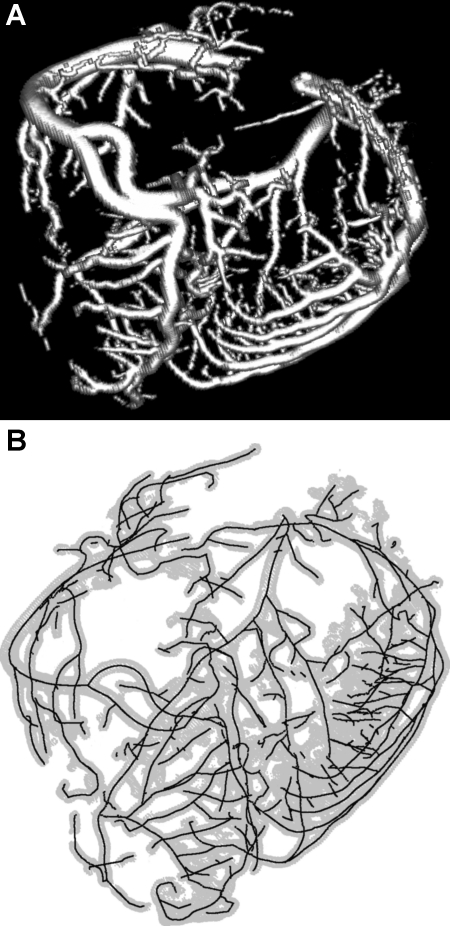
The LAD, RCA, and LCX were cannulated under saline to avoid air bubbles and perfused with cardioplegic solution to flush out the blood. The three major arteries (RCA, LAD, and LCX) were individually perfused at a pressure of 100 mmHg with three different colors of Microfil (MV-112, MV-117, and MV-130, Flow Tech) mixed with Cab-O-Sil to block the capillaries, resulting in the filling of only the arterial tree down to precapillary levels. After the Microfil was allowed to harden for 45–60 min, the hearts were kept in the refrigerator in saline solution until the day of the CT scan. Scans were made axially (120 mAs, 120 kV, 0.6 × 0.6 × 1.0 mm) on a 16-slice scanner (Siemens Somatom Sensation 16), resulting in ∼200 slices of 512 × 512 pixels each. An example of a volume-rendered image is shown in Fig. 1A.

Fig. 1.

A: volume rendering (with shading enabled) of a Microfil-perfused porcine heart, which was scanned using a computed tomography (CT) scanner. B: centerlines (solid lines) extracted from the CT scan shown in A. The boundaries of the vessel wall identified by the algorithm are shown in light gray.

Computer-assisted extraction of angular measurements from CT volumetric images.

The previously developed software package extracts morphometric data from a volumetric image (e.g., Fig. 1A) in several steps. Although a brief summary of the algorithm is given here, a detailed description can be found in a recent publication (22). The algorithm first segments the vessels within the volumetric image based on the image gradients. To get a more accurate representation of the vessel boundary, the points resulting from the segmentation step are moved along the gradient direction in such a way that they are located at the maximal gradient. This provides a more precise and smoother representation of the boundary compared with using the original voxel locations. This is important as representation of the boundary at a subvoxel level helps increase the accuracy of the morphometric measurements. A vector field is then computed in such a way that all vectors are pointing inward to the center of the vessel. In the simplest case, the image gradients can be used at the boundary. Using a trilinear interpolation, the vector field can be computed after a tetrahedrization of all the boundary points is determined. Finally, the points on the centerlines are computed using a topological analysis of the vector field within the cross-sectional area (CSA) of the vessels and connected based on the topology of the tetrahedrization. This describes the centerline at a subvoxel precision, which further contributes to the accuracy of this approach and results in a precise representation of the centerlines of all vessels within the volumetric image. The algorithm was validated with manual, optical measurements, and we found a RMS error between computed vessel diameters and manual measurements of 0.16 mm (<10% of the mean value) and an average deviation of 0.13 mm (22).

Using the above algorithm, the arterial centerlines were determined for all seven porcine hearts and for all vessels detected by the software. A centerline was defined as the curve centric to the individual vessel segments. These centerlines connecting at the vessel bifurcations form a skeleton of the vasculature, which can stretch over a consecutive sequence of vessels segments, as shown in Fig. 1B. Since the accuracy for vessels smaller than the scan resolution is questionable, as indicated by our previous study (22), vessels with a diameter of <1 mm were not included in the analysis.

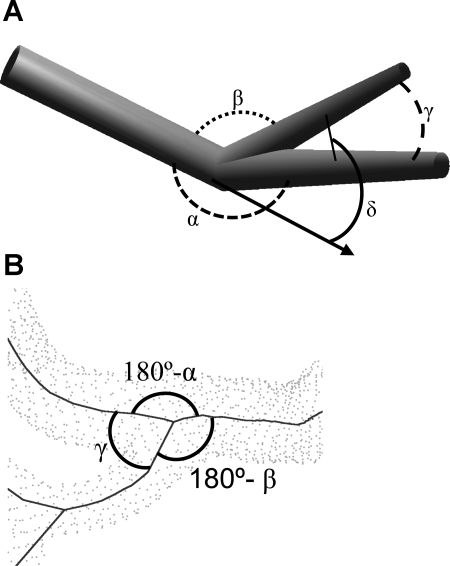
Based on the centerlines of the vessel segments, the software was extended to measure bifurcation angles, as shown in Fig. 2A. The out-of-plane angle is formed between the parent vessel and each of the two daughter vessels. The main angle (α) refers to the angle between the parent vessel and the larger daughter vessel, whereas the secondary angle (β) is determined by the angle between the parent vessel and the smaller daughter vessel. The two daughter vessels describe a plane as defined by the centerlines of those vessels. The angle between the two daughter vessels within that plane (χ) specifies the in-plane angle. Finally, the angle between the parent vessel and the plane defined by the daughter segments (δ) reflects the planarity of the bifurcations.

Fig. 2.

A: definition of bifurcation angles. Shown are the angles formed by the parent and daughter segments, namely, the main angle (α) between the parent and larger daughter vessel, the secondary angle (β) between the parent and smaller daughter vessels, the in-plane angle (γ) between the daughter vessels, and the out-of-plane angle (δ) between the plane defined by the daughter and parent vessels. B: example for a bifurcation in a typical dataset. Angles are marked using the same symbols as before; angle δ is not shown as it is hard to see due to the projection used in this image.

Since the first line segment of a centerline merely represents the connection of the vessel branches but not the direction of the daughter vessel due to possible curvature, more than the first line segments were included in the calculation of the bifurcation angle (Fig. 2B). The first centerline segment typically only leads out of the main vessel formed by the parent vessel and the larger daughter branch. Using this line segment alone would result in an erroneous bifurcation angle. Hence, the centerline segments starting with the first line segment after the bifurcation until the length of the daughter segment reaches two times the radius of the parent vessel were considered. The vectors representing the centerline segments identified in such a way were then averaged and weighed by the length of each vector to determine a representative for the orientation of the daughter vessels. These were used for the calculation of the bifurcation angles as described above.

In addition to bifurcation angles, diameters, and CSAs, vessel length and volume were computed based on the centerline and the geometric configuration of the vessel boundary. For the CSA, points on the vessel boundary were identified, which form a circular shape orthogonal to the centerline at every center point. One of these points was chosen as a starting point. The points were then sorted with respect to angle between the line connecting the current point and the center point and the line formed by the selected point and the center point. This results in a polygon encircling the center point, which represents the CSA. Hence, the CSA was then computed as the surface area of the slices formed by the center point and two neighboring points on the vessel boundary.

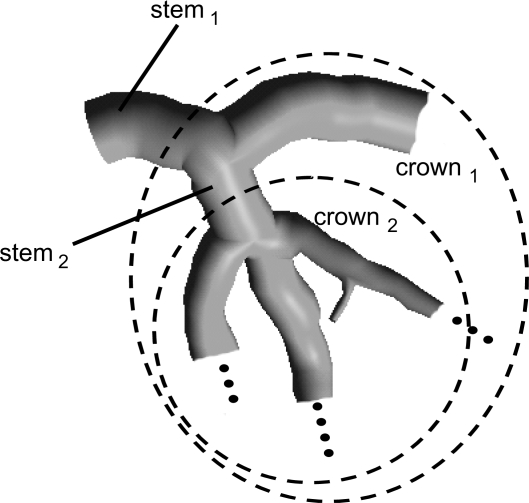
The previous software (22) was further extended to compute vessel lengths and vessel volumes for every crown. A crown was defined as the combination of all vessel segments from a vessel bifurcation downward, as shown in Fig. 3. The crowns were defined down to the point where the vessel diameter was 1 mm. The vessel volume was computed as the volume described by the vessel boundary enclosing the centerline. Similarly, the vessel length was computed for a crown as the sum of all the lengths of all vessel segments within that crown. Based on these methodologies, vessel volumes, CSAs, and vessel lengths were computed for all crowns. Hence, the length of a crown is the sum of all vessel segments down to vessel equal to 1 mm in diameter. Similarly, the crown volume can be computed as the sum of the volumes of all vessel segments included in the length computation. For the CSA, the parent vessel of the given bifurcation was used. To better compare the data of different hearts, the crown length and crown volume were normalized using the sum of the lengths and volumes of the entire branch, i.e., the LAD, LCX, or RCA, for a given heart. The CSA was normalized by the most proximal vessel segment of the main branch.

Fig. 3.

Definition of crowns used for the calculation of crown length and crown volume.

Data analysis.

For the statistical analysis, the bifurcations were grouped with respect to the order of the respective vessel segments. There is a unique relation between the range of diameter and order number, as defined previously (10). This relation was used to assign order numbers to the respective vessels measured here as shown in Table 1 for the LAD, LCX, and RCA. The bifurcations were then classified based on the order of the parent and daughter vessels. Bifurcations between vessel orders ranging from 9 to 11 for the LAD and RCA and from 9 to 10 for the LCX were considered since vessels of this size range can be extracted reliably from CT-scanned imagery with a resolution of 1 mm. Average angles and SDs within each of these groups were computed for each of the major coronary arterial branches.

Table 1.

Relation between the diameter and order number and statistical summary of the morphometric measurements for the RCA, LAD, and LCx

	Range, mm	Diameter, mm	Length, mm	n
RCA
Order 9	552–955	0.85±0.09	7.0±5.4	30
Order 10	955.1–2,319	1.4±0.31	7.9±7.3	157
Order 11	2,319.1–3,606	3.3±0.55	9.4±11.6	42
LAD
Order 9	554–986	0.86±0.08	7.1±5.3	109
Order 10	986.1–2,189	1.3±0.27	6.6±5.5	191
Order 11	2,189.1–3,830	2.8±0.31	5.7±4.5	47
LCx
Order 9	649–1,782	1.3±0.24	7.4±7.4	107
Order 10	1782.1–2,940	2.7±0.59	8.2±7.1	52

Values for diameter and length are means ± SD;

n, number of vessel segments. RCA, right coronary artery; LAD, left anterior descending coronary artery; LCx, left circumflex artery.

The out-of-plane angles, as defined previously, were used to estimate the planarity of the bifurcation. In the case of a completely planar bifurcation, the angle is 0. Similarly, the cosine of the angle can be computed to derive a value describing the planarity: a value of 1 represents a completely planar bifurcation, whereas a value of 0 describes an orthogonal bifurcation. Similar to the angles, the bifurcations were grouped according to their orders, and the planarity was determined. Average planarity and SDs were computed for each of the major arterial branches.

RESULTS

The process time for a full scan of coronary CT is only several minutes in the present version of the algorithm. All seven hearts (3 major coronary arteries in each heart) were processed similarly. Table 1 shows the vessel diameter (and range), length, and number of vessels measured for the LCX, LAD, and RCA of each respective order. Tables 2–6 provide statistical summaries of the bifurcation angles in the porcine coronary vasculature. The order numbers are provided for the daughter vessel (row) and for the parent vessel (column). There are only vessels coming off of equal or smaller order and, hence, there are no entries for other components. The tables list the average angles and number of measurements made.

Table 2.

Statistical summary of the main angle α, defined between the parent vessel segment and larger daughter segment

Parent Segment	Larger Daughter Vessel Segment
	Order 9	Order 10	Order 11
RCA
Order 9	26.0±17.5 (7)	24.8 (1)	34.4±5.5 (3)
Order 10		22.2±11.8 (67)	22.4±16.5 (15)
Order 11			15.3±7.3 (32)
LAD
Order 9	27.7±17.8 (26)	30.8±14.4 (9)	26.6±14.8 (10)
Order 10		23.4±14.7 (81)	34.6±19.9 (23)
Order 11			18.5±10.1 (36)
LCx
Order 9	21.4±18.7 (44)	31.6±16.5 (11)
Order 10		18.5±16.8 (36)

Values are means ± SD (in °); numbers in parentheses are numbers of measurements made. Shown are the averages and SDs for each group of bifurcations determined by the radius of the parent vessel segment and the daughter vessel segment.

Table 6.

Statistical summary of the planarity of the bifurcation where a value of unity describes a completely planar bifurcation and a value of 0 represents an orthogonal bifurcation

Parent Vessel Segment	Daughter Vessel Segment
	Order 9	Order 10	Order 11
RCA
Order 9	0.98±0.02 (7)	0.96 (1)	0.89±0.12 (3)
Order 10		0.97±0.05 (67)	0.95±0.10 (15)
Order 11			0.98±0.02 (32)
LAD	order 9	order 10	order 11
Order 9	0.94±0.10 (26)	0.88±0.11 (9)	0.93±0.13 (10)
Order 10		0.95±0.07 (81)	0.89±0.17 (23)
Order 11			0.97±0.04 (36)
LCx	order 9	order 10
Order 9	0.94±0.14 (44)	0.93±0.06 (11)
Order 10		0.95±0.11 (36)

Values are means ± SD; numbers in parentheses are numbers of measurements made. Shown are the averages and SDs for each group of bifurcations determined by the radius of the parent vessel segment and the daughter vessel segment. The number of measurements made for each order is the same as those shown in Table 2.

Bifurcation angles were computed based on the centerlines of the vessels. Table 2 shows the statistical summary of the main angles (α) of the bifurcations describing the angle between the parent vessel and the larger daughter vessel. Typically, the larger daughter vessel is a mere continuation of the parent vessel with a second vessel branching off. As a result, only relatively small angles α occur between the parent and larger daughter vessel, as shown in Table 2. Table 3 shows similar statistical values for the secondary angle (β) formed by the parent vessel and the small daughter vessel. Since this typically describes a smaller vessel branching off of a larger one, β is significantly larger than α (Table 2). The in-plane angles between the daughter vessels (γ) are shown in Table 4. These transmural or perforating vessels, which typically branch off of a larger vessel of order 11, have the largest angles (up to 90°). The larger angles are found for the larger orders, which include the transmural vessels compared with vessels of smaller orders. Table 5 shows the out-of-plane angle (δ), which describes the angle between the plane formed by the daughter vessels and the parent vessel. This is an index of planarity of the bifurcation, which is further analyzed in Table 6. A value of 1 represents total planarity (0 angle), whereas 0 indicates an orthogonal bifurcation (90° angle).

Table 3.

Statistical summary of the secondary angle β, defined between the parent vessel segment and smaller daughter segment

Parent Segment	Smaller Daughter Segment
	Order 9	Order 10	Order 11
RCA
Order 9	76.3±18.4 (7)	575.5 (1)	55.9±15.0 (3)
Order 10		63.4±31.7 (67)	57.9±14.7 (15)
Order 11			63.0±34.2 (32)
LAD
Order 9	64.1±33.0 (26)	65.2±20.3 (9)	46.7±25.8 (10)
Order 10		75.5±32.5 (81)	61.4±17.7 (23)
Order 11			75.3±30.1 (36)
LCx
Order 9	72.4±30.3 (44)	57.0±16.0 (11)
Order 10		74.6±36.5 (36)

Values are means ± SD (in °); numbers in parentheses are numbers of measurements made. Shown are the averages and SDs for each group of bifurcations determined by the radius of the parent vessel segment and the daughter vessel segment. The number of measurements made for each order is the same as those shown in Table 2.

Table 4.

Statistical summary of the in-plane angle χ, defined between the daughter segments

Larger Daughter Segment	Smaller Daughter Segment
	Order 9	Order 10	Order 11
RCA
Order 9	83.7±27.4 (7)	51.5 (1)	58.2±31.5 (3)
Order 10		73.4±34.7 (67)	67.2±21.1 (15)
Order 11			68.0±31.7 (32)
LAD
Order 9	67.8±31.7 (26)	70.8±32.2 (9)	59.8±27.2 (10)
Order 10		81.8±32.9 (81)	72.8±26.1 (23)
Order 11			81.9±31.3 (36)
LCx
Order 9	77.1±30.2 (44)	70.1±28.1 (11)
Order 10		77.0±38.2 (36)

Values are means ± SD (in °); numbers in parentheses are numbers of measurements made. Shown are the averages and SDs for each group of bifurcations determined by the radius of the larger daughter vessel segment and the smaller daughter vessel segment. The number of measurements made for each order is the same as those shown in Table 2.

Table 5.

Statistical summary of the out-of-plane angle δ, defined between the parent vessel segment and plane defined by the daughter segments

Parent Vessel Segment	Plane Defined by the Daughter Segments
	Order 9	Order 10	Order 11
RCA
Order 9	9.5±7.3 (7)	17.2 (1)	21.8±19.53 (34)
Order 10		11.4±9.8 (67)	13.8±13.7 (15)
Order 11			8.4±5.6 (32)
LAD
Order 9	16.1±13.6 (26)	25.3±13.5 (9)	16.1±14.7 (10)
Order 10		13.7±11.2 (81)	20.2±20.0 (23)
Order 11			11.1±8.7 (36)
LCx
Order 9	12.6±15.5 (44)	18.6±10.8 (11)
Order 10		10.0±13.2 (36)

Values are means ± SD (in °); numbers in parentheses are numbers of measurements made. Shown are the averages and SDs for each group of bifurcations determined by the radius of the parent vessel segment and the plane defined by daughter vessel segments. The number of measurements made for each order is the same as those shown in Table 2.

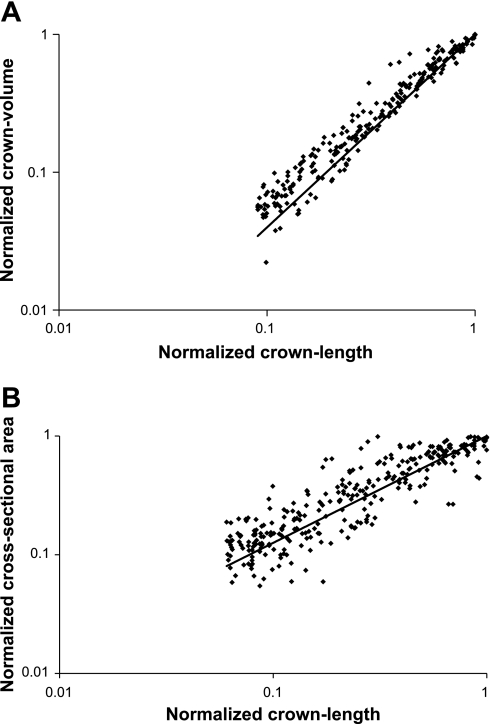
Figure 4, A and B, shows the relation between normalized crown length and normalized crown volume as well as vessel length and CSA for various crowns, respectively (Fig. 3). For the crown volume, each crown was represented as a single data point where the normalized crown length was plotted against the normalized crown volume on a logarithmic scale. A least-squares trend line with an exponential curve for the relation between crown length and crown volume is also shown in Fig. 4A. An exponent of 1.4 was found with a correlation coefficient of R² = 0.97. Similarly, the normalized CSAs were plotted against the normalized crown length on a logarithmic scale (Fig. 4B). For the relation between the CSA and the crown length, an exponent of 0.9 (R² = 0.65) was determined as the scaling relation between these two parameters.

Fig. 4.

A: normalized crown volume versus normalized crown length for all porcine hearts. The solid line represents the least-squares fit with an exponent of 1.4 and R² = 0.97. B: normalized cross-sectional area versus normalized crown length for all porcine hearts. The solid line represents the least-squares fit with an exponent of 0.9 and R² = 0.65.

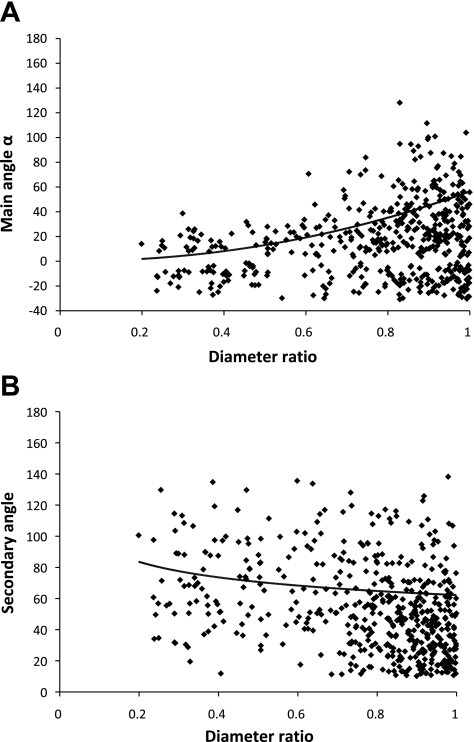
Theoretically, it has been shown that branching planar angles obey the minimum energy hypothesis to render them physiologically efficient (15). We considered the relation between the diameter ratio of the daughter branches and the main and secondary angles to evaluate the agreement with the predicted optimum angles. Figure 5, A and B, shows the data for the main angle and secondary angles, respectively.

Fig. 5.

A: main angle α plotted against the ratio of the radius of the smaller daughter vessel over the radius of the larger daughter vessel, including the trend line for the optimal angles. B: secondary angle β plotted against the ratio of the radius of the smaller daughter vessel over the radius of the larger daughter vessel, including the trend line for the optimal angles.

It should be noted that the computation of the main angle differs slightly from the one used for the results shown in Table 2 to match Zamir and Chee's definition (25) since they only consider planar bifurcation in a two-dimensional projection. As a result, negative angles for the main angle are possible if both daughter vessels are located on the same side with respect to the parent vessel, e.g., if daughter vessels are oriented to the left. Based on the radius of the parent and daughter vessels, the optimal angles were calculated according to Murray's physiological principle of minimum work (15) and are shown as a solid trend line.

DISCUSSION

In the present study, the morphological features (CSA, length, and vascular volume) and 3-D branching angles of the porcine coronary vasculature were quantitatively described using a time-efficient, semiautomatic extraction method from CT images. This is a labor-saving methodology for extracting labor-intensive morphometric data from volume-rendered images. These morphological data are necessary for modeling vascular structures and hemodynamics, to elucidate scaling laws, for the diagnosis and assessment of therapeutics interventions, and so on.

Morphometry of coronary arteries.

The novelty of this study is the extension of the previous algorithm (22) to the entire arterial vasculature visible with CT images, which results in a detailed morphological analysis that includes not only vessel diameter and lengths but also 3-D bifurcation angles, crown volume, and length. The diameters and lengths of the first several orders of RCA, LAD, and LCx vessel elements are shown in Table 1. The diameter of largest vessels (order 11 for the RCA and LAD and order 10 for the LCx) are lower than previously reported (10). This is due to the fact that the most proximal vessels (larger diameter) were not included in the extraction due to the presence of the cannuale used to perfuse the Microfil cast. The algorithm was validated (within 10% error), however, when the same segment of the artery extracted from CT and optical measurements was compared (15). Hence, this algorithm achieves a higher accuracy compared with other techniques found in the literature. Lee et al. (14) used an artifical data set to validate their method for determining vessel radius and reported an error of 0.5 voxels compared with the present algorithm with an error of only 0.27 voxels. Based on measurements extracted from micro-CT scans, Nordsletten et al. (17) generated similar plots for the relation between CSA and volume and diameter ratio versus the ratio of Zamir's cost functions for a renal vasculature of a rat. While their findings are similar in that they also confirmed Murray's law, current micro-CT technology is not clinically translatable.

Branching angles.

The bifurcation angles are thought to be optimized based on the minimization of energy (15, 25). While the mean measured angles tended to reflect the optimal values (Fig. 5), it can be observed that the individual angles showed significant scatter. This finding is in agreement with the observations made by Zamir et al. (25) in human hearts. The general trend here provides further validation for the extraction algorithm of angles.

It is commonly assumed that arterial bifurcations are planar, i.e., the daughter and parent vessels reside in the same plane (5). However, other publications have shown that this is not necessarily the case for the human aortic bifurcation (1, 18). Our measurements (Table 6) show that, for porcine hearts, the arterial bifurcations are mostly planar with planarity values of >90%.

Scaling laws.

Several studies have suggested a correlation between coronary artery lumen size at any point in the arterial tree, the sum of arterial branch lengths distal to that point, the volumetric flow in the entire arterial tree, and regional myocardial mass (for a review, see Ref. 3). Seiler and colleagues (19, 20) have reported a power-law relationship between the CSA of the stem vessel and the cumulative length of the crown perfusing a myocardial region. The power-law relationship was shown to be comparable in both canine and human studies, thereby confirming the fundamental physical principles underlying the structure of the coronary arterial tree in different species. Kassab (13) has demonstrated that different vascular trees (coronary, pulmonary, and vascular systems of various skeletal muscles, mesentery, omentum, and conjunctiva) in various species (rat, hamster, cat, rabbit, pig, and human) obey a set of design rules or scaling power laws based on the minimum energy hypothesis.

A power law exists between crown volume and crown lengths as well as CSA and crown length to ensure optimal flow (12). The exponent of this relation is expected to be 1.4, which was confirmed by our measurements (R² = 0.97; Fig. 4A). The RMS error between the expected and actual values is 0.042, and the average deviation is 0.017. The small scatter and high correlation of this relation makes it ideal for the evaluation of diffuse coronary artery disease. The volume-length relation can define the signature of normality (through the slope of exponent), and the deviation thereof in diffuse disease can determine the extent of the disease. This is a significant future application of the extraction algorithm from patient CT images.

The measurements of the CSA are usually expected to have larger scatter compared with the volume measurements. Regardless, a significant trend can be seen in the results shown in Fig. 4B, indicating a significant relation between CSA and normalized crown length as being a power law with an exponent of 0.9. Seiler et al. (19, 20) found a power-law relationship between the stem CSA and crown cumulative arterial length in both canine and human studies. They reported a value of 0.82 for in vivo human studies of left coronary arteries and similar values for canine studies. In previous studies, we provided a physical basis for the proposed relation based on the minimum energy cost function and conservation of energy for steady-state flow (10, 13). The power exponents for the CSA-length relationship were ∼0.93 in the previous study (10, 13). The agreement in the exponent determined in the present study provides further validation for the proposed extraction algorithm.

Critique of methods.

The present study is based on CT images of excised hearts. The clinical application will need in vivo analysis. It should be noted that ex vivo images were obtained with a 16-slice CT. There are 64- and 256-slice CT available clinically with significantly higher resolution. Hence, the present analysis is translatable to clinical CT imaging.

The current version of the algorithm is still only semiautomatic, i.e., it requires some user intervention. Mainly, the user has to select the root of the main branch, i.e., the LAD, RCA, and LCx, and, in some rare cases, a connection has to be inserted at the bifurcations if the algorithm does not recognize it and fails to insert it. This occurs more frequently (<10%) in distal bifurcations, and a manual correction simply entails a small interpolation of the connection. The user interface of the software for performing these manual corrections in a more user-friendly fashion is currently underway. Once this is completed, we plan to make the software publicly available.

Significance and potential utility.

A large-scale reconstruction of the coronary vasculature has been undertaken to understand the distribution of pressure and flow throughout the vasculature (1, 8, 21). Such realistic anatomic models allow computational fluid dynamic analysis to understand the local distribution of velocity, wall shear stress magnitude, and gradients (temporal and spatial) as well as understanding regions of disturbed flow (6, 7). The previous reconstructions were based on labor-intensive data collection, which limits the speed of progress. The algorithm described here provides data that serve as a foundation for such models in a time-efficient approach. The efficient reconstruction of coronary anatomy in health and disease will allow us to quantitatively assess a number of hypotheses relating to the coronary circulation and cardiology.

CT angiography is clinically used to improve the management of patients with acute chest pain (13). Furthermore, the introduction of the newest technology in this field (i.e., 64-slice CT with improved temporal and spatial resolution as well as 256-slice multidetector CT and dual-source CT) makes this imaging modality a very promising screening and diagnostic tool for cardiac patients. Despite the potential utility, the images remain qualitative, and there is no validated and reliable algorithm to extract quantative and precise data automatically (or at least semiautomatically) from the CT images. The proposed validated algorithm addresses this issue and will, in future studies, allow the translation of patient-specific analysis to the clinic.

GRANTS

This work was supported in part by National Heart, Lung, and Blood Institute Grants HL-092048 and HL-084529.