Abstract
Lepidopterists have long acknowledged that many uncommon butterfly species can be extremely abundant in suitable locations. If this is generally true, it contradicts the general macroecological pattern of the positive interspecific relationship between abundance and distribution, i.e. locally abundant species are often geographically more widespread than locally rare species. Indeed, a negative abundance–distribution relationship has been documented for butterflies in Finland. Here we show, using the Finnish butterflies as an example, that a positive abundance–distribution relationship results if the geographically restricted species are missed, as may be the case in studies based on random or restricted sampling protocols, or in studies that are conducted over small spatial scales. In our case, the abundance–distribution relationship becomes negative when approximately 70 per cent of the species are included. This observation suggests that the abundance–distribution relationship may in fact not be linear over the entire range of distributions. This intriguing possibility combined with some taxonomic biases in the literature may undermine the generalization that for a given taxonomic assemblage there is a positive interspecific relationship between local abundance and regional distribution.
Keywords: abundance–distribution relationship, Lepidoptera, macroecology
1. Introduction
The positive interspecific relationship between local abundance and regional distribution is argued to be an almost universal feature of species assemblages (Brown 1984; Gaston et al. 1997; hereafter abundance–distribution relationship). That is, locally abundant species tend to be more widespread than species that are locally rare. Besides a positive relationship, some studies have also documented an inverse relationship between abundance and distribution (e.g. Arita et al. 1990; Ford 1990; Gaston & Lawton 1990; Johnson 1998; Cowley et al. 2001a,b; Päivinen et al. 2005). Contradictory results can stem from the phenomenon being partly scale dependent: positive relationships may emerge at a local scale but no relationship, or indeed a negative relationship, at a larger spatial scale (Gaston & Lawton 1990; Hughes 2000; Cowley et al. 2001a). We feel, however, that the negative relationship is often considered to emerge only under restricted circumstances and commonly explained away, rather than considered a real pattern.
Our thesis is that an apparently general positive abundance–distribution relationship can result from incomplete sampling of species assemblages. Sampling artefact has been proposed to be able to generate an artefactual positive relationship: the distribution of widespread species with low local abundance will be underestimated because they are recorded from fewer localities than equally widespread species occurring at higher densities (Gaston et al. 1997). We propose, however, that the positive abundance–distribution relationship can emerge because it is the locally abundant but geographically restricted species that are missed. A negative abundance–distribution relationship has been documented for butterflies in Finland (Päivinen et al. 2005). Using these data, we here examine how the percentage of species of an assemblage included in the analysis affects the sign and slope of the abundance–distribution relationship.
2. Material and methods
Data are based on the literature and include the 95 resident butterfly species in Finland. The distribution of species is the number of 10 by 10 km grid squares on the Finnish national coordinate system from which a species was recorded during 1988–1997 (Huldén et al. 2000). Abundance is derived from the National Butterfly Scheme in Finland (NAFI) 1991–2000, which is based on surveys by volunteer lepidopterists and includes over 1.5 million individuals (see details in Päivinen et al. 2005). Each lepidopterist reports the species observed, the number of individuals for each species and the total number of field days (i.e. sampling effort) for each grid square they have been surveying. To calculate the mean local abundance, we divided the total number of individuals of each butterfly species by the number of grids occupied by the species. To circumvent the problem of mathematical non-independence of the national distribution and mean local abundance arising from the necessity of dividing the total number of individuals with the distribution, we used two independent distribution datasets. The distribution data from the NAFI were used to calculate the mean local abundance, while the distribution data from the Atlas of Finnish Macrolepidoptera (Huldén et al. 2000) were used to examine the relationship between local abundance and regional distribution. To make the monitoring reliable, the lepidopterists participating in NAFI have been instructed to report all the species, not just the rare ones. However, rare butterfly species with known occurrence sites may face proportionally higher sampling effort than common species. To control for the effects of sampling effort on abundance, we divided the mean local abundance by the number of observation days in each grid cell that a given species occupied; the observation days are the days when the observer was observing at a given grid square, and thus include also days when a given species was not observed. The number of observation days for each species averages 20 815 (min–max = 53–50 595). To demonstrate the importance of controlling for sampling effort, we also present results using uncorrected data. Similarly to most other studies (see Gaston et al. 1997), the abundance–distribution relationship in Finnish butterflies is unaffected by the control of phylogenetic relatedness of the species (Päivinen et al. 2005).
Random sampling techniques are likely to yield species records in a positive relationship to species distribution such that the most widely distributed species will be observed first and as the sampling effort is increased, species with more restricted distributions start appearing in the data. Following this logic, we divided our data such that we first included 30 per cent of species in the analysis, and then proceeded by adding 10 per cent at each step. Species were included in the order of species distribution in Finland, starting from the most widespread species. From these data, we extracted Pearson's correlation coefficients between abundance and distribution for each proportion of the data (30, 40, 50, … , 100%).
3. Results
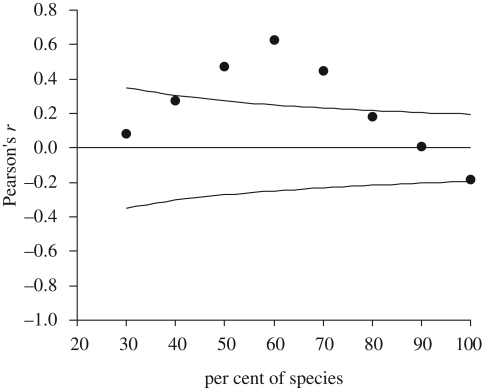
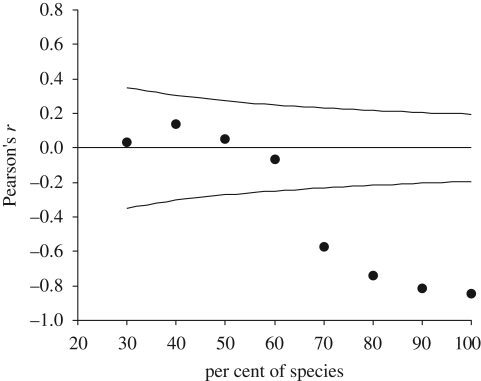
There was no relationship between local abundance and national distribution of Finnish butterflies (F1,93 = 3.34, p = 0.071). However, after correcting for sampling effort, the relationship became strongly negative (F1,93 = 230.0, p < 0.001). With the data uncorrected for sampling effort, the correlation coefficient between local abundance and national distribution was non-significant or significantly positive, depending on the percentage of species included in the analysis (figure 1). Using the data corrected for sampling effort however, the relationship became significantly negative when 70 per cent or more of the species were included in the analysis (figure 2).
Figure 1.
Pearson's correlation coefficients between local abundance and national distribution (uncorrected for sampling effort) of Finnish butterflies in relation to the percentage of species included in the analysis; species were entered in order of decreasing national distribution. The horizontal line represents correlation coefficient 0 and the curved lines represent the area above and under which the correlation coefficients are significantly different from zero.
Figure 2.
Pearson's correlation coefficients between local abundance and national distribution (corrected for sampling effort) of Finnish butterflies in relation to the percentage of species included in the analysis; see figure 1 legend for details.
4. Discussion
Our results show that a positive relationship between abundance and distribution of species can result if only a small proportion of species of a given assemblage is sampled; this is supported both by data corrected and uncorrected for sampling effort. Indeed, the proportion of species included in the analysis is often relatively small. Hughes (2000) documented a non-significant negative relationship between the local abundance and regional as well as continental distribution of lycaenid butterflies in North America. The data included only 15 per cent of the lycaenid species occurring in North America, so the true relationship among this taxonomic assemblage could well be significantly negative. Gutiérrez & Menéndez (1995) documented that increasing abundance had only a slight positive effect (R2 = 0.055) on species distribution in northern Spain; the study included 73 per cent of the butterfly species in the region, which is close to the threshold level for a significantly negative relationship in our data. For British butterflies, Cowley et al. (2001b) identified that the positive abundance–distribution relationship is only present, or is strongest, in the widespread, mobile species (i.e. ca 30% most widespread species).
The abundance–distribution relationship has been considered a fundamental macroecological pattern (Brown 1984; Gaston & Blackburn 2000). Paradoxically, however, the pattern seems to be the weakest at large spatial scales (Cowley et al. 2001a). Most studies are conducted over a limited geographical range, or they rely on some random sampling protocols, and thereby miss a great proportion of species and particularly those species with restricted distribution but high local abundance. Because the geographically restricted but locally abundant species are those that contribute to the negative abundance–distribution relationship (Cowley et al. 2001a,b; Päivinen et al. 2005), inadequate sampling may result in apparently general positive relationships. Because only the best quality patches can sustain viable populations in the long run, the negative pattern could be more common in northern- and southernmost latitudes where most species meet the edge of their distribution (Päivinen et al. 2005), or when the focal habitat is rare at the landscape scale (Gaston & Lawton 1990). Both of these patterns can result from differences in extinction probability, i.e. only the largest local populations of species with restricted distribution are able to persist, whereas the locally rare species can persist only if they are widespread (Johnson 1998). We stress that in studies on abundance–distribution relationships, particularly, strong effort should be made to include the species with only a few known sites of occurrence.
Our results suggest an intriguing possibility that the abundance–distribution relationship may in fact not be linear over the entire range of distributions. If the relationship was intrinsically negative as we have earlier suggested (Päivinen et al. 2005), then missing the rarest species should lead to less significant negative or non-significant relationships, not positive ones. However, as we have shown here, the relationship is weakly positive for the most widespread species, while strongly negative for the rarer species. The widespread and rare species do seem to behave differently in other systems as well. Cowley et al. (2001a,b) showed that butterfly species which occurred at high densities relative to their distribution used aggregated resources and were relatively sedentary, whereas mobile generalist species were more widespread and less abundant (see also Päivinen et al. 2005). Gaston & Blackburn (2000) data on birds demonstrate that in some cases there is no relationship or only weak positive relationship for the rarer species, but very strong positive relationship for the common species.
The reason for the apparent general positive abundance–distribution relationship might relate to a taxonomic bias in the literature: there is an overwhelming number of studies on birds (references in Gaston & Blackburn 2000). This might present a problem because birds are generally territorial and as such there are stronger biological restrictions for a high local abundance in comparison with invertebrates. This also means that there is a stronger positive relationship between abundance and distribution because each breeding pair inhabits a new piece of land leading to rapid increase in distribution with abundance; this mechanism can be expected to be much weaker for non-territorial species. Also, a bird species can be represented year after year by a single breeding pair—even at macroecological scales—whereas an isolated insect population must have hundreds or thousands of individuals for long-term persistence. These biological facts have especially strong influence on the slope of the abundance–distribution relationship at the rarer end of the range size continuum.
As a conclusion, the possibility that the nonlinear relationship between abundance–distribution applies not only to specialist invertebrates, but other organisms as well, may undermine the general macroecological pattern that for a given taxonomic assemblage there is a positive interspecific relationship between local abundance and regional distribution.
Acknowledgements
We thank J. Niemelä for a discussion that inspired this work. The manuscript was substantially improved by comments from an anonymous referee pointing out the possible importance of the nonlinearity. This work was supported by the Academy of Finland.
References
- Arita H. T., Robinson J. G., Redford K. H.1990Rarity in neotropical forest mammals and its ecological correlates. Conserv. Biol. 4, 181–192 (doi:10.1111/j.1523-1739.1990.tb00107.x) [Google Scholar]
- Brown J. H.1984On the relationship between abundance and distribution of species. Am. Nat. 124, 255–279 (doi:10.1086/284267) [Google Scholar]
- Cowley M. J. R., et al. 2001aDensity–distribution relationships in British butterflies. I. The effect of mobility and spatial scale. J. Anim. Ecol. 70, 410–425 (doi:10.1046/j.1365-2656.2001.00508.x) [Google Scholar]
- Cowley M. J. R., Thomas C. D., Wilson R. J., León-Cortés J. L., Gutiérrez D., Bulman C. R.2001bDensity–distribution relationships in British butterflies. II. An assessment of mechanisms. J. Anim. Ecol. 70, 426–441 (doi:10.1046/j.1365-2656.2001.00509.x) [Google Scholar]
- Ford H. A.1990Relationships between distribution, abundance and foraging niche breadth in Australian land birds. Ornis Scand. 21, 133–138 (doi:10.2307/3676809) [Google Scholar]
- Gaston K. J., Lawton J. H.1990Effects of scale and habitat on the relationship between distribution and density. Oikos 58, 329–335 (doi:10.2307/3545224) [Google Scholar]
- Gaston K. J., Blackburn T. M.2000Pattern and process in macroecology Oxford, UK: Blackwell Science [Google Scholar]
- Gaston K. J., Blackburn T. M., Lawton J. H.1997Interspecific abundance–range size relationships: an appraisal of mechanisms. J. Anim. Ecol. 66, 579–601 [Google Scholar]
- Gutiérrez D., Menéndez R.1995Distribution and abundance of butterflies in a mountain area in the northern Iberian peninsula. Ecography 18, 209–216 (doi:10.1111/j.1600-0587.1995.tb00123.x) [Google Scholar]
- Hughes J. B.2000The scale of resource specialization and the distribution and abundance of lycaenid butterflies. Oecologia 123, 375–383 (doi:10.1007/s004420051024) [DOI] [PubMed] [Google Scholar]
- Huldén L., Albrecht A., Itämies J., Malinen P., Wettenhovi J.2000Atlas of Finnish Macrolepidoptera Helsinki, Finland: Suomen Perhostutkijain Seura, Luonnontieteellinen keskusmuseo [Google Scholar]
- Johnson C. N.1998Species extinction and the relationship between distribution and abundance. Nature 394, 272–274 (doi:10.1038/28385) [Google Scholar]
- Päivinen J., Grapputo A., Kaitala V., Komonen A., Kotiaho J. S., Saarinen K., Wahlberg N.2005Negative density–distribution relationship in butterflies. BMC Biol. 3, 5 (doi:10.1186/1741-7007-3-5) [DOI] [PMC free article] [PubMed] [Google Scholar]