Evaluation of Agile Designs in First-in-Human (FIH) Trials—A Simulation Study

Abstract

The aim of the investigation was to evaluate alternatives to standard first-in-human (FIH) designs in order to optimize the information gained from such studies by employing novel agile trial designs. Agile designs combine adaptive and flexible elements to enable optimized use of prior information either before and/or during conduct of the study to seamlessly update the study design. A comparison of the traditional 6 + 2 (active + placebo) subjects per cohort design with alternative, reduced sample size, agile designs was performed by using discrete event simulation. Agile designs were evaluated for specific adverse event models and rates as well as dose-proportional, saturated, and steep-accumulation pharmacokinetic profiles. Alternative, reduced sample size (hereafter referred to as agile) designs are proposed for cases where prior knowledge about pharmacokinetics and/or adverse event relationships are available or appropriately assumed. Additionally, preferred alternatives are proposed for a general case when prior knowledge is limited or unavailable. Within the tested conditions and stated assumptions, some agile designs were found to be as efficient as traditional designs. Thus, simulations demonstrated that the agile design is a robust and feasible approach to FIH clinical trials, with no meaningful loss of relevant information, as it relates to PK and AE assumptions. In some circumstances, applying agile designs may decrease the duration and resources required for Phase I studies, increasing the efficiency of early clinical development. We highlight the value and importance of useful prior information when specifying key assumptions related to safety, tolerability, and PK.

Electronic supplementary material

The online version of this article (doi:10.1208/s12248-009-9141-0) contains supplementary material, which is available to authorized users.

INTRODUCTION

With an increasing emphasis on moving go/no-go decisions to Phase I, innovation in the pharmaceutical industry has resulted in the early development evaluation of an unprecedented number of new molecular entities. This increase in the number of investigational compounds, often for unprecedented mechanisms and targets with low or uncertain probability of success (1), has engendered an increased emphasis on execution in Phase I, notably exploratory INDs and microdosing screening multiple compounds at the same time leading to selection of the one with the highest probability of developmental success (2–4). Recent initiatives have focused on knowledge and information management (5,6) and a better understanding of the probability of success at a portfolio level to make effective decisions regarding advancing these compounds. One particular aspect in the successful implementation of model-based drug development for any particular development candidate is the use of prior information for guiding and executing informed and intelligent clinical designs (7). As the term indicates, a first-in-human (FIH) study in healthy subjects is done to discern the initial safety, tolerability, pharmacokinetics (PK), and pharmacodynamics (PD) of escalating doses of a drug candidate for the very first time in humans (8).

Due to the uncertainty about the risks related with the compound, such studies, either as alternating panel or serial panel designs, are typically conducted in small groups (usually six treated with active treatment and two with placebo) of young adult healthy volunteers and with doses that typically range from one associated with no engagement of the target to one that is normally a maximal tolerated dose, as much as a 1,000-fold dose range. Due to uncertainty in translating animal model findings to humans, particularly for unprecedented mechanisms, a wide dose range is expected to cover the entire exposure–response curve. As a result, the same number of subjects are given doses that are associated with an absence of an effect, with a relevant clinical effect and those that produce no incremental effect over the maximum effect. It is quite interesting in that such a uniform design was already challenged by Sheiner (9,10) and others as to whether they allow for a better characterization of dose/response (11,12).

A modification of the typically used designs includes flexible designs that are based on optimal adaptive design methodology (13–15). Such studies are being increasingly recognized as yielding the best performance characteristics from a modeling and simulation perspective, guided by use of all applicable information prior to the start of the study and adapting to new information gained from initial cohorts of the study to adjust the scope of subsequent cohorts. Informative adaptive designs have been widely used in oncology applications as accelerated development is particularly desired in such disease states.

Because of the importance of exposure–toxicity relationships in oncology, a valuable application of leveraging prior information, for example, from adults to guide starting dose and the escalation regimen in pediatrics, and using dose-limiting toxicity (DLT) has been successfully adopted by many investigators (16–19). A newly proposed rolling six design for reducing the time to complete phase I trials in pediatrics has been recently proposed as an alternative to the conventional oncology 3 + 3 design (20). These investigators have used a discrete event simulation methodology to develop dose escalation/de-escalation and stopping rules based on a priori assumptions of DLT frequencies. Other authors have similarly advocated for the use of optimal adaptive design methodologies to improve the performance characteristics of dose/response studies (21). Maloney et al. have used assumptions related to dose–response models such as linear, log-linear, four-parameter sigmoidal E_max, and exponential models to demonstrate the superior capability of the adaptive designs to "learn" the true dose–response as compared to fixed optimal designs (21). Clearly, emerging evidence from a number of seminal works now support the use of adaptive designs to improve dose–response modeling and dose selection in later phases of development (14,22). Such innovative approaches have several other advantages, including minimizing exposure of the investigational drug or biologic to healthy subjects, better guidance to define effective doses, reducing sample sizes, and provide for a seamless and efficient drug development program.

The Current Designs and the Need for Agile Designs

Merck and other sponsors are already implementing a flexible, while not adaptive, approach to FIH study designs. These studies are typically designed as two-panel, five-period alternating panel rising single dose designs in eight healthy subjects (six active, two placebo), aged 18 to 45 years, with a minimum of 7–10 days washout between periods. They are often combined with sequential, rising multiple-dose designs (23). Such a design provides for valuable within-subject information on variability related to PK or PD. A predefined decision tree for interim analysis provides the flexibility to dose downwards, if needed, based on review of safety, PK or PD prior to dose escalation. These designs provide superior performance characteristics (including smaller overall sample size) as compared to serial panel cohorts.

It is increasingly evident that clinical pharmacology plays an important role in early clinical development by characterizing the safety, tolerability, pharmacokinetics, and pharmacodynamics of a compound, which may provide an early indicator of the viability for continued development for novel investigational compounds. With the rise in the number of investigational agents in the Phase I space, it is also important that resources are efficiently used and information is optimally collected to inform early decision making and use Phase I as a stage-gate at which the continuation of the development process is decided. To effectively address this overarching goal, we need to underscore the elements of speed, nimbleness, and quality of information. Therefore, our goals were, specifically, to evaluate, using stochastic simulations, the performance characteristics of alternative agile FIH study designs as compared to current FIH study design as a reference, in an effort to optimize the study designs, maintain the quality of information gained, and improve the speed and nimbleness of the execution.

When the agile manifest was introduced to the software development field, it presented a more adaptive, value-driven approach. It soon made its way into the software mainstream delivering significant improvements in innovation, quality, productivity, and competitive advantage (24). We propose using the term agile design for clinical trials. It combines features of flexible and adaptive elements to enable optimized use of prior information either before and/or during conduct of the study to seamlessly update the study design. An agile design predefines a relevant dose level or exposure for increased investigation, rapidly escalating through a wider dose range. This relevant dose level can also be subject to additional biopharmaceutics or other evaluation including effect assessment of food or formulation. The agile designs evaluated are consistent with other similar trials including N of 1 trials (7,25,26). When coupled with eIND/eCTA paradigms for accelerated clinical assessments, such agile designs provide an added mechanism to better and quickly understand the viability of new molecular entities.

METHODS

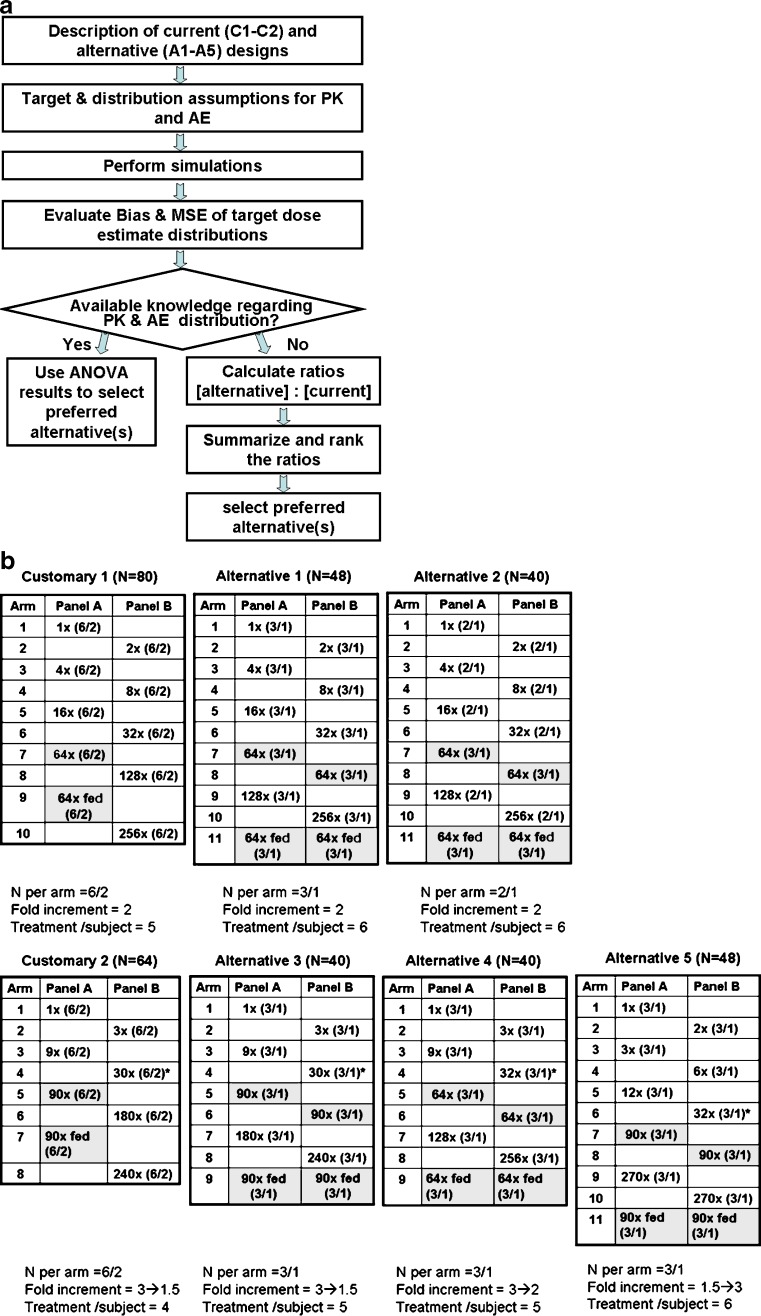
A simulation approach was used to evaluate the performance of several alternate FIH study designs. Simulations were performed using a number of assumptions related to safety, tolerability, PK, and PD data. The flow chart provided in Fig. 1a illustrates the processes roadmap described in this section, from introducing the agile designs to the selection of preferred alternative.

Fig. 1.

Study designs and selection process. a Selection algorithm for agile designs. b Customary and alternative designs evaluated (top row of designs have fixed dose increments while the dose increments in the bottom row change during the trial. Details are provided for each design: top number of total treatments N; tables fold increase is indicated with numbers of subjects in parentheses (drug/placebo), last doses administered prior PK review are indicated by *. Dose of interest is highlighted; bottom number of subjects per arm, fold increments and number of treatments per subject.)

Study Designs

The simulation strategy focused on evaluating designs with crossover alternating panels since it was previously reported to require fewer subjects than a sequential panel design would in FIH studies (27). Specifically, the study designs evaluated were defined as customary (base case with the 6 + 2 design per dose, usually six treated with active treatment and two with placebo; defined as designs C1 and C2) and alternatives alternative agile designs (defined as A1 through A5); these are illustrated in Fig. 1b. Other biopharmaceutics evaluations such as food effect or formulation assessments can also be incorporated. The tested dose range was defined as up to 270-fold, specifically, doses that will produce PK exposures ranging from a mean area under the curve (AUC) = 1 (in arbitrary units) and up to a mean AUC = 270 for dose-proportional kinetics. In all the evaluated designs, one dose level was selected as an expected efficacious dose and six subjects were treated with this dose. A predetermined dose, in the center of the dose range (doses related with a mean AUC of 64 or 90) was used as the expected efficacious dose. In the first occasion, it was given in the fasted state. The second time the dose was given was following consumption of high fat meal toward the end of the study allowing the estimation of the effect of food consumption on the PK of the compound. In this manuscript, the assumed AUCs and adverse event (AE) rates are considered to be the same with and without the consumption of food.

Since doses other than the expected efficacious dose produce exposures that are assumed to be either less effective or higher than required, smaller number of subjects were tested with the alternative designs at these doses (sample size per arm of N = 3/1 or N = 2/1).

Dose escalation schemes included a fixed twofold increment and a modified Fibonacci scheme starting with a threefold increment decreasing as doses escalate to twofold and to 1.3-fold. An alternative with opposite increasing dose increment scheme (from 1.5- to threefold) was also evaluated. Other dose increment schemes were not assessed.

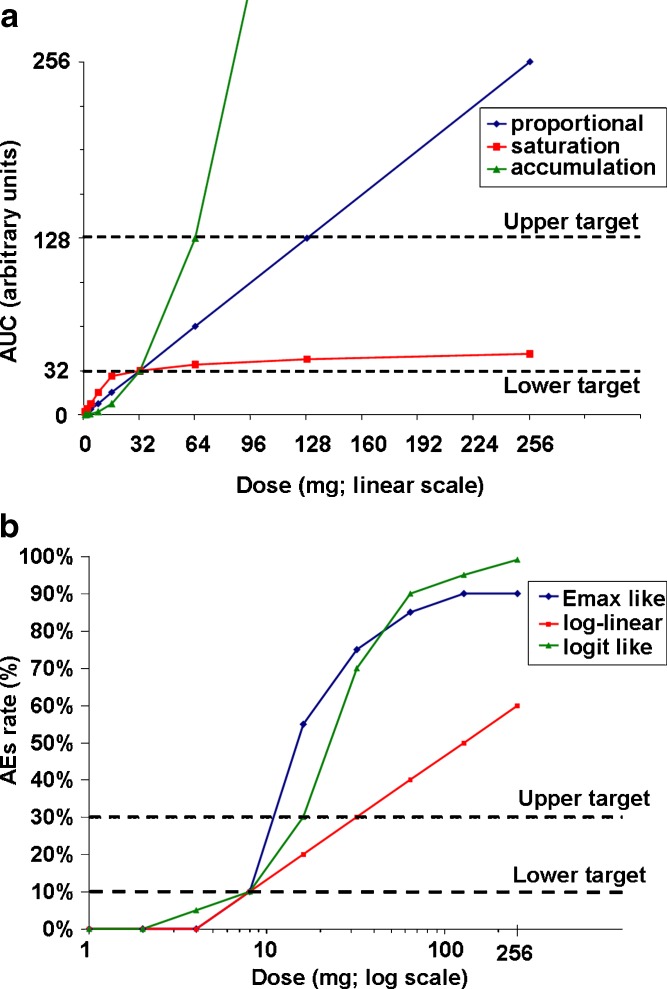
For PK and PD, the tested exposure ranged from AUC = 1 to AUC = 270 (arbitrary units). A dose lower than the expected efficacious dose (associated with AUC = 32) was used as a target dose for minimal expected efficacy and one higher dose (associated with AUC = 128) was used as a target for maximal expected efficacy (Fig. 2a).

Fig. 2.

Underlying PK and AE relationships. a Underlying PK relationships—AUC mean by dose. The maximal predetermined mean exposure is 256 AUC. Dotted lines indicate lower and upper exposure targets (32 AUC and 128 AUC). b Underlying safety and toxicity/dose relationships—probability of AE by dose. Dotted lines indicate true underlying AE rate targets of 10% and 30%

For safety and tolerability, doses associated with AE rates of 10% (representing mild AEs) and 30% (representing moderate AEs) were used (Fig. 2b). These AE values were chosen for pragmatic reasons and could differ from actual scenarios in that the mild and moderate AEs may have unrelated relationships and be different percentages. Additional simulations were carried out to investigate a case where the maximal target doses for AUC rates were reduced to AUC of 64 arbitrary units (instead of an AUC of 128 arbitrary units) representing cases where efficacy is limited by preclinical exposure (efficacious level is close to the preclinical no-effect level).

The effect of one PK pause, meaning the analysis of plasma concentrations of the drug and a pharmacokinetic data review step prior to dose escalation, was assessed on the performance of the evaluated study designs. The purpose of the PK pause is to simulate ability to stop the study if there is possibility of exceeding a maximum drug exposure level based on AUC; such an exposure level would typically be estimated based on animal toxicity studies. The option of not conducting a PK review prior to dose escalation was also investigated in the simulation evaluation.

Key Considerations

We studied three types of true underlying AE relationships and three types of PK relationships. The key assumptions for PK were made as follows. AUC dose–response relationships were constructed as representative of the following true underlying relationships: (1) dose-proportional, (2) a saturation model, and (3) a steep-accumulation model. The assumed minimal efficacious dose of 32× is the true underlying dose with target AUC of 32 arbitrary units in all cases (Fig. 2a). This assumption mimics the situation in which robust human PK predictions are known. CVs of 30% and 50% were used for estimating variability around the mean AUC values. These CVs are intended to encompass all sources of variability: within-subject, between-subject, individual subject AUC calculations, etc. For safety and tolerability, AEs were defined according to the frequency and not according to the severity. Three AE rate dose–response relationships were constructed as examples of potential true underlying relationships consistent with: (1) an E_max model, (2) a log-linear model, and (3) an S-shaped logit-like model (Fig. 2b).

Analysis Methods of Each Simulated Scenario

The data from each simulation were first smoothed using isotonic regression (28). Isotonic regression generates a non-decreasing dose–response curve fit by averaging responses of adjacent doses at which the response of the higher dose is lower than that of the lower dose. This process is applied iteratively until a non-decreasing set of estimated means at each dose is obtained. Then, linear interpolation was used to estimate the dose with response equal to the target.

To simulate a PK review in each simulation, the smoothed AUC data at doses yielding arbitrary values of 16 and 32 were used to extrapolate by a straight line an estimated mean AUC at each higher dose. If the 90% confidence interval, using the pooled within-dose SD, for estimated mean AUC at any of the doses yielding exposures higher than 32 arbitrary units exceeded the expected maximal efficacy target level of 128 arbitrary units, the data for that dose and all higher doses was ignored in estimation of the target doses, as if the simulated study had been terminated at the PK review. The entire set of simulations was also analyzed without any PK pause, that is, based on all the available data generated.

Performance Characteristics for Comparing the Designs

Box-plots were used to display the distribution of target dose estimates for each design and example dose–response curve. To yield an indication of directional closeness of the target dose estimates to the true underlying target, we computed the difference between the estimated target dose and the true underlying value for each simulation. We summarized the median of these differences across all simulations for each design and example dose–response curve as a measure of bias. We used median since the distributions were not necessarily symmetric. To yield an indication of spread of the distribution estimates of target doses across all simulations, the median of the squared bias values was computed. This is referred to as MSE (median squared error). The bias and squared error results from the simulations were each compared among the designs using analysis of variance (ANOVA), with and without the PK pause, for safety/tolerability and PK relationships.

Prior Knowledge

While no clinical information is available regarding compounds reaching FIH study, in some cases, assumptions regarding the clinical pharmacokinetics, safety, and/or tolerability relationships may be made with some level of confidence based on information obtained from other related compounds (prior knowledge). Specifically, such prior knowledge may arise with a more advanced compound(s) with similar physiochemical properties and mechanism of action—for example, an internal "lead" compound(s) if a "backup" compound is being developed or a more advanced competitor in case data was publicly disclosed. In either circumstance, assumptions regarding the clinical data of the new compound will be based on (1) whether the compound is in the same structural class, (2) whether there is some shared similarity in the preclinical finding of the new compound and the lead/competitor; and (3) whether there is reasonable ability to translate animal findings to humans for the lead or the competitor. If these conditions are met, we may assume the new compound may have similar clinical PK and/or safety profiles to the lead/ competitor, until more experience with the compound is gained. Use of this prior knowledge allows for an alternative design to be selected that best matches the specific PK and/or AE distributions.

Computing Details

The agile design simulations and summaries, ANOVA analysis, as well as pre-processing of optimization summary data were conducted using SAS Version 8.2. The final local and global optimizations were carried out in Excel, using the Solver tool. When generating the AE observation per subject per period, the ranbin function in SAS was used with the specified AE rate to generate an AE observation: 0 for no AE, 1 for AE. Likewise, when generating the AUC observation, the rannor function in SAS was used to generate a normally distributed observation with mean 0 and standard deviation 1. The standard normal observation was transformed by adding the appropriate mean and multiplying by the appropriate SD for the case according to the particular study design scenario. Thus, the AE and AUC observations were generated for each period and each subject in the particular design case. For each simulated case, the estimated doses for AE targets were summarized for the PK cases combined; thus, for AE targets, there were 21 cases, each comprised of 3,000 simulations because the PK cases (three PK relationships, each with 1,000 simulations) were combined as they had no bearing on the AE relationships. Similarly, the estimated doses for PK targets were summarized for the AE cases combined (three AE relationships, each with 1,000 simulations); thus, for PK targets, there were 42 cases, each comprised of 3,000 simulations because the AE cases were combined as they had no bearing on the PK relationships. The relationships used for PK and safety/tolerability are illustrated in Fig. 2.

Alternative Selection When Prior Knowledge is Available

Performance assessments were carried out in two multiple-step parts. Firstly, the designs were compared for each distribution. Such a comparison is pragmatic in cases where prior knowledge about the relationships is available (PK, safety, and/or tolerability) either for a backup compound in the presence of an advanced lead compound or if data with a more advanced competitor are available. Bias and MSE were compared across designs using ANOVA of the overall Tukey normalized ranks of the data since the raw data demonstrated substantial departures from the normality assumption. The ANOVA model for the AE simulations contained these factors (levels): design (C1, C2, A1, A2, A3, A4, A5), dose–response curve (E_max-like, linear, logit), and design-by-curve interaction. The ANOVA model for the PK simulations contained these factors (levels): design (C1, C2, A1, A2, A3, A4, A5), dose–response curve (proportional, saturated, steep), CV (30%, 50%), CV-by-design interaction, and design-by-curve interaction. The mean normalized ranks were compared between the designs using the Hochberg multiplicity adjustment method to control the type I error at 0.05 for comparisons among the seven designs for each scenario.

Alternative Selection When No Prior Knowledge is Available

Secondly, preferred alternative designs were selected based on the overall performances for sets of relationships and for the entire group of relationships. Such a comparison may be useful in cases where the mechanism of action is novel and no prior knowledge about the relationships is available. A desired preferred alternative design will outperform any other design for all the distributions. However, due to the large number of tested scenarios, no single design can be declared as preferred for all the distributions. Thus, the authors developed a scoring system to rank the designs. Briefly, the computed ratios of bias and MSE, the two key performance metrics, between the alternative designs and the customary designs (C1 and C2, separately) were first calculated. Ratios below an empiric value of 1.20 were considered acceptable. Estimates that were better than the customary design (<0.8) were assigned a value of +1 and estimates within the range 0.8 to 1.2 were assigned a value of 0. Estimates that were considered unacceptable (>1.2) were assigned a value of −1. Summing the score for each alternative design for sets of relationships and for the entire group of relationships provided a robust ranking method to select the overall preferred designs.

RESULTS

The percent of simulations in which the PK pause resulted in stopping the study due to a predicted AUC having upper 90% confidence limit that is greater than the targeted value was computed. This rule was chosen to simulate a conservative approach to stopping for PK exceeding a predefined target estimated from animal toxicity studies. If the 90% CI for mean AUC is entirely below the target AUC level, then the study would proceed. However, if not, then there would be some non-negligible chance that the mean AUC could be at the target level, and the study could be stopped. When a CV of 30% is assumed, all designs stopped correctly early in over 90% of simulations for the proportional AUC dose–response curve scenario. This was observed for the saturated AUC dose–response curve assumption only for designs C1, C2, A1, and A4 and for the steep curve only for designs C1 and A5; others stopped early from ∼70% to 87% of simulations. When a CV of 50% is assumed, designs C1, C2, and A5 stopped close to 90% of simulations for the proportional curve, and other designs stopped close to 80% of simulations. This was also the case for the saturated curve, except that design A5 stopped closer to 80% of simulations. For the steep curve, design C1 stopped in 69% of simulations, design A5 in 57%, and other designs in 32% to 43% of simulations. With regard to stopping at the PK pause, there is not much lost when using design A1 in comparison to designs C1 and C2 except for steep dose–response curves. Similar results were observed when the upper target for PK is considered as 64 arbitrary units (see Supplementary data).

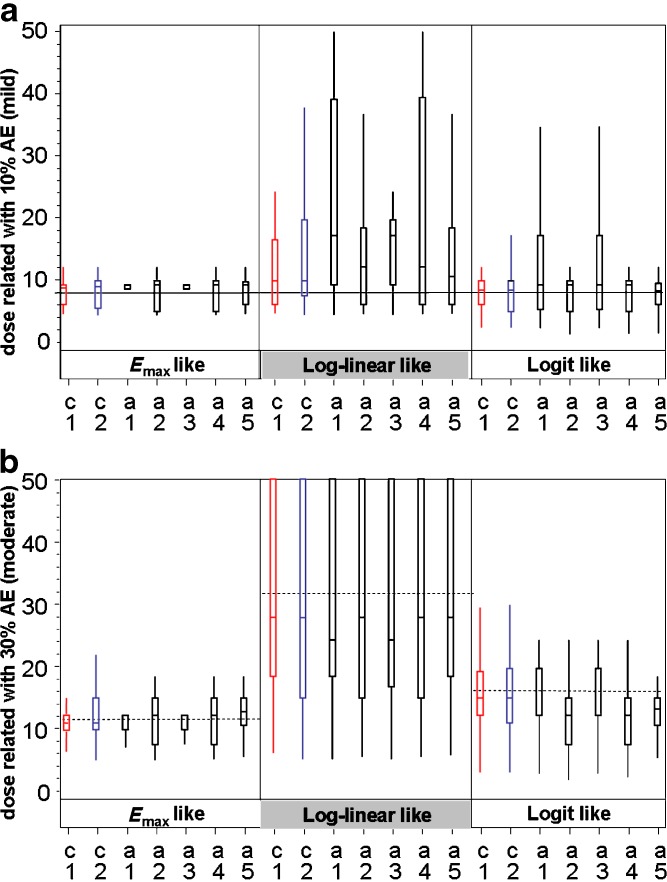
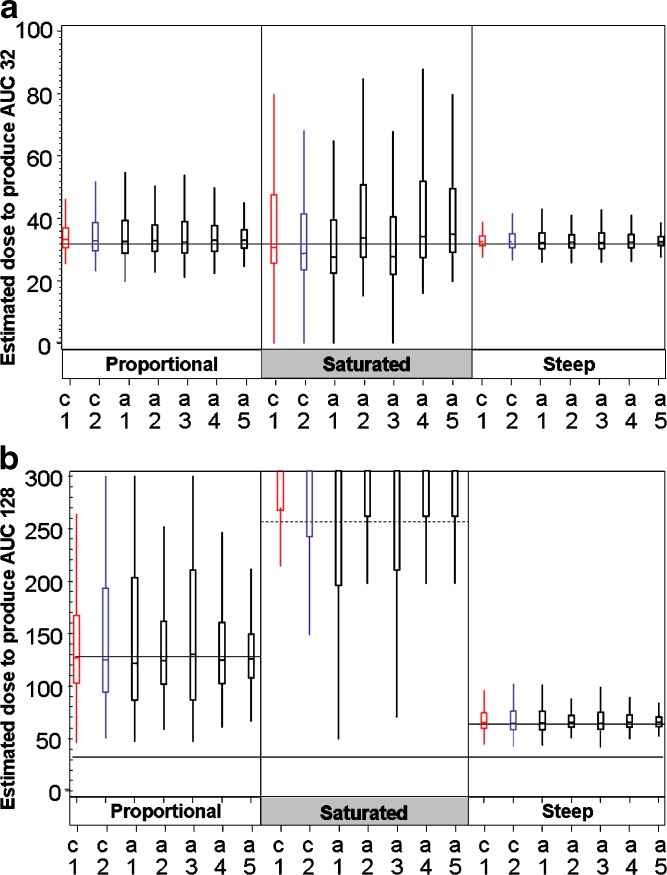
Figures 3 and 4 graphically illustrate (box-plots) representative distributions of target dose estimates. Distributions of estimated doses that are targeted to have 10% (mild) and 30% (moderate) AE rate (case of 30% CV for PK) are presented in Fig. 3a and b, respectively. The distributions corresponding to 50% CV were generally similar, since all parameters were comparable (data not shown). Distributions of estimated doses to yield exposures related to minimal and maximal efficacious doses (corresponding to an AUC of 32 and an AUC of 128 arbitrary units) are presented in Fig. 4a and b, respectively, for the 30% CV case for PK. The distributions corresponding to 50% CV were generally similar, since all parameters were comparable (data not shown).

Fig. 3.

Box-plots describing the distribution of estimated doses for AE relationships. For each of the three AE relationships, seven designs are shown. Each box represents 3,000 simulations of the design + distribution situation. Alternative designs (in black) are compared with the 6/2 customary designs (C1 in red and C2 in blue). a distribution of estimated doses to have 10% (mild) AE rate safety target (case of 30%CV for PK): reference line indicates the correct dose for 10% rate (8×). b Distribution of estimated doses to have 30% (mild) AE rate safety target (case of 30% CV for PK): reference lines (dashed) indicate the correct dose for E _max-like distribution (11.5×) log-linear (32×) and logit-like relationships (16×). Figures of 50% CV are provided in the Supplementary data. Box-plot description: median line is positioned inside the box. Boxes stretch vertically from the 25th to 75th percentiles of the distribution of values. Whiskers stretch from the box to the second and 98th percentile of the distribution of values

Fig. 4.

Box-plots describing the distribution of estimated doses to produce exposure of AUC = 32 and AUC = 128. For each of the three PK distribution seven designs are compared. Each box represents 3,000 simulations of the design + distribution situation. Alternative designs (in black) are compared with the 6/2 customary designs (C1 in red and C2 in blue) a distribution of estimated doses to produce AUC32 (30% CV) b distribution of estimated doses to have exposure of AUC128 for safety target (30% CV): solid reference lines indicate the correct dose-proportional PK (128×) and steep PK (64×) note that for saturated PK estimated doses to produce AUC128 were above the maximal predetermined dose of the study (256×; dashed line)

PK-related estimates were primarily organized by AUC target (assuming arbitrary AUC values of 32 or 128) and CV% (assumed to be either 30 or 50) and secondarily organized by the three AUC relationships and ordinal manner of study design. Similarly, AE-related dose estimates were primarily organized by the AE rate target (assumed as 10% or 30%) and CV% (assumed as 30 or 50) and secondarily organized by the three AE relationships and ordinal manner of study design.

Table I summarizes the ANOVA results for designs at each distribution. These ANOVA results report statistically significant differences between each pair of designs. Such a comparison is useful for cases where prior knowledge of relationship is available for similar compounds if specific relationships are known. Designs are listed in increasing order of mean normalized rank. Statistically significant differences are indicated by "<" meaning that a design with "<" to its right is statistically significantly different from all designs to its right. A design with "∼" to its right is not statistically significantly different from the design immediately to its right. The number of "∼" symbols indicates how many designs to the right are not significantly different from the design at the left of those symbols.

Table I.

ANOVA Results for Comparing Designs at each Distribution (AUC = 128 for Maximal Efficacious Dose)

PK Pause	Target	Distribution	Metric	ANOVA results
Yes	PK	Proportional	Bias	A1<A4∼∼A2∼∼C2∼∼A5∼c3∼C1
			MSE	A5<C1∼∼A4∼A2<C2<A1<A3
		Saturated	Bias	A3∼A1<C2<C1<A4∼A2<A5
			MSE	A5<C1∼A2∼A4<C2<A1∼A3
		Steep	Bias	A1∼∼A3∼c2∼∼∼A2∼∼A4∼c1>A5
			MSE	A5<A2∼A4∼C1<C2∼∼A3∼A1
	Safety and tolerability	E max-like	Bias	C1<C2<A3∼∼A5∼A1<A2∼A4
			MSE	C1<C2∼A3∼A1∼A5<A2∼A4
		Log-Linear	Bias	C2<C1∼A2∼A5<A4<A3<A1
			MSE	C1∼C2<A5<A2<A4<A3<A1
		Logit	Bias	A5<A4∼A2<C1<c2<A1∼A3
			MSE	A5<C1<A2∼∼C2∼A4<A1<A3
No	PK	Proportional	Bias	A1<A2∼A4∼C2<A5∼C1<A3
			MSE	C1∼A5<C2∼∼A2∼∼A4∼A1<A3
		Saturated	Bias	A1<A3∼c2<C1∼∼A4∼A2<A5
			MSE	A4∼∼∼∼∼A2∼∼∼∼A5∼∼∼A1∼∼C2∼C1<A3
		Steep	Bias	A1∼∼A2∼∼A4∼C2∼A5∼C1<A3
			MSE	A5∼C1∼∼A4∼∼∼A2∼∼C2∼A1<A3
	Safety and tolerability	E max-like	Bias	C1<C2<A3∼∼A1∼A5<A2∼A4
			MSE	C1<C2∼∼A3∼A1<A5<A2∼A4
		Log-linear	Bias	C1<A5∼C2<A4∼A2<A1∼A3
			MSE	C1<C2∼A5<A4∼∼A1∼A2<A3
		Logit	Bias	A5<A4∼A2<C1∼C2<A3∼A1
			MSE	A5<C1<A2∼∼A4∼C2<A1∼A3

The designs are listed in increasing order of mean normalized rank. Statistically significant differences are indicated by "<" meaning that a design with "<" to its right is statistically significantly different from all designs to its right. A design with "∼" to its right is not statistically significantly different from the design immediately to its right. The number of "∼" symbols indicates how many designs to the right are not significantly different from the design at the left of those symbols

Table II summarizes the ranking results for selecting overall preferred alternative designs for the base case (maximal efficacious does related to an AUC of 128 arbitrary units with PK review). Ranking results for selecting overall preferred alternative designs for other scenarios (cases with no PK pause and a lower maximal dose target) are provided in the Supplementary data.

Table II.

Selection Process for Overall Preferred Alternative Designs (Base Case: AUC=128 for Maximal Efficacious Dose with PK Review)

Alternative Design	A1	A2	A3	A4	A5
PK and PD distribution (C1 and C2 combined) with PK review [12 cases]
Bias Summed score	2	-1	5	-3	-9
MSE Summed score	-13	3	-14	0	11
Combined Summed scores	-11	2	-9	-3	2
Rank	5	1	4	2	3
Safety and Tolerability distribution (C1 and C2 combined) with PK review [6 cases]
Bias Summed score	-4	-6	-4	-6	-6
MSE Summed score	-6	-8	-6	-8	-2
Combined Summed scores	-10	-14	-10	-14	-8
Rank	2	4	2	3	1
All data with equal weight for PK and Safety/Tolerability (BIAS and MSE)
Summed scores	-31	-26	-29	-31	-14
Rank	3	2	4	5	1

The computed ratios of bias and MSE, the two key performance metrics, between the alternative designs and the customary designs (C1 and C2, separately) were calculated as described in the “Methods” section. Each bias and MSE summed score value represents comparison of two targets at three relationships. The combined bias and MSE summed score was also used for ranking (on 1–5 scale, with one as the best rank). The more positive the combined summed score the better the rank. Cases with summed score value less than −5 may suggest poor estimate thus were also considered in the ranking process. For overall summation and ranking (all data with equal weight), since PK and PD were rated twice (30% CV and 50% CV) the safety & tolerability were assigned equal weight prior to summing and ranking

Estimated Dose with 10% AE Rate in Designs with PK Pause

For the logit AE dose–response model, all designs except A1 and A3 seem to estimate close to the correct value of eight. Designs A1 and A3 seem biased upwards, i.e., >25% of estimates were above 16, i.e., more than twofold above target. For the E_max and linear dose–response models, estimates seemed generally biased upwards, but only slightly so for the E_max distribution. Designs A1 and A3 seem to perform the worst; other designs seem generally similar.

Estimated Dose with 30% AE Rate in Designs with PK Pause

For the E_max-like dose–response model, all designs estimate reasonably close to the correct value (11.5), with designs C1, A1, and A3 similarly best. For the linear dose–response model, all designs estimate with distributions biased low (medians ∼ −4 for all designs except A1 and A3 with medians ∼ −8); all designs yielded highly variable estimates. For the logit model, designs A2, A4, and A5 estimate lower than target in nearly all cases (centered on doses 12 or 13). The other designs perform generally similarly and estimate generally close to and centered on the target. Figure 3a and b provide box-plot illustrations of the distribution of estimated doses for the 10% and 30% AE relationships for the 30% CV case.

Estimated Doses with AUC = 32 and AUC = 128 in Designs with PK Pause

For all dose–response curves, the medians of estimate distributions are close to the respective targets, but the distributions are skewed towards being biased higher than target. The spread in estimates are generally similar for all designs within each type of dose–response curve. The greatest variability was observed for the saturated model, the least for steep model with one exception: for the proportional model with CV = 30, designs C2, A1, and A3 were more variable than the others. Estimates for doses with AUC of 128 arbitrary units were more variable than those for AUC of 32 arbitrary units. Results were substantially more variable for a CV of 50% than for a CV of 30%. Figure 4a and b provide box-plot illustrations of the distribution of estimated doses for the 32 AUC and 128 AUC PK relationships for the 30% CV case.

Estimated Doses with AE Rates 10% and 30% in Designs with No Review of PK Prior to Dose Escalation

Results for the E_max and logit dose–response curves were generally similar to the respective results of those designs with a PK pause, enabling review of the PK data prior to dose escalation which allows for adjusting the prior information. For the linear dose–response curves, designs C1, C2, and A5 did similarly with no PK pause as with the PK pause; however, designs A1 and A4 were less variable with no PK pause than with PK pause, and, curiously, designs A2 and A3 were more variable with no PK pause than with PK pause.

Estimated Doses with AUC = 32 and AUC = 128 in Designs with No PK Pause

For the proportional and steep dose–AUC–response curves, estimates of doses with an AUC value of 32 arbitrary units were generally similarly distributed for all designs when PK pause was not included. As expected, the spread in the distributions were narrower when there was no PK pause than when a PK pause was included. This is likely due to having more data from which to estimate the respective dose targets, enabling adjustment of the prior information. For the saturated dose–response curve, estimates were biased upwards more so when there was no PK pause than with a PK pause. This is likely due to use of simple linear regression, which was employed across all cases since dose-proportionality was assumed. In practice, post-hoc analysis accounting for curvature in PK responses with dose can correct for this behavior.

For all cases, estimated doses with AUC of 128 arbitrary units approximated the target generally well in designs with no PK pause, except for design A3 which was substantially biased upwards for the proportional and steep dose–response curves. Estimates of dose with AUC of 128 arbitrary units were all appropriately out of the dose range for the saturated dose–response curve. The distributions of estimates for cases with no PK pause showed considerably less spread than corresponding cases with a PK pause.

In general, lowering the upper AUC target had no impact on the recommendations cited above for the AUC of 128 (arbitrary units) target cases.

Effect of Changing Upper PK Target from AUC = 128 to AUC = 64 (with PK Pause)

The change in upper PK target had little impact on the distributions of AE target estimates, except that for the linear AE distribution, estimates of AE targets when AUC of 128 arbitrary units were closer to target and much less variable than with the AUC = 64 target. PK AUC estimates of the dose producing an AUC of 32 were generally similar for PK pause targets AUC of 128 and 64. Estimates of doses with a target AUC of 128 were similarly distributed around the respective target as they were for a target AUC of 64. Variability in the estimates for a target AUC of 128 was less than that for a target AUC of 64 for the steep dose–response curve, but similar for the other two dose–response curves.

Effect of Changing Upper PK Target from AUC = 128 to AUC = 64 (with No PK Pause)

Distributions of estimates of AE targets were generally similar when the upper AUC target was 128 as when it was 64. For the proportional and steep dose–response curves, distributions of estimates of dose with AUC = 32 were generally similar when the upper PK target was AUC = 128 as when it was AUC = 64. For the saturated dose–response curve, results were biased higher for AUC = 128 target compared to corresponding cases for AUC = 64 target. This is likely due to the use of simple linear regression, which was employed across all cases since dose-proportionality is usually assumed. Design A4 performed poorly in estimating dose with AUC = 128. Other designs were generally on target for the proportional and steep dose–response curves in estimating doses with AUC = 128.

DISCUSSION

The primary aim of the current investigation was to explore alternatives to standard FIH designs in order to evaluate how information gained from novel agile designs compares to conventional designs. Agile designs are proposed for cases where prior knowledge about pharmacokinetics and/or adverse event relationships is available or appropriately assumed. It is envisaged that agile designs for a FIH study may decrease the duration and resources required for phase I studies, with no meaningful loss of information as it relates to PK and AE. Specifically, we assessed the impact of a sample size reduction from N = 6, typically used in current (customary) FIH study designs, to N = 3 on most active treatments. One thousand subsets of three active treatment observations were sampled from the complete data. In general, when sample size was reduced, the estimates of PK and AE target doses generally were acceptable, where the targets were the values computed via isotonic regression based on the complete data (data not shown). There was some evidence of slight bias, but bias, if any, was small.

In reviewing results across relationships, our hope was that one or two of the alternative designs would emerge as most meaningful design in terms of bias and MSE similar to the conventional designs. This was, however, not the case, as the design with least bias and MSE varied across the scenarios studied. We used a wide variety of dose-response scenarios, each of which was substantially different from the others. In general, the choice of agile alternative design should depend on the likelihood of true underlying distribution and balance between PK and AE objectives for each particular application. However, in an attempt to combine the information from this simulation study across various scenarios, we have also developed a single metric in order to evaluate the overall appropriateness for alternative design to be considered as a replacement for the current designs. In this simulation study, the scenarios tested included commonly encountered situations within the context of a FIH study, namely, a base case with relatively large dose range, a case with no a priori PK review prior to dose escalation, and a case with a lower maximal dose target representing a case where efficacy is limited by preclinical exposure.

We describe two key selection processes. In the first case, prior knowledge is available (or appropriately assumed) regarding the distribution of PK, safety, and/or tolerability, or of both. In cases where data from other similar compounds are available, whether internal lead compounds of the same or similar structural class or external information from competitor drugs or investigational molecules), the ANOVA results (Table I) may assist in the selection of a preferred alternative design by indicating statistically significant differences between distributions of target dose estimates. Furthermore, if the new compound is believed to behave similar to a compound with more advanced clinical experience, the selected alternative design may be verified with the available clinical data from the advanced compound. However, caution should still be exercised because similarity in mechanism of action or structural characteristics will not necessarily produce similarity in the response distribution in question. In the second case, no specific assumptions can be made regarding the different relationships. Such cases are presumably common when evaluating compounds with novel or unprecedented mechanisms of action in FIH studies. In the subsequent sections, we will focus on this latter selection process with an aim of suggesting a general alternative design as a replacement to the current design(s).

Several alternative designs appeared to provide superior performance characteristics, when assumptions for the base case (a maximal efficacious dose associated with an AUC of 128, and PK review) were made. From the perspective of PK target, while A5 design received the highest summed scores (bias and MSE combined), its summed bias score received a value smaller than −5, which may indicate the likelihood of a poor estimate. When the safety and tolerability targets are considered, A5 has the best score followed by designs A1 and A3. When both targets are considered together, design A5 outperformed the rest of the alternative designs with A2 tending to be somewhat better as compared to others. Design A2 may serve as replacement if fixed increments are accepted (ranked #2) and if decreasing increments are desired design, then A3 (decreasing increments) may be considered (ranked #4). In the absence of a PK review, however, all the designs except design A3 performed similarly with preference for design A1. When both PK and AE are considered together, designs A1 and A5 outperformed the rest of the alternative designs with modest preference for design A1.

When assumptions for a narrower dose range are made with maximal target dose associated with an AUC of 64 (instead of 128) and with PK review, design A4 is recommended as the preferred alternative. Considering the AE target alone, both designs A1 and A5 were found to be the preferred designs with equal summed scores. When both PK and AE are considered together, the A5 design outperformed the rest of alternatives with much more accepted cases and summed score. The rest of the designs performed similarly with designs A1 and A4 ranked second and third, respectively.

One could argue that the acceptance of design A5 may be questionable especially in cases where the dose range is narrow, wherein with increasing dose escalation there may be an increased risk of exceeding the pre-specified safety exposure level. It is also assumed that the accuracy of PK estimates in this case is also highly desired therefore the more realistic designs will be design A1 if fixed increments are accepted or design A4 if decreasing increments are desired.

Although the study designs, PK data, and AE data described in this study are all hypothetical, some real data of a completed clinical trial (in a censored fashion) was used as the basis for simulation sampling, with replacement, to support some of the conclusions of our findings (data not shown). The case for reduced sample size designs have been long argued with the continued management of the pipeline, necessitating creative but meaningful ways to improve both the efficiency and the productivity of Phase I development. Such improvements have been argued to have a meaningful impact on pediatric drug development (20,29,30). While their focus has been on oncology and on pediatrics, we believe that agile study designs that are based on sound assumptions would still provide meaningful information on the drug candidate, minimizing human exposure, and in a learn/confirm manner, provide impetus for the design of subsequent hypothesis testing clinical study designs. Our results and approaches are consistent with similar simulation evaluations (31,32). While dose-proportionality is desired for new compounds, several relationships were evaluated in the simulation evaluation due to the high uncertainty in the FIH study regarding PK and AEs. These agile study designs can provide a quick assessment of an early decision point in Phase I to accelerate investigational agents with high probability of successful development and decelerate or terminate ones without.

STUDY LIMITATIONS

Choice of agile design should be based on simulations. To the extent that this set of simulations encompasses potential true underlying situations, this set could be used to substantiate choice of agile design. However, many situations might not be encompassed and would require developing software and simulations, maybe like those described herein, to substantiate choice of agile design. We acknowledge several limitations in the context of simulations performed in this exercise. These are as follows:

1. Only reductions in sample size per arm to N = 3/1 and N = 2/1 from the classical N = 6/2 were studied. Furthermore, these designs considered fixed sample sizes. It is possible that adaptively changing sample size based on interim PK and AE assessments could improve performance characteristics. However, since there are numerous potential adaptation rules and scenarios, it is likely that simulations similar to those in this manuscript would be needed to substantiate particular choices for a given protocol. However, if it could be rationalized that such adaptations would likely improve performance characteristics, then these simulations, as "worst case" scenarios, could support their use. That is, if the performance characteristics without adaptation are adequate, and if those with adaptation are thought to be better, then use of adaptation is supportable.

2. The dose–response curves studied all included the target dose. We did not study situations with target dose outside of the dose range because all designs have high precision based on regression analysis to estimate a flat dose–response curve due to the large number of doses studied.

3. AUC was simulated separately from AE to evaluate the designs for AUC directly and for AE distributions directly. The dose–AUC–AE relationship was not the purpose of the simulation study.

4. Inclusion of additional PK pauses for interim analyses, even after each arm, could improve performance characteristics of the designs but were not specifically evaluated.

5. The effect of biomarkers and pharmacodynamics on the performance metrics of agile designs were not explicitly made since those downstream links would encompass too many potential types of relationships to include in a single simulation exercise. Our assumption here is that in cases with no hysteresis in the PK/PD profile, PK could be used as a surrogate for PD and herein we consider an indirect application. Alternatively, the PK relationships studied could be considered instead as PD dose–response relationships. To better define the role of agile designs for rapid determination of PD and PK/PD relationships, additional work is required.

SUMMARY

We propose, using agile design, which combines features of flexible and adaptive elements to enable the use of prior information either before and/or during conduct of the study, to seamlessly update the study design. Simulations demonstrated that the agile design is a robust and feasible approach to FIH clinical trials, with no meaningful loss of relevant information, as it relates to PK and AE assumptions. In some circumstances, applying agile designs may decrease the duration and resources required for Phase I studies, increasing the efficiency of early clinical development. More investigation is necessary with prospective examples to fully explore the performance characteristics of such agile designs, and whether additional efficiencies are possible in conjunction with adaptive approaches.