Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2009 Nov 5;3(11):3513–3520. doi: 10.1021/nn9010494

Understanding the Electronic Structure of Metal/SAM/Organic−Semiconductor Heterojunctions

Ferdinand Rissner †, Gerold M Rangger †, Oliver T Hofmann †, Anna M Track †, Georg Heimel ‡, Egbert Zojer †,*
PMCID: PMC2782352  PMID: 19891441

Abstract

graphic file with name nn-2009-010494_0001.jpg

Computational modeling is used to describe the mechanisms governing energy level alignment between an organic semiconductor (OSC) and a metal covered by various self-assembled monolayers (SAMs). In particular, we address the question to what extent and under what circumstances SAM-induced work-function modifications lead to an actual change of the barriers for electron and hole injection from the metal into the OSC layer. Depending on the nature of the SAM, we observe clear transitions between Fermi level pinning and vacuum-level alignment regimes. Surprisingly, although in most cases the pinning occurs only when the metal is present, it is not related to charge transfer between the electrode and the organic layer. Instead, charge rearrangements at the interface between the SAM and the OSC are observed, accompanied by a polarization of the SAM.

Keywords: computational modeling, density functional theory, electronic structure/processes/mechanisms, monolayers, organic electronics, molecular electronics, self-assembly, metal/organic interfaces

In organic (opto)electronics, the performance of devices strongly depends on the energy level alignment at interfaces between different functional materials and the electrodes. Deviations from optimum charge carrier injection barriers often imply a significant loss of efficiency.1−3 A method of optimizing the device performance is to introduce self-assembled monolayers (SAMs) between electrodes and organic semiconductors (OSCs). They can be used to adjust the work function Φ of the electrode, and significant steps toward understanding the mechanisms that govern SAM-induced work-function modifications, ΔΦSAM, have been made.4−13 SAMs have also been shown to reduce carrier injection barriers in devices.4,14 However, to what extent and under which conditions ΔΦSAM actually translates into a change of the carrier injection barriers(15) and the crucial question what are the microscopic mechanisms responsible for deviations is not yet really understood. Resolving that matter is the purpose of the present study.

To achieve that we rely on density functional theory (DFT)-based slab-type band structure calculations to obtain an in-depth understanding of the electronic processes in metal/SAM/OSC systems. Depending on the actual magnitude of ΔΦSAM, we observe clear-cut transitions between pinning of the metal Fermi level at the frontier orbitals of the OSC (and thus a SAM-independent carrier injection barrier) and vacuum-level alignment, where ΔΦSAM more or less directly translates into a modification of electron and hole injection properties. Interestingly, in spite of the fact that the presence of the metal is what causes the pinning, it is found to be not related to long-range charge transfer between the metal and the OSC, but rather results from a polarization of the SAM, accompanied by charge transfer between the SAM and the OSC layer. To further elucidate how the presence of the substrate affects the vacuum-level shift and charge rearrangements, we compare the full metal/SAM/OSC system to the SAM/OSC interface in the absence of the metal. Finally, in the appendix, it is discussed to what extent the integer charge transfer (ICT) model16,17 and the unified IDIS (induced density of interface states) model(15) can provide a satisfactory rationale for the properties of the present structures, which is useful as both approaches have been applied to organic/organic interfaces and the ICT model is often used to describe pinning effects.

Results and Discussion

The Systems

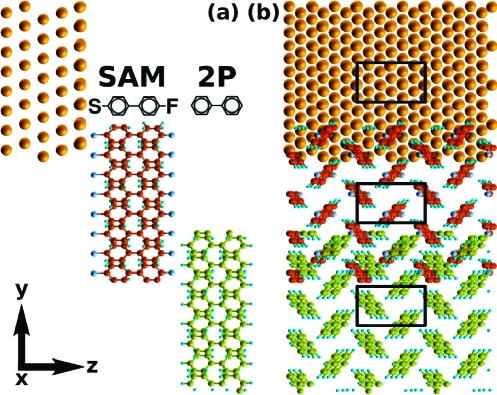
The studied model interfaces consist of a Au(111) surface, a SAM interlayer, and on top of it an additional monolayer of biphenyl, 2P (regarding the choice of the semiconductor compare the discussion in the Methods section). The latter represents a computationally viable model system for the bulk of an OSC. The SAMs, used as “tools” to vary the metal work function are biphenyl derivatives assumed to pack in a herringbone patterned p(3 × √3̅) surface unit cell (1).(18) They are substituted at the two terminal positions (4 and 4′) by a docking group (directed toward the electrode) and a head group (pointed at the OSC). The net change in the metal work function induced by such a SAM, ΔΦSAM, is determined, on the one hand, by the dipole moment and the electron-donating or -withdrawing character of the head group and, on the other hand, by the nature of the docking group and the resulting charge rearrangements at the interface induced by the bonding to the metal.11,19 It has been shown that the net effect of head and docking groups is essentially additive.(20) Independently varying the docking groups and head group substituents, thus, provides a handle for tuning the work function of the metal/SAM system over a wide range.

Figure 1.

Figure 1

Open in a new tab

Side (a) and top (b) view of the representative system Au|S|2P|F∥2P. The two monolayers (S|2P|F and 2P) are shifted for the sake of clarity. The black rectangles mark the p(3 × √3) surface unit cell.

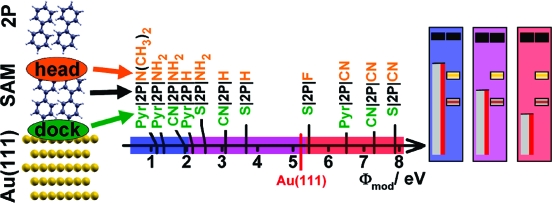
In the following, the systems are denoted as metal|docking group|number of rings|head group∥2P. Here, ∥2P refers to the weakly bound monolayer of 2P on top of the SAM. They include (sorted by ascending ΔΦSAM) Au|Pyr|2P|N(CH3)2∥2P (1), Au|Pyr|2P|NH2∥2P (2), Au|CN|2P|NH2∥2P (3), Au|Pyr|2P|H∥2P (4), Au|S|2P|NH2∥2P (5), Au|CN|2P|H∥2P (6), Au|S|2P|H∥2P (7), Au|S|2P|F∥2P (8), Au|Pyr|2P|CN∥2P (9), Au|CN|2P|CN∥2P (10), and Au|S|2P|CN∥2P (11). The pyridine docking group gives rise to the largest work function decrease, followed by the isocyanide (CN−) and the thiolate (S−).(20) As head groups, we studied the dimethylamine and amine group (−N(CH3)2 and −NH2) as strong donors, hydrogen, the (weak) σ-acceptor −F and the cyano group (−CN) as a strong acceptor.(11) This allowed modifying the Au(111) work function over a huge range with a calculated ΔΦSAM ranging from −4.06 eV (1)(21) to +2.66 eV (11).(22)

A challenge when setting up the model system is to determine the geometry of the SAM∥2P interface. Its structure is primarily determined by van der Waals forces, which are not properly accounted for in DFT calculations based on state-of-the-art functionals such as the chosen PW91. Hence, the relative position of 2P with respect to the SAM had to be set “manually” starting from the experimentally determined bulk structure of 2P.(23) The 2P unit cell is, however, incommensurate with the dimensions of the p(3 × √3) surface unit cell dictated by the periodicity of the SAM. We, therefore, assumed that at least the first monolayer of 2P at the SAM∥2P interface adopts the same unit cell as the SAM with the 2P bulk unit cell stretched in x- and compressed it in y-direction (+0.74/−0.52 Å). The atomic positions within the distorted unit cell were then reoptimized (while fixing the z-coordinates of the lower-most hydrogens to keep the layer flat). This is reasonable, as (i) the distortion of the 2P unit cell leaves its volume virtually unchanged and (ii) the ability of organic thin films to act as templates for the heteroepitaxial growth of other organic layers has been observed experimentally.24,25 The orientation of the substrate molecules was found to be the primary factor determining in organic/organic heteroepitaxial growth.(26) We, therefore, only studied upright standing 2P molecules and did not consider any geometries with 2P lying flat on the SAM. The distance between the SAM and the 2P layer was chosen to avoid overlapping van der Waals spheres, and its influence was carefully tested (for further details, see Methods section).

Level Alignment

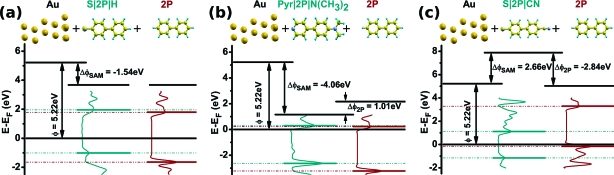
The key question to be addressed here is how the SAM-induced work-function change11,20 affects the actual alignment of the electrode Fermi level relative to the energy levels of the subsequently deposited OSC, that is, the highest occupied and the lowest unoccupied π-states (HOPS/LUPS) of 2P. Three representative examples are shown in 2, where the Fermi energy (determined de facto by the metal) and the densities of states projected onto the SAM and the 2P regions are shown. HOPS and LUPS energies (EHOPS and ELUPS) are determined from the maxima of the corresponding peaks. The top horizontal lines in 2 denote the calculated vacuum-level energies above the respective surfaces (metal, metal|SAM, and complete system).

Figure 2.

Figure 2

Open in a new tab

Energy level schemes for three selected systems. The systems’ Fermi level is shown together with the density of states projected onto the SAM and 2P atoms (cyan and red curves); the HOPS and LUPS are drawn as horizontal lines. The work-function Φ of gold and the work-function changes due to the SAM adsorption, ΔΦSAM, and the inclusion of the 2P layer, ΔΦ2P, are also shown (when present). Vacuum-level alignment between the SAM and the OSC applies to system 7 (a). The Fermi level is pinned at the LUPS of 2P in system 1 (b) and at the HOPS of 2P in system 11 (c).

The system containing the biphenyl thiolate SAM (7) shown in 2 is an example for vacuum-level alignment at the SAM∥2P interface. The work function of gold is decreased by ΔΦSAM = −1.54 eV due to adsorption of the biphenylthiol SAM, and the addition of a monolayer of 2P on top of the SAM has no further effect on Φ. Here, the energetic distances of the Fermi level EF to the HOPS and LUPS of 2P, EF−E2PHOPS and E2PLUPS− EF, which can be taken as measures for the hole and electron injection barriers, are directly controlled by ΔΦSAM.

The situation changes dramatically for metal electrodes covered by SAMs that induce particularly large work-function increases/decreases. If ΔΦSAM became negative (positive) enough, the LUPS (HOPS) of 2P would be shifted below (above) the Fermi level for vacuum-level alignment. In thermodynamic equilibrium, this is not possible. Instead, the Fermi level gets pinned close to the LUPS (HOPS) of the 2P layer (2). The consequence of this is a work function modification ΔΦ2P that counteracts ΔΦSAM. For the systems investigated here, pinning16,27,28 of EF close to the LUPS is seen in 1−3 and pinning close to the HOPS in systems 8−11. The level diagrams for the case with the largest positive and negative ΔΦ2P, systems 1 and 11, are shown in 2, respectively.

The level alignments for all investigated SAM interlayers are summarized in 3 as a function of the work function of the SAM-covered Au(111) electrode, Φmod. The energetic difference between the Fermi level (characterizing the energy up to which the states in the metal are filled) and the 2P HOPS (EF−E2PHOPS, cyan diamonds) and 2P LUPS (E2PLUPS− EF, red circles) peaks is a measure for the electron and hole injection barriers. We find that the level alignments can be organized in three regimes: Fermi level pinning close to the LUPS of 2P, vacuum-level alignment (i.e., the Schottky−Mott limit), and pinning close to the HOPS. Consequently, the SAM-induced work-function modification directly controls the charge carrier injection barriers only for a limited number of systems (4−7). In the other cases, the positions of the 2P states are almost independent of ΔΦSAM. The three regimes can also be distinguished on the basis of the slope parameter S:10,27,29,30

graphic file with name nn-2009-010494_m001.jpg

A value of S close to 1 is found when the vacuum levels align, and S ≈ 0 when EF is pinned close to the HOPS or LUPS of the 2P layer.

Figure 3.

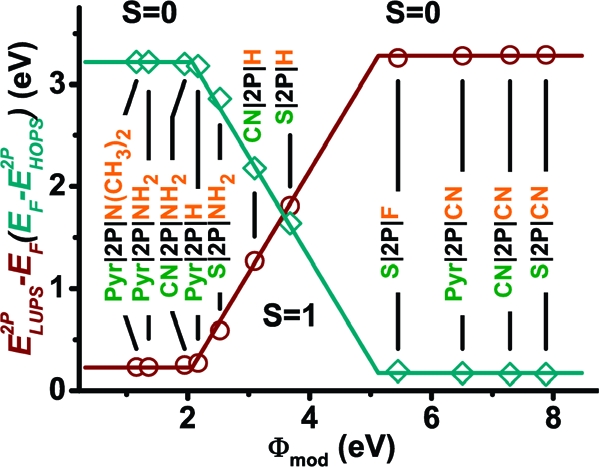
Figure 3

Open in a new tab

E2PLUPS− EF (red circles) and EF−E2PHOPS (cyan diamonds) as a function of the work function of the SAM covered Au(111) electrode, Φmod. For the definition of the slope parameter S, see text. The values of E2PLUPS and E2PHOPS correspond to the peak positions in the respective molecular DOS. E2PLUPS−EF and EF−E2PHOPS are measures for the electron and hole injection barriers. The lines serve as guides to the eye.

Organic−organic Interface

In the absence of the metal, a completely different situation is encountered. In that case, pinning can occur only at the organic/organic interface to prevent the HOMO-derived band of one of the organic layers from lying above the LUMO-derived band of the other organic material. As examples, in 4, the situations for 2P on Pyr|2P|N(CH3)2 and HS|2P|CN are shown. In both cases, pinning of the Fermi level close to the LUPS and HOPS occurred in the full system (see 2 and 3). In the absence of the metal, however, there is vacuum-level alignment at the Pyr|2P|N(CH3)2∥2P interface, while pinning still occurs for HS|2P|CN∥2P. Nevertheless, also in the latter case, the level alignment at the organic/organic interface is markedly different from the situation encountered when the metal is present; that is, ΔΦ2P is reduced from −2.84 to −1.39 eV (cf.2 and 4).

Figure 4.

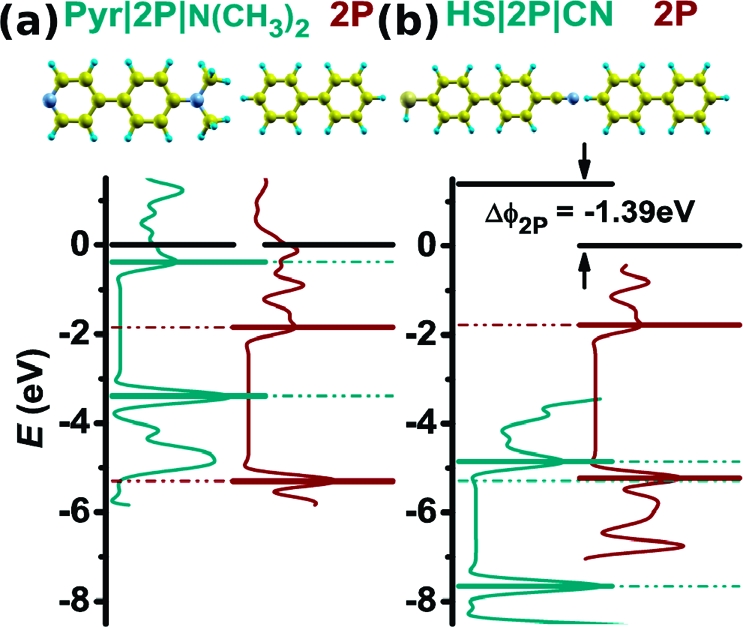
Figure 4

Open in a new tab

Energy level schemes for the organic/organic interfaces Pyr|2P|N(CH3)2∥2P (a) and HS|2P|CN∥2P (b) in the absence of the substrate metal. The density of states projected onto the SAM and 2P atoms is shown around the band gap (cyan and red curves); the HOPS and LUPS are drawn as horizontal lines. The black horizontal lines show the vacuum levels at the substituent side of the SAM before 2P deposition (left part of each plot) and at the 2P side in the SAM∥OSC system (right part). The latter is set as the origin of the energy axis. ΔΦ2P denotes the step in the electron electrostatic potential due to contact between the layers in analogy to the work-function changes in 2.

A summary of the situation for all investigated systems is given in 5. There, the changes in the work function due to the presence of the OSC layer for the situations with and without metal substrate are compared. When the metal is present, ΔΦ2P≈ 0 eV only for systems 4−7, consistent with the vacuum-level alignment for these three systems shown in 3; for 1−3 and 8−11, a linear dependence of ΔΦ2P on Φmod with a slope of approximately −1 is observed as expected for Fermi level pinning. In contrast, for the mere organic/organic interface, a significant deviation from vacuum-level alignment (ΔΦ2P ≈ 0 eV) is observed only for the three −CN substituted systems. There, if ΔΦ2P were also vanishingly small, the particularly large ionization potential on the −CN side of the SAM(11) would result in the HOPS of the 2P layer above the LUPS of the SAM inconsistent with thermodynamic equilibrium. The magnitude of ΔΦ2P in all three cases is independent of the docking group, in sharp contrast to the situation when the metal is present. This can be well understood by the fact that in the free-standing film only the head group modifies the ionization potential of the SAM on the side of the SAM where the OSC layer is deposited, which is the determining quantity for level alignment in that situation. The docking group impacts only the potential landscape at that respective side of the SAM(20) and, thus, has no impact on the level alignment between the SAM and the OSC (cf. the extensive discussion of SAM electrostatics in ref (19)).

Figure 5.

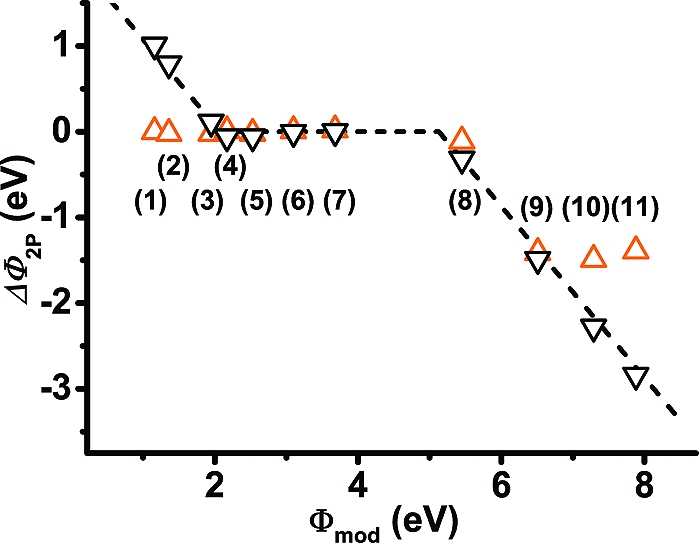
Figure 5

Open in a new tab

Vacuum-level shift at the SAM∥2P interface, ΔΦ2P, as a function of the work function of the SAM-modified gold surface, Φmod. The downward triangles denote the situation for the three-component systems consisting of metal, SAM, and the organic semiconductor; the upward triangles represent the case when removing the metal (keeping Φmod unchanged). The dashed straight lines (with slopes of −1 and 0) serve as guides to the eye.

Charge Rearrangements

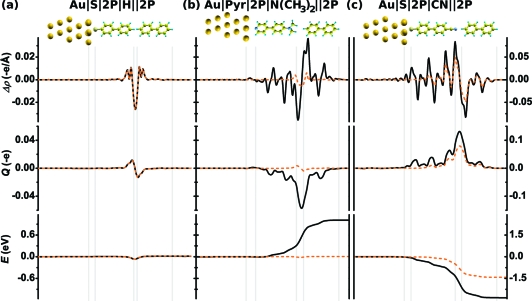
As the investigated systems including the metal substrate cover both vacuum-level alignment (ΔΦ2P ≈ 0 eV) as well as different degrees of Fermi level pinning (ΔΦ2P ≠ 0 eV), they allow a detailed analysis of the processes which lead to a nonvanishing ΔΦ2P in the latter case. The work-function modification ΔΦ2P is connected via the Poisson equation to a change in the charge density upon addition of 2P (Δρ = ρmetal|SAM∥2P− (ρmetal|SAM+ ρ2P); cf.Methods section).(11) As long as the charge transfer to/from the 2P layer remains small enough so that its eigenstates are not significantly modified, Δρ also directly affects the carrier injection barriers.(20)

For system 7, which represents the vacuum-level alignment regime (S = 1), the charge rearrangements (integrated over the x,y plane of the unit cell) are depicted as solid lines in the uppermost panel of 6. Reminiscent of Pauli repulsion at metal/organic contacts, electron density is pushed back from the interface into the two monolayers in a close to symmetric way. The net charge transfer across the SAM∥2P interface can be obtained by integrating over Δρ(z). The quantity Q(z) = ∫z0Δρ(z′)dz′ describes the total amount of charge per unit cell which is shifted from above to below a plane at position z (see middle panel of 6). The fact that Q = 0 right at the interface between the SAM and 2P for system 7 means that there is no net charge transfer between the two layers. Consistently, the electrostatic energy E(z) obtained from solving the one-dimensional Poisson equation shows a small dip directly at the interface, but then virtually recovers its original value (6, bottom panel). The situation changes slightly for substituted SAMs: there, the interface becomes “asymmetric”, that is, there is a nonvanishing charge transfer between the head group and the neighboring part of the biphenyl layer. The consequence of this effect on the electron potential energy, E, however, remains <0.2 eV in the “vacuum-level alignment” regime.

Figure 6.

Figure 6

Open in a new tab

Plane-integrated charge rearrangements, Δρ, per unit cell (topmost panels), cumulative charge transfer along the z-axis per unit cell, Q (middle panels), and change in the potential energy of an electron, E, upon addition of 2P to the system (bottom panels) for systems 7 (a), 1 (b), and 11 (c); Δρ > 0 indicates an increase of the electron density, and Δρ < 0 a decrease. Black lines show the results for the addition of 2P to a metal|SAM systems, dashed orange lines for the pure SAM∥2P interfaces. The y-scales in (c) differ by a factor of 2.5 from the respective scales in (a) and (b). Vertical lines and schematic pictures of the systems in the background serve as guides to the eye.

In contrast, in the pinning cases, the significant values of ΔΦ2P must be caused by some charge transfer. Intuitively, one might expect that this charge transfer should be between the OSC layer and the metal, as it prevents the occupied (unoccupied) states of the 2P layer from lying above (below) the metal Fermi level in thermodynamic equilibrium. Bearing in mind the large charge transfer distance, the absolute magnitude of the transferred charge could be comparably small to yield the necessary shift of the levels. The dominant role of the metal for the Fermi level pinning is also underlined by the observation that the pinning situation described above is observed only as long as the metal is present. Indeed, in a purely inorganic system, namely, for small Au islands separated from a Ag(001) surface by an insulating MgO layer, Simic-Milosevic et al.(31) found that electrons were transferred from the Ag/MgO interface region onto the Au islands.

Considering all that, it comes as a surprise that nothing like a metal to OSC charge transfer is observed in any of the investigated systems (cf. solid lines in 6): The situation for the HOPS pinning case with the largest ΔΦ2P (Au|S|2P|CN∥2P; system 11) is depicted in the uppermost panel of 4. There is no long-range charge transfer between 2P and the Au substrate. Instead, two other effects give rise to ΔΦ2P: (i) Significant electron transfer occurs in the SAM∥2P interface region from the 2P layer to the SAM as evidenced by pronounced peaks in Δρ and Q, which result in a sharp drop in the electrostatic energy E. (ii) Additionally, the SAM is polarized; that is, charge is redistributed within the SAM giving rise to a series of dipoles (see Δρ plot). The long-range transfer within the SAM remains relatively small as seen in the plot of Q. As a net effect, the potential energy drops by −2.84 eV, preventing the 2P HOPS from lying above EF (compare 2). The overall situation for LUPS pinning in Au|Pyr|2P|N(CH3)2∥2P (system 1) is depicted in 6. The main qualitative difference to HOPS pinning is a reversal of the sign of the charge rearrangements, which is consistent with a reversal of the sign of ΔΦ2P. The notion that the observed charge rearrangements are characteristic of Fermi level pinning for OSCs on SAM-covered metals rather than a mere consequence of some type of surface reaction between the head groups of the SAM and the 2P layer is supported (i) by the fact that a qualitatively similar behavior is observed in all studied pinning cases and (ii) by the observation that Δρ extends over the whole SAM instead of just across the interfacial region.

As far as the metal-free systems are concerned (dashed lines in 6), there is no difference to the full system for 7. As expected, also in 1 nothing but Pauli pushback in the immediate vicinity of the interface is observed (here in sharp contrast to the situation when the metal is present). For the situation where pinning occurs also at the organic/organic interface (shown here for 11), the structure of the charge rearrangements in the region of the SAM∥2P interface is similar to the situation observed when the metal is present (albeit with a smaller magnitude of Δρ). The charge rearrangements on the phenyl ring next to the metal substrate, however, vanish in the purely organic/organic case; that is, the role of SAM polarization diminishes in the metal-free case.

In conclusion, inserting a SAM allows controlling the energy level alignment between an electrode and an organic semiconductor over a certain range in which vacuum-level alignment occurs between the SAM and the OSC. Beyond that range, which is determined by the energy gap of the OSC, Fermi level pinning close to the OSC states is observed and an additional work-function change ΔΦ2P counteracts the SAM-induced work-function modification. The pinning situation changes completely in the absence of the metal. Nevertheless, in spite of the fact that the pinning and the magnitude of ΔΦ2P are a clear consequence of the presence of the metal substrate, they are not related to any (long-range) charge transfer between the metal and the OSC. Instead, pinning is found to be a consequence of SAM backbone polarization in addition to local charge transfer at the organic−organic interface.

Methods

The density functional theory calculations were performed using the VASP code.(39) Valence electrons were described by a plane wave basis set (kinetic energy cutoff approx. 20 Ry) and valence-core electron interactions by the projector augmented wave (PAW) method.(40) A 5 × 8 × 1 Monkhorst−Pack(41)k-point grid was chosen. A Methfessel−Paxton(42) occupation scheme with a broadening of 0.2 eV was used. In one case, CN|2P|H∥2P, the smearing was reduced to 0.05 eV to prevent artifacts due to negative occupancies near EF. Geometry relaxations were stopped as soon as all forces fell below 0.01 eV/Å. For electronic relaxations, two separate convergence criteria were applied: a stable dipole moment (tolerance: Δμz < ± 0.002 eÅ) over several self-consistent cycles, and a total energy ΔE < 1.10−4 eV. The metal was resembled by five layers of Au(111) atoms. During geometry relaxations, the coordinates of the lower three layers were fixed (representing the bulk), while the upper two layers (representing the surface) were free to move. The pure organic/organic systems differ from the complete systems only by the removal of the metal atoms. No additional geometry optimizations were performed. Only in case of the thiolate docking group, a saturating hydrogen was added to the sulfur. The charge density differences Δρ were obtained by subtraction of the densities of the isolated parts of a system from the density of the corresponding system, that is, Δρ = ρmetal|SAM∥2P − (ρmetal|SAM + ρ2P) and Δρ = ρSAM∥2P − (ρSAM + ρ2P) for the full systems and the pure organic/organic interfaces, respectively. The one-dimensional plots were then generated by integration over the x,y plane of the unit cell, hence displaying the charge rearrangements per unit cell. Further details regarding the applied computational methodology and the used parameters are given in ref (12). Three-dimensional representaions of the systems were generated using XCrysDen.(43)

It should be noted that DFT calculations are known to notoriously underestimate the band gap of semiconductors (most relevant here for the 2P layer). An improved description could, for example, be achieved within the GW approximation.(44) Also, the band gap reduction in the vicinity of a metal as observed in three-terminal single-molecule devices(45) reminiscent of the Newns−Andersen model46,47 could be accounted for in this way.(44) GW calculations for the present systems are, however, far beyond computational capacities. As our work is concerned with conceptual effects at metal/SAM/OSC interfaces, this poses no major problem. Moreover, focusing on the relative positions of energy levels, the following fundamental conclusions can be expected to hold largely independent of the chosen conjugated system. In fact, the “1/n law” that the band gap of oligophenylenes decreases with increasing number n of phenyl rings renders DFT-calculated 2P de facto a suitable model for some longer chain oligomers.

When putting the 2P layer on top of the SAM, the strategy described in the Results and Discussion section was pursued. In particular, the distance between the SAM and the 2P layer was chosen to avoid overlapping van der Waals spheres. The used geometries are supplied in Supporting Information. We also carefully tested the dependence of the results on the variation of the distance between the SAM and 2P (Δz = ±0.3 Å) and on their relative in-plane alignment. The maximum changes in energy level alignments due to both kinds of variation were <0.05 eV for all SAM head groups. Also, as far as the charge rearrangements and related quantities were concerned, the qualitative picture remained unchanged and also quantitative deviations were minor.

Acknowledgments

Support by the European Commission through the STREP project ICONTROL (EC-STREP-033197) and by the FWF through project P20972-N20 is gratefully acknowledged. We thank the ZID of the TU Graz for providing computational resources. G.H. acknowledges financial support by the DFG through Sfb448 “Mesoscopically Organized Composites”.

Appendix

In this section, the above-described results shall be discussed in the context of the ICT (integer charge transfer)17,27,28,32−35 and IDIS (induced density of interface states)17,36−38 models. This is useful as (i) both models have been used to explain the properties of organic/organic interfaces also including the influence of a metal substrate,15,16 and (ii) in particular the ICT approach has been used to successfully rationalize Fermi level pinning.17,35

Within the IDIS model, a notable perturbation of the molecular DOS is assumed when a molecule approaches a surface, even if the interaction between the two materials can be regarded as weak.(37) This modified DOS can be determined,(37) and by filling it with the charge of the isolated, neutral molecule, the charge neutrality level (CNL) is obtained. The position of the CNL is found to be quite insensitive to the interaction strength between the organic and the metal36−38 and can hence be treated as an intrinsic property of the organic. If an organic heterojunction is in contact with a substrate, the unified IDIS model predicts the vacuum-level shift to be

graphic file with name nn-2009-010494_m002.jpg

where ECNL is the charge neutrality level of the topmost organic layer (in our case 2P), Φmod is the Fermi energy of the SAM-covered substrate (cf. Fig. 5) and SOO is a screening parameter depending only on the two organic materials.(15) The problem that arises when applying this model to the full set of systems that we investigated here is that, as ECNL is regarded as an intrinsic property of the OSC, the screening parameter has to be one in the vacuum-level alignment regime (systems 4−7) and then needs to change abruptly to zero when pinning occurs. Even if this were the case, pinning at the HOPS would be observed only if ECNL were equivalent to the HOPS energy (8−11), while it needed to correspond to the LUPS for 1−3. In that case, ECNL can no longer be a materials parameter of the OSC in contradiction to the original assumption of the IDIS model. For a CNL within the gap, SOO would effectively have to be a function of Φmod in order to predict the results depicted in Fig. 5, and hence would not only be determined by the two organic materials.

In contrast to the IDIS model, the ICT approach assumes that no significant hybridization occurs between the states at the interface.16,17,32,35 This appears reasonable, as the model is typically applied to systems, where the OSC in question is separated from the conducting substrate by an insulating layer or another relatively thick OSC layer. A consequence of this lack of hybridization is that only an integer number of charges can be transferred between the conducting substrate and the organic layer. The slope parameter, S, becoming zero for certain substrate work functions as observed also in 3(16) is then associated with charge transfer to polaronic or bipolaronic levels of the OSC (the ICT states) together with a pinning of the Fermi level at these states. The ICT states are often found deep within the gap of the organic semiconductor, in particular, when dealing with amorphous materials or systems disordered at least at the interface. In such materials, charges are highly localized. The situation changes in highly crystalline and well-ordered substances with delocalized charges, where the pinning levels approach the original positions of the bands of the molecular crystals.17,35 Intrinsically, only the latter case can be the outcome of a band structure calculation (unless inaccessibly large super cells were used). Considering these aspects, the results of the ICT model well match the outcomes of our study. Here, it needs to be mentioned that, in our calculations, the actual pinning position is influenced by the applied smearing of the electronic occupations which amounts 0.2 eV in the presented data.

Supporting Information Available

Cartesian coordinates of the three-component systems. This material is available free of charge via the Internet at http://pubs.acs.org.

Funding Statement

National Institutes of Health, United States

Supplementary Material

nn9010494_si_001.pdf (91.6KB, pdf)

References

  1. Baldo M. A.; Forrest S. R. Interface-Limited Injection in Amorphous Organic Semiconductors. Phys. Rev. B 2001, 64, 085201. [Google Scholar]
  2. Parker I. D. Carrier Tunneling and Device Characteristics in Polymer Light-Emitting Diodes. J. Appl. Phys. 1994, 75, 1656–1666. [Google Scholar]
  3. van Woudenbergh T.; Blom P. W. M.; Huiberts J. N. Electro-optical Properties of a Polymer Light-Emitting Diode with an Injection-Limited Hole Contact. Appl. Phys. Lett. 2003, 82, 985–987. [Google Scholar]
  4. Campbell I. H.; Kress J. D.; Martin R. L.; Smith D. L.; Barashkov N. N.; Ferraris J. P. Controlling Charge Injection in Organic Electronic Devices Using Self-Assembled Monolayers. Appl. Phys. Lett. 1997, 71, 3528–3530. [Google Scholar]
  5. Bruner E. L.; Koch N.; Span A. R.; Bernasek S. L.; Kahn A.; Schwartz J. Controlling the Work Function of Indium Tin Oxide: Differentiating Dipolar from Local Surface Effects. J. Am. Chem. Soc. 2002, 124, 3192–3193. [DOI] [PubMed] [Google Scholar]
  6. Bock C.; Pham D. V.; Kunze U.; Käfer D.; Witte G.; Woll C. Improved Morphology and Charge Carrier Injection in Pentacene Field-Effect Transistors with Thiol-Treated Electrodes. J. Appl. Phys. 2006, 100, 114517-7. [Google Scholar]
  7. Yan H.; Huang Q. L.; Cui J.; Veinot J. G. C.; Kern M. M.; Marks T. J. High-Brightness Blue Light-Emitting Polymer Diodes via Anode Modification Using a Self-Assembled Monolayer. Adv. Mater. 2003, 15, 835–838. [Google Scholar]
  8. Asadi K.; Gholamrezaie F.; Smits E.; Blom P. W. M.; de Boer B. Manipulation of Charge Carrier Injection into Organic Field-Effect Transistors by Self-Assembled Monolayers of Alkanethiols. J. Mater. Chem. 2007, 17, 1947–1953. [Google Scholar]
  9. Ishii H.; Sugiyama K.; Ito E.; Seki K. Energy Level Alignment and Interfacial Electronic Structures at Organic/Metal and Organic/Organic Interfaces. Adv. Mater. 1999, 11, 605–625. [Google Scholar]
  10. Koch N. Organic Electronic Devices and Their Functional Interfaces. ChemPhysChem 2007, 8, 1438–1455. [DOI] [PubMed] [Google Scholar]
  11. Heimel G.; Romaner L.; Bredas J. L.; Zojer E. Interface Energetics and Level Alignment at Covalent Metal−Molecule Junctions: π-Conjugated Thiols on Gold. Phys. Rev. Lett. 2006, 96, 196806. [DOI] [PubMed] [Google Scholar]
  12. Heimel G.; Romaner L.; Bredas J. L.; Zojer E. Organic/Metal Interfaces in Self-Assembled Monolayers of Conjugated Thiols: A First-Principles Benchmark Study. Surf. Sci. 2006, 600, 4548–4562. [Google Scholar]
  13. Sushko M. L.; Shluger A. L. Intramolecular Dipole Coupling and Depolarization in Self-Assembled Monolayers. Adv. Funct. Mater. 2008, 18, 2228–2236. [Google Scholar]
  14. de Boer B.; Hadipour A.; Mandoc M. M.; van Woudenbergh T.; Blom P. W. M. Tuning of Metal Work Functions with Self-Assembled Monolayers. Adv. Mater. 2005, 17, 621–625. [Google Scholar]
  15. Betti M. G.; Kanjilal A.; Mariani C.; Vázquez H.; Dappe Y. J.; Ortega J.; Flores F. Barrier Formation at Organic Interfaces in a Cu(100)−Benzenethiolate−Pentacene Heterostructure. Phys. Rev. Lett. 2008, 100, 027601-4. [DOI] [PubMed] [Google Scholar]
  16. Braun S.; de Jong M. P.; Osikowicz W.; Salaneck W. R. Influence of the Electrode Work Function on the Energy Level Alignment at Organic−Organic Interfaces. Appl. Phys. Lett. 2007, 91, 202108-3. [Google Scholar]
  17. Braun S.; Salaneck W. R.; Fahlman M. Energy-Level Alignment at Organic/Metal and Organic/Organic Interfaces. Adv. Mater. 2009, 21, 1450–1472. [Google Scholar]
  18. Azzam W.; Fuxen C.; Birkner A.; Rong H. T.; Buck M.; Woll C. Coexistence of Different Structural Phases in Thioaromatic Monolayers on Au(111). Langmuir 2003, 19, 4958–4968. [Google Scholar]
  19. Heimel G.; Romaner L.; Zojer E.; Bredas J.-L. The Interface Energetics of Self-Assembled Monolayers on Metals. Acc. Chem. Res. 2008, 41, 721–729. [DOI] [PubMed] [Google Scholar]
  20. Heimel G.; Romaner L.; Zojer E.; Bredas J. L. Toward Control of the Metal−Organic Interfacial Electronic Structure in Molecular Electronics: A First-Principles Study on Self-Assembled Monolayers of -Conjugated Molecules on Noble Metals. Nano Lett. 2007, 7, 932. [DOI] [PubMed] [Google Scholar]
  21. The analysis of the charge rearrangements resulting from the bond formation between systems 1 and 2 and the Au(111) surface (calculations performed in analogy, for example, to ref 11) displays certain features related to electron accumulation, which are located clearly above the head groups. Their origin is not yet fully understood, but intensive tests have shown that they do not depend on the input parameters of the band structure calculations. A consequence of these features is that the obtained work function modifications of −4.06 and −3.86 eV for 1 and 2 have to be regarded as a lower limit to the actual values. Moreover, the charge rearrangements at the SAM∥2P interface are qualitatively consistent with the situations observed for all other SAMs. Consequently, we are confident that these issues bear no relevance for the conclusions drawn in the current paper.
  22. These numbers represent fully self-consistent calculations; i.e., effects like the mutual depolarization of neighboring molecules are fully taken into account. Moreover, in the computer experiments, SAM formation does not constitute a problem. In the real world, however, one can expect dipole−dipole repulsion to provide a significant experimental challenge for SAM formation especially for the systems implying the extreme values of ΔΦSAM.
  23. Charbonneau G. P.; Delugeard Y. Biphenyl: Three-Dimensional Data and New Refinement at 293 K. Acta Crystallogr., Sect. B 1977, 33, 1586–1588. [Google Scholar]
  24. Koller G.; Berkebile S.; Krenn J. R.; Netzer F. P.; Oehzelt M.; Haber T.; Resel R.; Ramsey M. G. Heteroepitaxy of Organic−Organic Nanostructures. Nano Lett. 2006, 6, 1207–1212. [DOI] [PubMed] [Google Scholar]
  25. Käfer D.; Ruppel L.; Witte G. Growth of Pentacene on Clean and Modified Gold Surfaces. Phys. Rev. B 2007, 75, 085309-14. [Google Scholar]
  26. Oehzelt M.; Koller G.; Ivanco J.; Berkebile S.; Haber T.; Resel R.; Netzer F. P.; Ramsey M. G. Organic Heteroepitaxy: p-Sexiphenyl on Uniaxially Oriented α-Sexithiophene. Adv. Mater. 2006, 18, 2466–2470. [Google Scholar]
  27. Crispin A.; Crispin X.; Fahlman M.; Berggren M.; Salaneck W. R. Transition between Energy Level Alignment Regimes at a Low Band Gap Polymer−Electrode Interfaces. Appl. Phys. Lett. 2006, 89, 213503-3. [Google Scholar]
  28. Osikowicz W.; de Jong M. P.; Salaneck W. R. Formation of the Interfacial Dipole at Organic−Organic Interfaces: C60/Polymer Interfaces. Adv. Mater. 2007, 19, 4213–4217. [Google Scholar]
  29. Seki K.; Ito E.; Ishii H. Energy Level Alignment at Organic/Metal Interfaces Studied by UV Photoemission. Synth. Met. 1997, 91, 137–142. [Google Scholar]
  30. Kahn A.; Koch N.; Gao W. Electronic Structure and Electrical Properties of Interfaces between Metals and π-Conjugated Molecular Fims. J. Polym. Sci., Part B 2003, 41, 2529–2548. [Google Scholar]
  31. Simic-Milosevic V.; Heyde M.; Lin X.; Konig T.; Rust H.-P.; Sterrer M.; Risse T.; Nilius N.; Freund H.-J.; Giordano L.; Pacchioni G. Charge-Induced Formation of Linear Au Clusters on Thin MgO Films: Scanning Tunneling Microscopy and Density-Functional Theory Study. Phys. Rev. B 2008, 78, 235429-6. [Google Scholar]
  32. Braun S.; Osikowicz W.; Wang Y.; Salaneck W. R. Energy Level Alignment Regimes at Hybrid Organic−Organic and Inorganic−Organic Interfaces. Org. Electron. 2007, 8, 14–20. [Google Scholar]
  33. Braun S.; Salaneck W. R. Fermi Level Pinning at Interfaces with Tetrafluorotetracyanoquinodimethane (F4-TCNQ): The Role of Integer Charge Transfer States. Chem. Phys. Lett. 2007, 438, 259–262. [Google Scholar]
  34. Tengstedt C.; Osikowicz W.; Salaneck W. R.; Parker I. D.; Hsu C.-H.; Fahlman M. Fermi-Level Pinning at Conjugated Polymer Interfaces. Appl. Phys. Lett. 2006, 88, 053502-3. [Google Scholar]
  35. Fahlman M.; Crispin A.; Crispin X.; Henze S. K. M.; de Jong M. P.; Osikowicz W.; Tengstedt C.; Salaneck W. R. Electronic Structure of Hybrid Interfaces for Polymer-Based Electronics. J. Phys.: Condens. Matter 2007, 19, 183202. [DOI] [PubMed] [Google Scholar]
  36. Vázquez H.; Flores F.; Kahn A., Induced Density of States Model for Weakly-Interacting Organic Semiconductor Interfaces. Org. Electron. 2007, 8, 241−248. [Google Scholar]
  37. Vázquez H.; Oszwaldowski R.; Pou P.; Ortega J.; Perez R.; Flores F.; Kahn A. Dipole Formation at Metal/PTCDA Interfaces: Role of the Charge Neutrality Level. Europhys. Lett. 2004, 65, 802–808. [Google Scholar]
  38. Vázquez H.; Gao W.; Flores F.; Kahn A. Energy Level Alignment at Organic Heterojunctions: Role of the Charge Neutrality Level. Phys. Rev. B 2005, 71, 041306. [Google Scholar]
  39. Kresse G.; Furthmüller J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169–11186. [DOI] [PubMed] [Google Scholar]
  40. Kresse G.; Joubert D. from Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar]
  41. Monkhorst H. J.; Pack J. D. Special Points for Brillouin-Zone Integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar]
  42. Methfessel M.; Paxton A. T. High-Precision Sampling for Brillouin-Zone Integration in Metals. Phys. Rev. B 1989, 40, 3616–3621. [DOI] [PubMed] [Google Scholar]
  43. Kokalj A. Comput. Mater. Sci. 2003, 28, 155; code available from http://www.xcrysden.org/. [Google Scholar]
  44. Neaton J. B.; Hybertsen M. S.; Louie S. G. Renormalization of Molecular Electronic Levels at Metal−Molecule Interfaces. Phys. Rev. Lett. 2006, 97, 216405-4. [DOI] [PubMed] [Google Scholar]
  45. Kubatkin S.; Danilov A.; Hjort M.; Cornil J.; Bredas J.-L.; Stuhr-Hansen N.; Hedegard P.; Bjornholm T. Single-Electron Transistor of a Single Organic Molecule with Access to Several Redox States. Nature 2003, 425, 698–701. [DOI] [PubMed] [Google Scholar]
  46. Norsko J. K. Chemisorption on Metal Surfaces. Rep. Prog. Phys. 1990, 53, 1253–1295. [Google Scholar]
  47. Newns D. M. Self-Consistent Model of Hydrogen Chemisorption. Phys. Rev. 1969, 178, 1123. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nn9010494_si_001.pdf (91.6KB, pdf)

Articles from ACS Nano are provided here courtesy of American Chemical Society

RESOURCES