Kinetic Studies of Biological Interactions By Affinity Chromatography

Abstract

The rates at which biological interactions occur can provide important information on the mechanism and behavior of such processes in living systems. This review will discuss how affinity chromatography can be used as a tool to examine the kinetics of biological interactions. This approach, referred to here as biointeraction chromatography, uses a column with an immobilized binding agent to examine the association or dissociation of this agent with other compounds. The use of HPLC-based affinity columns in kinetic studies has received particular attention in recent years. Advantages of using HPLC with affinity chromatography for this purpose include the ability to reuse the same ligand within a column for a large number of experiments, and the good precision and accuracy of this approach. A number of techniques are available for kinetic studies through the use of affinity columns and biointeraction chromatography. These approaches include plate height measurements, peak profiling, peak fitting, split-peak measurements, and peak decay analysis. The general principles for each of these methods are discussed in this review and some recent applications of these techniques are presented. The advantages and potential limitations of each approach are also considered.

1 Introduction

1.1 General principles of affinity chromatography

The method of affinity chromatography has been used for decades as a selective means for the purification and analysis of chemicals in biological systems [1-6]. Affinity chromatography can be defined as a type of liquid chromatography in which a biologically-related agent is used as the stationary phase [1, 7]. This biologically-related agent, referred to as the “affinity ligand”, can consist of an immobilized sequence of DNA or RNA, a protein or enzyme, a biomimetic dye, an enzyme substrate or inhibitor, or a small target molecule, among others [2]. The specific nature with which these ligands can interact with their targets provides the basis for the selective separations that can be obtained when using affinity chromatography, making this an important tool in modern biochemistry and chemical analysis [1, 3-6].

In the past, many affinity separations were conducted using low-performance supports such as agarose or polyacrylamide [8]. However, HPLC media like silica and monolithic supports can also be used as the support material in affinity separations, resulting in a technique known as high-performance affinity chromatography (HPAC) [2, 8-11]. Along with providing an efficient and rapid means of selective separation and analyzing chemicals in complex biological samples, the development of HPAC has further resulted in a series of new tools that can be used to study biological interactions. This review will examine the use of affinity chromatography and HPAC in such studies, with particular attention being given to the use of these methods in examining the rate constants and kinetics of biological binding processes.

1.2 Biointeraction chromatography

The use of affinity chromatography to characterize a biological interaction is a method that is referred to as biointeraction chromatography (also known as quantitative affinity chromatography or analytical affinity chromatography) [12-16]. There are a number of advantages to utilizing affinity chromatography, and especially HPAC, for studying biological interactions. For instance, the immobilized ligand in an affinity column can often be used for a large number of sample injections. This feature helps to provide optimum run-to-run precision and minimizes batch-to-batch variations in the experiments because the same preparation of ligand is used for multiple studies. The same feature reduces the total amount of ligand that is needed for the experiments and lowers the cost when expensive ligands such as monoclonal antibodies or cell receptors are used. In addition, biointeraction studies that are conducted by using HPAC can be easily automated and used as the basis for relatively high-throughput measurements [16].

The proper use of biointeraction chromatography (and affinity chromatography in general) does require that careful attention be given to the nature of the affinity ligand and the way in which this ligand is used to study a biological interaction. Fortunately, many immobilization techniques are available for this purpose (see reviews in Refs. [3-6, 17]). In addition, it has been shown for some biological systems that good agreement can be obtained in the binding behavior of the immobilized and native forms of a ligand (e.g., as noted for drug-protein binding in Refs. [15-17]). It is also now possible to physically entrap some ligands in a support such as a sol gel to directly use the soluble form of a ligand in binding studies [17].

Most past applications of biointeraction chromatography have involved its use in obtaining information on binding equilibria and thermodynamics (see reviews and examples in Refs. [12, 15, 16, 18]). However, this technique can also be used to examine the kinetics of a biological interaction. The kinetics of such a binding process can be studied by using one of a pair of interacting agents as a ligand within an affinity column while the second, complementary binding agent is injected or applied onto this column. The observed peak or elution profile for the injected analyte is then used to provide information on the rate of the analyte-ligand interaction. This general approach has been used examine the rates of several biological systems, including antibody-antigen interactions, lectin/sugar binding, and drug-protein interactions, among others (see Table 1) [19-53].

Table 1.

Examples of applications of biointeraction chromatography in kinetic studies

Ligand	Analyte [Refs.]
Human serum albumin	Imipramine [48], R/S-propranolol [48], D/L-tryptophan [47, 50, 53] R/S-warfarin [20, 31]
Antibodies	2,4-Dichlorophenoxyacetic acid and related herbicides [37], human serum albumin [24, 43-45, 51], β-lactoglobulin [41, 42]
Concanavalin A	4-Methylumbelliferyl-α-D-mannopyranoside [19, 36], p-nitrophenyl-α-D-mannopyranoside [19, 36, 38-40, 52]
Protein A and protein G	Human IgG [30], rabbit IgG [22, 23, 46]
Cibacron Blue 3G-A	Lysozyme [29, 32]
Nicotinic acetlylcholine receptors	Various inhibitors [25-28, 34, 35]
Heat shock protein 90	Novobiocin [33]
Bovine neurophysin II	Vasopressin [49]
Peptides	Fibrinogen [21]

Figure 1 depicts a common model used to describe the kinetic processes that lead to the interaction of an analyte (A) with an immobilized ligand on a chromatographic support. In this model, as the analyte travels through the column in the flowing mobile phase, the analyte can undergo mass transfer from the flowing region of the mobile phase to a stagnant layer of mobile phase that surrounds, and is contained within, the interior of each support particle. This stagnant mobile phase mass transfer is described in Figure 1 by the forward and reverse mass transfer rate constants k₁ and k_-1, respectively. Once the analyte is inside of the support pores, it can then interact with the immobilized ligand that is in contact with the stagnant mobile phase region. This interaction of A with L is represented in Figure 1 by a simple 1:1 reversible interaction with association and dissociation rate constants given by the terms k_a and k_d. The ratio of these rate constants in this model gives the association equilibrium constant (K_a) for the formation of the analyte-ligand complex, where K_a = k_a/k_d.

Figure 1.

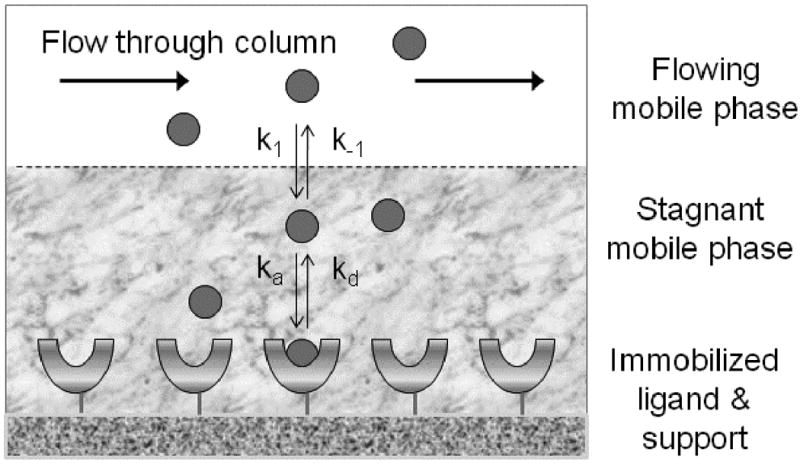
General model for describing the association and dissociation of an analyte with an immobilized ligand in an affinity column, and the movement of this analyte through mass transfer between the flow mobile phase and stagnant mobile phase regions of the column.

The overall strength and rate of analyte-ligand binding will determine the types of methods that can be used to characterize the interaction kinetics with biointeraction chromatography. However, all of these methods are based on either the injection of a small plug of the analyte (i.e., zonal elution) or the continuous application of an analyte (i.e., frontal analysis, or frontal affinity chromatography). It is further possible to characterize these methods according to whether they use a trace amount of applied analyte (i.e., linear elution conditions, giving a result that is independent of the amount of injected analyte) or a significant amount of analyte versus ligand (i.e., non-linear elution conditions, where the response is affected by the amount of applied analyte) [54]. A variety of techniques that cover all of these categories will be discussed in Sections 2-4 of this review.

1.3 Biointeraction chromatography versus surface plasmon resonance

In considering the potential applications of biointeraction chromatography, it is useful to also consider surface plasmon resonance (SPR), a technique which forms the basis for affinity and kinetic measurements in instruments such as Biacore [15, 55, 56]. SPR-based sensors are closely related to affinity chromatography in that they employ a flow-based system to monitor the association and dissociation of an analyte from a surface that contains an immobilized ligand. However, in SPR the interaction is examined directly within the sensor and at the sensor's surface; in biointeraction chromatography the interaction is examined through its affect on the retention or elution profile for an analyte, as observed at the exit of the column [15]. Although a detailed discussion of SPR is beyond the scope of this current review, a rigorous treatment of this topic can be found in a number of recent reports [15, 55, 56].

In both SPR and biointeraction chromatography it is necessary to use the proper experimental conditions and appropriate models or methods for data analysis to obtain accurate rate constants. The conditions and models that should be used in biointeraction chromatography have been discussed in previous reports [15-17], as well as in this current review. Various mathematical treatments and systematic precautions to follow in SPR have also been discussed in the past [55, 57-61]. Both biointeraction chromatography and SPR have similar considerations concerning the need to have an immobilized ligand that mimics the binding behavior of the same ligand in its native state. It is also necessary in both to make corrections for mass transfer to obtain accurate kinetic measurements for the binding of an analyte with the ligand. If these requirements are met, either biointeraction chromatography or SPR can be used successfully for examining the kinetics of biological systems [56, 62].

One key difference between SPR and biointeraction chromatography is the way in which the analyte-ligand interaction is detected and monitored. The use of surface plasmon resonance to monitor such a reaction will give a signal that is proportional to the amount of analyte that has been bound by the immobilized ligand. This signal, in turn, is related to the size of the analyte, the concentration of the analyte, and the affinity of this analyte for the ligand [56, 63]. The nature of this signal can make it difficult to detect small analytes or to work with analytes that are present at low concentrations [59, 63, 64], such as those that have limited solubility in an aqueous buffer. It is possible to improve analyte concentration and the corresponding signal in SPR by adding an organic modifier or solubilizing agent, but the presence of this agent may also alter the nature of the analyte-ligand interaction [9, 63]. Unlike SPR, biointeraction chromatography is not limited to a particular detection method because the support/surface that contains the ligand is separate from the means used for analyte detection. A large variety of detectors have been used in biointeraction chromatography, with UV-Vis absorption spectroscopy, fluorescence spectroscopy, and mass spectrometry being the most common. The greater range of detection modes and the ability of these detectors to monitor lower concentration species than SPR make it easier to use biointeraction chromatography with chemicals that are present at low concentrations, that have low solubility or that have only weak to moderate affinities for a ligand.

The ability to detect a binding curve with SPR does not necessarily mean that accurate rate constants can be measured from this curve. The effect of rebinding and the balance between mass transfer and chemical interaction kinetics in this approach places a limit on the association and dissociation rate constants measurable by SPR [58, 59]. Accurate and precise kinetic measurements in SPR have typically been limited to systems with moderate to strong binding (i.e., K_a = 10⁵ M^-1 or larger), with decreased precision being noted for systems with weaker binding and/or those with fast association or dissociation kinetics [63, 65]. On the other hand, biointeraction chromatography has been used in several studies to examine the kinetics of drug interactions with serum proteins, which often involve chemicals that may be present at low concentrations or have binding constants in the range of 10⁵ M^-1 or lower (see reviews in Refs. [15-17]). In contrast to this, little comparable work has been conducted with SPR with this type of system and the work that has been done has involved only drug-protein interactions with relatively high affinities [63]. Many different approaches are available in biointeraction chromatography to examine the kinetics of an analyte-ligand interaction. Some of these approaches (e.g., frontal analysis) are similar to SPR in that they make use of binding and saturation curves, while others make use of zonal elution profiles or measurements of non-retained analyte fraction for such work. The availability of this broad range of approaches makes it possible for biointeraction chromatography to be used in examining a wide range of rate constants for analyte-ligand interactions.

2 Band-broadening measurements

The measurement and use of band-broadening was the earliest approach developed for using affinity chromatography to study the kinetics of biological reactions. This type of study is typically performed by using zonal elution and injections of small pulses of the analyte to achieve linear elution conditions. Two specific approaches for kinetic studies by biointeraction chromatography that are based on band-broadening measurements are the plate height method and peak profiling.

2.1 Plate height method

The plate height method (also known as the band-broadening method) makes use of plate height and band-broadening measurements to obtain information on the rate of an analyte-ligand interaction [19, 31, 53, 66]. In this method the affinity column is viewed as being divided into a series of equal sized regions (i.e., “theoretical plates”, N) that each represents a single interaction between the analyte and stationary phase. According to chromatographic theory, the value of N is equal to the ratio ${{(\text{t}}_{\text{R}}}^2/{\sigma }_{\text{R}}^2)$, where t_R is the retention time observed for the analyte, σ_R is the standard deviation of the elution profile for the analyte, and ${\sigma }_{\text{R}}^2$ is the corresponding variance (Note: each of these terms should be corrected for extra-column contributions, as measured by performing sample injections with no column present). The distance along the column that makes up each theoretic plate is described by using the “plate height” (H), where H = L/N and L is the total length of the column [66, 67].

Several processes contribute to the broadening of a chromatographic peak as an analyte travels through an affinity column. Each of these processes, in turn, can be described by its own plate height term. For instance, the plate height contribution due to mobile phase mass transfer and eddy diffusion (H_m) describes the broadening that occurs due to differential migration paths and interparticle flow profiles. The plate height contribution due to the longitudinal diffusion term (H_L) describes broadening due to axial diffusion of solutes. Two other important plate height contributions are those due to stagnant mobile phase mass transfer (H_sm) and stationary phase mass transfer (H_k), which are related to the mass transfer and interaction processes, respectively, that were given in Figure 1. As shown in Eq. (1), the total observed plate height for the analyte (H_total) is equal to the sum of each of these individual contributions to band-broadening, where the value of H_total has already been corrected for the plate height contribution due to extra-column band-broadening contributions (H_ec) through the measurements made when no column is present in the system.

$${\text{H}}_{\text{total}}=\frac{\text{L}\cdot {\sigma }_{\text{R}}^2}{{\text{t}}_{\text{R}}^2}={\text{H}}_{\text{m}}+{\text{H}}_{\text{L}}+{\text{H}}_{\text{sm}}+{\text{H}}_{\text{k}}$$ (1)

To make kinetic measurements in the plate height method, it is typically assumed that the contribution of H_L to the total plate height is negligible and that H_m is constant, as is often true at the flow rates that are commonly used in affinity chromatography. The following equations are then used to provide estimates of H_sm and H_k or to measure these terms from independent band-broadening studies with retained and non-retained solutes, respectively [66].

Stationary phase mass transfer:

$${\text{H}}_{\text{k}}=\frac{2\cdot \text{u}\cdot k}{{\text{k}}_{\text{d}}\cdot {\left(1+k\right)}^2}$$ (2)

Stagnant mobile phase mass transfer:

$${\text{H}}_{\text{sm}}=\frac{2\cdot \text{u}\cdot {\text{V}}_{\text{P}}{\left(1+\frac{{\text{V}}_{\text{M}}}{{\text{V}}_{\text{P}}}\cdot k\right)}^2}{{\text{k}}_{-1}\cdot {\text{V}}_{\text{M}}{\left(1+k\right)}^2}$$ (3)

In these equations, u is the linear velocity of the flowing mobile phase (as measured using a non-retained void marker capable of sampling all inter- and intraparticle space), V_P is the pore volume of the support, V_M is the column void volume, k is the retention factor of the analyte, and all other terms are as described previously. It is also useful to note that for a non-retained solute (k = 0), Eq. (3) reduces to the following form [23, 66].

For a non-retained solute (k = 0):

$${\text{H}}_{\text{sm}}=\frac{\text{2}\cdot \text{u}\cdot {\text{V}}_{\text{P}}}{{\text{k}}_{-\text{1}}{\text{V}}_{\text{M}}}$$ (4)

In the plate height method, the analyte of interest is first injected onto an inert control column or a non-retained species is injected onto a column containing the desired ligand. These injections are made at various flow rates to obtain plate height measurements at k = 0. A plot of H_total versus u is then made and examined by linear regression. An example of such a plot is shown in Figure 2(a). The resulting best-fit parameters are then analyzed by combining Eqs. (1) and (4). If the values of V_P and V_M are known for the column, as can be determined from independent measurements, it is then possible to obtain k_-1 from the best-fit slope. The value of H_m can also be estimated as being equal to the intercept of this plot [31, 53, 66].

Figure 2.

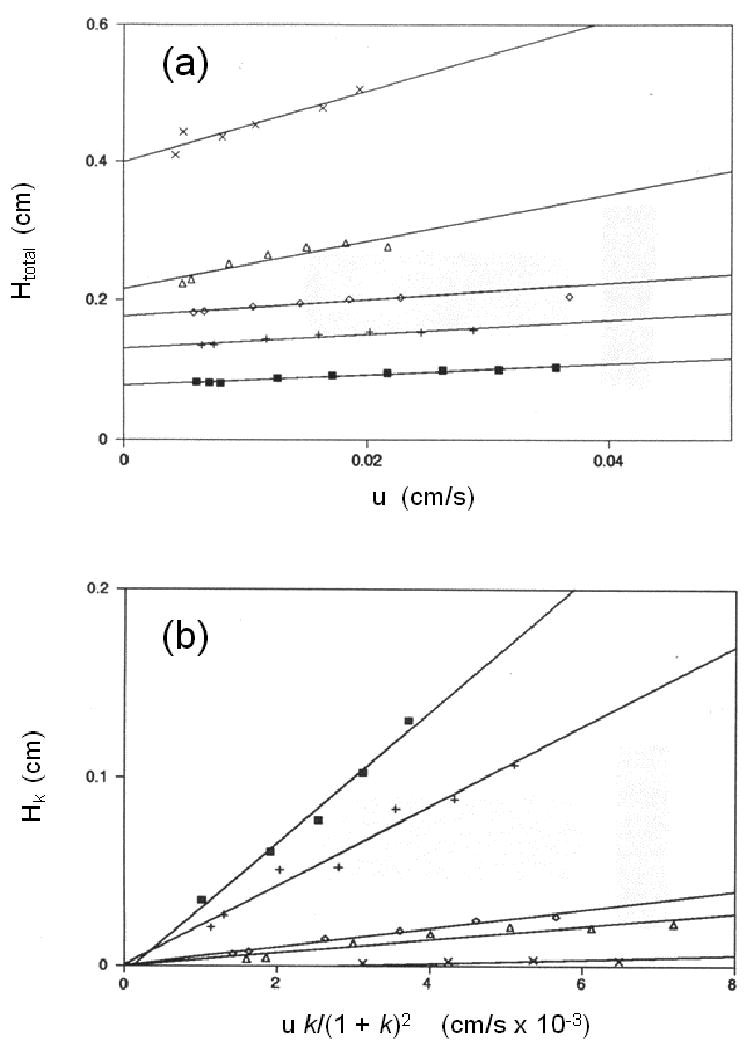
Typical results obtained in the plate height method at several temperatures for (a) plots of the total plate height (H_tot) versus linear velocity (u) for the injection of R-warfarin onto an immobilized HSA column, and (b) the corresponding plots of the plate height contribution due to stationary phase mass transfer (H_k) versus u k/(1+k)² after correcting the data for other band-broadening contributions. (Adapted with permission from Ref. [31])

In the second step of this approach, injections of the analyte are made onto an affinity column (at several flow rates) containing the desired immobilized ligand and both the total plate height and retention factor are measured. The value of k_-1 that was determined in the first set of experiments is then used along with Eq. (3) and estimates of V_P and V_M to estimate the value for H_sm at each of tested flow rates. These values for H_sm and the previous estimate of H_m are then subtracted from the total observed plate height for the analyte in Eq. (1) to give the plate height contribution due to stationary phase mass transfer (H_k). Finally, a plot of the calculated value of H_k is made versus the term [u k/(1+k)²]. The result, as predicted by Eq. (3), should be a plot with an intercept of zero, and a slope that can be used to provide the dissociation rate constant for the analyte/ligand system [31, 66]. This type of plot is illustrated in Figure 2(b).

The dissociation rate constant that is measured by the plate height method is identical to the term k_d that is shown for the general reaction model in Figure 1. This is the case because other sources of band-broadening, such as mobile phase mass transfer and stagnant mobile phase mass transfer, are corrected for during the data analysis process. It is also possible to obtain the value of the association rate constant (k_a) for this interaction if the calculated value of k_d is used along with an independent measure of the association equilibrium constant K_a, since K_a = k_a/k_d. The value of K_a in this case can be obtained through separate biointeraction studies that are based on frontal analysis or zonal elution, as previously discussed in detail in Refs. [12, 15, 16].

An early application of the plate height method involved its use to examine the rates at which various sugars bind to concanavalin A [19]. This technique has also been used to measure the rate constants for interactions of R/S-warfarin and D/L-tryptophan with the protein human serum albumin (HSA) [31, 53]. The dissociation rate constants found for the interactions of warfarin with HSA using the plate height method were in the same general range but slightly smaller than those reported with racemic warfarin using stopped flow analysis; however, this small difference was thought to be a result of the high concentrations of warfarin used in the stopped flow analysis studies, which may have led to a larger contribution from non-specific interactions [31]. A kinetic analysis of warfarin-HSA interactions using SPR gave results that were in good agreement with those obtained via the plate height method [31, 63].

The kinetic studies on tryptophan and warfarin were performed at several temperatures and used along with separate estimates of K_a to obtain dissociation and association rate constants for each of these temperatures. This information was then examined through the use of Arrhenius-type plots to obtain more details on the kinetics and transition states for the interactions of HSA with each solute. Similar work looking at the effects of pH, ionic strength and solvent polarity on the association and dissociation kinetics were conducted for D/L-tryptophan [31, 53]. The information obtained from these studies was found to be important in optimizing chiral separations for R/S-warfarin and D/L-tryptophan on HSA columns [31, 53]. This type of kinetic data has since been shown to be useful in describing the pharmacokinetics of drugs that bind to HSA [68, 69] and in developing new assays for measurement of free drug or hormone fractions in serum [70, 71].

The plate height method requires that the association and dissociation rates for the analyte-ligand interaction are reasonably fast to allow multiple binding and dissociation steps to occur as the analyte passes through the affinity column. This requirement means that the plate height method is most useful for ligands that have weak-to-moderate strength binding (i.e., K_a values that are 10⁶ M^-1 or lower). It is also necessary in this approach to ensure that a sufficiently small amount of analyte is being injected to provide linear elution conditions. The use of efficient columns and support materials is another desirable feature in this type of experiment because this helps minimize the plate height contributions due to H_m and H_sm and makes it easier to obtain estimates of H_k. In addition, it is important to measure and use the true retention times and peak variances in these studies. A correction should also be made for extra-column band-broadening and extra-column components to the observed elution time by injecting the analyte onto the chromatographic system when all components except the column are present [16, 31, 53].

2.2 Peak profiling

An approach that is closely related to the plate height method is the technique of peak profiling. This is another example of a method that is performed by using zonal elution and linear elution conditions. A theoretical derivation for this approach in affinity chromatography was first reported in 1975 by Denizot and Delaage, who based their work on the molecular dynamic theory of chromatography that was previously developed by Giddings and Eyring [72, 73]. In the peak profiling method, the retention times and variances are measured on an affinity column for both a retained analyte and a non-retained solute (see Figure 3). In the original peak profiling method, these values were then used with the following equation to calculate the apparent dissociation rate constant (k_d,app) for this interaction [72],

Figure 3.

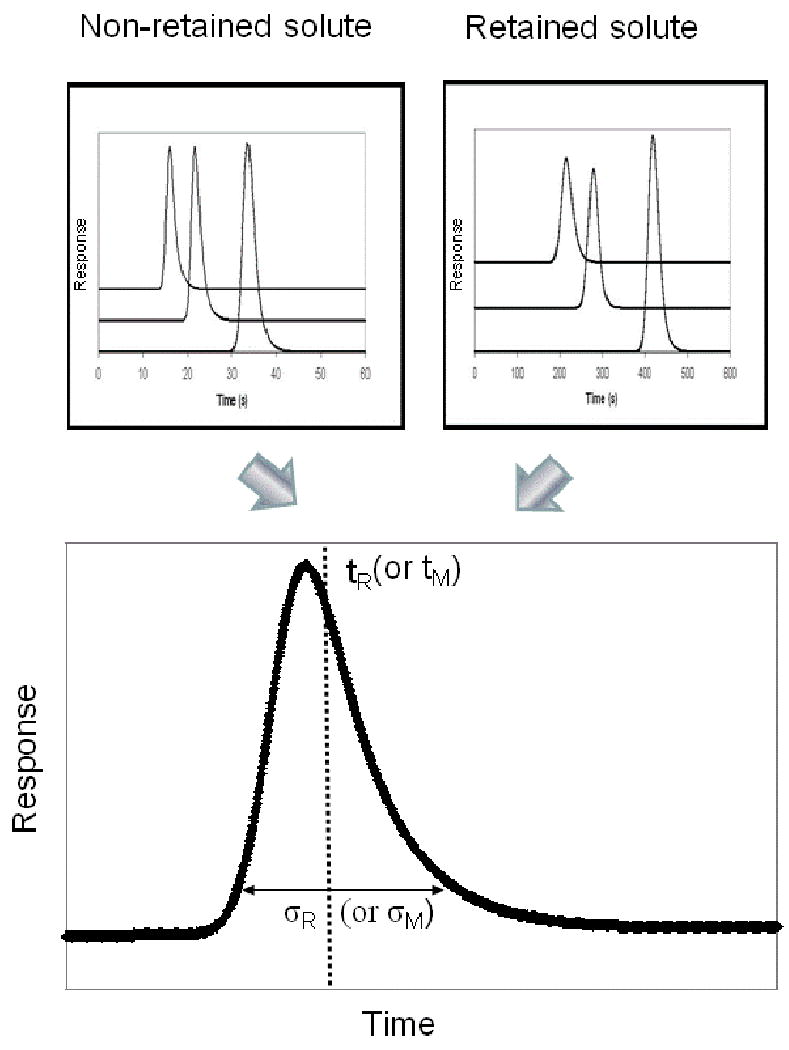
General approach used in peak profiling for obtaining kinetic information on a solute-ligand interaction. In this figure, t_M is the column void time (or elution time for a non-retained solute), t_R is the retention time for a retained analyte, σ_M is the standard deviation of the peak for the non-retained solute, and σ_R is the variance of the peak for the retained analyte (Note: the corresponding peak variances would be σ_M² and σ_R², respectively). These parameters are typically measured in peak profiling by using peak fitting software and an exponentially-modified Gaussian model. The set of three chromatograms shown for the non-retained and retained species represent results that were obtained at three different flow rates.

$${\text{k}}_{\text{d},\text{app}}=\frac{2\cdot {\text{t}}_{\text{M}}^2\cdot \left({\text{t}}_{\text{R}}-{\text{t}}_{\text{M}}\right)}{{\sigma }_{\text{R}}^2\cdot {\text{t}}_{\text{M}}^2-{\sigma }_{\text{M}}^2\cdot {\text{t}}_{\text{R}}^2}$$ (5)

In Eq. (5), t_R is again the retention time for the analyte and t_M represents the elution time of a non-retained solute (i.e., the column void time). The peak variances for the analyte and non-retained solute are described by the terms ${\sigma }_{\text{R}}^2$ and ${\sigma }_{\text{M}}^2$, respectively. Although this method is relatively simple to perform, it does assume that all sources of band-broadening other than stationary phase mass transfer are either negligible or the same for the retained and non-retained species. It is for this reason that Eq. (5) is shown as providing an apparent dissociation rate constant (k_d,app), which may be affected by some of these other band-broadening processes.

An early application of the original peak profiling method was its use in studying the kinetics of bovine neurophysin II (BNP II) self-association and the binding of BNP II with the neuropeptide Arg⁸-vasopressin (AVP). These experiments utilized BNP II that was immobilized on either non-porous or porous glass beads. However, it was found that the rate constants determined by this approach were underestimated by orders of magnitude compared to solution phase values, especially when using porous supports [49, 74]. This difference may have been due to differences in the stagnant mobile phase mass transfer contributions for the retained and non-retained species or the use of relatively low flow rates and fraction collection for these experiments. Later, a mathematically equivalent approach employing plate height measurements was used with HPAC to examine the dissociation kinetics of sugars on an immobilized concanavalin A column [38]. Further analysis of this system indicated these results were also underestimated due, in part, to working under non-linear conditions [38, 52]. Later work with this approach used measurements at high flow rates to examine the binding of L-tryptophan with HSA that was immobilized to a monodisperse HPLC support material; in this case, reasonably good agreement was obtained with literature values [50].

A modified form of the peak profiling method has recently been developed that uses HPAC and work at multiple flow rates for band-broadening measurements. An alternative form of Eq. (5) was developed for this work, which was now expressed in terms of the plate heights for the retained and non-retained species (H_R and H_M), the retention factor for the retained species, and the linear velocity of the mobile phase, as shown below [47].

$${\text{H}}_{\text{R}}-{\text{H}}_{\text{M}}=\frac{2\cdot \text{u}\cdot k}{{\text{k}}_{\text{d},\text{app}}\cdot {\left(1+k\right)}^2}={\text{H}}_{\text{k}}$$ (6)

Eq. (6) was found to be useful for peak profiling studies because it predicts that a plot of (H_R - H_M) versus [u k/(1+k)²] will give a linear relationship with a slope that can be used to provide the value of k_d,app (see Figure 4). The results of this approach were compared to those obtained by traditional peak profiling at a single linear velocity by using L-tryptophan and HSA as a model system. It was found that the traditional method gave k_d,app values that varied with linear velocity, while the use of Eq. (6) and data obtained at multiple linear velocities allowed for more precise and accurate estimates of dissociation rate constants [47]. An expanded form of this approach that includes a correction for non-specific binding processes has also been used to study binding kinetics of HSA with imipramine and propranolol [48].

Figure 4.

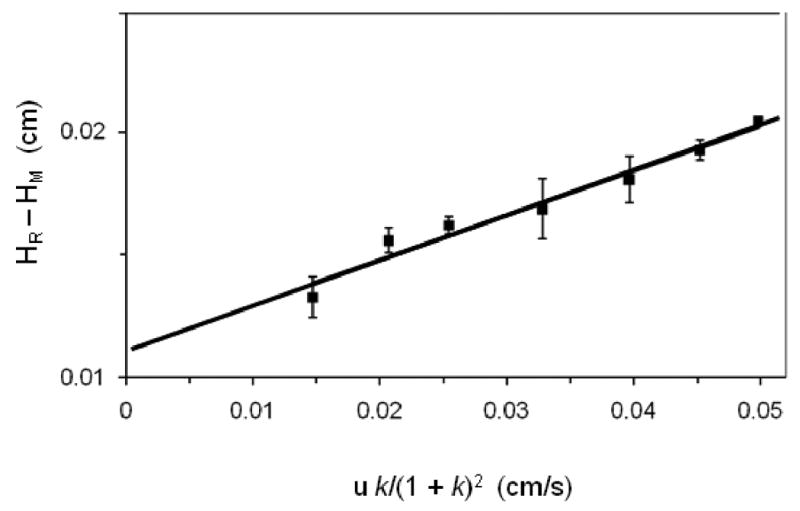
Peak profiling plots prepared according to Eq. (6) for data obtained on an immobilized HSA column for R/S-propranolol.

One advantage of using multiple flow rates for peak profiling is that Eq. (6) can be expanded to correct for the contribution of stagnant mobile phase mass transfer. The expression that is used for data analysis in this case is given by Eq. (7) [47].

$${\text{H}}_{\text{R}}-{\text{H}}_{\text{M}}=\frac{\text{u}\cdot k}{{\left(1+k\right)}^2}\cdot \left[\frac{2}{{\text{k}}_{\text{d}}}+\frac{{\text{d}}_{\text{p}}^2\left(2+3\cdot k\right)}{60\cdot \gamma \cdot \text{D}}\right]$$ (7)

In this equation, d_P is the particle diameter of the support packing material, γ is the tortuosity factor, and D is the diffusion coefficient of the analyte in the mobile phase. This expression has been used to determine the dissociation rate constant for the L-tryptophan/HSA system by using a series of columns that contained supports with different particle diameters. In this method, a series of plots are made of H_R-H_M versus [u k/(1+k)²] for a group of columns that have different values for d_p. The best-fit of these plots are then determined and used to prepare a second graph in which the resulting best-fit slope is plotted versus d_p². It is then possible from the intercept of this new graph to obtain the true dissociation rate constant (k_d) for the system [47].

Peak profiling is similar to the plate height method in that it works best with a solute-ligand system that has relatively fast rates of association and dissociation rates and weak-to-moderate strength binding. It is also again necessary to do this type of experiment under linear elution conditions and to correct for extra-column contributions to band-broadening and elution times. In addition, the use efficient columns and support materials again helps to minimize plate height contributions other than H_k, providing for easier measurements of dissociation rate constants. An advantage of the peak profiling method is that it can allow for higher-throughput kinetic measurements than the plate height method because it can be conducted at higher flow rates [47, 48, 50]. However, the use of higher flow rates also requires a fast sampling rate for data to minimize the effect of any electronic dampening on the measured peak variances.

It can be seen from this discussion and the previous section that there are many similarities between the peak profiling and plate height methods. This similarity is a result of the fact that the peak profiling method is essentially a subset of the plate height method which uses higher flow rates and a more direct calculation method. In the plate height method, the void marker is used to gain information on the factors that contribute to band broadening, where each contribution is calculated or measured and subtracted from the total plate height for an analyte. In peak profiling several band-broadening factors are dealt with simultaneously by comparing the total plate height that is measured for the analyte with that measured for a non-retained solute. Both methods should yield comparable results and are capable of correcting for mass transfer contributions, but the peak profiling method has the possibility of allowing for faster data collection and analysis.

3 Peak fitting methods

Although the plate height and peak profiling methods both use dilute amounts of analyte and linear elution conditions, similar methods have also been developed that allows the use of much higher analyte concentrations in such work (i.e., non-linear elution conditions). The advantage of using non-linear conditions is that the high concentrations of applied analyte make it possible to have easier analyte detection. Non-linear peak fitting is one approach that can be used for kinetic measurements of analyte/ligand kinetics under such conditions. Techniques have been described for such experiments that make use of either zonal elution or frontal analysis, as will be discussed in this section.

3.1 Peak fitting in zonal elution

Peak fitting has been used with zonal elution to study analyte-ligand kinetics in work conducted under non-linear elution conditions. This work has been conducted by using the following equation to fit elution profiles [52, 75].

$$\text{y}=\frac{{\text{a}}_{\text{0}}}{{\text{a}}_{\text{3}}}\left[1-e^{\left({-\text{a}}_{\text{3}}{/\text{a}}_{\text{2}}\right)}\right]\cdot \left[\frac{\sqrt{\frac{{\text{a}}_{\text{1}}}{\text{x}}}\cdot I_1\left(\frac{\text{2}\sqrt{{\text{a}}_{\text{1}}\text{x}}}{{\text{a}}_{\text{2}}}\right)e^{{-\text{x}-\text{a}}_{\text{1}}/{\text{a}}_{\text{2}}}}{\text{1}-\text{T}\left(\frac{{\text{a}}_{\text{1}}}{{\text{a}}_{\text{2}}},\frac{\text{x}}{{\text{a}}_{\text{2}}}\right)\left[\text{1}-{\text{e}}^{{-\text{a}}_{\text{3}}/{\text{a}}_{\text{2}}}\right]}\right]$$ (8)

This equation is written in a form in which y represents the intensity of the measured signal at a given point in time in the elution profile, x is the reduced retention time at which y is measured, T is a switching function, and I₁ is a modified Bessel function. The terms a₀ through a₃ are the best-fit parameters used to fit this equation to the experimental peak. These parameters are then used, in turn, to estimate the value of the rate constants and equilibrium constant for the analyte-ligand interaction. For instance, the values of k, k_d,app, and K_a can be determined by using the relationships k = a₁, k_d,app = 1/a₂t_M, and K_a = a₃/C_o, where t_M is the column void time and C_o is the concentration of injected solute multiplied by the ratio of sample volume to column dead volume [35].

An example of the peak shape and experimental fit that can be expected from this type of experiment is given in Figure 5. This fit is based on the same general non-linear model that is often used in fitting frontal analysis data in biointeraction chromatography (see next section); however, the difference in these two approaches is that Eq. (8) uses an impulse input to model sample application in order to obtain a zonal elution profile [52]. The fit of this model in Figure 5 and in related applications tends to be best early in the elution profile but not quite as good towards the tail of a peak. Ligand heterogeneity has been cited as the cause for these observed deviations at the peak tail [52]. Despite these deviations, the resulting fit has been found in one study to be sufficient to allow the relative ranking of compounds according to their dissociation rates, which correlate with the duration of an inhibitory effect [34].

Figure 5.

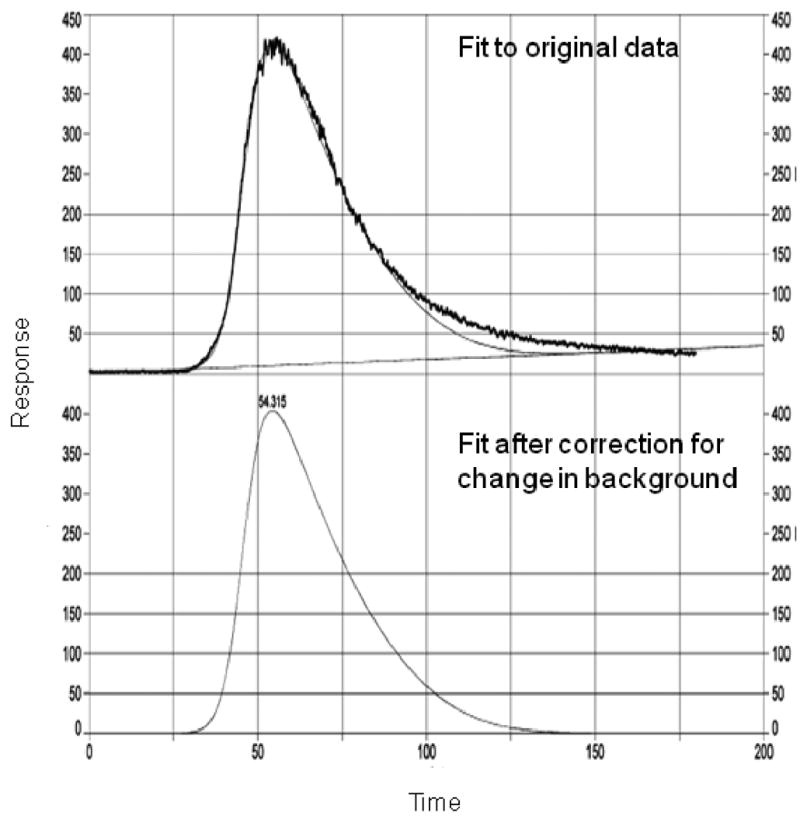
A chromatogram and results of peak fitting according to Eq. (8) for the elution of verapamil from a column containing an immobilized nicotinic acetylcholine receptor. The upper tracing shows both the experimental data and initial fit to this data, while the lower tracing shows just the best-fit response after a correction has been made for the baseline. (Adapted with permission from Ref. [34])

Eq. (8) was original developed and used to study the binding of pNp-mannoside binding to an immobilized concanavalin A column [52]. This equation has also been used to characterize the binding of various inhibitors to immobilized nicotinic acetylcholine receptor (nAChR) membrane affinity HPLC columns [25-28, 34, 35]. These experiments have been used to estimate both the binding constant and rate constants for these interactions, as well as to develop quantitative-structure activity relationships (QSARs) for these inhibitor/nAChR interactions. This approach has also been used to perform studies on immobilized heat shock protein 90, a molecular chaperone protein that has been noted to have increased activity in some types of cancer [33].

An expression similar to Eq. (8) was derived to describe peak shapes for the non-specific elution of an otherwise irreversibly retained solute [30]. This alternative equation was then used to fit data obtained for the use of a pH step gradient to elute human IgG-class antibodies from a column containing protein A that was immobilized onto non-porous silica. A good fit between the experimental data and best-fit peaks was obtained, giving an estimated dissociation rate constant of 1.5 s^-1 for IgG from protein A in the presence of a pH 3.0 buffer [30]. The same technique has also utilized in examining the elution of lysozyme from a Cibacron Blue 3GA columns in the presence of elution buffers that contain various concentrations of sodium chloride [29].

An advantage of this peak fitting approach is that it does not require the use of linear elution conditions. The utilization of Eq. (8) for this approach assumes that the interaction being monitored has reasonably fast association/dissociation kinetics, which generally means that the system has weak-to-moderate binding. However, the method reported in Ref. [30] can allow this method to also be used with high affinity systems under mobile phase conditions that allow for measurable analyte dissociation. One precaution with the use of these equations is that they do assume that the contribution of some kinetic processes are negligible compared to analyte binding and/or dissociation form the ligand. For instance, the past use of Eq. (8) for kinetic studies has treated stagnant mobile phase mass transfer as a contributing factor to the measured rate constant instead of treating this as a separate entity. Similarly, work in Refs. [29, 30] that has examined analyte dissociation kinetics from affinity columns has assumed that the contribution of stagnant mobile phase mass transfer to the apparent rate of analyte desorption is negligible. It is for this reason that the rate constants determined by this technique are typically apparent values that are actually a function or more than one kinetic process occurring within the column.

3.2 Peak fitting in frontal analysis

Frontal analysis can also be used with peak fitting to examine the kinetics of solute-ligand interactions by affinity chromatography. A substantial amount of work has been performed in this area using low-performance supports for affinity chromatography,[76-79] however, this current review will focus on applications using HPAC. Many of the models and expressions that are used for this purpose are based on the initial work of Thomas [75]. This model gives an apparent rate constant for analyte adsorption to the column (k_a,app), in which it is assumed that mass transfer is infinitely fast and analyte adsorption is described by second-order Langmuir kinetics based on interaction at a single type of homogeneous ligand binding site [32, 54, 75]. Numerous variations of this model have been used, but in each the simulated frontal profiles are compared with experimental results to estimate k_a,app. For example, work examining the adsorption of lysozyme to a Cibacron Blue F3GA column with a non-porous support used a general Langmuir adsorption model but treated mass transfer as a film resistance mechanism [32]. Simulated profiles were then used to examine the effects of particle diameter, concentration, flow rate, and association rate constants on the expected profiles and compared to experimental results to determine the apparent association rate constants for adsorption. The simulated profiles showed good correlation with experimental breakthrough curves at the application front, but ligand heterogeneity was thought to decrease the goodness of fit near the plateau region [32].

The binding of HSA to columns containing immobilized anti-HSA antibodies was examined by using frontal analysis along with a Langmuir adsorption model and a rectangular isotherm, in which dissociation of the analyte was assumed to be negligible on the timescale of the experiment (i.e., k_d was essentially zero) [43]. This model gave a good fit with experimental breakthrough curves at low HSA concentrations, however, a flow rate dependence of the measured apparent association rate constant was observed due to the contribution of mass transfer. Apparent association rate constants were determined on columns of various load capacities and used along with the following equation to correct for such contributions.

$$\frac{1}{{\text{k}}_{\text{a},\text{app}}}=\frac{1}{{\text{k}}_{\text{a}}}+\frac{{\text{q}}_{\text{x}}{\text{V}}_{\text{M}}}{{\text{Fn}}_{\text{mt}}}$$ (9)

In this equation, n_mt is a global mass transfer coefficient that is dependent on the packing and column dimensions, F is the flow rate, V_M is the column void volume, and q_x is the loading capacity of the column. A plot of 1/k_a,app versus q_x was then prepared, and the intercept used to calculate the true association rate constant k_a for the HSA-antibody interaction, giving results in good agreement with those reported in the literature [43]. A similar approach for correcting for mass transfer contributions has been utilized to study the interaction of fibrinogen with immobilized peptides [21].

A bi-Langmuir model based on two independent binding sites has been employed in some studies to examine the rates of analyte-ligand interactions by frontal analysis. This type of model has been employed to compare the adsorption of HSA to various columns [24] and to describe the adsorption of β-lactoglobulin to immobilized antibodies for this protein [41]. In this latter study, it was found that β-lactoglobulin/antibody interaction was not irreversible on the timescale of the experiment, making it impossible to determine equilibrium constants under such conditions. This led instead to the development of an approach making use of sequential frontal applications of the analyte that were separated by a rinsing step of a predefined duration [42]. During this rinsing step some, but not all, of the adsorbed analyte was able to desorb as a function of the dissociation rate constant, affecting the results of the second frontal application. Figure 6 demonstrates how the breakthrough time of the second frontal application was reduced compared to the initial application. Column saturation occurred more quickly in the second application because some binding sites were already filled due to incomplete desorption following the first application and rinsing step. A bi-Langmuir adsorption model was then fit to these curves to provide the apparent association and dissociation rate constants for this system [42].

Figure 6.

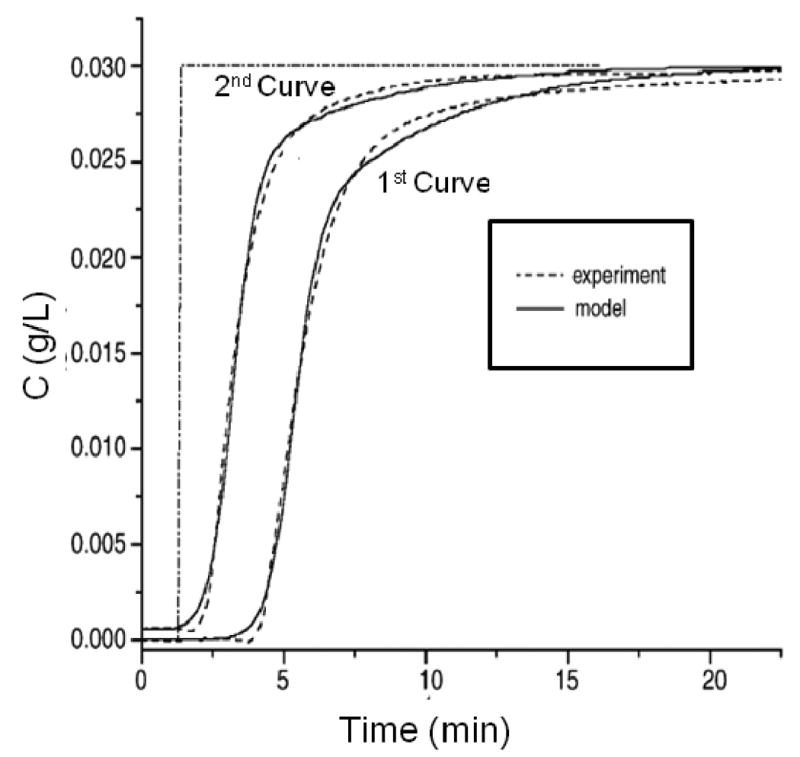
Comparison of two sequential breakthrough curves for the binding of β-lactoglobulin to an affinity column containing antibodies against this agent. The dashed lines show the experimental data and the solid lines show the results obtained through peak fitting to a bi-Langmuir kinetic model. Each curve in this figure begins when a step change is made to apply a sample solution to the column. (Adapted with permission from Ref. [42])

Another variation on the frontal analysis approach has involved the use of linear chromatographic theory to determine concentration-dependent rate constants, and then to extrapolate these values to those that would be expected at infinite dilution. This technique makes use of the following equation that is true under linear elution conditions [15, 40, 80-82],

$${\text{k}}_{\text{d}}=\frac{\text{2}\left({\text{V}}_{\text{A}}-{\text{V}}_{\text{A}}^{\ast }\right)}{{\text{d}\sigma }_{\text{A}}^{\text{2}}/\text{dF}}$$ (10)

Where V_A is the measured breakthrough volume for the analyte, and V_A* is the breakthrough volume for a non-retained solute, F is the flow rate, and ${\sigma }_{\text{A}}^2$ is the variance of the breakthrough curve. A plot of ${\sigma }_{\text{A}}^2$ versus F is prepared for data obtained at a range of flow rates and gives a slope which yields ${(\text{d}{\sigma }_{\text{A}}^2/\text{df)}}_{\text{app}}$. The effects of slow mass transfer in this experiment can be corrected empirically by making analyte injections on a column that does not contain any immobilized ligand [40] or by using an exact analytical solution [39] to obtain the corrected value of $\text{d}{\sigma }_{\text{A}}^2/\text{df}$. This process is done over a range of concentrations and the resulting values of $\text{d}{\sigma }_{\text{A}}^2/\text{df}$ are then each used to calculate an apparent value for the dissociation rate constant, k_d,app. These values for k_d,app are then analyzed as a function of the applied concentrations and extrapolated to infinite dilution to give the true value of k_d. This approach has been used to examine the binding of p-nitrophenyl-α-D-mannopyranoside with immobilized concanavalin A [39, 40].

The advantages and disadvantages of using peak fitting in frontal analysis are similar to those noted in the previous section for zonal elution. This approach again does not require the use of linear elution conditions; however, it does make certain inherent assumptions about the kinetics of the system that is being monitored. Examples of these assumptions are that the data fits a certain type of adsorption isotherm (e.g., a Langmuir or bi-Langmuir model) and that the effects of stagnant mobile phase mass transfer are negligible compared to the rates of solute association and/or dissociation with the immobilized ligand. The presence of these assumptions means that the rate constants that are measured through this approach will actually be apparent values that may vary with the experimental conditions. In addition, although frontal analysis tends to be easier to perform than a zonal elution experiment, this method can also require a larger amount of analyte.

4 Miscellaneous methods

A number of other techniques have also been developed for examining the kinetics of solute-ligand interactions by affinity chromatography. Examples include the split-peak method and peak decay analysis. The principles behind each of these approaches will now be examined, as well as their applications. The combined use of these two methods will also be examined.

4.1 Split-peak method

The split-peak method can be used to examine affinity interactions in which there is essentially irreversible binding of a solute with a ligand on the timescale of application step. This approach is based on the idea that there is a given probability during any separation process that a small fraction of analyte will elute non-retained from the column without interacting with the stationary phase. This phenomenon is known as the “split-peak effect”. This effect increases as the flow rate of application is increased or as the residence time for the analyte in the column decreases, as illustrated in Figure 7 [83]. The result is two peaks even for the injection of a pure solute onto an affinity column.

Figure 7.

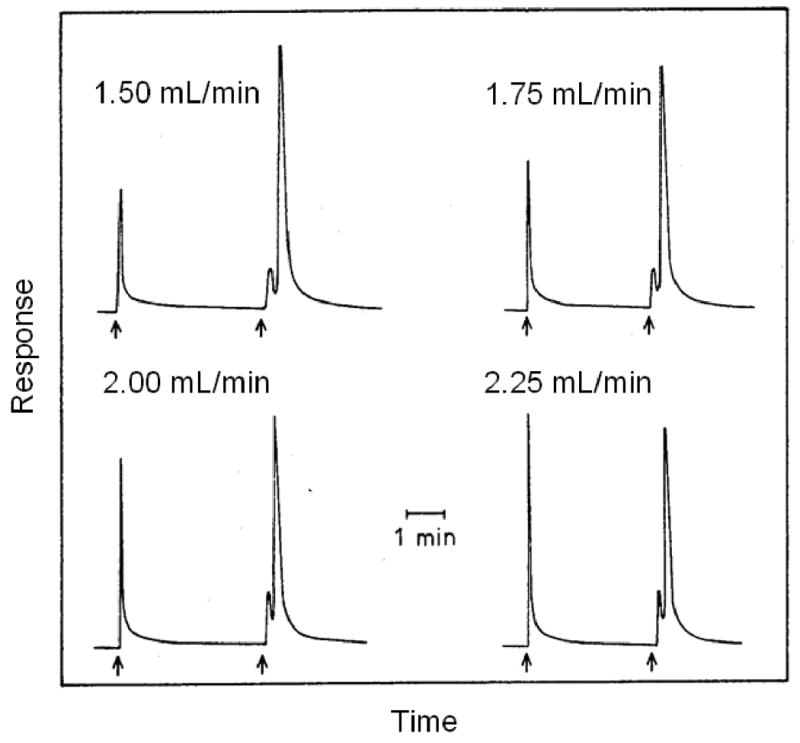
An illustration of the split-peak effect, as observed during the injection of rabbit IgG onto an immobilized protein A column at several flow rates. The sample was injected at the first arrow in each chromatogram and the retained analyte was eluted by a pH change at the second arrow. (Adapted with permission from Ref. [83])

The following equation has been derived to describe the split-peak effect for work under linear elution conditions. This equation shows how the presence of either slow mass transfer, as represented by 1/(k₁V_e), or slow adsorption, represented by 1/(k_a m_L), will affect the free fraction (f) of a solute that elutes non-retained from the column.

$$\frac{-1}{\text{ln f}}=\text{F}\left(\frac{1}{{\text{k}}_{\text{1}}{\text{V}}_{\text{e}}}+\frac{1}{{\text{k}}_{\text{a}}{\text{m}}_{\text{L}}}\right)$$ (11)

In this equation, F is the flow rate of sample application, m_L is the active moles of immobilized ligand or binding sites in the column, and V_e is the excluded (interparticle) volume of mobile phase in the column. The term k₁ is the forward mass transfer rate constant, and k_a is the association rate constant for analyte-ligand binding, as defined earlier in Figure 1 [23]. Eq. (11) can be used for rate constant measurements by first making a plot of -1/ln f versus F for each tested analyte concentration. The size of this slope for any given concentration of applied analyte may depend on the type of column and support that is used in such an experiment, as shown in Figure 8. Figure 8 also shows the typical sample size dependence of these plots, in which measured slope increases as larger amounts of an analyte are used in the study; a correction for this effect can then be made by extrapolating these measured slope to an infinitely dilute sample [23, 66]. Either mass transfer or adsorption may be the rate-limiting step in analyte retention and dominate the extrapolated slope term in Eq. (11) [23, 46, 84]. For some systems, the rate-limiting step can also be identified by comparing the measured slope with independent estimates of the mass transfer contribution for the analyte [23, 66].

Figure 8.

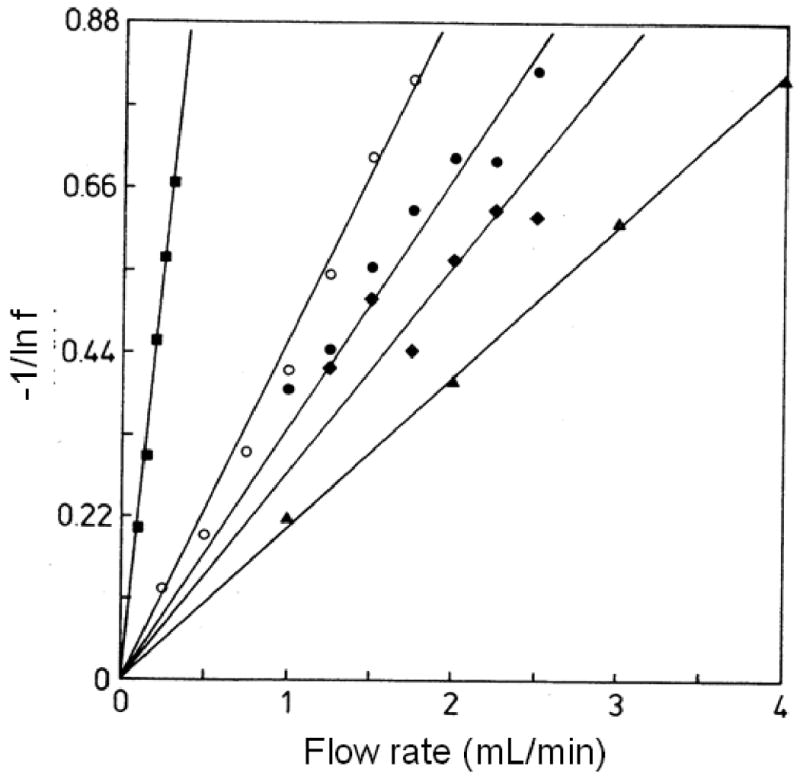
Analysis of data obtained for split-peak studies, as analyzed according to Eq. (11). These results show plots that were obtained for the binding of rabbit IgG to protein A columns in experiments that involved the use of various sample sizes; the Schiff base (SB), carbonyldiimidazole (CDI) or ester amide (EA) immobilization methods; and 10 μm diameter support materials with pore sizes of 50 or 500 Å. The conditions for each plot were as follows: SB method, 500 Å pore size, 22 μg IgG (○); SB method, 500 Å pore size, 11 μg IgG (●); SB method, 50 Å pore size, 15 μg IgG (▲); CDI method, 500 Å pore size, 2.7 μg IgG (■); and EA method, 500 Å pore size, 8.2 μg IgG (◆). (Adapted with permission from Ref. [23])

A split-peak method based on Eq. (11) was originally used by Hage et al. to study the binding kinetics of rabbit IgG on various affinity columns containing immobilized protein A. The results suggested that the rate limiting process for analyte retention of these columns was dependent on the type of support and immobilization method that was being used [23]. This information made it possible to determine the apparent rate constant for IgG binding to protein A and to optimize the performance of protein A affinity supports for the analysis of clinical samples [23, 66, 85]. Computer simulations have been used to predict the response of this method as a function of sample load for a homogeneous ligand under both mass transfer- and adsorption-limited conditions [22], as well as the effect of sample load for the adsorption-limited case in the presence of a heterogeneous ligand for columns that contained mixtures of protein A and protein G [46].

It is possible in some cases to obtain an exact solution for the split-peak effect under non-linear elution conditions. The most common example is given in Eq. (12), which has been derived in various forms to describe the binding of an analyte to a homogeneous ligand under adsorption-limited conditions [44-46, 51, 84, 86].

$$\text{f}=\frac{{\text{S}}_{\text{o}}}{\text{LoadA}}ln\left[1+\left(e^{\text{LoadA}/{\text{S}}_{\text{o}}}-1\right)e^{-\text{1}/{\text{S}}_{\text{o}}}\right]$$ (12)

The term Load A is the relative moles of solute applied versus the total moles of active ligand in the column, and S_o is a combination of system parameters, where S_o = F/(k_a m_L). This method has been employed to study the binding kinetics of HSA to various types of anti-HSA antibodies [44, 45, 51]. Such kinetic measurements have also been combined with studies of epitopes and equilibrium constants to obtain a more complete picture of the antibody interactions with HSA [51].

Eq. (12) has also been used in the derivation of equations to describe the response of chromatographic-based competitive binding immunoassays that are based on the split-peak effect [84, 87, 88], as illustrated in Figure 9. In this example, a sample of HSA was injected onto an anti-HSA column, followed by an injection of a fixed and known concentration of HSA (used in this case as a “label”). A plot was then prepared based on the ratio of the measured quantity of the label that was bound by the column following the injection of the sample (B) versus the amount of bound label in the absence of any injected sample (B_o). The resulting calibration plot of B/B_o versus log[analyte] gave a good fit with the response that was predicted based on an expression derived from Eq. (11). This fit also made it possible to estimate the association rate constant for the HSA/anti-HSA system and provided a result that was in good agreement with values reported for other antigen/antibody interactions [84]. A similar approach based on Eq. (11) has been used with frontal analysis to measure the apparent association rate constants for 2,4-dichlorophenoxyacetic acid (2,4-D) and related herbicides to immobilized monoclonal anti-2,4-D antibodies [89, 90] and the binding of L-thyroxine to anti-thyroxine antibodies and aptamers [37].

Figure 9.

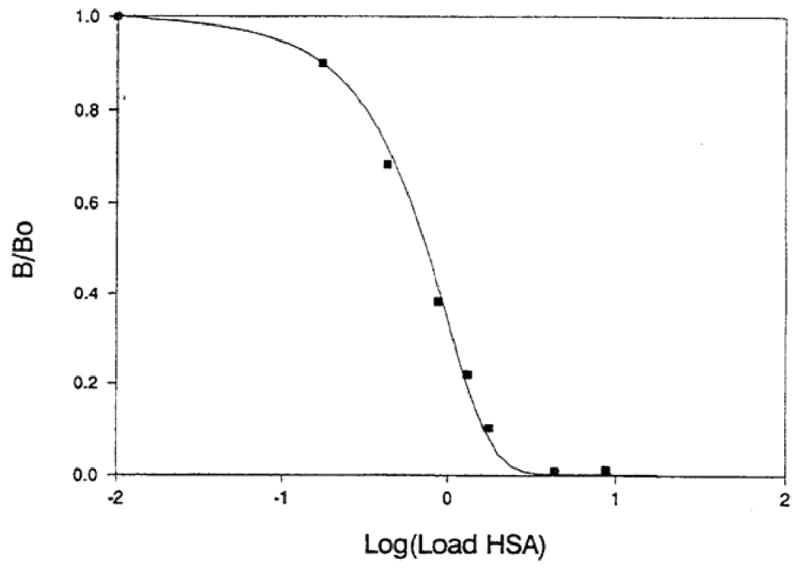
A calibration curve for a sequential addition, competitive binding immunoassay performed using HSA as the analyte and immobilized anti-HSA antibodies as the ligand in an affinity column. The ratio B/B_o represents the relative fraction of a known quantity of labeled HSA that was bound to the column with or without the previous injection of an unlabeled analyte sample. The symbols represent the experimental results, while the line is the best-fit response that was used to estimate the association rate constant for this interaction. (Reproduced with permission from Ref. [84])

An important advantage of using the split-peak method for rate constant determinations is it requires only area measurements. This latter feature makes this method attractive because peak areas are much easier to measure than peak variances or profiles, as are required in the other techniques discussed previously in this review. The main limitation of this approach is it is limited to analytes that have relatively slow dissociation kinetics, which typically indicates the presence of high affinity interactions. It can also be difficult with some types of affinity columns to reach appropriate experimental conditions to observe the split-peak effect. Eqs. (11) and (12) indicate that the extent of this effect will increase as the application flow rate is raised, as the column size is decreased, or as the amount of active ligand in the column is decreased. All of these changes act to lower the probability of any given analyte being retained by the affinity column and will increase the likelihood that a measurable free fraction will be observed.

4.2 Peak decay method

The peak decay method is another technique for rate constant measurements in biointeraction chromatography. As its name implies, this approach is performed under conditions in which part of the analyte elution profile gives a decay curve that can be related to the dissociation rate for the analyte from the column. This method was originally performed by injecting a small pulse of analyte on the column, followed by continuous application of a high concentration of a competing agent that prevented any momentarily dissociated analyte from rebinding to the ligand. This created a situation in which the analyte washed from the column as it dissociated from the ligand. The result was a decay curve that could be used under appropriate experimental conditions to estimate the dissociation rate constant for the analyte-ligand system. High flow rates are typically utilized during this experiment to minimize the effect of mobile phase mass transfer kinetics on the decay profile and to lower the chance that the dissociated analyte will rebind to the immobilized ligand [66].

The peak decay method and theoretical basis of this approach were first reported in 1987 by Moore and Walters [36]. This work was followed by computer modeling studies which examined conditions that were needed to obtain accurate dissociation rate constants through this method [66]. In the case where analyte dissociation is slower than mobile phase mass transfer, Eq. (13) can be used to find the apparent dissociation rate constant for the analyte. This involves collecting data on the elution profile for the analyte from the column and then determining the slope of this elution profile by plotting the natural logarithm of the peak response versus time [36].

$$ln\left(\frac{{\text{dm}}_{{\text{E}}_{\text{e}}}}{\text{dt}}\right)=ln\left({\text{m}}_{{\text{E}}_{\text{o}}}{\text{k}}_{\text{d}}\right)-{\text{k}}_{\text{d}}\text{t}$$ (13)

In this equation, m_Ee represents the moles of analyte that elute from the column at any given time, and m_Eo is the initial moles of analyte that were bound to the column. Other terms in this equation are the same as defined earlier. This expression indicates that a plot of ln(dm_Ee/dt) versus t should result in a linear relationship with a slope of −k_d, which provides the dissociation rate constant for the analyte/ligand system, as illustrated at the bottom of Figure 10.

Figure 10.

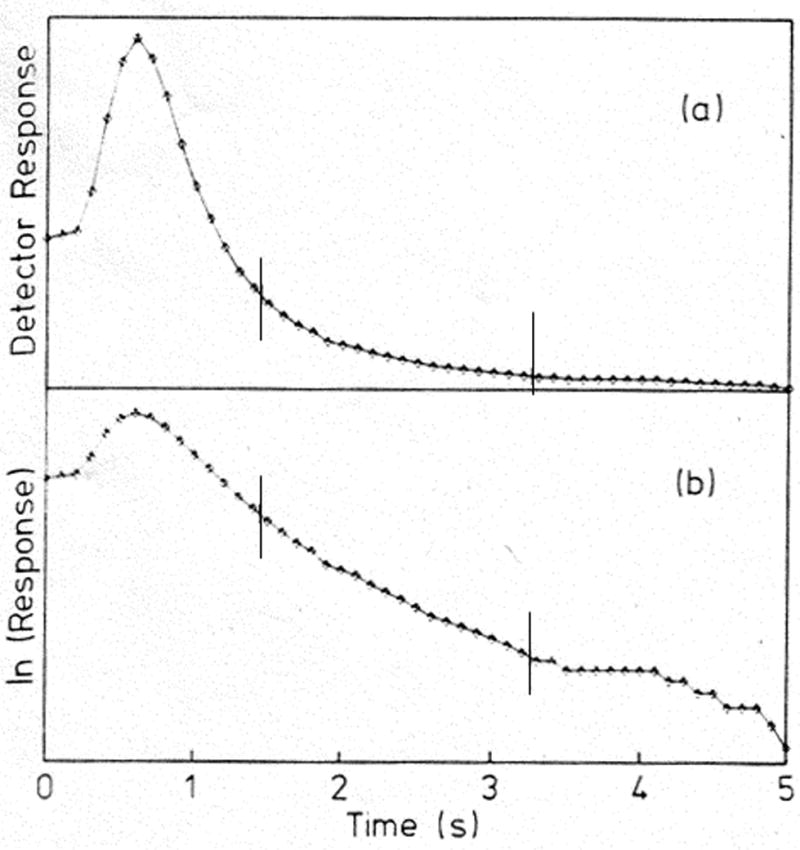
Examples of (a) a typical peak decay curve and (b) a logarithmic transform of this curve as determined for elution of the sugar methylumbilliferyl α-D-mannopyranoside (MUM) from an immobilized concanavalin A column after a step change was made to the continuous application of 0.1 M mannose as a competing agent. These chromatograms were collected on a 6.3 mm × 2.1 mm i.d. column at 10 mL/min. The slope of the curve in (b) was analyzed according to Eq. (13) to obtain the dissociation rate constant for MUM from this column. (Adapted with permission from Ref. [36])

The peak decay method was first used to examine the dissociation of 4-methylumbelliferyl-α-D-mannopyranoside (MUM) from immobilized concanavalin A. Figure 10(a) depicts the elution profile that was observed for MUM as this analyte was eluted after a step change was made to pass through the column a mobile phase that contained a fixed concentration of mannose as a competing agent. After the response of this elution profile was converted to a logarithmic scale, as shown in Figure 10(b), the new plot of this data was analyzed according to Eq. (13) to find the dissociation rate constant from the slope of the central linear region of this graph. It was found that the peak decay method allowed for accurate and precise dissociation rate constants to be obtained for this system as long as sufficiently high competing agent concentration and flow rates were used [36].

One limitation of this original technique is that it required the use of a competing agent for analyte elution. This factor limits the usefulness of this method to systems in which the competing agent and analyte have significantly different signals that can be monitored for selective measurement of the decay profile. It has recently been shown that the peak decay method can also be used with weak to moderate affinity systems without requiring any competing agent. This was accomplished by using short affinity columns (e.g. 2.5 mm in length) and high flow rates to reduce the probability of analyte re-association to the point where no competing agent was necessary. This non-competitive peak decay method was used to measure the dissociation rates of R/S-warfarin from immobilized HSA and gave comparable results to previous rate constant measurements for this system [20]. The peak decay method has also been used to estimate dissociation rate constants for analytes from immobilized ligands in the presence of a step change in the pH of the mobile phase, as has been demonstrated in work looking at the conditions needed to release 2,4-D and related agents from anti-2,4-D antibodies [89, 90].

The peak decay method can be used with either weak or moderate affinity analytes, making it complementary to the split-peak method [20]. The peak decay method can also be employed in the identifying conditions for the elution of analytes from ligands with high binding affinity [89, 90]. The main disadvantage of the peak decay method is that it requires the presence of experimental conditions that cause analyte dissociation from the ligand to be the rate-limiting step in desorption of analyte from the column. Factors that can be adjusted to help create such a condition are the elution flow rate, the column size, the type of support material and (if a competing agent is to be used) the concentration of the competing agent.

5 Concluding remarks

This review has demonstrated how affinity columns and the method of biointeraction chromatography can be a valuable tool in studying the kinetics of biological interactions. Particular emphasis was given to methods that combine affinity ligands with HPLC columns for this type of analysis. Important advantages of affinity columns and HPLC to examine the kinetics of biological systems include the ability of this approach to reuse a biological ligand for a large number of experiments, and the good precision and accuracy of this approach. This approach is complementary to SPR in terms of its ability to measure kinetics for moderate to strong affinity systems. However, biointeraction chromatography is also capable of working with systems that involve small analytes, weak binding or relatively fast association/dissociation kinetics. Increasing the flow rate and reducing ligand density in SPR (i.e., to reduce mass transfer and rebinding effects) can be used to examine small analytes or those with weak binding to a ligand, but the reliability and reproducibility of kinetic measurements in SPR are affected by such modifications [58]. The efficiency of modern HPAC columns and the speed at which they can be used represent other advantages of biointeraction chromatography as a tool for characterizing biological interactions.

A variety of approaches for studying the kinetics of biological interactions have been reported for use with affinity columns (see summary in Table 2). These approaches have included those that are based on plate height measurements, peak profiling, and peak fitting, as well as techniques that make use of the split-peak effect or peak decay analysis. These methods have made it possible to perform kinetic studies for systems that range from weak-to-moderate affinities to those with high affinities. Some of these methods are performed under linear elution conditions (e.g., plate height measurements and peak profiling), while others can be used under non-linear conditions (e.g., peak fitting in zonal elution or frontal analysis methods). The range of methods that are available in biointeraction chromatography is another advantage of this technique that allows kinetic parameters for nearly any analyte/ligand system to be measured.

Table 2.

Summary of methods for kinetic measurements by biointeraction affinity chromatography

Method	Application conditions	Usable range of affinitiesa	Information obtainedb
Plate height measurements	Linear zonal elution	Weak to moderate affinity	kd
Peak profiling	Linear zonal elution	Weak to moderate affinity	kd,app or kd
Zonal elution peak fitting	Non-linear zonal elution	Weak to moderate affinity	kd,app or kd
Frontal analysis curve fitting	Non-linear frontal analysis	Moderate to strong affinity	ka,app or ka
Frontal analysis moment analysisc	Non-linear frontal analysisd	Moderate to strong affinity	ka,app or ka
Peak decay method	Non-linear zonal elution	Weak to moderate affinity	kd or k-1
Split peak method	Non-linear or linear zonal elutiond	Strong affinity	k1 or ka

^aWeak affinity, K_a < 10⁴ M^-1; moderate affinity, K_a = 10⁴ − 10⁶ M^-1; Strong affinity, K_a > 10⁶ M^-1.

^bSymbols and abbreviations: k_d, dissociation rate constant; k_d,app, apparent dissociation rate; k_a, association rate constant; k_a,app, apparent association rate constant; k_-1, reverse mass transfer rate constant for movement of a solute from the stagnant mobile phase to the flowing mobile phase in a column; k₁, forward mass transfer rate constant for movement of a solute from the flowing mobile phase to the stagnant mobile phase.

^cThis approach refers to the analysis of frontal analysis curves through the use of Eq. (10).

^dThe results in this method can be extrapolated to infinite dilution to correct for any concentration dependence in the results.

A variety of applications for kinetic analysis by biointeraction chromatography were discussed in this review. Some examples included the use of this method to examine the interactions of drugs with proteins, sugars with lectins, receptors with their inhibitors, and antibodies with various antigens. This range of systems should continue to grow as new techniques are developed in this field and as more work is conducted to obtain a better understanding of the theoretical and practical aspects of such studies. Recent correlation of inhibitory effects and rate constants measured using bioaffinity chromatography have shown the promise of this method as a tool for the selection of lead drug candidates and in developing quantitative-structure activity relationships useful for drug discovery and development [28]. In addition, kinetic measurements for serum-protein binding can assist in prediction of the pharmacokinetic properties of drug candidates and in optimizing chiral separations of drugs [31, 53, 69]. It is expected from current trends that the future will see an even greater use of affinity columns and biointeraction chromatography as a valuable tool in examining the kinetics of biological interactions for pharmaceutical development and optimizing separations utilizing immobilized ligands.

Abbreviations

AVP

Arg⁸-vasopressin

BNPII

bovine neurophysin II

2,4-D

2,4-dichlorophenoxyacetic acid

HPAC

high-performance affinity chromatography

HSA

human serum albumin

MUM

4-methylumbelliferyl-α-D-mannopyranoside

nAChR

nicotinic acetylcholine receptor

QSAR

quantitative-structure activity relationship

SPR

surface plasmon resonance

a₀…a₃

Non-linear peak fitting parameters for zonal elution

B

Quantity of label bound in a competitive binding assay in the presence of sample

B_o

Quantity of label bound in a competitive binding assay in the absence of sample

C_o

Concentration of injected solute multiplied by the ratio of sample volume to the column dead volume

D

Diffusion coefficient for a solute in the mobile phase

d_p

Particle diameter of a support material

f

Fraction of solute eluting free, or non-retained, from a column

F

Flow rate

I₁

Modified Bessel function used in peak fitting

H or H_total

Total plate height

H_ec

Plate height contribution due to extra column band-broadening

H_k

Plate height contribution due to stationary phase mass transfer

H_L

Plate height contribution due to longitudinal diffusion

H_m

Plate height contribution due to mobile phase mass transfer and eddy diffusion

H_M

Total plate height for a non-retained species

H_R

Total plate height for a retained species

H_sm

Plate height contribution due to stagnant mobile phase mass transfer

k

Retention factor

k₁

Rate constant describing movement of a solute from the flowing mobile phase to the stagnant mobile phase

k_-1

Rate constant describing movement of a solute from the stagnant mobile phase to the flowing mobile phase in a column

K_a

Association equilibrium constant

k_a

Association rate constant

k_a,app

Apparent association rate constant

k_d

Dissociation rate constant

k_d,app

Apparent dissociation rate constant

L

Column length

Load A

Relative moles of applied solute versus the total moles of active ligand

m_Ee

Moles of analyte eluting for a column at a given time

m_Eo

Initial moles analyte bound to a column

m_L

Moles of active ligand

N

Number of theoretical plates

n_mt

Global mass transfer coefficient

q_x

Column loading capacity

S_o

Split-peak constant, where S_o = F/(k_a m_L) for a homogeneous ligand

T

Switching function

t_M

Column void time

t_R

Retention time for an analyte

u

Linear velocity of the mobile phase

V_A

Breakthrough volume for a retained analyte during frontal analysis

V_A*

Breakthrough volume for a non-retained solute during frontal analysis

V_M

Column void volume

V_P

Pore volume within a column

V_e

Excluded volume of mobile phase within a column

x

Reduced retention time in peak profiling

y

Signal intensity at a given time in peak profiling

γ

Tortuosity factor

σ_M

Standard deviation for the peak of a non-retained solute

σ_M²

Variance for the peak of a non-retained solute

σ_R

Standard deviation for the peak of a retained analyte

σ_R²

Variance for the peak of a retained analyte