A layered neural architecture for the consolidation, maintenance, and updating of representations in visual working memory

Abstract

Many everyday tasks rely on our ability to hold information about a perceived stimulus in mind after that stimulus is no longer visible and to compare this information with incoming perceptual information. This ability has been shown to rely on a short-term form of visual memory that has come to be known as visual working memory. Research and theory at both the behavioral and neural levels has begun to provide important insights into the basic properties of the neuro-cognitive systems underlying specific aspects of this form of memory. However, to date, no neurally-plausible theory has been proposed that addresses both the storage of information in working memory and the comparison process in a single framework. The present paper presents a layered neural field architecture that addresses these limitations. In a series of simulations, we show how the model can be used to capture each of the components underlying performance in simple visual comparison tasks—from the encoding, consolidation, and maintenance of information in working memory, to comparison and updating in response to changed inputs. Importantly, the proposed model demonstrates how these elementary perceptual and cognitive functions emerge from the coordinated activity of an integrated, dynamic neural system.

1. Introduction

Human thought and behavior arises within dynamic and often highly complex visual environments. Within such environments, objects are distributed in space and the events within which they are embedded unfold over time. Although the general properties of a complex scene can be obtained in a single fixation (1976; Schyns & Oliva, 1994), acquiring detailed visual information from spatially separated regions requires the sequential inspection of different objects through movements of the eyes (see review in Henderson & Hollingworth, 1999). This allows objects of interest to be centered over the fovea, a region of the retina containing over 30,000 densely packed photoreceptors that provides high-acuity information to the visual system. However, the detailed perceptual representations formed during each fixation quickly fade as the eyes move on to inspect new objects (Irwin, 1993; Simons & Levin, 1997). As a result, some form of visual memory is needed to maintain continuity in perceptual processing. In addition, the use of visual memory is necessary whenever we need to compare visual percepts created at different points in time.

Imagine, for example, that you are sitting at your desk drinking a cup of morning coffee. At some point, you set the coffee cup down and turn away to retrieve a paper from your briefcase. When you turn back towards the desk and reach for the coffee mug, you notice that the cup is different from the cup you were drinking from previously (e.g., its color has changed). What's the cause of this change? Looking around, you realize that a colleague sitting at a nearby desk has picked up your coffee mug, mistakenly identifying it as her own. To detect simple changes such as this, the properties of the first cup must have been held for a brief period of time in memory and subsequently compared to the second cup.

A considerable amount of research has begun to elucidate the properties of the perceptual and cognitive systems supporting behavior in tasks like these. This work has suggested that performance in such tasks relies on a short-term form of visual memory, which we will refer to simply as visual working memory (VWM). This form of memory can be differentiated from much shorter-term iconic memory (see, e.g., Averbach & Coriell, 1961; Irwin, 1992; Phillips, 1974; Sperling, 1960), and from much longer-term forms of memory (see discussion in Luck, in press). Although much has been learned about the neuro-cognitive systems underlying VWM, and detailed theories have been proposed that capture aspects of this system, to date, no neurally-plausible theory has been proposed that addresses both the storage of information in working memory and the process by which the contents of memory are compared to new perceptual inputs. The present report describes a new neurally-based process model that begins to address these challenges.

1.1. Visual working memory and change detection

One of the primary tasks used to study the properties of the visual memory systems supporting behavior in situations like the one described above is the change detection task depicted in Figure 1. A typical trial in this task involves the presentation of a sample array containing one or more simple objects (e.g., colored squares), which observers are asked to remember. This is followed by a brief (e.g., 1000-ms) delay interval, and the appearance of a test array that is either identical to the original sample array, or differs from it in the color of a single object. Participants then make a two-alternative forced choice (2-AFC) response, indicating whether the items in the test array are the same as or different than the items that were present in the sample array. This task mimics the structure of the real-world task described above, but the perceptual and motor demands of the task are minimized, making it a useful method for exploring the properties of VWM.

Figure 1.

Change detection task used to explore properties of visual working memory for simple features (adapted from Luck & Vogel, 1997). Different fill patterns represent different solid colors.

Behavioral studies of change detection have suggested that representations in VWM are established very rapidly (Gegenfurtner & Sperling, 1993; Vogel, Woodman, & Luck, 2006), and in an all-or-none fashion (Zhang & Luck, in press); that the capacity of VWM is highly limited to ∼3-4 items (Cowan, 2001; Vogel, Woodman, & Luck, 2001); and that the detection of changes at test elicits rapid shifts of attention and the eyes to the location of the change (Hyun, Woodman, Vogel, Hollingworth, & Luck, in press). At another level, evidence from functional magnetic resonance imaging (fMRI) (Pessoa, Gutierrez, Bandettini, & Ungerleider, 2002; Pessoa & Ungerleider, 2004; Todd & Marois, 2004; Xu & Chun, 2006) and event related potential (ERP) (Vogel & Machizawa, 2005) studies of change detection have begun to elucidate the specific brain areas supporting these functions (Pessoa et al., 2002; Todd & Marois, 2004; Vogel & Machizawa, 2005; Xu & Chun, 2006). Additionally, single unit recording studies with non-human primates have uncovered the rich spatio-temporal dynamics underlying working memory at the cellular and network levels (see, e.g., Amit & Mongillo, 2003; Fuster & Alexander, 1971; Goldman-Rakic, 1987).

Studies of change detection have begun to make significant contributions to our understanding of VWM at both the behavioral and neural levels. Nevertheless, few theoretical models have been formulated within a neurally-plausible framework that could effectively address both lines of research. This is due in part to the fact that theories in this area have tended to live at two different levels: the verbal/conceptual level of cognitive psychology, and the neurodynamical/biophysical level of computational neuroscience.

Although large-scale integrative theories of working memory have been proposed within cognitive psychology (see, e.g., Baddeley & Logie, 1999; Cowan, 1995), most theories that interface directly with the change detection literature have focused on particular aspects of performance in such tasks. For example, a number of verbal/conceptual models have focused on maintenance, addressing capacity limits and the nature of the representations held in VWM (Alvarez & Cavanagh, 2004; Luck & Vogel, 1997; Wheeler & Treisman, 2002; Zhang & Luck, in press). Such models have been a fruitful source of behavioral hypotheses, however, they have not addressed the question of how such representations are integrated with incoming percepts. In addition, although links to neurophysiology have been suggested, the conceptual models in this domain have not been formalized in a way that explains how the properties of VWM emerge from the complex dynamical processes underlying neural function. Nonetheless, theories within cognitive psychology have a clear strength—a firm commitment to rigorous behavioral research and hypothesis testing.

At the neural level, sustained excitatory reverberation among visually-selective populations of cells has been proposed as a mechanism for maintenance in working memory (see, e.g., Amit, 1995; Grossberg, 1978; Hebb, 1949; Wang, 2001). This proposal has been strongly supported by the discovery of “memory cells” in the prefrontal cortex exhibiting elevated spike discharges during the delay interval of delayed response spatial memory tasks (Funahashi, Bruce, & Goldman-Rakic, 1989; Fuster & Alexander, 1971). Memory cells selective for spatial and non-spatial object properties, tactile stimuli, and other task-relevant information have also been found in cortical areas both within and outside the prefrontal cortex (see, e.g., Andersen, Bracewell, Barash, Gnadt, & Fogassi, 1990; Fuster & Jervey, 1981; E. K. Miller, Li, & Desimone, 1993). The persistent neural activity found in these studies has been recognized as the most likely candidate for the neural basis of maintenance in working memory.

Several neuronally detailed accounts of maintenance have been formulated using integrate and fire and Hodgkin-Huxley neurons (see, e.g. Amit & Brunel, 1997; Compte, Brunel, Goldman-Rakic, & Wang, 2000; Tegner, Compte, & Wang, 2002). For example, Compte et al. (2000) have proposed a model of the prefrontal cortex that captures working memory for single spatial locations through localized peaks of activation in neural fields. Within this model, neurons coding for similar spatial locations are linked through recurrent excitatory connections, with the strength of excitatory coupling decreasing as a function of the distance between their preferred cues. Spatial tuning is further shaped by broad lateral inhibition among neurons preferring differing cues (Rao, Williams, & Goldman-Rakic, 1999). This type of tuning allows localized peaks of activation, or “bump attractors”, representing particular spatial locations, to be sustained in the absence of continuing external input.

Although models such as these capture the maintenance function of working memory, performance of simple visual comparison tasks requires the integration of working memory representations with perceptual representations that are stimulus driven. That is, once a working memory representation has been created, it must be updateable when new, changed sensory information arises. Several models have been developed that address the integration of perception and working memory in the context of specific discrimination paradigms (see, e.g., Machens, Romo, & Brody, 2005; P. Miller & Wang, 2006). For instance, Miller and Wang described a neural model of two-interval vibrotactile frequency discrimination using a rate-coding principle where particular frequencies are represented by different average sustained firing rates. In this task, the specific vibrational frequency of an initial stimulus (S1) is remembered across a short delay interval, and is compared to the frequency of a second stimulus (S2). The animal then makes a binary decision, indicating whether the frequency of S2 is greater than or less than S1. In their model, graded mnemonic activity reflecting the frequency of S1 in working memory provides an inhibitory signal to upstream neurons responding to S2. The inhibitory signal gates later inputs to the model on the basis of the difference in amplitude between S1 and S2. When S2 > S1, upstream neurons overcome the inhibition from working memory and their firing rate increases, whereas when S2 < S1, upstream neurons do not respond. Such differential frequency-dependent responding to S2 provides a plausible means of generating the binary decision required in the frequency discrimination task.

Such models provide a framework for thinking about how both maintenance and comparison functions can arise within a single integrated system. However, because the same population of neurons cannot simultaneously maintain different average firing rates, a general approach to multi-item VWM and change detection using the rate coding principle is not conceptually possible. Because of this, we adopt a space coding principle in the present report where working memory for metric information is realized through sustained peaks of activation in neural fields. Models in this class have primarily focused on working memory for single spatial locations (see discussion of Compte et al., above), and to date have not been extended to address the comparison process (but see Simmering, Spencer, & Schöner, 2006 for steps in this direction). However, such approaches have been rigorously tied to both behavioral and neural data looking at spatial working memory and, therefore, provide a fertile ground to explore the properties of VWM.

In the sections below, we show how a multi-layered dynamic neural network can be used to implement basic perceptual and memory functions, including the encoding and maintenance of information about multiple items in VWM, and the comparison of working memory representations with perceptual representations required in change detection tasks. The proposed model goes beyond existing formulations, showing how the separate functions necessary for performance in change detection tasks may emerge from a single, integrated dynamic neural network. As such, this framework can serve as a bridge between the behavioral models of cognitive psychology and the neural models of computational neuroscience.

2. Dynamic Field Theory of VWM and Change Detection

To begin addressing VWM and change detection within an integrated neural system, we have developed a new model that builds on the Dynamic Field Theory (DFT) of spatial cognition (see, Simmering, Spencer, & Schutte, forthcoming; Spencer & Schöner, 2003; Spencer, Simmering, Schutte, & Schöner, 2007). The DFT is in a class of bistable attractor neural network models that were originally developed to capture the dynamics of neural activation in visual cortex (see, e.g., Amari, 1977; Buerle, 1956; Griffith, 1963, 1965; Grossberg, 1980; Wilson & Cowan, 1972). This framework has been used to account for the processes that underlie saccadic eye movements (Kopecz & Schöner, 1995; Wilimzig, Schneider, & Schöner, 2006), motor planning (Erlhagen & Schöner, 2002; Schutte & Spencer, 2007), infants' performance in Piaget's A-not-B task (Thelen, Schöner, Scheier, & Smith, 2001), the dynamics of neural activation in motor and premotor cortex (Bastian, Riehle, Erlhagen, & Schöner, 1998; Bastian, Schöner, & Riehle, 2003a), and the behavior of autonomous robots (Bicho, Mallet, & Schöner, 2000; Engels & Schöner, 1995; Schöner, Dose, & Engels, 1995). In other work, neural fields have been used to explore single- and multi-item working memory (see, e.g., Laing & Chow, 2001; Laing, Troy, Gutkin, & Ermentrout, 2002; Macoveanu, Klingberg, & Tegner, 2006; Tegner et al., 2002) and the processes underlying visual attention (Rougier & Vitay, 2006), among other things. In the present report, we expand the framework of the DFT to address the maintenance of multiple items in VWM and the process of change detection.

2.1. Two-layer neural field models of elementary perceptual and memory processes

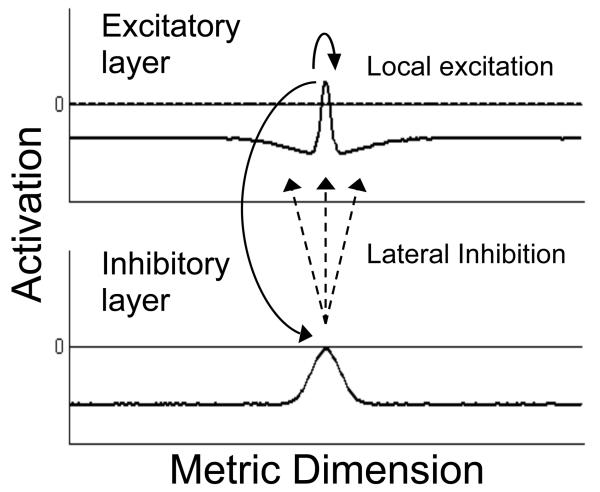
A simple two-layer network of the type analyzed by Amari (1977; Amari & Arbib, 1977) is shown in Figure 2. The basic model consists of a single population of visually-selective excitatory neurons reciprocally coupled to a second population of similarly tuned inhibitory neurons. These neurons are arranged by their topographic position in cortex, thereby forming a continuous dynamic neural field. Thus, the discrete sampling of inputs by individual neurons that is more typical in neural network approaches is replaced in this formulation by a continuous neural field that represents the metric structure of the represented dimension. Such dimensions could be spatial in nature, representing, for instance, the retinal location of a perceived stimulus, or non-spatial, representing the color or orientation of the stimulus.

Figure 2.

Two-layer neural field model of the type analyzed by Amari (1977). The model consists of a single layer of feature-selective excitatory neurons reciprocally coupled to a similarly-tuned layer of inhibitory interneurons. Neurons coding for similar values along the metric dimension in the excitatory field engage in locally excitatory interactions (curved solid arrow), and transmit excitatory activation to the inhibitory layer. Neurons in the inhibitory layer transmit broad lateral inhibition back to the excitatory field (dashed arrows). See text for additional details

Although the field concept was originally developed to address neural dynamics in topographically organized visual areas (e.g., V1), the same methods have been used where no clear topographic organization exists on the cortical surface (e.g., in the motor cortex; see Bastian et al., 1998; Erlhagen, Bastian, Jancke, Riehle, & Schöner, 1999; Georgopoulos, 1995). In this case, neurons within the field are ordered according to their functional topography—that is, by each neuron's “preferred” stimulus, with nearby neurons in the field coding for similar properties (e.g., similar colors), and distant neurons coding for distinct properties (e.g., different colors).

Patterns of activation within such fields can live in different attractor states. For instance, in the absence of input, the activation level across the population of neurons remains at a stable baseline rate, indicating that no relevant features are currently present. However, in the presence of input, reflecting, for instance, the appearance of a particular colored object in the task space, activation increases for those neurons selectively tuned to this feature. If input is sufficiently strong, the stable baseline firing state is destabilized and the field moves into an “on” state, characterized by the formation of a localized peak of activation within the field. The location of the resultant peak along the represented dimension reflects the field's estimation of the metric values present in the task space (e.g., the detection of a particular color), in keeping with the space coding principle. Two or more instances along the dimension are represented by a double or multi-peaked distribution, with the level of activation providing an estimate of the certainty of each informational source. For instance, a high level of certainty about the presence of a particular feature (e.g., blue) is represented by a higher level of activation than a less probable feature (e.g., red).

Although the picture sketched thus far parallels many of the concepts used by feed-forward networks, it is important to emphasize that activation in dynamic neural fields does not simply mimic the structure of input (though that is one potential limit case of the model's dynamics). Rather, activation in dynamic neural fields can take on a life of its own due to the internal dynamics that govern the evolution of activation through time. The model developed here uses the generic locally excitatory and laterally inhibitory, or “Mexican hat”, form of interaction among neurons described by Amari (1977), and commonly found in models of cortical function (Durstewitz, Seamans, & Sejnowski, 2000; Rao et al., 1999). With this form of interaction, neurons coding for similar properties (e.g., similar locations, features, objects, etc.) enter into mutually supportive interactions via excitatory synaptic connections (curved solid arrow in Figure 2), and neurons coding for very different properties enter into mutually suppressive interactions (dashed arrows in Figure 2) mediated by a field of inhibitory interneurons.

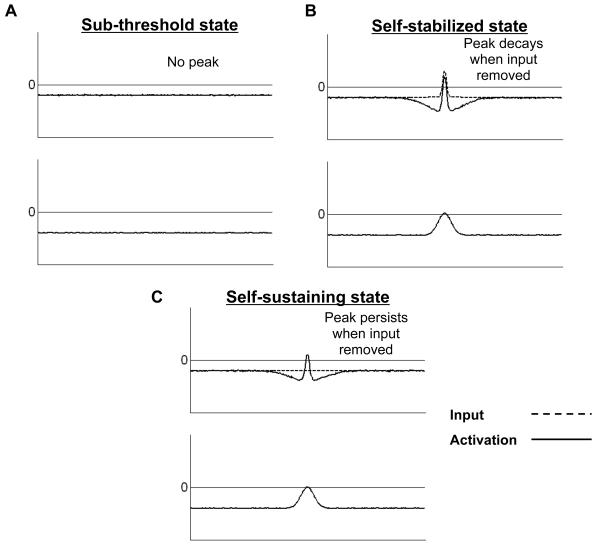
The simulations in Figure 3 illustrate the three basic attractor states that arise in the 2-layer dynamic neural field model. The first attractor state is illustrated in Figure 3A, which shows the state of the field prior to input. At this point, the field is characterized by a stable sub-threshold state of activation, reflecting the absence of information along the metric dimension. In Figure 3B, the field has transitioned to a self-stabilized state, wherein one or more above-threshold peaks of activation are formed in response to specific input. Such peaks remain above threshold as long as the input remains on, but quickly transition back to the sub-threshold state when input is removed. Finally, in the simulation shown in Figure 3C, the strength of excitatory recurrence among neurons in the excitatory layer has been increased slightly. In this case, the field enters a self-sustaining state where peaks of activation can remain above threshold after the input has been removed, a form of working memory that is central to the work presented here.

Figure 3.

Three basic attractor states arising in the two-layer dynamic neural field model. (A) A stable sub-threshold state, where activation at all field sites is negative, reflecting the absence of information along the represented dimension. (B) A self-stabilize state, where localized peaks of activation, representing the detection of a particular feature (e.g., a certain color) in the task space, are formed in the presence of input but decay once input is removed. (C) A self-sustaining state where localized peaks of activation are maintained in the absence of input, implementing a form of working memory. In each panel, input to the model is represented by a dashed line, whereas the pattern of activation within the field is indicated by a solid line.

Which attractor regime a field is in depends on several factors, all of which depend on the dynamic balance between excitation and inhibition. If inhibition is too strong relative to excitation, peaks will transition back to the sub-threshold state once the stimulus has been removed. However, changing the strength of excitatory and inhibitory neural interactions is not the only way to move the network into a given regime. With all other parameters held constant, a given network can be made to function in either the self-stabilized, input-driven regime or the self-sustained regime through global modulation of the resting level of neurons in the field. This changes the functional balance between excitation and inhibition without requiring specific changes to the neural interaction parameters that determine the strength of excitatory and inhibitory projections among layers. Such modulations could play a role in “executive” processes (e.g., processes believed to be implemented by the PFC) which maintain task demands, in part, by determining what types of information are maintained in working memory for use in ongoing tasks (see, e.g., D'Esposito, 2007; Fuster, 2003). For instance, in a task where color is the relevant behavioral dimension, the resting level of neurons in color-selective regions of cortex could be boosted slightly, allowing them to enter the self-sustained state following stimulus presentation (Buss & Spencer, 2008). Conversely, the resting level of neurons coding for task-irrelevant dimensions (e.g., orientation) could be reduced through global inhibitory input, diminishing the role these neurons play in the control of ongoing behavior and mental processes (see also Gruber, Dayan, Gutkin, & Solla, 2006, which explores the role of dopaminergic modulation in gating access to working memory).

2.2. Integrating perceptual and memory processes in a three-layer dynamic neural field model

The simple two-layer networks introduced in the last section can serve either a perceptual or a working memory function. Thus, taken separately they capture some of the requirements of a model of VWM and change detection. For instance, a two-layer network operating in the self-stabilized regime, where peaks of activation are formed in response to input but die out when input is removed, could be used to capture the perceptual encoding of the test array. Additionally, a two-layer network operating in the self-sustaining regime, where peaks of activation remain above threshold after input has been removed, can be used to implement maintenance in VWM. However, as discussed previously, modeling working memory and change detection requires that each of these functions be integrated to explain how items currently maintained in VWM are compared to perceived items in the test array.

To address this, we have developed a three-layer architecture consisting of two layers of excitatory neurons coupled to a single layer of inhibitory neurons. This framework allows simple perceptual and working memory functions, including the detection of stimuli in the task space and their retention in working memory, to be implemented in the same neural architecture. In addition, excitatory and inhibitory interactions among the layers gives rise to emergent decisions about detected change. The next section describes the architecture and patterns of connectivity of the model, and presents a series of simulations illustrating the model's functionality. These simulations demonstrate that the model can serve as an integrated neural framework that captures the encoding, consolidation, and maintenance of information in WM, in addition to the coordination of WM and perception leading to updating and change detection in the face of changing sensory inputs.

2.2.1. Model Architecture

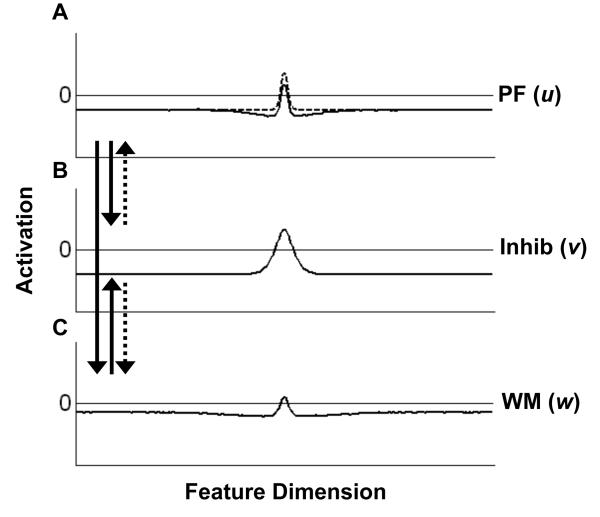
To combine basic perceptual and working memory functions in a single neural architecture, we have developed the three-layer dynamic neural field model depicted in Figure 4 (for equations and parameter details, see Appendix A and Table 1, respectively). The model consists of an excitatory perceptual field (PF(u); Figure 4A), an excitatory working memory field (WM(w); Figure 4C), and a shared inhibitory field (Inhib(v); Figure 4B). In each field, the x-axis consists of a collection of neurons tuned to particular metric features (e.g., specific colors), and the y-axis shows each neuron's activation level. Excitatory and inhibitory connections among the layers are indicated by solid and dashed arrows, respectively. With respect to this coupling, it is important to note that only positive levels of activation are significant. That is, only sufficiently activated field sites transmit their activation to other neurons, and thus contribute to the evolving patterns of activation across the network. This is captured by the sigmoidal nonlinearity characteristic of neuronal dynamics (Grossberg, 1973).

Figure 4.

The three-layer dynamic neural field model of visual working memory and change detection. The model consists of an excitatory perceptual field, PF(u), (A), and an excitatory working memory field, WM(w), (C), which are reciprocally coupled to a single layer of inhibitory neurons (B). Excitatory and inhibitory patterns of connectivity among the layers are indicated by solid and dashed arrows, respectively. In addition, neurons in both PF and WM engage in localized excitatory interactions (curved solid arrow). Input to the network is indicated by the dashed lines in PF and WM.

Perceptual inputs to the network take the form of Gaussians positioned at particular locations in the field and having a particular strength and width. As its name suggests, PF is the primary target of perceptual input to the model. However, the neurons in the WM field also receive weak direct input (see parameter details in Table 1)¹. Additionally, nearby neurons (i.e., neurons coding for similar colors) in both fields interact via local excitatory connections. With respect to coupling among the layers, PF provides excitatory input to both Inhib and WM, and Inhib provides inhibitory input to both PF and WM. Significantly, WM only interacts with PF via the inhibitory layer. That is, the only external source of excitatory input to PF is direct stimulus input. Note, however, that the fundamental pattern of interactions is symmetrical for PF and WM: both project excitation to the inhibitory layer and receive inhibition in return, and neurons in both fields engage in locally excitatory interactions. The primary difference between them, therefore, is the source of their excitatory input. PF is primarily excited by direct afferent input, whereas WM is primarily excited by PF. This asymmetry of input channels leads to the emergence of different functional roles, with PF being responsible for detecting new inputs, and WM serving to maintain activation patterns consistent with past inputs (see discussion below). To serve this role, WM must be buffered from external input to some degree, which is why its primary input comes from PF, rather than directly from earlier visual areas. Finally, because the projection from PF or WM to other neuronal structures, such as motor structures responsible for generating behavioral responses, is subject to the same rule of non-linear sigmoidal transmission, only sufficiently activated sites in either layer have behavioral significance. That is, activation levels in the field and the associated sigmoid are normalized such that sites with positive levels of activation successfully transmit their state to downstream structures, whereas sites with negative levels of activation do not. Note that to explain the model's functionality we have opted to show patterns of activation at particular moments in time in all figures; however, patterns of activation evolve continuously over time.

3. Model simulations

In the present section, we present a series of simulations that demonstrate the emergent functionality of the three-layer model described above. Our model's ability to capture specific data sets, and the impact of noise and distractors on the functioning of the model are explored elsewhere (see, e.g., Johnson, Spencer, Luck, & Schöner, submitted; Spencer, Perone, & Johnson, in press). We begin by showing how the model behaves when a single input is applied, moving from perceptual encoding, to working memory consolidation and maintenance, to comparison and updating. After this, we discuss the multi-item case, showing how the model can capture multi-item VWM and change detection.

3.1. Single-item perception and working memory

3.1.1. Perceptual encoding

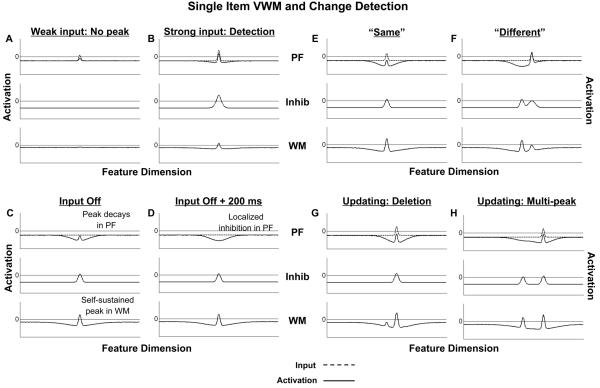
The resting level of neurons in each field, h < 0, ensures that interaction among neurons only plays a role in the presence of sufficiently strong input. For localized inputs, S(x), with low amplitude, PF, and to a lesser extent WM, begins to assume the form of the input, but activation values across all field sites remain negative (see Figure 5A). That is, PF and WM remain in the stable sub-threshold activation state. When the amplitude of the input is sufficiently strong (see Figure 5B), however, interactions among neurons come into play. At this point, PF transitions to the self-stabilized state consisting of a localized peak of activation centered at the location of the input. The size and shape of the peak reflects both the input state, as well as locally excitatory and laterally inhibitory interactions among neurons (via recurrence between PF and Inhib). The transition from the sub-threshold state to the self-stabilized state as a function of input strength involves a dynamical instability and is the mechanism by which detection decisions, or perceptual encoding, emerges in the model. Thus, for the model to detect a stimulus, input to PF needs to be sufficiently strong and of sufficient duration to generate a self-stabilized peak of activation.

Figure 5.

Simulations demonstrating the emergent functionality of the three-layer model in response to a single input. Dashed lines show the input to the model, whereas activation within each of the layers is represented by solid lines. (A) With weak input all field sites remain below threshold. (B) When input strength is increased, the field goes through an instability, resulting in the formation of a self-stabilized peak in PF. (C) When input is removed, the peak decays in PF, but is sustained in the WM layer. (D) During the delay interval, the only input to PF is from Inhib, which receives excitatory activation from the sustained peak in WM. This produces a region of localized inhibition in PF surrounding the maintained value. (E) and (F) show the generation of “same” and “different” responses in the model. A new peak is built in PF only when a new input that is sufficiently different than the value being held in WM is presented to the model. The presence of a peak in PF at test serves as the basis for a “different” response. (G) and (H) show the updating of WM in response to new input. In the first case, the original peak is destabilized and replaced by a new peak, whereas, in the second case, a second peak is added to the field without destabilizing the original peak.

3.1.2. Consolidation and maintenance in working memory

In addition to activating neurons in Inhib, above-threshold activation in PF is propagated to WM, which also receives weak direct input as described above. With sufficiently strong input, a single peak of activation begins to build in WM (see Figure 5B). As before, this peak is stabilized by locally excitatory interactions in WM together with broad lateral inhibition from Inhib (see solid arrows from PF to Inhib and from WM to Inhib in Figure 4). Figure 5C shows the consequences of removing the input from PF. This event leads to the destabilization of the peak in PF. In contrast, a self-sustaining peak of activation remains in the WM field. This occurs as a result of the large reduction of excitatory input to PF when the input is removed, and a consequent reduction of inhibitory input to WM (note lower levels of activation in middle layer of Figure 5C), which also continues to receive excitatory input as long as above-threshold activation is present in PF. The strength of recurrent excitatory connections among neurons in WM is somewhat stronger than in PF, giving WM a competitive advantage once the input is removed. Although this contributes to both the maintenance of the peak in WM as well as the destabilization of the peak in PF via shared inhibition, sustained activation also arises in a variant of the model where the strength of excitatory recurrence in PF and WM is identical. Thus, the different functional roles of PF and WM do not merely reflect differential tuning, but arise, in part, as a function of the asymmetry in their input channels, which allows self-sustained activation to emerge in the WM layer as a result of the flow of incoming activation directly to PF and indirectly to WM.

3.1.3. Emergent change detection and updating in WM

In the absence of continuing perceptual input, the only input to PF comes from Inhib, whose activation is driven by the presence of a self-sustaining peak in WM. As a result, a region of inhibition is formed in PF at the location of the sustained peak in WM (see Figure 5D, top layer). This leads to a failure to re-ignite a peak in PF when a second input that matches the value being maintained in WM is presented to the model (see Figure 5E). As a result, the model remains in its previous state, with a single stable peak of activation sustained in WM, and negative activation in PF. The presence of a peak in WM, but no peak in PF at test serves as the basis for a “same” decision in the model.

Compare this with a trial where a metrically very different input is applied at test. In this case, the input enters PF at a relatively uninhibited site, which allows an above-threshold peak to be built in PF at the location of the new input (see Figure 5F). The presence of a new peak in PF at test serves as the basis for a “different” response.

Thus, responding “different” relies on a specific neural response to novel input, whereas “same” responses are generated by activation that is already present in WM. This mode of operation is consistent with the findings of Hyun et al. (in press), showing that the detection of changes at test generates an active change signal that produces rapid shifts of attention and the eyes to the location of the change (see also Beck, Rees, Frith, & Lavie, 2001; Pessoa & Ungerleider, 2004)². Moreover, because “different” responses must wait for activation to build in PF and overtake activation associated with maintenance in WM, “same” responses tend to be generated faster than “different” responses, in keeping with previous findings (see review in Farell, 1985; Hyun, 2006). Thus, the model has clear potential for addressing RT effects in visual comparison tasks, although this topic is not explored in detail here.

In addition to signaling that a change has occurred, the presence of an above threshold peak in PF leads to the updating of WM. When the new peak in PF is metrically relatively close to the old peak in WM, interference can arise. In some cases, this can result in the deletion of the old peak in WM and its replacement by a new peak at the value specified by input from PF (see WM field in Figure 5G). However, as shown in Figure 5H, when peaks are metrically far apart, a multi-peak solution can arise where the new peak in PF is added to WM without destabilizing the old working memory peak (for similar functionality in a somewhat different framework, see Gutkin, Laing, Colby, Chow, & Ermentrout, 2001). This would reflect, for instance, the sequential loading of WM with different featural information obtained across successive eye movements or successive presentation of stimuli.

3.2. Multi-item perception and working memory

The goal of the present section is to show that the basic functionality of the model illustrated for single items in the previous section can be extended to the multi-item case. Recall that rate coded models have been used to address discrimination, but are conceptually incapable of multi-item memory. Thus, it is important to demonstrate that the neural field model proposed here goes beyond such models by addressing multi-item VWM and change detection.

3.2.1. Multi-peak encoding, consolidation, and maintenance

The presence of multiple high-amplitude inputs results in the formation of peaks of activation in PF, representing the detection of multiple features in the task space. In general, because PF operates in the self-stabilized mode, where locally excitatory recurrence is somewhat weaker than in WM, several peaks can be simultaneously formed as long as the input remains on. This is demonstrated in Figure 6A. In Figure 6B, these three inputs have been successfully consolidated in the WM layer and are self-sustained even though the input has been removed. In this case, the “Mexican hat” interaction profile, where inhibition declines as a function of the distance from the focus of excitation, allows the locally excitatory interactions associated with each peak to be isolated by lateral inhibition, while keeping the total amount of inhibition in the field relatively low. This makes it possible for multiple items to be maintained simultaneously in VWM (see also, Laing et al., 2002; Macoveanu et al., 2006; Trappenberg, 2003).

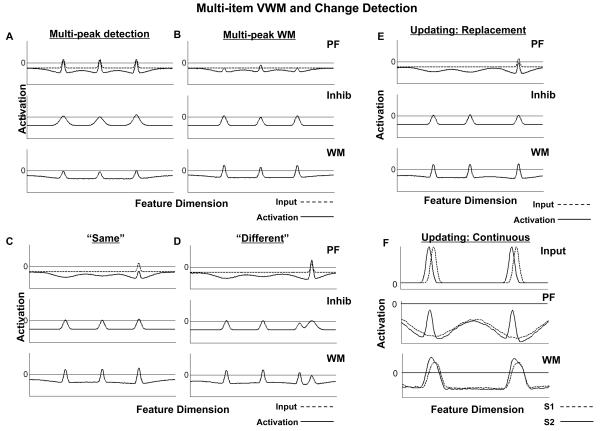
Figure 6.

Simulations of the three-layer model in response to multiple simultaneous inputs. (A) and (B) show the detection of the inputs by PF, and their consolidation and maintenance in WM, respectively. The simulations in (C) and (D) show the generation of “same” and “different” responses in the multi-item case. Finally, (E) and (F) show two different forms of updating in the model. In the first case, the presentation of a changed input at test results in the destabilization of the original peak in WM and its replacment by the new value. In the second case (F), activation in WM is updated in a continuous fashion in response to new input. Note, that the scale of the simulations shown in (F) have been magnified, and the inputs to the model are now shown in the top panel. The first (S1) and second (S2) stimuli presented to the model are indicated by dashed and solid lines, respectively.

3.2.2. Multi-peak change detection

The simulations shown in Figure 6C-D demonstrate robust change detection performance when three items are held in working memory (i.e., when the number of items in memory is below capacity). As with the single-item case, when a new input that matches one of the original inputs is presented (Figure 6C), a new peak fails to be reignited in PF, and the model generates a “same” response. Similarly, when a new input that does not match one of the original items is presented (Figure 6D), a robust peak is built in PF, which serves as the basis for the generation of a “different” response. Note that the model behaves identically when three items, rather than one, are presented at test. When all three items match the original items, no new peak builds in PF. Conversely, when one of the items is different, a peak builds in PF at a location matching the changed input.

3.2.3. Updating in multi-peak WM

Figures 6E-F show two different forms of updating in multi-item VWM. In the first case, the presentation of a new input that is distinct but metrically relatively close to the original value produces interference in WM. This leads to the deletion of the original peak in WM and its replacement by a peak at the new value, that is, the value specified by the peak in PF (compare WM peaks in Figures 6D and 6E).

Figure 6F shows a case where new inputs are presented that are not identical to the original inputs, but are too similar to support explicit change detection. Note that the scale of the simulations has been changed so that this rather subtle effect is visible in the figure. Also, for these simulations, the inputs presented to the model are illustrated in the top panel, rather than in the PF layer, with dashed lines representing the first input (S1), and solid lines representing the second input (S2), which was presented following a 1000-ms delay interval. The bottom two panels show the PF and WM layers of the three-layer model—Inhib has been left out for simplicity. The dashed lines in PF and WM show the patterns of activation in these layers after the offset of the first input. As before, two self-sustained peaks of activation are present in WM following stimulus offset, and neurons representing similar features are inhibited in PF. When the second input is applied, peaks try to build in PF, but are unable to do so because of strong inhibition at those locations. In addition, because WM receives weak direct input when S2 is on, the peaks in WM begin to shift in the direction of the new inputs. That is, WM is updated in a continuous fashion to reflect the values of the new stimulus, even though the change was not large enough to provoke the generation of a “different” response (see Hollingworth & Henderson, 2004).

3.2.4. Capacity limits in VWM

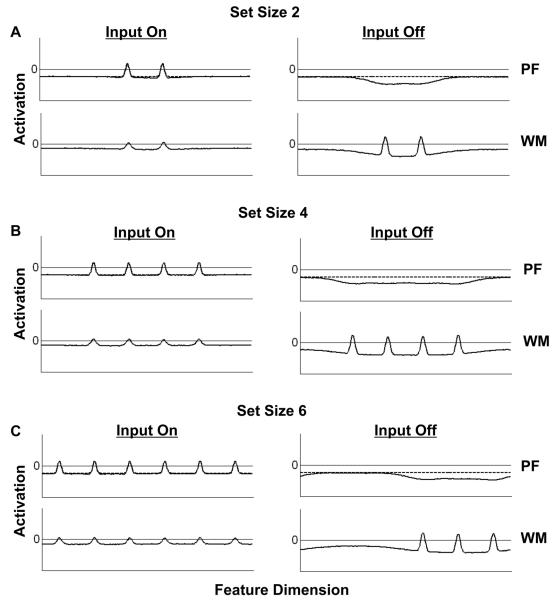
Thus far, we have demonstrated the functionality of the model when the number of items to be remembered (i.e., the number of peaks) is relatively small. What happens when the number of items is increased beyond three? Figures 7A-C show the consequences of adding more and more items to WM. Although the Mexican hat function underlying maintenance in the model allows a multi-peak solution of the field dynamics, the capacity of working memory is not unlimited. As more items are added to working memory, the net excitatory activation increases, which in turn increases the overall amount of inhibition. Figures 7A-B show that the model can stably maintain up to four items in WM. However, when two more inputs are added (Fig. 7C), the level of inhibition overtakes excitation. Recall that inhibition is not homogenous throughout the field, but is governed by an inhibitory interaction kernel of a given strength and width. In addition, activation within the field is influenced by the presence of internal noise. As a result, individual peaks will vary somewhat in their strength and accuracy, and will be subject to varying amounts of inhibition. Thus, as shown in Figure 7C, when additional inputs are added, inhibition selectively prevents several peaks from forming in WM, rather than weakening all peaks equally. Under these circumstances, if a new input were to be presented that matches one of the “forgotten” items, the model would incorrectly generate a “different” response by building a peak at that location in PF³.

Figure 7.

Simulations showing capacity limits in the three-layer neural field model. The simulations in (A) and (B) show the model successfully maintaining up to four peaks of activation simultaneously in WM. However, when two more items are added, inhibitory input to WM outweighs excitation, and three of the items failed to be sustained in the absence of input. Note that, for simplicity, the inhibitory layer is not shown here.

Thus, the proposed model, and bistable attractor network models of maintenance more generally, suggest that capacity limits in change detection arise as a result of limitations in the number of representations that can be simultaneously maintained in working memory (for similar proposals, see Cowan, 2001; Luck & Vogel, 1997; Pashler, 1988; Zhang & Luck, 2008)⁴. This view has been contrasted with a resource-based view of change detection (see, e.g, Wilken & Ma, 2004) which holds that observers can store a potentially large number of representations, with resolution decreasing at larger set sizes due to increased internal noise. Although models based on this latter conceptualization do provide better fits to change detection results than high-threshold approaches in some cases (Macmillan & Creelman, 1991), Zhang and Luck (2008) have demonstrated that this does not hold for limited-capacity models of working memory more generally. Indeed, their work, which applies a signal detection conceptualization to a small and potentially variable number of fixed-resolution representations, provides strong support for the idea that discrete items (e.g., individual objects) are encoded in working memory in an all-or-none fashion. This is consistent with the detection instability underlying encoding in the neural field model proposed here. In each case, when capacity is exceeded, a small number of items are selected for encoding and maintenance in working memory, and the other items are simply forgotten, as shown in Figure 7C.

3.2.5. Selection of inputs for consolidation in working memory

Although the model shows robust change detection performance at smaller set sizes, self-sustained peaks can fail to be established in WM in some cases even though the number of items to be remembered is within the capacity of WM. Thus far, we have assumed that all inputs were more or less identical in strength. This is not entirely unreasonable. For example, normalization of input strength could be mediated through other layers of perceptual processing not implemented here. It is likely, however, that the strength of perceptual inputs arising from different objects in multi-item arrays could vary considerably. Such variations might arise through spontaneous fluctuations, or due to factors such as the relative salience of the objects (e.g., their relative luminance), or the spatial distribution of attention within the display. In this case, less salient objects, or objects that are unattended would produce lower amplitude inputs to PF. This would decrease their likelihood of going through the detection instability and their probability of being consolidated in WM.

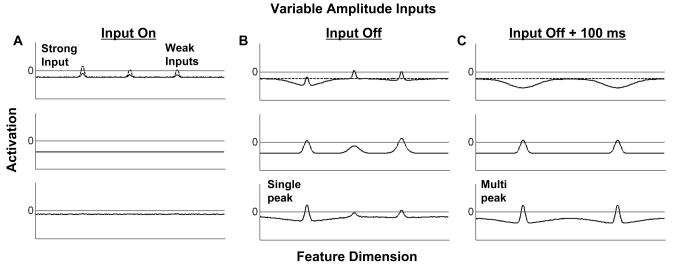
The simulations presented in Figure 8 show the consequences of presenting variable amplitude inputs to the model. For these simulations, the model was presented with one strong input, and two relatively weak inputs (Figure 8A). In this case, the strongest of the three inputs is successfully consolidated and sustained in WM after the input is turned off (Figure 8B), whereas the two weaker inputs remain below threshold. However, when the model is probed a short time later (Figure 8C), a second peak has formed at the location of one of the weaker inputs. Thus, with variable amplitude inputs, the model shows an emergent property of sequential consolidation in WM. In addition, these simulations provide a plausible basis for the finding that attended inputs are more likely to be consolidated in WM (Schmidt, Vogel, Woodman, & Luck, 2002).

Figure 8.

Simulations of the three-layer model with variable amplitude inputs. When one strong and two weak inputs are presented to the model (A), the strong input is successfully consolidated and maintained in WM (B). In addition, a short time later, one of the weaker inputs is also consolidated (C).

4. Discussion

The present paper provided a survey of a new approach to visual working memory and change detection based on the principles of the Dynamic Field Theory that bridges the gap between neural and behavioral levels of theorizing. Although theories at the cognitive level have maintained a tight back and forth with behavioral research looking at VWM, such theories have not been formulated at the level of neural processes, and have not addressed the comparison process in change detection. Conversely, theories at the neural level have shed light on the biophysical and neurodynamical properties of the neural systems supporting maintenance in working memory, but have made little contact with the human behavioral literature looking at change detection. In addition, such approaches have focused primarily on single-item memory for spatial information, and have not addressed multi-item maintenance and the process of change detection in a single, integrated neural system. In the present paper, we described a new neural process model of VWM and change detection that addresses these limitations.

The basic functionality of the proposed model was demonstrated in a series of exemplary simulations showing how the model can be used to capture different aspects of the change detection task. Recall that the first step in change detection involves the detection of items in the memory array and their successful consolidation in working memory. When inputs of sufficient strength and duration are presented to the model, the system goes through a detection instability, marked by an abrupt transition from a stable sub-threshold state of activation to an above-threshold state where localized peaks of activation can be formed and, in some cases, maintained once the input has been removed. Whether peaks of activation are maintained in the absence of input depends on the balance of excitatory and inhibitory inputs to the field.

Excitatory recurrence in PF and laterally inhibitory input from Inhib can move PF into a self-stabilized state in response to input, where one or more peaks of activation are maintained as long as input is present. Once input is removed, however, PF quickly transitions back to the sub-threshold state, where activation at all field sites remains at baseline. In contrast, neurons in the WM layer, where excitatory recurrence is stronger, enter a self-sustaining state in response to input, where localized peaks of activation are maintained after the input is removed. Once a stable self-sustaining peak of activation is formed in the WM layer, the model can be said to have consolidated the information in WM.

The self-sustained state persists unless systematic or random perturbations (e.g., noise) destabilize the peak. One source of systematic perturbation of particular interest here is the case where new inputs are presented to the model some time after the original inputs are consolidated in WM. Under these circumstances, several functions emerge, depending on the nature of the new inputs. When the new inputs are the same as the original inputs, neurons in PF coding for those features fail to enter the self-stabilized state. The failure to build a peak in PF occurs as a result of strong inhibitory recurrence from Inhib, whose activation is driven by the presence of self-sustaining peaks in WM. Thus, in this case, the self-sustained state is maintained in WM, and PF remains in the sub-threshold state.

In contrast, when a new input that is different than the original is presented to the model, patterns of activation in the model are changed depending on the metric similarity of the new and old inputs. When the new inputs are only slightly different than the original inputs, no new peak is built in PF, but the peaks in WM may be updated in a continuous fashion to reflect the new values. In contrast, when a new input is presented that is sufficiently metrically different from the original inputs, PF transitions to the self-stabilized state, signaling that a change has occurred, and working memory is updated to reflect the new value. If the new inputs are metrically similar to the original inputs, the original peak in WM is destabilized, and is replaced by the new value. However, when the new input is metrically very different than the original input, the new item may be added to the WM field without destabilizing the old peak.

Thus, the proposed model realizes each of the basic components needed to capture performance in change detection tasks, from encoding and consolidation, to maintenance, to comparison and updating in response to changed inputs. Importantly, the model shows how these different functions can arise within an integrated, dynamic neural system.

4.1. Neural plausibility of the proposed model

We have claimed that the model proposed here represents a neurally-plausible approach to VWM and change detection. In what sense is our neural field model grounded in neural principles? First of all, there is a demonstrated link between a population dynamics approach to cortical activation and patterns of activation in neural fields, as well as clear methods that can be used to map single-unit recordings onto dynamic population representations that can be directly compared to dynamic field models. For instance, Bastian et al. (Bastian et al., 1998; Bastian, Schöner, & Riehle, 2003b; Erlhagen et al., 1999) have used population coding techniques to compare single-unit neural activity in motor cortex to time-dependent changes in neural activation in a dynamic field model of motor planning. The first step in making this comparison was to map the responses of neurons in motor cortex to basic stimuli and create a continuous field by ordering the neurons based on their “preferred” stimulus. This was followed by a behavioral precuing task that probed predictions of a dynamic field theory of movement preparation (Erlhagen & Schöner, 2002). A similar procedure was used in studies of neuronal interaction in the cat visual cortex (Jancke et al., 1999). In both cases, the reported results suggested a robust relationship between predictions of dynamic field models and neural measures.

Additionally, because cortical neurons never project both excitatorily and inhibitorily onto targets, the inhibitory lateral interaction must be mediated through an ensemble of interneurons. We used a generic, two-layer formulation (Amari & Arbib, 1977) to realize this interaction where an inhibitory activation field receives input from an excitatory activation field and in turn inhibits that field.

Finally, the model presented here incorporates additional insights gained from studies of the layered structure of cortex. Specifically, the three-layered architecture was inspired by a cortical circuit model of the neocortex that was derived from decades of research investigating the cytoarchitecture of the neocortex (Douglas & Martin, 1998). This basic circuit model consists of two interacting populations of excitatory pyramidal cells distributed across different layers of cortex, coupled to a single population of inhibitory neurons. The basic structure and patterns of connectivity within the model are therefore consistent with known principles of cortical organization. It is also possible, however, to achieve the same functionality using a four-layer architecture where each excitatory layer projects to a local inhibitory population in addition to the inhibitory population of the other excitatory field (see, e.g., Edin, Macoveanu, Olesen, Tegner, & Klingberg, 2007). This four-layered architecture would be consistent with the proposal that the perceptual field resides in posterior cortex and the working memory field in another area such as the prefrontal cortex. Future work will be required to assess which of these possibilities is most likely.

4.2. Behavioral plausibility of the proposed model

In addition to providing a framework for capturing existing data and relating behavioral phenomena to neural processes, a central challenge for any model is to make novel predictions that can be empirically tested. How does the model perform in this respect? An interesting property of dynamic neural field models is their metrics, which is reflected in the topographic organization of neurons within the field. As a result, when more than one peak of activation is present in working memory, peaks interact as a function of their metric similarity. For instance, when peaks are relatively far apart in feature space, reflecting, for instance, memory for multiple highly distinctive colors, they either do not interact, or they interact in a weakly inhibitory fashion. In contrast, when items are moved closer together in feature space they interact in a strongly inhibitory fashion. In some cases, this can lead to competition between peaks, with one peak being suppressed by another nearby peak. In other cases, shared lateral inhibition can lead to a narrowing of the range of local excitation associated with each peak in WM, and a consequent narrowing of the inhibitory projection from WM to PF via the inhibitory field. As a result, when a different color is presented a fixed distance away from the original color in color space, neurons coding for the color of the test stimulus are less inhibited for close versus far colors. In the context of our model of change detection, this suggests that it should be easier to detect changes when one of two similar colors are changed at test. This counterintuitive prediction has been confirmed in a series of change detection experiments probing working memory for both color and orientation (Johnson, Spencer, & Schoner, 2006; see also, Lin & Luck, in press).

A second prediction arising as a result of close metrics in VWM is that shared lateral inhibition among similar items will lead to mutual repulsion between nearby peaks. This arises as a result of the fact that when two similar peaks are held in WM at the same time, inhibition is stronger in-between the peaks than it is on the “outer side” of each peak. As a result, it is easier for the excitation associated with each peak to grow in a direction away from the other peak (i.e., away from the other item in memory) across the delay interval. This leads to the prediction that when similar features are held in VWM, they will be systematically biased away from each other over delays. This prediction has been confirmed in a cued color recall experiment comparing memory for a “far” color with memory for two “close” colors (Johnson & Spencer, in preparation).

5. Conclusions

In conclusion, we contend that the three-layer neural field architecture described here provides a useful framework for thinking about how elementary perceptual and cognitive functions can emerge from the coordinated activity of an integrated, dynamic neural system. The proposed model captures each of the primary components required in simple visual comparison tasks such as change detection, and is consistent with general principles of neural function. An important future direction for this approach will be to move beyond general principles and more tightly link the model to behavioral phenomena in this area. The tests of novel behavioral predictions discussed above represent our initial efforts in this direction. The early success of these efforts suggests that the model is in a position to bridge the gap between neural processes and behavioral phenomena.

Appendix A

Model Equations

Activation in the perceptual field, PF (u), is captured by:

$$\begin{array}{cc}\hfill \tau u\acute{Y}(x,t)& =-u(x,t)+h_u+\int c_{\mathit{uu}}(x-x^{\prime }){\Lambda }_{\mathit{uu}}\left(u(x^{\prime },t)\right){\mathit{dx}}^{\prime }\hfill \\ \hfill & -\int c_{\mathit{uv}}(x-x^{\prime }){\Lambda }_{\mathit{uv}}\left(v(x^{\prime },t)\right){\mathit{dx}}^{\prime }+s_{\mathit{tar}}(x,t)\hfill \end{array}$$ (1)

where uY(x,t) is the rate of change of the activation level for each neuron across the feature dimension, x, as a function of time, t. The constant τ determines the time scale of the dynamics. The first factor that contributes to the rate of change of activation in PF is the current activation in the field,-u(x,t), at each site x. This component is negative so that activation changes in the direction of the resting level h_u.

Next, activation in PF is influenced by the local excitation / lateral inhibition interaction profile, defined by self-excitatory projections, ∫ c _uu (x – x′) Λ _uu (u(x′, t)) dx′, and inhibitory projections from the Inhibitory layer (Inhib; v), ∫ c _uv (x – x′) Λ _uv (v(x′, t)) dx′. These projections are defined by the convolution of a Gaussian kernel with a sigmoidal threshold function. In particular, the Gaussian kernel was specified by:

$$c(x-x^{\prime })=c\exp \left[-\frac{{(x-x^{\prime })}^2}{2{\sigma }^2}\right],$$ (2)

with strength, c, width, σ, and resting level, k. The sigmoidal function is given by:

$$\Lambda \left(u\right)=\frac{1}{1+\exp [-\beta u]},$$ (3)

where β is the slope of the sigmoid, that is, the degree to which neurons close to threshold (i.e., 0) contribute to the activation dynamics. Lower slope values permit graded activation near threshold to influence performance, while higher slope values ensure that only above-threshold activation contributes to the activation dynamics. At extreme slope values, the sigmoid function approaches a step function.

Inputs to the model take the form of a Gaussian:

$$S_{{\mathit{tar}}_{\mathit{space}}}(x,t)=c\exp \left[-\frac{{(x-x_{\mathit{center}})}^2}{2{\sigma }^2}\right]\chi \left(t\right)$$ (4)

centered at x_center, with width, σ, and strength, c. These inputs could be turned on and off through time (e.g., the target appears and then disappears). This time interval was specified by the function χ(t). This is referred to as the “index function”, because it is set to one in a given interval, when the stimulus is on, and zero elsewhere.

The second layer of the model, Inhib (v), is specified by the following equation:

$$\begin{array}{cc}\hfill \tau \stackrel{.}{v}& =-v(x,t)+h_v+\int c_{\mathit{vu}}(x-x^{\prime }){\Lambda }_{\mathit{vu}}\left(u{x}^{\prime },t)\right){\mathit{dx}}^{\prime }\hfill \\ \hfill & +\int c_{\mathit{vw}}(x-x^{\prime }){\Lambda }_{\mathit{vw}}\left(w{x}^{\prime },t)\right){\mathit{dx}}^{\prime }.\hfill \end{array}$$ (5)

As before, vÝ(x,t) specifies the rate of change of activation across the population of feature-selective neurons, x, as a function of time, t; the constant τ sets the time scale; v(x,t) captures the current activation of the field; and h_v sets the resting level of neurons in the field. Note that Inhib receives activation from two projections—one from PF, ∫ c_vu (x – x′)Λ _vu (u(x′, t)) dx′, and one from WM, ∫ c _vw (x – x′) Λ _vw (w (x′, t)) dx′. As described above, these projections are defined by the convolution of a Gaussian kernel (Equation 2.2) with a sigmoidal threshold function (Equation 2.3).

The third layer, WM (w), is governed by the following equation:

$$\begin{array}{c}\hfill \tau \stackrel{.}{w}(x,t)=-w(x,t)+h_w+\int c_{\mathit{ww}}(x-x^{\prime }){\Lambda }_{\mathit{ww}}\left(w(x^{\prime },t)\right){\mathit{dx}}^{\prime }\hfill \\ \hfill -\int c_{\mathit{wv}}(x-x^{\prime }){\Lambda }_{\mathit{wv}}\left(v(x^{\prime },t)\right){\mathit{dx}}^{\prime }+\int c_{\mathit{wv}}(x-x^{\prime }){\Lambda }_{\mathit{wu}}\left(u(x^{\prime },t)\right){\mathit{dx}}^{\prime }\hfill \\ \hfill +c_s{s}_{\mathit{tar}}(x,t)\hfill \end{array}$$ (6)

Again, wÝ(x,t) is the rate of change of activation across the population of feature-selective neurons, x, as a function of time, t; the constant τ sets the time scale; w(x,t) captures the current activation of the field; and h_w sets the resting level. WM receives self excitation, ∫ c _ww (x – x′) Λ _ww (w (x′, t)) dx′, lateral inhibition from Inhib (v), ∫ c _wv (x – x′) Λ _wv (v (x′, t)) dx′, and input from PF(u), ∫ c _wu (x – x′) Λ _wu (u (x′, t)) dx′. WM also receives direct target, S_tar(x,t), inputs scaled by c_s.

Table A1.

Parameter values for simulations

Layer	τ	h	self- excitation	excitatory projection(s)	inhibitory projection(s)	target input
u (PF)	80	−7	cuu = 2.0 σuu = 3		cuv = 1.55 σuv = 26	ctar = 121 σtar = 3
v (Inhib)	10	−12		cvu = 2.0 σvu = 10 cvw = 1.95 σvw = 5
w (WM)	80	−4	cww = 3.15 σww = 3	cwu = 1.85 σwu = 5	cwv = 1.05 σwv = 42	[scaled by cs = 0.2]

¹Input strength for the variable amplitude simulations were 12 for the strong input, and 8 for each of the weak inputs.