Flow-Dependent Entrapment of Large Bioparticles in Porous Process Media

Abstract

The need for purification of biomolecules extends to larger bioparticles as well. For example, virus purification is required for production of many vaccines and gene delivery vectors, and understanding virus removal in porous media is also important in downstream processing of therapeutic proteins and in purification of water in soils. A convective entrapment mechanism for retention of large bioparticles is discussed here based on retention of large bioparticles in pore constrictions at high enough flow rates, even under non-binding conditions. A simple equation to predict whether such entrapment is expected to occur in a given system is derived based on a Péclet number that is proportional to the flow rate and to the cube of the bioparticle diameter. To test the theory, adenovirus was spiked onto chromatographic beds. As expected from the theory, under non-interacting conditions a progressively larger amount of virus becomes trapped with increasing flow rate. The entrapment is reversible upon flow rate reduction, which, within the proposed model, is based on the possibility of diffusive escape from pore constrictions. This mechanism can be exploited for virus purification or removal, and the theory also explains the anecdotal evidence that monoliths and membranes are more difficult to clean than conventional chromatographic beds, especially at high flow rates.

Introduction

Purified viruses are used in several different fields, including gene therapy (Flotte 2007), where they serve as gene delivery vectors, vaccines (Morenweiser 2005; Ulmer et al. 2006), and oncolytic viruses (Working et al. 2005). In addition to virus purification, removal of viruses and virus-like particles is an important concern in downstream processing of therapeutic proteins. Not only must the separation steps be capable of removing viruses, regulatory agencies also require understanding of the removal mechanisms to ensure robustness. The mechanism postulated here is based on size, so it applies to bioparticles in general, although special emphasis is placed here on viruses.

Although a variety of separation techniques can be applied to viruses (Braas et al. 1996), this study deals primarily with chromatography, which has been shown to be potentially more efficient for virus purification than density gradient ultracentrifugation, the traditional method for virus purification (Green et al. 2002; Huyghe et al. 1995; Kamen and Henry 2004; Konz et al. 2005; Zhang et al. 2001). Other large therapeutic bioparticles, such as DNA and whole cells, can also be purified by chromatography (Arvidsson et al. 2002; Urthaler et al. 2005). Development of chromatographic processes for virus purification and removal has been been primarily empirical and understanding of the underlying mechanisms is limited. This work reports a nonadsorptive mechanism for virus retention in chromatographic media that may confound conventional interpretations of chromatographic behavior. This mechanism, convective entrapment, applies to large bioparticles that are transported into pores by convection and are unable to traverse the pores fully because of the presence of throats or other constrictions. The particles are able to emerge only if the convective transport is reduced sufficiently to allow escape by diffusion back to the proximal end of the pore.

The postulated mechanism may also be relevant to retention in depth filters and natural porous media, such as soils. Indeed, phenomena similar to that presented here, known as “straining,” “wedging,” and “bridging,” have been described previously in studies of water flow through natural porous media and in depth filtration (Bradford and Bettahar 2006; Bradford et al. 2007; Cushing and Lawler 1998; McDowell-Boyer et al. 1986; Torkzaban et al. 2008), and should apply to removal of viruses and bacteria in soils, an important concern for water resources. In these earlier studies, however, diffusion of the trapped particles has generally been neglected. This may be reasonable for bacteria and other cells, but does not necessarily hold for viruses, since they are an order of magnitude smaller.

The peculiar nature of the postulated mechanism makes it applicable especially in certain classes of chromatographic media used in biotechnology applications. The different types of chromatographic stationary phases (Curling and Gottschalk 2007; Jungbauer 2005) can be divided into four main categories: 1) conventional narrow-pore media, 2) perfusive resins (Afeyan et al. 1990), 3) monoliths (Plieva et al. 2004; Podgornik et al. 2002; Švec et al. 2003), and 4) adsorptive membranes (Giovannini et al. 1998; Han et al. 2005; van Reis and Zydney 2007; Yang et al. 2002), which are essentially thin monoliths. Conventional resins typically have pore diameters that are less than about 100 nm, and therefore smaller than many viruses. Perfusive resins have at least a subset of pores of much wider mean diameter, of order hundreds of nm, but due to the distribution of pore sizes could potentially trap the majority of virus types. Monoliths and membranes are even more likely to trap large bioparticles since their continuous structure resembles those of some filters. In this work we compare virus retention on narrow-pore, perfusive, and monolithic phases, all under non-adsorptive conditions, and present results consistent with the postulated convective entrapment mechanism. We complement these results with a quantitative model describing the balance of convection and diffusion in porous media that can be used to assess the likelihood of retention in pore constrictions in a given system.

Theory

The proposed physical basis for the retention mechanism is shown in Figure 1. If a porous medium contains pores with constrictions through which a bioparticle, e.g., a virus, cannot pass (Figure 1A), there is a possibility that some fraction of the bioparticles flowing through the porous medium will become convectively trapped in these pores. Once a particle reaches such a constriction, the only way for it to escape is by diffusion. If downstream convection >> upstream diffusion, the virus particle will remain trapped (Figure 1B). At sufficiently low flow rates, however, diffusion is capable of moving the virus particle against the flow to wider pores (Figure 1C).

Fig 1.

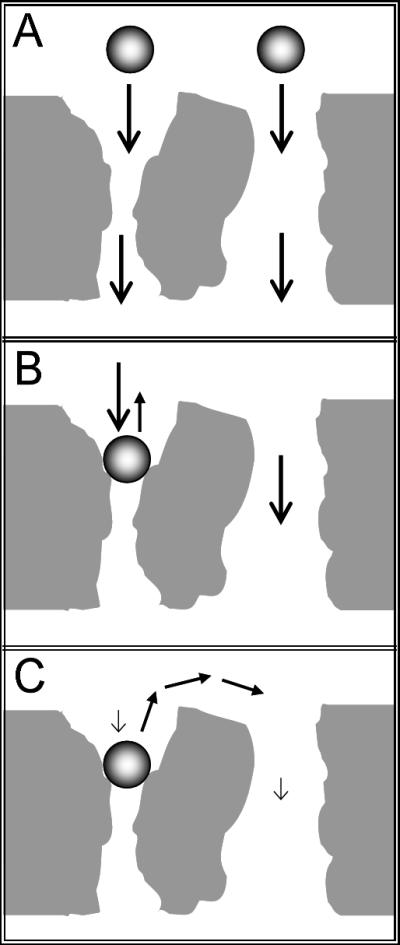
Schematic representation of a bioparticle, e.g., a virus, in a porous medium at high and low flow rates: A) Although the average pore size may be larger than the bioparticle, porous media can contain pore constrictions, i.e., throats, through which the bioparticle cannot pass. B) If convective transport is dominant relative to diffusive motion, the bioparticle remains trapped by the flow. C) If the flow velocity is sufficiently small that convective transport is slow compared to diffusion, the bioparticles can move from constricted pores into wider ones, which allows them to elute.

The explanation in Figure 1 can be quantified by defining a Péclet number (Pe) for the trapping phenomenon as

$$Pe\equiv \frac{u_{c}L}{D},$$ (1)

which represents the ratio of convective transport into the constriction to diffusion out of the trap. Here D is the bioparticle diffusivity and L is a measure of the length that the bioparticle would have to diffuse to escape from a constriction. The key to defining Pe properly in Equation 1 is u_c, the flow velocity through the constriction. Since the flow velocity in a pore is expected to be proportional to the square of the pore diameter (Batchelor 1967), the ratio of u_c to the average flow velocity is approximately equal to the ratio of the corresponding diameters squared, so u_c can be estimated as

$$u_c\approx \frac{u_s}{\epsilon }{\left(\frac{d_c}{d_p}\right)}^2,$$ (2)

where d_p is the average pore diameter, d_c is the diameter of the pore constriction, which is comparable to the bioparticle diameter (d_b), ε is the total bed porosity, and u_s is the superficial linear velocity. Combining equations 1 and 2 with the Stokes-Einstein equation gives

$$Pe\approx \frac{L{u}_s{d}_c^2}{\epsilon D{d}_p^2}\approx \frac{3\pi \mu d_{b}L{u}_s{d}_c^2}{\epsilon d_p^{2}kT}.$$ (3)

in which k is the Boltzmann constant and T is the temperature. For order of magnitude estimation, L ≈ d_p and d_c ≈ d_b, so Equation 3 simplifies to

$$Pe\approx \frac{3\pi \mu u_s{d}_b^3}{d_p\epsilon kT}.$$ (4)

This order-of-magnitude estimate provides a basis for estimating the likely significance of convective entrapment in a particular medium as a function of bioparticle size. Convective entrapment should be negligible when Pe << 1, which is usually the case for small molecules and proteins. For larger bioparticles, such as viruses, Pe can be of order 1, as demonstrated in the Results section. Pe is directly proportional to d ³_b and, therefore, molecular weight, for bioparticles with similar specific volumes. Since the dependence on bioparticle size is so strong, for very large bioparticles, such as cells, Pe >> 1 in most practical cases. However, the theory predicts that, under non-binding conditions, there exists a flow rate low enough to allow bioparticles to escape by diffusion and pass through the porous medium, provided there is a path free of constrictions that can trap the particles.

Of course, the likelihood of convective entrapment also depends strongly on the structure of the stationary phase. In most cases, entrapment is not expected to occur on conventional (nonperfusive) chromatographic resins due to their pore structure. Not only would many viruses not be able to fit into the pores of these resins, convection in the small-pore beads is likely to be minimal. For example, in a bed of 100 μm beads that have 100 nm pores, the fraction of the flow passing through the resin beads rather than around them is expected to be on the order of 10⁻⁵. In contrast, in 10 μm perfusive beads with 400 nm pores, the fraction of the flow passing through the beads is estimated to be around 2%. As long as the resin beads are an order of magnitude larger than the bioparticles of interest and the intrabead pores of the resin are smaller than the bioparticles, entrapment is unlikely.

For the large bioparticles of interest here, the pore size distribution of packed beds, including perfusive ones, can be estimated as being bimodal: pores between the beads are usually significantly wider than pores within the beads. Resin manufacturers typically provide the average diameter of the pores within the beads (d_w) and the resin bead diameter (d_r). The interstitial porosity between resin beads (ε_i), approximately 0.35−0.42 (DePhillips and Lenhoff 2000; Matheson 1974), and the porosity within the resin beads themselves (ε_w) sum up to the total bed porosity (ε). A pulse of an unretained small molecule can be used to estimate ε. The diameter of the smallest possible constriction in a bed packed with spherical beads is about 0.15d_r. If d_r >> d_b, which is usually the case, entrapment between resin beads will not occur, so L ≈ d_w and Equation 4 can be written more accurately for packed beds as

$$Pe\approx \frac{3\pi \mu u_s{d}_w{d}_b^3}{d_p^2\epsilon kT},$$ (5)

where $\stackrel{‒}{d_p^2}$ is the mean square pore diameter, estimated as

$$\stackrel{‒}{d_p^2}\approx \frac{d_w^2{\epsilon }_w+{\left(0.15d_r\right)}^2{\epsilon }_i}{\epsilon }.$$ (6)

Experimental methods

Small samples of adenovirus were passed through chromatographic anion-exchange columns under non-interacting conditions. The model virus was purified human adenovirus serotype 5 (Ad5), purchased from the Vector Development Lab of the Baylor College of Medicine (cat. Ad5-CMV-eGFP, lot 102307). Ad5 is about 100 nm in diameter, its diffusivity is 3.67×10⁻¹² m²/s, and it has a molecular weight of 1.7×10⁸ and a pI of 4.5 (Fabry et al. 2005; Nermut 1975; Oliver et al. 1976; Trilisky and Lenhoff 2007). The virus solutions were used at room temperature and pH 7.8 at an approximate concentration of 3.5 × 10¹¹ p/mL (0.1 g/L) in 20 mM HEPES, 1.5 M NaCl, 1.7% glycerol, which was also used as the running buffer (isocratic elution). The virus is known to be intact and monodisperse at these conditions (Trilisky and Lenhoff 2007), and the NaCl concentration is high enough to ensure that the conditions were non-binding on all stationary phases that were studied (there were no significant changes in Ad5 retention beyond 1 M NaCl).

Five different stationary phases were used (Table I): three polymeric monoliths, a narrow-pore resin and a perfusive resin. Monoliths were supplied with their own housings and the resins were packed into Waters AP-Minicolumns (0.5 cm ID, bed height given in Table I). The average pore diameter of Q Sepharose XL beads is 12 nm (Yao and Lenhoff 2004), which is much smaller than the diameter of Ad5 (100 nm), so the virus does not enter the pores of this resin, nor should there be significant flow through these resin beads; this is also the case if the dextran grafted into the pores is neglected, leaving the base matrix as Sepharose FF, with a mean pore diameter of around 50 nm (DePhillips and Lenhoff 2000). For the perfusive resin, PL-SAX, the diameter of the macropores in the beads is about 400 nm and the bead diameter is about 10 μm (manufacturer's data). Using small-molecule tracers, the total porosity of the PL-SAX bed was measured to be 0.91. Pore size information for Uno Q is not available, but an order-of-magnitude estimate was obtained using the equivalent pore diameter of 2000 nm from the permeability data (Trilisky 2009).

Table I.

Characteristics of the stationary phases investigated.

Stationary phase	Manufacturer	Lot #	Bed dimensions (cm)		d (μm)	ε	Type	Base matrix	Functional group
			Diameter	Height
4 DEAE CIM disks	BIA Separations	05-GE01−012−001B	1.2	1.2	1.0	0.57	monolithic	poly-methacrylate	tertiary amine (DEAE)
ProSwift WAX-1S	Dionex	006−06−012	0.46	4.4	1.8	0.54
UNO Q-1	Bio-Rad	Q1−4188	0.7	3.5	2.0	0.77		poly-(acrylamide / vinyl)	quaternary amine (Q)
PL-SAX 4000Å 10μm	Varian / Polymer Labs	10M-SAX40−199A	0.5	4.8	dw ≈ 0.4 dr ≈ 10	0.91	perfusive (wide-pore)	PS-DVB
Q Sepharose XL	GE Healthcare	10004024	0.5	5.5	dw ≈ 0.012 dr ≈ 100	n/a	conventional (narrow-pore)	agarose + dextran

All chromatographic experiments were performed on an ÄKTA Explorer 100 (GE Healthcare). Since Ad5 was pure, it was detected at 260 nm, which is proportional to the concentration of the virus in this range (Trilisky and Lenhoff 2007). The UV-900 detector was set to acquire data at the fastest available rate of every 0.1 s with the smallest available averaging time of 0.01 s. To minimize sample dilution due to non-plug flow during filling of the sample loop (30 μL), 100 μL of Ad5 solution was slowly passed through the sample loop. After column equilibration and the start of sample injection, the injection valve was left in the inject mode for the remainder of the run to ensure that the entire sample entered the column. Control runs were performed without a column in place to ensure that there were no losses due to extra-column effects.

Results and discussion

The entrapment phenomenon was postulated to explain an apparent failure to close the mass balance on the virus, i.e., by a reduction in the peak area, in units of absorbance × volume, for a given non-adsorbing pulse. While peak area was conserved for small molecules (NaCl and uridine-5’-monophosphate) and proteins (BSA and ovalbumin) (data not shown), the virus peak area decreased drastically with increasing flow rate. Figure 2 shows an example of such a decrease and Figure 3 shows that the decrease occurred on all the monolithic and perfusive stationary phases that were studied. The entrapment is expected to occur on membranes with appropriate pore size distributions too, although they were not tested experimentally in this work. There was no reduction in the Ad5 peak area for no-column control runs or on the Q Sepharose XL column (Figure 4). Q Sepharose XL and other small-pore resins generally do not contain constrictions that would be expected to trap viruses as large as Ad5.

Fig 2.

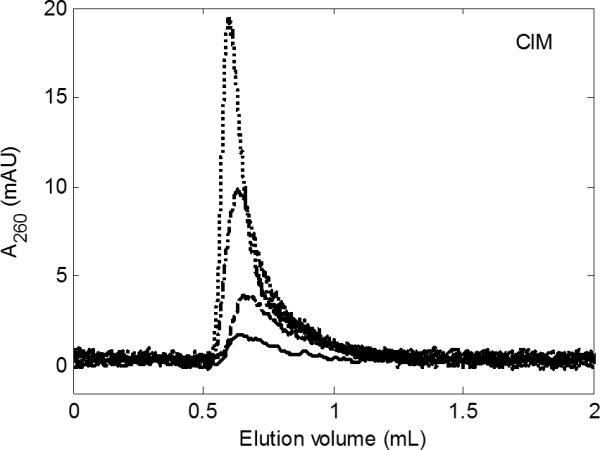
Reduction in Ad5 peak area with increasing flow rate under non-adsorbing conditions. Four DEAE CIM disks; u_s = 0.2 cm/min (········), 0.4 cm/min (- · -), 1 cm/min (- - -), and 2.7 cm/min (—). Pulse and background: 1.5 M NaCl, 20 mM HEPES, 1.7% glycerol, pH 7.8. Concentration of Ad5 in the pulse was 3.5 × 10¹¹ p/mL (0.1 g/L).

Fig 3.

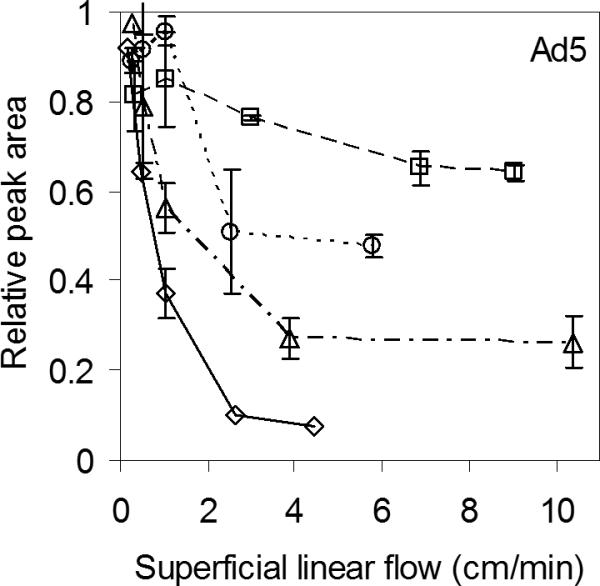
Decrease in Ad5 peak area with increasing flow rate on the three monoliths, 4 CIM disks (—◇—), ProSwift (- -□ - -), Uno Q (- · Δ - ·), and on the perfusive resin, PL-SAX (····○····). Error bars represent one standard deviation based on replicates (n=2-3). Same pulse and background as in Figure 2.

Fig 4.

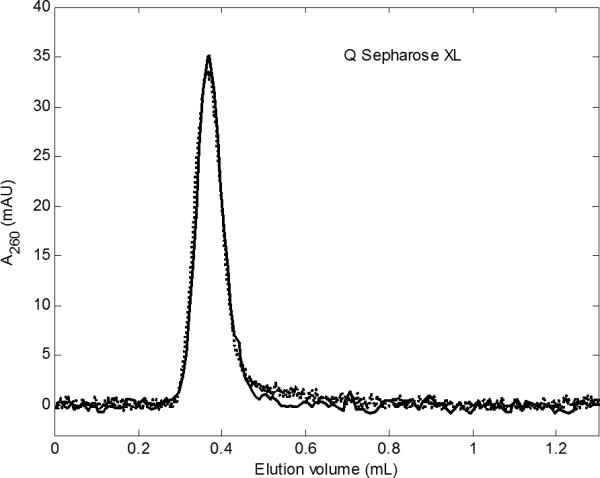
Ad5 pulse on Q Sepharose XL at 1 cm/min (········) and at 25 cm/min (—). The two curves overlap closely. Same pulse and background as in Figures 2 and 3.

The missing virus from the other stationary phases was recovered when the flow rate was reduced, as exemplified in Figure 5 for CIM and PL-SAX. One run was carried out at the lowest flow rate, which was held constant throughout the run, while for higher flow rates, the flow was reduced to the lowest flow rate after about 1.5−2 column volumes, leading to elution of the remainder of the expected peak area. If the flow rate was increased again during elution, the signal dropped down to nearly zero and the elution did not resume until the flow rate was reduced again.

Fig 5.

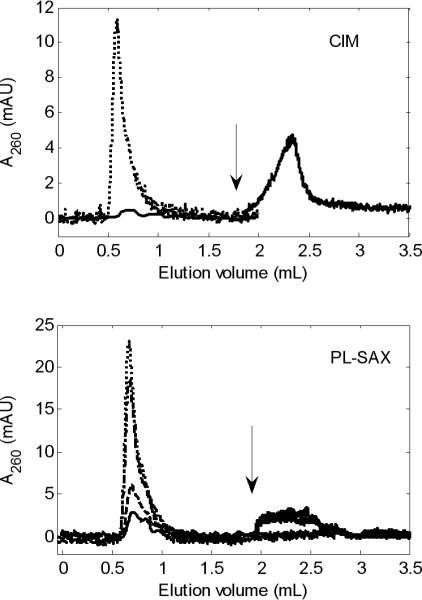
Ad5 pulse on 4 CIM disks (top) and on PL-SAX (bottom). In the top panel, u_s = 0.18 cm/min (Pe ≈ 0.12; ········) and 4.4 cm/min (Pe ≈ 3.1; —). In the lower panel, u_s = 0.25 cm/min (Pe ≈ 0.041; ········), 1 cm/min (Pe ≈ 0.16; - · -), 5.8 cm/min (Pe ≈ 0.93; - - -), and 10 cm/min (Pe ≈ 1.6; —). The arrow indicates where the flow rate was reduced to the lowest value. Same pulse and background as in Figures 2-4.

To explain the results, Pe values estimated using the data in Table I and Equations 4 and 5 are shown in Figure 6. For the highest flow rates, Pe > 1, indicating that convection overcomes diffusion, and for the lowest flow rates, Pe < 1, i.e. diffusion is capable of moving the virus particles out of the constriction traps, allowing them to elute. Since proteins are typically an order of magnitude smaller than viruses, Pe for proteins is 3 orders of magnitude less than unity in these monoliths and the perfusive resin at typical flow rates used in chromatography (∼1−10 cm/min), which explains why the entrapment is usually negligible for proteins, although not completely absent. At the opposite end of the spectrum, for bioparticles significantly larger than Ad5, Pe >> 1. Bacteria, for example, are on the order of 1 μm in diameter, so Pe for bacteria is 3 orders of magnitude greater than unity under the conditions studied here.

Fig 6.

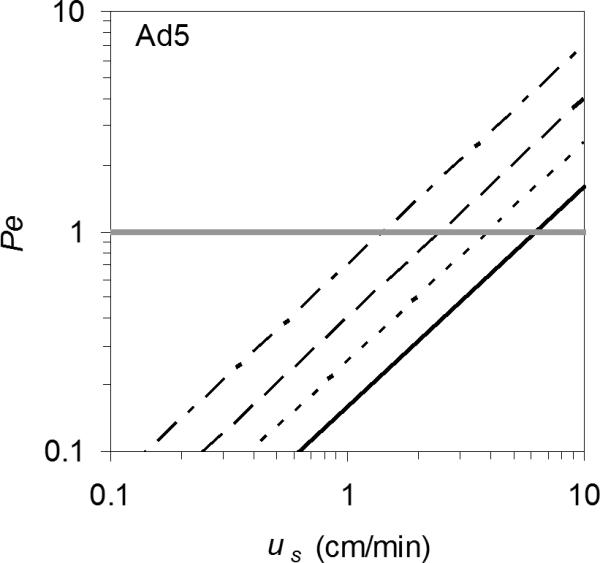
Order of magnitude estimates for Péclet numbers are consistent with the theory that peak area reduction with increasing flow rate occurs due to entrapment of the Ad5 particles by the flowing liquid at pore constrictions in the monoliths, 4 CIM disks (- · - ·), ProSwift (- - -), Uno Q (·········), and in the perfusive resin, PL-SAX (—). The horizontal gray line at Pe = 1 indicates where diffusion and convection are approximately in balance.

It is ironic that monoliths and perfusive resins were designed specifically for faster purification of larger biologics, yet larger bioparticles are much more likely to become convectively trapped in these stationary phases and can only be fully eluted at very low flow rates. For fast purification of viruses and other large bioparticles, using either non-porous beads or beads with pores smaller than the bioparticle may be better than using monoliths or perfusive resins that have pores with diameters comparable to those of the bioparticles of interest because this would avoid the entrapment of the bioparticles. Since entrapment is a size-based separation, the mechanism applies not only to viruses but to other particles as well. Although only ionexchangers were used in this work, the entrapment is likely to occur in all chromatography modes since it occurs even under non-interacting conditions.

The theory can also help explain anecdotal reports that monoliths and membranes are more difficult to clean than packed columns and can become occluded over a few usage cycles. These observations are consistent with entrapment of large bioparticles, e.g., cell debris or aggregates, inside the monoliths due to the flow. Since escape is less likely at high flow rates, it may be advisable to use low flow rates during cleaning. Column cleaning is often carried out with the flow direction reversed, but this helps mainly with impurities that are too large to enter the bed deeply, and it may not be adequate for impurities that can enter the bed. Flow reversal may be more effective if coupled with a reduction in flow rate to the extent that time constraints permit. Periodic pauses in the flow during cleaning may be helpful as well since they would allow bioparticles to diffuse out of the constrictions.

The entrapment mechanism is relevant only in media in which a significant fraction of the flow passes through pores smaller than the bioparticle of interest. Few real porous media have monodisperse pore size distributions and there is often a fraction of sufficiently small pores present, especially since smaller pores provide more specific surface area for adsorption. The theory then raises a natural question about just how much constrictive space is there in a column and how it compares to the amount of virus that becomes trapped. A pore size distribution from accessible pore volume for a range of particle sizes shows that, in CIM disks, the volume of pores smaller than Ad5 constitutes a significant fraction of the pore space – roughly 15% (Trilisky 2009). The volume of the virus particles that was spiked onto the columns in the experiments here is 4−8×10⁻⁶ of the column volume, so even sparsely distributed constrictions are likely to be adequate for trapping a noticeable amount of virus. Multiple virus particles could be trapped in a single constriction, but trapping reduces the flow rate through the constriction and the characteristic distance for diffusive escape, thus reducing the likelihood of entrapment of other particles. It is expected that the fractional entrapment would be less dramatic for larger loads. Increasing the pulse volume for CIM from 30 μL (about 2% of V_T) to 70 μL (about 5% of V_T) reduced the loss in Ad5 peak area by about 13%. Therefore, entrapment is expected to be especially critical in analytical chromatography, where samples are usually small and flow rates are high. Ad5, for example, could be incorrectly quantified or be completely undetected.

Convective entrapment could also be exploited for virus purification: a column with a high concentration of appropriate constrictions can be loaded at a high flow rate and eluted by reducing the flow rate. The experiments here were performed under non-interacting conditions, i.e., the virus particles are neither attracted nor repelled by the pore surface. Under attractive conditions, the retention of virus particles can only increase. Under repulsive conditions, for instance, if the adsorbent and the virus have the same charge, the entrapment may decrease and it may be possible to purify virus particles by loading them at high salt concentration and high flow rate and eluting them by reducing the salt concentration and the flow rate.

Conclusions

This study bridges several fields in which virus removal is a major concern: chromatography of proteins (virus removal), purification of viruses by chromatography, depth filtration, and purification of water by flow through natural porous media. In all of these fields, convective entrapment presents a potential mechanism for reversibly trapping large bioparticles in porous media even under non-binding conditions and even if the average pore size is much larger than the bioparticle of interest. Such entrapment could allow removal of trace amounts of viruses and other large contaminants on perfusive resins and monoliths. Although membranes were not tested in this work, the entrapment could occur on them as well because membranes are essentially thin monoliths and are likely to have pore constrictions too. Entrapment generally does not occur on conventional narrow-pore resins because the constrictions in the interstitial pore space are too large and the intraparticle pores are too small. Since flow velocity controls the entrapment, virus removal can be enhanced in flow-through purification of therapeutic proteins by using higher flow rates. In bind-elute mode, eluting the protein at a higher flow rate could improve viral clearance. The entrapment mechanism can also be used to purify viruses by loading at a high flow rate and elution at a lower flow rate.

The likelihood of convective entrapment increases linearly with flow rate and with the molecular weight of the bioparticle, or, alternatively, the cube of its diameter. To avoid entrapment, Pe << 1 must be satisfied. If a yield loss is observed during filtering of bioparticles from larger impurities, a lower filtration rate may help. To improve column cleaning, it should be carried out at very low or pulsating flow to allow convectively trapped bioparticles to diffuse out of constrictions.