Global Medical Shape Analysis Using the Laplace-Beltrami Spectrum

Abstract

This paper proposes to use the Laplace-Beltrami spectrum (LBS) as a global shape descriptor for medical shape analysis, allowing for shape comparisons using minimal shape preprocessing: no registration, mapping, or remeshing is necessary. The discriminatory power of the method is tested on a population of female caudate shapes of normal control subjects and of subjects with schizotypal personality disorder.

1 Motivation and Background

Morphometric studies of brain structures have classically been based on volume measurements. More recently, shape studies of gray matter brain structures have become popular. Methodologies for shape comparison may be divided into global and local shape analysis approaches. While local shape comparisons [1,2] yield powerful, spatially localized results that are relatively straightforward to interpret, they usually rely on a number of preprocessing steps: one-to-one correspondences between surfaces need to be established, shapes need to be registered and resampled, possibly influencing shape comparisons. While global shape comparison methods cannot spatially localize shape changes they may be used to indicate the existence of shape differences between populations. Global approaches may be formulated with a significantly reduced number of assumptions and preprocessing steps in comparison to local approaches, staying as true as possible to the original data.

This paper describes a methodology for global shape comparison based on the Laplace-Beltrami spectrum (LBS) [3,4] of a Riemannian manifold (of closed surfaces in space). Previous approaches for global shape analysis in medical imaging include the use of invariant moments [5], the shape index [6], and global shape descriptors based on spherical harmonics [7]. The proposed methodology based on the LBS differs in the following ways from these previous approaches:

• It works for any Riemannian manifold, whereas spherical harmonics based methods are restricted to surfaces with spherical topology, and invariant moments do not easily generalize to arbitrary Riemannian manifolds. It may thus be used to analyze surfaces, solids, non-spherical objects, etc.

• The only preprocessing required is the extraction of a surface approximation from a manually segmented binary volume. No registration, remeshing, or additional mappings are necessary. Further the description is invariant to isometries and remeshing.

2 Shape-DNA: The Laplace-Beltrami Spectrum

In this section we introduce the necessary background for the computation of the LBS beginning sequence (also called ”Shape-DNA”). The ”Shape-DNA” is a signature computed only from the intrinsic geometry of an object. It is the beginning sequence of the spectrum of the LB operator defined for real valued functions on Riemannian manifolds and can be used to identify and compare objects like surfaces and solids independent of their representation, position and, if desired, independent of their size. This methodology was first introduced in [8] with a first description of basic ideas given in [9]. The LBS can be regarded as the set of squared frequencies (the so called natural or resonant frequencies) that are associated to the eigenmodes of an oscillating membrane defined on the manifold. (E.g., the eigenmodes of a sphere are the spherical harmonics.) Let us review the basic theory in the general case (see [3,4] for details).

Let f be a real-valued function, with f ∈ C², defined on a Riemannian manifold M. The Laplace-Beltrami Operator Δ is: Δf := div(grad f) with grad f the gradient of f and div the divergence on the manifold. The LB operator is a linear differential operator. It can be calculated in local coordinates. Given a local parametrization ψ : ℝⁿ → ℝ^n+k of a submanifold M of ℝ^n+k with

$$g_{\mathit{\text{ij}}}≔\langle {\partial }_i\psi , {\partial }_j\psi \rangle , G≔(g_{\mathit{\text{ij}}}), W≔\sqrt{\text{det}G}, (g^{\mathit{\text{ij}}})≔G^{-1}$$ (1)

(where i, j = 1(1)n, det is the determinant) we get:$\Delta f=\frac{1}{W}{\displaystyle {\sum }_{i,j}{\partial }_i(g^{\mathit{\text{ij}}}W{\partial }_{j}f)}$. If M is a domain in the Euclidean plane M ⊂ ℝ² the LB operator is the well known Laplacian$\Delta f=\frac{{\partial }^{2}f}{{(\partial x)}^2}+\frac{{\partial }^{2}f}{{(\partial y)}^2}$. The Laplacian eigenvalue problem is

$$\Delta f=-\lambda f,$$ (2)

its solutions represent the spatial part of the solutions of the wave eq. (with an infinite number of eigenvalue λ and eigenfunction f pairs). In the case where the Riemannian manifold M is a planar region, f(u, v) in eq. (2) can be understood as the natural vibration form (also eigenfunction) of a homogeneous membrane with eigenvalue λ. Any properties of the material are ignored. The standard boundary condition of a fixed membrane is f ≡ 0 on the boundary of the surface domain (Dirichlet boundary condition).

The spectrum is defined to be the family of eigenvalues of eq. 2, consisting of a diverging sequence 0 ≤ λ₁ ≤ λ₂ ≤ ⋯ ↑ +∞, with each eigenvalue repeated according to its multiplicity and with each associated finite dimensional eigenspace. In the case of a closed manifold without a boundary the first eigenvalue λ₁ is always equal to zero, because in this case the constant functions are non-trivial solutions of the Laplacian eigenvalue problem.

The spectrum is an isometric invariant as it only depends on the gradient and divergence which in turn are defined to be dependent only on the Riemannian structure of the manifold, i.e., the intrinsic geometry. Furthermore, scaling an n-dimensional manifold by a factor a results in eigenvalues scaled by a factor$\frac{1}{a^2}$. Thus, by normalizing the eigenvalues, shape can be compared regardless of the object’s scale and position. The spectrum depends continuously on the shape of the manifold [10]. We use cubic triangular finite elements for the computation of the spectra [3,4].

Normalization

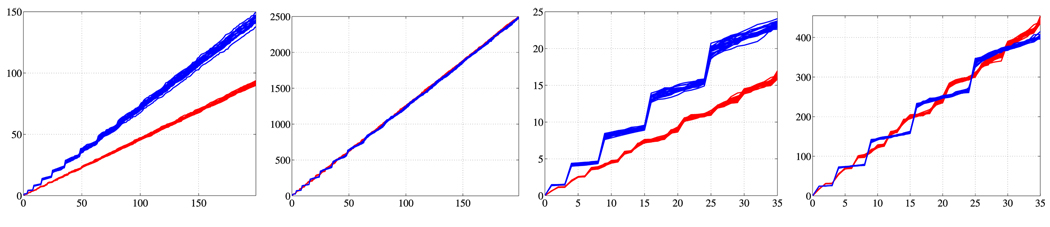
The LBS is a diverging sequence. Analytic solutions for the spectrum are only known for a limited number of shapes. For the unit 2-sphere the eigenvalues are λ_i = i(i + 1), i ∈ ℕ₀ with multiplicity 2i + 1. In general the eigenvalues asymptotically tend to a line with a slope dependent on the surface area of the 2D manifold$M:{\lambda }_n\sim \frac{4\mathrm{\pi }n}{\text{area}(M)}$, as n ↑ ∞. Therefore, a difference in surface area manifests itself in different slopes of the eigenvalue asymptotes. Fig. 1 shows the behavior of the spectra of a population of spheres and a population of ellipsoids respectively. The sphere population is based on a unit sphere where Gaussian noise is added in the direction normal to the surface of the noise-free sphere. Gaussian noise is added in the same way to the ellipsoid population. Since the two basic shapes (sphere and ellipsoid) differ in surface area, their unnormalized spectra diverge (Fig. 1 a). Area normalization greatly improves the spectral alignment (Fig. 1 b). Figs 1 c) and d) show zoom-ins of the spectra for small eigenvalues. For the unnormalized as well as for the surface area normalized case, the spectra of the two populations clearly differ, demonstrating that the LBS can detect shape- as well as size-differences.

Fig. 1.

Spectral behavior from left to right: (a) unnormalized, (b) Area normalized, (c) unnormalized (zoom), (d) Area normalized (zoom). Eigenvalue (ordinate) versus eigenvalue number (abscissa).

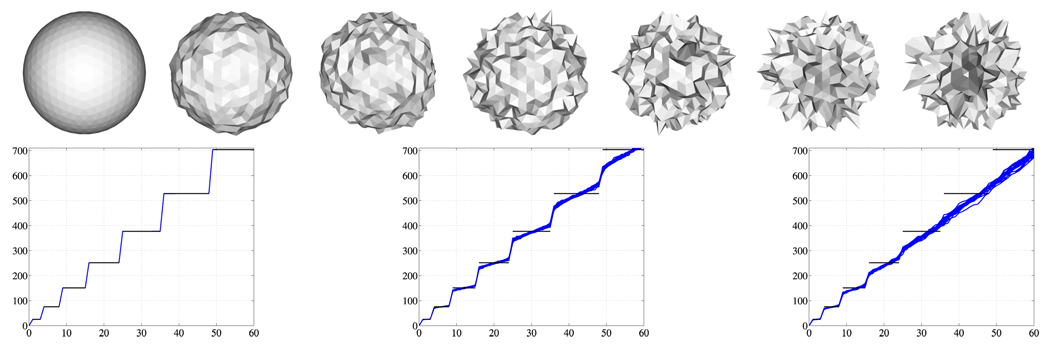
Statistical testing results depend on the chosen normalization. When unnormalized spectra of populations with widely different surface areas are compared, larger eigenvalues lead to better discrimination of the groups (Fig. 1 a), however, this mainly reflects the surface area differences. A surface area normalization shows if additional shape differences exist. Having identical noise levels for the populations under investigation is essential, since different noise levels will affect surface areas differently, with increased surface areas for increased noise levels (see Fig. 2 for an illustration). Violating this assumption may yield to the detection of noise level differences as opposed to shape differences, as demonstrated in Fig. 2. For the analysis of identically acquired and processed shapes – e.g., obtained through manual segmentations – identical noise levels are a reasonable assumption; also, the expected accuracy of the spectra calculations is expected to be independent of population.

Fig. 2.

Spectra of a sphere with different noise levels. The noise-free case on the left demonstrates the accuracy of the numerical eigenvalue computations. Spectra were normalized to unit surface area. Black horizontal lines: analytic spectrum of the noise-free sphere. Increasing levels of noise from left to right. Eigenvalue (ordinate) versus eigenvalue number (abscissa).

3 Statistical Analysis of Groups of LB Spectra

Given the (possibly normalized) LB spectra we use permutation tests to compare group features to each other (200,000 permutations were used for all tests). We use three different kinds of statistical analyses¹ (see [11] for details on permutation testing): (i) A two-sided, nonparametric, permutation test to analyze the scalar quantities: volume and surface area; (ii) a two-sided, nonparametric, multivariate permutation test based on the maximum t-statistic to analyze the high-dimensional spectral feature vectors (Shape-DNA); and (iii) independent permutation tests of the spectral feature vector components across groups (as in (ii)), followed by a false discovery rate (FDR) approach to correct for multiple comparisons, to analyze the significance of individual vector components.

To test scalar values the absolute mean difference is used as the test statistic s = |μ_a − μ_b|, where the μ_i indicates the group means. Due to the small number of samples compared to the dimensionality of the feature vectors (preventing the use of the Hotelling T² statistic), the maximum t-statistic

$$t_{\mathit{\text{max}}}=\underset{1\le j\le N}{\mathit{\text{max}}}\frac{\left|{\overline{e}}_{a,j}-{\overline{e}}_{b,j}\right|}{S{E}_j}$$ (3)

is chosen as the test statistic for the spectral feature vectors. Here, N is the vector dimension, ē_a,j indicates the mean of the j-th vector component of group a, and SE_j is the pooled standard error estimate of the j-th vector component, defined as

$$S{E}_j=\frac{\sqrt{(n_a-1){\sigma }_{a,j}^2+(n_b-1){\sigma }_{b,j}^2}}{\sqrt{\frac{1}{n_a}+\frac{1}{n_b}}},$$ (4)

where n_i is the number of subjects in group i and σ_i,j is the standard deviation of vector component j of group i. To account for the multiple comparison problem when testing individual vector components, the significance levels are corrected based on an FDR of 5% [12].

4 Results

Volume measurements are the simplest means of morphometric analysis. While volume analysis results are easy to interpret, they only characterize one morphometric aspect of a structure. The following Sections introduce the LBS as a method for a more complete global structural description using the analysis of a caudate as an exemplary brain structure. For brevity all results are presented for the right caudate only.

Populations

Magnetic Resonance (MR) images of the brains of 32 neurolepticnaïve female subjects diagnosed with Schizotypal Personality Disorder (SPD) and of 29 female normal control subjects were acquired on a 1.5-T General Electric MR scanner. Spoiled-gradient recalled acquisition images (voxel dimensions, 0.9375 × 0.9375 × 1.5 mm) were obtained coronally. The images were used to delineate the caudate nucleus and to estimate the intracranial content [13].

Preprocessing

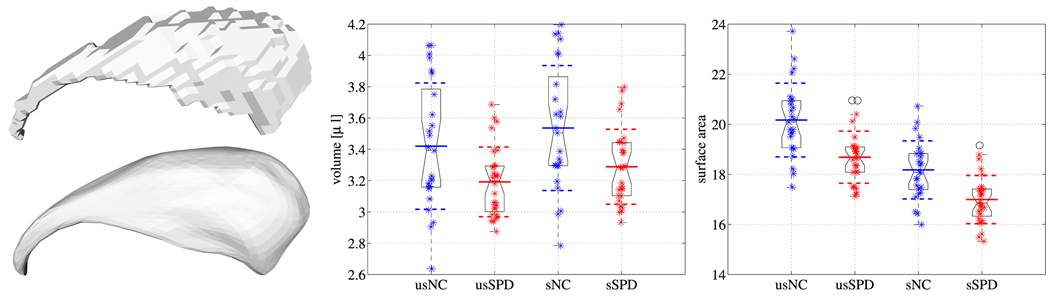
The caudate nucleus was delineated manually by an expert. Interrater reliability (based on intraclass correlation coefficients) among three raters for the right caudate volume were high (r=.94). Interrater reliabilities were computed by three raters on the brain scans of five randomly selected subjects from the pool of subjects [13]. The isosurfaces separating the binary label maps of the caudate shapes from the background were extracted using marching cubes (assuring spherical topology). Analysis was performed on the resulting triangulated surfaces directly (referred to as unsmoothed surfaces) as well as on the same set of surfaces smoothed and resampled using spherical harmonics² (referred to as smoothed surfaces). The unsmoothed surfaces are used as a benchmark dataset subject to only minimal preprocessing, whereas the smoothed surfaces are used to demonstrate the influence of additional preprocessing. See Fig. 3 for an example of a smoothed and an unsmoothed caudate.

Fig. 3.

Exemplary caudate shape unsmoothed and with spherical harmonics smoothing (left). Group comparisons for volume differences (middle) and surface area differences (right). Smoothed results prefix ’s’, unsmoothed results prefix ’us’. Volume and surface area reductions are observed for the SPD population in comparison to the normal control population.

Volume and Area Analysis

For comparison, results for a volume and a surface area analysis are shown in Fig. 3. As has been previously reported for this dataset [13], subjects with schizotypal personality disorder exhibit a statistically significant reduction compared to the normal control subjects. While smoothing plays a negligible role for the results (smoothed: p = 0.008, loss 7.0%, i.e., there is a chance of p = 0.008 that the loss is a random effect; unsmoothed: p = 0.013, loss 6.7%), the absolute values of the surface area are affected more, since smoothing impacts surface area more than volume. While surface smoothing is desirable to reduce noise effects, the result for the female caudates shows the same trend for the surface areas (but not for magnitude) in the smoothed and the unsmoothed cases (smoothed: p = 0.00019; unsmoothed: p = 0.000085).

Laplace-Beltrami Spectrum Analysis

The LB spectrum was computed for the female caudate population using surface area normalization. A maximum t-statistic permutation test on a 100-dimensional spectral shape descriptor shows significant shape differences (see Tab. 1) for surface area normalization for the unsmoothed surfaces, but not for the smoothed ones. Surface area normalization is the strictest normalization in terms of spectral alignment. Testing for surface area independently yields statistically significant results.

Table 1.

Shape comparison results for the maximum t-statistic permutation test for the unsmoothed and smoothed dataset. Volume and area results for comparison.

	normalization	p-value (unsmoothed)	p-value (smoothed)
LBS (N=20)	unit brain volume	0.0026	0.0013
	unit caudate surface area	0.0050	0.63
LBS (N=100)	unit brain volume	0.00032	0.00092
	unit caudate surface area	0.026	0.84
Volume	unit brain volume	0.013	0.0078
	unit caudate surface area	0.0011	0.011
Area	unit brain volume	0.000045	0.00022
	unit caudate volume	0.001	0.011

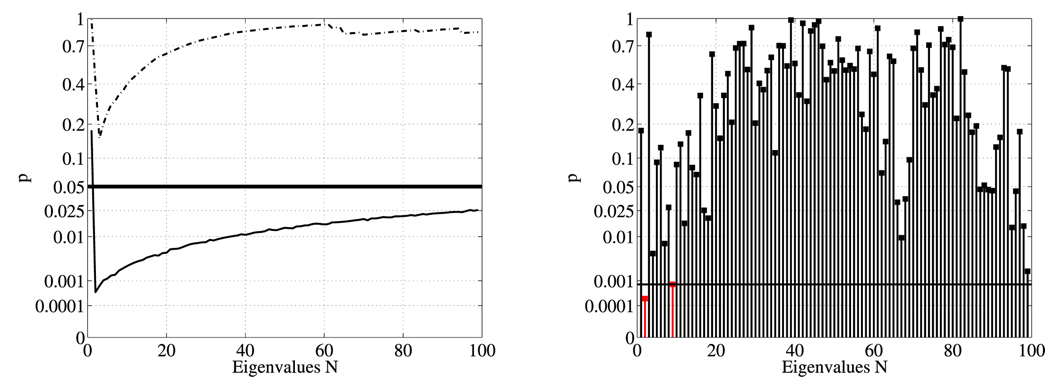
Fig. 4 indicates that using too many eigenvalues has a slightly detrimental effect on the observed statistical significance. This is sensible, since higher order modes correspond to higher frequencies and are thus more likely noise, which can overwhelm the statistical testing. In this particular example, a few small eigenvalues distinguish the shapes (explaining the sharp initial drop in Fig. 4), while the upward slope is explained by adding an increasing number of eigenvalues that no longer contribute to the shape discrimination of the two populations. It is thus sensible to restrict oneself only to a subset of the spectrum (e.g., the first 20). However, this subset needs to be agreed upon before the testing and cannot be selected after the fact. Note, that the LBS results of Tab. 1 show statistically significant shape differences even when the strong influence of surface area is removed, which suggests that the LBS indeed picks up shape differences that complement area and volume findings. The LBS can detect surface area differences (since the surface areas may be extracted from the spectrum) and can distinguish objects with identical surface area or volume based on their shape. Future work, computing the LBS of solids, will try to disentangle the influence of volume and area differences further. Our shape difference findings are consistent with results previously reported in [6,13] for a population of male caudates and the same population of female caudates used in this paper.

Fig. 4.

Maximum t-statistic results of area normalized case (left) for the first n eigenvalues (solid line: unsmoothed, dashed line: smoothed) and (right) for individual eigenvalues (unsmoothed case) with FDR multiple comparison correction. The black horizontal lines correspond to the 5% significance level and the 5% FDR corrected significance level respectively. The left plot shows statistical results for the analysis of shape-DNAs of different lengths. The right plot shows statistical results for individual spectral components. Since the statistically most significant eigenvalue cannot be selected after the statistical analysis, a shape-DNA-based analysis with prespecified length is useful.

5 Conclusion

This paper showed the applicability and utility of the LBS for shape analysis in medical imaging. The maximum t-statistic was used for a group analysis of LB spectra. In particular, the paper demonstrates that the LBS can reliably be computed on (iso)surfaces without preprocessing, e.g., surface smoothing, and that the normalizations of the spectra greatly influence the outcome of the statistical procedure. In particular, the surface area normalized results indicate that there are true shape differences. Future work will focus on the computation of volume spectra.