Compressed and Distributed Sensing of Neuronal Activity for Real Time Spike Train Decoding

Abstract

Multivariate point processes are increasingly being used to model neuronal response properties in the cortex. Estimating the conditional intensity functions underlying these processes is important to characterize and decode the firing patterns of cortical neurons. This paper proposes a new approach for estimating these intensity functions directly from a compressed representation of the neurons’ extracellular recordings. The approach is based on exploiting a sparse representation of the extracellular spike waveforms, previously demonstrated to yield near-optimal denoising and compression properties. We show that by restricting this sparse representation to a subset of projections that simultaneously preserve features of the spike waveforms in addition to the temporal characteristics of the underlying intensity functions, we can reasonably approximate the instantaneous firing rates of the recorded neurons with variable tuning characteristics across a multitude of time scales. Such feature is highly desirable to detect subtle temporal differences in neuronal firing characteristics from single-trial data. An added advantage of this approach is that it eliminates multiple steps from the typical processing path of neural signals that are customarily performed for instantaneous neural decoding. We demonstrate the decoding performance of the approach using a stochastic cosine tuning model of motor cortical activity during a natural, nongoal-directed 2-D arm movement.

I. Introduction

SPIKE trains are the fundamental neural communication mechanism used by cortical neurons to relay, process, and store information in the central nervous system. Decoding the information in these spike trains is a fundamental goal in systems neuroscience in order to better understand the complex mechanisms underlying brain function. In motor systems, these spike trains were demonstrated to carry important information about movement intention and execution [1], and were shown to be useful in the development of neuroprosthetic devices and brain-machine interface (BMI) technology to assist people suffering from severe disability in improving their lifestyle [2], [3].

Cortically-controlled BMI systems rely fundamentally on instantaneous decoding of spike trains from motor cortical neurons recorded during a very limited interval. This interval, often referred to as the movement planning period, is estimated to be around 100–200 ms [4]. The decoding process is typically a cascade of processing steps illustrated in Fig. 1. It features amplification and filtering, followed by spike detection and sorting to segregate single unit responses in the form of binary spike trains. The spike trains are then filtered using a variable-width kernel function (e.g., a Gaussian) to yield a smoothed estimate of the instantaneous firing rate [5], [6]. These steps have to be performed within the movement preparation period to enable the subject to experience a natural motor behavior.

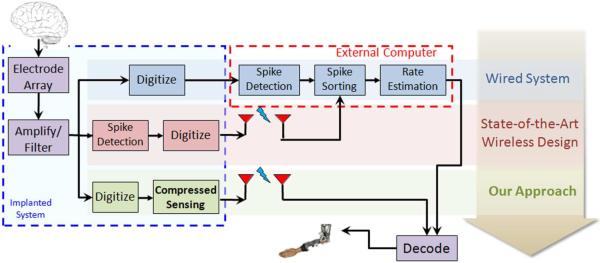
Fig. 1.

Schematic diagram of a typical data flow in a neuro-motor prosthetic application. Ensemble neural recordings are first amplified and filtered prior to telemetry transmission to the outside world. Three data processing paths are considered. (1) Wired systems (top): information is extracted through the cascade of spike detection and sorting followed by rate estimation with a massive computational power [2]. (2) Wireless systems (middle): Telemetry bandwidth is reduced by moving the spike detection block inside the implantable device [12], [13]. (3) Proposed system (bottom): the spike detection, sorting and rate estimation blocks are replaced with one “compressed sensing” block that permits adaptive firing rate estimation in real time for instantaneous decoding to take place.

The spike sorting step is arguably the most computationally prohibitive in that sequence. This step requires two modes of analysis: a training mode and a runtime mode. During the training mode, spikes are detected, aligned, and sorted based on certain discriminating features, such as principal component analysis (PCA) scores [7]. During runtime, an observed spike’s features are compared to the stored features to determine which neuronal class it belongs to. Both steps require significant amount of computations to enable this identification/classification process to run smoothly. As a result, most of existing systems feature a wired connection to the brain to permit streaming the high-bandwidth neural data to the outside world where relatively unlimited computing power can carry out this task with close to real time performance.

In our extensive body of prior work, we have proposed an approach for neural data denoising and compression [8] as well as spike detection and sorting [9], [10], based on a sparse representation of the recorded data prior to telemetry transmission. We have further reported on the suitability of computing this representation within the resource-constrained environment of a wireless implantable system [11]. In this paper, we show that this same sparse representation not only overcomes the severe bandwidth limitations of a wireless implantable system, but also enables adequate estimation of neuronal firing rates without the need to decompress, reconstruct, and sort the spikes off-chip in the traditional sense. This is illustrated in the bottom of Fig. 1, where decoding neural discharge patterns can be directly performed using the compressed data.

The paper is organized as follows. Section II introduces the application of point processes to model neuronal firing and outlines how the mapping of the data to spike train realizations of these point processes can be achieved through a sparse representation operator that is further used to estimate their underlying intensities. Section III describes the details of the methods used to collect real spike data and simulate neural activity encoding 2-D arm movement. Results of these experiments are reported and discussed in Sections IV and V, respectively.

II. Theory

A. Single Neuron Point Process Model

In a typical recording experiment, the observations of interest are the times of occurrence of events from a population of neurons, expressesing the discharge pattern of pattern these neurons. In an arbitrary neuron p, the firing can be modeled as a realization of an underlying point process with conditional intensity function—or firing rate—λ_p(t|F) [14]. This intensity function is conditioned on some set, F, of intrinsic properties of the neuron itself and the neurons connected to it, and some extrinsic properties such as the neuron’s tuning characteristics to external stimuli features during that trial. Because many of these properties are hard to measure, the number of events in a given interval, N_p, is typically random by nature. The integral of λ_p over a finite time interval [T_a, T_b] represents the expected value N_p within a single trial [15]

$$E\left[N_p\right]={\int }_{T_a}^{T_b}{\lambda }_p(t\mid F)dt.$$ (1)

Estimating λ_p from the set of event times {t_p} is typically achieved by binning the data into time bins of equal width, T_w = T_b − T_a, and counting the number of events occurring within each bin. The resulting spike counts, often referred to as a rate histogram, constitute an instantaneous firing rate estimate λ̂_p. In traditional signal processing, this is equivalent to convolving the spike train with a fixed-width rectangular window. This approach assumes that variations in the rate pattern over the bin width do not carry information that is destroyed if aliasing occurs, for example, when the bin width is not optimally selected to satisfy the Nyquist sampling rate of λ_p.

The binning approach can detect the presence of the type of spike bursts that may exist within the fixed-length bins. However, bursts come in a variety of lengths within a given trial reflecting the heterogeneous characteristics of cortical neurons, and can range from very short bursts (3–4 spikes within 2–3 ms [16]) to much longer bursts that can last for more than 2 s [17]. This implies that the firing rate of individual neurons is highly nonstationary and that temporal and spectral variations in λ_p are believed to occur over a multitude of time scales that reflect the complex temporal structure of neuronal encoding while subjects carry out similar behavioral tasks [18], [19], or depending on the demands of distinct behavioral tasks [20]. This nonstationarity arises in part because of the dependence of the firing rate on multiple factors such as the degree of tuning (sharp or broad) to behavioral parameters, the behavioral state, the subject’s level of attention to the task, level of fatigue, prior experience with the task, etc. While across-trial averaging of rate histograms (peristimulus) helps to reduce this variability, it destroys any information about the dynamics of interaction between neurons that are widely believed to affect the receptive fields of cortical neurons, particularly when plastic changes occur across multiple repeated trials. Typically, a nonparametric kernel smoothing step (e.g., a Parzen window [21]) is needed. The temporal support T_w of the kernel function is known to strongly impact the rate estimator [22]. Moreover, the selection of T_w is arguably important to determine the type of neural response property sought. For small T_w (<2–3 ms), precise event times can be obtained. As T_w approaches the trial length, we obtain the overall average firing rate over that trial. In between these two limits, T_w needs to be adaptively selected to capture any nonstationarities in λ_p that may reflect continuously varying degrees of neuronal inhibition and excitation indicative of variable degree of tuning to behavioral parameters.

B. Sparse Extracellular Spike Recordings

We ultimately seek to estimate λ_p directly from the recorded raw data. However, two complications arise. First, the detected events are not directly manifested as binary sequence of zeros and ones to permit direct convolution with a kernel to take place, but rather by full action potential (AP) waveforms. Second, these events are typically a combination of multiple single unit activity in the form of AP waveforms with generally distinct—but occasionally similar—shapes. This mandates the spike sorting step before the actual firing rate can be estimated.

Let’s assume that the actual spike waveforms are uniformly sampled over a period T_s. Each spike from neuron p is a vector of length N_s samples that we will denote by g_p. For simplicity assume the event time is taken as the first sample of the spike waveform (this can be generalized to any time index, e.g., that of a detection threshold crossing). The discrete time series corresponding to the entire activity of neuron p over a single trial of length T can be expressed as

$${\mathrm{s}}_p=\sum _{i\in \left\{t_p\right\}}\sum _{k=0}^{N_s-1}{g}_p\left[k\right]\delta [i+k]$$ (2)

where the time index i includes all the refractory and rebound effects of the neuron and takes values from the set {t_p}, while δ( · ) is the Dirac delta function. For compression purposes, it was shown in [8] and [9] that a carefully-chosen sparse transformation operator, such as a wavelet transform, can significantly reduce the number of coefficients representing each spike waveform to some N_c ⪡ N_s. This number is determined based on the degree of sparseness q as N_c ≈ ε^(q−2)/2q where 0 < q < 2 (q = 0 implies no sparsness, while q = 2 implies fully sparse) and ε denotes some arbitrarily chosen signal reconstruction error [23]. Mathematically, an observerd spike, g, is represented by the transform coefficients obtained from the inner product g^j = 〈g, w_j〉, where w_j is an arbitrary wavelet basis at time scale j. When multiple units are simultaneously recorded, the spike recordings from the entire population can be expressed as

$$s^j=\sum _{i\in \left\{t_s^j\right\}}\sum _{k=0}^{N_{c-1}^j}{g}^j\left[k\right]\delta [i+k]$$ (3)

where $N_c^j$ is the number of nonzero transform coefficients at time scale j, and i takes values from the set of spike times for all neurons in the whole trial, $\left\{t_s^j\right\}$. Note that $N_c^j⪡N_s$ and the total number of coefficients obtained is $N_c=\sum N_c^j$.

To minimize the number of the most important coefficients/event, ideally to a single feature, we note that the magnitude of the coefficients g^j carry information about the degree of correlation of the spike waveforms with the basis w^j. Therefore, this information can be used to single out one feature out of “the most significant” coefficients per event from neuron p via a thresholding process. One way to obtain this single feature, fg^j[k] is to locally average the coefficient before thresholding. We define a neuron-specific sensing threshold at time scale jj, denoted ${\gamma }_p^j$. This threshold is selected to preserve the ability to discriminate neuron p’s events from those belonging to other neurons using this single feature. Specifically, in every time scale j, we cast the problem as a binary hypothesis test in which

$$f_g^j\left[k\right]\underset{H_0}{\overset{H_1}{\gtrless }}{\gamma }_p^{j}k=0,1,\dots ,N_c^j,j=0,1,\dots ,J.$$ (4)

Using a top-down approach, ${\gamma }_p^j$ is selected based on a standard likelihood ratio test (given predetermined level of false positive). The outcome of this statistical binary test is one time index per event, k*, for which the alternative hypothesis H₁ is in effect. In other words, the sensing threshold in a given time scale should allow only one feature to be kept per event. Once this is achieved, fg^j [k] at indices where H₀ is in effect are automatically set to zero. Note that this step allows suppressing both noise coefficients as well as those belonging to neurons’ other than neuron p’s. In such case, the thresholded signal can be expressed as

$${\stackrel{‒}{s}}_p^j=\sum _{i\in \left\{t_p^j\right\}}{f}_g^j\left[k^{\ast }\right]\delta [i-k^{\ast }].$$ (5)

The outcome of (5), after proper normalization fg^j[k*], is an estimate of the true binary spike train vector. It can be readily seen that the temporal characteristics of this estimate will exactly match that of the binary spike train of neuron p and consequently preserves all the critical information such as spike counts and interspike interval (ISI) statistics allowing rate estimation to be readily implemented [24]. The simple example in Fig. 2 illustrates this idea. In each wavelet decomposition level, the binary hypothesis test (i.e., the thresholding) is equivalent to a two-class discrimination task whereby one unit at a time is identified at each level. The spike class separability (defined below) is compared to that in the time domain and a unit is extracted (i.e., its coefficients removed) from the data set if the unit separability is higher than that of the time domain. This process is repeated until the separability no longer exceeds that of the time domain, or the size of the remaining events is smaller than a minimum cluster size (typically five events), or the maximum number of decomposition levels has been reached (typically 4–5 levels).

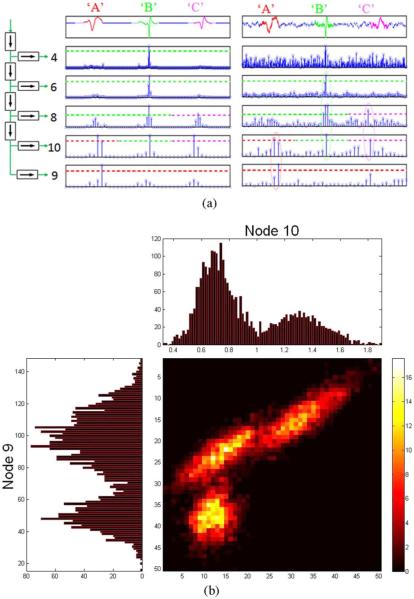
Fig. 2.

(a) Sparse representation of sample events from three units, “A,” “B,” and “C” in the noiseless (middle) and noisy (right) neural trace for five wavelet decomposition levels indicated by the binary tree (left). First level high-pass coefficients (node 2) are omitted as they contain no information in the spectral band of spike waveforms. Sensing thresholds are set to allow only one feature/event to survive in a given node. In this case, it is a local average of 32/2^j coefficients. For example, nodes 4 and 6 can either be used to mark events from unit “B,” while node 9 can be used to mark events from unit “A.” When noise is present (right), the sensing threshold also serves as a denoising one. (b) 1-D and 2-D joint distributions of wavelet features for nodes 9 and 10 for the three units over many spike occurrences from each unit showing three distinct clusters. These projections can be used when spikes from different units result in identical sparse representations in a particular node (e.g., node 10). This can be used to resolve the ambiguity provided that these units were not already discriminated in earlier nodes.

C. Instantaneous Rate Estimation

A fundamental property of the DWT sparse representation suggests that as j increases, ${\stackrel{‒}{s}}_p^j$ becomes more representative of the intensity function rather than the temporal details of neuron p’s spikes, which were eventually captured in finer time scales. This is because the coefficients that survive the sensing threshold will spread their energy across multiple adjacent time indices, thereby performing the same role as the kernel smoothing approach, but at a much less computational overhead as will be shown later. Mathematically, extending the DWT of the vector ${\stackrel{‒}{s}}_p^j$ after normalization to higher level requires convolving it with a wavelet basis kernel with increasing support. This support, denoted t_L at level L, is related to the sampling period T_s by

$$t_L=T_s{n}_w{2}^{(L-2)}$$ (6)

where n_w is the wavelet filter support. For the symmlet4 basis used in this paper (n_w = 8), this temporal support is equivalent to ~1.2 ms at level 4 (at 25 kHz sampling rate), which roughly corresponds to one full event duration. Extending the decomposition to level 5 will include refractory and rebound effects of neurons typically observed in the cerebral cortex [18]. Therefore, temporal characteristics of the firing rate will be best characterized starting at level 6 and beyond where the basis support becomes long enough to include two or more consecutive spike events.

D. Computational Complexity

Herein, we compare the cost of estimating the firing rate through the standard time domain spike sorting using PCA scores followed by kernel smoothing to the proposed compressed sensing approach. Both involve calculating the computational cost in two different modes of operation, the training mode and the “runtime mode. In the training mode, features are extracted and the population size is estimated using cluster cutting in the feature space. This should ideally correspond to the number of distinct spike templates in the data. Using a Bayesian classifier with equal priors

$$\begin{array}{cc}\hfill p=& \underset{p}{\mathrm{argmax}}P(C_p\mid g)=\underset{p}{\mathrm{argmax}}\frac{P(g\mid C_p)}{P\left(C_p\right)}P\left(g\right)\hfill \\ \hfill \Rightarrow & p\cong \underset{p}{\mathrm{argmax}}P(g\mid C_p)\hfill \\ \hfill P(g\mid C_p)=& \frac{1}{{\left(2\pi \right)}^{N_s∕2}{\mid {\Sigma }_p\mid }^{N_s}}\hfill \\ \hfill & \times \exp [-\frac{1}{2}{(g-{\mu }_p)}^T{\Sigma }_p^{-1}(g-{\mu }_p)]\hfill \end{array}$$ (7)

where C_p is the class of neuron p. It is assumed that each class is multivariate Gaussian distributed, where μ_p and Σ_p are the N_s × 1 mean vector and N_s × N_s temporal covariance matrix for each neuron p = 1, . . . , P. The overall computations for the Bayesian classifier are in the order of $~O\left(N_s^{2}P\right)$.

First, spikes are aligned by searching for a local extreme followed by cropping the waveform symmetrically around that location, which requires computations in the order of ~O(2N_sN_P). Finding the eigenvalues and eigenvectors, for example, using a cyclic Jacobi method [25], requires $O(N_s^3+N_s^2{N}_P)$ computations. For projection onto a PCA space, an O(2N_sN_P operations are needed to reduce the dimensionality of spike waveforms to a 2-D feature space.

A cluster-cutting algorithm, such as expectation-maximization (EM), is performed on the obtained 2-D feature space. Optimizing EM clustering requires $~O\left(d^2{N}_P^{2}P\right)$ computations, where P here indicates the number of Gaussian models and d is the dimension of the space (here d = 2). To detect various spike prototypes, the EM clustering is implemented for different P’s, and the best fit is selected. The overall computations required for EM clustering for a maximum number of P units is in the order of $~{\sum }_{k=1,\dots ,P}O\left(4N_P^{2}k\right)=O\left(2N_P^2(P+1)P\right)$. Consequently, the overall computations required for training the PCA-based spike sorter is $~O(4N_s{N}_P+N_s^3+N_s^2{N}_P+2N_P^2(P+1)P)$. In the runtime mode, detected spikes are aligned and projected, and then classified to one of the predefined units using the Bayesian classifier, requiring computations in the order of ~O(4N_s + 4P).

In contrast, a five-level wavelet decomposition requires operations in the order of ~O(23N_s) if classical convolution is used. However, this number can be significantly reduced by using the approach we reported in [11]. Local averaging, typically used to remedy the shift variance property of the DWT and to obtain the single feature, with a node-dependent filter requires computations in the order of ~O(8N_s), since this filter is only applied to nodes 4, 6, 8, 9, and 10 in which spike features are mostly captured. At each node, one unit is discriminated at a time using a two-class cluster cutting (binary classification). This requires computations in the order of $~5\times O\left(2N_P^2\right)$. Consequently, the overall computations required for the training mode using the compressed sensing method is in the order of $~O(21N_s{N}_P+10N_P^2)$. In the runtime mode, every detected event is decomposed, filtered, and classified using a 1-D Bayesian classifier with computations in the order of ~O(21N_s + P).

For rate estimation, three methods were considered: the rectangular kernel (rate histogram), the Gaussian kernel, and the extended DWT (EDWT) we propose. In EDWT, the firing rate is directly obtained by normalizing the thresholded vectors and extending the decomposition to lower levels (higher frequency resolution). This requires $~O\left(45N_s{n}_W{\sum }_{l=5}^{\infty }{2}^{-l}\right)=O(22.5\times N_s)$. In the kernel based methods, a kernel function is convolved with the spike train and the rate is estimated by sampling the result. Assuming 45 ms bin width, and 2 ms refractory period, the number of computation required is in the order of ~O(22.5 × n_w). A Gaussian kernel width of n_w = 100 is typically used to limit the amount of computations. The computational cost comparison is summarized in Table I and further plotted in the results section.

TABLE I.

Computational Cost for the Training and Runtime Modes

	Training mode	Runtime mode
PCA/EM	O(4NsNP + Ns3 + Ns2NP + 2NP2(P+1)P)	O(4Ns + 4P + 22.5nw)
Compressed sensing	O(21NsNP + 10NP2)	O(43.5Ns + P)

III. Methods

Because our purpose was to demonstrate the ability to decode movement trajectory directly from neural data using the compressed signal representation, and given that the nature of cortical encoding of movement remains a subject of current debate in the neuroscience community [1], [3], [4], [26], investigation of the methods developed in this paper required generation of neural data with known spike train encoding properties. This section describes in details the methods we used to model and analyze the data to demonstrate the validity of the approach.

A. Spike Class Generation and Separability

Spike waveforms were detected and extracted from spontaneous activity recorded in the primary motor cortex of an anesthetized rat using a 16-channel microelectrode array. All procedures were approved by the Institutional Animal Care and Use Committee at Michigan State University following NIH guidelines. Details of the experimental procedures to obtain these recordings are described elsewhere [8]. These spikes were manually aligned and sorted using a custom spike sorting algorithm [9]. Out of 24 units recorded, the actual action potential waveforms are shown in Fig. 3 for five representative units recorded on one electrode.

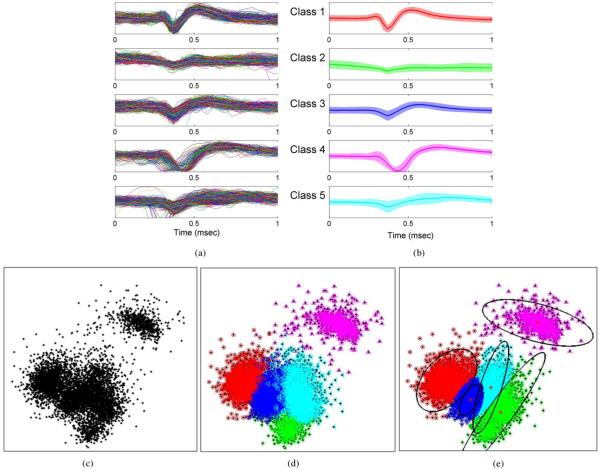
Fig. 3.

Five units obtained from spontaneous recordings in an anesthetized rat preparation. Units were chosen to posses significant correlation among their spike waveforms as seen in the PCA feature space in (c). (a) Events from each recorded unit, aligned and superimposed on top of each other for comparison. (b) Corresponding spike templates obtained by averaging all events from each unit on the left panel. (c) PCA 2-D feature space. Dimensions represent the projection of spike events onto the two largest principal components. (d) Clustering result of manual, extensive, offline sorting using hierarchical clustering using all features in the data. (e) Clustering result using the two largest principal components and EM cluster-cutting based on Gaussian mixture models. This is an example of a suboptimal sorting method with relatively unlimited computational power.

The separability of spike classes was calculated to determine the sensing thresholds for each neuron at any given time scale j. Specifically, we used the dimensionless measure

$$\Gamma \left\{C\right\}=\frac{\text{Between Cluster Separability}}{\text{Within Cluster Separability}}=\frac{S_B}{S_W}$$ (8)

for a set of clusters, {C_i|i = 1, 2, . . . , P}. The between-cluster separability is defined by [27]

$$S_B=\sum _{i=1}^P\frac{\sum _{x\in C_i}\sum _{y\notin C_i}\parallel x-y\parallel }{\mid C_i\mid \sum _{j\ne i}\mid C_j\mid }$$ (9)

where |C_i| equals the number of spikes belonging to cluster C_i, x and y are elements from the set of all spike waveforms and || · || represents the Euclidean distance (l₂ norm) between two elements. The quantity in (9) provides a factor proportional to the overall separation between clusters. For improved separability, a large S_B is desired. On the other hand, the within-cluster separability is defined as

$$S_W=\sum _{i=1}^P\frac{\sum _{x\in C_i}\sum _{y\in C_i}\parallel x-y\parallel }{\mid C_i\mid \left(\mid C_i\mid -1\right)}$$ (10)

and is proportional to the overall spread within each of the individual clusters. For improved separability, a small S_W is desired. Therefore, a large Γ indicates a greater overall separability.

We computed a separability ratio (SR) as the ratio between Γ{2} (i.e., a two-class separability) in every node of DWT decomposition to that in the time domain. Therefore, an SR ratio of 1 indicates equal degree of separability in both domains, while ratios larger than 1 indicate superior separability in the sparse representation domain. This later case implies that at least one unit can be separated in that node’s feature space better than the time domain’s feature space. This detected unit is subsequently removed from the data by removing its coefficients and the decomposition process continues until all possible units are detected, or all nodes have been examined on any given electrode. On the other hand, if the same unit can be discriminated in more than one node, the “best node” for discrimination of this unit is the node that provides the largest SR. For a given probability of false positives (typically 0.1), the sensing threshold ${\gamma }_p^j$ is determined by maximizing the separability of at least one spike class in each node. Since the sensing threshold is chosen to discriminate between spike events and not to minimize the mean squared error (MSE) of the reconstructed spike, this selection rule results in thresholds that are typically higher than those obtained from the thresholding rule for compression and near-optimal signal reconstruction [8], [28]. As a result, the number of false positives that may be caused by classifying noise patterns as unit-generated spikes is automatically reduced.

B. Population Model of 2-D Arm Movement

Since instantaneous decoding of spike trains is the ultimate goal in this application, we used the decoding performance as a measure of success of this method. To simulate spike trains from motor cortex neurons during movement planning and execution, we used a probabilistic population encoding model of a natural, nongoal directed, 2-D arm movement trajectory. The arm movement data were experimentally collected to ensure realistic kinematics. The discrete time representation of the conditional intensity governing each neuron firing rate was modeled as a variant of the cosine tuning model of the neuron’s preferred direction θ_p (ranging from 0 to 2π) [1]

$$\begin{array}{cc}\hfill {\lambda }_p(t_k\mid {\mathrm{x}}_p)=& \exp \left({\beta }_p+{\delta }_p\stackrel{.}{\theta }\cos \left(\frac{\theta \left(t_k\right)-{\theta }_p}{{\omega }_p}\right)\right)\hfill \\ \hfill & p=1,2,\dots ,P\hfill \end{array}$$ (11)

where β_p denotes the background firing rate, θ(t_k) denotes the actual movement direction, $\stackrel{.}{\theta }$ denotes velocity magnitude (kept constant during the simulation), X_p = [θ_p,δ_p,ω_p] is a parameter vector governing the tuning characteristics of neuron p, where it was assumed that the tuning depth δ_p was constant (δ_p and β_p where fixed for all neurons and equal to 1 and log(5), respectively), the preferred direction θ_p was uniformly distributed, while the tuning width ω_p was varied across experiments. Using this model, event times were obtained using an inhomogeneous Poisson process with 2 ms refractory period as

$$\mathrm{Pr}\left\{\text{spike from neuron}p\text{in}(t_k,t_k+\Delta ]\right\}\approx {\lambda }_p\left(t_k\right)\cdot \Delta$$ (12)

where Δ is a very small bin (~1 ms).

The tuning term in (11) incorporates a neuron-dependent tuning width ω_p, an important parameter that affects the bin width choice for rate estimation prior to decoding. Variability in this term (ω_p ranged from 0.25 to 4 in each experiment) resulted in firing rates that are more stochastic in nature and served to closely approximate the characteristics of cortical neurons’ firing patterns [18]. We used the mean squared error between the rate functions obtained from the simulated trajectory data and the estimated rates using the EDWT method as

$${\mathrm{MSE}}_j=\frac{1}{N}\sum _{n=1}^N{(\lambda \left[n\right]-{\widehat{\lambda }}_j\left[n\right])}^{2}j=1,2,\dots ,J.$$ (13)

While (13) provides a simple and obvious measure of performance, it should be noted that in practice the true rate function is unknown. Information theoretic measures are useful in such cases since they assess higher order statistical correlation between the estimators and measurable quantities such as the observed movement and can be useful to determine the time scale that best characterize the information in the instantaneous firing rate. We used a node-dependent mutual information metric between the encoded movement parameter and the rate estimator [29] defined as

$$I_j=\sum _{\theta ,{\widehat{\lambda }}_j}p(\theta ,{\widehat{\lambda }}_j)\log \frac{p(\theta ,{\widehat{\lambda }}_j)}{p\left(\theta \right)p\left({\widehat{\lambda }}_j\right)},j=1,2,\dots ,J.$$ (14)

This metric is particularly useful when the instantaneous rate function is not Gaussian distributed.

IV. Results

A. Spike Class Separability

We first report results of the spike sorting component of the algorithm. Fig. 3(c) shows a scatter plot of the first two principal components of the five representative spike classes in Fig. 3(a). These units were selected from the recorded pool to have poorly isolated clusters. Results of manual, extensive, offline sorting using hierarchical clustering of all the features in the data are displayed in Fig. 3(d). In Fig. 3(e), the clustering result using automated, PCA/EM cluster-cutting with two principal features is illustrated. Examination of these figures reveals that the lack of separability in the feature space, particularly for units 1, 2, 3, and 5, results in significant differences between the manual, extensive, offline sorting result and the automated PCA/EM result. Alternatively, when a two-class situation is considered where one single cluster is isolated in a given node while all other spike classes are lumped together, Fig. 4 illustrates that each spike class is separable in at least one node of the sparse representation. The different degrees of separability across nodes permit isolating one class at a time, owing to the compactness property of the transform in nodes that are best representative of that class. For example, class 1 appears poorly isolated from class 5 in the time-domain feature space, yet it is well separated from all the other classes in node 6.

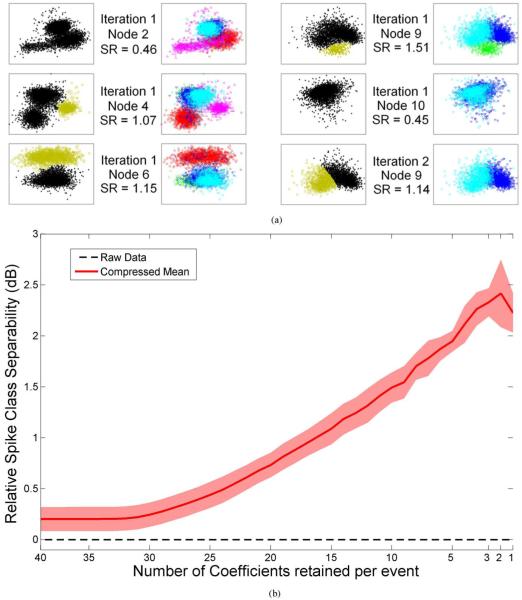
Fig. 4.

(a) Unit isolation quality of the data in Fig. 3. Each cell in the left side shows the separation (displayed as a 2-D feature space for illustration only) obtained using the compressed sensing method. The highest magnitude coefficients that survive the sensing threshold in a given node are considered irregular samples of the underlying unit’s firing rate and are marked with the “Gold” symbols in the left panel. The feature space of the sorted spikes using the manual, extensive, offline spike sorting is re-displayed in the right side (illustrated with the same color code as Fig. 3) for comparison. If a gold cluster from the left panel matches a single colored cluster from the right panel in any given row, this implies that the corresponding unit is well isolated in this node using the single feature/event magnitude alone. The unit is then removed from the data before subsequent DWT calculation is performed in the next time scale. Using this approach, three out of five units (pink, red, and green) in the original data were isolated during the first iteration in nodes 4, 6, and 9, respectively, leaving out two units to be isolated with one additional iteration on node 9’s remaining coefficients. In the first iteration, node 2 shows weak separation (SR = 0.45) between units. Unit 4 has larger separability in node 4 (SR = 1.07). Units 1 and 2 are separated in nodes 6 and 9 (SR = 1.15 and 1.51, respectively). Units 3 and 5 are separated in node 9 afterwards (SR = 1.14). (b) Quantitative analysis of spike class separability versus number of coefficients retained per event (40 coefficients retained implies 0% compression of the spike waveforms, while 1 coefficient retained implies 100% compression) (i.e., thresholding) for 24 units recorded in the primary motor cortex of anesthetized rat. A 2.5 dB (> 75%) improvement can be observed when the two most significant coefficients are averaged compared to time domain separability (Raw data).

It can be seen from Fig. 4 that in most nodes, the SR ratio is larger than 1 (except for nodes 2 and 10). For the 24 units recorded in this data set, the performance of the compressed sensing strategy was 92.88 ± 6.33% compared to 93.49 ± 6.36% for the PCA-EM. Performance of the sensing threshold selection process was quantified as a function of the number of coefficients retained in Fig. 4(b). As we increase the sensing threshold, the number of retained coefficients logically decreases thereby improving compression. However, the most interesting result is the improved separability by 2.5 dB compared to time domain separability, when preserving only the two most significant coefficients. This implies that discarding some of the coefficients that may be needed for optimal spike reconstruction and sorting in the time domain in a classical sense does improve the ability to discriminate between spike classes based on their magnitude only. Maximum separability is reached when we compute a single feature from the two most significant coefficients/event.

B. Firing Rate Estimation

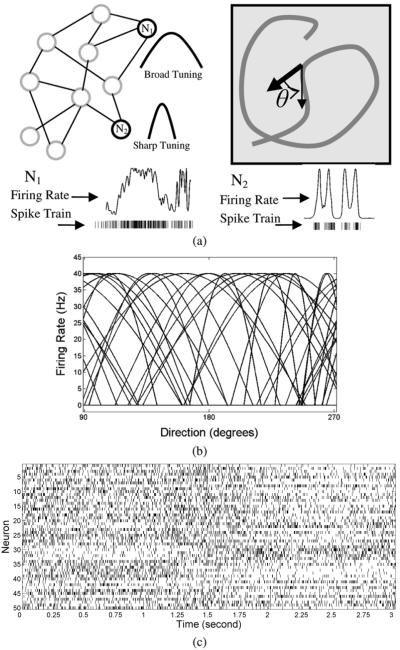
A sample trajectory, rate functions from neurons with distinct tuning characteristics and their spike train realizations are shown in Fig. 5. It can be clearly seen in Fig. 5(a) that the tuning width has a direct influence on the spike train statistics, particularly the ISI. A broadly tuned neuron exhibits more regular ISI distribution, while a sharply tuned neuron exhibits a more irregular pattern ISI. Fig. 5(b) illustrates the tuning characteristics of a subpopulation of the entire population over a limited range (for clarity) to demonstrate the heterogeneous characteristics of the model we employed. A 3-s raster plot in Fig. 5(c) illustrates the stochastic patterns obtained for the trajectory illustrated later in Fig. 8.

Fig. 5.

(a) Schematic of encoding 2-D, nongoal-directed arm movement: the sample network of neurons is randomly connected with positive (excitatory), and negative (inhibitory) connections. Right panel demonstrates a symbolic movement trajectory to indicate the movement parameter encoded in the neural population model. Sample firing rates and corresponding spike trains are shown to illustrate the distinct firing patterns that would be obtained with broad and sharp tuning characteristics. (b) Sample tuning characteristics (over a partial range) of a subset of the 50 neurons modeled with randomly chosen directions and widths. (c) Sample 3-s raster plot of spike trains obtained from the population model.

Fig. 8.

Decoding performance of a sample 2-D movement trajectory. The black line is the average over 20 trials, while the gray shade around the trajectory represents the estimate variance. Top left: one unit is observed on any given electrode (i.e., neural yield = 1) and therefore no spike sorting is required. The variance observed is due to the network interaction. Top right: every electrode records two units on average (neural yield = 2) and no spike sorting is performed. Bottom left: PCA/EM/Gaussian kernel spike sorting and rate estimation is implemented. Bottom right: Compressed sensing decoding result.

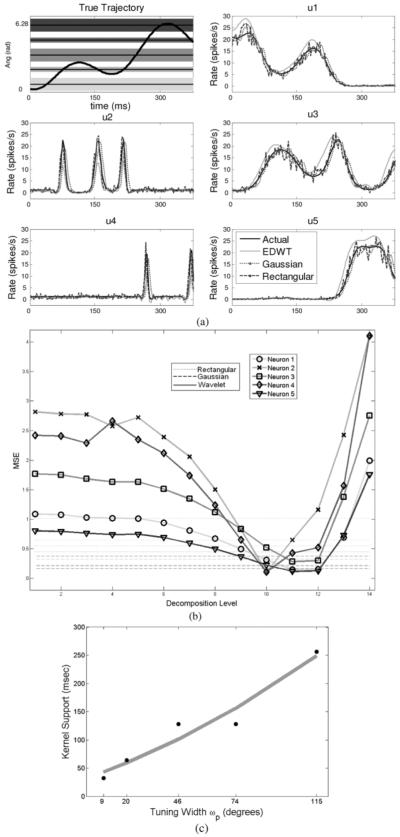
In Fig. 6, a 400-ms segment of the movement’s angular direction over time is illustrated superimposed on the neuronal tuning range of five representative units with distinct tuning widths. The resulting firing rates and their estimators using the rate histogram, Gaussian kernel, and extended DWT methods are illustrated for the five units, showing various degrees of estimation quality. As expected, the rate histogram estimate is noisy owing to the fixed width of the kernel, while the Gaussian and EDWT methods perform better. In Fig. 6(b), the relation between the wavelet kernel size and the MSE is quantified. As expected, decomposition levels with shorter kernel width (i.e., fine time scales) tend to provide the lowest MSE for neurons that are sharply tuned. In contrast, a global minimum in the MSE is observed for broadly tuned neurons at coarser time scales, suggesting that these decomposition levels are better suited for capturing the time varying-characteristics of the firing rates. Interestingly, the MSE for the EDWT method attains a lower level than both the rectangular and Gaussian kernel methods at the optimal time scale, clearly demonstrating the superiority of the proposed approach. The relation between the tuning width and the kernel size for the entire population is illustrated in Fig. 6(c). As the tuning broadens, larger kernel sizes (i.e., deeper decomposition levels) are required to attain a minimum MSE and vice versa.

Fig. 6.

(a) Top-left: 400 ms segment of angular direction from a movement trajectory superimposed on tuning “bands” of five representative units. Top right, middle, and bottom panels: Firing rates obtained from the point process model for five units and their extended DWT (EDWT), Gaussian, and rectangular kernel estimators. As expected, the rectangular kernel estimator is the noisiest, while the Gaussian and EDWT estimators are closest to the true rates. (b) Mean square error between the actual (solid black line) and the estimated firing rate for each neuron with the three methods. Each pair of dotted and dashed lines is the MSE for rectangular and Gaussian kernel methods, respectively, for the five units in (a). These remain flat as they do not depend on the DWT kernel window length. For the sharply tuned neurons, on average, ten levels of decomposition result in a minimum MSE that is lower than the MSE for rectangular and Gaussian kernel methods. For broadly tuned neurons, 12 levels of decomposition result in optimal performance. (c) Tuning width versus optimal kernel size. As the tuning broadens, larger kernel windows (i.e., coarser time scales) are needed to obtain optimal rate estimators.

The mutual information between the actual movement trajectory and the rate estimators are shown in Fig. 7. There is a steady increase in the mutual information versus kernel support until a maximum is reached at the optimal decomposition level that agrees with the minimum MSE performance. This maximum coincides with a rate estimator spectral bandwidth matching that of the underlying movement parameter. Rate estimators beyond the optimal time scale do not carry any additional information about the movement trajectory.

Fig. 7.

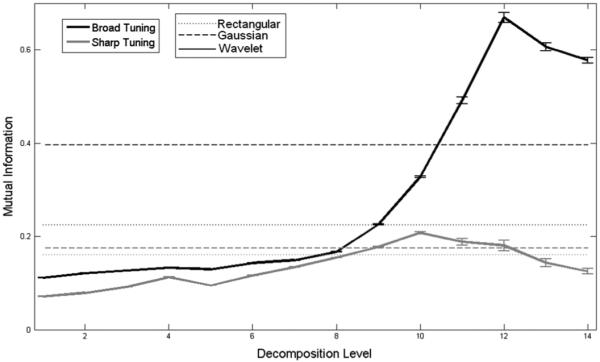
Average mutual information (in bits) between movement direction, θ, and rate estimators averaged across the two subgroups of neurons in the entire population as a function of decomposition level (i.e., kernel size). Solid lines indicate the performance of the EDWT method (dark for the broad tuning group and gray for the sharp tuning group). The two dashed lines represent the Gaussian kernel method (broad tuning and sharp tuning groups), while the two dotted lines represent the rectangular kernel method in a similar way. As expected, sharply tuned neurons require smaller kernel size to estimate their firing rates. Overall, the EDWT method achieves higher mutual information than either the fixed width Gaussian or rectangular kernels for broadly tuned neurons, while slightly less for sharply tuned neurons owing to the relatively more limited response time these neurons have, limiting the amount of data.

C. Decoding Performance

A sample trajectory and the decoded trajectory are shown in Fig. 8 for four different cases. First, when no spike sorting is required. This is the ideal case in which every electrode records exactly the activity of one unit, but is hard to encounter in practice. Second, when two or more units are recorded on a single electrode but no spike sorting is performed prior to rate estimation. Third, when spike sorting is performed for the later case using the PCA/EM/Gaussian kernel algorithm. And fourth, when combined spike sorting and rate estimation are performed using the compressed sensing method. We used a linear filter for decoding in all cases [30]. It is clear that the proposed method has a decoding error variance that is comparable to the PCA/EM/Gaussian kernel algorithm, suggesting that the performance is as good as, if not superior, to the standard method.

D. Computational Cost

An important aspect to validate and confirm the superiority of our approach is to compare the computational complexity of the standard PCA/EM/Gaussian kernel rate estimator to the compressed sensing method for different event lengths (N_s) and different number of events (N_p) per neuron.

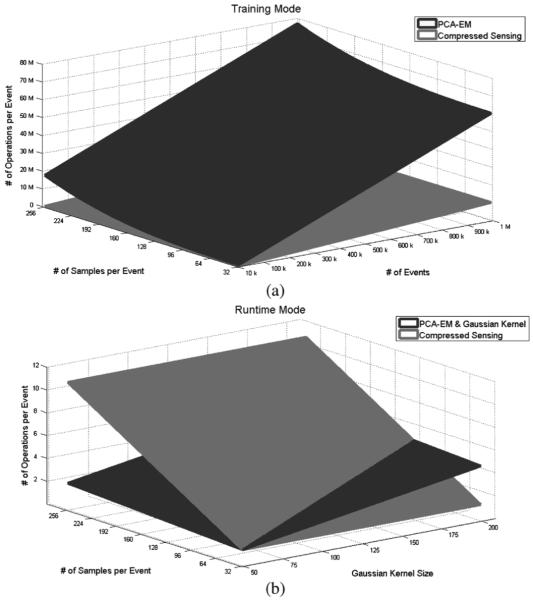
The results illustrated in Fig. 9 show that the proposed method requires significantly less computations for training. This is mainly attributed to the complexity in computing the eigenvectors of the spike data every time a new unit is recorded. In contrast, wavelets serve as universal approximators to a wide variety of transient signals and therefore do not need to be updated with the occurrence of events from new units. In the runtime mode, the computational cost for the proposed method becomes higher when the number of samples/event exceeds 128 samples. At a nominal sampling rate of 40 kHz (lower rates are typically used), this corresponds to a 3.2 ms interval, which is much larger than the typical action potential duration (estimated to be between 1.2–1.5 ms). We conclude that the proposed method is also superior in the runtime mode.

Fig. 9.

Computational complexity of PCA/EM/Gaussian kernel and the compressed sensing method. (a) Computations per event versus number of events and number of samples per event in the training mode. (b) Computations per event versus number of samples per event and kernel size in the runtime mode. At a sampling rate of 40 KHz and ~1.2–1.5 ms event duration (48–60 samples), the compressed sensing method requires less computations than the PCA/EM/Gaussian kernel method. The number of units is assumed fixed in the training mode for both methods (P = 50).

V. Discussion

In this work, we have proposed a new approach to directly estimate a critical neuronal response property, the instantaneous firing rate, from a compressed representation of the recorded neural data. The approach has three major benefits. First, the near-optimal denoising and compression allows to efficiently transmit the activity of large populations of neurons while simultaneously maintaining features of their individual spike waveforms necessary for spike sorting, if desired. Second, firing rates are estimated across a multitude of timescales, an essential feature to cope with the heterogeneous tuning characteristics of motor cortex neurons. These characteristics are important to consider in long term experiments where plasticity in the ensemble interaction is likely to affect the optimal time scale for rate estimation. Third, as our extensive body of prior work has demonstrated [11], [31], the algorithm can be efficiently implemented in low-power, small size electronics to enable direct decoding of the neural signals to take place without the need for massive computing power. Taken together, these are highly desirable features for real-time adaptive decoding in BMI applications.

We have used a particular model for encoding the 2-D hand trajectory for demonstration purposes only. It should be noted, however, that the method is completely independent of that model. What is important to consider is the fact that the sparse representation preserves all the information that needs to be extracted from the recorded neural data to permit faithful decoding to take place downstream. This includes the features of the spike waveforms as well as the temporal characteristics of the underlying rate functions.

In the tests performed here we have used the same wavelet basis, the symmlet4, for both spike sorting and rate estimation. This basis was previously demonstrated to be near-optimal for denoising, compression, and hardware implementation. However, the possibility exists to use this basis in the first few levels, and then extend the decomposition from that point on using a different basis that may better represent other features present in the rate functions that were not best approximated by the symmlet4. For example, the “bumps” in the sparse rate estimates in Fig. 6 are not as symmetrical in shape as those in the original rate, or those in the Gaussian estimator. For this particular example a more symmetric basis may be better suited.

Estimation of the rate using a fixed bin width may be adequate for certain applications that utilize firing rates as the sole information for decoding cortical responses during instructed behavioral tasks such as goal-directed arm reach tasks [3]-[4], [32], [33]. These operate over a limited range of behavioral time scales. However, natural motor behavior is characterized by more heterogeneous temporal characteristics that reflect highly-nonstationary sensory feedback mechanisms from the surrounding cortical areas. The firing rates of motor neurons during naturalistic movements are highly stochastic and require a statistically-driven technique that can adapt to the expected variability [18]. This is particularly important given the significant degrees of synchrony typically observed between cortical neurons during movement preparation [34], and also observed during expected and unexpected transitions between behavioral goal representations [35].

While it has been argued that precise spike timing does not carry information about motor encoding [36], one must note that most of the BMI demonstrations to date were carried out in highly-trained subjects performing highly stereotypical, goal-directed behavioral tasks. Very few studies, if any, have been carried out to characterize naturally occurring movements in naïve subjects. Thus, the potential still exists for new studies that may demonstrate the utility of both neuronal response properties, namely precise spike timing and firing rate, in decoding cortical activity. For that, the sparse representation is able to simultaneously extract these two important elements that are widely believed to be the core of the neural code [37]. Therefore, our proposed approach will be the first to offer the solution for extracting both properties within a single computational platform in future generations of BMI systems.

We note that for a fully implantable interface to the cortex to be clinically viable, spike detection, sorting, and instantaneous rate estimation need to be implemented within miniaturized electronics that dissipate very low power in the surrounding brain tissue. More recently, it has been shown that tethering the device to the subject’s skull to maintain a wired connection to the implant significantly increases brain tissue adverse reaction, which is believed to negatively affect implant longevity [38]. Therefore, the interface needs to feature wireless telemetry to minimize any potential risk of infection and discomfort to the patient and to elongate the implant’s lifespan. We believe that eliminating any of the steps from the signal processing path while preserving the critical information in the neural data will significantly reduce the computational overhead to permit small size, low power electronics to be deployed and accelerate the translation of this promising technology to clinical use.

VI. Conclusion

We have proposed a new approach to directly estimate instantaneous firing rates of cortical neurons from their compressed extracellular spike recordings. The approach is based on a sparse representation of the data and eliminates multiple blocks from the signal processing path in BMI systems. We used the decoding of simulated 2-D arm trajectories to demonstrate the quality of decoding obtained using this approach. We also demonstrated that regardless of the type of neural response property estimated, the approach efficiently captures the intrinsic elements of these responses in a simple, adaptive, and computationally efficient manner. The approach was compared to other methods classically used to estimate firing rates through a more complex processing path. We further demonstrated the improved performance attained with our approach, while maintaining a much lower computational complexity.

Quantitative measures were applied to show that the sparse representation allows for better unit separation compared to classical PCA techniques, currently employed by many commercial data acquisition systems. This suggests that full reconstruction of the spike waveforms for traditional time domain sorting is not necessary, and that more accurate spike sorting performance could ultimately be achieved when the proposed method is used. This translates into substantial savings in computational and communication costs for implantable neural prosthetic systems to further improve their performance and potential use in clinical applications.

Biography

Mehdi Aghagolzadeh received the B.Sc. degree in electrical engineering with honors from University of Tabriz, Tabriz, Iran, in 2003, and the M.Sc. degree in electrical engineering from University of Tehran, Tehran, Iran, in 2006. He is currently working toward the Ph.D. degree in the Department of Electrical and Computer Engineering, Michigan State University, East Lansing.

He has held various academic scholarships throughout his academic career. His research interest includes statistical signal processing, neural engineering, information theory, and system identification.

Karim Oweiss (S’95-M’02) received the B.S. degree (1993) and the M.S. (1996) with honors in electrical engineering from the University of Alexandria, Alexandria, Egypt, and the Ph.D. degree in electrical engineering and computer science from the University of Michigan, Ann Arbor, in 2002. He completed postdoctoral training with the Biomedical Engineering Department at the University of Michigan, Ann Arbor, in the summer of 2002.

In August 2002, he joined the Department of Electrical and Computer Engineering and the Neuroscience program at Michigan State University, where he is currently an Assistant Professor and Director of the Neural Systems Engineering Laboratory. His research interests span diverse areas that include statistical signal processing, information theory, machine learning, neural integration and coordination in sensorimotor systems, and computational neuroscience. He is the editor of the book “Statistical Signal Processing for Neuroscience” (forthcoming) to be published by Academic Press in fall 2009.

Prof. Oweiss is a member of the Society for Neuroscience. He is also a member of the Board of Directors of the IEEE Signal Processing Society on Brain Machine Interfaces, the technical committees of the IEEE Biomedical Circuits and Systems, the IEEE Life Sciences, and the IEEE Engineering in Medicine and Biology Society. He is an Associate Editor of IEEE Signal Processing Letters, the Journal of Computational Intelligence and Neuroscience, and the EURASIP Journal on Advances in Signal Processing. He was awarded the excellence in Neural Engineering award from the National Science Foundation in 2001.