Early Math Matters: Kindergarten Number Competence and Later Mathematics Outcomes

Abstract

Children’s number competencies over 6 time points, from the beginning of kindergarten to the middle of 1st grade, were examined in relation to their mathematics achievement over 5 later time points, from the end of 1st grade to the end of 3rd grade. The relation between early number competence and mathematics achievement was strong and significant throughout the study period. A sequential process growth curve model showed that kindergarten number competence predicted rate of growth in mathematics achievement between 1st and 3rd grades as well as achievement level through 3rd grade. Further, rate of growth in early number competence predicted mathematics performance level in 3rd grade. Although low-income children performed more poorly than their middle-income counterparts in mathematics achievement and progressed at a slower rate, their performance and growth were mediated through relatively weak kindergarten number competence. Similarly, the better performance and faster growth of children who entered kindergarten at an older age were explained by kindergarten number competence. The findings show the importance of early number competence for setting children’s learning trajectories in elementary school mathematics.

Poor achievement in mathematics is a major concern in U.S. schools. Advanced study in high school mathematics is a pillar for success in college science (Sadler & Tai, 2007) and serves as a gateway for a wide range of vocations in science, technology, engineering, and mathematics disciplines. Unfortunately, many U.S. students do not develop the foundations for learning advanced mathematics. Mathematics difficulties are cumulative and worsen with time. For example, difficulties with whole numbers are obstacles to learning fractions, and difficulties with fractions lead to failure in algebra (National Mathematics Advisory Panel, 2008). Mirroring U.S. national trends, recent data from the state of Delaware showed approximately 25% of students failed to meet state mathematics standards in third grade, with the percentage of failing students increasing each grade thereafter through ninth grade, where 49% failed (Delaware Department of Education, 2007).

National statistics in the United States reveal persistent income disparities in mathematics achievement across grade levels, with low-income students scoring substantially lower than middle-income students (National Assessment of Educational Progress, 2007). Yet, low-income youth who acquire strong mathematical skills by the end of middle school are much more likely to graduate from college than their peers who do not acquire such skills (National Mathematics Advisory Panel, 2008).

Early Number Competence

There is growing consensus that many mathematics difficulties in elementary school can be traced to weaknesses in basic whole number competencies, that is, in understanding the meaning of numbers and number relationships (e.g., Gersten, Jordan, & Flojo, 2005; Malofeeva, Day, Saco, Young, & Ciancio, 2004; National Mathematics Advisory Panel, 2008). Number competencies refer to ability to apprehend the value of small quantities immediately, make judgments about numbers and their magnitudes (e.g., 4 is closer to 3 than to 6), grasp counting principles (e.g., the final number of a set indicates the total number of objects), and join and separate sets (e.g., 3 and 2 makes 5, and 5 take away 2 is 3). They also involve a linear representation of small numbers, such that each number is one more than the one that comes before it or one less than the one that comes after (Siegler & Booth, 2004). Number competencies allow children to make connections among mathematical relationships, principles, and procedures (Gersten et al., 2005). Early number competencies can be differentiated from a more complex, but related, kind of mathematics knowledge (e.g., principles of place value) that children acquire primarily through formal teaching (National Mathematics Advisory Panel, 2008).

Number Competence and Mathematics Difficulties

Weak general number competence is reflected in poorly developed counting procedures, slow fact retrieval, and inaccurate computation—all characteristics of children with mathematics difficulties (Geary, Hamson, & Hoard, 2000; Jordan, Hanich, & Kaplan, 2003a, 2003b). Mastery of number combinations is tied to fundamental number knowledge (Baroody & Rosu, 2006; Locuniak & Jordan, 2008). It is difficult to memorize arithmetic facts by rote without understanding how combinations relate to one another on a number line (e.g., 3 + 2, 2 + 3, 5 − 2, and 5 − 3). Accurate and efficient counting facilitates children’s learning of number relations, leading to strong connections between a problem and its solution and reducing the need for rote memorization (Siegler & Shrager, 1984). Developmental dyscalculia, a severe form of mathematics difficulties, is attributed to domain-specific cognitive impairments in number knowledge rather than domain-general deficits in memory, spatial processing, or language (Butterworth & Reigosa, 2007). Children with dyscalculia show particular weaknesses in recognizing and comparing numbers as well as in counting and enumerating sets (Landerl, Bevan, & Butterworth, 2004).

Malleability of Number Competencies

It has been argued that infants have a natural number sense or ability to represent numbers in a nonverbal manner. These preverbal systems (e.g., an object file system for the precise representation of small sets of objects and an analogue magnitude system for capturing approximate representations of large sets) develop without input or instruction (Berch, 2005; Dehaene, 1997; Feigenson, Dehaene, & Spelke, 2004) and are shared by humans from differing cultural background as well as other species (Gordon, 2004). They provide a foundation for acquiring number competencies involving words and symbols.¹ Knowledge of the verbal or symbolic number system is heavily influenced by experience or the input the child receives (Case & Griffin, 1990; Geary, 1995; Levine, Jordan, & Huttenlocher, 1992). Engaging young children in number activities and games (e.g., board games that emphasize one-to-one correspondences, counting, and number representations) is important for building number competence (Baroody, 1987; Booth & Siegler, 2008; Copley, 2000; Gersten et al., 2005). Efforts to teach number competencies to high-risk kindergartners have resulted in significant gains on first-grade mathematics outcomes compared with control groups (Griffin, Case, & Siegler, 1994).

Predictability of Early Number Competence

Measures of early number competence have shown promise for predicting conventional mathematics outcomes in school. The ability to identify numbers, discriminate between quantities, and identify missing numbers in sequences at the end of kindergarten is a strong predictor of mathematics outcomes at the end of first grade (Chard et al., 2005; Clarke & Shinn, 2004). Jordan, Kaplan, Olah, and Locuniak (2006) examined number competencies (e.g., counting, number comparisons, and calculation) in kindergartners of different economic backgrounds. Longitudinal assessment over four kindergarten time points revealed three reliably distinct growth patterns: children who started and finished kindergarten with strong number competence, children who came to kindergarten with low number competence but made progress in school, and children who came to kindergarten with low number competence and did not progress. Not surprisingly, low-income children were overrepresented in the low-performing, low-growth trajectory group and had particular weaknesses on number tasks with strong verbal components (i.e., story problems vs. calculations presented in a nonverbal context). After controlling for age of kindergarten entry, income level, and gender, it was also found that number competence level and growth were highly predictive of mathematics achievement at the end of first grade (Jordan, Kaplan, Locuniak, & Ramineni, 2007). Studies also have shown that early number competence predicts mathematics outcomes over and above supporting cognitive competencies, including verbal, spatial, and memory skills (Locuniak & Jordan, 2008; Mazzocco & Thompson, 2005).

Although kindergarten number competence is clearly predictive of mathematics outcomes in relative proximity (e.g., kindergarten number competence to first-grade mathematics), it is possible that the relation fades and becomes less important with time. Because typical first-grade mathematics curricula focus on simple number concepts and calculation, measures of number competence and first-grade mathematics achievement are similar. In fact, Chard et al. (2005) used a number knowledge test as a marker for achievement in first grade, one that assesses the same constructs as the number measures that were used in kindergarten. Mathematics expectations, however, become more complex in elementary school. By the end of third grade, the point at which many U.S. children start taking state-mandated mathematics assessments, the curriculum layers Base 10 place value concepts, written computation with multidigit numbers, rational numbers, and so forth onto basic whole-number constructs (Kilpatrick, Swafford, & Findell, 2001). Children are required to apply their number knowledge to solve novel problems. Although the elementary school mathematics curriculum diversifies, it still incorporates many elements of number competence. Algebra and even geometry (e.g., calculating perimeters and areas) depend on skill with numbers. Mazzocco and Thompson (2005) found that children who were identified with learning disabilities in mathematics also performed poorly on specific number competence items (e.g., magnitude judgments of one-digit numbers and mental addition) on a standardized early mathematics test in kindergarten.

Present Study

The aim of the present study was to examine the predictive relationship between early number competence and later mathematics achievement. It is the end piece of the Children’s Math Project, a multiyear longitudinal investigation of children’s mathematics difficulties. The present work extends previous studies (Jordan et al., 2007; Mazzocco & Thompson, 2005) by examining number competence and growth over multiple time points in relation to later mathematics achievement and growth. Children were assessed in number competence six times, from the beginning of kindergarten through the middle of first grade. Our measure was designed to tap number skills that are relevant to the mathematics curriculum in primary school rather than more general cognitive abilities. It assessed competencies related to counting, number comparisons, and calculation, which are strongly related to one another (Jordan et al., 2007). Then children’s mathematics achievement was measured on five occasions, from the end of first grade through the end of third grade, on a standardized test assessing both written computation and applied problem solving. This design allowed us to use a sequential process growth curve model to examine level of and growth in number competence (kindergarten to early first grade) in relation to mathematics performance and growth from late first grade to late third grade. Recent studies (e.g., Fuller, Wright, Gesicki, & Kang, 2007) have emphasized the importance of understanding students’ patterns of growth as well as their levels of proficiency.

We asked the following questions: (a) Does level of number competence in kindergarten predict level of mathematics performance after first grade? (b) Does level of kindergarten number competence predict rate of achievement in mathematics between first and third grades? (c) Does rate of growth in early number competence predict later mathematics level and growth? Because age (older children performed better than younger children), gender (boys performed better than girls), and income level (middle-income children performed better than low-income children) were significant predictors of number competence in previous studies (e.g., Jordan et al., 2006), we considered each of these background variables in the present analyses.

Method

Participants

Participants were drawn from six schools in the same public school district in northern Delaware. The schools were selected because they served children from both low-income and middle-income families. Background characteristics of participants in kindergarten (where we set the intercept for number competence; n = 378) and third grade (where we set the intercept for children’s mathematics achievement; n = 196) are presented in Table 1. In the kindergarten sample, 54% of the children were boys, 56% were minority, and 33% were low income. In the third-grade sample, 52% were boys, 45% were minority, and 23% were low income. For both samples, the mean age at the beginning of kindergarten was 5.5 years. The attrition rate was similar across the participating schools. All children were taught mathematics with the Math Trailblazers curriculum (Teaching Integrated Mathematics and Science, 2004) throughout the course of the study, with the exception of 15 children who were taught with Investigations in Number, Data, and Space (TERC, 1998) in second and third grades. The two curricula are similar in content and approach. The mean standard scores in mathematics achievement were about 100 in our third-grade sample (see Table 1), which is also the mean of the national normative sample (on the Woodcock–Johnson III Achievement Tests; McGrew, Schrank, & Woodcock, 2007).

Table 1.

Demographic Information for Participants in Kindergarten (n = 378) and Third Grade (n = 196)

Demographic variable	Kindergarten	Grade 3
Gender
Male	54%	52%
Female	46%	48%
Race
Minoritya	56%	45%
Nonminority	44%	55%
Incomeb
Low income	33%	23%
Middle income	67%	77%
Mean kindergarten start age	5 years, 6 months   (4 months)	5 years, 6 months   (4 months)
Mean WJMath Calculation    standard score		102 (17)
Mean WJMath Applied    Problems standard    score		104 (14)

Note. Standard errors in parentheses. WJMath = Woodcock–Johnson III Achievement Tests–Mathematics.

^aMinority refers to African American (61%), Asian (10%), and Hispanic (29%) in kindergarten and African American (63%), Asian (11%), and Hispanic (26%) in third grade.

^bLow income was determined by eligibility for the school district’s free or reduced-price lunch program.

Materials

Number competence

The number competency core battery was developed as a part of a larger longitudinal study of children’s mathematics development (see Jordan et al., 2007). We used items and tasks that were given to children at all six time points in kindergarten and first grade. The 42-item measure has good internal reliability for kindergartners and first graders (coefficient alpha > .80 at each level, with an average reliability of .87, SD = .03). Administration and scoring procedures were standardized to reduce potential bias (Jordan et al., 2006). Testers read instructions verbatim, and all scoring questions and ambiguities were discussed and resolved by the research team.

The test items tapped counting and number recognition, number comparisons, nonverbal calculation, story problems, and number combinations. The measure is not timed and typically takes about 25–30 min to administer. The subtasks were always presented to each child in the following order: counting and number recognition, number comparisons, nonverbal calculation, story problems, and number combinations. The total possible score on the measure was 42 points.

Counting and number recognition involved 10 items. Children were first asked to count to 10 and were given one point if they succeeded. Children were allowed to restart counting only once but were always allowed to self-correct. Children’s knowledge of counting principles (Geary, Hoard, & Hamson, 1999) was assessed after viewing a set of either five or nine alternating yellow and blue dots. A finger puppet told the child he or she was learning to count. The child was then asked to indicate whether the puppet counted “OK” or “not OK.” Correct counting involved counting from left to right and right to left. Unusual but correct counts involved counting the yellow dots first and then the blue dots or counting the blue dots first and then the yellow dots. For incorrect counts, the puppet counted left to right but counted the first dot twice (“1, 2”). Children received a score of correct/incorrect for each of eight trials. (Children were screened for color blindness prior to the task, and no child failed the screen.) Finally, children were asked to name a visually presented number (i.e., 13).

Number comparisons, adapted from Griffin (2002), consisted of eight items. Given a number (e.g., 7), children were asked what number comes after that number and what number comes two numbers after that number. Given two numbers (e.g., 5 and 4), children were asked which number was bigger or which number was smaller. Children also were shown visual arrays of three numbers (e.g., 6, 2, and 5), each placed on the point of an equilateral triangle. They were then asked to identify which number was closer to the target number (e.g., 5) at the triangle’s apex.

On nonverbal calculations the tester and child sat facing each other, with a box of 20 chips placed off to the side. The experimenter also had a box lid with an opening on the side. Four addition and four subtraction calculations were presented: 2 + 1, 4 + 3, 2 + 4, 3 + 2, 3 − 1, 7 − 3, 5 − 2, 6 − 4. The tester placed a number of chips on her mat (in a horizontal line) and told the child how many chips were on the mat. The examiner then covered the chips with the box lid. The researcher either added or removed chips (through the side opening) one by one and at the same time told the child how many chips were being added or taken away. For each item, the children were asked to indicate how many chips were left hiding under the box, either with chips or by stating the number word. Children’s errors were corrected on the initial addition and subtraction calculations. The nonverbal calculation task was adapted from and validated by Levine et al. (1992).

Story problems involved four oral addition and four oral subtraction story problems, read one at a time. The calculations were the same as those used in nonverbal calculation. The addition problems were phrased “Sue has m pennies. Bill gives her n more pennies. How many pennies does Sue have now?” whereas the subtraction problems were phrased “Darrel has m pennies. Karen takes away n of his pennies. How many pennies does Darrel have now?”

Finally, four addition and four subtraction number combinations were given, with the same calculations that were presented on nonverbal calculation and story problems. The items were orally phrased as “How much is m and n?” and “How much is n take away m?”

Mathematics achievement

Children were given the Calculation and Applied Problems portions of the Woodcock–Johnson III for a composite mathematics achievement score (WJMath; McGrew et al., 2007). The WJMath is an individually administered, standardized diagnostic battery with strong reliability (coefficient alpha > .80 for ages 6–8). The WJMath has high content validity and is significantly correlated with performance on the third-grade math portion of the Delaware State Testing Program (r = .77, p < .01). The Calculation (WJCalc) subtest measures the ability to perform computations in a conventional written format. The Applied Problems (WJApp) subtest requires the child to analyze and solve orally presented mathematics problems in various contexts. The correlation between the two subtests is .68 for ages 6–8. The WJMath measures are not timed and have a total administration time of about 30 min.

Procedure

Children were assessed longitudinally a total of 11 times between kindergarten and third grade. They were given the number measure on six occasions: four times in kindergarten (September, November, February, and April) and twice in first grade (September and November). Children’s later achievement was assessed on the WJMath five times: April of first grade, September and April of second grade, and September and April of third grade. One of several trained graduate research assistants in school psychology assessed children individually in their schools. Each testing period lasted about a month, and schools were visited in approximately the same order over the various time points.

Results

Raw scores were used for all analyses. Correlations between WJMath and number competence at the various time points are presented in Table 2. All the correlations are positive and significant (p < .01). On the 42-item number competence measure (in February of kindergarten, where we set the intercept in the subsequent growth curve analyses), a raw score of 18 was at the 25th percentile, a score of 22 was at the median, and a score of 29 was at the 75th percentile.

Table 2.

Correlations Between Early Number Competence and Later Math Achievement Across All Time Points

Time of testing	Grade 1 spring			Grade 2 fall			Grade 2 spring			Grade 3 fall			Grade 3 spring
	WJMath	WJApp	WJCalc	WJMath	WJApp	WJCalc	WJMath	WJApp	WJCalc	WJMath	WJApp	WJCalc	WJMath	WJApp	WJCalc
Kindergarten
September	.70	.68	.58	.64	.63	.55	.68	.70	.55	.64	.65	.52	.63	.65	.52
November	.66	.66	.55	.63	.61	.53	.64	.65	.51	.66	.65	.55	.60	.61	.50
February	.69	.69	.56	.67	.65	.56	.72	.72	.60	.71	.70	.59	.65	.66	.53
April	.73	.72	.61	.66	.64	.57	.68	.67	.58	.70	.68	.59	.66	.65	.56
Grade 1
September	.71	.72	.56	.71	.69	.62	.66	.68	.53	.66	.68	.52	.65	.67	.52
November	.72	.71	.61	.67	.62	.63	.63	.61	.55	.60	.58	.51	.60	.58	.52

Note. All correlations are significant (p < .01). WJMath = Woodcock–Johnson III Achievement Tests–Mathematics; WJApp = Woodcock–Johnson III Applied Problems subtest; WJCalc = Woodcock–Johnson III Calculation subtest.

Problems of Attrition

A common feature of longitudinal studies is loss of participants over time. Attrition gives rise to the usual problems of missing data in longitudinal studies. To assess this problem, we used a logistic regression analysis to examine the extent to which absence at the final time point is related to gender, income, minority status, and age. The results are shown in Table 3. Low-income and minority children were approximately 1.2 times more likely to be absent from the study at the last time point compared with their middle-income and majority children counterparts. These effects are statistically significant. Gender and age did not predict the odds of being absent from the study. The finding of differential attrition may limit the generalizability of the findings and should be kept in mind when interpreting the results.

Table 3.

Summary of Logistic Regression Analysis for Variables Predicting Absence From the Study at Time 14 (End of Third Grade)

Predictor	B	SE B	eB
Gender	0.05	0.05
Income	0.16**	0.06	1.2
Race	0.18**	0.06	1.2
Age	0.00	0.00

Note. Gender is coded as 1 for male and 0 for female, income is coded as 1 for low income and 0 for middle income, and race is coded as 1 for minority and 0 for nonminority. e^B = exponentiated B, also known as the odds ratio.

^**p < .01.

The most restrictive assumption that can be made regarding missing data in this context is that they are missing completely at random; that is, the missing data patterns are independent of both observed and missing data on all variables. A more realistic assumption regarding missing data is they are not missing at random, in which the missing data at any point in time t is due to observed responses at that time point and possibly previous time points. Statistical modeling for data not missing at random, however, requires a model for the process that led to missing data, and typically such modeling is not attempted.

A reasonable alternative in longitudinal studies is to assume that the missing data are missing at random, in which “missingness” (including attrition) at time t may be due to levels of responses at time t – 1, or perhaps earlier. Attrition in this study was found to be due primarily to children moving from the school district (rather than withdrawing from the study or being absent on the day of the testing), and there is no evidence that it resulted from the actual performance of the children at either time t or earlier time points. Thus, in the following growth curve analyses, missing data were handled by an imputation procedure based on full information maximum likelihood under the assumption that missing data are missing at random (Little & Rubin, 2002). This procedure was developed by Arbuckle (1996) and implemented in the Mplus program (Muthén & Muthén, 2007). It allows us to use all available data in the estimation of the sequential growth curve models discussed next.

Sequential Process Growth Curve Modeling

Number Competence and Woodcock–Johnson General Mathematics Achievement (WJMath)

A sequential process growth curve model was used to estimate the intercepts and slopes for number competence and mathematics achievement (WJMath). In keeping with the structural equation modeling specification of growth curve modeling (Willett & Sayer, 1994), we refer to the intercepts and slopes as the growth factors. A sequential process growth curve model is a variant of multivariate growth curve modeling (Kaplan, 2009; Willett & Sayer, 1994) that joins two conventional growth curve models but allows for the growth factors of one process to be predicted by the growth factors of the other, through the specification of regression relations among the growth parameters. In the present study, the sequential process growth curve model enables us to test whether the growth factors (i.e., intercepts and slopes) associated with WJMath can be predicted by the growth factors of number competence. All growth curve analyses used the Mplus software program (Muthén & Muthén, 2007).

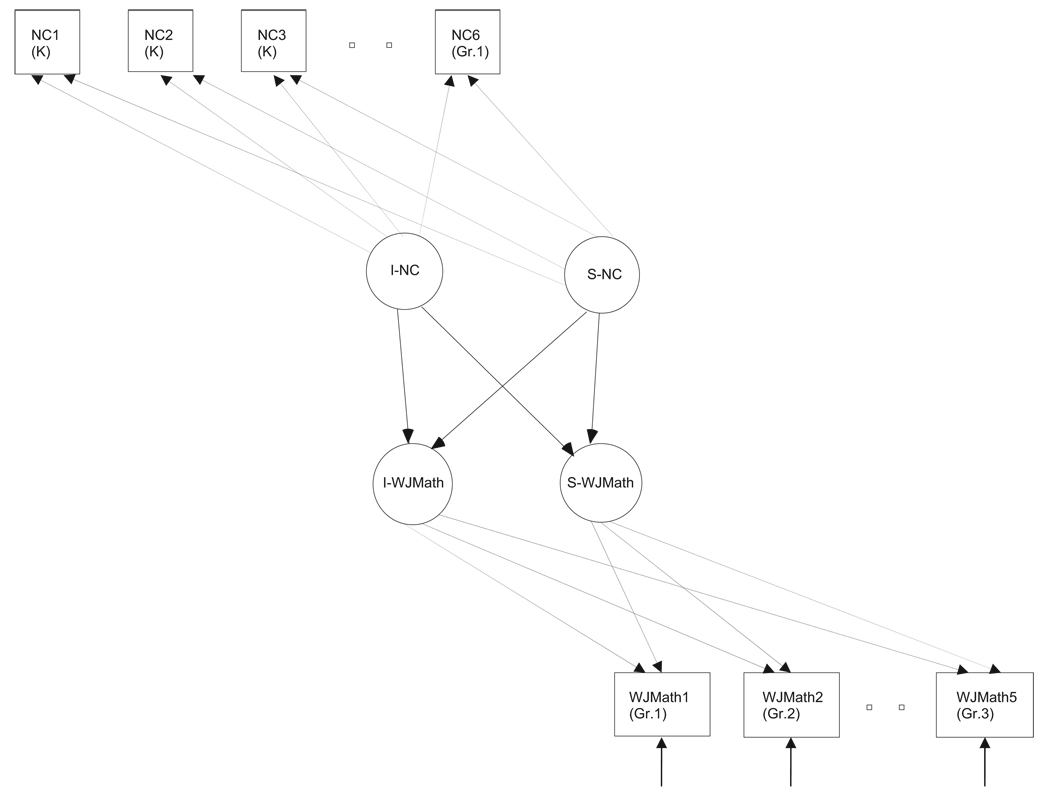
Two models are considered. Model 0 is the sequential process growth curve model without the addition of background predictors and serves as the baseline model. The path diagram in Figure 1 shows how the sequential process model is specified. The squares indicate the repeated measures of number competence (i.e., four times in kindergarten and twice in first grade), the rectangles indicate the repeated measures of mathematics achievement as measured by the WJMath (i.e., once in first grade, twice in second grade, and twice in third grade), and the circles represent the intercepts and slopes for number competence and the intercepts and slopes for WJMath. The manner in which the repeated measures provide estimates of the growth factors is based on the structural modeling approach to growth curve modeling (see, e.g., Kaplan, 2009; Willett & Sayer, 1994). Our primary interest is in the relationships among the growth factors of number competence and WJMath, and the single-headed arrows among the growth factors themselves indicate this.

Figure 1.

Path diagram of sequential growth curve model for number competence (NC) from the beginning of kindergarten (K) through the middle of first grade and math achievement (Woodcock–Johnson III Achievement Tests–Mathematics [WJMath]) from the end of first grade through the end of third grade. Growth parameters for WJMath are regressed on the NC growth parameters (I = intercept, S = linear slope). Not all time points are shown because of space limitations.

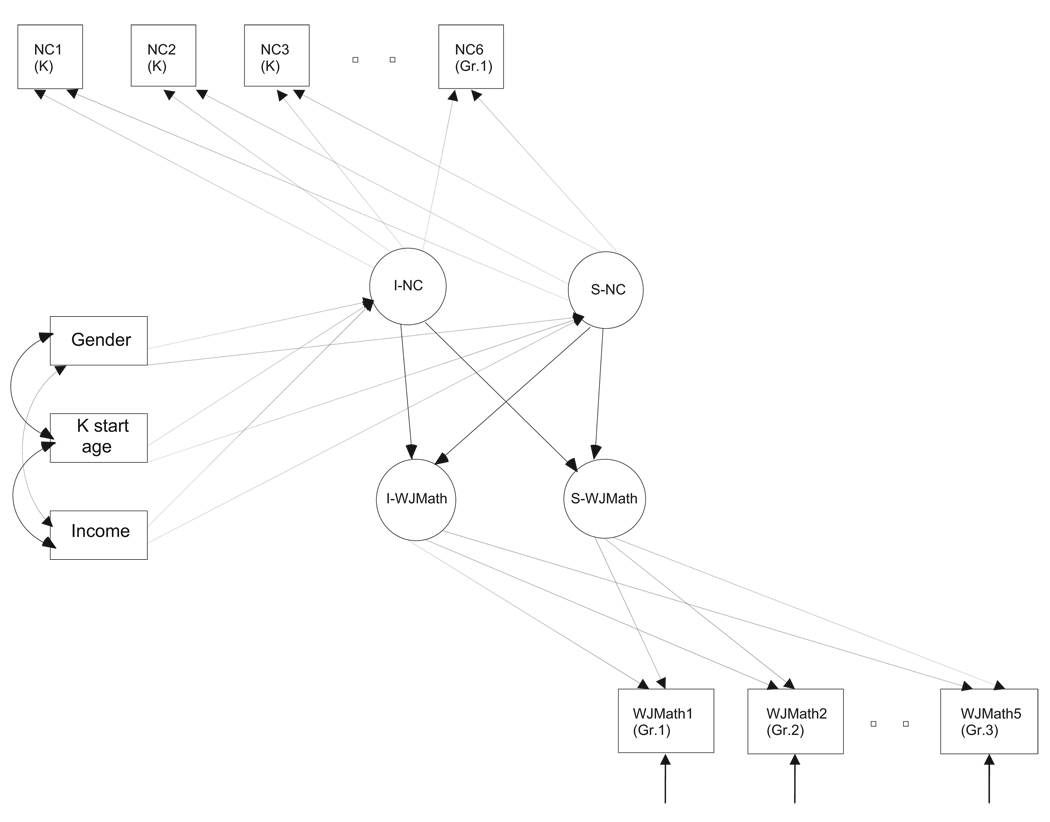
Model 1 adds the background predictors of income (1 = low income, 0 = middle income), gender (1 = male, 0 = female), and kindergarten start age (centered around the sample mean). A path diagram of Model 1 is given in Figure 2. In contrast to Figure 1, Figure 2 shows the regressions of the growth factors on the background predictors (gender, income level, and kindergarten start age), indicated by the single-headed arrows from the predictors to the growth factors. Note also that Model 1 is a mediating effects model, in which the background predictors are hypothesized to influence the growth factors of WJMath only through the growth factors of kindergarten number competence.

Figure 2.

Path diagram of sequential growth curve model for number competence (NC) from the beginning of kindergarten (K) through the middle of first grade and math achievement (Woodcock–Johnson III Achievement Tests–Mathematics [WJMath]) from the end of first grade through the end of third grade, with background variables of gender, income status, and kindergarten start age. Growth parameters for NC are regressed on the background variables, and the growth parameters for math achievement are regressed on the number competence growth parameters (I = intercept, S = linear slope). Not all time points are shown because of space limitations.

Table 4 presents the parameter estimates for the baseline Model 0 and for Model 1, which incorporates the background predictors of gender, income level, and kindergarten start age. On the basis of inspection of the empirical trajectories of number competence and WJMath, we specified a linear growth curve model for both models. The intercept for number competence was centered at the third number competence time point, corresponding to February of kindergarten, and the intercept for WJMath was set at the last time point, corresponding to April of third grade.

Table 4.

Parameter Estimates for the Number Competence and WJMath Sequential Growth Curve Model

Measure	Model 0			Model 1
	Estimate		95% CI	Estimate		95% CI
Growth parameters
NC intercept	23.37*		22.70, 24.00	24.57*		23.61, 25.53
NC slope	0.79*		0.75, 0.84	0.80*		0.72, 0.88
Variance (NC intercept)	38.34*		33.94, 42.74	30.59*		26.74, 34.44
Variance (NC slope)	0.10*		0.08, 0.13	0.10*		0.07, 0.12
WJMath intercept	21.27*		17.18, 25.35	21.17*		17.16, 25.18
WJMath slope	0.41*		0.23, 0.59	0.40*		0.22, 0.58
Variance (WJMath intercept)	20.12*		14.72, 25.51	19.84*		14.40, 25.28
Variance (WJMath slope)	0.03*		0.02, 0.04	0.03*		0.02, 0.04
Regression coefficients
WJMath intercept on NC intercept	0.96*		0.84, 1.09	0.96*		0.84, 1.09
WJMath intercept on NC slope	3.53*		0.44, 6.61	3.74*		0.79, 6.69
WJMath slope on NC intercept	0.01*		0.00, 0.02	0.01*		0.00, 0.02
WJMath slope on NC slope	0.00		−0.14, 0.13	0.01		−0.13, 0.14
NC intercept on boys				0.80		−0.31, 1.92
NC slope on boys				0.07		−0.02, 0.16
NC intercept on low income				−4.79*		−5.89, −3.70
NC slope on low income				−0.14*		−0.23, −0.04
NC intercept on kindergarten start age				1.51*		0.85, 2.16
NC slope on kindergarten start age				−0.05		−0.10, 0.00
BIC		18164.52			17964.47
R2 statistics
WJMath intercept					.66
WJMath slope					.10
NC intercept					.20
NC slope					.07

Note. Model 0 is baseline, and Model 1 is baseline plus the background variables. Variance stands for conditional variance of the parameters. WJMath = Woodcock–Johnson III Achievement Tests–Mathematics; CI = confidence interval; NC = number competence; BIC = Bayesian information criterion.

^*p < .05.

Typical measures of model fit are sensitive to the fact that structural models are being specifically constrained to yield estimates of growth. Moreover, in the context of this study, models to be compared are nonnested, in the sense that we will be adding additional variables to the model and not additional structural paths to the baseline model. Conventional measures of model fit, such as the likelihood ratio chi-square test and the root-mean-square error of approximation, are used for nested comparisons. In comparing improvement in the model when adding variables, we rely on the Bayesian information criterion (BIC). The BIC is a measure that balances the fit of the model with a penalty function for adding parameters to the model and can be used when comparing nonnested models. Among competing models, the model with the lower BIC value is recommended.

Baseline Model 0

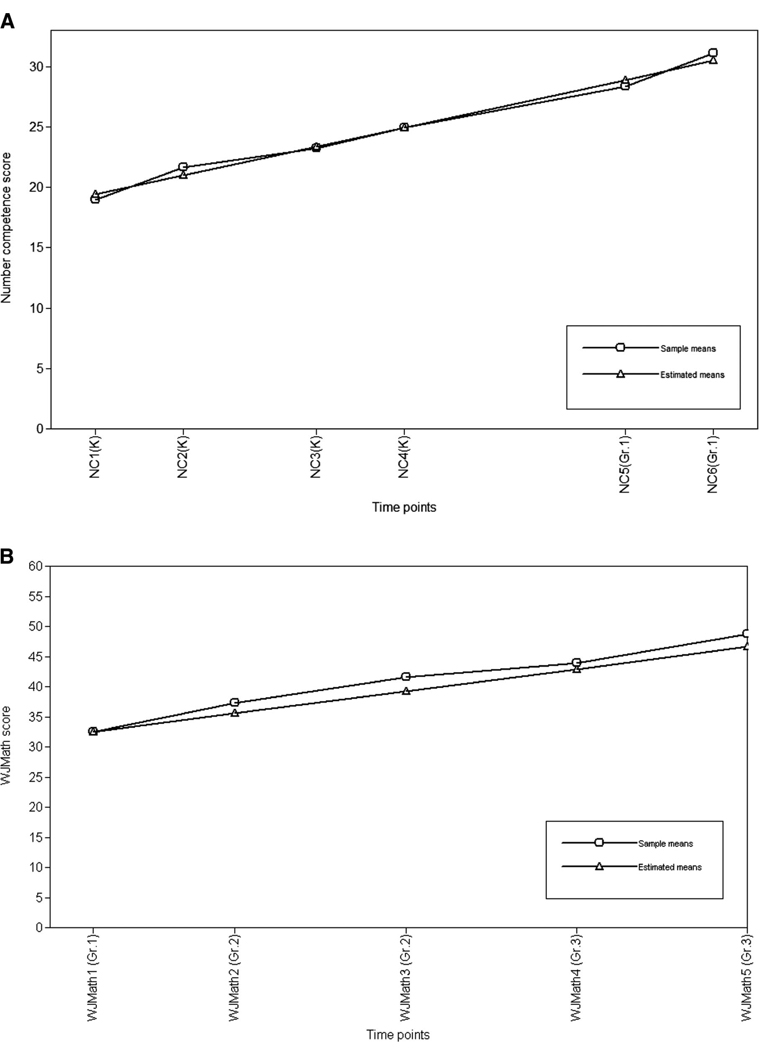
Inspection of the first column of Table 4 under Model 0 shows that the growth factors (i.e., intercepts and slopes) for both outcomes (i.e., number competence and WJMath) are statistically significant (p < .05). Both number competence and WJMath show significant and positive growth over their respective periods. The observed and estimated mean raw scores for number competence over the six time points are displayed in Figure 3A and for WJMath over the five time points in Figure 3B.

Figure 3.

Observed and estimated means for (A) number competence (NC) raw scores and (B) Woodcock–Johnson III Achievement Tests–Mathematics (WJMath) raw scores. The x-axis reflects the waves of the study in months.

In the interest of space, the standardized solutions are not shown. However, we report effect sizes in terms of standard deviation change in WJMath growth factors (intercepts and slopes) for a one standard deviation increase in number competence growth factors (intercepts and slopes). The means and standard deviations for the growth factor scores are intercept number competence, M = 23.26, SD = 6.01; slope number competence, M = 0.79, SD = 0.23; intercept WJMath, M = 46.56, SD = 6.83; and slope WJMath, M = 0.61, SD = 0.11.

The results under Model 0 of Table 4 also show the regressions of the growth factors for WJMath on the growth factors of number competence. Higher average performance on number competence in kindergarten is associated with higher average performance on WJMath in third grade (b = 0.96, z = 14.97, p < .05, CI[confidence interval]_.95 = 0.84 – 1.09). Thus, for a one standard deviation increase in number competence (corresponding to 6 points), there is a 5.3-point increase in WJMath in the third grade. Moreover, steeper rates of growth in number competence over kindergarten until the middle of first grade are associated with higher average performance on WJMath in third grade (b = 3.53, z = 2.24, p < .05, CI_.95 = 0.44 – 6.61). This result indicates that for a one standard deviation increase in the rate of growth in number competence (corresponding to 0.23 points), there is approximately a 1-point increase in WJMath in the third grade. We also observe that higher average performance on number competence in kindergarten is associated with steeper rates of growth in WJMath between first and third grades (b = 0.01, z = 3.23, p < .05, CI_.95 = 0.00 – 0.02). In terms of effect sizes, this result indicates that for a one standard deviation increase in number competence (corresponding to 6 points), there is a 0.03-point increase in the rate of growth in WJMath. Finally, rate of growth in number competence was not significantly related to rate of growth in WJMath.

Overall, we found modest (though significant) effects of higher levels of number competence with respect to growth over time in WJMath. The large effects for this baseline model were related to the intercepts; namely that higher levels of kindergarten number competence were predictive of statistically significant and substantively meaningful performance on WJMath in the third grade.

Model 1: Addition of background variables

Model 1 in Table 4 shows the results of adding the background predictors of income, gender, and kindergarten start age in performance on number competence and WJMath. The results relative to Model 0 do not change appreciably. Of interest, however, is that low-income children demonstrated poorer average performance and poorer average growth in number competence in kindergarten compared with their middle-income counterparts. Older children showed higher average performance on number competence than younger children. There were no significant effects of gender. Adding the regression of number competence on background predictors yielded an improvement in the fit of the model as measured by the BIC. In total, 20% of the variance in number competence performance and 7% of the variance of the number competence growth can be accounted for by gender, income, and kindergarten start age. Regarding WJMath, approximately 66% of the variance in WJMath performance at the end of third grade and 10% of the variance in the WJMath growth can be accounted for by the number competence growth factors.

Indirect effects

As noted earlier, Model 1 specified only indirect effects from the background predictors to the WJMath growth factors through the number competence growth factors. It is important to determine whether the process by which the background predictors influence WJMath is mediated only through number competence (pure mediation) or whether there are direct effects from the background predictors to WJMath over and above any indirect effect through number competence (partial mediation). One way that this can be determined is through an inspection of the modification indices and expected parameter changes (see Kaplan, 2009, for further explanation). An inspection of the modification indices and expected parameter changes associated with omitted direct effects (not shown) does not suggest that the model will be greatly improved if these direct effects are included. Thus, evidence supports a fully mediating model, and we now turn to the indirect effects.

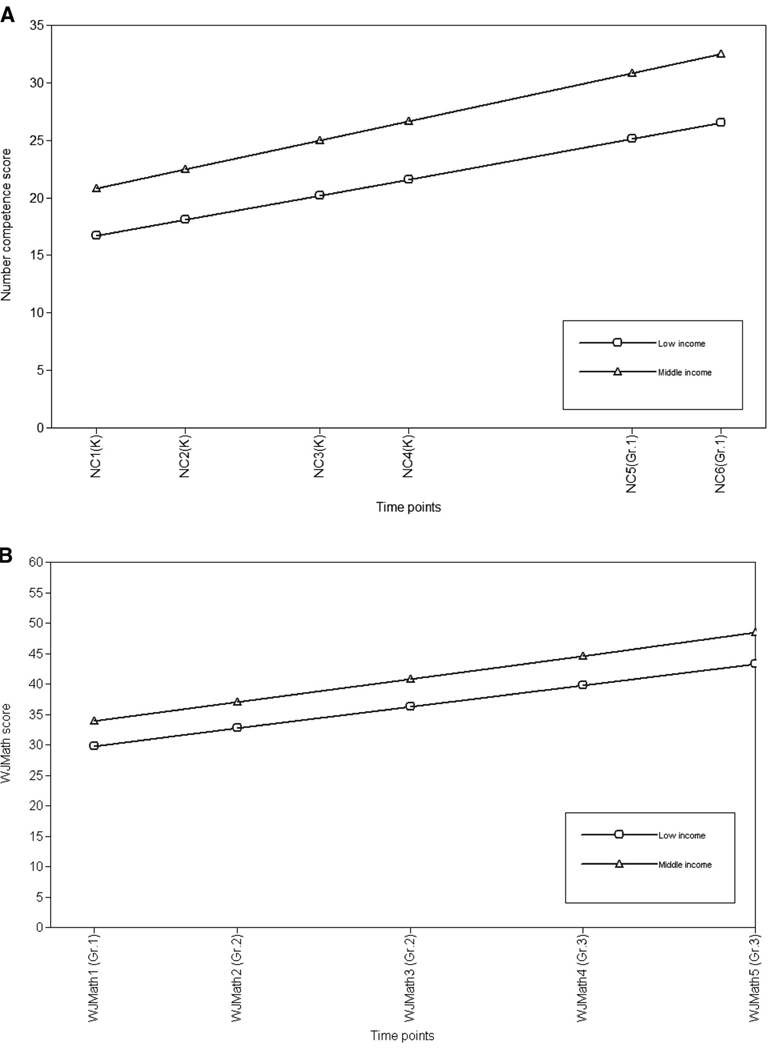
Table 5 presents the estimates for indirect effects of income and kindergarten start age for WJMath growth factors as mediated by the number competence growth factors. (Effects for gender were not significant in Model 1 and thus are not reported.) There were significant indirect effects for income and kindergarten start age on mathematics achievement growth factors by the number competence intercept only. Low-income children performed almost five points less than middle-income children on WJMath at the end of third grade (b = −4.62, z = −7.48, p < .05, CI_.95 = −5.83 – −3.41) and achieved at a slower rate (b = −0.04, z = −2.98, p < .05, CI_.95 = −0.07 – −0.02) as mediated through their level of number competence in kindergarten. The estimated means for number competence and WJMath at their respective time points are plotted for income in Figures 4A and 4B. The actual means, standard deviations, and range of scores, broken down by income level, are shown in Table 6. The standard deviations are roughly the same for the income groups, and the ranges reveal considerable overlap in the distributions.

Table 5.

Indirect Effects of Background Variables for WJMath From Number Competence

Variable	Estimate	95% CI
WJMath intercept on low income
Total indirect effect via NC	−5.13*	−6.48, −3.76
Specific indirect effects
Via NC intercept	−4.62*	−5.83, −3.41
Via NC slope	−0.51	−1.04, 0.02
WJMath slope on low income
Total indirect effects via NC	−0.04*	−0.08, −0.01
Specific indirect effects
Via NC intercept	−0.04*	−0.07, −0.02
Via NC slope	0.00	−0.02, 0.02
WJMath intercept on kindergarten start age
Total indirect effects via NC	1.28*	0.63, 1.93
Specific indirect effects
Via NC intercept	1.45*	0.80, 2.10
Via NC slope	−0.17	−0.40, 0.06
WJMath slope on kindergarten start age
Total indirect effects via NC	0.01*	0.00, 0.03
Specific indirect effects
Via NC intercept	0.01*	0.00, 0.02
Via NC slope	0.00	−0.01, 0.01

Note. WJMath = Woodcock–Johnson III Achievement Tests–Mathematics; CI = confidence interval; NC = number competence.

^*p < .05.

Figure 4.

Estimated growth trajectories for (A) number competence (NC) raw scores and (B) Woodcock–Johnson III Achievement Tests–Mathematics (WJMath) raw scores by income status. The x-axis reflects the waves of the study in months.

Table 6.

Raw Score Means, Standard Deviations, and Range for Early Number Competence and Later Math Achievement Across All Time Points for Sample Overall and by Income Level

Time of testing	Overall			Low income			Middle income
	M	SD	Range	M	SD	Range	M	SD	Range
NC
Kindergarten
September	18.90	6.32	7–39	16.34	4.48	7–28	20.20	6.71	8–39
November	21.72	6.94	8–40	18.71	4.95	10–32	23.27	7.31	8–40
February	23.48	7.34	9–40	19.79	5.89	9–37	25.33	7.31	10–40
April	25.17	7.85	7–41	20.98	6.51	11–39	27.22	7.64	7–41
Grade 1
September	28.75	7.48	12–42	24.62	7.10	12–40	30.57	6.92	12–42
November	31.36	7.08	13–42	27.71	7.20	14–41	33.03	6.37	13–42
WJMath
Grade 1 fall	32.47	6.41	13–56	29.18	6.28	13–42	33.85	5.96	16–56
Grade 2
Fall	37.32	5.48	20–59	34.35	5.20	23–44	38.38	5.19	20–59
Spring	41.61	6.30	24–64	38.50	5.74	24–54	42.75	6.13	25–64
Grade 3
Fall	43.91	6.81	27–68	40.11	6.10	28–58	45.04	6.61	27–68
Spring	48.73	8.15	25–73	44.24	7.16	27–62	50.07	7.97	25–73
WJApp
Grade 1 fall	24.38	4.02	11–40	22.42	3.76	13–32	25.20	3.84	11–40
Grade 2
Fall	27.41	3.68	15–41	25.60	3.22	18–31	28.06	3.62	15–41
Spring	29.93	4.04	18–41	27.78	3.83	18–38	30.71	3.83	20–41
Grade 3
Fall	31.27	4.50	22–43	28.67	3.77	22–37	32.05	4.42	22–43
Spring	33.60	5.24	16–47	30.84	4.67	16–44	34.42	5.14	22–47
WJCalc
Grade 1 fall	8.09	2.94	0–16	6.75	3.09	0–12	8.66	2.69	0–16
Grade 2
Fall	9.91	2.23	3–18	8.76	2.47	3–14	10.32	1.99	4–18
Spring	11.69	2.70	4–23	10.72	2.33	4–17	12.04	2.75	4–23
Grade 3
Fall	12.64	2.84	3–25	11.43	2.85	6–22	12.99	2.74	3–25
Spring	15.13	3.48	3–26	13.40	3.12	5–19	15.65	3.42	3–26

Note. NC = number competence; WJMath = Woodcock–Johnson III Achievement Tests–Mathematics; WJApp = Woodcock–Johnson III Applied Problems subtest; WJCalc = Woodcock–Johnson III Calculation subtest.

In terms of kindergarten start age, older children performed better on WJMath at the end of third grade (b = 1.45, z = 4.36, p < .05, CI_.95 = 0.80 – 2.10) and achieved at a faster rate (b = 0.01, z = 2.68, p < .05, CI_.95 = 0.00 – 0.02) owing to better number competence in kindergarten. In terms of effect sizes, these results indicate that each month older a child is when starting kindergarten confers a 1.45-point advantage on the WJMath as mediated through kindergarten number competence. Regarding achievement growth, the findings indicate that for a 1-month age difference, a child will achieve at a rate of approximately two thirds of a standard deviation on the WJMath as mediated through kindergarten number competence.

Number Competence and Components of Mathematics Achievement

To provide more information about the relation between level of early number competence and growth in later mathematics outcomes, we performed parallel sequential growth curve analyses on each of the two subareas on the WJMath: WJApp and WJCalc. In the interest of space, we do not present baseline model results. Instead, Table 7 presents the parameter estimates for the model, which incorporates the background predictors. The intercept for number competence was centered at the third number sense time point, corresponding to February of kindergarten, and the intercept for both WJApp and WJCalc was set at the last time point, corresponding to April of third grade. The pattern of results for both applied problems and calculation was the same as the pattern for composite mathematics (WJMath). The only exception was that the number competence slope predicted the WJCalc intercept but not the WJApp intercept.

Table 7.

Parameter Estimates for the Number Competence and WJApp and WJCalc Sequential Growth Curve Models

Measure	WJApp			WJCalc
	Estimate		95% CI	Estimate		95% CI
Growth parameters
NC intercept	24.60*		23.67, 25.52	24.55*		23.62, 25.47
NC slope	0.80*		0.73, 0.88	0.80*		0.72, 0.87
Variance (NC intercept)	30.47*		25.95, 34.99	30.42*		25.91, 34.94
Variance (NC slope)	0.10*		0.07, 0.13	0.10*		0.07, 0.13
WJ intercept	5.29*		3.29, 7.28	15.83*		13.19, 18.47
WJ slope	0.21*		0.11, 0.31	0.19*		0.07, 0.31
Variance (WJMath intercept)	3.80*		2.58, 5.03	8.00*		5.86, 10.14
Variance (WJMath slope)	0.01*		0.00, 0.01	0.01*		0.01, 0.02
Regression coefficients
WJ intercept on NC intercept	0.34*		0.28, 0.40	0.63*		0.55, 0.71
WJ intercept on NC slope	1.18		−0.25, 2.61	2.47*		0.53, 4.41
WJ slope on NC intercept	0.00*		0.00, 0.01	0.01*		0.00, 0.01
WJ slope on NC slope	−0.01		−0.09, 0.06	0.01		−0.08, 0.10
NC intercept on boys	0.78		−0.34, 1.89	0.84		−0.27, 1.96
NC slope on boys	0.06		−0.03, 0.15	0.07		−0.02, 0.16
NC intercept on low income	−4.81*		−5.99, −3.64	−4.83*		−6.00, −3.66
NC slope on low income	−0.13*		−0.23, −0.04	−0.13*		−0.23, −0.04
NC intercept on kindergarten start age	1.51*		0.95, 2.07	1.50*		0.94, 2.05
NC slope on kindergarten start age	−0.05*		−0.09, 0.00	−0.05*		−0.09, 0.00
BIC		19083.19			19513.43
R2 statistics
WJ intercept		.55			.67
WJ slope		.06			.12
NC intercept		.21			.21
NC slope		.07			.07

Note. Variance stands for conditional variance of the parameters. WJApp = Woodcock–Johnson III Applied Problems subtest; WJCalc = Woodcock–Johnson III Calculation subtest; CI = confidence interval; NC = number competence; WJMath = Woodcock–Johnson III Achievement Tests–Mathematics; BIC = Bayesian information criterion.

^*p < .05.

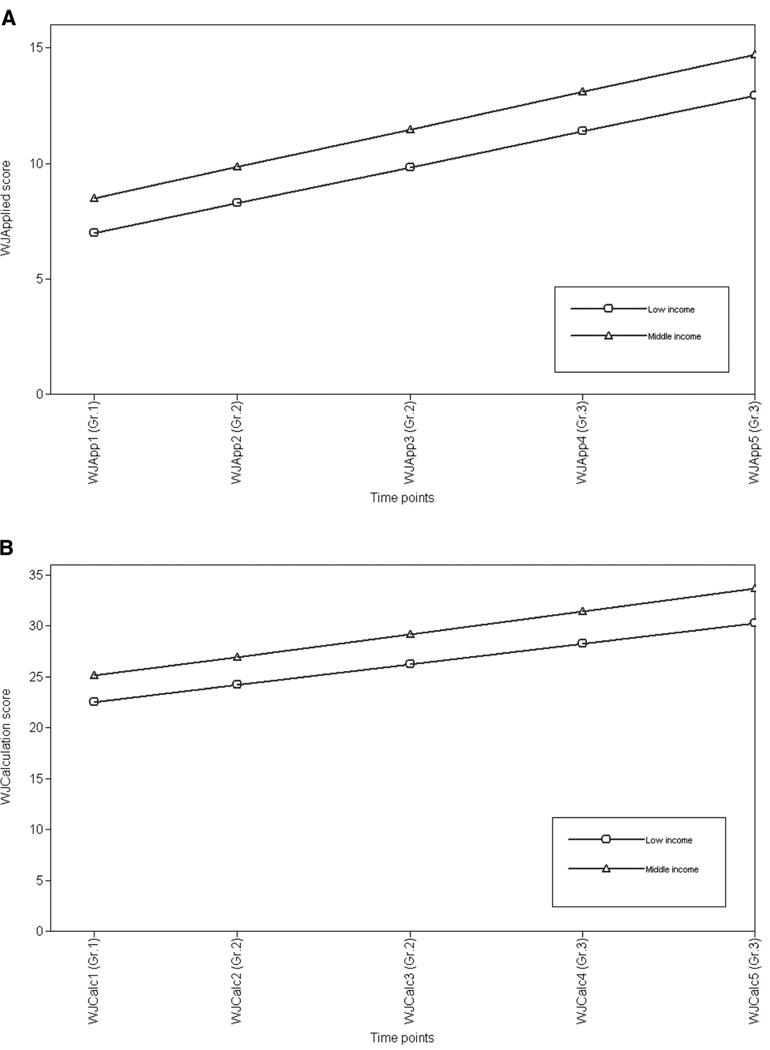
Table 8 presents the estimates for indirect effects of income and kindergarten start age for WJApp and WJCalc as mediated by the number sense growth factors. Again, the pattern of results is the same as the one from the initial analysis with WJMath. The one exception was for kindergarten start age, in which there was an indirect effect through the number competence intercept for WJCalc slope but not for WJApp slope. The estimated means for WJApp at their respective time points are plotted for income in Figure 5A and for WJCalc in Figure 5B. The actual means, standard deviations, and range of scores, broken down by income level, are shown in Table 6.

Table 8.

Indirect Effects of Background Variables for WJApp and WJCalc From Number Competence

Variable	WJApp		WJCalc
	Estimate	95% CI	Estimate	95% CI
WJ intercept on low income
Total indirect effect via NC	−1.78*	−2.32, −1.24	−3.37*	−4.27, −2.48
Specific indirect effects
Via NC intercept	−1.62*	−2.11, −1.14	−3.04*	−3.87, −2.22
Via NC slope	−0.16	−0.45, 0.07	−0.33	−0.69, 0.02
WJ slope on low income
Total indirect effects via NC	−0.01	−0.03, 0.01	−0.03*	−0.06, −0.01
Specific indirect effects
Via NC intercept	−0.01	−0.03, 0.0	−0.03*	−0.05, −0.01
Via NC slope	0.00	−0.01, 0.01	0.00	−0.01, 0.01
WJ intercept on kindergarten start age
Total indirect effects via NC	0.45*	0.23, 0.67	0.83*	0.44, 1.22
Specific indirect effects
Via NC intercept	0.51*	0.30, 0.72	0.94*	0.57, 1.31
Via NC slope	−0.06	−0.14, 0.03	−0.12	−0.26, 0.03
WJMath slope on kindergarten start age
Total indirect effects via NC	0.01	0.00, 0.01	0.01*	0.00, 0.02
Specific indirect effects
Via NC intercept	0.01	0.00, 0.01	0.01*	0.00, 0.02
Via NC slope	0.00	0.00, 0.00	0.00	0.00, 0.00

Note. WJApp = Woodcock–Johnson III Applied Problems subtest; WJCalc = Woodcock–Johnson III Calculation subtest; CI = confidence interval; NC = number competence.

^*p < .05.

Figure 5.

Estimated growth trajectories for (A) Woodcock–Johnson III Applied Problems subtest (WJApp) raw scores and (B) Woodcock–Johnson III Calculation subtest (WJCalc) raw scores by income status. The x-axis reflects the waves of the study in months.

Number Competence Subtask Analyses

A coefficient alpha of .70 or above is considered the minimum acceptable level for reliability of a test (Reynolds, Livingston, & Willson, 2006). Two of our number subtasks reached this threshold: story problems (mean alpha coefficient of .73, SD = .08) and number combinations (mean alpha coefficient of .83, SD = .04). Thus, we performed separate sequential growth curve analyses on these subtasks. The results are presented in Table 9 and Table 10. The intercept for both story problems and number combinations was centered at the third time point, corresponding to February of kindergarten, and the intercept for WJMath was set at the last time point, corresponding to April of third grade. (We do not present outcome math data broken down by WJCalc and WJApp because preliminary analyses showed not appreciable differences.)

Table 9.

Parameter Estimates for Number Competence Subtask and WJMath Sequential Growth Curve Models

Measure	Story problems			Number combinations
	Estimate		95% CI	Estimate		95% CI
Growth parameters
NT intercept	3.20*		2.94, 3.45	3.55*		3.25, 3.85
NT slope	0.21*		0.18, 0.24	0.23*		0.20, 0.26
Variance (NT intercept)	2.08*		1.73, 2.43	2.96*		2.48, 3.44
Variance (NT slope)	0.02*		0.01, 0.02	0.02*		0.02, 0.03
WJMath intercept	33.76*		31.43, 36.09	34.90*		32.70, 37.15
WJMath slope	0.49*		0.40, 0.59	0.52*		0.42, 0.62
Variance (WJMath intercept)	19.23*		13.23, 25.23	21.44*		15.44, 27.43
Variance (WJMath slope)	0.03*		0.02, 0.04	0.03*		0.02, 0.04
Regression coefficients
WJMath intercept on NT intercept	3.44*		2.94, 3.95	2.89*		2.49, 3.30
WJMath intercept on NT slope	15.98*		7.80, 24.16	12.27*		6.01, 18.54
WJMath slope on NT intercept	0.04*		0.02, 0.06	0.03*		0.01, 0.05
WJMath slope on NT slope	0.11		−0.02, 0.44	0.04*		−0.22, 0.31
NT intercept on boys	0.04		−0.27, 0.35	0.15*		−0.22, 0.51
NT slope on boys	0.04*		0.01, 0.08	0.03		−0.01, 0.07
NT intercept on low income	−1.15*		−1.48, −0.83	−1.57*		−1.95, −1.18
NT slope on low income	−0.07*		−0.11, −0.03	−0.05*		−0.10, −0.01
NT intercept on kindergarten start age	0.29*		0.14, 0.45	0.41*		0.22, 0.59
NT slope on kindergarten start age	0.00		−0.02, 0.02	0.00		−0.03, 0.02
BIC		16862.78			17209.05
R2 statistics
WJMath intercept		0.65			0.63
WJMath slope		0.12			0.09
NT intercept		0.16			0.20
NT slope		0.11			0.04

Note. Variance stands for conditional variance of the parameters. WJMath = Woodcock–Johnson III Achievement Tests–Mathematics; CI = confidence interval; NT = number competence subtask; BIC = Bayesian information criterion.

^*p < .05.

Table 10.

Indirect Effects of Background Variables Income and Kindergarten Start Age for WJMath From Number Competence Subtask

Variable	Story problems		Number combinations
	Estimate	95% CI	Estimate	95% CI
WJMath intercept on low income
Total indirect effect via NT	−5.14*	−6.57, −3.71	−5.18*	−6.58, −3.78
Specific indirect effects
Via NT intercept	−3.98*	−5.23, −2.73	−4.53*	−5.79, −3.27
Via NT slope	−1.16	−2.02, −0.31	−0.65	−1.29, 0.00
WJMath slope on low income
Total indirect effects via NT	−0.05*	−0.09, −0.02	−0.05*	−0.08, −0.01
Specific indirect effects
Via NT intercept	−0.04*	−0.07, −0.02	−0.04*	−0.07, −0.01
Via NT slope	−0.01	−0.03, 0.02	0.00	−0.02, 0.01
WJMath intercept on kindergarten start age
Total indirect effects via NT	1.07*	0.46, 1.68	1.13*	0.52, 1.73
Specific indirect effects
Via NT intercept	1.01*	0.45, 1.56	1.18*	0.62, 1.73
Via NT slope	0.07	−0.24, 0.37	−0.05	−0.32, 0.22
WJMath slope on kindergarten start age
Total indirect effects via NT	0.01*	0.00, 0.02	0.01*	0.00, 0.02
Specific indirect effects
Via NT intercept	0.01*	0.00, 0.02	0.01*	0.00, −0.02
Via NT slope	0.00	0.00, 0.00	0.00	0.00, 0.00

Note. WJMath = Woodcock–Johnson III Achievement Tests–Mathematics; CI = confidence interval; NT = number competence subtask.

^*p < .05.

The pattern of effects for story problems and number combinations is the same as the pattern seen in the initial analysis with general number competence. However, we did find that boys had a slightly faster rate of growth than girls on story problems but not on number combinations—an effect not seen on the analysis with the general number competence measure. The actual means, standard deviations, and range of scores, broken down by income level and problem type, are shown in Table 11.

Table 11.

Raw Score Means, Standard Deviations, and Range for Story Problems and Number Combinations Across All Time Points for Sample Overall and by Income Level

Time of testing	Overall			Low income			Middle income
	M	SD	Range	M	SD	Range	M	SD	Range
Story problems (n = 8)
Kindergarten
September	1.96	1.70	0–8	1.53	1.36	0–6	2.18	1.81	0–8
November	2.37	2.04	0–8	1.69	1.38	0–6	2.72	2.24	0–8
February	2.71	2.18	0–8	1.89	1.74	0–8	3.13	2.27	0–8
April	3.12	2.37	0–8	1.91	1.81	0–8	3.71	2.39	0–8
Grade 1
September	4.15	2.44	0–8	3.03	2.17	0–8	4.64	2.39	0–8
November	5.14	2.45	0–8	4.08	2.49	0–8	5.62	2.28	0–8
Number combinations (n = 8)
Kindergarten
September	2.00	2.16	0–8	1.21	1.43	0–8	2.40	2.35	0–8
November	2.65	2.31	0–8	1.73	1.56	0–8	3.12	2.48	0–8
February	3.05	2.54	0–8	1.79	1.81	0–8	3.68	2.61	0–8
April	3.50	2.72	0–8	2.20	2.25	0–8	4.14	2.71	0–8
Grade 1
September	4.73	2.73	0–8	3.52	2.67	0–8	5.26	2.59	0–8
November	5.50	2.56	0–8	4.23	2.73	0–8	6.08	2.26	0–8

Discussion

Although kindergarten number competencies predict mathematics outcomes in first grade, few studies have examined whether the relation continues in subsequent grades, when the subject matter becomes more complex. Even fewer studies have examined early number competence in relation to rate of achievement in mathematics, even though growth rates are important for gauging children’s progress under the U.S. No Child Left Behind Act (Fuller et al., 2007).

Our findings provide compelling evidence that before first grade children develop foundational number competence that supports more complex mathematics. Higher levels of kindergarten number competence predicted statistically significant and substantively meaningful performance in composite mathematics achievement at the end of third grade. Level of kindergarten number competence was a modest but significant predictor of rate of achievement between first and third grades, and rate of growth in number competence was a modest but significant predictor of level of achievement at the end of third grade. Our findings did not vary appreciably when we examined kindergarten number competence in relation to elementary mathematics subareas of written calculation procedures and applied problem solving separately. Early understanding of number relations and operations provides support for learning complex calculation procedures involving larger numbers as well as problem solving in varied contexts. This is in keeping with arguments that conceptual knowledge and procedural skill are iterative, each prompting the learning of the other (National Mathematics Advisory Panel, 2008; Rittle-Johnson, Siegler, & Alibali, 2001).

We were further interested in the relative importance of the subtasks on our number competence measure, although all are connected conceptually (Jordan et al., 2007). There were two reliable subtasks within the battery: story problems and number combinations. Both tasks were presented orally, and both involved addition and subtraction. Previous work suggests that before formal instruction in school, children perform better on story problems than on number combinations (Levine et al., 1992). Story problems have meaningful referents (e.g., pennies) that allow children to draw on their everyday knowledge, whereas number combinations do not. It has been argued that the ability to solve number combinations is not a meaningful activity (e.g., Ashcraft, 1992), that they are learned primarily through rote verbal associations between a problem and its answer. However, our finding that kindergarten performance on both number combinations and story problems predicts achievement and growth between first and third grades (in terms of calculation procedures as well as applied problem solving) supports the view that early competence on verbal arithmetic problems reflects understanding of how quantities are combined and separated rather than mere rote associations (Baroody, 1985; Booth & Siegler, 2008; Jordan et al., 2007). Basic operational knowledge and skills allow children to benefit from the primary school mathematics curriculum from the start and should have a central role in early intervention programs.

Consideration of background variables revealed poorer long-term mathematics outcomes (in general achievement and subareas) for children from low-income families than for those from middle-income families—a finding that extends previous work (e.g., Jordan, Huttenlocher, & Levine, 1992; Jordan et al., 2007; Siegler, in press). Low-income children performed more poorly than middle-income children in mathematics achievement at the end of third grade and achieved at a slower rate between first and third grades. More important, however, was the finding that the poor mathematics performance of low-income children in third grade was mediated by their relatively weak number competence in kindergarten. Low-income children enter kindergarten with fewer number-related experiences than their middle-income counterparts—at home, in their communities, and in their preschools (Clements & Sarama, 2008)—and it is likely that early learning opportunities contributed to the substantial advantage of middle-income children in the present study. Because number competence is achievable for most children (Ginsburg, Lee, & Boyd, 2008), the finding of its intermediate effect in predicting complex mathematics has practical relevance for teachers and families.

The better performance and faster growth (between first and third grades) in mathematics achievement of older children also was explained by kindergarten number competence. It is not clear, however, why starting kindergarten at an older age confers a modest but reliable advantage over younger children in number competence. Possibly, some younger children enter kindergarten with less mature behavior or weak attention, which in turn makes them less available for learning. Further research is needed to investigate this issue and to verify similar age effects in other samples of children. There were no meaningful gender effects in our study.

It could be argued that our findings reflect general cognitive competence, rather than number competence per se. However, Jordan, Glutting, and Ramineni (2008) found a divergent association between number competence at the end of kindergarten and reading performance at the end of third grade (r = .29), as opposed to a convergent association between number competence at the end of kindergarten and mathematics performance at the end of third grade (r = .63). Moreover, Locuniak and Jordan (2008) found that early number skills are uniquely predictive of mathematics fluency when general verbal and spatial factors were considered.

Why are early number competencies important to later mathematics functioning? Understanding of numbers and number relations makes formal mathematics more accessible. It helps children make sense of the count sequence, develop a mental number line, and reason about numbers (Baroody, 1985; Siegler & Booth, 2004; Siegler & Robinson, 1982). Counting knowledge allows children to count on or up from addends to solve novel number combinations—a key arithmetic strategy in early elementary school (Geary, Hoard, Byrd-Craven, & DeSoto, 2004). Reasoning about numbers and number relationships also helps children develop strategies for solving complex word problems (Kilpatrick et al., 2001).

Our findings demonstrate the importance of kindergarten number competence for setting children’s developmental learning trajectories in elementary school mathematics. Theories of development with atypical populations (e.g., specific language impairment) indicate that timing of skill acquisition plays a critical role in development (Karmiloff-Smith, 1998). A seemingly circumscribed problem early on can trigger more problems as development progresses (Karmiloff-Smith, 1998; Thomas & Karmiloff-Smith, 2003). If children leave kindergarten with weak number competencies, especially with respect to operational knowledge and skills, they will enter first grade at a disadvantage and may never catch up to children who started with good number competencies. Children who start first grade ahead are likely to advance their mathematics learning, whereas children who are behind are still acquiring basic skills. In the reading area, Juel (1988) found that children who entered first grade with little or no phonemic awareness—an early reading-related skill—almost always became poor readers, a finding also supported more recently by Schatschneider, Fletcher, Francis, Carlson, and Foorman (2004), who demonstrated the importance of letter–sound knowledge to reading. Although many children in the Juel study made steady progress in phonemic skills during first grade, they still entered second grade with less phonemic awareness than children who became average or good readers and continued to show reading delays into fourth grade. The early reading difficulties created a vicious cycle, such that children who had poor reading skills in first grade began to dislike and avoid reading; avoidance of reading then led to poor vocabulary and conceptual development and so on. Such a cycle, if not interrupted, results in permanent gaps between good and poor readers. In a similar vein, early weaknesses in number competence may lead to a cascade of mathematics failure in school.

Number competencies, especially with respect to addition and subtraction, are closely tied to the mathematics curriculum in elementary school (in contrast to general cognitive competencies, such as working memory or spatial facility), and thus it is not altogether surprising that they are predictive over time. Similarly, kindergarten skills that are closely tied to the reading curriculum are more predictive of reading than are general language or perceptual skills (Schatschneider et al., 2004). However, it should be kept in mind that children enter kindergarten with large individual differences in number competence and varied growth trajectories; some children with initial delays in number skills are responsive to typical kindergarten experiences and catch up to their peers, whereas others have intractable weaknesses (Jordan et al., 2006).

The sustained predictability of kindergarten number competence to later mathematics outcomes has important implications for educational policy. Improving number competence in children from low-income families as well as in younger children should be a priority in preschool, kindergarten, and first grade. Until recently, early interventions related to mathematics have generated far less interest than have early reading interventions (Fuchs, 2005; Gersten et al., 2005). In fact, mathematics difficulties in kindergarten and early primary school are largely overlooked (Dowker, 2005), even though number competencies can be achieved through targeted instruction (Booth & Siegler, 2008; Griffin et al., 1994). For example, using a randomized controlled trial with a low-income preschool sample, Ramani and Siegler (2008) found that a short numeracy development program (four 15–20-min sessions over a 2-week period) involving number board games produced moderate effect sizes on number competence measures (e.g., picking which of two numbers is larger) that persisted at least 9 weeks after the intervention. However, further research needs to investigate whether gains in specific numerical competencies in early childhood contribute to later mathematics development.

In conclusion, early number competence is important for setting children’s learning trajectories in mathematics. Our study demonstrates a robust and sustained predictive relation between number competence (addition and subtraction number combinations and story problems in particular) and later mathematics outcomes, in terms of level of performance and, to a lesser extent, rate of development. Although the strength of the relation between early number competence and mathematics achievement beyond third grade was not tested, recent work suggests the connection is lasting (Duncan et al., 2008). The effects of weak number competence, if not addressed, are likely to be felt throughout the school years.