Abstract
Cross-adaptation is widely used to probe whether different stimuli share common neural mechanisms. For example, that adaptation to second-order stimuli usually produces little aftereffect on first-order stimuli has been interpreted as reflecting their separate processing. However, such results appear to contradict the cue-invariant responses of many visual cells. We tested the novel hypothesis that the null aftereffect arises from the large difference in the backgrounds of first- and second-order stimuli. We created second-order faces with happy and sad facial expressions specified solely by local directions of moving random dots on a static-dot background, without any luminance-defined form cues. As expected, adaptation to such a second-order face did not produce a facial-expression aftereffect on the first-order faces. However, consistent with our hypothesis, simply adding static random dots to the first-order faces to render their backgrounds more similar to that of the adapting motion face led to a significant aftereffect. This background similarity effect also occurred between different types of first-order stimuli: real-face adaptation transferred to cartoon faces only when noise with correlation statistics of real faces or natural images was added to the cartoon faces. These findings suggest the following: (1) statistical similarities between the featureless backgrounds of the adapting and test stimuli can influence aftereffects, as in contingent adaptation; (2) weak or null cross-adaptation aftereffects should be interpreted with caution; and (3) luminance- and motion-direction-defined forms, and local features and global statistics, converge in the representation of faces.
Introduction
A central question in sensory processing is whether different classes of stimuli for the same sensory attribute share a common neural representation. The standard signature of such sharing is the transfer of an aftereffect in cross-adaptation. For vision, this question has been prominently raised with respect to the comparison between first-order, luminance-defined stimuli and second-order stimuli defined by variations in contrast, motion, texture, phase, and spatial or temporal frequency, etc., without modulation of mean luminance. The common psychophysical and neuroimaging finding that adaptation to second-order stimuli does not substantially transfer to first-order stimuli (Nishida et al., 1997; Larsson et al., 2006; Ashida et al., 2007; Schofield et al., 2007) has duly been interpreted as indicating that the two classes of stimuli are processed separately.
Such separation, however, appears to be at odds with cue-invariant responses found at many stages along the visual hierarchy. For example, some V1 cells and a larger fraction of V2 cells have similar tuning to first-order and second-order (illusory-contour) orientations (von der Heydt et al., 1984; Sheth et al., 1996). Likewise, subsets of MT and MSTd cells show similar tuning to first- and second-order motion patterns (Albright, 1992; Geesaman and Andersen, 1996). Moreover, shape selectivity does not depend on whether the shapes are defined by first- or second-order cues (Sary et al., 1993; Grill-Spector et al., 1998). If such cells contribute significantly to adaptation, then aftereffects should transfer, at least partially, from second- to first-order stimuli. Conversely, if they do not contribute, then adaptation seems an inadequate probe for shared neural mechanisms.
One hitherto unexplored confounding factor is that, with the notable exception of the one study (Georgeson and Schofield, 2002) that did find significant interorder cross-adaptation transfer, first- and second-order stimuli, by their construction, often have different background patterns. For instance, a typical first-order orientation stimulus is a black bar on a uniform white background; however, its second-order counterpart might involve flickering dots in a virtual rectangle embedded in a larger background of static dots. Featureless backgrounds could be important since, for instance, their size makes them contribute substantially to the statistics of images, and visual adaptation is highly sensitive to such statistics (Field, 1987; Atick and Redlich, 1990; Barlow, 1990; Dan et al., 1996; Wainwright, 1999; Brenner et al., 2000; Simoncelli and Olshausen, 2001; Zhaoping, 2006; Schwartz et al., 2007). However, theories considering image statistics focus on predicting visual receptive fields rather than cross-adaptation aftereffects, whereas theories treating aftereffects consider only statistics of features but not backgrounds.
Therefore, we investigated the role of background statistics in the transfer of the facial-expression aftereffect between different classes of faces. We chose face stimuli because cue convergence may be more pronounced at higher levels of processing; we will report similar studies for lower-level stimuli separately. We found that background statistics can be critically important for interactions not only between first- and second-order stimuli but also between different types of first-order stimuli. These findings have implications for the function and mechanisms of adaptation and the representation of faces.
Materials and Methods
Subjects
A total of eight subjects consented to participate in the experiments of this study. Among them, two were experimenters, and the rest were naive to the purpose of the study. All subjects had normal or corrected to normal vision. Each experimental condition had four subjects, two of whom were naive. All subjects showed highly consistent results. The study was approved by the Institutional Review Board of the New York State Psychiatric Institute.
Apparatus
The visual stimuli were presented on a 21 inch ViewSonic P225f monitor controlled by a Macintosh G4 computer. The vertical refresh rate was 100 Hz, and the spatial resolution was 1024 × 768 pixels. In a dimly lit room, subjects viewed the monitor from a distance of 75 cm, using a chin rest to stabilize head position. Each pixel subtended 0.029° at this distance. All luminance values cited in the paper were measured with a Minolta LS-110 photometer. All experiments were run in Matlab with Psychophysics Toolbox extensions (Brainard, 1997; Pelli, 1997).
Visual stimuli
A black (0.23cd/m2) fixation cross was always shown at the center of the white (56.2 cd/m2) screen. It consisted of two orthogonal line segments, each 0.29° in length and 0.06° in width. All stimuli were grayscale. They included second-order cartoon faces with motion gradient-defined facial expressions, first-order cartoon faces with luminance-defined facial expressions, and first-order real faces derived from the Ekman Pictures of Facial Affect (PoFA) database (Ekman and Friesen, 1976). Synthetic noises were used as backgrounds for some of the face stimuli (see below). Each stimulus was shown with the fixation cross at its center.
Motion gradient cartoon faces.
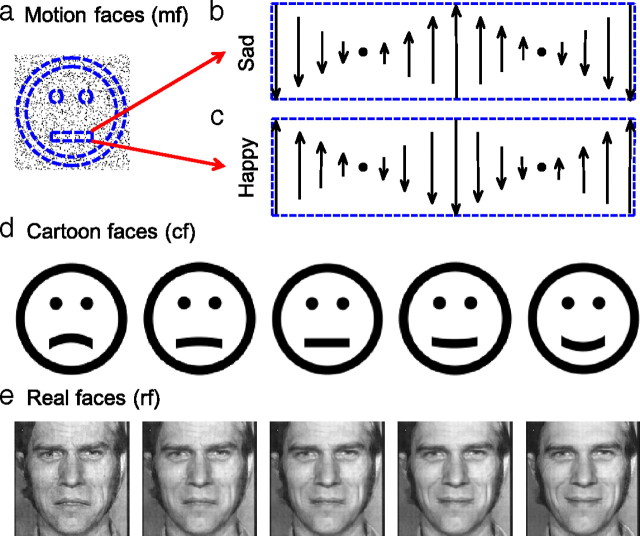
We generated these dynamic, second-order faces in a 3.7° × 3.7° (129 × 129 pixels) square containing black random dots on a white background. Each dot had a size of 1 pixel (0.029°). The dot density was 15%. On this random-dot field, we defined a virtual ring for the face outline, two virtual disks for the eyes, and a horizontally oriented virtual rectangle for the mouth (Fig. 1a). The outline ring had inner and outer radii of 1.77° and 1.48°, respectively, containing 500 dots on average. Each eye disk had a radius of 0.17°, containing 17 dots on average. The mouth rectangle was 0.29° × 1.28°, containing 66 dots on average. The mouth center was 0.64° below the face center. The distance between the eye and mouth levels was 1.22°. The center-to-center distance between the eyes was 0.85°. The dots within the face-outline ring and the eye disks randomly flickered at 10 Hz. This was achieved by letting each dot have a lifetime of 100 ms (10 frames) and get replotted to a random location within its original region when its lifetime was reached. The initial lifetimes of different dots were randomized to avoid synchronous flicker. The dots within the mouth rectangle had different motion gradient patterns to produce sad and happy expressions, as explained in the text (Fig. 1b,c). The motion along each vertical line of the mouth rectangle was created by moving a window of 1 pixel width on a large field of random dots at the desired velocity; this avoided dots' jumping between opposite edges of the rectangle. To generate a set of motion faces with expressions varying gradually from sad to happy, we let a fraction of the dots (noise dots) in the mouth rectangle flicker at 10 Hz. These stimuli are referred to as motion faces.
Figure 1.
Examples of face stimuli used in this study. a, An illustration for second-order motion faces with motion gradient-defined expressions. Dashed blue curves and lines define virtual regions for the face outline, eyes, and mouth. Dots inside the face outline and eye regions flickered at 10 Hz. b, c, Dots inside the mouth rectangle carried opposite motion gradient patterns to produce sad and happy expressions. The vertical arrows indicate the velocity of the dots in that column. d, Static cartoon faces generated by our anti-aliasing program. The mouth curvature varied from concave to convex to produce a spectrum of sad to happy expressions. e, Real faces derived from two images from the Ekman PoFA database with MorphMan 4.0.
Static cartoon faces.
As in a previous study (Xu et al., 2008), we generated black cartoon faces on white background with an anti-aliasing method. The dimensions of the face outline ring and eye disks exactly matched those of the motion faces (Fig. 1d). The length and thickness of the mouth curve also matched those of the motion faces. However, unlike the motion faces whose mouths were a flat rectangle, the mouths of the static cartoon faces had curvature varying from concave to convex (−0.34, −0.25, −0.17, −0.08, 0, 0.08, and 0.17 in the units of 1/°) to produce a spectrum of sad to happy expressions. The positions of the eyes and mouth within the static cartoon faces were also identical to those in the motion faces.
Real-face images.
These stimuli were derived from images from Ekman PoFA database (Ekman and Friesen, 1976) in the same way as a previous study (Xu et al., 2008), except that we cropped and scaled the image size to 3.7° × 3.7° and presented them at a higher contrast (mean mouth contrast, 0.27). We applied MorphMan 4.0 (STOIK Imaging) to a sad and a happy face of the same person to generate 21 images with the proportion of the happy face varying from 0 (saddest) to 1 (happiest) in steps of 0.05 (Fig. 1e). Those with proportions equal to 0, 0.15, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, and 0.7 were used in the experiments.
Noise backgrounds with various correlation statistics.
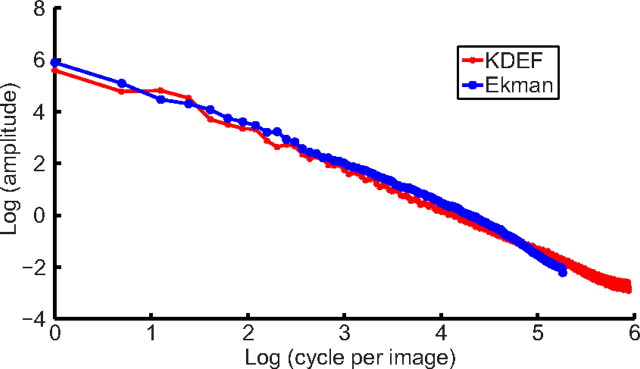
We generated 3.7° × 3.7° noise patterns as backgrounds for static cartoon faces in the last experiment. We first computed correlation statistics of real faces by calculating the average amplitude spectrum of the front-view faces in the Ekman PoFA database (Ekman and Friesen, 1976) and Karolinska Directed Emotional Faces (KDEF) database (Lundqvist et al., 1998). We used the standard procedure of first computing the 2D Fourier transform of the images and then combining the amplitude spectrum across different orientations to obtain a 1D spectrum. We found that the spectrum follows the 1/fk law with k = 1.63, where f is the spatial frequency.
We then generated 1/fk noise patterns with k equal to 0, 0.5, 1.0, 1.5, 2.0, and 2.5. The k = 0 noise had a flat spectrum and we generated it as spatial white noise. For other k values, we inverse transformed the 1/fk amplitude spectrum and a random phase spectrum to the spatial domain. Finally, we applied the standard histogram equalization procedure (MATLAB histeq function) to equalize the first-order distributions of the noises to that of the saddest real face. Therefore, noises with different k values all had the same first-order distributions but different second-order correlation structures.
Procedures
We used the method of constant stimuli and the two-alternative forced-choice paradigm in all experiments. Subjects received no feedback on their performances at any time. We measured facial expression perception in the motion faces (mf) and in the controls whose mouth region was frame randomized to destroy motion (mfr). These conditions did not involve adaptation and are denoted as 0-mf and 0-mfr. For the 0-mf condition, we randomly interleaved the upside-down happiest and saddest motion faces as catch trials for the two naive subjects to ensure that they judged facial expression, instead of motion direction (see Results). We also cross-adapted the motion faces and the static cartoon faces (cf). The adapting stimulus was either the saddest mf or the saddest cf and the test stimuli were either the set of the motion faces or the set of the static cartoon faces. The four possible combinations are denoted as mf-mf, mf-cf, cf-mf, and cf-cf, where, for example, mf-cf represents the condition with the saddest mf as the adapting stimulus and the cf set as the test stimuli. Similarly, we measured cross-adaptation aftereffects between the motion faces and the real faces (rf), resulting in four possible conditions: mf-mf, mf-rf, rf-mf, and rf-rf. We also included baseline conditions without adaptation for cf and rf, and they are denoted as 0-cf and 0-rf. (The baseline condition for mf was the same as the 0-mf condition mentioned above.) In total, there were 11 different conditions (0-mf, 0-mfr, 0-cf, 0-rf, mf-mf, cf-cf, rf-rf, mf-cf, cf-mf, mf-rf, and rf-mf).
The 11 conditions were run in separate blocks with two blocks per condition. Although in Results we described these conditions in a specific order, they were randomized for each subject. Over the two blocks for each condition, each test stimulus was repeated 20 times. The trials for different test stimuli in a block were also randomized. There was a break of at least 10 min after each adaptation block to avoid carryover of the aftereffects to the next block. Data collection for each block started after subjects had sufficient practice trials (∼10–20) to feel comfortable with the task.
Subjects started each block of trials by fixating the central cross and pressing the space bar. After 500 ms, for each adaptation block the adapting stimulus appeared for 4 s. After a 500 ms interstimulus interval (ISI), a test face appeared for 100 ms if it was a static cartoon face or real face and for 1 s if it was a motion face. The longer duration for the motion face was needed for subjects to perform the task well. For the baseline blocks without adaptation, only a test stimulus was shown in each trial. A 50 ms beep was then played to remind subjects to report their perception of the test stimulus. Subjects had to press the “A” or “S” key to report happy or sad expression, respectively. After a 1 s intertrial interval, the next trial began.
After the completion of the above 11 conditions, we ran additional conditions to study how adaptation to the contrast-matched cartoon face (cfc) and modified real face (rfm) affected the perception of the motion faces (the cfc-mf and rfm-mf conditions). cfc was the saddest static cartoon face, with its foreground and background luminance values set to the means of the mouth and surrounding areas of the saddest real face. rfm was the saddest real face, with the mouth curve of cfc pasted over. Moreover, we investigated whether motion-face adaptation could produce an aftereffect on the static cartoon faces with random dots added (cfd) to make their background more similar to the motion face (the mf-cfd and 0-cfd conditions). We also ran two control experiments. The first used test cartoon faces whose uniform background luminance matched that of the cfd stimuli but without any dots (the mf-cfl and 0-cfl conditions). The second experiment repeated the mf-cfd condition but subjects were asked to judge motion direction (up or down) around the midpoint of the mouth curves of the test static faces (the mf-cfd-dir condition). The rationale for running these seven conditions was explained in Results.
Finally, we cross-adapted real faces and static cartoon faces. We started with four adaptation conditions, namely, cf-cf, cf-rf, rf-cf, and rf-rf (where rf-cf, for example, means adapting to the saddest real face and testing on the cartoon faces), and two baseline conditions, 0-cf and 0-rf. We then repeated the rf-cf and 0-cf conditions after adding 1/fk noises to the background of the test cartoon faces (the rf-cfk and 0-cfk conditions). We used k = 0, 0.5, 1.0, 1.5, 2.0, and 2.5 in different blocks with randomized order. The noise in each trial was generated online. Therefore, although noise backgrounds in the same block all had the same correlation statistics (same k), there was no repetition of a specific sample. We also included a uniform background whose luminance equaled the mean of the other backgrounds. This corresponds to a very large k and is labeled as k = ∞. The rationale for running these 20 conditions was explained in Results.
Data analysis
For each condition, the data were sorted into fraction of “happy” responses to each test stimulus. The test stimuli were parameterized according to the fraction of the signal dots in the motion faces, the mouth curvature of the static cartoon faces, or the proportion of the happy face in the morphed real faces. The fraction of “happy” responses was then plotted against the test stimulus, and the resulting psychometric curve was fitted with a sigmoidal function of the form f(x) = 1/[1 + e−a(x−b)], where a determines the slope and b gives the test stimulus parameter corresponding to the 50% point of the psychometric function [the point of subjective equality (PSE)]. An aftereffect is measured by the difference between the PSEs of the adaptation condition and the corresponding baseline condition. To determine whether an aftereffect was significant, we calculated the p value by comparing subjects' PSEs of the adaptation condition against those of the corresponding baseline condition via a two-tailed paired t test. For the 0-mfr and mf-cfd-dir conditions, we determined whether the slopes of the psychometric curves were significantly different from zero via a two-tailed t test. In the last experiment, in which the k value of the noise background was varied, we used ANOVA to test the dependence on k.
Results
We first describe a novel class of second-order faces in which facial expressions are either sad or happy depending on local directions of motion. We then present our cross-adaptation studies using these second-order faces and conventional first-order cartoon and real faces and demonstrate the importance of statistical similarity between the featureless backgrounds of the adapting and test stimuli.
Facial expressions solely specified by motion gradients in second-order faces
We programmed second-order cartoon faces with motion gradient-defined expressions (Fig. 1a). On a white screen, we generated black random dots with a 15% dot density over a 3.7° × 3.7° square. We then defined a virtual ring for the face outline, two virtual disks for the eyes, and a horizontally oriented virtual rectangle for the mouth. Unlike first-order stimuli, these regions were not drawn with a luminance different from the background. Instead, they were virtual regions within which dots were dynamic and thus perceptually segregated from the background static dots. The dots within the outline ring and the eye disks randomly flickered at 10 Hz. The dots within the mouth rectangle had different motion gradient patterns to produce sad and happy expressions. For the sad expression (Fig. 1b), the dots along the middle vertical line of the rectangle moved upward and those at the two ends of the rectangle moved downward at a speed of 2.9°/s. The velocity of other dots in the rectangle was determined by a linear interpolation. Owing to the motion mislocalization effect (Ramachandran and Anstis, 1990; De Valois and De Valois, 1991; Fu et al., 2004), this motion gradient pattern made the mouth rectangle look concave even though it was physically flat. For the happy expression, the direction of each dot in the mouth rectangle was reversed (Fig. 1c). The first supplemental file, available at www.jneurosci.org as supplemental material, contains two movies showing that indeed these stimuli appear sad and happy, respectively. Playing the movies backward to reverse the directions of motion exchanges the sad and happy expressions. Stopping the movies at any frame causes both the faces and their expressions to vanish. When we randomized the frames of the mouth rectangle (see the second supplemental file, available at www.jneurosci.org as supplemental material), the perceived differences between sad and happy faces disappeared, further proving the lack of static form cues for the expressions.
To conduct formal psychophysical experiments, we generated a set of faces with expressions that gradually changed from sad to happy by letting a fraction of the dots (signal dots) within the mouth rectangle follow the above-prescribed motion gradients while the remaining dots (noise dots) randomly flickered at 10 Hz. We use negative and positive fractions to label the motion gradient patterns for the sad and happy expressions, respectively. Thus, the original sad and happy faces with 100% signal dots in the mouth region have signal dot fractions of −1 and 1, respectively. A fraction of 0 means that all dots are noise dots. We generated a total of nine stimuli with fractions from −1 to 1, in steps of 0.25. Subjects initiated a block of trials after fixating on a central cross. In each trial, a stimulus was pseudorandomly selected and shown centered at fixation. Subjects reported whether the perceived expression was sad or happy via a key press. At no point was feedback given in this or the other experiments.
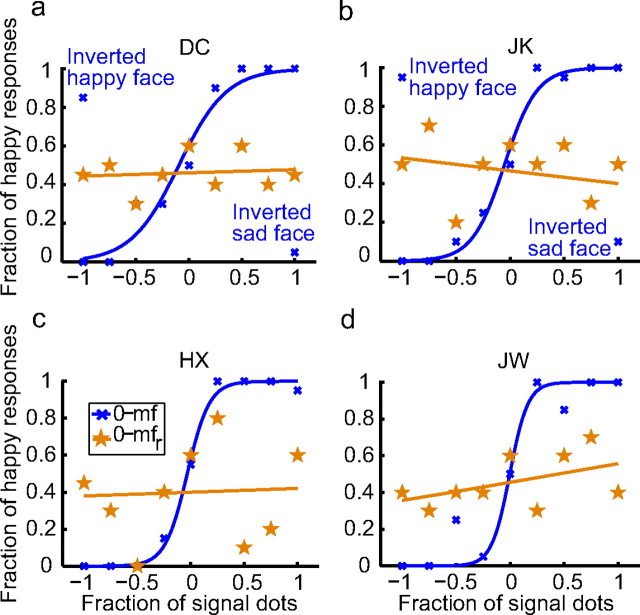
The psychometric data for four subjects (two of them naive) are shown as the blue curves (the 0-mf condition) in Figure 2a–d. As the fraction of signal dots varied from −1 to 1, the fraction of “happy” responses increased gradually from 0 to 1 for all subjects, indicating that the perceived expressions varied from sad to happy in an orderly manner. One might raise the possibility that subjects did not really perceive any facial expressions but simply judged local motion directions. This is unlikely for three reasons. First, none of the subjects performed a motion direction task under this condition so there was little chance of confusion. Second, if the subjects could not see facial expression and decided to use motion direction as a substitute, it would be hard to explain why all subjects happen to choose the same motion pattern to indicate happy or sad expressions. Third, when they were given the instructions, all subjects understood the task immediately and found it to be straightforward. To rule out this possibility directly, for the two naive subjects, we randomly interleaved catch trials in which the stimuli were the saddest and happiest faces (signal dot fractions of −1 and 1) shown upside-down. When the face with a signal dot fraction of 1 (or −1) was inverted, its motion gradient pattern was identical to that of the upright face with a signal dot fraction of −1 (or 1). If the subjects judged local motion directions, they would consider the inverted saddest face as “happy” and the inverted happiest face as “sad.” The data, marked as inverted happy or sad face in Figure 2, a and b, show the opposite results, indicating that the subjects indeed judged the faces' expressions. The fact that the catch trials did not produce chance performances (0.5) also suggests that for simple cartoon faces, inversion does not destroy the perception of facial expressions (Xu et al., 2008).
Figure 2.
Facial-expression perception with the motion faces. a–d, Psychometric functions from two naive subjects (DC, JK) and two experimenters (HX, JW). For each subject, the perceived expression varied gradually from sad to happy as the fraction of the signal dots varied from −1 to 1 (blue curve, the 0-mf condition). The perception of expression was destroyed with randomized motion frames (brown curve, the 0-mfr condition). For the two naive subjects, catch trials with the inverted saddest and happiest motion faces were shown to indicate that they judged facial expressions instead of motion directions (see Results for details).
To ensure that the perceived facial expressions in the above experiment were completely specified by motion instead of by static form cues, we conducted a control experiment that randomized the motion frames of the mouth rectangle for all nine face stimuli. The results of the subjects' judgments are shown as the brown curves (the 0-mfr condition) in Figure 2a–d. The slopes of these psychometric curves do not significantly differ from zero (mean, 0.023; p = 0.47), indicating that the subjects could not distinguish between sad and happy expressions once the coherent motion gradients were destroyed by randomization. We conclude that there was no first-order form cue in the original stimuli.
Cross-adaptation between the second-order motion faces and first-order static cartoon faces and real faces
After establishing facial-expression perception in the second-order motion faces, we cross-adapted them with first-order, luminance-defined faces to gain insight into interactions between different cues in face processing. Previous studies on cross-adaptation between first- and second-order stimuli have been limited to low-level stimuli (Nishida et al., 1997; Larsson et al., 2006; Ashida et al., 2007; Schofield et al., 2007).
As in our previous study (Xu et al., 2008), we generated first-order static cartoon faces and real faces with expressions varying from sad to happy; examples are shown in Figure 1, d and e. The physical dimensions of the static cartoon faces exactly matched those of the motion faces except that the sad to happy expressions were generated by luminance-defined curvature rather than motion gradients. We also closely matched the motion faces and the real faces, paying special attention to align the mouth positions of the real faces to that of the motion faces, since the mouth is particularly important for facial expressions (Gosselin and Schyns, 2001; Xu et al., 2008).
We first report how the second-order motion faces and the first-order static cartoon faces interacted. We used either the saddest mf or the saddest cf we generated as the adapting stimulus and then our set of mf or cf faces as the test stimuli. The total of four possible combinations are denoted as mf-mf, mf-cf, cf-cf, and cf-mf conditions, where, for example, cf-mf means adapting to the saddest cartoon face and testing on the motion faces. We also included baseline conditions without adaptation for the motion faces and static cartoon faces, denoting them as 0-mf (already described above) and 0-cf.
The psychometric data from four subjects (two of them naive) for the 0-mf, mf-mf, and cf-mf conditions are shown in Figure 3a–d as blue, green, and dashed black curves, respectively. Similarly, the data for the 0-cf, cf-cf, and mf-cf conditions are shown in Figure 4a–d as blue, green, and dashed black curves, respectively. As expected, the two within-category adaptation conditions (mf-mf and cf-cf) generated large facial-expression aftereffects, indicated by the shifts of the psychometric curves from the corresponding baseline conditions (0-mf and 0-cf). The leftward shifts mean that subjects perceived happy expressions more often after adapting to sad faces, consistent with previous face adaptation experiments (Leopold et al., 2001; Webster et al., 2004; Xu et al., 2008). For the cross-adaptation conditions (cf-mf and mf-cf), the results were asymmetric: first-order cartoon-face adaptation generated a significant aftereffect on the second-order motion faces (cf-mf), yet second-order motion-face adaptation failed to generate an aftereffect on the first-order cartoon faces (mf-cf). Similar asymmetric interactions have been reported previously for low-level stimuli (Smith et al., 2001; Ellemberg et al., 2004; Schofield et al., 2007).
Figure 3.
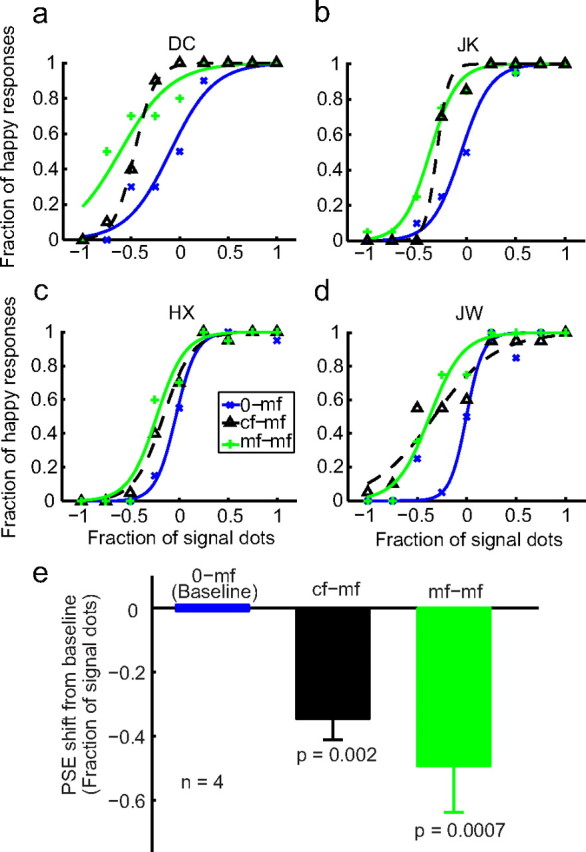
The effect of cartoon adaptation on the perceived expression of the motion faces. a–d, Psychometric functions from two naive subjects (DC, JK) and two experimenters (HX, JW). The test stimuli were always the mf. The adapting stimuli varied with conditions as follows: 0-mf, no-adaptation baseline (blue, copied from Fig. 2); cf-mf, adaptation to the saddest cartoon face (dashed black); mf-mf, adaptation to the saddest motion face (green). e, Summary of all four subjects' data. For each condition, the average PSE relative to the baseline condition was plotted, with the error bar representing ±SEM. The p value shown for each condition in the figure was calculated against the baseline condition using a two-tailed paired t test.
Figure 4.
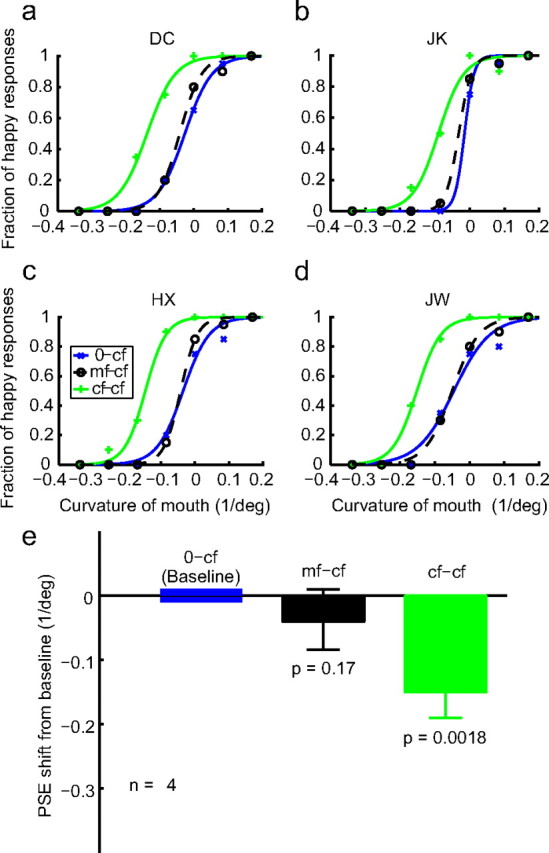
The effect of motion-face adaptation on the perceived expression of the static cartoon faces. a–d, Psychometric functions from two naive subjects (DC, JK) and two experimenters (HX, JW). The test stimuli were always the static cf. The adapting stimuli varied with conditions as follows: 0-cf, no-adaptation baseline (blue); cf-cf, adaptation to the saddest cartoon face (green); mf-cf, adaptation to the saddest motion face (dashed black). e, Summary of all four subjects' data.
To quantify the aftereffects and summarize the results from all four subjects, we determined the PSE—the x-axis value corresponding to 50% “happy” responses—for each psychometric curve of each subject. Figure 3e shows the mean PSEs of the mf-mf (green bar) and cf-mf (black bar) conditions relative to the baseline 0-mf condition. Similarly, Figure 4e shows the mean PSEs of the cf-cf (green bar) and mf-cf (black bar) conditions relative to the baseline 0-cf condition. A negative value means a leftward shift of the psychometric curve from the baseline. The error bars indicate ±1 SEM. The asymmetry in the aftereffect is apparent, with the cf-mf, but not the mf-cf, condition being significantly different from the corresponding baseline (Figs. 3e and 4e, p values).
We also cross-adapted first-order real faces and the second-order motion faces and found little aftereffect transfer in either direction (see the third supplemental file, available at www.jneurosci.org as supplemental material). Similar results have also been reported for low-level stimuli (Nishida et al., 1997; Larsson et al., 2006; Ashida et al., 2007). Note, in particular, that the first-order cartoon face, but not the first-order real face, produced an aftereffect on the second-order motion faces. This is not attributable to different contrasts or mouth shapes of the stimuli (see the third supplemental file, available at www.jneurosci.org as supplemental material).
The role of background similarity in determining aftereffect transfer from second- to first-order faces
As mentioned in the Introduction, to understand the above results and the role of cue-invariant cells in cross-adaptation, we considered a new contingent factor that could contribute to the transfer of an aftereffect, namely, the similarity between the backgrounds of the adapting and test stimuli. By background we mean the luminance distributions of the largely featureless areas surrounding the facial features. We hypothesized that strong aftereffects are induced only when adapting and test stimuli have sufficiently similar backgrounds. The hypothesis implies the surprising prediction that although featureless backgrounds cannot produce a facial expression aftereffect by themselves, they will significantly influence the aftereffect. We designed experiments to test this prediction.
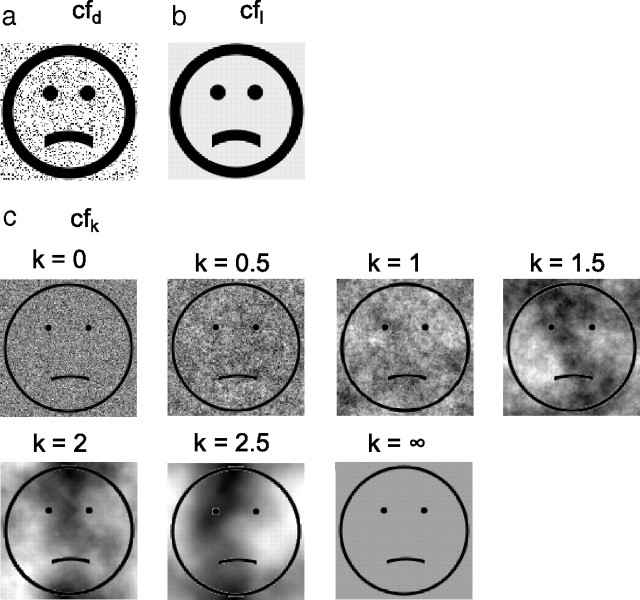
In Figure 4, we showed that motion-face adaptation failed to produce an aftereffect on the test static cartoon faces (the mf-cf condition). By the background-similarity hypothesis, we expected to observe the aftereffect in the mf-cf condition simply by adding random dots to the test cartoon faces to make them more similar to the adapting motion face. Importantly, this experiment could also address the question of whether it is possible for a second-order face to produce an aftereffect on first-order faces. We therefore generated a new set of test cartoon faces (cfd) (Fig. 5a) by adding random dots to the original set shown in Figure 1d. The dot density was the same as for the motion faces (15%). The dots were added online for each trial so that no dot pattern was repeated across trials. We ran the motion-face adaptation condition (mf-cfd) and the no-adaptation baseline condition (0-cfd) in exactly the same way that we ran the original mf-cf and 0-cf conditions. The data from four subjects (two of them naive) are shown as dashed and solid red curves in Figure 6a–d. Motion-face adaptation indeed produced a significant aftereffect on the cartoon faces with added dots (Fig. 6e, hatched red bar), supporting the notion that background similarity influences the aftereffect. The result suggests that the lack of aftereffect in the original mf-cf condition (Fig. 4) is not entirely because the adapting motion face is not as salient as the test cartoon faces. It further suggests that second-order stimuli can produce aftereffects on first-order stimuli when their backgrounds are more similar.
Figure 5.
Manipulations of background similarity between adapting and test faces. Each face set contained expressions ranging from sad to happy, but only the saddest one is shown here. a, Cartoon face set with random dots added (cfd). Random dots of 15% density were added to the original static cartoon face set in Figure 1d. b, Luminance-matched cartoon face set (cfl). The background luminance was matched to the mean background luminance of cfd set. c, Cartoon face sets with 1/fk noise backgrounds, with k = 0, 0.5, 1, 1.5, 2, and 2.5, respectively. Noises with different k values had the same first-order luminance distribution but different second-order correlation structures. A uniform background was also included and labeled as k = ∞.
Figure 6.
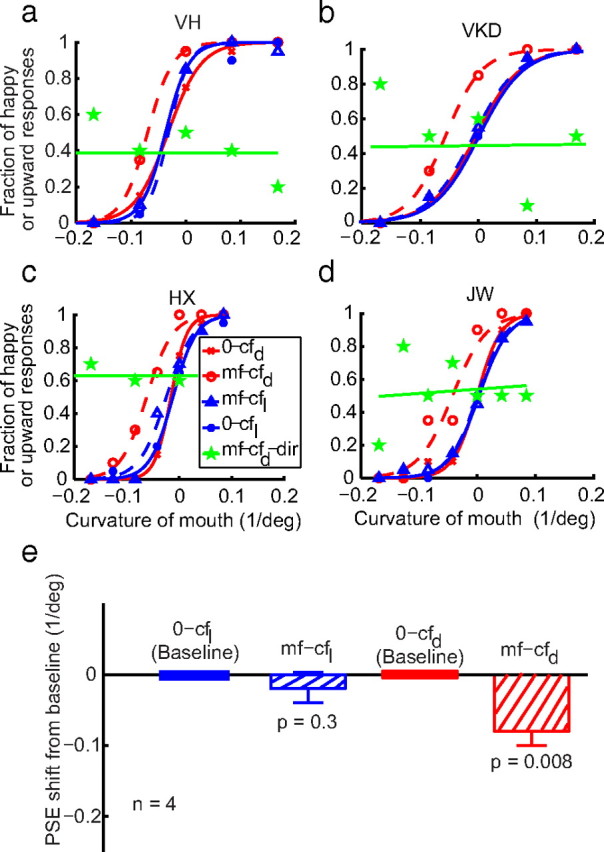
The role of background similarity in aftereffect transfer from second-order motion faces to first-order static cartoon faces. a–d, Psychometric functions from two naive subjects (VH, VKD) and two experimenters (HX, JW) under the following conditions: 0-cfd, no adaptation and test on the dot-added cartoon faces (solid red); mf-cfd, adaptation to the saddest motion face and test on the dot-added cartoon faces (dashed red); 0-cfl, no adaptation and test on the background-luminance-matched cartoon faces (solid blue); mf-cfl, adaptation to the saddest motion face and test on the background-luminance-matched cartoon faces (dashed blue); mf-cfd-dir, same as mf-cfd, but the subjects judged motion direction (up or down) above the midpoint of the mouth curves of the test cfd faces (solid green). e, Summary of all four subjects' data.
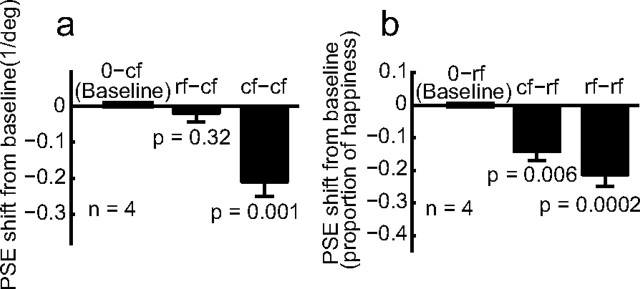
We excluded two alternative explanations. The first depends on the fact that the added black dots reduced the mean background luminance of the cfd set (47.6 cd/m2) compared with the original cartoon faces (56.2 cd/m2), resulting in a slightly lower contrast for the features in the cfd faces. If the lowered contrast produced the aftereffect, we would expect to observe the motion-face-induced aftereffect on dot-free cartoon faces with reduced background luminance (47.6 cd/m2) (Fig. 5b, cfl). We ran the motion-face adaptation condition (mf-cfl) and no-adaptation baseline condition (0-cfl) in this luminance-matched case in exactly the same way that we ran the mf-cfd and 0-cfd conditions. The data (Fig. 6a–d, dashed and solid blue curves, and 6e, blue hatched bar) show no aftereffect, suggesting that luminance is not a critical factor. Furthermore, the slopes of the psychometric functions for the cfl and cfd conditions do not differ significantly (mean = 23.2 and 25.1, respectively; p = 0.32), suggesting that the different aftereffects cannot be attributed to different saliencies of the test stimuli.
The second alternative explanation is that the added dots produced a motion aftereffect which then biased the perceived facial expressions. This is very unlikely because the added dots were outside the mouth curves (Fig. 5a) and thus had little or no spatial overlap with the moving dots inside the mouth of the adapting motion face. To rule out this possibility formally, we repeated the mf-cfd condition but asked the subjects to report the direction of motion for the dots above the midpoint of the mouth curves of the test cartoon faces. The data for this condition (mf- cfd-dir) are shown as green curves in Figure 6a–d. That the slopes of these curves are not significantly different from zero (mean, 0.014; p = 0.62) indicates that the subjects did not see motion aftereffects in this experimental condition. Indeed, the subjects complained that they could not perform this task because they could not see motion anywhere in the test faces.
The role of background similarity in determining aftereffect transfer between different types of first-order faces
We further investigated whether background similarity also contributes to aftereffect transfer between different types of first-order faces. We used real faces as in Figure 1e and static cartoon faces similar to those in Figure 1d but with a 30% pen width since there was no need to match the motion faces in this experiment. We first cross-adapted rf and cf stimuli without any background manipulations. There were four adaptation conditions rf-rf, cf-cf, rf-cf, and cf-rf, and two baseline conditions 0-rf and 0-cf. We found that cartoon-face adaptation generated a facial-expression aftereffect on the real faces (the cf-rf condition) but real-face adaptation failed to produce an aftereffect on the cartoon faces (the rf-cf condition). This is similar to the asymmetry between the motion and cartoon faces (Figs. 3 and 4), and we show only the summary data in Figure 7.
Figure 7.
Cross-adaptation between first-order cartoon and real faces. Only the summary data from two naive subjects and two experimenters are shown. a, The test stimuli were always the cartoon faces. The adapting stimuli varied with conditions as follows: 0-cf, no-adaptation baseline; cf-cf, adaptation to the saddest cartoon face; rf-cf, adaptation to the saddest real face. b, The test stimuli were always the real faces. The adapting stimuli varied with conditions as follows: 0-rf, no-adaptation baseline; rf-rf, adaptation to the saddest real face; cf-rf, adaptation to the saddest cartoon face.
We then examined whether we can increase the aftereffect in the rf-cf condition by adding proper backgrounds to the test cartoon faces. One possibility would be to remove eyes, nose, and mouth from the adapting real face and use the remainder as the background for the test cartoon faces. However, the remainder might still carry some facial expression information or contain other features that could complicate the interpretation of the results. We therefore generated noise backgrounds based on the correlation statistics of real faces. For this purpose, we first computed the amplitude spectrum of real faces and found that it follows the 1/fk law with k = 1.63 (Fig. 8), where k is the spatial frequency, in agreement with a recent study (Keil, 2008). Comparing with natural image statistics (k = 1) (Field, 1987; Ruderman, 1994), front-view faces have less energy in high-frequency range, presumably because of less abrupt occlusions.
Figure 8.
Correlation statistics of front-view real-face images measured by the Fourier amplitude spectrum of the KDEF database (red) and Ekman database (blue). The log–log plots show nearly straight lines, indicating a 1/fk relationship between amplitude and spatial frequency. The KDEF curve extends to higher frequencies because of the larger image size. Curve fitting yields k values of 1.61 for the KDEF faces and 1.65 for Ekman faces, with an average of 1.63.
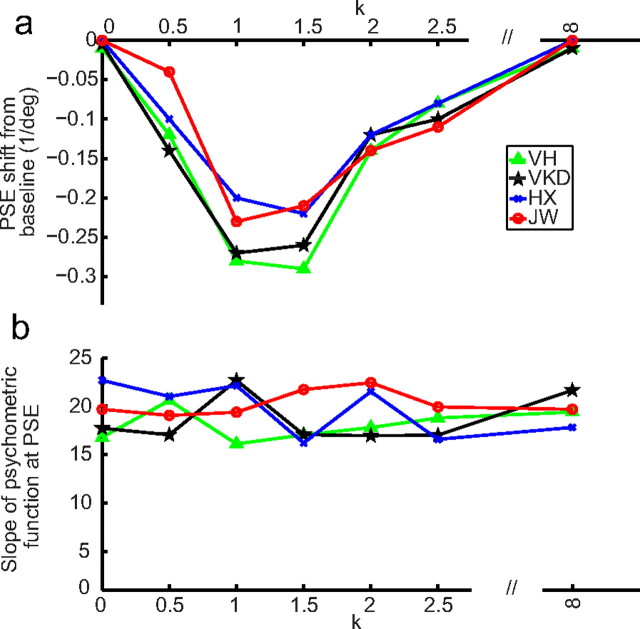
We then repeated the rf-cf condition after adding 1/fk noises to the test cartoon faces (denoted as the rf-cfk conditions). We also run the corresponding baseline conditions 0-cfk. In separate blocks with randomized order, we let k = 0, 0.5, 1, 1.5, 2.0, and 2.5. By histogram equalization, noises with different k values all had the same first-order distribution but different second-order correlation structures. (Note that first- and second-order image statistics should not be confused with first- and second-order stimuli.) We also included a uniform background whose luminance matches the mean of the other backgrounds; it is labeled as k = ∞. Samples of different backgrounds are shown in Figure 5c. The background in each trial was generated online. Consequently, although backgrounds for different trials in a block had identical statistics (same k), no sample was repeated. This ensures that any effect is not due to accidental “features” in a particular sample. Figure 9a shows the facial-expression aftereffect transfer from real-face adaptation to the test cartoon faces, measured as the PSE shift from the corresponding baseline condition, as a function of k. When the noise backgrounds had k values of 1 and 1.5, matching the correlation statistics of natural images and real-face images, the transfer was maximal. For k values outside this range, the transfer declines to 0. An ANOVA test indicates a significant dependence of the aftereffect on k (p = 0.03). Since all backgrounds (except the uniform one labeled as k = ∞) had the same first-order luminance distribution but different second-order correlation structures, Figure 9a suggests that the second-order statistics of the real and cartoon faces have to be similar to produce a sizable aftereffect.
Figure 9.
The role of background similarity in aftereffect transfer from first-order real faces to first-order static cartoon faces. The adapting stimulus was always the saddest read face. The test stimuli were cartoon face sets with 1/fk noise backgrounds. a, The aftereffect, measured as the PSE shift from the corresponding baseline, as a function of k for four subjects. b, The slope (at PSE) of psychometric curves for the baseline conditions as a function of k.
An alternative interpretation of Figure 9a is that the test cartoon faces had different saliencies against different noise backgrounds even though they all had identical first-order luminance distributions, and differences in saliency led to different aftereffect transfer. To rule out this interpretation, we measured the slopes (at PSE) of the psychometric functions for different k values, and the results for the baseline conditions are shown in Figure 9b. An ANOVA test showed no significant dependence of the slope, and thus saliency, on k (p = 0.41). A similar lack of dependence on k was found for the slopes in the adaptation conditions (p = 0.37).
Discussion
We investigated the role of background statistics in aftereffect transfer between different classes of faces. We first generated a novel class of second-order faces in which local directions of motion define sad and happy facial expressions, without any static form cue. Reversing motion directions in these stimuli exchanges happy and sad expressions. We then examined interactions between these second-order motion faces and first-order cartoon and real faces. Adaptation to a second-order motion face failed to produce a facial-expression aftereffect on the first-order real or cartoon faces, whereas adaptation to a first-order cartoon face, but not a real face, generated the aftereffect on the second-order motion faces, a difference that was not due to differences in contrast or mouth shape. These results agree with previous studies using simpler nonface stimuli, namely, that second-order adaptation typically does not transfer to first-order stimuli whereas first-order adaptation sometimes, but not always, transfers to the second-order stimuli (Nishida et al., 1997; Larsson et al., 2006; Ashida et al., 2007; Schofield et al., 2007). Such results have been widely interpreted as indicating separate processing for first- and second-order stimuli.
However, as mentioned in Introduction, cue-invariant cells with similar tuning to first- and second-order stimuli have been reported in many visual areas, raising the question of why aftereffect transfer is not more frequently observed, particularly from second- to first-order stimuli,. We therefore searched for conditions that may facilitate transfer. We found that, surprisingly, the degree of similarity between the featureless backgrounds of adapting and test faces is a critical factor. Specifically, adaptation to a second-order motion face could be made to transfer to the first-order cartoon faces by simply adding static random dots to the latter making their backgrounds more similar to that of the adapting motion face (Fig. 6, the mf-cfd condition). Moreover, background similarity also controlled transfer between different classes of first-order faces: Real-face adaptation transferred to static cartoon faces only when noise with the correlation statistics of real faces or natural images was added to the background of the cartoon faces (Fig. 9a). We ruled out contrast, motion-aftereffect, or saliency-based explanations for these findings. Our results have implications for mechanisms of adaptation, the interpretation of null aftereffects, and the representation of faces.
The background similarity effect in visual adaptation
The background similarity effect we described could be considered a new form of contingent aftereffect. The best-known contingent aftereffect was reported by McCollough (1965), who induced two different color aftereffects simultaneously, for two different orientations. This implies that a particular color aftereffect is observed only when the test and adapting stimuli have the same orientation. Similar contingent aftereffects have been reported for face adaptation (Rhodes et al., 2004; Yamashita et al., 2005; Ng et al., 2006; Little et al., 2008); in particular, facial-expression aftereffects are larger when the identities of adapting and test faces are shared (Fox and Barton, 2007). Our work extends these studies, showing the even greater importance of sharing gross statistical characteristics of otherwise featureless backgrounds.
The background similarity effect depends on both first- and second-order statistics. We originally demonstrated the effect by showing that transfer from motion faces with only first-order, white noise, random-dot backgrounds, to cartoon faces, occurred when similar, first-order, random dots were added to the latter. However, the backgrounds of real faces have second-order structure; substantial transfer from them to cartoon faces depended on matching this; simply matching the first-order distribution was insufficient. Of course, faces (and natural images in general) obviously contain higher-order structures. It would be interesting to test what aspects of higher-order statistics, notably those important for the determination of face identity (Fox and Barton, 2007), could further enhance the background similarity effect.
At a neuronal level, contingent aftereffects likely arise from cells jointly selective to multiple aspects of stimuli. The background similarity effect, in particular, predicts joint selectivity to stimulus features and background statistics. Variation in firing rates coming from the background may therefore have resulted in an underestimation of the degree of invariance to features or cues defining the features, effectively comprising a novel nonclassical influence on visual responses. However, face-identity aftereffects are not influenced by differing facial expressions (Fox et al., 2008), showing that identity coding is invariant to expression-related statistics. How selectivity and invariance depends on tasks and levels of the visual hierarchy is an open question.
It thus becomes pressing to ask whether background manipulations can enhance aftereffect transfer between first- and second-order low-level stimuli such as orientation and translational motion. Cue-invariant responses to orientation and motion have been found in areas V1, V2, and MT (von der Heydt et al., 1984; Albright, 1992; Sheth et al., 1996). Computational models also assume that separate first- and second-order motion processing in V1 and V2, respectively, converges on MT (Wilson et al., 1992). However, it is possible that cue convergence is progressively stronger at higher-level areas coding more complex stimuli, with the fraction of cue-invariant cells in relatively low-level areas being too small (O'Keefe and Movshon, 1998) to have a perceptual impact. We are currently investigating this issue. Interestingly, the rare study that did find strong cross-adaptation aftereffects between first- and second-order orientations used stimuli of very similar backgrounds (Georgeson and Schofield, 2002).
At a functional level, our study suggests that statistical similarity between featureless backgrounds of stimuli can gate their temporal interactions. Although the statistical rationale for the adaptation effects that are observed is not yet completely clear (Schwartz et al., 2007; Xu et al., 2008), by restricting the scope of adaptation, the background similarity effect will avoid overgeneralization.
Adaptation treats the temporal context of stimuli. However, there are many similarities between the effects of spatial and temporal context (Clifford et al., 2000; Schwartz et al., 2007), as in the relationship between the tilt aftereffect and the tilt illusion. It is not known if the latter is gated by statistical similarity between the backgrounds of the stimuli involved. Crowding is another form of contextual spatial interaction and it is known to be stronger when the features in the target and flanks are more similar (Levi, 2008). However, it is also unknown if featureless backgrounds modulate the crowding effect.
Interpretation of null aftereffects
Our results suggest that if adaptation to A has no impact on B, then it is not necessarily true that A and B are processed separately. Our initial null findings might have tempted one to conclude that facial expressions in motion faces, real faces, and static cartoon faces are all processed separately, despite expression being a universal property. Our later finding of significant transfer for sufficiently similar backgrounds suggests that different cues do indeed converge in the course of creating facial-expression representation. The same issue may affect the design and interpretation of a range of future adaptation experiments. Nevertheless, that transfer depends on appropriate background manipulations suggests limitations in the extent of shared neural processing for the stimuli. In this sense, our results complement, rather than contradict, previous suggestions of separate processing of first- and second-order stimuli. A probable scenario is that there are both separate and shared representations of different classes of stimuli. Previous studies emphasized the former whereas our method of background manipulation is sensitive enough to reveal the latter.
The notion of background similarity is symmetric: if A is similar to B, then B is similar to A; yet the interactions between different classes of stimuli are often asymmetric. An obvious explanation is that the outcome of a particular adaptation experiment depends on multiple factors including saliency and separate processing as well as background similarity.
Face representation
Our results suggest the possibility that background statistics are an integral component of facial-expression representation even when the backgrounds do not contain any information about facial expression. In other words, featureless backgrounds are not discarded after feature extraction. For example, when adapting to the saddest motion face, the context provided by the featureless stationary dots in the background may be encoded together with the dots that define the mouth shape (and facial expression). This integration could occur either at face areas or at lower-level areas feeding the face areas, and may be related to the holistic view of face representation (Tanaka and Farah, 2003).
The perceived expressions in our motion-face stimuli also suggest strong interactions between motion processing and face perception, functions that have been assigned to dorsal and ventral pathways, respectively (Ungerleider and Mishkin, 1982; Felleman and Van Essen, 1991). Although there have already been demonstrations of the interactions (Bassili, 1978; Berry, 1990; Knappmeyer et al., 2003; Farivar et al., 2009), our motion-face stimuli are unique in that the happy and sad expressions are solely defined by local directions of motion according to the motion mislocalization effect. Since reversing the directions exchanges the happy and sad expressions, our stimuli link face perception to directional processing, instead of general motion detection. Directional tuning and the associated mislocalization effect start as early as V1 (Hubel and Wiesel, 1968; Fu et al., 2004). Thus, our stimuli suggest that local, low-level directional processing contributes to face perception, supporting the notion of a strong local component in face representation, in addition to a holistic component (Xu et al., 2008).
In summary, we have shown that statistical similarity between featureless backgrounds of the adapting and test stimuli is a novel factor in determining aftereffect transfer between different classes of stimuli. This result has implications for the design and interpretation of future adaptation studies. We have also shown that facial expressions can be solely defined by local directions of motion gradient patterns, thus establishing a strong link between face and motion-direction processing. Our findings suggest that luminance- and motion-direction-defined forms, and local features and background statistics, converge in the representation of faces.
Footnotes
This work was supported by National Institutes of Health Grant EY016270 (N.Q.) and by the Gatsby Charitable Foundation and the Biotechnology and Biological Sciences Research Council, Engineering and Physical Sciences Research Council, and Wellcome Trust Grant BB/E002536/1 (P.D.). We are very grateful to an anonymous reviewer for suggesting that we relate our results to contingent aftereffects and to Richard Lipkin for editorial assistance.
References
- Albright TD. Form-cue invariant motion processing in primate visual cortex. Science. 1992;255:1141–1143. doi: 10.1126/science.1546317. [DOI] [PubMed] [Google Scholar]
- Ashida H, Lingnau A, Wall MB, Smith AT. FMRI adaptation reveals separate mechanisms for first-order and second-order motion. J Neurophysiol. 2007;97:1319–1325. doi: 10.1152/jn.00723.2006. [DOI] [PubMed] [Google Scholar]
- Atick JJ, Redlich AN. Towards a theory of early visual processing. Neural Comput. 1990;2:308–320. [Google Scholar]
- Barlow H. A theory about the functional role and synaptic mechanism of visual aftereffects. In: Blakemore C, editor. Vision: coding and efficiency. Cambridge, UK: Cambridge UP; 1990. [Google Scholar]
- Bassili JN. Facial motion in the perception of faces and of emotional expression. J Exp Psychol Hum Percept Perform. 1978;4:373–379. doi: 10.1037//0096-1523.4.3.373. [DOI] [PubMed] [Google Scholar]
- Berry DS. What can a moving face tell us? J Pers Soc Psychol. 1990;58:1004–1014. doi: 10.1037//0022-3514.58.6.1004. [DOI] [PubMed] [Google Scholar]
- Brainard DH. The Psychophysics Toolbox. Spat Vis. 1997;10:433–436. [PubMed] [Google Scholar]
- Brenner N, Bialek W, de Ruyter van Steveninck R. Adaptive rescaling maximizes information transmission. Neuron. 2000;26:695–702. doi: 10.1016/s0896-6273(00)81205-2. [DOI] [PubMed] [Google Scholar]
- Clifford CW, Wenderoth P, Spehar B. A functional angle on some after-effects in cortical vision. Proc R Soc Lond B Biol Sci. 2000;267:1705–1710. doi: 10.1098/rspb.2000.1198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dan Y, Atick JJ, Reid RC. Efficient coding of natural scenes in the lateral geniculate nucleus: experimental test of a computational theory. J Neurosci. 1996;16:3351–3362. doi: 10.1523/JNEUROSCI.16-10-03351.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Valois RL, De Valois KK. Vernier acuity with stationary moving Gabors. Vision Res. 1991;31:1619–1626. doi: 10.1016/0042-6989(91)90138-u. [DOI] [PubMed] [Google Scholar]
- Ekman P, Friesen W. Pictures of facial affect. Palo Alto, CA: Consulting Psychologists; 1976. [Google Scholar]
- Ellemberg D, Allen HA, Hess RF. Investigating local network interactions underlying first- and second-order processing. Vision Res. 2004;44:1787–1797. doi: 10.1016/j.visres.2004.02.012. [DOI] [PubMed] [Google Scholar]
- Farivar R, Blanke O, Chaudhuri A. Dorsal–ventral integration in the recognition of motion-defined unfamiliar faces. J Neurosci. 2009;29:5336–5342. doi: 10.1523/JNEUROSCI.4978-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felleman DJ, Van Essen DC. Distributed hierarchical processing in the primate cerebral cortex. Cereb Cortex. 1991;1:1–47. doi: 10.1093/cercor/1.1.1-a. [DOI] [PubMed] [Google Scholar]
- Field DJ. Relations between the statistics of natural images and the response properties of cortical-cells. J Opt Soc Am A Opt Image Sci Vis. 1987;4:2379–2394. doi: 10.1364/josaa.4.002379. [DOI] [PubMed] [Google Scholar]
- Fox CJ, Barton JJ. What is adapted in face adaptation? The neural representations of expression in the human visual system. Brain Res. 2007;1127:80–89. doi: 10.1016/j.brainres.2006.09.104. [DOI] [PubMed] [Google Scholar]
- Fox CJ, Oruç İ, Barton JJS. It doesn't matter how you feel. The facial identity aftereffect is invariant to changes in facial expression. J Vis. 2008;8:11.1–13. doi: 10.1167/8.3.11. [DOI] [PubMed] [Google Scholar]
- Fu YX, Shen Y, Gao H, Dan Y. Asymmetry in visual cortical circuits underlying motion-induced perceptual mislocalization. J Neurosci. 2004;24:2165–2171. doi: 10.1523/JNEUROSCI.5145-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geesaman BJ, Andersen RA. The analysis of complex motion patterns by form/cue invariant MSTd neurons. J Neurosci. 1996;16:4716–4732. doi: 10.1523/JNEUROSCI.16-15-04716.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Georgeson MA, Schofield AJ. Shading and texture: separate information channels with a common adaptation mechanism? Spat Vis. 2002;16:59–76. doi: 10.1163/15685680260433913. [DOI] [PubMed] [Google Scholar]
- Gosselin F, Schyns PG. Bubbles: a technique to reveal the use of information in recognition tasks. Vision Res. 2001;41:2261–2271. doi: 10.1016/s0042-6989(01)00097-9. [DOI] [PubMed] [Google Scholar]
- Grill-Spector K, Kushnir T, Edelman S, Itzchak Y, Malach R. Cue-invariant activation in object-related areas of the human occipital lobe. Neuron. 1998;21:191–202. doi: 10.1016/s0896-6273(00)80526-7. [DOI] [PubMed] [Google Scholar]
- Hubel DH, Wiesel TN. Receptive fields and functional architecture of monkey striate cortex. J Physiol. 1968;195:215–243. doi: 10.1113/jphysiol.1968.sp008455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keil MS. Does face image statistics predict a preferred spatial frequency for human face processing? Proc R Soc Lond B Biol Sci. 2008;275:2095–2100. doi: 10.1098/rspb.2008.0486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knappmeyer B, Thornton IM, Bülthoff HH. The use of facial motion and facial form during the processing of identity. Vision Res. 2003;43:1921–1936. doi: 10.1016/s0042-6989(03)00236-0. [DOI] [PubMed] [Google Scholar]
- Larsson J, Landy MS, Heeger DJ. Orientation-selective adaptation to first- and second-order patterns in human visual cortex. J Neurophysiol. 2006;95:862–881. doi: 10.1152/jn.00668.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leopold DA, O'Toole AJ, Vetter T, Blanz V. Prototype-referenced shape encoding revealed by high-level after effects. Nat Neurosci. 2001;4:89–94. doi: 10.1038/82947. [DOI] [PubMed] [Google Scholar]
- Levi DM. Crowding–an essential bottleneck for object recognition: a mini-review. Vision Res. 2008;48:635–654. doi: 10.1016/j.visres.2007.12.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Little AC, DeBruine LM, Jones BC, Waitt C. Category contingent aftereffects for faces of different races, ages and species. Cognition. 2008;106:1537–1547. doi: 10.1016/j.cognition.2007.06.008. [DOI] [PubMed] [Google Scholar]
- Lundqvist D, Flykt A, Öhman A. The Karolinska Directed Emotional Faces (KDEF), CD-ROM from Department of Clinical Neuroscience, Psychology section, Karolinska Institutet, ISBN 91-630-7164-9 [Google Scholar]
- McCollough C. Color adaptation of edge-detectors in the human visual system. Science. 1965;149:1115–1116. doi: 10.1126/science.149.3688.1115. [DOI] [PubMed] [Google Scholar]
- Ng M, Ciaramitaro VM, Anstis S, Boynton GM, Fine I. Selectivity for the configural cues that identify the gender, ethnicity, and identity of faces in human cortex. Proc Natl Acad Sci U S A. 2006;103:19552–19557. doi: 10.1073/pnas.0605358104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nishida S, Ledgeway T, Edwards M. Dual multiple-scale processing for motion in the human visual system. Vision Res. 1997;37:2685–2698. doi: 10.1016/s0042-6989(97)00092-8. [DOI] [PubMed] [Google Scholar]
- O'Keefe LP, Movshon JA. Processing of first- and second-order motion signals by neurons in area MT of the macaque monkey. Vis Neurosci. 1998;15:305–317. doi: 10.1017/s0952523898152094. [DOI] [PubMed] [Google Scholar]
- Pelli DG. The VideoToolbox software for visual psychophysics: transforming numbers into movies. Spat Vis. 1997;10:437–442. [PubMed] [Google Scholar]
- Ramachandran VS, Anstis SM. Illusory displacement of equiluminous kinetic edges. Perception. 1990;19:611–616. doi: 10.1068/p190611. [DOI] [PubMed] [Google Scholar]
- Rhodes G, Jeffery L, Watson TL, Jaquet E, Winkler C, Clifford CW. Orientation-contingent face aftereffects and implications for face-coding mechanisms. Curr Biol. 2004;14:2119–2123. doi: 10.1016/j.cub.2004.11.053. [DOI] [PubMed] [Google Scholar]
- Ruderman DL. The statistics of natural images. Netw Comput Neural Syst. 1994;5:517–548. [Google Scholar]
- Sary G, Vogels R, Orban GA. Cue-invariant shape selectivity of macaque inferior temporal neurons. Science. 1993;260:995–997. doi: 10.1126/science.8493538. [DOI] [PubMed] [Google Scholar]
- Schofield AJ, Ledgeway T, Hutchinson CV. Asymmetric transfer of the dynamic motion aftereffect between first- and second-order cues and among different second-order cues. J Vis. 2007;7(8):1. doi: 10.1167/7.8.1. [DOI] [PubMed] [Google Scholar]
- Schwartz O, Hsu A, Dayan P. Space and time in visual context. Nat Rev Neurosci. 2007;8:522–535. doi: 10.1038/nrn2155. [DOI] [PubMed] [Google Scholar]
- Sheth BR, Sharma J, Rao SC, Sur M. Orientation maps of subjective contours in visual cortex. Science. 1996;274:2110–2115. doi: 10.1126/science.274.5295.2110. [DOI] [PubMed] [Google Scholar]
- Simoncelli EP, Olshausen BA. Natural image statistics and neural representation. Annu Rev Neurosci. 2001;24:1193–1216. doi: 10.1146/annurev.neuro.24.1.1193. [DOI] [PubMed] [Google Scholar]
- Smith S, Clifford CW, Wenderoth P. Interaction between first- and second-order orientation channels revealed by the tilt illusion: psychophysics and computational modelling. Vision Res. 2001;41:1057–1071. doi: 10.1016/s0042-6989(01)00015-3. [DOI] [PubMed] [Google Scholar]
- Tanaka JW, Farah MJ. The holistic face representation. In: Perception of faces, objects and scenes. In: Peterson MA, Rhodes G, editors. Analytic and holistic processes. New York: Oxford UP; 2003. pp. 53–74. [Google Scholar]
- Ungerleider LG, Mishkin M. Two cortical visual systems. In: Ingle DJ, Goodale MA, Mansfield RJW, editors. Analysis of visual behavior. Cambridge, MA: MIT; 1982. pp. 549–586. [Google Scholar]
- von der Heydt R, Peterhans E, Baumgartner G. Illusory contours and cortical neuron responses. Science. 1984;224:1260–1262. doi: 10.1126/science.6539501. [DOI] [PubMed] [Google Scholar]
- Wainwright MJ. Visual adaptation as optimal information transmission. Vision Res. 1999;39:3960–3974. doi: 10.1016/s0042-6989(99)00101-7. [DOI] [PubMed] [Google Scholar]
- Webster MA, Kaping D, Mizokami Y, Duhamel P. Adaptation to natural facial categories. Nature. 2004;428:557–561. doi: 10.1038/nature02420. [DOI] [PubMed] [Google Scholar]
- Wilson HR, Ferrera VP, Yo C. A psychophysically motivated model for 2-dimensional motion perception. Vis Neurosci. 1992;9:79–97. doi: 10.1017/s0952523800006386. [DOI] [PubMed] [Google Scholar]
- Xu H, Dayan P, Lipkin RM, Qian N. Adaptation across the cortical hierarchy: low-level curve adaptation affects high-level facial-expression judgments. J Neurosci. 2008;28:3374–3383. doi: 10.1523/JNEUROSCI.0182-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamashita JA, Hardy JL, De Valois KK, Webster MA. Stimulus selectivity of figural aftereffects for faces. J Exp Psychol Hum Percept Perform. 2005;31:420–437. doi: 10.1037/0096-1523.31.3.420. [DOI] [PubMed] [Google Scholar]
- Zhaoping L. Theoretical understanding of the early visual processes by data compression and data selection. Netw Comput Neural Syst. 2006;17:301–334. doi: 10.1080/09548980600931995. [DOI] [PubMed] [Google Scholar]