Driving force dependence of rates for nonadiabatic proton and proton-coupled electron transfer: Conditions for inverted region behavior

Abstract

The driving force dependence of the rate constants for nonadiabatic electron transfer (ET), proton transfer (PT), and proton-coupled electron transfer (PCET) reactions are examined. Inverted region behavior, where the rate constant decreases as the reaction becomes more exoergic (i.e., as ΔG⁰ becomes more negative), has been observed experimentally for ET and PT. This behavior was predicted theoretically for ET but is not well understood for PT and PCET. The objective of this Letter is to predict the experimental conditions that could lead to observation of inverted region behavior for PT and PCET. The driving force dependence of the rate constant is qualitatively different for PT and PCET than for ET because of the high proton vibrational frequency and substantial shift between the reactant and product proton vibrational wavefunctions. As a result, inverted region behavior is predicted to be experimentally inaccessible for PT and PCET if only the driving force is varied. This behavior may be observed for PT over a limited range of rates and driving forces if the solvent reorganization energy is low enough to cause observable oscillations. Moreover, this behavior may be observed for PT or PCET if the proton donor-acceptor distance increases as ΔG⁰ becomes more negative. Thus, a plausible explanation for experimentally observed inverted region behavior for PT or PCET is that varying the driving force also impacts other properties of the system, such as the proton donor-acceptor distance.

According to standard Marcus theory of nonadiabatic electron transfer (ET),¹ the dependence of the logarithm of the ET rate constant on the driving force ΔG⁰ is represented by an inverted parabola. The maximum rate corresponds to the activationless regime with –ΔG⁰ = λ, and the inverted region is defined as –ΔG⁰ = λ, where λ is the reorganization energy of the reaction. The existence of the inverted region, where the ET rate constant decreases as the reaction becomes more exoergic (i.e., as ΔG⁰ becomes more negative), has been confirmed experimentally.^1,2 The inverted region behavior has also been experimentally observed for proton transfer (PT) reactions,^3-5 although the theoretical basis for these experimental observations has not been well understood.⁶ To our knowledge, the inverted region behavior has not yet been experimentally observed for proton-coupled electron transfer (PCET) reactions, in which an electron and proton transfer simultaneously with no stable intermediate.^7-9 The objectives of this Letter are to elucidate the fundamental differences in the driving force dependence of the rate constants for ET, PT, and PCET and to identify the experimental conditions that could lead to observation of inverted region behavior for PT and PCET.

Our analysis is based on the following form of the rate constant for a vibronically nonadiabatic charge transfer reaction:^9-11

$$k=\sum _{\mu }{P}_{\mu }\sum _{\nu }\frac{V_{\mu \nu }^2}{\hslash }\sqrt{\frac{\pi }{\lambda k_{\mathrm{B}}T}}\exp \left[-\frac{{(\Delta G^0+\lambda +{\epsilon }_{\nu }-{\epsilon }_{\mu })}^2}{4\lambda k_{\mathrm{B}}T}\right]$$ (1)

where P_μ is the Boltzmann probability for the reactant state μ and V_μν is the nonadiabatic coupling between the reactant and product vibronic states μ and ν with vibrational energies ε_μ and ε_ν relative to their ground states. In the vibronically nonadiabatic limit, V_μψ ⪡ k_BT and the solvent timescale is much faster than the timescale associated with the nonadiabatic transitions.

For PCET reactions, typically the proton transfer is electronically nonadiabatic (i.e., the proton tunneling timescale is much faster than the electronic transition timescale). In this case, the vibronic coupling is the product of the electronic coupling V^el and the overlap integral S_μν between the reactant and product proton vibrational wavefunctions:^9,12,13

$$V_{\mu \nu }=V^{\mathrm{el}}{S}_{\mu \nu }.$$ (2)

For nonadiabatic ET reactions that are coupled to intramolecular vibrational quantum modes, the rate constant is also given by Eq. (1) with the vibronic coupling of the form in Eq. (2).¹¹

In general, vibronically nonadiabatic PT reactions could be either electronically adiabatic or electronically nonadiabatic. The form of the rate constant in Eq. (1) is valid for both cases, but the form of the vibronic coupling will correspond to Eq. (2) for the electronically nonadiabatic case and to a tunneling matrix element for the electronically adiabatic case.¹⁴ The latter case is related to hydrogen atom transfer reactions, which may be viewed as vibronically nonadiabatic PCET reactions in which the proton transfer is electronically adiabatic.¹³ Note that PT reactions could also be completely adiabatic, where the system remains in the ground electronic and vibrational states throughout the reaction. In this case, the rate constant is given by a standard transition state theory expression modified to account for the zero point energy of the transferring proton.¹⁵

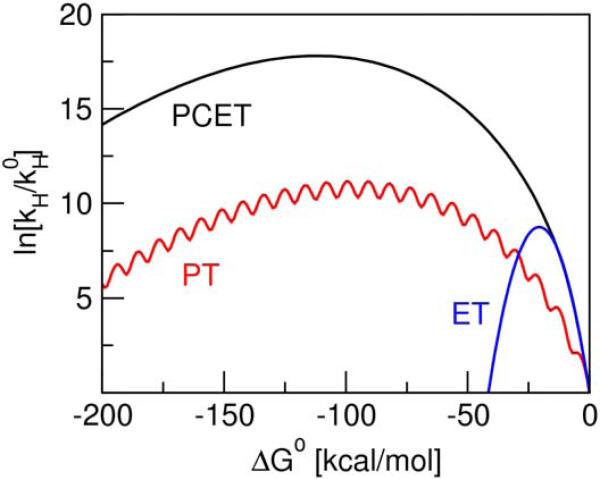
We investigated model systems corresponding to vibronically nonadiabatic ET, PT, and PCET. In the first set of calculations, we assumed that the proton transfer reaction was electronically nonadiabatic, so the vibronic coupling was of the form given in Eq. (2). The solvent reorganization energy was chosen to be 20 kcal/mol for ET and PCET and 5 kcal/mol for PT. For simplicity, the vibrational modes were represented by harmonic potentials with the minima for the reactant and product states separated by δx. The frequency of the proton vibrational mode was chosen to be 3000 cm⁻¹ with δx = 0.5 Å for both PT and PCET, and the frequency of the intramolecular solute mode was chosen to be 400 cm⁻¹ with δx = 0.1 Å for ET. The dependence of the rate constant on the driving force for these three models is depicted in Figure 1. The ET model exhibits the typical inverted region behavior with a maximum corresponding to –ΔG⁰ = λ =20 kcal/mol. The PCET and PT models exhibit significant asymmetry with a substantial shift in the maximum,¹⁶ resulting in maxima at ΔG⁰ ≈ –125 kcal/mol and –100 kcal/mol for PCET and PT, respectively. Thus, observation of the inverted region behavior is predicted to be experimentally inaccessible for the PCET and PT models.

Figure 1.

Driving force dependence of the nonadiabatic rate constant for the PCET (black), PT (red), and ET (blue) models. In the PCET model, λ = 20 kcal/mol, ω = 3000 cm⁻¹, and δx = 0.5 Å. In the PT model, λ = 5 kcal/mol, ω = 3000 cm⁻¹, and δx = 0.5 Å. In the ET model, λ = 20 kcal/mol, ω = 400 cm⁻¹, and δx = 0.1 Å. The reduced mass of the vibrational mode is 1 amu for PCET and PT and 10 amu for ET. The proton transfer is assumed to be electronically nonadiabatic for all models. The temperature is 300 K, and $k_H^0$ is the rate constant for ΔG⁰ = 0.

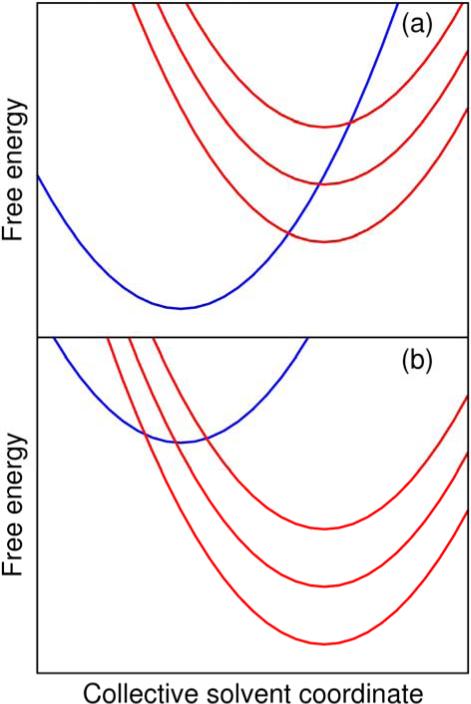
The free energy dependence of the rate constants can be understood by analysis of the contributions to the expression given in Eq. (1). The free energy curves along the collective solvent coordinate for the PCET model with two different driving forces are illustrated in Figure 2. The free energy curves corresponding to the ground reactant and the ground and first two excited product vibronic states are depicted. The relative contributions of the pairs of reactant/product vibronic states to the overall rate constant are determined primarily by a balance between the free energy barrier, ΔG^‡ = (ΔG⁰ + λ ε_ν – ε_μ)²/4λ, and the vibronic coupling V_μν.⁹ The Boltzmann probability for the reactant state is also relevant when excited reactant states are considered, but for simplicity we consider only the ground reactant vibronic state in this analysis, although the excited reactant states are included in the calculations. In the normal Marcus region, where –ΔG⁰ < λ, the free energy barrier is lowest for the ground product vibronic state, but in the inverted Marcus region, the free energy barrier becomes lowest for an excited product vibronic state.

Figure 2.

The free energy as a function of the collective solvent coordinate generated for the PCET model using standard Marcus theory for (a) ΔG⁰ = 10 kcal/mol, corresponding to the normal Marcus region with –ΔG⁰ < λ, and (b) ΔG⁰ = –30 kcal/mol, corresponding to the inverted Marcus region with –ΔG⁰ > λ.

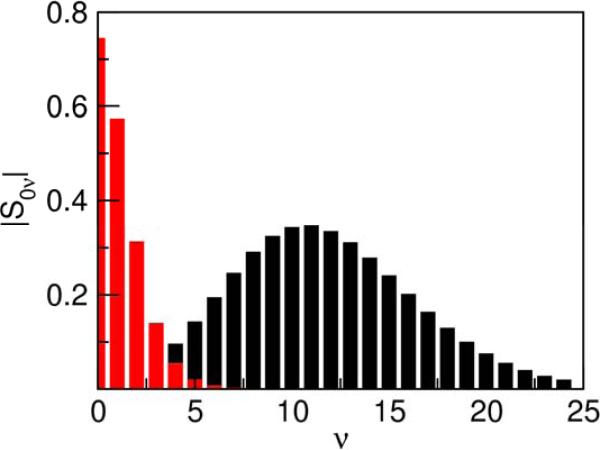
In general, the vibronic coupling varies significantly for different pairs of reactant/product vibronic states due to differences in the overlap integrals. Figure 3 depicts the dependence of the overlap integral on the vibrational quantum number of the product state for the ET and PCET models. For the ET model, the overlap integral decreases monotonically as the vibrational quantum number of the product state increases because of partial destructive interference effects arising from the nodal structure of the excited vibrational states. As a result, the ET rate constant decreases as ΔG⁰ becomes more negative because the dominant product state corresponds to a higher vibrational quantum number with smaller vibronic coupling. The participation of such a vibrational quantum mode in ET has been found to lead to asymmetry and shifting of the maximum in the driving force dependence.¹¹ For the PCET and PT models, however, initially the overlap increases as the vibrational quantum number of the product state increases because the overlap integral is dominated by the tails of the vibrational wavefunctions, and the excited proton vibrational wavefunctions are more delocalized. For highly excited states, the oscillations of the proton vibrational wavefunctions lead to cancellation effects that result in a decrease in the overlap integral, as in the ET model. Due to this behavior of the overlap integrals, the PCET and PT rate constants continue to increase as –ΔG⁰ becomes greater than λ because the excited product states with greater vibronic coupling become accessible. Eventually the rate constant decreases when the vibronic coupling decreases for highly exoergic reactions.

Figure 3.

Overlap integral between the reactant and product proton vibrational wavefunctions as a function of the product state quantum number ν for the PCET (black) and ET (red) models. All overlap integrals correspond to the ground reactant vibronic state. Note that these overlap integrals for harmonic oscillators behave as a Poisson distribution.

The qualitatively different behavior that arises for PT and PCET compared to ET is due to the higher frequency of the proton and the larger shift between the reactant and product proton vibrational wavefunctions. To further analyze the relative significance of these properties, we performed calculations for different combinations of the vibrational frequency ω and shift δx. For ω = 400 cm⁻¹ and δx = 0.5 Å, the free energy dependence of the rate constant is very similar to that for the ET model. For ω = 3000 cm⁻¹ and δx = 0.1 Å, the curve is much more asymmetric than that for the ET model, but the maximum is still at –ΔG⁰ ≈ λ. These figures are provided in Supporting Information. Thus, the combination of a high vibrational frequency and a relatively large shift leads to the qualitative driving force dependence depicted in Figure 1 for the PT and PCET models.

We also investigated the impact of other vibrational modes on the free energy dependence of the PCET and PT rates. We performed calculations with two uncoupled quantum modes, where one mode is the proton and the second mode is either another dimension of the proton motion or another intramolecular mode. The second mode was assigned a frequency of ω = 400 cm⁻¹ and a shift of δx = 0.1 Å. The resulting free energy dependence of the rate constant is virtually indistinguishable from that of the original model with only the proton vibrational mode because the overlap integrals between the ground reactant and excited product vibrational states of the second mode are very small, so these excited states do not contribute significantly to the overall rate constant. Thus, the driving force dependence is dominated by the high-frequency mode and is not significantly affected by the inclusion of additional low-frequency modes. In addition, we analyzed the rate constant expressions that include the proton donor-acceptor motion^9,17 and determined that the inclusion of this mode should not impact the qualitative driving force dependence of the rate constant.

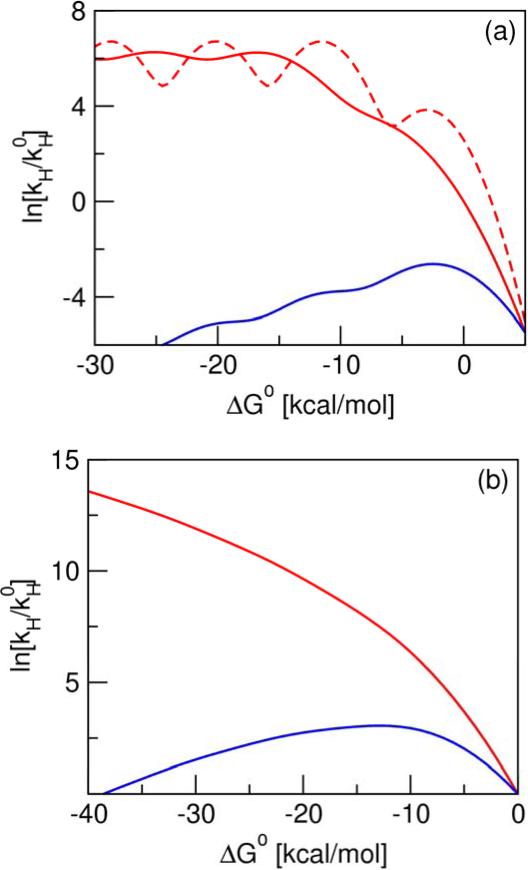
Since many PT reactions are electronically adiabatic, we also investigated the free energy dependence of the PT rate constant in this regime. For the proton vibrational states below the barrier of the electronically adiabatic proton potential, the vibronic coupling is a tunneling matrix element that can be estimated using the semiclassical expression for tunneling through a parabolic barrier.¹⁸ For the proton vibrational states above the barrier, the vibronic coupling can be estimated as half of the splitting between the adiabatic vibrational energy levels.¹⁹ As shown in Figure 4a, the driving force dependence of the rate constant for this type of electronically adiabatic PT model exhibits a plateau as ΔG⁰ becomes more negative because the coupling becomes virtually constant for the excited vibrational states. The oscillations exhibited in Figures 1 and 4a for the PT models are due to the relatively small reorganization energy for PT. These oscillations arise from effects that occur when the dominant product state is changing from state ν to state ν+1 as ΔG⁰ becomes more negative. When the width $\sqrt{2\lambda k_{\mathrm{B}}T}$ of the Gaussian term in Eq. (1) is smaller than the splitting between adjacent vibrational energy levels, the driving force dependence of the total rate constant exhibits oscillations with a period that is approximately equal to the vibrational energy level splitting. As illustrated in Figure 4a, the amplitude of these oscillations increases as the reorganization energy decreases.

Figure 4.

Driving force dependence of the rate constant for (a) electronically adiabatic PT and (b) PCET models. In the electronically adiabatic PT model, ω = 3000 cm⁻¹, and the proton transfer barrier frequency and height are 2500 cm⁻¹ and 7 kcal/mol, respectively. The reorganization energy is λ = 8 kcal/mol for the two solid curves and λ = 3 kcal/mol for the dashed curve. In this model, the red curves correspond to a fixed proton transfer barrier, and the blue curve corresponds to the increase of the barrier as a function of ΔG⁰ with a slope of 0.6667, leading to an increase in the barrier height from 7 kcal/mol to 25 kcal/mol for the range of ΔG⁰ shown here. In both cases, the vibronic coupling for vibrational states above the barrier was estimated as half the splitting between the third and fourth vibrational states for the fixed barrier. In the PCET model, λ = 20 kcal/mol, ω = 3000 cm⁻¹, and δx = 0.5 Å. In this model, the red curve corresponds to a fixed proton donor-acceptor distance, and the blue curve corresponds to the increase of this distance as a function of ΔG⁰ with a slope of 0.00714 Å (kcal/mol)⁻¹, leading to an increase in δx from 0.5 Å to 0.8 Å for the range of ΔG⁰ shown here. The temperature is 300 K for all models, and $k_H^0$ is the rate constant for ΔG⁰ = 0 for the PT model with fixed barrier and λ = 8 kcal/mol in (a) and for both PCET models in (b).

As mentioned above, the inverted region behavior has been observed experimentally for PT reactions.^3-5 This discrepancy between theory and experiment has been denoted a “conundrum” in the literature.⁶ The calculations presented above also suggest that the inverted region behavior is not expected to be observed experimentally for vibronically nonadiabatic PT in either the electronically adiabatic or electronically nonadiabatic regime. For reasons discussed above, the inclusion of the three-dimensional motion of the transferring proton, low-frequency intramolecular modes, or the proton donor-acceptor mode is not expected to impact the qualitative driving force dependence of the PT rate constant. If the additional modes are strongly coupled to the proton vibrational mode, however, multidimensional tunneling effects could potentially impact the driving force dependence. Moreover, additional modes corresponding to substantial geometrical changes associated with high frequencies and large shifts between the reactant and product states could impact the relative weightings of the pairs of reactant/product vibronic states and thus the driving force dependence. In general, PT reactions could be completely adiabatic in the normal region, and the conversion to the nonadiabatic regime or to alternative mechanisms in the inverted region could lead to a decrease in the overall rate constant.

One possibility is that the experiments could be probing one of the oscillations observed in the PT curves of Figures 1 and 4a. This explanation could apply to the experimental data on PT within benzophenone/aniline contact radical ion pairs in a series of different solvents.^4-6 In this case, the inverted region behavior is observed experimentally for rates that typically vary by only a factor of ~2 over a relatively small range of driving forces. Moreover, the inverted region behavior is observed for nonpolar solvents corresponding to lower solvent reorganization energies but is not observed for polar solvents corresponding to higher solvent reorganization energies.^4,5 These experimental data are consistent with Figure 4a, which illustrates that the amplitude of the theoretically predicted oscillations is larger for lower solvent reorganization energies. According to the theoretical calculations, the oscillations may not be experimentally observable for highly polar solvents. Furthermore, the maximum of the first oscillation will occur at a more negative value of ΔG⁰ for higher solvent reorganization energies. In contrast, the more pronounced inverted region behavior observed experimentally in Ref. 3 for rates that vary by more than two orders of magnitude over a range of driving forces spanning ~10 kcal/mol does not appear to be consistent with the theoretically predicted period and amplitude of these oscillations, particularly because these PT reactions were studied in a polar solvent.

An alternative explanation for the experimentally observed inverted region behavior in PT reactions is that the driving force is varied in a manner that also impacts another property of the system, such as the proton donor-acceptor distance or vibrational frequency, the proton vibrational frequencies, or the electronic coupling. This explanation could apply to the experimental data on PT between acids and diphenylmethyl carbanion in dimethylformamide studied in Ref. 3. In this case, the driving force is varied by altering the pK_a values of the proton donor for a fixed proton acceptor. As discussed in the literature,^20,21 ΔpK_a, the difference in pK_a values between the proton donor and acceptor, is strongly correlated with the hydrogen bond length and energy. Specifically, the proton donor-acceptor distance is expected to increase as the magnitude of ΔpK_a increases (i.e., as ΔG⁰ becomes more negative for the series of complexes studied in Ref. 3). This effect can be incorporated into the electronically adiabatic PT model by increasing the intrinsic proton transfer barrier, which depends strongly on the proton donor-acceptor distance, as ΔG⁰ becomes more negative. As depicted in Figure 4a, this modified PT model clearly exhibits inverted region behavior. Similarly, this effect can be incorporated into the electronically nonadiabatic PT and PCET models by increasing the proton donor-acceptor distance as ΔG⁰ becomes more negative. Figure 4b illustrates that this modified PCET model also exhibits inverted region behavior. In these models, initially the rate increases as ΔG⁰ becomes more negative, despite the increase in the proton donor-acceptor distance, but eventually the increasing donor-acceptor distance causes the rate to decrease. Thus, the inverted region behavior could be observed experimentally for both PT and PCET systems if the driving force is varied in a manner that also impacts the properties of the proton transfer interface. In contrast to PT and PCET, varying the driving force experimentally for ET reactions is not expected to significantly impact the overlap integrals corresponding to the intramolecular vibrational modes or the electronic coupling.

The calculations in this Letter elucidate the underlying physical principles dictating the driving force dependence of the rate constants for ET, PT, and PCET reactions and predict the experimental conditions that could lead to observation of inverted region behavior for PT and PCET. The driving force dependence of the rate constant is qualitatively different for PT and PCET than for ET because the overlap integrals corresponding to excited vibronic states initially increase for PT and PCET but decrease monotonically for ET. This difference in the overlap integrals is due to a combination of the higher proton vibrational frequency and the larger shift between the reactant and product proton vibrational wavefunctions. As a result, these types of theories predict that the inverted region behavior will not be experimentally accessible for PT and PCET reactions if only the driving force is varied. The experiments measuring inverted region behavior for PT over a limited range of rates and driving forces could be probing an oscillation arising from the relatively small reorganization energy. Another plausible explanation for the experimentally observed inverted region behavior for PT is that varying the driving force also impacts other properties of the system, such as the proton donor-acceptor distance. The analysis presented in this Letter suggests that this possibility should be considered when the inverted region behavior is observed experimentally for PT or PCET reactions.