RECENT IMPROVEMENTS IN SMALL ANGLE X-RAY DIFFRACTION FOR THE STUDY OF MUSCLE PHYSIOLOGY

Abstract

The molecular mechanism of muscle contraction is one of the most important unresolved problems in Biology and Biophysics. Notwithstanding the great advances of recent years, it is not yet known in detail how the molecular motor in muscle, the class II myosin, converts the free energy of ATP hydrolysis into work by interacting with its track, the actin filament, neither it is understood how the high efficiency in energy conversion depends on the cooperative action of myosin motors working in parallel along the actin filament. Researches in muscle contraction imply the combination of mechanical, biochemical and structural methods in studies that span from tissue to single molecule. Therefore, more than for any other research field, progresses in the comprehension of muscle contraction at molecular level are related to, and in turn contribute to, the advancement of methods in Biophysics.

This review will focus on the progresses achieved by time resolved small angle X-ray scattering (SAXS) from muscle, an approach made possible by the highly ordered arrangement of both the contractile proteins myosin and actin in the ca 2 μm long structural unit the sarcomere that repeats along the whole length of the muscle cell. Among the time resolved structural techniques, SAXS has proved to be the most powerful method of investigation, as it allows the molecular motor to be studied in situ, in intact single muscle cells, where it is possible to combine the structural study with fast mechanical methods that synchronize the action of the molecular motors. The latest development of this technique allows Angstrom-scale measurements of the axial movement of the motors that pull the actin filament toward the centre of the sarcomere, by exploiting the X-ray interference between the two arrays of myosin motors in the two halves of the sarcomere.

1. INTRODUCTION

Force and shortening in muscle are driven by cyclical interaction of the “head” portion of the molecular motor myosin II, extending from the myosin filament, with the actin filament. During the attachment to actin, the myosin head undergoes a structural working stroke that drives the actin filament towards the centre of the myosin filament. In skeletal and cardiac muscle, myosin and actin are organized in well-ordered and parallel arrays of filaments, the sarcomere, that constitutes the structural and functional unit of muscle. The myosin filament overlaps with the actin filament originating from the Z line bounding the sarcomere. The parallel and series arrangement of sarcomeres accounts for the macroscopic force and shortening of the muscle. An array of ca 300 motors work cooperatively in each half-sarcomere, and thus the structure-function relation of the motor cannot be fully described at single molecule level but only preserving the integrity of the sarcomere. The necessity to preserve the sarcomeric structure and to extend the time resolution of mechanical measurements to the submillisecond range, appropriate to the kinetics of the myosin motor, makes the single fibre from the skeletal muscle the best preparation for these studies. In the single fibre, information on the size and kinetics of the acto-myosin interaction can be obtained by synchronisation of the action of the molecular motors by means of length or force step perturbation, controlled at the level of the sarcomere. The combination of sarcomere mechanics with the small angle X-ray scattering from single muscle fibres has allowed the description of Angstrom-scale movement and submillisecond kinetics of the molecular motor in muscle.

2. STRUCTURAL AND MECHANICAL BACKGROUND

2.1 The structural unit: the sarcomere

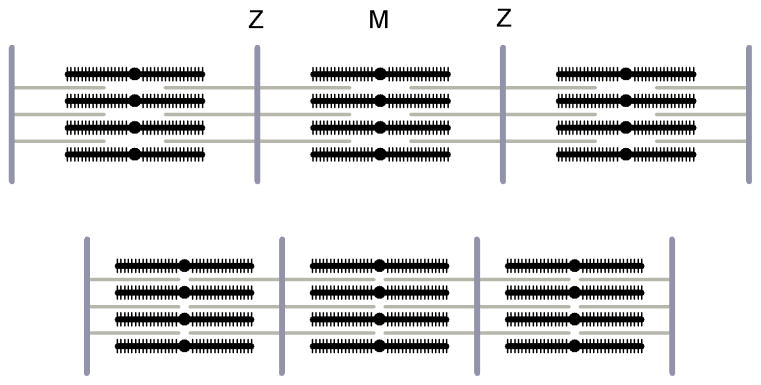
The skeletal muscle is made up of elongated cells, also called muscle fibres, 20–200 μm in diameter and running the length of the muscle. The contractile material in the fibre is arranged in bundles of filaments called myofibrils, with a diameter of about 1 μm (figure 1,a). The myofibrils are constituted by parallel arrays of thin actin containing and thick myosin-containing filaments (figure 1,b). The structural unit of the contractile machinery, the sarcomere, is delimited at its ends by the Z-line, which holds the thin filaments in a regular lateral array. The actin filaments extend from the Z-line for ca 1.0 μm and partially overlap with the myosin filaments placed on the centre of the sarcomere and about 1.6 μm long. The length of the sarcomere varies with the degree of overlap between the myosin and actin filaments, and it is about 2.2 μm in the muscle at rest. The centre of the sarcomere is crossed by the M-line, a structure that connects each thick filament with its neighbours. The sarcomeres are in register across the myofibrils, giving the whole fibre a striated appearance when observed under the optical microscope.

Figure 1.

a. Levels of structural organization in a typical vertebrate skeletal muscle. The muscle consists in bundles of long, cylindrical fibres, each fibre is a muscle cell. Each fibre contains a bundle of cylindrical myofibrils, mainly composed by the contractile proteins. The contractile proteins are organized in filaments arranged into repeating units, the sarcomeres. b. Longitudinal section of frog sartorious muscle, as seen by electron microscopy, together with the diagram showing the overlapping actin (gray) and myosin (black) filaments (adapted from H.E. Huxley, 1972). c. Scheme of the cross section of a sarcomere in the overlap region, with myosin (black) and actin (gray) filaments arranged on regular hexagonal arrays. The elementary cell contains one myosin filament and two actin filaments. The crystallographic planes 1,0 and 1,1 are also indicated. The interplanary distances are $d(1,0)=\sqrt{3}·d(1,1)$.

As revealed by electron microscopy (EM) on transversal section of the fibre, the actin and myosin filaments are arranged inside the myofibrils on a hexagonal lattice, formed by the 2D repeat of an elementary cell containing one myosin filament and two actin filaments (figure 1,c). The side of the cell is ca 40 nm at 2.2 μm sarcomere length (Matsubara and Elliott 1972) and reduces when the sarcomere length is increased, to keep constant the volume of the sarcomere.

2.2 The contractile proteins

Force and shortening are generated at the molecular level by the globular portion of the motor protein myosin II that extends from the thick filament and forms the “cross bridge” with the actin filament.

The myosin molecule is a dimer with molecular weight (MW) ca 520,000 (figure 2,a) and consists of two heavy chains (MW 220,000), each composed by a 150-nm “tail” and a globular “head” at one end, and two pairs of light chains (each light chain with MW 20,000). The myosin molecule can be split by proteolytic enzymes into various fragments. Digestion by trypsin results in two fragments, the light meromyosin (LMM), made of most of the tail, and the heavy meromyosin (HMM), that contains the two heads. Digestion by papain produces a further split of HMM into three subfragments: two S1 portions, the heads, and a rod-like S2 portion.

Figure 2.

a. Schematic diagram of the myosin molecule, with flexible link between LMM and HMM and between S2 and S1 subfragments. The LMM is about 90 nm long. The S2 portion of HMM is about 60 nm and links the two S1 “heads”.

b. Arrangement of the myosin molecules to form the thick filament. The bare zone is indicated, where the LMM “tails” arrange antiparallel and leave the region free of myosin heads.

The ca 95 nm-long LMM part of the myosin molecules interact to form the backbone of the thick filament. The thick filament is bipolar: on each half of the thick filament, the end of the tail of the myosin molecules points toward the centre of the sarcomere. As a consequence of this antiparallel arrangement of the molecules in the two halves of the thick filament, a region of ca 160 nm in the centre of the filament, called the bare zone, is free of heads (figure 2,b).

For each myosin molecule the two heads project from the backbone of the filament. The myosin heads are arranged around the backbone in a crown-like appearance of three pairs of heads, with an axial repeat of 14.3 nm and a rotation of 40° between successive crowns (figure 3,a). With this arrangement, the pairs of heads form a three-stranded helix with a pitch of 14.3×3=42.9 nm.

Figure 3.

a. Diagram showing the arrangement of myosin heads on the myosin filament in vertebrate striated muscle. The myosin heads (black) emerge axially from the thick filament (gray) as crown of three pairs with 14.5 nm periodicity. In each crown the pairs of heads are separated azimuthally by 120° and adjacent crowns are rotated by 40°, forming a three stranded helix with period ca 43 nm (dotted lines). b. Helical symmetry of the actin filament. Successive monomers can be arranged on two primitive helices (black lines). The right handed helix has a pitch of 5.1 nm and the left handed helix has a pitch of 5.9 nm. The overall appearance is of two interwining helices with a pitch of ca 37.5 nm. The gray dashed line marks one of the two long helix.

The S2 rod shows some degree of flexibility (Elliott and Offer 1978) and also the head can swing freely about its junction with the S2 rod (the head-rod junction), this allows a wide range of movement of the head relative to the filament backbone.

Actin is a globular protein with MW about 42,000. In the thin filament the actin monomers, separated by p_A=2.73 nm, arrange on two genetic helices, a right-handed helix with pitch p_RH about 5.1 nm and a left-handed helix with pitch p_LH about 5.9 nm. These give the filament the overall appearance of a two-stranded right-handed helix, with a pitch P of ca 37.5 nm (figure 3,b). The values of p_A and P can be determined from the pitches of the two primitive helices according to the the relations: 1/p_A=1/p_RH+1/p_LH and 1/P=1/p_RH−1/p_LH (Squire 1981). Thin filaments interacting with a solution of HMM moieties in the absence of adenosine triphosphate (ATP) become HMM labeled. In these “decorated” thin filaments, all myosin heads point in the same direction, giving an appearance of arrowheads that reveals a polarity of the thin filament (Huxley 1963). Decorated thin filaments still attached to either sides of the Z-line show that the thin filaments have opposite polarity across the Z-line, with arrowheads pointing away from the Z line.

2.3 Regulatory proteins

In the resting muscle, the interaction of myosin with actin is inhibited by the regulatory proteins tropomyosin and troponin. Tropomyosin is a filamentous protein ca 40 nm long, which runs along the actin filament and binds to seven actin monomers on each of the two long-pitch actin helices. Tropomyosin is bound to its end by troponin, which repeats along the thin filament with a periodicity of 38.5 nm (figure 4; Ebashi et al 1969). Depolarisation of the plasmalemma (surface membrane) of the muscle cell initiates a series of events that end with the release of Ca⁺⁺ from the sarcoplasmic reticulus. Ca⁺⁺ binds to troponin, inducing a conformational change, which causes a shift in the position of tropomyosin along the actin filament to uncover the sites of actin for the interaction with myosin.

Figure 4.

Schematic drawn of the thin filament. Tropomyosin molecules (black strip) run in the groove between the two actin helices (white spheres), and bind to seven actin monomers on each helix. At one end of tropomyosin binds a troponin molecule (gray).

2.4 Mechanics and energetics of muscle contraction

Muscle contraction is induced by the excitation of the muscle fibre that consists in the rapid depolarization of the plasmalemma. In nature, excitation is produced by the action potential that originates at the neuromuscular junction under the control of the nerve cell. In experimental conditions, the excitation of muscle cells is produced by electrical stimulations with current pulses. A single current pulse induces a transitory increase in force, called twitch, which then decays in a few tens of milliseconds. In isometric conditions, the mechanical responses to repeated stimuli add up, increasing the force developed. If the frequency of stimulation reaches the fusion frequency, the force response, called tetanus, attains a maximum steady value, T₀. For the skeletal muscle of the frog at 4°C the fusion frequency is about 20 Hz, and increases for higher temperatures. If a load lower than the force T₀ is applied on the fibre, the fibre shortens at constant velocity (isotonic contraction); the velocity is higher the lower the force, and attains a maximum value when the force is zero. The force-velocity relation (Hill 1938) is the basic active property of muscle.

Shortening is due to the relative sliding of the two sets of actin and myosin filaments in the region of overlap in each sarcomere, while the length of the filaments remains constant (figure 5; Huxley and Hanson 1954; Huxley and Niedergerke 1954). The driving force for shortening is generated by the cyclic interaction of myosin heads with the actin filament. The force exerted on actin is proportional to the number of cross-bridges acting in parallel in each half-sarcomere that represents the functional unit for force generation. Accordingly, increasing the sarcomere length above full overlap (> 2.2 μm) reduces the isometric tetanic force as the number of cross-bridges reduces (Gordon et al 1966). The generation of force by the myosin cross-bridge is attributed to a structural working stroke in the myosin head that pulls the actin filaments toward the centre of the sarcomere. Due to the bipolar nature of the sarcomere, the actin filaments attached on opposite Z-lines are driven toward the centre of the myosin filament, with consequent shortening of the sarcomere.

Figure 5.

Diagram to show the change in overlap of the thick (black) and thin (gray) filament with changing sarcomere length (between Z lines), according to the sliding filaments theory. The length of the filaments remain constant as they slide past each other.

The work produced in an actin-myosin interaction is accounted for by the hydrolysis of one molecule of ATP in the myosin head (Lymn and Taylor 1971). In the muscle in physiological conditions, the energy released by the hydrolysis of ATP is ca 10⁻¹⁹ J/molecule.

According to the force-velocity relation, during muscle contraction the rate of work production, the power, is zero in the isometric contraction, when the shortening velocity is zero, and rises to a maximum for isotonic contractions at intermediate loads. The power reduces at high velocity, to become again zero when the force is zero. During contraction the rate of heat production by the muscle rises two orders of magnitude above the resting level (Hill and Hartree 1920); the rate of heat production increases even more if the muscle shortens and produces power. Thus, the rate of energy liberation by a contracting muscle increases with increase in shortening velocity (Fenn effect; Fenn 1923) and this is explained by a corresponding increase in rate of ATP splitting (Kushmerick and Davies 1969). Another fundamental property of active muscle is that the efficiency of energy conversion varies with the load and has a maximum (ca 0.5) in the region of high loads (Hill 1964; Woledge 1973)

The forces of the half-sarcomeres working in parallel in the cross section of the fibre add up to attain the macroscopic force exerted by the muscle during an isometric contraction (ca 300 kN·m⁻² or kPa at 4°C). In principle, by scaling down this figure for the number of thick filaments in the cross section of the fibre and for the number of myosin heads in each half-thick filament it would be possible to calculate the force exerted by the single head. The length of the myosin filament covered by the heads is about 700 nm: since every 14.3 nm there is a crown of six heads, on each half-thick filament there are about 50 crowns and 300 heads. The cross sectional density of myosin filament is about 5·10¹⁴ m⁻² (Mobley and Eisenberg 1975), thus the force per half-thick filament is 3·10⁵ N·m⁻²/5·10¹⁴ m⁻² = 6·10⁻¹⁰ N. If all the heads were attached and bearing force, then force per head would be 6·10⁻¹⁰ N/3·10² = 2 pN. However, since the heads go through a cycle of attachment and detachment, they spend only a fraction of the cycle attached to actin and bearing force. This fraction is called the duty ratio (r) and its value coincides with the fraction of heads that are attached at each given time. The value of r for the skeletal muscle myosin is still under debate, though it is a fundamental parameter for mechanical and biochemical characterisation of the acto-myosin interaction. If the fraction of interacting heads is 0.2 as indicated by spectroscopic studies (Cooke et al 1982; Corrie et al 1999) then force per attached head will be five times larger than the value given above, i.e. ca 10 pN.

To investigate the mechanism of force production in muscle, the action of the attached heads can be synchronised by applying a step perturbation (100 μs duration) in length or force on an otherwise isometrically contracting fibre. Huxley and Simmons (1971) pioneered the technique using length step controlled at the sarcomere length level and recording the force with a capacitance force transducer fast enough to resolve the fast components of the force transient. Because the sarcomere is symmetric about its centre, and each set of myosin heads would have experienced local filament sliding of half the sarcomere shortening, the length changes of the fibre are conventionally expressed in units of nanometers per half-sarcomere (nm/hs). The force transient elicited by a step release consists of a decrease of force synchronous with the length step (phase 1; figure 6), which is the response of the undamped elasticity of the attached myosin heads and of the myofilaments. In single muscle fibre of Rana temporaria force drops to zero for a release of about 5 nm/hs that represents the strain in the undamped elasticity of the sarcomere at T₀. Following the release, force recovers towards the isometric value with a complex time course. The quick component of force recovery (phase 2) is complete in 1–2 ms and is the mechanical manifestation of the working stroke by the myosin heads that have been unloaded. In phase 2, force recovers almost completely for releases up to 5 nm/hs, while for larger releases the force recovery progressively reduces and becomes zero for releases larger than 12 nm/hs. This latter value is therefore considered the amplitude of the unloaded working stroke. The subsequent phases of the force transient (phase 3 and phase 4) are related to detachment of the perturbed heads and substitution by freshly attached heads that bring the force to the original isometric value.

Figure 6.

Force transient response in muscle fibre upon length step perturbation. Upper trace: length change at the level of the half-sarcomere, the length step is imposed on the otherwise isometrically contracting fibre. Middle trace: force response, with indicated the various phases (1–4) of the force transient, as described in par. 2.4. Lower trace: baseline for force. (Frog muscle; adapted from A.F. Huxley 1974).

3. THE MOLECULAR MECHANISM OF FORCE GENERATION

3.1 The tilting head model

The cross-bridges were first observed in electron micrographs of muscle in rigor as connections between the actin and myosin filaments (Huxley 1957). The rigor state can be experimentally induced in a demembranated fibre by depletion of ATP, a condition that occurs in nature post mortem, and implies that all the myosin heads are bound to actin in a conformation that corresponds to the end of the working stroke. The discovery of the cross-bridges as linkages between the thick and the thin filaments immediately led to the conclusion that if they are responsible for force and filaments sliding, then their action must be a cyclic process, since the cross-bridges are too short to account for the length changes that may occur in the sarcomere when the muscle shortens.

The first evidence in support of the hypothesis of a working stroke in the myosin head while attached to actin was obtained in early electron microscope and X-ray diffraction studies in insect flight muscle (Reedy et al 1965), which established that in resting muscle the myosin heads stick out at right angles from the myosin filament, while in rigor they form an angle of 45° with the filament axis, with the end that is attached to actin closer to the centre of the myosin filament.

In 1969, H.E. Huxley suggested that the conformational changes for the attached heads consisted in a rotation of the S1 head about its attachment on the actin filament (figure 7). The force and/or displacement generated by the rotation of the S1 would then be transmitted to the backbone of the thick filament through the S2 rod. The flexible linkage between HMM and S2 and between S2 and S1 allow for a wide range of movement of S1 which justify the observed independence of the force from the transverse distance between filaments. The “tilting head” model is consistent with the different orientation of cross-bridges observed with EM between rest and rigor state, and was later supported by in vivo X-ray diffraction studies (Huxley et al 1981; Irving et al 1992).

Figure 7.

The tilting head model originally proposed by Huxley 1969. The myosin head S1 is linked to the filament backbone through the S2 rod-like portion of the molecule. The S1 attaches to the actin filament (a, left S1) and undergoes a rotational movement (b, left S1) that pulls actin filament toward the centre of the myosin filament. Meantime, other molecules which have already rotated (a, right S1) detach to start the cycle again (b, right S1). (From H.E. Huxley 1969).

However, this model was challenged by structural studies with spectroscopic probes (Cooke et al 1982), which showed that most of the head does not move when attached to actin. The apparent contradiction has been solved with the definition of crystallographic model of the myosin head, which suggests that the working stroke is due to an inter-domain movement inside S1, rather than changes at the interface between S1 and actin.

3.2 The crystallographic structure and the tilting lever arm model

The definition in the early 90’s of the structure of actin and myosin at atomic level by protein crystallography has been a major breakthrough in the understanding of the molecular mechanism of muscle contraction.

The crystallographic structure of the actin monomer, G actin, showed that it is composed of four globular sub-domains (Kabsch and Holmes 1990). The crystallographic model of the G actin combined with lower resolution information obtained by X-ray diffraction of actin filaments, F actin, allowed the arrangement of the monomers in the filament to be determined (Holmes et al 1990).

The crystallographic structure of the S1 subfragment of the myosin molecule, isolated from skeletal muscle of chicken, was determined in 1993 (Rayment et al 1993a). In vitro motility experiments had demonstrated that the myosin head (the S1 subfragment) is the site of the motor capacity of the myosin molecule (Toyoshima et al 1987). Thus, the crystallographic structure of myosin S1 has been the first high-resolution structure of a molecular motor to be solved.

The crystal structure of the myosin head showed that it is composed of a globular portion (motor domain or catalytic domain, CD; figure 8) that binds to actin and hydrolyses ATP, and a 9 nm-long α-helix that binds the myosin light chains (light chain domain, LCD; figure 8).

Figure 8.

Ribbon representation of the subfragment S1 of the myosin molecule. Data from the crystallized S1 molecule in absence of ATP and the products of ATP hydrolysis (nucleotide-free). The catalytic domain (CD) and the light chain domain (LCD) are indicated. (From Rayment et al 1993.)

The helical segment ends with a hook that connects the head with the S2 portion of the molecule, the head-rod junction.

This suggested that while the CD firmly attaches to actin, the LCD acts as a lever arm that amplifies an inter-domain movement in the converter region at the base of the lever (tilting lever arm model). The S1 structure solved by Rayment and coworkers was nucleotide-free, which should correspond to the conformation the myosin head has in the rigor state, when the products of the hydrolysis of ATP have been released and the head is firmly attached to actin in a conformation that corresponds to the end of the working stroke.

The high resolution structure of the myosin head was then fit in the three-dimensional reconstruction of the actomyosin complex obtained by EM of actin filaments decorated with myosin heads in rigor and was found that the crystallographic model of the myosin head could fit reasonably well into the electron density of the actin-attached myosin head, with the CD attached to actin and the LCD pointing Z ward (Rayment et al 1993b).

The first direct evidence for the mechanism of the tilting lever arm was provided by combined cryo-EM of actin decorated with vertebrate smooth muscle S1 (Whittaker et al 1995) showing that upon release of ADP (adenosine diphosphate) the lever arm domain rotates by ca 20° resulting in 3.0–3.5 nm axial displacement at the distal end of the lever arm. A model for the conformation of the lever arm at the beginning of the working stroke was provided by crystal structure of a construct of smooth muscle myosin motor domain (a truncated S1 without part of the lever arm region) with a transition state analog ADP·AlF₄⁻ (Dominguez et al 1998). In this structure, the converter domain is rotated by 70° relative to the nucleotide-free skeletal S1 (figure 9). By propagating this tilting to the lever arm in the whole S1, a potential working stroke of about 10 nm was found, consistent with the values determined with fast mechanical experiments in vivo (Huxley and Simmons 1971).

Figure 9.

Atomic model for the working stroke. Gray spheres represents monomers of the actin filament; myosin head is shown in ribbon representation in both the nucleotide-free, or rigor, conformation (left) and in the adenosine triphosphate (ADP)AlF₄⁻ conformation (right). In the two conformations the catalytic domains (CD, residues 1–707) are made to coincide. The orientation of the light chain domain in the ADP AlF₄⁻ structure was determined by assuming that the converter-light chain domain (LCD), residues 711–843) moves as a rigid body about residue 707. The white circles between CD and LCD identify the position of the converter domain (residues 711–781) in the two conformations. (Adapted from Irving et al 2000).

The lever arm model predicts that the step size and thus the sliding velocity depend linearly on the length of the lever arm. Direct support for this view came from the finding that the sliding velocity of fluorescently labeled actin filaments in in vitro assays depends on the length of the lever arm, changed by using mutant myosins (Uyeda et al 1996). By extrapolating the relation between the length of the lever arm and the sliding velocity to zero speed it was possible to determine the position of the fulcrum, which coincided with the converter domain, as predicted by the crystallographic model.

4. SMALL ANGLE X-RAY SCATTERING STUDIES OF MUSCLE

The function of muscle myosin in the native system depends on the interaction between its conformational changes and force or movement exerted on the actin filament, and this cannot be reproduced in crystallographic studies. The quasi-crystalline arrangement of the motor proteins in the three-dimensional lattice of a muscle makes it possible to use small-angle X-ray scattering (SAXS) to investigate the conformational changes in the myosin motor, at a lower spatial resolution than that of crystallography, but in the unperturbed sarcomeric arrangement. Among other structural techniques, only fluorescence spectroscopy allows the structural dynamics of motor proteins to be recorded in situ. However, to provide spectroscopic probes at the right position in the motor it is necessary to use demembranated fibres and in this preparation the sarcomeric order is poorly maintained during mechanical responses, making the application of fast mechanical methods difficult.

In most of the X-ray studies on muscle the preparation is the whole skeletal muscle dissected from the frog hind limb, usually the sartorius muscle, which can be easily kept alive for hours after dissection and has been extensively used in the past physiological studies. Once dissected, the muscle is kept in a solution with ionic composition and pH similar to the extracellular medium. Muscle is composed of water for 80% of its weight and the contractile structure, made by proteins, has a weak diffraction power. Thus, a high X-ray flux is needed to collect enough photons in the X-ray pattern. Before the use of the synchrotron sources, several hours of exposure time were needed to collect a good quality pattern from the whole muscle. This prevented time-resolved studies on the time scale of the myosin motor kinetics. The availability of the synchrotron sources for muscle studies in the early 80’s (for a review see Holmes and Rosenbaum 1998) and the parallel development of suitable detectors, made it possible to attain the time resolution adequate to follow structural events during muscle contraction.

Further increase in intensity and fine focusing of the beam obtained with the advent of third-generation synchrotrons, opened the possibility to further enhance the time and spatial resolution and to apply the method to the single muscle fibre. This preparation is a 100 times weaker diffractor than the whole muscle but allows the structural study to be combined with fast mechanics controlled at the sarcomere level and thus follow the structural dynamics of the molecular motors synchronized by step perturbations in length or force.

4.1 The muscle at rest

Pioneering studies (Huxley and Brown, 1967 and reference therein) have characterised the 2D X-ray diffraction pattern from the skeletal muscle of frog in different physiological conditions up to 0.2 nm⁻¹ in the reciprocal space.

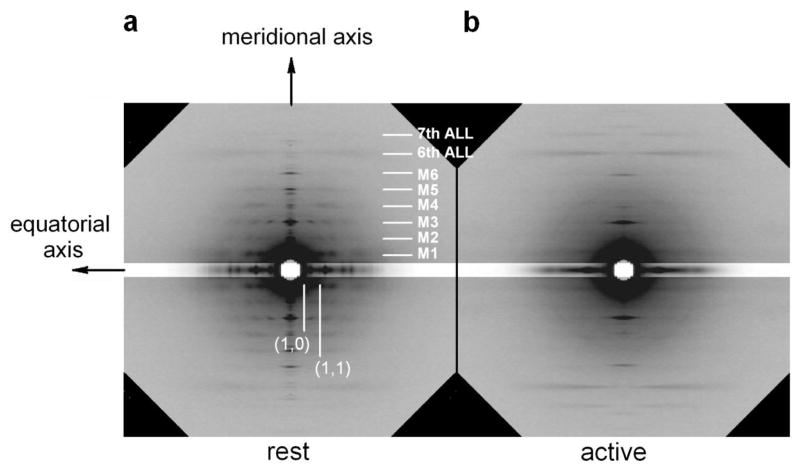
The diffraction pattern from muscle can be divided into four quadrants, separated by two axes of symmetry: the meridional axis, parallel to the fibre axis, and the equatorial axis, perpendicular to the fibre axis (figure 10,a).

Figure 10.

Diffraction pattern from frog fibre at rest (a.) and during an isometric contraction (b.) In a are indicated the meridional and the equatorial axis, parallel and perpendicular to the fibre axis respectively. The white marks indicate the position of the meridional myosin-based reflections (M series), and of the actin-based layer lines (6^th and 7^th ALL). The equatorial reflection (1,0) and (1,1) are also indicated. The equatorial bands shown in the patterns have the intensity reduced to 1/3, to avoid saturation in the figure. Patterns collected at the ID2A beamline (ESRF synchrotron; Boesecke et al 1995) on the FReLoN CCD detector. Fibre dissected from the tibialis anterior muscle of Rana temporaria (4°C, 2.2 μm s.l.). The exposure time is 120 ms for each pattern.

The most prominent feature of the small-angle X-ray pattern from the muscle at rest is a series of regularly spaced layer-lines arising from a periodicity of ca 42.9 nm, consisting of both a component on the meridional axis and an off-meridional component, running parallel to the equatorial axis. These layer-lines come from the quasi-helicoidal repeat of the myosin heads on the myosin filament and are commonly referred to as M1, M2, M3 … according to their order.

In particular, the first-order layer line M1 at 42.9 nm has a strong off-meridional component, signaling the pitch of the helical arrangement of the myosin heads, and the third order M3 at 14.3 nm has the most prominent component on the meridional axis, signaling the axial repeat of the heads. These features combined with the estimate of the density of myosin molecules along the thick filament (Knight et al 1986) lead to the conclusion that crowns of three myosin pairs project from the filament every 14.3 nm, with a rotation of 40° between successive crowns, forming a the three-stranded helix (Squire 1974; see par. 2.2).

However, from a structure with a regular subunit repeat of 14.3 nm within a 42.9 nm helical repeat, only reflections that index to orders of 14.3 nm (M3, M6, M9 …) are expected to appear on the meridional axis.

The presence of the “forbidden” reflections (M1, M2, M4, M5…) from the resting muscle should indicate systematic perturbations in the 14.34 nm axial repeat of the myosin heads (Yagi et al 1981; Squire 1981; Malinchik and Lednev 1992). Models proposed to explain the presence of the forbidden reflections have the common feature that the myosin crowns are grouped in triplets: each triplet of crowns is separated by 42.9 nm from the next, and the crowns within each triplet are separated by less than 14.3 nm.

The meridional reflections are quite sharply localised across the meridional pattern, with a cross-meridional width that fades to zero at about ±1/400 nm⁻¹ in the reciprocal space, indicating that the myosin filaments at rest are in register for an extent of about 400 nm across the muscle fibres.

The M3 reflection at rest shows also a strong sampling across the meridional axis, with the off-meridional peaks at a position corresponding to the interplanary distance between the myosin filaments, as marked by the (1,0) equatorial reflection (see below).

Layer-lines reflections indexing on a ca 38 nm helicoidal repeat originate from the two-stranded actin helix (par. 2.2). Of these, the most prominent are at 5.9 nm and at 5.1 nm, the pitch of the two primitive helices. The meridional component of the 2.73 nm actin-based reflection marks the axial repeat of the actin monomers along the filament.

Other reflections, which do not index at either the myosin or the actin repeat, have been observed on the meridional axis. Of these, a pair of reflections at 44.2 and 41.8 nm that have been associated to the protein C (Rome et al 1973a), which binds to the myosin filament with a function still to be fully clarified (Moos et al 1975; Moos and Feng 1980; Squire et al 2003). Another pair of reflections at 38.3 and 39.5 nm likely originating from the troponin repeat along the actin filament (Rome et al 1973b).

The equatorial axis is dominated by two reflections at spacing of about 35 nm and 20 nm. They arise respectively from the (1,0) and (1,1) crystallographic planes of the hexagonal lattice on which the myosin filaments are arranged (figure 1,c). The intensity of the (1,0) reflection, I_1,0, is 2.5 times higher than the intensity of the (1,1) reflection, I_1,1. The I_1,1 is enhanced by the increase in overlap with the actin filaments, and the ratio I_1,0/I_1,1 depends on the relative mass of the two sets of overlapping filaments.

4.2 The active muscle

During an isometric contraction (figure 10,b), the off-meridian myosin-based layer-lines weaken indicating a disordering of the helicoidal arrangement of the myosin heads. This is the consequence of actin-myosin interaction and force generation. The forbidden reflections on the meridional axis disappear too, and only the M3 and its higher orders remain strong, indicating the formation of a regular axial repeat. The spacing of the repeat increases to 14.57 nm, ca 1.5% higher than in the resting muscle. Such a large change is one order of magnitude larger than that expected from the elastic property of the thick filament (see below) and can be explained only by structural changes in the filament. The ca 1.5% increase in spacing of myosin-based reflections produced by the activation and force development going from the rest to the isometric contraction is not a general feature for all the types of muscle: in insect flight muscle, the periodicity of the M3 reflection is ca 14.57 nm both at rest and during contraction. For a comparative summary on this point see Tregear et al 1984.

The radial width of the reflection increases upon activation. Once corrected for the size of the beam, the radial width is twofold the value at rest. Moreover, sampling of the M3 along the radial direction is lost. The increase of the cross-meridional width indicates that the coherent diffractor responsible for the reflection is reduced in size, that is the myosin filaments are no longer in register during contraction. Since the radial width increases with force, the misalignment of the filaments is thought to be induced by the force exerted on them. As a consequence of the misalignment, the M3 layer-line is no longer sampled across the meridional axis. To make the total intensity of the reflection at rest and during isometric contraction comparable, it is necessary to correct for the loss of register, estimated by the increase in radial width. To compare the intensities, they should be multiplied by a factor proportional to the radial width of the reflection (Huxley et al 1982).

The weakening of the off-meridional M1 reflection allows the detection of the actin-based layer-line at 37 nm (Bordas 1993), which at rest is masked by the higher intensity of M1.

The actin-based layer-lines at 5.1 and 5.9 nm, as well as the meridional 2.73 nm, increase their intensity upon activation by a factor of about 2, indicating the transfer of mass from the myosin filament to actin, as a consequence of the myosin heads attachment to the actin monomers (Huxley and Brown 1967).

The intensity of the equatorial (1,0) reflection decreases and the intensity of (1,1) increases also as a consequence of the radial transfer of mass of myosin toward the actin filament, the intensity ratio I_1,0/I_1,1 is inverted relative to the resting value, becoming 0.8.

4.3 The phase problem

The intensity distribution in the X-ray diffraction pattern is the squared amplitude of the Fourier Transform (FT) of the electron density of the sample. As proteins are mainly formed by light atoms, the electron density of muscle fibres is approximately proportional to their mass density.

In particular, the myosin-based meridional reflections originate from the myosin heads that repeat along the myosin filament. An array of N repeating mass distribution with a periodicity d will give an intensity distribution of scattered light along the meridional axis described by the equation:

$$I(R)\propto F^2(R){\left[\frac{sin(N\pi Rd)}{sin(\pi Rd)}\right]}^2$$ (1)

where R is the coordinate in the reciprocal space and the term F²(R) is the squared amplitude of the Fourier transform (FT) of the axial mass density of the repeating structure, which modulates the amplitude of the peaks described by the Laue function (sin(NπRd)/sin(πRd); Vainshtein, 1966). Changes in d would change the positions of the intensity peaks, while a change in its axial mass density would change the way the peak intensities are modulated.

X-ray detectors cannot record the electric field but only the diffracted intensity, which is proportional to the squared value of the field, and thus the phase information of the FT is lost in the diffraction pattern. This prevents the application of Fourier synthesis to the spatial distribution of the electric field and so to determine directly the structure of the sample. The lack of phase information is a problem shared with crystallographic methods. Even with this limitation, SAXS is a powerful method for studying the structural dynamics of muscle motor in situ, by integrating the information from other approaches, such as EM or protein crystallography. In the next paragraphs it will be described how it has been possible to partially recover the phase information, either using specific mechanical protocols or the X-ray interference between the mirror structures inside the sarcomere.

4.4 The structural dynamics of muscle myosin at low spatial resolution

The changes in the X-ray patterns from muscle in different states give general support to the cross-bridge theory, but do not provide conclusive evidence that some kind of axial movement of attached cross-bridges produces the relative sliding of actin and myosin filaments. In the isometric contraction, since the cross-bridge cycle occurs asynchronously, the signals from their ensemble will only give information on their average conformation during the cycle.

Mechanical experiments have shown that rapid length perturbation imposed on an otherwise isometrically contracting fibre can be used to synchronise the cross-bridge action, and that the force transient that follows has a rapid component, complete within 1–2 ms, that is the mechanical manifestation of the execution of the working stroke by the myosin heads attached to actin (Huxley and Simmons 1971; see 2.4). During the working stroke, according to the tilting head model, which was postulated to consist in a rotation of the head, the mass density of the heads along the meridional axis should change. Consequently, the intensity of the myosin-based meridional reflections, and in particular the strong M3 reflection, should change as predicted by eq. (1) where the term F(R) represents the FT of the axial mass density of the heads.

This effect is complete within the time of the quick force recovery following a release, thus the time of exposure must be in the millisecond time scale and conventional X-ray sources cannot provide enough photons in the reflections of interest. With the intense light from synchrotron radiation made available in 1980 the key experiment was actually carried out for the first time on the whole sartorius muscle of the frog (Huxley et al 1981). These experiments showed that the intensity of the M3 meridional reflection reduces following a ca 1% shortening in muscle length and that the observed decrease lags the fall in force by about 0.5 ms. Since the M3 reflection originates directly from the axial repeat of the myosin heads, the intensity decrease indicated an increased spread of the mass density of the heads along the filament axis as a consequence of the mechanical perturbation. This evidence was the first experimental support for the idea that tilting of the head drives filament sliding.

Though the whole muscle diffracts ca 100 times stronger than the single fibre, there is a series of factors that limit the possibility to apply fast mechanical perturbations, such as the higher mass and the compliance of tendon attachments. Moreover, different fibres within the same muscle can have different time courses of activation and force development and a different kinetic of the response to mechanical perturbations. Only in single muscle fibres it is possible to apply length step under sarcomere length control.

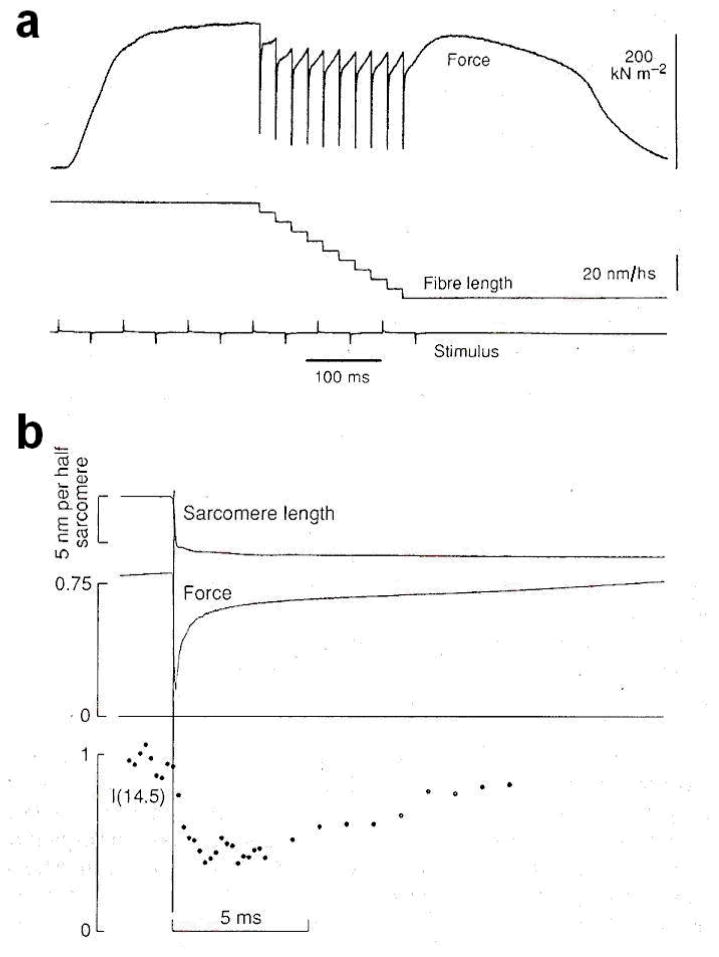
The X-ray investigation on the structural working stroke in single fibres has started about ten years later (Irving et al 1992). Measurements of I_M3 from the single fibre with the submillisecond time resolution, necessary to resolve the structural changes accompanying the quick recovery of force, became feasible thanks to brighter X-ray beams available at the British synchrotron source SRS (Synchrotron Radiation Source, Daresbury, U.K.). Increase of signal to noise ratio for such a short exposure was obtained by signal averaging during the same phases over cycles of step perturbations repeated at intervals long enough to allow the complete repriming of the ability to execute the working stroke (Lombardi et al 1992). Step releases complete in 120 μs were applied to a single muscle fibre and the intensity of the M3 reflection (I_M3) was monitored with a proportional counter gas-filled detector (Towns-Andrew et al 1989) at 200 μs time resolution (figure 11).

Figure 11.

Changes in force and intensity of the 14.5 nm X-ray reflection resulting from a staircase length change in an active single muscle fibre. a. Records of force and length changes with slow time base. The 10 shortening steps, each complete in 120 μs and resulting in filament sliding of about 6 nm/hs, are repeated at 20 ms interval. The lower line marks the time the electrical stimuli are delivered. b. Fast time base records of sarcomere length, force response and intensity of the M3 reflection, I(14.5), showing the average response to 6 nm/hs steps in a series of 10 steps at 20 ms interval, as in a. The sarcomere length and force traces are averaged from five fibres. Intensity data are recorded at 0.2 ms time frame during the length step and the rapid force recovery, and at 1 ms time frame during the slower force recovery to the isometric value. The vertical line marks the midpoint of the length step. Sarcomere length is monitored by a Striation Follower (Huxley et al 1981). Force is normalized to the isometric value and intensity is normalized to its value before the step. From Irving et al 1992.

The results showed that for a 6 nm/hs release I_M3 doesn’t change during the length step itself while the force decreases to ca 0.25 T₀ (phase 1 of Huxley and Simmons transients, 1971). In the next 2 ms, I_M3 decreases by ca 50% while the force recovers to 0.8 T₀ (phase 2), as actin-attached myosin heads execute their working stroke.

This behaviour shows that the axial movement of the myosin heads, that spreads their axial mass density, reducing the I_M3, does not passively follow changes in force but is associated with active force generation. Following the elementary force recovery process, as the heads detach and reattach farther along the actin filament, I_M3 recovers the value before the step, with a half-time of about 8 ms. This is similar to the half-time for the repriming of the capacity to repeat the working stroke determined with mechanics (Lombardi et al 1992). Thus, the tilting of the heads is synchronous with the mechanical manifestation of the working stroke and the recovery of a tilt closer to the perpendicular to the filament axis tracks the subsequent detachment-attachment responsible for the repriming process.

4.5 The orientation of the lever arm in isometric contraction

Even if the intensity of the M3 reflection lacks phase information, the previous experiments suggest that myosin heads in the isometric contraction preceding the step has the main axis oriented near the perpendicular to the filament axis. This hypothesis can be tested by extending the mechanical protocol to step stretches. The force transient elicited by a step stretch is composed of the elastic increase in force during the step itself (phase 1) followed by a quick recovery that within the first 4 ms is mainly determined by the reversal of the working stroke elicited by the stretch (phase 2; Piazzesi et al 1997). The behaviour of I_M3 is not symmetric for step releases and step stretches. As seen above, I_M3 does not change in phase 1 for a release of 6 nm/hs. Following smaller releases (ca 2 nm/hs), I_M3 does not change or slightly increases both in phase 1 and in phase 2 (Piazzesi et al 1995). On the contrary, I_M3 sharply decreases also in phase 1 following stretches (Lombardi et al 1995).

However, when a stretch to the original length of the fibre is applied 1 ms after a release, I_M3 increases (figure 13; Irving et al 2000). When a small shortening step is followed 1 ms later by another shortening step, I_M3 shows no change in response to the first step, but decreases during both phase 1 and 2 response after the second step (Irving et al 2000).

Figure 13.

Changes in force and intensity of the M3 reflection, I_M3, produced by a ca 6 nm/hs shortening step followed after 1 ms by a stretch during active contraction. a. Superimposed slow time base force records in the presence and absence of the 40 length changes cycles imposed at 50 ms intervals. Changes in length (b.) and force (c.) in the same fibre as panel a, sampled at 10 μs intervals, and I_M3 (d., filled circles, 100 μs time windows) averaged from 402 tetani in 14 fibres. I_M3 is normalised for the average value before the shortening step. (Adapted from Irving et al 2000.)

All these results can be interpreted by using the crystallographic model of the head with the assumption that the CD of the myosin head is rigidly attached to the actin and the LCD tilts about a fulcrum in the converter domain (residue 707) during both the elastic response and the working stroke response. The tilt produces an axial displacement (Δz) of the tip of the lever arm, the head-rod junction (residue 843), with respect to the CD, and a change in the axial mass distribution of the head.

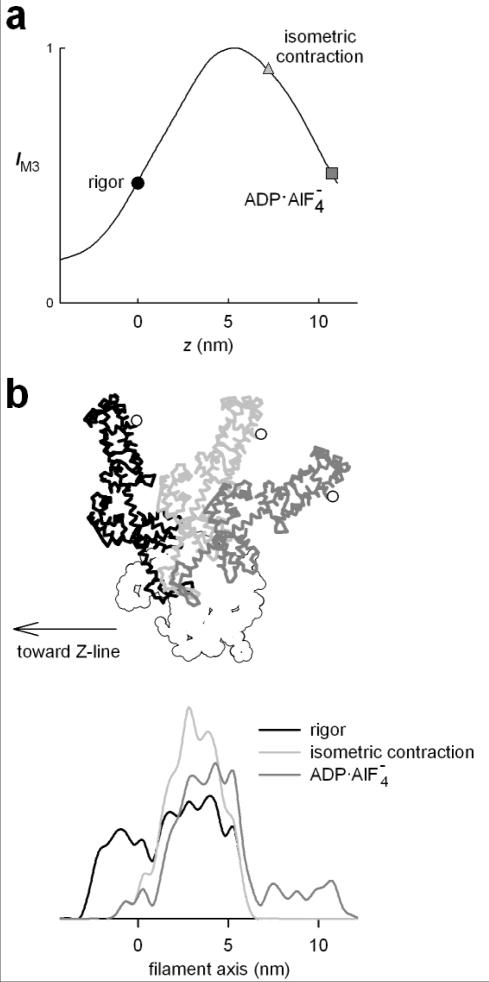
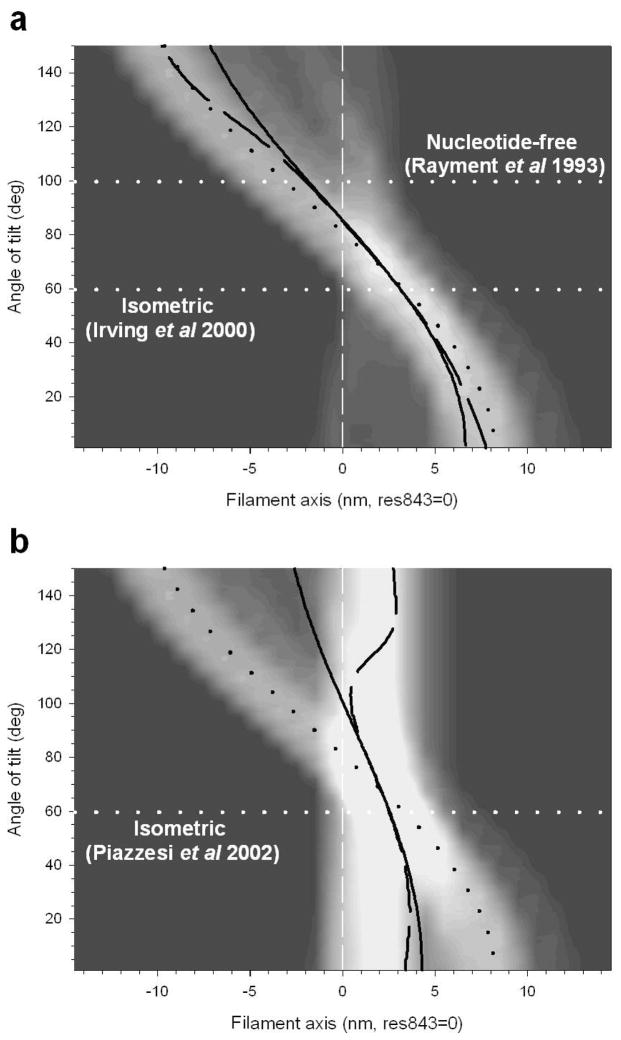
The solid line in figure 12,a shows the relation between I_M3 and Δz predicted by the model. The rigor conformation (Rayment et al 1993b) is taken as the origin for the axial displacement (Δz=0). For any Δz, I_M3 has been calculated as the value at 1/14.5 nm⁻¹ of the FT of the axial mass density of the head conformation, and it has been normalised by its maximum value, reached for Δz=5 nm. The circle represents I_M3 predicted for the rigor conformation, and the square at Δz=10 nm represents the ADP·AlF₄⁻ conformation, assumed to correspond to the beginning of the working stroke (Dominguez et al 1998). The changes in I_M3 produced by step releases and stretches reported above are consistent with the model if Δz is 7 nm during the isometric contraction (Irving et al 2000; figure 12, triangle). I_M3 stays almost constant during phase 1 of a large shortening step or during either phase 1 or phase 2 of a smaller shortening, because Δz is decreasing from 7 nm, across the maximum of the I_M3: Δz relation. I_M3 decreases during phase 2 after a large release step or during phase 1 of a second release imposed 1 ms after a conditioning release, because Δz has been moved to the ascending limb of the I_M3: Δz relation. Application of a stretch from the isometric state increases Δz from 7 nm, on the descending limb of the I_M3: Δz relation, so I_M3 decreases during both phase 1 and phase 2 responses to a stretch. If the stretch is imposed 1 ms after a 6 nm release (figure 13) phase 1 of the stretch response is on the ascending limb of the I_M3: Δz relation, so I_M3 increases in phase 1, but there is little change in phase 2 because the final part of the change in Δz occurs in the plateau region.

Figure 12.

a. Relation between calculated intensity of the M3 reflection (I_M3) and Δz, the axial displacement of the tip of the lever arm from the position in the rigor conformation (black circle). Dark gray square and light gray triangle indicate the conformation of S1 with the ADP AlF₄⁻ compound and during isometric contraction respectively. (Adapted from Irving et al 2000). b. Model used to calculate the relation I_M3:Δz shown in a. The catalytic domain (white) is at fixed position and the light chain domain is oriented according to the three different conformations: rigor (black); isometric contraction (light gray); ADP AlF₄⁻ (dark gray). The white circle identifies the tip of the lever arm (residue 843). The lower traces show the axial mass density in the three conformations.

The I_M3 versus Δz curve in figure 12 has been calculated under the assumption that the myosin heads in all the crowns along the thick filament have the same orientation, but the shape of the curve is basically unchanged for a constant dispersion of a few nanometres (Irving et al 2000). Thus the critical assumption for the interpretation of the data is that the dispersion of the head orientation does not change during either phase 1 and phase 2 of the force transient, which is satisfied if, as supported by mechanical evidence (Lombardi et al 1992), the heads attached just before the length step remain attached during the force transient up to a few milliseconds after the step.

4.6 The compliance of the myofilaments

Originally the experiments on the force transient elicited by length step were interpreted assuming that the 4–5 nm/T₀ compliance of the half-sarcomere was located in the myosin molecule, either in the S2 region that connects the head to the myosin backbone (Huxley 1969) or in the myosin head itself, so that the working stroke was thought to stretch a compliant structure in the cross-bridge itself (Huxley and Simmons 1971; Ford et al 1981).

Subsequently, by precisely measuring the spacing of the actin-based and myosin-based X-ray reflections from frog muscle both at rest and during contraction or by stretching a contracting muscle it has been shown that a considerable amount of the half-sarcomere compliance is contributed by the myofilaments (Huxley et al 1994; Wakabayashi et al 1994). The actin compliance measured from the spacing changes of the relatively strong actin-based meridional reflection at 2.73 nm and of the 5.9 nm and 5.1 nm off meridional layer-lines is 0.2–0.3 %/T₀. One group (Wakabayashi et al 1994) reported also a difference in the spacing changes of the 2.73 nm and of the 5.1 nm and 5.9 nm layer-lines, which suggested that the right-handed primitive helix with 5.1 nm pitch untwists to a greater extent upon stretch. However, the overall change in the azimuthal angle of each monomer relative to its neighbors would be only 0.4° at most between rest and contraction.

The compliance of the myosin filament, unlike actin, cannot be deduced from the spacing changes which occur on the myosin-based reflections between rest and isometric contraction, because, as reported in par. 4.2, a major structural change of the myosin filament accompanies activation and isometric force development (Huxley and Brown 1967).

The compliance of the myosin filament can be reliably estimated by measuring the spacing changes accompanying length perturbation of the contracting muscle. The spacing change of the high order myosin-based reflection like M6 or M15 is 0.2–0.3%/T₀ (Huxley et al 1994; Wakabayashi et al 1994; Reconditi et al 2004). Higher order reflections are preferred to measure the compliance of the myosin filament because i) they are far from the center of the pattern, so that the relative errors on their position are smaller and ii) they mainly originate from the backbone of the filament rather than from the attached heads (Huxley et al 2003). In this respect it must be noted that the M3 reflection, that mainly originates from the myosin heads attached to both myosin and actin filament, will show spacing changes related to the strain in both myosin and actin filaments. In fact, depending on the mechanical protocol, changes in spacing of M3, S_M3, can be significantly different from those of M6, S_M6. In the length step experiments, S_M3 changes by 0.14%/T₀ from T₀ to T₁, while it changes by 0.34%/T₀ from T₀ to T₂ (Piazzesi et al 2002b). On the contrary, S_M6 changes are independent on the phase of the mechanical transients. In load step experiments, S_M6 changes by 0.26%/T₀ in each phase of the velocity transient (Reconditi et al 2004).

4.7 Distribution of force along the myofilaments

The force between actin and myosin filaments is generated by the cross-bridge. The force in a given point of a myosin or actin filament is the cumulative resultant of all the forces exerted by cross-bridges from the free end of the filament, where force and strain are zero, to that point. Each cross-bridge contributes equally, so that the cumulative force increases linearly and reaches the maximum in the bare zone of the myosin filament and at the end of the overlap region in the actin filament (figure 14; Linari et al 1998). In the overlap region both filaments experience on average half the maximum force.

Figure 14.

Distributed strain in the half-sarcomere. a. Schematic representation of the structure of the half-sarcomere at sarcomere length 2.1 μm. l_M, the length of the myosin filament, is 0.8 μm; ζ, the length of the overlap region, is 0.7 μm; l_A, the length of the actin filament from the Z line to the beginning of the bare zone, is 0.95 μm. b. Distribution of the force along the myosin and actin filament. (Adapted from Linari et al 1998.)

The signals of the actin-based X-ray reflections come from the whole actin filament (though enhanced in the overlap region by the mass of the heads attached), with the 300 nm segment from the Z line to the beginning of the overlap region bearing the maximum force T, and the 700 nm segment in the overlap region bearing an average force T/2. Thus, the average force in the whole actin filament is (0.3 T + 0.7 T/2 =) 0.65T (Wakabayashi et al 1994; Linari et al 1998). The observed 0.2–0.3%/T₀ spacing change of the actin-based layer lines must be scaled for the average force in the filament, and indicates a compliance of the actin filaments of 0.31–0.46%/T₀.

The structure of the myosin filament is more complex than the actin filament, and it is not known from what region of the filament the higher order myosin-based reflections come from. However, the bare zone is only ca 1/10 the length of the whole myosin filament, and the average force on the whole filament can be approximated to half the maximum force T. Thus, the observed 0.2–0.3%/T₀ spacing change of the myosin-based reflections indicates a compliance of 0.4–0.6%/T₀ for the myosin filaments.

By taking into account of the value of T₀ in standard units (3·10⁵ Nm⁻²) and of the density of actin and myosin filaments per cross-sectional area (10¹⁵ m⁻² and 5 10¹⁴ m⁻² respectively), these results indicate a compliance per unit length of 10–15 m/N/μm for actin and 7–10 m/N/μm for myosin.

The value found for the compliance of actin is consistent with the estimate from mechanical measurements on isolated actin filaments (Kojima et al 1994), where an actin filament is attached with one end to a calibrated microlever to measure both applied force and lengthening. In this way, it was found that the actin filament has a compliance per unit length of 23 m/N/μm and 15 m/N/μm with and without tropomyosin respectively.

Knowing the compliance of the myofilaments allows the contribution of the cross-bridges to the half-sarcomere stiffness to be calculated. This contribution is linearly related to the number of attached myosin heads. The value of the myofilament compliance is also indispensable to deduce the axial movements of the myosin heads for a given filament sliding at any value of force.

4.8 Estimate of cross-bridge compliance

Based on the formalism in Ford et al (1981), the half-sarcomere compliance may be derived from the compliances of the myofilaments and of the cross-bridges by the formula:

$$C_{\text{hs}}=c_{\text{A}}(l_{\text{A}}-\frac{2}{3}\zeta )+c_{\text{M}}(l_{\text{M}}-\frac{2}{3}\zeta )+\frac{1}{\beta K_{\text{c}}\zeta }$$ (2)

where C_hs is the compliance of the half-sarcomere; c_A and c_M are the compliance per unit length of the actin and myosin filaments respectively; β is the fraction of attached heads and K_C is the stiffness per unit length of the cross-bridges if all the heads were attached; l_A is the length of the actin filament, from the Z line to its end; l_M is the length of the myosin half-filament, from the M line to its end; ζ is the length of the overlap region. This formula is a good approximation when K_c(c_A+c_M) is small, and neglects minor contributions to the half-sarcomere compliance, such as that from the Z line. One can define the equivalent compliance of the actin and myosin filaments as C_eqA=c_A(l_A−2ζ/3) and C_eqM=c_M(l_M−2ζ/3), which represent the contribution of the filaments to the half-sarcomere compliance.

Thus by knowing the contribution of the myofilaments to the half-sarcomere compliance C_hs, from eq. (2) it is possible to obtain the contribution of the array of cross-bridges. Length step experiments allow C_hs to be measured either in rigor (C_hsrig), when all heads are attached (β=1, Cooke and Franks 1980), or during the isometric contraction (C_hs0). Then the fraction of the myosin heads attached during isometric contraction (β₀) can be determined by the equation:

$${\beta }_0=\frac{C_{\text{hsrigor}}-C_{\text{eqA}}-C_{\text{eqM}}}{C_{\text{hs}0}-C_{\text{eqA}}-C_{\text{eqM}}}$$ (3)

The figure for β₀ depends very critically on the estimates of the filament compliance. For fibres of Rana esculenta, Linari et al (1998) reported the value β₀=0.4, a value likely overestimated by the assumption of c_M=3 nm/T₀/μm for the myosin filament compliance. With the more reliable value of c_M=5 nm/T₀/μm (Wakabayashi et al 1994; Reconditi et al 2004) the fraction of attached heads is reduced to 0.2.

Mechanical experiments alone do not allow the compliance of the S1 or S2 fragment to be distinguished, since, from the mechanical point of view, what matters is the total compliance of the link between actin and myosin filaments.

SAXS experiments allow the structural source of the compliance to be discriminated. In fact, the intensity of the M3 reflection would change during elastic response elicited by a length step only if the step implies a change in the axial mass density as it occurs only if the compliance is in the myosin head. The experiments already reported on length step and with rapid sinusoidal oscillations in length (Lombardi et al 1995; Irving et al 2002; Dobbie et al 1998) have suggested that the larger part of the cross-bridge compliance resides in the S1 rather in the S2 subfragment.

The changes in I_M3 in these experiments can be simulated by using the crystallographic structure of S1 (Rayment et al 1993a). In this way, the intensity changes are found consistent with a structural model where the cross-bridge compliance is all due to a relative axial motion of the tip of the lever arm relative to the CD attached to actin, excluding any detectable contribution from the S2 region of the myosin molecule. However, the low resolution of the data obtained with SAXS from single fibres does not allow the origin of the compliance to be determined; it could be associated with rotation of the whole head on the actin monomer (Lombardi et al 1995), bending of the lever arm region, or distortion of a small region in the fulcrum of the lever arm (Dobbie et al 1998).

The changes in the I_M3 upon mechanical perturbations gave strong support to the tilting lever arm model, however they did not give a direct measure of the size and direction of the motion because I_M3 lacks the phase information. The direction of the tilt was obtained using mechanics: sliding of the filaments in the direction of shortening implies that the CD of the myosin head moves toward the centre of the sarcomere.

5. THE FINE STRUCTURE OF THE MYOSIN-BASED MERIDIONAL REFLECTIONS

5.1 Origin of the fine structure

When observed with a spatial resolution of ca 1000 nm (1/1000 nm⁻¹ in the reciprocal space), the myosin-based reflections along the meridional axis look finely sampled by a system of fringes (figure 15). To achieve the high spatial resolution required to observe the fine structure of these reflections, SAXS beamlines have developed finely focused beams and suitable detectors with a small point spread function (see Appendix A1).

Figure 15.

High spatial resolution 2D pattern from single fibre of frog at rest. The meridional reflections are sampled by the interference fringes. The 2D pattern has been mirrored and the intensity profile is obtained from integration between 1/100 nm⁻¹ on both side of the meridional axis. The myosin based meridional reflections are indicated. Exposure time 700 ms; fibre dissected from the tibialis anterior muscle of frog. The high spatial resolution is obtained thanks to the finely focused beam at BioCAT beamline (APS synchrotron; Irving et al 2000) and 65μm-PSF CCD detector (Phillips et al 2002).

The fine structure of the meridional reflections is produced by interference effects between diffraction from mirror structures in each half-sarcomere and seems to concern all the meridional reflections whatever their origin. For instance, the doublet at 39.5 and 38.3 nm originates from the actin filament (Huxley and Brown 1967), and has been later attributed to the repeat of troponin along the filament axis (Rome et al 1973b), which gives rise to a reflection sampled by interference effects across the Z line. The doublet at 44.2 and 41.8 nm has been associated with the periodicity of C-protein (Rome 1973a), which lies close to the central region of the thick filament. The split of the reflection is due to interference of the two arrays of C-protein across the M line. Haselgrove (1975) observed that in the pattern from the muscle at rest the M3 reflection at 14.3 nm and possibly the M2 reflection at 21.4 nm are sampled by interference effect of the two arrays of myosin heads on each half of the bipolar myosin filament.

How the X-ray interference of mirror structures in the sarcomere generates the sampling of the meridional reflections is explained here in relation to the myosin heads. As a first approximation, each crown of heads can be represented by a point diffractor, with its position coinciding with the centre of mass of the heads. In this approximation, the bipolar myosin filament can be thought as the convolution between the 49 point diffractors in each array and two points separated by the centre-to-centre distance between the two arrays (the interference distance).

Since the FT of the convolution of two structures is the product of the FT of each structure, the diffraction pattern from the 49 point diffractors on the two separate arrays would be the series of meridional reflections sampled by the interference fringes (figure 16).

Figure 16.

Schematic representation of the pattern produced by two arrays of point diffractors with periodicity d, separated by a centre-to-centre distance D. a. The double array can be seen as the convolution of the single array with two points separated by D. b. The intensity distribution from the two arrays (right, thicker line) is given by the product of the intensity distributions of a single array (left, black line) and the two points (middle, gray line). The n order of the interference fringes in the middle panel is the integer closest to D/d.

The 49 point array produces a diffracted intensity along the meridional axis, which is the square of the Laue function:

$$I(R)={\left[\frac{sin(N\pi Rd)}{sin(\pi Rd)}\right]}^2$$ (4)

where R is the reciprocal space coordinate and d is the repeat of the N diffractors (N=49 here). The width of each peak that rises at R=n/d (n=1, 2, 3…) is inversely proportional to N·d.

The two points separated by the interference distance D would produce an intensity distribution described by the equation (4) with N=2 and the repeat D:

$$I(R)={\left[\frac{sin(2\pi RD)}{sin(\pi RD)}\right]}^2\propto {cos}^2(\pi RD)$$ (5)

Thus, the total intensity distribution on the meridional axis produced by the two arrays of point diffractors would be:

$$I(R)\propto {\left[\frac{sin(N\pi Rd)}{sin(\pi Rd)}\right]}^2{cos}^2(\pi RD)$$ (6)

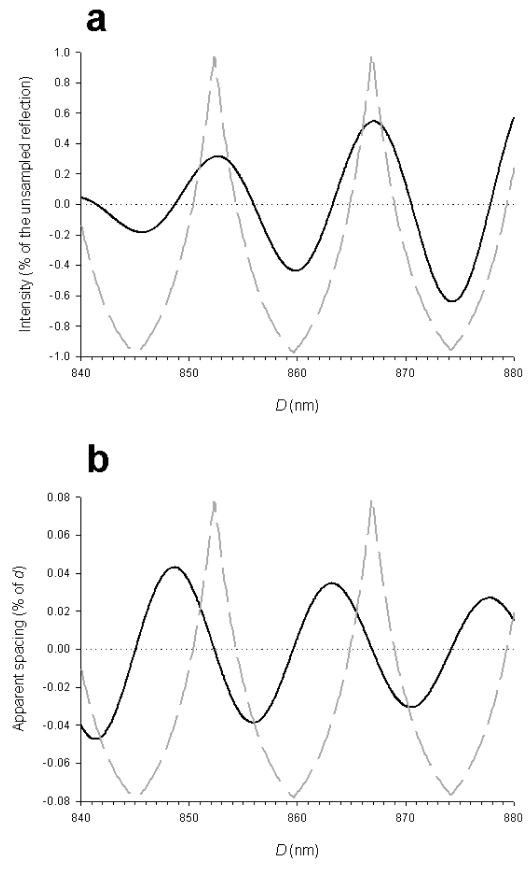
The interference fringes described by eq. (5) are narrower than the whole meridional reflections, described by eq. (5), by a factor 2D/Nd = 2.4. Thus, the interference fringes sample the meridional reflections by splitting them into two narrower peaks. To resolve the peaks the spatial resolution of the beam-detector system must be higher than 900 nm, which is the approximate value of the interference distance.

From eqs. (5) and (6) it follows that whenever D is an integer multiple of d, the reflection is sampled with a peak on its centre, because at the centre of the reflection Rd=1 and thus the argument of the cosine function is a multiple of π. If D is an odd multiple of d/2, then the centre of the reflection coincides with a minimum of the interference fringes and the two major sampling peaks have the same amplitude. It is easy to see that a change of the interference distance of ca 7.2 nm (d/2) would produce a dramatic effect on the interference fine structure of the M3 reflection, while a change of 14.34 nm (d) or its integral multiples will not produce a detectable change.

In principle, it would be easy to calculate the interference distance D from the spacing of the sampling peaks, by the relation:

$$D={(1/p_1-1/p_2)}^{-1}$$ (7)

where p₁ and p₂ are the spacing of the two sampling peaks. In practice, the envelope of the Laue function that describes the unsampled reflection moves the interference peaks close together (figure 16), so that eq. (7) gives an overestimate of the interference distance.

5.2 The fine structure of the forbidden reflections

A remarkable study on the interference sampling of the meridional pattern from frog muscle at rest was done by Malinchick and Lednev (1992). To account for the forbidden reflections, they proposed a model for the axial arrangement of the crowns of myosin heads along the filament. As seen before (par. 4.1), the presence of forbidden reflections suggests that the crowns of heads emerge in groups of three (triplets) with period 42.9 nm, in which each crown repeats a distance close but not equal to 14.3 nm (figure 17). In the X-ray patterns collected with a high spatial resolution (up to 0.02 nm⁻¹) by Malinchick and Lednev (1992) it was possible to resolve the position of the peaks that sample the forbidden reflections and to find that the distance between the peaks was consistent with an interference distance of about 705 nm. This is lower than the centre-to-centre distance between the two whole arrays of myosin heads, that is about (160+14.3·49=) 860 nm. This result suggested a model where the perturbation on the regular 14.3 nm repeat was not occupying the whole array but was concentrated in the proximal region of each array. A detailed simulation with one-dimensional model led to the conclusion that starting from the centre of the filament, the first 13 triplets (39 crowns) emerge with a spacing 42.9 nm between the central crown of each triplet and with a spacing inside the triplet of 13.1 nm, while the remaining 11 crowns outside the perturbation region are regularly separated by 14.3 nm. The perturbation region coincides approximately with the C-protein zone, and therefore it was suggested that the interaction between the myosin heads and the C-protein array could be responsible for the axial perturbation of the myosin periodicity. Upon activation, the forbidden reflections vanish because, as the heads leave the myosin filament to attach to actin, the interaction with the C-protein weakens and a regular 14.5 nm periodicity is assumed. The large spacing increase from 14.3 nm at rest to 14.5 nm during contraction still remains unsolved.

Figure 17.

Model for the heads arrangement on the myosin filament at rest. Each vertical bar represents the axial position of a crown of heads. a. On each half filament, starting from the bar zone, the first 39 crowns are grouped in triplets (black bars). The axiual distance between the centres of next triplets is 42.9 nm and the distance of next crown in each triplet is 13.1 nm. On the free end of the half filament, the crowns repeat with a regular spacing of 14.3 nm (gray bars). b. On the whole filament, the centre-to-centre distance between the two arrays of triplets is 704 nm. Bare zone is ca 160 nm. (Adapted from Malinchik and Lednev 1992).

5.3 Testing the nature of the fine structure in isometric contraction

The analysis of the fine structure of the meridional reflections reported above concern resting muscle. In fact, at that time technical limitations did not allow adequate time and spatial resolution for corresponding observations in contracting muscle.

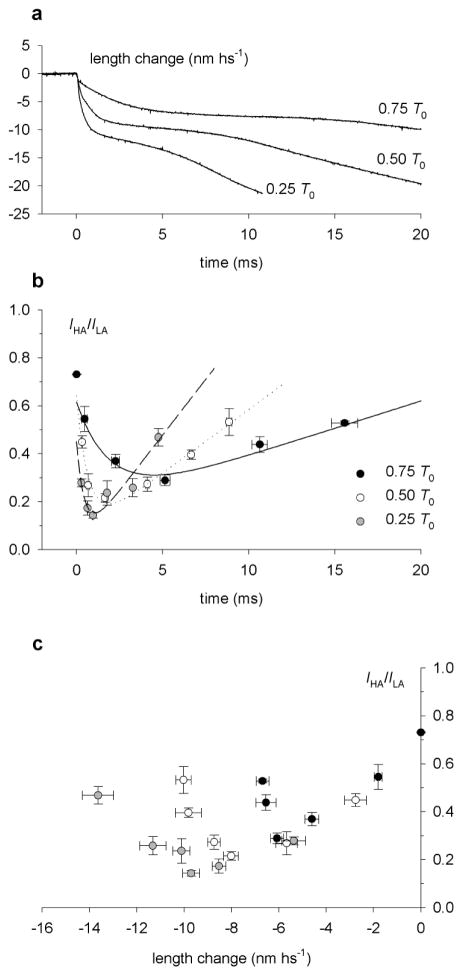
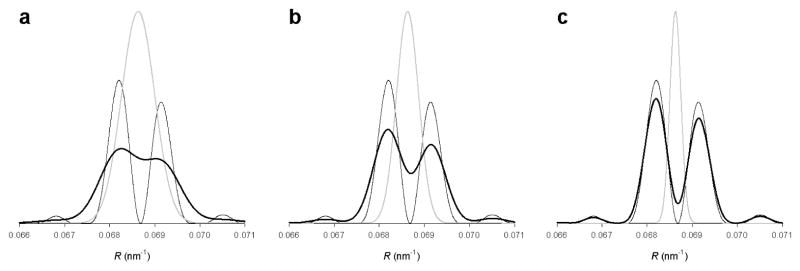
An important technical breakthrough for the in vivo dynamical study of muscle was the advent of third generation synchrotrons, the European Synchrotron Radiation Facility (ESRF), Grenoble, France, and the Advanced Photon Source (APS), Argonne, IL – USA, where a high X-ray flux (10¹³ photons/s) is combined with a finely focused beam. Using an image plate detector at ESRF, Bordas et al (1995) observed that the M3 reflection from a contracting muscle (8°C) was composed of two closely spaced peaks at 14.62 and 14.41 nm, with the intensity of the higher angle peak (I_HA) ca 0.6 the intensity of the lower angle peak (I_LA). H.E. Huxley suggested that, as in the resting muscle, the two peaks were the effect of the interference between the two arrays of myosin heads from the same thick filament (Bordas et al 1995).

This explanation for the origin of the fine structure of the M3 reflection was tested by measuring the intensity distribution in tetani at various sarcomere lengths (Linari et al 2000). The experiments were made using single muscle fibres, where the length of the sarcomere can be reliably determined.

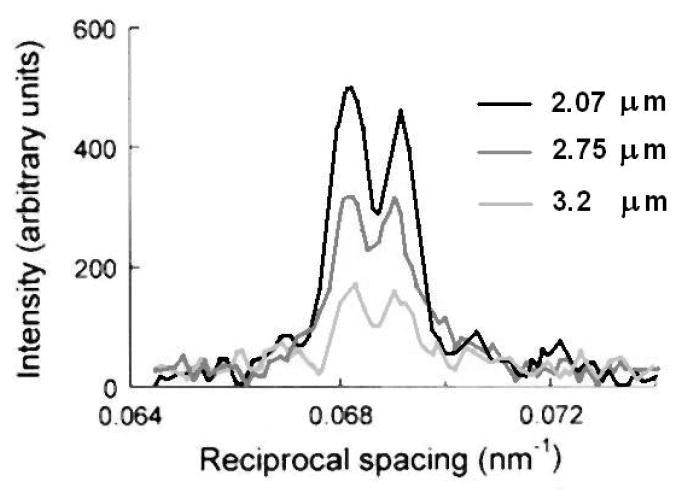
The X-ray beam from a synchrotron source allows a higher resolution along the vertical direction, and consequently, to maximise the resolution and to observe the interference sampling on the meridional reflections, it is necessary to mount the specimen with the axis vertical. For this reason, the experimental set-up for single fibre mechanics had to be adapted to mount the fibre vertically (Linari et al 2000). The fine structure of the M3 reflection from the single fibre during isometric contraction at 4°C and at ca 2.1 μm sarcomere length (s.l.) showed two major peaks at 14.67 and 14.46 nm, with I_HA/I_LA ≈ 0.8 (figure 18).

Figure 18.

Axial X-ray diffraction patterns from a single muscle fibre at rest (a) and at the plateau of an isometric tetanus (b). Sarcomere length 2.06 μm; exposure time 6 s in both conditions. The meridional myosin-based reflection are indicated on the left. The scale on the right refers to the reciprocal space.

In the s.l. range 2.1–2.2 μm the actin filament fully overlaps with the array of myosin heads, and the overlap region is about 700 nm. When the fibre is lengthened so that s.l. is 3.2 μm, the overlap is reduced to 200 nm. The isometric tetanic force, which is proportional to the number of cross-bridges (Gordon et al 1966), reduces in proportion to the reduction of overlap. In the range of s.l. investigated (2.1–3.2 μm), the actin and myosin filaments passed from the condition with the whole array of heads on each half-thick filament overlapped with actin, to the condition with only ca 25% of the array overlapped with actin. The intensity of the M3 reflection, I_M3, decreased linearly with increasing s.l. and thus was directly proportional to the extent of overlap between the array of heads and the actin filament. I_M3 extrapolated to zero for s.l.=3.6 μm, the length at which the overlap of the heads with actin becomes zero. The linear behaviour of I_M3 with the extent of overlap suggested that only the heads interacting with actin contributed to the intensity. It must be noted that the number of diffractors increases with the length of the array, and, from eq. (4), the intensity of the reflection increases with the square of the length, while the width of the reflection decreases with the inverse of the length. Consequently the integrated intensity of the reflection is proportional to the number of diffractors and thus to the length of the array. This analysis implies that the heads outside the overlap region are too disordered to make a substantial contribution to the M3 reflection. The fine structure of the M3 reflection did not undergo major changes with the increase in s.l., showing two main peaks of roughly comparable intensity in the whole range of s.l. (figure 19). At full overlap, the interference distance was calculated as 867 nm, close to 59.5 times the 14.57 nm repeat of the heads during isometric contraction. The interference distance, measured from the separation between the two main peaks of the M3 reflection, increased with s.l. as expected from the increased distance between the two arrays of actin-attached myosin heads. As noticed before, a change in the nanometer-scale of the interference distance would change dramatically the fine structure of the reflection, while a change by a multiple of the axial repeat of the heads would have a small effect on it, basically reducing only to an axial shift of the sampling peaks closer or farther from each other as the interference distance increases or decreases respectively.

Figure 19.

Sarcomere length dependence of the axial intensity distribution of the M3 reflection at the plateau of the isometric tetanus. As the sarcomere length increases, the intensity of the reflection decreases while the peak ratio does not change. (Adapted from Linari et al 2000).

These results provided the experimental evidence to support the idea that the fine structure of the M3 reflection is due to the interference between myosin heads in the two halves of the thick filament.

The finding that the two sampling peaks maintain roughly the same relative intensity for the whole range of s.l. clearly indicated that the interference distance is increased by a multiple of the periodicity.

In this respect, the experiments also provide a constrain for theories of the origin of the ca 1.5% increase in the spacing of the M3 reflection between rest and isometric contraction. In fact, the interference distance increases by a multiple of the periodicity only if the spacing increase to 14.5 nm upon activation involves the whole myosin filament, therefore the myosin heads in the non overlap region have also increased their periodicity by the same extent as the heads attached to actin and contributing to I_M3.

These experiments do not imply changes in tilting of the myosin heads, and indicate that the conformation of the heads does not change between isometric contraction at different s.l. Indeed, it can be shown that the interference distance as measured from the fine structure of the M3 reflection depends, with a good approximation, only on the axial displacement of the centre of mass of the myosin heads from the centre of the M-line and not on their conformation (see Appendix A4).

5.4 The interference effect provides the phase information

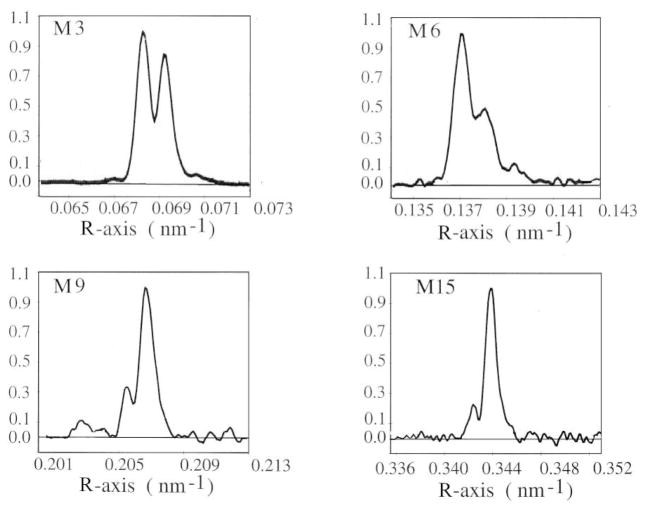
The approximation of the heads as point diffractors implies that the splitting of all the myosin-based meridional reflections have the same interference distance, while this is not the case. For example, as the M3 reflection during isometric contraction is split into two peaks of comparable intensity, say the n^th and the (n+1)^th order of the interference distance, almost equidistant from the centre of M3, then at the level of the M6 reflection (the 2^nd order of the M3) the 2n^th and the (2n+2)^th order should still be almost equidistant from the centre of the reflection, with the (2n+1)^th order sampling the M6 close to its centre and the satellite peaks of about 0.1 its intensity. This is not the case, as the M6 is still sampled by two unequal peaks but with an intensity ratio much higher than expected (ratio HA/LA peaks about 0.5; Juanhuix et al 2001). Thus, the fine structure of the meridional reflections seems to originate from a slightly different interference distance because the diffractor, the myosin head, is asymmetric along the meridional axis. To qualitatively understand this point, it may help to think that the reflections at different orders of the 14.5 nm repeat have contributions of different weight from different parts of the molecule. In this way the splitting of the M3 and M6 reflections during isometric contraction can both be reproduced by a model in which the myosin head is approximated by two rectangular masses of different weights (3.5:1) displaced by ca. 3 nm, with an average interference distance of ca. 867 nm (Reconditi 1998; figure 20). However, this solution is not unique.

Figure 20.

a. Schematic model for the myosin head during isometric contraction. The thick filamenti s composed by two arrays of 50 heads, with 14.57 nm repeat. Each head is represented as two rectangular parts, extending for 7 nm (a) and 2.5 nm (b) along the filament axis. The mass of a is 3.5 the mass of b. The centre-to-centre distance of the two arrays formed by the a and b masses are 868.6 nm and 861.1 nm respectively. b. Predicted intensity distribution of the M3 reflection during isometric contraction. Upper panel: dashed lines: Fourier Transform of the a mass (gray) and of the b mass (black); thin continuous lines: interference fringes generated from the two arrays of a masses (gray) and b masses (black); thick black line, intensity distribution predicted by the complete model. In this model, the region of the head attached to actin (a) influences more the M3 reflection, while the region closet to the myosin filament (b) influences more the M6 reflection. c. Comparison of the intensity distribution predicted by the model (thin line) with the intensity distribution observed during the isometric contraction (thick line), for the M3 and the M6 reflections.

A more detailed analysis of the fine structure of the myosin-based reflections from isometrically contracting muscle is described in Juanhuix et al 2001. High-resolution meridional patterns collected at the ESRF synchrotron up to the M15 reflection (at about 2.83 nm; figure 21) were subjected to a theoretical analysis based on the polarity of the myosin filament and produced the phase information required for defining the axial mass profile attributed to the myosin heads. The heads on the two halves of the thick filament may be represented as two diffraction units with their centers of mass separated by a distance D. Each unit is composed by N levels of the motif, repeating with a periodicity d. In a one-dimensional model, the motif is considered to be the axial mass projection of the repeating structure, in this case the pair of heads. Because the polarity across the M-line, the repeating motifs in one diffraction unit are the mirror image of those in the other. Taking the M-line as the origin of the coordinates in the real space, the meridional FT of the motif on one half of the filament is represented as F(R)e^iφ(R), where F(R) is the amplitude and φ(R) the phase of the complex FT. The lattice transform for the array is the Laue function, whose phase is zero when the center of the lattice coincides with the origin of the coordinates. In our case the centre of the lattice is displayed by half the bare zone (BZ) plus half the array length, [BZ+(N−1)d]/2, then its FT is [sin(πNRd)/sin(πRd)]·e^{−iπR[BZ +(N−1)d]}. The array of heads is the convolution of the repeating motif and the lattice, thus its FT is the product of the FT of the motif and the FT of the lattice:

$$F(R)e^{i\phi (R)}[sin(\pi \mathit{NRd})/sin(\pi Rd)]·e^{i\pi R[BZ+(N-1)d]}$$

Figure 21.

Aaxial intensity distribution of the myosin-based meridional reflections at the plateau of the isometric tetanus after background subtraction. For each reflection the intensity is scaled to normalise the height of the main peak. The intensity of the M12 reflection does not rise above the noise level and is not shown. (Adapted from Juanhuix et al 2001).

The mirror array on the other half of the filament has the same modulus and opposite phase:

$$F(R)e^{-i\phi (R)}[sin(\pi \mathit{NRD})/sin(\pi RD)]·e^{+i\pi R[BZ+(N-1)d]}$$

The total FT of the system is the sum of the FT’s of the two arrays, and taking into account that D=[BZ+(N−1)d], the following formula was found to describe the axial intensity distribution of the myosin-based reflections:

$$I(R)\propto F^2(R){\left[\frac{sin(N\pi Rd)}{sin(\pi Rd)}\right]}^2{cos}^2[\pi RD-\phi (R)]$$ (8)

This is a modified form of eq. (6) to take into account the form factor of the scattering mass.

If the amplitude and the phase of the FT are known, one can apply Fourier synthesis and reconstruct the mass distribution that produces the reflections. With the observed fine structures of four nonzero-intensity reflections (the M3, M6, M12 and M15) the mass distribution could be reconstructed with the approximation allowed by the sum of four sinusoidal profiles.

The relative values of F(R) at R=1/14.54 nm⁻¹ and its multiples can be measured from the intensity of the whole reflections. The phase φ(R) is deduced from the R value for which πRD−φ(R)=± π/2, which produces the minimum between the interference peaks. The origin of the phase can be arbitrarily chosen as φ=0 for the M3, which in turn determines the value of D. The phase at the level of the other three reflections has still an ambiguity of π radians, which ambiguity allows 2³=8 possible mass distributions. The authors assumed that all the mass which produces the M series of reflections is due to the myosin heads, and among the possible mass distributions chose the one that best fit the crystal structure of the pair of myosin heads with a given conformation.

However, other time-resolved experiments on whole muscle suggest that the mass profile which generates the M series reflections does not come exclusively from the myosin heads but also from structures on the thick filament with the same periodicity (Huxley et al 2003). This idea found definitive support from the finding that the intensity and fine structure of M6 reflection is scarcely influenced by rapid mechanical maneuvers that induce the axial movement of the myosin heads (Reconditi et al 2004).

5.5 The axial movement of the centre of mass

When the mass projection of the myosin head changes its shape from a profile 1 to a profile 2, its centre of mass moves from C₁ to C₂ and the phase of its FT changes from φ₁(R) to φ₂(R). The interference distance D in eq. (8) changes by ΔD=[φ₁(R)−φ₂(R)]/π R.

When the axial mass distribution of the diffracting unit is symmetric about the coordinate C in real space, then φ(R)=−2πRC (Appendix A4) and ΔD=2(C₂−C₁). This latter relation is equivalent to saying that the interference distance changes with the shape of the head as if the head were approximated by a point diffractor in the position of its centre of mass.

It can be shown that the approximation of the centre of mass is very good for large changes of orientation of the lever arm around the isometric conformation for the myosin head (figure A4).

Figure A4.

Axial mass density of the myosin head S1 for various angles of tilt of the light chain domain (LCD) relative to the filament axis, with the catalytic domain (CD) in the conformation of Rayment et al 1993b. The origin of the axis is on the residues 843, the tip of the lever arm. Lighter gray means higher mass density. Solid line: centre of mass of the molecule; dotted line: centre of mass of the CD; dashed line: apparent changes in the interference distance due to the change of φ(R) at the level of the M3 reflection, for R=1/14.5 nm. The dashed line is calculated as φ(R)/2πR for R=1/14.57 nm⁻¹, as described in the text and in par. 5.5. a. Mass density of a single myosin head. The white dotted lines indicate the conformation of S1 in rigor as in Rayment et al 1993b and in isometric contraction as in Irving et al 2000. b. Mass density of two heads, sharing the head-rod junction at residue 843. One head has the LCD at a fixed angle of 70° to the filament axis. The white dotted line indicates the conformation in isometric contraction as in Piazzesi et al 2002b.

In the myosin filament, the separation between the centres of mass of the two arrays of heads is about 860 nm: the length of one array, ca 700 nm, plus the whole bare zone, ca 160 nm. Thus the interference fringes which sample the M3 reflection at ca 14.5 nm are the ca 59^th (860/14.5) order of the fringe series. A ΔC movement of the centre of mass of the myosin heads (thought to be symmetrical in the two arrays) would change the interference distance by 2·ΔC, and in reciprocal space R it would look amplified about 59 times at the level of the M3. Moreover, the movement of the interference fringes changes the way they sample the reflection, and therefore the intensity ratio of the two peaks that constitute the fine structure of the reflection. This change is very sensitive to the movement, and an axial shift of the centre of mass of the heads of a few Angstroms can change the peak intensity ratio by ca 0.1–0.2, which is easily detectable (see Appendix A2, figure A2).

Figure A2.

Relation between the peak ratio of the M3 reflection and D, the centre-to-centre distance between the two arrays of heads. a. Relation between I_HA/I_LA and D in the range 860–867 nm. b. Relation between I_HA/I_LA (solid lines) or I_LA/I_HA (dashed lines) and D in the range 840–880 nm. The circle indicates the value of I_HA/I_LA in isometric contraction and the triangle indicates the value of I_LA/I_HA in rigor.

It is evident from the argument above that observing the changes in the fine structure of the M3 reflection is a powerful method to measure the elastic and working stroke response elicited in the myosin head by length or force steps imposed on single muscle fibres (Piazzesi et al 2002b; Reconditi et al 2004). Moreover, the interference effect can be used to study the different static conformations assumed by the myosin heads under different biochemical conditions that are relevant for investigating the coupling between the biochemical and the structural-mechanical steps of the myosin-actin interaction (Reconditi et al 2003)

5.6 Different biochemical states

Though not a physiological state, the rigor state of muscle is interesting since in this state, reached after depletion of ATP, the myosin head is strongly bound to the actin filament in a conformation that mimics that at the end of the working stroke.

The first evidence in support of this hypothesis was obtained in early electron microscope and X-ray diffraction studies (Reedy et al 1965; see par. 3.1), showing that in resting muscle the myosin heads stick out from the myosin filament at right angles, while in rigor they are at an angle of 45°. This finding is consistent with the idea of a working stroke that pulls the actin filaments toward the centre of the sarcomere. However, for the characterisation of the working stroke it is important to compare the head conformation in rigor with that in the isometric contraction, a state in which the heads can be considered to be biased towards the beginning of the working stroke.

The pattern from the muscle in rigor is quite rich, with a series of layer-lines that index on the ca 38 nm axial repeat of the actin helix and a series of meridional reflections that index on the ca 43 nm axial repeat of the myosin filament (Huxley and Brown 1967), but the structural interpretation of the reflections on the basis of their intensity alone is complicated by disorder and by the complexity of the structure (Squire and Harford 1988; Takezawa et al 1999; Koubassova and Tsaturyan 2002). However, when the X-ray diffraction patterns are recorded at the high spatial resolution that allows the fine structure of the meridional reflection to be observed, the axial position of the pair of heads relative to the M-line can be determined unambiguously.

In experiments at high spatial resolution the small angle X-ray scattering pattern has been recorded up to 0.145 nm⁻¹ from single fibres at the plateau of the isometric contraction (T₀) and in rigor at both low and high force at about 0.5 T₀, reached by slowly stretching the rigor fibre (figure 22,d–f; Reconditi et al 2003).

Figure 22.

M3 intensity profiles calculated from the two-head model. a. and d. Isometric contraction. b. and e. Low-force rigor. c. and f. High force rigor. in a–c, the two heads of one myosin molecule are shown in light and dark gray; actin monomers are shown as white spheres. In d–f, experimental intensity profiles (black circles) and calculated profiles from the two-head model convolved with the point spread function of the X-ray beam and detector (continuous line; from Reconditi et al 2003).

As already seen, the axial pattern from the fibre at rest shows the various orders of the ca 43 nm quasi-helical periodicity of the myosin heads along the thick filament, with the intense M3 reflection originating from the 14.34 nm axial repeat of the myosin heads. During isometric contraction, only the M3 and M6 reflections remain intense in the meridional pattern and their spacing increases by about 1.6%. The meridional pattern from the fibre in rigor still shows a prominent M3 reflection, with about 30% the intensity during isometric contraction, at a spacing of 14.44 nm, almost half-way between the value at rest and that during contraction (Haselgrove 1975; Reconditi et al 2003). The nature of these changes in head periodicity from rest to isometric contraction and to rigor is not clear, and cannot be explained solely in terms of elastic strain. However, assuming that the change of the periodicity involves a homogeneous change along the whole thick filament, the spacing change would not affect per se the fine structure of the reflection (see Appendix A5). Thus, the comparison between the fine structure of the M3 reflection during the isometric contraction and in rigor allows the changes in the axial position of the heads to be measured, relative to the head-rod junction.

As previously seen, the M3 reflection from the active fibre is split into two peaks, one at 14.46 nm (HA) and the other at 14.66 nm (LA) with intensity ratio I_HA/I_LA ca 0.8, while in rigor the M3 fine structure changes to a main peak at about 14.41 nm and a minor one at 14.60 nm, with ratio I_HA/I_LA = 4.0. Such a change implies an axial movement of the centre of mass by ca 4.5 nm relative to the head-rod junction, towards the centre of the filament (Appendix A2, figure A2). The corresponding amount of tilting of the lever arm depends on the structural model used for the myosin head. If I_M3 were due only to attached heads and only one head per molecule were attached to the actin filament either in the active fibre or in rigor, the predicted axial shift between the catalytic domain and the tip of the lever arm would be about 5.8 nm (see Appendix A4). This axial shift corresponds to a tilt of the lever arm by 36° from isometric contraction to rigor. During isometric contraction the angle between the residue 707-residue 843 vector and the filament axis is ca 65° (Irving et al 2000, Piazzesi et al 2002b), so the mean angle of the vector in rigor would be 101°, which is consistent with the value measured by cryoelectron microscopy of myosin S1 fragments bound to isolated actin filaments in the absence of ATP (102°, Rayment et al 1993b).

However, the myosin molecule is composed of two head domains, which share the head-rod junction, and there is evidence that in rigor both are bound to actin, on subsequent monomers along the actin helix (Cooke and Franks 1980; Thomas and Cooke 1980; Lovell et al 1981; Reconditi et al 2003). With these constraints, the two heads cannot have the same conformation. It is likely that due to steric hindrance the heads in rigor undergo some sort of distortion with respect to the S1 conformation in the decorated actin filament (Rayment et al 1993b). Under the assumption that the two heads attach to two consecutive monomers on the same actin filaments, their catalytic domains are separated by a fixed distance, the 5.46 nm between actin monomers. Thus, the axial tilts of the two heads are not independent and the best fit between the model and data can be searched by varying a single parameter. The best agreement with the data was found for tilts of 92° and 127° for the Z-ward and the M-ward head respectively (figure 22,a–c). These values encompass the value found for the angle of the lever arm in myosin heads decorating the actin filament in the absence of ATP, when pairs of heads do not share the head-rod junction. The conclusions reached by studying the changes of the fine structure of the M3 reflection can only define the axial tilt of the lever arm of the myosin head. However, this results obtained in situ give results consistent with that in the isolated actin-myosin complex in the absence of ATP, and suggests that the amplitude of the working stroke is ca 6 nm from the isometric contraction.

5.7 Angstrom-scale measurements of the working stroke

The possibility of observing the fine structure of the M3 reflection with submillisecond time windows allowed by the intense and finely focused beams available at the third generation synchrotron like ESRF and APS, together with suitable detectors, made it possible to reinvestigate the 1/1000 s⁻¹ conformational changes responsible for force generation and filament sliding.

Length step experiments

The length step experiment (see par. 2.4 and 4.4) has been repeated while monitoring the intensity and the fine structure of the M3 reflection. The intensity profiles of the M3 reflection were collected during isometric contraction just before the length step (figure 23,a; 2 ms time window, T₀), at the end of the step release (100 μs time window, T₁) and at the end of quick recovery of force (2 ms time window, T₂). The shortening step reduced the value of I_HA/I_LA and shifted both peaks to a higher angle (figure 23,b), as expected for displacement of the two arrays of actin-attached myosin heads toward the centre of the sarcomere. Most of the change occurred at the end of the shortening step (T₁) and only a small further reduction occurred during the subsequent rapid force recovery phase (T₁ to T₂ transition). The reduction of I_HA/I_LA is larger the larger the step, and saturates for steps larger than 7 nm/hs (figure 24).

Figure 23.

Change in the interference fine structure of the M3 reflection following a shortening step. a. Length change and force response. The thick gray segments in the force trace mark the X-ray exposure windows: T0, before the step; T1, at the end of the elastic response; T2, at the end of quick recovery. b. Axial intensity distribution of the M3 reflection, normalised to the height of the lower angle peak, recorded in the three time windows shown in a. (Adapted from Piazzesi et al 2002).

Figure 24.

Changes in I_HA/I_LA following shortening steps of different sizes. White circles and black triangles are the values at T₁ and at T₂ respectively. The black square represents the value just before the length step. The lines are calculated from the model described in the text: gray, T₁; black, T₂. Continuous lines indicate that only one head of each myosin responds to the length step; gray dashed line (T₁) is the prediction of a model where all the heads in the fibre respond to the step; black dashed line (T₂) is the prediction of the rapid detachment-attachment model. (From Piazzesi et al 2002).

From the experimental values of I_HA/I_LA it is possible to deduce the interference distance D, using the theoretical intensity distribution described in eq. (6) and figure A2. Eq. (6) applies exactly if each layer of myosin heads can be considered as point diffractors, but parallel analysis using the mass projection of the myosin head in the isometric contraction as described by Irving et al 2000 gives the same value for D (see Appendix A4). Thus the change in D responsible for the change of I_HA/I_LA can be used as an estimate of the average displacement (ΔC) of the centre of mass of the myosin heads with respect to their attachment to the myosin filament (the tip of the LCD). As shown in figure 25, ΔC, negative for displacement towards the center of the thick filament, is proportional to the size of the shortening step for steps up to 7 nm/hs, but is about 5 times smaller than the imposed filament sliding.

Figure 25.

Axial motion (ΔC) of myosin head centre of mass with respect to the myosin filament attachment. White circles and black triangles are the values at T₁ and at T₂ respectively. The values of ΔC are obtained from the values of I_HA/I_LA in figure 24. Negative values of ΔC denote motion toward the centre of the myosin filament. Gray and black line represents the linear regression on the T₁ and T₂ data respectively, except the point at −9nm/hs. (From Piazzesi et al 2002).

The value of ΔC at T₂ (figure 25, triangles) is similar to that at T₁ (circles). This result is consistent with models where the force recovery is due to the working stroke in myosin heads that remain attached to actin in phase 2, but not with models where the force is due to the attachment of heads with a strain loaded by Brownian motion (Huxley 1957, Howard 2001). In this latter case, the recovery of force would be due to strained heads newly attached to actin sites farther from the centre of the myosin filament, and this implies that an increase of ΔC would be observed, rather than the small decrease shown by the data. To quantitatively interpret the observed axial motion of the myosin heads during the elastic response and the subsequent quick force recovery, the compliance of both actin filament (here assumed 0.26%/T₀, Dobbie et al 1998; Linari et al 1998) and myosin filament (0.26%/T₀, Wakabayashi et al 1994; Huxley et al 1994) must be taken into account. These values are needed to calculate the actual axial movement Δz undergone locally by the heads for any given change of the half-sarcomere length and force (see par. 4.7 and par. 4.9), which is calculated by the formula:

$$\mathrm{\Delta }z=\mathrm{\Delta }\mathit{hsl}-(C_{\text{eqA}}+C_{\text{eqM}})·\mathrm{\Delta }T$$ (9)

Where Δhsl is the amplitude of the imposed step in half-sarcomere length, C_eqA and C_eqM are the equivalent compliance of the actin and myosin filament as defined in par. 4.6, and ΔT is the force change from T₀.

The axial movement Δz is then used in the simulation of the fine structure of M3, where each layer of myosin heads is represented by the crystallographic model of S1 (Rayment et al 1993b), with the CD attached to actin and the LCD at a variable angle of tilt. The changes in the ratio I_HA/I_LA calculated with this model are shown by the black dashed line in figure 24, and are much larger than the observed changes (circles). The reduced changes in the interference fine structure during the length step can be explained if part of the M3 intensity is due to myosin heads with sufficient axial order to contribute to the M3 reflection but not responding to the length step. The most obvious conclusion is that this latter population of heads is made up of the detached heads that are partner of the attached heads from the same myosin dimer. The contribution of the partner heads to I_M3 can be larger than that of heads in fully detached dimers if the head attached to actin imposes order on its partner since they are joined at the head-rod junction. The changes in I_HA/I_LA during the elastic response, calculated by introducing the partner head in the model, produce a better fit to the data (figure 24, black solid line). In this model, the displacement Δz of the CD relative to the head-rod junction produces a movement of the centre of mass ΔC 0.4 times smaller (Piazzesi et al 2002b), whereas it would have been 0.8 times smaller without the contribution of the partner heads.

During the quick force recovery, attached heads tilt to increase the strain on the actin and myosin filaments and on the heads themselves. The calculated values for the interference changes at T₂ (figure 24, gray solid line) are close to the observed data (triangles). In contrast, if the quick force recovery were due to heads newly attached to actin, the intensity ratio would rise (figure 24, gray dashed line) because these heads would be in the isometric conformation, with their centres of mass far from the centre of the thick filament. This is clearly inconsistent with the results of the experiments. The residual discrepancy between the model and the data is likely to be due to the detachment of a small (<0.1) fraction of heads during the quick force recovery for releases larger than 5 nm (Irving et al 2000).

The small change of I_HA/I_LA observed during the quick recovery of force seems to contradict the idea of a working stroke as the tilting of the LCD, which would displace the CD farther towards the M line. However, it must be taken into account that during the quick force recovery the working stroke increases the strain of the elastic element of the S1 portion, producing a back tilting of the tip of the lever arm. Small angle scattering does not provide enough resolution to distinguish the structural detail of the strain distribution. However, by definition, the strain of the head is the displacement between the tip of the lever arm and the CD produced by a step change of force.

In conclusion, the X-ray interference changes measured during the elastic and working stroke response elicited by length steps do not allow a direct measurement of the axial motion of myosin heads, but provide definitive evidence in favor of a mechanism of force generation based on a ca 10 nm working stroke in the myosin head, and against the idea of force generation based on attachment of already strained heads.

Load step experiments

An alternative method of synchronising the working stroke in the myosin heads is to superimpose step changes in force on isometric contraction (Podolsky 1960). Only recently, improvement in the mechanical techniques for single fibre experiments has made possible to isolate the early phase of the velocity transient following a force step (Piazzesi et al 2002a). The transient induced by a step decrease in force from the isometric value T₀ to 0.5 T₀ (figure 26,a), is composed of elastic shortening in phase 1, followed by a rapid shortening that lasts for ca 2 ms (phase 2, associated with the working stroke in the myosin heads). The shortening velocity then decreases (phase 3), before increasing once again to attain the steady state characteristic of the force-velocity relation (phase 4).

Figure 26.

Changes in the interference fine structure of the M3 reflection following a load step, and explanation in terms of the axial motions of the myosin heads. a. Force step and length change. Numbers 1–4 indicate the phases of the velocity transient as described in the text. The thick gray segments in the length trace mark the X-ray exposure windows: L₀, before the load step; L_2s, start of phase 2; L_2e, end of phase 2; L₃, end of phase 3. b. Axial intensity distribution of the M3 reflection recorded in the four time windows shown in a. c–f Motions of the myosin heads at the four phases of the velocity transient shown in a. (Adapted from Reconditi et al 2004).

The elastic response to the load step is the same as that to a length step, but the following velocity transient occurs at constant load, and therefore at constant strain in both the filaments and the heads. Thus, with the load-step protocol, X-ray interference measures directly the axial movement of working heads. The fine structure of the M3 reflection (figure 26,b) has been recorded during the isometric contraction preceding the step load (L₀), at the start and end of phase 2 of the velocity transient following the step (L_2s and L_2e respectively), and at the end of phase 3 (L₃). I_HA/I_LA decreased during phase 1, and in contrast with the length step protocol, continued to decrease during phase 2 of the velocity transient, before recovering in phase 3. These results show that myosin heads remain attached to actin and move toward the centre of the sarcomere during both phase 1 and phase 2 of the velocity transient (figure 26,c–e). The recovery of the ratio I_HA/I_LA during phase 3 of the velocity transient while shortening continues shows that myosin heads detach from actin in this phase and reattach to new actin monomers farther from the centre of the sarcomere (figure 26,f).

The change of the load in the range 0.75 to 0.25 T₀ shows that the speeds of both the working stroke and the subsequent detachment from actin depend on the load and are slower at higher load (Reconditi et al 2004; figure 27,a). The effect of the load on the size of the working stroke is made clear in figure 27,c, where I_HA/I_LA is plotted against the extent of filament sliding in each half-sarcomere: data for phase 2 of the velocity transient follow the same relation, independent of the load. In fact, the extent of axial motion of the heads while they are attached depends only on the amount of filament sliding and not on time (that changes by a factor of 4; figure 27,b and c). The recovery of I_HA/I_LA during the velocity transient marks when the heads start to detach from actin. This deviation occurs after different extents of filament sliding at different loads: at the lowest load (0.25 T₀), the working stoke accounts for 12 nm sliding, but at the highest load (0.75 T₀), the working stroke proceeds for only 6 nm before detachment of the heads. The working stroke at low load, 12 nm, is consistent with that from the crystallographic model (Dominguez et al 1998). At higher loads, the myosin head detaches from actin before reaching the structural limit defined by the crystallographic model. The load dependence of the size and the speed of the working stroke are basic molecular parameters to understand the macroscopic performance of muscle contraction. For instance, for an increase in load by a factor of three (0.25 to 0.75 T₀) the size of the working stroke in the attached myosin heads reduces only by a factor of two. Thus, the mechanical work produced in one actin-myosin interaction is higher at higher load and this gives a molecular explanation of the dependence of the efficiency of energy conversion in muscle (par. 2.4).

Figure 27.

Load dependence of the axial motions of myosin heads. a. Velocity transients following step reductions in force to 0.75, 0.5, and 0.25 T₀. b. I_HA/I_LA plotted against time for the three different loads: 0.75 T₀ (black); 0.5 T₀ (white); 0.25 T₀ (gray). The lines are drawn for visual help to follow the time courses. c. Relation between I_HA/I_LA and the extent of filament sliding, from the same experiments as b. (From Reconditi et al 2004).

This study is the clearest demonstration that even if small angle X-ray scattering has lower resolution than crystallography, the combination of X-ray interference between the two arrays of myosin heads with fast mechanics makes this approach the most powerful for the structural study of the molecular motor in muscle.

CONCLUSION

The size of myosin II stroke at low loads agrees with the movement expected from the difference between the crystallographic model of the myosin head with bound nucleotides (Dominguez et al, 1998, assumed as the pre-working stroke conformation) and that without nucleotide (Rayment et al, 1993, rigor-like conformation assumed as the post-working stroke conformation). Whether the reduced size of the stroke at high load is the result of a lower proportion of motors going through a switch-like conformational change, as postulated by crystallographers, or it is the result of a reduced movement in myosin II motor is a question for the future. A challenge to the switch-like model is the increasing evidence that the myosin II motor has a very small compliance: the strain in the myosin head generating its maximum isometric force is ~1.5 nm from mechanical - X-ray studies in situ, almost one order of magnitude smaller than the 11 nm working stroke. Also the recent finding that in a dynein molecule the size of the movement can be modulated by the load (Mallik et al., 2004) makes more solid the second view. Another fundamental question that will drive future investigations is strictly related to the peculiar polymeric organization of myosin II motor. How are the size of the stroke and the nature of myosin II interaction with actin modified by the load at the steady state of isotonic shortening? Can a structural explanation be found for the reduced rate of energy use at high shortening speed? Answers to these questions will provide the molecular and supramolecular bases for complete understanding of the energetics of muscle contraction.

APPENDIX

A1. Beamline characteristics to observe the fine structure

The system of fringes produced by the X-ray interference between the two arrays of myosin heads in each half-thick filament are described in terms of the reciprocal space coordinate R by the eq. (5): I (R) ∞ cos² (πRD), with D the centre-to-centre distance between arrays. Each fringe has a maximum for R = n/D, with n integer, and reaches 1/2 the maximum for R = (n ±1/4)/D. The full width at half maximum (FWHM) of a fringe is then 1/(2D), half the separation between two consecutive fringes 1/D. The relation between R and the linear coordinate l on the detector is R = sin(θ)/λ ≈ l/Lλ and l = RLλ, with L the camera length and λ the X-ray wavelength. Thus, in linear coordinates, the FWHM of a fringe is Lλ/2D and their separation is Lλ/D. If the system beam-detector has a point spread function (PSF) with FWHMδ_s, the observed fringes are convoluted with the PSF of the system, with a resulting width δ_f given by ${\delta }_f=\sqrt{{\delta }_s^2+{(L\lambda /2D)}^2}$. To discriminate between two consecutive fringes their separation must be higher than their width (Rayleigh criterion) and thus $L>\frac{2}{\sqrt{3}}\frac{{\delta }_{s}D}{\lambda }$. With the values D=860 nm and λ=0.1 nm, L > 10·δ_s, where L is measured in metres and δ_s is measured in millimeters. This relation shows that the higher the PSF of the system, the longer the camera must be to discriminate the fringes that sample the reflection (figure A1). In practice, to discriminate the sampling fringes, the lower limit for L is larger than10·δ_s. This is due to different factors: i) the actual axial width of the sampling peak is reduced by the envelope of the overall reflection, described by the Laue function; ii) the height of the two peaks is not the same, and this causes the smaller peak to be masked by the higher peak when convoluted with the system PSF.

Figure A1.

Convolution of the Point Spread Function (PSF) of the beam and detector system with the predicted intensity distribution. Thin black line, intensity profile predicted by the model for the two arrays of myosin heads; thin gray line: PSF of the system (FWHM δ_s); thick line: convolution between the two profiles. a. Camera length L=12δ_s;; b. L=17δ_s; c. L=30δ_s. Where δ_s is measured in millimeters and L in metres.

A2. Sensitivity of the fine structure of the M3 reflection to the interference distance

As seen in par. 5.1, two arrays of N point diffractors each, separated by a centre-to-centre distance D, produces the in the reciprocal space R the axial intensity distribution given by eq. (6):

$$I(R)\propto {\left[\frac{sin(N\pi Rd)}{sin(\pi Rd)}\right]}^2{cos}^2(\pi RD)$$

with d the periodicity of each array. A change of D is amplified by a factor D/d at the level of R=1/d in reciprocal space. The most evident effect of changes of D is on the ratio I_HA/I_LA (par. 5.3) between the two main peaks that sample the Laue function (figure A2). Starting from I_HA/I_LA=0.8, a change of D by ±0.2 nm changes I_HA/I_LA by ±0.05. It is to be noted that a change in D is twice the axial movement of each of the two arrays. Thus, the sensitivity of I_HA/I_LA to axial movement of the centre of mass of each array is about 0.5 nm⁻¹.

A3. Influence of the fine structure on intensity and spacing of the M3 reflection

The interference between the two arrays of myosin heads samples the M3 reflection that would arise from a single array, and changes the apparent spacing and intensity of the reflection in a way that depends on the interference distance. In a wide range around D=59·d the changes in the total intensity of the reflection are less that 1% (figure A3, A). This effect is lower than the uncertainty in the intensity measurements, estimated to be about 5% in the best data from muscle fibre experiments, and thus negligible for practical purposes. The apparent spacing change due to interference effect would change at maximum by ca 0.08% (figure A3,b). This value is comparable with the spacing changes observed in the step perturbation experiments, and it is a further reason for not using the spacing changes of the M3 reflection to measure the compliance of the filaments. On the contrary, M6 reflection does not show significant changes in its fine structure following mechanical maneuvers (Reconditi et al 2003; Reconditi et al 2004), and thus its spacing changes are not influenced by changes of the interference distance D.

Figure A3.

Solid line: relation between the apparent intensity (a.) and spacing (b.) of the sampled M3 reflection and D, the centre-to-centre distance between the two arrays of heads. The values are relative to the unsampled reflection. Dashed line: peak ratio as in figure A2.

A4. The approximation of the centre of mass

If the axial mass density of a myosin head is described by a function f(z) symmetric about the origin for the coordinates in the real space z, f(−z)=f(z), then its FT is real and the phase is zero. In fact the FT of f(z) is:

$$\text{F}.\text{T}.(R)=\underset{-\infty }{\overset{+\infty }{\int }}f(z)·e^{-2\pi \mathit{iRz}}dz=\underset{-\infty }{\overset{+\infty }{\int }}f(z)·cos(2\pi Rz)dz-i\underset{-\infty }{\overset{+\infty }{\int }}f(z)·sin(2\pi Rz)dz$$

and the last integral is zero because it integrates in a symmetrical interval a function symmetrical about the centre of the coordinates.

If the myosin head would change its shape still keeping a symmetrical distribution about the axial coordinate C, the new position of its centre of mass, the phase of its FT would change by −2πRC through the whole reciprocal space R. Thus, according to eq.(8) (Juanhuix et al 2001):

$$I(R)\propto F^2(R){\left[\frac{sin(N\pi Rd)}{sin(\pi Rd)}\right]}^2{cos}^2[\pi RD-\phi (R)]=F^2(R){\left[\frac{sin(N\pi Rd)}{sin(\pi Rd)}\right]}^2{cos}^2[\pi R(D+2C)]$$

This latter result shows that, for a symmetrical mass density, the change in the interference distance would correspond exactly to twice the axial movement of the centre of mass of the myosin heads.

In general, the axial mass density of the myosin heads is not symmetric and changes with the tilt of the LCD. However, the result obtained for symmetrical mass density is a good approximation also for non-symmetrical mass density, if it is not too spread too far along the axis of the filaments. For a large range of tilts, the axial movement of the myosin head produces a fine structure of the M3 reflection that is undistinguishable from the fine structure produced by point diffractors at the position of the centre of mass of the heads. If the diffracting mass is constituted by only one head, the range of axial tilts where the approximation is applicable is for angles of tilt between 35° and 100° from the filament axis (figure A4,a). If the diffracting mass consists of a moving head and its partner head with a fixed LCD at 70° from the filament axis (Piazzesi et al 2002b; Reconditi et al 2004), the range for the approximation is for angle of tilt between 35° and 90° (figure A4,b). The approximation of the centre of mass for calculating the axial movement of the myosin heads from the changes in the fine structure of M3 is then largely model independent. On the other hand, the relation between the axial movement of the centre of mass ΔC (figure A4, black solid line) and the axial displacement Δz of the tip of the LCD relative to the CD attached to actin (figure A4, gray line) depends on the model for the diffracting mass. The change in shape of the myosin head modulates the F²(R) factor and the intensity of the reflections in a way that also depends on the model for the h ead. The changes in both the fine structure and the intensity of the M3 and higher order reflection upon mechanical maneuvers set the constraints for building a model of the diffracting mass (Piazzesi et al 2002b; Reconditi et al 2004).

A5. Effect of the filament strain on the fine structure

A uniform extension or shortening of the bipolar myosin filament would change by the same proportion both the periodicity of the heads and the interference distance. Then, if the shape of the head does not change, the effect of the uniform length change on the M3 reflection would be a change of scale in reciprocal space, with the reflection and the sampling peaks moving together along the meridional axis, and changing their meridional width by the same amount. The intensity ratio of the sampling peaks, which is the most sensitive parameter for the axial movement of the heads, would remain the same.

However, a uniform force along the active muscle fibre does not mean a uniform force along the myosin and actin filaments. In fact, the force T between the filaments is mediated by a number N of layers of cross-bridges along the filament, each layer contributes with a force T/N. The distribution of the force along the myosin filament has then the maximum value T at the bare zone, and decreases uniformly to zero at the end of the filament (figure 14). The non-uniform force along the myosin filament could mimic the effect of an axial movement of the heads. The following calculations are to evaluate this effect.

Let us indicate with d₀ the constant spacing between heads when there is no force along the myosin filament and with HBZ₀ the extent of the half-bare zone. A force T at the end of the fibre, with each of the N heads contributing with a force t = T/N, stretches HBZ₀ to HBZ_T = HBZ₀(1+ c_BZ T), where c_BZ is the compliance of the bare zone, not necessarily the same as the compliance of the myosin filament in the region of the heads c_M. Starting from the first head after the HBZ, the i^th segment between heads is stretched to a length d_i = d₀[1+ c_M t (N−i)]=d₀+ δ (N−i), having defined δ= d₀ c_M t

The whole length of the array of heads is:

$$A=\sum _{i=1}^{N-1}[d_0+\delta (N-i)]=(N-1)d_0+\delta \sum _{i=1}^{N-1}i=(N-1)d_0+\delta \frac{N(N-1)}{2}$$ A1

and the average periodicity is:

$$d_{\text{T}}=\frac{A}{N-1}=d_0+\delta \frac{N}{2}=d_0(1+c_{\text{M}}\frac{T}{2})$$ A2

Therefore, the average force along the filament in the region of the heads is half the force along the fibre.

In the non-stretched filament, the centre of mass of the array of heads is c.m.₀=HBZ₀+d₀(N−1)/2, relative to the M-line. With a force T along the fibre, the centre of mass of the array moves to

$$c.m{.}_{\text{T}}={\mathit{HBZ}}_{\text{T}}+[\sum _{i=1}^{N-1}(i{d}_0+\sum _{j=N-1}^{N-i}j\delta )]/N=HB{Z}_{\text{T}}+\frac{(N-1)}{2}{d}_0+\delta \sum _{i=1}^{N-1}{i}^2/N$$ A3

By induction from N=1, is can be shown that

$$\sum _{i=1}^N{i}^2=\frac{1}{6}N(N+1)(2N+1)$$ A4

and the A3 becomes:

$$c.m{.}_{\text{T}}=HB{Z}_{\text{T}}+\frac{N-1}{2}{d}_0+\delta \frac{2N^2-3N+1}{6}=HB{Z}_0(1+c_{BZ}T)+d_0[\frac{N-1}{2}+c_{M}T(\frac{N}{3}-\frac{1}{2}+\frac{1}{6N})]$$ A5

If the centre of mass would change by the same percentage amount as the average periodicity, it should be:

$$c.m{.}_{\text{T}}=(HB{Z}_0+d_0\frac{N-1}{2})(1+c_M\frac{T}{2})$$ A6

and the peak ratio of the sampled M3 would be unchanged.

The difference between (A5) and (A6) mimics the effect on the peak ratio of an axial movement of the centre of mass of the heads, which may be calculated as:

$$\mathrm{\Delta }z=HB{Z}_0(c_{\text{BZ}}T-c_{\text{M}}\frac{T}{2})+d_0{c}_{M}T(\frac{N}{12}-\frac{1}{4}+\frac{1}{6N})$$ A7

The first term on the right shows the contribution of the elastic strain of the HBZ to the apparent axial movement of the head. In the simplest hypothesis that the compliance of the bare zone is the same as the rest of the myosin filament, c_BZ=c_M=0.0026/T_0, this contribution would be ca (80·0.0013=)0.10 nm/T₀. The contribution of the second term would be ca (14.5·0.0026·3.84=)0.14 nm/T₀, for a total of ca 0.24 nm/T₀.