Short Term Gains, Long Term Pains: How Cues About State Aid Learning in Dynamic Environments

Abstract

Successful investors seeking returns, animals foraging for food, and pilots controlling aircraft all must take into account how their current decisions will impact their future standing. One challenge facing decision makers is that options that appear attractive in the short-term may not turn out best in the long run. In this paper, we explore human learning in a dynamic decision-making task which places short- and long-term rewards in conflict. Our goal in these studies was to evaluate how people’s mental representation of a task affects their ability to discover an optimal decision strategy. We find that perceptual cues that readily align with the underlying state of the task environment help people overcome the impulsive appeal of short-term rewards. Our experimental manipulations, predictions, and analyses are motivated by current work in reinforcement learning which details how learners value delayed outcomes in sequential tasks and the importance that “state” identification plays in effective learning.

In Aesop’s fable “The Ant and the Grasshopper,” an industrious ant spends the summer months collecting supplies for the winter while a lazy grasshopper wastes time making music. However, when winter arrives, the grasshopper finds himself starving and begs the ant for food only to be turned away with the lesson that “idleness brings want.” In other words, what looks attractive today may not be best tomorrow. Conflicts between our desire for immediate satisfaction and our long-term well-being are characteristic of many real-world situations. For example, a student may be more likely to experience long-term success by studying for an important exam rather than attending a party even though the party is the more attractive option in the short-term. Similarly, the decision making pathologies associated with substance abusing populations are often characterized by the impulsive desire for immediate rewards over higher utility future outcomes (Bechara et al., 2001; Bechara & Damasio, 2002; Grant, Controreggi, & London, 2000).

In this report, we examine how people learn strategies that maximize their long-term well-being in a dynamic decision making task that we refer to as the “Farming on Mars” task. In our experiments, participants were asked to make repeated choices between two alternatives with the goal of maximizing the rewards they receive over the entire session. On any given trial, one option always returns more reward than the other. However, each time the participant selects this more attractive alternative, the future utility of both options is lowered. Thus, the strategy which provides the most reward over the experiment is to choose what appears to be the immediately inferior option on each and every trial. Just like the fabled grasshopper, participants must learn to make choices that appear, at least in the short-term, to move them away from their current goal in order to ultimately reach it.

The reward structure of our task borrows from a number of recent studies that place short-term and long-term response strategies in conflict (Bogacz, McClure, Li, Cohen, & Montague, 2007; Egelman, Person, & Montague, 1998; Herrnstein, 1991; Herrnstein & Prelec, 1991; Montague & Berns, 2002; Neth, Sims, & Gray, 2006; Tunney & Shanks, 2002). Interestingly, the conclusion from much of this work has been that humans and other animals often fail to inhibit the tendency to select an initially attractive option even when doing so leads to lower rates of reinforcement, a phenomena referred to as melioration. Melioration appears at odds with rational accounts, which dictate that decision makers follow a strategy that maximizes their long-term expected utility (see Tunney and Shanks, 2002 for a similar discussion). However, the rational account fails to specify how this optimal strategy is discovered in an unknown environment. In this paper, we attempt to better understand the learning mechanisms that participants use to find advantageous behavioral strategies in situations where the structure of the environment is not clearly defined in advance.

Like many situations in the real world, success in the Farming on Mars task depends on a variety of cognitive processes including the appropriate exploration of alternatives and the ability to learn the value of actions when these values are contingent upon past behavior in non-obvious ways. In order to better understand the complex interplay of learning, exploration, and decision making in the task, we develop and test a set of simple computational models based on the framework of reinforcement learning (RL, Sutton & Barto, 1998). RL is an agent-based approach to learning through interaction with the environment in pursuit of reward-maximizing behavior. The RL approach has been successful in both practical applications (Bagnell & Schneider, 2001; Tesauro, 1994), and in the modeling of biological systems (Daw & Touretzky, 2002; Montague, Dayan, & Sejnowski, 1996; Montague, Dayan, Person, & Sejnowski, 1995; Schultz, Dayan, & Montague, 1997; Suri, Bargas, & Arbib, 2001). An attractive feature of RL for the present report is that it emphasizes the concept of a situated learner interacting with a responsive environment, making it an ideal framework for studying human learning and decision making in dynamic tasks.

The central goal of the present studies was to examine how people’s mental representation of the structure of a task influences their ability to learn a control strategy that maximizes their long-term benefit. Our experiments were specifically motivated by the RL framework that we describe later and by issues of cognitive representation and generalization in dynamic decision-making tasks. In Experiment 1, we present an exploratory study of behavior in the Farming on Mars task. Our goal was to establish that behavior in the task replicates previous work (Herrnstein, 1991; Herrnstein & Prelec, 1991; Tunney & Shanks, 2002) and to assess the effect that different types of feedback may have on performance in the task. In Experiment 2, we present a novel extension of the task by providing participants with different types of cues indicative of the underlying state of the dynamic system. Consistent with our simple RL model, we find that an important component of optimal behavior in the task is correctly identifying the current state of the environment and appropriately generalizing experience from one state to others. In the absence of cues about system state, learners tend to collapse together functionally distinct situations, which greatly complicates learning the underlying reward structure of the task. We next compare human performance in our task to a number of simple RL models to identify the cognitive mechanisms that drive performance in our tasks. Finally, we consider the implications of this work.

The Farming on Mars Task

In the Farming on Mars task, participants interact with a simple video game. The cover story for the game is that two agricultural robots were sent to the planet Mars to establish a farming system capable of generating oxygen for later human inhabitants. Participants are told that each robot specializes in a different set of farming practices, but that only one can be active at a given moment. Participants’ job as controller is to repeatedly select which robot should be active at each point in time in order to maximize the total amount of oxygen generated over the entire experiment. On each trial, participants simply indicate which robot should do the farming, and are given feedback about how much oxygen was immediately generated as a result of their choice.

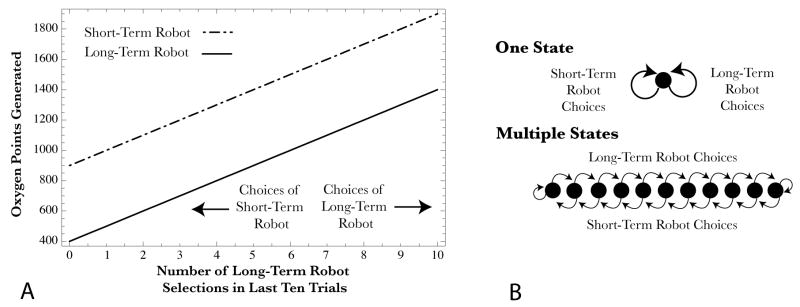
Figure 1A shows an example of the payoff structure in the task. Unknown to participants, one robot always generates more oxygen than the other robot for any given trial. For example, at the midpoint along the horizontal axis, selecting the more productive robot (referred to as the Short-Term robot with payouts corresponding to the upper-diagonal line) would generate 1300 oxygen units, whereas selecting the other robot (referred to as the Long-Term robot with payouts corresponding to the lower-diagonal line) would generate only 800 oxygen units. However, each time the Short-Term robot is selected, the expected output of both robots is lowered on the following trial (i.e., the state of the system shifts to the left in Figure 1A). For example, selecting the Short-Term robot again after it generated 1300 oxygen units would result in only 1200 units on the subsequent trial. In contrast, selecting the Long-Term robot twice in this situation would transition the payout from 700 to 800 units.

Figure 1. Panel A.

The payout function for the Farming on Mars task. The horizontal axis is the number of choices out of the last ten in which the Long-Term robot was selected. The vertical axis is the number of oxygen units generated as a result of choosing one of the robots on a trial. The two diagnonal lines show the reward associated with each robot for each task state. By design the Short-Term robot is better at every point, but the best long-term strategy is to exclusively choose the Long-Term robot because the selection of the Short-Term robot transitions the state to the left, whereas selection of the Long-Term robot transitions the state to the right. Panel B: Two potential representations of the state structure of the task are shown. States are depicted as black circles. In the top figure, the problem consists of a single state. In this representaton, trials which differ from one another in terms of the available rewards are aliased together. In the bottom panel, eleven distinct states are shown. Actions (such as selecting the Short-Term robot) push the system into an adjacent state. In this case, states directly correspond to the positions along the horizontal axis in panel A and better capture the underlying structure of the task.

Selections of the Long-Term robot behave in the opposite fashion. When this robot is selected, the output of both robots is increased on the next trial (shifted to the right in Figure 1A). Critically, over a window of ten trials, the reward received from repeatedly selecting the Long-Term robot exceeds that from always selecting the Short-Term robot (i.e., the highest point of the Long-Term robot curve is above the lowest point for the Short-Term robot curve in Figure 1A). As a result, the optimal strategy is to select the Long-Term robot on every trial, even though selecting the Short-Term robot would earn more on any single trial. Participants were not given any relevant information about the differences between the robots, and thus could only arrive at the optimal strategy by interactively exploring the behavior of the system (cf. Berry & Broadbent, 1988; Stanley, Mathew, Russ, & Kotler-Cope, 1989).

The Importance of State and Problem of Perceptual Aliasing

An important challenge facing any learning agent is adopting an appropriate mental representation of the environment. For example, when trying to navigate a simple maze, distinct locations can be perceptually identical (e.g., two hallways which have the same junctions). In this case, the agent must deal with the problem of perceptual aliasing (McCallum, 1993; Whitehead & Ballard, 1991), where multiple states or situations in the world may map to a single percept. When an agent is unsure of their current state, it is difficult to determine the most effective course of action, and to learn effectively from that experience. In many real-world situations, determining the mapping from observations in the world to relevant states about which the agent can learn is often a non-trivial problem. Imagine yourself as a traveler stepping off an elevator in a unfamiliar hotel. Each floor might be hard to distinguish based on perceptual cues alone (i.e., floors have similar decor). This aliasing can make deciding which action to take next a challenge. Is your room to the left or right? Should you step back inside the elevator? Note, however, that when distinct perceptual cues are available which veridically map onto task-relevant states (e.g., distinct and salient labels on each floor of the hotel), the decision problem can be somewhat simplified.

Participants in the Farming on Mars task face a related challenge. Each time a player makes a choice, the underlying state of the system changes so that the reward received on the next trial is different than it was on the previous trial. However, from the perspective of a naïve participant situated in the task, it is not clear whether there are multiple states or a single state with rewards drifting or fluctuating over time (see Figure 1B, top). To the degree that participants adopt the later psychological representation of the system, it inherently leads to the aliasing of functionally distinct states, making the true reward structure of the task difficult to detect.

An alternative view (that is not transparently available to participants at the start of the task) is that the task involves a number of distinct states and that participants can transition from state to state depending on their actions. Under this view, the value associated with any particular action depends on the the current state of the system (see Figure 1B, bottom). Participants who can correctly identify the current state are better positioned to uncover the dynamics determining rewards in the task¹. With this representation, each state is clearly disambiguated from the next and the problem of perceptual aliasing is reduced. Of course, an even more effective representation might allow for generalization between related states, so that experience in one situation can quickly be extended to others without the need to directly experience many outcomes in each state. As we will see in our experiments and simulations, mental representations of state that are well-matched to the underlying structure of the task lead to significantly better performance. In some cases, melioration may simply be a consequence of learners adopting a poorly matched representation of the task dynamics.

Issues concerning state identification and generalization are central to contemporary work in RL and are an active area of research in computer science and engineering (c.f., Littman, Sutton, & Sigh, 2002). Indeed, many popular algorithms for learning sequential decision strategies in complex environments such as Q-learning (Watkins, 1989) and SARSA (Sutton, 1996; Sutton & Barto, 1998) require learning agents to correctly identify changes in the state of the environment as a consequence of their actions. The experimental manipulations that follow were inspired by this formal framework for sequential decision making and make interesting predictions about how appropriately structured cues in the environment can aid decision making in dynamic tasks.

Experiment 1

In Experiment 1, we sought to validate our experimental paradigm by replicating past work with dynamic decision making tasks that place short- and long-term rewards in conflict. In addition, this basic version of the task provides a baseline for our later studies. We were particularly interested in the effect that different types of reward structures would have on participant’s performance. Tunney and Shanks (2002) reported that participants learned to maximize reward in a situation similar to the Farming on Mars task when the magnitude of the reward varied from one task state to the next, but settled on a melioration strategy when rewards were probabilistic. Since we were unsure of of how to most effectively convey rewards to participants, we began by testing participants in an analogous version of the Farming on Mars task. In the continuous rewards condition, participants were given a reward (oxygen points) on each trial, the magnitude of which was a linear function of the number of Long-Term robot selections they made over the past 10 trials (similar to Figure 1A).

In the second condition, called the probabilistic rewards condition, the function that determined the reward on any given trial was probabilistic. Instead of generating a particular number of oxygen units on each trial, the reward function determined the probability of earning either a smaller or larger fixed reward (i.e., the rewards were essentially binary: more or less). In all other ways, the two conditions were identical. For example, more selections of the Long-Term robot increased total output of the system (i.e., the percentage of trials in which the larger number of oxygen units were generated by selecting either robot), while more selections of the Short-Term robot lowered the productivity of the system (increasing the percentage of trials in which smaller number of oxygen units were generated). Similarly, the probability of generating the larger number of oxygen units was always higher for the Short-Term robot than it was for the Long-Term robot, but, as in the continuous condition, the optimal strategy was to select the Long-Term robot on as many trials as possible.

A key difference between these conditions is how much information is conveyed by the reward on a single trial. In the continuous rewards condition, the magnitude of the reward correlated with the current task state and is a stable indicator of the expected value of that state. In contrast, in the probabilistic rewards condition, the reward signal is more variable and participants must integrate over a number of trials in order to evaluate the value of each action. In addition, in this condition, trial-to-trial changes in the magnitude of the reward signal no longer provide a stable cue about changes in the state of the system (changed in the magnitude of the reward no longer clearly indicate changes in the operation of the farming system). To the degree that participants take advantage of the structure inherent to the reward signal, their performance should be negatively impacted by the probabilistic reward signal since these values convey less overall information about the task.

Method

Participants

Eighteen University of Texas undergraduates participated for course credit and a small cash bonus which was tied to performance. Participants were randomly assigned to either a continuous rewards condition (N = 9) or a probabilistic rewards condition (N = 9).

Materials

The experiment was run on standard desktop computers using an in-house data collection system written in Python. Stimuli and instructions were displayed on a 17-inch color LCD positioned approximately 47 centimeters away from the participant. Participants were tested individually in a single session. Extraneous display variables, such as which robot corresponds to the left or right choice option, were counterbalanced across participants.

Design

Participants were given a simple two-choice decision making task described above. Prior to the start of the experiment, participants were given instructions that described the basic cover story and task. Critically, participants were informed that their goal was to maximize the total output from the “Mars Farming system” over the entire experiment by selecting one of two robot systems on each trial. Unknown to the participant, the number of oxygen units generated at any point in time was a function of their choice history over the last ten trials (h). At the start of the experiment, h was initialized to 5 (so as to not favor either option). The payoffs associated with each robot system were manipulated so that one option was better than the other in the long-term, despite appearing worse in the short-term. In the continuous rewards condition, the payoff for any selection of the Long-Term Robot was $10+70\ast \frac{h}{10}$ while the payoff for the Short-Term robot was $30+70\ast \frac{h}{10}$. These reward functions are structurally equivalent to the one shown in Figure 1. In the probabilistic rewards condition, rewards were always either 15 or 85 units (set so as to make the qualitative distinction between “more” and “less” reward obvious). However, the probability of generating the 85-unit outcome when selecting the Long-Term robot was $\frac{2}{3}\ast \frac{h}{10}$ while the probability of generating the 85 unit outcome when selecting the Short-Term robot was $\frac{1}{3}+\frac{2}{3}\ast \frac{h}{10}$ (this is the same payoff function used by Neth et al., 2006). Note that the probability of earning the 85 unit outcome was always higher for the Short-Term robot than it was for selecting the Long-Term on any individual trial, but repeated selections of the Long-Term robot would earn more on average than repeated selections of the Short-Term robot.

Procedure

The 500 trials of the experiment were divided into five blocks of 100 trials each. At the end of each block, participants were given a short break and each successive block picked up where the last block left off. In order to maintain motivation, participants were told that they could earn a small cash bonus of $2–5 which was tied to their oxygen generating performance in the task. However, they were not told how oxygen points would translate into cash rewards, only that generating more oxygen would yield a larger bonus.

On each trial, participants were shown a control panel with two response buttons labeled either System 1 or System 2. Between these two buttons was a video display where trial-relevant feedback and instructions were presented. Participants clicked one of the two response buttons using a computer mouse. After a selection was made, a short animation (lasting approximately 800 ms) indicated that the response was being sent to the Mars base. Following this animation, the amount of oxygen generated on that trial was shown. The number of oxygen points earned was visually depicted using a 10×10 grid of green dots. The number of dots that were active in this grid indicated the amount of oxygen that was generated on the current trial (i.e., more dots meant more oxygen was generated on that trial). A short auditory beep was presented when the oxygen points display was updated indicating that the reward for that trial had been received. The points display was shown for 800 ms, after which the screen reset to a “Choose” prompt that indicated the start of the next trial. No information about the cumulative oxygen generated across trials was provided.

The optimal strategy in the task is to select the Long-Term robot as much as possible. However, if participants know that the experiment is about to end shortly, the optimal strategy switches to selecting the Short-Term robot because it provides a greater immediate reward. At the start of the task, we did not provide specific information about the length of the task or the number of trials, other than it would not last more than one hour (in reality the task took around 35–40 minutes). However, in order to evaluate the impact that changing participants’ temporal horizon has on performance, on the last five trials of the experiment, a prompt was displayed above the control panel that initiated a count-down (i.e., “5 trials left”, “4 trials left”, and so on).

Results

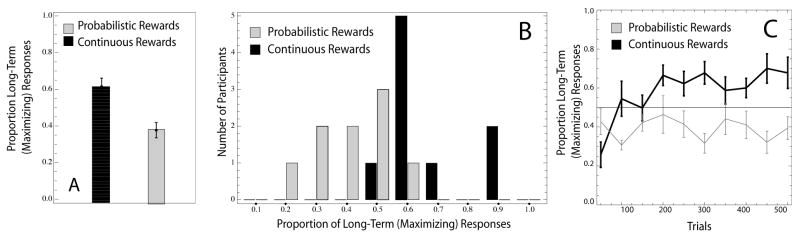
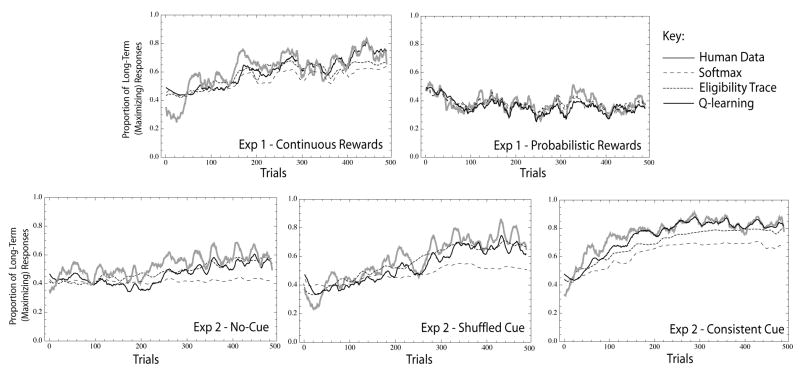
The primary dependent measure was the number of Long-Term robot selections the participants made. Figure 2A shows the proportion of trials in which this option was chosen for each condition (excluding the last 5 trials of the task). Overall, participants made far fewer choices of the Long-Term robot in the probabilistic rewards condition (M =.38, SD =.13) compared to the continuous rewards condition (M =.61, SD =.14), t(16) = 3.74, p <.002. In addition, responding in both conditions reliably differed from chance performance (t(8) = 2.78, p <.03 and t(8) = 2.53, p <.04 for the probabilistic and continuous reward conditions, respectively). Figure 2B shows a histogram which bins participants based on the proportion of Long-Term robot selections they made over the entire experiment. A far greater number of participants in the probabilistic rewards condition selected the Short-Term option on the majority of trials.

Figure 2.

Overall results of Experiment 1. Panel A shows the average proportion of Long-Term responses made throughout the experiment as a function of condition. Panel B show the full distribution of participant’s performance. Panel C presents the average proportion of Long-Term responses considered in blocks of 50 trials for both conditions. Error bars are standard errors of the mean.

Time-Course Data

Figure 2C shows the proportion of Long-Term choices calculated in non-overlapping blocks of 50 trials at a time averaged across participants. In the continuous rewards condition, participants adopted an early strategy favoring the Short-Term, implusive option (participants in this condition allocated 31.1% of their choice to the Long-Term option in the first 50 trials, a level below chance responding, t(8) = 2.41, p <.043). In contrast, participants in the probabilistic reward condition allocated 47.1% of their choices to the Long-Term option in the first 50 trials, t < 1.

A two-way repeated measures ANOVA on condition and experimental block (1–5) revealed an effect of training condition, F(1; 64) = 14.07, p <.002, and training block, F(4, 64) = 2.71, p <.04, and a significant interaction F(4, 64) = 5.32, p <.001. While early selections of the Short-Term option were more frequent in the continuous rewards condition, participants in this condition eventually increased the number of Long-Term (maximizing) selections as the experiment progressed, which was confirmed by a significant effect of training block in this condition, F(4, 32) = 6.36, p <.001. In addition, we found that selections of the Long-Term robot in the last block of 95 trials exceed those from the first block of 100 in the continuous rewards condition, t(8) = 3.12, p <.014. In contrast, a one-way repeated measures ANOVA on training block in the probabilistic reward condition failed to reach significance, F < 1. In addition, performance during the last block of 95 trials did not significantly differ from performance in the first block of 100 trials for this condition, t < 1.

Last Five Trials Analysis

Collapsing across both conditions, responses during the last five trials of the experiment (after participants were informed that the experiment was about to end) revealed fewer Long-Term responses than in the preceding five trials of the experiment, t(17) = 3.29,p <.005. Considered within each condition, in the continuous rewards condition, 86% of responses were Long-Term responses on trials 490–495 compared to only 51% on trials 495–500, t(8) = 3.41, p =.009. In the probabilistic rewards condition, the proportion of Long-Term responses fell from 40% to 28% in the last five trials, a result which failed to reach significance, t(8) = 1.35, p =.21.

Discussion

Participants in the continuous rewards condition were initially attracted to the Short-Term, impulsive option but show evidence of gradually increasing the number of Long-Term selections they made over the course of the experiment. In contrast, participants in the probabilistic rewards condition appear to have slightly favored the Short-Term option throughout. While the magnitude of the reward signal correlated with the current state of the system in the continuous rewards condition, there was no stable relationship between the magnitude of the reward and system state in the probabilistic rewards condition. In addition, participants in the probabilistic rewards condition had to integrate the value of particular actions over a number of trials in order to derive a good estimate, contributing to the aliasing of distinct task states.

Overall, the results of the probabilistic rewards condition appear consistent with previous work that reports a strong and consistent preference for short term strategies in probabilistic tasks. For example, Neth et al. (2006) tested participants in a similar task using a probabilistic reward schedule and found that participants selected the Long-Term, maximizing option on rougly 37% of trials (Experiment 1, no feedback condition). Likewise, Tunney and Shanks (2002) report that participants selected the Long-Term option 33% of the time and showed little learning in a task with a probabilistic reward schedule (Experiment 2). In contrast, in the continuous rewards condition we found that participants selected the Long-Term option around 61% of the time. This level of performance actually exceeds the performance reported by Tunney and Shanks (2002, Experiment 1) where participants only selected a long-term option 45% of the time in the first 500 trial session of a task that provided continuously varying rewards. This difference, while small, may be explained by participants being more engaged by the Farming on Mars cover story.

The results of Experiment 1 establish two facts. First, we demonstrate that we are able to replicate previous findings comparing probabilistic and continuous reward signals using our Farming on Mars task. Second, we conclude that manipulations involving continuous reward signals are most likely to show learning as the sparse feedback in the probabilistic case is a factor that strongly limits performance (at least in the context of a single 1-hour training session). Thus, in the experiments that follow, we chose to focus on conditions that provide participants with continuous feedback.

Experiment 2

Having established the viability of our paradigm, in Experiment 2, we test the impact that different kinds of cues about the current state of the environment can have on participants’ learning and decision making abilities. Our predictions, consistent with the RL model described later, are that providing participants with simple perceptual cues that readily align with the state structure of the task will improve their ability to learn a reward maximizing strategy by limiting the aliasing of functionally distinct states.

Each subject was randomly assigned to one of three conditions. The conditions were identical with respect to the number of trials and the payoff function (shown in Figure 1A), but differed in the types of cues that were provided on the display. In the no-cue condition, participants were tested in the two-choice Farming on Mars task and were given no additional information about the state of the system. This condition matches most closely with previous investigations of maximization/melioration behavior (Herrnstein, 1991; Herrnstein & Prelec, 1991; Tunney & Shanks, 2002) and is virtually identical to Experiment 1’s continuous condition. In the shuffled-cue and consistent-cue conditions, participants’ control panel was augmented to include a horizontal row of lights (see Figure 3, right) that indicated the underlying system state. At any given time, only one of these lights was active. Which light was lit was determined by the number of times the Long-Term robot was selected over the previous ten trials of the experiment (note that participants did not know at the start of the experiment how the two robots varied). The function of the light was to indicate to participants the current state of the Mars farming system (i.e., the current point along the horizontal axis in Figure 1A).

Figure 3.

Examples of the task interface used in Experiment 2. The left panel shows the display in the no-cue condition. The right panel shows the indicator lights used in both the consistent-cue and shuffled-cue conditions. In addition, the right panel illustrates how rewards were conveyed to participants.

In the consistent-cue condition, the indicator lights were organized in a regular fashion such that the active light moved one position either to the left or to the right as the state was updated. In the shuffled-cue condition, the relationship between successive state cues was obscured by randomizing the arrangement of the indicator lights on a per-participant basis. Like in the consistent-cue condition, the position of the light was perfectly predictive of the underlying state of the farming system, but the relationship between successive states and the magnitude of the reward signal was more irregular. We predict that systematic cues (such as those in the consistent-cue condition), will bolster performance by allowing experience in one state to be generalized to related states. Note that the addition of the perceptual cue in the consistent-cue and shuffled-cue conditions does not render the task trivial. To excel at the task, participants must still learn that the Short-Term robot yields less reward than the Long-Term robot over the course of the experiment.

Method

Participants

Fifty-one University of Texas undergraduates participated for course credit and a small cash bonus which was tied to performance. Participants were randomly assigned to one of the three conditions: the no-cue condition (N = 17), the shuffled-cue condition (N = 17), and the consistent-cue condition (N = 17).

Materials and Design

The materials and basic design were the same as in Experiment 1. However, the payoff function differed. On each trial, the payoff for selecting the Long-Term Robot was $400+1000\ast \frac{h}{10}$, where h is the number of times the Long-Term robot was selected in the last 10 trials. In contrast, the payoff on each trial for the Short-Term robot was $900+1000\ast \frac{h}{10}$.

Procedure

The procedure was nearly identical to Experiment 1. However, in the consistent-cue and shuffled-cue conditions (but not in the no-cue condition), the display was augmented to include a row of eleven indicator lights as described above and shown in Figure 3. No mention of these lights was made in the instructions. The current position of the indicator light was updated at the same time as the oxygen reading. The active light indicated the underlying state of the reward function (i.e., position along the horizontal axis in Figure 1A). In contrast to Experiment 1, feedback in this experiment was provided in numerical terms (i.e., “New Oxygen Added: 800.00”, see Figure 3).

In the consistent-cue condition, selections of the Long-Term robot moved the active light one way across the screen, while selections of the Short-Term robot shifted it the other direction. The polarity of the light arrangement (e.g., whether the far left light indicated a preponderance of recent Short- or Long-Term robot selections) was counterbalanced across participants. The shuffled-cue condition differed from the consistent-cue condition in that the arrangement of the indicator lights was randomly shuffled on a per participant basis. Thus, like the consistent-cue condition, the active light was determined by the recent response history, but unlike the consistent-cue condition, the indicator light did not necessarily move to a neighboring location as the underlying state transitioned to adjacent states (e.g., the far left light could illuminate, then following a state transition, the light three positions to the right could be illuminated on the next trial).

Results

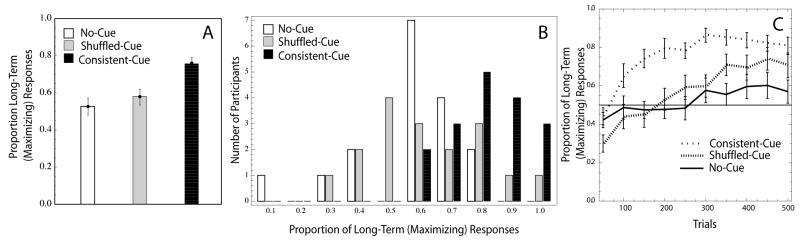
Figure 4A shows the proportion of trials in which the Long-term option was chosen for each condition (excluding the last 5 trials of the task). A one-way ANOVA revealed a significant effect of condition, F(2, 50) = 9.32, p <.001. In both the no-cue and shuffled-cue conditions, the proportion of Long-Term choices did not significantly differ from.5, M =.52, SD =.18, t < 1 and M =.57, SD =.18, t(16) = 1.79, p =.093, respectively. In contrast, participants in the consistent-cue condition chose the Long-Term robot more often than the Short-Term robot, M =.76, SD =.13, t(16) = 8.38, p <.001. Planned comparison revealed that the proportion of Long-Term responses did not differ between the no-cue and shuffled-cue conditions, t < 1. However, a significantly larger proportion of Long-Term responses was recorded in the consistent-cue condition compared to the shuffled-cue, t(32) = 3.42, p <.002, and no-cue conditions, t(32) = 4.28, p <.001.

Figure 4.

Overall results of Experiment 2. Panel A shows the average proportion of Long-Term responses made throughout the experiment (excluding the last five trials) as a function of condition. Panel B shows population distribution of participant’s performance. Panel C presents the average proportion of Long-Term responses considered in blocks of 50 trials for all three conditions. Error bars are standard errors of the mean.

Figure 4B shows a histogram which bins participants based on the proportion of Long-Term robot selections they made over the entire experiment. All of the participants in the consistent-cue condition allocated more than half of their responses to the Long-Term robot. In contrast, a few participants in both the no-cue and shuffled-cue condition appear to have settled on a sub-optimal, implusive strategy by selecting the Short-Term robot on the majority of trials. In addition, it appears that the shuffled-cue may have helped some participants uncover the Long-Term, reward-maximizing strategy, however the impact of this information appears more variable than in the consistent-cue condition.

Note that in the consistent-cue condition, the direction that the indicator light moved in response to Long-Term or Short-Term selections was counterbalanced along with the location of the response button itself. However, participants likely brought with them pre-existing associations concerning the left-right axis of the display (Dehaene, Bossini, & Giraux, 1993). Thus, one possibility is that the effect of the consistent light cue increased in conditions where the response button and direction of movement were compatible. However, in our data, we failed to find an effect of compatibility relative to participants for whom these two factors moved in opposing directions, t < 1. In addition, there was no separate effect of the direction that the indicator light moved (left vs. right) on performance within the consistent-cue condition, t < 1.

Time-Course Data

Figure 4C shows the proportion of Long-Term choices calculated in non-overlapping blocks of 50 trials at a time. Overall, the movement of the indicator light in the consistent-cue condition appears to have helped participants uncover a maximizing strategy at a faster rate than in the other conditions. Early in learning, some participants developed a preference to choose the Short-Term (impulsive) option. This was particularly true in the shuffled-cue condition where only 30% of participants’ selections were towards the Long-Term option over the first 50 trials, a result significantly below chance responding, t(16) = 4.67, p <.001. Similarly, in the no-cue condition, participants selected the Long-Term option on 42% of the first 50 trials. However, this result failed to reach significance, t(16) = 2.03, p =.06. Finally, in the consistent-cue condition, participants allocated 43% of their selections to the long-term robot, which did significantly differ from chance, t(16) = 1.51, p =.15.

However, in all three conditions, participants gradually increased the proportion of Long-Term responses they made by the end of the experiment. For example, a two-way repeated measures ANOVA on condition and experimental block (1–5) revealed a significant effect of training condition, F(2, 192) = 9.32, p <.001, and training block, F(4, 192) = 21.2, p <.001, and a significant interaction F(8, 192) = 3.08, p =.003. Planned comparisons within each condition found a significant effect of block only in the shuffled-cue condition, F(4, 64) = 13.7, p <.001. However, comparing the proportion of selections allocated to the Long-Term option in the first block of 100 trials compared to the last block of 95 trials revealed a significant increase in both the shuffled-cue (mean difference =.31, t(16) = 5.32, p <.001) and consistent-cue conditions (mean difference =.23, t(16) = 5.23, p <.001) with no difference in the no-cue condition (mean difference =.08, t(16) = 1.16, p =.26).

Last Five Trials Analysis

Collapsing across conditions, responses during the last five trials of the experiment (after participants were informed that the experiment was about to end) revealed fewer Long-Term responses than in the preceding five trials, t(50) = 3.08, p <.005. Overall, this result suggests that participants were able to adjust their behavior when the relevant temporal horizon was reduced. A similar pattern was observed within each condition, although the reliability of the effects was limited due to statistical power. In the no-cue condition, 56% of responses were to the Long-Term response on trials 490–495 compared to 42% on trials 495–500, t(16) = 1.95, p =.07. Similarly, in the shuffled-cue condition, the proportion of Long-Term responses fell from 75% to 57% in the last five trials, t(16) = 2.1, p =.05. Finally, in the consistent-cue condition, Long-Term responses fell from 81% to 71%, t(16) = 1.22, p =.23.

Discussion

The results of Experiment 2 demonstrate how cues about system state can impact learning in a dynamic task. In the no-cue condition, we found that participants chose the Short-Term robot on roughly half the trials. In addition, it appears that few individual participants discovered the reward-maximizing strategy of selecting the Long-Term robot on the majority of trials. However, when given a simple cue which reflected the underlying state of the system (the purpose of which was never explicitly explained), participants’ performance dramatically improved. In the no-cue and shuffled-cue conditions, participants appear to have been drawn towards the Short-Term option early in the task, with participants in the shuffled-cue condition eventually overcoming this tendency and making more selections of the Long-Term robot.

The finding of near-optimal behavior in the consistent-cue condition (almost 80% of choices were towards the Long-Term option) stands in contrast with previous attempts at encouraging maximizing behavior in human participants, which have been met with limited success. For example, in a similar task, Neth, Sims, and Gray (2006) gave participants global feedback about their performance every few trials which indicated how close to the optimal their current strategy was. In spite of this global perspective, the authors report that they were unable to detect a significant improvement on maximizing behavior. Our results show that a more effective manipulation is to provide participants with information about the current state of the task environment and how it changes in response to their actions.

Overall, performance in the consistent-cue condition exceeded that of the shuffled-cue condition, despite the fact that both conditions provided identical information about the current state (i.e., both conditions provided participants with cues which perfectly correlated with the reward structure of the task). While there are a number of differences between these conditions (including the fact that the state cues in the consistent-cue condition may have been more discriminable or more easily memorized than those in the shuffled-cue condition), one important distinction is the fact that the indicator light in the consistent-cue condition moved in a predictable way from one state to the next. If participants detect that the light moving one place to the left or right was associated with increased reward, they might be able to generalize this to other states, even if they had not yet been directly experienced. In contrast, the less transparent movement of the cue in the shuffled-cue condition limited this type of generalization due to the fact that adjacent states did not map onto adjacent indicator light positions. In our later RL simulations, we consider the role that generalization between states might play in accounting for the observed differences in performance.

One question left unanswered by Experiment 2 is the degree to which state cues might improve performance when the feedback provided to participants is probabilistic. To this end, we tested a separate set of 51 New York University undergraduates (17 in each condition) in an experiment that replicated Experiment 2 (i.e., participants were assigned to a no-cue, shuffled-cue, or consistent-cue as above) but which used the probabilistic reward structure from Experiment 1. Overall we found that consistent state cues did have a positive influence on the number of Long-term options made by participants over the experiment. For example, we found a significantly higher number of long-term selections in the consistent-cue condition compared to both the no-cue and shuffled cue conditions. Examination of the time-course of performance in this experiment revealed that participants had a tendency to prefer a melioration strategy early in the task, but there was evidence of a shift toward a long-term strategy near the end of the task in both the consistent-cue and shuffled-cue conditions. Nevertheless, the dramatic influence of the state cues was somewhat reduced in the probabilistic rewards case (overall percentage of trials in which the Long-term option was selected for all three groups remained below chance). One likely reasons is that the sparse feedback in the probabilistic reward case was a strong limiting factor (for the reasons described earlier). Our data suggest, however, that with extended training, participants in this experiment could eventually leverage the state-cues to support a long-term strategy even in a probabilistic task. Nevertheless, these follow-up results confirm that the state-cues in Experiment 2 do not automatically suggest a reward-maximizing strategy to participants, but that the cues must be integrated along with learning the value of particular actions in order to have a positive effect.

Reinforcement Learning-Based Analyses

The experiments just reviewed highlight how cues that are congruent with the state structure of a dynamic task may support effective decision making. In the following section, we describe an extensive computational analysis of human performance in our experiments. The primary goal of these simulations was to gain a better understanding of the learning mechanisms that participants engage in the task. As mentioned earlier, the experimental manipulations we considered in the first part of the paper were primarily motivated by the principals of contemporary RL models including issues of state identification, generalization, and the appreciation of future outcomes. Before considering the specific models tested and our results, we highlight some the key theoretical issues addressed in our simulations.

What cues do learners utilize in the Faming on Mars task to disambiguate the current task state?

The first question addressed by our simulations has to do with the perceptual cues that participants rely on in constructing a mental representation of the task. Our claim in the first part of the paper was that cues such as the indicator lights could help participants identify distinct task states and generalize experience from one state to the next. In our simulations, we systematically evaluate how providing our RL-based models with similar types of information improves the ability of the model to account for the trial-by-trial choices of participants in our experiments. Our goal was to understand how participants might rely on these cues to inform their choice strategies, and how changes in the structure and informativeness of these cues should impact performance.

States cues or Memory cues?

A second question, related to the first, assessed the degree to which the state cues in our task helped participants overcome the perceptual aliasing of functionally distinct tasks states, or if they simply served as a memory cue about recent actions. RL theorists have long recognized how an effective memory may help agents overcome some of the issues surrounding perceptual aliasing (Chapman & Kaelbling, 1991; McCallum, 1993, 1995). The intuition is that two states which appear identical (for example, the highly confusable floors of a hotel) may be distinguished by the recent behavioral history of the agent. Starting in the hotel lobby, if the agent has already opted to go up four floors in the elevator, it is unlikely that the next state will be to arrive on the flrst floor. Thus, in some environments, it may be possible to disambiguate the current task state using memory for recent actions. Neth et al. (2006) and Bogacz et al. (2007) provide an account of human learning in a task similar to the Farming on Mars task, which explains reward-maximizing behavior without reference to distinct state cues but via a simple memory system (known as eligibility traces). By this account, the cues provided on the screen in the consistent-cue condition from Experiment 2 might simply help participants maintain a memory for recent actions. In contrast, other models we consider hold that perceptual cues in the task helped participants directly represent and identify distinct task states.

Overview of Models Tested

We begin by explaining the basic operation and formalism of the models that we tested in order of increasing complexity.

Baseline Model

In order to provide a standard for our model comparisons, we tested a simple baseline model which assumed that participants choose either the Long-term or Short-term option with a constant probability across all trials. If the probability of choosing the Long-term option is denoted p_max then the probability of choosing the Short-term option is simply 1−p_max. Unlike the RL-based models considered next, this model assumes that choices are independent on each trial and not influenced by learning. However, this model captures the base rates of responding to each choice option for each subject and can often provide an excellent fit. Most importantly, this baseline comparison allows us to evaluate the degree to which the trial-by-trial dynamics generated by individual participants are explained by our learning models (see Busemeyer & Stout, 2002 for a similar approach and motivation).

Softmax Model

Next, we considered a version of the Softmax action selection model (Sutton & Barto, 1998; Daw, O’Doherty, Seymour, Dayan, & Dolan, 2006; Worthy, Maddox, & Markman, 2007). In this model, the probability of selecting either the Short-term or Long-term option is based on an estimate of value of each action which is learned through experience. The model’s current estimate of the value of the selected action, a_i, is updated on each trial according to:

$$Q(a_i)=Q(a_i)+\alpha ·\delta$$ (1)

where

$$\delta =r_{t+1}-Q(a_i)$$ (2)

Q(a_i) refers to the current estimate of the value of option a_i, and α is a recency parameter (0 ≤ α ≤ 1.0) that controls the degree to which the current estimate depends on the most recent rewards. When α is small, the value of Q(a_i) depends on a larger historical window of past rewards, while if α = 1.0 then Q(a_i) depends only on the reward from the last trial. Finally, δ is the error between current predictions and actual experienced reward on trial t+1, denoted r_t+1. The probability of choosing action a_i on any trial is given by:

$$P(a_i)=\frac{e^{Q(a_i)·\tau }}{{\sum }_{j=1}^2{e}^{Q(a_j)·\tau }}$$ (3)

where τ is a parameter which determines how closely the choice probabilities are biased in favor of the value of Q(a_i). In general, the probability of choosing option a_i is an increasing function of the estimated value of that action, Q(a_i), relative to the other action (Luce, 1959). However, the τ parameter controls how deterministic responding is. When τ → 0 each option is chosen randomly (the impact of learned values is effectively eliminated). Alternatively, as τ → ∞ the model will always select the highest valued option (also known as “greedy” action selection). In summary, the Softmax model includes two free parameters: a recency parameter, α, and a decision parameter, τ.

Eligibility Trace (ET) Model

While the Softmax model improves upon the baseline model, it ultimately predicts that participants will favor selections of the Short-term option. This is because the model has no way of taking into account the gain in future rewards available from actions many steps into the future. Instead, the model bases its actions entirely on the average reward experienced from each choice option. Since the Short-term option always returns a larger magnitude reward, the model will necessarily settle into an impulsive strategy².

One extension of the Softmax model described above, which allows it to learn to choose the reward-maximizing, Long-term option, is to augment the model with a memory for recent actions known as eligibility traces (Bogacz et al., 2007; Neth et al., 2006). In this model, each possible action in the task is associated with a decaying trace which encodes the number of times each action was selected in the recent past. These decaying traces provide a way of linking the value of the Short- and Long-term options. If the RL agent selects the Short-Term option after a run of selections of the Long-Term option, the spike in reward will reinforce not only the value of the Short-Term option but also the Long-Term option, as this option’s eligibility trace will remain strongly activated in memory. Thus, memory for the recent history of actions provides the model with a way of “crediting” actions that may indirectly lead to increased reward. With an appropriate rate of memory decay, the inclusion of eligibility traces can allow the Softmax model to maximize reward in the task by choosing the Long-Term option on most trials.

Formally, the Eligibility Trace (ET) model we considered is identical to the one described in Bogacz et al. (2007) and extends the Softmax model above by modifying Equation 1 to include an additional term that represents a decaying trace for recent selections of action a_j:

$$Q(a_j)=Q(a_j)+\alpha ·\delta ·{\lambda }_j$$ (4)

where δ is as defined in Equation 2. Unlike the Softmax model, this Equation 4 is updated for each available action j rather than just for the selected option, j = i. In addition, on each trial, λ_j for every action decays according to λ_j = λ_j * zeta; with 0.0 ≤ ζ ≤ 1.0. However, each time a particular action a_i is selected, the trace for only that action is incremented according to λ_i = λ_i + 1. The addition of the memory decay parameter (ζ) in this model raises the number of free parameters to three.

Q-learning Network Model

According to the ET model, the perceptual state cues we provided in Experiment 2 might boost participant’s performance by improving their memory for recent choices and for how these selections relate to reward outcomes. An alternative view is that the main challenge in the task is for participants to adopt a mental representation of the state structure of the task that is well-matched to the actual task dynamics. The model based on Q-learning (Watkins, 1989), which we describe next, leverages these perceptual cues in order to learn a long-term reward maximizing strategy³.

The Q-learning network model differs from the Softmax and ET model just described in two key ways. First, in the Q-learning network model, estimates of the value of particular actions depend not only on recently experienced outcomes, but also include a discounted estimate of the value of future actions. Second, this model incorporates a representation of the task based on cues in the environment (including experimenter provided cues and/or the reward signal itself). In this sense, the Q-learning network model is more complex than any of the models considered so far. However, in our simulations, we systematically evaluate many aspects of the model in order to justify the increased complexity.

Learning the Value of Actions

In order to maximize the reward received in the task, the Q-learning network model attempts to estimate the long-term value of selecting a particular action a in state s, a value referred to as Q(s, a). These so-called “Q-values” in the model represent an estimate of the discounted future reward the agent can expect to receive given that it selects action a in state s and thereafter behaves optimally. In our task, there are only two actions available to the RL agent at each state, which correspond to selections of either the Short-Term or Long-Term robot. Each time an action is selected, the model computes the error between its current estimate of the value of that action in that state, Q(s_t, a_t), and the actual reward received according to:

$$\delta =[r_{t+1}+\gamma \underset{a}{max}Q(s_{t+1},a)-Q(s_t,a_t)]$$ (5)

where δ is the Q-learning error term, r_t+1 is again the reward received as a result of taking action a_t, γ is a parameter influencing the relative weight given to immediate versus delayed rewards, and max_a Q(s_t+1, a) is a estimate of the best action available in the next state, s_t+1, which results from taking action a_t. Overall, δ in Equation 5 measures the difference in our current estimate of the long-term value of the current state and action, Q(s_t, a_t), and a discounted estimate of future rewards we expect to receive, r_t+1 + γ max_a Q(s_t+1, a). This difference enables the model to incrementally bootstrap new estimates of the long-term value of particular actions on the basis of older estimates and allows the model’s value estimates to extend beyond the immediate time step.

The asymptotic value of each action depends on the relative weight given by the agent to immediate versus delayed rewards. In our model, the degree to which learners value short-or long-term rewards is determined by a simple discounting parameter, γ. Note that when γ = 0, the error term in the model reduces to the standard delta rule (Rescorla & Wagner, 1972; Wagner & Rescorla, 1972; Widrow & Hoff, 1960). Accordingly, under these conditions, the model strongly favors immediate rewards and thus predicts melioration behavior in the task. As the value of γ increases, the model gives more weight to future rewards, eventually allowing it to favor selections of the Long-Term option.

Learning a Representation of the Task

Note that a critical challenge facing a learner following Equation 5 is to appropriately identify and distinguish different task states (i.e., appropriately distinguishing the Q(s, a) pairs). We assume that cues in the task, such as the magnitude of the reward signal or the indicator lights given to participants on the screen, help learners to elaborate these representations. In our account, the estimate of the value of a particular action on trial t is not stored directly, but is instead calculated as a simple linear function of the current input (i.e., cues presented in the task):

$$Q(s_t,a_t)=\sum _{j=1}^N{w}_{ja}^t·I_j^t$$ (6)

where N is the number of inputs, $I_j^t$ is the activation of the jth input unit on trial t (described below), and w_ja is a learned weight from the jth input unit to action a. Thus, the model attempts to learn the mapping between input cues (i.e., current state) and the Q-values associated with that state as approximated by a simple single-layer network (Widrow & Hoff, 1960). Changing the type and structure of input cues modulates the ability of the model to learn the appropriate representation of the state structure of the task and ultimately influences its ability to uncover an optimal response strategy.

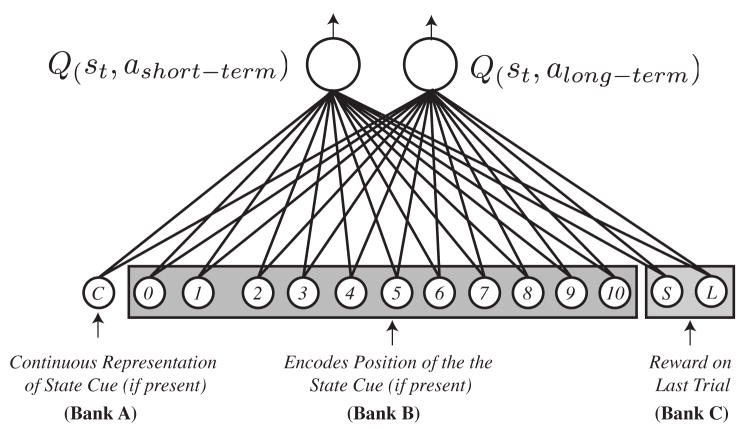
Figure 5 shows a diagram of the basic architecture. In order to characterize the information available to human participants, the model was provided with a bank of 14 input units. Activation on the first unit in this set coded the position of the active indicator light (if present on the display) on a continuous scale from 0.0 to 1.0 (labeled with a C in the figure). For example, if the left-most light was to be active on a particular trial, the activation of this input unit was set to 0.0. The right-most position was coded as 1.0. Intermediate positions were coded in equal increments of 0.1. This continuous input representation allows generalization of the value learned in one state to nearby states. If the model receives a small reward while the indicator light was in position state 0 (far left) and a slightly larger reward in state 1, then the linear network can “extrapolate” this to predict even larger rewards in unexperienced states (i.e., 2, 3, or 4, and so on).

Figure 5.

Diagram of the architecture of the Q-learning network model. These models use cues such as experimenter-provided state cues or the reward on the previous trial in order to estimate the value of each action. Input was a single vector of length 14 which encoded various aspects of the display (see the main text for details). A set of learned connection weights passed activation from the input units to the output nodes which, in turn, estimate the current value of the state-action pair Q(s, a). Critically, the models must learn through experience how perceptual cues in the task relate to the goal of maximizing reward.

In addition to the continuous input unit, the model was provided with a bank of 11 binary input units. On each trial, the activation of one of these units was set to 1.0 and the rest were set to 0.0. Which of these 11 units was activated depended on the position of the active indicator light on the display. In contrast to the continuous input, this discrete coding of the light position is equivalent to a lookup table representation (learning about one position does not generalize to others). The purpose of this redundant coding of the display information was to formalize distinct hypotheses participants might entertain for how cues in the environment relate to experienced rewards. The final two inputs were used to encode the reward signal received on the previous trial (consistent with the idea that the magnitude of recent rewards can actually contribute to the identification of the current state). In each simulation, rewards (used for prediction) were numerically coded according to the functions defined for each experiment, however when reward was used as an input to the network, these values were scaled between 0.0 and 1.0 so that they would have the same range of values as other input units. If the agent selected the Short-Term option and received r oxygen units, the first of these two units (labeled S in the figure) would be set to r on the next trial and the other (L) set to zero, and vice versa following selections of the Long-Term option.

The error, δ, calculated in Equation 5 is used to adjust weights in the model according to:

$$w_{ja}^t=w_{ja}^{t-1}+\alpha ·\delta ·I_j^{t-1}$$ (7)

where $w_{ja}^t$ is the new value of the weight, $w_{ja}^{t-1}$ is the old value of the weight, and α is a learning rate parameter. Finally, the probability of selecting action a_i is given by Eqn. 3 where the Q(a_i) for each action are replaced with the value Q(s_t, a_i). Thus, the choice the model makes on each trial depends not only on the estimated value of each action but also the current state, s_t. In summary, our simple Q-learning network model has three interpretable parameters: a learning rate (α), a parameter controlling exploratory actions (τ), and the discounting parameter (γ) which controls the weight given to future rewards.

Model Comparison Procedure

Table 1 summarizes the key differences between the four architectures we considered. The basic logic behind our simulations are as follows. First, by testing the baseline and Softmax model, we provide a standard against which to judge the improvement in fit expected by the ET and Q-learning network model (which actually can account for maximizing behavior in the task). Without these baseline comparisons, we are unable to judge the relative quality of our fit, and rule out simpler explanations of our results. Next, by comparing the relative fit of the ET and Q-learning network model, we are able to assess if the improvements in performance with state-cues were mitigated by improvement memory for recent actions (as predicted by the ET account), or if such cues helped subject disambiguate successive task states (as suggested by the Q-learning network model). Finally, by changing the structure of the input cues provided to the Q-learning network model, we can assess the degree to which such cues contributed to performance in the task and assess which cues participants likely utilized.

Table 1.

Summary of models tested. The column labeled k_m denotes the number of free parameters in the model (see Equation 8).

Name	km	Description
Baseline	1	No error term. Chooses each option with a fixed probability across all trials. A standard comparison against which to evaluate the other models.
Softmax	2	Error Term: δ = rt+1 − Q(ai) Estimates the average outcome from each action. Does not take into account different states or future outcomes. Predicts melioration.
Eligibility Trace (ET)	3	Error Term: δ = rt+1 − Q(ai) Estimates the average outcome from each action but includes a decaying memory for recent action selections (eligibility traces). With an appropriate decay term, can predict maximizing behavior.
Q-learning Network	3	Error Term: δ = rt+1 + γ maxaQ(st+1; a) − Q(st; at) Utilizes a linear network to approximate distinct state representations. Error term include a discounted estimate of future reward. Depending on the setting of the discounting term, γ, and the nature of state cues that are provided, can predict maximizing behavior.

The first step in our analysis was to evaluate the ability of the models to fit to the trial-by-trial choices of individuals in our experiments. For each model, we searched for parameters that maximized the log-likelihood of the choice sequence for each subject in each condition of our experiments. Predicted response probabilities for each trial were generated by providing the model with the entire choice history (and relevant rewards and state cues) for all trials up to t − 1, then allowing the model to predict the choice probabilities on trial t. Summing the log of the probability of the model making the same response as the subject across the entire 495 trial sequence results in a likelihood measure, $L_i^m$, which measures the quality of the fit for model m to subject i. A parameter search was conducted to find the free parameters which maximized the value of $L_i^m$ for each subject and model using the Nelder-Mead simplex method with 200 random starting points (Nelder & Mead, 1965)⁴.

Due to the fact that some of the models tested differed in the number of free parameters they possessed, direct comparison of the fit quality between models requires a correction. We used the Akaike Information Criterion (AIC) which compares the fit quality of each model while correcting for the number of free parameters (Akaike, 1974)⁵. The value of the AIC for subject i and model m can be computed as follows:

$$AI{C}_i^m=2·L_i^m-2·k_i^m$$ (8)

where k_a are the number of free parameters in the model. Larger values of $AI{C}_i^m$ mean that model m provides a better account of subject i’s choice data. We can compare the improvement in $AI{C}_i^m$ for different models in order to determine the model which best accounts for the data. In our analysis, we compared each learning model (i.e., Softmax, ET, and the Q-learning network) to the performance of the baseline model by simply computing the difference in the AIC value between the particular RL model and baseline. This measure, which we denote, $AI{C}_i^{m-b}$, quantifies the improvement in model fit provided by model m over the baseline model for participant i, correcting for the number of free parameters in each. Positive values indicate conditions where the tested model provided a better fit than did the baseline model. Furthermore, if model x provides a better fit than model y then $AI{C}_i^{x-b}>AI{C}_i^{y-b}$.

Results

Table 2 shows the $AI{C}_i^{m-b}$ score averaged over participants for each model and in each experimental condition. To give a sense of how closely each model was able to fit the trial-by-trial choices on participants in the task, Figure 6 displays the predicted choices sequence for each model (averaged across participants) to the one actually generated by participants in our task⁶. In the following section we consider the results for each model.

Table 2.

Comparison of mean $AI{C}_i^{m-b}$ score for each model, m, relative to the baseline for all participants in a particular condition. In parentheses is the percentage of participants for whom model m provides a better fit than baseline (i.e., $AI{C}_i^{m-b}$ is positive). The best fit model in each condition is indicated in bold.

	Experiment 1		Experiment 2
Model (m)	cont.	prob.	no-cue	shuffled	consistent
Softmax	18.4 (0.78)	130.0 (1.00)	−11.2 (0.47)	1.0 (0.59)	−26.9 (0.53)
ET	41.1 (1.00)	96.3 (1.00)	30.5 (0.76)	78.6 (0.82)	11.1 (0.76)
Q-learning	105.3 (1.00)	137.5 (1.00)	93.2 (0.94)	166.7 (0.94)	118.2 (0.94)

Figure 6.

A comparison between the human results and the best-fit model predictions for each of the three learning models. Using the best fit parameters for each subject, we found the predicted probability of selecting the Long-term option on trial t given the response history of that subject for all trials up to trial t − 1. For presentation purposes, proportion of long-term responses for human participants and predicted probabilities of long-term responses for the model were smoothed using a sliding window of 15 trials. Note that although the Softmax model does not predict that participants will select more from the Long-term option, when linked to individual choice histories, it can end up slightly favoring the long-term option. Overall, the Q-learning network model provides the best account across all five conditions.

Softmax Model

As expected, the Softmax model only slightly out-performed the baseline model (see Table 2). For example, in the no-cue and shuffled-cue condition of Experiment 2 and the continuous reward condition of Experiment 1, the Softmax model often performs roughly the same (or worse) relative to the baseline model. Note, however, that the Softmax model provides a much better fit to the probabilistic rewards condition of Experiment 1. In this condition, participants mostly meliorated in the task (making around 30% selections toward the maximizing response). Given that the Softmax model is unable to predict maximizing behavior in the task, it makes sense that it would provide the best fit to the condition where participants also failed to maximize. In contrast, the Softmax model performs worse than baseline in the consistent-cue condition of Experiment 2, where participants were much more likely to adopt the long-term, reward maximizing strategy. This is clearly visible in Figure 6 where the Softmax model consistently under-predicts performance in all conditions except the probabilistic reward condition of Experiment 1.

ET Model

Unlike the Softmax model which is unable to predict maximizing behavior, the Eligibility trace model can account for a shift to the Long-term option given an sufficiently low rate of decay (i.e., additional memory for recent actions). However, despite this additional capability (and an additional parameter), the ET model provides only a marginally improved fit relative to the Softmax model. In particular, Table 2 shows that the the ET model provides a superior fit in continuous rewards condition from Experiment 1 and the nearly equivalent no-cue condition from Experiment 2 relative to the Softmax model. In both of these conditions, participants showed some evidence of a shift towards a reward maximizing strategy. This finding simply reflects the advantage the ET model has over the Softmax model at predicting maximizing behavior in the task. However, despite this ability, the ET model fails to provide an account of human performance in the consistent-cue condition of Experiment 1 that exceeds the Q-learning network model (considered next). In this condition, human participants made roughly 80% of their selections to the Long-term option. Thus, the rapid rate of learning in the consistent-cue condition appears to rule out an account based solely on improved memory for recent actions.

Nevertheless, the best-fit parameters of the ET model did recover the predicted relationship between increased task performance and improved memory. For example, the average decay parameter (ζ) recovered across the no-cue, shuffled-cue, and consistent-cue conditions of Experiment 2 was M=.5 (SD=.29), M=.57 (SD=.34), and M=.70 (SD=.18), respectively. The recovered best-fit ζ was lower in the no-cue condition compared to the consistent-cue condition, t(32) = 2.53, p =.02, however, all other pairwise differences between conditions in Experiment 1 were not significant at the.05 level. On the other hand, with a sufficiently high rate of decay (i.e., ζ → 0), the ET model reduces to the Softmax model. Thus, like the Softmax model, the ET model can also provide an excellent fit in the probabilistic rewards condition of Experiment 1 by assuming rapid forgetting (in this condition the average recovered ζ value was.08 (SD=.21) which was significantly lower than in the continuous rewards condition M=.69 (SD=.26), t(16) = 5.45, p <.001). Pooling across all five conditions, the magnitude of ζ was positively correlated with overall proportion of Long-term responses made in the task, R² =.60, t(67) = 6.16, p <.001. Thus, improved task performance was associated with increased memory for recent actions as assessed by the ET model. Nevertheless, our results suggest that while the inclusion of eligibility traces can improve the account of our data in some conditions, additional memory alone is insufficient to account for the full pattern of results (particularly in the consistent-cue condition from Experiment 2).

Q-Learning network Model

The Q-learning network model achieved a superior fit across all five experimental conditions in Table 2. In Figure 6, the model clearly matches the trial-by-trial dynamics of responding in each condition. Give that this model provides the best overall fit, we subjected it to further analysis.

Parameter Analyses for Q-learning Network Model

Table 3 shows the mean and median parameter values recovered in each condition for the Q-learning network model. In Experiment 1, the best fit parameters reveal greater discounting of future rewards in the probabilistic reward condition (as indicated by a lower setting of γ relative to the continuous rewards case, t(16) = 3.69, p =.002). In all but one case, the best fit value of γ actually approached zero, effectively reducing the Q-learning network model to the Rescorla-Wagner model (Rescorla & Wagner, 1972; Wagner & Rescorla, 1972). Although a higher setting of γ appears to account for the differences in performance between the two conditions of Experiment 1, in general, the γ parameter did not significantly predict final task performance across all five conditions, R² =.19, t(16) = 1.58, p <.11. In addition, we found no significant differences between the setting of γ across the three conditions of Experiment 1.

Table 3.

Recovered parameters for the Q-learning network model including both state-cues (when appropriate) and the magnitude of the reward signal on the last trial as input. The first number in each cell is the mean value of the parameter across all participants assigned to the respective condition. The second number reports the median. Finally, standard deviations are shown in parentheses.

Condition	α	τ	γ
Experiment 1
cont.	.3,.2 (.28)	.02,.01 (.02)	.73,.88 (.38)
prob.	.05,.04 (.4)	.09,.08 (.03)	.1, 0.0 (.32)
Experiment 2
no-cue	.41,.36 (.31)	.03,.001 (.13)	.48,.44 (.42)
shuffled-cue	.16,.13 (.12)	.002,.001 (.002)	.77,.81 (.26)
consistent-cue	.12,.09 (.12)	.002,.001 (.002)	.69,.86 (.34)

The magnitude of the best-fit τ parameter was significantly higher in the probabilistic rewards condition relative to the continuous rewards condition of Experiment 1 (t(16) = 5.32, p < 0.001), suggesting that participants in the probabilistic reward condition were more exploitative of early rewards and less likely to explore. However, few of the other parameters varied in a systematic way across conditions in either experiment. In general, systematic parameter differences between conditions were not expected, as all the participants tested in our experiments came from the same general population and were randomly assigned to conditions. In fact, our inability to detect strong parameter difference in the Q-learning network model between conditions (except for γ in Experiment 1) supports the idea that aspects of the task environment (i.e., the state cues provided in the display) were the primary factors influencing performance.

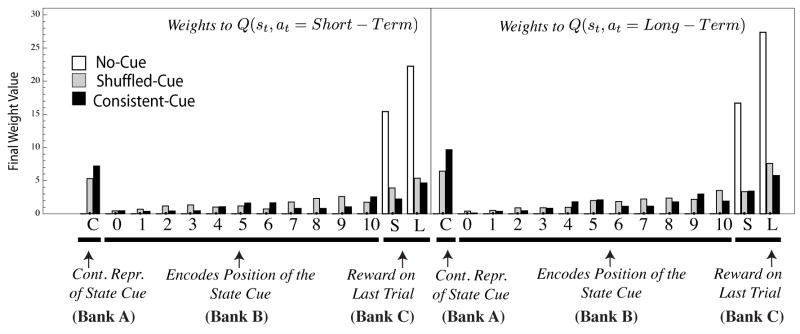
Analyses of Learning Weights

To give further insight into how the Q-learning network model solves the task, Figure 7 shows learning weights in the model in each condition of Experiment 2. For brevity, we focus here on Experiment 2, since the conditions tested predict the strongest differences in the cues used by participants to solve the task (although a similar analysis applies to Experiment 1). These weights are the final setting for each subject following the same procedure used to generate Figure 6⁷. In Figure 7, the horizontal axis of each panel displays the 14 input units to the model. The panels are divided in half, with the left side showing the weights from the input units to the output unit predicting the value of Q(s_t, a_t = Short – Term) (i.e, the Short-term action) and the right side showing the weights to the Q(s_t, a_t = Long – Term) (i.e., the Long-term action).

Figure 7.

The final setting of the learning weights in the Q-learning network model in Experiment 2. For each subject, in each condition, the model predicted the participant’s choices on a trial-by-trial basis and the weights were updated. The setting of the weights following the last trial of the experiment were recorded and averaged within each condition. The horizontal axis of each panel displays the 14 input units to the model shown in Figure 5. The input labeled C represents the continuous representation of the state cue provided in the shuffled-cue and consistent-cue conditions. The inputs labeled 0–10 reflect the discrete encoding of the same cue. Finally, the inputs labeled S and L encoded the magnitude of the reward signal on the previous trial as a result of selecting either the Short-term (S) or Long-term (L) action. The panels are divided in half, with the left side showing the weights from the input units to the output unit predicting the value of Q(s_t, a_t = Short – Term) (i.e, the Short-term action) and the right side showing the weights to the Q(s_t, a_t = Long –; Term) (i.e., the Long-term action) unit.

In the no-cue condition, participants were not provided with any cues about system state, thus the weights coming from the state-cue input units are all zero. However, strong positive weights developed from the input units encoding the reward on the last trial (the bars label S and L in the figure). In addition, the magnitude of the weights connecting these units to the Long-term option (i.e., the right side of the figure) are greater than those connecting to the Short-term option (on the left). In this condition, participants are predicted to have heavily relied on the magnitude of the reward signal on the last trial in constructing a representation of the task. In addition, the weights suggest that participants were able to incorporate an estimate of the future reward available from each state as opposed to just immediate outcomes, since the weights leading to the Short-term output units are smaller in magnitude.

In the consistent-cue condition, the model learned a strong weight from the continuous representation of the state cue (labeled C in the figure). In effect, the model learned to associate the position of the indicator light with increasing future reward. In addition, notice the generally increasing positive weights as you move from left to right along the 11 discrete state-cue input units (reflecting the greater reward available in the higher “numbered” states). In the shuffled-cue condition, a similar pattern emerges⁸. Finally, note that in both the shuffled-cue and consistent-cue condition, the strongest weights in the model are from the continuous state cue input unit (C) to the output units, suggesting the the model’s predictions most heavily relied on presented state cues.

The increased emphasis on input unit C in the shuffled-cue and consistent-cue conditions provides an explanation of the model’s performance. As the value of the weight connecting C to the output units is increased, it allows the model to predict that the estimated value of an action (calculated at the output node) will increase as a function of the current state (i.e., states with larger value on input C result in higher estimated values of reward). The linear input weight allows the model to “extrapolate” learned values from one region of the state space to (as-of-yet) unexperienced states, rapidly improving performance in the task. In the shuffled-cue condition, this “extrapolation” is less effective (since the value of input C does not linearly map onto output values) meaning that the model has to rely more on the discrete cue encoding (inputs 0–10) in order to “bootstrap” the value of particular actions. Overall, this simple principal illustrates how cues which are predictable (in the sense that they allow the value of some state-action pairs to be generalized to other, non-experienced states) can support rapid performance increases.

Evaluating the Role of Inputs

While the Q-learning network model just reported provides an excellent account of human performance in the task, the model assumes a complex set of input cues (as shown in Figure 5). In order to evaluate the specific role that each of these inputs played in contributing to the model fits, we conducted a set of follow-up simulations where we limited the information provided to the Q-learning network model in systematic ways. By comparing the relative fit of the model with and without these various input cues, we can better understand the role that each plays in driving performance. Table 4 summarizes these results. The values reported in the table reflect the improvement (or lack of improvement) in the model fits relative to the baseline model. New parameter fits were conducted in each situation. As in Table 2, positive values in the table reflect instances where the model fit better than baseline and the values are comparable between different models.

Table 4.

Comparison of mean $AI{C}_i^{m-b}$ score for the Q-learning network model when only certain types of inputs are provided relative to baseline. The bank A, B, and C refer to the different types of input illustrated in Figure 5 (i.e., the continuous state cue, the 11 discrete state cues, or the reward from the previous trial, respectively). Again, positive values indicate conditions where the tested model provided a better fit than did the standard while negative value indicate a worse fit. In parentheses is the percentage of participants for whom the model provides a better fit than baseline. The top row (Bank A, B, & C) refers to the full model reported in Table 2.

	Experiment 1
Provided Inputs	no-cue	shuffled-cue	consistent-cue
Bank A, B, & C	93.2 (0.94)	166.7 (0.94)	118.2 (0.94)
No Inputs	−80.2 (0.00)	−81.7 (0.00)	−189.7 (0.00)
Bank A & B only	−80.2 (0.00)	108.8 (0.94)	73.8 (0.88)
Bank A Only	−80.2 (0.00)	−17.5 (0.59)	61.8 (0.88)
Bank B Only	−80.2 (0.00)	93.9 (0.94)	−3.1 (0.47)

The first row of Table 4 shows the results of fitting the full Q-learning network model (also reported in Table 2). This model incorporated both continuous and discrete state cues (when appropriate for the experimental condition) and the reward on the previous trial as input (i.e., input banks, A, B, and C were all enabled). The next row shows a restricted model, where the Q-learning network model was given neither reward or state cues as input (labeled “No Inputs” in the table). Here, the performance of the fit suffers considerably, particular in the shuffled-cue and consistent-cue conditions. Without inputs to distinguish successive task states, the Q-learning network model is unable to learn much in the task and performs well below the baseline model.

Next, we compared the model with the full set of state cues but no reward inputs (i.e., Banks A and B only), continuous state cues only (bank A only), or discrete cues only (Bank B only). When the reward signal from the preceding trial was removed as an input (Bank A & B only), the overall fit of the model dropped somewhat, particularly in the no-cue condition since there was no other information provided to the model that could disambiguate successive task states. The introduction of the continuous state cue (Bank A only) strongly improves performance in only the consistent-cue conditions. This highlights how the irregular behavior of the continuous input cue is of little use in the shuffled-cue condition. In contrast, providing the model with only discrete state cues (Bank B only) improves performance mostly in the shuffled-cue condition. This reflects the fact that participants in the consistent-cue were likely making use of additional information in the task (i.e., a representation that allowed extrapolation such as the continuous state cue). Note that even when the rewards were not provided as input to the Q-learning network model (i.e., Bank C was disabled), fits for the shuffled-cue and consistent-cue conditions exceeded that of the ET model. The fact that even this more limited model (in terms of inputs) out fits the ET model provides further support the idea that state-cues do not simply play the role of a memory cue for participants.

Evaluating the combination of state cues and memory traces

The previous discussion suggests that the ET account alone is insufficient to explain the pattern of results we found in our experiments. However, this is not to say that memory for recent actions does not play a role in task performance. One way to leverage both of these ideas is to include eligibility traces in the Q-learning model to see if they, in combination with state cues, can further improve the fit of the model. We considered two different kinds of eligibility traces. The first were equivalent to the decaying action traces used in Bocagz et al. (2007) (i.e., λ_j in Equation 4). These eligibility traces are additional inputs which effectively track the relative frequency that each action (i.e., a_t = Short – Term or a_t = Long – Term) has been selected in the recent past and are not tied to any particular task state. A second type of eligibility traces is more consistent with Watkins’ (1989) Q(λ) algorithm where eligibility traces are associated with particular state-action pairs, Q(s, a). In order to implement this in our network model, we simply assumed that the discrete inputs (bank B) decayed according to a procedure similar to that used to decay action traces in the ET model above. Each time a state-action pair is visited, the input for that unit is set to 1.0, and traces decay on each time step according to parameter ζ. While this procedure, known as replacing-traces (Sutton & Barto, 1998), differs slightly from the action traces methods (the value is reset to 1.0 instead of incremented by one), it makes the contribution of these cues to the prediction of the network comparable. The key difference between the action traces and state-action traces fits is whether memory was associated with previous actions or with previous state-action pairs. Overall, the inclusion of traces in the Q-learning model raises the number of free parameters to four, however the correction in $AI{C}_i^m$ still allows us to make comparisons between the fit of different models. Besides the inclusion of these additional memory and decay processes, these new models were identical to the Q-learning network tested above (i.e., the same inputs were used and the same simulation procedure).

Table 5 shows the result of two additional fits of the shuffled-cue and consistent-cue conditions from Experiment 2 (we focus here on the shuffled-cue and consistent-cue conditions given that these conditions have the greatest potential for revealing the interaction of eligibility traces and state cues). Unlike previous tables (which compared various models to a baseline), the fit scores shown here compare the standard Q-learning network model to the extended model that included eligibility traces. In many cases, we found that the combination of eligibility traces along with state information allows the Q-learning model to provide a slightly better fit to participant’s choice data. For example, the addition of Bocagz-style action-only eligibility traces (denoted Action Only in the table) provided an improved AIC score for 94% of the participants in the shuffled-cue and consistent-cue condition when compared with the original model. Interestingly, the Q(λ)-style traces (denoted State-Action in the table) provide less of an advantage, only improving the fit for around 60% of the participants. Taken together, these analyses show that including eligibility traces in the Q-learning network at least moderately improves the fit of the model and suggests that both state-cues and memory for past actions (or state-action pairs) may contribute to performance in the task. However, despite the small differences in fit, at this point we are unable to strongly differentiate between the accounts provided by the action-only or state-action traces.

Table 5.

The difference between the $AI{C}_i^m$ score for the standard Q-learning network model described above and the various extensions of this model to include eligibility traces. The first row shows the improvement in fit quality when state cues are combined with the decaying action traces proposed by Bocagz, et al. (2007). The second row shows the improvement in fit quality using decaying state-action traces associated with previous inputs to the network (consistent with the Q(λ) algorithm of Watkins, 1989). As in the previous tables, positive values indicate conditions where the extended model provided a better fit on average than did the more restricted model controlling for the additional parameters. In parentheses is the percentage of participants for whom the extended model provides a better fit than the original.

	Experiment 1
Types of Traces	shuffled-cue	consistent-cue
Action Only	11.4 (0.94)	8.8 (0.94)
State-Action	6.8 (0.65)	4.1 (0.59)

Discussion

Returning to the questions posed at the beginning of this section, our simulations show how learners may draw upon a variety of perceptual cues in order to overcome the problem of perceptual aliasing. Simulations with our Q-learning network model provided a better fit to individual participant’s choice sequences than did a number of other learning mechanisms. This model predicts that participants utilize cues in the environment to help construct a representation of the state structure of the task. Indeed, our motivation for the manipulations reported in Experiment 2 was the central role that such state representations play in contemporary RL approaches.

We found that systematically changing the types of input cues provided to the Q-learning network model dramatically modulates its ability to account for participant’s behavior in different conditions. When the experimenter-provided cues were absent (such as in the Experiment 2, no-cue condition), the model often failed to elaborate the full state representation of the task and, as a result, had trouble learning the reward structure. When provided with cues that were in concert with the underlying state structure of the task environment (e.g., consistent-cue condition, Experiment 2), participants generalized across related states and learned to choose the long-term (optimal) option. In our simulations of the shuffled-cue condition, we found the model accounted for the intermediate levels of performance we observed in our experiment. In some fits, the model was able to use the structure of input cues to disambiguate task-relevant states, while in other cases, the lack of continuity between the state cues caused the model (and participants) to become trapped in sub-optimal solutions. Overall, these differences were well explained in the model by assuming that the perceptual cues in the task helped participants to disambiguate successive task states and to generalize the experience from one state to others. In fact, we failed to find strong differences between the best-fit parameter distribution across the three conditions of Experiment 2, which is consistent with the idea that aspects of the task environment were the major factors influencing performance.

Concerning the second question raised at the beginning of this section, we found evidence that the primary function of the perceptual cues was to make apparent when states of the environment were changing as a results of participants’ actions. An alternative account, provided by the ET model, is that state cues simply help participants remember their relative allocation of choices to each option. While our fits with the ET model did recover the predicted relationship between state cues and the rate of memory decay (participants given the more predictable cues also were better fit using a lower rate of memory decay), the ET model failed to account for the rapid improvement in learning we found in the consistent-cue condition. The key difference between the ET and Q-learning network model was how experience was generalized from one state to the next. In the Q-learning network model, consistent state cues facilitated “extrapolation” of the estimated value from one state to related states. Thus, the ability to generalize experience between states appears to be a critical factor influencing optimal behavior in the task.

General Discussion

In this paper, we evaluated human performance in a dynamic decision making task which placed short- and long-term rewards in conflict. Optimal performance in the task required learners to engage a complex set of cognitive processes including learning, generalization, exploration/exploitation, and the appreciation of delayed rewards. In order to better understand the contribution of these processes to performance in the task, we tested a number of simple computational models based on contemporary work in RL (Sutton & Barto, 1998). The results establish how learners’ mental representations of the task environment can influence their ability to discover an optimal response strategy. In our experiments, participants who were given perceptual cues, which limited the aliasing of distinct task states, outperformed participants lacking these cues. In dynamic and complex task environments, the state representation that the learner adopts may act as a kind of “framework” for effectively structuring, integrating, and generalizing experiences. Overall, our results are consistent with the account provided by the simple network model that motivated our studies and join a number of recent papers providing encouraging support for using RL methods to model human behavior in sequential decision making tasks (Fu & Anderson, 2006; Neth et al., 2006; Sun, Slusarz, & Terry, 2005). In the following sections we highlight some of the contributions and implications of our results.

The Importance of “State”

First, while the concept of “state” is central to RL systems that are rooted in the mathematics of Markov Decision Processes, little work has directly examined how this construct might apply in human learning tasks. Our results demonstrate how the state representations participants use to structure their experiences can have an important impact on their learning performance. In Experiment 2, we presented participants with cues that reflected the current underlying state of the Mars farming system. In a condition where these cues were absent, participants settled on a largely sub-optimal response strategy. However, when present, cues about system state helped participants overcome the allure of the short-term rewards and instead make choices that maximized their long-term benefit. In addition, our results showed that cues that were predictable and well matched to the underlying state-transition dynamics of the environment (such as those in the consistent-cue condition of Experiment 2) were more effective than those which were incongruent with the task structure (the shuffled-cue condition).

These findings are largely consistent with work demonstrating how signals indicative of the current state of the environment may help decision makers develop optimal strategies. For example, Herrnstein et al. (1993, Experiment 1) used a task similar to our own and found that participants were more likely to maximize when provided with an arrow that indicated the number of responses the participant made to the maximizing choice option over the relevant choice history. Similarly, Sanabria et al. (2003) had pigeons “play” the iterated prisoner’s dilemma against a computer opponent that followed a tit-for-tat strategy (Axelrod, 1984). Consistent with work in the maximization/melioration paradigm, pigeons preferred a short-term “defect” strategy on every trial. However, when the pigeons were given a secondary cue reflecting their choice on the last trial (i.e., the current state of the tit-for-tat opponent), behavior shifted toward the reward-maximizing “cooperate” option.

Taken together, our experimental results and simulations highlight how state representations that are poorly matched or incongruent with the true dynamics of the environment can lead to sub-optimal responding. Our results suggest a theoretical distinction between evaluating behavior with respect to the structure of reward in the environment or with respect to a learner’s representation of that environment. The RL models we tested learn to approximate optimal or rational solutions to the problem at hand, but are largely limited by the representation of the task that the model adopts. Thus, failures of rational choice in particular situations may be illusory when we fully consider the cognitive representations over which behavior operates.

Memory in the World and in the Head

Our simulations comparing the ET model and the Q-learning network model raise an interesting question about the function of state cues in the task. On the one hand, cues about task state may help to disambiguate situations that call for different behavioral responses (preventing aliasing). On the other hand, such cues may serve as a memory aid about the recent history of actions. While our simulations appear to support the state-based interpretation, these two perspectives may not be completely at odds. In a sense, the perceptual cues provided in the task may serve as a kind of externalized memory (Triesch, Ballard, Hayhoe, & Sullivan, 2003), helping to reduce the load on cognitive resources by offloading memory into the environment. One prediction following from this idea is that performance in the Farming on Mars task may be more resistant to the effects of additional working memory load when highly discriminable state cues are available in the task environment.

On a related point, Bocagz et al. (2007) report a series of experiments showing that the time between successive trials in a similar decision making task can influence the degree to which participants uncover a long-term strategy. In their account, participants maintain a memory (using eligibility traces) of recent actions that decay over time. Faster inter-trial interval allow less decay, and thus improve task performance. While the account we provide based on state representations does not directly address the issue of stimulus timing, it would be possible to augment our Q-learning network model with time-based eligibility traces as well (the final model fits combining eligibility traces in the model assumed trial-based decay). Thus, while in our simulations we report evidence favoring a state-based account over one based entirely on memory, these two perspectives are not necessarily at odds. Indeed, our follow up fits combining state cues and eligibility traces suggest both processes may contribute to participant’s choices. Manipulations that improve participant’s memory for the task and which make task-relevant states more distinguishable are likely complementary, albeit psychologically distinct, routes to improving performance.

Limitations and Future Work

While we found that our Q-learning network model accounts for human performance across a variety of manipulations, the model cannot account for all aspects of our data. For instance, in our studies, participants were more likely to choose the Short-Term robot selection when informed that the experiment was about to end. However, the simple model we developed is not equipped to alter its preferences based on knowledge of the task horizon online in the task. One possible extension to our model that addresses this shortcoming is for the model to maintain multiple estimates of state-action values based on different settings of the temporal discounting parameter, γ, and to use the setting suggested by current knowledge of the task horizon. Alternatively, participants may have engaged explicit reasoning processes about the nature of the reward contingency and realized that the most effective strategy near the end of the experiment was to select the impulsive, short-term option (a behavior that might be accounted for with RL models that incorporate planning, Daw, Niv, & Dayan, 2005). Similarly, we are unable to assess yet the role that explicit reasoning processes may have played in accounting for the differences between the shuffled-cue and consistent-cue conditions of Experiment 2 (although the Q-learning model appears to provide an excellent fit to participant’s trial-by-trial choices).

On the theoretical side, our results provide a first step in linking work in category learning and generalization into models of sequential choice (see also Redish, Jensen, Johnson, & Kurth-Nelson, 2007 for recent work on this issue). In our simulations, we showed how cues that allowed extrapolation or generalization of the experience in one part of the state space to others could improve performance. This opens opportunities for evaluating the role that generalization and category creation (Carpenter & Grossberg, 1988; Love, Medin, & Gureckis, 2004; Sutton, 1996) have on performance in online, sequential choice tasks. In our experiments, we manipulated how apparent particular representations of the world were to participants, however, additional work is needed to understand how learners might uncover these regularities for themselves through experience.

Finally, while our results and discussion appear to suggest a universally positive role of state information, it is also important to keep in mind that the usefulness of state information may interact with the reward structure of the task. For example, if the Farming on Mars task was changed so that the option which earned the most reward in the short-term also earned the most in the long-term, it would be much easier to learn a policy that exploits the globally superior option on every trial even when underlying task states are not clearly distinguished. Ultimately, the representation that a learner should adopt is likely influenced by their current goals and the reward structure of the task.

Implications

Humans posses an amazing capacity for interacting with and controlling the ongoing dynamics of their environment across a variety of tasks and situations (c.f., Berry & Broadbent, 1988; Chhabra & Jacobs, 2006; Stanley et al., 1989). However, like Aesop’s grasshopper, when we fail to take into account how immediately attractive options might conflict with our longer-term well-being, we often suffer the consequences. For example, patients with medical conditions such as heart disease may continue to maintain an unhealthy diet despite the best advice from their doctors. One reason for this failure to appreciate the consequences of delayed outcomes may be that it is often difficult to perceive the relevant cues about our health state (e.g., high blood pressure, weight gain) that are changing as a result of our actions. The conclusion from the present studies is that the preference for Short-Term rewards can, in some circumstances, be overcome by providing informative cues that make clear the underlying structure and dynamics of the environment.