Super-Resolution Laser Scanning Microscopy through Spatiotemporal Modulation

Abstract

Super-resolution optical microscopy has attracted great interest among researchers in many fields, especially in biology where the scale of physical structures and molecular processes fall below the diffraction limit of resolution for light. As one of the emerging techniques, structured illumination microscopy can double the resolution by shifting unresolvable spatial frequencies into the pass-band of the microscope through spatial frequency mixing with a wide-field structured illumination pattern. However, such a wide-field scheme typically can only image optically thin samples and is incompatible with multiphoton processes such as two-photon fluorescence, which require point scanning with a focused laser beam. Here, we propose two new super-resolution schemes for laser scanning microscopy by generalizing the concept of a spatially nonuniform imaging system. One scheme, scanning patterned illumination (SPIN) microscopy, employs modulation of the excitation combined with temporally cumulative imaging by a nondescanned array detector. The other scheme, scanning patterned detection (SPADE) microscopy, utilizes detection modulation together with spatially cumulative imaging, in this case by a nondescanned single-element detector. When combined with multiphoton excitation, both schemes can image thick samples with three-dimensional optical sectioning and much improved resolution.

It has been well known since the late nineteenth century¹ that the resolution of optical microscopes is limited by diffraction. This phenomenon is clearly explained by the theory of Fourier optics^2,3 in which the resolution limit of a microscope is given by the extent of its optical transfer function (OTF), the normalized Fourier transform of the point spread function (PSF). The microscope essentially functions as a low-pass filter, rejecting spatial frequencies in the specimen that lie beyond the bandwidth of the OTF.

The length scale of many biological structures and molecular processes is, however, below the diffraction limit, so they cannot be resolved with conventional optical microscopes. This situation has motivated many attempts to break the diffraction limit and achieve super-resolution. Prior knowledge about the object (e.g., its finite size and nonnegativity) has been utilized to recover or extrapolate the object spectrum beyond the pass-band of the microscope.^4–13 Nonlinear effects in fluorescence excitation have been exploited to confine fluorescence emission to a volume smaller than defined by the diffraction limit, as demonstrated in two-photon laser scanning microscopy (2PLSM).^14–17 Utilizing saturated stimulated emission to spatially restrict the fluorescence PSF, stimulated emission depletion (STED) microscopy achieved a true far-field diffraction-unlimited spatial resolution for the first time.^18–23 In particular, a record of 5.8 nm resolution has been recently reported with STED.²² The introduction of photoswitchable molecules enables activation and imaging of a random, sparse set of individual molecules, each of which can be localized to the centroid of its PSF with a precision much smaller than the diffraction limit. This feature has been utilized in recently developed photoactivated localization microscopy (PALM),^24–28 fluorescence photoactivation localization microscopy (FPALM),^29–31 and stochastic optical reconstruction microscopy (STORM).^32–35 Finally, particularly relevant to the present study is the use of nonuniform illumination fields to “shift” out-of-band specimen frequencies into the pass-band of the microscope through spatial frequency mixing with the illumination field, as in structured illumination microscopy (SIM) for wide-field fluorescent imaging.^36–42 One particular advantage of SIM over other super-resolution techniques is that SIM does not require special fluorescent probes or high-intensity radiation.

We will briefly review the principles of SIM in the background section. Here it suffices to point out that in current implementations of SIM, the illumination field is generated through interference of coherent light over the entire field of view, using either diffraction gratings⁴¹ or spatial light modulators.⁴³ Such wide-field illumination has its limitations. It is incompatible with optical processes that require high intensity of excitation light (e.g., two-photon fluorescence), which is only practical when focused laser beams are scanned through the specimen. Furthermore, wide-field illumination limits imaging depth so typically only thin samples, such as cultured cells, can be effectively imaged.

In this paper, we propose and compare two new super-resolution microscopy schemes. These schemes generalize the concept of a spatially nonuniform imaging system to laser scanning microscopy with either spatial or temporal modulation. Both schemes can image thick samples with optical sectioning when two-photon excitation is used. In addition, they are compatible with nonfluorescent processes such as spontaneous Raman scattering. They achieve maximal resolution improvement by a factor of 2 over conventional wide-field microscopy.

Background

As incoherent imaging is exemplified by fluorescent microscopy, we will use the term “fluorophore” to refer to any incoherent point light source for brevity. Furthermore, we assume that fluorescence excitation and detection are not saturated, so the signal is linear with respect to the distribution of fluorophore concentration. For notational simplicity we write equations mostly for the one-dimensional (1D) system, and only explicitly write equations for the 2D system when significant differences arise between 1D and 2D cases. Without loss of generality, we assume the magnification of the microscope to be unity, and omit unessential constant factors in the equations.

Let h_ex(•) denote the excitation PSF, and h_em(•) the emission PSF. Both PSFs are normalized so that the peak value is 1. Let I_ex(r),r ∈ ℝ be the illumination field, the intensity distribution of excitation light, where r indicates position on the specimen plane (Figure 1). Let I_em(r) be the fluorescence emission field, the intensity of fluorescence emitted at point r on the specimen plane. When fluorophore excitation is not saturated, I_em is proportional to the illumination field and to the fluorophore concentration, I_em(r) = I_ex(r)s(r).

Figure 1.

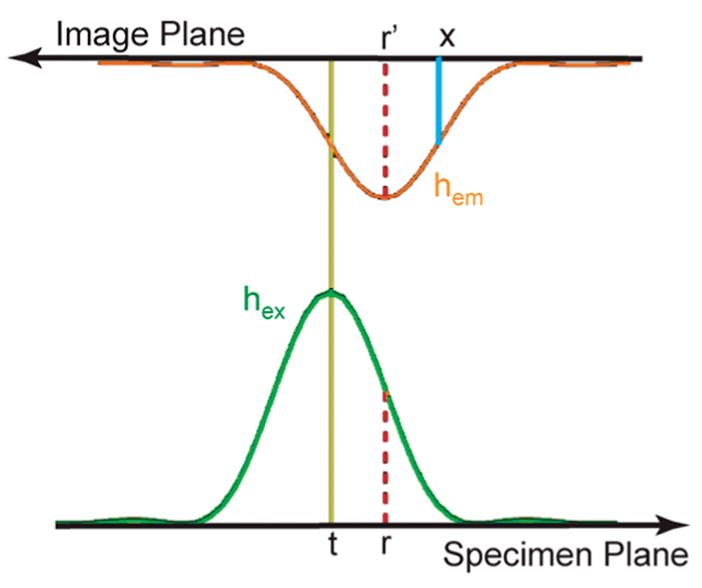
Schematic of image formation with a focused spot illumination. A focused excitation light spot, given by the excitation PSF h_ex (green trace) centered at t, is imposed on the specimen plane. Fluorophores at position r are excited with intensity h_ex(r − t) as indicated with the red dotted line. Emitted fluorescence is focused onto the image plane as an emission PSF h_em (orange trace). Note that the positive direction of the image plane has been reversed so that point r and its conjugate point r′ are aligned in the schematic (red dotted lines). Its contribution to the pixel value at x is proportional to h_em(x − r).

Let I_im(x),x ∈ ℝ be the light intensity distribution on the image plane (Figure 1). We shall refer to I_im as the image field, which is given by

$$\begin{array}{rl}{I}_{\text{im}}(x)& =\int I_{\text{em}}(r)h_{\text{em}}(x-r)\text{d}r\\ & =\int I_{\text{ex}}(r)s(r)h_{\text{em}}(x-r)\text{d}r\end{array}$$ (1)

An absorbing mask with transmittance M(x) may be inserted at the image plane, and the signal that is transmitted is given by M(x)I_im(x) as linearity is assumed. To avoid confusion, we reserve the term “image” for the light distribution on the image plane, and refer to final images produced by the detector as “pictures” denoted by p(•).

We will now briefly review the principle of SIM with wide-field illumination (henceforth referred to as WF-SIM) in 1D. Detailed formulas for the 2D case have been given previously^38,44 and will not be repeated here. In WF-SIM, the structured illumination field I_ex is created through interference of coherent waves, and assumes for example the form

$$I_{\text{ex}}(r)=\frac{1}{2}[1+cos({\omega }_{\text{r}}•r)]$$ (2)

where ω_r is the spatial frequency of the illumination field in radians per unit length.

In Fourier space, this illumination field is represented as

$${\stackrel{\sim }{I}}_{\text{ex}}(k)=\pi \left[\delta (k)+\frac{\delta (k-{\omega }_{\text{r}})}{2}+\frac{\delta (k+{\omega }_{\text{r}})}{2}\right]$$ (3)

where k is the spatial frequency, δ(•) is the Dirac delta function, and tilde over a function indicates its Fourier transform. In particular, h̃_ex and h̃_em will denote the excitation and emission OTF, respectively.

Wide-field fluorescence is detected with a charge-coupled device (CCD) camera and gives

$$\begin{array}{rl}p(x)& =\int I_{\text{ex}}(r)s(r)h_{\text{em}}(x-r)\text{d}r\\ & =[I_{\text{ex}}(x)s(x)]\otimes h_{\text{em}}(x)\end{array}$$ (4)

where ⊗ denotes convolution.

With the structured illumination field given in eq 2, Fourier transform of eq 4 yields

$$\begin{array}{rl}\stackrel{\sim }{p}(k)& =[{\stackrel{\sim }{I}}_{\text{ex}}(k)\otimes \stackrel{\sim }{s}(k)]{\stackrel{\sim }{h}}_{\text{em}}(k)\\ & =\pi \left[\stackrel{\sim }{s}(k)+\frac{\stackrel{\sim }{s}(k-{\omega }_{\text{r}})}{2}+\frac{\stackrel{\sim }{s}(k+{\omega }_{\text{r}})}{2}\right]{\stackrel{\sim }{h}}_{\text{em}}(k)\end{array}$$ (5)

where we have used the fact δ(x − x₀) ⊗ f(x) = f(x − x₀).

Equation 5 shows that frequency components k ± ω_r of s̃ are shifted by the structured illumination field into the pass-band given by h̃_em. Now each p̃ (k) in the recorded picture is the linear combination of three terms, as shown in eq 5. In order to solve for each term, two additional equations are needed. These extra relations are given by shifting the illumination pattern with respect to the specimen as

$$I_{\text{ex}}^{\pm \varphi }(r)=\frac{1}{2}[1+cos({\omega }_{\text{r}}•r\pm \varphi )]$$ (6)

where ϕ ≡ ω_r•r₀ indicates displacement in the specimen plane. In Fourier space, such shifts contribute phase factors to the pictures

$$\begin{array}{rl}{\stackrel{\sim }{p}}^{\pm \varphi }(k)=& \{\pi [\delta (k)+\frac{1}{2}\delta (k-{\omega }_{\text{r}})exp\left(\pm i\frac{\varphi }{{\omega }_{\text{r}}}k\right)+\frac{1}{2}\delta (k+{\omega }_{\text{r}})\\ & exp\left(\pm i\frac{\varphi }{{\omega }_{\text{r}}}k\right)]\otimes \stackrel{\sim }{s}(k)\}{\stackrel{\sim }{h}}_{\text{em}}(k)\\ =& \pi \left[\stackrel{\sim }{s}(k)+\frac{\stackrel{\sim }{s}(k-{\omega }_{\text{r}})e^{\pm i\varphi }}{2}+\frac{\stackrel{\sim }{s}(k+{\omega }_{\text{r}})e^{\pm i\varphi }}{2}\right]{\stackrel{\sim }{h}}_{\text{em}}(k)\end{array}$$ (7)

where the sifting property of δ-function has been used, as well as the fact that the Fourier transform of f(x − a) is f̃(k)e^−iak. Notice that the phase factor e^±iϕ does not depend on the frequency k.

For each frequency k, s̃(k), s̃(k − ω_r), and s̃(k + ω_r) can be solved by combining eq 5 and 7, if the emission OTF h̃_em and the shift φ are known. Out-of-band frequencies in s̃ can be then “shifted back.” Because I_ex is diffraction-limited, the maximal spatial frequency it introduces is ${\omega }_{\text{r}}={\omega }_{\text{ex}}^{\text{c}}$, the cutoff frequency of h̃_ex. The final picture p is band-limited by ${\omega }_{\text{em}}^{\text{c}}$, the cutoff frequency of h̃_em. Therefore, the effective bandwidth of WF-SIM is ${\omega }_{\text{eff}}^{\text{c}}={\omega }_{\text{ex}}^{\text{c}}+{\omega }_{\text{em}}^{\text{c}}$, which gives approximately twice the resolution of conventional microscopy if the difference between excitation and emission wavelengths is ignored.

In the 2D system, applying the modulation pattern along a particular direction (not necessarily a coordinate axis) extends the bandwidth only along the corresponding direction in the (k_x,k_y) space. Thus in order to extend the bandwidth isotropically in the (k_x,k_y) space, it is in theory necessary to apply modulation patterns along an infinite number of directions. In practice, however, modulating along the x- and y-axis gives substantial, although nonisotropic, improvement in resolution,³⁸ whereas using a set of three orientations of the modulation pattern separated by 2π/3 radians gives an almost isotropic improvement in resolution.³⁷

Results. 1. Laser Scanning Microscopy with Modulated Scanning and Temporally Cumulative Imaging

The first scheme we propose is scanning patterned illumination (SPIN) microscopy. In this scheme (Figure 2), excitation intensity is modulated as scanning proceeds. Pictures are cumulatively built up with a nondescanned, spatially resolved detector such as a CCD camera located at the image plane. Similar detector arrangement has been utilized in multifocal multiphoton imaging.^45,46

Figure 2.

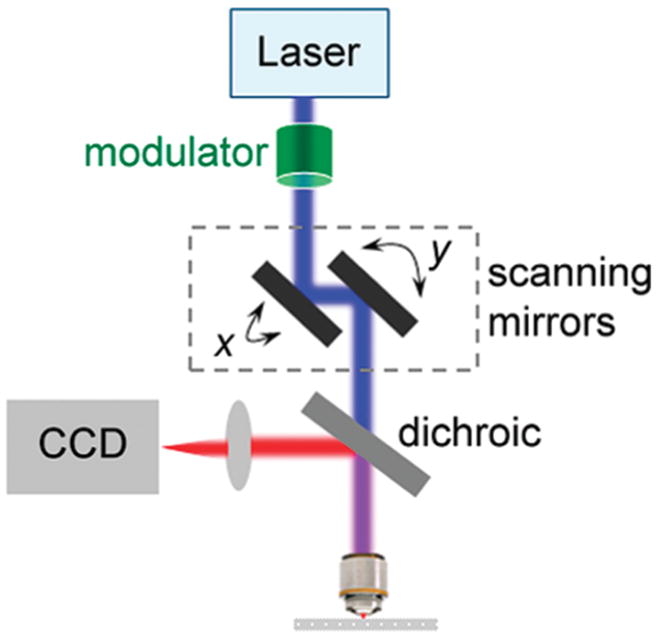
Schematic of laser scanning super-resolution microscopy through modulated scanning and temporally cumulative imaging. On top of a standard laser scanning microscope, the peak intensity of the focused excitation spot is temporally modulated in a controlled manner, while the spot scans across the specimen. The epi-collected fluorescence signal, after spectrally separated from the excitation light by a dichroic and/or a filter, is imaged onto a nondescanned CCD camera. Each complete frame scanning with a particular modulation sequence builds up one CCD-picture cumulatively. Several such CCD-pictures are generated with a set of modulation sequences that are phase-shifted in space in order to reconstruct a super-resolution image of the specimen.

Assume that scanning proceeds at constant speed v ≡ 1, and we shall henceforth use t to refer to both time and the position of the scanning spot center at that particular time. The emission field I_em(r) is given by:

$$I_{\text{em}}(r,t)=I_{\text{ex}}^{max}(t)h_{\text{ex}}(r-t)s(r)$$ (8)

where $I_{\text{ex}}^{max}\in [0,1]$ is the normalized peak intensity of the scanning Airy disk. $I_{\text{ex}}^{max}$ is modulated over time as

$$I_{\text{ex}}^{max}(t)=\frac{1}{2}[1+cos({\omega }_{\text{t}}•t)]$$ (9)

where ω_t is the temporal modulation frequency, and the DC component serves to ensure that $I_{\text{ex}}^{max}\ge 0$.

As scanning proceeds, the detector cumulatively builds up I_im(x,t), which is given in a form similar to eq 1. This temporal integration yields the picture

$$\begin{array}{rl}p(x)& =\iint I_{\text{ex}}^{max}(t)h_{\text{ex}}(r-t)s(r)h_{\text{em}}(x-r)\text{d}r\text{d}t\\ & =\int [\int I_{\text{ex}}^{max}(t)h_{\text{ex}}(r-t)\text{d}t]s(r)h_{\text{em}}(x-r)\text{d}r\\ & =\{[I_{\text{ex}}^{max}(x)\otimes h_{\text{ex}}(x)]s(x)\}\otimes h_{\text{em}}(x)\end{array}$$ (10)

where the order of integration has been exchanged, and the fact that PSFs are even functions is used.

In eq 10 the term $I_{\text{ex}}^{max}(x)\otimes h_{\text{ex}}(x)$ plays the role of the structured illumination field I_ex in WF-SIM as shown in eq 4. In other words, the spatially structured illumination field has been synthesized through modulation of the peak intensity of the scanning spot. This fact can be better appreciated by examining eq 10 in the Fourier space, which yields

$$\stackrel{\sim }{p}(k)=\{[{\stackrel{\sim }{I}}_{\text{ex}}^{max}(k){\stackrel{\sim }{h}}_{\text{ex}}(k)]\otimes \stackrel{\sim }{s}(k)\}{\stackrel{\sim }{h}}_{\text{em}}(k)$$ (11)

${\stackrel{\sim }{I}}_{\text{ex}}^{max}(k)$ has the same form as Ĩ_ex(k) in eq 3. Because of the sifting property of the δ-function, ${\stackrel{\sim }{I}}_{\text{ex}}^{max}$ picks up the DC as well as the ± ω_t components of h̃_ex, which yields the following effective illumination field Ẽ_eff(k)

$$\begin{array}{l}{\stackrel{\sim }{E}}_{\mathit{eff}}(k)=\\ \pi \left[{\stackrel{\sim }{h}}_{ex}(0)\delta (k)+\frac{1}{2}{\stackrel{\sim }{h}}_{ex}({\omega }_t)\delta (k-{\omega }_t)+\frac{1}{2}{\stackrel{\sim }{h}}_{ex}(-{\omega }_t)\delta (k+{\omega }_t)\right]\end{array}$$ (12)

Because h̃_ex is bandwidth-limited with cutoff frequency ${\omega }_{\text{ex}}^{\text{c}}$, the temporal modulation frequency ω_t of $I_{\text{ex}}^{max}$ must be chosen to lie within the pass-band [ $-{\omega }_{\text{ex}}^{\text{c}},{\omega }_{\text{ex}}^{\text{c}}$]. The effect of subsequent convolution with s̃(k) and multiplication with h̃_em(k) is completely analogous to the process described for WF-SIM and gives the relationship

$$\begin{array}{l}\stackrel{\sim }{p}(k)=\\ \pi \left[{\stackrel{\sim }{h}}_{\text{ex}}(0)\stackrel{\sim }{s}(k)+\frac{1}{2}{\stackrel{\sim }{h}}_{\text{ex}}({\omega }_{\text{t}})\stackrel{\sim }{s}(k-{\omega }_{\text{t}})+\frac{1}{2}{\stackrel{\sim }{h}}_{\text{ex}}({\omega }_{\text{t}})\stackrel{\sim }{s}(k+{\omega }_{\text{t}})\right]{\stackrel{\sim }{h}}_{\text{em}}(k)\end{array}$$ (13)

In order to solve for each s̃(k), the intensity modulation pattern $I_{\text{ex}}^{max}(t)$ should be shifted as described in eq 6 to produce additional pictures p̃^±ϕ(k). The same algorithm as used in WF-SIM can then be applied to solve and back-shift s̃(k). Again, the maximal effective bandwidth is given by ${\omega }_{\text{ex}}^{\text{c}}+{\omega }_{\text{em}}^{\text{c}}$, just as in WF-SIM. The effect of SPIN is simulated on an image of a (very small) zebra with custom-written Matlab scripts assuming the following parameters: objective lens numerical aperture NA = 1.4, excitation wavelength λ_ex= 488 nm, emission wavelength λ_em= 535 nm, and temporal modulation period T_t = 1/ω_t = 300 nm, which is slightly larger than the resolution limit (~200 nm) to ensure sufficient signal-to-noise ratio. For simplicity we followed Frohn et al.³⁸ and applied the modulation pattern only along the x- and y-axis. As mentioned before, more isotropic resolution improvement can be achieved by applying modulation patterns along a set of 3 orientations. The SPIN reconstructed picture is shown in Figure 4C. The “true” object (Figure 4A) and simulated wide-field fluorescence image (Figure 4B) are given for comparison.

Figure 4.

Simulation of SPIN and SPADE microscopy (A) The object is assumed to have 50 nm pixels. In all images shown here, gray levels are normalized to [0,1] to facilitate visual comparison. (Insets here and below) Magnified views of the boxed region of the zebra head. In all panels below, the coordinate axes are defined as shown here. Scale bar: 1 μm. (B) Simulated wide-field fluorescence image with Poisson noise. The number of expected photons per pixel is set to ~3000 on average and ~10 000 at maximum. Emission wavelength λ_em = 535 nm, objective lens numerical aperture (NA) = 1.4, and the theoretical emission PSF is given by h_em(r) = [2J₁(v)/v]², where v ≡ 2πrNA/λ is the normalized lateral or transversal optical coordinate, and J₁ is the Bessel function of the first kind of order 1. This gives the resolution limit d ≡ λ_em/(2NA) = 191 nm, defined as the inverse of the highest spatial frequency passed by the microscope. (C) An example of the spatial and temporal modulation patterns along the x-axis. Pictures reconstructed with SPIN and SPADE were both generated using sinusoidal modulation patterns along the x- and y-axis with three shifts along each axis (φ = 0, ± ω_t). The modulation period is 300 nm. This modulation scheme is similar to the WF-SIM illumination pattern used by Frohn et al.³⁸ (D) Picture reconstructed with SPIN. Excitation λ _ex = 488 nm, emission λe_em = 535 nm, and the modulation period T_t = 300 nm. Poisson noise was applied to pictures generated with structured illumination (not shown), as described in (B). Each set of x-shifted frequencies s̃(k_x − ω_t,k_y), s̃(k_x,k_y), and s̃(k_x + ω _t,k_y) were reconstructed from three pictures with modulations along the x-axis. Analogously, each set of y-shifted frequencies were reconstructed from three pictures with modulations along the y-axis. Wiener filtering is used to invert the multiplication with h̃_em(k_x,k_y) in which the regularization parameter (1/SNR) is set to 1.4%. The effective resolution is $d_{\text{eff}}={(d^{-1}+T_{\text{t}}^{-1})}^{-1}=117\text{nm}$. Notice the vertical stripes on the nose of the zebra; they show up with SPIN and SPADE (E) but are unresolved in the wide-field image (B). (E) Picture reconstructed with SPADE. Imaging parameters identical to (D) with mask patterns the same as intensity modulation patterns in (D). Mask spatial modulation period T_s = 300 nm. Poisson noise was applied to pictures generated with structured detection (not shown), as described in (B), and reconstruction of each frequency s̃(k_x,k_y) proceeded as in (D). The effective resolution is the same as (D).

The intensity modulation $I_{\text{ex}}^{max}$ does not have to be sinusoidal. In two dimensions, a practically simpler implementation is to “jump scan”, that is, scan a few lines, then skip the next few lines, while the intensity on the scanned lines is kept constant. This makes $I_{\text{ex}}^{max}(x,y)$ a square wave along the direction perpendicular to the fast axis (say, the x-axis) of the scanning pattern. This square wave contains an infinite number of harmonics of the fundamental spatial frequency ω_y along the y-axis. However, ω_y can be chosen such that all higher harmonics are cutoff by the excitation OTF, and eq 12 remains valid with only changes in constant factors.

When choosing $I_{\text{ex}}^{max}$ in two dimensions, one has to consider the available scanning mechanism. Modulation along the coordinate axes is compatible with both point-wise intensity modulation (e.g., through an acousto-optical modulator, AOM) and the “jump scan” discussed above. Modulation oblique to the coordinate axes can be implemented with AOM. Jump scan oblique to the coordinate axes, however, cannot be performed straightforwardly if the two scanning mirrors are not equivalent (e.g., one strictly fast and one slow).

When SPIN is combined with 2PLSM, the nonlinearity in 2-photon excitation yields the following relationship

$$\begin{array}{rl}p(x)& =\iint {[I_{2\text{P}}^{max}(t)h_{2\text{P}}(r-t)]}^{2}s(r)h_{\text{em}}(x-r)\text{d}r\text{d}t\\ & =\{[{(I_{2\text{P}}^{max}(x))}^2\otimes h_{2\text{P}}^2(x)]s(x)\}\otimes h_{\text{em}}(x)\end{array}$$ (14)

where $I_{2\text{P}}^{max}$ is the peak intensity of the 2-photon scanning spot, and h_2P is the 1-photon PSF at the infrared wavelength used in 2PLSM, which has cutoff frequency ${\omega }_{\text{ex}}^{\text{c}}$. Thus $h_{2\text{P}}^2$ is the effective 2-photon PSF, which has cutoff frequency $2{\omega }_{\text{ex}}^{\text{c}}$. If $I_{2\text{P}}^{max}$ assumes the form as in eq 9, it gives ${(I_{2\text{P}}^{max})}^2={[1+cos({\omega }_{\text{t}}•t)]}^2=3/2+2cos({\omega }_{\text{t}}•t)+cos(2{\omega }_{\text{t}}•t)/2$, where the prefactor 1/2 in eq 9 is omitted. Thus the harmonic 2ω_t is introduced. If ω_t is larger than ${\omega }_{\text{ex}}^{\text{c}}$, this harmonic falls outside the pass-band of the effective 2-photon OTF. Otherwise, this harmonic contributes to p(x), which complicates subsequent manipulations and thus should be avoided. Alternatively, as the modulation pattern $I_{2\text{P}}^{max}$ is created by controlling laser intensity and can take arbitrary functional forms, a nonsinusoidal pattern can be employed. For instance, as suggested by one reviewer, $I_{2\text{P}}^{max}(t)={[1+cos({\omega }_{\text{t}}•t)]}^{1/2}$ yields ${(I_{2\text{P}}^{max})}^2=1+cos({\omega }_{\text{t}}•t)$ as desired.

2. Laser Scanning Microscopy with Modulated Detection and Spatially Cumulative Imaging

In the above scheme of SPIN, when $I_{\text{ex}}^{max}(t)$ is a constant, I_im(x,t) has the functional form

$$I_{\text{im}}(x,t)=\int h_{\text{ex}}(r-t)s(r)h_{\text{em}}(x-r)\text{d}r$$ (15)

As h_ex and h_em are both even functions, there is clearly a symmetry between x and t in eq 15 if we ignore the difference between h_ex and h_em. It suggests an alternative scheme for super-resolution. In this scheme (Figure 3), the peak intensity of the scanning spot is kept constant, and modulation is imposed by inserting a mask with transmittance M(x) =(1/2)[1 + cos(ω_s•x)] on the image plane, where ω_s is the spatial modulation frequency. We thus term this scheme scanning patterned detection (SPADE) microscopy. In SPADE, a single-element detector (e.g., a photomultiplier tube, PMT) with a large detection area is placed behind the mask. The detector sums up all transmitted signals through the mask and assigns the sum to the pixel corresponding to the current scanning position. This scheme produces the following picture

Figure 3.

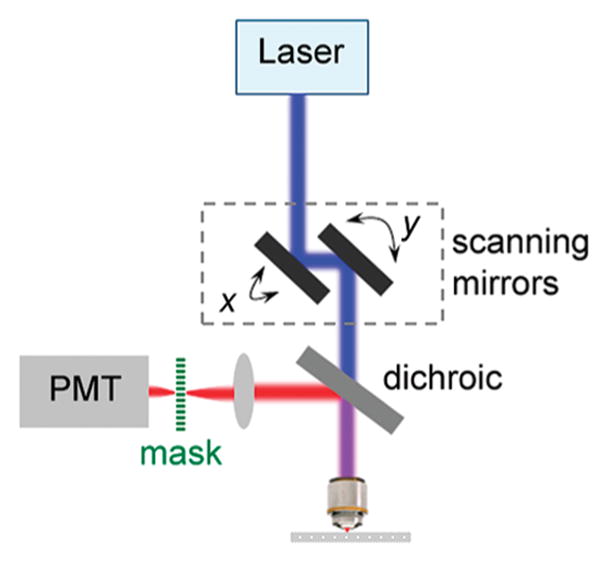
Schematic of laser scanning super-resolution microscopy through modulated detection and spatially cumulative imaging. Built on a standard laser scanning microscope, a mask with modulated transmittance is positioned at the image plane of the epi-fluorescence signal, and a single element large-area nondescanned detector such as a PMT is placed behind the mask. For each scanning position, the detector sums up all transmitted signal through the mask and assigns the integrated intensity to the single pixel corresponding to the current scanning position. After each complete frame is scanned with a particular mask, one PMT-picture is built up. Several such PMT-pictures are generated with a set of masks whose modulated transmittance is phase-shifted in space, in order to reconstruct a super-resolution image of the specimen.

$$\begin{array}{rl}p(t)& =\iint h_{\text{ex}}(r-t)s(r)h_{\text{em}}(x-r)M(x)\text{d}r\text{d}x\\ & =\int h_{\text{ex}}(r-t)s(r)[\int h_{\text{em}}(x-r)M(x)\text{d}x]\text{d}r\\ & =h_{\text{ex}}(t)\otimes \{s(t)[h_{\text{em}}(t)\otimes M(t)]\}\end{array}$$ (16)

where the order of integration has been exchanged, and the evenness of h_ex and h_em is exploited.

Fourier transform of eq 16 yields:

$$\stackrel{\sim }{p}(k)={\stackrel{\sim }{h}}_{\text{ex}}(k)\{\stackrel{\sim }{s}(k)\otimes [{\stackrel{\sim }{h}}_{\text{em}}(k)\stackrel{\sim }{M}(k)]\}$$ (17)

where the maximal frequency shift of s̃(k) is limited by the cutoff frequency ${\omega }_{\text{em}}^{\text{c}}$ of the emission OTF h̃_em. The overall effective bandwidth, however, is still ${\omega }_{\text{ex}}^{\text{c}}+{\omega }_{\text{em}}^{\text{c}}$.

The similarity between eqs 16 and 10 is obvious. Formally, M(x) corresponds to $I_{\text{ex}}^{max}(t)$, and the roles of h_ex and h_em are swapped. In order to recover out-of-band frequencies in s̃(k), M(x) also needs to be shifted according to eq 6 to generate additional images. The same algorithmic manipulations are then applied to obtain super-resolved s̃(k). The effect of SPADE is simulated with the same parameters as for SPIN, with spatial modulation period T_s = 1/ω_s = 300 nm. The SPADE reconstructed picture is shown in Figure 4D.

Because SPADE applies the modulation to the image plane, its mathematical formalism remains unchanged when it is combined with 2PLSM, except that the effective two-photon excitation PSF should be used.

3. Comparison between SPIN and SPADE

Both SPIN and SPADE depend critically on the fact that light intensity from different incoherent point sources is linearly summed. This property of incoherent imaging enables spatial structures to be first decomposed and encoded into a temporal sequence and subsequently synthesized from the sequence through summation.

The mathematical formalisms of SPIN and SPADE exhibit clear symmetry between eqs 10 and 16, which stems from the symmetry between x and t in eq 15. Mathematically, eqs 10 and 16 are weighed sums over t and x with the temporal and spatial modulation terms being the weights, respectively. Therefore, both SPIN and SPADE can be viewed as linear filtering approaches to the ill-posed problem of solving s(r) from the integral equation eq 15.

The symmetry between SPIN and SPADE also leads to some interesting alternative descriptions of image formation. As Heintzmann et al. pointed out,⁴⁷ the emission field I_em is linear in I_ex only when excitation is not saturated, but is always linear in fluorophore concentration s because fluorophores do not interact. Thus one may introduce the “emittability field” E(x) to represent the dependence of fluorescence emission on excitation intensity and describe image formation with a spatially resolved detector as

$$\begin{array}{rl}p(x)& =\int E[I_{\text{ex}}(r)]s(r)h_{\text{em}}(x-r)\text{d}r\\ & =[E(x)s(x)]\otimes h_{\text{em}}(x)\end{array}$$ (18)

For image formation in scanning microscopy with single-element detection, we may analogously define D(x) = h_em(x) ⊗ M(x), where M(x) is the transmittance on the image plane. Equation 16 then assumes the form

$$p(t)=h_{\text{ex}}(t)\otimes [s(t)D(t)]$$ (19)

We call D(x) “detectability” to emphasize its analogous role to the emittability E(x). When spatial integration is used with scanning, the system behaves as if fluorescence from each point light source is detected with a different detectability, and the limited resolution in p(t) comes from the fact that signals from the entire illuminated spot are assigned to a single pixel.

4. Digital Implementation of SPIN and SPADE

It is in principle possible to implement the spatial or temporal integration utilized in SPIN and SPADE digitally rather than physically. In order to do so, individual pictures corresponding to I_im(x,t) must be taken for each scanning position t. Modulations and integrations are then carried out as weighed sums over these pictures. The sum may be performed either over different pictures, following the integration over t in eq 10, or over different pixels in each picture, following the integration over x in eq 16.

This digital implementation is essentially a linear filter approach to inversion of the pictures. It shares the spirit of some inversion formulas previously proposed.^48,49 The difference is that previous approaches involve manipulating an infinite number of frequencies, whereas our schemes only use finite number of “carrier” frequencies.

Although physical integration is much faster in the image acquisition process, digital processing may carry one advantage. When the illumination pattern is physical, it cannot take negative values. The mask’s transmittance cannot be negative either, unless special detection configurations are utilized.⁵⁰ Thus there is always a DC component in the “carrier wave”, corresponding to the h̃_ex(0)δ(k) term in eq 12. Typically its amplitude is much larger than the harmonics at ±ω_t, which shift the specimen frequencies, because the harmonics are attenuated by the OTF. This has the tendency to bury the harmonics in the noise. With digital implementation of these schemes, the weights can take any value, so the “modulation patterns” can be a single sinusoid wave without the DC offset.

Discussion

In this paper, we propose two new schemes of super-resolution scanning microscopy that improve the resolution by a factor of 2. The first scheme, scanning patterned illumination (SPIN) microscopy, synthesizes an effective structured illumination field through modulation of the peak intensity of the scanning spot and temporally cumulative imaging on a spatially resolved wide-field detector. The second scheme, scanning patterned detection (SPADE) microscopy, exploits the formal symmetry between x and t in the image field I_im as given in eq 15 and uses a mask at the image plane to accomplish the spatial frequency shift. Although we focused on one-photon fluorescence, both schemes can be combined with multiphoton excitation to image thick samples with optical sectioning, as well as nonfluorescent incoherent optical processes such as spontaneous Raman scattering. Neither SPIN nor SPADE per se requires special fluorophores or special light sources to generate extreme light intensities.

The classical resolution limit of optical microscopy holds only when the optical system is linear and space-invariant.⁵¹ Scanning microscopy, however, is not space-invariant, because illumination is no longer spatially uniform. Thus out-of-band frequencies in the specimen are actually shifted into the pass-band of the microscope through beating with frequencies in the scanning spot. If a spatially resolved detector is used to take a separate picture for each scanning spot, it is in principle possible to invert the pictures to achieve super-resolution.^11,48,52,53 However, recovery of out-of-band specimen frequencies from such imaging schemes is complicated, because the scanning spot contains a continuous distribution of frequencies, rather than a few discrete ones as in WF-SIM. Taking one full image for each location of the scanning spot also severely limits the speed of imaging.

SPIN and SPADE avoid this problem in a way equivalent to heterodyne detection in the spatial frequency domain. They lock-in to a particular “carrier” frequency from the excitation or emission OTF. This “carrier” frequency shifts out-of-band specimen frequencies into the pass-band, which can then be recovered with exactly the same algorithm as in WF-SIM.