MEAN VOLUME FLOW ESTIMATION IN PULSATILE FLOW CONDITIONS

Abstract

To verify a previously reported three-dimensional (3D) ultrasound method for the measurement of time-average volumetric blood flow, experiments were performed under pulsatile flow conditions, including in vivo investigations, and results were compared with accepted, but invasive, “gold standard” techniques. Results showed that volume averaging results in the correct time-average volume flow without the need for cardiac gating. Unlike other currently employed methods, this method is independent of Doppler angle, flow profile and vessel geometry. A GE Logiq 9 ultrasound system (GE Medical Systems, Milwaukee, WI, USA) and a four-dimensional (4D) 10L and 4D 16L probe were used to acquire 3D Doppler measurements in the femoral and carotid arteries of four canines. Two invasive blood flow meters were used (electromagnetic for one canine and ultrasonic for three canines) as the gold standard techniques. Transcutaneous color flow measurements were taken to obtain 3D volume data sets encompassing the vessel. Constant depth planes were used to integrate color flow pixels encompassing the entire vessel cross-section. Power Doppler data were used to correct for partial volume effects. An artificial stenosis was induced to vary the ambient volume flow. Unrestricted, bidirectional flow was measured as high as 400 mL min⁻¹. Several flow restrictions were imposed that decreased the measured volumetric flow rate to as low as 30 mL min⁻¹. All flow rate estimates (n = 38) were plotted against results obtained via the gold standards. A general line fit resulted in y = 0.926 × − 0.87 (r² = 0.95), which corresponds to a 0.6% flow offset relative to the average flow rate of 142 mL min⁻¹, as well as a 7.4% error in the linearity of our estimate. A secondary curve fit was performed that required the slope to be 1 and the intercept to be 0, which yielded an r²-value of 0.93. The percent-error distribution was computed and fitted to a Gaussian function, which yielded μ = −7.04% and σ = 9.52%. Theoretical studies were conducted to estimate the expected error in our volume flow measurements as a function of number of samples (N) used for averaging pulsatile waveforms. Experiments showed the same $1∕\sqrt{N}$ dependence as theory. Direct comparisons of volume flow rate estimates using volumetric color Doppler and independent standards showed that our method has good accuracy under in vivo pulsatile blood flow conditions.

INTRODUCTION

The use of a newly developed three-dimensional (3D) ultrasound method to measure volume blood flow (Kripfgans et al. 2006b) is reported. This method was originally proposed by Hottinger (1978) and Hottinger and Meindl (1974). At the time they performed their studies, however, suitable 3D scanning technology was not available. A wide variety of clinical applications might benefit from this tested technique, including estimation of cardiac output, monitoring of cerebrovascular diseases and evaluation of intrauterine growth restriction during pregnancy. Methods currently used are either invasive (e.g., insertion of a Swan-Ganz catheter) or have limited accuracy. An example of the latter is ultrasound-based Doppler estimates (i.e., unknown Doppler angle, vessel geometry and flow profile), which may also suffer from poor signal-to-noise ratios (SNRs) for large angles even if the angle is manually adjusted (Gill 1985; Wells 1994).

Therefore, the goal of this paper was to verify the performance of an angle-independent, robust, volumetric flow measurement technique that can be implemented using data obtained from current clinical scanner architecture. The advent of 3D/four-dimensional (4D) ultrasound systems has made this technique a reality, and we hope this research will serve to move noninvasive ultrasonic volume flow measurements to clinical application.

Specifically, we tested the method of surface integration of velocity vectors (SIVV) on a highly sampled cross-plane, which takes advantage of the color flow Doppler firings commonly used in ultrasound systems. Because ultrasound imaging techniques have expanded to include 3D technology, a surface can be defined through a vessel in which the summation of the color flow Doppler velocities will yield the volume flow. This method requires no a priori knowledge of the flow direction (i.e., it is angle independent) or of the vessel geometry; it only requires that the surface completely intersects the vessel of interest. This technique is a substantial improvement over previous methods such as vector Doppler (Kripfgans et al. 2006a) or decorrelation-based volume flow estimators (Rubin et al. 2001). In addition, current research by Forsberg et al. (2006, 2008) in vector Doppler acquisitions include a novel, semiautomatic 4D Doppler ultrasound scanner dedicated to measure volume flow.

In this work, mean and peak systolic velocities of the carotid arteries (common, internal and external) were estimated by reconstructing vector Doppler blood flow data. Mean volume flow estimates ranging from 10 to 80 mL min⁻¹ were measured in vivo with coefficients of determination (r²) of 0.86 and 0.62 for mean and peak systolic flow, respectively. Corresponding root mean square errors were 6.9% and 61.2% for mean and peak systolic volume flow measurements, respectively. Another approach to volume flow estimation, proposed by Bohs et al. (1998, 2000, 2001), utilizes two-dimensional (2D) velocity estimations, and is based on speckle and ensemble tracking for 2D vector measurements. This technique could be extended to 3D, in which three ultrasound receive beams would be used to compute 3D blood flow velocities, ultimately yielding blood volume flow. However, from an implementation point of view, three transmit beams are not easily obtained on a commercial system. Secondarily, the triangulation will suffer as depths become large compared to the transducer aperture, because the angles between the three beams will narrow and reduce estimation accuracy.

Sun et al. experimentally tested the method of surface integration of velocity vectors in 1995, and they listed three approaches to obtain volume flow. In their general approach, the surface used for integration is a variable surface geometry with a variable velocity profile. According to Sun et al. (1995): “Based on the equation of continuity, flow can be computed through any arbitrary surface geometry, as long as the flow path is completely intercepted.” This approach, although mathematically and physically correct, is not practical because an arbitrary surface is not natural to the scanning geometry of clinical imaging arrays.

The geometry of the second approach, the proximal isovelocity surface area (PISA) method, is dictated by the flow profile and consists of an isovelocity surface that, in turn, yields a fixed velocity profile and variable surface geometry, which also does not resemble typical clinical transducer–scanning geometries. In contrast, the SIVV method operates on a fixed surface geometry and variable velocity profile, which is a practical approach because the fixed surface directly maps to the transducer surface geometry through the requirement that the surface of integration be perpendicular to the Doppler beam.

Whereas the term surface integration suggests the use of data from a well-sampled surface, Sun et al. (1995) were using velocity data located on a polar grid with a radial sampling of approximately 60 data points (60 axial-lateral angles over a 42° sector) and 4 polar angles. Using a 2D ultrasound transducer, an axial-lateral image plane was recorded; the transducer was then rotated about its own axis by 90° and another axial-lateral image plane was recorded. The resulting two image planes can be seen as 4 angular sample points in the lateral-elevational image plane. Despite the low angular sampling, Sun et al.'s (1995) results for experimental verification in vitro were within 10% of the true flow.

Recording a limited number of data points as well as cardiac gating allowed Sun et al. (1995) to measure time-resolved volume flow rates. From the two rotational positions of the ultrasound transducer, one position was used to image the flow 48 times; the transducer was then rotated to image the second view. A delay generator was used to trigger the Doppler data acquisition as a function of the cardiac pump cycle such that each Doppler image was taken 10 ms further into the cardiac cycle. Because the data acquisition time (60 ms) was slow compared to the cardiac cycle, it was suggested that a time-correction method by Eidenvall et al. (1992) should be implemented to reduce the likelihood of desynchronization.

Noninvasive volume flow acquisitions by other modalities include magnetic resonance (MR) imaging. Lew et al. (2007) reported a fast MR imaging sequence in which a single-slice plane can be acquired in 200 to 250 s and in a reduced time by using a fast scan sensitivity encoding technique (SENSE-PCx3), which requires 60 to 80 s at the cost of increased noise and decreased SNR. Frydrychowicz et al. (2007) introduced a flow-sensitive in vivo 4D MR imaging system to analyze aortic hemody-namics and to derive vessel wall parameters. Scanning times are of the order of 12 to 18 min; in addition, there is the necessity of respiratory gating. Even though MR-based techniques require an inherently long data acquisition time, they perform well in acoustically difficult anatomical locations such as the brain.

In this study, we will show that volume averaging can result in the correct time-averaged volume flow without the need for cardiac gating. This average volume flow is the primary information needed clinically at this time. Other conditions and parameters affecting in vivo blood flow estimation, such as heart rate, waveform, vessel size and flow rate, were investigated preliminarily. Finally, in vivo data are shown for measurements from 38 flow conditions in the femoral and carotid arteries of four canines.

Stenoses were induced to vary the natural flow rate and flow profiles. Alteration of the flow profile, although not directly measured, is assumed to have occurred because the introduced occlusion was located upstream of our volume flow volume of interest (VOI). Color flow (CF)–based volume flow estimates were compared to two techniques considered to be “gold standards.”

MATERIALS AND METHODS

Experimental setup

Flow tube

A GE Logiq 9 ultrasound system (GE Medical Systems, Milwaukee, WI, USA) for 3D static/4DD real-time imaging was used to acquire flow both in a Doppler flow tube phantom and in an in vivo canine model. The ultrasound scanner was equipped with the current Digital Imaging and Communications in Medicine (DICOM) standard software (developed by the National Electrical Manufacturers Association), which allows the user to store 3D duplex mode data and the associated scanner settings.

Scans were performed using two wideband (range: 3.5 to 11 MHz and 4.5 to 16 MHz, respectively), linear-volume arrays, which are curved along the mechanically swept direction (4D10L/4D16L) intended for small parts or superficial vascular exams. These arrays have a built-in sweep motor that is fully controlled by the Logiq 9 ultrasound scanners (GE Medical Systems). A 6-axis, computer-controlled, stepper motor positioning setup held the transducer array to allow vessel alignment and angle control between the array and measured vessels (Kripfgans et al. 2006a, 2006b).

For flow phantom experiments, a CompuFlow 1000 System (Shelly Medical Imaging Technologies, London, Ontario, Canada) was used to circulate blood-mimicking fluid (Orgasol EXD, ELF Atochem, France, 5-mm particle size). This system utilizes a positive-displacement pump that is driven by a microstepping motor under the control of an embedded microprocessor, resulting in accurate, user-specified pulsatile flow (~0.5 to 3 mL s⁻¹ time-averaged volume flow for this study). Pulsatility frequencies were selected that mimicked heart rate values ranging from 60 to 120 beats per minute (bpm) in 20-bpm steps.

Thin-walled, natural rubber tubing (Kent Elastomer Products Inc., Kent OH, USA, 4.8 and 9.5 mm, i.e., 3/16 and 3/8 inch, in diameter and 380-μm, i.e., 0.015-inch, wall thickness) was embedded in a tissue-mimicking phantom (custom phantom obtained from CIRS Inc., Norfolk, VA, USA, a = 0.3 dB MHz⁻¹ cm⁻¹). Volume flow estimates were compared for both 4.8-mm and 9.5-mm diameter tubes.

Data acquisition

Conventional CF region of interest positioning in the duplex image is followed by out-of-plane (elevational) volume of interest (VOI) alignment with the flow tube. Figure 1A shows conventional axial-lateral duplex B-mode with overlaid CF. Figure 1B and C show the intersecting orthogonal image planes, namely axial-elevational and elevational-lateral, respectively. Typically, a 20- to 30-mL scan volume resulted from the VOI selection. The 3D CF VOI in Fig. 1 was set to full lateral linear aperture and a 29° elevational angle, which encompassed the entire vessel, including additional surrounding tissue in the 3D sweep, thus requiring a scan time of less than 7 s.

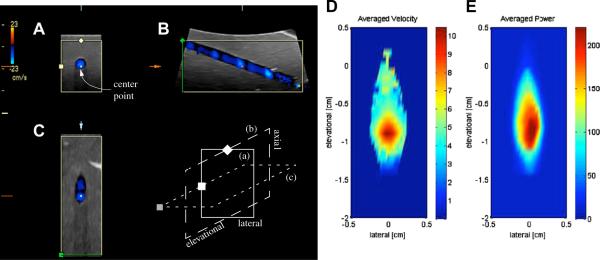
Figure 1.

Three-panel view of a single 3-D color flow acquisition reproduced in a flow phantom for a carotid (panels A to C) volume flow profile. The acquisition shows the pulsatile nature of the observed flow. The three panel types shown are: (A) axial-lateral view, (B) axial-elevational view and (C) elevational-lateral view. The schematics below (B) illustrate the spatial relationship of the three views; here (a) corresponds to (A), etc. All three panels coincide at the center point that is labeled in (A) and marked in each view. The pulsatility of carotid flow leads to the acquisition of blue bands in the elevational direction (B) in the observed vessel due to the finite time of the volumetric acquisition of the mechanical probe used. (D) shows the averaged velocity from 21 acquisitions as shown in (C). Averaged (linear) Doppler power is shown in (E).

A total of 38 in vivo data sets were acquired. Each data set is computed as the average of 50 volumetric scans; hence, there were 1900 acquisitions. The GE Logiq 9 ultrasound scanner (GE Medical Systems) sweeps a 3D volume and simultaneously records B-mode and CF data throughout the scanned volume. One example volumetric scan is shown in Fig. 1; the images are in a standard panel view of the Logiq 9 scanner (GE Medical Systems) in 3D mode. After a 3D volume sweep, the center planes in the axial-lateral direction, the axial-elevational direction and the elevational-lateral direction are displayed in Fig. 1A, B and C, respectively.

For navigational purposes, the images have markers that demonstrate their spatial relationships. Each panel is set in a rectangular, beige-colored frame. One to two symbols are on the frame, and the center of each frame bears a colored square (labeled and marked in Fig.1). The schematics below panel B in Fig. 1 illustrates the spatial relationship of the three planes in panels A through C; the frames in the schematics that are labeled with lowercase letters correspond to their uppercase-labeled counterparts in the panels.

Given the spatial orientations of the acquired data, there are several items worth noting about this example. First, at the left and right edge of the axial-elevational panel (panel B), the flow tube is at distinctively different angles with respect to the Doppler beam. Close to the left edge of this axial-elevational image plane, the Doppler angle is nearly perpendicular to the flow, so that the CF tapers off as the recorded flow transitions into the wall filter. In addition, the measured velocities increase toward the right side of the image plane as the Doppler angle approaches 0°. A previous study demonstrated that, for all practical purposes, this angle change does not affect the estimation of volume flow (Kripfgans et al. 2006b).

Second, the pulsatile nature of the flow can be seen as the 3D scan moves elevationally. Because the mechanical sweep time is long compared to the cardiac cycle, the CF records a different phase at each volume sweep position. This phenomenon can be observed in both the axial-elevational panel (Fig. 1B) as well as the elevational-lateral panel (Fig. 1C). As shown in Fig. 1D and E, and discussed later in this study, averaging a large number of 3D acquisitions taken at non-synchronous time points with respect to the heart beat yields the average CF velocity and Doppler power. This observation also holds true for blood flow with flow reversal as recorded in vivo in femoral flow.

Volume flow was measured by the integration of CF velocity data in the C-plane of the acquired 3D volume, as proposed by Hottinger and Meindl (1974). At the CF center frequency of 5 MHz (λ ~ 0.3 mm), CF pixel sizes in the C-plane ranged from 0.23 to 0.28 mm². Investigated vessel diameters were 4.8 and 9.5 mm and were variable for the flow tube experiments but of the order of 5 mm for the in vivo experiments. For each spatial velocity voxel in the 3D data set, the associated Doppler power (same resolution) and the 3D spatial location of the voxels were obtained from the scanner. Ultrasound data sets were stored in a proprietary digital DICOM file format to which the authors had full access.

The scanner acquired 3D volume data in the same fashion as any other standard clinical, 3D–equipped, GE Logiq 9 (GE Medical Systems). The only difference is that we used a more convenient acquisition method by which the scanner can be told to acquire, for example, 50 data sets and automatically save them after each acquisition. Moreover, the scanner was instructed to pause for a (normally distributed) random time interval between 0 and 1 s before each acquisition to prevent synchronization between scanning and subject heart beat. Specifics on data analysis are provided in the corresponding section below.

Animal preparation

Four mongrel canines were used as acute in vivo models for the procedures used to measure volume flow. The procedures were previously approved by the University of Michigan's Committee on the Care and Use of Animals (UCUCA) the University of Michigan. Dogs were pre-anesthetized with an intra-muscular injection of acepromazine (0.8 mg/kg⁻¹ intravenous (IV)), administered thiopental (8 to 12 mg/kg⁻¹ IV) for induction of anesthesia, and intubated. Full anesthesia was maintained by inhalation of isoflurane. After anesthesia, the animal received a continuous IV infusion of 0.9% saline at 2 mL kg⁻¹ h⁻¹ for hydration. Venous access was provided through the right cephalic vein using a 21-gauge, 3/4-inch long butterfly catheter.

The animal was instrumented to monitor electrocar-diogram (contact probes), SpO₂ (lingual probe) and temperature (rectal probe). Fur was removed from selected areas initially by shaving; a depilatory cream was applied to remove additional hair. The left-and right-side femoral arteries were scanned transcutaneously, and ultrasonic access estimates were made from various scan angles. Then, sites were selected distally to these locations, and an acute dissection (3-cm incision) was performed to expose the desired artery. A flow meter cuff, used as the standard comparative measure, was then placed around the vessel, and ultrasonic volume flow acquisitions were carried out with simultaneous data-logging using the flow meter. Stenoses were induced to vary the natural flow rate in the femoral and carotid arteries. A pneumatic vascular occluder (Harvard Apparatus, Holliston, MA, USA, 4-mm lumen diameter, 5-mm cuff width) was placed around the artery being tested.

The gold standard flow meter (described in the next section) was used as a measure of the degree of the stenosis with respect to the unrestricted flow. An electronic syringe pump (Harvard Apparatus) allowed convenient control of the artificial stenosis cuff cutoff to adjust the effective volume flow rate. Any side branches located between the flow cuff and the ultrasound sampling position were ligated. After all measurements were completed, the animal was euthanized using standards approved by the UCUCA in accordance with the Institutional Animal Care & Use Committee (IACUC) guidelines consistent with the recommendations of the Panel on Euthanasia of the American Veterinary Medical Association.

Two types of invasive flow meters were used: an electromagnetic flow meter (Carolina Medical, King, NC, USA, model FM501D) and an ultrasonic flow meter (Transonic Systems Inc., Ithaca, NY, USA, model TS420). Both systems are recognized gold standards for in situ blood volume flow estimations and bear a 5% error in volume estimates.

Data analysis

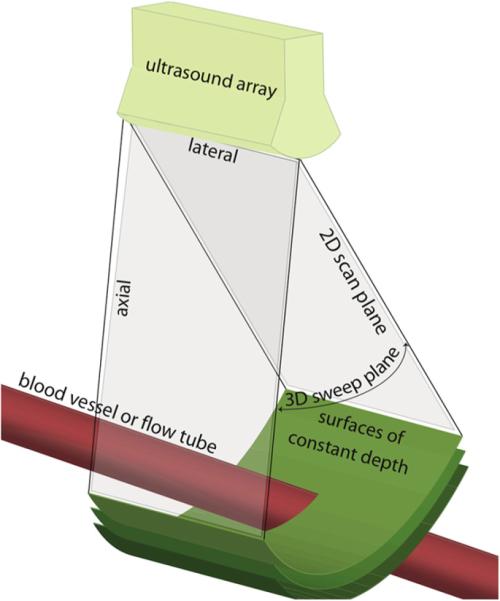
After data were exported to an off-line computer for analysis, MatLab software (The MathWorks Inc., Nat-nick, MA, USA) was used to define a cross-sectional surface through the vessel or flow tube. Figure 2 shows a depiction of a volume scan. The linear array on top of Fig. 2 is mechanically swept to scan an approximately pie-slice-shaped, 3D volume. Surfaces of constant depth, which fully intersect the vessel of interest, are shown in green. These elevational-lateral scan surfaces are used for flow estimation. DICOM data from the Logiq 9 scanner (GE Medical Systems) are obtained as a 3D digital data set, in which the desired surface of constant depth is extracted off-line. The SIVV method is based on Gauss's theorem, which relates the divergence of the quantity in an enclosed volume V to the flux q through the surface S covering V. In other words, a surface integral over the enclosing boundary S will yield the volume flow Q, as follows:

$$Q={\int }_s\stackrel{‒}{v}•d\stackrel{‒}{A},$$ (1)

where $d\stackrel{‒}{A}$ is the local area element vector, which is collinear to $\stackrel{‒}{v}$. More details on the method of surface integration can be found in publications by Hottinger and Meindl (1974) and Hottinger (1978), Sun et al. (1995) and Tsujino et al. (1995), as well as our previous paper showing results for constant velocity volume flow (Kripfgans et al. 2006b).

Figure 2.

Display of surfaces (green) over which Doppler-measured velocities can be integrated to obtain multiple realizations of blood (red vessel) volume flow for averaging.

Power weighting

Each voxel's velocity was weighted by an associated coefficient based on Doppler power. Previously, we have found this to be effective in accounting for partial volume averaging (Rubin et al. 1995; Kripfgans et al. 2006b). The highest Doppler power is typically found inside the vessel and rolls off to the smallest Doppler power (ideally zero) for tissue background voxels. This roll-off is due, in part, to the effect of the Doppler wall filter, but it is assumed that the dominant cause is partial volume effect and therefore the power in the roll-off is directly proportional to the amount of blood in the voxel reference. Therefore, the power can be used to weight the cross-sectional area of the voxel containing flux.

To determine the proper Doppler power-weighting function, one needs to identify the corresponding voxels that represent 100% blood. This identification is obtained by inspection of the histogram of the average over the 50 acquisitions Doppler power values from each voxel in the C-plane surface (green surface in Fig. 2). Background voxels were identified and removed by their large peak, near-zero power. Then the assumption is that, in the histogram of the remaining voxels, a peak exists that results from the large number of voxels inside the vessel, i.e., those containing 100% blood. To find this peak, we assume that it is the last local maximum in the histogram, moving from the low-power values to high-power values.

Power weighting factors w_i were introduced by Kripfgans et al. (2006b) and range from 0 in tissue to 1 inside the flow. Here, X denotes the spatial position of each voxel and the subscript i is meant to index overall spatial voxels of the lateral, elevational and axial positions. To obtain these values, time-averaged power values were calculated for each voxel position via the following equation:

$${\widehat{p}}_i=\frac{1}{N}\sum _{j=1}^{N}p(X_i,t_j).$$ (2)

Here, t_j is the volume acquisition time, which is indexed for each new volume and is explained in more detail below. Then the time-averaged Doppler power values ${\widehat{p}}_i$, from the surfaces of integration (seven used in this study) were grouped to form a 64-bin histogram. The position of the peak in the histogram, as described above, is used to identify p_100%. To facilitate finding the location of the p_100% peak, the peak amplitude is enhanced by multiplication of the histogram amplitude by the power value, i.e., power X histogram frequency at a given power value. Voxels at or above p_100% are assumed to be 100% blood. Blood flow voxel cross-sectional areas s_i with less Doppler power, ${\widehat{p}}_i$, are scaled to compensate for partial volume-averaging by a coefficient w_i as follows:

$$w_i\left({\widehat{p}}_i\right)=\{\begin{array}{cc}0\hfill & \text{for}{p}_{\text{background}}\ge {\widehat{p}}_i\hfill \\ \frac{{\widehat{p}}_i}{p_{100\%}}\hfill & \text{for}{p}_{100\%}>{\widehat{p}}_i\ge p_{\text{background}}\hfill \\ 1\hfill & \text{for}{\widehat{p}}_i\ge p_{100\%}.\hfill \end{array}\phantom{\}}$$ (3)

An automatic velocity-masking algorithm was generated, which uses the Doppler power histogram analysis described above to form a modified SIVV method using the following equation:

$$Q=\sum _{i\in s}{s}_i.w_i.v_i.$$ (4)

Here the v_i-values are the local Doppler velocity estimates obtained from the ultrasound scanner, color flow–processing engine. Each v_i-value is perpendicular to the corresponding surface area s_i. Multiple surfaces can be averaged to improve the SNR. Typically, seven surfaces were utilized in calculating the average volume flow, three of which are shown in Fig. 2. The histogram analysis described above can be seen as a system calibration scheme or a normalization procedure for this method of volume flow estimation.

Statistical analysis

Acquiring pulsatile flow with the current ultrasound scanner setup yields results drawn from different phases in the cardiac cycle. Under the assumption that the flow waveform is smooth and well behaved, it can be shown that sufficient random sampling across the cardiac cycle, as was performed here, will provide the average volume flow rate without cardiac gating. The sample average as follows:

$$E\left(Y\right)=\frac{Y_1+Y_2+Y_3+\dots +Y_N}{N}\to \mu ,$$ (5)

converges toward the expectation value μ for the number of acquisitions N approaching infinity. In eqn (5), the values Y₁, Y₂,… are an infinite sequence of identically, independently distributed random variables with finite expectation values E(Y₁)=E(Y₂)=…=μ<∞. For an assumed periodic temporal flow profile, which is sampled randomly in time over its period, the value of the resulting instantaneous flow measurements can also be assumed random. Therefore, we can randomly sample our population of flow values, and they will converge toward the mean of the flow with a standard error of the mean of $\pm \sigma ∕\sqrt{N}$, where σ is the standard deviation of the flow over a period. In our case, we are estimating local velocities in time and position in the blood vessel. Specifically, we estimated the mean local velocity ${\widehat{v}}_i$ as follows:

$${\widehat{v}}_i=E\left(v_i\left(X_i\right)\right)=\frac{\sum _{j=1}^{N}v(X_i,t_j)}{N},$$ (6)

where E(v_i(X_i)) is the expected value of the local velocity estimates. v(X_i,t_j) are the local velocity estimates that are measured at randomly selected time increments defined by t_j as follows:

$$t_{j+1}=t_j+t_s+t_r,$$ (7)

where t_s is defined as the sampling time for one 3D sweep (approximately 7 s), and t_r are equally distributed, random, time offsets between 0 and 1 s, to avoid synchronization of our sampling with the cardiac cycle.

Also, notice that this random sampling accounts for the changing diameter with the heart cycle. v_i(X_i,t_j) is a function of position and time. The time is randomly sampled, as shown above. The position variable X_i does not assume a location relative to the vessel. For those values falling outside of the flow stream during portions of the cardiac cycle, eqn (6) will be zero for those instances. However, the mean value will still be correct, because the mean averages these zeros in with those values in which there is flow at position X_i. The local area s_i at X_i will be multiplied by the local mean, and so the flux will be correct. Thus, pulsatility and changing area creates no difficulty for the SIVV method.

To obtain the average volume flow in the presence of pulsatility, 50 random time points distributed across the equivalent of a cardiac cycle were collected and averaged at each location. Power Doppler data were then used to correct for partial volume effects as described in the previous section. Then, using the seven surfaces for our flow estimate, the equation for the modified SIVV method, rewritten from eqn (4), becomes the following:

$$Q=\frac{1}{M}\sum _{i\in S_M}{s}_i•w_i•{\widehat{v}}_i,$$ (8)

where M is the number of integration surfaces and the surface of integration (S) has been modified to include the M surfaces (S_M).

RESULTS

Flow tube experiments

Flow tube experiments were conducted to investigate how pulsatile flow could be recorded and processed for planned in vivo work. The following parameters were varied: time average volume flow, heart rate and tube size.

Time-averaged volume flow variation

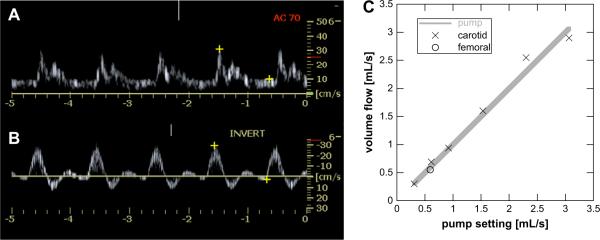
Time-averaged volume flow was measured from 0.3 to 3.0 mL s⁻¹. This flow range was anticipated for the planned in vivo verification. Either a typical carotid or a typical femoral artery waveform was selected from the preprogrammed waveforms in the CompuFlow 1000 System (Shelly Medical Imaging Technologies) and are shown as pulsed wave Doppler in Fig. 3A and B, respectively. Figure 3C shows six volume flow measurements for carotid flow (X) and one volume flow measurement for femoral flow (O). The carotid waveform is composed of time-varying forward flow and the femoral waveform of forward and reverse flow in Fig. 3A and B, respectively. The data have an average error of 6.4% between the true pump output and the estimated volume flow, with a maximum error of 12.5%. A least-squares regression using a linear function yields a fit of y = 0.98x + 0.07 (r² = 0.984). Forcing this fitting function to go through the origin with unity slope (y = x) yields an r² of 0.981. A 9.5-mm diameter flow tube was used in conjunction with a 60-bpm carotid or femoral waveform.

Figure 3.

Doppler waveforms for carotid (A) and femoral flow (B) were generated by the pump system and 3D Doppler data obtained and processed for volume flow. (C) The measured average volume flow rates compare favorably to the actual rates across a range of velocities and for the femoral waveform, which includes reverse flow in its pump cycle. Each point is the result for 50 random volume acquisitions across the cardiac cycle. Rates were within 7.1% of the actual value.

Artificial heart rate and vessel size variation

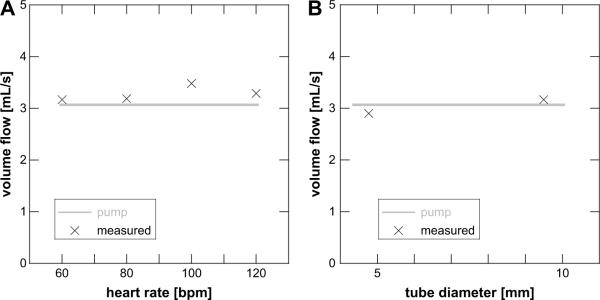
Next, variations in heart rate and vessel diameter were investigated using carotid waveform flow. Figure 4 shows the results for a volume flow of 3 mL s⁻¹ for four heart rates ranging from 60 to 120 bpm. These are typical values to be anticipated in vivo. All four values overestimated the true volume flow with an average error of 7.1% and a maximum error of 13.5% relative to the chosen time-averaged flow of 3 mL s⁻¹ for a 9.5-mm diameter flow tube.

Figure 4.

(A) The measured volume flow rate remains constant in the flow tube experiment across a range of equivalent heart rates of 60 to 120 beats per minute (bpm). Each point is the result for a single data acquisition of 50 random points across the simulated cardiac cycle. (B) Effect of changing flow tube diameter. Note that despite a factor of 2 change in diameter, the measured volume flow rate remains near the actual value. Each point is the result of 50 random volume acquisitions across the cardiac cycle.

Finally, two tube sizes were used to compare volume flow estimations of carotid waveform flow in a larger versus a smaller vessel. A large vessel might be a common carotid artery in humans, which is approximately 1 cm in diameter. The investigated femoral artery in our canine model was approximately 4 mm in diameter. Here, the large-diameter tubing measured 9.5 mm across, whereas the small-diameter tubing measured 4.8 mm. The observed errors were −5.4% and +3.4%, respectively, relative to the chosen time-averaged flow of 3 mL s⁻¹ for a 60-bpm carotid waveform.

In vivo results — Arterial flow estimation

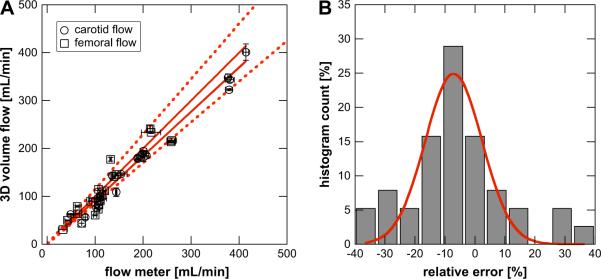
Figure 5A shows blood volume flow measurement for 38 cases at two anatomic locations: the femoral and the carotid arteries. At each site, blood flow was controlled by the flow cuff, resulting in a distribution of volume flow rates. The abscissa in the Figure shows values as measured by the gold standard device (either electromagnetic or ultrasonic flow meters), whereas the ordinate gives the blood volume flow as measured by the SIVV method. Two fitting functions were tested. First, a general line fit yielded y = 0.926x − 0.87 (r² = 0.95). Second, the identity function (y = x) was tested and yielded an r²-value of 0.93. The first line fit demonstrates constant bias (<1 mL min⁻¹), whereas both fits show that the SIVV technique's scale-factor is close to unity, i.e., it is a direct measurement of volume flow (0.925 and 1.00, respectively).

Figure 5.

(A) Comparison of volume flow measured by the method of surface integration of velocity vectors and two gold standard flow meters (see Methods). In vivo results of four canines are shown. Blood flow was measured in each femoral artery (open square) and carotid artery (open circle). In addition to baseline flows, stenosed flows and flows after recovery from the stenoses were measured. Two line fits are shown, which partially overlap. A general line fit yields y = 0.926x − 0.87 (r² = 0.954). Second, a fit using the identity function (y = x) yielding an r² = 0.928. The dashed lines indicate the ±15% absolute error interval for the identity fit. Experimental errors are indicated for flow meter as well as 3D volume flow analysis as one standard deviation error bars along the abscissa and ordinate, respectively. (B) The percent error distribution was computed and fitted to a Gaussian function, which yielded μ = −7.04% and σ = 9.52%.

The average error ${\stackrel{‒}{e}}_i$ and average absolute error $\stackrel{‒}{\mid e_i\mid }$ of all 38 estimates equal −6.3% and 14.0%, respectively. A histogram and associated Gaussian fit $(f\left(x\right)=\frac{1}{\sigma \sqrt{2\pi }}{e}^{\frac{-{(x-\mu )}^2}{2{\sigma }^2}})$ of the error e_i is shown in Fig. 5B. The standard deviation σ of the fit yields 9.52%.

Figure 6 shows pulse-wave Doppler traces for three flow conditions: baseline, medium and high stenosis. Figure 6A shows the above-mentioned forward and reversed flow in the vessel, which is typical for femoral flow. The flow cuff imposed a restriction, which resulted in a change in the Doppler waveform confirmed by pulse-wave Doppler. Figure 6B shows that the reversed flow in the vessel disappears after the medium flow restriction is applied. Subsequent volume flow estimation, however, showed that the time-averaged flow was minimally altered, reduced from 115.8 mL min⁻¹ (111.6 mL min⁻¹) to 114 mL min⁻¹ (107.4 mL min⁻¹), i.e., 2.7%, where the values in parentheses refer to the standard flow meter. Further restriction of the vessel showed high stenosis, manifesting in a large flow degradation as seen in pulse-wave Doppler (Fig. 6C). Associated volume flow estimation for this particular case showed a 35% reduction in blood flow, down to approximately 65.4 mL min⁻¹ (67.8 mL min⁻¹).

Figure 6.

Volume flow measurements were accompanied by pulse wave Doppler interrogations before each acquisition. Unrestricted femoral flow showed forward and reverse flow, as can be seen in panel (A). Moderate restriction of the lumen (B) showed disappearance of reverse flow, but no reduction in volume flow. Further restriction of the lumen (C) led to diminished flow through the vessel.

Sample size variation and statistical considerations

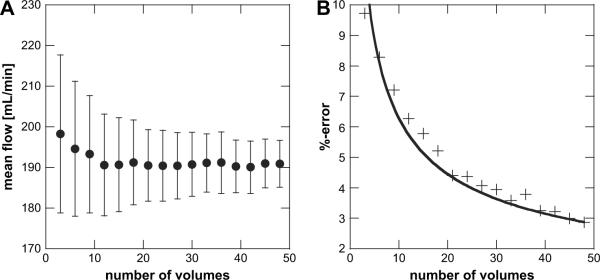
The effect of the number of random temporal samples used for averaging is of interest especially when using mechanically swept arrays, because the acquisition of many 3D color flow volumes can be a time-consuming task. A re-sampling technique was used on a volume flow data set consisting of 100 3D Doppler acquisitions to investigate the effect of varying the sample size on the resulting volume flow estimate. To obtain statistical estimates of volume flow, random subsets of size N, where N is varied from 4 to 47, were extracted to compute the average volume flow and its associated standard deviation eqn (6) and eqn (8)). Results are plotted in Fig. 7A as a function of subset size N.

Figure 7.

A re-sampling technique was used to verify that our measurement accuracy improves as a function of $1∕\sqrt{N}$. By using multiple random subsets of varying size, a mean and standard deviation of the flow calculated from the subsets were estimated (i.e., bootstrapping). Subsets were drawn from a total measurements population of two individual volume acquisitions of 50 data sets each. (A) Carotid volume flow estimates are shown as a function of number of measurement samples used to obtain the average flow. Error bars show one standard deviation. (B) Percent error, calculated as one standard deviation over the true flow (flow meter) as a function of the number of measurement samples used to obtain the average flow. The data shows a $1∕\sqrt{N}$ dependence and was fitted as such, yielding $19.9∕\sqrt{N}$, r² = 0.92. It is assumed that for N ≥ 50, the selected data subsets are not statistically independent and thus are not plotted.

Mean flow estimates appear to be largely insensitive to sample size reduction, as can observed in Fig. 7A. However, as expected, the statistical variation decreases as the sample size is increased. The percent error (standard error normalized by the true flow calculated from the flow meter) in our measurement for various sample sizes are shown in Fig. 7B. A sample size of greater than 15 volumes results in an error of ±5% or less, assuming a correct reading from the flow meter.

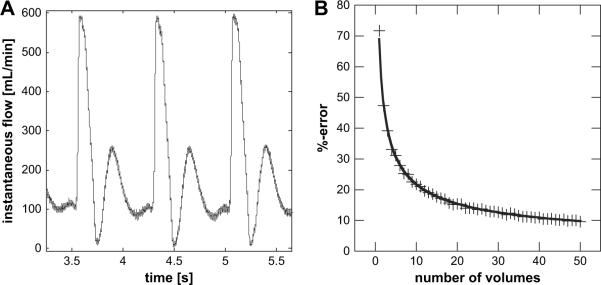
Sample size variation and its effect on volume flow measurements using the flow meter data was again investigated using the same statistical re-sampling technique as described above. Subsets of N randomly selected samples were taken from points on the time resolved, flow meter waveform shown in Fig. 8A. The flow meter waveform used here was acquired during the 3D color flow volume measurements used for Fig. 7 and consists of approximately 12 cardiac cycles (only three are shown). Each subset was used to calculate a flow measurement and 100 random realizations were drawn for each choice of N. These 100 subsets were then used to compute a respective mean and standard deviation of the flow estimates.

Figure 8.

An ultrasonic flow meter waveform was used to test the theoretical prediction for the %-error of a volume flow estimate as given in eqn (9). (A) A sample of the carotid waveform in the canine for data in Fig. 7, with an average flow of approximately 200 mL min⁻¹ and a standard deviation of 137.8 mL min⁻¹. (B) The estimated relative error was computed as waveform standard deviation over waveform mean. A fit of the estimated percent error yields $\%-\text{error}=68.9∕\sqrt{N}$ with r² = 0.998.

Figure 8B shows the expected percent error for each choice of N ranging from 3 to 48. The associated percent error is plotted in panel B of Fig. 8. It should be noted that Figs. 7 and 8 are derived from the same re-sampling methods, using 3D SIVV data and flow meter data, respectively. In the case of Fig. 7, however, a given volume flow estimate was measured via eqn (6) and eqn (8). For Fig. 8, a given volume flow estimate was found by averaging the randomly selected points on the waveform.

A theoretical expression for the percent error (standard error normalized by the true mean) expected for a flow estimate (in the absence of speckle and electronic noise), as a function of the number of samples used to calculate that estimate, can be expressed as follows (Taylor 1997):

$$\%-\text{error}=100\frac{{\sigma }_{\text{waveform}}}{{\mu }_{\text{waveform}}}\frac{1}{\sqrt{N}}•$$ (9)

Here, σ_waveform is the standard deviation of the underlying time varying blood flow waveform, μ_waveform is the corresponding mean of the flow waveform. N represents the number of independent flow measurements randomly sampled in time. In other words, the confidence in our measurement is dependent on the original waveform (i.e., the mean and standard deviation of the waveform) and the amount of sampling of that waveform. It should be noted that this analysis does not account for noise variations separately from that of actual flow variations in their effects on flow estimates. The data in Fig. 7B and Fig. 8B were both fit to show the $1∕\sqrt{N}$ dependence. Figure 7B shows a $\%-\text{error}=19.9∕\sqrt{N}$ as well as a coefficient of determination r²) of 0.92. Figure 8 shows a $\%-\text{error}=68.9∕\sqrt{N}$ as well as a coefficient of determination (r²) of 0.998. It is clear, however, that there is a factor of 3.46 difference between the error estimated from the flow meter waveform and error measured from the 3D color Doppler data. The fact that our Doppler flow error is significantly lower than the predicted error (from the flow meter waveform) for a given number of volumes may be due to some combination of the frame averaging (two frames used) and the color flow packet-size of 16, which was used in these experiments.

SUMMARY AND DISCUSSION

Previously we have reported on the use of SIVV in constant flow conditions (Kripfgans et al. 2006b). During these measurements, volume flow varied between 2.5 and 15 mL s⁻¹, and angles from the Doppler beam to the flow tube were in the range of 40° to 140°. Current efforts in this study were concentrated on the case of pulsatile flow conditions, including those that allow flow reversal as found in femoral arteries. Benchtop experiments providing pulsatile flow in Doppler phantoms were used to modify our previously published techniques (Kripfgans et al. 2006b) for application in vivo.

Volume flow estimation using the modified method of SIVV is shown to be robust in pulsatile flow situations under controlled flow tube conditions as well as in vivo, yielding a mean error of −7.04% with respect to our gold standard and an associated standard deviation of 9.52%. This error estimation results from 38 in vivo measurements using 50 volume flow acquisitions each to obtain the average flow. Although the mean error is negative, one cannot statistically conclude that the error is biased, given the standard deviation in the error estimate overlaps an error of zero. Parameter variations for flow profile, tubing size, heart rate, etc. in flow tube experiments have predicted the stability of SIVV and subsequent flow acquisition, and analysis in a canine model has confirmed this prediction.

Linearity of canine data showed r²>0.93 depending on the fitting function. This observation holds true for femoral and carotid flows, keeping in mind that femoral flow is not only pulsatile but shows flow reversal as seen in Fig. 6A. A total of 50 scan volumes per data point of volume flow estimation were used for the results in this study. Current technology using mechanically swept 3D probes is restricted to relatively slow acquisition times; however, we have shown that the associated error of reducing the number of volumes leads to a well-defined additional error, which may be tolerated. This finding makes patient scanning feasible without the need for 2D arrays, if the average volume flow is of interest. When 2D arrays are available, however, this technique may be robust enough to perform real-time volume flow imaging throughout the cardiac cycle.

During our image volume acquisitions, the wall filter cutoff frequency was set to the lowest value allowed by the system to minimize partial volume-averaging effects. This value was typically 5 to 8% of the pulse repetition frequency. Future work will investigate different methods for removing or suppressing wall motion or static tissue signal and its ultimate effect on volume flow estimation. It is the presence of a wall filter that leads to the partial averaging effect, which then necessitates our use of the compensatory power-weighted mask. In addition to the wall filter, the Doppler gain was set to maximize the dynamic range in our Doppler power values within the blood vessel of interest. In the absence of digitization error, however, our methods and results are expected to be relatively independent of the Doppler gain settings.

Effects of red blood cell aggregation, also called Rouleaux formation, are present under certain flow conditions, such as in the inferior vena cava (IVC), and will influence the Doppler power weighting method. For example as in the IVC, the Doppler power would be elevated in the center of the vessel where the velocity gradient, and therefore the shear stress, is minimized. Rubin et al. (1997) have commented on the effects of Rouleaux formation and suggested the computation of a cumulative Doppler power distribution function over the region of interest.

Results from sample size variation estimate show that our volume flow estimate will follow the law of large numbers with a $1∕\sqrt{N}$ dependence. This error will be inherent in the estimation of volume flow. For a sample size of 15 acquisitions, this error will be approximately 5% and should continue to decrease with increasing sample size. However, large sample sizes are not desirable due to the direct increase in acquisition time. Current 3D acquisitions using a mechanical sweep mechanism are capable of recording 5 or more B-mode volumes per second. One could imagine that future electronically swept 3D acquisitions will be capable of performing color flow at 5 or more volumes per second. Neglecting noise, this leads to a 3-s acquisition time for a 5% error volume flow estimate. Our in vivo estimates showed an average error of −6.3% for a sample size of 50. The fact that there should be at least an error of approximately 2.8% implies that our residual error is of the order of 3.5%.

No hardware or software modifications were made to the CF processing stream in the GE Logiq 9 scanner (GE Medical Systems). Because this scanner is an off-the-shelf machine, the same processing can be performed with any scanner that is capable of 3D CF scanning. The demonstrated Doppler acquisition and processing scheme does not use any audio Doppler output or spectral Doppler information. One fundamental assumption of the method of velocity vector integration, as presented here, is that the scanner performs adequately in estimating CF velocity and Doppler power. The internal CF processing could be examined by evaluating IQ data, which would then serve to identify sources of error and parametric dependencies.

Additionally, investigations are needed to examine the effect of the CF point spread function, because over-lapping CF beams will result in spatial averaging of Doppler power and velocity. Although this averaging is not expected to interfere with estimating the integral of the average velocity and average Doppler power, it is necessary to formulate estimations for the number of independent voxels needed for a given vessel and their level of separation. The latter are especially important for time-resolved volume flow, where fast acquisitions are needed. Despite the reliance on system-specific CF processing, the off-line processing performed using off-the-shelf hardware can facilitate transcutaneous, noninvasive blood volume flow estimation in vivo.

A clinical implementation of the regular SIVV method could be synchronized with cardiac gating, which would ensure a constant heart cycle phase across the integration plane, preferably peak systole. However, we have shown in this study that volume averaging results in the correct time-averaged volume flow without the need for cardiac gating. This average volume flow is the primary information needed clinically at this time. Yet, it does assume a reproducible volume flow from one cardiac cycle to the next. However, this is no different from similar assumptions proven effective for retrospective gating in ultrasound as well as other modalities.

More importantly, cardiac gating might be needed only if time-resolved volume flow is desired. The common use of cardiac gating in ultrasound as well as other imaging applications makes it highly probable that one could, if clinically indicated, obtain reliable, time-resolved volumetric flow measurements throughout the cardiac cycle. Even in the case of time-resolved volumetric flow, cardiac gating is only necessary now due to the speed of the 3D image acquisition. With future use of 2D arrays in 3D ultrasound, temporal limitations should be eliminated to a significant degree.