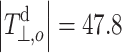Abstract
Hyperfine couplings and g-values of nitroxyl spin labels are sensitive to polarity and hydrogen bonding in the environment probed. The dependences of these electronic paramagnetic resonance (EPR) properties on environmental dielectric permittivity and proticity are reviewed. Calibrations are given, in terms of the Block–Walker reaction field and local proton donor concentration, for the nitroxides that are commonly used in spin labeling of lipids and proteins. Applications to studies of the transverse polarity profiles in lipid bilayers, which constitute the permeability barrier of biological membranes, are reviewed. Emphasis is given to parallels with the permeation profiles of oxygen and nitric oxide that are determined from spin-label relaxation enhancements by using nonlinear continuous-wave EPR and saturation recovery EPR, and with permeation profiles of D2O that are determined by using 2H electron spin echo envelope modulation spectroscopy.
Introduction
The great power of the spin-label electron paramagnetic resonance (EPR) method in biological systems lies in its sensitivity to rotational motion [1–8]. Compared with studies of dynamics, those on the sensitivity to environmental polarity are less extensive but have received a considerable impetus in recent years from the application of high-field/high-frequency EPR [9–11], an area in which Wolfgang Lubitz and collaborators, both past and present, are extremely active. Thus, a review of current progress and achievements, particularly in the area of biological membranes, is timely.
Because hydrogen bonding to the –NO moiety produces pronounced g-shifts and hyperfine shifts, the polarity sensitivity of nitroxyl spin labels can be divided into two regimes [12, 13]: that in protic environments, and that in aprotic environments. These two are considered separately here below. Then follows a consideration of the application to biological membranes, including a comparison with complementary EPR techniques: electron spin echo envelope modulation (ESEEM) [14] and continuous-wave (CW) T 1e-relaxation studies [15].
Aprotic Environments
Reaction Fields
In the absence of hydrogen bonding, the polarity sensitivity of the EPR spectrum arises from the response to the reaction field, E R, of the polarizable environment that is induced by the spin-label electric dipole, p (see, e.g., Ref. [16]):
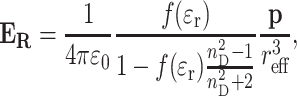 |
1 |
where ε r is the relative dielectric permittivity of the spin-label environment, ε 0 is the permittivity of free space, and r eff is the effective interaction molecular radius of the spin label. The term involving the refractive index n D of the pure spin label accounts for the polarizability of the spin label. Its inclusion is important because it effectively renormalizes the bare reaction field, f(ε r).
The function f(ε r) in Eq. (1) that determines the sensitivity to dielectric environment depends on the model assumed for calculating the reaction field. Various models have been proposed for the radial dependence of the dielectric permittivity of the surroundings (see Fig. 1). Onsager’s original model assumes a dipole of molecular radius r eff embedded in a homogeneous dielectric (i.e., a step function for ε r) and yields: f(ε r) = 2(ε r − 1)/(2ε r + 1) [17]. In this model, the reaction field saturates too rapidly with increasing dielectric permittivity of the medium, ε r. A survey of different models for the radial dependence of ε r (Fig. 1), including additionally a direct statistical mechanical calculation, has revealed that a model with an exponential transition to the bulk dielectric constant, which depends inversely on the radial distance, best describes the polarity dependence of spin-label EPR parameters [16]. In this analytical model, due to Block and Walker [18], the Onsager result is modified to
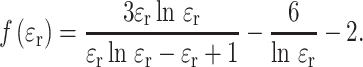 |
2 |
For ε
r close to unity, Eq. (2) becomes 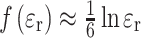 [19], confirming that E
R = 0 for ε
r = 1. For very large dielectric constants
[19], confirming that E
R = 0 for ε
r = 1. For very large dielectric constants 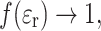 but far less rapidly than in the Onsager model. Recently, the Block–Walker model has also been applied to analyze the polarity dependence of fluorescent probes, which allows transfer of data on environmental polarity between these and spin labels [20]. Interestingly, the Block–Walker model was used to represent the effects of solvation in EPR simulations with the Gaussian quantum chemical package [21], whereas other packages still use the Onsager approach.
but far less rapidly than in the Onsager model. Recently, the Block–Walker model has also been applied to analyze the polarity dependence of fluorescent probes, which allows transfer of data on environmental polarity between these and spin labels [20]. Interestingly, the Block–Walker model was used to represent the effects of solvation in EPR simulations with the Gaussian quantum chemical package [21], whereas other packages still use the Onsager approach.
Fig. 1.
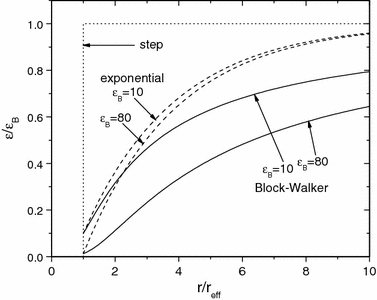
Radial dependence of the relative dielectric permittivity for different models of the reaction field. Dotted line step function, Onsager [17]. Solid line exponential-inverse transition, Block and Walker [18]. Dashed line direct exponential transition, Ehrenson [69]. r eff is the effective molecular radius of the spin label. The starting level is ε r = 1, for r/r eff ≤ 1. Dependences are given for two values of the bulk dielectric permittivity that is attained at large distances: ε B = 10 and ε B = 80, as indicated
Isotropic Hyperfine Couplings
The isotropic 14N-hyperfine coupling, a N0, of nitroxyl spin labels depends linearly on the unpaired electron spin density on the nitrogen atom (ρ Nπ) and to a lesser extent on that on the oxygen atom (ρ Oπ):
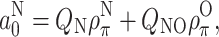 |
3 |
where 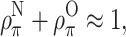 and the leading term is that involving Q
N (≫Q
NO). The spin density distribution, and hence the hyperfine coupling, is perturbed linearly by the reaction field from the polar environment [22]. The isotropic coupling therefore depends on the dielectric permittivity of the environment according to [23]
and the leading term is that involving Q
N (≫Q
NO). The spin density distribution, and hence the hyperfine coupling, is perturbed linearly by the reaction field from the polar environment [22]. The isotropic coupling therefore depends on the dielectric permittivity of the environment according to [23]
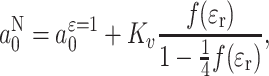 |
4 |
where a ε=10 is the extrapolated isotropic hyperfine coupling in a medium of relative dielectric permittivity ε r = 1. The coefficient, K v, of the polarity-dependent term is given by:
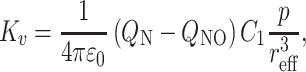 |
5 |
which is a constant for a particular nitroxide (C
1 is the factor relating changes in ρ
Nπ to the strength of the reaction field). In Eq. (4), it is assumed that 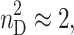 for the refractive index of the nitroxide [19].
for the refractive index of the nitroxide [19].
Values of the calibration constants in Eq. (4), for various nitroxides of relevance to biological spin labeling (see Fig. 2), are listed in Table 1. These values of a ε=10 and K v are obtained by using the Block–Walker model Eq. (2) for the reaction field. The 4,4-dimethyl-oxazolidine-N-oxyl (DOXYL) nitroxide is used for site-specific spin labeling of lipid chains, which is important for determining transmembrane polarity profiles. The other spin-label moieties in Table 1 are involved mostly in spin labeling proteins. (1-Oxyl-2,2,5,5-tetramethylpyrroline-3-methyl) methanethiosulfonate (MTSSL) is the standard reagent, in combination with cysteine-scanning mutagenesis, for site-directed spin labeling of proteins. 2,2,6,6-Tetramethylpiperidine-1-oxyl-4-amino-4-carboxylic acid (TOAC) is a nitroxyl amino acid that can be introduced into the protein backbone by peptide synthesis.
Fig. 2.
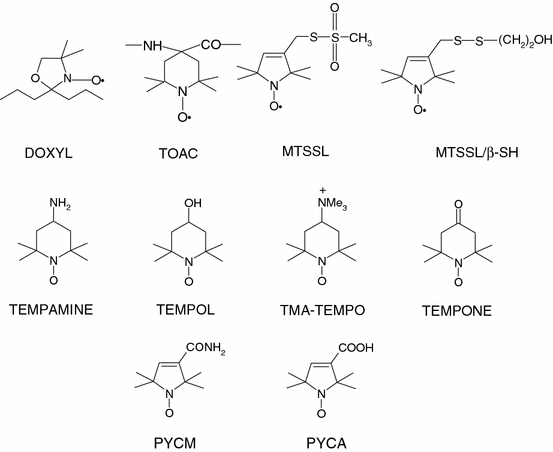
Chemical structures of spin-label nitroxide moieties. DOXYL moiety is attached to the hydrocarbon chain in a spin-labeled lipid; TOAC is an amino acid unit in spin-labeled peptides; MTSSL is used for spin labeling cysteine residues in proteins and peptides; MTSSL/β-SH is an S–S adduct of MTSSL. TOAC, 4-amino-TEMPO (TEMPAMINE), 4-hydroxy-TEMPO (TEMPOL), 4-trimethylammonium-TEMPO (TMA-TEMPO) and 4-oxo-TEMPO (TEMPONE) are based on the 6-membered piperidine ring (i.e., 2,2,6,6-tetramethyl-piperidine-1-oxyl [TEMPO]-based). MTSSL, PYCM and PYCA are based on the 5-membered pyrroline ring
Table 1.
Dependence of isotropic nitrogen hyperfine couplings, a
N0, of nitroxyl spin labels on solvent polarity, 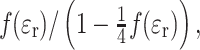 in aprotic media, according to Eqs. (2) and (4) for the Block–Walker model
in aprotic media, according to Eqs. (2) and (4) for the Block–Walker model
| Spin label | K v (μT) | a N0 (μT) | Reference |
|---|---|---|---|
| Lipid spin labels | |||
| DOXYL | 87 ± 12 | 1410 ± 5 | [23] |
| Protein spin labels | |||
| MTSSLa | 81 ± 55 | 1421 ± 17 | [23] |
| MTSSL/β-SHa | 63 ± 31 | 1437 ± 10 | [23] |
| Peptide spin labels | |||
| TOAC | 89 ± 16 | 1464 ± 6 | [23] |
| 71 ± 20 | 1464 ± 8 | ||
| Piperidinyl nitroxides | |||
| TEMPAMINE | 98 ± 11 | 1524 ± 4 | [16] |
| TEMPOL | 99 ± 13 | 1519 ± 6 | [16] |
| TMA-TEMPO | 96 ± 13 | 1513 ± 6 | [16] |
| Pyrrolinyl nitroxides | |||
| PYCM | 109 ± 13 | 1404 ± 4 | [16] |
| 99 ± 14 | 1410 ± 6 | ||
| PYCA | 154 ± 21 | 1400 ± 9 | [16] |
aSimulated by using the Onsager reaction field
The values of K v in Table 1 reflect the relative sizes of the different nitroxides. Taking (Q N − Q NO) = 2.04 mT [24], p = 3 Debye (10−29 Cm) [25] and C 1 = 1.9 × 10−11 V−1 m [26], effective molecular radii of: r eff = 0.35 ± 0.10 and 0.38 ± 0.07 nm are obtained for MTSSL and MTSSL/β-SH, respectively, compared with r eff = 0.31 ± 0.01 nm for the smaller di-tert-butyl nitroxide (DTBN) [23]. For both the DOXYL and TOAC nitroxides, an effective radius of 0.34 ± 0.02 nm is obtained, which must correspond only to a segment of the entire spin-labeled lipid or peptide. Effective radii estimated from group contributions to the molecular volume, V w [27], are r eff = (3V w/4π)1/3 = 0.385, 0.386 and 0.341 nm for MTSSL, MTSSL/β-SH and DTBN, respectively. These are in qualitative accord with the values deduced from the EPR data. For TOAC, the effective radius deduced from the molecular volume of the TOAC ring alone is r eff = 0.335 nm, which is close to the effective experimental value. The DOXYL unit has a considerably smaller molecular volume: including two methylene groups on either side of the point of chain attachment is needed to bring the effective radius, r eff = 0.341 nm, close to that deduced from Eq. (5).
These results imply that an electric field of strength E x = 109 V m−1 produces a change in isotropic hyperfine coupling of Δa N0 = 40 μT (cf. Refs. [22, 26]). From the molecular volumes of MTSSL, MTSSL/β-SH, DTBN and the peptide moiety of TOAC, the mean experimental polarity sensitivity of the isotropic hyperfine coupling is given by K v = (4.21 ± 0.39 μT nm3) × (1/r 3eff) [23]. This relation can prove useful for prediction of the polarity dependence of other nitroxides.
Anisotropic Hyperfine Couplings
The polarity dependence of the principal z-element of the hyperfine tensor is determined by both the isotropic and anisotropic terms:
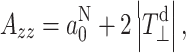 |
6 |
where 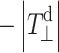 is the perpendicular element of the traceless hyperfine tensor that arises from the electron–nuclear dipolar interaction. Clearly, the latter depends directly on the unpaired spin density on the nitrogen:
is the perpendicular element of the traceless hyperfine tensor that arises from the electron–nuclear dipolar interaction. Clearly, the latter depends directly on the unpaired spin density on the nitrogen: 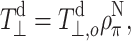 where
where  is the value of
is the value of 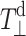 for ρ
Nπ = 1. Combining Eqs. (3) and (6), A
zz is related to the isotropic coupling constant, a
N0, by
for ρ
Nπ = 1. Combining Eqs. (3) and (6), A
zz is related to the isotropic coupling constant, a
N0, by
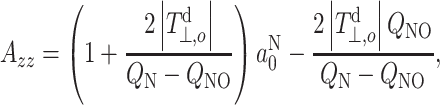 |
7 |
which predicts a linear dependence. The value of 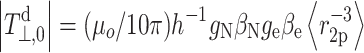 is 47.8 MHz (≈1.70 mT) for a 14N 2p-orbital [28]. Values of Q
N and Q
NO depend on the particular nitroxide and may be estimated by using Eq. (7) [24].
is 47.8 MHz (≈1.70 mT) for a 14N 2p-orbital [28]. Values of Q
N and Q
NO depend on the particular nitroxide and may be estimated by using Eq. (7) [24].
Griffith et al. [22] demonstrated an approximately linear relation between A
zz and a
N0 for DOXYL spin-labeled stearic acids or their methyl esters in a number of glass-forming media. Linear regression yields A
zz = (2.19 ± 0.27) × a
N0+(0.14 ± 0.39) mT, implying from Eq. (7) that Q
NO ≈ 0. Table 2 lists values of the mean ratio of anisotropic to isotropic hyperfine couplings, A
zz/a
N0, for different nitroxide spin labels. Also listed are the values of Q
N that are deduced from Eq. (7) with Q
NO = 0 and 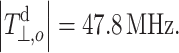
Table 2.
Mean ratios of anisotropic to isotropic 14N-hyperfine couplings, A zz/a N0, for different nitroxides, and resulting values of Q N in Eq. (3) [23]a
| Spin label | A zz/a N0 | Q N/MHz (mT) |
|---|---|---|
| DOXYL | 2.33 ± 0.05 | 72 ± 3 (2.57 ± 0.09) |
| 2.29 ± 0.02 | 74 ± 1 (2.64 ± 0.04) | |
| MTSSL | 2.34 ± 0.04 | 71 ± 2 (2.52 ± 0.08) |
| MTSSL/β-SH | 2.36 ± 0.02 | 70 ± 1 (2.50 ± 0.04) |
| TOAC | 2.32 ± 0.07 | 72 ± 4 (2.58 ± 0.13) |
Isotropic g-Values
The g-factors of nitroxides depend on the unpaired spin density, ρ Oπ, on the oxygen atom and additionally on the energies and distribution of the lone pair orbitals. Therefore, the isotropic g-values respond to environmental polarity, but the sign of the polarity dependence is opposite to that of the hyperfine coupling. The major contribution to the polarity dependence of the nitroxide g-tensor comes from the g xx element [11, 29]:
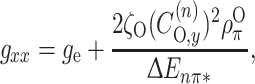 |
8 |
where g
e = 2.002319 is the free-electron g-value, ζO is the spin–orbit coupling of oxygen, 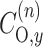 is the coefficient of the oxygen 2p
y orbital in the lone pair orbital, and ΔE
nπ* is the n → π* excitation energy. The g
yy tensor element is considerably less sensitive to polarity than the g
xx element because the energy denominators for g
yy involve the bonding and antibonding N–O σ-orbitals, which do not lie as close in energy to the unpaired electron orbital as does the lone pair. The g
zz tensor element is practically insensitive to polarity, i.e., g
zz ≈ g
e.
is the coefficient of the oxygen 2p
y orbital in the lone pair orbital, and ΔE
nπ* is the n → π* excitation energy. The g
yy tensor element is considerably less sensitive to polarity than the g
xx element because the energy denominators for g
yy involve the bonding and antibonding N–O σ-orbitals, which do not lie as close in energy to the unpaired electron orbital as does the lone pair. The g
zz tensor element is practically insensitive to polarity, i.e., g
zz ≈ g
e.
The g-factor, like the hyperfine coupling, also responds approximately linearly to the polarization reaction field (see, e.g., Refs. [13, 30]). Consequently, the polarity dependence of the isotropic g-value in aprotic environments is given similarly by [cf. Eq. (4)]
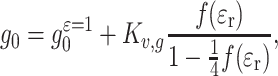 |
9 |
where g ε=10 is the isotropic g-factor in a medium of relative dielectric permittivity ε r = 1, and K v,g is a constant for a particular nitroxide. Values of the linear regression parameters, K v,g and g ε=10, for some spin labels of biological interest in aprotic solvents are listed in Table 3.
Table 3.
Dependence of isotropic g-values, g
0, of nitroxyl spin labels on solvent polarity, 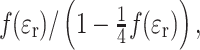 in aprotic media according to Eqs. (2) and (9) for the Block–Walker model [23]
in aprotic media according to Eqs. (2) and (9) for the Block–Walker model [23]
| Spin label | K v,g × 103 | (g ε=10 − g e) × 103 |
|---|---|---|
| DOXYL | −0.19 ± 0.06 | 3.60 ± 0.02 |
| MTSSL | −0.22 ± 0.09 | 3.65 ± 0.03 |
| MTSSL/β-SH | −0.36 ± 0.15 | 3.69 ± 0.04 |
| TOAC | −0.37 ± 0.06 | 3.91 ± 0.02 |
Protic Environments
Isotropic Hyperfine Couplings
For protic media, the effects of hydrogen bonding on the hyperfine couplings mostly far outweigh those of the solvent polarity. Figure 3 shows the dependence of the isotropic 14N-hyperfine coupling constants of a DOXYL fatty acid and a TOAC-containing dipeptide on the dielectric permittivity of protic solvents with differing polarities. For the more apolar protic solvents, an approximately linear dependence on polarity is obtained with the Block–Walker model, in accordance with Eq. (4) for aprotic media. The values of the slope of the dependence, K v, are comparable to those obtained with aprotic solvents, but the intercepts, a ε=10, are considerably larger (see Ref. [23]). As the proton donor concentration increases at higher polarities, the dependence on polarity shows a steep nonlinearity when hydrogen-bonding contributions to a N0 come to overwhelm those from polarization of the medium.
Fig. 3.
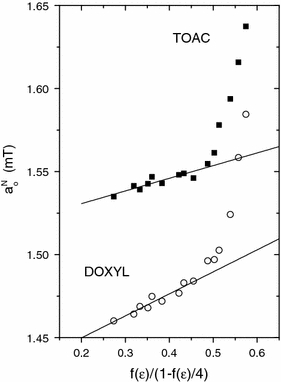
Dependence of the isotropic hyperfine coupling, a
N0, on solvent polarity, 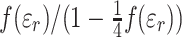 with the Block–Walker model Eq. (2), for DOXYL (circles) and TOAC (squares) spin labels in protic solvents. Solid lines are linear regressions for a limited range of data from the more apolar protic media [23]
with the Block–Walker model Eq. (2), for DOXYL (circles) and TOAC (squares) spin labels in protic solvents. Solid lines are linear regressions for a limited range of data from the more apolar protic media [23]
Levelling-off of the polarity dependence for the more apolar protic solvents in Fig. 3 arises because the bulkier alcohol molecules form hydrogen bonds less efficiently. In the presence of a proton donor, chemical exchange takes place between free and hydrogen-bonded nitroxides, which have isotropic 14N-hyperfine couplings 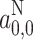 and
and 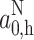 , respectively. Because exchange is fast compared with the difference in hyperfine couplings, the isotropic coupling constant that is observed experimentally is given by (see, e.g., Ref. [31])
, respectively. Because exchange is fast compared with the difference in hyperfine couplings, the isotropic coupling constant that is observed experimentally is given by (see, e.g., Ref. [31])
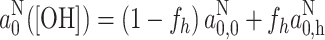 |
10 |
where f
h([OH]) is the fractional population of hydrogen-bonded nitroxides. The latter depends directly on the concentration of proton-donor –OH groups in the different solvents: f
h([OH]) = K
A,h[OH], where K
A,h is an effective association constant. Figure 4 illustrates the linear dependence of a
N0 on molar concentration, [OH], of hydroxyl groups that is obtained for DOXYL and TOAC spin labels in alkanol solvents and their mixtures with water. Parameters of the linear regressions for these and other spin labels are given in Table 4. The values of 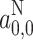 for the non-hydrogen-bonded nitroxides are close to the hyperfine couplings that are predicted for an aprotic solvent of polarity
for the non-hydrogen-bonded nitroxides are close to the hyperfine couplings that are predicted for an aprotic solvent of polarity 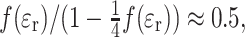 from the data in Table 1. The gradients of the dependences on –OH concentration,
from the data in Table 1. The gradients of the dependences on –OH concentration,  in Table 4 are similar for the different nitroxides. Density functional theory (DFT) calculations for MTSSL [32] predict values of a
0,h − a
0,0 ≈ 82 and 145 μT for one and two hydrogen bonds, respectively, which implies that K
A,h ~ 0.02–0.03 M−1 [cf. Eq. (10)]. The standard state to which K
A,h refers here is that of a pure hydrogen-bonding solvent.
in Table 4 are similar for the different nitroxides. Density functional theory (DFT) calculations for MTSSL [32] predict values of a
0,h − a
0,0 ≈ 82 and 145 μT for one and two hydrogen bonds, respectively, which implies that K
A,h ~ 0.02–0.03 M−1 [cf. Eq. (10)]. The standard state to which K
A,h refers here is that of a pure hydrogen-bonding solvent.
Fig. 4.
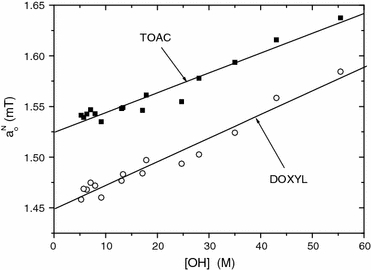
Dependence of the isotropic hyperfine coupling, a N0, on concentration, [OH], of hydroxyl proton-donor groups in alkanols and their mixtures with water, for DOXYL (circles) and TOAC (squares) spin labels. Solid lines are linear regressions [23]
Table 4.
Coefficients for the linear dependence of isotropic hyperfine splittings, a N0, on –OH concentration for different spin labels in protic media [see Eq. (10)] [23]
| Spin label |
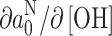 (μT M−1) (μT M−1) |
a N0,0 (μT) |
|---|---|---|
| DOXYL | 2.3 ± 0.1 | 1449 ± 3 |
| MTSSL | 2.2 ± 0.3 | 1472 ± 7 |
| MTSSL/β-SH | 2.2 ± 0.2 | 1484 ± 5 |
| TOAC | 2.0 ± 0.1 | 1524 ± 3 |
Much higher association constants for hydrogen bonding are expected and found with nitroxides as acceptors in aprotic media [31, 33]. Figure 5 shows the dependence of the isotropic 14N-hyperfine splitting on concentration of the H-bond donor trifluoroethanol (TFE) in the apolar solvents toluene or benzene, for a DOXYL and a TEMPO-based nitroxide. These clearly have the appearance of a binding curve. Applying the law of mass action, together with Eqs. (4) and (10), the dependence on proton donor concentration is given by [31]
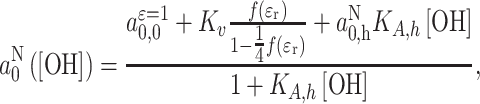 |
11 |
where ε r is the dielectric permittivity of the mixture of protic and aprotic solvents, which also depends on [OH]. The solid lines in Fig. 5 are nonlinear least-squares fits of Eq. (11), which yield association constants of K A,h ~ 1.0 M−1 for H-bonding of TFE with both DOXYL and TEMPONE. (The corresponding values of a 0,h − a 0,0 are ≈120 and 130 μT for DOXYL and TEMPONE, respectively.) The association constant for hydrogen bonding with water is likely to be larger than K A,h ~ 1.0 M−1, because assuming this value also for water predicts effective internal water concentrations in lipid membranes that are rather high compared with those expected from the solubility of water in oil [33].
Fig. 5.
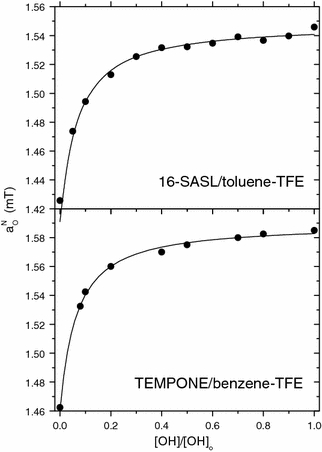
Dependence of the isotropic hyperfine coupling, a N0, of 16-DOXYL-stearic acid and TEMPONE spin labels on proton donor concentration, [OH], in mixtures of TFE with toluene or benzene. Solid lines are fits of Eq. (11) to the experimental data with the Onsager model, yielding K A,h = 0.96 ± 0.14 and 1.01 ± 0.07 M−1 for H-bonding of TFE with DOXYL and TEMPONE, respectively [31, 33]
Isotropic g-Values
As with hyperfine couplings, the effects of hydrogen bonding on the g-values in protic media considerably outweigh those of polarity. Because line shifts arising from g-value differences are small compared with the magnitude of the overall resonance field, fast chemical exchange between free and hydrogen-bonded nitroxides effectively averages the g-values. An expression similar to that for the hyperfine couplings therefore holds for the isotropic g-values in protic solvents [cf. Eq. (10)]:
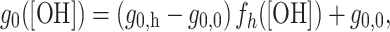 |
12 |
where g 0,h and g 0,0 are the isotropic g-values of the hydrogen-bonded and free nitroxides, respectively, and f h([OH]) = K A,h[OH] is again the fraction of nitroxides that are hydrogen bonded.
As for hyperfine couplings, isotropic g-values depend linearly on the concentration of hydroxyl groups in hydrogen-bonding solvents, in accordance with Eq. (12). Data for various spin labels are given in Table 5. From DFT calculations, it is estimated that (g 0,h − g 0,0) ≈ −1.7 × 10−4 and −3.2 × 10−4 for one and two hydrogen bonds, respectively [32]. With the values for ∂g 0/∂[OH] in Table 6, this gives K A,h ~ 0.02–0.04 M−1, in agreement with the corresponding estimate from the isotropic hyperfine couplings.
Table 5.
Coefficients for the linear dependence of isotropic g-values, g 0, on –OH concentration for various spin labels in protic media [see Eq. (12)] [23]
| Spin label |
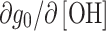 (M−1) (M−1) |
g 0,0 − g e |
|---|---|---|
| DOXYL | −(5.9 ± 0.3) × 10−6 | (3.543 ± 0.007) × 10−3 |
| MTSSL | −(5.7 ± 0.7) × 10−6 | (3.544 ± 0.017) × 10−3 |
| MTSSL/β-SH | −(5.5 ± 0.5) × 10−6 | (3.510 ± 0.011) × 10−3 |
| TOAC | −(6.6 ± 0.4) × 10−6 | (3.709 ± 0.010) × 10−3 |
Table 6.
Correlation of isotropic g-values, g 0, with isotropic hyperfine couplings, a N0, for different nitroxyl spin labels in protic media [23]
| Spin label |
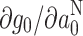 (T−1) (T−1) |
|---|---|
| DOXYL | −2.52 ± 0.11 |
| MTSSL | −2.52 ± 0.12 |
| MTSSL/β-SH | −2.46 ± 0.10 |
| TOAC | −3.33 ± 0.14 |
| DFTa | −2.1, −2.2 |
aDFT calculations. Data from Owenius et al. [32]. Contributions solely from hydrogen bonding: 1 and 2 hydrogen-bonds, respectively
The isotropic g-value is the trace of the g-tensor: g 0 = (1/3)(g xx+g yy+g zz), and is therefore related to polarity and hydrogen-bonding via changes in g xx and to a lesser extent in g yy. From Eq. (8), changes in g-value, δg 0, are related to the terms dependent on polarity and hydrogen-bonding by (cf. [34])
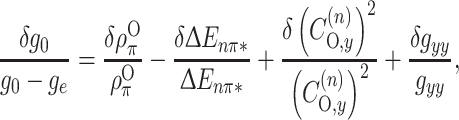 |
13 |
where the first two terms on the right are likely to dominate [29]. In contrast, changes in the isotropic hyperfine coupling depend only on the unpaired spin density [see Eq. (3)]. Therefore, g-values are preferentially sensitive to hydrogen-bonding, as compared with hyperfine couplings. Table 6 lists the gradients, 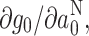 of the approximately linear correlation between g
0 and a
N0 in protic solvents. Predictions from DFT calculations [32] that are included in Table 6 suggest that a large part of this gradient in strongly polar solvents is contributed by hydrogen bonding to the nitroxide. For comparison, a similar gradient
of the approximately linear correlation between g
0 and a
N0 in protic solvents. Predictions from DFT calculations [32] that are included in Table 6 suggest that a large part of this gradient in strongly polar solvents is contributed by hydrogen bonding to the nitroxide. For comparison, a similar gradient 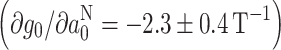 was obtained between the outer and inner chain regions for DOXYL-labeled lipids in phosphatidylcholine bilayer membranes [35].
was obtained between the outer and inner chain regions for DOXYL-labeled lipids in phosphatidylcholine bilayer membranes [35].
g-Tensor-Anisotropy
Fully exploiting the polarity dependence of the g xx tensor element [see Eq. (8)] was first possible in spin-label spectroscopy with the development of high-field EPR spectrometers. As correspondingly noted in connection with isotropic g-values, the advantage over hyperfine couplings is the enhanced sensitivity to hydrogen bonding. From Eq. (8), the polarity sensitivities of the two are related by [10]
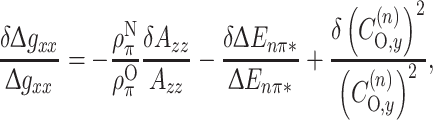 |
14 |
where  and
and 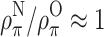 for nitroxides. Use of the g
xx tensor element is preferable over use of isotropic g-values because the former incorporates almost the entire polarity sensitivity of the g-tensor, but it requires high-field EPR spectrometers.
for nitroxides. Use of the g
xx tensor element is preferable over use of isotropic g-values because the former incorporates almost the entire polarity sensitivity of the g-tensor, but it requires high-field EPR spectrometers.
The gradient 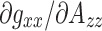 has proved to be a useful diagnostic indicator for distinguishing protic from aprotic environments. Steinhoff et al. [12] assign a gradient of
has proved to be a useful diagnostic indicator for distinguishing protic from aprotic environments. Steinhoff et al. [12] assign a gradient of 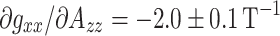 to a protic (i.e., water-accessible) environment and of −1.35 ± 0.1 T−1 to an aprotic environment, for MTSSL in the membrane protein bacteriorhodopsin. Corresponding values for MTSSL in homogeneous media are −1.8 T−1 and approximately −0.8 T−1 for protic and aprotic solvents, respectively [32]. Quantum theoretical (DFT) calculations of the incremental changes, ΔA
zz and Δg
xx, in the hyperfine and g-tensors that are induced by hydrogen bonding of water to the nitroxide support the assignment of large g
xx versus A
zz gradients to protic environments (see Table 7). For comparison, a gradient of
to a protic (i.e., water-accessible) environment and of −1.35 ± 0.1 T−1 to an aprotic environment, for MTSSL in the membrane protein bacteriorhodopsin. Corresponding values for MTSSL in homogeneous media are −1.8 T−1 and approximately −0.8 T−1 for protic and aprotic solvents, respectively [32]. Quantum theoretical (DFT) calculations of the incremental changes, ΔA
zz and Δg
xx, in the hyperfine and g-tensors that are induced by hydrogen bonding of water to the nitroxide support the assignment of large g
xx versus A
zz gradients to protic environments (see Table 7). For comparison, a gradient of  is obtained between DOXYL labels situated close to the polar interface and close to the hydrophobic center of lipid membranes [35], indicating a dominant contribution of water penetration to the polarity profile in biological membranes.
is obtained between DOXYL labels situated close to the polar interface and close to the hydrophobic center of lipid membranes [35], indicating a dominant contribution of water penetration to the polarity profile in biological membranes.
Table 7.
Contributions of water hydrogen bonding to g xx (and A zz) from DFT calculations for MTSSL model nitroxides
| Medium | Δg xx | Δg xx/ΔA zz (T−1) | Reference | ||
|---|---|---|---|---|---|
| 1H2O | 2H2O | 1H2O | 2H2O | ||
| Vacuuma | −4.4 × 10−4 | −8.2 × 10−4 | −2.0 | −2.3 | [32] |
| Vacuum | −5.5 × 10−4 | – | −2.4 | – | [72] |
| Waterb | −4.6 × 10−4 | – | −3.2 | – | [72] |
a g-Tensor for nitroxide in vacuum. A-tensor calculated with a polarizable medium by using the Onsager reaction field
bSimulated by using the Onsager reaction field
A valuable feature of high-field EPR is the ability to detect g-strain that arises from a heterogeneous population of hydrogen-bonded spin labels, and even to resolve discrete levels of hydrogen bonding [35–37]. Figure 6 shows 94 and 360 GHz spectra that illustrate the polarity-associated g-strain for a spin label at the n = 5 position of the lipid chains (5-PC) in hydrated membranes. A single, inhomogeneously broadened peak with frequency-dependent width is observed in the g xx-region at the low-field side of the spectrum from 5-PC. In contrast, at the n = 9 position (i.e., 9-PC), broadening of the g xx-feature in the 94 GHz spectrum is considerably smaller and the 14N-hyperfine splitting (2A xx) is partially resolved. Relative to 9-PC (for which ΔH 1/2 = 47 μT), the inhomogeneous broadening of 5-PC increases almost fourfold between 94 and 360 GHz (from δΔH 1/2 = 41 μT to δΔH 1/2 = 153 μT), i.e., scales directly with the microwave frequency. The equivalent g xx-strain corresponds to a distribution width of δΔg xx ≈ 2 × 10−4. This represents a statistical distribution of water molecules in the region of the membrane close to the top of the chain, whereas water is almost absent towards the center of the membrane. The n = 8 segment of the chain (i.e., 8-PC) represents a transition region, where the EPR spectrum consists of a superposition of partially resolved components corresponding to the two flanking regions n < 8 and n > 8.
Fig. 6.
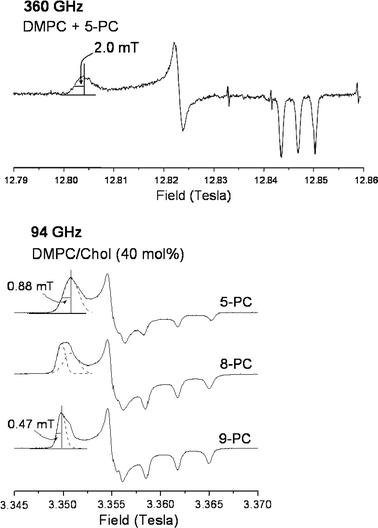
Upper 360-GHz EPR spectrum of 5-DOXYL-phosphatidylcholine (5-PC) in membranes of dimyristoyl phosphatidylcholine at −100°C [70]. Lower 94-GHz EPR spectra of n-DOXYL-phosphatidylcholines (n-PC) in membranes of dimyristoyl phosphatidylcholine + 40 mol% cholesterol at −100°C (data from Ref. [35]). Dashed lines in the g xx-regions indicate: an individual hyperfine component in the non-H-bonded state (9-PC), inhomogeneous broadening from a distribution of H-bonding states (5-PC), and coexistence of these two states (8-PC)
The results of DFT calculations, which are presented in Table 7, suggest that hydrogen bonding of one water molecule causes a g-shift of Δg xx = −(4.4–5.5) × 10−4. The g-shift measured between the outer (5-PC) and inner (10-PC) regions of the membrane is Δg xx ≈ −6.2 × 10−4. Thus, the mean of number water molecules that are hydrogen-bonded to a spin label positioned in the upper part of the chain is ~1, and the distribution width (see above) is approximately ±0.5 water molecules. Considering that a given nitroxide can have up to two strong H-bonds with water, these estimates are not unreasonable.
Membrane Polarity Profiles
The transmembrane polarity profile, or permeability barrier, of biological membranes can be determined at high spatial resolution by using lipids systematically spin-labeled at single sites down their hydrocarbon chains with the DOXYL moiety [38] (see Fig. 2). A considerable range of EPR techniques are available for such studies with spin-labeled lipids. Membrane polarity profiles can be detected from conventional CW-EPR determinations of isotropic hyperfine couplings [2, 39–45] or A zz-values [22, 46], or from HF-EPR determinations of g xx [35]. Profiles of water penetration can be determined from ESEEM spectroscopy of D2O using pulse EPR [14, 47, 48]. Finally, penetration profiles of hydrophobic paramagnetic gases, such as nitric oxide [49, 50] and molecular oxygen [51–53], can be obtained from enhancements of spin-label T 1e-relaxation that are determined from nonlinear CW-EPR (progressive saturation [54–56], saturation transfer [57, 58], or first harmonic phase-quadrature spectra [59, 60]) or from saturation recovery pulse-EPR [61, 62].
Oxygen (Hydrophobicity) Profiles
Figure 7 shows the transmembrane profile of spin–lattice relaxation enhancement by oxygen in lipid bilayers. T 1e-enhancements measure the local concentration–diffusion product, D T[O2], where D T is the translational diffusion coefficient of oxygen in the membrane. Oxygen is more soluble in oil than in water and therefore accumulates in the hydrophobic interior of the lipid membrane. The ensuing relaxation enhancements measured by both the line broadening and the CW-EPR saturation parameters of spin-labeled lipids [53] are in good agreement with those measured by saturation recovery EPR of a spin-labeled α-helical transmembrane peptide [63]. Spin-labeled lipids are able to map the profile with better resolution than spin-labeled peptides, because the transmembrane increment of Δz = 0.1 nm/CH2 segment for lipid chains is shorter than that of Δz = 0.15 nm/amino-acid residue for a peptide α-helix. A transmembrane peptide has the considerable advantage, however, that it can be spin-labeled systematically in regions corresponding to the lipid headgroups and beyond, and also that it extends continuously across both halves of the bilayer. In Fig. 7, the lipid profile has been reflected across the bilayer midplane with a separation that gives best alignment with the peptide profile.
Fig. 7.
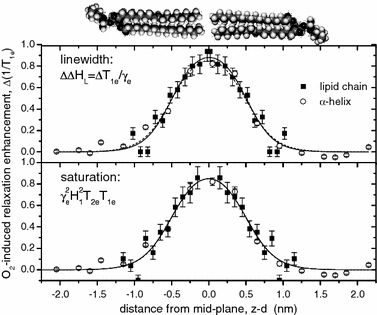
Transmembrane profile of oxygen-induced T 1-relaxation enhancement of spin-labeled DOXYL-lipids, n-PC (solid squares), and spin-labeled peptide, GW2(LA)mC[MTSSL](LA)pLW2A (open circles), in fluid phospholipid bilayer membranes. Upper Lipid relaxation enhancements deduced from convolution line widths: ΔΔH L = Δ(1/T 1e)/γe, compared with peptide relaxation enhancements deduced from saturation recovery EPR. Lower Lipid relaxation enhancements deduced from CW-EPR saturation parameters: P = γ2e H 21 T 2e T 1e, compared with peptide relaxation enhancements. Solid and dashed lines are nonlinear least-squares fits of Eq. (16) to the data for spin-labeled lipids and peptides, respectively. Relaxation enhancements are normalized such that R 1 − R 2 = 1 and R 2 = 0, for the fits of Eq. (16); transmembrane distances, z, are referred to the membrane midplane as origin (2d is the membrane thickness) [64]
The diffusion–concentration profile for oxygen that is registered by spin-labeled lipids exhibits a sigmoidal Boltzmann shape that was established for the transmembrane polarity profile based on measurements of a N0 [40], and also of g xx and A zz [35]:
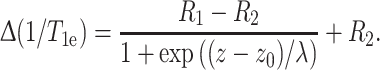 |
15 |
Equation 15 corresponds to a two-phase distribution between membrane regions with transverse coordinate z > z 0 and z < z 0, where the free energy of transfer for oxygen depends linearly on the distance from the dividing plane at z = z 0. The oxygen-induced enhancements in the two regions are R 1 and R 2, respectively, and λ is the decay length that characterizes the width of the transition region. Equation (15) describes only one lipid leaflet of the symmetrical bilayer membrane. The complete transmembrane profile that incorporates two leaflets back-to-back is given by
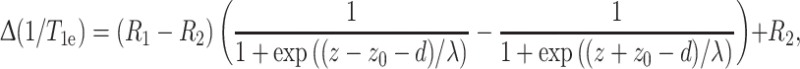 |
16 |
where d is the thickness of one lipid leaflet of the membrane. Fitting Eq. (16) to the T 1e-enhancement data for the spin-labeled peptides gives z 0 = 0.49 ± 0.09 nm and λ = 0.20 ± 0.05 nm, and the membrane midplane corresponds to residue position (d) 11.7 ± 0.2 (see dashed lines in Fig. 7). After alignment, comparable values are also obtained from the profiles for spin-labeled lipids [64].
Hyperfine and g-Value (Polarity) Profiles
Oxygen is a hydrophobic molecule and the profile in Fig. 7 reflects the hydrophobic barrier to permeation of the membrane by polar solutes. The transmembrane polarity profile which is registered by the spin-label hyperfine couplings and g-values (see, e.g., lower trace in Fig. 5) is the inverse of that in Fig. 7, i.e., achieves a minimum at the membrane midplane. Table 8 summarizes data, characterizing the transmembrane profiles that are obtained from the different EPR techniques, including D2O-ESEEM which directly reflects the profile of water penetration [14]. All data are obtained with spin-labeled lipids, and the parameters z 0 and λ are expressed in terms of the C-atom position, n, in the sn-2 chain of phosphatidylcholine. Mostly, the profiles are rather similar: the decay length is λ ~ 1–1.5 CH2 groups, with the exception of the data from frozen samples (g xx, A zz, and ESEEM) for which a sharper profile is found. The midpoint of the profile is at the n 0 ~ 8–10 position of the lipid chain, with a tendency to the higher end of this range for membranes containing cholesterol (at least from measurements of a N0 in fluid membranes). Integration over the entire oxygen profile in Fig. 7 allows estimation of the membrane permeability coefficient, P. Permeabilities of P ~ 210, 160 and 5–7 × 10−3 cm s−1 are obtained for oxygen [53], nitric oxide [50] and water [40], respectively.
Table 8.
Parameters for fitting the polarity profiles, recorded for n-PC spin labeled phosphatidylcholine chains in different lipid membranes, according to Eq. 15)a
| Lipidb | Indicator | n 0 | λ | Reference |
|---|---|---|---|---|
| diC16:0PC | a N0 | 7.8 ± 0.1 | 0.8 ± 0.1 | [40] |
| diC16:0PC +chol | a N0 | 9.2 ± 0.1 | 0.8 ± 0.1 | [40] |
| D2O-ESEEM | 7.6 ± 0.2 | 0.4 ± 0.1 | [48] | |
| diC14:0PC | a N0 | 8.00 ± 0.06 | 0.44 ± 0.06 | [40] |
| O2, saturation | 9.8 ± 0.7 | 1.4 ± 0.6 | [53] | |
| O2, linewidth | 9.0 ± 0.1 | 1.4 ± 0.1 | [53] | |
| O2, saturation | 7.8 ± 0.2 | 0.5 ± 0.2 | [50] | |
| NO, saturation | 10.2 ± 0.3 | 1.4 ± 0.3 | [50] | |
| diC14:0PC +chol | a N0 | 9.37 ± 0.09 | 0.83 ± 0.08 | [40] |
| g xx | 7.63 ± 0.08 | 0.25 ± 0.05 | [35] | |
| A zz | 7.60 ± 0.09 | 0.36 ± 0.06 | [35] | |
| C16:0C18:1PC | a N0 | 8.35 ± 0.14 | 1.03 ± 0.13 | [40] |
| C16:0C18:1PC +chol | a N0 | 9.38 ± 0.14 | 1.25 ± 0.13 | [40] |
| diC18:1PC | a N0 | 8.24 ± 0.24 | 0.96 ± 0.22 | [40] |
| diC18:1PC +chol | a N0 | 10.0 ± 0.1 | 1.0 ± 0.1 | [40] |
a n 0 and λ are expressed in CH2 units for C-atom position in the sn-2 chain of phosphatidylcholine
b diC 16:0 PC dipalmitoyl phosphatidylcholine, diC 14:0 PC dimyristoyl phosphatidylcholine, C 16:0 C 18:1 PC 1-palmitoyl-2-oleoyl phosphatidylcholine, diC 18:1 PC dioleoyl phosphatidylcholine, chol cholesterol (40 or 50 mol%), a N0 isotropic 14N-hyperfine coupling, O 2 and NO relaxation enhancements by molecular oxygen and nitric oxide, respectively, g xx anisotropic g-tensor element, A zz anisotropic 14N-hyperfine tensor element
Intramembrane Location of Proteins and Peptides
The pronounced intramembrane polarity profile that is registered by the hyperfine couplings and g-values (Table 8), allows to determine the intramembrane depth at which a spin label on a membrane protein or peptide is situated and, hence, to locate the entire protein or peptide within the membrane. Because the transmembrane profiles of a N0, for example, are established with DOXYL labels, whereas proteins and peptides are spin-labeled with other nitroxides such as MTSSL or TOAC, calibrations of the polarity dependence of the different spin labels that are given in Tables 1, 3, 4 and 5 are needed to transfer the EPR data between lipids and proteins [23].
TOAC (see Fig. 2) is a nitroxyl amino acid that can substitute isosterically for β-alanine (Aib) in peptides that contain this amino acid, and more generally in helical peptides [65]. Alamethicin is a highly hydrophobic, 20-residue, channel-forming peptide antibiotic that contains a high proportion of Aib [66]. Figure 8 (left) gives the isotropic hyperfine couplings, Δa N0, suitably normalized, for TOAC substituted at the 1-, 8- or 16-position in alamethicin, relative to a N0-profiles for spin-labeled lipids n-PC in the corresponding fluid lipid-bilayer membranes. For all three TOAC positions, the values of a N0 correspond to a lower polarity in diC16:0PC bilayers than in the thinner diC14:0PC bilayers: the TOAC1 residue, for instance, is in a more polar location than the 4-C atom of the lipid sn-2 chain in diC14:0PC, but at the level of the 4–6 C-atom in diC16:0PC. The TOAC8 residue is situated towards the center of the bilayer (C-atom 10–14) in diC16:0PC, but at the depth of the 8–9 C-atom in diC14:0PC. The TOAC16 residue is close to the 8 C-atom in diC16:0PC, and between the 7 and 8-C atoms in diC14:0PC. Clearly, the alamethicin helix spans the membrane with TOAC16 residing in the opposite bilayer leaflet from that of TOAC8 and TOAC1. Comparison between the two lipid hosts of different chain length reflects the general trend that, in membranes of different thickness, the hydrophobic alamethicin peptide preserves the same transmembrane location relative to the bilayer midplane [67].
Fig. 8.
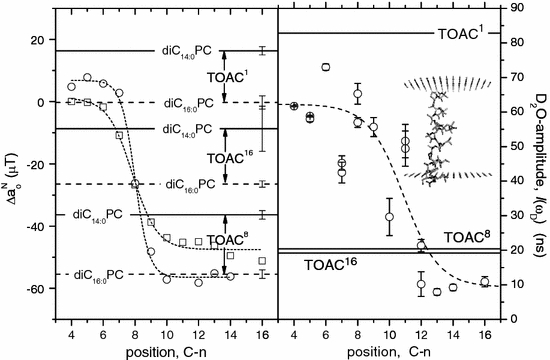
Location of TOAC-substituted alamethicin peptide in phospholipid membranes. Left isotropic hyperfine couplings, a
N0, for alamethicin-TOAC1, -TOAC8 and -TOAC16 in fluid diC14:0PC (solid horizontal lines) and diC16:0PC (dashed horizontal lines) bilayers, relative to the a
N0-profiles of DOXYL phosphatidylcholines n-PC (dotted lines) in fluid diC14:0PC (circles) and diC16:0PC (squares) bilayers [40]. All values of a
N0 are corrected to those in methanol, i.e., 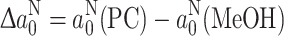 [67, 71]. Right D2O-ESEEM amplitudes of alamethicin-TOAC1, -TOAC8 and -TOAC16 in diC18:1PC bilayers (solid horizontal lines), relative to the profile of D2O-amplitudes for DOXYL phosphatidylcholines n-PC in diC16:0PC bilayers (solid circles) [48, 68]
[67, 71]. Right D2O-ESEEM amplitudes of alamethicin-TOAC1, -TOAC8 and -TOAC16 in diC18:1PC bilayers (solid horizontal lines), relative to the profile of D2O-amplitudes for DOXYL phosphatidylcholines n-PC in diC16:0PC bilayers (solid circles) [48, 68]
Complementary information on the location of alamethicin in lipid bilayer membranes is provided by the hyperfine modulation of the TOAC electron spin-echo envelope in an aqueous D2O medium (i.e., 2H-ESEEM). Figure 8 (right) shows the profile of D2O penetration in lipid membranes that is recorded by the 2H-ESEEM amplitudes from spin-labeled lipids, n-PC (symbols and dashed line). The solid lines give the corresponding D2O-ESEEM amplitudes for the alamethicin-TOACm positions. The D2O-ESEEM amplitude from the N-terminal TOAC1 residue correlates with the lipid polar headgroup region of the membrane. The D2O-ESEEM amplitudes for the TOAC8 and TOAC16 analogues are similar, indicating that these residues are situated at similar locations on opposite sides of the bilayer midplane. Comparing the ESEEM data in frozen membranes with the a N0 data from fluid membranes (Fig. 8, right and left), it is seen that the TOAC1 and TOAC8 residues are located at comparable positions in the two cases. The TOAC16 residue, on the other hand, although situated in the apposing bilayer leaflet, correlates with a position closer to the bilayer midplane in the thicker frozen membranes than in the thinner fluid bilayers. This indicates a more asymmetric location of alamethicin with respect to the membrane midplane in frozen membranes, which may be a feature of proto-assembled alamethicin ion channels [68].
Conclusions
- In aprotic environments, isotropic hyperfine couplings and g-values depend on dielectric permittivity, ε r, of the medium according to expressions of the form
where f(ε r) = 3ε r ln ε r/(ε r ln ε r − ε r+1) − 6/ln ε r − 2. For a N0, K v ~ 80–100 μT and a ε=10 depends on the particular spin label (see Table 1). For g 0, K v,g ~ −(0.2–0.4) × 10−3 and g ε=10 is given in Table 3.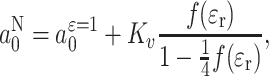
- In protic environments, isotropic hyperfine couplings and g-values depend linearly on the concentration of hydroxyl groups, [OH], according to expressions of the form
For a N0,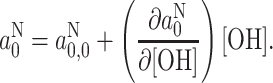
 ~ 2.2 μT M−1 and
~ 2.2 μT M−1 and 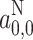 depends on the particular spin label (see Table 4). For g
0,
depends on the particular spin label (see Table 4). For g
0, 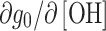 ~ −(5.5–6.6) × 10−6 M−1 and g
0,0 is given in Table 5.
~ −(5.5–6.6) × 10−6 M−1 and g
0,0 is given in Table 5. The g-value versus hyperfine coupling gradients,
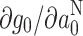 and
and 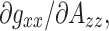 are diagnostic for hydrogen-bonding environments, with values of −(2–3) T−1 in protic media and considerably smaller in aprotic media. A hydrogen bond to one water molecule produces a g-shift of Δg
xx ≈ −4.5 × 10−4 (Table 7).
are diagnostic for hydrogen-bonding environments, with values of −(2–3) T−1 in protic media and considerably smaller in aprotic media. A hydrogen bond to one water molecule produces a g-shift of Δg
xx ≈ −4.5 × 10−4 (Table 7).- The profiles of polarity and permeation of O2, NO and H2O in lipid bilayer membranes follow a Boltzmann sigmoid with respect to the C-atom position, n, in the lipid chains of the form:
where λ ~ 1–1.5 CH2 groups and the midpoint of the profile is at n 0 ~ 8–10 (Table 8). This profile is established by measurement of: a N0, g xx and A zz; relaxation enhancements by O2 and NO; and D2O-ESEEM amplitudes.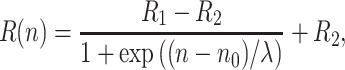
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
References
- 1.Schorn K, Marsh D. Chem. Phys. Lipids. 1996;82:7–14. doi: 10.1016/0009-3084(96)02550-9. [DOI] [Google Scholar]
- 2.Pates RD, Marsh D. Biochemistry. 1987;26:29–39. doi: 10.1021/bi00375a005. [DOI] [PubMed] [Google Scholar]
- 3.Horváth LI, Brophy PJ, Marsh D. Biochemistry. 1988;27:46–52. doi: 10.1021/bi00401a009. [DOI] [PubMed] [Google Scholar]
- 4.Horváth LI, Brophy PJ, Marsh D. J. Magn. Reson. 1994;B105:120–128. doi: 10.1006/jmrb.1994.1111. [DOI] [PubMed] [Google Scholar]
- 5.Livshits VA, Kurad D, Marsh D. J. Phys. Chem. B. 2004;108:9403–9411. doi: 10.1021/jp035915p. [DOI] [Google Scholar]
- 6.Livshits VA, Kurad D, Marsh D. J. Magn. Reson. 2006;180:63–71. doi: 10.1016/j.jmr.2006.01.005. [DOI] [PubMed] [Google Scholar]
- 7.Erilov DA, Bartucci R, Guzzi R, Marsh D, Dzuba SA, Sportelli L. J. Phys. Chem. B. 2004;108:4501–4507. doi: 10.1021/jp037249y. [DOI] [Google Scholar]
- 8.Marsh D. Appl. Magn. Reson. 2007;31:387–410. doi: 10.1007/BF03166592. [DOI] [Google Scholar]
- 9.Keeler J, Lubitz W, Möbius K, Dinse K-P. Magn. Reson. Chem. 2005;43:S1–S266. doi: 10.1002/mrc.1608. [DOI] [Google Scholar]
- 10.Möbius K, Savitsky A, Schnegg A, Plato M, Fuchs M. Phys. Chem. Chem. Phys. 2005;7:19–42. doi: 10.1039/b412180e. [DOI] [PubMed] [Google Scholar]
- 11.Marsh D, Kurad D, Livshits VA. Chem. Phys. Lipids. 2002;116:93–114. doi: 10.1016/S0009-3084(02)00022-1. [DOI] [PubMed] [Google Scholar]
- 12.Steinhoff HJ, Savitsky A, Wegener C, Pfeiffer M, Plato M, Möbius K. Biochim. Biophys. Acta. 2000;1457:253–262. doi: 10.1016/S0005-2728(00)00106-7. [DOI] [PubMed] [Google Scholar]
- 13.Plato M, Steinhoff HJ, Wegener C, Törring JT, Savitsky A, Möbius K. Mol. Phys. 2002;100:3711–3721. doi: 10.1080/00268970210166246. [DOI] [Google Scholar]
- 14.Bartucci R, Erilov DA, Guzzi R, Sportelli L, Dzuba SA, Marsh D. Chem. Phys. Lipids. 2006;141:142–157. doi: 10.1016/j.chemphyslip.2006.02.009. [DOI] [PubMed] [Google Scholar]
- 15.D. Marsh, T. Páli, L.I. Horváth, in Spin Labeling. The Next Millenium, vol. 14, ed. by L.J. Berliner (Plenum Press, New York, 1998), pp. 23–82
- 16.Marsh D. J. Magn. Reson. 2008;190:60–67. doi: 10.1016/j.jmr.2007.10.004. [DOI] [PubMed] [Google Scholar]
- 17.Onsager L. J. Am. Chem. Soc. 1936;58:1486–1493. doi: 10.1021/ja01299a050. [DOI] [Google Scholar]
- 18.Block H, Walker SM. Chem. Phys. Lett. 1973;19:363–364. doi: 10.1016/0009-2614(73)80380-X. [DOI] [Google Scholar]
- 19.Reddoch AH, Konishi S. J. Chem. Phys. 1979;70:2121–2130. doi: 10.1063/1.437756. [DOI] [Google Scholar]
- 20.Marsh D. Biophys. J. 2009;96:2549–2558. doi: 10.1016/j.bpj.2009.01.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Barone V. Chem. Phys. Lett. 1996;262:201–206. doi: 10.1016/0009-2614(96)01070-6. [DOI] [Google Scholar]
- 22.Griffith OH, Dehlinger PJ, Van SP. J. Membrane Biol. 1974;15:159–192. doi: 10.1007/BF01870086. [DOI] [PubMed] [Google Scholar]
- 23.Marsh D, Toniolo C. J. Magn. Reson. 2008;190:211–221. doi: 10.1016/j.jmr.2007.11.005. [DOI] [PubMed] [Google Scholar]
- 24.Cohen AH, Hoffman BM. J. Am. Chem. Soc. 1973;95:2061–2062. doi: 10.1021/ja00787a083. [DOI] [Google Scholar]
- 25.Rosantzev EG. Free Nitroxyl Radicals. New York/London: H. Ulrich/Plenum; 1970. [Google Scholar]
- 26.Schwartz RN, Peric M, Smith SA, Bales BL. J. Phys. Chem. B. 1997;101:8735–8739. doi: 10.1021/jp970555p. [DOI] [Google Scholar]
- 27.Bondi A. J. Phys. Chem. 1964;68:441–451. doi: 10.1021/j100785a001. [DOI] [Google Scholar]
- 28.Whiffen DH. J. Chim. Phys. 1964;61:1589–1591. [Google Scholar]
- 29.Kawamura T, Matsunami S, Yonezawa T. Bull. Chem. Soc. Jpn. 1967;40:1111–1115. doi: 10.1246/bcsj.40.1111. [DOI] [Google Scholar]
- 30.Gullá AF, Budil DE. J. Phys. Chem. B. 2001;105:8056–8063. doi: 10.1021/jp0109224. [DOI] [Google Scholar]
- 31.Marsh D. J. Magn. Reson. 2002;157:114–118. doi: 10.1006/jmre.2002.2572. [DOI] [PubMed] [Google Scholar]
- 32.Owenius R, Engström M, Lindgren M, Huber M. J. Phys. Chem. A. 2001;105:10967–10977. doi: 10.1021/jp0116914. [DOI] [Google Scholar]
- 33.Marsh D. Eur. Biophys. J. 2002;31:559–562. doi: 10.1007/s00249-002-0245-z. [DOI] [PubMed] [Google Scholar]
- 34.Ondar MA, Grinberg OYa, Dubinskii AA, Lebedev YaS. Sov. J. Chem. Phys. 1985;3:781–792. [Google Scholar]
- 35.Kurad D, Jeschke G, Marsh D. Biophys. J. 2003;85:1025–1033. doi: 10.1016/S0006-3495(03)74541-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Finiguerra MG, Blok H, Ubbink M, Huber M. J. Magn. Reson. 2006;180:197–202. doi: 10.1016/j.jmr.2006.02.011. [DOI] [PubMed] [Google Scholar]
- 37.Polovyanenko DN, Bagryanskaya EG, Schnegg A, Möbius K, Coleman AW, Ananchenko GS, Udachin KA, Ripmeester JA. Phys. Chem. Chem. Phys. 2008;10:5299–5307. doi: 10.1039/b803296c. [DOI] [PubMed] [Google Scholar]
- 38.Marsh D. Methods. 2008;46:83–96. doi: 10.1016/j.ymeth.2008.07.001. [DOI] [PubMed] [Google Scholar]
- 39.Fretten P, Morris SJ, Watts A, Marsh D. Biochim. Biophys. Acta. 1980;598:247–259. doi: 10.1016/0005-2736(80)90003-6. [DOI] [PubMed] [Google Scholar]
- 40.Marsh D. Proc. Natl. Acad. Sci. USA. 2001;98:7777–7782. doi: 10.1073/pnas.131023798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Swamy MJ, Ramakrishnan M, Angerstein B, Marsh D. Biochemistry. 2000;39:12476–12484. doi: 10.1021/bi000699l. [DOI] [PubMed] [Google Scholar]
- 42.Schorn K, Marsh D. Biochemistry. 1996;35:3831–3836. doi: 10.1021/bi952688b. [DOI] [PubMed] [Google Scholar]
- 43.Rama Krishna YVS, Marsh D. Biochim. Biophys. Acta. 1990;1024:89–94. doi: 10.1016/0005-2736(90)90211-6. [DOI] [PubMed] [Google Scholar]
- 44.Bartucci R, Gambacorta A, Gliozzi A, Marsh D, Sportelli L. Biochemistry. 2005;44:15017–15023. doi: 10.1021/bi051101i. [DOI] [PubMed] [Google Scholar]
- 45.Hoffmann P, Sandhoff K, Marsh D. Biochim. Biophys. Acta. 2000;1468:359–366. doi: 10.1016/S0005-2736(00)00276-5. [DOI] [PubMed] [Google Scholar]
- 46.Subczynski WK, Wisniewska A, Yin JJ, Hyde JS, Kusumi A. Biochemistry. 1994;33:7670–7681. doi: 10.1021/bi00190a022. [DOI] [PubMed] [Google Scholar]
- 47.Bartucci R, Guzzi R, Marsh D, Sportelli L. Biophys. J. 2003;84:1025–1030. doi: 10.1016/S0006-3495(03)74918-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Erilov DA, Bartucci R, Guzzi R, Shubin AA, Maryasov AG, Marsh D, Dzuba SA, Sportelli L. J. Phys. Chem. B. 2005;109:12003–12013. doi: 10.1021/jp050886z. [DOI] [PubMed] [Google Scholar]
- 49.Subczynski WK, Lomnicka M, Hyde JS. Free Rad. Res. Commun. 1996;24:343–349. doi: 10.3109/10715769609088032. [DOI] [PubMed] [Google Scholar]
- 50.Nedieanu S, Páli T, Marsh D. Biochim. Biophys. Acta. 2004;1661:135–143. doi: 10.1016/j.bbamem.2003.12.008. [DOI] [PubMed] [Google Scholar]
- 51.Subczynski WK, Hyde JS, Kusumi A. Proc. Natl. Acad. Sci. USA. 1989;86:4474–4478. doi: 10.1073/pnas.86.12.4474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Subczynski WK, Hyde JS, Kusumi A. Biochemistry. 1991;30:8578–8590. doi: 10.1021/bi00099a013. [DOI] [PubMed] [Google Scholar]
- 53.Dzikovski BG, Livshits VA, Marsh D. Biophys. J. 2003;85:1005–1012. doi: 10.1016/S0006-3495(03)74539-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Páli T, Horváth LI, Marsh D. J. Magn. Reson. 1993;A101:215–219. [Google Scholar]
- 55.Livshits VA, Páli T, Marsh D. J. Magn. Reson. 1998;133:79–91. doi: 10.1006/jmre.1998.1434. [DOI] [PubMed] [Google Scholar]
- 56.Livshits VA, Dzikovski BG, Marsh D. J. Magn. Reson. 2003;162:429–442. doi: 10.1016/S1090-7807(03)00076-4. [DOI] [PubMed] [Google Scholar]
- 57.Horváth LI, Marsh D. J. Magn. Reson. 1983;54:363–373. [Google Scholar]
- 58.Páli T, Livshits VA, Marsh D. J. Magn. Reson. B. 1996;113:151–159. doi: 10.1006/jmrb.1996.0168. [DOI] [PubMed] [Google Scholar]
- 59.Livshits VA, Páli T, Marsh D. J. Magn. Reson. 1998;134:113–123. doi: 10.1006/jmre.1998.1471. [DOI] [PubMed] [Google Scholar]
- 60.Livshits VA, Marsh D. J. Magn. Reson. 2000;145:84–94. doi: 10.1006/jmre.2000.2069. [DOI] [PubMed] [Google Scholar]
- 61.Kusumi A, Subczynski WK, Hyde JS. Proc. Natl. Acad. Sci. USA. 1982;79:1854–1858. doi: 10.1073/pnas.79.6.1854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Yin JJ, Hyde JS. Z. Phys. Chem. 1987;153:57–65. [Google Scholar]
- 63.Nielsen RD, Che K, Gelb MH, Robinson BH. J. Am. Chem. Soc. 2005;127:6430–6442. doi: 10.1021/ja042782s. [DOI] [PubMed] [Google Scholar]
- 64.Marsh D, Dzikovski BG, Livshits VA. Biophys. J. 2006;90:L49–L51. doi: 10.1529/biophysj.106.081042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Marsh D. J. Magn. Reson. 2006;180:305–310. doi: 10.1016/j.jmr.2006.02.007. [DOI] [PubMed] [Google Scholar]
- 66.Bartucci R, Guzzi R, De Zotti M, Toniolo C, Sportelli L, Marsh D. Biophys. J. 2008;94:2698–2705. doi: 10.1529/biophysj.107.115287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Marsh D, Jost M, Peggion C, Toniolo C. Biophys. J. 2007;92:4002–4011. doi: 10.1529/biophysj.107.104026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Bartucci R, Guzzi R, Sportelli L, Marsh D. Biophys. J. 2009;96:997–1007. doi: 10.1016/j.bpj.2008.10.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Ehrenson S. J. Am. Chem. Soc. 1981;103:6036–6043. doi: 10.1021/ja00410a008. [DOI] [Google Scholar]
- 70.Marsh D, Kurad D, Livshits VA. Magn. Reson. Chem. 2005;43:S20–S25. doi: 10.1002/mrc.1680. [DOI] [PubMed] [Google Scholar]
- 71.Marsh D, Jost M, Peggion C, Toniolo C. Biophys. J. 2007;92:473–481. doi: 10.1529/biophysj.106.092775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Savitsky A, Dubinskii AA, Plato M, Grishin YA, Zimmermann H, Möbius K. J. Phys. Chem. B. 2008;112:9079–9090. doi: 10.1021/jp711640p. [DOI] [PubMed] [Google Scholar]