Nonlocal means-based speckle filtering for ultrasound images

Abstract

In image processing, restoration is expected to improve the qualitative inspection of the image and the performance of quantitative image analysis techniques. In this paper, an adaptation of the Non Local (NL-) means filter is proposed for speckle reduction in ultrasound (US) images. Originally developed for additive white Gaussian noise, we propose to use a Bayesian framework to derive a NL-means filter adapted to a relevant ultrasound noise model. Quantitative results on synthetic data show the performances of the proposed method compared to well-established and state-of-the-art methods. Results on real images demonstrate that the proposed method is able to preserve accurately edges and structural details of the image.

I. Introduction

In ultrasound imaging, denoising is challenging since the speckle artifacts cannot be easily modeled and are known to be tissue-dependent. In the imaging process, the energy of the high frequency waves are partially reflected and transmitted at the boundaries between tissues having different acoustic impedances. The images are also log-compressed to make easier visual inspection of anatomy with real-time imaging capability. Nevertheless, the diagnosis quality is often low and reducing speckle while preserving anatomic information is necessary to delineate reliably and accurately the regions of interest. Clearly, the signal-dependent nature of the speckle must be taken into account to design an efficient speckle reduction filter. Recently, it has been demonstrated that image patches are relevant features for denoising images in adverse situations [1]–[3]. The related methodology can be adapted to derive a robust filter for US images. Accordingly, in this paper we introduce a novel restoration scheme for ultrasound (US) images, strongly inspired from the NonLocal (NL-) means approach [1] introduced by Buades et al. [1] to denoise 2D natural images corrupted by an additive white Gaussian noise. In this paper, we propose an adaptation of the NL-means method to a dedicated US noise model [4] using a Bayesian motivation for the NL-means filter [3]. In what follows, invoking the central limit theorem, we will assume that the observed signal at a pixel is a Gaussian random variable with mean zero and a variance determined by the scattering properties of the tissue at the current pixel.

The remainder of the paper is organized as follows. In Section II, we give an overview of speckle filters and related methods. Section III described the proposed Bayesian NL-means filter adapted to speckle noise. Quantitative results on artificial images with various noise models are presented in Section IV. Finally, qualitative result on real 2D and 3D US images are proposed in Section V.

II. Speckle Reduction: related work

The speckle in US images is often considered as undesirable and several noise removal filters have been proposed. Unlike the additive white Gaussian noise model adopted in most denoising methods, US imaging requires specific filters due to the signal-dependent nature of the speckle intensity. In this section, we present a classification of standard adaptive filters and methods for speckle reduction.

A. Adaptive Filters

The adaptive filters are widely used in US image restoration because they are easy to implement and control. The commonly-used adaptive filters - the Lee’s filter [5], Frost’s filter [6], and Kuan’s filter [7] - assume that speckle noise is essentially a multiplicative noise. Many improvements of these classical filters have been proposed since. At the beginning of the 90’s, Lopes et al. [8] suggested to improve the Lee’s and Frost’s filters by classifying the pixels in order to apply specific processing to the different classes. Based on this idea, the so-called Adaptive Speckle Reduction filter (ASR) exploits local image statistics to determine specific areas to be processed further. In [9], the kernel of the adaptive filter is fitted to homogeneous regions according to local image statistics. Analyzing local homogeneous regions was also investigated in [10], [11] to spatially adapt the filter parameters. Note that the Median filter has been also examined for speckle reduction in [4]. Very recently, a stochastic approach to ultrasound despeckling (SBF) has been developed in [12], [13]. This local averaging method removes the local extrema assumed to be outliers in a robust statistical estimation framework. Finally, the Rayleigh-Maximum-Likelihood (R-ML) filter has been derived with similar methodological tools in [14].

B. Partial Differential Equations (PDE) -based approaches

Adapted formulations of the Anisotropic Diffusion filter (AD) [15] and the Total Variation minimization scheme (TV) [16] have been developed for US imaging. In [17], [18], the Speckle Reducing Anisotropic Diffusion (SRAD) was introduced and involves a noise-dependent instantaneous coefficient of variation. In [19] the Nonlinear Coherent Diffusion (NCD) filter is based on the assumption that the multiplicative speckle in US signals is transformed into an additive Gaussian noise in Log-compressed images. Recently, the Oriented SRAD (OSRAD) filter has been proposed in [20]; this filter takes into account the local directional variance of the image intensity, i.e., the local image geometry. Finally, the TV minimization scheme has been adapted to ultrasound imaging in [21], [22]. Unlike the previous adaptive speckle filters, all the considered PDE-based approaches are iterative and produce smooth images while preserving edges. Nevertheless, meaningful structural details are unfortunately removed during iterations.

C. Multiscale methods

Several conventional wavelet thresholding methods [23]–[25] have also been investigated for speckle reduction [26]–[28] with the assumption that the logarithm compression of US images transforms the speckle into an additive Gaussian noise. In order to relax this restrictive assumption, Pizurica et al. [29] proposed a wavelet-based Generalized Likelihood ratio formulation and imposed no prior on noise and signal statistics. In [30]–[33], the Bayesian framework was also explored to perform wavelet thresholding adapted to the non-Gaussian statistics of the signal. Note that other multiscale strategies have been also studied in [34]–[36] to improve the performance of the AD filter; in [37], the Kuan’s filter is applied to interscale layers of a Laplacian pyramid.

D. Hybrid approaches

The aforementioned approaches can be also combined in order to take advantage of the different paradigms. In [38], the image is preprocessed by an adaptive filter in order to decompose the image into two components. A Donoho’s soft thresholding method is then performed on each component. Finally, the two processed components are combined to reduce speckle. PDE-based approaches and a wavelet transform have been also combined as proposed in [39].

III. Method

The previously mentioned approaches for speckle reduction are based on the so-called locally adaptive recovery paradigm [40]. Nevertheless, more recently, a new patch-based non local recovery paradigm has been proposed by Buades et al [1]. This new paradigm proposes to replace the local comparison of pixels by the non local comparison of patches. Unlike the aforementioned methods, the so-called NL-means filter does not make any assumptions about the location of the most relevant pixels used to denoise the current pixel. The weight assigned to a pixel in the restoration of the current pixel does not depend on the distance between them (neither in terms of spatial distance nor in terms of intensity distance). The local model of the signal is revised and the authors consider only information redundancy in the image. Instead of comparing the intensity of the pixels, which may be highly corrupted by noise, the NL-means filter analyzes the patterns around the pixels. Basically, image patches are compared for selecting the relevant features useful for noise reduction. This strategy leads to competitive results when compared to most of the state-of-the-art methods [3], [41]–[46]. Nevertheless, the main drawback of this filter is its computational burden. In order to overcome this problem, we have recently proposed a fast and optimized implementation of the NL-means filter for 3D Magnetic Resonance (MR) images [46].

In this section, we rather revise the traditional formulation of the NL-means filter, suited to the additive white Gaussian noise model, and adapt this filter to spatial speckle patterns. Accordingly, a dedicated noise model used for US images is first considered. A Bayesian formulation of the NL-means filter [3] is then used to derive a new speckle filter.

A. The Non Local means Filter

Let us consider a gray-scale noisy image u = (u(x_i))_xi∈Ω^dim defined over a bounded domain Ω^dim ⊂ ℝ^dim, (which is usually a rectangle of size |Ω^dim|) and u(x_i) ∈ ℝ₊ is the noisy observed intensity at pixel x_i ∈ Ω^dim. In the following, dim denotes the image grid dimension (dim = 2 or dim = 3 respectively for 2D and 3D images). We also use the notations given below:

Original pixelwise NL-means approach

• Δ_i: square search volume centered at pixel x_i of size |Δ_i| = (2M + 1)^dim, M ∈ ℕ;

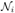• : square local neighborhood of x_i of size |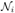| = (2d + 1)^dim, d ∈ ℕ;

• u(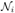): vector (u⁽¹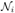⁾(), …, u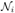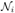^(||)())^T gathering the intensity values of ;

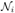• • v(x_i): true intensity value at pixel x_i ∈ Ω^dim;

• NL(u)(x_i): restored value of pixel x_i;

• w(x_i, x_j): weight used for restoring u(x_i) given u(x_j) and based on the similarity of patches u(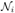) and u().

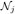Blockwise NL-means approach

• B_i: square block centered at x_i of size |B_i| = (2α + 1)^dim, α ∈ ℕ;

• • v(B_i): unobserved vector of true values of block B_i;

• u(B_i): vector gathering the intensity values of block B_i;

• NL(u)(B_i): restored block of pixel x_i;

• w(B_i, B_j): weight used for restoring u(B_i) given u(B_j) and based on the similarity of blocks u(B_i) and u(B_j).

Finally, the blocks B_ik are centered on pixels x_ik with i_k = (k₁n, …, k_dimn), (k₁, …, k_dim) ∈ ℕ^dim and n represents the distance between block centers.

1. Pixelwise approach

In the original NL-means filter [1], the restored intensity NL(u)(x_i) of pixel x_i, is the weighted average of all the pixel intensities u(x_i) in the image Ω^dim:

$$NL(u)(x_i)=\sum _{x_j\in {\mathrm{\Omega }}^{\mathit{dim}}}w(x_i,x_j)u(x_j)$$ (1)

where w(x_i, x_j) is the weight assigned to value u(x_j) for restoring the pixel x_i. More precisely, the weight evaluates the similarity between the intensities of the local neighborhoods (patches) 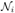and 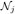centered on pixels x_i and x_j, such that w(x_i, x_j) ∈ [0, 1] and Σ_xi∈Ω^dim w(x_i, x_j) = 1 (see Fig. 1). The size of the local neighborhoo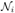d and is (2d + 1)^dim. The traditional definition of the NL-means filter considers that the intensity of each pixel can be linked to pixel intensities of the whole image. For practical and computational reasons, the number of pixels taken into account in the weighted average is restricted to a neighborhood, that is a “search volume” Δ_i of size (2M+1)^dim, centered at the current pixel x_i.

Fig. 1.

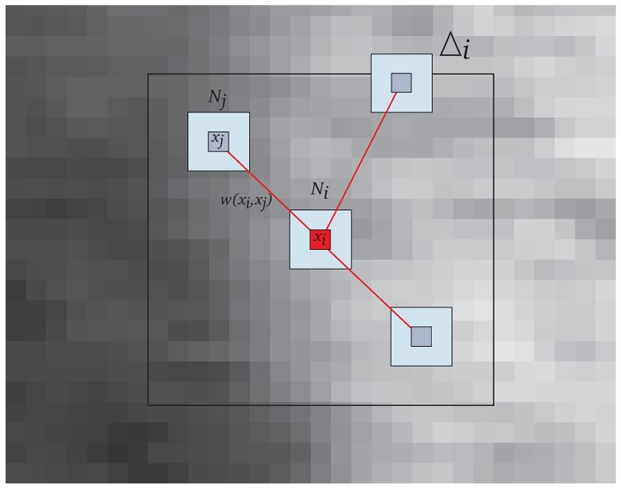
Pixelwise NL-means filter (d = 1 and M = 8). The restored value at pixel x_i (in red) is the weighted average of all intensity values of pixels x_j in the search volume Δ_i. The weights are based on the similarity of the intensity neighborhoods (patches) u() and u().

For each pixel x_j in Δ_i, the Gaussian-weighted Euclidean distance ${\left|\right|·\left|\right|}_{2,a}^2$ is computed between the two image patches u() and u(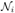) as explained in [1]. This distance is the traditional L₂-norm convolved with a Gaussian kernel of standard deviation a. The standard deviation of the Gaussian kernel is used to assign spatial weights to the patch elements. The central pixels in the patch contribute more to the distance than the pixels located at the periphery. The weights w(x_i, x_j) are then computed as follows:

$$w(x_i,x_j)=\frac{1}{Z_i}exp-\frac{{\left|\right|\mathbf{u}({\mathcal{N}}_i)-\mathbf{u}({\mathcal{N}}_j)\left|\right|}_{2,a}^2}{h^2}$$ (2)

where Z_i is a normalization constant ensuring that Σ_xi∈Ω^dim w(x_i, x_j) = 1, and h acts as a filtering parameter controlling the decay of the exponential function.

2. Blockwise approach

As presented in [46], a blockwise implementation of the proposed NL-means-based speckle filter is able to decrease the computational burden. The blockwise approach consists of: i) dividing the volume into blocks with overlapping supports; ii) performing a NL-means-like restoration of these blocks; iii)) restoring the pixel intensities from the restored blocks. Here, we describe briefly these three steps and refer the reader to [46] for additional detailed explanations:

1. a partition of the volume Ω^dim into overlapping blocks B_ik containing P = (2α + 1)^dim elements is performed, i.e. Ω^dim =∪_k B_ik. These blocks are centered on pixels x_ik which constitute a subset of Ω^dim. The pixels x_ik are equally distributed at positions i_k = (k₁n, k₂n, k₃n), (k₁, k₂, k₃) ∈ ℕ^dim where n represents the distance between the centers of B_ik;

2. a block B_ik is restored as follows:

   $$\mathbf{NL}(u)(B_{i_k})=\sum _{B_j\in {\mathrm{\Delta }}_{i_k}}w(B_{i_k},B_j)\mathbf{u}(B_j)\text{with}w(B_{i_k},B_j)=\frac{1}{Z_{i_k}}exp-\frac{{\left|\right|\mathbf{u}(B_{i_k})-\mathbf{u}(B_j)\left|\right|}_2^2}{h^2}$$ (3)

   where u(B_i) = (u⁽¹⁾(B_i), …, u^(P)(B_i))^T is an image patch gathering the intensities of the block B_i, Z_ik is a normalization constant ensuring Σ_Bj∈Δik w(B_ik,B_j) = 1 and

   $${\left|\right|\mathbf{u}(B_{i_k})-\mathbf{u}(B_j)\left|\right|}_2^2=\sum _{p=1}^P{(u^{(p)}(B_i)-u^{(p)}(B_j))}^2;$$ (4)

3. for a pixel x_i included in several blocks B_ik, several estimates of the same pixel x_i from different NL(u)(B_ik) are computed and stored in a vector A_i of size L (see Fig 2). We denote A_i(l) the lth element of vector A_i. The final restored intensity of pixel x_i is the mean of the restored values NL(u)(B_ik).

Fig. 2.

Blockwise NL-means Filter (n = 2, α = 1 and L = 4). For each block B_ik centered at pixel x_ik, a NL-means-like restoration is performed from blocks B_j. The restored value of the block B_ik is the weighted average of all the blocks B_j in the search volume. For a pixel x_i included in several blocks, several estimates are obtained and fused. The restored value of pixel x_i is the average of the different estimations stored in vector A_i.

The main advantage of this approach is to significantly reduce the complexity of the algorithm. Indeed, for a volume Ω^dim of size |Ω^dim|, the global complexity is $\mathcal{\theta }({(2\alpha +1)}^{\mathit{dim}}{(2M+1)}^{\mathit{dim}}{(\frac{N}{n})}^{\mathit{dim}})$. For instance, if we set n = 2, the complexity is divided by a factor of 4 in 2D and 8 in 3D.

B. The NL Means-based Speckle Filter

1. Bayesian formulation

In [3], a Bayesian formulation of the NL-means filter was proposed. Equivalent to the conditional mean estimator, it has been shown that an empirical estimator v̂ (B_ik) of a block B_ik can be defined as (see the appendix):

$$\widehat{\mathbf{v}}(B_{i_k})=\frac{\frac{1}{\mid {\mathrm{\Delta }}_{i_k}\mid }{\displaystyle \sum _{j=1}^{\mid {\mathrm{\Delta }}_{i_k}\mid }}\mathbf{v}(B_j)p(\mathbf{u}(B_{i_k})\mid \mathbf{v}(B_j))}{\frac{1}{\mid {\mathrm{\Delta }}_{i_k}\mid }{\displaystyle \sum _{j=1}^{\mid {\mathrm{\Delta }}_{i_k}\mid }}p(\mathbf{u}(B_{i_k})\mid \mathbf{v}(B_j))}$$ (5)

where p(u(B_ik)|v(B_j)) denotes the probability density function (pdf) of u(B_ik) given the noise free and unknown patches v(B_j). Since v(B_j) is unknown, an estimator is classically computed by substituting u(B_j) for v(B_j). Hence, we get

$$\widehat{\mathbf{v}}(B_{i_k})=\frac{{\displaystyle \sum _{j=1}^{\mid {\mathrm{\Delta }}_{i_k}\mid }}\mathbf{u}(B_j)p(\mathbf{u}(B_{i_k})\mid \mathbf{u}(B_j))}{{\displaystyle \sum _{j=1}^{\mid {\mathrm{\Delta }}_{i_k}\mid }}p(\mathbf{u}(B_{i_k})\mid \mathbf{u}(B_j))}$$ (6)

where p(u(B_ik)|u(B_j)) denotes the pdf of u(B_ik) conditionally to u(B_j). In the case of an additive white Gaussian noise, the likelihood p(u(B_ik)|u(B_j)) will be proportional to $e^{-\frac{{\left|\right|\mathbf{u}(B_{i_k})-\mathbf{u}(B_j)\left|\right|}_2^2}{h^2}}$, and the corresponding Bayesian estimator v̂(B_ik) is then similar to the initial NL-means method (see (3)).

In what follows, this general Bayesian formulation is used to derive an adapted filter to a dedicated ultrasound noise model.

2. Noise models for log-compressed US images

The relevant noise pdfs useful for US image denoising cannot be easily exhibited. Basically, we should consider the complex image formation process, i.e.: i) local correlation due to periodic arrangements of scatterers [17] and finite beamwidth; ii) envelope detection and logarithm amplification of radio-frequency signals performed on the display image [19]; iii) additive Gaussian noise of sensors [19]; iv) additive Gaussian noise introduced by the acquisition card. All these factors tend to prove that the Rayleigh model used for RF signals is not suitable for analyzing US Log-compressed images. Usually, in the wavelet denoising domain [19], [26], [27], multiplicative speckle noise is supposed to be transformed into an additive Gaussian noise by the logarithmic compression. However, recent studies related to US images demonstrate also that the distribution of noise is satisfyingly approximated by a Gamma distribution [47] or a Fisher-Tippett distribution [48].

Consequently, we have decided to choose the following general speckle model:

$$u(x)=v(x)+v^{\gamma }(x)\eta (x)$$ (7)

where v(x) is the original image, u(x) is the observed image, η(x) ~ (0, σ²) is a zero-mean Gaussian noise. This model is more flexible and less restrictive than the usual RF model and is able to capture reliably image statistics since the factor γ depends on ultrasound devices and additional processing related to image formation.

Contrary to additive white Gaussian noise model, the noise component in (7) is image-dependent. In [4], based on the experimental estimation of the mean versus the standard deviation in Log-compressed images, Loupas et al. have shown that γ = 0.5 model fits better to data than the multiplicative model or the Rayleigh model. Since, this model has been used successfully in many studies [38], [49]–[51]. Clearly, this model is relevant since it is confirmed that the speckle is higher in regions of high intensities versus regions of low intensities [47], [49].

3. A new statistical distance for patch comparison: the Pearson distance

Based on the Bayesian formulation (see (6)), we introduce a new distance to compare image patches if we consider the noise model (7). For each pixel we assume:

$$u(x)\mid v(x)\sim \mathcal{N}(v(x),v{(x)}^{2\gamma }{\sigma }^2)$$ (8)

which yields

$$p(u(x)\mid v(x))\propto exp-\frac{{(u(x)-v(x))}^2}{2v{(x)}^{2\gamma }{\sigma }^2}.$$ (9)

Given a block B_i, the likelihood can be factorized as (conditional independence hypothesis):

$$\begin{array}{l}p(\mathbf{u}(B_i)\mid \mathbf{u}(B_j))=\prod _{p=1}^{P}p(u^{(p)}(x_i)\mid u^{(p)}(x_j))\\ \propto exp-\sum _{p=1}^P\frac{{(u^{(p)}(x_i)-u^{(p)}(x_j))}^2}{2{(u^{(p)})}^{2\gamma }(x_j){\sigma }^2}.\end{array}$$ (10)

Accordingly, the so-called Pearson distance defined as

$$d_P(\mathbf{u}(B_i),\mathbf{u}(B_j))=\sum _{p=1}^P\frac{{(u^{(p)}(B_i)-u^{(p)}(B_j))}^2}{{(u^{(p)})}^{2\gamma }(B_j)}$$ (11)

is substituted to the usual L₂-norm (see (4)). In the reminder of the paper, γ = 0.5 is considered in the proposed filter.

A pixel selection scheme similar to [46] based on tests on the mean will be used to select the most relevant patches. This selection is controlled by the thresholding μ₁ as previously described in [46]. As a result, the denoising results are improved and the algorithm is faster. In addition, a parallel implementation is used in all experiments to speed up the algorithm.

IV. Synthetic images experiments

In this section, we propose to compare different filters with experiments on synthetic data, with different noise models, image data and quality criteria. Two simulated data are described in this section:

• in section IV-A, a 2D phantom and a noise model available in MATLAB are considered for the experiments, and the signal-to-noise Ratio (SNR) is used to compare objectively several methods;

• in section IV-B, the realistic speckle simulation proposed in Field II is performed and the ultrasound despeckling assessment index (Q̃) proposed in [12], [13] is chosen for objective comparisons;

A. 2D phantom corrupted by the theoretical (MATLAB) noise model

1. Speckle model and quality criterion

In this experiment, the synthetic image “Phantom” (see Fig. 3), available in MATLAB, was corrupted with different levels of noise. The “Phantom” image is a 32 bit image of 256 × 256 pixels. First, an offset of 0.5 was added to the image (to avoid naught areas) before performing a multiplication of intensities by a factor 20. Then, the MATLAB speckle simulation based on the following image model

Fig. 3.

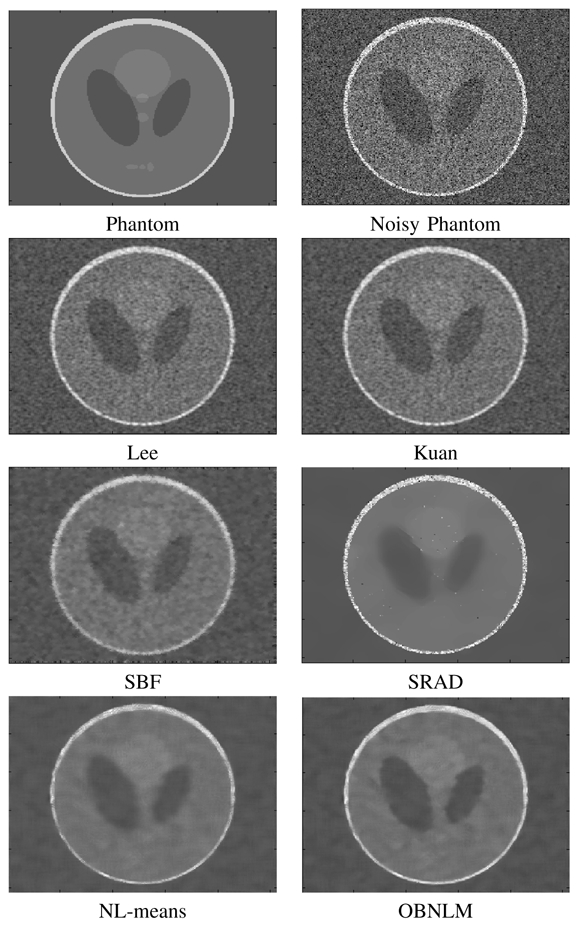
Results obtained with different filters applied to the “Phantom” image corrupted with signal-dependent noise (σ = 0.4). The quantitative evaluation, measured using the signal-to-noise ratio, is presented in Table II.

$$u(x_i)=v(x_i)+v(x_i)\nu (x_i),\nu (x_i)\sim \mathcal{N}(0,{\sigma }^2)$$ (12)

was applied to the “Phantom” image. Three levels of noise were tested by setting σ = {0.2; 0.4; 0.8}. To assess denoising methods, the SNR values [52] were computed between the “ground truth” and the denoised images:

$$\mathit{SNR}=10{log}_{10}\frac{{\sum }_{x_i\in {\mathrm{\Omega }}^2}(v{(x_i)}^2+\widehat{v}{(x_i)}^2)}{{\sum }_{x_i\in {\mathrm{\Omega }}^2}{(v(x_i)-\widehat{v}(x_i))}^2}$$ (13)

where v(x_i) is the true value of pixel x_i and v̂(x_i) the restored intensity of pixel x_i.

2. Compared methods

In this experiment, we compared several speckle filters and the parameters were adjusted to get the best SNR values:

• Lee’s filter (2D MATLAB implementation) [5]

• Kuan’s filter (2D MATLAB implementation) [7]

• SBF filter (2D MATLAB implementation provided by the authors) [12]

• Speckle Reducing Anisotropic Diffusion (SRAD) (MATLAB implementation of Virginia University¹) [17]

• blockwise implementation of the classical NL-means filter [1]

• blockwise implementation of the proposed method denoted as Optimized Bayesian NL-means with block selection (OBNLM).

In this experiment, we have chosen to compare our method with well-known adaptive filters, such as the Lee’s and Kuan’s filters, and with two competitive state-of-the-art methods: SRAD and SBF filters. We limited the comparison to this set of methods but the results produced by other recent filters could be also analyzed further (e.g. see [14]). Moreover, the usual NL-means filter has been applied to the same images in order to quantitatively evaluate the performance of our speckle-based NL-means filter. For each method and for each noise level, the optimal filter parameters were searched within large ranges. These parameters are given in Table I.

TABLE I.

Optimal set of parameters used for the matlab “Phantom” experiment. For the NL-means based filters, we set n = 2 and |Δ_ik| = 11 × 11.

Filter	iteration number σ = {0.2; 0.4; 0.8}	smoothing parameter σ = {0.2; 0.4; 0.8}	threshold	patch size
Lee’s filter	-	-	-	2 × 2
Kuan’s filter	-	-	-	2 × 2
SBF	{5; 8; 30}	-	-	3 × 3
SRAD	{500; 1000; 2000}	dt = {0.1; 0.2; 0.1}	-	-
NL-means	-	h = {20.0; 25.0; 30.0}	-	5 × 5
OBNLM	-	h = {12.0; 14.0; 16.0}	μ1 = 0.9	5 × 5

3. Results

Table II gives the SNR values obtained for each method. The denoised images corresponding to σ = 0.4 are presented in Fig. 3. For all levels of noise, the OBNLM filter obtained the best SNR value. For this experiment, the use of the Pearson distance combined with block selection enabled to improve the denoising performances of the NL-means filter for images corrupted by signal-dependent noise. Visually, the NL-means based filter satisfyingly removed the speckle while preserving meaningful edges.

TABLE II.

SNR values obtained with several filters applied to the 2D matlab “Phantom” image.

SNR (dB)
Filter	σ = 0.2	σ = 0.4	σ = 0.8
Noisy phantom	39.32	25.96	14.11
Lee’s filter	49.41	42.71	32.31
Kuan’s filter	49.43	42.71	32.33
SBF	49.61	43.86	38.04
SRAD	57.17	44.07	33.29
NL-means	62.15	47.92	38.72
OBNLM	64.13	53.12	42.13

B. Field II simulation

1. Speckle model and quality assessment

In order to evaluate the denoising filters with a more relevant and challenging simulation of speckle noise, the validation framework proposed in [12], [13] was used. This framework is based on Field II simulation [53]. The “Cyst” phantom is composed of 3 constant classes C_r presented in Fig. 4. The result of the Field II simulation is converted into an 8 bit image of size 390 × 500 pixels. Since the geometry of the image is known, but not the true value of the image (i.e. without speckle), the authors introduced the ultrasound despeckling assessment index (Q̃) defined as:

$$Q=\frac{{\sum }_{r\ne l}{({\mu }_{C_r}-{\mu }_{C_l})}^2}{{\sum }_r{\sigma }_{C_r}^2}$$ (14)

to evaluate the performance of denoising filters for this simulation. We denote μ_Cr as the mean and ${\sigma }_{C_r}^2$ as the variance of class C_r after denoising. To avoid the sensitivity to image resolution, Q is normalized by Q_id. The new index Q̃ = Q/Q_id is high if the applied filter is able to produce a new image with well separated classes and small variances for each class. According to [12], [13], an image is satisfyingly denoised if Q̃ is high enough.

Fig. 4.

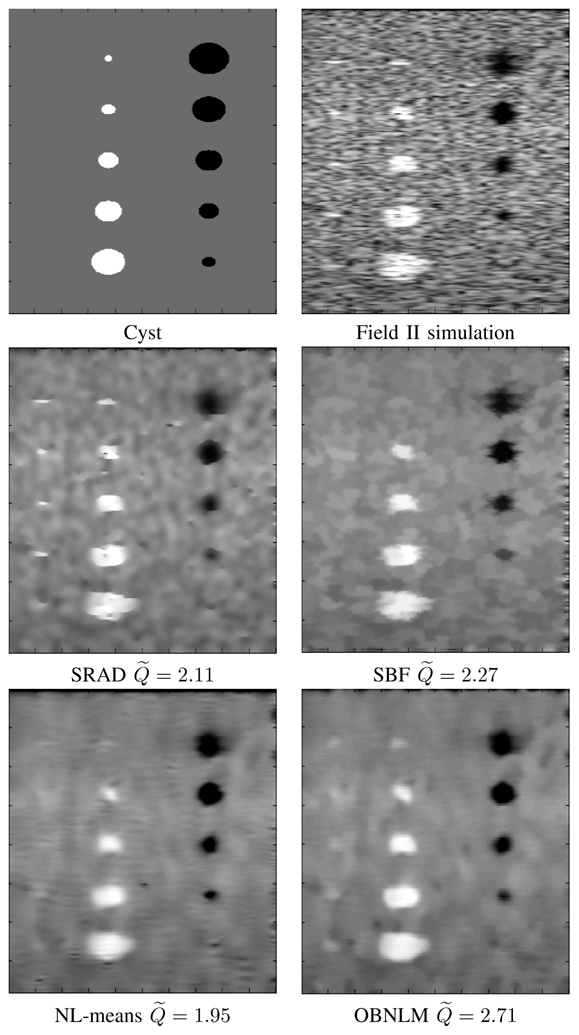
Denoised images obtained with the compared filters for the Field II experiment and the corresponding Q̃ indexes.

2. Method Comparison

For this experiment, we compared the SBF filter, SRAD filter, NL-means filter and the proposed OBNLM filter. The filter parameters are given in Table III. Compared to the previous experiment, the patch size by using the NL-means-based filters is increased. Indeed, the patch size reflects the scale of the “noise” compared to the image resolution. In the previous experiment, the resolution of the added noise was about one pixel. In this experiment, the objects to be removed are composed of several pixels, thus the patch size is increased to evaluate the restoration performance of each object.

TABLE III.

Optimal set of parameters used for validation on the 2D synthetic data simulated with Field II. For the NL-means-based filters n = 4 and |Δ_ik| = 33 × 33.

Filter	iteration number	smoothing parameter	threshold	patch size
SBF	400	-	-	5 × 5
SRAD	500	dt = 0.05	-	-
NL-means	-	h = 50	-	11 × 11
OBNLM	-	h = 50	μ1 = 0.75	11 × 11

3. Results

The denoised images and the quantitative results are given in Fig. 4. In this evaluation framework, the OBNLM filter produced the highest Q̃ index. Similar values than those presented in [12], [13] were found for the SRAD and SBF filters. Compared to the original NL-means filter, the proposed adaptations for US images improved the Q̃ index of the denoised image.

V. Experiments on real data

In this section, a visual comparison of 2D intraoperative ultrasound brain images (Section V-A) and a visual inspection of 3D ultrasound image of a liver (Section V-B) are proposed.

A. Intraoperative ultrasound brain images

In this paragraph, we propose a visual comparison of the SBF and SRAD filters and the OBNLM method on real intraoperative brain images. The parameters for the SBF and SRAD filters are the parameters given respectively in [17] and [12]. The parameters of the OBNLM filter were set as follows: h = 8, n = 2, α = 3, M = 6 and μ₁ = 0.6.

Figure 5 shows the denoising results. Visually, the OBNLM filter efficiently removes the speckle component while enhancing the edges and preserving the image structures. The visual results produced on real image by our method are competitive compared to SRAD and SBF filters.

Fig. 5.

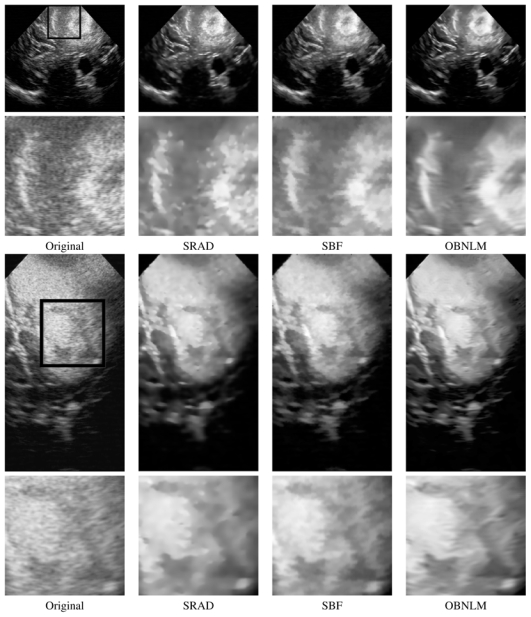
Results obtained with the SRAD and SBF filters and the proposed filters on real intraoperative brain images. The OBNLM filter efficiently removes the speckle while enhancing the edges and preserving the image structures.

B. Experiments on a 3D liver image

In this section, result of the proposed filter on 3D US image is proposed. These data are freely available on Cambridge University website². The B-scans were acquired with a Lynx ultrasound unit (BK Medical System) and tracked by the magnetic tracking system miniBIRD (Ascension Technology). The reconstruction of the volume was performed with the method described in [54]. The reconstructed volume size was 308 × 278 × 218 voxels with an isotropic resolution of 0.5 × 0.5 × 0.5 mm³.

The denoising results obtained with the OBNLM method on the liver volume are shown in Fig. 6. As for the previous experiment on 2D US brain images, the visual results on this 3D dataset show edge preservation and efficient noise removal produced by our filter.

Fig. 6.

Top: 3D volume of the liver. Bottom: the denoising result obtained with the OBNLM filter with h = 8, n = 2, α = 1, M = 5 and μ₁ = 0.6.

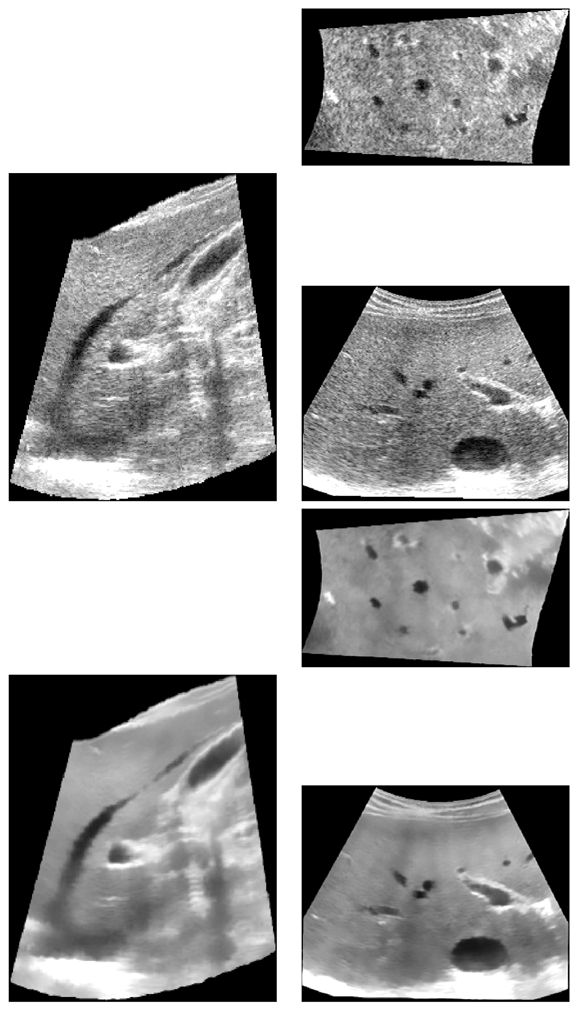
Figure 7 shows zooming views of hepatic vessels. The edge preservation of the OBNLM filter is visible on the removed noise image that does not contain structures. Moreover, the difference in dark areas (hepatic vessels) and gray areas (hepatic tissues) shows the smoothing adaptation according to the signal intensity. The noise in brighter areas is drastically reduced.

Fig. 7.

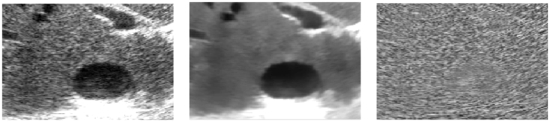
From left to right: the original “noisy” volume, the denoising result obtained with the OBNLM filter with h = 8 and μ₁ = 0.6 and the removed noise component. The edge preservation of the OBNLM is visually appreciated by inspecting the removed noise component which contains few structures. Moreover, the level of noise estimated for the dark areas (hepatic vessels) and the gray areas (hepatic tissues) demonstrates the relevance of the signal-dependent modeling.

VI. Conclusion

In this paper, we proposed a Non Local (NL)-means-based filter for ultrasound images by introducing the Pearson distance as a relevant criterion for patch comparison. Experiments were carried out on synthetic images with different simulations of speckle. During the experiments, quantitative measures were used to compare several denoising filters. Experiments showed that the Optimized Bayesian Non Local Means (OBNLM) filter proposes competitive performances compared to other state-of-the-art methods. Moreover, as assessed by quantitative results, our adaptation of classical NL-means filter to speckle noise proposes a filter more suitable for US imaging. Experiments on real ultrasound data were conducted and showed that the OBNLM method is very efficient at smoothing homogeneous areas while preserving edges. Further work will be pursued on the automatic tuning of the OBNLM filter and on the influence study on post-processing tasks such as image registration or image segmentation.

Appendix

Details of the Bayesian NL-means filter

The following Bayesian definition of the NL-means filter is presented in [3]. By considering the quadratic loss function, the optimal Bayesian estimator of a noise-free patch v̂_opt(B) can be written as:

$${\widehat{\mathbf{v}}}_{\mathit{opt}}(B)=\underset{\mathbf{v}(B)}{\text{argmin}}\sum _{\mathbf{v}(B)}{\left|\right|\mathbf{v}(B)-\widehat{\mathbf{v}}(B)\left|\right|}^{2}p(\mathbf{v}(B)\mid \mathbf{u}(B))=\sum _{\mathbf{v}(B)}\mathbf{v}(B)p(\mathbf{v}(B)\mid \mathbf{u}(B))$$ (15)

where p(v(B)|u(B)) denotes the probability density function (pdf) of v(B) conditionally to u(B), u(B) is the observed intensity and v(B) is the true intensity of block B. According to the Bayes’ and marginalization rules, the so-called conditional mean estimator can be rewritten as (see [3]):

$${\widehat{\mathbf{v}}}_{\mathit{opt}}(B)=\sum _{\mathbf{v}(B)}\mathbf{v}(B)\frac{p(\mathbf{v}(B)\mid \mathbf{u}(B))}{p(\mathbf{u}(B))}=\frac{{\sum }_{\mathbf{v}(B)}\mathbf{v}(B)p(\mathbf{u}(B)\mid \mathbf{v}(B))p(\mathbf{v}(B))}{{\sum }_{\mathbf{v}(B)}p(\mathbf{u}(B)\mid \mathbf{v}(B))p(\mathbf{v}(B))}$$ (16)

where p(u(B)|v(B)) denotes the distribution of u(B) conditionally to v(B). Since p(u(B)|v(B)) and p(u(v)) cannot be estimated from only one realization of the image, these pdfs are estimated from observations (blocks B_j) taken in a search window Δ_i of a block B_i. According to [3], [55], the following approximations can be written:

$$\frac{1}{\mid {\mathrm{\Delta }}_i\mid }\sum _{j=1}^{\mid {\mathrm{\Delta }}_i\mid }\mathbf{v}(B_j)p(\mathbf{u}(B_i)\mid \mathbf{v}(B_j))\stackrel{P}{\to }{\sum }_{\mathbf{v}(B)}\mathbf{v}(B)p(\mathbf{u}(B)\mid \mathbf{v}(B))p(\mathbf{v}(B))$$ (17)

$$\frac{1}{\mid {\mathrm{\Delta }}_i\mid }\sum _{j=1}^{\mid {\mathrm{\Delta }}_i\mid }p(\mathbf{u}(B_i)\mid \mathbf{v}(B_j))\stackrel{P}{\to }{\sum }_{\mathbf{v}(B)}p(\mathbf{u}(B)\mid \mathbf{v}(B))p(\mathbf{v}(B)),$$ (18)

If we assume the prior distribution p(v(B)) uniform. This leads to the empirical Bayesian estimator v̂(B_ik) uses in (5):

$$\widehat{\mathbf{v}}(B_i)=\frac{\frac{1}{\mid {\mathrm{\Delta }}_i\mid }{\displaystyle \sum _{j=1}^{\mid {\mathrm{\Delta }}_i\mid }}\mathbf{v}(B_j)p(\mathbf{u}(B_i)\mid \mathbf{v}(B_j))}{\frac{1}{\mid {\mathrm{\Delta }}_i\mid }{\displaystyle \sum _{j=1}^{\mid {\mathrm{\Delta }}_i\mid }}p(\mathbf{u}(B_i)\mid \mathbf{v}(B_j))}.$$ (19)

We refer the reader to [3] for detailed explanations.