tRNA–guanine transglycosylase from E. coli: a ping-pong kinetic mechanism is consistent with nucleophilic catalysis

Abstract

tRNA–guanine transglycosylase (TGT) is a key enzyme in the post-transcriptional modification of certain tRNAs with the pyrrolopyrimidine base queuine. TGT is required for pathogenicity in Shigella flexneri, a human pathogen, and therefore is potentially a novel antibacterial target. Previous work has indicated that the TGT reaction proceeds through a covalent enzyme–tRNA complex [Biochemistry 40 (2001) 14123]. To further substantiate this mechanism, the determination of the kinetic mechanism for the TGT reaction was undertaken. Computational and graphical analyses of initial velocity data are most consistent with a ping-pong kinetic mechanism. The modes of inhibition of 7-methylguanine with respect to both guanine (competitive) and tRNA (uncompetitive) indicate that tRNA binds first to the enzyme. This kinetic mechanism is consistent with the covalent intermediate chemical mechanism and with our earlier study of a mechanism-based inhibitor [7-fluoromethyl -7-deazaguanine, Biochemistry 34 (1995) 15539] in which TGT inactivation was dependent upon the presence of tRNA.

1. Introduction

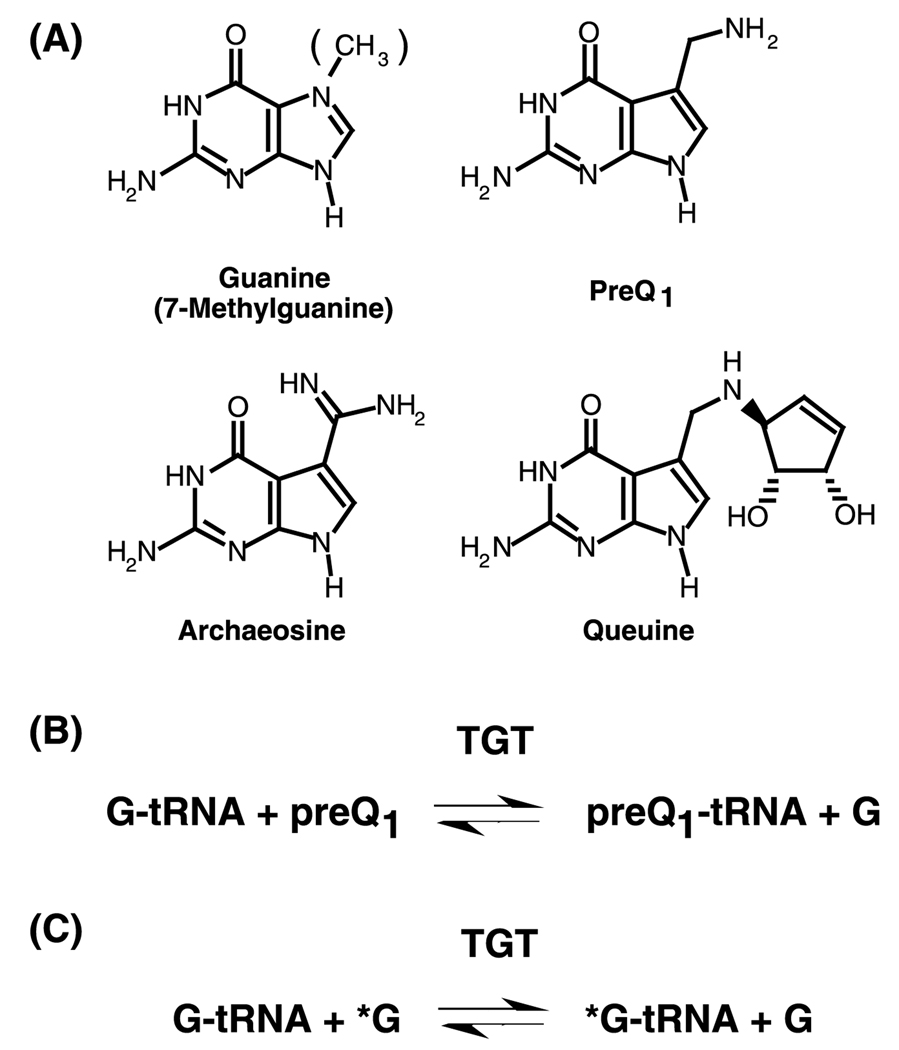
tRNA–guanine transglycosylase (TGT)¹ is a key enzyme involved in the post-transcriptional modification of tRNA leading to queuine in eubacteria and eukaryotes and to archaeosine in archaea. In eubacteria, TGT catalyzes the exchange of guanine at position 34 of the tRNA with the queuine precursor, preQ₁ (Fig. 1), which is subsequently modified to queuine. In the absence of preQ₁, TGT will catalyze the exchange of guanine 34 with guanine free base. The tgt gene has been found to be required for virulence in the human pathogen Shigella flexneri [1]. This suggests that TGT itself may be a novel antibiotic target. A fuller understanding of the chemical and kinetic mechanisms of the TGT reaction is desirable as a prelude to rational drug design.

Fig. 1.

Structures of TGT substrates and the TGT reaction: (A) Guanine (7-methylguanine), preQ₁, archaeosine, and queuine, (B) the TGT reaction incorporating preQ₁, (C) the TGT reaction exchanging guanine for guanine.

The crystal structure of the TGT from Zymomonas mobilis bound to preQ₁ has been solved [2]. Visual examination of this structure suggests the existence of only a single binding site that would accommodate either preQ₁ or guanine [2]. Subsequent mutagenesis studies have implicated aspartate 89 (Escherichia coli numbering) as a nucleophilic catalyst in an associative mechanism involving a covalent TGT–tRNA complex [3,4]. Such a chemical mechanism would predict that the TGT reaction should follow ping-pong kinetics. In order to confirm this, we have performed experiments to determine the kinetic mechanism of the guanine exchange reaction catalyzed by the E. coli TGT.

Initial rate kinetics and inhibition studies described herein indicate that TGT follows ping-pong kinetics with tRNA binding first. This is consistent with nucleophilic catalysis by aspartate 89 [3,4] and with our observation that guanine does not appear to bind to free TGT (Goodenough-Lashua and Garcia, unpublished).

2. Materials and methods

2.1. Reagents

Unless otherwise specified, reagents were purchased from Sigma or Aldrich. Yeast extract and bactotryptone were from Difco. Agarose, isopropyl β-d-thiogalactopyranoside (IPTG), and dithiothreitol (DTT) were from Gibco BRL. BstNI was from New England BioLabs. Buffered phenol, glycerol, Hepes, and NTPs were from Amersham Pharmacia. RNase inhibitor, pyrophosphatase, and urea were from Roche/Boehringer–Mannheim. BSA standards and the Bradford reagent were from Bio-Rad. [8-³H]Guanine (1–10 Ci/mmol) was from Moravek. Precast PhastGels were from Pharmacia. T7 RNA polymerase was isolated from E. coli pAR1219/BL21 following the procedure of Grodberg and Dunn [5]. E. coli tRNA^Tyr (ECY) was prepared and purified via in vitro transcription as previously described [6]. The tRNA was characterized by both native and denaturing PAGE (not shown) as described previously [7,8]. tRNA concentrations were determined using the UV extinction coefficient at 260nm corrected for hyperchromicity as previously described [9].

2.2. Preparation of tRNA–guanine transglycosylase

E. coli tRNA–guanine transglycosylase was prepared from an over-expressing clone as described previously [10,11]. Typically, 7.5 mg of TGT is obtained per liter of cell culture. TGT was characterized by denaturing and native PAGE (not shown) as described previously [7,8].

2.3. Initial velocity kinetics

The TGT reaction was monitored by following the incorporation of radiolabeled guanine into tRNA essentially as previously described [6]. Reaction mixtures consisting of 200mM Hepes (pH 7.3), 20mM MgCl₂, 5mM DTT, and varying concentrations of both tRNA and [³H]guanine (350mCi/mmol), were treated with 10nM TGT. Guanine concentrations were varied from 0.15 to 0.7 µM and tRNA concentrations were varied from 0.1 to 1.0 µM. Because the [³H]guanine is dissolved and diluted in 0.1 M HCl, an equivalent volume of 0.1 M NaOH was added to each assay and the usual buffer concentration (100mM) was doubled. The total volume of each assay mixture was 400 µl. During a 15 min time course, 70 µl aliquots were removed every 3 min and quenched in 2mL of 5% trichloroacetic acid. The precipitated RNA was collected on glass fiber filters (GF/C, Whatman) and quantitated via liquid scin-tillation counting. The data were analyzed using Kaleidagraph where the initial velocities (v_i) of guanine incorporation were determined from plots of pmol guanine incorporated versus time.

2.4. Kinetic mechanism data analysis

For these studies, the reactions were limited to initial velocity conditions. Therefore, it is assumed that the amount of product formed is negligible and all terms containing either product are essentially zero. The data were fit by three dimensional, non-linear regression to the initial velocity rate equations described by Cornish-Bowden [12] using the pre-programmed equations in GraFit [13]. The results were then plotted using Kaleidagraph to display both the data and the fitted lines.

The rate equation for a ternary complex mechanism is given by Eq. (1), where [A] and [B] correspond to the substrate concentrations, K_M(A) and K_M(B) correspond to the Michaelis constants for substrates A and B, respectively, and K_i(A) is the dissociation constant for A from the E-A complex [12]

$$v_{\mathrm{i}}=\frac{V_{\text{max}}[\mathrm{A}][\mathrm{B}]}{K_{i(\mathrm{A})}{K}_{\mathrm{M}(\mathrm{B})}+K_{\mathrm{M}(\mathrm{B})}[\mathrm{A}]+K_{\mathrm{M}(\mathrm{A})}[\mathrm{B}]+[\mathrm{A}][\mathrm{B}]}.$$ (1)

For the ping-pong mechanism, the initial rate equation is defined as

$$v_{\mathrm{i}}=\frac{V_{\text{max}}[\mathrm{A}][\mathrm{B}]}{K_{\mathrm{M}(\mathrm{B})}[\mathrm{A}]+K_{\mathrm{M}(\mathrm{A})}[\mathrm{B}]+[\mathrm{A}][\mathrm{B}]}$$ (2)

where the parameters are as defined above. Note that the only difference between these two equations is the term K_i(A)K_M(B) in the denominator of the ternary complex equation.

2.5. 7-Methylguanine (7-MeG) inhibition with respect to guanine

Reaction mixtures consisting of 100mM Hepes (pH 7.3), 20mM MgCl₂, 5mM DTT, a saturating concentration of tRNA (10 µM), varying concentrations of [³H]guanine (350 mCi/mmol) (0.075–0.35 µM), and varying concentrations of 7-MeG (0–20 µM) were treated with 10nM TGT. The total volume of each assay mixture was 400 µl. During a 15 min time course, 70 µl aliquots were removed every 3 min, filtered, and quantitated as described above. The data were analyzed using Kaleidagraph, where initial velocities were calculated from pmol guanine incorporated versus time plots. The initial velocity data were analyzed as described below.

2.6. 7-Methylguanine (7-MeG) inhibition with respect to tRNA

The K_i determination for 7-MeG with respect to tRNA was carried out as described for guanine with the following exceptions. The [³H]guanine (300mCi/mmol) concentration was held constant at 0.35 µM while the tRNA concentration was varied from 0.05 to 2 µM and the 7-MeG concentration ranged from 0 to 10 µM. As described above, it was necessary to add NaOH to neutralize the HCl associated with the guanine. The total volume of the assay mixture was 550 µl, from which 100 µl aliquots was removed every 4 min for 20 min.

2.7. Inhibition data analysis

The 7-methylguanine inhibition data were fit by three-dimensional, non-linear regression to a competitive (with respect to guanine) inhibition equation (3) and an uncompetitive (with respect to tRNA) inhibition equation (4) using the preprogrammed equations in GraFit. The results were then plotted using Kaleidagraph to display both the data and the fitted lines:

$$v_{\mathrm{i}}=\frac{V_{\text{max}}[\mathrm{S}]}{K_{\mathrm{M}}(1+[\mathrm{I}]/K_{\mathrm{i}})+[\mathrm{S}]},$$ (3)

$$v_{\mathrm{i}}=\frac{V_{\text{max}}[\mathrm{S}]/(1+[\mathrm{I}]/K_{\mathrm{i}})}{K_{\mathrm{M}}(1+[\mathrm{I}]/K_{\mathrm{i}})+[\mathrm{S}]}.$$ (4)

For graphical analysis of the data, these equations can be rearranged in the form of 1=v_i vs. [I] (Dixon method) [14] or [S]/v_i vs. [I] (the Cornish-Bowden method) [15]. In fact, both plots are complementary when analyzing data such as these. Therefore, the data were plotted by both methods based on the methodology described below. In the case of competitive inhibition, Eq. (5) holds, and plots of 1/v_i vs. [I] (Dixon) are intersecting. Plots of [S]/v_i vs. [I] (Cornish-Bowden) are parallel as the [S] term in the slope falls out

$$\frac{1}{v_{\mathrm{i}}}=\frac{K_{\mathrm{M}}}{V_{\text{max}}[\mathrm{S}]K_{\mathrm{i}}}[\mathrm{I}]+\frac{1}{V_{\text{max}}}\left(1+\frac{K_{\mathrm{M}}}{[\mathrm{S}]}\right).$$ (5)

In the case of uncompetitive inhibition, Eq. (6) holds, and plots of 1/v_i vs. [I] (Dixon) are parallel. Plots of [S]/v_i vs. [I] (Cornish-Bowden) are intersecting

$$\frac{1}{v_{\mathrm{i}}}=\frac{1}{V_{\text{max}}{K}_{\mathrm{i}}}[\mathrm{I}]+\frac{1}{V_{\text{max}}}\left(1+\frac{K_{\mathrm{M}}}{[\mathrm{S}]}\right).$$ (6)

3. Results

3.1. Determination of the kinetic mechanism for TGT using initial velocity kinetics

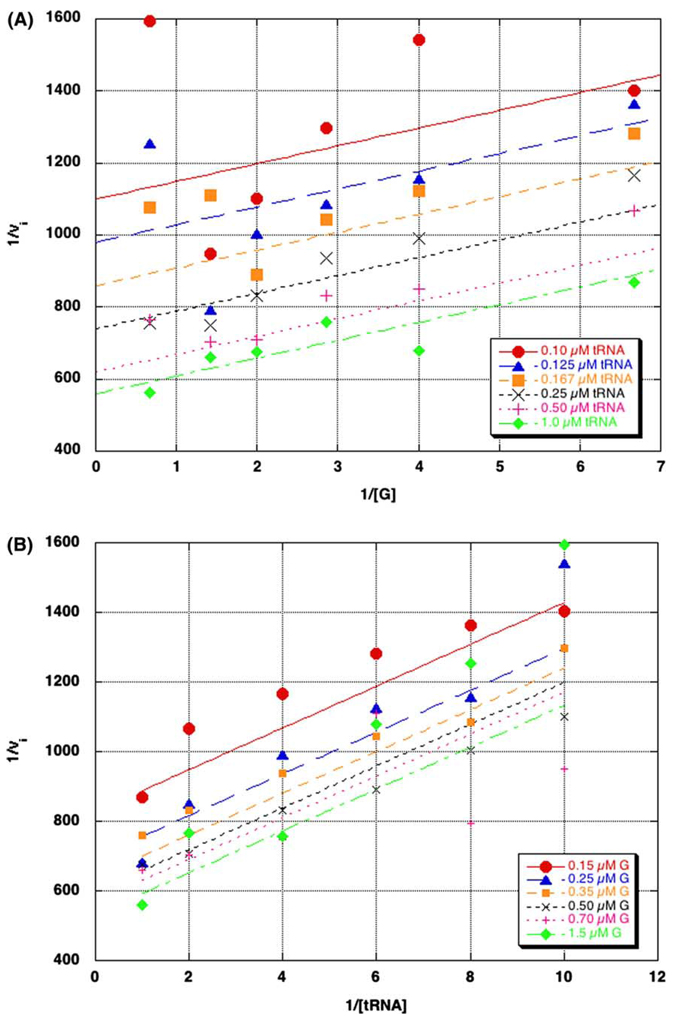
The kinetic mechanism of TGT was determined from initial velocity studies by varying the concentrations of both substrates. Each substrate was varied over a concentration range of approximately 0.5–5 times K_M. The reciprocal of the initial velocity (1/v_i) was plotted against the reciprocal of one of the substrates (1/[S]) at a fixed concentration of the second substrate to give a straight line. Repeating this data analysis at several concentrations of the second substrate, resulted in a series of lines. The data were fit to both ping-pong and ternary complex equations (Eq. (1) and Eq. (2)) as described in Section 2. The kinetic parameters obtained from these fits are displayed in Table 1. When the initial velocities were plotted against either guanine (Fig. 2A) or tRNA (Fig. 2B), parallel lines were obtained.

Table 1.

Kinetic parameters for ping-pong and ternary complex fits

Kcata (10−3 s−1)	KM Guaninea (µM)	KM tRNAa (µM)	KiA (µM)b
Ping-pong fit
2.0 (0.1)	0.0988 (0.023)	0.12 (0.017)	n/a
Ternary complex fit
2.0 (0.1)	0.101 (0.036)	0.12 (0.029)	−0.006 (0.07)

^aStandard errors are shown in parentheses. Kinetic parameters are determined from the average of three independent determinations of initial velocity data fit via non-linear regression to a three-dimensional equation for either a ping-pong or ternary complex mechanism (GraFit [13]).

^bK_iA is as defined by Cornish-Bowden and Wharton [12] and corresponds to $K_{\mathrm{A}}^{\prime }$ in GraFit.

Fig. 2.

Primary plots of kinetic mechanism data (1/v_i vs. 1/[substrate]). Initial velocities were determined by varying the concentration of guanine ([G], 0.15–0.7 µM), at several constant concentrations of tRNA (A), or by varying the concentration of tRNA ([tRNA], 0.1–1 µM) at several constant concentrations of guanine (B). The data points were generated from three independent determinations of the initial velocity data. The data were fit to a two-substrate ping-pong model (Eq. (2)). Error bars were left out for clarity.

Visual inspection of the data fit to the ternary complex equations (not shown) showed no difference from that of the ping-pong model (i.e., the lines still exhibited a parallel relationship). This is consistent with the kinetic parameters obtained from this fit which are essentially identical to those from the ping-pong fit with the addition of K_i(A) (−0.006) µM. Because K_i(A) is so small, the K_i(A) * K_M(B) term in Eq. (1) becomes negligible and the equation simplifies to the ping-pong equation (Eq. (2)).

3.2. Determination of the order of substrate binding

To determine the order of substrate binding, initial velocities of guanine exchange were measured in the presence of 7-methylguanine (7-MeG). It was previously shown that 7-MeG was a competitive inhibitor of guanine exchange [16]; presumably competitive with respect to guanine. The type of inhibition exhibited by 7-MeG with respect to each substrate was determined by three dimensional, non-linear regression fits of the data to both competitive (Eq. (3)) and uncompetitive (Eq. (4)) inhibition equations as described in Section 2. To confirm the mode of inhibition with respect to each substrate, each dataset was analyzed graphically by two methods: 1/v_i vs. [7-MeG] according to the method of Dixon [14] or [S]/v_i vs. [7-MeG] following the method of Cornish-Bowden [15].

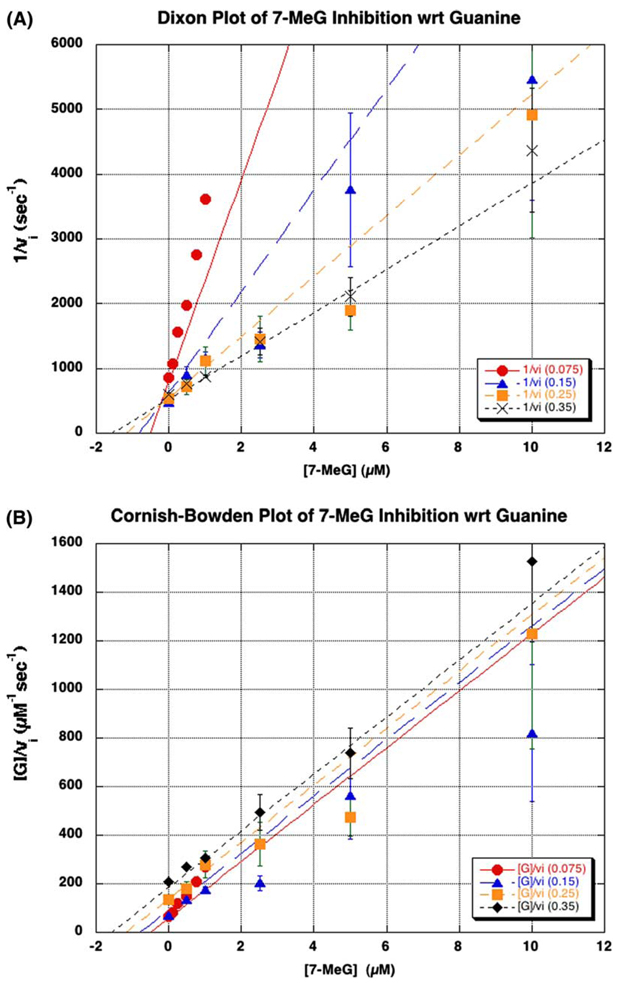
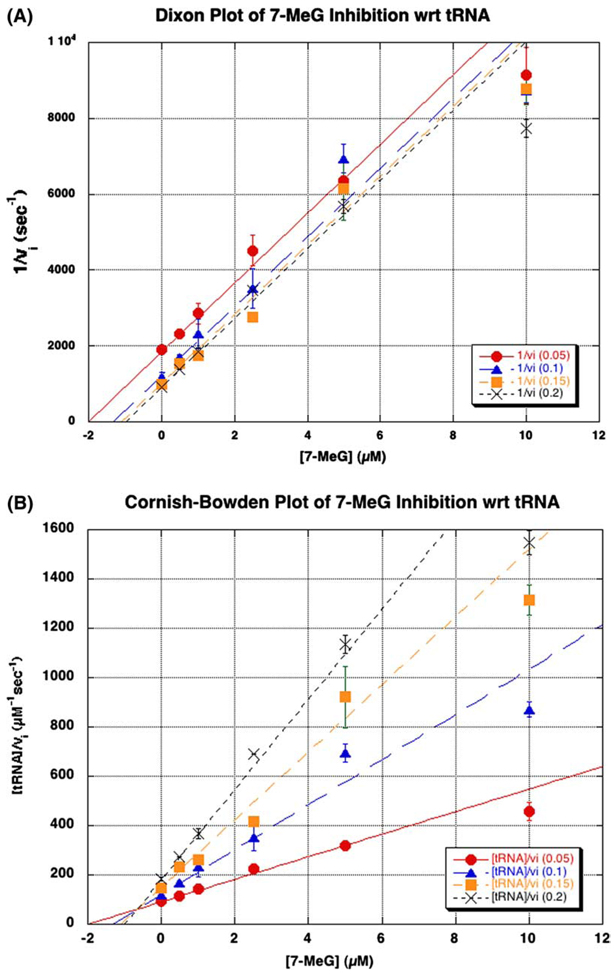
With respect to guanine, the data for 7-MeG inhibition were most consistent with competitive inhibition. This was further substantiated by the graphical analysis of the fit of the data to the calculated lines in a Dixon plot (intersecting lines, Fig. 3A), and when plotted according to the method of Cornish-Bowden (parallel lines, Fig. 3B). On the other hand, 7-MeG was found to be uncompetitive with respect to tRNA by a similar fit to the uncompetitive inhibition equation. Similar graphical analysis of the fit of the data to the calculated lines revealed parallel lines in the Dixon plot (Fig. 4A) and intersecting lines in the Cornish-Bowden plot (Fig. 4B). The calculated kinetic parameters for these fits are shown in Table 2.

Fig. 3.

Inhibition of guanine by 7-methylguanine (7-MeG). The mode of inhibition of the guanine kinetics by 7-MeG was determined by varying the concentrations of guanine (0.075–0.35 µM) and 7-MeG (0–10 µM), while holding tRNA constant at a saturating concentration (10 µM). The data were analyzed graphically by plotting either (A) 1/v_i vs. [7-MeG] or (B) [guanine]/v_i vs. [7-MeG] and fitting the data to the competitive inhibition equation (3) using GraFit. K_i corresponds to the point of intersection in the Dixon plot (A). The data points arise from an average of three independent determinations of initial velocities under these conditions. The error bars are the standard deviation of these three determinations for each point.

Fig. 4.

Inhibition of tRNA by 7-methylguanine (7-MeG). The mode of inhibition of the tRNA kinetics by 7-MeG was determined by varying the concentrations of tRNA (0.05–0.2 µM) and 7-MeG (0–10 µM), while holding guanine constant at its K_M (0.35 µM). The data were analyzed graphically by plotting either (A) 1/v_i vs. [7-MeG] or (B) [tRNA]/v_i vs. [7-MeG] and fitting the data to the uncompetitive inhibition equation (4) using GraFit. K_i corresponds to the point of intersection in the Cornish-Bowden plot (B). The data points arise from an average of two independent determinations of initial velocities under these conditions. The error bars are the standard deviation of these two determinations for each point.

Table 2.

Kinetic parameters for 7-methylguanine inhibition

Kcata (10−3 s−1)	KMa (µM)	Kia (µM)
With respect to guanine
2.2 (0.2)	0.056 (0.024)	0.22 (0.08)b
With respect to tRNA
1.7 (0.1)	0.106 (0.01)	0.64 (0.04)c

^aStandard errors are shown in parentheses. Kinetic parameters are determined from the average of two (tRNA) or three (guanine) independent determinations of initial velocity data fit via non-linear regression to a three-dimensional equation for either competitive inhibition (guanine) or uncompetitive inhibition (tRNA) using GraFit.

^bCompetitive with respect to guanine.

^cUncompetitive with respect to tRNA.

4. Discussion

TGT catalyzes the incorporation of queuine (ultimately) into tRNA. The reaction involves breaking and reformation of the glycosidic bond to the base at position 34 of the substrate tRNAs. The initial velocity data reported here fit best to the ping-pong model (Eq. (2)). These data exhibit parallel lines for both substrates in plots of 1/v_i vs. 1/[substrate] (Fig. 2). It should be noted that the effects of substrate inhibition can cause lines that look parallel for a sequential mechanism [17]. In the TGT assay (which follows the incorporation of radiolabeled guanine), the forward and reverse reactions are chemically identical. Therefore, for all practical purposes, the substrates and products are also identical. In most studies, the radiolabeled guanine is present in excess and the amount of unlabeled guanine that is reincorporated is negligible. Since both the tRNA (which contains the unlabeled guanine) and the radiolabeled guanine are at low concentrations in these studies it was especially important to ensure that initial velocity conditions were maintained. Consequently, substrate inhibition is not a problem in the current work. The value for k_cat predicted by the fit to the ping-pong model is consistent with previously determined values and the K_M values for both substrates are consistent with K_M values determined currently in our lab. (It should be noted that these K_M values are ca. 10-fold lower than K_M values that we have previously published [7,9,18]. The current studies utilize a higher specific activity guanine substrate, allowing for a more sensitive assay. Therefore, reliable data can be obtained at lower TGT concentrations (10nM) than were previously required (ca. 250 nM). This may account for the discrepancy in K_M values.)

Fitting the data to the ternary complex equation (1) yielded values for the kinetic parameters that are essentially identical to those for the ping-pong fit (Table 1) with the addition of a value of −0.006 for K_i(A). This non-sensical value for K_i(A) causes this term to drop out and the ternary complex equation reduces to that for the ping-pong mechanism. The fact that the fit of the data to the ternary complex mechanism reduces to the ping-pong equation lends strong support to the conclusion that TGT follows a ping-pong mechanism.

In a ping-pong mechanism, substrate binding must be ordered. Given the nature of the TGT reaction, the only chemically reasonable order would be for tRNA to bind first. To provide experimental evidence to confirm this, the order of substrate binding was investigated through the use of a methylated guanine analogue (7-methylguanine, 7-MeG, Fig. 1) that has been previously reported to inhibit the TGT reaction [16,19]. The type of inhibition caused by 7-MeG with respect to each substrate was determined. Using a guanine analogue inhibitor, competitive inhibition with respect to guanine would be expected independent of the order of substrate binding. Therefore, the key issue (or goal) is to determine the type of inhibition observed by 7-MeG when tRNA is the variable substrate. As summarized in Table 3, uncompetitive inhibition with respect to tRNA would be expected if tRNA binds first. Alternatively, if guanine binds first, non-competitive inhibition with respect to tRNA would be expected by 7-MeG. 7-MeG was competitive with respect to guanine (Fig. 5) and uncompetitive with respect to tRNA (Fig. 4). These results are consistent with tRNA binding first.

Table 3.

Predicted inhibition pattern for 7-methylguanine dependent upon order of substrate binding

	Varying guanine	Varying tRNA
G-tRNA binds first	Competitive	Uncompetitive
Guanine binds first	Competitive	Non-competitive

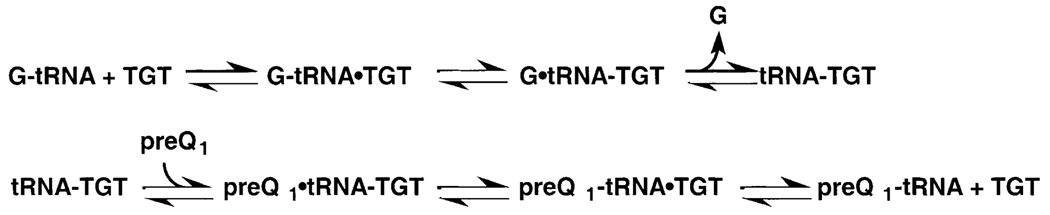
Fig. 5.

Proposed kinetic mechanism for the TGT reaction.

Ideally, these inhibition studies would have been repeated with an inhibitory tRNA analogue. Although the minihelix analogue SCFMH(TΨC)(G₅₃C) has been reported as a competitive inhibitor of guanine exchange [20], its K_i = 135µM limits its availability in quantities suitable for these studies. To our knowledge, no other tRNA-competitive inhibitor has been reported for TGT. A mechanism in which tRNA binds first is most consistent with the crystal structure which exhibits only a single binding site, and the failure to observe guanine binding in the absence of tRNA (Goodenough-Lashua and Garcia, unpublished).

Chemically, the reaction catalyzed by pseudouridine synthase is most similar to that of TGT. Pseudouridine synthase is responsible for the formation of pseudouridine (Ψ) from uridine. The first step of the reaction involves cleavage of the N–C glycosidic bond. This is followed by rotation of the uracil base. The final step results in the formation of a C-C glycosidic bond. Unfortunately, since the glycosidic bond formation step utilizes the base removed in the initial step, and not exogenous uracil [21], this enzyme is not a relevant model for our kinetic mechanism studies.

A family of enzymes which includes AMP nucleosidase and nucleoside hydrolase catalyze reactions whose end products are similar to the product of the first half of the TGT reaction. The reactions catalyzed by AMP nucleosidase [22] and nucleoside hydrolase [23,24] involve excision of the base through hydrolysis. No covalent enzyme intermediate is involved in catalysis by these enzymes and a ternary complex mechanism (involving enzyme, nucleoside, and water) is employed.

The second step of the TGT reaction involves glycosidic bond formation. The best model for this reaction comes from the phosphoribosyltransferases (PRTases) which play key roles in nucleotide biosynthesis. There is much uncertainty surrounding the study of the kinetic mechanisms of this family of enzymes. The reports of ping-pong kinetics among this family have come into question following more recent studies. For example, Victor et al. [25] proposed a ping-pong mechanism for yeast orotate PRTase (OPRTase), in which PP_i release precedes orotate binding. However, Bhatia et al. [17] reported that Salmonella typhimurium OPRTase employs a sequential mechanism; citing a contamination of the commercial OMP by PP_i as a source of uncertainty and a need to reconsider the 1979 work. Furthermore, early studies with human hypoxanthine-guanine PRTase (HGPRTase) demonstrated that at high magnesium concentrations, parallel lines in a double reciprocal plot were observed suggesting a ping-pong mechanism; although, low concentrations of magnesium led to a sequential mechanism [26]. Further studies on the human, yeast, and bacterial enzymes over the next two decades continued to give conflicting results. Evidence was obtained for a purely sequential [27–29], as well as, a sequential with an alternative ping-pong mechanism [30]. Most recently, kinetic, binding, and structural data have maintained the sequential mechanism for HGPRTase [31]. Finally, yeast uracil PRTase (UPRTase) was reported to follow a ping-pong mechanism [32], but studies with the E. coli enzyme clearly support a sequential mechanism [33]. It should be noted that in the cases of OPRTase and UPRTase, it is possible that various organisms utilize different mechanisms, explaining the discrepancies observed.

The strongest precedence for a ping-pong mechanism in a similar enzyme comes from nucleoside 2′-deoxyribosyltransferase, which exhibits both transferase and hydrolase activities [34]. Similar to TGT, nucleoside 2′-deoxyribosyltransferase initiates the cleavage of the glycosidic bond of a nucleoside to release the base. The base can either be transferred to a different deoxyribose, or be released from the enzyme. The cleavage reaction proceeds through an acyl enzyme intermediate in which an active site glutamate acts as the nucleophile [35,36]. Kinetic evaluation of the enzyme has revealed that nucleoside 2′-deoxyribosyltransferase utilizes a ping-pong kinetic mechanism [37].

The current data strongly suggest a ping-pong reaction, in which tRNA binds first, as the most likely kinetic mechanism for TGT. Ping-pong kinetics are consistent with the proposed chemical mechanism involving a covalent intermediate between tRNA and aspartate 89 [4]. The failure of guanine to bind in the absence of tRNA is also consistent with ping-pong kinetics, but alone not does not rule out an ordered sequential mechanism. The single binding site observed in the structural data [2] further supports a ping-pong mechanism, although in the absence of a tRNA–TGT co-crystal structure the possibility of a second site forming upon tRNA binding cannot be completely eliminated. In previous studies of preQ₁ analogues as substrates for TGT, we noted that in the absence of any heterocyclic substrate, TGT will catalyze the “wash-out” of radiolabeled guanine from tRNA [18]. This “wash-out”, presumably hydrolysis, occurs at a rate ca. 0.1% of that of the normal reaction. Although this rate of wash-out is low (slow) it does provide evidence that the first chemical step can occur in the absence of the second substrate. Finally, ping-pong kinetics are consistent with our earlier study of a mechanism-based inhibitor of TGT, 7-fluoromethyl-7-deazaguanine (FMPP) [38]. In those studies, we observed that FMPP inactivation of TGT was dependent upon tRNA and that FMPP is competitive with respect to guanine, consistent with FMPP interacting with a covalent TGT–tRNA intermediate.

Based upon these results for the guanine exchange reaction, we propose a kinetic mechanism for the TGT reaction as presented in Fig. 5. In this mechanism, the first half reaction involves tRNA binding, followed by guanine release and dissociation. Once the active site is accessible, the preQ₁ binds and glycosidic bond formation occurs. This step results in release of the enzyme from the covalent intermediate and dissociation of the modified tRNA can occur.