A Semiparametric Transition Model with Latent Traits for Longitudinal Multistate Data

SUMMARY

We propose a general multistate transition model. The model is developed for the analysis of repeated episodes of multiple states representing different health status. Transitions among multiple states are modeled jointly using multivariate latent traits with factor loadings. Different types of state transition are described by flexible transition-specific nonparametric baseline intensities. A state-specific latent trait is used to capture individual tendency of the sojourn in the state that cannot be explained by covariates and to account for correlation among repeated sojourns in the same state within an individual. Correlation among sojourns across different states within an individual is accounted for by the correlation between the different latent traits. The factor loadings for a latent trait accommodate the dependence of the transitions to different competing states from a same state. We obtain the semiparametric maximum likelihood estimates through an expectation-maximization (EM) algorithm. The method is illustrated by studying repeated transitions between independence and disability states of activities of daily living (ADL) with death as an absorbing state in a longitudinal aging study. The performance of the estimation procedure is assessed by simulation studies.

1. Introduction

Many health studies involve conditions whereby subjects make repeated transitions over time among a set of defined states representing different health status. A popular analytic framework uses intensity-based methods (Andersen et al., 1993) in which state transition intensities are specified.

The methodological development in this article is motivated by a longitudinal study of activities of daily living (ADL) among older persons (Gill, Hardy, and Williams, 2002). Participants who needed help from another person or were unable to complete at least one of the four ADL tasks (dressing, bathing, walking, transferring) were considered disabled. Many older persons made multiple transitions between ADL independence and disability before death. Repeated transition between community stay and hospital stay before remission in schizophrenia patients is another example. In kidney transplant patients, total organ rejection is regarded as a nonabsorbing state but not a repeated state because the state of total organ rejection usually cannot be revisited. Important questions arise such as: Does the duration of a healthier state continually lengthen (improved health) or shorten (worsening health) over time? Can such a progressive pattern be tested and the magnitude be estimated?

In our approach, each nonabsorbing state can have its own latent trait. This state-specific individual latent trait represents an unobserved risk factor associated with transitioning from that state or an intrinsic individual tendency of sojourn in the state that cannot be fully explained by measured covariates. Thus, the latent trait accounts for correlation among the repeated sojourns in that state within the same individual (association type I). The use of multivariate latent traits accounts for correlation (positive or negative) among the sojourns in different states within an individual (association type II). A positive correlation indicates that longer (or shorter) gap times in all the involved states are more likely so that the transitions are less likely (or more likely). A negative correlation indicates that a longer gap time in one state is associated with a shorter gap time in the other involved states. A novel feature of our model is the introduction of factor loadings into the semiparametric model. The factor loadings conveniently account for the possible dependence (either positive or negative) among the competing transitions to different states from a same state within an individual (association type III). A positive (negative) dependence indicates that an increased likelihood of transitioning to one state is associated with an increased (decreased) likelihood of transitioning to another state from a same state. For multistate data with more than two states, all the three types of association can be present. The semiparametric model with latent traits introduced in this article simultaneously accommodate all these three types of association.

Previous work using a single shared frailty (a latent variable) to characterize heterogeneity in multivariate survival data has some deficiencies. In most cases, univariate frailty only induces positive association within the cluster (Joe, 1993). In the correlated gamma frailty models considered by Parner (1998), a common cluster-specific frailty plus an individual-specific frailty are used so that an individual has his/her own frailty that is correlated but not shared with the frailty of another individual in the same cluster. However, the correlated gamma frailties still can only accommodate positive correlation within the cluster. Often, there are situations when event times within a same cluster are negatively associated. For example, alternating community stay and hospital stay among severe schizophrenia patients, and independence and disability states in our ADL example may be negatively correlated. The bivariate log-normal frailty considered by Xue and Brookmeyer (1996) naturally accommodates negative correlation between sojourns in different states. However, without introducing factor loadings, possible dependence arising from competing transitions to different states from a same state cannot be accommodated using the usual log-normal frailties when there exist more than two states. In our ADL example, recovery from disability and death in a disability state are competing transitions that may well be dependent. Liu, Wolfe, and Huang (2004) modeled the intensity functions of point processes of repeated hospitalizations and death in transplant candidates suffering from severe kidney diseases by using a single gamma frailty with a factor loading. However, their model also treated the hospitalization as a point event neglecting the length of stay and is not suitable for data with more than two states.

The article is organized as follows. In Section 2, we describe in more detail our ADL example. In Section 3, we present our multistate latent traits model. We describe its estimation procedure in Section 4. In Section 5, we present the results from the analysis of the ADL data set. We conduct the simulation studies in Section 6, and conclude with a discussion in Section 7.

2. The ADL Example in Longitudinal Aging Study

The participants were all in the independence state of ADL at entry. The data set consists of monthly follow-up interviews for the first 84 months on 754 subjects; 228 participants died after a median follow-up of 42 months, and 35 dropped out of the study after a median follow-up of 21 months. Complete details of this longitudinal aging study regarding the follow-up assessments, including formal tests of reliability and accuracy, have been published previously (Gill et al., 2002).

Table 1 presents summary statistics of our ADL data set. Briefly, both genders spent less time in disabled state than independent state with women being in disabled state longer than men. Overall, women made slightly more transitions and were followed for a longer time before death, that is, they lived longer with lower overall mortality (27.5% for women vs. 35.5% for men). These results can be explained by the finding that older age and longer follow-up times as indicated by more transitions are both associated with being in a disability state (see Section 5.2.1). For both genders, death was much more likely to occur in a disability state. In analyzing the data, we address questions such as: whether a shorter sojourn in disabled state indicates a higher likelihood of recovery and a longer sojourn in independent state; whether death dependently censors the stay in an ADL state or is simply a result of older age; and whether death is more related to one ADL state than the other.

Table 1.

Summary statistics on states, transitions, and death by gender

	Male (nM = 265)		Female (nF = 487)
	Independence	Disability	Independence	Disability
Min, median, mean, max of total times in months	1, 67, 54, 83	0, 2, 7, 72	1, 64, 53, 84	0, 3, 13, 78
Min, median, mean, max of total number of transitions	0, 2, 3, 24		0, 2, 4, 32
Min, median, mean, max of months since entry to death	1, 37, 38, 80		1, 47, 43, 80
Total number of deaths (%)	24 (25.5%)	70 (74.5%)	28 (20.9%)	106 (79.1%)

3. A Semiparametric Multistate Model with Latent Traits

3.1 Model Specification

Suppose there are n independent individuals indexed by i = 1,…n and K + M states with K nonabsorbing states indexed by k = 1,…,K and M absorbing states indexed by k = K + 1,…,K + M. Let j(j = 1,…,J_ik) index the jth visit of state k by individual i and max_{i∈{1,…,n}} J_ik ≥ 2 if state k is nonabsorbing and can be revisited. It should also be noted that sometimes a transition from one state to another nonabsorbing state is not biologically plausible, for example, the transition from total organ rejection to no rejection is not possible in a kidney transplant patient.

We specify an intensity function for transition from a nonabsorbing state k(k = 1,…,K) to a different state l(l = 1,…,K + M) in the following semiparametric multiplicative model:

$${\lambda }_{ijkl}(t)=R_{ijkl}(t){\lambda }_{0kl}(t)\text{exp}\{{\mathbf{X}}_{ijkl}^{\mathrm{T}}(t){\beta }_{kl}+{\gamma }_{kl}{\eta }_{ik}\}.$$ (1)

In this model, t is the gap time since the last transition, and R_ijkl is the observed at-risk process for individual i with R_ijkl(t) = 1 if subject i is at risk for transition to state l in the jth visit of state k and not censored at time t and zero otherwise. If the transition from state k to l is not possible at t for individual i, then R_ijkl(t) = 0. λ_ijkl is the intensity of transition from state k to l during jth visit to state k by individual i, λ_0kl is the unspecified baseline intensity function with cumulative intensity Λ_0kl, X_ijkl is a column vector of possibly time-dependent covariates for individual i associated with the transition to state l during jth visit of state k, β_kl is the corresponding vector of regression coefficients for X_ijkl, η_ik is the individual i’s latent variable of trait for sojourn in state k, and γ_kl is the loading representing the effect of the latent trait measure on the transition from state k to state l. The maximum number of latent traits equals the number of repeated nonabsorbing states, so there can be only two latent traits in our ADL example.

Let η_i = (η_i1,…,η_iK)^T and η_i is assumed to have a multivariate normal distribution with mean zero and variance–covariance matrix G. The choice of the multivariate normal distribution conveniently accommodates any possible negative correlation due to sojourn among different states within the same individual. The covariates in X_ijkl may contain the number of transitions individual i made since the beginning of follow-up to capture the possible “instability” effect in that increased number of transitions indicates a decreased tendency for staying in the same state.

Our model only requires K + M ≥ 2 but not M ≥ 1 and is general enough to accommodate both repeated and/or forward transitions.

3.2 Summary of the Data

Let D_ijk be the index of the state that is transited to from the jth visit of state k, and U_ijk be the gap time of jth visit in state k for individual i. Define the counting process N_ijkl(t) = I(U_ijk ≤ t, D_ijk = l) and write dN_ijkl(t) = N_ijkl{(t + dt)−} − N_ijkl(t−) as dt → 0. Using this notation, N_ijkl(U_ijk) = 1 and N_ijkl′(U_ijk) = 0 for any l′ ≠ l if D_ijk = l.

Define X_i… = {X_i.1.;,…,X_i.K.} as all the covariates for subject i with X_i.k. = {R_ijklX_ijkl(t)}, N_i… = {N_i.1.,…,N_i.K.} denote all the counting processes for subject i with N_i.k. = {N_ijkl(t)}, and R_i… = {R_i.1.,…,R_i.K.} denote all the at-risk processes for subject i with R_i.k. = {R_ijkl(t)}. In all the above, j = 1,…,J_ik; l = 1,…,K + M; l ≠ k, t ∈ [0, U_ijk]. Therefore, the observed data for subjects can be written as O_‥‥ = {O_i…; i = 1,…,n} with O_i… = {X_i…, N_i…, R_i…} denoting observed data for subject i. We assume O_i… and O_i′… are independent for any i ≠ i′.

3.3 Model Interpretation and Identification

As discussed by Manton, Stallard, and Vaupal (1986), often the fit of a model is more sensitive to assumptions in the form of the baseline intensity or hazards than in the form of the frailty distribution, so we adopt a nonparametric flexible baseline intensity function that is specific for both the current state and the state to be transited to. The use of a gap time scale implies that the process of multistate transition is “renewed” right after a transition to a nonabsorbing state is made, so the “full” capacity of multistate transitions is resumed.

The novel feature in our model is the use of latent trait η_ik with loading γ_kl. The state-specific individual latent trait captures an individual’s tendency of sojourn in that state and naturally induces correlation among repeated sojourns in the state within an individual. Dependence arising from the competing transitions from the same state to different states is accounted for by using the factor loadings. Our latent traits with loadings are different from random effects or frailties in that both the latent traits and the loadings are unknown, whereas unknown random effects of regression coefficients are used with observed covariates and frailties have loadings of one.

For the model to be identified, the smallest l in the loading γ_kl is assumed to be one for each k, that is, γ_{k,min(l:l≠k}) = 1. This restriction is imposed because the variance components in G are allowed to vary freely. Imposing a γ_kl = 1 implies that a greater value of the latent trait η_kl is associated with increased likelihood of transition from state k to l. With the transition to state l with the smallest number in the label serving as the reference level, the sign and the size of γ_kl′(l′ ≠ l) determine the direction and the extent of the association between the latent trait for the transition from state k to l′ and the latent trait for the transition from state k to l. When K = 2 and M = 0, model (1) reduces to the bivariate log-normal model of Xue and Brookmeyer (1996) for two alternating states. Furthermore, when K = 1 and M = 1, model (1) is the frailty model with a single event considered by Barker and Henderson (2005).

4. An Estimation Procedure

We use semiparametric maximum likelihood (SPML) methods to simultaneously estimate the parameters in our model via the expectation-maximization (EM) algorithm. Let Ψ denote the collection of all parametric components of the parameters β’s, γ’s, and G, Λ_0‥ denote the collection of the nonparametric cumulative baseline intensity functions Λ_0kl’s and [A|B] denote the conditional density of A given B. The log likelihood of the observed data O_‥‥ given the covariates X_i… is written as $l_n(\mathbf{\Psi },{\mathbf{\Lambda }}_{0‥};{\mathbf{O}}_{‥‥})={\displaystyle {\sum }_{i=1}^n\text{log}{\displaystyle \int [{\mathbf{N}}_{i\cdots ,}{\mathbf{R}}_{i\cdots }|{\mathit{\eta }}_{i,}{\mathbf{X}}_{i\cdots }]}}[{\mathit{\eta }}_i]\mathrm{d}{\mathit{\eta }}_i$. This observed log likelihood is computationally difficult to maximize because of the presence of the integration within the logarithm. Therefore we use the EM algorithm to maximize the complete data log likelihood, which is written as

$$\begin{array}{c}{\displaystyle \sum _{i=1}^n\{\text{log}[{\mathbf{N}}_{i\cdots },{\mathbf{R}}_{i\cdots }|{\mathit{\eta }}_i,{\mathbf{X}}_{i\cdots }]+\text{log}[{\mathit{\eta }}_i]\}}\hfill \\ ={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{k=1}^K{\displaystyle \sum _{j=1}^{J_{ik}}{\displaystyle \sum }_{l=1}^{K+M}}}}\hfill \\ \times [{\displaystyle {\int }_0^{U_{ijk}}\{\text{log}\{{\lambda }_{0kl}(t)\}+{\mathbf{X}}_{ijkl}^{\mathrm{T}}(t){\beta }_{kl}+{\gamma }_{kl}{\eta }_{ik}\}}{\mathrm{d}N}_{ijkl}(t)\hfill \\ -{\displaystyle {\int }_0^{U_{ijk}}{R}_{ijkl}(t){\lambda }_{0kl}(t)\text{exp}\{{\mathbf{X}}_{ijkl}^{\mathrm{T}}(t){\beta }_{kl}+{\gamma }_{kl}{\eta }_{ik}\}}\mathrm{d}t]\hfill \\ +{\displaystyle \sum _{i=1}^n\text{log}[\{2\pi \mathit{\text{det}}(\mathbf{G}){\}}^{-\frac{1}{2}}\text{exp}\{-{\mathit{\eta }}_i^{\mathrm{T}}{\mathbf{G}}^{-1}{\mathit{\eta }}_i/2\}].}\hfill \end{array}$$ (2)

The calculation for the conditional expectation of a function g of the latent traits given the observed data, $\mathrm{E}\{g({\mathit{\eta }}_i)|{\mathbf{O}}_{i\cdots }\}=\frac{{\displaystyle \int g({\mathit{\eta }}_i)[{\mathit{\eta }}_i][{\mathbf{N}}_{i\cdots },{\mathbf{R}}_{i\cdots }|{\mathit{\eta }}_i,{\mathbf{X}}_{i\cdots }]}\mathrm{d}{\mathit{\eta }}_i}{{\displaystyle \int [{\mathit{\eta }}_i][{\mathbf{N}}_{i\cdots },{\mathbf{R}}_{i\cdots }|{\mathit{\eta }}_i,{\mathbf{X}}_{i\cdots }]}\mathrm{d}{\mathit{\eta }}_i}$, is given as

$$\frac{{\displaystyle \int g({\mathit{\eta }}_i)\text{exp}\left[{\displaystyle \sum _{k=1}^K{\displaystyle \sum _{j=1}^{J_{ik}}{\displaystyle \sum }_{l=1}^{K+M}}}\{{\gamma }_{kl}{\eta }_{ik}{N}_{ijkl}(U_{ijk})-{\mathrm{\Lambda }}_{ijkl}(U_{ijk})e^{{\gamma }_{kl}{\eta }_{ik}}\}\right]}\varphi ({\mathit{\eta }}_i)\mathrm{d}{\mathit{\eta }}_i}{{\displaystyle \int \text{exp}\left[{\displaystyle \sum _{k=1}^K{\displaystyle \sum _{j=1}^{J_{ik}}{\displaystyle \sum }_{l=1}^{K+M}}}\{{\gamma }_{kl}{\eta }_{ik}{N}_{ijkl}(U_{ijk})-{\mathrm{\Lambda }}_{ijkl}(U_{ijk})e^{{\gamma }_{kl}{\eta }_{ik}}\}\right]}\varphi ({\mathit{\eta }}_i)\mathrm{d}{\mathit{\eta }}_i}$$ (3)

with ${\mathrm{\Lambda }}_{ijkl}(U_{ijk})={\displaystyle {\int }_0^{U_{ijk}}{R}_{ijkl}(t){\lambda }_{0kl}(t)\text{exp}\{{\mathbf{X}}_{ijkl}^{\mathrm{T}}(t){\beta }_{kl}\}}\mathrm{d}t$ and ϕ(η_i) is the multivariate normal density for η_i. Equation (3) follows because the terms without η_ik cancel out in the numerator and the denominator for [N_i…, R_i…|η_i, X_i…]. Because there are no closed forms for the integrals in (3), a Monte Carlo integration method with antithetic simulation in the E-step as described by Henderson, Diggle, and Dobson (2000) is used. There are also no closed-form solutions for β_kl and γ_k, so one-step Newton–Raphson is used in the M-step. Other details of the EM algorithm are given in Appendix A. Because problems such as multiple solutions and convergence to a stationary point may exist, the EM was repeated from different starting values to ensure convergence to a global maximum.

The standard errors for Ψ are estimated using the bootstrap. As a comparison, they are also approximated with the submatrix of the inverse of empirical information for {Ψ, Λ_0‥} (McLachlan and Krishnan, 1997). This empirical information is used to approximate the observed information under EM algorithm using the Louis formula (Louis, 1982). The empirical information matrix reduces to the empirical Fisher information matrix when evaluated at the SPML estimates, {Ψ̂, Λ̂_0‥}, as

$${\displaystyle \sum _{i=1}^{n}S({\mathbf{N}}_{i\cdots },{\mathbf{R}}_{i\cdots },}{\mathbf{X}}_{i\cdots };\mathbf{\Psi },{\mathbf{\Lambda }}_{0‥})S^{\mathrm{T}}({\mathbf{N}}_{i\cdots },{\mathbf{R}}_{i\cdots },{\mathbf{X}}_{i\cdots };\mathbf{\Psi },{\mathbf{\Lambda }}_{0‥}),$$

where the observed score vector, S(N_i…, R_i…, X_i…; Ψ̂, Λ̂_0‥), can be calculated from the expected complete data score obtained at the convergence of the EM algorithm as

$$\begin{array}{cc}{\mathrm{E}}_{\mathbf{\Psi },{\mathbf{\Lambda }}_{0‥}}\hfill & \{S_{\mathrm{C}}({\mathbf{N}}_{i\cdots },{\mathbf{R}}_{i\cdots },{\mathbf{X}}_{i\cdots };{\mathit{\eta }}_i;\mathbf{\Psi },{\mathbf{\Lambda }}_{0‥})|\hfill \\ \hfill & \hfill {\mathbf{N}}_{i\cdots },{\mathbf{R}}_{i\cdots },{\mathbf{X}}_{i\cdots },\}{|}_{\mathbf{\Psi }=\widehat{\mathbf{\Psi }},{\mathbf{\Lambda }}_{0‥}={\widehat{\mathbf{\Lambda }}}_{0‥}}.\hfill \end{array}$$

The complete score S_C is much easier to calculate and has a closed-form expression, which motivated the use of the above EM algorithm.

We did not obtain the estimates of the standard errors via the profile likelihood with {λ_0kl} being profiled out because Hsieh, Tseng, and Wang (2006) found the standard errors via the profile likelihood are underestimated as compared to those via bootstrap in the semiparametric joint model of longitudinal and survival outcomes. This underestimation likely results because the dimension of the parameters Ψ is much smaller in the profile likelihood than that of {Ψ, Λ_0‥} in the Louis formula and that the covariance between Ψ and Λ_0‥ is nonzero. So the variance estimates from inverting the observed information matrix for Ψ in the profile likelihood are smaller than those from inverting the observed information matrix for {Ψ, Λ_0‥}. Because the asymptotically estimated standard errors based on the empirical information without using profile likelihood may still be smaller than those via bootstrap in finite samples, we base the inferences about covariate effects on the bootstrap standard errors whenever there is a difference in the significance of the findings.

5. Analysis of the Longitudinal ADL Data

5.1 Description of the Variables

The response variable is ADL status (independence or disability) from monthly telephone interviews or death. Time-dependent covariates were recorded through comprehensive in-home assessments that were conducted at baseline and every 18 months. The data set analyzed consists of the observations from 752 out of the 754 participants because 2 participants died before their first interview. We use k = 1, 2, and 3 to index the states of independence, disability, and death, respectively. Covariates with meaningful two-way interactions were selected according to the overall clinical relevance and statistical significance from fitting univariate event data. The covariates include baseline age in years (age), indicator of female gender (sex), and some important time-varying indicators such as living alone (alone), depression (depres), and a slower gait speed (frail).

5.2 Solution from Fitting the Latent Trait Model to the ADL Data

The X_ijkl in the final fitted model includes only the aforementioned covariates with two-way interactions that have p-values less than 0.1 as judged by the univariate analysis. Table 2 shows that the conclusions on the covariates effects and the loadings are consistent based on the bootstrap and the asymptotics except for sex:frail. The significance of the effects is assessed by the Wald statistics. The asymptotic estimates of the standard errors for β̂_kl and γ̂_kl are close to or smaller than those from the bootstrap except for the effect of tran in β̂₂₁. The asymptotic estimates of the standard errors for the variance components in Ĝ are larger than those from the bootstrap. The asymptotic estimates of the standard errors based on the profile likelihood are always smaller than those from the approximation of Louis’ formula described in Section 4 (not shown).

Table 2.

Estimates of β_kl, γ_kl and, G

	Transition from independence state
	To nonabsorbing state of disability			To absorbing state of death
	β̂ 12a	Standard error		β̂13a	Standard error
Covariate	Estimate	Bootstrap	Asymptotic	Estimate	Bootstrap	Asymptotic
Age	0.0365	0.0042	0.0013	0.0754	0.0201	0.0009
Tran	0.1623	0.0149	0.0150
Frail	0.9035	0.1053	0.1052
Frail:tran	−0.0837	0.0131	0.0109
Alone	−0.2642	0.0780	0.0645
Alone:tran	0.0326	0.0106	0.0098
Depres	0.2842	0.0645	0.0344
Sex	0.0150	0.1060	0.0865
Sex:frail	0.1858	0.1222	0.0886
Sex:tran	−0.0133	0.0118	0.0113
	Transition from disability state
	To nonabsorbing state of independence			To absorbing state of death
	β̂21a	Standard error		β̂23a	Standard error
Covariate	Estimate	Bootstrap	Asymptotic	Estimate	Bootstrap	Asymptotic
Age	−0.0151	0.0032	0.0017
Tran	−0.0119	0.0072	0.0095	−0.1306	0.0639	0.0640
Frail	−0.2620	0.1075	0.0505	−0.8099	0.2313	0.2279
Frail:tran				0.1188	0.0608	0.0585
Sex				−0.8057	0.1923	0.1914
	Estimates of variance–covariance matrix for the latent traits
	$\widehat{\text{var}}({\widehat{\eta }}_{i1})$ a	Standard error		$\widehat{\text{var}}({\widehat{\eta }}_{i2})$ a	Standard error
	Estimate	Bootstrap	Asymptotic	Estimate	Bootstrap	Asymptotic
	0.1612	0.0443	0.0526
$\widehat{\text{Cov}}({\widehat{\eta }}_{i1},{\widehat{\eta }}_{i2})$ a	−0.0572	0.0159	0.0100	0.0212	0.0059	0.0079
	γ̂12	Standard error		γ̂13	Standard error
Loadinga	Estimate	Bootstrap	Asymptotic	Estimate	Bootstrap	Asymptotic
	1	NA	NA	−0.4855	1.4860	0.4938
	γ̂21	Standard error		γ̂23	Standard error
Loadinga	Estimate	Bootstrap	Asymptotic	Estimate	Bootstrap	Asymptotic
	1	NA	NA	5.3678	1.1854	0.8820

^aWe use k = 1 and 2 to index the states of independence and disability, respectively. We use l = 2 and 3 to denote the states of disability and death that can be transited to from the state of independence (state 1). We use l = 1 and 3 to denote the states of independence and death that can be transited to from the state of disability (state = 2).

5.2.1 Fixed effects

The top left panel of Table 2 presents the fixed effects on the transition from ADL independence to disability. Increased age, the number of previous state transitions (tran), depression (depres), and physical frailty (frail) all significantly increase the likelihood of transition. The interaction term of frail:tran is significant, but has the opposite effect of either main effect because frail and tran are partially overlapping in their effects on the transition, so that their combined effect is less than additive. The effect of living alone (alone) on the transition depends on the number of previous transitions due to the presence of a significant interaction effect of alone:tran. Living alone initially decreases the likelihood of the transition, but for those having made at least two previous transitions (consisting of a transition from ADL independence to disability and back to independence) it increases the likelihood, that is, once an individual experiences disability, living alone (in an independence state) increases the risk of becoming disabled again. Neither the main effect of sex nor the two interaction effects with sex are significant for the transition.

The top right panel of Table 2 shows that for an ADL-independent person, age is the only significant predictor for death. There also does not seem to exist any latent trait associated with dying in independence after accounting for just age (see the second paragraph in Section 5.2.3).

Increased age and physical frailty (frail) are the two significant factors that reduce the chance of recovery from disability (Table 2, middle left panel). In sum, older age is associated with being in a disability state such that other risk factors would come into play (to increase the likelihood of death).

Being female is a significant protective factor for death for disabled persons (Table 2, middle right panel). Physical frailty is also a significant protective factor, together with the effects shown in the middle left panel, these findings indicate that a physically frail person may live with disability for a long time without dying or recovering. Increased number of previous state transitions (tran) also significantly reduces the likelihood of death with disability, indicating that the previous recoveries from disability as evidenced by many transitions seem to protect an ADL-disabled person from death. The opposite sign of frail:tran versus frail and tran on death has a similar interpretation as for the transition from ADL independence to disability.

5.2.2 Transition intensities

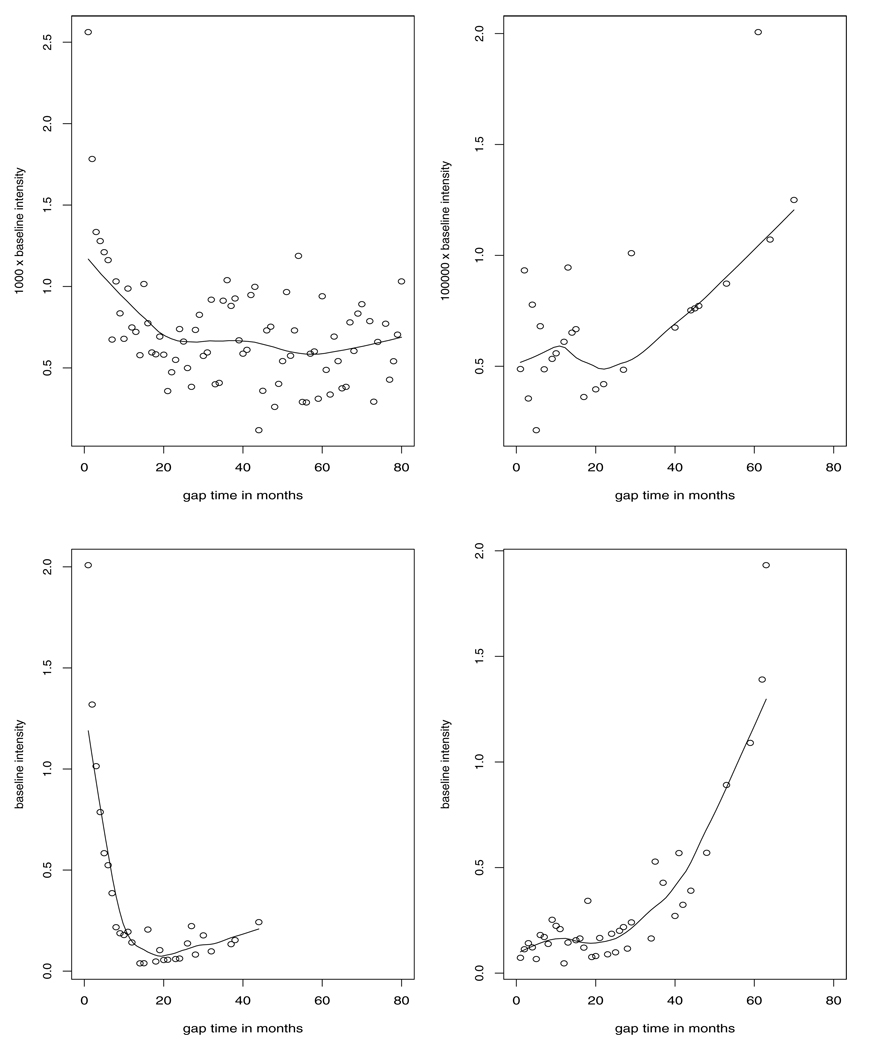
Scatter plots of the nonparametric estimates of and of the corresponding smoothed baseline intensities are shown in Figure 1. After recovery from ADL disability, the likelihood of transition back to disability among survivors significantly decreases during the first 20 months and then stabilizes (Figure 1, top left). During the first 10 months in disability state, the likelihood of recovery sharply decreases (Figure 1, bottom left). There is also an increased overall trend for death after an ADL transition (Figure 1, right panels). That is, the likelihood of death is relatively constant for the first 20 months in either the independence or disability state and then increases rapidly thereafter. The data suggest that prolonged sojourn in an independence state after 70 months will only result in transition to the disability state and death is unlikely to occur. After 45 months in a disability state, recovery is unlikely but the likelihood of death continues to increase. It is evident that the disability state is relatively unstable compared to the independence state because the overall intensities of recovery and of death are significantly greater than the transition intensities in the independence state, therefore the sojourn in the disability state is much shorter.

Figure 1.

Plots of the baseline intensities. Circles are nonparametric estimates of the baseline intensities. Lines are the loess-smoothed estimates. Top left: transition from ADL independence to disability, the scale of the intensity is amplified by 1000 times; top right: transition from ADL independence to death, the scale of the intensity is amplified by 100,000 times; bottom left: transition from ADL disability to independence; bottom right: transition from ADL disability to death.

5.2.3 Effects of the latent traits

Prediction of the latent traits, denoted by η̃_ik, for each individual is calculated as the conditional expectation of the latent traits given the individual’s observed data, that is, η̃_ik = E(η_ik|O_i…) in the last iteration of the EM algorithm.

Here a latent trait denotes the intrinsic individual tendency of transitioning out of a particular state (or sojourn in that state) that cannot be explained by the listed covariates in Table 2 and captures dependence between repeated sojourns in the same state within an individual. In our example, there exist significant individual effects on the transitions between the two ADL states because both latent traits for the independence state and the disability state are significant as judged by the significance of their variance components (Table 2, bottom panel). The significant covariance between the two latent traits means the likelihood of a transition from ADL independence to disability state is negatively correlated with the reverse transition. That is, an older person who tends to stay longer in an independence state (i.e., whose value of the latent trait 1 is smaller) will be more likely to recover (if s/he happens to be disabled), and one who tends to stay longer in a disability state (i.e., whose latent trait 2 value is smaller) will be more likely to transit from an independence state (if s/he happens to be in it) back to a disability state.

The loading for independence-state-specific latent trait 1 in terms of transition to the disability state is set to one. The estimated loading of latent trait 1 for transition to death, γ̂₁₃, is not significant (Table 2, bottom panel), indicating that the competing transitions from ADL independence to disability and to death are two independent events, that is, not associated after accounting for the covariates in the top and middle panels of Table 2. There is not any significant individual effect associated with death in independence beyond that of age (Table 2, top right panel). Thus, latent trait 1 can be interpreted as individual tendency for the transition to disability state without dying.

The loading for disability-state-specific latent trait 2 in terms of transition to independence (recovery) is set to one. The estimated loading for transition to death (dying in disability), γ̂₂₃, is highly significant (Table 2, bottom panel), indicating that recovery and dying in disability are two associated competing events even after accounting for the covariates and that there also exists individual tendency for dying in disability beyond what can be explained by the listed covariates. The positive sign of γ̂₂₃ indicates that the likelihood of recovery and of death is positively dependent, that is, the ADL disability state is highly dynamic in that an ADL-disabled older person either recovers or dies in a much shorter time period than the sojourn time in an independence state. Thus, latent trait 2 can be interpreted as an individual capacity to transit out of a disability state.

5.2.4 Empirical assessment of model assumptions

We are not aware of any formal testing or other methods of inference for assessing model assumptions for multivariate survival models with latent variables, so we focus on exploratory techniques to detect serious departures from model assumptions. We make use of measures that can be readily obtained during the usual computation for model fitting.

To empirically assess the conditional independence between two transition times of the same type from independence (disability) to disability (independence) state, predicted latent traits for individual i, η̃_i1(η̃_i2) is used as a covariate in fitting the usual time-to-event model. The gap times to disability (independence) state are treated as independent survival outcomes both within and between individuals and other covariates include those in X_ij12(X_ij21), and the sojourn time of the previous independence (disability) state. Only individuals with two or more independence (disability) states were included. The p-values of the Wald test for the coefficients associated with the previous sojourn time in the same state are 0.41 (0.88) for the independence (disability) state with the latent traits included and the p-values of the Wald test for the coefficients associated with previous sojourn time in same state are 0.035 (0.042) for independence (disability) state without including the latent traits. The results indicate that repeated visits in the same state are correlated and the latent traits successfully account for such correlation. Similar empirical assessment of conditional independence between transitions of different types was performed. The p-values of the Wald test for the coefficients associated with the sojourn time in the last state (of different type) are 0.20 (0.96) for the independence (disability) state with the latent traits included, and the p-values of the Wald test for the coefficients associated with sojourn time in the last state are 0.020 (0.094) for independence (disability) state without including the latent traits as covariates. The results indicate that repeated visits to different states are correlated and the latent traits successfully account for such correlation.

We are not aware of methods for checking the proportional hazards (PH) assumption in the presence of frailty or random effects and future work in this area is warranted. We assessed the PH assumption given the latent traits by using the predicted latent traits η̃_ik, X_ijkl and a vector of the interaction terms of log t × X_ijkl in fitting the independent model for the gap times of occurrence/recurrence of disability, of recovery, of death in independence, and of death in disability. The interaction terms between log t and X_ijkl are not significant except for age. We found that the interaction term between log t and age is significant for both directions of transitions between independence and disability and for death in an independence state. These results indicate that the PH assumption is met for all the covariates except for age. Schoenfeld residuals for age also indicate possible violation of the PH assumption. Although the effect of age needs to be further studied, its effect in the presence of nonproportionality can be interpreted as an average effect of age over time. Time-varying coefficients models for nonproportional covariates effects have been studied; however, these models have different fitting algorithms and were studied in the absence of frailty or latent variables (Marzec and Marzec 1997; Tian, Zucker, and Wei, 2005).

There is little work in the literature studying the impact of model departure from the normality assumption of the multivariate latent traits. Future work is needed for testing normality assumptions of latent traits. We choose to use multivariate normal latent traits due to the consideration that the independence and disability states may be negatively correlated, which is confirmed by the result from analyzing our ADL data.

6. Simulation Study

In this section, we examine the performance of the estimation procedure with respect to the bias and asymptotic standard error estimates under two settings that have different complexity in terms of covariates. Only one covariate for each type of transition is present in the first setting and the covariates in the second setting mimic those in our ADL data set described above. In each setting, the sample size is n = 752 and the number of replications is 100. For each subject, gap times for the two nonabsorbing, repeated states that mimic the independence and the disability state in the ADL data set are generated; gap time for one absorbing state is also generated after a transition of state. The gap times are generated from an exponential distribution with hazards of $c_{kl}\text{exp}\{{\mathbf{X}}_{ijkl}^{\mathrm{T}}{\beta }_{kl}+{\gamma }_{kl}{b}_{ik}\}$, where b_i = (b_i1, b_i2)^T are bivariate normal with mean 0 and variance matrix

$$\left(\begin{array}{cc}\hfill 0.16\hfill & \hfill -0.05\hfill \\ \hfill -0.05\hfill & \hfill 0.02\hfill \end{array}\right)$$

and the constant c_kl is used to adjust the overall transition rate from state k to l so that the rate is comparable with the corresponding transition rate in the original data.

In the first setting, a covariate X_ijkl was generated from a normal distribution with mean 78 and standard deviation 5 and used as a single fixed covariate for the mutual transitions between the two nonabsorbing states and the transition from the independence state to the absorbing state. For the transition from the disability state to the absorbing state, the single time-dependent covariate is the number of previous transitions. In the second setting, we use the baseline covariates corresponding to the ADL data set as X_i1kl(0). For an individual starting from ADL independence: (i) the gap time in months is designated as the minimum of the simulated time-to-disability state and time-to-death from the two exponential distributions with the covariates {X_ij1.} and β. that mimic those in the ADL data set and, (ii) if the individual does not die, at the transition of the state, the covariates are updated with the most recent covariate values in the ADL data set for the individual, and the gap time in the disability state is designated as the minimum of the simulated time-to-independent state and time-to-death from the two exponential distributions with the covariates {X_ij2.} and β₂. that mimic those in the ADL data set. (i) and (ii) are repeated until either death is encountered or the minimum of 84 cumulative months and a random normal variable representing administrative censoring with a mean of 77 months and a standard deviation of 10 months are reached.

Table 3 presents the findings from setting 1. If we assume the transitions are all independent without using the latent traits model, the estimates for the regression coefficients β_kl are all biased downward toward the null hypothesis. The estimated standard errors for the estimates are very close to the standard deviations of the estimates from the 100 Monte-Carlo-simulated data sets (the last three columns in Table 3). Using the joint analysis with the latent traits, we can see that the estimates for the regression coefficients β_kl are almost all unbiased but the standard deviations of the estimates from the 100 Monte-Carlo-simulated data sets are larger than those from the asymptotic calculation. The estimates for the variance components in G are biased downward in value and the estimates for the factor loadings γ_kl are biased upward probably to compensate for the downward bias of the estimated variance components in G. The Monte Carlo standard deviations for the estimates of the variance components are uniformly smaller than those from the asymptotic calculation. The Monte Carlo standard deviations for the estimates of the factor loadings remain larger than those from asymptotic calculation.

Table 3.

Results from simulation study under setting 1

		Joint analysisa			Separate analysisa
Type of parameterb	True value	Mean estimate	Sample SE	Mean Asy. SE	Mean estimate	Sample SE	Mean Asy. SE
β12	0.036	0.036	0.0048	0.0016	0.032	0.0068	0.0065
β13	0.075	0.075	0.024	0.0031	0.069	0.028	0.028
β21	−0.015	−0.015	0.0045	0.0035	−0.012	0.0067	0.0068
β23	−0.13	−0.11	0.074	0.074	−0.096	0.067	0.063
γ12	1	1	0	0
γ13	−0.5	−0.7	1.26	0.93
γ21	1	1	0	0
γ23	5.0	5.29	2.01	1.95
var(ηi1)	0.16	0.14	0.043	0.062
cov(ηi1, ηi2)	−0.05	−0.042	0.014	0.021
var(ηi2)	0.02	0.016	0.0053	0.0073

^aIn joint analysis, the variance components and the loadings of the latent traits are estimated. In separate analysis, each type of transition is estimated separately assuming no association and without using the latent traits. The “Sample SE” denotes the standard deviation of the parameter estimates from 100 simulated data sets and the “Mean Asy. SE” denotes the average of the asymptotic standard errors obtained from the 100 simulated data sets.

^bWe use k to index the state from which transition is made. We use l = 2 and 3 to denote the states of disability and death that can be transited to from state 1. We use l = 1 and 3 to denote the states of independence and death that can be transited to from state 2.

Table 4 presents the findings from setting 2 and shows similar results to those in setting 1 except that the Monte Carlo standard deviation for tran in β₂₁ is smaller than the corresponding asymptotic estimate. This smaller Monte Carlo standard deviation reflects the configuration of the covariate with respect to the event of the transition because the same is observed for the original data set (Table 2, middle left panel). The overall pattern of discrepancy in the estimated standard errors between the Monte Carlo estimates and the asymptotic calculation in the simulation follows the pattern of discrepancy between the bootstrap and the asymptotic estimates in the original data.

Table 4.

Results from simulation study under setting 2

Type of parameterb		True value	Mean estimate	Sample SEa	Mean Asy. SEa	Mean bootstrap SE
β12	Age	0.036	0.037	0.0060	0.0016	0.0062
	Tran	0.16	0.15	0.042	0.035	0.039
	Frail	0.90	0.87	0.190	0.120	0.190
	Frail:tran	−0.084	−0.081	0.039	0.020	0.040
	Alone	−0.26	−0.28	0.096	0.074	0.099
	Alone:tran	0.037	0.038	0.031	0.024	0.030
	Depress	0.28	0.25	0.094	0.053	0.095
β13	Age	0.075	0.075	0.020	0.003	0.019
β21	Age	−0.015	−0.015	0.0054	0.003	0.0056
	Tran	−0.012	−0.015	0.012	0.019	0.017
	Frail	−0.26	−0.27	0.17	0.14	0.17
β23	Frail	−0.81	−0.82	0.27	0.26	0.27
	Tran	−0.13	−0.12	0.066	0.066	0.069
	Frail:tran	0.12	0.13	0.057	0.057	0.062
	Sex	−0.81	−0.81	0.18	0.19	0.19
γ12		1	1	0	0	0
γ13		−0.5	−0.66	1.30	1.07	1.32
γ21		1	1	0	0	0
γ23		5.0	5.36	1.79	1.44	1.82
Variance	var(ηi1)	0.16	0.13	0.050	0.052	0.049
Components	cov(ηi1, ηi2)	−0.05	0.036	0.013	0.016	0.012
	var(ηi2)	0.02	0.015	0.006	0.008	0.006

^aThe “Sample SE” denotes the standard deviation of the parameter estimates from 100 simulated data sets and the “Mean Asy. SE” denotes the average of the asymptotic standard errors obtained from the 100 simulated data sets.

^bWe use k to index the state from which transition is made. We use l = 2 and 3 to denote the states of disability and death that can be transited to from state 1. We use l = 1 and 3 to denote the states of independence and death that can be transited to from state 2.

Using a similar approach to that of Hsieh et al. (2006), we also investigated whether the bootstrap method provides reliable estimates of standard errors for Ψ. Among the 100 simulated data sets under setting 2, we resampled 50 bootstrap samples from each single simulated data set. The mean of the 50 bootstrap standard error estimates for the parameters are given in the last column of Table 4. The result suggests that the bootstrap estimates of the standard error are quite reliable as they are close to the corresponding Monte Carlo standard deviations.

In summary, we found that the SPML estimates obtained with the EM algorithm are satisfactory for the regression parameters. The estimates for the variance components of the latent traits are underestimated in value. The Wald test for a variance component using the SPML estimate obtained via EM and the asymptotic estimate for the standard error of the estimate appears to be underpowered. The estimated standard errors from the asymptotic calculation are reliable for the independent multistate models without latent traits. For the latent trait model, the bootstrap estimates for the standard errors should be adopted.

7. Discussion

This article considered multistate data under heterogeneity. Using multivariate normal latent traits with loadings has a particular advantage when the sojourn times in different states may be negatively associated and/or when competing transitions to different states are dependent.

Because social behavior aspects are often difficult to capture with measured covariates, our example illustrates the utility of latent traits that are specific for certain correlated states of health. Another important aspect is that the meaning of a latent trait is not predetermined and the interpretation only becomes evident after fitting the model. This can be seen from the interpretation of the two latent traits in our ADL example in Section 5.2.3.

As in the case of gamma frailty models studied by Nielsen et al. (1992) and Barker and Henderson (2005), we also found that the SPML estimates using EM for the variance components of the latent traits are underestimated in value. The problem with such bias needs further research on the estimation procedure, that is, investigating whether the local likelihood approach described by Barker and Henderson (2005) could alleviate the bias. With respect to the estimated standard errors for Ψ, the asymptotic calculation works well for the model without latent traits. In the presence of latent traits, however, the bootstrap estimates for the standard errors should be adopted.

Regarding the ADL data set from the ongoing longitudinal aging study, it should be noted that the first independence state is left truncated because all the participants were in ADL independence at entry. Different intensities can be used for the first transition either by having different baseline intensities or by including additional covariates associated with the first transition. When we used a different baseline intensity for the first transition from the rest of the transitions from independence to disability state, the results were very similar to Table 2. The latent trait model we proposed can easily accommodate both of these situations and is applicable when the starting state, with possible left truncation, is different across study participants.

Limitations of our latent trait model include the lack of commercial software for fitting our model, and the intensive computation required to fit the model. The Matlab code for fitting our model can be obtained from the first author. With respect to estimating the standard errors, although the bootstrap method is advocated, a bootstrap estimate for a covariate effect may well be dependent upon the empirical configuration of the covariate among those who experienced the corresponding event outcome in the finite sample, and, therefore, is sometimes smaller than the asymptotic estimate. Further investigation into the relationship between the asymptotic and the bootstrap methods will be of much interest. Future work could also include developing approaches for simultaneously handling dropouts in the data, possibly relaxing the normality assumption for the latent traits, and investigating the utility of time-dependent latent traits.

APPENDIX A

Calculations in the EM Algorithm

We denote the conditional expectation in the (r + 1)th iteration of the EM algorithm as E^(r+1)(·|O_i…).

In the M-step, after taking the derivative of (2) with respect to λ_0kl(t) and setting the derivative to zero, the nonparametric estimate of λ_0kl(t) has a closed form that is given by

$$\begin{array}{c}{\lambda }_{0kl}^{(r+1)}(t)\hfill \\ =\frac{{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{J_{ik}}\mathrm{d}{N}_{ijkl}(t)}}}{{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{J_{ik}}{R}_{ijkl}(t)\text{exp}\{{\mathbf{X}}_{ijkl}^{\mathrm{T}}(t){\beta }_{kl}^{(r)}\}{\mathrm{E}}^{(r+1)}\{\text{exp}({\gamma }_{kl}^{(r)}{\eta }_{ik})|{\mathbf{O}}_{i\cdots }\}}}}.\hfill \end{array}$$

No closed-form solutions exist for β_kl and γ_kl. They can be updated in (r + 1)th iteration using the following one-step Newton–Raphson algorithm:

$$\begin{array}{cc}{\beta }_{kl}^{(r+1)}={\beta }_{kl}^{(r)}+I_C^{-1}({\beta }_{kl}^{(r)})S_C({\beta }_{kl}^{(r)})\hfill & \text{and}\hfill \\ {\gamma }_{kl}^{(r+1)}={\gamma }_{kl}^{(r)}+I_C^{-1}({\gamma }_{kl}^{(r)})S_C({\gamma }_{kl}^{(r)}),\hfill & \hfill \end{array}$$

where the complete-data scores $S_C({\beta }_{kl}^{(r)})$ and $S_C({\gamma }_{kl}^{(r)})$ are given respectively as

$$\begin{array}{c}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{J_{ik}}{\mathbf{X}}_{ijkl}{N}_{ijkl}(U_{ijk})-{\displaystyle {\int }_0^{\infty }{\lambda }_{0kl}^{(r+1)}}(t){\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{J_{ik}}{R}_{ijkl}(t){\mathbf{X}}_{ijkl}(t)}}}}\hfill \\ \times \text{exp}\{{\mathbf{X}}_{ijkl}^{\mathrm{T}}(t){\beta }_{kl}^{(r)}\}{\mathrm{E}}^{(r+1)}\{\text{exp}({\gamma }_{kl}^{(r)}{\eta }_{ik})|{\mathbf{O}}_{i\cdots }\}\mathrm{d}t,\hfill \\ {\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{J_{ik}}\mathrm{E}({\eta }_{ik}|{\mathbf{O}}_{i\cdots })N_{ijkl}(U_{ijk})-{\displaystyle {\int }_0^{\infty }{\lambda }_{0kl}^{(r+1)}(t)}}}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{J_{ik}}{R}_{ijkl}(t)}}\hfill \\ \times \text{exp}\{{\mathbf{X}}_{ijkl}^{\mathrm{T}}(t){\beta }_{kl}^{(r+1)}\}{\mathrm{E}}^{(r+1)}\{{\eta }_{ik}\text{exp}({\gamma }_{kl}^{(r)}{\eta }_{ik})|{\mathbf{O}}_{i\cdots }\}\mathrm{d}t.\hfill \end{array}$$

The complete-data informations $I_C({\beta }_{kl}^{(r)})$ and $I_C({\gamma }_{kl}^{(r)})$ are given respectively as

$$\begin{array}{c}{\displaystyle {\int }_0^{\infty }{\lambda }_{0kl}^{(r+1)}}(t){\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{J_{ik}}{R}_{ijkl}(t){\mathbf{X}}_{ijkl}(t){\mathbf{X}}_{ijkl}^{\mathrm{T}}(t)}}\hfill \\ \times \text{exp}\{{\mathbf{X}}_{ijkl}^{\mathrm{T}}(t){\beta }_{kl}^{(r)}\}{\mathrm{E}}^{(r+1)}\{\text{exp}({\gamma }_{kl}^{(r)}{\eta }_{ik})|{\mathbf{O}}_{i\cdots }\}\mathrm{d}t,\hfill \\ {\displaystyle {\int }_0^{\infty }{\lambda }_{0kl}^{(r+1)}}(t){\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{J_{ik}}{R}_{ijkl}(t)\text{exp}\{{\mathbf{X}}_{ijkl}^{\mathrm{T}}(t){\beta }_{kl}^{(r+1)}}\}{\mathrm{E}}^{(r+1)}}\hfill \\ \times \{{\eta }_{ik}^2\text{exp}({\gamma }_{kl}^{(r)}{\eta }_{ik})|{\mathbf{O}}_{i\cdots }\}\mathrm{d}t.\hfill \end{array}$$

The updated G estimate in the (r + 1)th iteration of the EM is given as

$${\mathbf{G}}^{(r+1)}={\displaystyle \sum _{i=1}^n{\mathrm{E}}^{(r+1)}}({\mathit{\eta }}_i{\mathit{\eta }}_i^{\mathrm{T}}|{\mathbf{O}}_{i\cdots })/n.$$