Abstract
Intussusceptive angiogenesis is a process that forms new blood vessels by the intraluminal division of a single blood vessel into two lumens. Referred to as nonsprouting or intussusceptive angiogenesis, this angiogenic process has been described in morphogenesis and chronic inflammation. Mechanical forces are relevant to the structural changes associated with intussusceptive angiogenesis because of the growing evidence that physiologic forces influence gene transcription. To provide a detailed analysis of the spatial distribution of physiologic shear stresses, we developed a 3D finite element model of the intraluminal intussusceptive pillar. Based on geometries observed in adult intussusceptive angiogenesis, physiologic shear stress distribution was studied at pillar sizes ranging from 1μm to 10μm. The wall shear stress calculations demonstrated a marked spatial dependence with discrete regions of high shear stress on the intraluminal pillar and lateral vessel wall. Further, the intussusceptive pillar created a “dead zone” of low wall shear stress between the pillar and vessel bifurcation apex. We conclude that the intraluminal flow fields demonstrate sufficient spatial resolution and dynamic range to participate in the regulation of intussusceptive angiogenesis by intraluminal flow fields.
Introduction
Angiogenesis is a physiologic process that produces new blood vessels from pre-existing vessels. This process is essential in normal growth and development as well as in the repair and regeneration of injured tissue. The most commonly recognized form of angiogenesis occurs as the result of new vessels “sprouting” from pre-existing vessels (Folkman and D’Amore, 1996). In addition, there is an angiogenic process that forms new blood vessels by the intraluminal division of a single blood vessels into two vessels (Djonov et al., 2003; Patan et al., 1996). Referred to as nonsprouting or intussusceptive angiogenesis, this angiogenic process has been previously described in morphogenesis (Burri and Djonov, 2002). Recently, intussusceptive angiogenesis has been described in adult inflammation (Konerding et al., 2009).
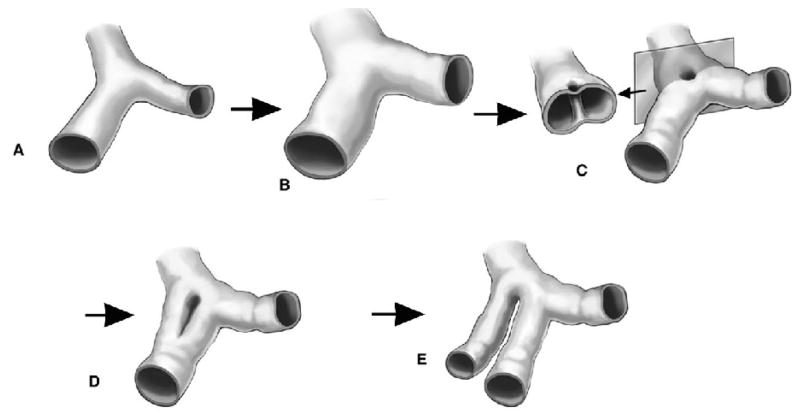
Attempts to understand intussusceptive angiogenesis have focused on the morphologic features of the process. The process of intussusceptive angiogenesis begins with the development of a transluminal “pillar” (Figure 1). In the chorioallantoic membrane model, the intussusceptive pillar is a cylindrical column or post that appears as a “hole” in luminal corrosion casts (Burri and Tarek, 1990; Caduff et al., 1986). As the process evolves, the intussusceptive pillar expands down the lumen of the blood vessel. Within hours to days, this process of luminal division results in the development of two blood vessels from a single lumen (Djonov et al., 2003).
Figure 1.
Schematic of the process of intussusceptive angiogenesis. After dilatation of the vessel (B), intraluminal pillars form at vessel bifurcations (C). Extensions of the pillars down the vessel axis (D) produce a replicated vessel (E).
Although it is theoretically possible that intussusceptive angiogenesis reflects a pure developmental program, increasing evidence suggests that the process involves physiologic shear stresses within the vessel lumen. The chick chorioallantoic membrane is composed of three layers of which the central layer is the capillary plexus or blood sinus (Breier, 2000; Wilting and Christ, 1996). The development of the capillary plexus between incubation day 7 and 12 is associated with a striking increase in size, blood flow and blood pressure (Mulder et al., 1998; Ruijtenbeek et al., 2002). Coincident with these increases in volumetric flow, the chick chorioallantoic membrane develops pillars that mark the onset of intussusceptive angiogenesis (Patan et al., 1996). Similarly, adult murine colitis demonstrates significant changes in mucosal plexus blood flow within a week of the onset of inflammation (Miele et al., 2009; Ravnic et al., 2007; Tsuda et al., 2008; Turhan et al., 2007). It is this period of perturbed blood flow that precedes the development of intussusceptive pillars.
Intraluminal blood flow is relevant to the structural changes associated with intussusceptive angiogenesis because of the growing evidence that physiologic forces influence gene transcription. To provide a detailed analysis of the spatial distribution of physiologic forces, we developed a 3D computational model of the intraluminal intussusceptive pillar. Analysis of multiple pillar diameters indicated that the distribution of forces within the vessel bifurcation provided sufficient spatial information to potentially regulate the process of pillar extension and intussusceptive angiogenesis.
Methods
Mice
Balb/c mice (Jackson Laboratory, Bar Harbor, ME), 25–33g, were used in all experiments. The care of the animals was consistent with guidelines of the American Association for Accreditation of Laboratory Animal Care (Bethesda, MD).
Trinitrobenzenesulfonic acid administration
The 2,4,6- Trinitrobenzenesulfonic acid (TNBS) (Sigma, St.Louis, MO) model of colitis was similar to that described previously (Ravnic et al., 2007). After the mouse abdomen was sheared and cleansed with water, 36ul of a 2.5% 2,4,6- Trinitrochlorobenzene (TNCB)(ChemArt, Egling, Germany) in a 4:1 acetone:olive oil solution was sprayed onto a 1.5cm diameter circular PhastTansfer Filter Paper (Pharmacia, Upsala, Sweden). The TNCB soaked filter paper was applied to the sheared abdomen and secured with Tegaderm (3M, St.Paul, MN) and Durapore Surgical Tape (3M, St.Paul, MN). The TNCB patch was removed 24 hours after application. On post-sensitization day six, 125ul of 1.75% TNBS in a 50% ethanol solution was instilled into the rectum. Control mice had only the 50% ethanol solution instilled intrarectally. Acute colitis was defined as 5 to 7 days after TNBS exposure.
Scanning electron microscopy
After systemic heparinization, PBS perfusion and intravascular fixation with 2.5% buffered glutaraldehyde, the systemic circulation was perfused with 10–20ml of Mercox (SPI, West Chester, PA) diluted with 20% methyl methacrylate monomers (Aldrich Chemical, Milwaukee, WI) as described previously (Ravnic et al., 2006). After complete polymerization, the tissues were harvested and macerated in 5% potassium hydroxide followed by drying and mounting for scanning electron microscopy. The microvascular corrosion casts were imaged after coating with gold in an argon atmosphere with a Philips ESEM XL30 scanning electron microscope (Eindhoven, Netherlands). In some mice, stereo-pair images were obtained using a tilt angle of 6 degrees. The quality of the filling of the corrosion casts was also checked by comparisons with the vascular densities in semithin light microscopic sections stained with methylene blue. The corrosion casts demonstrated filling of the whole capillary bed from artery to vein without evidence of extravasation or pressure distension.
Morphometry and image analysis
Corrosion casts of the mucosal plexus of the mouse colon have been previously described in detail (Ravnic et al., 2005; Ravnic et al., 2007). Images were processesed with the MetaMorph Imaging System 7.5 software (Molecular Devices, Brandywine, PA). The 14-bit grayscale images were thresholded and SEM-derived distance calibration was applied. The MetaMorph’s region measurements and caliper applications were used to measure the vessel dimensions and estimate pillar diameter. The data was logged into Microsoft Excel 2003 (Redmond WA) by dynamic data exchange.
Computational flow dynamics
The development of the numerical model was developed using custom code using the C++ object oriented programming language and OpenGL graphic library (Filipovic et al., 2003; Kojic et al., 2008a; Kojic et al., 2008b). The custom code was used because of convenience and efficiency; comparable flow modeling is available commercially. The finite element mesh was constructed as a vessel bifurcation. Although vessel diameters were selectable, the current experiments used a vessel diameter of 20μm to facilitate experimental manipulations of pillar size. To reflect the pillar dimensions observed in vivo, the pillar diameters in the computational model were 1μm, 5μm and 10μm. The computational algorithm was designed to ensure a smooth transition from the proximal tube to the distal limbs. The mesh of the luminal pillar was generated by projecting a circle of prescribed radius in the 2D XY plane. Consistent with corrosion cast observations, the centroid of the pillar was placed in the geometric center of the bifurcation. The continuous nonpulsatile flow used in this model reflected previous intravital microscopy observations (Ravnic et al., 2007; Turhan et al., 2007).
Spatial statistics
Selected bifurcations in the mucosal plexus of the mouse colon were identified using corrosion casts and distance calibrated images were obtained. The images were superimposed based on the geometric center of the bifurcations. The 14-bit grayscale images were converted to a numerical matrix and arithmetically combined. The 2-dimensional contour limits reflected the 95% confidence limits of the combined data was plotted in Origin 7.5 (www.originlab.com) and used for modeling geometries. Morphometry analysis was based on measurements in at least three different mice.
Results
Pillar geometry
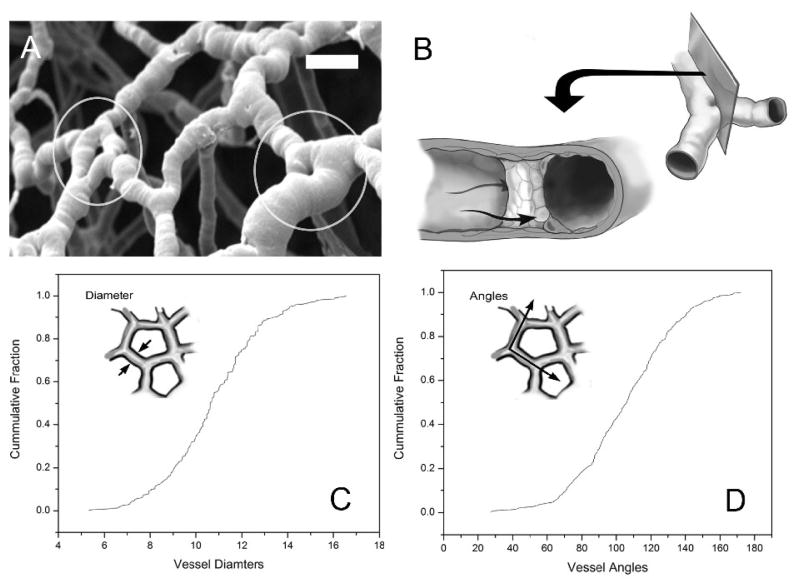
The geometry of the vessel bifurcation model was addressed by statistically extracting essential geometric features of vessel bifurcations from detailed morphologic measurements of the murine mucosal plexus (Figure 2). Casts of the mucosal plexus demonstrated small holes close to the geometric center of the vessel bifurcations. Consistent with the morphology of intussusceptive pillars, the location of the pillars within the corrosion casts precluded absolute (tilt-angle) morphometry; nonetheless, surface features demonstrated pillar diameters 21±18% of the axial vessel diameter (N=36 pillars; N=3 mice). These geometric measurements were used for the subsequent development of the computational model.
Figure 2.
Structure of the intussceptive pillar based on vessel structure in vivo. A) Scanning electron microscopy of corrosion casts of the mucosal plexus microcirculation. Because of the intraluminal cast formed by the injected polymer, the pillars appear as filling defects (circles) (bar=25μm). B) Schematic diagram of the pillar within the flow stream. Quantitative morphometry of the mucosal plexus microcirculation demonstrating microvessel diameter (C) and branch angles (D).
Finite element mesh of vessel bifurcation
To develop a finite element mesh of the vessel bifurcation, a simplified model was constructed with three tubes of the same diameter D (current calculation, D=20μm), smoothly connected with equal angles θ and radius of curvature R, and developed with and without the intussusceptive pillar (Figure 3). The pillar-wall interface required curved distortion of the mesh to match the morphology of the corrosion casts.
Figure 3.
Finite element mesh of bifurcation pillar. Based on a 3D spatial coordinate system, the model was constructed of 3 tubes of the same diameter that were smoothly connected with equal angles θ and radius of curvature R.
Flow solver
The modeling was performed using a continuum approach. Governed by the Navier-Stokes equations and the continuity equation, the three-dimensional flow of a viscous incompressible fluid was expressed:
| (1) |
| (2) |
where vi was the blood velocity in direction xi, ρ was the fluid density (1.05 g/cm3), and p was pressure, μ was the dynamic viscosity (0.03675g/cm/sec). Summation was assumed on the repeated (dummy) indices, i,j=1,2,3. Equation (1) represented the balance of linear momentum, while equation (2) expressed the incompressibility condition. The code was validated using the analytical solution for shear stress and velocities through a straight expanding tube (Filipovic et al., 2003).
Boundary conditions
A parabolic velocity profile was prescribed for all calculations at the inlet of the proximal vessel; the inlet was more than 10 diameters away from the bifurcation region. A zero free traction boundary condition was kept at the outlet sections of distal limbs. This assumption was based on a steady flow condition and the parabolic velocity profile at the outlet cross-section. Reynolds number (Re) was defined as
| (3) |
where V̄ was the mean velocity of the prescribed inlet parabolic velocity profile, D=20μm was the vessel diameter (both proximal and distal limbs) and ν =0.035 cm2/s was the kinematic viscosity for the blood and Re was less than 1.0 (Secomb et al., 2003).
Velocity and shear stress maps
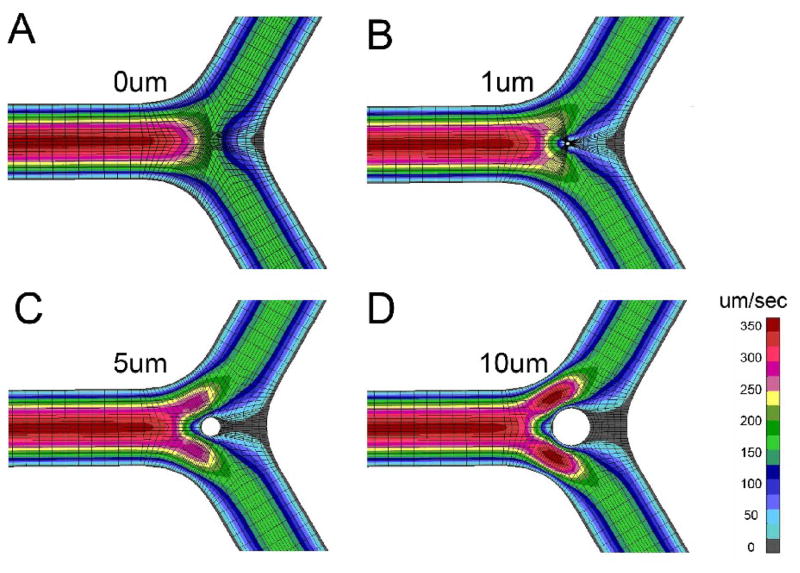
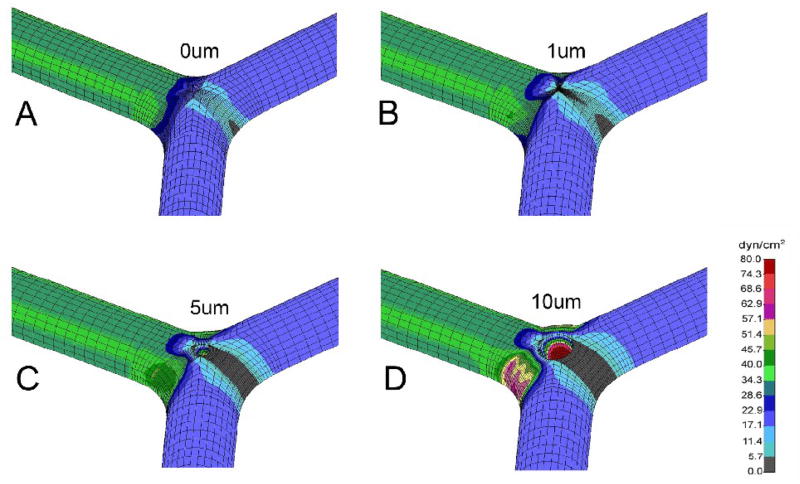
Velocity profiles demonstrated the most significant changes within the bifurcation; specifically, around the pillar surface and along the lateral wall of the bifurcation (Figure 4). The shear stress map reflected these effects with focal high shear regions at the mid-portion of the pillar and on the lateral vessel wall (Figure 5).
Figure 4.
Maps of velocity isolines in the mid-plane of the vessel are shown for control (A) and pillar sizes of 1μm (B), 5μm (C), and 10μm (D) diameter.
Figure 5.
Wall shear stress maps of the vesselsl are shown for symmetric flow conditions. The shear maps are shown for control (A) and pillar sizes of 1μm (B), 5μm (C), and 10μm (D) diameter.
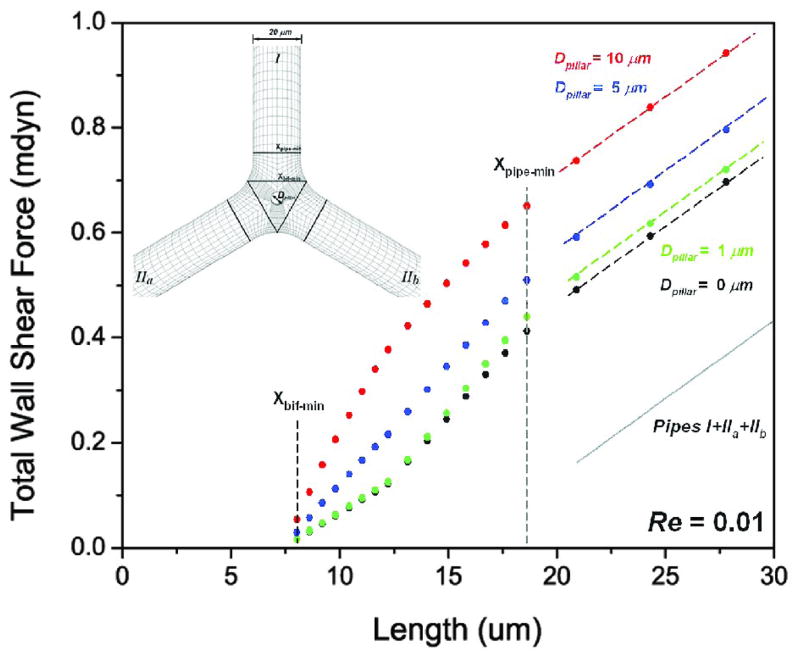
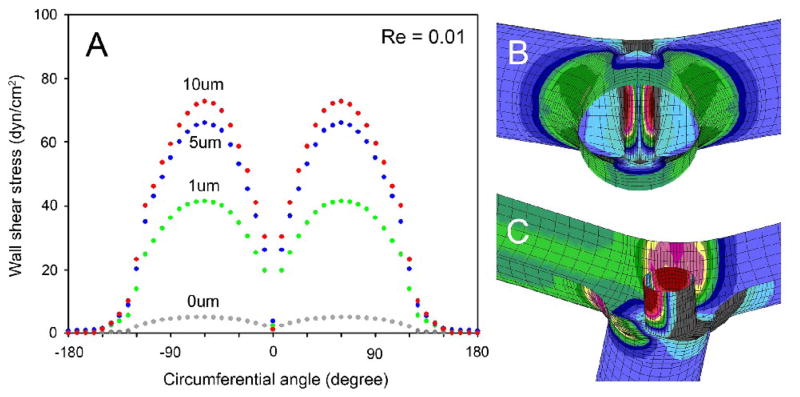
The pillar surface demonstrated two spatial shear stress gradients (Figure 6). The first gradient was along the longitudinal axis of the pillar. Relatively low wall shear stress was mapped at the interface between the pillar and the vessel wall (Figure 6B,C). The shear rates at the pillar-wall interface were largely unresponsive to geometric variation (mesh distortion; not shown). Higher shear stresses were mapped to the midpoint of the pillar. The second gradient was mapped on the circumference of the pillar. Assuming the centerline of the flow stream at 0 degrees, the wall shear stress was low at 0 degrees (front of pillar) and maximal at 60 degrees of the pillar circumference. Of note, a “dead zone,” defined as wall shear stress <3dyn/cm2, was located between the pillar and the bifurcation apex (180 degrees from the flow stream).
Figure 6.
The spatial distribution of wall shear stress on the circumferential surface of the intraluminal pillar at the vessel midplane. A) The vessel centerline was designated as 0 degrees (B). The distribution of pillar wall shear stress from the midplane of the vessel to the vessel wall is also shown (C). Re=0.01.
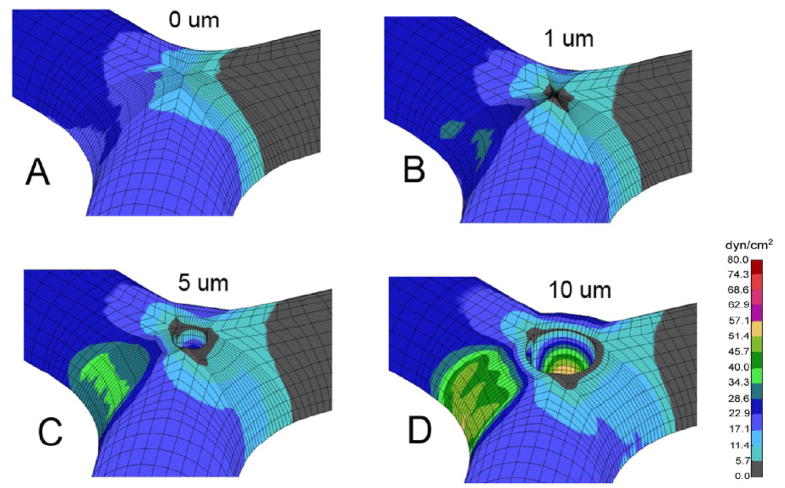
Flow perturbations associated with intussusceptive angiogenesis—such as inflammation-associated segmental flow occlusion (Miele et al., 2009)—were also analyzed. Occlusion of one limb of the bifurcatiuon resulted in asymmetry of the wall shear stress distribution (Figure 7). In particular, high shear stress mapped to the contralateral vessel wall. In addition, the low shear zone shifted toward the axis of the patent vessel. The re-orientation of the low shear areas toward the patent vessel centerline was reminiscent of pillar extension observed in advanced intussusceptive angiogenesis (Figure 8A–C). A comparison of symmetric and asymmetric flow fields (Figulre 8D–E) suggests that intraluminal flow fields provide a potential mechanism for shaping septal extension in intussusceptive angiogenesis.
Figure 7.
Wall shear stress maps of the vessel after occlusion of single limb of the bifurcation. The shear maps are shown for control (A) and pillar sizes of 1μm (B), 5μm (C), and 10μm (D) diameter.
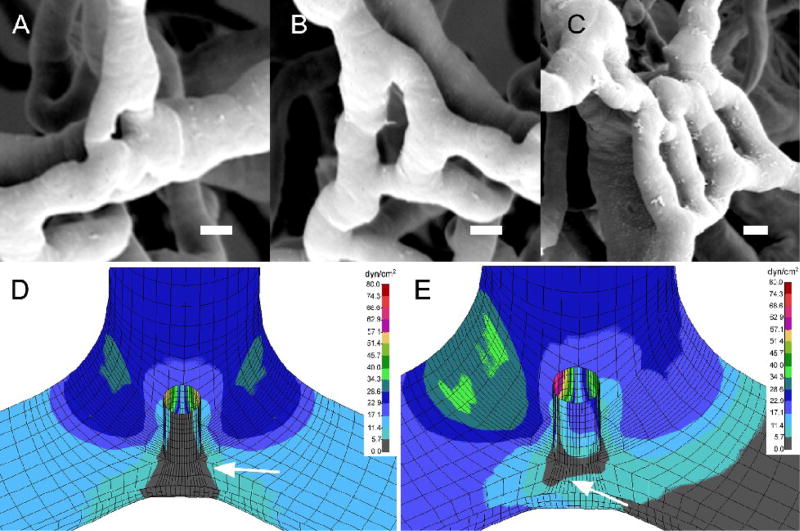
Figure 8.
Potential role of flow dynamics in shaping the process of intussusceptive angiogenesis. A–C) Corrosion casting and scanning electron microscopy of the inflammatory colon mucosal plexus at various stages of intussusceptive angiogenesis. The intussusceptive pillar (A) expands to form a septum (B). In some cases, multiple parallel lumens can form (C). Although the spatial distribution of shear stress in symmetric flow (D) suggests the likelihood of vessel angle remodeling (arrow, gray=low shear), the occlusion of one limb of the bifurcation (E) results in re-orientation of the low shear zone toward the vessel axis (arrow, gray=low shear). A–C) Bar=5um; D–E) shear map is shown in dyn/cm2.
Discussion
In this report, we developed a finite element computational flow dynamics simulation of the pillar phase of intussusceptive angiogenesis. Based on geometries observed in adult intussusceptive angiogenesis, physiologic shear stress distribution was studied at pillar sizes ranging from 1μm to 10μm. The wall shear stress calculations demonstrated a marked spatial dependence with discrete regions of high shear stress on the intraluminal pillar and lateral vessel wall. Further, the intussusceptive pillar created a “dead zone” of low wall shear stress between the pillar and vessel bifurcation apex. Vessel occlusion resulted in a reorientation of the low shear zone toward the patent vessel axis. We conclude that the spatial resolution and dynamic range of these forces are consistent with intraluminal flow field participation in the process of intussusceptive angiogenesis.
A contribution of our study was the development of a 3-dimensional finite element model based on in vivo vessel geometry; that is, we extracted the essential structural features of vessels undergoing intussusceptive angiogenesis in vivo. Previous attempts at computational flow modeling of intussusceptive angiogenesis have focused on the larger-scale network implications of the process. Although limited to the network scale, these 2-dimensional models have suggested the importance of flow-driven remodeling (Godde and Kurz, 2001; Szczerba and Szekely, 2005). To investigate the implications of these findings on a smaller scale, we used the specialized structural methods of corrosion casting and scanning electron microscopy. SEM was necessary because the intussusceptive pilar is too small to be visualized by standard light microscopy (Burri et al., 2004). Further, tilt-angle SEM provided accurate quantitative morphometry of the vessel bifurcation for the construction of the 3-dimensional finite element model (Konerding et al., 2001; Malkusch et al., 1995).
Although our treatment of the blood as a Newtonian fluid discounted the mechanical effects of blood cells, we have chosen this computational approach for two reasons. First, the blood cell concentrations in two models of intussusceptive angiogenesis--the chorioallantoic membrane and chronic colitis models--are strikingly different. Intussusceptive angiogenesis occurs with a normal blood concentration in the murine model, but in the presence of a lower concentration of blood cells in the chorioallantoic membrane model. This observation suggests that the process is relatively insensitive to blood cell concentration. Second, the alternative to continuum modeling is a discretized approach such as discrete particle dynamics (DPD) (Filipovic et al., 2008a; Filipovic et al., 2008b; Haber et al., 2006). We have successfully applied DPD to the analysis of blood components in a parallel-plate flow chamber (Filipovic et al., 2008c); however, the computational demands of this promising technique currently preclude its application to the complex geometry of intussusceptive angiogenesis. Despite the theoretical limitations of a continuum approach, we suspect that our computational model closely approximates the distribution of forces in vivo and will provide useful insights into intravascular flow regulation.
A potential limitation of our study is the focus on a divergent flow stream. The predominance of viscous forces (low Reynold’s number flow) in most mucosal plexus vessels suggests reversibility; that is, the wall shear stress should be the same regardless of the direction of flow. Nonetheless, subtle differences in convergent and divergent flow streams may exist in vivo. Future in vivo studies should evaluate the potential differences between convergent and divergent flows in regulating the process of intussusceptive angiogenesis.
Mapping the distribution of physiologic shear stresses in the process of intussusceptive angiogenesis is relevant to the growing evidence that vascular lining cells respond to mechanical factors such as fluid shear stress. Mechanical stresses acting on the luminal surface of the vessel wall include the shear stress produced by flow. The pattern of these shear stresses are different between straight, branched and curved regions of the vascular tree (Chien, 2003; Colangelo et al., 1994; Karino and Goldsmith, 1980; Karino et al., 1987; Nerem, 1993). Here, we demonstrate another pattern of shear stress distribution created by the intussusceptive pillar.
The shear stress acting on the luminal endothelial cells activate a variety of mechanosensors (Labrador et al., 2003). Membrane molecules include receptor tyrosine kinases (Chen et al., 1999; Wang et al., 2002), integrins (Jalali et al., 2001; Schwartz, 2001), ion channels (Olesen et al., 1988; Yamamoto et al., 2006), G protein receptors (Kuchan et al., 1994) and even lipids (Haidekker et al., 2000). These mechanosensors trigger signaling pathways that activate multiple genes associated with cell growth and proliferation (Ingber, 2006; Resnick et al., 2003). In vitro studies using cultured endothelial cells suggest that gene expression is sensitive to both the pattern and duration of shearing (Chien, 2007). While an integrated understanding of gene expression remains elusive, flow regulation of gene expression is an indication that structural adaptations such as intussusceptive angiogenesis are responsive to intraluminal flow fields. Similarly, our model provides an illustration of the spatial resolution of shear stress gradients in intussusceptive angiogenesis. We speculate that these mechanical forces play an important role in structural adaptation.
To illustrate a potential mechanism of flow regulation, it is conceivable that the extension of the luminal pillar is limited to low shear regions. In symmetric flows, the pillar would extend through the low shear “dead zone” to the bifurcation apex to produce vessel angle remodeling. In contrast, asymmetric flows, associated with the inflammation-induced occlusion of one limb of the bifurcation would produce pillar extension down the axis of the patent limb. Pillar extension down the vessel axis would reflect the vessel replication observed in intussusceptive angiogenesis. The recent description of microvascular flow perturbations spatially associated platelet aggregates suggests that such occlusion does occur in vivo (Miele et al., in press). The association of pillar extension with low shear stress “dead zones” suggests that the intial endothelial actvation is triggered by extraluminal events; for example, inflammatory mediators in chronic colitis and growth signals in the chorioallantoic membrane model. We suspect that the intravascular flow fields may not be sufficient to initiate pillar formation, but are necessary to shape pillar extension. Further, intravascular flow fields provide a mechanism of local feedback control.
Finally, our model also illustrates a unique feature of flow fields within a bifurcation containing an intraluminal pillar. In addition to providing a low resistance region for pillar extension, the “dead zone” is an area with microhemodynamic conditions suitable for cell-cell interactions. Experiments performed in PDMS microchannels suggest that the intraluminal pillar may increase residence time and wall contact time within the bifurcation (Turhan et al., 2008). These observations suggest that the structural features of intussusceptive angiogenesis, combined with the changing micro-hemodynamic conditions, may contribute to cell transmigration and perivascular inflammation.
Acknowledgments
Supported in part by NIH Grants HL47078, HL75426, HL054885, HL074022 and HL070542
Abbreviations
- 2D
2-dimensional
- 3D
3- dimensional
- DPD
discrete particle dynamics
- PBS
phosphate buffered saline
- PDMS
poly-dimethyl siloxane
- SEM
scanning electron microscopy
- TNBS
Trinitrobenzenesulfonic acid
- TNCB
Trinitrochlorobenzene
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Breier G. Angiogenesis in embryonic development--a review. Placenta. 2000;21(Suppl A):S11–5. doi: 10.1053/plac.1999.0525. [DOI] [PubMed] [Google Scholar]
- Burri PH, Djonov V. Intussusceptive angiogenesis--the alternative to capillary sprouting. Mol Aspects Med. 2002;23:S1–27. doi: 10.1016/s0098-2997(02)00096-1. [DOI] [PubMed] [Google Scholar]
- Burri PH, et al. Intussusceptive angiogenesis: its emergence, its characteristics, and its significance. Dev Dyn. 2004;231:474–88. doi: 10.1002/dvdy.20184. [DOI] [PubMed] [Google Scholar]
- Burri PH, Tarek MR. A novel mechanism of capillary growth in the rat pulmonary microcirculation. Anat Rec. 1990;228:35–45. doi: 10.1002/ar.1092280107. [DOI] [PubMed] [Google Scholar]
- Caduff JH, et al. Scanning electron microscope study of the developing microvasculature in the postnatal rat lung. Anat Rec. 1986;216:154–64. doi: 10.1002/ar.1092160207. [DOI] [PubMed] [Google Scholar]
- Chen KD, et al. Mechanotransduction in response to shear stress. Roles of receptor tyrosine kinases, integrins, and Shc. J Biol Chem. 1999;274:18393–400. doi: 10.1074/jbc.274.26.18393. [DOI] [PubMed] [Google Scholar]
- Chien S. Molecular and mechanical bases of focal lipid accumulation in arterial wall. Prog Biophys Mol Biol. 2003;83:131–51. doi: 10.1016/s0079-6107(03)00053-1. [DOI] [PubMed] [Google Scholar]
- Chien S. Mechanotransduction and endothelial cell homeostasis: the wisdom of the cell. Am J Physiol Heart Circ Physiol. 2007;292:H1209–24. doi: 10.1152/ajpheart.01047.2006. [DOI] [PubMed] [Google Scholar]
- Colangelo S, et al. Three patterns of distribution characterize the organization of endothelial microfilaments at aortic flow dividers. Cell Tissue Res. 1994;278:235–42. doi: 10.1007/BF00414165. [DOI] [PubMed] [Google Scholar]
- Djonov V, et al. Vascular remodeling by intussusceptive angiogenesis. Cell Tissue Res. 2003;314:107–17. doi: 10.1007/s00441-003-0784-3. [DOI] [PubMed] [Google Scholar]
- Filipovic N, et al. Dissipative particle dynamics simulation of flow generated by two rotating concentric cylinders: II. Lateral dissipative and random forces. J Phys D: Appl Phys. 2008a;41 doi: 10.1103/PhysRevE.74.046701. In press. [DOI] [PubMed] [Google Scholar]
- Filipovic N, et al. Modelling thrombosis using dissipative particle dynamics method. Philosophical Transactions of the Royal Society a-Mathematical Physical and Engineering Sciences. 2008b;366:3265–3279. doi: 10.1098/rsta.2008.0097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Filipovic N, et al. Interactions of blood cell constituents: experimental investigation and computational modeling by discrete particle dynamics algorithm. Microvasc Res. 2008c;75:279–84. doi: 10.1016/j.mvr.2007.09.007. [DOI] [PubMed] [Google Scholar]
- Filipovic ND, et al. An implicit algorithm within the arbitrary Lagrangian-Eulerian formulation for solving incompressible fluid flow with large boundary motions. Comp Meth Appl Mech Engng. 2003;195:6347–6361. [Google Scholar]
- Folkman J, D’Amore PA. Blood vessel formation: what is its molecular basis? Cell. 1996;87:1153–5. doi: 10.1016/s0092-8674(00)81810-3. [DOI] [PubMed] [Google Scholar]
- Godde R, Kurz H. Structural and biophysical simulation of angiogenesis and vascular remodeling. Dev Dyn. 2001;220:387–401. doi: 10.1002/dvdy.1118. [DOI] [PubMed] [Google Scholar]
- Haber S, et al. Dissipative particle dynamics simulation of flow generated by two rotating concentric cylinders. Part I: Boundary conditions. Phys Rev E. 2006 doi: 10.1103/PhysRevE.74.046701. In press. [DOI] [PubMed] [Google Scholar]
- Haidekker MA, et al. Fluid shear stress increases membrane fluidity in endothelial cells: a study with DCVJ fluorescence. Am J Physiol Heart Circ Physiol. 2000;278:H1401–6. doi: 10.1152/ajpheart.2000.278.4.H1401. [DOI] [PubMed] [Google Scholar]
- Ingber DE. Cellular mechanotransduction: putting all the pieces together again. Faseb J. 2006;20:811–27. doi: 10.1096/fj.05-5424rev. [DOI] [PubMed] [Google Scholar]
- Jalali S, et al. Integrin-mediated mechanotransduction requires its dynamic interaction with specific extracellular matrix (ECM) ligands. Proc Natl Acad Sci U S A. 2001;98:1042–6. doi: 10.1073/pnas.031562998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karino T, Goldsmith HL. Disturbed flow in models of branching vessels. Trans Am Soc Artif Intern Organs. 1980;26:500–6. [PubMed] [Google Scholar]
- Karino T, et al. Flow patterns in vessels of simple and complex geometries. Ann N Y Acad Sci. 1987;516:422–41. doi: 10.1111/j.1749-6632.1987.tb33063.x. [DOI] [PubMed] [Google Scholar]
- Kojic M, et al. Computer modeling in bioengineering: Th oretical Background, Examples and Software. John Wiley and Sons; Chichester, England: 2008a. [Google Scholar]
- Kojic M, et al. A mesoscopic bridging scale method for fluids and coupling dissipative particle dynamics with continuum finite element method. Computer Methods in Applied Mechanics and Engineering. 2008b;197:821–833. doi: 10.1016/j.cma.2007.09.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Konerding MA, et al. 3D microvascular architecture of pre-cancerous lesions and invasive carcinomas of the colon. Br J Cancer. 2001;84:1354–62. doi: 10.1054/bjoc.2001.1809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Konerding MA, et al. Intussusceptive angiogenic replication of the mucosal plexus in murine colitis. 2009. Submitted. In review. [Google Scholar]
- Kuchan MJ, et al. Role of G proteins in shear stress-mediated nitric oxide production by endothelial cells. Am J Physiol. 1994;267:C753–8. doi: 10.1152/ajpcell.1994.267.3.C753. [DOI] [PubMed] [Google Scholar]
- Labrador V, et al. Interactions of mechanotransduction pathways. Biorheology. 2003;40:47–52. [PubMed] [Google Scholar]
- Malkusch W, et al. A simple and accurate method for 3-D measurements in microcorrosion casts illustrated with tumour vascularization. Anal Cell Pathol. 1995;9:69–81. [PubMed] [Google Scholar]
- Miele LF, et al. Blood flow patterns spatially associated with platelet aggregates in murine colitis. Anat Rec. 2009 doi: 10.1002/ar.20954. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mulder AL, et al. Cardiac output distribution in response to hypoxia in the chick embryo in the second half of the incubation time. J Physiol. 1998;508(Pt 1):281–7. doi: 10.1111/j.1469-7793.1998.281br.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nerem RM. Hemodynamics and the vascular endothelium. J Biomech Eng. 1993;115:510–4. doi: 10.1115/1.2895532. [DOI] [PubMed] [Google Scholar]
- Olesen SP, et al. Haemodynamic shear stress activates a K+ current in vascular endothelial cells. Nature. 1988;331:168–70. doi: 10.1038/331168a0. [DOI] [PubMed] [Google Scholar]
- Patan S, et al. Implementation of intussusceptive microvascular growth in the chicken chorioallantoic membrane (CAM): 1. pillar formation by folding of the capillary wall. Microvasc Res. 1996;51:80–98. doi: 10.1006/mvre.1996.0009. [DOI] [PubMed] [Google Scholar]
- Ravnic DJ, et al. Vessel painting of the microcirculation using fluorescent lipophilic tracers. Microvasc Res. 2005;70:90–96. doi: 10.1016/j.mvr.2005.06.002. [DOI] [PubMed] [Google Scholar]
- Ravnic DJ, et al. Inflammation-responsive focal constrictors in the mouse ear microcirculation. J Anat. 2006;209:807–816. doi: 10.1111/j.1469-7580.2006.00656.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ravnic DJ, et al. Structural adaptations in the murine colon microcirculation associated with hapten-induced inflammation. Gut. 2007;56:518–523. doi: 10.1136/gut.2006.101824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Resnick N, et al. Fluid shear stress and the vascular endothelium: for better and for worse. Prog Biophys Mol Biol. 2003;81:177–99. doi: 10.1016/s0079-6107(02)00052-4. [DOI] [PubMed] [Google Scholar]
- Ruijtenbeek K, et al. The chicken embryo in developmental physiology of the cardiovascular system: a traditional model with new possibilities. Am J Physiol Regul Integr Comp Physiol. 2002;283:R549–50. doi: 10.1152/ajpregu.00107.2002. author reply R550–1. [DOI] [PubMed] [Google Scholar]
- Schwartz MA. Integrin signaling revisited. Trends Cell Biol. 2001;11:466–70. doi: 10.1016/s0962-8924(01)02152-3. [DOI] [PubMed] [Google Scholar]
- Secomb TW, et al. Microangioectasias: structural regulators of lymphocyte transmigration. Proc Natl Acad Sci U S A. 2003;100:7231–7234. doi: 10.1073/pnas.1232173100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szczerba D, Szekely G. Computational model of flow-tissue interactions in intussusceptive angiogenesis. J Theor Biol. 2005;234:87–97. doi: 10.1016/j.jtbi.2004.11.014. [DOI] [PubMed] [Google Scholar]
- Tsuda A, et al. Bimodal oscillation frequencies of blood flow in the inflammatory colon microcirculation. Anat Rec. 2008 doi: 10.1002/ar.20767. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turhan A, et al. Bridging mucosal vessels associated with rhythmically oscillating blood flow in murine colitis. Anat Rec. 2007;291:74–92. doi: 10.1002/ar.20628. [DOI] [PubMed] [Google Scholar]
- Turhan A, et al. Effect of intraluminal pillars on particle motion in bifurcated microchannels. In Vitro Cell Dev Biol. 2008 doi: 10.1007/s11626-008-9134-9. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y, et al. Interplay between integrins and FLK-1 in shear stress-induced signaling. Am J Physiol Cell Physiol. 2002;283:C1540–7. doi: 10.1152/ajpcell.00222.2002. [DOI] [PubMed] [Google Scholar]
- Wilting J, Christ B. Embryonic angiogenesis: a review. Naturwissenschaften. 1996;83:153–64. doi: 10.1007/BF01143056. [DOI] [PubMed] [Google Scholar]
- Yamamoto K, et al. Impaired flow-dependent control of vascular tone and remodeling in P2X4-deficient mice. Nat Med. 2006;12:133–7. doi: 10.1038/nm1338. [DOI] [PubMed] [Google Scholar]