Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 2009 Nov 10;106(47):19780–19784. doi: 10.1073/pnas.0911705106

Viscosity of glass-forming liquids

John C Mauro a,1, Yuanzheng Yue b, Adam J Ellison a, Prabhat K Gupta c, Douglas C Allan a
PMCID: PMC2785243  PMID: 19903878

Abstract

The low-temperature dynamics of ultraviscous liquids hold the key to understanding the nature of glass transition and relaxation phenomena, including the potential existence of an ideal thermodynamic glass transition. Unfortunately, existing viscosity models, such as the Vogel–Fulcher–Tammann (VFT) and Avramov–Milchev (AM) equations, exhibit systematic error when extrapolating to low temperatures. We present a model offering an improved description of the viscosity–temperature relationship for both inorganic and organic liquids using the same number of parameters as VFT and AM. The model has a clear physical foundation based on the temperature dependence of configurational entropy, and it offers an accurate prediction of low-temperature isokoms without any singularity at finite temperature. Our results cast doubt on the existence of a Kauzmann entropy catastrophe and associated ideal glass transition.

Keywords: modeling, supercooled liquids, configurational entropy, relaxation

Perhaps the most intriguing feature of a supercooled liquid is its dramatic rise in viscosity as it is cooled toward the glass transition. This sharp, super-Arrhenius increase is accompanied by very little change in the structural features observable by typical diffraction experiments. Several basic questions remain unanswered:

  1. Is the behavior universal (i.e., is the viscosity of all liquids described by the same underlying model)?

  2. Does the viscosity diverge at some finite temperature below the glass transition (i.e., is there a dynamic singularity)?

  3. Is the existence of a thermodynamic singularity the cause of the dramatic viscous slowdown?

Answers to these questions are critical for understanding the behavior of deeply supercooled liquids. Unfortunately, equilibrium-viscosity measurements cannot be carried out at temperatures much below the glass transition owing to the long structural relaxation time. It thus becomes critical to find a model that best describes the temperature dependence of viscosity by using the fewest possible number of fitting parameters (1, 2). Because two parameters are needed for a simple Arrhenius description, modeling of super-Arrhenius behavior requires a minimum of three parameters. We focus on three-parameter models only, with the goal of describing the universal physics of supercooled liquid viscosity in the most economical form possible.

The most popular viscosity model is the Vogel–Fulcher–Tammann (VFT) equation (3)

graphic file with name zpq04709-0454-m01.jpg

where T is temperature, x is composition, and the three VFT parameters (η∞, A, and T0) are obtained by fitting Eq. 1 to experimentally measured viscosity data. In the polymer science community, Eq. 1 is also known as the Williams–Landel–Ferry (WLF) equation (4). Although VFT has met with notable success for a variety of liquids, there is some indication that it breaks down at low temperatures (3, 5). Another successful three-parameter viscosity model is the Avramov–Milchev (AM) equation (6), derived based on an atomic hopping approach:

graphic file with name zpq04709-0454-m02.jpg

where η∞, τ, and α are fitting parameters. Eq. 2 had been proposed (albeit empirically) by several authors (1, 7, 8) before the work of Avramov and Milchev. Although another three-parameter model has recently been proposed by Elmatad et al. (9), the quadratic form adopted by these authors applies only over a narrow range of temperatures and breaks down in both the high- and low-temperature tails. Here we are interested only in those models, such as VFT and AM, that cover the full range of temperatures by using a single three-parameter form.

Model.

We revisit the problem of viscous liquid dynamics starting with the Adam–Gibbs equation (10), relating viscosity to the configurational entropy of the liquid, Sc(T,x):

graphic file with name zpq04709-0454-m03.jpg

which has met with remarkable success in describing the relaxation behavior of a wide variety of systems (11) and has proved a key enabler for the theoretical study of dynamical heterogeneities in supercooled liquids (12, 13). Here, B(x) is an effective activation barrier, which is typically left as a fitting parameter. The configurational entropy Sc(T,x) is a complex quantity in a glassily entangled system, but it can be modeled by using constraint theory. [Constraint theory is general approach that has given an accurate description of the phase diagrams of thermal, kinetic, vibrational, and other properties of many network glasses, especially near the glass transition (14).] Following the energy landscape analysis of Naumis (15) and the temperature-dependent constraint model of Gupta and Mauro (16), the configurational entropy can be related to the topological degrees of freedom per atom (17, 18), f(T,x), by

graphic file with name zpq04709-0454-m04.jpg

where N is the number of atoms, k is Boltzmann's constant, and Ω is the number of degenerate configurations per floppy mode (16). To obtain the most economical model for f(T,x), we consider a simple two-state system in which the network constraints are either intact or broken, with an energy difference given by H(x):

graphic file with name zpq04709-0454-m05.jpg

In the limit of high temperature, Eq. 5 gives three translational degrees of freedom per atom. The network becomes completely rigid at absolute zero temperature, f(0,x) = 0, where there is no thermal energy to break the bond constraints. Defining K(x) = B(x)/3NklnΩ and C(x) = H(x)/k, we obtain the following three-parameter model for viscosity:

graphic file with name zpq04709-0454-m06.jpg

Eq. 6 was proposed empirically as one of several expressions by Waterton in 1932 (19), but we are unaware of any subsequent work with this expression. Although Eq. 6 could be obtained by assuming an exponential form for activation barrier in the Arrhenius formula for viscosity, this would be physically unrealistic because (i) the activation barrier would become infinite in the limit of zero temperature and (ii) the high-temperature kinetics are dominated by entropic effects, which are not considered by using a simple activation-barrier model. Here we obtain Eq. 6 through a physically realistic model for configurational entropy based on a constraint approach.

Although the viscosity models of Eqs. 1, 2, and 6 have different sets of adjustable parameters, each model can be rewritten in terms of the same set of physically meaningful quantities: (i) the glass-transition temperature, Tg(x); (ii) the fragility, m(x); and (iii) the extrapolated infinite temperature viscosity, η∞(x). For any composition x, the glass-transition temperature is defined where the shear viscosity is equal to 1012 Pa-s (16, 20), i.e., η(Tg(x),x) = 1012 Pa-s. Fragility (21) is defined as

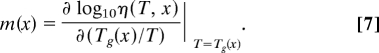graphic file with name zpq04709-0454-m07.jpg

With these definitions, the VFT expression of Eq. 1 becomes

graphic file with name zpq04709-0454-m08.jpg

the AM expression of Eq. 2 becomes

graphic file with name zpq04709-0454-m09.jpg

and the current model in Eq. 6 can be rewritten as

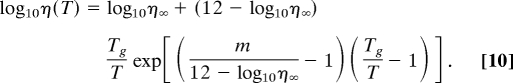graphic file with name zpq04709-0454-m10.jpg

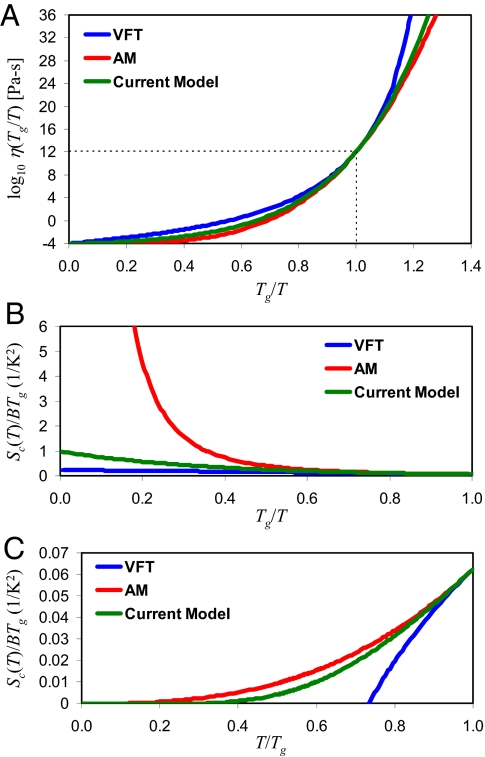
To illustrate the differences among the three models, Eqs. 8–10 are plotted in Fig. 1A assuming m = 60 and log10η∞ = −4. The intrinsic differences among these models can be elucidated by equating each of Eqs. 8–10 with the Adam–Gibbs relation of Eq. 3 and solving for the configurational entropy, Sc(T). As shown in Fig. 1B, the AM model predicts divergent configurational entropy in the limit of high temperature. This is a physically unrealistic result because only a finite number of configurations are available to any system (22). Both VFT and Eq. 10 correctly yield convergent Sc(T) in the high-temperature limit.

Fig. 1.

Fig. 1.

Open in a new tab

Comparison of the viscosity models. (A) Temperature dependence of viscosity with Eqs. 8–10, assuming m = 60 and log10η∞ = −4. (B) Plot of Sc(T)/BTg for T > Tg, obtained by equating each of Eqs. 7–9 with the Adam–Gibbs relation of Eq. 3. The AM model of Eq. 9 yields a divergent configurational entropy in the limit of T →∞. (C) Plot of Sc(T)/BTg for T < Tg. The VFT model of Eq. 8 predicts a vanishing of configurational entropy at T = T0.

The low temperature scaling of Sc(T), shown in Fig. 1C, is a matter of controversy. Although both AM and the current model predict Sc(T) = 0 only at absolute zero temperature, VFT predicts Sc(T0) = 0 at some finite temperature T0. As a result, the T0 parameter is often associated with the Kauzmann temperature, TK, at which the extrapolated liquid-entropy curve apparently intersects that of the crystal (23). The apparent success of the VFT equation, combined with Kauzmann's notion of an entropy catastrophe at TK, has led many theorists to suggest the existence of an ideal thermodynamic glass transition (24, 25). Both the AM equation and our current model avoid introducing such a singularity at a finite temperature. Although the issue remains contentious, the energy-landscape analysis of Stillinger (26) presents a compelling physical argument against the notion of vanishing liquid entropy at a finite temperature: Because a liquid cannot be truly confined in a single microstate at any finite temperature, the configurational entropy is necessarily positive for all T > 0. The recent work of Hecksher et al. (27) has also raised doubts about the existence of dynamic divergence at T0. In particular, they showed that the relaxation times of 42 organic liquids can be described equally well by other empirical expressions with the same number of fitting parameters as VFT but without incorporating a singularity at a finite temperature. In this work, we show that our model in Eq. 10 provides an improved description of viscosity scaling, especially at low temperatures, thus providing stronger evidence against the notion of dynamic divergence and the vanishing of liquid entropy at T0.

Results

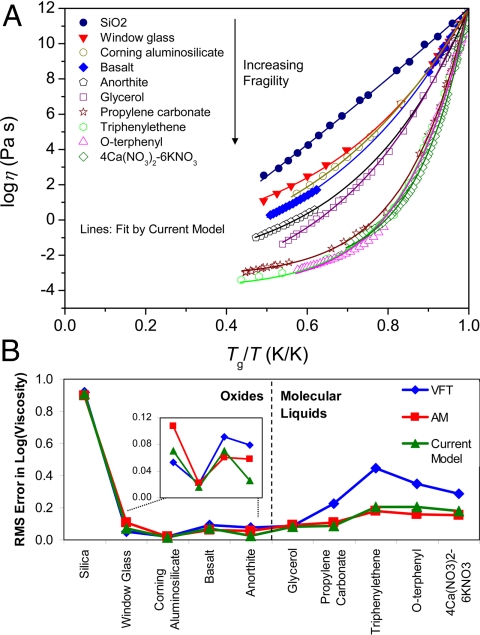
Let us first consider the glass-forming liquids in Fig. 2A, including five oxide and five molecular liquids, covering a wide range of fragility values from 20 to 115. Fig. 2B shows that the current model of Eq. 10 provides either the best fit or a close second-best fit for all ten of these diverse liquids. VFT performs worst overall, faring especially poorly with the higher-fragility molecular liquids. The poor performance of VFT with high-fragility liquids was also found by Angell (21), who tested several other two- and three-parameter equations (not including AM or the current model) but found that none performed significantly better than VFT (21, 28). Here we show that Eq. 10 performs much better than VFT across the full range of fragility values.

Fig. 2.

Fig. 2.

Open in a new tab

Model fits. (A) Viscosity curves of five oxide and five molecular liquids covering a range of fragility values from 20 to 115. (B) Root mean square error in the fitted viscosity curves using the three models of Eqs. 8–10.

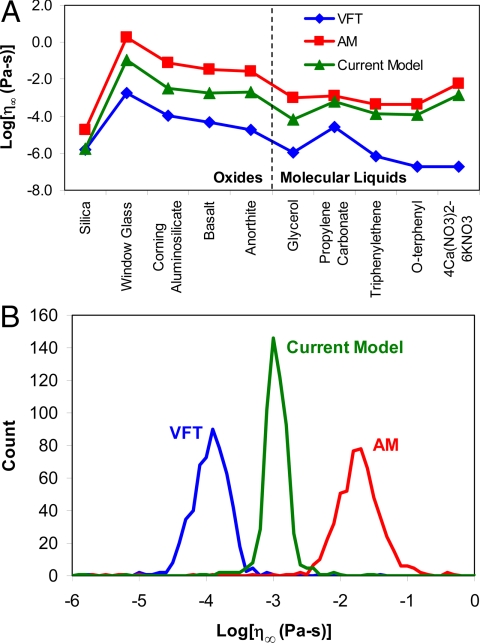
The relatively good fitting quality of AM in Fig. 2B is marred by an unphysical extrapolation to high temperatures. The relaxation time at an infinitely high temperature is given by the quasilattice vibration period (τ∞ ≈ 10−14 s), corresponding to the time between successive assaults on the energy barriers to structural rearrangement (29, 30). With an infinite frequency shear modulus of G∞ ≈ 29 GPa for silicate liquids (31), Maxwell's equation yields η∞ = G∞τ∞ ≈ 10−3.5 Pa-s. This extrapolated viscosity is expected to be somewhat lower for molecular liquids owing to their lower G∞; also, silica is expected to have a lower η∞ because of its anomalous strong-to-fragile cross-over (32). As shown in Fig. 3A, the values of η∞ obtained by using AM are unrealistically high, a result that follows directly from the unphysical divergence of configurational entropy exhibited in Fig. 1B. Previous studies by Hecksher et al. (27) and Yue (20) have shown that when η∞ is held to a physically realistic value, the fit quality of AM is significantly worse than that of VFT.

Fig. 3.

Fig. 3.

Open in a new tab

Extrapolated infinite temperature viscosity. (A) Distribution of η∞(x) values for the compositions in Fig. 2. (B) Histogram of η∞(x) values for the best-fit viscosity curves of 568 different Corning aluminosilicate compositions. The current model produces the narrowest distribution of η∞(x) values.

Next we consider fits to 568 different silicate liquids developed through composition research at Corning Incorporated. The liquids cover a wide range of composition space, from simple calcium aluminosilicate ternaries through complex borosilicates with up to 11 unique oxide components. Each composition is represented by 6–13 data points in the range of 10–106 Pa-s, obtained via a rotating-spindle method. Of these, 85 compositions are also represented by data points at 106.6 Pa-s (the softening point, obtained via parallel-plate viscometry) and 1011 Pa-s (obtained via beam bending viscometry). The measured isokom temperatures are accurate to within ±1 K. Fitting the full set of viscosity data, the current model of Eq. 10 yields the lowest RMS error of 0.0347 log10(Pa-s), compared with 0.0350 for VFT and 0.0470 for AM. Fig. 3B shows that the current model produces the narrowest distribution of η∞ values, in agreement with arguments concerning the universality of the η∞ parameter for a given class of materials (33–35), viz., in the limit of infinite temperature, the details of the interatomic potentials are no longer important because the system is dominated by kinetic energy. We note that this argument for a universal η∞ implicitly assumes simple exponential relaxation in the high-temperature limit (36). Fig. 3B also shows that the AM model produces unphysically high values of η∞ for nearly all of the Corning compositions.

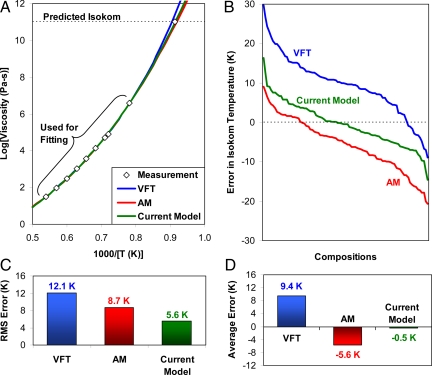
Near the glass-transition temperature, molecular glasses (like o-terphenyl) begin to form large clusters (as precursors to crystallization) or simply begin to crystallize (37). Thus, the low-temperature behavior is best studied with network glass data where crystallization is strongly inhibited. To investigate the low-temperature scaling of viscosity, we perform an extrapolation test on the 85 Corning compositions that include 106.6 and 1011 Pa-s data. As illustrated in Fig. 4A, the three viscosity models are fit to the high-temperature viscosity data only (including the softening point at 106.6 Pa-s). The models are then extrapolated to low temperatures to predict the 1011 Pa-s isokom temperature. The error in the isokom prediction is plotted in Fig. 4 B–D, where it is apparent that both the VFT and AM expressions exhibit systematic error, albeit in opposite directions. The AM equation exhibits too little curvature, underpredicting the 1011 Pa-s isokom temperature by an average of 5.6 K. In contrast, VFT exhibits too much curvature and overpredicts the 1011 Pa-s isokom by an average of 9.4 K. This systematic error is a direct result of VFT's spurious assumption of dynamic divergence at T0, which leads to an overly steep rise in viscosity at low temperatures. As shown in Fig. 4D, our current viscosity model of Eq. 10 exhibits no such systematic error when performing low-temperature extrapolation; its average error of −0.5 K falls within the experimental error bars of ±1 K. [As an aside, the recent model of Elmatad et al. (9) underpredicts the 1011 Pa-s isokom temperatures by an average of 72.0 K under exactly the same test as above, a result that demonstrates the dramatic breakdown of simple parabolic scaling when extending to low temperatures. Hence, this model is not in the same ballpark as any of the three other models considered.]

Fig. 4.

Fig. 4.

Open in a new tab

Results of the low-temperature extrapolation test. (A) Low-temperature extrapolation test, where the viscosity models are fit to high-temperature viscosity data and then extrapolated to predict the 1011 Pa-s isokom temperature. (B) Error in the predicted 1011 Pa-s isokom for 85 Corning compositions. The compositions on the horizontal axis are ordered in terms of descending error for the three models. A given position on the horizontal axis generally corresponds to three different liquids. (C) Root mean square error in the predicted isokom temperature using the three different models. (D) Average error in the predicted isokom temperature.

Discussion

The substantially enhanced extrapolation ability of Eq. 10 offers a cogent argument against the existence of dynamic divergence and the vanishing of configurational entropy at finite temperature, a view that is also supported by the low-temperature experiments of Simon et al. (38). Our results therefore cast doubt on the existence of an equilibrium second-order transition temperature T2 (10, 24) equivalent to T0 (21) and TK (23). According to Adam–Gibbs entropy function, Sc = ΔCp ln(T/T2), the configurational entropy would vanish at T = T2, where ΔCp is the difference in isobaric heat capacity between the equilibrium liquid and the glass at Tg (10). Another problem with the Adam–Gibbs Sc function is divergence in the high-temperature limit. Please note that although the derivation of our current model is based on the Adam–Gibbs relation between thermodynamics (Sc) and kinetics (η), it does not rely on the specific form of Sc(T) assumed by Adam and Gibbs in their discussion of the ideal glass transition.

Of the three viscosity models in Eqs. 8–10, only the current model of Eq. 10 offers a realistic extrapolation of configurational entropy in both the high- and low-temperature limits. As a result, Eq. 10 provides for physically reasonable values of η∞, as well as a more accurate description of the low-temperature scaling of viscosity. The failure of the VFT and AM models in either limit can be attributed to finite size effects, a common problem in complex systems (39). In the high-temperature limit, shear flow can be described by single-atom motion. As the temperature is lowered, the shear flow becomes cooperative and the length scale of the cooperatively rearranging regions increases (10). Such length-scale effects are critical for understanding other aspects of supercooled liquid and glassy behavior, such as stretched exponential relaxation (40) and dynamical heterogeneities (41–43). In a more general sense, by demanding good limits for both the high- and low-temperature scaling of viscosity, we have extended some of the basic ideas of complex analysis to glass-forming systems. The interested reader is encouraged to examine the recent work of Naumis and Cocho (39). Building on the notion of multiple length scales, these authors present an elegant N/D formula (44) for integrating rank distributions (39). Owing to the convolution of multiple length scales, the expressions for N (the numerator) and D (the denominator) in glass-forming systems need not be polynomials.

The improved accuracy of Eq. 10 in performing low-temperature extrapolations, combined with its absence of a singularity at finite temperature, offers strong evidence against the existence of dynamic divergence in glass-forming liquids. Any realistic model of the supercooled liquid and glassy states must account correctly for the low-temperature thermodynamics and kinetics. A particularly promising approach is the energy-landscape model of Stillinger (26, 45). Whereas the current paper deals solely with equilibrium liquid viscosity, a separate investigation by Mauro et al. (46) extends the analysis to viscosities up to 1016 Pa-s, providing a thorough theoretical and experimental analysis of the nonequilibrium viscosity of glass accounting for the effects of thermal history in the sub-Tg regime, including the cross-over to Arrhenius scaling at temperatures below the glass transition (47).

Acknowledgments.

We thank our colleagues at Corning Incorporated, particularly D. Keller, R. Irion, W. Muffly, and D. Walmsley, for obtaining reliable viscosity data. We also thank L.-M. Wang for providing the viscosity data of molecular liquids and R. Keding and G. G. Naumis for valuable discussions.

Footnotes

The authors declare no conflict of interest.

References

  • 1.Sturm VKG. On the temperature dependence of viscosity of liquids (Translated from German) Glastechn Ber. 1980;53:63–76. [Google Scholar]
  • 2.Mysen BO, Richet P. Silicate Glasses and Melts: Properties and Structure. Amsterdam: Elsevier; 2005. [Google Scholar]
  • 3.Scherer GW. Editorial comments on a paper by Gordon S. Fulcher. J Am Ceram Soc. 1992;75:1060–1062. [Google Scholar]
  • 4.Williams ML, Landel RF, Ferry JD. The temperature dependence of relaxation mechanisms in amorphous polymers and other glass-forming liquids. J Am Chem Soc. 1955;77:3701–3707. [Google Scholar]
  • 5.Laughlin WT, Uhlmann DR. (1972) Viscous flow in simple organic liquids. J Phys Chem. 1972;76:2317–2325. [Google Scholar]
  • 6.Avramov I, Milchev A. (1988) Effect of disorder on diffusion and viscosity in condensed systems. J Non-Cryst Solids. 1988;104:253–260. [Google Scholar]
  • 7.Hutton JF, Phillips MC. In: Amorphous Materials. Douglas RW, Ellis B, editors. New York: Wiley; 1972. p. 215. [Google Scholar]
  • 8.Utracki LA. Temperature dependence of liquid viscosity. J Macromol Sci B. 1974;10:477–505. [Google Scholar]
  • 9.Elmatad YS, Chandler D, Garrahan JP. Corresponding states of structural glass formers. J Phys Chem B. 2009;113:5563–5567. doi: 10.1021/jp810362g. [DOI] [PubMed] [Google Scholar]
  • 10.Adam G, Gibbs JH. On the temperature dependence of cooperative relaxation properties in glass-forming liquids. J Chem Phys. 1965;43:139–146. [Google Scholar]
  • 11.Scherer GW. Use of the Adam–Gibbs equation in the analysis of structural relaxation. J Am Ceram Soc. 1984;67:504–511. [Google Scholar]
  • 12.Capaccioli S, Ruocco G, Zamponi F. Dynamically correlated regions and configurational entropy in supercooled liquids. J Phys Chem B. 2008;112:10652–10658. doi: 10.1021/jp802097u. [DOI] [PubMed] [Google Scholar]
  • 13.Karmakar S, Dasgupta C, Sastry S. Growing length and time scales in glass-forming liquids. Proc Nat Acad Sci USA. 2009;106:3675–3679. doi: 10.1073/pnas.0811082106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Boolchand P, Lucovsky G, Phillips JC, Thorpe MF. Self-organization and the physics of glassy networks. Philos Mag. 2005;85:3823. [Google Scholar]
  • 15.Naumis GG. Glass transition phenomenology and flexibility : An approach using the energy landscape formalism. J Non-Cryst Solids. 2006;352:4865–4876. [Google Scholar]
  • 16.Gupta PK, Mauro JC. Composition dependence of glass transition temperature and fragility. I. A topological model incorporating temperature-dependent constraints. J Chem Phys. 2009;130 doi: 10.1063/1.3077168. 094503. [DOI] [PubMed] [Google Scholar]
  • 17.Phillips JC. Topology of covalent non-crystalline solids I: Short-range order in chalcogenide alloys. J Non-Cryst Solids. 1979;34:153–181. [Google Scholar]
  • 18.Phillips JC, Thorpe MF. Constraint theory, vector percolation and glass formation. Solid State Commun. 1985;53:699–702. [Google Scholar]
  • 19.Waterton SC. The viscosity-temperature relationship and some inferences on the nature of molten and of plastic glass. J Soc Glass Technol. 1932;16:244–249. [Google Scholar]
  • 20.Yue YZ. The iso-structural viscosity, configurational entropy and fragility of oxide liquids. J Non-Cryst Solids. 2009;355:737–744. [Google Scholar]
  • 21.Angell CA. Formation of glasses from liquids and biopolymers. Science. 1995;267:1924–1935. doi: 10.1126/science.267.5206.1924. [DOI] [PubMed] [Google Scholar]
  • 22.Stillinger FH. Enumeration of isobaric inherent structures for the fragile glass former o-terphenyl. J Phys Chem B. 1998;102:2807–2810. [Google Scholar]
  • 23.Kauzmann W. The nature of the glassy state and the behavior of liquids at low temperatures. Chem Rev. 1948;43:219–256. [Google Scholar]
  • 24.Gibbs JH, DiMarzio EA. Nature of the glass transition and the glassy state. J Chem Phys. 1958;28:373–383. [Google Scholar]
  • 25.Stillinger FH, Debenedetti PG, Truskett TM. The Kauzmann paradox revisited. J Phys Chem B. 2001;105:11809–11816. [Google Scholar]
  • 26.Stillinger FH. Supercooled liquids, glass transitions, and the Kauzmann paradox. J Chem Phys. 1988;88:7818–7825. [Google Scholar]
  • 27.Hecksher T, Nielsen AI, Olsen NB, Dyre JC. Little evidence for dynamic divergences in ultraviscous molecular liquids. Nat Phys. 2008;4:737–741. [Google Scholar]
  • 28.Angell CA, Poole PH, Shao J. Glass-forming liquids, anomalous liquids, and polyamorphism in liquids and biopolymers. Nuovo Cimento D. 1994;16:993–1025. [Google Scholar]
  • 29.Martinez LM, Angell CA. A thermodynamic connection to the fragility of glass-forming liquids. Nature. 2001;410:663–667. doi: 10.1038/35070517. [DOI] [PubMed] [Google Scholar]
  • 30.Angell CA, Ngai KL, McKenna GB, McMillan PF, Martin SW. Relaxation in glassforming liquids and amorphous solids. J Appl Phys. 2000;88:3113–3157. [Google Scholar]
  • 31.Bornhoft H, Brückner R. Elastic and inelastic properties of soda lime silicate glass melts. Glass Sci Technol. 1999;72:315–328. [Google Scholar]
  • 32.Saika–Voivod I, Poole PH, Sciortino F. Fragile-to-strong transition and polyamorphism in the energy landscape of liquid silica. Nature. 2001;412:514–517. doi: 10.1038/35087524. [DOI] [PubMed] [Google Scholar]
  • 33.Angell CA. Relaxation in liquids, polymers and plastic crystals—strong/fragile patterns and problems. J Non-Cryst Solids. 1991;131–133:13–31. [Google Scholar]
  • 34.Giordano D, Russell JK, Dingwell DB. Viscosity of magmatic liquids: A model. Earth Planet Sci Lett. 2008;271:123–134. [Google Scholar]
  • 35.Mazurin OV, Startsev YK, Stoljar SK. (1982) Temperature dependences of viscosity of glass-forming substances at constant fictive temperatures. J Non-Cryst Solids. 1982;52:105–114. [Google Scholar]
  • 36.Gupta PK, Mauro JC. Two factors governing fragility: Stretching exponent and configurational entropy. Phys Rev E. 2008;78 doi: 10.1103/PhysRevE.78.062501. 062501. [DOI] [PubMed] [Google Scholar]
  • 37.Sun Y, Xi HM, Chen S, Ediger MD, Yu L. Crystallization near glass transition: Transition from Diffusion-controlled to diffusionless crystal growth studied with seven polymorphs. J Phys Chem B. 2008;112:5594–5601. doi: 10.1021/jp7120577. [DOI] [PubMed] [Google Scholar]
  • 38.Simon SL, Sobieski JW, Plazek DJ. Volume and enthalpy recovery of polystyrene. Polymer. 2001;42:2555–2567. [Google Scholar]
  • 39.Naumis GG, Cocho G. Tail universalities in rank distributions as an algebraic problem: The beta-like function. Phys A. 2008;387:84–96. [Google Scholar]
  • 40.Phillips JC. Stretched exponential relaxation in molecular and electronic glasses. Rep Prog Phys. 1996;59:1133–1207. [Google Scholar]
  • 41.Berthier L. Time and length scales in supercooled liquids. Phys Rev E. 2004;69 doi: 10.1103/PhysRevE.69.020201. 020201(R) [DOI] [PubMed] [Google Scholar]
  • 42.Pan AC, Garrahan JP, Chandler D. Heterogeneity and growing length scales in the dynamics of kinetically constrained lattice gases in two dimensions. Phys Rev E. 2005;72 doi: 10.1103/PhysRevE.72.041106. 041106. [DOI] [PubMed] [Google Scholar]
  • 43.Trachenko K. The Vogel–Fulcher–Tammann law in the elastic theory of glass transition. J Non-Cryst Solids. 2008;354:3093–3906. [Google Scholar]
  • 44.Sugawara M, Kanazawa A. N/D method. Phys Rev. 1962;126:2251–2255. [Google Scholar]
  • 45.Mauro JC, Loucks RJ. Selenium glass transition: A model based on the enthalpy landscape approach and nonequilibrium statistical mechanics. Phys Rev B. 2007;76:174202. [Google Scholar]
  • 46.Mauro JC, Allan DC, Potuzak M. Nonequilibrium viscosity of glass. Phys Rev B. 2009;80 094204. [Google Scholar]
  • 47.Trachenko K, Brazhkin VV. Understanding the problem of glass transition on the basis of elastic waves in a liquid. J Phys: Condens Matter. 2009;21:425104. doi: 10.1088/0953-8984/21/42/425104. [DOI] [PubMed] [Google Scholar]

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES