Joint Segmentation of Thalamic Nuclei from a Population of Diffusion Tensor MR Images

Abstract

Several recent studies explored the use of unsupervised segmentation methods for segmenting thalamic nuclei from diffusion tensor images. These methods provide a plausible segmentation on individual subjects; however, they do not address the problem of consistently identifying the same functional areas in a population. The lack of correspondence between the segmented nuclei make it more difficult to use the results from the unsupervised segmentation tools for morphometry. In this paper we present a novel segmentation algorithm to automatically segment the gray matter nuclei while ensuring consistency between subjects in a population. This new algorithm, referred to as Consistency Clustering, finds correspondence between the nuclei as the segmentation is achieved through a single model for the whole population, similar to the brain atlases experts use to identify thalamic nuclei.

1 Introduction

Diffusion tensor imaging (DTI) is a relatively new imaging modality that measures free water diffusion, i.e. Brownian motion, of the endogenous water in tissue [1]. In human brain tissue, the water diffusion is not the same in all directions, since it is obstructed by structural elements such as cell membranes or myelin [1]. When this obstruction constrains the water diffusion in a coherent direction, such as within the cerebral white matter, the resulting water diffusion tensor becomes anisotropic, containing information about the directionality of the white matter connectivity. Thus, quantification of water diffusion in tissue through DTI provides a unique way to analyze white matter organization of the brain.

Unlike white matter, the tissue in gray matter is less organized in orientation. The lack of coherent orientation limits the use of DTI for gray matter analysis in some areas, such as the cerebral cortex. However, there are certain gray matter structures that exhibit coherence in diffusion direction due to the presence of coherent white matter near these structures, such as the thalamus. The thalamus acts as the central relay station of the brain with nearly all of the sensory tract projections reach to the cortex passing through the thalamus. Since functionally related pathways target the same region of cortex once they leave the thalamus, they result in organization of diffusivity within the thalamus. This organized diffusion can be measured in DTI, and it has been proposed that the thalamic nuclei can be distinguished by their characteristic diffusion orientation [2].

Precise identification of the thalamic nuclei is essential in a clinical setting, since many motor-control disorders are surgically corrected by applying chronic electrical stimulation to the appropriate functional area of the thalamus. Currently, these regions are detected qualitatively before the operation using generic atlases along with structural MRI [6], which does not provide adequate contrast to identify the distinct nuclei. Changes have also been reported in the thalamic nuclei during the progression of a large number of diseases, including schizophrenia [7] and Parkinson’s disease [8].

Since the realization that thalamic nuclei can be resolved through DTI, several segmentation algorithms have been proposed to segment the thalamic nuclei. The earliest segmentation method, which depends on DTI data only from within the thalamus, uses the k-means clustering algorithm [2]. Later, other clustering methods have been proposed that use spectral clustering [3], level-sets [4] and the mean-shift algorithm [5]. These later methods avoid some of the weaknesses of the k-means, which includes a bias toward ellipsoidal clusters and sensitivity to initialization. Even though each of these clustering algorithms produce plausible segmentations for any given subject in a population, they do not find a correspondence between the segments acquired from different subjects.

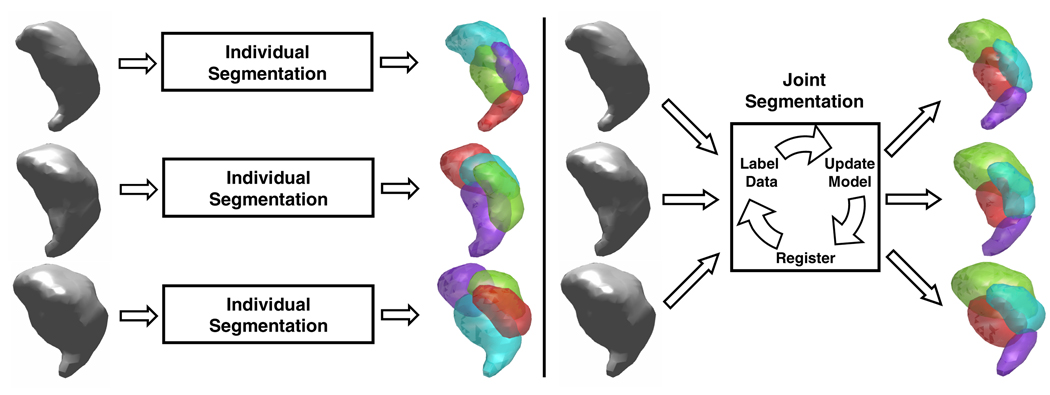
In this paper, we present a new approach to the segmentation of thalamic nuclei. Unlike the previous methods, this new algorithm, referred to as Consistency Clustering (CC), is designed to segment multiple subjects simultaneously and find a correspondence between the segmentation results (Figure 1). CC achieves these goals by learning a thalamic model of the population under investigation, which serves as a probabilistic atlas of the thalamic nuclei. This model involves a spatial component as well as a directional component for each nuclei. CC also performs a poly-rigid registration to account for inter-subject variability. Since the segmentation of each individual subject is done according to a common model, the consistency of segmentations between subjects is ensured. This joint segmentation approach results in a segmentation for each subject and determines a correspondence between subjects. Also, the thalamic model, which is learned from a population of labeled or unlabeled data, serves as an anatomical atlas for the population under investigation.

Fig. 1.

Schematic description of previous thalamus segmentation algorithms [2,3,4,5] (left) as opposed to the Consistency Clustering (right)

In the following sections, we first describe the theory behind the method, and then present results from several experiments that demonstrate the feasibility of the proposed method with DTI data from 10 healthy participants.

2 Theory

In this section we formulate the problem of joint segmentation of thalamic nuclei as a maximum likelihood problem and solve it using the generalized expectation maximization algorithm [9]. The algorithm iteratively increases the joint probability of observing the set of thalami under investigation. The joint probability is measured in terms of a mixture density model that accounts for spatial distribution of the nuclei as well as the principal diffusion orientation. The inter-subject variability is also handled within the same framework by introducing a set of parameters describing a poly-rigid registration.

The DTI data is modeled with a set of parametersi, Θ = {π_c,μ_c,Σ_c, ν_c, κ_c} ∪ {R_s}, where c is an index over clusters, i.e. c ∈ {1, 2, …, C} and s is an index over subjects, i.e. s ∈ {1, 2, …, S}. Given these parameters, the likelihood of the subjects becomes:

$$\Lambda (X,V;\Theta )={\displaystyle \prod _{i=1}^N{\displaystyle \sum _{c=1}^C{\pi }_c{f}_x({\mathit{x}}_i;\Theta )f_{\upsilon }({\mathit{\upsilon }}_i;\Theta ),}}$$

where we assume independence between every observed sample (voxel) and also independence between the spatial location x_i and principal diffusion orientation υ_i. We model the spatial distribution with a Gaussian:

$$f_x(\mathit{x};\Theta )=f_x(\mathit{x};{\mathit{\mu }}_c,{\mathit{\Sigma }}_c)=\frac{1}{{\left(2\pi \right)}^{3/2}|{\mathit{\Sigma }}_c{|}^{1/2}}\text{exp}\left(-\frac{1}{2}{(\mathit{x}-{\mathit{\mu }}_c)}^T{\mathit{\Sigma }}_c^{-1}(\mathit{x}-{\mathit{\mu }}_c)\right),$$

where µ_c is the mean vector and Σ_c is the covariance matrix. We model the distribution of the principal diffusion directions with a von Mises-Fisher distribution:

$$f_{\upsilon }(\mathit{\upsilon };\Theta )=f_{\upsilon }(\mathit{\upsilon };{\mathit{\nu }}_c,{\kappa }_c)=C({\kappa }_c)\exp ({\kappa }_c{{\mathit{\nu }}_c}^T\mathit{\upsilon }),$$

where ν_c is the mean orientation and κ_c is the concentration parameter. The constant, C(κ) = κ^1/2/(2π)^3/2I_1/2(κ), and I_1/2(κ) is a modified Bessel function of the first kind and order 1/2. Under this model, we formulate our problem as a maximum likelihood estimation of the parameter set Θ:

$${\Theta }^{*}=\underset{\Theta }{\arg \max }\Lambda (X,V;\Theta ).$$

In the next sections we present the update equations for our formulation to iteratively estimate Θ*. Detailed derivations have been omitted due to limited space.

2.1 E-Step

In the E-step, CC updates the membership probabilities for each voxel, given the estimate of the parameter set at iteration (n), Θ⁽ⁿ⁾:

$$\begin{array}{cc}p(c|{\mathit{x}}_i,{\mathit{\upsilon }}_i;{\Theta }^{(n)})\hfill & \propto {\pi }_c^{(n)}{f}_x({\mathit{R}}_s^{(n)}○{\mathit{x}}_i;{\mathit{\mu }}_c^{(n)},{\mathit{\Sigma }}_c^{(n)})f_{\upsilon }({\mathit{R}}_s^{(n)}○{\mathit{\upsilon }}_i,{\mathit{\nu }}_c^{(n)},{\kappa }_c^{(n)}),\hfill \\ \hfill & \triangleq p_{\mathit{\text{ci}}}^{(n)},\hfill \end{array}$$

where $p_{\mathit{\text{ci}}}^{(n)}$ is normalized at every iteration, so that ${\sum }_c{p}_{\mathit{\text{ci}}}^{(n)}=1$ for all voxels.

2.2 M-Step

In the M-step, CC updates the parameter set Θ to maximize the expected value of the log likelihood. Ignoring constant term that does not depend on Θ, the expected value of the log likelihood is derived as:

$$\beta (X,V;\Theta )={\displaystyle \sum _{\mathit{i}=1}^{\mathit{N}}{\displaystyle \sum _{\mathit{c}=1}^{\mathit{C}}{p}_{\mathit{c}\mathit{i}}^{(\mathit{n})}(\log \mathit{}{\pi }_{\mathit{c}}+\log {\mathit{f}}_{\mathit{x}}({\mathit{R}}_{\mathit{s}}^{(\mathit{n})}○{\mathit{x}}_{\mathit{i}};{\mathit{\Theta }}^{(\mathit{n})})+\log {\mathit{f}}_{\mathit{\upsilon }}({\mathit{R}}_{\mathit{s}}^{(\mathit{n})}○{\mathit{\upsilon }}_{\mathit{i}};{\mathit{\Theta }}^{(\mathit{n})})})}$$ (1)

For a given parameter set Θ⁽ⁿ⁾, the update equations for Θ⁽ⁿ⁺¹⁾ are derived using Lagrange multipliers for the corresponding constraints and setting the derivative of (1) to zero. Let $P_c^{(n)}\triangleq {\sum }_{i=1}^N{p}_{\mathit{\text{ci}}}^{(n)},$ then the resulting update equations are:

$$\begin{array}{ll}\hfill {\pi }_c^{(n+1)}=& P_c^{(n)}/N,\hfill \\ \hfill {\mathit{\mu }}_c^{(n+1)}=& (1/P_c^{(n)})\times {\displaystyle \sum _{i=1}^N{p}_{ci}^{(n)}{\mathit{x}}_i,}\hfill \\ \hfill {\mathit{\Sigma }}_c^{(n+1)}=& (1/P_c^{(n)})\times {\displaystyle \sum _{i=1}^N{p}_{ci}^{(n)}({\mathit{x}}_i-{\mathit{\mu }}_c^{(n+1)}){({\mathit{x}}_i-{\mathit{\mu }}_c^{(n+1)})}^T,}\hfill \\ \hfill {\mathit{r}}_c=& {\displaystyle \sum _{i=1}^N{p}_{ci}^{(n)}{\mathit{\upsilon }}_i,}\hfill \\ \hfill {\overline{r}}_c=& \Vert {\mathit{r}}_c\Vert /P_c^{(n)},\hfill \\ \hfill {\mathit{\nu }}_c^{(n+1)}=& {\mathit{r}}_c/\Vert {\mathit{r}}_c\Vert ,\hfill \\ \hfill {\kappa }_c^{(n+1)}\approx & (3{\overline{r}}_c-{\overline{r}}_c^3)/(1-{\overline{r}}_c^2),\hfill \end{array}$$

where the last equation is an approximation to the true parameter κ_c [10].

Registration

Registration parameters are also updated in the m-step. We parametrize the registration as one rigid transformation per cluster per subject, i.e.,

$$\begin{array}{cc}{\mathit{R}}_s^{(n)}○{\mathit{x}}_i\hfill & ={\mathit{R}}_{sc}^{(n)}({\mathit{x}}_i-{\mathit{\mu }}_{sc}^{(n)})+{\mathit{\mu }}_{sc}^{(n)}+{\mathit{t}}_{sc}^{(n)},\hfill \\ {\mathit{R}}_s^{(n)}○{\mathit{\upsilon }}_i\hfill & ={\mathit{R}}_{sc}^{(n)}{\mathit{\upsilon }}_i,\hfill \end{array}$$

where ${\mathit{\mu }}_{\mathit{\text{sc}}}^{(n)}={\sum }_{i\in s}{p}_{\mathit{\text{ci}}}^{(n-1)}{\mathit{x}}_i/{\sum }_{i\in s}{p}_{\mathit{\text{ci}}}^{(n-1)},$ and represents the weighted mean of the voxel locations in a given subject. Similar to other parameters, setting the derivative of (1) to zero, we get:

$${\mathit{t}}_{sc}^{(n+1)}={\mathit{\mu }}_c^{(n+1)}-{\mathit{\mu }}_{sc}^{(n+1)},$$

where ${\mathit{\mu }}_c^{(n+1)}={\sum }_{i\in s}{\sum }_c{p}_{\mathit{\text{ci}}}^{(n)}{\mathit{x}}_i/{\sum }_{i\in s}{\sum }_c{p}_{\mathit{\text{ci}}}^{(n)}.$ Unfortunately, the same technique does not lead into a simple analytical solution for the rotation matrices,${\mathit{R}}_{\mathit{\text{sc}}}^{(n+1)}.$ However, we derive a maximum likelihood optimization function and optimize the function using a numerical scheme. The resulting optimization function is:

$$\begin{array}{ll}{\mathit{R}}_{sc}^{(n+1)}\hfill & =\underset{{\mathit{R}}_{sc}}{\arg \max }{\displaystyle \sum _{i\in s}2{\kappa }_c^{(n+1)}{\mathit{\nu }}_c^{(n+1),T}{\mathit{R}}_{sc}{\mathit{\upsilon }}_i-{\mathit{x}}_i^T{\mathit{R}}_{sc}^T{\mathit{\Sigma }}_c^{(n+1),T}{\mathit{R}}_{sc}{\mathit{x}}_i}\hfill \\ \hfill & \text{s}.\text{t}.{\mathit{R}}_{sc}{\mathit{R}}_{sc}^T=I\text{and}|\mathrm{R}|\text{=1}.\hfill \end{array}$$

We further parametrize R_sc using Euler angles so that the constraints are automatically met. Then we find optimal values for the Euler angles (and therefore R_sc) using a simplex search method [11].

3 Methods

3.1 Image Acquisition and Pre-processing

DTI data were acquired using a twice-refocused spin-echo EPI sequence [12] on a 3 Tesla Siemens Trio MRI scanner using an 8-channel head coil. The sequence parameters were TR/TE=8400/82 ms, b=700 s/mm², gmax=26 mT/m, 10 T2 images, 60 diffusion gradient directions. The resulting images had 2 × 2 mm in-plane resolution with a slice thickness of 2 mm with 0 mm gap.

Correction for motion and residual eddy current distortion was achieved by registering all of the scans to the first acquired non-diffusion-weighted scan for each participant. The registration used a 12 degree-of-freedom global affine transformation and a mutual information cost function [13]. Trilinear interpolation was used for the resampling. The diffusion tensor were calculated for each voxel using the formulas of [14].

The diffusion tensor volumes were normalized to MNI-space (Montreal Neurological Institute) by registering each participant’s T2 volume to a skull-stripped version of the MNI 152-subject T2 template [15] and then applying the transformation to the diffusion tensor volumes with 12 degree-of-freedom global affine transformation. The tensors were reoriented using the rotational portion of the atlas transformation.

Thalamus masks were then drawn manually for each individual by a trained neuro-anatomist. The masks were drawn for each hemisphere on each individual’s MNI-normalized FA map following the guidelines from [16]. Each hemisphere was further segmented into its seven nuclei on the corresponding tensor map by the neuro-anatomist following the drawings of [16].

3.2 Experiments

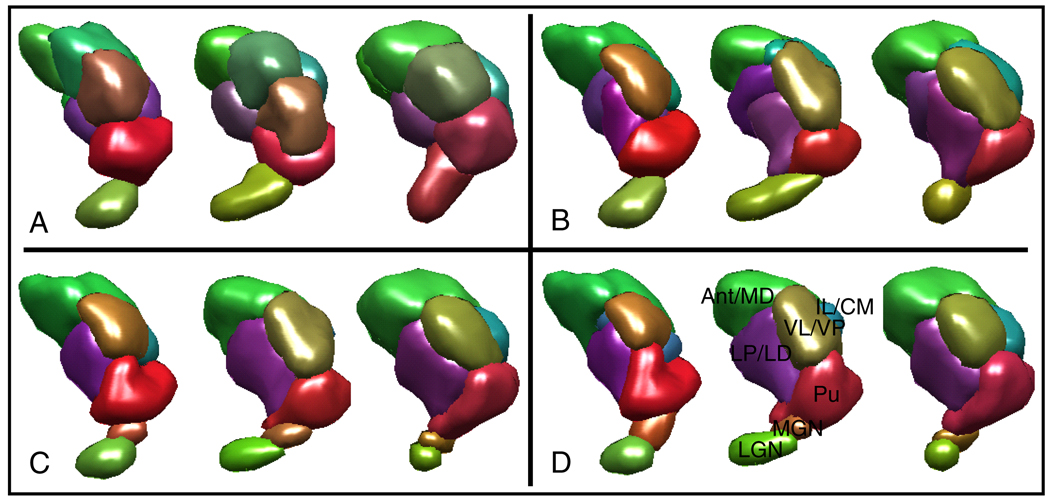
CC was validated on 10 normal subjects’ DTI datasets. Each subject’s thalami (only the left hemispheres) were segmented individually using the k-means algorithm as described in [2] and spectral clustering as described in [3] to create benchmarks. The same thalami were then segmented jointly using CC with the same (uniform) initialization used for the k-means algorithm. The joint segmentation resulted in corresponding segmentations in all subjects, whereas the k-means clustering did not (Figure 2A, B). To test the use of prior information, we repeated the joint segmentation experiment 10 times for each thalami in a leave-one-out fashion. For each joint segmentation, we fixed the voxel labels for 9 of the subjects at the expert labels (to “anchor” the model), and let the last subject’s labels vary. The resulting segmentations were not only consistent among subjects (Figure 2C), but also matched well qualitatively with the expert labels (Figure 2D).

Fig. 2.

Segmentation results from three subjects’ left thalamic hemispheres are shown. Colors indicate the mean diffusion orientation in each cluster. (A) Segmentations obtained using k-means have an ellipsoidal bias and they do not correspond well between subjects. (B) Segmentations obtained using CC with no prior information are consistent among subjects. (C) Segmentation using CC with prior information are both consistent among subjects and match well with the expert segmentations. (D) Expert labeled thalami are shown. Note that even though the segmentations in (C) and (D) look very similar, they are not exactly the same (see Figure 3).

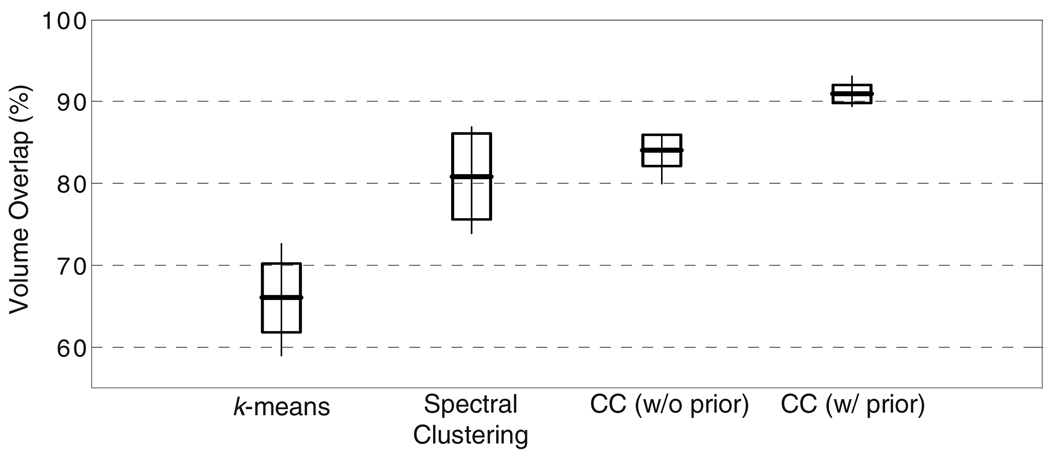
We also quantified the accuracy of the segmentation results against the expert labels using the Dice volume overlap measure [17] (Figure 3). Both spectral clustering and CC without prior information resulted in comparable volume overlaps, while k-means performed the worst due to its simple nature. Furthermore, CC resulted in a slightly higher average overlap and less variability around this average among subjects, indicating a better performance overall. The decrease in the variability is due to the increased consistency of segmentations between the subjects. Not surprisingly, the use of prior information improved the volume overlaps, indicating the need for prior information and the weakness of the unsupervised algorithms for replicating expert preference.

Fig. 3.

Volume overlaps between the expert segmentations and segmentations obtained using k-means [2], spectral clustering [3] and Consistency Clustering (CC), without and with prior information on the expert labels, from the left hemispheres from 10 subjects. The boxes indicate one standard deviation around the mean, and the thin lines indicate the range.

The algorithm took under 2 minutes to converge on a desktop personal computer with a non-optimized MATLAB implementation for the joint segmentation of 10 subjects. The algorithm’s complexity is linear with the number of voxels for fixed number of clusters, similar to the simple k-means clustering.

4 Discussion and Conclusion

In this paper we presented a novel algorithm, called Consistency Clustering, for jointly segmenting a population of diffusion tensor images of the deep gray matter. The joint segmentation resulted not only in plausible segmentations for each subject, but also correspondence between the subjects. This is an important difference between the CC and previous algorithms proposed to segment the gray matter, since without correspondence between the segmentations of individual subjects, it is difficult to assign consistent anatomical labels to the resulting segmentations. Also, without consistent and anatomically meaningful segmentations, the quantitative morphometry becomes a challenge in the gray matter.

CC not only provided consistent segmentations for the population, but it was also able to handle prior information about the expert labels. Also, through the use of labels from other subjects in the population, the algorithm was able to produce segmentations that were both qualitatively and quantitatively very similar to the expert’s preference. Therefore, CC can be used in two different ways to produce consistent segmentations in a population. The first way involves running the algorithm unsupervised on the population, and then assigning anatomical labels to the segmentations only on one of the subjects. The labels are then automatically transferred to the rest of the subjects since the correspondence problem is already solved at this stage. The second way involves labeling one or several subjects by hand, and then using these labeled subjects as prior information to label the rest of the population according to the expert preference.

Either way, CC (or a variant with an improved model for the thalamic nuclei) is a powerful tool that provides fast and consistent segmentation of the deep gray matter and has a use in a variety of applications such as in quantitative morphometry studies and pre-surgical planning.