Redistribution by insurance market regulation: Analyzing a ban on gender-based retirement annuities

Abstract

We illustrate how equilibrium screening models can be used to evaluate the economic consequences of insurance market regulation. We calibrate and solve a model of the United Kingdom’s compulsory annuity market and examine the impact of gender-based pricing restrictions. We find that the endogenous adjustment of annuity contract menus in response to such restrictions can undo up to half of the redistribution from men to women that would occur with exogenous Social Security-like annuity contracts. Our findings indicate the importance of endogenous contract responses and illustrate the feasibility of employing theoretical insurance market equilibrium models for quantitative policy analysis.

1. Introduction

Regulators often restrict the use of race, gender, and other buyer characteristics in pricing insurance policies. These restrictions are likely to become more prevalent as genetic testing and other technologies enrich the information set that insurers might use in setting individual-specific prices. Several theoretical studies, including Hoy (1982), Crocker and Snow (1986), and Rea (1987), analyze restrictions on characteristic-based pricing and show that they have unavoidable negative efficiency consequences. Empirical work supports the key predictions of the models that underlie these efficiency analyses. Buchmueller and DiNardo (2002) and Simon (2005), for example, show a decline in insurance coverage when characteristic-based pricing is banned in health insurance markets. Hoy and Witt (2007) is the only study we know of that offers estimates of the efficiency costs of restricting characteristic-based pricing. It focuses on the case of genetic testing bans in term life insurance. We are not aware of any empirical research that simultaneously measures the efficiency and distributional consequences of such restrictions.

This paper takes a first step toward developing such estimates. We extend existing theoretical models and adapt them to estimate both the efficiency and redistributive effects of a unisex pricing requirement for pension annuities in the United Kingdom. Restrictions on characteristic-based pricing are usually thought to transfer resources from individuals with a low risk of a loss to those with greater risks. Since women are at greater risk of living for many years after they purchase an annuity than men, unisex pricing restrictions on pensions redistribute from men to women. We find that the extent of such redistribution depends critically on the nature of insurance market equilibrium and on the way insurance companies respond to the unisex pricing requirement. Our findings extend Rea’s (1987) analysis of how a unisex pricing rule would affect the policies purchased by prospective annuitants.

The redistribution associated with pricing restrictions in insurance markets is similar to that associated with a broad class of other regulatory policies. Conditional on an individual’s gender, the redistribution from men to women of a unisex pricing rule is similar to the redistribution from low-cost to high-cost consumers under uniform pricing regulations in industries such as telephone and electricity distribution. Posner (1971) labels such redistribution “taxation by regulation.” Hirshleifer (1971) argues for a different approach to such redistribution, however, that takes an ex ante perspective. Before individual characteristics are known, the redistribution associated with gender-blind pricing may be viewed as a form of insurance against drawing a high-cost characteristic. In the annuity market, belonging to a long-lived group, as women do, corresponds to being a high-cost annuity buyer.

The pension annuity market provides a convenient setting for applying theoretical models of asymmetric information to quantify regulatory impact. It is also interesting in its own right because of its size, its importance for retiree welfare, and the salience of its unisex pricing regulations. Private annuity arrangements, typically defined benefit pension payouts, represent an important source of income for many elderly households. Employers in the United States were once free to offer different pension annuity payouts to men and women, but litigation in the 1970s and early 1980s eliminated this practice. The European Union is currently debating regulatory reforms that may eliminate gender-based pricing in insurance markets, including those for annuities. Analyzing how restrictions affect annuity markets may also have broader implications for the design and regulation of annuitized payout structures associated with defined contribution Social Security systems.

Our institutional analysis focuses on the U.K. retirement annuity market. Workers who have accumulated tax-preferred retirement savings are required to purchase an annuity. This eliminates the possibility that unisex pricing regulations might alter the set of annuity market participants. Participants nevertheless have substantial flexibility in choosing their annuity policy, and Finkelstein and Poterba (2004) suggest that this choice is affected by private information about mortality risk. The compulsory participation requirements in this market simplify our analysis, but they also suggest caution in generalizing our quantitative findings on the efficiency and distributional consequences of a ban on gender-based pricing to annuity markets or other insurance markets where participation is voluntary.

We are not aware of any previous attempts to calibrate and solve a stylized theoretical model of insurance market equilibrium. Doing so requires adapting a model to incorporate many institutional features of actual insurance markets. For example, it is important to determine whether individuals have recourse to any informal, if inefficient, substitutes for insurance. Our analysis recognizes that policyholders may save against the contingency of a long life, and that insurance companies may not observe this saving. When insurance companies can observe and contract on saving, banning gender-based pricing may not have any redistributive or efficiency consequences. This lack of efficiency consequences is a special case of a result in Crocker and Snow (2007): when there are no informal substitutes for insurance, the efficiency consequences of introducing asymmetric information are minimal whenever the dimensionality of insurance contracts is sufficiently large. In contrast, regulatory interventions may have non-trivial consequences when individuals can draw on unobservable savings as a substitute for buying annuities.

Our analysis demonstrates that theoretical models of insurance market equilibrium can be adapted to offer quantitative predictions on regulatory issues. We find that estimates of the impact of regulation are substantially affected by recognizing that insurers may alter their product offerings in response to regulation. Insurer response may substantially reduce the amount of redistribution from men to women associated with a ban on gender-based pricing. This finding highlights the importance of modeling insurance market equilibrium when analyzing regulatory policy. Golosov and Tsyvinski (2007) make a similar observation with regard to tax policy. Even after we allow for insurance companies to alter their menu of annuity products, we find that banning gender-based pricing in the U.K. retirement annuity market would redistribute resources. In most cases we consider, men would be worse off by an amount equivalent to losing at least 3% of their retirement wealth. We also estimate small efficiency costs associated with this redistribution, although our estimates of these costs are likely to be very sensitive to the compulsory nature of the U.K. retirement annuity market. This feature rules out the possibility that some individuals who might buy annuities when gender-based prices are permitted would chose not to do so when prices are gender-blind. This potentially important source of inefficiency associated with regulation of voluntary insurance markets is not relevant to our analysis, but it could be substantial in other markets.

This paper is organized as follows. Section 2 briefly reviews the qualitative impact of uniform pricing requirements in insurance markets with asymmetric information. Section 3 models the range of possible contracts offered and purchased in equilibrium under the assumption that the annuity market equilibrium is constrained Pareto efficient. It also introduces our algorithm for solving for equilibrium contract structure; a technical appendix provides further details. In Section 4 we calibrate our theoretical model, using data on annuitants in the U.K. retirement annuity market, and present estimates of a two-type mixture model for mortality rates. Section 5 describes the measures that we use for evaluating the efficiency and distributional effects of insurance market regulation. Section 6 presents our quantitative results on the range of possible distributional and efficiency effects of adopting gender-blind pricing under different assumptions concerning the constraints on annuity buyers and insurance companies. A brief conclusion in Section 7 discusses how our results bear on a number of ongoing policy debates and describes how our approach might be generalized to other insurance markets.

2. A framework for analyzing regulation in insurance markets

This section reviews the qualitative efficiency and distributional effects of banning categorization in a two-state, two-type model of competitive insurance markets with asymmetric information. This framework considers two distinct types of individuals who are indistinguishable to an insurance company but who face different risks of a loss. Individuals can insure themselves against a loss by purchasing a single insurance contract from a firm in a competitive insurance market.

2.1. Qualitative analysis of the “perfect categorization” case

Hellwig (1987) explains that previous research suggests several potential equilibrium concepts for insurance markets with asymmetric information. We are agnostic about the “right” concept and therefore refrain from explicitly modeling equilibrium. Instead, we follow Crocker and Snow’s (1986) analysis of the efficiency impact of banning categorization by focusing on constrained efficient outcomes. This approach is consistent with equilibrium behavior. For example, the equilibrium concept developed by Miyazaki (1977), Wilson (1977), and Spence (1978) (hereafter MWS) results in a constrained efficient outcome. We describe this outcome in more detail after characterizing the entire efficient frontier.

To characterize the efficient frontier, denote the high-risk and low-risk types by H and L, respectively. Let Vⁱ (A) denote the indirect utility achieved by type i when she purchases insurance contract A, and let Πⁱ(A) denote the expected profit a firm earns by selling contract A to type i. Points on the Pareto frontier solve the following program, where λ is the proportion of high-risk types:

$$\begin{array}{l}\underset{A^L,A^H}{max}{V}^L(A^L)\\ \mathit{subject}to\\ ({IC}_H)V^H(A^H)\ge V^H(A^L)\\ ({IC}_L)V^L(A^L)\ge V^L(A^H)\\ (MU)V^H(A^H)\ge {\overline{V}}^H\\ (BC)(1-\lambda ){\mathrm{\Pi }}^L(A^L)+\lambda {\mathrm{\Pi }}^H(A^H)\ge 0,\end{array}$$ (1)

where (IC_i) is the incentive compatibility constraint stating that i types must be willing to choose the contract designed for them, (BC) is a budget constraint that requires that on average policies break even, and (MU) is a minimum utility constraint for the high-risk types. Varying the minimum utility V̄^H in (MU) allows us to trace out the entire Pareto frontier, as in Fig. 1 below. Crocker and Snow (1985) characterize this constrained Pareto frontier in the standard two period, one-accident setting by instead varying the Lagrange multiplier on constraint (MU) in (1).

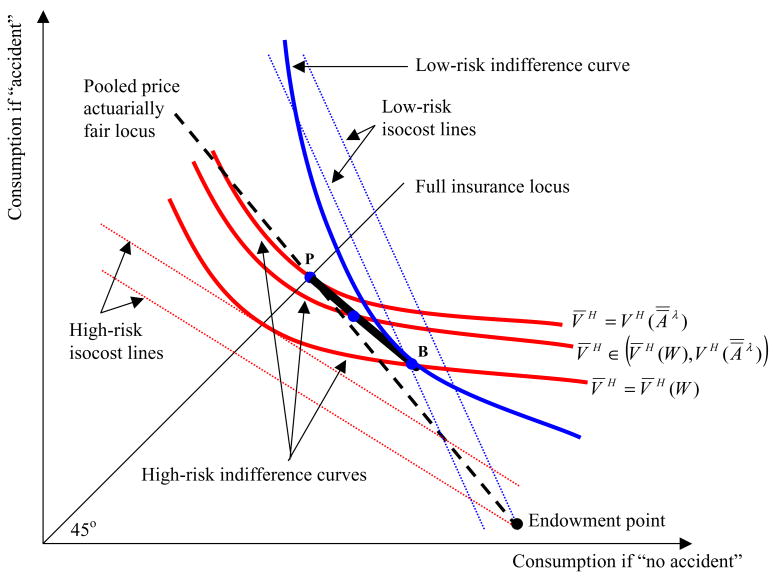
Fig. 1.

A stylized constrained Pareto frontier. The dark curve connecting B to P depicts the range of consumption bundles for low-risk (L) types achievable in the constrained Pareto optimal insurance market described in Eq. (1). More precisely, it depicts the consumption bundles for low-risk types consistent with: (i) high-risk (H) types receiving full insurance; (ii) a binding high-risk incentive compatibility constraint; (iii) firms breaking even in aggregate; (iv) high-risk types being no better off than at the pooled actuarially fair full insurance bundle (point P); (v) high-risk types being no worse off than with their full insurance actuarially fair insurance contract. It can be traced out by solving (1) for each minimum required level of high-risk type utility V̄^H between V̄^H (W) (the high-risk types’ utility with their full insurance actuarially fair bundle; point B) and $V^H({\overline{\overline{A}}}^{\lambda })$ (their utility with the pooled actuarially fair full insurance; point P).

Fig. 1 describes insurance contracts as state-contingent consumption vectors A = (a₀, a₁), where the subscript 0 refers to the “no loss” state. Insurance providers supply consumption promises A in exchange for a buyer’s state-contingent endowment wealth vector W = (w₀, w₀ − ℓ). High-risk types have a higher probability of experiencing State 1 than low-risk types but they are otherwise identical. Both types are expected utility maximizers with a strictly concave utility function.

For low values of V̄^H, (MU) may be slack. For example, if ${\overline{V}}^H=\underset{\left\{A:{\mathrm{\Pi }}^H(A)=0\right\}}{max}{V}^H(A)$, so that (MU) dictates that high-risk types must be at least as well off as they would be with their full insurance actuarially fair consumption point, then (MU) will be slack when the Rothschild and Stiglitz (1976) equilibrium either fails to exist or exists but is not constrained efficient. Such a situation is depicted at point M, which illustrates the low-risk types’ consumption in the constrained efficient allocation that is best for low-risk types. This corresponds to the MWS equilibrium. Fig. 1 shows that even this best-for-low-risks allocation can involve cross subsidies from low to high-risk types.

The dark curve connecting points B and P depicts a portion of the locus of low-risk types’ consumption points that correspond to constrained Pareto optimal outcomes. Point P is the unique pooling outcome on the frontier—the only unique constrained efficient outcome with A^L = A^H It is on the 45-degree line and therefore provides full insurance. Point P involves larger cross subsidies from low to high-risk types than point B does. There are additional constrained efficient outcomes not depicted in Fig. 1 which involve even larger low to high-risk cross subsidies than those at point P. Such outcomes involve the low-risk types being fully insured and the high-risk types being over-insured—a possibility that Crocker and Snow (1985) note does not obtain in standard models of insurance market equilibrium. As a result, we do not consider this portion of the frontier. We consider the set of outcomes in the region of the frontier bounded by P and B, but we do not try to select any particular constrained efficient outcome from this set.

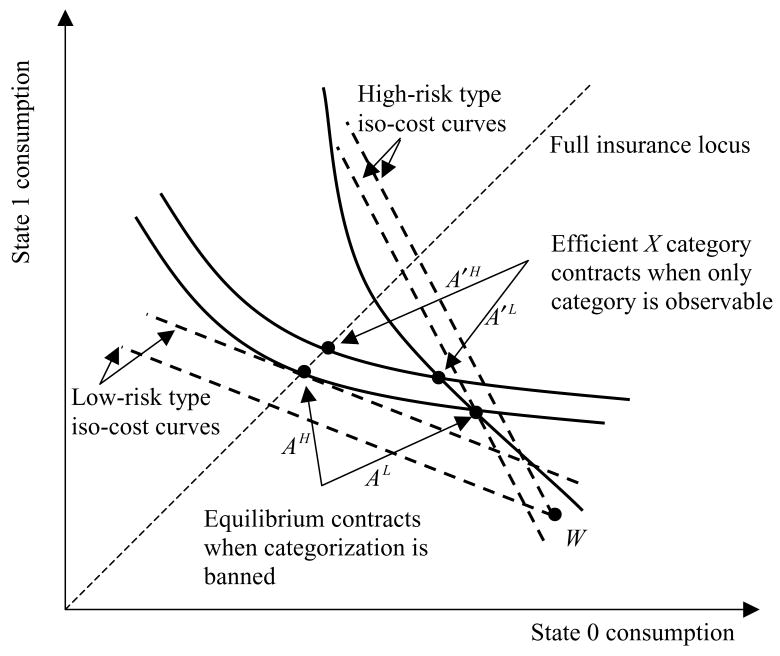
Because the program in (1) permits—and, as in the case of Fig. 1, may even require—the market to implement a contract pair involving cross subsidies, bans in characteristic-based pricing can have both distributional and efficiency consequences. This is illustrated in Fig. 2, which depicts a constrained efficient pair of contracts. When insurers can observe type and condition policy type on it, the competitive equilibrium will provide each type with actuarially fair full insurance. A^H* and A^L* depict the full insurance actuarially fair contracts that we assume emerge when type is observable and can be contracted upon. Consumption for each type is independent of the realized state of nature.

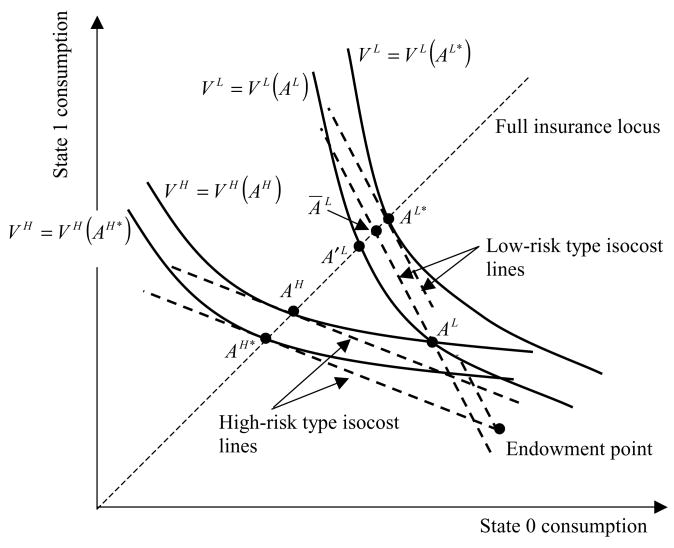
Fig. 2.

A constrained efficient annuity pair. This figure illustrates a constrained efficient pair of contracts (A^L, A^H) solving Eq. (1). A^H lies above A^H*, the full insurance actuarially fair contract for high-risk types. Hence, (A^L, A^H) involves redistribution from low to high-risk types. Since the low-risk (high-risk) types’ indirect utility V^L is lower (higher) with A^L (A^H) than with A^L* (A^{H *}), low-risk (high-risk) types are worse (better) off with (A^L, A^H) than they are with the pair of individually fair full insurance contracts (A^L*, A^H*). When type is observable, (A^L, A^H) is also inefficient (in the sense of Eq. (14)) because each type could be made equally well off with the contract pair (A′^L, A^H) at a lower expected cost to firms; the distance between A′^L and Ā^L (the full insurance contract with the same actuarial cost for the low-risk type as A^L) is a measure of this inefficiency.

When type-based pricing is banned, we assume that the market implements a pair of contracts, A^H and A^L, which is constrained efficient given the ban’s rules. Note that, as depicted, this contract pair involves positive cross subsidies between types. High-risk types are better off, and low-risk types are worse off, when categorization is banned. This illustrates the distributional consequences of a ban on category-based pricing. The ban is efficiency reducing in this example as well. Since type is observable, it is in principle possible to make low-risk types as well off as with A^L via contract A′^L, which costs less to provide than A^L.

1.2 Residual private information

The foregoing discussion assumes that type is observable, so banning characteristic-based pricing moves the economy from perfect to imperfect information. In practice, information such as gender or a test outcome may be related to risk type, but even conditional on this information, insurers are unlikely to be able to completely determine the policy-buyer’s risk type. The relevant comparison is therefore between two equilibria with different levels of imperfect information.

Our analysis builds on previous studies, such as Hoy (1982) and Crocker and Snow (1986), which consider the most parsimonious possible model for capturing the presence of residual private information. There are two risk types, but risk type is not directly observable. Instead, insurers observe a signal that is correlated with risk type. There are two possible signals, X and Y, and we refer to individuals as falling in category X or category Y. A fraction λ_k of category-k individuals are high-risk types, with 0 < λ_X < λ_Y < 1. Category Y, which accounts for a fraction θ of individuals, is the higher-risk category but it still includes some low-risk types.

Our analysis assumes that markets will operate in a constrained efficient manner given the information that is available and can be used in writing contracts. When characteristic-based pricing is permitted, we further assume that the market will not implement contracts involving cross subsidies across observable categories. We imposed this assumption in Fig. 2 by assuming that the contracts A^H* and A^L* emerge when type-based pricing was allowed. A ban on categorical pricing in this imperfect information setting will have the same qualitative effects as it does in the perfect information setting described above.

3. Applying the model to gender-based pricing in the U.K. pension annuity market

Individuals in self-directed defined contribution pension plans in the United Kingdom, the analogues of IRAs and 401(k)’s in the United States, must annuitize a substantial share of their accumulated balance by the date when they retire. Although annuitization is compulsory, annuitants can select among a range of different annuity contracts. Finkelstein and Poterba (2004, 2006) find evidence of self-selection in contract choice, apparently reflecting private information about mortality risk. From the perspective of an insurance company, high-risk annuitants are those who are at substantial risk of living longer than the characteristics used in pricing, such as age and gender, would suggest. There are currently no regulations in the U.K. annuity market limiting the characteristics used in pricing annuities although annuities are priced almost exclusively on age at purchase and gender. Several small firms have recently entered the annuity market with discounted annuities for heavy smokers.

While the two-state model discussed above suffices for understanding the qualitative impacts of a ban on categorical pricing, it is too stylized to plausibly measure the quantitative impact of regulatory interventions in the annuity market. We extend the analysis to many “states,” since individuals can live to receive payments many years after purchasing an annuity. Townley and Boadway (1988) use the only other contract theoretic model we have found that includes more than three periods in an analysis of an annuity market with asymmetric information. We relax that study’s restrictions on the set of possible contracts. Rea (1987) considers the multi-period consumption problem of annuity buyers, and recognizes the possibility that insurers will offer annuities with different age-specific payments and that men and women will make different choices when confronting these product options. Our analysis embeds this insight in a model which allows for asymmetric information other than that created by a gender-based pricing ban.

Our baseline model allows for unobservable savings. This is a crucial assumption because in our model, insurance companies can screen so effectively when they can observe and contract on savings that informational asymmetries created by a ban on gender categorization have neither efficiency nor distributional consequences. Although the sharpness of this result is likely to depend on particular modeling assumptions, the intuition is general and can be illustrated by considering an extreme case. If long-lived individuals have a non-zero probability of surviving to an age by which short-lived individuals are certain to have died, and if consumption must equal the annuity payment for each period, then insurance companies can perfectly screen out the long-lived by offering an annuity contract which provides zero consumption at advanced ages. A ban on gender-based pricing will not alter the separating equilibrium because insurance companies offer a menu of products that achieves complete selection.

In contrast, when savings are not observable, insurers may not be able to screen different types of observationally equivalent annuity buyers. This was noted by Eichenbaum and Peled (1987) and Brunner and Pech (2005). Intuitively, accumulating assets is an imperfect substitute for buying an annuity: both provide longevity insurance. While annuities are tailored precisely to this need, annuity buyers can nevertheless use unobserved savings to mitigate the distortions introduced by insurance companies for screening purposes. The derivation and solution method that we develop below illustrates this result, provides insight on the importance of the limitations on screening that follow from unobservable savings, and shows why the model is substantially more difficult to solve when savings are unobservable. Even in this case, however, we can find the set of contracts on the constrained Pareto frontier.

When we apply our model to the market for retirement annuities in the United Kingdom, we consider a ban on gender-based annuities in employer-sponsored retirement plans. Most households accumulate retirement wealth in tax-deferred accounts like the ones we analyze and in other accounts as well. It seems unlikely that insurance companies offering annuities within retirement plans would be able to observe all household wealth holdings, which suggests that unobservable savings is likely to be a key feature of the annuitization environment. Assets held either in taxable accounts or in tax-deferred accounts could be used to support consumption at extreme ages and thereby to counter attempts by insurance companies to screen annuity buyers by offering age-related annuity payout structures.

3.1. Defining annuity market outcomes

Our model applies to any number of periods t =0, ···, N, where t is the number of years after retirement at age R=65. In practice, we take N=35, thereby assuming individuals do not live past age 100. To capture the compulsory purchase requirement, we assume that individuals must use their retirement wealth W to purchase an annuity. Individuals exponentially discount the future for time, at rate δ=1/1+r per year, where r is the interest rate. They also discount for their probability S_t of living to age R+t. The two risk types, H and L, differ only in their survival probabilities. There is a continuum of individuals, with a fraction λ of high-risk types. We assume $S_{t+1}^H/S_t^H>S_{t+1}^L/S_t^L$ for each t, i.e., the higher-longevity type has a lower mortality hazard at every age.

The direct utility of a consumption stream Γ = (c₀, ···, c_N) for an individual of type σ is:

$$U^{\sigma }(c_0,\cdots ,c_N)=\sum _{t=0}^N{\delta }^t{S}_t^{\sigma }u(c_t)=\sum _{t=0}^N{\delta }^t{S}_t^{\sigma }\frac{c_t^{1-\gamma }}{1-\gamma },$$ (2)

where γ is the risk-aversion parameter. Annuity streams, which are denoted by A, specify a life-contingent payment a_t in each of the N + 1 periods. Our baseline model imposes no structure on annuity payments a_t; we later restrict their possible time profile.

Individual savings earn an interest rate r. Individuals have no bequest motive, and they cannot borrow against their annuity. This means that individuals with an annuity stream A can obtain any consumption stream that satisfies $\mathrm{\Gamma }\in F(A)\equiv \left\{\mathrm{\Gamma }\mid {\displaystyle \sum _0^t}{\delta }^s{c}_s\le {\displaystyle \sum _0^t}{\delta }^s{a}_s\forall t\right\}$. This induces indirect utility functions and type-specific actuarial cost functions

$$V^{\sigma }(A)=\underset{\mathrm{\Gamma }\in F(A)}{max}{U}^{\sigma }(\mathrm{\Gamma }),$$ (3)

and

$$C^{\sigma }(A)\equiv \sum _0^N{\delta }^n{S}_t^{\sigma }{a}_t.$$ (4)

Because individuals discount the future at the rate of interest, “full insurance” annuities have level real payouts. Let V̄^σ (X) denote the utility that type σ gets by consuming the full insurance annuity Ā with C^σ (Ā) = X. Let ${\overline{\overline{A}}}^{\lambda }$ denote the pooled-fair full insurance annuity—i.e., the full insurance annuity satisfying $\lambda C^H({\overline{\overline{A}}}^{\lambda })+(1-\lambda )C^L({\overline{\overline{A}}}^{\lambda })=W$. In a constrained efficient market, the two risk types purchase a pair of annuities A^H and A^L that solve:

$$\begin{array}{l}\underset{A^L,A^H}{max}{V}^L(A^L)\\ \mathit{subject}to\\ ({IC}_H)V^H(A^H)\ge V^H(A^L)\\ ({IC}_L)V^L(A^L)\ge V^L(A^H)\\ (MU)V^H(A^H)\ge {\overline{V}}^H\\ (BC)(1-\lambda )C^L(A^L)+\lambda C^H(A^H)\le W\end{array}$$ (5)

for some V̄^H We further assume that ${\overline{V}}^H(W)\le {\overline{V}}^H\le V^H({\overline{\overline{A}}}^{\lambda })$, where V̄^H (W) is the utility of high-risk types, with initial wealth W, with full insurance at the actuarially fair rate for their risk type. Hence, we focus on outcomes that make high-risk types at least as well off as they would be if they revealed their type, and no better off than they would be in a pooling equilibrium with fair full insurance. This range corresponds to a portion of the efficient frontier in Fig. 1. Solving (5) involves solving for the N+1 year-specific annuity payments for each of the two types. Furthermore, the functions V^σ (A) are themselves implicitly defined via (3), which is an optimization problem over N + 1 variables.

In spite of this complex structure, four factors make (5) computationally tractable. First, the assumption that ${\overline{V}}^H\le V^H({\overline{\overline{A}}}^{\lambda })$ implies that the low-risk type incentive compatibility constraint (IC_L) is slack at the solution. We therefore drop this constraint and later verify that it is indeed satisfied. Second, the budget constraint (BC) trivially binds at the optimum. Third, once (IC_L) is dropped, it is easy to see that A^H will be a full insurance annuity. Any allocation with an A^H that does not offer full insurance can be improved upon by replacing A^H with the full insurance bundle Ã^H for which V^H (Ã^H) = V^H (A^H), as this replacement affects (5), without (IC_L), only by making (BC) slack. Since A^H is a full insurance annuity, we can parameterize it by T ≡ W − C^L (A^L), the size of the cross subsidy from low to high-risk types expressed in per low-risk type terms. For a given T, $V^H(A^H)={\overline{V}}^H(W+\frac{1-\lambda }{\lambda }T)$, i.e., the utility they would receive with full insurance at their actuarially fair rate and an initial wealth of $\left(W+\frac{1-\lambda }{\lambda }T\right)$. This means that the solution to (5) must have T ≥ T̄, where T̄ solves ${\overline{V}}^H={\overline{V}}^H\left(W+\frac{1-\lambda }{\lambda }\overline{T}\right)$. This permits us to write (5) in the simpler form:

$$\begin{array}{l}\underset{A^L,T}{max}{V}^L(A^L)\\ \mathit{subject}to\\ (I{C}^{\prime })V^H(A^L)\le {\overline{V}}^H(W+\frac{1-\lambda }{\lambda }T)\\ (M{U}^{\prime })T\ge \overline{T}\\ (B{C}^{\prime })C^L(A^L)\le W-T.\end{array}$$ (6)

In practice, we solve this program for a given T and then search over different values of T to find the optimum.

Fourth, we observe that neither type chooses to save at an efficient contract pair. This is obvious for high-risk types since A^H is a full insurance annuity. The low-risk types have no incentive to save in a constrained efficient setting because, when mortality is uncertain and there are neither bequest motives nor administrative loads, accumulating assets is a less efficient way of transferring income forward in time than buying an annuity. The life-contingency of annuity payments allows a given consumption stream to be provided with fewer resources. Alternatively, it enables the annuity buyer to earn a return conditional on surviving that is enhanced because there is a risk of death and corresponding termination of payments. Constraints (BC) and (BC′) in (5) and (6) reflect our assumption of zero administrative loads. This is not a crucial assumption in our compulsory setting; assuming that loads are independent of contract structure would be sufficient. It is more efficient to use life-contingent payments than savings so that resources are not “wasted” at death. If a low-risk type receives an annuity A^L that induces her to save at some age, then her consumption stream, say Ã^L, would differ from the annuity stream. That same consumption stream could be achieved directly via an annuity at a lower actuarial cost to the annuity provider. There is therefore some surplus to be created by reducing the annuity’s payouts in its early years and raising its payouts in later years. Insurers in an efficient market will take advantage of such opportunities to repackage the timing of cash flows until the surplus is eliminated and low-risk types no longer wish to save out of their annuity payments. Formally, consider replacing A^L with Ã^L in (6). Low-risk types would be exactly as well off as before, but when A^L ≠ Ã^L the budget constraint would be strictly looser. Furthermore, the incentive compatibility constraint will be no tighter, and possibly strictly looser. Therefore, A^L can only solve (6) when A^L = Ã^L

The observation that neither type chooses to save means that, in equilibrium, V^L (A^L) = U^L (A^L) and V^H (A^H) =U^H (A^H), so both can be computed directly instead of by solving the non-trivial (3). The only part of (6) that is difficult to compute is V^H (A^L) the utility that high-risk types get if they deviate, purchase the low-risk type annuity, and save optimally. The structure of (6) allows us to evaluate V^H (A^L) in solving for equilibrium without explicitly solving (3). In particular, with our assumptions about the parametric forms for survival probabilities and preferences, V^H (A^L) = Ṽ^H (A^L; n^*) at any solution to (6) for some n^*, where

$${\stackrel{\sim }{V}}^H(A_L;n^{\ast })=\sum _{t=0}^N{\delta }^t{S}_t^{H}u({\stackrel{\sim }{c}}_t^H)$$ (7)

and

$${\stackrel{\sim }{c}}_t^H=\left\{\begin{array}{cc}{a}_t^L& ift<n^{\ast }\\ \frac{{\left(\frac{S_t^H}{S_{n^{\ast }}^H}\right)}^{\frac{1}{\gamma }}{\sum }_{n=n^{\ast }}^N{\delta }^n{a}_n^L}{{\sum }_{n=n^{\ast }}^N{\delta }^n{\left(\frac{S_n^H}{S_{n^{\ast }}^H}\right)}^{\frac{1}{\gamma }}}& ift\ge n^{\ast }\end{array}\right\}.$$ (8)

Eqs. (7) and (8) describe the utility achieved by a high-risk type with an annuity stream A^L when she consumes the payments before period n^*, and thereafter follows the consumption pattern she would follow if the remaining annuity stream $\left(a_{n^{\ast }}^L,\cdots ,a_N^L\right)$ were a bond against which she could save and borrow at the constant rate r. Hence, saying that V^H (A^L) = Ṽ^H (A^L; n^*) for some n^* is a solution to (6) is tantamount to saying that the optimal consumption pattern of high-risk types who deviate and buy annuity stream A^L is of this form. For their utility to be given by a consumption pattern of this form, the stream A^L must be such that this consumption pattern of deviating high-risk types does not involve borrowing.

The Appendix shows that annuity stream A^L has the property that deviating high-risk types will optimally consume in accord with (8). The intuition behind this result offers insights into the critical importance of saving in determining the optimal annuity streams. Suppose that annuitants could not save. Then we could solve (6) by replacing V^H (A^L) with U^H (A^L) and using first order conditions. To illustrate such a solution, Fig. 3 plots the annuity streams A^L and A^H for a special case of the general problem. This case corresponds to the T̄ = 0 extreme, i.e., to the MWS equilibrium. We consider only the male population in the baseline parameterization of our model, as developed below. The special case also assumes a constant relative risk aversion coefficient of γ = 3 and r = .03. Fig. 3 shows that A^H is a full insurance annuity and A^L is an annuity which is almost a full insurance annuity with significantly higher annuity payments. The payments provided by A^L decline with time, but this decline is only significant at late ages—indeed, it is negligible until age 97. The payments fall off sharply thereafter, but the A^L annuity payment only falls below the A^H payment at age 100—the oldest age considered. Between ages 99 and 100, however, the payment falls off so sharply that the incentive compatibility constraint is satisfied. Qualitatively similar plots would hold for less extreme values of T̄.

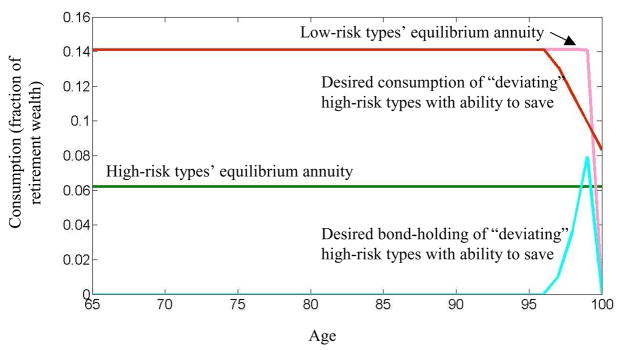
Fig. 3.

Efficient annuities when savings are observable and contractible. This figure plots the pair of annuity contracts solving Eq. (5) when savings is observable and contractible and when V̄^H (high-risk types’ minimum utility) is equal to the utility high-risk types get from their full insurance actuarially fair contract. The annuity curves plot the size of the life-contingent annuity payments as a function of the age of annuitant. “Desired consumption (bond-holding) of ‘deviating’ high-risk types” refers to the hypothetical optimal consumption (bond-holding) pattern for high-risk types who are given the low-risk types’ equilibrium annuity and can freely save.

A^L falls off steeply and at an advanced age because this is when S^L/S^H is smallest. Low annuity payments translate directly into low consumption when individuals cannot save. This reduces the utility of high-risk types much more than that of low-risk types at old ages, since high-risk types are relatively much more likely to still be alive at those ages. The best way from the perspective of low-risk types to satisfy incentive compatibility for high-risk types involves providing a downward tilt in annuity payouts at extreme old ages, when the relative probability of low-risk types being alive, compared to high-risk types, is lowest. In practice, many governments and families provide an implicit safety net for individuals who exhaust their resources. This can limit the capacity of late-life punishments to serve as screening devices, thereby reducing the disparity between the efficient frontier with and without savings.

When individuals can save, such a steep drop-off is far less useful as a self-selection device because it can always be undone—albeit inefficiently—by saving. Indeed, Fig. 3 also shows the optimal consumption pattern ${\stackrel{\sim }{c}}_t^H$ and bond-wealth holding of high-risk types who receive annuity A^L but who can also save. These high-risk types optimally choose to consume the annuity payments until age 96. At older ages they use their savings to smooth out the sharp drop-off in the annuity stream. Because such saving reduces the power of downward-sloping payout schedules as a selection device, when annuitants can save, the extremely sharp fall-off of payments A^L will no longer be optimal. The incentive for positive saving by deviating high-risk types, however, will still be as in (8).

3.2. Optimal structure of contracts

We find the optimal structure of annuity contracts when annuitants can save by solving (6). We cannot offer general analytic solutions, so our findings necessarily require assumptions about the underlying functional forms of the utility functions and mortality rates as well as various parameter values. Using the same baseline parameters that we used in Fig. 3, and the same assumption that T̄ = 0, Fig. 4 plots the solution to (6) and shows the actuarially fair full insurance annuities for both high-risk and low-risk individuals, as well as the optimal consumption stream of a high-risk type who deviates and purchases annuity A^L Qualitatively similar graphs would obtain for other values of T̄.

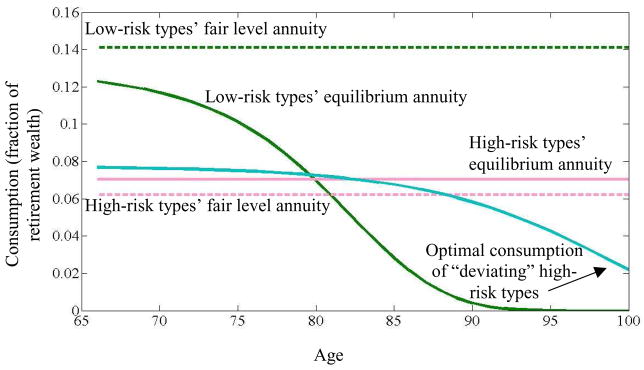
Fig. 4.

Efficient annuities when saving is unobservable or non-contractible. This figure plots the pair of annuity contracts solving Eq. (5) when savings is unobservable or non-contractible and when V̄^H (high-risk types’ minimum utility) is equal to the utility high-risk types get from their full insurance actuarially fair contract. The annuity curves plot the size of the life-contingent annuity payments as a function of the age of annuitant. “Optimal consumption of ‘deviating’ high-risk types” refers to the optimal consumption pattern for high-risk types who “deviate” and purchase the low-risk types’ equilibrium annuity. Calculations are for the baseline parameters described in Section 4 and Table 1.

Several features of Fig. 4 are worthy of note. First, the solution involves substantial cross subsidies. This is clear from a comparison of the level of the high-risk type fair level annuity and the high-risk type optimum annuity A^H, as A^H offers strictly higher payouts. Second, while A^L provides a downward sloping annuity stream, it declines much more gradually than the annuity stream shown in Fig. 3, which corresponds to the case in which annuitants could not save. Third, the optimal consumption stream of a high-risk type deviating to A^L reveals that the deviating high-risk type who purchases A^L will immediately begin to save: n^* = 0 in (7) and (8).

Comparing Figs. 3 and 4 shows how allowing for unobservable saving affects the structure of the optimal annuity streams. Though it is more difficult to find the optimal annuities with unobservable saving than without, the evident realism that allowing for such saving provides leads us to choose this as our benchmark case. Indeed, the results in Fig. 3 suggest that if unobservable saving is not possible, asymmetric information is essentially irrelevant because the optimal annuity streams are virtually identical to the annuity streams that would obtain with symmetric information. The findings more generally suggest caution in using applied contract theoretic models for quantitative purposes when there are inefficient and unobservable behaviors the insured can undertake as a substitute for formal insurance.

3.3. Discussion of key assumptions

The discussion of unobservable saving highlights one of several extensions we have made to the standard stylized model of insurance markets with asymmetric information. These extensions add realism to our framework for analyzing the impact of a ban on gender-based pricing. Nonetheless, the model that we develop in (5) and (6), and then solve, makes a number of assumptions for tractability and still falls short of a fully realistic model. Some of our assumptions, such as the use of constant relative risk aversion utility or the assumption that individuals discount the future at the rate of interest, are standard. Others are more specific to this application.

First, our model does not include bequest motives. The potential role of bequest motives in explaining saving behavior has been widely debated, for example by Kotlikoff and Summers (1981), Hurd (1987, 1989), Bernheim (1991), Brown (2001), and De Nardi (2004), but no robust consensus has emerged. Conceptually, the presence of bequest motives can easily be incorporated into our framework. We would simply add utility from consumption in states when the annuitant is dead. Since our solution algorithm relies heavily on the shape of preferences, however, this extension can pose practical issues of computational tractability. In part for this reason, we have addressed the analytically more convenient setting without bequests, while recognizing that this limits the potential applicability of our findings. We suspect that bequest motives would make screening more difficult and less efficient, thereby magnifying the efficiency consequences of requiring unisex pricing.

Second, we have followed previous theoretical models in modeling mortality heterogeneity via two risk types. The computational challenge of finding optimal contracts is much more difficult in a many-type setting, although solution algorithms similar to the ones we developed here would, in principle, also apply. We show below that our data cannot reject the parsimonious two-type model in favor of one which allows the underlying types to differ by gender. We focus on a setting with a single dimension of heterogeneity. Smart (2000) and Wambach (2000) show that adding dimensions, such as preference heterogeneity with regard to risk aversion, can significantly change equilibrium contracts. Recent empirical evidence presented by Finkelstein and McGarry (2006) and Cohen and Einav (2007) suggests that heterogeneity in risk aversion may be a quantitatively important feature of insurance markets.

Third, while our model incorporates some important features of the U.K. annuity market, it does not capture many others. For example, in assuming that markets are efficient, we abstract away from administrative loads in annuity pricing. We also abstract away from other annuitant choices, such as the option to purchase limited term guarantees on their contracts, or the options of couples to purchase joint-and-survivor annuity products instead of the single-life annuities on which we focus our attention. We ignore the presence of wealth outside retirement accounts, thereby abstracting from other assets, such as housing wealth, which may serve as a partial hedge against longevity risk. We additionally abstract from the possible presence of risks other than longevity risk, such as liquidity risks or health shocks. Crocker and Snow (2005) discuss how such “background risks” can affect insurance market equilibrium.

Finally, our model does not allow for the possibility of individuals learning over time about their risk type. Polborn et al. (2006) show that allowing for such dynamic considerations when individuals can time their insurance purchases may have important qualitative effects on the analysis of restrictions on characteristic-based pricing. In part because of these and other modeling abstractions, the optimal annuity contracts that emerge from our analysis do not match actual U.K. retirement annuity contracts. We discuss this further below.

4. Model calibration

To calibrate our model and quantify the efficiency and distributional consequences of mandating unisex prices, we must fix the relative risk aversion parameter γ; the real interest rate r; the fraction of high-risk individuals among men (λ^M) and women (λ^F); the fraction θ of women in the relevant population; and the survival curves for each risk type (S^H and S^L). We present results for risk aversion coefficients of 1, 3, and 5, assume the interest rate r is equal to 0.03, and set the discount rate δ=1/1+r. We set θ = 0.5 in our baseline case, but we also report results for other values.

We estimate the remaining parameters using micro-data on a sample of compulsory annuitants who bought annuities from a large U.K. life insurance company between 1981 and 1998. We have information on their survival experience through the end of 1998. These data, which are described in more detail in Finkelstein and Poterba (2004), appear to be reasonably representative of the U.K. annuity market. We restrict our attention to annuities that insure a single life and we focus on individuals who purchased annuities at the modal age for men (age 65). We exclude annuitants who died before their 66^th birthday and consider only mortality after age 66. Our sample consists of 12,160 annuitants. Only 1,216 are women, so our inferences regarding mortality rates for women are necessarily less precise than those for men. Our sample represents roughly one-third of Finkelstein and Poterba’s (2004) sample of annuities purchased by buyers of all ages.

We estimate the survival curves for two underlying, unobserved risk types H and L. In the spirit of Heckman and Singer (1984), we assume a parametric form for the baseline mortality hazard and jointly estimate the parameters of the baseline and the two multiplicative parameters that capture unobserved heterogeneity. We follow the actuarial literature on mortality modeling, such as Horiuchi and Coale (1982), and assume a Gompertz functional form for the baseline hazard. This is particularly well suited to our context because our data are sparse in the tails of the survival distribution. Formally, for a given risk type σ, the mortality hazard at age x_i is given by:

$$\mu (x_i\mid \sigma )={\alpha }_{\sigma }·exp(\beta (x_i-b)),$$ (9)

where b is the base age, 65 in our case. We assume that the growth parameter β is common to both risk types and to both genders. This means that β determines the shape of the mortality curves for both types, which differ only in their values of α_σ. Using the notation t_i = x_i − b, this form of the hazard implies risk-type-specific survival functions of the form:

$$S(t_i\mid \sigma )=exp\left\{\frac{{\alpha }_{\sigma }}{\beta }(1-exp(\beta ·t_i))\right\}.$$ (10)

When the two underlying risk types are the same for males and females, so that only the mix of these two risk types differs across genders, this model depends on a parameter vector Θ = {α_L, α_H, β, λ_f, λ_m}.

The likelihood function in this case is:

$$\begin{array}{l}L(\mathrm{\Theta })\equiv \sum _i{1}_m·\left({\lambda }_m{l}_i^H+(1-{\lambda }_m)l_i^L\right)+1_m·\left({\lambda }_f{l}_i^H+(1-{\lambda }_f)l_i^L\right)\\ \mathit{where}\\ l_i^{\sigma }=S(t_i\mid {\alpha }_{\sigma },\beta )(d_{\sigma }+(1-d_i)\mu (t_i\mid {\alpha }_{\sigma },\beta )),\sigma =\{H,L\}.\end{array}$$ (11)

The variable d_i in (11) is an indicator for whether the individual observation is censored and 1_m and 1_f are indicator variables for whether the individual is male or female, respectively. An individual’s contribution to the likelihood function is a weighted average of the likelihood function of a high-risk and low-risk type, with the weights equal to the gender-specific fraction of high and low-risk individuals. Of the observations in our sample, 81% are censored because the annuitant is still alive at the end of the sample period, December 31, 1998.

Table 1 presents our estimates of the mortality model in (10) and (11). Our estimates yield aggregate mortality statistics that are similar to those published by the Institute of Actuaries (1999) for all 65 year-old U.K. pensioners in 1998. The life expectancies implied by our model differ from those in the aggregate tables by only 0.26 years for women and 0.45 years for men. The estimated mortality rates for the high and low-risk types are substantially different. For example, the estimates in Table 1 imply that life expectancy at 65 is only 8.8 years for low-risk types, compared to 23.2 years for high-risk types. The estimate in column 5 of Table 1 shows that over 80% of women are classified in the high-risk (long-lived) group, compared to only about 60% of men (column 4). The estimates therefore imply a three-year difference in life expectancy at age 65 for men and women. Survival differences this large imply substantial potential redistribution toward women from unisex pricing restrictions.

Table 1. Estimates of two-type Gompertz mortality hazard model, same types for both genders.

Results are based on estimating Eq. (11) using micro-data on annuitant mortality patterns for a sample of compulsory annuities purchased from a large U.K. life insurer between 1981 and 1998. Standard errors are in parentheses. Column 6 contains the total log likelihood. Column 7 reports the χ²(3) statistic (P-value) for the Likelihood Ratio test of this restriction relative to the more flexible specification in Table 2.

Sample	Multiplicative factor on hazard for high risk (αH)	Multiplicative factor on hazard for low risk (αL)	Common growth factor in hazard model (β)	Fraction of men who are high risk (λM)	Fraction of women who are high risk (λF)	log(L)	χ2(3) (P-value)
	(1)	(2)	(3)	(4)	(5)	(6)	(7)
65 Year olds (N=12160)	0.0031 (0.0003)	0.0405 (0.0013)	0.1485 (0.0056)	0.6051 (0.0096)	0.8192 (0.0231)	−10347.45	1.94 (0.59)

We investigated the restrictiveness of our five-parameter model by estimating a more flexible eight-parameter model that allows for gender-specific risk types. In addition to having a gender-specific fraction of high-risk types, λ, the parameters α_L, α_H, and β are also permitted to be gender specific. Table 2 shows the results. For men, the estimates of the mortality parameters look qualitatively similar to those in Table 1. This is not surprising, since most of the sample is male. The estimates for women do not reject the null hypothesis of a single underlying risk type. The one-type model actually exhibits the best fit. The likelihood function for women varies very little as the model parameters change, which explains why we cannot reject the validity of the implicit parameter restrictions involved in using the five- instead of the eight-parameter model. In light of these results, we use the parameter estimates from our more parsimonious model.

Table 2. Estimates of two-type gender-specific Gompertz mortality model.

Results are based on estimating Eq. (11) separately for each gender using the same data as in Table 1 Standard errors are in parentheses. The estimation for females led to a single type model. The final column reports the total log likelihood.

Sample	Multiplicative factor on hazard for high risk (αH,m/αH,f)	Multiplicative factor on hazard for low risk (αL,m/αL,f)	Common growth factor in hazard model (βm/βf)	Fraction who are high risk (λm/λf)	log(L), by gender	log(L)
	(1)	(2)	(3)	(4)	(5)	(6)
65 Year old males (m) (N=10944)	0.0030 (0.0003)	0.0423 (0.0014)	0.1566 (0.0058)	0.6305 (0.0091)	−9568.59	−10346.4
65 Year old females (f) (N=1216)	0.0111 (0.0009)	NA	0.0882 (0.0228)	NA	−777.89

5. Measuring the efficiency and distributional effects of banning gender-based pricing

This section briefly describes the measures that we use to quantify the efficiency and distributional effects of a unisex pricing restriction in the model described above. Standard measures of the distributional and efficiency effects of regulatory policies, such as compe nsating variation, equivalent variation, and their corresponding measures of deadweight burden, do not naturally extend to settings with asymmetric information. It is not clear what it means to estimate the transfer that a consumer of a given type requires to be as well off after a policy intervention as beforehand when it is not possible for the government to identify the consumer and carry out the transfer. Our measure of inefficiency is in the spirit of Debreu (1951, 1954), and it is also the natural quantification of the efficiency notion used by Crocker and Snow (1986) when they demonstrate that restrictions on categorical pricing in insurance markets are efficiency reducing.

To measure efficiency and redistribution, we use the actuarial cost function C^σ (A) from (4), which gives the expected cost to an insurance company of honoring contract A when it is owned by an individual of risk type σ. The cost, for a vector A^i,σ of contracts for each type i ∈ {X,Y} and category σ ∈ {H,L}is given by the total actuarial cost function:

$$\begin{array}{l}TC(A^{i,\sigma })\equiv \theta \left({TC}^Y(A^{Y,\sigma })\right)+(1-\theta )\left({TC}^X(A^{X,\sigma })\right)\\ \equiv \theta \left({\lambda }_Y{C}^H(A^{Y,H})+(1-{\lambda }_Y)C^L(A^{Y,L})\right)+(1-\theta )\left({\lambda }_X{C}^H(A^{X,H})+(1-{\lambda }_X)C^L(A^{X,L})\right),\end{array}$$ (12)

where the total cost functions for each category, TC^X and TC^Y, are defined implicitly, and A^Y,σ and A^X,σ denote category-specific vectors of contracts. The minimum expenditure function is defined by:

$$E\left(A^{i,\sigma }\right)\equiv \{\begin{array}{cc}\underset{\{{\stackrel{\sim }{A}}^{X,L},{\stackrel{\sim }{A}}^{Y,L},{\stackrel{\sim }{A}}^{X,H},{\stackrel{\sim }{A}}^{Y,H}\}}{\mathit{\text{Min}}}& TC({\stackrel{\sim }{A}}^{i,\sigma })\\ \mathit{\text{Subject to}}& (IC):V^{\sigma }({\stackrel{\sim }{A}}^{i,\sigma },S^{\sigma })\ge V^{\sigma }({\stackrel{\sim }{A}}^{i,{\sigma }^{\prime }},S^{\sigma })\forall i\in \{X,Y\}\mathit{\text{and}}\forall \sigma ,{\sigma }^{\prime }\in \{H,L\}\\ \mathit{and}& (MU):V^{\sigma }({\stackrel{\sim }{A}}^{i,\sigma },S^{\sigma })\ge V^i(A^{i,{\sigma }^{\prime }},S^{\sigma })\forall i\in \{X,Y\}\mathit{and}\forall \sigma \in \{H,L\}.\end{array}$$ (13)

The minimum expenditure function maps a proposed allocation A^i,σ of contracts to each type within each category into the minimum total actuarial cost of ensuring that each type within each category is at least as well off as with A^i,σ, while respecting the economy’s inherent informational constraints. These inherent constraints are captured by (IC) in (13), which requires that within each category, individuals need to be willing to choose the contract à designed for them. Because category is observable, however, incentive compatibility does not have to be satisfied across categories.

An efficient allocation A^i,σ solves (13). Any other informationally feasible contract set Ã^i,σ that makes each individual as well off as A^i,σ has at least as high a total actuarial cost. Other allocations are inefficient, and the quantity TC(A^i,σ) − E(A^i,σ) is a measure of the inefficiency. If $A_1^{i,\sigma }$ and $A_2^{i,\sigma }$ denote any two vectors of contracts, then the efficiency cost of moving from the former to the latter is

$$EC(A_1^{i,\sigma },A_2^{i,\sigma })\equiv \left(TC(A_2^{i,\sigma })-E(A_2^{i,\sigma })\right)-\left(TC(A_1^{i,\sigma })-E(A_1^{i,\sigma })\right).$$ (14)

For our analysis of a ban on categorical pricing, this expression simplifies because, by assumption, the market outcome prior to the ban is efficient. The efficiency cost of a ban is therefore exactly the inefficiency of the post-ban equilibrium contract set.

Since both TC(·) and E(·) decompose by category, the efficiency cost of a ban on characteristic-based pricing can be decomposed by category as TCⁱ (A^i,σ) = Eⁱ (A^i,σ) + Inefficiencyⁱ (A^i,σ). This expression decomposes the actuarial cost, or the resource use, of a given category into two components: the minimum resources needed to make the types that well off, and the resources that are wasted because of an inefficient allocation. We interpret the former as a money-metric measure of the well being of the individuals in the category, since the wasted resources do not contribute to well being. We can therefore quantify redistribution at the category level from a policy that changes the contract set from $A_1^{i,\sigma }$ to $A_2^{i,\sigma }$ as the increase in this money-metric measure. Redistribution towards category Y is therefore given by $R^Y\left(A_1^{i,\sigma },A_2^{i,\sigma }\right)\equiv \left(E^Y(A_2^{Y,i})-E^Y(A_1^{Y,i})\right)$. There is a similar expression for the redistribution towards category X.

When a policy change has efficiency consequences, the weighted sum of redistribution across categories will not be zero, even when the policy change does not affect the total actuarial cost. This is because some of the redistribution away from category X can be dissipated via an increase in the inefficiency of the allocations and might never reach category Y. Since some may find it appealing to have a measure of redistribution for which the entire amount redistributed away from one group is redistributed to the other group, we construct the re-centered measure:

$${\stackrel{\sim }{R}}^Y\left(A_1^{i,\sigma },A_2^{i,\sigma }\right)\equiv R^Y\left(A_1^{i,\sigma },A_2^{i,\sigma }\right)-\left(\theta R^Y\left(A_1^{i,\sigma },A_2^{i,\sigma }\right)+(1-\theta )R^X\left(A_1^{i,\sigma },A_2^{i,\sigma }\right)\right).$$ (15)

This expresses the re-centered redistribution per member of category Y; again there is a similar expression for category X.

Fig. 2 can be used to illustrate the efficiency and distributional measures when category is perfectly predictive of type (i.e., λ_X = 0 = 1 − λ_Y). In this setting, the efficiency metric equals the sum of certainty equivalent consumptions across types. Prior to the ban on categorical pricing, the competitive market gives actuarially fair full insurance contracts A^L* and A^H* to the two types; this allocation, which entails state-independent consumption, is efficient. When categorical pricing is banned, the market implements a pair of contracts labeled A^L and A^H which is as efficient as possible given the government imposed pricing constraints. This set of allocations is nevertheless inefficient because A^L could, in principle, be replaced by the full insurance consumption contract A′^L which makes low-risk types equally well off, while saving resources. The efficiency cost of the ban is precisely the difference in the actuarial costs of A^L and A′^L, scaled by the number of low-risk types in the market.

The policy also redistributes resources from low to high-risk types. The amount redistributed to each of the high-risk types, computed without re-centering, is the actuarial difference between A^H and A^H* computed using the high-risk types’ mortality. We measure the amount redistributed away from each of the low-risk types via the actuarial difference between A^L* and A′^L, in this case computed using low-risk type’s mortality rates. The change in actual resource use or in the actuarial cost of the low-risk types’ contract is measured by the actuarial difference between A^L* and Ā^L, again using low-risk type mortality rates.

When categorization is imperfect, the same sort of analysis applies, but summing certainty equivalents across individuals is no longer a valid measure of efficiency. Because contract outcomes are assumed to be constrained efficient when categorical pricing is allowed, we need only consider the inefficiency of the post-ban equilibrium. Fig. 5 illustrates this. The post-ban allocation is given by the contract pair A^X,H = A^Y,H ≡ A^H and A^X,L = A^Y,L ≡ A^L. This allocation is inefficient because of the inefficient allocation within the X category. Having fewer high-risks within that category means that additional (break even) cross subsidies from low-risk types to high-risk types within that category can make both types in the X category better off. Hence, both X category types could be made at least as well off with fewer resources. The pair of contracts shown in Fig. 5 illustrates how this could be done. On the other hand, because the Y category has a greater fraction of high-risks, additional cross subsidies within that category do not yield Pareto improvements—the original contracts are, in fact, the efficient way for Y category types to achieve their original level of well being. The efficiency cost of the ban is measured by the difference in the actuarial costs of the market allocations and the associated efficient allocations.

Fig. 5.

The inefficiency of categorical pricing bans. This figure illustrates the efficiency and re-distribution metrics described in Eqs. (14) and (15). When categorization is banned, the market provides the contract A^H (A^L) to high-risk (low-risk) types of both categories. Since this allocation involves positive cross subsidies from low-risk to high-risk types, it also involves redistribution across categories with different risk type fractions. Eq. (15) quantifies this redistribution. Insofar as category is observable, the allocation (A^L, A^H) is also inefficient. In this example, the inefficiency stems from the fact that one category has fewer high-risk types. This means that each risk type within that category can be made at least as well off with the contract pair (A′^L, A′^H) at a lower expected cost to annuity providers. Eq. (14) quantifies this inefficiency.

Because we consider the set of constrained Pareto efficient market outcomes, there is a range of possible market allocations both prior to and subsequent to a ban on categorical pricing—hence a range of possible estimates of the consequences of a ban. The efficiency and distributional measures developed above allow us to summarize all possible efficiency and distributional effects of a ban via a single-parameter family of consequences. This family ranges from a “high efficiency cost, low redistribution” end-member to a “low efficiency cost, high redistribution” end-member. To see this, note that prior to a ban in gender-based pricing, the market is, by assumption, efficient. The efficiency cost of a ban is therefore equal to the inefficiency of the post-ban allocation. Moreover, because the market does not implement cross subsidies across genders in the absence of a ban, the total “welfare,” measured by Eq. (13), of each gender prior to the ban is W. The distributional consequences of a ban can be measured from the “welfare” of each gender in the allocation which obtains when a ban is implemented, regardless of the specifics of the market allocation in the absence of a ban.

The range of possible efficiency and distributional consequences of banning gender-based pricing can be computed from the range of possible post-ban market outcomes, namely by the solutions to (5) as V̄^H varies from the utility V̄^H (W) that H-types obtain from their full insurance actuarially fair contract to the utility $V^H\left({\overline{\overline{A}}}^{\lambda }\right)$ that they obtain from an actuarially fair full insurance contract that pools across types and genders. Furthermore, one can show that the redistribution towards women is monotone increasing in V̄^H and that the efficiency cost is strictly decreasing in V̄^H until the efficiency cost reaches zero. Hence, bounding the possible efficiency and distributional consequences of a ban amounts to computing the solution to (5) at the two endpoints, where the lower end of this range corresponds precisely with the MWS equilibrium, and the upper end corresponds with the pooled-fair full-insurance outcome. While this leaves a potentially large range of consequences, it has the advantage of characterizing the full set of feasible constrained efficient outcomes. Those who are willing to choose a particular equilibrium concept—such as the MWS equilibrium—can narrow the range of possible consequences to a single point.

6. Estimates of the efficiency and distributional consequences of banning gender-based pricing

We begin by reporting findings for our baseline model, in which firms have full flexibility in designing the payment profile of the annuities they offer, individuals can save out of their annuity income, and insurance companies cannot observe saving. We then consider results in several restricted models and then evaluate the sensitivity of our findings to changing several key parameters.

6.1. Baseline model results

Table 3 summarizes the results associated with both the MWS and the pooled-fair outcome, with the latter labeled SS. The first six columns of Table 3 present the minimum expenditure functions for women, men, and the total population at each of the two extreme contracts which may obtain when categorization is banned. These are E^F, E^M, and E, in the notation used above (see (13)). They denote the minimum per person resources needed to ensure that each type is at least as well off as in the equilibrium while respecting the inherent informational constraints of the model. Since each person is endowed with one unit of resources, the difference between the fifth and sixth columns and 1.0 gives the efficiency cost of the ban when the post-ban contracts are given by the MWS and the pooled-fair outcomes, respectively. This percentage difference is reported in the seventh and eight columns. For a risk aversion coefficient of 1, the high-end (MWS-end) efficiency cost is 0.04% of retirement wealth W. For risk aversion coefficients of 3 and 5, the comparable costs are about 0.02%. If, subsequent to a ban, the market implements the pooled-fair endpoint outcome, then there are no associated efficiency costs. The low upper bound on efficiency costs in part reflects our focus on a compulsory annuity market. The efficiency costs of eliminating characteristic-based pricing in voluntary insurance markets could be very different from our estimates. In a simpler model of a voluntary annuity market, Rea (1987) estimates efficiency costs of 0.15%. Rea’s model counterfactually implies that all retirees fully annuitize, however. We believe that efficiency costs are likely to be even larger when individuals choose whether or not to participate in the insurance market.

Table 3. Range of efficiency and distributional consequences of unisex pricing.

Estimates are based on the model and algorithm described in Section 3. Columns labeled MWS refer to the high efficiency cost/low redistribution end of the range of possible consequences of a ban on gender-based pricing. This obtains if the market implements the Miyazaki (1977), Wilson (1977), Spence (1978) equilibrium when gender-based pricing is banned. Columns labeled SS refer to the zero efficiency cost/high redistribution end of the range. This obtains if the market implements a pooled-fair full insurance “Social Security-like” outcome when gender-based pricing is banned. The MWS contracts are computed using Eq. (5) and the risk type-distributions estimated in Table 1, pooled across genders. Columns (1)–(6) are computed using Eq. (14) and columns (9)–(10) are computed using Eq. (15).

Relative risk aversion	Required per-person endowment needed to achieve utility level from non-categorizing equilibrium when categorization is allowed								Redistribution to women (R̃W), per woman, % of endowment		Efficiency cost per dollar of redistn
	Women (EW)		Men (EM)		Total population(E)		Efficiency cost as % of total endowment
	MWS	SS	MWS	SS	MWS	SS	MWS	SS	MWS	SS	MWS
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)
γ=1	1.020	1.071	0.979	0.929	0.9996	1	0.038%	0%	2.08%	7.14	3.66%
γ=3	1.033	1.071	0.966	0.929	0.9998	1	0.025	0	3.39	7.14	1.45
γ=5	1.040	1.071	0.959	0.929	0.9998	1	0.018	0	4.06	7.14	0.89

The eleventh and twelfth columns of Table 3 report summary statistics for redistribution from men to women. This is the re-centered redistribution per woman defined in (15). For a risk aversion coefficient of one, we estimate that 2.1% of the endowment is redistributed when the market implements the MWS-endpoint outcome in the unisex setting. For risk aversion coefficients of 3 and 5, the comparable estimates are 3.4% and 4.1%, respectively. The last column of Table 3 reports the efficiency costs as a percentage of the amount of redistribution for the high-end MWS case. This ratio varies from 3.6% for a risk aversion of one to under 1.0% for a risk aversion of five.

When the market implements the pooled-fair outcome instead, it redistributes a total of 7.1% of resources towards women. This is between 1.8 and 3.4 times more redistribution than the low-end redistribution estimates of Table 3. In addition to providing an endpoint for the possible consequences of a ban in gender-based pricing in our setting, the 7.1% redistribution and zero-efficiency cost endpoint are also interpretable as the effect of banning gender-based pricing in a compulsory full-insurance setting such as the U.S. Social Security system. In such a setting individuals are, in effect, required to purchase level inflation-protected annuities with their retirement accumulations W. If categorization by gender is allowed and pricing is actuarially fair, men get larger per-period annuity payouts than women for a given initial premium. If categorization is not allowed, all buyers receive the same full insurance annuity with an intermediate payout level. Because there is no scope for insurers to adjust the menu of policies that they offer in response to the ban, such a ban would not have any efficiency costs. The consequences in such a setting are thus identical to the high-distribution endpoint calculations in Table 3.

The smaller redistributive effect of eliminating gender-based pricing in the MWS-endpoints in Table 3, relative to the “Social Security” setting, results from the endogenous adjustment of optimal annuity profiles, not of reduced demand for annuities by men, since annuitization is mandatory in our benchmark setting. The reduction in redistribution results from the fact that firms can sell annuity contracts that vary in the time profile of their payout stream and that, by using these profiles for screening, they can partially undo the transfers that take place as a result of the ban on gender-based pricing. This highlights how recognition of how the structure of insurance contracts responds to government regulation can have important effects on analyses of the regulatory policy.

6.2. Results in restricted models

We compare the results from our baseline model with those from two alternative models. The first restricts the behavior of annuity buyers by disallowing saving, and the second restricts the behavior of annuity providers by limiting the set of contracts they can offer. These exercises help to expand our understanding of how various provisions in our model affect our results and they illustrate the importance of extending the basic model to account for real-world features such as access to savings or limits on the set of contracts insurers can offer. In both cases, we focus exclusively on the high-efficiency cost low-redistribution endpoint. The other endpoint is unaffected by these changes.

Table 4 summarizes our findings from the two alternative models. We explained earlier that if annuitants cannot save, or if their saving can be observed and contracted upon by insurance companies, then the MWS equilibrium annuities of short-lived types are characterized by contracts that are level until very old ages, at which point payments fall off rapidly. Because long-lived types have a substantial chance of being alive at those old ages, relative to short-lived types, this shape enforces self-selection at very little cost to the short-lived types. In practice, this means that the MWS equilibrium contracts offered to each sub-population, whether males alone, females alone, or the pooled population, involve no cross subsidies from the short-lived to the long-lived types, and the MWS equilibrium coincides with the Rothschild-Stiglitz equilibrium. Banning categorization has neither efficiency nor distributional consequences in this setting.

Table 4. Efficiency and distributional effects of ban on gender-based pricing in restricted models.

Unrestricted (Baseline) Model calculations are as in Table 3. The Restricted Contracts Model calculations are described in Section 6.2. In the Restricted Contracts Model, firms can only offer contracts with constant escalation or declination rates. In the No Savings Model, individuals are assumed to have no access to savings technology. Redistribution and efficiency metrics are described in Eqs. (15) and (14), respectively. ‘MWS’ refers to the Miyazaki (1977), Wilson (1977), Spence (1978) equilibrium. This is the constrained efficient market outcome with the least redistribution. ‘SS’ refers to the constrained efficient market outcome with pooling of risk types. This is the constrained efficient outcome with the highest amount of redistribution that we consider); it loosely corresponds to banning gender-based pricing in a compulsory Social Security setting.

	Redistribution to women (R̃W), per woman (as % of endowment)		Efficiency cost as % of endowment
	MWS	SS	MWS	SS
	γ=1
Unrestricted (baseline) model	2.0838	7.14	0.0381	0
No savings model	0	7.14	0	0
Restricted contracts model	1.3326	7.14	0.1000	0
	γ=3
Unrestricted (baseline) model	3.3874	7.14	0.0246	0
No savings model	0	7.14	0	0
Restricted contracts model	2.2504	7.14	0.1358	0
	γ=5
Unrestricted (baseline) model	4.0549	7.14	0.0180	0
No savings model	0	7.14	0	0
Restricted contracts model	2.8690	7.14	0.1352	0

In contrast, restricting the set of contracts that insurers can offer can increase the efficiency costs of a ban on gender-based pricing while reducing the amount of redistribution. We consider a restriction that makes the set of observed annuity policies more consistent with those in our modeling exercise. While U.K. annuity companies appear to use the time-profile of annuity payments to screen individuals according to their risk type, Finkelstein and Poterba (2002, 2004) report that insurers offer only a limited number of simple alternative payment profiles. Most policies involve level nominal payments, and the few exceptions involve nominal payments that escalate at a constant rate over time. Neither of these profiles is consistent with the annuity payout profiles generated in our model. It is possible that a richer and more realistic model might yield annuities with a structure that more closely accords with observed policies. Alternatively, we may have overlooked restrictions on the form of annuities that can be offered by insurance firms, such as explicit or implicit regulations on legal pension payment profiles or costs to either the consumer or producer from product complexity.

We modify our model by restricting insurance firms to offer only policies which provide benefits that rise or fall at a constant real rate: a_t+1 = ηa_t for some constant η and for all t. Subject to this additional requirement, market outcomes are still characterized by (5). As in the unrestricted program, the long-lived types purchase a full-insurance annuity, and short-lived types purchase a declining annuity. For the baseline parameters and a risk aversion of 3, the MWS equilibrium rate of decline is 12.1% per annum when gender-based pricing is banned, and is 9.5% and 13.3% for males and females, respectively, when gender-based pricing is allowed. Table 4 indicates that for a risk aversion of 3, a ban in gender-based pricing in this restricted contract model redistributes approximately 2.25% of retirement wealth towards women, at an efficiency cost of 0.136% of retirement wealth. The maximum amount of redistribution achievable by a ban on gender-based pricing falls by about one-third in a model with contract restrictions relative to a model without such restrictions. The efficiency costs, while still modest on an absolute scale, rise by an order of magnitude. These findings highlight how the nature of the contracting environment and the potential endogenous response to regulation can have substantial effects on the consequences of regulation.

These results also provide insight into why the efficiency costs are so small in the baseline model. There are two mechanisms for satisfying self-selection constraints in an MWS equilibrium. First, the short-lived (low-risk) types can be offered a highly distorted contract, such as a contract with front loading. This distortion makes the low-risk type contract less attractive to both types, but it is a distortion which is particularly unattractive to high-risk types. Second, there can be cross subsidies from the low-risk types’ contracts to the high-risk types’ contracts. These help satisfy self-selection by making the high-risk type annuity contracts more desirable and the low-risk type annuity contracts less desirable. The efficiency costs will tend to be large when a change in the mix λ of high and low-risk types has substantial effects on the optimal amount of distortion in the contract space.

Without saving, there is essentially no tradeoff between efficiency and redistribution. Distortions can be used to enforce self-selection at virtually no cost, so the equilibrium never relies on cross subsidies. This means that there is no change in the distortion when a ban is put in place, and therefore no efficiency cost. More generally, whenever the marginal cost of distortion is very small for low distortions, and very high at high distortions—with a sharp transition between these two regions—the efficiency cost of a ban will tend to be low, as the optimal mix of distortion and cross-subsidization will take place near the transition, irrespective of the relative fraction of low and high-risk types.

Restricting the contract space raises the efficiency cost of a ban on gender-based pricing because the transition is not as sharp in the restricted contracts case. With an unrestricted contract space, it is possible to target an optimal distortion, for example, by making the low-risk type annuity more downward sloping at old ages than at young ages. With this flexibility, a small distortion is very helpful, and additional distortions are less helpful, in achieving self-selection. In contrast, with the restricted contract space we consider, the distortion cannot be targeted: the size of the distortion is fully captured by the downward tilt of the low-risk type annuity. Relative to the unrestricted space, the tradeoff between distortion and cross subsidy is therefore flatter, raising the efficiency cost of banning category-based pricing.

6.3. Comparative statics

To provide some insight into the sensitivity of our results to various parameter choices, we compute the redistributive consequences and the efficiency cost of banning categorization under two alternative sets of parameter vectors.

First, we vary the fraction θ of women in the population. Our base case assumed that half of the population was female. Decreasing θ, to reflect the fact that most participants in the compulsory U.K. annuity market are male, increases the per-woman distributional effects of banning categorization. When there are relatively more men, women gain more by being pooled with them.

The efficiency cost of a ban is non-monotonic in θ because of two offsetting effects. First, the efficiency cost mechanically falls as the relative size of the male population decreases, since the efficiency cost of a ban in categorization in the MWS framework is entirely due to the inefficiency of the post-ban allocation amongst the low-risk category—in this case men. Second, as the number of women increases, the equilibrium payout in the non-categorizing case moves away from the men’s categorizing payout and toward the women’s. This raises the efficiency cost per male, counterbalancing the first effect. Finkelstein and Poterba (2004, 2006) report that about 70% of U.K. annuitants are male. The results in Table 5 suggest that this raises the amount of redistribution to women and decreases the efficiency cost per dollar of redistribution by about 40% compared to our baseline estimates with equal numbers of men and women.

Table 5. Sensitivity analysis for redistribution and efficiency cost calculations (γ = 3).

Same calculations as in Table 3 with varying parameters. Table 3’s baseline results appear in bold. Panel 1 considers the effects of varying the fraction of females in the annuitant pool, holding all other parameters constant at the Table 3 baseline levels. Panel 2 considers the effects of varying the mortality hazards for high and low-risk types at age 65. These hazards are varied so as to keep the aggregate mortality rate at age 65 constant. All other parameters are held at the Table 3 baseline levels. The redistribution and efficiency cost metrics are described in Eqs. (15) and (14), respectively. ‘MWS’ refers to the Miyazaki (1977), Wilson (1977), Spence (1978) equilibrium. This is the constrained efficient market outcome with the least redistribution. ‘SS’ refers to the constrained efficient outcome with pooling of risk types. This is the outcome that we consider with the most redistribution; it loosely corresponds to banning gender-based pricing in a compulsory Social Security setting.

Parameter(s) being varied and new value(s)	Redistribution to women (R̃W), per woman as % of endowment		Efficiency cost as % of endowment		Efficiency cost per dollar of distribution
	MWS	SS	MWS	SS	MWS	SS
Panel 1: Varying θ (fraction female)
θ = 0.1	6.37%	13.63%	0.00%	0%	0.32%	0%
0.3	4.84	10.30	0.01	0	0.89	0
0.5	3.39	7.14	0.02	0	1.45	0
0.7	2.00	4.17	0.03	0	1.97	0
0.9	0.66	1.35	0.01	0	2.40	0
Panel 2: Varying αH, αL = mortality hazards at age 65 for high-risk and low-risk types
αH, αL =.001, .046	4.72%	8.63%	0.02%	0%	0.91%	0%
.002, .043	3.98	7.85	0.02	0	1.18	0
.0031, .041	3.39	7.14	0.02	0	1.45	0
.005, .036	2.62	6.01	0.03	0	1.97	0
.008, .028	1.65	4.16	0.03	0	3.27	0

The second comparative static we consider involves varying the mortality hazards at retirement for the two different risk types. We hold constant the relative number of men and women, θ, as well as the relative numbers of high-risk types in each gender, λ_M and λ_F, and we vary the mortality hazards α_H and α_L in a way that keeps the population average mortality hazard at age 65 approximately constant. The gap between the two risk types in our baseline parameterization may be too large, since, at best, our estimates describe the differences in actual risks across types, as opposed to the private information individuals have when they make annuity purchases. Table 5 indicates that the amount of redistribution that takes place as a result of a unisex pricing rule is increasing in the difference between the mortality rates. The total efficiency cost, however, appears to be robust to the gap in the mortality rates. As a result, the efficiency cost per dollar of redistribution rises as the relative hazard declines.

In Finkelstein, Poterba, and Rothschild (2006), we considered a third comparative static which involved jointly varying α_H and α_L and the gender-specific fractions of each risk type, λ_M and λ_F, in such a way that life expectancies of the two genders remain constant and the aggregate fraction of high-risk and low-risk types remains unchanged. This had small but non-zero effects on our estimates of the distributional impact of unisex pricing. When we considered a smaller mortality gap, we found smaller distributional consequences of unisex pricing than in our baseline case. In contrast with the previous comparative static, however, the efficiency consequences of unisex pricing were as much as six times larger than in the baseline case.

7. Conclusion

This paper employs a model of insurance market equilibrium in the presence of asymmetric information to study the efficiency costs and the redistributive effects of regulations that restrict the set of individual characteristics that can be used in pricing insurance contracts. It moves beyond the qualitative observation that such regulations may entail efficiency costs to explore the quantitative effects of such policies. We develop, calibrate, and solve an equilibrium insurance contracting model for the United Kingdom’s compulsory retirement annuity market. While our model does not fully capture this market’s institutional features, it suggests the power of using equilibrium models in applied policy analysis.

Our findings underscore the importance of considering the endogenous response of insurance contracts to regulatory restrictions. Recognizing that insurers can vary the menu of contracts they offer may reduce estimates of the amount of redistribution from men to women under a ban on gender-based pricing by as much as 50%. The redistribution associated with a unisex pricing requirement, even accounting for the endogenous contract response, is substantial. Our baseline estimates suggest that at least 3.4% of retirement wealth is redistributed from men to women. In contrast, we find only modest efficiency costs of a requirement for unisex pricing in the compulsory annuity market. We suspect that this finding would not generalize to other settings in which insurance market participation is voluntary, and in which some consumers might choose not to participate in the market after various regulations were imposed.

Our analysis offers a starting point for comparing the consequences of unisex pricing in government provided social insurance programs with mandatory participation and no choice over annuity contract, such as the U.S. Social Security system, with the consequences of unisex pricing requirements in annuity markets with mandatory participation but choice over privately-supplied annuitant contracts, as in our U.K. setting. Our analysis, however, does not consider any of the potential long-run behavioral responses to a ban on gender-based annuity pricing. For example, a change in annuity pricing could affect the savings and labor supply decisions of those who will subsequently face compulsory annuitization requirements. Changes on these margins might affect our efficiency cost analysis. Annuity companies might also respond to unisex pricing requirements by conditioning annuity prices on observables that are not currently used in pricing, such as occupation or residential location. These characteristics might in turn adjust endogenously to the pricing, with resultant efficiency consequences. These are all important directions for further theoretical and empirical work.

Restrictions on gender-based pricing of retirement annuities are just one of many examples of regulatory constraints on insurance pricing. In the United States, for example, where insurance is regulated at the state level, there are many restrictions on the information set insurers may use in setting automobile insurance prices. Blackmon and Zeckhauser’s (1991) analysis of automobile insurance in Massachusetts raises issues similar to those in the current paper in a different context, although it does not explore how the menu of policy offerings might respond to regulation. Insurers also face restrictions in the markets for homeowner’s insurance and small-group and non-group health insurance. The growing field of medical and genetic testing promises to create new tensions between insurers and regulators, as medical science provides new information that insurers could potentially use to predict the future morbidity and mortality of life and health insurance buyers.

Our framework provides a natural starting point for evaluating the efficiency and distributional consequences of restrictions on characteristic-based pricing in a range of insurance markets more generally. A convincing analysis in these other settings will require attention to issues that we have not confronted in the compulsory annuity market. Analyzing the role of choice on the extensive margin of whether or not to purchase insurance is a key issue. In addition, while moral hazard is likely to be relatively unimportant in the annuity market, it may be pronounced in the automobile or health insurance market. Moral hazard effects need to be considered in analyzing the efficiency consequences of regulations.

Finally, the use of insurance market regulations to redistribute among various population groups raises interesting questions that range far beyond our study. These include why a society might wish to carry out transfers between men and women, or between other groups, the extent to which transfers in insurance markets are simply undone by other transfers within the household or in the private sector, and why insurance markets rather than, say, the tax system, are a natural locus for such transfers. These issues warrant discussion and research.