Abstract
A variety of studies have demonstrated that organizing stimuli into categories can affect the way the stimuli are perceived. We explore the influence of categories on perception through one such phenomenon, the perceptual magnet effect, in which discriminability between vowels is reduced near prototypical vowel sounds. We present a Bayesian model to explain why this reduced discriminability might occur: it arises as a consequence of optimally solving the statistical problem of perception in noise. In the optimal solution to this problem, listeners’ perception is biased toward phonetic category means because they use knowledge of these categories to guide their inferences about speakers’ target productions. Simulations show that model predictions closely correspond to previously published human data, and novel experimental results provide evidence for the predicted link between perceptual warping and noise. The model unifies several previous accounts of the perceptual magnet effect and provides a framework for exploring categorical effects in other domains.
Keywords: perceptual magnet effect, categorical perception, speech perception, Bayesian inference, rational analysis
Introduction
The influence of categories on perception is well-known in domains ranging from speech sounds to artificial categories of objects. Liberman, Harris, Hoffman, and Griffth (1957) first described categorical perception of speech sounds, noting that listeners’ perception conforms to relatively sharp identification boundaries between categories of stop consonants and that whereas between-category discrimination of these sounds is nearly perfect, within-category discrimination is little better than chance. Similar patterns have been observed in the perception of colors (Davidoff, Davies, & Roberson, 1999), facial expressions (Etcoff & Magee, 1992), and familiar faces (Beale & Keil, 1995), as well as the representation of objects belonging to artificial categories that are learned over the course of an experiment (Goldstone, 1994; Goldstone, Lippa, & Shiffrin, 2001). All of these categorical effects are characterized by better discrimination of between-category contrasts than within-category contrasts, though the magnitude of the effect varies between domains.
In this paper, we develop a computational model of the influence of categories on perception through a detailed investigation of one such phenomenon, the perceptual magnet effect (Kuhl, 1991), which has been described primarily in vowels. The perceptual magnet effect involves reduced discriminability of speech sounds near phonetic category prototypes. For several reasons, speech sounds, particularly vowels, provide an excellent starting point for assessing a model of the influence of categories on perception. Vowels are naturally occurring, highly familiar stimuli that all listeners have categorized. As will be discussed later, a precise two-dimensional psychophysical map of vowel space can be provided, and using well-established techniques, discrimination of pairs of speech sounds can be systematically investigated under well-defined conditions so that perceptual maps of vowel space can be constructed. By comparing perceptual and psychophysical maps, we can measure the extent and nature of perceptual warping and assess such warping with respect to known categories. In addition, the perceptual magnet effect shows several qualitative similarities to categorical effects in perceptual domains outside of language, as vowel perception is continuous rather than sharply categorical (Fry, Abramson, Eimas, & Liberman, 1962) and the degree of category influence can vary substantially across testing conditions (Gerrits & Schouten, 2004). Finally, the perceptual magnet effect has been the object of extensive empirical and computational research (e.g. Grieser & Kuhl, 1989; Kuhl, 1991; Iverson & Kuhl, 1995; Lacerda, 1995; Guenther & Gjaja, 1996). This previous research has produced a large body of data that can be used to provide a quantitative evaluation of our approach, as well as several alternative explanations against which it can be compared.
We take a novel approach to modeling the perceptual magnet effect, complementary to previous models that have explored how the effect might be algorithmically and neurally implemented. In the tradition of rational analysis proposed by Marr (1982) and J. R. Anderson (1990), we consider the abstract computational problem posed by speech perception and show that the perceptual magnet effect emerges as part of the optimal solution to this problem. Specifically, we assume that listeners are optimally solving the problem of perceiving speech sounds in the presence of noise. In this analysis, the listener’s goal is to ascertain category membership but also to extract phonetic detail in order to reconstruct coarticulatory and non-linguistic information. This is a difficult problem for listeners because they cannot hear the speaker’s target production directly. Instead, they hear speech sounds that are similar to the speaker’s target production but that have been altered through articulatory, acoustic, and perceptual noise. We formalize this problem using Bayesian statistics and show that the optimal solution to this problem produces the perceptual magnet effect.
The resulting rational model formalizes ideas that have been proposed in previous explanations of the perceptual magnet effect but goes beyond these previous proposals to explain why the effect should result from optimal behavior. It also serves as a basis for further empirical research, making predictions about the types of variability that should be seen in the perceptual magnet effect and in other categorical effects more generally. Several of these predictions are in line with previous literature, and one additional prediction is borne out in our own experimental data. Our model parallels models that have been used to describe categorical effects in other areas of cognition (Huttenlocher, Hedges, & Vevea, 2000; Köording & Wolpert, 2004; Roberson, Damjanivic, & Pilling, 2007), suggesting that its principles are broadly applicable to these areas as well.
The paper is organized as follows. We begin with an overview of categorical effects across several domains, then focus more closely on evidence for the perceptual magnet effect and explanations that have been proposed to account for this evidence. The ensuing section gives an intuitive overview of our model, followed by a more formal introduction to its mathematics. We present simulations comparing the model to published empirical data and generating novel empirical predictions. An experiment is presented to test the predicted effects of speech signal noise. Finally, we discuss this model in relation to previous models, revisit its assumptions, and suggest directions for future research.
Categorical Effects
Categorical effects are widespread in cognition and perception (Harnad, 1987), and these effects show qualitative similarities across domains. This section provides an overview of basic findings and key issues concerning categorical effects in the perception of speech sounds, colors, faces, and artificial laboratory stimuli.
Speech Sounds
The classic demonstration of categorical perception comes from a study by Liberman et al. (1957), who measured subjects’ perception of a synthetic speech sound continuum that ranged from /b/ to /d/ to /g/, spanning three phonetic categories. Results showed sharp transitions between the three categories in an identification task and corresponding peaks in discrimination at category boundaries, indicating that subjects were discriminating stimuli primarily based on their category membership. The authors compared the data to a model in which listeners extracted only category information, and no acoustic information, when perceiving a speech sound. Subject performance exceeded that of the model consistently but only by a small percentage: discrimination was little better than could be obtained through identification alone. These results were later replicated using the voicing dimension in stop consonant perception, with both word-initial and word-medial cues causing discrimination peaks at the identification boundaries (Liberman, Harris, Kinney, & Lane, 1961; Liberman, Harris, Eimas, Lisker, & Bastian, 1961). Other classes of consonants such as fricatives (Fujisaki & Kawashima, 1969), liquids (Miyawaki et al., 1975), and nasals (J. L. Miller & Eimas, 1977) show evidence of categorical perception as well. In all these studies, listeners show some discrimination of within-category contrasts, and this within-category discrimination is especially evident when more sensitive measures such as reaction times are used (e.g. Pisoni & Tash, 1974). Nevertheless, within-category discrimination is consistently poorer than between-category discrimination across a wide variety of consonant contrasts.
A good deal of research has investigated the degree to which categorical perception of consonants results from innate biases or arises through category learning. Evidence supports a role for both factors. Studies with young infants show that discrimination peaks are already present in the first few months of life (Eimas, Siqueland, Jusczyk, & Vigorito, 1971; Eimas, 1974, 1975), suggesting a role for innate biases. These early patterns may be tied to general patterns of auditory sensitivity, as non-human animals show discrimination peaks at category boundaries along the dimensions of voicing (Kuhl, 1981; Kuhl & Padden, 1982) and place (Morse & Snowdon, 1975; Kuhl & Padden, 1983), and humans show similar boundaries in some non-speech stimuli (J. D. Miller, Wier, Pastore, Kelly, & Dooling, 1976; Pisoni, 1977). Studies have also shown cross-linguistic differences in perception, which indicate that perceptual patterns are influenced by phonetic category learning (Abramson & Lisker, 1970; Miyawaki et al., 1975). The interaction between these two factors remains a subject of current investigation (e.g. Holt, Lotto, & Diehl, 2004).
The role of phonetic categories in vowel perception is more controversial: vowel perception is continuous rather than strictly categorical, without obvious discrimination peaks near category boundaries (Fry et al., 1962). However, there has been some evidence for category boundary effects (Beddor & Strange, 1982) as well as reduced discriminability of vowels specifically near the centers of phonetic categories (Kuhl, 1991), and we will return to this debate in more detail in the next section.
Colors
It has been argued that color categories are organized around universal focal colors (Berlin & Kay, 1969; Rosch Heider, 1972; Rosch Heider & Oliver, 1972), and these universal tendencies have been supported through more recent statistical modeling results (Kay & Regier, 2007; Regier, Kay, & Khetarpal, 2007). However, color terms show substantial cross-linguistic variation (Berlin & Kay, 1969), and this has led researchers to question whether color categories influence color perception. Experiments have revealed discrimination peaks corresponding to language-specific category boundaries for speakers of English, Russian, Berinmo, and Himba, and perceivers whose native language does not contain a corresponding category boundary have failed to show these discrimination peaks (Winawer et al., 2007; Davidoff et al., 1999; Roberson, Davies, & Davidoff, 2000; Roberson, Davidoff, Davies, & Shapiro, 2005). These results indicate that color categories do influence performance in color discrimination tasks.
More recent research in this domain has asked whether these categorical effects are purely perceptual or whether they are mediated by the active use of linguistic codes in perceptual tasks. Roberson and Davidoff (2000) demonstrated that linguistic interference tasks can eliminate categorical effects in color perception (see also Kay & Kempton, 1984). Investigations have shown activation of the same neural areas in naming tasks as in discrimination tasks (Tan et al., 2008) as well as left-lateralization of categorical color perception in adults (Gilbert, Regier, Kay, & Ivry, 2006). These results suggest a direct role for linguistic codes in discrimination performance, indicating that categorical effects in color perception are mediated largely by language. Nevertheless, categorical effects may play a large role in everyday color perception. Linguistic codes appear to be used in a wide variety of perceptual tasks, including those that do not require memory encoding (Witthoft et al., 2003), and verbal interference tasks fail to completely wipe out verbal coding when the type of interference is unpredictable (Pilling, Wiggett, ÖOzgen, & Davies, 2003).
Faces
Categorical effects in face perception were first shown for facial expressions of emotion in stimuli constructed from line drawings (Etcoff & Magee, 1992) and photograph-quality stimuli (Calder, Young, Perrett, Etcoff, & Rowland, 1996; Young et al., 1997; Gelder, Teunisse, & Benson, 1997). Stimuli for these experiments were drawn from morphed continua in which the endpoints were prototypical facial expressions (e.g. happiness, fear, anger). With few exceptions, results showed discrimination peaks at the same locations as identification boundaries between these prototypical expressions. Evidence for categorical effects has been found in seven-month-old infants (Kotsoni, Haan, & Johnson, 2001), nine-year-old children (Gelder et al., 1997), and older individuals (Kiffel, Campanella, & Bruyer, 2005), indicating that category structure is similar across different age ranges. However, these categories can be affected by early experience as well. Pollak and Kistler (2002) presented data from abused children showing that their category boundaries in continua ranging from fearful to angry and from sad to angry were shifted such that they interpreted a large portion of these continua as angry; discrimination peaks were shifted together with these identification boundaries.
In addition to categorical perception of facial expressions, discrimination patterns show evidence of categorical perception of facial identity, where each category corresponds to a different identity. Beale and Keil (1995) found discrimination peaks along morphed continua between faces of famous individuals, and these results have been replicated with several different stimulus continua constructed from familiar faces (Stevenage, 1998; Campanella, Hanoteau, Seron, Joassin, & Bruyer, 2003; Rotshtein, Henson, Treves, Driver, & Dolan, 2005; Angeli, Davidoff, & Valentine, 2008). The categorical effects are stronger for familiar faces than for unfamiliar faces (Beale & Keil, 1995; Angeli et al., 2008), but categorical effects have been demonstrated for continua involving previously unfamiliar faces as well (Stevenage, 1998; Levin & Beale, 2000). The strength of these effects for unfamiliar faces may derive from a combination of learning during the course of the experiment (Viviani, Binda, & Borsato, 2007), the use of labels during training (Kikutani, Roberson, & Hanley, 2008), and the inherent distinctiveness of endpoint stimuli in the continua (Campanella et al., 2003; Angeli et al., 2008).
Learning Artificial Categories
Several studies have demonstrated categorical effects that derive from categories learned in the laboratory, implying that the formation of novel categories can affect perception in laboratory settings. As proposed by Liberman et al. (1957), this learning component might take two forms: acquired distinctiveness involves enhanced between-category discriminability, whereas acquired equivalence involves reduced within-category discriminability. Evidence for one or both of these processes has been found through categorization training in color perception (Özgen & Davies, 2002) and auditory perception of both speech sounds (Pisoni, Aslin, Perey, & Hennessy, 1982) and white noise (Guenther, Husain, Cohen, & Shinn-Cunningham, 1999). These results extend to stimuli that vary along multiple dimensions as well. Categorizing stimuli along two dimensions can lead to acquired distinctiveness (Goldstone, 1994), and similarity ratings for drawings that differ along several dimensions have shown acquired equivalence in response to categorization training (Livingston, Andrews, & Harnad, 1998). Such effects may arise partly from task-specific strategies but likely involve changes in underlying stimulus representations as well (Goldstone et al., 2001).
Additionally, several studies have demonstrated that categories for experimental stimuli are learned quickly over the course of an experiment even without explicit training. Goldstone (1995) found that implicit shape-based categories influenced subjects’ perception of hues and that these implicit categories changed depending on the set of stimuli presented in the experiment. A similar explanation has been proposed to account for subjects’ categorical treatment of unfamiliar face continua (Levin & Beale, 2000), where learned categories seem to correspond to continuum endpoints. Gureckis and Goldstone (2008) demonstrated that subjects are sensitive to the presence of distinct clusters of stimuli, showing increased discriminability between clusters even when those clusters receive the same label. Furthermore, implicit categories have been used to explain why subjects often bias their perception toward the mean value of a set of stimuli in an experiment. Huttenlocher et al. (2000) argued that subjects form an implicit category that includes the range of stimuli they have seen over the course of an experiment and that they use this implicit category to correct for memory uncertainty when asked to reproduce a stimulus. Under their assumptions, the optimal way to correct for memory uncertainty using this implicit category is to bias all responses toward the mean value of the category, which in this case is the mean value of the set of stimuli. The authors presented a Bayesian analysis to account for bias in visual stimulus reproduction that is nearly identical to the one-category model derived here in the context of speech perception, reflecting the similar structure of the two problems and the generality of the approach.
Summary
The categorical effects in all of these domains are qualitatively similar, with enhanced between-category discriminability and reduced within-category discriminability. Though there is some evidence that innate biases contribute to these perceptual patterns, the patterns can be influenced by learned categories as well, even by implicit categories that arise from specific distributions of exemplars. Despite widespread interest in these phenomena, the reasons and mechanisms behind the connection between categories and perception remain unclear. In the remainder of this paper we address this issue through a detailed exploration of the perceptual magnet effect, which shares many qualitative features with the categorical effects discussed above.
The Perceptual Magnet Effect
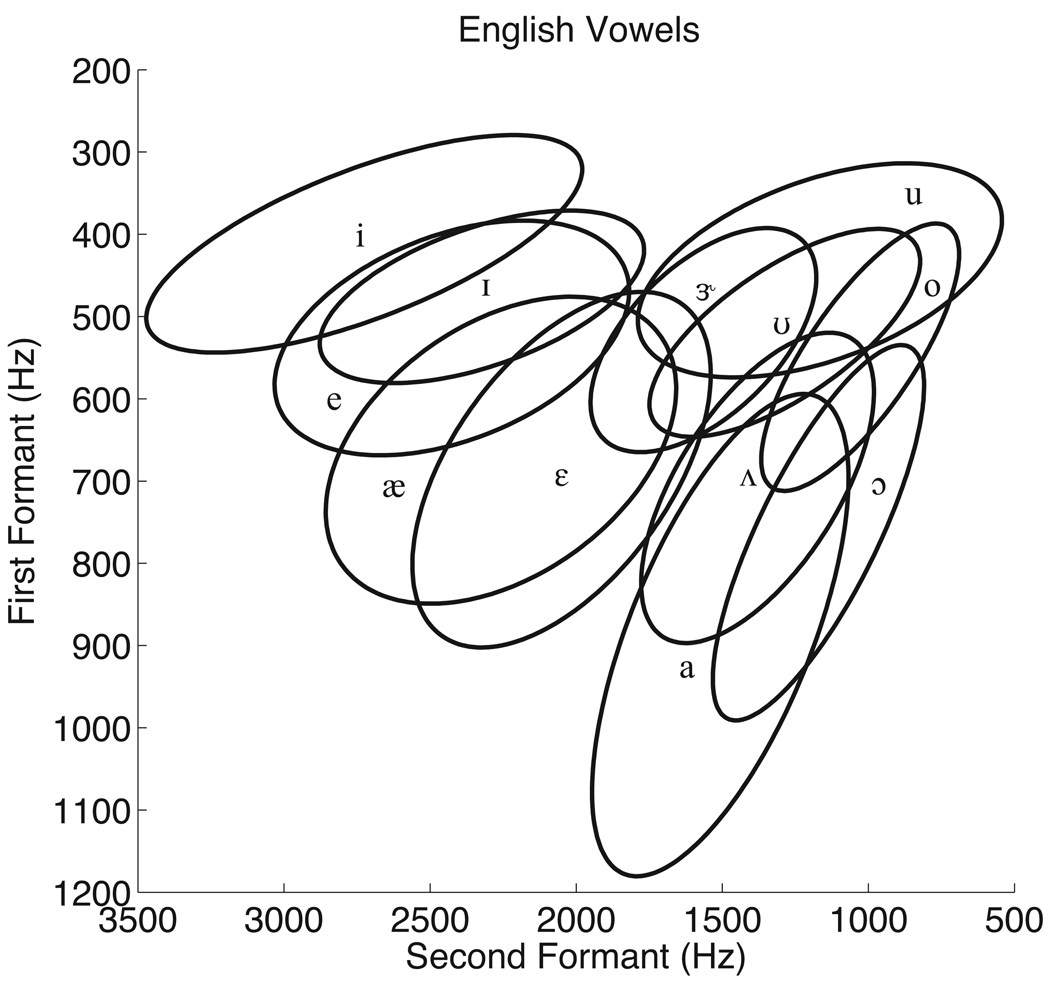
The phenomenon of categorical perception is robust in consonants, but the role of phonetic categories in the perception of vowels has been more controversial. Acoustically, vowels are specified primarily by their first and second formants, F1 and F2. Formants are bands of frequencies in which acoustic energy is concentrated – peaks in the frequency spectrum – as a result of resonances in the vocal tract. F1 is inversely correlated with tongue height, whereas F2 is correlated with the proximity of the most raised portion of the tongue to the front of the mouth. Thus, a front high vowel such as /i/ (as in beet) spoken by a male talker typically has center formant frequencies around 270 Hz (F1) and 2290 Hz (F2), and a back low vowel such as /a/ (as in father) spoken by a male typically has center formant frequencies around 730 Hz and 1090 Hz (Peterson & Barney, 1952). Tokens of vowels are distributed around these central values. A map of vowel space based on data from Hillenbrand, Getty, Clark, and Wheeler (1995) is shown in Figure 1. Though frequencies are typically reported in Hertz, most research on the perceptual magnet effect has used the mel scale to represent psychophysical distance (e.g. Kuhl, 1991). The mel scale can be used to equate distances in psychophysical space because difference limens, the smallest detectable pitch differences, correspond to constant distances along this scale (S. S. Stevens, Volkmann, & Newman, 1937).
Figure 1.
Map of vowel space from Hillenbrand et al.’s (1995) production experiment. Ellipses delimit regions corresponding to approximately 90% of tokens from each vowel category.
Early work suggested that vowel discrimination was not affected by native language categories (K. N. Stevens, Liberman, Studdert-Kennedy, & Öhman, 1969). However, later findings have revealed a relationship between phonetic categories and vowel perception. Although within-category discrimination for vowels is better than for consonants, clear peaks in discrimination functions have been found at vowel category boundaries, especially in tasks that place a high memory load on subjects or that interfere with auditory memory (Pisoni, 1975; Repp, Healy, & Crowder, 1979; Beddor & Strange, 1982; Repp & Crowder, 1990). In addition, between-category differences yield larger neural responses as measured by event related potentials (Näätäanen et al., 1997; Winkler et al., 1999). Viewing phonetic discrimination in spatial terms, Kuhl and colleagues have found evidence of shrunken perceptual space specifically near category prototypes, a phenomenon they have called the perceptual magnet effect (Grieser & Kuhl, 1989; Kuhl, 1991; Kuhl, Williams, Lacerda, Stevens, & Lindblom, 1992; Iverson & Kuhl, 1995).
Empirical Evidence
The first evidence for the perceptual magnet effect came from experiments with English-speaking six-month-old infants (Grieser & Kuhl, 1989). Using the conditioned headturn procedure to assess within-category generalization of speech sounds, the authors found that a prototypical /i/ vowel based on mean formant values in Peterson and Barney’s production data was more likely to be generalized to sounds surrounding it than was a non-prototypical /i/ vowel. In addition, they found that infants’ rate of generalization correlated with adult goodness ratings of the stimuli, so stimuli that were judged as the best exemplars of the /i/ category were generalized most often to neighboring stimuli. Kuhl (1991) showed that adults, like infants, can discriminate stimuli near a non-prototype of the /i/ category better than stimuli near the prototype. Kuhl et al. (1992) tested English- and Swedish-learning infants on discrimination near prototypical English /i/ (high, front, unrounded) and Swedish /y/ (high, front, rounded) sounds, again using the conditioned headturn procedure; they found that while English infants generalized the /i/ sounds more than the /y/ sounds, Swedish-learning infants showed the reverse pattern. Based on this evidence, the authors described the perceptual magnet effect as a language-specific shrinking of perceptual space near native language phonetic category prototypes, with prototypes acting as perceptual magnets to exert a pull on neighboring speech sounds (see also Kuhl, 1993). They concluded that these language-specific prototypes are in place as young as six months.
Iverson and Kuhl (1995) used signal detection theory and multidimensional scaling to produce a detailed perceptual map of acoustic space near the prototypical and non-prototypical /i/ vowels used in previous experiments. They tested adults’ discrimination of 13 stimuli along a single vector in F1−F2 space, ranging from F1 of 197 Hz and F2 of 2489 Hz (classified as /i/) to F1 of 429 Hz and F2 of 1925 Hz (classified as /e/, as in bait). In both analyses, they found shrinkage of perceptual space near the ends of the continuum, especially near the /i/ end. They found a peak in discrimination near the center of the continuum between stimulus 6 and stimulus 9. This supported previous analyses, suggesting that perceptual space was shrunk near category centers and expanded near category edges. The effect has since been replicated in the English /i/ category (Sussman & Lauckner-Morano, 1995), and evidence for poor discrimination near category prototypes has been found for the German /i/ category (Diesch, Iverson, Kettermann, & Siebert, 1999). In addition, the effect has been found in the /r/ and /l/ categories in English but not Japanese speakers (Iverson & Kuhl, 1996; Iverson et al., 2003), lending support to the idea of language-specific phonetic category prototypes.
Several studies have found large individual differences between subjects in stimulus goodness ratings and category identification, suggesting that it may be difficult to find vowel tokens that are prototypical across listeners and thus raising methodological questions about experiments that examine the perceptual magnet effect (Lively & Pisoni, 1997; Frieda, Walley, Flege, & Sloane, 1999; Lotto, Kluender, & Holt, 1998). However, data collected by Aaltonen, Eerola, Hellström, Uusipaikka, and Lang (1997) on the /i/−/y/ contrast in Finnish adults showed that discrimination performance was less variable than identification performance, and the authors argued based on these results that discrimination operates at a lower level than overt identification tasks. A more serious challenge has come from studies that question the robustness of the perceptual magnet effect. Lively and Pisoni (1997) found no evidence of a perceptual magnet effect in the English /i/ category, suggesting that listeners’ discrimination patterns are sensitive to methodological details or dialect differences, though the authors could not identify the specific factors responsible for these differences. The effect has also been difficult to isolate in vowels other than /i/: Sussman and Gekas (1997) failed to find an effect in the English /i/ (as in bit) category, and Thyer, Hickson, and Dodd (2000) found the effect in the /i/ category but found the reverse effect in the /ɔ/ (as in bought) category and failed to find any effect in other vowels. While there has been evidence linking changes in vowel perception to differences in interstimulus interval (Pisoni, 1973) and task demands (Gerrits & Schouten, 2004), much of the variability found in vowel perception has not been accounted for.
In summary, vowel perception has been shown to be continuous rather than categorical: listeners can discriminate two vowels that receive the same category label. However, studies have suggested that even in vowels, perceptual space is shrunk near phonetic category centers and expanded near category edges. In addition, studies have shown substantial variability in the perceptual magnet effect. This variability seems to depend on the phonetic category being tested and also on methodological details. Based on the predictions of our rational model, we will argue that some of this variability is attributable to differences in category variance between different phonetic categories and to differences in the amount of noise through which stimuli are heard.
Previous Models
Grieser and Kuhl (1989) originally described the perceptual magnet effect in terms of category prototypes, arguing that phonetic category prototypes exert a pull on nearby speech sounds and thus create an inverse correlation between goodness ratings and discriminability. While this inverse correlation has been examined more closely and used to argue that categorical perception and the perceptual magnet effect are separate phenomena (Iverson & Kuhl, 2000), most computational models of the perceptual magnet effect have assumed that it is a categorical effect, parallel to categorical perception.
Lacerda (1995) began by assuming that the warping of perceptual space emerges as a side-effect of a classification problem: the goal of listeners is to classify speech sounds into phonetic categories. His model assumes that perception has been trained with labeled exemplars or that labels have been learned using other information in the speech signal. In perceiving a new speech sound, listeners retrieve only the information from the speech signal that is helpful in determining the sound’s category, or label, and they categorize and discriminate speech sounds based on this information. Listeners can perceive a contrast only if the two sounds differ in category membership. Implementing this idea in neural models, Damper and Harnad (2000) showed that when trained on two endpoint stimuli, neural networks will treat a voice onset time (VOT) continuum categorically. One limitation of the models proposed by Lacerda (1995) and Damper and Harnad (2000) is that they do not include a mechanism by which listeners can perceive within-category contrasts. As demonstrated by Lotto et al. (1998), this assumption cannot capture the data on the perceptual magnet effect because within-category discriminability is higher than this account would predict.
Other neural network models have argued that the perceptual magnet effect results not from category labels but instead from specific patterns in the distribution of speech sounds. Guenther and Gjaja (1996) suggested that neural firing preferences in a neural map reflect Gaussian distributions of speech sounds in the input and that because more central sounds have stronger neural representations than more peripheral sounds, the population vector representing a speech sound that is halfway between the center and the periphery of its phonetic category will appear closer to the center of the category than to its periphery. This model implements the idea that the perceptual magnet effect is a direct result of uneven distributions of speech sounds in the input. Similarly, Vallabha and McClelland (2007) have shown that Hebbian learning can produce attractors at the locations of Gaussian input categories and that the resulting neural representation fits human data accurately. The idea that distributions of speech sounds in the input can influence perception is supported by experimental evidence showing that adults and infants show better discrimination of a contrast embedded in a bimodal distribution of speech sounds than of the same contrast embedded in a unimodal distribution (Maye & Gerken, 2000; Maye, Werker, & Gerken, 2002).
These previous models have provided process-level accounts of how the perceptual magnet effect might be implemented algorithmically and neurally, but they leave several questions unanswered. The prototype model does not give independent justification for the assumption that prototypes should exert a pull on neighboring speech sounds; several models cannot account for better than chance within-category discriminability of vowels. Other models give explanations of how the effect might occur but do not address the question of why it should occur. Our rational model fills these gaps by providing a mathematical formalization of the perceptual magnet effect at Marr’s (1982) computational level, considering the goals of the computation and the logic by which these goals can be achieved. It gives independent justification for the optimality of a perceptual bias toward category centers and simultaneously predicts a baseline level of within-category discrimination. Furthermore, it goes beyond these previous models to make novel predictions about the types of variability that should be seen in the perceptual magnet effect.
Theoretical Overview of the Model
Our model of the perceptual magnet effect focuses on the idea that we can analyze speech perception as a kind of optimal statistical inference. The goal of listeners, in perceiving a speech sound, is to recover the phonetic detail of a speaker’s target production. They infer this target production using the information that is available to them from the speech signal and their prior knowledge of phonetic categories. Here we give an intuitive overview of our model in the context of speech perception, followed by a more general mathematical account in the next section.
Phonetic categories are defined in the model as distributions of speech sounds. When speakers produce a speech sound, they choose a phonetic category and then articulate a speech sound from that category. They can use their specific choice of speech sounds within the phonetic category to convey coarticulatory information, affect, and other relevant information. Because there are several factors that speakers might intend to convey, and each factor can cause small fluctuations in acoustics, we assume that the combination of these factors approximates a Gaussian, or normal, distribution. Phonetic categories in the model are thus Gaussian distributions of target speech sounds. Categories may differ in the location of their means, or prototypes, and in the amount of variability they allow. In addition, categories may differ in frequency, so that some phonetic categories are used more frequently in a language than others. The use of Gaussian phonetic categories in this model does not reflect a belief that speech sounds actually fall into parametric distributions. Rather, the mathematics of the model are easiest to derive in the case of Gaussian categories. As will be discussed later, the general effects that are predicted in the case of Gaussian categories are similar to those predicted for other types of unimodal distributions.
In the speech sound heard by listeners, the information about the target production is masked by various types of articulatory, acoustic, and perceptual noise. The combination of these noise factors is approximated through Gaussian noise, so that the speech sound heard is normally distributed around the speaker’s target production.
Formulated in this way, speech perception becomes a statistical inference problem. When listeners perceive a speech sound, they can assume it was generated by selecting a target production from a phonetic category and then generating a noisy speech sound based on the target production. Listeners hear the speech sound and know the structure and location of phonetic categories in their native language. Given this information, they need to infer the speaker’s target production. They infer phonetic detail in addition to category information in order to recover the gradient coarticulatory and non-linguistic information that the speaker intended.
With no prior information about phonetic categories, listeners’ perception should be unbiased, since under Gaussian noise, speech sounds are equally likely to be shifted in either direction. In this case, listeners’ safest strategy is to guess that the speech sound they heard was the same as the target production. However, experienced listeners know that they are more likely to hear speech sounds near the centers of phonetic categories than speech sounds farther from category centers. The optimal way to use this knowledge of phonetic categories to compensate for a noisy speech signal is to bias perception toward the center of a category, toward the most likely target productions.
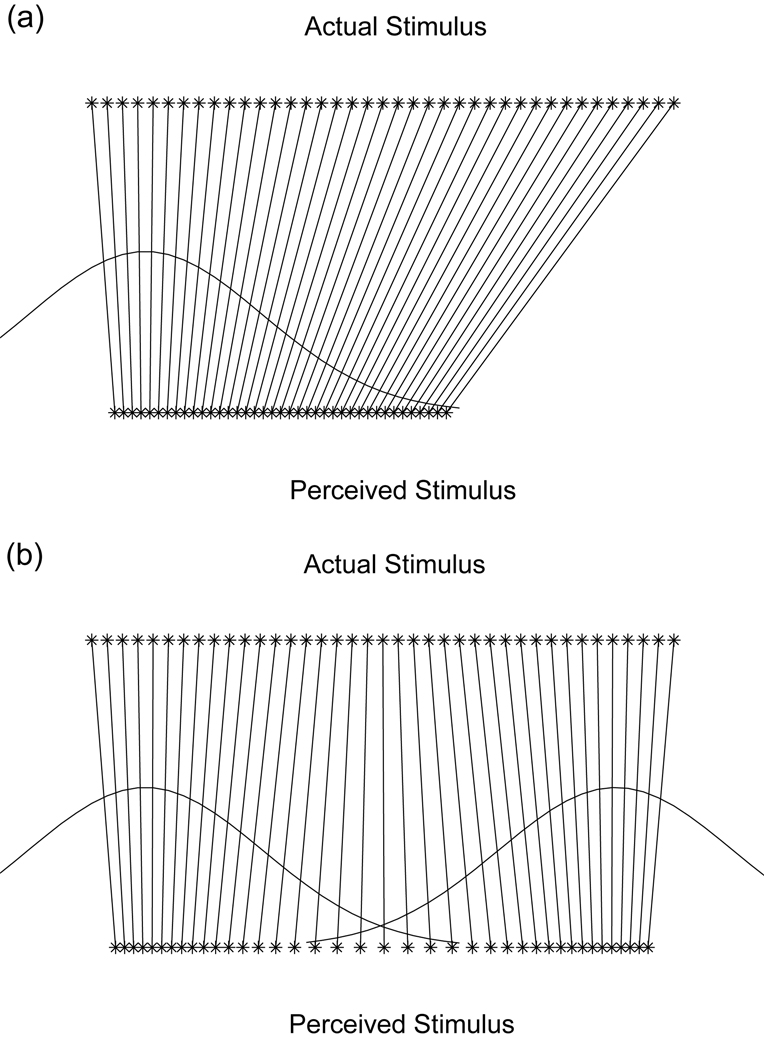
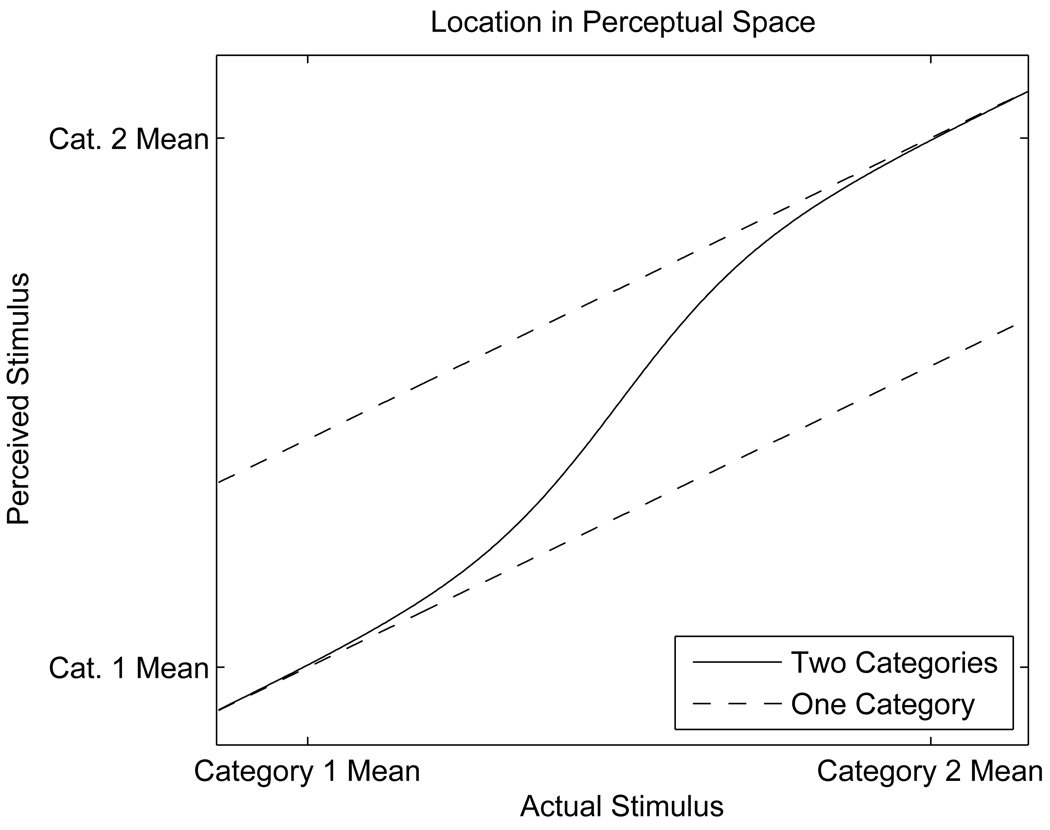
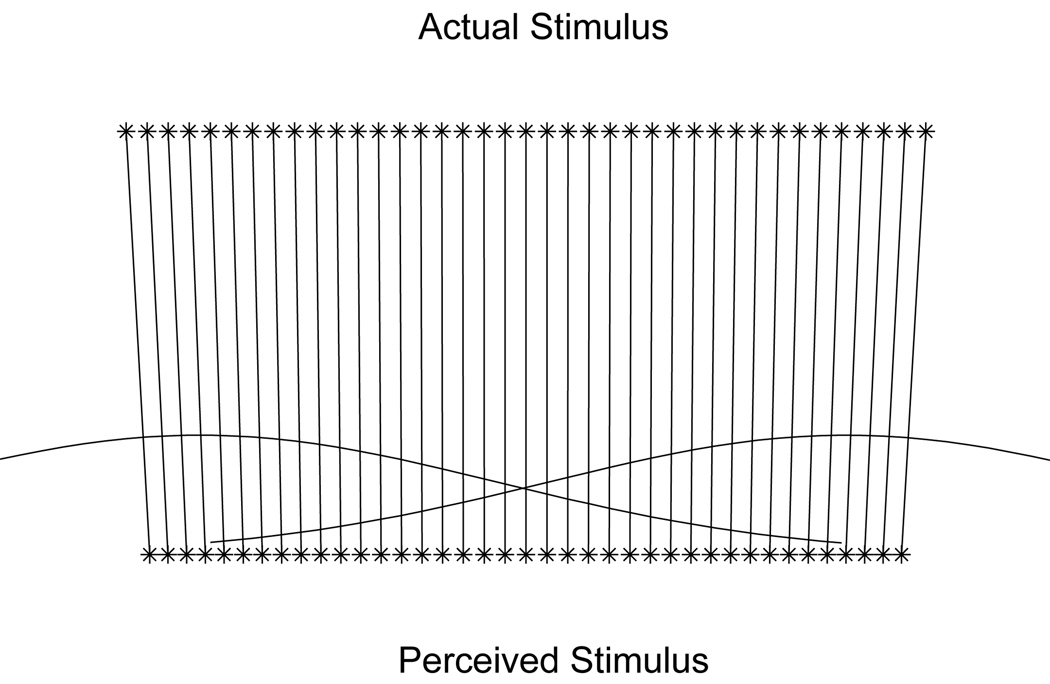
In a hypothetical language with a single phonetic category, where listeners are certain that all sounds belong to that category, this perceptual bias toward the category mean causes all of perceptual space to shrink toward the center of the category. The resulting perceptual pattern is shown in Figure 2 (a). If there is no uncertainty about category membership, perception of distant speech sounds is more biased than perception of proximal speech sounds so that all of perceptual space is shrunk to the same degree.
Figure 2.
Predicted relationship between acoustic and perceptual space in the case of (a) one category and (b) two categories.
In order to optimally infer a speaker’s target production in the context of multiple phonetic categories, listeners must determine which categories are likely to have generated a speech sound. They can then predict the speaker’s target production based on the structure of these categories. If they are certain of a speech sound’s category membership, their perception of the speech sound should be biased toward the mean of that category, as was the case in a language with one phonetic category. This shrinks perceptual space in areas of unambiguous categorization. If listeners are uncertain about category membership, they should take into account all the categories that could have generated the speech sound they heard, but they should weight the influence of each category by the probability that the speech sound came from that category. This ensures that under assumptions of equal frequency and variance, nearby categories are weighted more heavily than those farther away. Perception of speech sounds precisely on the border between two categories is pulled simultaneously toward both category means, each cancelling out the other’s effect. Perception of speech sounds that are near the border between categories is biased toward the most likely category, but the competing category dampens the bias. The resulting pattern for the two-category case is shown in Figure 2 (b).
The interaction between the categories produces a pattern of perceptual warping that is qualitatively similar to descriptions of the perceptual magnet effect and other categorical effects that have been reported in the literature. Speech sounds near category centers are extremely close together in perceptual space, whereas speech sounds near the edges of a category are much farther apart. This perceptual pattern results from a combination of two factors, both of which were proposed by Liberman et al. (1957) in reference to categorical perception. The first is acquired equivalence within categories due to perceptual bias toward category means; the second is acquired distinctiveness between categories due to the presence of multiple categories. Consistent with these predictions, infants acquiring language have shown both acquired distinctiveness for phonemically distinct sounds and acquired equivalence for members of a single phonemic category over the course of the first year of life (Kuhl et al., 2006).
Mathematical Presentation of the Model
This section formalizes the rational model within the framework of Bayesian inference. The model is potentially applicable to any perceptual problem in which a perceiver needs to recover a target from a noisy stimulus, using knowledge that the target has been sampled from a Gaussian category. We therefore present the mathematics in general terms, referring to a generic stimulus S, target T, category c, category variance , and noise variance . In the specific case of speech perception, S corresponds to the speech sound heard by the listener, T to the phonetic detail of a speaker’s intended target production, and c to the language’s phonetic categories; the category variance represents meaningful within-category variability, and the noise variance represents articulatory, acoustic, and perceptual noise in the speech signal.
The formalization is based on a generative model in which a target T is produced by sampling from a Gaussian category c with mean μc and variance . The target T is distributed as
| (1) |
Perceivers cannot recover T directly, but instead perceive a noisy stimulus S that is normally distributed around the target production with noise variance such that
| (2) |
Note that integrating over T yields
| (3) |
indicating that under these assumptions, the stimuli that perceivers observe are normally distributed around a category mean μc with a variance that is a sum of the category variance and the noise variance.
Given this generative model, perceivers can use Bayesian inference to reconstruct the target from the noisy stimulus. According to Bayes’ rule, given a set of hypotheses H and observed data d, the posterior probability of any given hypothesis h is
| (4) |
indicating that it is proportional to both the likelihood p(d|h), which is a measure of how well the hypothesis fits the data, and the prior p(h), which gives the probability assigned to the hypothesis before any data were observed. Here, the stimulus S serves as data d; the hypotheses under consideration are all the possible targets T; and the prior p(h), which gives the probability that any particular target will occur, is specified by category structure. In laying out the solution to this statistical problem, we begin with the case in which there is a single category and then move to the more complex case of multiple categories.
One Category
Perceivers are trying to infer the target T given stimulus S and category c, so they must calculate p(T|S, c). They can use Bayes’ rule:
| (5) |
The likelihood p(S|T), given by the noise process (Equation 2), assigns highest probability to stimulus S, and the prior p(T|c), given by category structure (Equation 1), assigns highest probability to the category mean. As described in Appendix A, the right-hand side of this equation can be simplified to yield a Gaussian distribution
| (6) |
whose mean falls between the stimulus S and the category mean μc.
This posterior probability distribution can be summarized by its mean (the expectation of T given S and c),
| (7) |
The optimal guess at the target, then, is a weighted average of the observed stimulus and the mean of the category that generated the stimulus, where the weighting is determined by the ratio of category variance to noise variance.1 This equation formalizes the idea of a perceptual magnet: the term μc pulls the perception of stimuli toward the category center, effectively shrinking perceptual space around the category.
Multiple Categories
The one-category case, while appropriate to explain performance on some perceptual tasks (e.g. Huttenlocher et al., 2000), is inappropriate for describing natural language. In a language with multiple phonetic categories, listeners must consider many possible source categories for a speech sound. We therefore extend the model so that it applies to the case of multiple categories.
Upon observing a stimulus, perceivers can compute the probability that it came from any particular category using Bayes’ rule
| (8) |
where p(S|c) is given by Equation 3 and p(c) reflects the prior probability assigned to category c.
To compute the posterior on targets p(T|S), perceivers need to marginalize, or sum, over categories,
| (9) |
The first term on the right-hand side is given by Equation 6 and the second term can be calculated using Bayes’ rule as given by Equation 8. The posterior has the form of a mixture of Gaussians, where each Gaussian represents the solution for a single category. Restricting our analysis to the case of categories with equal category variance , the mean of this posterior probability distribution is
| (10) |
which can be rewritten as
| (11) |
A full derivation of this expectation is given in Appendix A.
Equation 11 gives the optimal guess for recovering a target in the case of multiple categories. This guess is a weighted average of the stimulus S and the means μc of all the categories that might have produced S. When perceivers are certain of a stimulus’ category, this equation reduces to Equation 7, and perception of a stimulus S is biased toward the mean of its category. However, when a stimulus is on a border between two categories, the optimal guess at the target is influenced by both category means, and each category weakens the other’s effect (Figure 2 (b)). Shrinkage of perceptual space is thus strongest in areas of unambiguous categorization – the centers of categories – and weakest at category boundaries.
This analysis demonstrates that warping of perceptual space that is qualitatively consistent with the perceptual magnet effect emerges as the result of optimal perception of noisy stimuli. In the next two sections, we provide a quantitative investigation of the model’s predictions in the context of speech perception. The next section focuses on comparing the predictions of the model to empirical data on the perceptual magnet effect, estimating the parameters describing category means and variability from human data. In the subsequent section, we examine the consequences of manipulating these parameters, relating the model’s behavior to further results from the literature.
Quantitative Evaluation
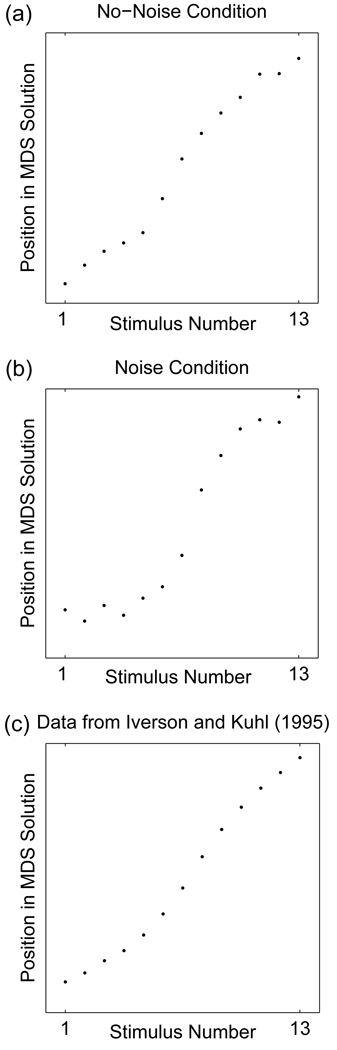
In this section, we test the model’s predictions quantitatively against the multidimensional scaling results from Experiment 3 in Iverson and Kuhl (1995). These data were selected as a modeling target because they give a clean, precise spatial representation of the warping associated with the perceptual magnet effect, mapping 13 /i/ and /e/ stimuli that are separated by equal psychoacoustic distance onto their corresponding locations in perceptual space. Because these multidimensional scaling data constitute the basis for both this simulation and the experiment reported below, we describe the experimental setup and results in some detail here.
Iverson and Kuhl’s multidimensional scaling experiment was conducted with thirteen vowel stimuli along a single continuum in F1−F2 space ranging from /i/ to /e/, whose exact formant values are shown in Table 1. The stimuli were designed to be equally spaced when measured along the mel scale, which equates distances based on difference limens (S. S. Stevens et al., 1937). Subjects performed an AX discrimination task in which they pressed and held a button to begin a trial, releasing the button as quickly as possible if they believed the two stimuli to be different or holding the button for the remainder of the trial (2000 ms) if they heard no difference between the two stimuli. Subjects heard 156 “different” trials, consisting of all possible ordered pairs of non-identical stimuli, and 52 “same” trials, four with each of the 13 stimuli.
Table 1.
Formant values for stimuli used in the multidimensional scaling experiment, reported in Iverson and Kuhl (2000).
| Stimulus Number | F1 (Hz) | F2 (Hz) |
|---|---|---|
| 1 | 197 | 2489 |
| 2 | 215 | 2438 |
| 3 | 233 | 2388 |
| 4 | 251 | 2339 |
| 5 | 270 | 2290 |
| 6 | 289 | 2242 |
| 7 | 308 | 2195 |
| 8 | 327 | 2148 |
| 9 | 347 | 2102 |
| 10 | 367 | 2057 |
| 11 | 387 | 2012 |
| 12 | 408 | 1968 |
| 13 | 429 | 1925 |
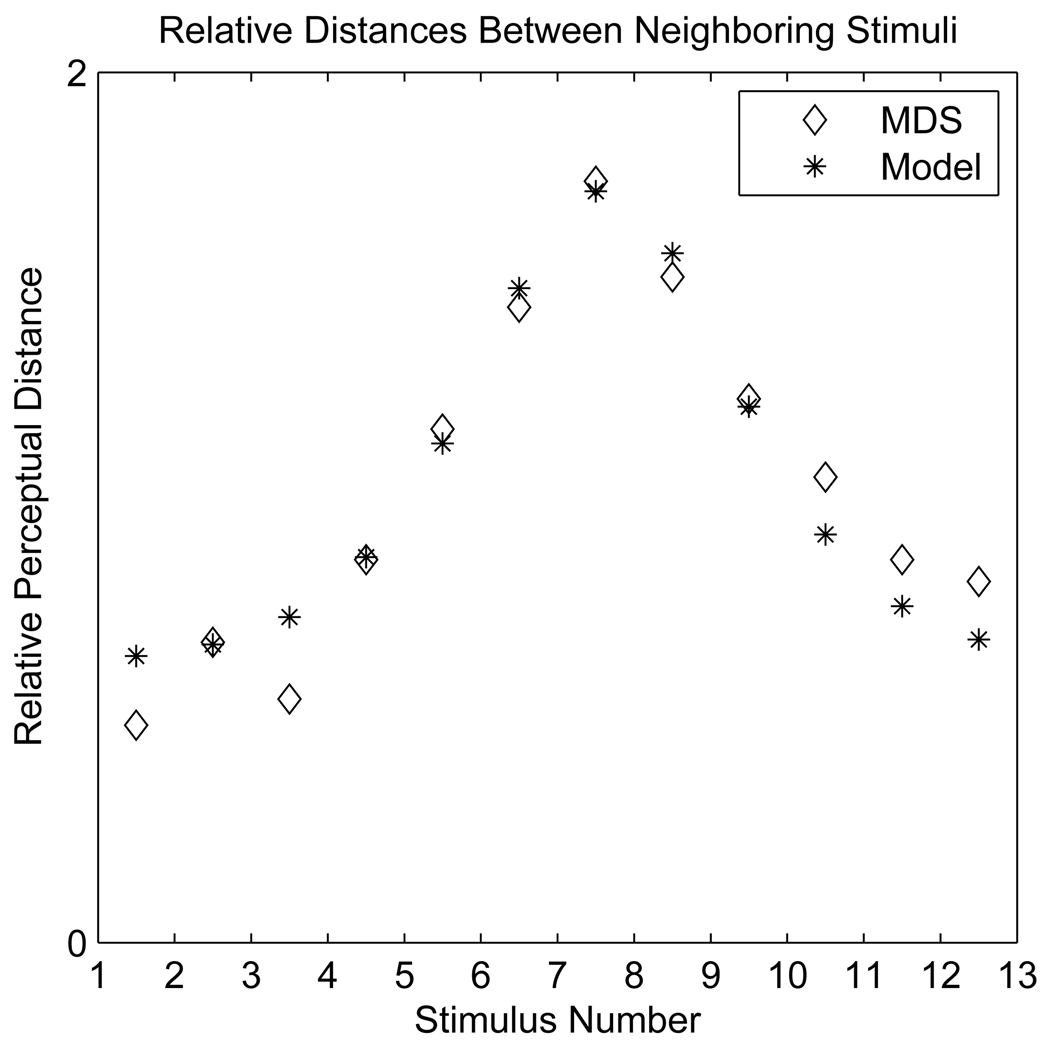
Iverson and Kuhl reported a total accuracy rate of 77% on “different” trials and a false alarm rate of 31% on “same” trials, but they did not further explore direct accuracy measures. Instead, they created a full similarity matrix consisting of log reaction times of “different” responses for each pair of stimuli. To avoid sparse data in the cells where most participants incorrectly responded that two stimuli were identical, the authors replaced all “same” responses with the trial length, 2000 ms, effectively making them into “different” responses with long reaction times. This similarity matrix was used for multidimensional scaling, which finds a perceptual map that is most consistent with a given similarity matrix. In this case, the authors constrained the solution to be in one dimension and assumed a linear relation between similarity values and distance in perceptual space. The interstimulus distances obtained from this analysis are shown in Figure 3. The perceptual map obtained through multidimensional scaling showed that neighboring stimuli near the ends of the stimulus vector were separated by less perceptual distance than neighboring stimuli near the center of the vector. These results agreed qualitatively with data obtained in Experiment 2 of the same paper, which used d′ as an unbiased estimate of perceptual distance. We chose the multidimensional scaling data as our modeling target because they are more extensive than the d′ data, encompassing the entire range of stimuli.
Figure 3.
Relative distances between neighboring stimuli in Iverson and Kuhl’s (1995) multidimensional scaling analysis and in the model.
We tested a two-category version of the rational model to determine whether parameters could be found that would reproduce these empirical data. Equal variance was assumed for the two categories and parameters in the model were based as much as possible on empirical measures in order to reduce the number of free parameters. The simulation was constrained to a single dimension along the direction of the stimulus vector. The parameters that needed to be specified were as follows:
Subject goodness ratings from Iverson and Kuhl (1995) were first used to specify the mean of the /i/ category, μ/i/. These goodness ratings indicated that the best exemplars of the /i/ category were stimuli 2 and 3, so the mean of the /i/ category was set halfway between these two stimuli.2
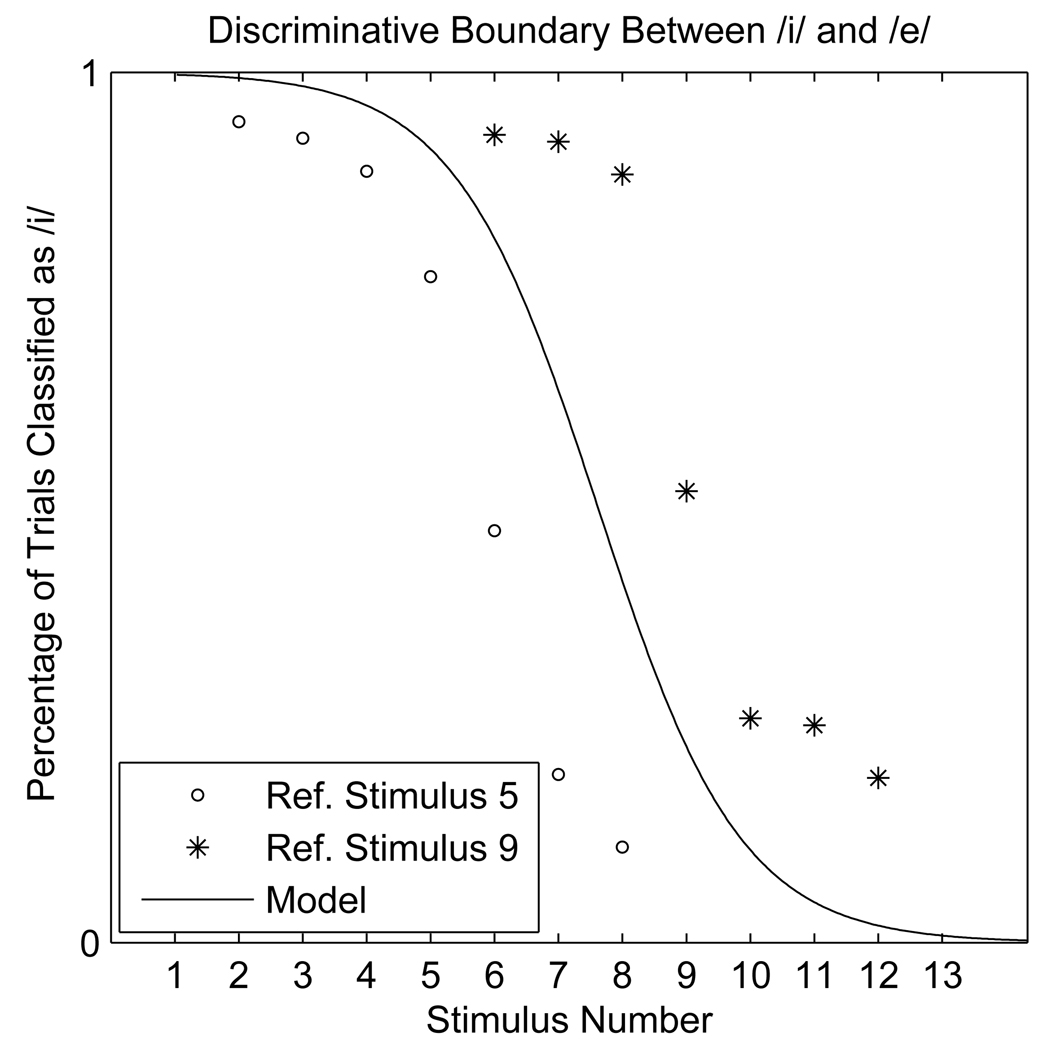
The mean of the /e/ category, μ/e/, and the sum of the variances, , were calculated as described in Appendix B based on phoneme identification curves from Lotto et al. (1998). These identification curves were produced through an experiment in which subjects were played pairs of stimuli from the 13-stimulus vector and asked to identify either the first or the second stimulus in the pair as /i/ or /e/. The other stimulus in the pair was one of two reference stimuli, either stimulus 5 or stimulus 9. The authors obtained two distinct curves in these two conditions, showing that the phoneme boundary shifted based on the identity of the reference stimulus. Because the task used for multidimensional scaling involved presentation of all possible pairings of the 13 stimuli, the phoneme boundary in the model was assumed to be halfway between the boundaries that appeared in these two referent conditions. In order to identify this boundary, two logistic curves were fit to the prototype and non-prototype identification curves. The two curves were constrained to have the same gain, and the biases of the two curves were averaged to obtain a single bias term. Based on Equation 34, these values indicated that μ/e/ should be placed just to the left of stimulus 13; Equation 35 yielded a value of 10,316 for . The resulting discriminative boundary is shown together with the data from Lotto et al. (1998) in Figure 4.
Figure 4.
Identification percentages obtained by Lotto et al. (1998) with reference stimuli 5 and 9 were averaged to produce a single intermediate identification curve in the model (solid line).
The ratio between the category variance and the speech signal noise was the only remaining free parameter, and its value was chosen in order to maximize the fit to Iverson and Kuhl’s multidimensional scaling data. This direct comparison was made by calculating the expectation E[T|S] for each of the 13 stimuli according to Equation 11 and then determining the distance in mels between the expected values of neighboring stimuli. These distances were compared with the distances between stimuli in the multidimensional scaling solution. Since multidimensional scaling gives relative, and not absolute, distances between stimuli, this comparison was evaluated based on whether mel distances in the model were proportional to distances found through multidimensional scaling. As shown in Figure 3, the model yielded an extremely close fit to the empirical data, yielding interstimulus distances that were proportional to those found in multidimensional scaling (r = 0.97). This simulation used the following parameters:
The fit obtained between the simulation and the empirical data is extremely close; however, the model parameters derived in this simulation are meant to serve only as a first approximation of the actual parameters in vowel perception. Because of the variability that has been found in subjects’ goodness ratings of speech stimuli, it is likely that these parameters are somewhat off from their actual values, and it is also possible that the parameters vary between subjects. Instead, the simulation is a concrete demonstration that the model can reproduce empirical data on the perceptual magnet effect quantitatively as well as qualitatively using a reasonable set of parameters, supporting the viability of this rational account.
Effects of Frequency, Variability, and Noise
The previous section has shown a direct quantitative correspondence between model predictions and empirical data. In this section we explore the behavior of the rational model under various parameter combinations, using the parameters derived in the previous section as a baseline for comparison. These simulations serve a dual purpose: they establish the robustness of the qualitative behavior of the model under a range of parameters, and they make predictions about the types of variability that should occur when category frequency, category variance, and speech signal noise are varied. We first introduce several quantitative measures that can be used to visualize the extent of perceptual warping, and these measures are subsequently used to visualize the effects of parameter manipulations.
Characterizing Perceptual Warping
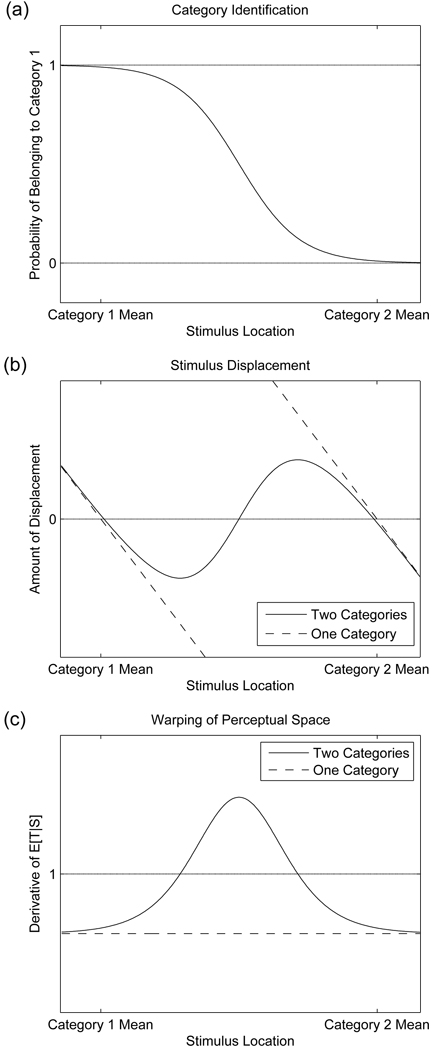
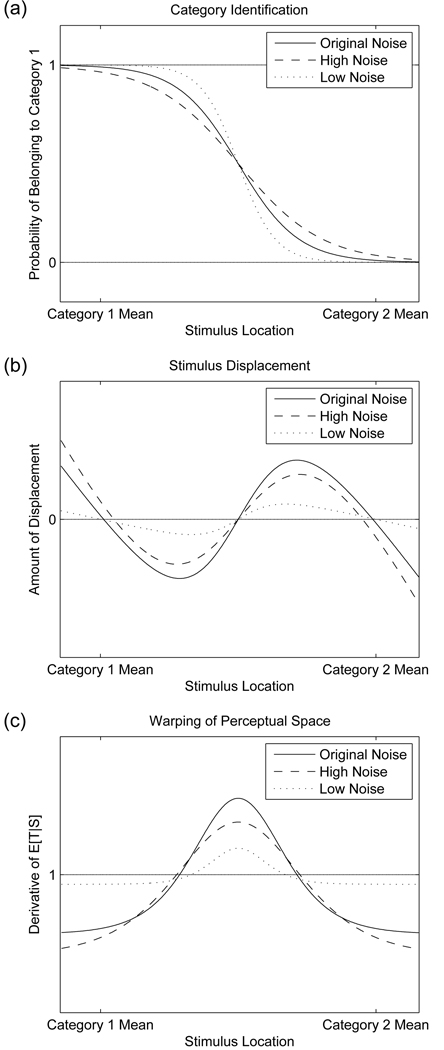
Our statistical analysis establishes a simple function mapping a stimulus, S, to a percept of the intended target, given by E[T|S]. This is a linear mapping in the one-category case (Equation 7), but it becomes non-linear in the case of multiple categories (Equation 11). Figure 5 illustrates the form of this mapping in the cases of one category and two categories with equal variance. Note that this function is not an identification function: the vertical axis represents the exact location of a stimulus in a continuous perceptual space, E[T|S], not the probability with which that stimulus receives a particular label. Slopes that are more horizontal indicate that stimuli are closer in perceptual space than in acoustic space. In the two-category case, stimuli that are equally spaced in acoustic space are nevertheless clumped near category centers in perceptual space, as shown by the two nearly horizontal portions of the curve near the category means. In order to analyze this behavior more closely, we examine the relationship between three measures: identification, the posterior probability of category membership; displacement, the difference between the actual and perceived stimulus; and warping, the degree of shrinkage or expansion of perceptual space.
Figure 5.
Model predictions for location of stimuli in perceptual space relative to acoustic space. Dashed lines indicate patterns corresponding to a single category; solid lines indicate patterns corresponding to two categories of equal variance.
The identification function p(c|S) gives the probability of a stimulus having been generated by a particular category, as calculated in Equation 8. This function is then used to compute the posterior on targets, summing over categories. In the case of two categories with equal variance, the identification function takes the form of a logistic function. Specifically, the posterior probability of category membership can be written as
| (12) |
where the gain and bias of the logistic are given by . An identification function of this form is illustrated in Figure 6 (a). In areas of certain categorization, the identification function is at either 1 or 0; a value of 0.5 indicates maximum uncertainty about category membership.
Figure 6.
Model predictions for (a) identification, (b) displacement, and (c) warping. Dashed lines indicate patterns corresponding to a single category; solid lines indicate patterns corresponding to two categories of equal variance.
Displacement involves a comparison between the location of a stimulus in perceptual space E[T|S] and its location in acoustic space S. It corresponds to the amount of bias in perceiving a stimulus. We can calculate this quantity as
| (13) |
In the one-category case, this means the amount of displacement is proportional to the distance between the stimulus S and the mean μc of the category. As stimuli get farther away from the category mean, they are pulled proportionately farther toward the center of the category. The dashed lines in Figure 6 (b) show two cases of this. In the case of multiple categories, the amount of displacement is proportional to the distance between S and a weighted average of the means μc of more than one category. This is shown in the solid line, where ambiguous stimuli are displaced less than would be predicted in the one-category case because of the competing influence of a second category mean.
Finally, perceptual warping can be characterized based on the distance between two neighboring points in perceptual space that are separated by a fixed step ΔS in acoustic space. This quantity is reflected in the distance between neighboring points on the bottom layer of each diagram in Figure 2. By the standard definition of the derivative as a limit, as ΔS approaches zero this measure of perceptual warping corresponds to the derivative of E[T|S] with respect to S. This derivative is
| (14) |
where the last term is the derivative of the logistic function given in Equation 12. This equation demonstrates that distance between two neighboring points in perceptual space is a linear function of the rate of change of p(c|S), which measures category membership of stimulus S. Probabilities of category assignments are changing most rapidly near category boundaries, resulting in greater perceptual distances between neighboring stimuli near the edges of categories. This is shown in Figure 6 (c), and the form of the derivative is described in more detail in Appendix C.
In summary, the identification function (Equation 12) shows a sharp decrease at the location of the category boundary, going from a value near one (assignment to category 1) to a value near zero (assignment to category 2). Perceptual bias, or displacement (Equation 13), is a linear function of distance from the mean in the one-category case but is more complex in the two-category case; it is positive when stimuli are displaced in a positive direction and negative when stimuli are displaced in a negative direction. Finally, warping of perceptual space (Equation 14), which has a value greater than one in areas where perceptual space is expanded and a value less than one in areas where perceptual space is shrunk, shows that all of perceptual space is shrunk in the one-category case but that there is an area of expanded perceptual space between categories in the two-category case. Qualitatively, note that displacement is always in the direction of the most probable category mean and that the highest perceptual distance between stimuli occurs near category boundaries. This is compatible with the idea that categories function like perceptual magnets and also with the observation that perceptual space is shrunk most in the centers of phonetic categories. The remainder of this section uses these measures to explore the model’s behavior under various parameter manipulations that simulate changes in phonetic category frequency, within-category variability, and speech signal noise.
Frequency
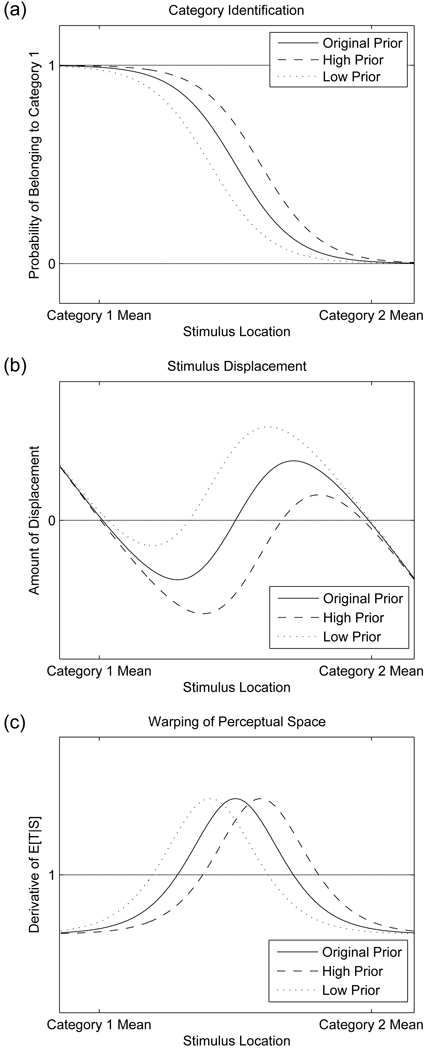
Manipulating the frequency of phonetic categories corresponds in our model to manipulating their prior probability. This manipulation causes a shift in the discriminative boundary between two categories, as described in Appendix B. In Figure 7 (a), the boundary is shifted toward the category with lower prior probability so that a larger region of acoustic space between the two categories is classified as belonging to the category with higher prior probability. Figure 7 (b) shows that when the prior probability of category 1 is increased, most stimuli between the two categories are shifted in the negative direction toward the mean of that category. This occurs because more sounds are classified as being part of category 1. Decreasing the prior probability of category 1 yields a similar shift in the opposite direction. Figure 7 (c) shows that the location of the expansion of perceptual space follows the shift in the category boundary.
Figure 7.
Effects of prior probability manipulation on (a) identification, (b) displacement, and (c) warping. The prior probability of category 1, p(c1), was either increased or decreased while all other model parameters were held constant.
This shift qualitatively resembles the boundary shift that has been documented based on lexical context (Ganong, 1980). In contexts where one phoneme would form a lexical item and the other would not, phoneme boundaries are shifted toward the phoneme that makes the non-word, so that more of the sounds between categories are classified as the phoneme that would yield a word. Similar effects have also been found for lexical frequency (Connine, Titone, & Wang, 1993) and phonotactic probability (Massaro & Cohen, 1983; Pitt & McQueen, 1998). To model such a shift using the rational model, information about a specific lexical or phonological context needs to be encoded in the prior p(c). The prior would thus reflect the information about the frequency of occurrence of a phonetic category in a specific context. The rational model then predicts that the boundary shift can be modeled by a bias term of magnitude and that the peak in discrimination should shift together with the category boundary.
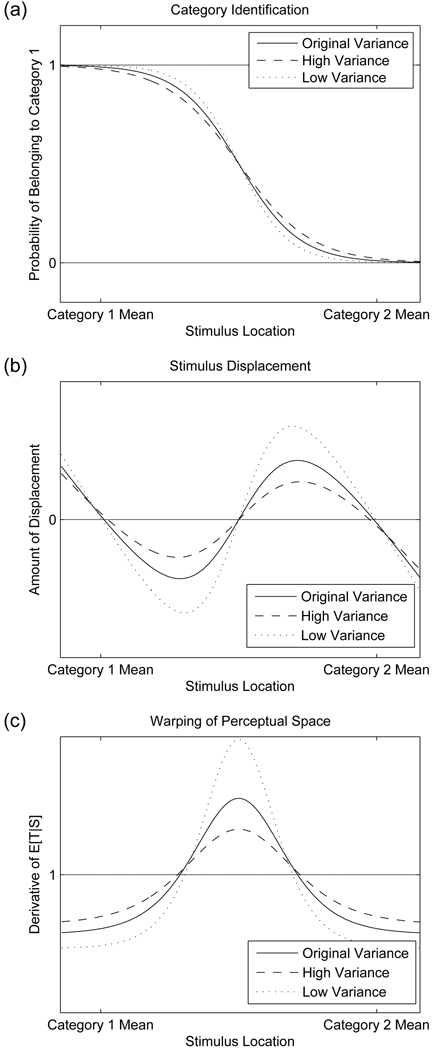
Variability
The category variance parameter indicates the amount of meaningful variability that is allowed within a phonetic category. One correlate of this might be the amount of coarticulation that a category allows: categories that undergo strong coarticulatory effects have high variance, whereas categories that are resistant to coarticulation have lower variance.3 In the model, categories with high variability should differ from categories with low variability in two ways. First, the discriminative boundary between the categories should be either shallow, in the case of high variability, or sharp, in the case of low variability (Figure 8 (a)). This means that listeners should be nearly deterministic in inferring which category produced a sound in the case of low variability, whereas they should be more willing to consider both categories if the categories have high variability. This pattern has been demonstrated empirically by Clayards, Tanenhaus, Aslin, and Jacobs (2008), who showed that the steepness of subjects’ identification functions along a /p/−/b/ continuum depends on the amount of category variability in the experimental stimuli.
Figure 8.
Effects of category variance on (a) identification, (b) displacement, and (c) warping. The category variance parameter was either increased or decreased while all other model parameters were held constant.
In addition to this change in boundary shape, the rational model predicts that the amount of variability should affect the weight given to the category means relative to the stimulus S when perceiving acoustic detail. Less variability within a category implies a stronger constraint on the sounds that the listener expects to hear, and this gives more weight to the category means. This should cause more extreme shrinkage of perceptual space in categories with low variance.
These two factors should combine to yield extremely categorical perception in categories with low variability and perception that is less categorical in categories with high variability. Figure 8 (b) shows that displacement has a higher magnitude than baseline for stimuli both within and between categories when category variance is decreased. Displacement is reduced with higher category variance. Figure 8 (c) shows the increased expansion of perceptual space between categories and the increased shrinkage within categories that result from low category variance. In contrast, categories with high variance yield more veridical perception.
Differences in category variance might explain why it is easier to find perceptual magnet effects in some phonetic categories than in others. According to vowel production data from Hillenbrand et al. (1995), reproduced here in Figure 1, the /i/ category has low variance along the dimension tested by Iverson and Kuhl (1995). The difficulty in reproducing the effect in other vowel categories might be partly attributable to the fact that listeners have weaker prior expectations about which vowel sounds speakers might produce within these categories.
This parameter manipulation can also be used to explore the limits on category variance: the rational model places an implicit upper limit on category variance if one is to observe enhanced discrimination between categories. This limit occurs when categories are separated by less than two standard deviations, that is, when the standard deviation increases to half the distance to the neighboring category. When the category variance reaches this point, the distribution of speech sounds in the two categories becomes unimodal and the acquired distinctiveness between categories disappears. Instead of causing enhanced discrimination at the category boundary, noise now causes all speech sounds to be pulled inward toward the space between the two category means, as illustrated in Figure 9. Shrinkage of perceptual space may be slightly less between categories than within categories, but all of perceptual space is pulled toward the center of the distribution. This perceptual pattern resembles the pattern that would be predicted if these speech sounds all derived from a single category, indicating that it is the distribution of speech sounds in the input, rather than the explicit category structure, that produces perceptual warping in the model.
Figure 9.
Categories that overlap to form a single unimodal distribution act perceptually like a single category: speech sounds are pulled toward a point between the two categories.
Noise
Manipulating the speech signal noise also affects the optimal solution in two different ways. More noise means that listeners should be relying more on prior category information and less on the speech sound they hear, yielding more extreme shrinkage of perceptual space within categories. However, adding noise to the speech signal also makes the boundary between categories less sharp so that in high noise environments, listeners are uncertain of speech sounds’ category membership (Figure 10 (a)). This combination of factors produces a complex effect: whereas adding low levels of noise makes perception more categorical, there comes a point where noise is too high to determine which category produced a speech sound, blurring the boundary between categories.
Figure 10.
Effects of speech signal noise on (a) identification, (b) displacement, and (c) warping. The speech signal noise parameter was either increased or decreased while all other model parameters were held constant.
With very low levels of speech signal noise, perception is only slightly biased (Figure 10 (b)) and there is a very low degree of shrinkage and expansion of perceptual space (Figure 10 (c)). This occurs because the model relies primarily on the speech sound in low-noise conditions, with only a small influence from category information. As noise levels increase to those used in the simulation in the previous section, the amount of perceptual bias and warping both increase. With further increases in speech signal noise, however, the shallow identification function begins to interfere with the availability of category information. For unambiguous speech sounds, displacement and shrinkage are both increased, as shown at the edges of the graphs in Figure 10. However, this does not simultaneously expand perceptual space between the categories. Instead, the high uncertainty about category membership causes reduced expansion at points between categories, dampening the difference between between-category and within-category discriminability.
The complex interaction between perceptual warping and speech signal noise suggests that there is some level of noise for which one would measure between-category discriminability as much higher than within-category discriminability. However, for very low levels of noise and for very high levels of noise, this difference would be much less noticeable. This suggests a possible explanation for variability that has been found in perceptual warping even among studies that have examined the English /i/ category (e.g. Lively & Pisoni, 1997). Extremely low levels of ambient noise should dampen the perceptual magnet effect, whereas the effect should be more prominent at higher levels of ambient noise.
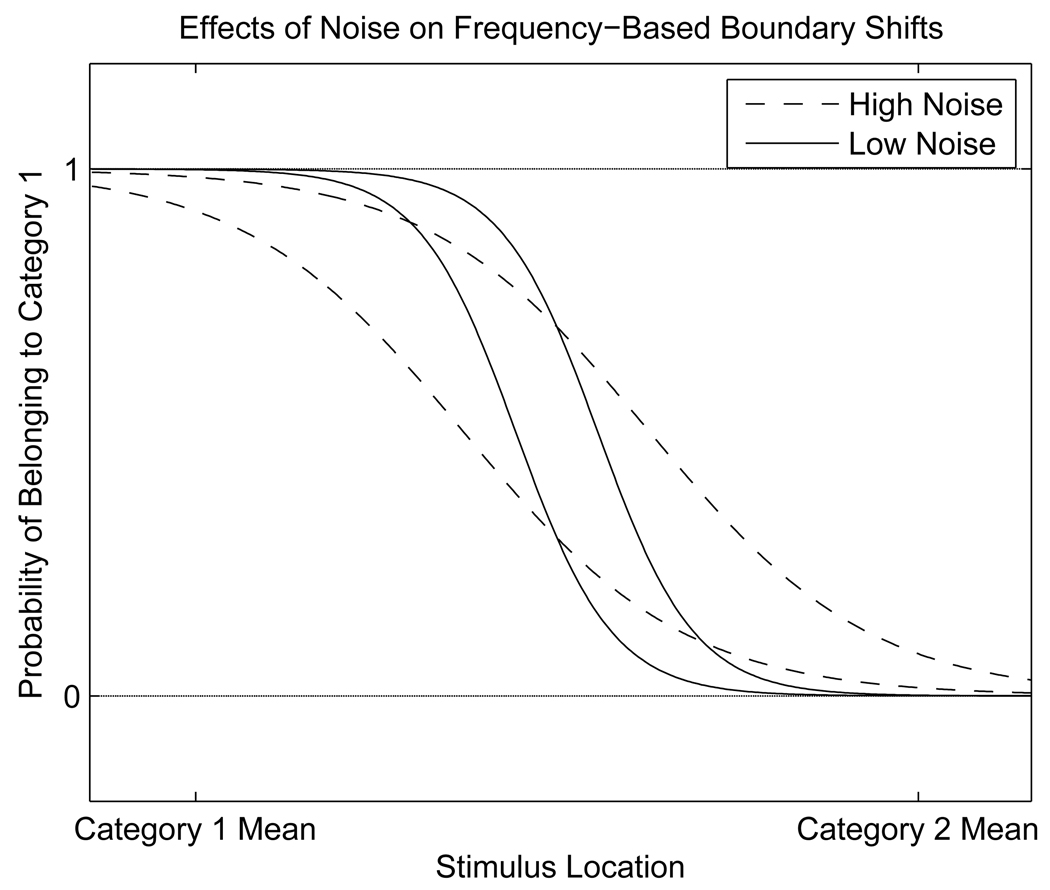
A further prediction regarding speech signal noise concerns its effect on boundary shifts. As discussed above, the rational model predicts that when prior probabilities p(c) are different between two categories, there should be a boundary shift caused by a bias term of . This bias term produces the largest boundary shift for small values of the gain parameter, which correspond to a shallow category boundary (see Appendix B). High noise variance produces this type of shallow category boundary, giving the bias term a large effect. This is illustrated in Figure 11, where for constant changes in prior probability, larger boundary shifts occur at higher noise levels. This prediction qualitatively resembles data on lexically driven boundary shifts: larger shifts occur when stimuli are low-pass filtered (McQueen, 1991) or presented in white noise (Burton & Blumstein, 1995).
Figure 11.
Effects of speech signal noise on the magnitude of a boundary shift. Simulations at both noise levels used prior probability values for c1 of 0.3 (left boundary) and 0.7 (right boundary). The boundary shift is nevertheless larger for higher levels of speech signal noise.
Summary
Simulations in this section have shown that the qualitative perceptual patterns predicted by the rational model are the same under nearly all parameter combinations. The exceptions to this are the case of no noise, in which perception should be veridical, and the case of extremely high category variance or extremely high noise, in which listeners cannot distinguish between the two categories and effectively treat them as a single, larger category. In addition, these simulations have examined three types of variability in perceptual patterns. Shifts in boundary location occur in the model due to changes in the prior probability of a phonetic category, and these shifts mirror lexical effects that have been found empirically (Ganong, 1980). Differences in the degree of categorical perception in the model depend on the amount of meaningful variability in a category, and these predictions are consistent with the observation that the /i/ category has low variance along the relevant dimension. Finally, the model predicts effects of ambient noise on the degree of perceptual warping, a methodological detail that might explain the variability of perceptual patterns under different experimental conditions.
Testing the Predicted Effects of Noise
Simulations in the previous section suggested that ambient noise levels might be partially responsible for the contradictory evidence that has been found in previous empirical studies of the perceptual magnet effect. In this section, we present an experiment to test the model’s predictions with respect to changes in speech signal noise. The rational model makes two predictions about the effects of noise. The first prediction is that noise should yield a shallower category boundary, making it difficult at high noise levels to determine which category produced a speech sound. This effect should lower the discrimination peak between categories at very high levels of noise and is predicted by any model in which noise increases the variance of speech sounds from a phonetic category. The second prediction is that listeners should weight acoustic and category information differentially depending on the amount of speech signal noise. As noise levels increase, they should rely more on category information, and perception should become more categorical. This effect is predicted by the rational model but not by other models of the perceptual magnet effect, as will be discussed in detail later in the paper. While this effect is overshadowed by the shallow category boundary at very high noise levels, examining low and intermediate levels of noise should allow us to test this second prediction.
Previous research into effects of uncertainty on speech perception has focused on the role of memory uncertainty. Pisoni (1973) found evidence that within-category discrimination shows a larger decrease in accuracy with longer interstimulus intervals than between-category discrimination. He interpreted these results as evidence that within-category discrimination relies on acoustic (rather than phonetic) memory more than between-category discrimination and that acoustic memory traces decay with longer interstimulus intervals. Iverson and Kuhl (1995) also investigated the perceptual magnet effect at three different interstimulus intervals; though they did not explicitly discuss changes in warping related to interstimulus interval, within-category clusters appear to be tighter in their 2500 ms condition than in their 250 ms condition. These results are consistent with the idea that memory uncertainty increases with increased interstimulus intervals.
Several studies have also studied asymmetries in discrimination, under the assumption that memory decay will have a greater effect on the stimulus that is presented first. However, many of these studies have produced contradictory results, making the effects of memory uncertainty difficult to interpret (see Polka & Bohn, 2003, for a review). Furthermore, data from Pisoni (1973) indicate that longer interstimulus intervals do not necessarily increase uncertainty: discrimination performance was worse with a 0 ms interstimulus interval than with a 250 ms interstimulus interval.
Adding white noise is a more direct method of introducing speech signal uncertainty, and its addition to speech stimuli has consistently been shown to decrease subjects’ ability to identify stimuli accurately. Subjects make more identification errors (G. A. Miller & Nicely, 1955) and display a shallower identification function (Formby, Childers, & Lalwani, 1996) with increased noise, consistent with the rational model’s predictions. While it is known that subjects rely to some extent on both temporal and spectral cues in noisy conditions (Xu & Zheng, 2007), it is not known how reliance on these acoustic cues compares to reliance on prior information about category structure. To test whether reliance on category information is greater in higher noise conditions than in lower noise conditions, we replicated Experiment 3 of Iverson and Kuhl (1995), their multidimensional scaling experiment, with and without the presence of background white noise.
The rational model predicts that perceptual space should be distorted to different degrees in the noise and no-noise conditions. At moderate levels of noise, we should observe more perceptual warping than with no noise due to higher reliance on category information. At very high noise levels, however, if subjects are unable to make reliable category assignments, warping should decrease; as noted, this decrease is predicted by any model in which subjects are using category membership to guide their judgments. Thus, while the model is compatible with changes in both directions for different noise levels, our aim is to find levels of noise for which warping is higher with increased speech signal noise. Moreover, manipulating the noise parameter in the rational model should account for behavioral differences due to changing noise levels.
Methods
Subjects
Forty adult participants were recruited from the Brown University community. All were native English speakers with no known hearing impairments. Participants were compensated at a rate of $8 per hour. Data from two additional participants were excluded, one because of equipment failure and one because of failure to understand the task instructions.
Apparatus
Stimuli were presented through noise cancellation headphones, Bose Aviation Headset model AHX-02, from a computer at comfortable listening levels. Participants’ responses were entered and recorded using the computer that presented the stimuli. The presentation of the stimuli was controlled using Bliss software (Mertus, 2004), developed at Brown University for use in speech perception research.
Stimuli
Thirteen /i/ and /e/ stimuli, modeled after the stimuli in Iverson and Kuhl (1995), were created using the KlattWorks software (McMurray, in preparation). Stimuli varied along a single F1−F2 vector that ranged from an F1 of 197 Hz and an F2 of 2489 Hz to an F1 of 429 Hz and an F2 of 1925 Hz. The stimuli were spaced at equal intervals of 30 mels; exact formant values are shown in Table 1. F3 was set at 3010 Hz, F4 at 3300 Hz, and F5 at 3850 Hz for all stimuli. The bandwidths for the five formants were 53, 77, 111, 175, and 281 Hz. Each stimulus was 435 ms long. Pitch rose from 112 to 130 Hz over the first 100 ms and dropped to 92 Hz over the remainder of the stimulus. Stimuli were normalized in Praat (Boersma, 2001) to have a mean intensity of 70 dB.
For stimuli in the noise condition, 435 ms of white noise was created using Praat by sampling randomly from a uniform [−0.5,0.5] distribution at a sampling rate of 11,025 Hz. The mean intensity of this waveform was then scaled to 70 dB. The white noise was added to each of the 13 stimuli, creating a set of stimuli with a zero signal-to-noise ratio.
Procedure
Participants were assigned to either the no-noise or the noise condition. After reading and signing a consent form, they completed ten practice trials designed to familiarize them with the task and stimuli and subsequently completed a single block of 208 trials. This block included 52 “same” trials, four trials for each of 13 stimuli, and 156 “different” trials in which all possible ordered pairs of non-identical stimuli were presented once each. In each trial, participants heard two stimuli sequentially with a 250 ms interstimulus interval. They were instructed to respond as quickly as possible, pressing one button if the two stimuli were identical and another button if they could hear a difference between the two stimuli. Responses and reaction times were recorded.
This procedure was nearly identical to that used by Iverson and Kuhl (1995), though the response method differed slightly in order to provide reaction times for “same” responses in addition to “different” responses. We also eliminated the response deadline of 2000 ms and instead recorded subjects’ full reaction times for each contrast, up to 10,000 ms.
Results and Discussion
Fourteen of the 8,320 responses were excluded from the analysis because subjects either responded before hearing the second stimulus or failed to respond altogether within the ten second response period. Table 2 shows the percentage of the remaining trials on which subjects responded “same” for each contrast. As expected, the percentage of “same” responses was extremely high for one-step discriminations and got successively lower as the psychoacoustic distance between stimuli increased. This correlation was significant in a by-item analysis for both the no-noise (r = −0.85; p < 0.01) and the noise (r = −0.87; p < 0.01) conditions.4 Figure 12 (a) shows these confusion data schematically, where darker squares indicate a higher percentage of “same” responses. This schematic representation highlights three differences between the conditions. First, the overall percentage of “same” responses was higher in the noise condition than in the no-noise condition, as evidenced by the higher number of dark squares. Second, the percentage of “same” responses declines more slowly in the noise condition than in the no-noise condition with increasing psychophysical distance, as reflected by a more gradual change from dark squares to light squares in the noise condition. Third, the difference between within-category and between-category contrasts was greater in the noise condition than in the no-noise condition. Whereas the no-noise condition shows fairly constant performance along any given diagonal, with only a small dip in the percentage of “same” responses toward the center of the stimulus continuum, the noise condition shows a much larger difference along the diagonal, with a strong decrease in “same” responses near the between-category contrasts at the center of the stimulus continuum. This third difference suggests that there is a larger degree of within-category shrinkage and between-category expansion of perceptual space in the noise condition, consistent with the predictions of the rational model.
Table 2.
Percentage of trials on which subjects responded “same” for each pair of stimuli in the no-noise (top) and noise (bottom) conditions.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 98.8 | 82.5 | 82.5 | 40 | 22.5 | 7.5 | 5 | 5 | 0 | 0 | 2.5 | 0 | 2.5 |
| 2 | 97.5 | 95 | 70 | 52.5 | 10 | 5 | 0 | 2.5 | 2.5 | 0 | 0 | 0 | |
| 3 | 91.3 | 97.5 | 75 | 32.5 | 12.5 | 5 | 2.5 | 0 | 2.5 | 2.5 | 0 | ||
| 4 | 97.5 | 87.5 | 40 | 12.5 | 5 | 2.5 | 0 | 2.5 | 0 | 0 | |||
| 5 | 97.5 | 77.5 | 27.5 | 12.5 | 5 | 2.5 | 0 | 0 | 0 | ||||
| 6 | 92.5 | 75 | 30 | 15 | 2.5 | 2.5 | 2.6 | 0 | |||||
| 7 | 91.3 | 75 | 42.5 | 17.5 | 5 | 5 | 0 | ||||||
| 8 | 95 | 80 | 50 | 32.5 | 7.5 | 5 | |||||||
| 9 | 93.75 | 87.5 | 67.5 | 27.5 | 22.5 | ||||||||
| 10 | 92.5 | 87.5 | 76.9 | 37.5 | |||||||||
| 11 | 97.5 | 87.5 | 65 | ||||||||||
| 12 | 96.3 | 97.5 | |||||||||||
| 13 | 100 | ||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
| 1 | 95 | 95 | 87.5 | 80 | 82.5 | 57.5 | 25 | 7 | 5 | 0 | 0 | 5 | 2.5 |
| 2 | 96.3 | 97.5 | 97.5 | 87.5 | 80 | 42.5 | 15 | 5 | 5 | 0 | 2.5 | 2.5 | |
| 3 | 95 | 97.5 | 90 | 80 | 42.5 | 30 | 7.5 | 0 | 2.5 | 2.5 | 0 | ||
| 4 | 92.5 | 95 | 90 | 55 | 20 | 10 | 7.5 | 2.5 | 2.5 | 7.5 | |||
| 5 | 95 | 90 | 67.5 | 27.5 | 5 | 12.5 | 2.5 | 15 | 10 | ||||
| 6 | 96.3 | 87.5 | 50 | 25 | 7.5 | 2.5 | 10 | 2.5 | |||||
| 7 | 91.3 | 75 | 42.5 | 20 | 12.5 | 12.5 | 10 | ||||||
| 8 | 87.5 | 72.5 | 52.5 | 40 | 20 | 10 | |||||||
| 9 | 90 | 92.5 | 72.5 | 47.5 | 37.5 | ||||||||
| 10 | 93.8 | 95 | 85 | 52.5 | |||||||||
| 11 | 95 | 100 | 85 | ||||||||||
| 12 | 95 | 97.5 | |||||||||||
| 13 | 95 | ||||||||||||
Figure 12.
Confusion matrices showing the percentage of “same” responses to each contrast in (a) subject data, (b) the full model in which the noise parameter varied between conditions, and (c) the restricted model in which the noise parameter was constrained to be the same between conditions. The left-hand plots show the no-noise condition and the right-hand plots show the noise condition. Darker cells indicate a higher percentage of “same” responses.
Same-Different Model
We used the rational model to simulate these confusion data, assuming that participants perceive speech sounds by sampling a target production from the posterior distribution on target productions, p(T|S). We extended the model to account directly for same-different responses by assuming that participants respond “same” if the sampled target productions for the two speech sounds are within a threshold distance ϵ of each other; otherwise they respond “different”. The parameter ϵ thus plays a similar role to the response criterion of the observer in Signal Detection Theory (Green & Swets, 1966), determining the magnitude of a difference that will yield a positive response. Under this model, the number of “same” responses to a given contrast is predicted to follow a binomial distribution B(n, p) where n is the number of trials in which a given contrast was presented and p is the probability that the two sampled target productions for that contrast are within a distance ϵ of each other, p(|TA − TB| ≤ ϵ|SA, SB). This probability can be computed as described in Appendix D.
The simulation used the same category means μ/i/ and μ/e/ and category variance as the simulation of the Iverson and Kuhl data. The noise variance was a free parameter that could vary between conditions to capture differences in perceptual warping; in addition, the decision threshold ϵ was a free parameter that could vary between the two conditions, allowing the model to capture the overall greater number of “same” responses in the noise condition. These free parameters were chosen to maximize the likelihood of the same-different data. The best-fitting model used parameters of ϵ=76 mels and (σS=30 mels) for the no-noise condition and ϵ=111 mels and (σS=46 mels) for the noise condition. Using these parameters, the percentage of “same” responses predicted by the model for each contrast was highly correlated with that found empirically (r = 0.98 for the no-noise condition; r = 0.97 for the noise condition), and these correlations remained high even after controlling for acoustic distance (r = 0.94 and r = 0.87 for the no-noise and noise conditions, respectively). Model performance is shown schematically in Figure 12 (b).
The key prediction for this experiment was that the noise variance parameter could account for differences in performance between the no-noise and noise conditions. However, in the above simulation, ϵ was an additional free parameter that could vary between conditions. To demonstrate quantitatively that noise parameter accounted for differences above and beyond those accounted for simply by varying the decision threshold, we used a generalized likelihood ratio test (e.g. Rice, 1995) to compare the full model described above with a restricted model (Figure 12 (c)) in which the noise parameter was constant across conditions. Like the full model, the restricted model used category means and the category variance from the previous simulations, and the decision threshold was a free parameter that could vary between the two conditions.5 The models differed only in their assumptions about the noise parameter. These two models thus constitute a nested hierarchy, and we can determine whether the additional noise parameter makes a statistically significant difference by examining the difference between the log likelihoods of the models, computed using the maximum likelihood estimates of the parameters. Under the null hypothesis that the data were generated from the restricted model, twice this difference has a χ2(1) distribution. The log likelihood of the data was −676 under the restricted model6 and −568 under the full model. The full model therefore accounted for these data significantly better than the restricted model (χ2(1) = 216, p < 0.0001); allowing the noise parameter to change between the noise and no-noise conditions resulted in a statistically significant improvement in fit.
This comparison indicates that the rational model accounts for additional differences between conditions beyond the overall increase in “same” responses. As noted earlier, there are two such differences apparent in the data. First, the decrease in “same” responses with psychophysical distance is more gradual in the noise condition than the no-noise condition. In the rational model, this occurs because listeners in the noise condition assume that the speech sound might have come from a wider range of target productions, leading to higher variability in the posterior distribution (Equation 25). Higher posterior variance leads to a shallower decline in “same” responses. Second, the responses are more categorical in the noise condition than the no-noise condition, as evidenced by response patterns along each diagonal. This occurs in the rational model due to increased weighting of category information in higher noise conditions (Equation 7).
While both these aspects of the data are compatible with the rational model, a straightforward alternative explanation is available for the first. In modeling these data we have made the assumption that the stimulus heard by experimental participants is identical to the stimulus played. This assumption allows the use of known stimulus values S when computing listeners’ optimal percepts. However, in reality there is likely to be some variability in the stimuli heard by listeners, and this variability should be higher in the noise condition than in the no-noise condition. The shallow decrease in “same” responses in the noise condition might then be a simple result of higher stimulus variability. Taking into account experimental noise might improve the performance of the restricted model by providing a mechanism to account for this shallower decrease in “same” responses in the noise condition.
To investigate this possibility, we simulated experimental noise in the restricted model by drawing values of S, the speech sound heard by listeners, from a Gaussian distribution centered around each stimulus value. The probability of a “same” response for a given contrast was approximated by drawing 100 samples of each speech sound in the pair and computing the probability of a “same” response for each pair of samples. These probabilities were then averaged to obtain the expected probability of a “same” response for each contrast, and a binomial model was used to compute the likelihood of the data. The experimental noise variance was a free parameter that varied between the two conditions, under the assumption that listeners in the two conditions heard the stimuli through different amounts of noise. A third noise parameter which governed listeners’ inferences was held constant between the two conditions, as in the restricted model, implementing an assumption that listeners weight category information equally in the two conditions. This model yielded a log likelihood of −618, significantly higher than the restricted model described above (χ2(2) = 116, p < 0.0001) but lower than the full model despite having one more free parameter.7 The remaining difference in likelihood between this model and the full model reflects listeners’ increased reliance on category information in higher noise conditions, as captured by our rational model.
Multidimensional Scaling
The two noise parameters used in the simulation of our confusion data were both lower than the noise variance estimated based on the Iverson and Kuhl data. However, the ambient noise level in Iverson and Kuhl’s experiment should have been comparable to that of our no-noise condition and was almost certainly lower than the zero signal-to-noise ratio in our noise condition. This discrepancy may reflect a difference in analysis methods. Whereas Iverson and Kuhl used multidimensional scaling to analyze their results, we based our analysis directly on subject confusion data. To draw a closer comparison to the results from Iverson and Kuhl, and to further help visualize the difference between the noise and no-noise conditions, we used multidimensional scaling to create perceptual maps from the behavioral data.
Our multidimensional scaling analysis incorporated information from both reaction times and same-different responses. Reaction time data were normalized across subjects by first taking the log transform to ensure normal distributions and then converting these to z-scores for each subject. Psychoacoustic distance had a significant positive correlation with these normalized reaction times for “same” responses (r = 0.45, p < 0.01 for the no-noise condition; r = 0.27, p < 0.02 for the noise condition),8 reflecting the predicted result that subjects who responded “same” were slower when the stimuli were separated by a greater psychoacoustic distance. Conversely, the data showed a significant negative correlation between psychoacoustic distance and normalized reaction times on “different” responses (r = −0.69, p < 0.01 for the no-noise condition; r = −0.56, p < 0.01 for the noise condition), indicating that subjects were faster to respond “different” when the stimuli were farther apart in psychoacoustic space. Both “same” and “different” reaction times were therefore included as measures of perceptual distance in our multidimensional scaling analysis.
The intuition behind our multidimensional scaling analysis, which is supported by the correlations presented above, is that reaction times and same-different responses are consistent with a subject’s perceptual map of the stimuli. “Different” responses with short reaction times indicate that stimuli are far apart in this perceptual map; “different” responses with long reaction times indicate that stimuli are closer together; “same” responses with long reaction times indicate that stimuli are even closer; and “same” responses with short reaction times indicate that stimuli are extremely close together in the perceptual map. Non-metric multidimensional scaling (Shepard, 1980) is an optimization method that aims to minimize violations of distance rankings in a perceptual map. It assumes a monotonic relation between reaction times and perceptual distance but does not assume any parametric form for this relation.9
A similarity matrix for each condition was constructed that mirrored these intuitions. This was implemented computationally by subtracting z-scores for “same” responses from a z-score of six,10 effectively transforming “same” responses into “different” responses with extremely long reaction times, such that shorter reaction times on a “same” response mapped onto longer reaction times on a “different” response. This is similar to the procedure used by Iverson and Kuhl, who substituted a reaction time of 2000 ms (the trial length in their experiment) for any “same” response. The median score across subjects for each contrast was then entered into the similarity matrix and scores were normalized to fall between zero and one.
Non-metric multidimensional scaling solutions based on these similarity matrices are shown in Figure 13. The plots are modeled after Figure 5: the horizontal axis shows acoustic space, and the vertical axis shows perceptual space. A linear function would indicate a linear mapping between acoustic and perceptual space, whereas non-linearities suggest that perceptual space is warped relative to acoustic space. Areas that are more nearly horizontal indicate greater shrinkage of perceptual space. These multidimensional scaling solutions suggest that there is a difference in subjects’ perceptual maps between the two conditions. Consistent with results from Iverson and Kuhl, there is some evidence of perceptual warping in the no-noise condition, but here interstimulus distances are relatively constant. As predicted by our model, perceptual space is more warped in the noise condition than in the no-noise condition. Unambiguous stimuli near category centers are very close together in perceptual space, whereas stimuli near the category boundary are much farther apart. The precise stimulus locations in these multidimensional scaling solutions are not compatible with the parameters used for the simulation of raw confusion data, suggesting that multidimensional scaling yields an imperfect perceptual map of the stimuli. It is possible that Iverson and Kuhl’s multidimensional scaling analysis produced a parallel exaggeration of the degree of warping, yielding the discrepancy in noise parameters discussed above. However, the multidimensional scaling solution illustrates the same qualitative difference between the conditions as is seen in the raw confusion data: subjects in the noise condition relied more on category information than subjects in the no-noise condition.
Figure 13.
Perceptual maps for the (a) no-noise and (b) noise conditions obtained through multidimensional scaling. Data from (c) Iverson and Kuhl’s (1995) multidimensional scaling experiment are shown for comparison.
As predicted for moderate noise levels, we observed increased perceptual warping with increased speech signal noise. These results provide evidence that listeners are sensitive to the level of speech signal noise and that their perception reflects these differing noise levels in a way that is compatible with the optimal behavior predicted by the rational model. This effect of noise is not directly predicted by previous models, though it may be compatible with some of them, as discussed in the next section.
Comparison to Previous Models
Our rational model has taken a new approach to explaining the perceptual magnet effect, framing it as the optimal solution to the inference problem of perceiving speech sounds in the presence of noise. However, the solution derived in this analysis shares elements with several previous computational models, which have implicitly incorporated mechanisms that implement reliance on prior information and optimal inference of category membership. These parallels allow the various approaches to be seen as complementary descriptions of the same system that we describe here, articulated at different levels of analysis (Marr, 1982). Previous models provide process-level accounts showing how a system like the one we propose might be implemented, while the rational model uses analysis of the computational-level problem to explain why the mechanisms proposed by previous models should work.
Exemplar Model
A direct mathematical connection occurs with Lacerda’s (1995) model, in which listeners’ discrimination abilities are the side effect of an exemplar-based categorization problem. Lacerda’s model rests on the assumption that phonetic categories have approximate Gaussian distributions and that listeners store labeled exemplars from these categories. Perception requires listeners to determine the category membership of a new speech sound. Lacerda defines a speech sound’s similarity to a category as the proportion of stored exemplars within some distance ϵ from the speech sound that belong to the category. Listeners’ discrimination of two speech sounds then depends on the difference between the two speech sounds’ similarity values.
In a system with two categories A and B, the similarity of a speech sound x to category A (sA) is defined in the exemplar model as
| (15) |
where N eighbA(x, ϵ) indicates the number of neighbors within range ϵ of speech sound x. The discrimination function depends on the difference in similarity between neighboring speech sounds; as the distance between neighboring speech sounds approaches zero, this corresponds to the derivative of the similarity function. The discrimination function is therefore defined as
| (16) |
where k is an arbitrary constant. This indicates that the discriminability at a point in perceptual space depends on the rate of change of category membership.
The mathematics underlying this exemplar model have a direct connection to our rational model. The first point of connection is that the similarity function in the exemplar model approximates the posterior probability of category membership in the rational model. This can be seen by noting that the exemplars are generated from a Gaussian distribution so that listeners who have heard N A exemplars from category A have heard approximately exemplars from category A within a range ϵ from speech sound x. As epsilon approaches zero, the number of neighbors is proportional to p(x|A)NA. The similarity metric then becomes
| (17) |
which is equivalent to Bayes’ rule as long as the number of stored exemplars in each category, NA and NB, are proportional to the prior probabilities of the categories, p(A) and p(B). This calculation yields the posterior probability p(A|x), indicating that the similarity metric used in the exemplar model approximates the posterior probability of category membership.
Furthermore, the discrimination function defined in the exemplar model is a component of the measure of warping defined in the rational model. This can be shown by substituting p(A|x) and its analogue p(B|x) into the discrimination function, yielding
| (18) |
Recall that Equation 14, which defined perceptual warping in the rational model, included the term . There is a direct correspondence between the derivative terms in the two equations: both indicate that the discriminability at a particular point in perceptual space is a linear function of the rate of change in the identification function. The constant k in the exemplar model corresponds in our model to a number that is based on the speech signal noise, category variance, and distance between the two category means, as discussed in Appendix C. Unlike in the exemplar model, discriminability in the rational model includes an additional component that is not based on category membership: listeners can discriminate speech sounds that differ acoustically to the extent that they rely on acoustic information from the speech sounds.
This analysis shows that the rational model incorporates the idea from Lacerda’s exemplar model that discrimination peaks occur near category boundaries due to the distributions of exemplars in phonetic categories. Our model also goes beyond the exemplar model to account for better than chance within-category discriminability and to provide independent justification for why discrimination should be best near those speech sounds where category uncertainty is highest. This maximum discriminability occurs because of the attractors that form at each phonetic category, based on optimal compensation for speech signal noise. The attractors pull equally on speech sounds that are on the boundary between phonetic categories, but as soon as a speech sound is to one side or the other of the boundary, perception is influenced more by the mean of the more probable category.
Despite their similarities, the two models differ in the goal they assign to the listener. Whereas Lacerda argues that listeners perceive only similarity to phonetic categories, shown here to be a measure of category membership, the rational model is based on the assumption that listeners are trying to extract acoustic detail from the speech signal. Because of this theoretical difference, the two models yield differing predictions on the role of speech signal noise in speech perception: Lacerda’s model does not predict the experimental result that reliance on category information should increase due to increased speech signal noise.
Neural Network Models
Additional links can be drawn between our rational model and several neural network models that have been proposed to account for categorical effects in speech perception. Guenther and Gjaja (1996) focused specifically on the perceptual magnet effect, proposing that Gaussian distributions of speech sounds can create a bias in neural firing preferences that favors category centers. In their model, most neurons preferentially respond to speech sounds near category centers, whereas few neurons favor speech sounds near category edges. This is a direct result of their unsupervised learning mechanism, which causes the distribution of neural firing preferences to mirror the distribution of speech sounds in the input. With such a distribution in place, a population vector computed over the entire population of neurons will include disproportionately many responses from neurons that detect sounds near category centers, biasing perception toward prototypical speech sounds.
While learning is not addressed in our model, the perceptual mechanism used in the neural model has a direct link to the model proposed here. Shi, Feldman, and Griffiths (2008) demonstrated that one can perform approximate Bayesian inference using an exemplar model by storing samples from the prior distribution, weighting each sample by its likelihood, and averaging over the values of these weighted samples. The neural model proposed by Guenther and Gjaja can be interpreted as implementing this type of approximate inference. In their model, the neural firing preferences come to mirror the distribution of speech sounds in the input so that the firing preference of each neuron represents a possible target production sampled from the prior. The activation of each neuron in the model then depends on the similarity of its firing preference to the speech sound heard. Specifically, the similarity is given by the dot product of the two unit vectors representing formant values, which has its maximum when the two formant values are equal. Though this differs from the Gaussian likelihood function we have proposed, it implements the idea that formant values most similar to the speech sound are given the highest weight. Finally, the percept of a sound is given by the population vector, which is a weighted average of neural firing preferences in which the weight assigned to each neuron is equal to its activation. Perception through the neural map therefore implements approximate Bayesian inference: the prior is given by neural firing preferences, and the likelihood function is given by the activation rule. While this neural implementation itself makes no predictions about the dependence of perceptual warping on speech signal noise, our analysis indicates that the dependence can be implemented in this framework through a mechanism that changes the neural activation rule, parallel to changing the likelihood function, based on noise levels.
Vallabha and McClelland (2007) present a neural model of the /r/ and /l/ categories that learns based on Gaussian distributions of speech sounds as well. This model has three layers of representation: an acoustic layer determined entirely by the input, a middle layer that represents perceptual space, and a final layer that represents category information. The category layer contains bidirectional connections with the perceptual layer such that the perception of a speech sound can help determine its category, but the category identification then exerts a bias on perception, moving the perceptual representation closer to the mean of a phonetic category. This is similar to the account of categorical perception provided by the TRACE model (McClelland & Elman, 1986). The model shares several theoretical components with the rational model, since it allows both category information and acoustic information to influence perception. However, we know of no explicit mathematical connections between the two models, and the authors do not address the neural model’s dependence on noise.
Several models of categorical perception are presented and reviewed by Damper and Harnad (2000). These models have in common that they are trained, in a supervised or unsupervised manner, on endpoint stimuli comprising voiced and voiceless tokens and tested on a VOT continuum between these endpoints. Results indicate that both a perceptron and a Brain-State-in-a-Box model (following J. A. Anderson, Silverstein, Ritz, & Jones, 1977) can reproduce the sharp category boundary between voiced and voiceless stops. In the perceptron, this categorization behavior likely results from the sigmoid activation function of the output unit, which resembles the logistic categorization function given in Equation 12. The Brain-State-in-a-Box model does not include this logistic categorization function but does include a mechanism mapping each input to its nearest attractor, creating a sharp change in behavior near the category boundary. These models therefore capture the idea that the discrimination function is dependent on categorization, but they fail to capture the within-category discriminability that has been shown for vowels. Because they only model categorization behavior, these models also fail to predict increased reliance on category information under noisy conditions.
These neural network models all implement some of the ideas contained in the rational model: either the idea that prior probability favors speech sounds near the center of a category, or the idea that discrimination is best near category boundaries. Models that implement the idea of bias toward category centers could theoretically be extended to account for increased bias under noisy conditions. However, the rational model goes further than this to explain why the dependence on noise should occur at all.
Acoustic and Phonetic Memory
Finally, the idea that both acoustic information from the speech sound and phonetic information from the category mean contribute to a listener’s percept has been suggested previously by Pisoni (1973) and others, who argue that the differences between vowel and consonant perception stem from the fact that vowels rely more on acoustic memory, whereas consonants rely more on phonetic memory. Like the Bayesian model, this account of acoustic and phonetic memory predicts that as the acoustic uncertainty increases, listeners should rely increasingly on phonetic memory, making perception more categorical. This idea has been tested in empirical studies that interfered with acoustic memory to obtain more categorical perception of vowels (Repp et al., 1979) or encouraged use of acoustic memory to obtain less categorical perception of consonants (Pisoni & Lazarus, 1974). In addition, tasks that required less memory load were found to increase especially the within-category discriminability of vowels (Pisoni, 1975).
This model is compatible with our Bayesian analysis, given some assumptions about the interaction between acoustic and phonetic memory and the degree to which each is used. The perception of speech sounds in the Bayesian model is a weighted average of the speech sound S and the means μc of a set of phonetic categories. One possible mechanism for implementing this approach would be to store the speech sound in acoustic memory and activate the phonetic category mean in phonetic memory. Under this assumption, the Bayesian model complements the process-level memory model by predicting the extent to which each mode of memory is used: for categories with high variability and in lower noise conditions, listeners should rely more on acoustic memory, whereas for categories with low variability and in higher noise conditions, listeners should rely more on phonetic memory.
It is worth noting that the closed-form solution given in Equation 11 holds only in the case of Gaussian phonetic categories and Gaussian noise. Qualitatively similar effects are predicted for any unimodal distribution of speech sounds, but these cases generally do not yield a quantitative solution that takes the form of a weighted average between acoustic and phonetic components. However, the weighted average may provide a close approximation to optimal behavior even in these cases.
Summary
In this section, we have shown that direct links can be drawn between the rational model and several process-level models that have been proposed to account for the perceptual magnet effect and categorical perception more generally. Any of these mechanisms might be consistent with the computational-level account we propose, and our analysis does not provide evidence for one particular implementation over another. Instead, our model contributes by providing a higher-level explanation of the principles that underlie the behavior of many of these models and by identifying phenomena such as the importance of speech signal noise that have not been predicted by previous accounts.
General Discussion
This paper has described a Bayesian model of speech perception in which listeners infer the acoustic detail of a speaker’s target production based on the speech sound they hear and their prior knowledge of phonetic categories. Uncertainty in the speech signal causes listeners to infer a sound that is closer to the mean of the phonetic category than the speech sound they actually heard. Assuming that a language has multiple phonetic categories, listeners use the probability with which different categories might have generated a speech sound to guide their inference of the acoustic detail. Simulations indicate that this model accurately predicts interstimulus distances in the detailed perceptual map from Iverson and Kuhl’s (1995) multidimensional scaling experiment as well as discrimination data from a novel experiment investigating the effect of noise on listeners’ use of category information. The remainder of the paper revisits the model’s assumptions and qualitative predictions in the context of previous research on the perceptual magnet effect, phonetic category acquisition, spoken word recognition, and categorical effects in other domains.
The Perceptual Magnet Effect
The rational model predicts that three factors are key in determining the nature of perceptual warping: category frequency, category variance, and speech signal noise. Nearly all values of these parameters imply the same pattern of perception, though to differing degrees. Speech sounds are pulled toward the means of nearby categories, yielding reduced discriminability near the centers of phonetic categories and increased discriminability near category edges. This is qualitatively in line with previous descriptions of the perceptual magnet effect. However, research on the perceptual magnet effect has found seemingly conflicting empirical data: several studies have found better discrimination near category boundaries than near the prototype, consistent with the idea of a perceptual magnet effect (Grieser & Kuhl, 1989; Kuhl, 1991; Iverson & Kuhl, 1995; Diesch et al., 1999; Iverson & Kuhl, 1996; Iverson et al., 2003), whereas other studies have found that the effect does not extend to other vowel categories (Sussman & Gekas, 1997; Thyer et al., 2000) or that methodological details affect the degree to which categorical effects are observed (Lively & Pisoni, 1997; Pisoni, 1973). The model’s predictions concerning differences in category variance and noise conditions suggest some avenues by which this debate might be resolved.
The predicted influence of category variance on perceptual warping may provide a reason why some categories show a higher degree of categorical perception than others. Data from Hillenbrand et al. (1995) suggest that the /i/ category has lower variance than other vowel categories in the direction tested by Iverson and Kuhl (1995), and it may be because of these higher levels of variability that the perceptual magnet effect has been difficult to find in other categories. Clayards et al. (2008) have demonstrated that adults are sensitive to the degree of within-category variability in an identification task, and our model predicts that this sensitivity carries over to discrimination tasks and makes perception less categorical in categories with high variability.
A second factor that should affect perceptual warping is the amount of speech signal noise, and the results of our experiment demonstrate that the perceptual magnet effect in the English /i/ and /e/ categories can be modulated by adding white noise. One immediate implication of this is that details of stimulus presentation are critical in speech perception experiments. Poor stimulus quality might actually yield better categorical perception results, and similar manipulations of memory uncertainty should also have this effect. This idea is consistent with results that show more pronounced discrimination peaks at category boundaries with longer interstimulus intervals, where memory uncertainty should be highest (Pisoni, 1973). Further research is necessary to determine the extent to which these factors can explain the variability in empirical results.
Another debate in the literature discusses the extent to which the perceptual magnet effect is a between-category or within-category phenomenon, and the rational model provides a way of reconciling these two characterizations. The within-category account involves speech sound prototypes that act as perceptual magnets, pulling the perception of speech sounds toward them (Kuhl et al., 1992). The idea of a perceptual magnet is formalized in Equation 7, where speech sounds are perceived based on the mean of the category that produced them. The between-category account ties the perception of speech sounds to the task of inferring category membership (Lacerda, 1995). In line with this, the Bayesian solution to the problem of speech perception with multiple categories (Equation 11) is consistent with the idea that listeners calculate the probability of each phonetic category having generated a speech sound. However, in contrast to Lacerda’s model, which assumes that listeners are perceiving only category membership, the present model predicts that listeners perceive speech sounds in terms of speakers’ intended target productions, a continuous variable that depends only partly on category membership. The rational model therefore synthesizes these two previous proposals into a single framework in which the perceptual magnet effect arises through the interaction between shrinkage of perceptual space toward category centers and enhanced discrimination between categories through optimal inference of category membership.
Similar to probabilistic models in visual perception (e.g. Yuille & Kersten, 2006), the use of the term inference here is not meant to imply that listeners are performing explicit computations, and the model does not attempt to distinguish between inference and perception. Likewise, in determining which categories might have generated a speech sound, listeners need not be making explicit categorization judgments. This computation may involve nothing more than implicit and automatic activation of the relevant phonetic categories, or even simple retrieval of stored exemplars (Shi et al., 2008). The argument presented here is that the perceptual magnet effect results from a process that approximates the mathematics of optimal inference and that this process is advantageous to listeners because it allows them to perceive speech sounds accurately.
Phonetic Category Acquisition
The rational model assumes that listeners have prior knowledge of phonetic categories in their language. While this is true of adult listeners, it poses an acquisition problem because infants need to learn which categories are present in their native language. This acquisition problem has been studied in the context of several computational models that learn Gaussian categories from unlabeled input using a mixture of Gaussians approach. Boer and Kuhl’s (2003) model learned from a batch of stored exemplars, using the Expectation Maximization algorithm (Dempster, Laird, & Rubin, 1977) to find an appropriate set of three vowel categories. More recently, McMurray, Aslin, and Toscano (2009) used an incremental algorithm to learn the category parameters for a voicing contrast and Vallabha, McClelland, Pons, Werker, and Amano (2007) applied this incremental algorithm to vowel formant and duration data from English and Japanese infant-directed speech. Incremental algorithms lend psychological plausibility to this account, allowing infants to learn from each speech sound as it is heard. The Gaussian categories learned by this type of algorithm would provide the necessary prior information assumed in our Bayesian model.
Learning explicit Gaussian categories yields a prior that is consistent with this model, but it is also possible to relax the assumptions of normality and of discrete categories so that the perceptual magnet effect arises simply as a result of listeners’ estimating the distribution of speech sounds in their language. Formal analyses of models of categorization have shown that simply storing exemplars can provide an alternative method for estimating the distribution associated with a category (Ashby & Alfonso-Reese, 1995). If it is assumed that probabilities are assigned to stimuli in a way that is determined by their similarity to previously observed exemplars, and that the distribution associated with a category results from summing the probabilities produced by each exemplar from that category, the result is a kernel density estimator, a nonparametric method for estimating probability distributions (Silverman, 1986). Given sufficiently many exemplars, the distribution estimated in this fashion will approximate the distribution associated with the category. If the category distribution is Gaussian, the result will be approximately Gaussian. However, listeners do not need explicit knowledge of this larger structure. Rather, they can obtain the same perceptual effect by treating each exemplar as its own category. In this scenario, listeners need to take many small overlapping categories, or kernels, into account using Equation 11. In our discussion of limits on category variance, we showed that if two Gaussian categories produce a collective unimodal distribution, all of perceptual space is biased inward toward a point between the categories. Here, kernels that represent speech sounds from a Gaussian phonetic category will combine to produce a unimodal Gaussian distribution. The mathematics of this case reduce to the mathematics of the case of a single discrete category, with the weight on speech sound S equal to the sum of the kernel width and the variance in the locations of kernels.
This method of learning distributions based on individual speech sounds removes the need for listeners to have knowledge of explicit categories, reducing the severity of the learnability problem. It suggests that the perceptual magnet effect requires prior knowledge of the distributions of speech sounds in the input but does not require knowledge of the discrete categories that these distributions represent. The mere presence of the perceptual magnet effect does not necessarily imply knowledge of discrete phonetic categories. Furthermore, this analysis can be used to relax the assumptions of Gaussian phonetic categories. Any unimodal distribution in the locations of exemplars should produce a qualitatively similar effect to that obtained with Gaussians, since as soon as the kernels representing exemplars are close enough together to yield a combined unimodal distribution, perception will be biased inward to a point between those exemplars.
Multiple Dimensions
This paper has examined a simplified problem in speech perception, involving stimuli that lie along a single psychoacoustic dimension. Real speech input contains multiple dimensions that are relevant for categorizing and discriminating stimuli, and in future work it will be interesting to examine discrimination patterns in categories that vary along multiple dimensions (e.g. Iverson et al., 2003) as well as patterns of trading relations in phoneme identification (e.g. Repp, 1982). Both of these problems require the use of more complex representations, such as multidimensional Gaussians, to represent phonetic categories and noise processes.
Preliminary simulations of the two-dimensional /r/−/l/ data from Iverson and Kuhl (1996) using multidimensional Gaussians suggest that our rational model captures some aspects of these data, but that the model would need to be extended to fully capture human data in multiple dimensions. These /r/−/l/ data show two basic effects. First, there is shrinkage toward category means along the F3 dimension, the dimension that separates the two categories. This shrinkage is weakest near the boundary between the categories, as predicted by the rational model. Second, the data show shrinkage in the F2 dimension, and this F2 shrinkage is strongest at F3 values that are near the category means. While the rational model predicts shrinkage in the F2 dimension, it predicts the same amount of F2 shrinkage at any value of F3.
This issue can potentially be addressed in two ways within the framework of the rational model. First, one can relax the assumption of Gaussian categories and Gaussian noise, an assumption that we have adopted only for computational simplicity. The neural map proposed by Guenther and Gjaja (1996) provides evidence that relaxing the Gaussian assumption will allow the model to capture human performance. As discussed above, Guenther and Gjaja’s model implements an approximate form of optimal Bayesian inference (Shi et al., 2008). The likelihood is given by their activation function, which is non-Gaussian, and the prior distribution is given by neural firing preferences in their neural map, which may be non-Gaussian as a result of their learning algorithm. This neural model therefore implements an approximation of our rational model that relaxes the Gaussian assumption. Their model obtains a close fit to the two-dimensional /r/−/l/ data, suggesting that in principle, the rational model is capable of capturing this pattern.
A second potential extension to the rational model would allow sounds to be generated from non-speech categories. Currently, all sounds are assumed to belong to the /r/ and /l/ categories, but incorporating a non-speech category would allow sounds that are different from native language categories to be classified as non-speech. In the data from Iverson and Kuhl (1996), sounds that are furthest from phonetic category centers are biased less than predicted by our current model. Consistent with this, a non-speech category with a uniform distribution over acoustic space would weaken the perceptual bias for sounds that are very different from native language categories. This would accord with suggestions from the speech perception literature that sounds dissimilar to native language phonetic categories remain perceptually unassimilated (e.g. Best, McRoberts, & Sithole, 1988). It would also parallel the suggestion by Huttenlocher et al. (2000) that participants performing a visual stimulus reproduction task are less likely to treat extreme stimulus values as belonging to the category of experimental stimuli, weakening the bias toward the edge of the category.
Phoneme Identification and Spoken Word Recognition
Speech perception involves recognizing not only speech sounds, but also words, and our framework is potentially compatible with several models of spoken word recognition. Shortlist B (Norris & McQueen, 2008) uses a Bayesian framework to characterize word recognition in fluent speech at a computational level, and a potential connection to this model comes through the quantity p(c|S), which is used as a primitive in Shortlist B to compute word and path probabilities for spoken utterances. On an implementational level, our model is potentially compatible with either interactive (McClelland & Elman, 1986) or feed-forward (Norris, McQueen, & Cutler, 2000) architectures, which give different accounts as to how acoustic and lexical information are combined during phoneme recognition. Any computation that ultimately yields the posterior on target productions p(T|S) is compatible with our model. Under a feed-forward account, acoustic and lexical information would combine at a decision level to generate the posterior distribution, whereas in an interactive account, an initial guess at the distribution on target productions might be recursively updated by lexical feedback until it settles on the correct posterior distribution. The model is also potentially compatible with either an episodic lexicon (e.g. Bybee, 2001) or a more abstract lexicon (e.g. McClelland & Elman, 1986) that nevertheless includes phonetic detail. As discussed above, groups of exemplars can produce perceptual patterns similar to those obtained using abstract categories. The presence of a perceptual magnet effect for isolated phonemes suggests that some prior information is available at the level of the phoneme (see also McQueen, Cutler, & Norris, 2006), but this might be achieved either through abstraction or through analogy with stored lexical items.
At the level of phoneme perception, the rational model is aimed primarily at explaining discrimination performance, but the quantity p(c|S) can potentially account for performance in explicit phoneme identification tasks as well. Consistent with our model’s predictions, Clayards et al. (2008) have demonstrated that listeners are sensitive to the degree of category variance when performing explicit categorization tasks. Nevertheless, we acknowledge the possibility that the quantity p(c|S) used for identification tasks is different from that used for discrimination tasks. Such divergence might be due to incorporation of additional information (e.g. lexical information) into explicit categorization tasks or to loss of information through imperfect approximations of the target production T before explicit categorization occurs. These possibilities remain open to further investigation.
Central to the rational model is the assumption that listeners have knowledge of phonetic categories but are trying to infer phonetic detail. This contrasts with previous models that have assumed listeners recover only category information about phonemes. Phonemes do distinguish words from one another; however, it is not clear that listeners abstract away from phonetic detail when storing and recognizing words (Goldinger, 1996; McMurray, Tanenhaus, & Aslin, 2002; Ju & Luce, 2006). Evidence has shown that listeners are sensitive to sub-phonemic detail at both neural and behavioral levels (Pisoni & Tash, 1974; Andruski, Blumstein, & Burton, 1994; Blumstein, Myers, & Rissman, 2005; Joanisse, Robertson, & Newman, 2007). Phonetic detail provides coarticulatory information that can help listeners identify upcoming words and word boundaries, and data from priming studies have suggested that listeners use this coarticulatory information on-line in lexical recognition tasks (Gow, 2001). This implies that listeners not only infer a speech sound’s category, but also attend to the phonetic detail within that category in order to gain information about upcoming phonemes and words. Though one could contend that listeners ultimately categorize speech sounds into discrete phonemes, their more direct goal must be to extract all relevant acoustic information from the speech signal. Because of its core assumption that listeners recover the phonetic detail of speech sounds they hear, the rational model is in accord with these behavioral results showing the use of phonetic detail in spoken word recognition.
Categorical Effects in Other Domains
The assumptions underlying the rational model are not specific to the structure of speech, and this makes the modeling results potentially applicable beyond the specific case of vowel perception. The extent to which this model can account for phenomena such as categorical perception of consonants, colors, or faces is an exciting question for future research. A generalization of these results to consonant perception would seem to be the most straightforward, and results that are qualitatively compatible with the rational model’s predictions have been found in stop consonant perception as measured by identification tasks (Ganong, 1980; Burton & Blumstein, 1995; Clayards et al., 2008). To the extent that consonants can be modeled as distributions of speech sounds along acoustic dimensions, the same principles that apply to vowel perception should yield insight into consonant perception. However, additional factors may need to be taken into account when modeling perception of consonants, especially stop consonants. Discrimination peaks have been found near stop consonant boundaries in animals (Kuhl & Padden, 1982, 1983) and very young infants (Eimas et al., 1971), suggesting that patterns in stop consonant perception are not solely the result of estimating distributions of speech sounds in the input, but also involve auditory discontinuities. Auditory discontinuities are found in non-speech stimuli as well (J. D. Miller et al., 1976; Pisoni, 1977) and might result from differential perceptual uncertainty depending on the stimulus value (Pastore et al., 1977). Influences of auditory discontinuities on category learning has been shown in adults (Holt et al., 2004), and future research might investigate how these discontinuities interact with learned categories in speech perception, and whether they continue to influence perception after phonetic categories are acquired.
The rational model suggests that cross-linguistic differences in speech perception result from differences in the distributions of speech sounds heard by listeners, where perception is biased toward peaks in these distributions. A key issue in applying these results to color and face perception therefore involves examining the extent to which categories in these domains can be characterized as clusters of exemplars. This seems plausible for both facial expressions and facial identities; however, the distribution of colors in the world is unlikely to depend on linguistic experience. Categorical perception of color appears instead to be mediated by linguistic codes, and effects of verbal interference on categorical perception of facial expressions parallel those in color perception (Roberson & Davidoff, 2000; Tan et al., 2008). The model presented here does not incorporate the notion of linguistic codes, and it may need to be extended to account for these results. Nevertheless, direct behavioral parallels have been drawn between color perception and speech perception (e.g. Bornstein & Korda, 1984). In the domain of face perception, stronger categorical effects in familiar faces than in unfamiliar faces (Beale & Keil, 1995) and shifts in the discrimination peak based on shifted category boundaries (Pollak & Kistler, 2002) are consistent with the rational model’s predictions. Indeed, categorical perception of facial identity has been argued to be more in line with prototype bias accounts than with labeling accounts (Roberson et al., 2007). These qualitative similarities may indicate that categories based on exemplar distributions and those based on linguistic codes are processed in a similar manner, but further investigation is required to determine the extent of these parallels.
Finally, evidence that our results are applicable beyond the specific case of speech perception comes from non-linguistic domains in which versions of this model have previously been proposed. Huttenlocher et al. (2000) used the same one-category model to explain category bias in visual stimulus reproduction, and this has been followed by demonstrations of similar effects with other types of visual stimuli (Huttenlocher, Hedges, Corrigan, & Crawford, 2004; Crawford, Huttenlocher, & Hedges, 2006). Köording and Wolpert (2004) explained subjects’ behavior in motor tasks using the same analysis. Similar ideas have also been used to describe optimal visual cue integration (Landy, Maloney, Johnston, & Young, 1995) and audiovisual integration (Battaglia, Jacobs, & Aslin, 2003). While this does not mean that the mechanisms being used in these domains are equivalent, it at least implies that several low-level systems use the same optimal strategy when combining sources of information under uncertainty, explaining why categories should influence perception in each of these cases.
Acknowledgments
This research was supported by Brown University First-Year and Brain Science Program Fellowships, NSF-IGERT grant 9870676, NSF grant 0631518, and NIH grant HD032005.
Appendix A
Computing Expected Target Productions
Given a generative model where and , we can use Bayes’ rule for the one-category case, p(T|S, c) ∝ p(S|T, c)p(T|c), to express the posterior on targets as
| (19) |
The normalizing constants can be eliminated while still retaining proportionality, so this expression becomes
| (20) |
Expanding the terms in the exponent and eliminating those terms that do not depend on T, we get
| (21) |
The expression in the exponent can be simplified into one term that depends on T2 and a second term that depends on T, so that
| (22) |
We make the form more similar to a Gaussian distribution,
| (23) |
and multiply by the constant to complete the square, preserving proportionality because this new term does not depend on T. The expression
| (24) |
now has the form of a Gaussian distribution with mean and variance . The posterior distribution in the one-category case is therefore
| (25) |
and the expected value of T is the mean of this Gaussian distribution,
| (26) |
To compute the expectation E[T|S] in the case of multiple categories, we use the formula E[T|S] = ∫Tp(T|S)dT where p(T|S) is computed by marginalizing over categories, p(T|S) = ∑c p(T|S, c)p(c|S). The expression for the expectation becomes
| (27) |
Bringing T inside the sum and then exchanging the sum and the integral yields
| (28) |
Since p(c|S) does not depend on T, this is equal to
| (29) |
where ∫ Tp(T|S, c)dT denotes E[T|S, c], the expectation in the one-category case (Equation 26). The expectation in the case of multiple categories is therefore
| (30) |
which is the same as the expression given in Equation 10.
Appendix B
Calculating Category Parameters from Identification Curves
Given a logistic identification curve for the percentage of participants that identified each stimulus as belonging to category 1 in a 2-category forced choice identification task, one can derive the category means and common variance by noting that the curve is an empirical measure of p(c1|S), which in a two-category forced choice task is defined according to Bayes’ rule (Equation 4) as
| (31) |
Each part of the fraction can be divided by the quantity in the numerator. Two inverse functions are applied to the last term, the exponential power and the natural logarithm, yielding
| (32) |
Assuming the two categories c1 and c2 have equal prior probability, and using the distribution for p(S|c) given in Equation 3, Equation 32 can be simplified to a logistic equation of the form
| (33) |
where . Thus given values for g, b, and μ1, one can calculate the value of μ2 and the sum as follows:
| (34) |
| (35) |
Without the assumption of equal prior probability, the bias term instead becomes , which produces a shift of the logistic toward the mean of the less probable category. Since the category boundary occurs where , this bias term produces a shift of magnitude where g is the gain of the logistic. The extra bias term therefore creates a larger shift in boundary locations for small values of the gain parameter, which can arise through high category variance , high noise variance , or small separation between category means μ1 − μ2.
Appendix C
Measure of Warping
Perceptual warping, which is a measure of the degree of shrinkage or expansion of perceptual space, corresponds mathematically to the derivative of the expected target E[T|S] with respect to S. We begin with the expectation from Equation 11
| (36) |
and compute its derivative, using the chain rule to compute the derivative of the second term.
| (37) |
This is the expression given in Equation 14. However, this derivative includes a term that corresponds to the derivative of the identification function. In the two-category case, the identification function has the form of a logistic function whose derivative is given by
| (38) |
where . Since p(c2|S) = 1 − p(c1|S) in the two-category case, the derivative of the logistic for p(c2|S) is identical to Equation 38 except that the gain has the opposite sign. Substituting this into Equation 37 and expanding the sum yields
| (39) |
which can be simplified to
| (40) |
or, substituting in the expression for the gain of the logistic,
| (41) |
Appendix D
Same-Different Task
Given two stimuli SA and SB, the posterior probability that the targets TA and TB are within range ϵ of each other is p(|TA − TB| ≤ ϵ|SA, SB), which is equivalent to p(−ϵ ≤ TA − TB ≤ ϵ|SA, SB). This probability can be computed analytically by marginalizing over category assignments for the two stimuli,
| (42) |
under the assumption that the two stimuli are generated independently (cA and SA are independent of cB and SB). To compute the first term, note that the distributions p(TA|cA, SA) and p(TB|cB, SB) are both Gaussians as given by Equation 6. Their difference therefore follows a Gaussian distribution with its mean equal to the difference between the two means and its variance equal to the sum of the two variances,
| (43) |
Given this density, the probability of falling within a range between −ϵ and ϵ can be expressed in terms of the standard cumulative normal distribution Φ,
| (44) |
where . The second and third terms in Equation 42 can then be computed independently for stimuli SA and SB using Equation 12.
Footnotes
Portions of this work were presented at the Mathematics and Phonology Symposium (MathPhon I), the 29th Annual Conference of the Cognitive Science Society, and the 2007 Northeast Computational Phonology Workshop. We thank Megan Blossom, Glenda Molina, Emily Myers, Lori Rolfe, and Katherine White for help in setting up and running the experiment, Laurie Heller and Tom Wickens for discussions on data analysis, and Sheila Blumstein, James McQueen, Dennis Norris, and an anonymous reviewer for valuable comments on previous versions of this manuscript.
The expectation is optimal if the penalty for misidentifying a stimulus increases with squared distance from the target.
Note that this is more extreme than the the mean value of the /i/ category produced by male speakers in Peterson and Barney (1952), which would instead correspond to stimulus 5.
Coarticulatory effects are context-dependent rather than being an inherent property of specific phonetic categories. However, listeners should be able to estimate the typical range of coarticulation that occurs within specific contexts and thus obtain a context-specific estimate of category variance.
All statistical significance tests reported in this paper are two-tailed.
Constraining ϵ to be the same between the two conditions significantly decreases the likelihood of the data; however, even under the assumption of a constant threshold, allowing the speech signal noise parameter to vary between conditions makes a statistically significant difference.
The maximum likelihood parameters for the restricted model were ϵ=85 mels and ϵ=103 mels for the no-noise and noise conditions, respectively, and (σS=38 mels).
This model cannot be compared to the full model in a generalized likelihood ratio test because the two models are not nested. To make a nested variant of the full model, we augmented it with the same two free parameters for experimental noise. This augmented full model had a log likelihood of −568. It therefore accounted for the data significantly better than the augmented restricted model (χ2(1) = 100, p < 0.0001), though it did not yield any improvement over the original full model. This again indicates that allowing the inference-related noise parameter to differ between the two conditions results in a statistically significant improvement in fit.
These correlations are relatively low due to sparse data in cells where most participants responded “different”. The correlations go up to r = 0.72 and r = 0.52 (both p < 0.01) for the no-noise and noise conditions, respectively, when the analysis is limited to only 0, 1, 2, and 3-step contrasts.
This differs from Iverson and Kuhl’s (1995) assumption of a linear relationship between log reaction times and perceptual distance.
The exact value did not affect the analysis, as long as the value was high enough that z-scores for “different” responses and z-scores for “same” responses did not overlap substantially.
References
- Aaltonen O, Eerola O, Hellströom A, Uusipaikka E, Lang AH. Perceptual magnet effect in the light of behavioral and psychophysical data. Journal of the Acoustical Society of America. 1997;101(2):1090–1105. doi: 10.1121/1.418031. [DOI] [PubMed] [Google Scholar]
- Abramson AS, Lisker L. Discriminability along the voicing continuum: Cross language tests. Proceedings of the 6th International Congress of Phonetic Sciences; Academia; Prague. 1970. pp. 569–573. [Google Scholar]
- Anderson JA, Silverstein JW, Ritz SA, Jones RS. Distinctive features, categorical perception, and probability learning: Some applications of a neural model. Psychological Review. 1977;84(5):413–451. [Google Scholar]
- Anderson JR. The adaptive character of thought. Hillsdale, NJ: Erlbaum; 1990. [Google Scholar]
- Andruski JE, Blumstein SE, Burton M. The effect of subphonemic differences on lexical access. Cognition. 1994;52:163–187. doi: 10.1016/0010-0277(94)90042-6. [DOI] [PubMed] [Google Scholar]
- Angeli A, Davidoff J, Valentine T. Face familiarity, distinctiveness, and categorical perception. The Quarterly Journal of Experimental Psychology. 2008;61(5):690–707. doi: 10.1080/17470210701399305. [DOI] [PubMed] [Google Scholar]
- Ashby FG, Alfonso-Reese LA. Categorization as probability density estimation. Journal of Mathematical Psychology. 1995;39:216–233. [Google Scholar]
- Battaglia PW, Jacobs RA, Aslin RN. Bayesian integration of visual and auditory signals for spatial localization. Journal of the Optical Society of America. 2003;20(7):1391–1397. doi: 10.1364/josaa.20.001391. [DOI] [PubMed] [Google Scholar]
- Beale JM, Keil FC. Categorical effects in the perception of faces. Cognition. 1995;57:217–239. doi: 10.1016/0010-0277(95)00669-x. [DOI] [PubMed] [Google Scholar]
- Beddor PS, Strange W. Cross-language study of perception of the oral-nasal distinction. Journal of the Acoustical Society of America. 1982;71(6):1551–1561. doi: 10.1121/1.387809. [DOI] [PubMed] [Google Scholar]
- Berlin B, Kay P. Basic color terms: Their universality and evolution. Berkeley: University of California Press; 1969. [Google Scholar]
- Best CT, McRoberts GW, Sithole NM. Examination of perceptual reorganization for nonnative speech contrasts: Zulu click discrimination by English-speaking adults and infants. Journal of Experimental Psychology: Human Perception and Performance. 1988;14(3):345–360. doi: 10.1037//0096-1523.14.3.345. [DOI] [PubMed] [Google Scholar]
- Blumstein SE, Myers EB, Rissman J. The perception of voice onset time: An fMRI investigation of phonetic category structure. Journal of Cognitive Neuroscience. 2005;17(9):1353–1366. doi: 10.1162/0898929054985473. [DOI] [PubMed] [Google Scholar]
- Boer B, de, Kuhl PK. Investigating the role of infant-directed speech with a computer model. Acoustics Research Letters Online. 2003;4(4):129–134. [Google Scholar]
- Boersma P. Praat, a system for doing phonetics by computer. Glot International. 2001;5(9/10):341–345. [Google Scholar]
- Bornstein MH, Korda NO. Discrimination and matching within and between hues measured by reaction times: some implications for categorical perception and levels of information processing. Psychological Research. 1984;46:207–222. doi: 10.1007/BF00308884. [DOI] [PubMed] [Google Scholar]
- Burton MW, Blumstein SE. Lexical effects on phonetic categorization: The role of stimulus naturalness and stimulus quality. Journal of Experimental Psychology: Human Perception and Performance. 1995;21(5):1230–1235. doi: 10.1037//0096-1523.21.5.1230. [DOI] [PubMed] [Google Scholar]
- Bybee J. Phonology and language use. Port Chester, NY: Cambridge University Press; 2001. [Google Scholar]
- Calder AJ, Young AW, Perrett DI, Etcoff NL, Rowland D. Categorical perception of morphed facial expressions. Visual Cognition. 1996;3(2):81–117. [Google Scholar]
- Campanella S, Hanoteau C, Seron X, Joassin F, Bruyer R. Categorical perception of unfamiliar facial identities, the face-space metaphor, and the morphing technique. Visual Cognition. 2003;10(2):129–156. [Google Scholar]
- Clayards M, Tanenhaus MK, Aslin RN, Jacobs RA. Perception of speech reflects optimal use of probabilistic speech cues. Cognition. 2008;108(3):804–809. doi: 10.1016/j.cognition.2008.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Connine CM, Titone D, Wang J. Auditory word recognition: Extrinsic and intrinsic effects of word frequency. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1993;19(1):81–94. doi: 10.1037//0278-7393.19.1.81. [DOI] [PubMed] [Google Scholar]
- Crawford LE, Huttenlocher J, Hedges LV. Within-category feature correlations and Bayesian adjustment strategies. Psychonomic Bulletin and Review. 2006;13(2):245–250. doi: 10.3758/bf03193838. [DOI] [PubMed] [Google Scholar]
- Damper RI, Harnad SR. Neural network models of categorical perception. Perception and Psychophysics. 2000;62(4):843–867. doi: 10.3758/bf03206927. [DOI] [PubMed] [Google Scholar]
- Davidoff J, Davies I, Roberson D. Colour categories in a stone-age tribe. Nature. 1999;398:203–204. doi: 10.1038/18335. [DOI] [PubMed] [Google Scholar]
- Dempster AP, Laird NM, Rubin DB. Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society. 1977;39:1–38. [Google Scholar]
- Diesch E, Iverson P, Kettermann A, Siebert C. Measuring the perceptual magnet effect in the perception of /i/ by German listeners. Psychological Research. 1999;62:1–19. doi: 10.1007/s004260050036. [DOI] [PubMed] [Google Scholar]
- Eimas PD. Auditory and linguistic processing of cues for place of articulation by infants. Perception and Psychophysics. 1974;16(3):513–521. [Google Scholar]
- Eimas PD. Auditory and phonetic coding of the cues for speech: Discrimination of the [r−l] distinction by young infants. Perception and Psychophysics. 1975;18(5):341–347. [Google Scholar]
- Eimas PD, Siqueland ER, Jusczyk P, Vigorito J. Speech perception in infants. Science. 1971;171(3968):303–306. doi: 10.1126/science.171.3968.303. [DOI] [PubMed] [Google Scholar]
- Etcoff NL, Magee JJ. Categorical perception of facial expressions. Cognition. 1992;44:227–240. doi: 10.1016/0010-0277(92)90002-y. [DOI] [PubMed] [Google Scholar]
- Formby C, Childers DG, Lalwani AL. Labelling and discrimination of a synthetic fricative continuum in noise: A study of absolute duration and relative onset time cues. Journal of Speech and Hearing Research. 1996;39:4–18. doi: 10.1044/jshr.3901.04. [DOI] [PubMed] [Google Scholar]
- Frieda EM, Walley AC, Flege JE, Sloane ME. Adults’ perception of native and nonnative vowels: Implications for the perceptual magnet effect. Perception and Psychophysics. 1999;61(3):561–577. doi: 10.3758/bf03211973. [DOI] [PubMed] [Google Scholar]
- Fry DB, Abramson AS, Eimas PD, Liberman AM. The identification and discrimination of synthetic vowels. Language and Speech. 1962;5:171–189. [Google Scholar]
- Fujisaki H, Kawashima T. On the modes and mechanisms of speech perception. Annual Report of the Engineering Research Institute. 1969;28:67–72.
- Ganong WF. Phonetic categorization in auditory word perception. Journal of Experimental Psychology: Human Perception and Performance. 1980;6(1):110–125. doi: 10.1037//0096-1523.6.1.110. [DOI] [PubMed] [Google Scholar]
- Gelder B. de, Teunisse J-P, Benson PJ. Categorical perception of facial expressions: Categories and their internal structure. Cognition and Emotion. 1997;11(1):1–23. [Google Scholar]
- Gerrits E, Schouten MEH. Categorical perception depends on the discrimination task. Perception and Psychophysics. 2004;66(3):363–376. doi: 10.3758/bf03194885. [DOI] [PubMed] [Google Scholar]
- Gilbert AL, Regier T, Kay P, Ivry RB. Whorf hypothesis is supported in the right visual field but not the left; Proceedings of the National Academy of Sciences; 2006. pp. 489–494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldinger SD. Words and voices: Episodic traces in spoken word identification and recognition memory. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1996;22(5):1166–1183. doi: 10.1037//0278-7393.22.5.1166. [DOI] [PubMed] [Google Scholar]
- Goldstone RL. Influences of categorization on perceptual discrimination. Journal of Experimental Psychology. 1994;123(2):178–200. doi: 10.1037//0096-3445.123.2.178. [DOI] [PubMed] [Google Scholar]
- Goldstone RL. Effects of categorization on color perception. Psychological Science. 1995;6(5):298–304. [Google Scholar]
- Goldstone RL, Lippa Y, Shiffrin RM. Altering object representations through category learning. Cognition. 2001;78:27–43. doi: 10.1016/s0010-0277(00)00099-8. [DOI] [PubMed] [Google Scholar]
- Gow DW. Assimilation and anticipation in continuous spoken word recognition. Journal of Memory and Language. 2001;45:133–159. [Google Scholar]
- Green DM, Swets JA. Signal detection theory and psychophysics. New York: Wiley; 1966. [Google Scholar]
- Grieser D, Kuhl PK. Categorization of speech by infants: Support for speech-sound prototypes. Developmental Psychology. 1989;25(4):577–588. [Google Scholar]
- Guenther FH, Gjaja MN. The perceptual magnet effect as an emergent property of neural map formation. Journal of the Acoustical Society of America. 1996;100(2):1111–1121. doi: 10.1121/1.416296. [DOI] [PubMed] [Google Scholar]
- Guenther FH, Husain FT, Cohen MA, Shinn-Cunningham BG. Effects of categorization and discrimination training on auditory perceptual space. Journal of the Acoustical Society of America. 1999;106:2900–2912. doi: 10.1121/1.428112. [DOI] [PubMed] [Google Scholar]
- Gureckis TM, Goldstone RL. The effect of the internal structure of categories on perception. In: Love BC, McRae K, Sloutsky VM, editors. Proceedings of the 30th Annual Conference of the Cognitive Science Society; Cognitive Science Society; Austin, TX. 2008. pp. 1876–1881. [Google Scholar]
- Harnad S. Introduction: Psychophysical and cognitive aspects of categorical perception: A critical overview. In: Harnad S, editor. Categorical perception: The groundwork of cognition. New York: Cambridge University Press; 1987. pp. 1–25. [Google Scholar]
- Hillenbrand J, Getty LA, Clark MJ, Wheeler K. Acoustic characteristics of American English vowels. Journal of the Acoustical Society of America. 1995;97(5):3099–3111. doi: 10.1121/1.411872. [DOI] [PubMed] [Google Scholar]
- Holt LL, Lotto AJ, Diehl RL. Auditory discontinuities interact with categorization: Implications for speech perception. Journal of the Acoustical Society of America. 2004;116(3):1763–1773. doi: 10.1121/1.1778838. [DOI] [PubMed] [Google Scholar]
- Huttenlocher J, Hedges LV, Corrigan B, Crawford LE. Spatial categories and the estimation of location. Cognition. 2004;93:75–97. doi: 10.1016/j.cognition.2003.10.006. [DOI] [PubMed] [Google Scholar]
- Huttenlocher J, Hedges LV, Vevea JL. Why do categories affect stimulus judgment? Journal of Experimental Psychology: General. 2000;129(2):220–241. doi: 10.1037//0096-3445.129.2.220. [DOI] [PubMed] [Google Scholar]
- Iverson P, Kuhl PK. Mapping the perceptual magnet effect for speech using signal detection theory and multidimensional scaling. Journal of the Acoustical Society of America. 1995;97(1):553–562. doi: 10.1121/1.412280. [DOI] [PubMed] [Google Scholar]
- Iverson P, Kuhl PK. Influences of phonetic identification and category goodness on American listeners’ perception of /r/ and /l/ Journal of the Acoustical Society of America. 1996;99(2):1130–1140. doi: 10.1121/1.415234. [DOI] [PubMed] [Google Scholar]
- Iverson P, Kuhl PK. Perceptual magnet and phoneme boundary effects in speech perception: Do they arise from a common mechanism? Perception and Psychophysics. 2000;62(4):874–886. doi: 10.3758/bf03206929. [DOI] [PubMed] [Google Scholar]
- Iverson P, Kuhl PK, Akahane-Yamada R, Diesch E, Tohkura Y, Kettermann A, et al. A perceptual interference account of acquisition difficulties for non-native phonemes. Cognition. 2003;87:B47–B57. doi: 10.1016/s0010-0277(02)00198-1. [DOI] [PubMed] [Google Scholar]
- Joanisse MF, Robertson EK, Newman RL. Mismatch negativity reflects sensory and phonetic speech processing. NeuroReport. 2007;18(9):901–905. doi: 10.1097/WNR.0b013e3281053c4e. [DOI] [PubMed] [Google Scholar]
- Ju M, Luce PA. Representational specificity of within-category phonetic variation in the long-term mental lexicon. Journal of Experimental Psychology: Human Perception and Performance. 2006;32(1):120–138. doi: 10.1037/0096-1523.32.1.120. [DOI] [PubMed] [Google Scholar]
- Kay P, Kempton W. What is the Sapir-Whorf hypothesis? American Anthropologist. 1984;86(1):65–79. [Google Scholar]
- Kay P, Regier T. Color naming universals: The case of Berinmo. Cognition. 2007;102:289–298. doi: 10.1016/j.cognition.2005.12.008. [DOI] [PubMed] [Google Scholar]
- Kiffel C, Campanella S, Bruyer R. Categorical perception of faces and facial expressions: The age factor. Experimental Aging Research. 2005;31:119–147. doi: 10.1080/03610730590914985. [DOI] [PubMed] [Google Scholar]
- Kikutani M, Roberson D, Hanley JR. What’s in the name? Categorical perception for unfamiliar faces can occur through labeling. Psychonomic Bulletin and Review. 2008;15(4):787–794. doi: 10.3758/pbr.15.4.787. [DOI] [PubMed] [Google Scholar]
- Körding KP, Wolpert DM. Bayesian integration in sensorimotor learning. Nature. 2004;427:244–247. doi: 10.1038/nature02169. [DOI] [PubMed] [Google Scholar]
- Kotsoni E, Haan M. de, Johnson MH. Categorical perception of facial expressions by 7-month-old infants. Perception. 2001;30:1115–1125. doi: 10.1068/p3155. [DOI] [PubMed] [Google Scholar]
- Kuhl PK. Discrimination of speech by nonhuman animals: Basic auditory sensitivities conducive to the perception of speech-sound categories. Journal of the Acoustical Society of America. 1981;70(2):340–349. [Google Scholar]
- Kuhl PK. Human adults and human infants show a “perceptual magnet effect” for the prototypes of speech categories, monkeys do not. Perception and Psychophysics. 1991;50(2):93–107. doi: 10.3758/bf03212211. [DOI] [PubMed] [Google Scholar]
- Kuhl PK. Early linguistic experience and phonetic perception: Implications for theories of developmental speech perception. Journal of Phonetics. 1993;21:125–139. [Google Scholar]
- Kuhl PK, Padden DM. Enhanced discriminability at the phonetic boundaries for the voicing feature in macaques. Perception and Psychophysics. 1982;32(6):542–550. doi: 10.3758/bf03204208. [DOI] [PubMed] [Google Scholar]
- Kuhl PK, Padden DM. Enhanced discriminability at the phonetic boundaries for the place feature in macaques. Journal of the Acoustical Society of America. 1983;73(3):1003–1010. doi: 10.1121/1.389148. [DOI] [PubMed] [Google Scholar]
- Kuhl PK, Stevens E, Hayashi A, Deguchi T, Kiritani S, Iverson P. Infants show a facilitation effect for native language phonetic perception between 6 and 12 months. Developmental Science. 2006;9(2):F13–F21. doi: 10.1111/j.1467-7687.2006.00468.x. [DOI] [PubMed] [Google Scholar]
- Kuhl PK, Williams KA, Lacerda F, Stevens KN, Lindblom B. Linguistic experience alters phonetic perception in infants by 6 months of age. Science. 1992;255(5044):606–608. doi: 10.1126/science.1736364. [DOI] [PubMed] [Google Scholar]
- Lacerda F. The perceptual-magnet effect: An emergent consequence of exemplar-based phonetic memory. In: Elenius K, Branderud P, editors. Proceedings of the XIIIth International Congress of Phonetic Sciences; KTH and Stockholm University; Stockholm. 1995. pp. 140–147. [Google Scholar]
- Landy MS, Maloney LT, Johnston EB, Young M. Measurement and modeling of depth cue combination: In defense of weak fusion. Vision Research. 1995;35(3):389–412. doi: 10.1016/0042-6989(94)00176-m. [DOI] [PubMed] [Google Scholar]
- Levin DT, Beale JM. Categorical perception occurs in newly learned faces, other-race faces, and inverted faces. Perception and Psychophysics. 2000;62(2):386–401. doi: 10.3758/bf03205558. [DOI] [PubMed] [Google Scholar]
- Liberman AM, Harris KS, Eimas PD, Lisker L, Bastian J. An effect of learning on speech perception: The discrimination of durations of silence with and without phonemic significance. Language and Speech. 1961;4:175–195. [Google Scholar]
- Liberman AM, Harris KS, Hoffman HS, Griffith BC. The discrimination of speech sounds within and across phoneme boundaries. Journal of Experimental Psychology. 1957;54(4):358–368. doi: 10.1037/h0044417. [DOI] [PubMed] [Google Scholar]
- Liberman AM, Harris KS, Kinney JA, Lane H. The discrimination of relative onset-time of the components of certain speech and nonspeech patterns. Journal of Experimental Psychology. 1961;61(5):379–388. doi: 10.1037/h0049038. [DOI] [PubMed] [Google Scholar]
- Lively SE, Pisoni DB. On prototypes and phonetic categories: A critical assessment of the perceptual magnet effect in speech perception. Journal of Experimental Psychology. 1997;23(6):1665–1679. doi: 10.1037//0096-1523.23.6.1665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Livingston KR, Andrews JK, Harnad S. Categorical perception effects induced by category learning. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1998;24(3):732–753. doi: 10.1037//0278-7393.24.3.732. [DOI] [PubMed] [Google Scholar]
- Lotto AJ, Kluender KR, Holt LL. Depolarizing the perceptual magnet effect. Journal of the Acoustical Society of America. 1998;103(6):3648–3655. doi: 10.1121/1.423087. [DOI] [PubMed] [Google Scholar]
- Marr D. Vision. San Francisco: W. H. Freeman; 1982. [Google Scholar]
- Massaro DW, Cohen MM. Phonological context in speech perception. Perception and Psychophysics. 1983;34(4):338–348. doi: 10.3758/bf03203046. [DOI] [PubMed] [Google Scholar]
- Maye J, Gerken L. Learning phonemes without minimal pairs. In: Howell SC, Fish SA, Keith-Lucas T, editors. Proceedings of the 24th Annual Boston University Conference on Language Development; Cascadilla Press; Somerville, MA. 2000. pp. 522–533. [Google Scholar]
- Maye J, Werker JF, Gerken L. Infant sensitivity to distributional information can affect phonetic discrimination. Cognition. 2002;82:B101–B111. doi: 10.1016/s0010-0277(01)00157-3. [DOI] [PubMed] [Google Scholar]
- McClelland JL, Elman JL. The TRACE model of speech perception. Cognitive Psychology. 1986;18:1–86. doi: 10.1016/0010-0285(86)90015-0. [DOI] [PubMed] [Google Scholar]
- McMurray B. Klattworks: A [somewhat] new systematic approach to formant-based speech synthesis for empirical research. (in preparation) [Google Scholar]
- McMurray B, Aslin RN, Toscano JC. Statistical learning of phonetic categories: Computational insights and limitations. Developmental Science. 2009;12(3):369–378. doi: 10.1111/j.1467-7687.2009.00822.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McMurray B, Tanenhaus MK, Aslin RN. Gradient effects of within-category phonetic variation on lexical access. Cognition. 2002;86:B33–B42. doi: 10.1016/s0010-0277(02)00157-9. [DOI] [PubMed] [Google Scholar]
- McQueen JM. The influence of the lexicon on phonetic categorization: Stimulus quality in word-final ambiguity. Journal of Experimental Psychology: Human Perception and Performance. 1991;17(2):433–443. doi: 10.1037//0096-1523.17.2.433. [DOI] [PubMed] [Google Scholar]
- McQueen JM, Cutler A, Norris D. Phonological abstraction in the mental lexicon. Cognitive Science. 2006;30:1113–1126. doi: 10.1207/s15516709cog0000_79. [DOI] [PubMed] [Google Scholar]
- Mertus J. Bliss user’s manual. Brown University; 2004. [Google Scholar]
- Miller GA, Nicely PE. An analysis of perceptual confusions among some English consonants. Journal of the Acoustical Society of America. 1955;27(2):338–352. [Google Scholar]
- Miller JD, Wier CC, Pastore RE, Kelly WJ, Dooling RJ. Discrimination and labeling of noise-buzz sequences with varying noise-lead times: An example of categorical perception. Journal of the Acoustical Society of America. 1976;60(2):410–417. doi: 10.1121/1.381097. [DOI] [PubMed] [Google Scholar]
- Miller JL, Eimas PD. Studies on the perception of place and manner of articulation: A comparison of the labial-alveolar and nasal-stop distinctions. Journal of the Acoustical Society of America. 1977;61(3):835–845. doi: 10.1121/1.381373. [DOI] [PubMed] [Google Scholar]
- Miyawaki K, Strange W, Verbrugge R, Liberman AM, Jenkins JJ, Fujimura O. An effect of linguistic experience: the discrimination of [r] and [l] by native speakers of Japanese and English. Perception and Psychophysics. 1975;18(5):331–340. [Google Scholar]
- Morse PA, Snowdon CT. An investigation of categorical speech discrimination by rhesus monkeys. Perception and Psychophysics. 1975;17(1):9–16. [Google Scholar]
- Näätänen R, Lehtokoski A, Lennes M, Cheour M, Huotilainen M, Iivonen A, et al. Language-specific phoneme representations revealed by electric and magnetic brain responses. Nature. 1997;385:432–434. doi: 10.1038/385432a0. [DOI] [PubMed] [Google Scholar]
- Norris D, McQueen J. Shortlist B: A Bayesian model of continuous speech recognition. Psychological Review. 2008;115(2):357–395. doi: 10.1037/0033-295X.115.2.357. [DOI] [PubMed] [Google Scholar]
- Norris D, McQueen JM, Cutler A. Merging information in speech recognition: Feedback is never necessary. Behavioral and Brain Sciences. 2000;23:299–325. doi: 10.1017/s0140525x00003241. [DOI] [PubMed] [Google Scholar]
- Özgen E, Davies IRL. Acquisition of categorical color perception: A perceptual learning approach to the linguistic relativity hypothesis. Journal of Experimental Psychology: General. 2002;131(4):477–493. [PubMed] [Google Scholar]
- Pastore RE, Ahroon WA, Baffuto KJ, Friedman C, Puleo JS, Fink EA. Common-factor model of categorical perception. Journal of Experimental Psychology: Human Perception and Performance. 1977;3(4):686–696. [Google Scholar]
- Peterson GE, Barney HL. Control methods used in a study of the vowels. Journal of the Acoustical Society of America. 1952;24(2):175–184. [Google Scholar]
- Pilling M, Wiggett A, Özgen E, Davies IRL. Is color “categorical perception” really perceptual? Memory and Cognition. 2003;31(4):538–551. doi: 10.3758/bf03196095. [DOI] [PubMed] [Google Scholar]
- Pisoni DB. Auditory and phonetic memory codes in the discrimination of consonants and vowels. Perception and Psychophysics. 1973;13(2):253–260. doi: 10.3758/BF03214136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pisoni DB. Auditory short-term memory and vowel perception. Memory and Cognition. 1975;3(1):7–18. doi: 10.3758/BF03198202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pisoni DB. Identification and discrimination of the relative onset time of two component tones: Implications for voicing perception. Journal of the Acoustical Society of America. 1977;61(5):1352–1361. doi: 10.1121/1.381409. [DOI] [PubMed] [Google Scholar]
- Pisoni DB, Aslin RN, Perey AJ, Hennessy BL. Some effects of laboratory training on identification and discrimination of voicing contrasts in stop consonants. Journal of Experimental Psychology: Human Perception and Performance. 1982;8(2):297–314. doi: 10.1037//0096-1523.8.2.297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pisoni DB, Lazarus JH. Categorical and noncategorical modes of speech perception along the voicing continuum. Journal of the Acoustical Society of America. 1974;55(2):328–333. doi: 10.1121/1.1914506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pisoni DB, Tash J. Reaction times to comparisons within and across phonetic categories. Perception and Psychophysics. 1974;15(2):285–290. doi: 10.3758/bf03213946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pitt MA, McQueen JM. Is compensation for coarticulation mediated by the lexicon? Journal of Memory and Language. 1998;39:347–370. [Google Scholar]
- Polka L, Bohn O-S. Asymmetries in vowel perception. Speech Communication. 2003;41:221–231. [Google Scholar]
- Pollak SD, Kistler DJ. Early experience is associated with the development of categorical representations for facial expressions of emotion; Proceedings of the National Academy of Sciences; 2002. pp. 9072–9076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Regier T, Kay P, Khetarpal N. Color naming reflects optimal partitions of color space; Proceedings of the National Academy of Sciences; 2007. pp. 1436–1441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Repp BH. Phonetic trading relations and context effects: New experimental evidence for a speech mode of perception. Psychological Bulletin. 1982;92(1):81–110. [PubMed] [Google Scholar]
- Repp BH, Crowder RG. Stimulus order effects in vowel discrimination. Journal of the Acoustical Society of America. 1990;88(5):2080–2090. doi: 10.1121/1.400105. [DOI] [PubMed] [Google Scholar]
- Repp BH, Healy AF, Crowder RG. Categories and context in the perception of isolated steady-state vowels. Journal of Experimental Psychology: Human Perception and Performance. 1979;5(1):129–145. doi: 10.1037//0096-1523.5.1.129. [DOI] [PubMed] [Google Scholar]
- Rice JA. Mathematical statistics and data analysis. 2 ed. Belmont, CA: Duxbury; 1995. [Google Scholar]
- Roberson D, Damjanivic L, Pilling M. Categorical perception of facial expressions: Evidence for a category adjustment model. Memory and Cognition. 2007;35(7):1814–1829. doi: 10.3758/bf03193512. [DOI] [PubMed] [Google Scholar]
- Roberson D, Davidoff J. The categorical perception of colors and facial expressions: The effect of verbal interference. Memory and Cognition. 2000;28(6):977–986. doi: 10.3758/bf03209345. [DOI] [PubMed] [Google Scholar]
- Roberson D, Davidoff J, Davies IRL, Shapiro LR. Color categories: Evidence for the cultural relativity hypothesis. Cognitive Psychology. 2005;50:378–411. doi: 10.1016/j.cogpsych.2004.10.001. [DOI] [PubMed] [Google Scholar]
- Roberson D, Davies I, Davidoff J. Color categories are not universal: Replications and new evidence from a stone-age culture. Journal of Experimental Psychology: General. 2000;129(3):369–398. doi: 10.1037//0096-3445.129.3.369. [DOI] [PubMed] [Google Scholar]
- Rosch Heider E. Universals in color naming and memory. Journal of Experimental Psychology. 1972;93(1):10–20. doi: 10.1037/h0032606. [DOI] [PubMed] [Google Scholar]
- Rosch Heider E, Oliver DC. The structure of the color space in naming and memory for two languages. Cognitive Psychology. 1972;3:337–354. [Google Scholar]
- Rotshtein P, Henson RNA, Treves A, Driver J, Dolan RJ. Morphing Marilyn into Maggie dissociates physical and identity face representations in the brain. Nature Neuroscience. 2005;8(1):107–113. doi: 10.1038/nn1370. [DOI] [PubMed] [Google Scholar]
- Shepard RN. Multidimensional scaling, tree-fitting, and clustering. Science. 1980;210:390–398. doi: 10.1126/science.210.4468.390. [DOI] [PubMed] [Google Scholar]
- Shi L, Feldman NH, Griffiths TL. Performing Bayesian inference with exemplar models. In: Love BC, McRae K, Sloutsky VM, editors. Proceedings of the 30th Annual Conference of the Cognitive Science Society; Cognitive Science Society; Austin, TX. 2008. pp. 745–750. [Google Scholar]
- Silverman BW. Density estimation. London: Chapman and Hall; 1986. [Google Scholar]
- Stevenage SV. Which twin are you? A demonstration of induced categorical perception of identical twin faces. British Journal of Psychology. 1998;89:39–57. [Google Scholar]
- Stevens KN, Liberman AM, Studdert-Kennedy M, Öhman SEG. Crosslanguage study of vowel perception. Language and Speech. 1969;12(1):1–23. doi: 10.1177/002383096901200101. [DOI] [PubMed] [Google Scholar]
- Stevens SS, Volkmann J, Newman EB. A scale for the measurement of the psychological magnitude pitch. Journal of the Acoustical Society of America. 1937;8:185–190. [Google Scholar]
- Sussman JE, Gekas B. Phonetic category structure of [i]: Extent, best exemplars, and organization. Journal of Speech, Language, and Hearing Research. 1997;40:1406–1424. doi: 10.1044/jslhr.4006.1406. [DOI] [PubMed] [Google Scholar]
- Sussman JE, Lauckner-Morano VJ. Further tests of the “perceptual magnet effect” in the perception of [i]: Identification and change/no-change discrimination. Journal of the Acoustical Society of America. 1995;97(1):539–552. doi: 10.1121/1.413111. [DOI] [PubMed] [Google Scholar]
- Tan LH, Chan AHD, Kay P, Khong P-L, Yip LKC, Luke K-K. Language affects patterns of brain activation associated with perceptual decision. Proceedings of the National Academy of Sciences. 2008;105(10):4004–4009. doi: 10.1073/pnas.0800055105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thyer N, Hickson L, Dodd B. The perceptual magnet effect in Australian English vowels. Perception and Psychophysics. 2000;62(1):1–20. doi: 10.3758/bf03212057. [DOI] [PubMed] [Google Scholar]
- Vallabha GK, McClelland JL. Success and failure of new speech category learning in adulthood: Consequences of learned Hebbian attractors in topographic maps. Cognitive, Affective, and Behavioral Neuroscience. 2007;7:53–73. doi: 10.3758/cabn.7.1.53. [DOI] [PubMed] [Google Scholar]
- Vallabha GK, McClelland JL, Pons F, Werker JF, Amano S. Unsupervised learning of vowel categories from infant-directed speech; Proceedings of the National Academy of Sciences; 2007. pp. 13273–13278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Viviani P, Binda P, Borsato T. Categorical perception of newly learned faces. Visual Cognition. 2007;15(4):420–467. [Google Scholar]
- Winawer J, Witthoft N, Frank MC, Wu L, Wade AR, Boroditsky L. Russian blues reveal effects of language on color discrimination; Proceedings of the National Academy of Sciences; 2007. pp. 7780–7785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winkler I, Lehtokoski A, Alku P, Vainio M, Czigler I, Csépe V, et al. Pre-attentive detection of vowel contrasts utilizes both phonetic and auditory memory representations. Cognitive Brain Research. 1999;7:357–369. doi: 10.1016/s0926-6410(98)00039-1. [DOI] [PubMed] [Google Scholar]
- Witthoft N, Winawer J, Wu L, Frank M, Wade A, Boroditsky L. Effects of language on color discriminability; Proceedings of the 25th Annual Conference of the Cognitive Science Society; 2003. [Google Scholar]
- Xu L, Zheng Y. Spectral and temporal cues for phoneme recognition in noise. Journal of the Acoustical Society of America. 2007;122(3):1758–1764. doi: 10.1121/1.2767000. [DOI] [PubMed] [Google Scholar]
- Young AW, Rowland D, Calder AJ, Etcoff NL, Seth A, Perrett DI. Facial expression megamix: Tests of dimensional and category accounts of emotion recognition. Cognition. 1997;63:271–313. doi: 10.1016/s0010-0277(97)00003-6. [DOI] [PubMed] [Google Scholar]
- Yuille A, Kersten D. Vision as Bayesian inference: analysis by synthesis? Trends in Cognitive Sciences. 2006;10(7):301–308. doi: 10.1016/j.tics.2006.05.002. [DOI] [PubMed] [Google Scholar]