Diffusion in Brain Extracellular Space

Abstract

Diffusion in the extracellular space (ECS) of the brain is constrained by the volume fraction and the tortuosity and a modified diffusion equation represents the transport behavior of many molecules in the brain. Deviations from the equation reveal loss of molecules across the blood-brain barrier, through cellular uptake, binding or other mechanisms. Early diffusion measurements used radiolabeled sucrose and other tracers. Presently, the real-time iontophoresis (RTI) method is employed for small ions and the integrative optical imaging (IOI) method for fluorescent macromolecules, including dextrans or proteins. Theoretical models and simulations of the ECS have explored the influence of ECS geometry, effects of dead-space microdomains, extracellular matrix and interaction of macromolecules with ECS channels. Extensive experimental studies with the RTI method employing the cation tetramethylammonium (TMA) in normal brain tissue show that the volume fraction of the ECS typically is about 20% and the tortuosity about 1.6 (i.e. free diffusion coefficient of TMA is reduced by 2.6), although there are regional variations. These parameters change during development and aging. Diffusion properties have been characterized in several interventions, including brain stimulation, osmotic challenge and knockout of extracellular matrix components. Measurements have also been made during ischemia, in models of Alzheimer's and Parkinson's diseases and in human gliomas. Overall, these studies improve our conception of ECS structure and the roles of glia and extracellular matrix in modulating the ECS microenvironment. Knowledge of ECS diffusion properties are valuable in contexts ranging from understanding extrasynaptic volume transmission to the development of paradigms for drug delivery to the brain.

I. INTRODUCTION

When substances diffuse in the brain, they predominantly move through the narrow extracellular space (ECS) that separates one cell membrane from another (Fig. 1A). Measurements of the diffusion properties of the ECS are important from two perspectives: first as a means of determining specific diffusion coefficients and second as a means of exploring the structure of the ECS.

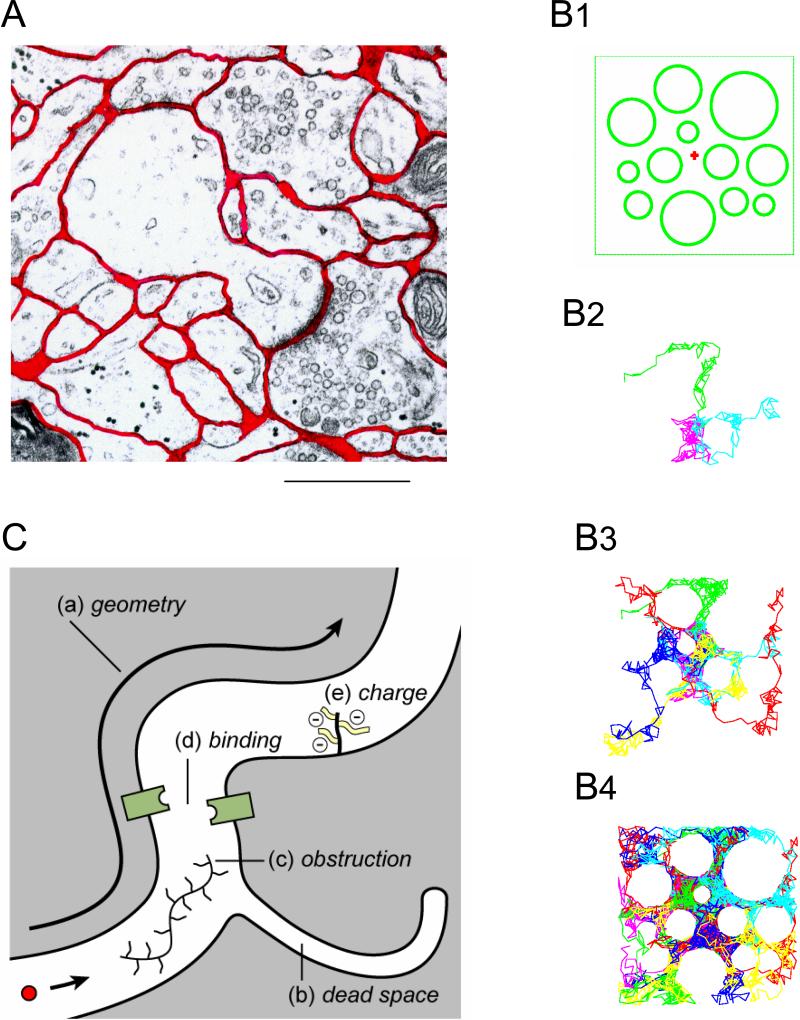
Fig. 1.

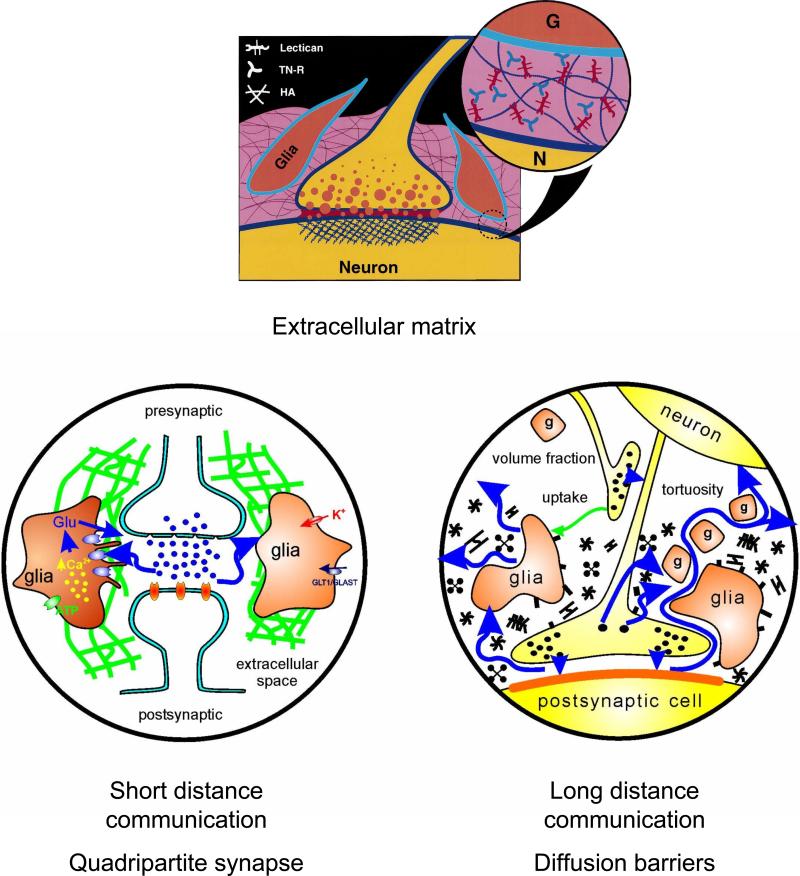
Basic concepts of ECS. A. Electronmicrograph of small region of rat cortex with dendritic spine and synapse. The ECS is outlined in red; it has a well-connected foam-like structure formed from the interstices of simple convex cell surfaces. Even though the ECS is probably reduced in width due to fixation procedure it is still evident that it is not completely uniform in width. Calibration bar approximately 1 μm. (Modified from Ref. 264). B₁-B₄. Molecules executing Random walks reveal structure. B₁: cross-section through an idealized 2D square brain region bounded by impermeable walls and containing a number of circular cellular profiles. The ECS width is exaggerated. B₂: Three molecules (different colors) have been released from the location marked with a red “+” in B₁ and allowed to execute up to 150 random steps. If the molecules encounter a cell boundary or wall, the step is canceled and the next random step selected. The profiles of the cells are omitted from this and the two subsequent panels, only the trajectories of the random walks are shown. The three trajectories in B₂ appear to have a random distribution. B₃: 12 molecules execute random walks and now the aggregate of their trajectories begins to reveal the presence of the cells. B₄: 48 random walks reveal an increasingly accurate view of the boundaries of the cells and the boundaries of the region. Note that the individual steps are large in this simulation to reduce the number required to reveal the geometry (Modified from Ref. 264). C. Factors affecting the diffusion of a molecule in the ECS. These are: a) geometry of ECS which imposes an additional delay on a diffusing molecule compared to a free medium. b) dead-space microdomain where molecules lose time exploring a dead-end. Such a microdomain may be in the form of a ‘pocket’ as shown but it may also take the form of glial wrapping or even a local enlargement of the ECS. c) Obstruction in the form of extracellular matrix molecules such as hyaluronan. d) binding sites for the diffusing molecule either on cell membranes or extracellular matrix. e) fixed negative charges, also on the extracellular matrix, that may affect the diffusion of charged molecules.

In order to predict the distribution of a substance it is essential to know the effective diffusion coefficient in brain tissue as well as the relative importance of diffusion versus clearance processes that may remove that substance from the ECS. The substance may be a neurotransmitter spilling over from a synapse to affect adjacent sites or a neuromodulator that utilizes the ECS as a conduit for signaling to other cells; this type of communication is variously called volume transmission, non-synaptic or extrasynaptic transmission. Knowledge of effective diffusion coefficients and diffusion properties are equally crucial for defining drug delivery within the CNS.

Structural information about the ECS may be arrived at by characterizing the distribution of well-chosen probe molecules. The underlying concept is that diffusing molecules execute random walks that allow them to explore the ECS (Fig. 1B). By accessing the results of this exploration, usually in the form of a concentration distribution, local structure may be revealed. Thus diffusion analysis provides a unique window onto a domain that has been largely inaccessible experimentally. In this context, when a given substance deviates from its expected diffusion behavior, such deviation can reveal additional information about local ECS characteristics, such as specific binding or clearance properties (Fig. 1C).

Several reviews have been written about diffusion in the ECS; a short paper by Nicholson and Syková (264) still provides a useful overview on the use of diffusion to explore structure and a longer review by Nicholson (254) may appeal to those who want a more detailed theoretical treatment. The present review should supersede most others. The subject of diffusion within the central nervous system includes many diverse topics, necessitating that we limit the scope of this review only to those areas with direct relevance to extracellular diffusion. Accordingly, intracellular diffusion and intercellular diffusion via gap junctions will not be covered. The diffusion of water within the brain is an important topic because of its role in diffusion-weighted magnetic resonance imaging (DW-MRI) but the biophysical issues are complex and not fully resolved so we only will address those aspects of this topic relevant to the ECS.

II. EXTRACELLULAR SPACE AND APPLICABLE CONCEPTS OF DIFFUSION

The ECS was vividly described (181) as like the water phase within a foam where the gaseous phase corresponds to the cells of the brain. This image captures the overall connectivity of the compartment but fails to do justice to the complex microscopic structure that is now emerging.

The ECS contains a fluid, sometimes referred to as the interstitial fluid (ISF) that is in contact with cerebrospinal fluid (CSF) at the ventricular surfaces. The composition of both fluids are thought to be similar, however, while much is known about CSF composition (18), direct assay of the ISF is not feasible. In one aspect the CSF and ISF do differ: the ISF is supplemented by an extracellular matrix (212, 322) (see below and Section VI.E). The extracellular matrix is composed of long-chain macromolecules many of which are tethered to cell surfaces while some, like hyaluronan, ‘float’ in the ECS (36).

Within the ECS, the dominant mechanism of molecular transport is diffusion constrained by the geometry of this compartment. Fortunately, extensive experimental studies have established that the labyrinthine nature of the ECS (Fig. 1A) makes the brain act like a porous medium for substances that do not cross cellular boundaries. This characterization allows application of established diffusion theory already developed in other disciplines.

Although diffusion predominates in the ECS, it is often modified by loss of molecules through removal across the blood-brain barrier (BBB), uptake into cells or binding to receptors. Indeed, these clearance processes are the determining factor in the distribution of some substances. It has also been suggested that bulk flow, i.e. transport by actual hydrodynamic flow of fluid, may play a role but it seems likely that such flow is confined to the perivascular spaces in normal (i.e. non-pathological) circumstances. All these topics will be addressed in this review.

The ECS is necessary for several reasons. One is to enable stable electrical signaling by providing a reservoir of extracellular ions sufficient to maintain resting, synaptic and action potentials. Another important role for the ECS, as noted above, is to mediate active chemical signaling through extrasynaptic volume transmission. The ECS also forms a conduit for essential substances to move between blood vessels and cells. Quantitative microscopy indicates that the average distance between a neuron and a microvessel in brain grey matter is about 20 μm (210, 333), even though the total brain volume occupied by blood vessels is less that 3% (42, 333). Finally, it is likely that the ECS is necessary to allow remodeling of synapses and connections. In this section we give an overview of our present concept of the ECS and how it may influence diffusion.

A. Extracellular space and its volume fraction

Studies with radiotracers, impedance measurements and electron microscopy led to contradictory ideas about the ECS in the early 1960's. The first study with electron microscopy (416) suggested that there was no space at all, then subsequent investigators came to believe that the ECS occupied only about 5% of the brain with the spaces between cell membranes averaging 10-20 nm (140, 160, 404). In contrast, Van Harreveld (398, 399) believed that the ECS occupied 15-20% the brain volume and considered that, while much of the space was about 20 nm wide, there were also expansions or ‘lakes’ (see also Ref. 46) that presumably accounted for the increased volume fraction. Van Harreveld based his conclusions on several methods; these included novel tissue preparation techniques for electron microscopy based on rapid freezing and freeze substitution of fixatives (399) that he believed preserved the water content of the tissue. He concluded that more accepted fixation techniques (281) almost certainly caused ischemia and this led to cellular swelling with concomitant shrinkage in the ECS. Post processing and embedding of brain tissue also likely caused water movement. A study of synaptic clefts with cryo-electromicroscopy (432) and work by Ohno et al. (278) using an in vivo cryotechnique substantiate the idea that the ECS is wider than seen in conventional electron microscopy but it is still difficult to accurately gauge the width from electron micrographs.

Today it is well established that the ECS occupies a volume fraction of between 15 and 30% in normal adult brain tissue with a typical value of 20% and that this falls to 5% during global ischemia (see Section V.A). Volume fraction is denoted by α and may be formally defined as

$$\alpha =V_{\mathrm{ECS}}∕V_{\text{Tissue}}$$ (1)

where the subscripts on V denote the respective volume of ECS or the whole tissue measured in a small region of brain (sometimes referred to as a Representative Elementary Volume) and written as a decimal i.e. 0.15 ≤ α ≤ 0.3 . In a ‘free’ medium, such as an aqueous solution or very dilute gel, α = 1. In other disciplines volume fraction is often called ‘porosity’ and denoted by a variety of symbols. We now know that Van Harreveld was correct about the magnitude of the volume fraction in brain tissue and about the errors introduced by classical tissue fixation.

It is less obvious what the true size of the spaces between cells is. The lakes that Van Harreveld and others saw may have been partly the result of local formation of ice crystals induced by the cryofixation techniques, although it remains plausible that the ECS is not uniform in size. A recent study (391) using quantum dot nanocrystals indicates that the true average width of the ECS in the in vivo rat cortex lies between 38-64 nm. As noted by Nicholson (247), there is a relationship between average cellular morphology, volume fraction, and the width of the ECS. If the average volume of a cell or cellular element is V_C and the corresponding cell surface area is S_C then one may imagine that each element of cell surface has an ‘atmosphere’ of ECS of thickness d where 2d is the average width of the ECS. Then

$$P=\frac{V_{\mathrm{c}}}{S_{\mathrm{c}}}=\left(\frac{1}{\alpha }-1\right)d$$ (2)

where P is the average volume-to-surface ratio for the cellular element. If, for simplicity, one imagines the brain as composed of cubical cells, each with a side of length a, so P = a/6, then combining the classic value of 2d = 20 nm with α = 0.2 yields a = 0.24 μm, whereas if the more recent estimate of ECS width is used, 2d = 60 nm with α = 0.2 then a = 0.72 μm. Most electron micrographs would suggest that the latter value is more representative of the diameter of a typical cellular profile (which could be a section through a dendrite, axon, glial process or occasional cell body) found in the CNS. Note, however, that if one takes the now discredited combination of α = 0.05 and 2d = 20 nm then a = 1.14 μm (c.f. 140, 309); as will be seen in Section V.A, these estimates are plausible in ischemic tissue, which is the expected state during classical fixation.

B. Hindered diffusion and tortuosity

How does a molecule behave within the narrow confines of the ECS? The early radiotracer work, interpreted according to the concepts of the physics of diffusion, showed that small molecules such as inulin and sucrose could diffuse through the ECS with an effective diffusion coefficient (D*) that was some two-to-three times less than the free diffusion coefficient (D) (194, 288). This result has been fully substantiated with the data that will be reviewed here. It has long been the practice when dealing with nervous tissues (e.g. Ref. 125) to characterize the hindrance to diffusion seen in the tissue compared to that in a free medium by the tortuosity λ, defined simply from the ratio of the two experimental measurements as:

$$\lambda =\sqrt{D∕D^{\ast }}.$$ (3)

Thus the radiotracer data indicated a tortuosity of between 1.4 and 1.7. A justification for the use the square root in the definition of tortuosity has been provided (326); note that, in other disciplines, tortuosity may have a different definition.

What is the origin of the hindrance that molecules experience as they diffuse through the brain? Among many factors we will focus on five possibilities (Fig. 1C): (a) An increase in geometric path-length as diffusing molecules are compelled to go around cellular obstructions; (b) Transient trapping of molecules in dead-space microdomains; (c) An increased interstitial viscous drag on migrating molecules arising from the obstruction imposed by the macromolecules that compose the extracellular matrix or drag arising from the walls of the channels when molecules are large; (d) Transient binding to membrane-attached or extracellular matrix-attached receptors specific for the diffusing molecule and (e) Non-specific interaction with fixed negative charges on the extracellular matrix when the diffusing molecule has adequate charge density. All five factors can be thought of as introducing a delay into the passage of a molecule in brain tissue relative to that in a free medium (a treatment in terms of increased dwell-time or diffusion retardation has been formulated (147, 144) (see Section II.H).

The increase in geometric path length, factor (a), represents the necessity for molecules in the brain ECS to travel a more circuitous path around cellular obstructions to arrive at their destination, as compared to their path in a free medium. The most simplistic way of thinking about this is just to compare the ratio of distance through the center of a spherical cell or obstruction to that encountered in traveling round the outside, which amounts to a tortuosity of π/2 = 1.57. The issue is more complex, however, because it is necessary to take a weighted average of all possible diffusion paths between two points (61). This is not trivial and many attempts at such calculations have led to a diversity of results. Nevertheless, we now know that the correct result for fairly general classes of packed cellular objects is that the component of λ attributable solely to geometry is no greater than 1.225 (380) (see Section II.H).

The discussion of geometric path length supposes that the ECS is well-connected, meaning that from any given location there are many different paths that may be taken to any other location. This is the commonly held view of the ECS and is supported by inspection of electron micrographs. This idea has been challenged by recent experiments (147, 148) suggesting the presence of factor (b), local dead-space microdomains or cul-de-sacs in the ECS, that transiently delay the diffusion of substances. Molecules that enter such a dead-space are constrained to explore it for a while before leaving at the site where they entered and consequently they will not have progressed in their overall journey but merely lost time.

The extracellular matrix likely plays a role in factors (c), (d) and (e) but the abundance and relative importance of this component of the ECS in determining tortuosity is not yet established. We know the extracellular matrix is composed of negatively charged glycosaminoglycans and proteoglycans (212, 269) and specifically hyaluronan (hyaluronate or hyaluronic acid), a nonsulfated glycosaminoglycan, and proteoglycans carrying side chains of either chondroitin sulfate glycosaminoglycan or heparan sulfate glycosaminoglycan (24, 269). The extracellular matrix composition and density vary with brain region (37, 134). A more detailed discussion of the extracellular matrix will be given in Section VI.E.

The obstructive capacity (c) of the extracellular matrix has been inferred from studies of polymeric solutions and gels (159, 275) and it is a fact that the diffusion coefficient is inversely proportional to local viscosity (see below and Equations 6 and 7), so if the interstitial medium has a greater viscosity than that of a free solution, it will contribute to the tortuosity. The amount of the contribution of the extracellular matrix to interstitial viscosity remains an open question, however, (94, 324). Increased drag on a molecule also may arise when the molecular size approaches the width of the ECS (84, 391). Binding interactions (d) between proteoglycans and external ligands are thought to modulate many physiological processes (24, 374). Other binding sites for many substances reside on neuronal or glial membranes in the form of receptor proteins. The non-specific effects of charge (e) are well-documented in cartilage and in solutions containing typical extracellular matrix components (213, 214, 215, 286, 296). Charge effects for monovalent ions, however, have not been clearly demonstrated in brain tissue (257). This may be because at the ionic strength of typical interstitial fluid, the Debye length of a monovalent ion is about 1 nm; the Debye length or screening constant is an indication of how far the electrostatic effect of the charge on the ion extends into the solution (132). The charges on the extracellular matrix would also be screened but still might harbor a local concentration or condensation of positive counterions, especially divalent ones, while excluding mobile anions. The local cloud of cations could exchange with fully mobile cations in solution at some unknown rate. All these speculations will remain unsubstantiated until better estimates the composition and concentration of the extracellular matrix are forthcoming.

At first sight it might seem impossible to offer a quantitative account of these varied and often ill-characterized factors. Fortunately this is not the case and there are theoretical reasons for believing that they can all be accommodated as components of the tortuosity. Starting with factor (a), the geometrical hindrance, we note that this is an inescapable consequence of the presence of cellular elements and will always result in an effective diffusion coefficient in brain, D_g, which is less than D, the free diffusion coefficient and, from the definition given in Equation 3, it follows that

$${\lambda }_g=\sqrt{D∕D_{\mathrm{g}}}$$ (4)

where λ_g is defined as the tortuosity attributable to the geometry. If all the other factors represent reversible processes with a ‘time-constant’ that is much faster than the local time-constant of the diffusion process (Ref 72) (Section 14.2), then the other factors may be expressed as tortuosities, each representing a feature of the internal milieu of the ECS (94) so that the measured tortuosity, λ, obtained by experimentally determining D*, is simply the product of these tortuosities

$$\lambda ={\lambda }_{\mathrm{g}}{\lambda }_1\dots {\lambda }_n=\sqrt{\frac{D}{D_{\mathrm{g}}}\frac{D_{\mathrm{g}}}{D_1}\frac{D_1}{D_2}\dots \frac{D_{n-1}}{D^{\ast }}}=\sqrt{\frac{D}{D^{\ast }}}$$ (5)

If the reversible process occurs on a similar time scale to that of the local diffusion then the basic diffusion equation will no longer be valid and neither will be Equation 5; this might occur for very extended dead-end pores, for example.

It is important to appreciate how λ is obtained in practice. For a selected molecule a measurement of D is made in a free solution (or a very dilute gel, to avoid thermal convection) and under similar conditions, a measurement of D* is made in brain tissue, then λ is simply defined according to Equation 3 as the square root of the ratio of these two quantities. The interpretation of λ in terms of tissue structure, increased diffusion path length or random walk behavior is a quite separate and optional issue and is not part of the operational definition of λ.

Diffusion coefficients are temperature dependent and it is necessary to use a value of D measured at, or corrected to, the same temperature as that used to determine D* when computing λ. The correction can be arrived at by considering the hydrodynamic diameter of a compact molecule (i.e. approximately spherical) estimated from the Stokes-Einstein equation (78) (Section 5.2.1)

$$d_{\mathrm{H}}=\frac{k_{\mathrm{B}}T}{3\pi \eta D}\times {10}^{13}$$ (6)

where d_H is the molecule or nanoparticle diameter (nm), k_B is Boltzmann's constant (1.38065 × 10⁻²³ J.K⁻¹), T is temperature (K), η is viscosity (Pa.s) and D is the free diffusion coefficient (cm² s⁻¹). The viscosity is usually taken as that of pure water and this also varies with temperature (195). Note that Equation 6 is sometimes referred to as the Sutherland-Einstein equation because it was published simultaneously and independently by both William Sutherland and Albert Einstein in 1905 (280).

Because the diameter of a molecule or nanoparticle is a fixed entity, the Stokes-Einstein equation can be used to correct a free diffusion coefficient measured at one temperature to another temperature, based on knowledge of the temperature dependence of the viscosity, i.e.

$$D_2=\frac{T_2}{T_1}\frac{{\eta }_1}{{\eta }_2}{D}_1$$ (7)

where T₁, T₂ are temperatures in degrees K. Despite the utility of this equation it is always preferable to measure D at the same temperature as that at which D* is obtained, and in a medium that approximates the interstitial fluid i.e. CSF.

C. Definition of concentration

Before proceeding it is worth noting that two definitions of concentration of a substance in a tissue are in use. Imagine a piece of the brain tissue bathed for a long time in a solution containing a substance at concentration C that can diffuse into the ECS but is excluded from the intracellular compartments. If the tissue is now homogenized and the concentration of substance measured in the homogenate, then a concentration per unit volume of tissue, C₁ will be measured and this will be less than C. This type of measurement is common in the biochemical literature and often expressed as concentration per weight of tissue or per protein content. It is important to appreciate that it is the concentration C, not C₁, that is experienced by the surfaces of the cells bounding the ECS and so it is this concentration that is the physiologically effective concentration as regards transport, receptor binding or even determination of membrane potential in the case of extracellular K⁺ concentration. For several common ions, the concentration C can be measured directly with an ion-selective microelectrode (250).

The concentrations C and C₁ are simply related by the volume fraction in the example discussed here, so C₁ = αC. More complex situations occur when the diffusing substance is lipid soluble or when cells actively transport and accumulate a substance, so that C₁ exceeds C. In such cases it is more appropriate to refer to a ‘distribution space’ for that substance, which can exceed 100% (e.g. Refs. 41, 100). Studies with such molecules were reviewed by Nicholson (254) and will not be considered here.

The distinction made above between C and C₁ is straightforward but it has another theoretical consequence when diffusion equations are derived for a two-phase medium like the brain. Depending on which definition of concentration is used, the effective diffusion coefficient may be either D* = D/λ², when C is employed in the derivation, or D* = αD/λ² when C₁ is employed. This distinction often is not made explicit and leads to confusion in the interpretation of some published work. In this review the first definition (D* = D/λ²) is always employed and results in the literature have been translated where necessary. This topic has been discussed further (275, 380).

D. Inhomogeneous and anisotropic diffusion parameters

The term ‘inhomogeneous diffusion parameters’ means that the diffusion parameters vary with location in the tissue. For example, the cerebellum exhibits inhomogeneity between the molecular layer and granule cell layer and both the tortuosity and volume fraction are different in the two layers (314).

Anisotropy is distinct from inhomogeneity and only manifests itself in the effective diffusion coefficient. So far it has been assumed that there is a single value of D*, and hence λ, associated with a location. In many brain regions, however, there are different values of these parameters associated with measurements along different axes in the tissue, often as a consequence of the local anatomical structure. For example, substances usually diffuse more readily along an axon bundle than across it, as seen in the myelinated corpus callosum (410). In these cases, D* and λ are tensor, not scalar, quantities and in theory there are up to three distinct values for each when measurements are made in the so-called principal axes of the tissue, which usually means they are aligned with distinct anatomical directions. If measurements are not so aligned, then as many as six tensor components may be required (255). The volume fraction α is always a scalar with a single value but in an anisotropic tissue it is not possible to correctly estimate α with the real-time iontophoretic method (see Section III.B) unless all the components of λ are determined. The theoretical analysis in anisotropic tissue is a straightforward extension of the isotropic case (254, 257, 314). Appropriate solutions to the diffusion equation for anisotropic conditions will be given in Section III.B and experimental results will be presented in Sections III.C.2 and IV.A.5. If D* and λ are the same when measured in any direction, then the tissue is said to be isotropic.

Anisotropic diffusion properties of brain tissue have gained considerable prominence with the extension of magnetic resonance techniques to delineate fiber tracts. This is known as diffusion tensor imaging (DTI) and will be briefly discussed in Section III.D.1.

E. Loss, clearance, uptake and binding

The contribution of factors (b) – (e), defined in section II.B, usually can be regarded as rapid reversible binding, which means that molecules only briefly leave the diffusion process before resuming their course and the net number of molecules in the whole ECS does not change with time. This is equivalent to an increase in tortuosity (Section 14.2 in Ref 72). In many instances, however, molecules are lost irreversibly from the ECS and this must be accounted for by a separate process. Molecules may be removed across the BBB (288) or lost at the surface of a brain slice bathed in flowing medium (150). They also may enter cells by passive or active transport, bind irreversibly to receptors, or become enzymatically degraded. In the simplest case, a molecule passively enters a cell when the internal concentration remains much lower than the concentration in the ECS (249) or passively leaves across the BBB (288), then the loss is proportional to the local concentration in the ECS. This means that loss = k′C where k′ (s⁻¹) is a rate constant. In the absence of diffusion, the decrease in concentration as a function of time would be represented by an exponential curve governed by k′ (249). The terms ‘uptake’ and ‘clearance’ are often used to refer to this process; in this review we will usually refer to it as ‘loss’.

Binding to receptors or transporters may also initially be proportional to extracellular concentration of the diffusing molecule but as the binding sites become increasingly occupied, saturation may occur and then the kinetics of the process becomes more complex. This situation is frequently represented by Michaelis-Menten kinetics and is exemplified by the behavior of dopamine in the ECS of the striatum (251, 413).

F. Bulk flow

The issues of the mechanism, importance and even the existence of endogenous bulk flow of interstitial fluid remain incompletely resolved at this time. The most accepted scenario would be that an osmotically balanced fluid is secreted into the brain across the BBB (47) but some may be generated by cells as a metabolic product (305) and the fluid, whatever its origin makes its way into the CSF (77) or leaves via lymphatic pathways (419). Cserr and collaborators provided the most direct evidence for bulk flow using blue dextran (76) and horseradish peroxidase (HRP) (Ref. 73); this was corroborated later by Weller et al. (412). Cserr and co-workers also measured the efflux of molecules with a range of molecular weights (48, 74, 373) and showed that they all cleared with a single rate constant. The investigators believed that these experiments argued against diffusion as a clearing mechanism because, if diffusion dominated, there should be a set of distinct rate constants each related to the individual effective diffusion coefficients. Cserr and colleagues (151) thought, however, that the actual conduit for bulk flow was restricted to the perivascular or Virchow-Robin space surrounding the capillaries, rather than being through the entire interstitial space. Rennels et al. (310) described the extensive penetration of HRP along perivascular routes after ventriculo-cisternal administration, although this may have been exaggerated by the sensitivity of the technique used to visualize the HRP.

Rosenberg et al. (320), using a different experimental approach to that of Cserr and co-workers, arrived at a bulk flow velocity of 10.5 μm min⁻¹ towards the ventricle in white matter under normal conditions, but gray matter showed flow only under osmotic stress. Ohata and Marmarou (277), however, concluded that diffusion alone was sufficient to explain clearance of brain edema and of high molecular weight dextrans and albumin. This was in agreement with the earlier conclusions of Davson (80) who explained the available data at that time in terms of the ‘CSF sink’ hypothesis, i.e. that substances are cleared from brain tissue simply by the diffusion gradient caused by the low concentration of substance in the ventricles. A study (117) supports the concept of convective removal of drugs and solutes from the brain and lends credence to the studies of Cserr and co-workers but also showed that the choice of anesthetic could influence results.

Abbott (1) has provided a review of bulk flow. At this time it appears most plausible that such flow is restricted to the perivascular spaces rather than taking place throughout the entire ECS. Over long distances and times this could be a significant mechanism but it has proved hard to quantify (see also Ref. 117).

G. Diffusion equation modified for ECS

Diffusion in the ECS can be described at two different levels, the microscopic and the macroscopic. This review will omit detailed theory (254, 257) but it is important to state here for reference the diffusion equations that underpin all the quantitative work to be discussed later.

Microscopically, diffusion of a chosen molecule consists of the sum total of the random walks that the molecule performs as it collides incessantly with water molecules and occasionally with obstructions such as cell membranes. The recognition of this fundamental process is usually attributed to the observations of Brown in 1827 on the ceaseless motion of pollen grains and may be said to have culminated with seminal papers on the theoretical basis of Brownian motion by Einstein in 1905 and Smoluchowski in 1906 (280). Such motion can be captured with computer-based Monte Carlo simulations of particles executing random walks (Fig. 1B) and this approach can be applied in a structured medium like the ECS of the brain; this represents a powerful approach to diffusion problems in the CNS (see Section II.H). A fundamental result of microscopic theory (32, 280) is that for a population of molecules or particles released from the origin at time zero, the mean of the square of their distances, r, from the release point after time t will be given by

$$\langle r^2\rangle =2dDt$$ (8)

where d is the dimension of the space (1, 2 or 3) and D is the diffusion coefficient. The distribution of particles is described by a Gaussian curve centered at r = 0 so that the highest density of particles remains at the origin.

With a suitable statistical treatment, the behavior of a large ensemble of random walks can be described by the equations of classical macroscopic diffusion. These were formulated largely by Adolf Fick in 1855 (see Ref. 105 for English translation) from other considerations before there was a detailed understanding of the microscopic theory. Fick's second law of diffusion forms the basis for present day analysis of molecular migration in brain tissue, but Fick's original formulation applies to molecules moving in a free medium like water, not the complex environment of the ECS.

Modification of the diffusion equation to brain tissue begins with the recognition that the brain is essentially a porous medium, allowing use of a vast amount of theory developed for treating such a medium in the disciplines of physics and engineering. Briefly, this means that some form of ‘volume averaging’ must be applied to the distribution of molecules in an appropriate representative elementary volume of brain tissue, enabling the diffusion equations to be re-derived using the new averaged variables. This approach was originally applied to brain tissue by Nicholson and Phillips (257) who showed that the form of the diffusion equation was unchanged but that the averaged properties of the medium came into play through the volume fraction and tortuosity. This had been implicitly assumed by previous investigators. In most of the experimental work reviewed here, diffusion measurements have been made over distances of the order of 100 μm and this experimental paradigm ensures that the local structural properties are averaged and the following macroscopic equation applies (254, 257, 264):

$$\frac{\partial C}{\partial t}=\frac{D}{{\lambda }^2}{\nabla }^{2}C+\frac{Q}{\alpha }-\mathbf{v}\cdot \nabla C-\frac{f\left(C\right)}{\alpha }.$$ (9)

The concentration, C, is the actual concentration in the interstitial space (see Section II.C) and it is a function both of time t and position, which is represented by the vector x = (x, y, z) in a rectangular Cartesian coordinate system, or the single radial coordinate r in a spherically symmetric realization. The symbols ▽ and ▽² symbolize the first and second spatial derivatives in the appropriate coordinate system.

The various terms of Equation 9 have the following interpretation. The term on the left of the equals sign represents the way that the concentration changes with time at a given location. The first term on the right of the equals sign brings in the contribution of diffusion itself. The free diffusion coefficient is D and the effective diffusion coefficient is D* = D/λ²; it is here that the tortuosity enters in the form of a reduction in the free diffusion coefficient. In the situation where the tissue structure causes anisotropic diffusion, λ becomes a tensor rather than scalar (254). The next term is the source-term, Q(x, t). This term is divided by the volume fraction, reflecting the fact that molecules released into the ECS are restricted to a smaller volume than if they had access to the entire brain tissue. The source may originate from local iontophoresis (249, 257), release of molecules by a pressure pulse (248), or even local release of a substance from a cell. There may be no source term if diffusion is driven by applying a substance to a brain surface; in such cases the driving force is accounted for by the boundary conditions of the diffusion equation. The third term represents the contribution of bulk flow, if present (Section II.F). Flow is defined by its velocity vector v and it forms a scalar product with the concentration gradient ▽C. If and when operative, bulk flow will have little influence on short-term and near-distance diffusion and is neglected in all subsequent theory in this review. Over longer times it might be significant. The final term, f(C), represents loss or clearance of material from the extracellular space, into cells, across the BBB, or by degradation through enzymatic attack or other processes. When such loss is proportional to local concentration, as it often is, f(C) = –k′αC (Section II.E). If f(C) represents Michaelis-Menten uptake, then Equation 9 becomes non-linear and the analysis is more complicated (251).

H. Theoretical models of diffusion in the ECS

Given a model of the brain composed of cells with specified shape packed together with a known volume fraction α it should be possible to calculate λ and D* (which, by Equation 2, are equivalent, so long as D is known). It turns out that this is indeed possible, but only when a specific model of the ECS is chosen. Note that usually only λ_g, the geometrical tortuosity Equation 3 is estimated in models, although attempts have been made to also include interstitial viscosity (e.g. Ref. 324).

Historically this problem goes back to work by Maxwell published in 1891 (Article 314 in Ref. 219) who derived an equivalent relationship for the net conductivity of an ensemble of dilute spheres each with a finite conductivity (which could be zero) embedded in a medium of different conductivity. It is interesting that Maxwell's result (interpreted in terms of impedance, the reciprocal of conductivity) often has been used to estimate the volume fraction of brain tissue, apparently fairly successfully (e.g. Refs. 102, 141), despite the fact that the inherent assumptions in Maxwell's derivation are violated. Recent work, described below, may resolve this paradox and show why Maxwell's result provides a reasonable estimate.

Specific models of brain tissue included more sophisticated variations of the λ/2 argument mentioned in Section II.B (e.g. Ref. 224) culminating in an insightful model by Mathias (218) that captured important aspects of the problem (Fig. 2A). These approaches all amount to taking a single model cellular element or ‘unit cell’ and attempting to calculate how much further a diffusing particle would have to go in traveling around it. The inherent difficulty can be seen in the paper by Rusakov and Kullman (324) who used a more elaborate statistical analysis but still essentially based on a single element and arrived at slightly different estimates of λ depending on whether a rectangular or polar coordinate system was used. This would violate a fundamental requirement for the measurement of λ, namely that one should obtain the same value regardless of the coordinate system used for the measurement. Indeed, one feature of attempts to compute λ has been that different analyses arrived at different values of λ.

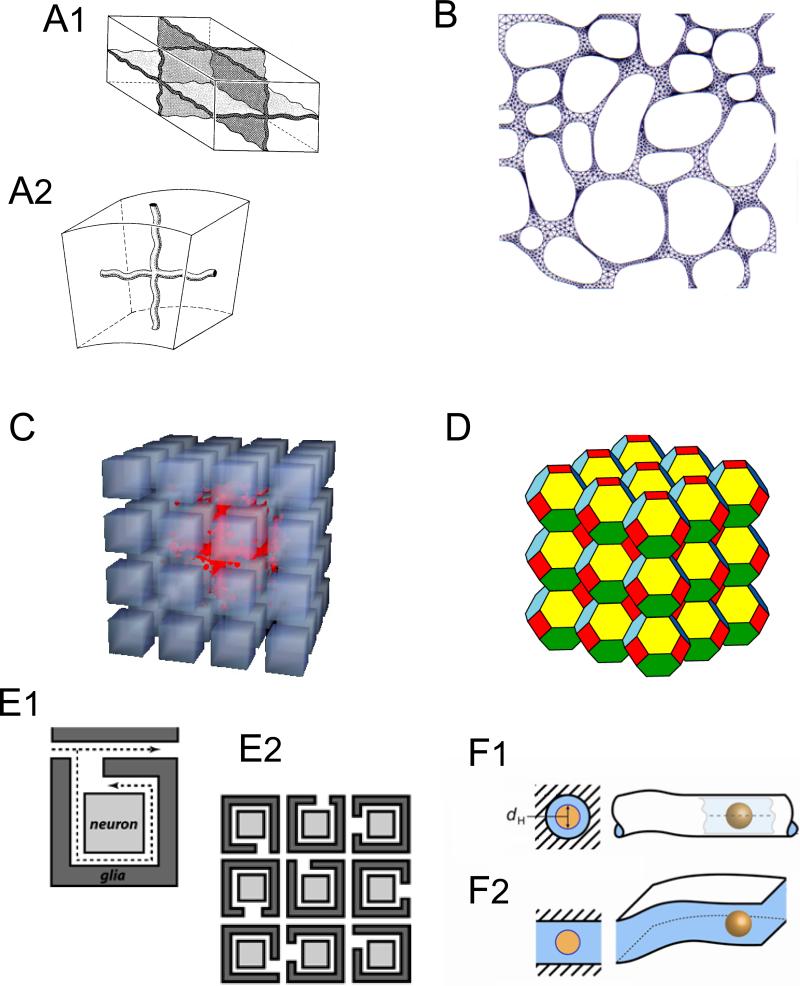
Fig. 2.

Theoretical models of ECS. A₁-A₂. ‘Unit cells’. Replication and stacking these elementary objects builds a simple ECS (stippled regions). A₁ shows intersection of eight cubical cells at center A₂ shows a system of 2D tubular channels between cells. (Modified from Ref. 218). B. ECS constructed as an asymmetric mesh in 2D for finite element method of computer solution for diffusion (Modified from Ref. 61). C. Monte Carlo simulation in ensemble of 3D cubic cells packing with small separation forming an ECS. A set of molecules (red) has been released at the center of the ensemble and are performing random walks causing the cloud of molecules to spread outwards and explore the local environment. (Hrabe and Hrabětová, unpublished). D. Ensemble of truncated octahedral cells. These also pack to fill 3D space but unlike ensembles of cubes have no aligned channels through the array of cells. (Modified from Ref. 380). E₁-E₂. Hypothetical wrapping of glial cells around neurons to form a dead-space microdomain. E₁ shows a single neuron-glial combination, dotted lines indicate two paths that a molecule might take. The path within the glial wrapping is obviously longer and will delay the diffusing molecule more than the path that avoids entering the wrapping. E₂ shows an ensemble of wrapped neurons. (Hrabětová, unpublished). F₁-F₂. Pore models of the ECS for analyzing diffusion of large molecules. F₁. A tubular pore where the molecule (yellow) with hydrodynamic diameter d_H takes up an appreciable amount of the pore leaving a small amount of ECS (blue) around the molecule. Here the total ECS is envisaged as a connecting set of tubes (c.f. panel A₂) possible formed within the extracellular matrix. F₂. Planar or sheet-like pores. Here the molecule has more lateral freedom to move (c.f. panel A₁). (Modified from Ref. 391).

The unit cell approach is fairly simple to implement and understand but it fails to capture the ensemble of paths that occur when there are many cells, a deficiency that was avoided by Maxwell in his original treatment. Approaches that do take into account ensemble paths require greater mathematical sophistication (43, 94). Blum et al. (43) were concerned with intracellular diffusion in the presence of obstacles, which is formally identical to the ECS problem, and derived results for 2D and 3D periodic lattices; El Kareh et al. (94) used homogenization theory to replicate and extend some of the work of Blum et al. (43) in the context of monoclonal antibody diffusion in tissue. El Kareh et al. (94) derived results for ensembles of packed cubical cells and speculated that Maxwell's result might apply to ‘un-elongated cells’. Later, Chen and Nicholson (61) (Fig. 2B) applied the methods of Blum et al. and El Kareh et al. to study how changes in cell shape affected λ, but only in 2D; indeed the application of these analytical techniques to 3D has remained challenging and usually necessitated final numerical solutions and quite restricted geometries. Recently, Hrabětová et al. (147) and Hrabe et al. (144) have advocated the summation of local dwell times instead of path lengths to deal with models of ECS geometry. This approach uses the quantity θ = 1/λ² as a retardation factor that reduces the problem in structured medium to a new problem in a free medium played out in ‘slow motion’.

Given the difficulties with attempts to derive analytical expressions for the relation between α and λ it is not surprising that the Monte Carlo method has been employed for this type of problem. In this method, a geometrical model is constructed within a computer and a population of point-particles is allowed to execute random walks within the geometry (Fig. 2C), making collisions with the bounding cell walls that can be represented by specular reflections (see Ref. 241). After the particles have been walking for some fixed time their positions are determined and D*, and hence λ, estimated from the statistics of the distribution. The advantage of the method is that ensembles of cells with complex geometries can be explored. The disadvantage is that reliable results require considerable computer time and it may not be possible to describe the results by means of a compact equation. Furthermore, although this method of simulation mimics molecular diffusion, the particle step sizes in the simulation are much greater than those actually occurring in an aqueous medium and the population of particles much less numerous than those found in reality.

An early application of the Monte Carlo method to the ECS was by Lipinski (197) based on 2D electron micrographs but it proved impossible to extract the correct volume fraction from the micrographs and we now know that his estimates of λ exceeded the theoretical limit for 2D (see below). An important tool became available for further work when Bartol and Stiles developed efficient Monte Carlo algorithms for studying the neuromuscular junction (25) and this has been made available as a general purpose package called MCell (345). Recently several studies (380, 144, 381) have applied MCell to modeling the 3D ECS (Fig. 2C, D). An alternative numerical approach using cellular automata based on the lattice Boltzmann equation has been implemented (79) for some simplified geometries. Yet another modeling approach based on the packing of fluid vesicles has been proposed (241).

The question addressed by Tao & Nicholson (380) was: Given the diversity of theoretical estimates for the value of λ in a packed ensemble of cells, can direct Monte Carlo simulation indicate which if any of the results are correct? In common with previous models, the cells were taken as convex and it was required that they could pack 3D space without gaps (spheres do not meet this requirement). Then, by moving the cells apart, different values of α could be obtained while maintaining a uniform ECS width. There are relatively few closed geometrical shapes that allow such packing and Tao and Nicholson used three models that do meet this requirement: cubes, truncated octahedra (Fig. 2D) and a mixture of rhombicuboctahedra, cubes and tetrahedra. It was found that for the three models, all the results could be fitted by the relation:

$$\lambda =\sqrt{(3-\alpha )∕2}.$$ (10)

Surprisingly, when the appropriate definition of D* is used (see Section II.C) this is equivalent to Maxwell's result for a dilute suspension of impermeable spheres (Section 12.4.1 in Ref. 72; Article 314 in Ref. 219) but the results of Tao and Nicholson imply that this has much wider validity, a conclusion that had been suggested by the study of El Kareh et al. (94) and also by an analog model (69). This result was already implicit in the impedance studies of the ECS that had relied upon Maxwell's equation. Several earlier theoretical studies, however, had arrived at larger estimates of λ (e.g. 92, 225, 324; see Ref. 380 for a survey of some other models).

Equation 10 implies that the maximum value of λ_g that can be obtained in an ECS formed by an ensemble of packed convex cells occurs as α → 0 and is $\sqrt{3∕2}=1.225$. This limit has been noted in systems of cellular elements by Mathias (Ref. 218) (Fig. 2A) and by others (94, 144). It is also known from these and other sources that the corresponding limit in 2D is $\sqrt{2}=1.414$, a result already noted in early work on muscle (3), so the limiting tortuosity actually decreases as one goes from 2D to 3D. This reduction in λ as dimension increases is not the case, however, if the 3D space is connected by cylindrical pores or tubes rather than sheets because for tubes the 3D limiting tortuosity is $\sqrt{3}=1.732$ (218).

These studies show that the basic geometrical tortuosity is not expected to be more than 1.225, whereas the experimental data to be reviewed later in depth shows that the typical value measured in the brain with small molecules is about 1.6. The increased value may be attributed to any or all of the factors (b) – (e) listed in Section II.B. One of these factors has been incorporated into models in the form of dead-space microdomains which lend themselves to Monte Carlo simulation. In the model of cellular ensembles studied by Tao and Nicholson (380) it was stipulated that the cells must be convex. It has long been known, however, that if an ensemble is composed of objects containing concavities or pits, the effective diffusion coefficient is reduced because diffusing molecules have to spend time exploring these cul de sacs where they become retained for brief periods of time (112, 411). Experimental analysis (147) along with theoretical and modeling studies (144, 147) (Fig. 2E) have shown that for narrow dead-space microdomains and volume fractions within the physiological range

$$\lambda ={\lambda }_{\mathrm{o}}\sqrt{\alpha ∕{\alpha }_{\mathrm{o}}}$$ (11)

where λ_o is the limiting geometrical volume fraction (1.225), α_o is the volume fraction of the well-connected space i.e. the space after the dead-space microdomains have been eliminated and α is the total volume fraction of the ECS (including dead-space). If α_d is the dead-space volume fraction (α_d = α – α_o) then application of Equation 11 to the experimental results has revealed that α_d:α_o would have to be 40:60 in normal cortical tissue and 60:40 in ischemic tissue to account for the measured tortuosities (147, 149; see also Section V.A.2); at this time we lack certainty about the anatomical basis for these numbers. This result was generalized to larger microdomains and the entire range of volume fractions by Tao et al. (381) based on detailed Monte Carlo simulation.

More elaborate models of cell ensembles can be generated from Voronoi tessellations (392) allowing some randomness in cell shape. This idea was employed by Hrabe et al. (144) as a basis for their 2D and 3D Monte Carlo simulations. Verkman and co-workers (211, 425) indicated that they had used a similar approach for some preliminary 2D simulations where they attempted to simulate variable width of the ECS and effect of finite molecular size. Their results appear similar to those already obtained (144, 381) for simulations with dead spaces.

A different type of model was recently proposed by Thorne and Nicholson (391) to explain the higher tortuosity (i.e. significantly greater than the value of 1.6 measured with small molecules) experimentally measured for larger substances such as dextrans and especially large synthetic quantum dot nanocrystals (treated in more detail in Section III.C.5). It was assumed that the quantum dots, with a hydrodynamic diameter of 35 nm were close to the average width of the ECS and so a restricted diffusion or pore model (53, 84, 285) would be appropriate. Depending on whether a planar or tubular model was adopted (Fig. 2F), the estimated ECS width was 38 – 64 nm (391). This model is not inherently inconsistent with those discussed above if one assumes that the mobility of large particles will mainly be restricted by the very local geometry of their microenvironment, while the mobility of smaller particles will be relatively unrestricted, so that small particle diffusion will be more sensitive to aspects of the larger domain such as overall geometry, dead-spaces, etc. An earlier model of restricted diffusion, using a less sophisticated pore model along with an attempt to incorporate interstitial viscosity, had been described by Rusakov and Kullmann (324). It remains an important question for future theoretical research to further reconcile these various models or to develop new ones to account for the expanding database of experimental results.

Another quantitative approach has been to look for an empirical relationship between α and λ and this quest has usually begun with a power law relationship based on Archie's Law (16). This approach is discussed briefly by Nicholson and Rice (260, 263) but does not work very well (183). Indeed, Mota et al. (238) carried out a detailed analysis of much of the available diffusion data for brain tissue and concluded that Archie's Law in its original form was not applicable; instead, Mota et al. (238) proposed a more general power law.

III. METHODS OF MEASUREMENT

The concept underlying methods of direct diffusion measurements is to introduce a detectable substance into the ECS and to subsequently measure its concentration distribution in space and time. In an ideal situation this distribution will be described by an appropriate solution to Equation 9 and, by fitting this solution to the measured concentration distribution, the parameters λ and α may be obtained. When there are other processes, such as loss characterized by a first-order kinetic constant k′, then the additional parameters may be extracted also. An important, but sometimes neglected, caveat is that the experimental concentration distribution must be accurately represented by the mathematical solution to the diffusion equation; otherwise, derived parameter values are meaningless. Therefore it is essential that a distribution curve can be obtained by the method of measurement, rather than a single value, to compare with theoretical predictions.

The choice of probe substance is important; the probe should be small enough to explore all regions of the ECS but remain predominantly in the ECS compartment. The probe should be non-toxic to brain tissue and of sufficiently low concentration that it does not affect interstitial osmolarity. Finally, it must be possible to measure the substance with adequate selectivity and sensitivity over endogenous compounds to determine a range of concentrations. These are quite stringent constraints. Once measurements with an ideal probe are available, the behavior can be compared with, for example, the non-ideal behavior of a drug that is taken up by cells or removed across the BBB to determine information about the elimination of the drug. Use of a larger probe compound that is more impeded in its diffusion by the narrow interstitial spaces of the ECS may provide additional information, such as an estimate of the size of the spaces.

The following sections will consider the older radiotracer method, the real-time iontophoresis (RTI) and real-time pressure (RTP) ejection methods, and the integrative optical imaging (IOI) method. After describing the techniques, the major results obtained with these methods will be reviewed with the exception of the large body of results obtained with the RTI method employing the cation tetramethylammonium (TMA⁺). The RTI-TMA data will be treated separately because this extensive and diverse collection of experiments forms the basis for much of our present understanding of the diffusion properties of the ECS and it has been the predominant technique for exploring the changed diffusion properties in development, aging, various forms of experimental intervention, and pathological states.

A. Radiotracers

Early attempts to quantitatively measure the diffusion properties of the ECS employed radiotracers (see Chapter 3 in Ref. 162) but were not very reliable until Rall, Fenstermacher, Patlak and their colleagues established a workable protocol that they then refined over several years (e.g. Refs. 101, 288, 303). These techniques are not in general use today but they are briefly reviewed here because the data obtained with them continue to provide an independent validation of the newer methods and the radiotracer technique remains sound.

1. Radiotracer technique

The basic method was to perfuse the bilateral ventriculoscisternal cavities of an anesthetized animal, usually a dog or monkey, with a radiolabeled probe molecule for a period that could extend to several hours (288). After perfusion, the brain was quickly removed, frozen, and sections made at 0.4 – 1 mm thickness from a rectangular block of tissue parallel to the perfused surface taken from an appropriate brain region (Fig. 3A). The caudate nucleus (part of the striatum) was often chosen because it was large and adjacent to the perfused ventricle but the method was also applied in the spinal cord and neocortex (see 254). Each section was weighed and the radioactivity measured to obtain a profile of the concentration of the marker at different distances from the surface at the time the animal was sacrificed (Fig. 3B). The value of D* was estimated by fitting these profiles of concentration C_x as a function of depth x to the appropriate one-dimensional solution of the diffusion equation (72, 288), i.e.

$$\frac{C_x}{C_0}=\text{erfc}\left(\frac{x}{2\sqrt{D^{\ast }t}}\right)$$ (12)

with boundary conditions that one surface was kept at a fixed concentration C₀ (the ventricle) and molecules diffused into an infinite medium (the brain). In practice the investigators plotted their data using special graph paper that had the ordinate scaled according to the complementary error function (erfc) as shown in Fig. 3B. This figure shows that sucrose obeys Equation 12 well but inulin deviates from ideal behavior. The value of the free diffusion coefficient, D, was obtained from similar measurements on a column of 2% agar gel (332). From these determinations λ was calculated.

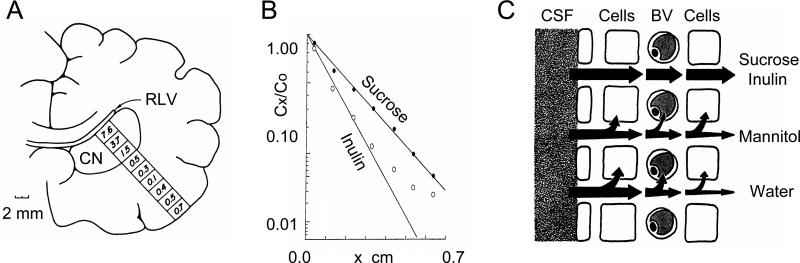
Fig. 3.

Radiotracer method. A. Tracer is perfused through the right lateral ventricle (RLV) and diffuses into the brain for 3-5 hours then the brain is fixed and removed. Small blocks of brain are cut as indicated and assayed for radioactivity. The number indicates percent of radiolabeled inulin or sucrose in a given tissue block. The caudate nucleus (CN) is immediately adjacent to the RLV so this structure has been most thoroughly analyzed. The scale bar of 2 mm is appropriate to a dog brain. (Modified from Ref. 303). B. Concentration of C¹⁴-sucrose and H³-inulin after four hours of ventriculocisternal perfusion in dog brain. Ordinate is plotted on complementary error function (erfc) scale (see Equation 12), C_x is concentration at distance x (abscissa) from ventricular border of caudate nucleus where concentration is C₀ (Modified from Ref. 104). C. Schematic of several possible pathways a molecule can follow after entering the brain tissue from the ventricular CSF. Arrows indicate the pathways; the thickness of the arrow represents the relative importance of that pathway. Sucrose and inulin remain predominantly extracellular, mannitol enters cells to some extent and a small amount crosses the BBB, water readily enters cells and crosses BBB. (Modified from Ref. 104).

By making the assumption that the ECS concentration in the first brain section adjacent to the ventricle had come into equilibrium with the perfusing concentration, the volume fraction α could be estimated also. This calculation was based on the expectation that the probe molecule was confined to the ECS in this section and that the weight of the section would be translated into a tissue volume and so the volume occupied by the radiolabeled substance could be found. In addition, because of the prolonged perfusion period, it was expected that some of the probe substance would cross the BBB and, by assuming a first order process, the relevant kinetic constants for this loss could be determined (288).

The main advantage of the radiotracer method is the ability to study the diffusion of a wide variety of compounds including many with therapeutic potential. The main disadvantages are that it requires an animal for each time point and it is most suited to large brains. Finally, the necessity to use radioactive compounds poses problems in some laboratories. These disadvantages have largely eliminated the method from contemporary use.

2.Radiotracer Results

The most effective ECS probe substances were found to be [³H]mannitol (M_r = 182), [¹⁴C]- and [³H]sucrose (M_r = 342), [¹⁴C]EDTA chelated with Ca²⁺ or Cr²⁺ (total M_r = 302 and 314 respectively) or [¹⁴C]- and [³H]inulin (M_r ~ 5000). All these compounds are uncharged, which may be an advantage given the fixed negative charges associated with the extracellular matrix. Fenstermacher and colleagues (104) concluded that mannitol was not entirely satisfactory while the molecular weight of inulin is not precisely defined and there is some evidence that this marker decomposes (108); later studies by Fenstermacher and colleagues settled on sucrose as the best marker. Even sucrose, however, may be sequestered over time by unidentified brain compartments (100, 118).

The radiotracer studies have been reviewed in detail (101, 254) and here we only include a selection of studies on the in vivo caudate nucleus for which values of λ and α were obtained (Table 1). The radiotracer studies included both ‘good’ and ‘bad’ ECS markers. The good ECS markers listed in Table 1 are Ca-EDTA, Cr-EDTA and sucrose. The reason for a marker failing to perform adequately as a means of measuring ECS parameters, i.e. a ‘bad’ marker, is largely caused by two processes (Fig. 3C). First, the marker may enter the intracellular compartment to a fairly modest degree (quasi-extracellular compound, QEC) or do so easily (intracellular substance, ICS). If the compound is actively taken up by cells, the volume fraction, as measured with the radiotracer method, can exceed unity and it is preferable to speak of a ‘distribution space’. Thus in Table 1 mannitol, methotrexate, metrizamide, sodium and p-aminohippurate (PAH) are all classified as QECs while α-aminoisobutyric acid (AiB), creatinine and hydroxyurea predominantly enter the intracellular space. Second, the marker may rapidly cross the BBB and so be lost from the tissue (e.g. water in Fig 3C); in this case diffusion parameters usually cannot be measured with radiotracers and these data have been omitted from the present review. Compounds ill-behaved from the perspective of diffusion probes of the ECS may still need to be characterized for their transport properties because they include such anti-cancer drugs as β-cytosine arabinoside, BCNU (N, N′-bis(2-chlorpethyl)-N-nitrosourea), and methotrexate (41). It should be noted that all substances will enter cells and may cross the BBB to some degree if given enough time but for ‘good’ ECS markers these processes do not have a major influence on the distribution of the radiotracers.

Table 1.

Caudate nucleus: Diffusion measurements using radiotracers

Molecule	Label	Mr	D × 106	Species	D* × 106	λ	α	Class	Refs.
			cm2 s−1		cm2 s−1
Ca-EDTA	14C	302	6.2	monkey	2.2	1.64	0.15	ECS	41, 101
Cr-EDTA	51Cr	314	8.4	rabbit	3.4	1.57	0.15	ECS	99, 101
Sucrose	3H	342	7.0a	rabbit	2.8	1.60	0.21	ECS	100, 101
Sucrose	3H	342	7.0a	dog	3.1	1.52	0.17	ECS	101, 288
Sucrose	3H	342	7.0a	cat	3.3	1.50	0.16	ECS	320
Mannitol	3H	182	8.5	dog	2.2	1.97	0.32	QEC	101, 288
Methotrexate	3H	508	5.3	monkey	0.9	2.43	0.28	QEC	41, 101
Metrizamide	125I	789	7.1	rabbit	2.2	1.80	0.19	QEC	99, 101
Na+	24Na	23	20.0	dog	5.9	1.82	0.16	QEC	101, 288
PAH	3H	194	8.3	dog	2.7	1.76	0.25	QEC	103, 104
AiB	14C	103	11.0	rabbit	0.9	3.50	3.34b	ICS	100, 101
Creatinine	14C	113	12.9	dog	1.9	2.61	0.61b	ICS	101, 288
Hydroxyurea	14C	76	13.6	monkey	1.8	2.79	0.56b	ICS	41, 101

Footnotes

Temperature for all measurements is 37 °C.

^acorrected to 37 °C using value of 5.209 × 10⁻⁶ cm²s⁻¹ at 25 °C from Ref. (200)

^bdistribution space

PAH = p-aminohippurate

AiB = aminoisobutyric acid

ECS = substance that remains predominantly in ECS

QEC = quasi-extracellular compound

ICS = substance that significantly enters intracellular space

Table 1 only offers a selection taken from studies on the caudate nucleus. Other studies focused on the spinal cord but the results were less reliable, perhaps because of the difficulties in adequately perfusing this region (see Ref. 254 for summary of these data). More recent work where diffusion of radiolabeled material has been analyzed includes studies of [¹²⁵I]-labeled nerve growth factor (NGF) released from polymer implants in rat brains (174, 175). Diffusion of [¹⁴C]-labeled sucrose and other compounds have also been studied after convection-enhanced delivery (CED) (44, 118). A modified radiotracer method has been applied to an extensive study of brain slices (289) and this will be reviewed in Section V.A.2.

In conclusion, the results summarized in Table 1, as well as other studies with ECS radiotracers, show that the value of λ obtained with this method is quite similar to that which is obtained with the point-source paradigm to be discussed next. The value of α obtained with the ECS radiotracers is around 15%, somewhat lower than the current estimates of about 20% obtained using TMA and described in detail later in this review. Quasi-extracellular compounds give more unreliable results but they are still quite close to the better ECS markers. In contrast, compounds that predominantly enter cells exhibit a distribution space that greatly exceeds the ECS volume fraction and may be greater that 100% when active transport is involved.

B. Real-time iontophoresis and real-time pressure ejection

Both the real-time iontophoresis (RTI) and real-time pressure (RTP) ejection method are realizations of the point-source paradigm. The techniques rely on microelectrodes or micropipettes for both delivering molecules and sensing them. Following a description of the methods, this section considers results obtained with ions other than TMA that employed the RTI or RTP method. The TMA results are so much more extensive that Sections IV and V will be devoted them.

1. Real-time iontophoresis technique

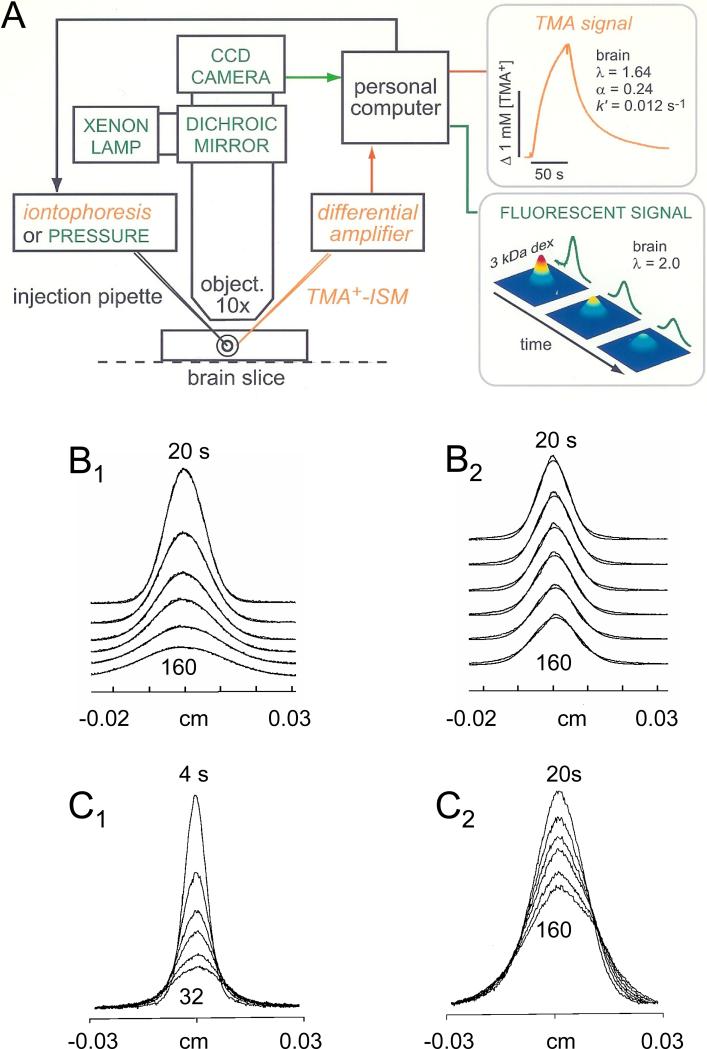
The advent of ion-selective microelectrodes (ISMs) made possible a new technique for diffusion measurements. These electrodes are constructed from double-barreled micropipettes (10, 150, 250, 361) and the first ones that became available were able to sense the local concentration of K⁺ in a volume of a few cubic micrometers around the tip of the microelectrode that was in local equilibrium with the ion concentration in the ECS (176, 177). This led Lux and Neher (208) to study the diffusion of K⁺ in the brain by using iontophoresis to release K⁺ from another micropipette about 30-60 μm away from the ISM. The resulting concentration changes at the ISM were interpreted according to a solution to the diffusion equation. Unfortunately, the original study was flawed by two unrecognized problems that acted in concert to make the results appear plausible. The first problem was the assumption that K⁺ would diffuse only through the ECS whereas it is now established that this ion rapidly enters brain cells by a variety of mechanisms (8, 169). The second problem was that, although it was recognized that the amplitude of the K⁺ signal in brain tissue was affected both by the restricted volume fraction and an altered diffusion coefficient, it was formally described only by a reduced diffusion coefficient (corresponding to a tortuosity factor alone) whereas, in the iontophoresis paradigm, both volume fraction and D* must be explicitly represented in the appropriate solution to the diffusion equation (see Equation 13 below). These errors were identified and resolved by Nicholson et al. (258) who went on to demonstrate the validity of the method by using tetramethylammonium (TMA⁺) or tetraethylammonium (TEA⁺) ions instead of K⁺. This was possible because the ion-exchanger originally used to measure K⁺ (Corning 477317: consisting of potassium tetrakis (p-chlorophenyl) borate dissolved in 2,3-dimethylnitrobenzene, Ref. 272) is about 600 times more sensitive to TMA⁺ or TEA⁺ than to K⁺ and therefore can sense micromolar concentrations of these quaternary ammonium ions. Combined with the correct modification of the diffusion equation, the diffusion properties of the ECS then could be measured accurately by the paradigm introduced by Lux and Neher (208). A full treatment of the theoretical and experimental aspects of the technique, including its extension to the anions α-naphthalenesulfonate (αNS⁻) and AsF₆⁻, was published by Nicholson and Phillips (257); some further extensions to the theory were added later (250, 254).

This method is capable of following many of the changes in diffusion properties of brain tissue in real-time and consequently is known as the real-time iontophoresis (RTI) method and otherwise as the TMA method and will be referred to here as the RTI-TMA method, when TMA⁺ is used. The setup and typical records from the original studies of Nicholson & Phillips (257) are illustrated in Figs. 4A and 4B. A micropipette releases TMA⁺, or another suitable probe ion, by iontophoresis with constant source strength Q into either brain tissue or an agarose gel. An ISM located about 100 μm from the release point measures the rising concentration of the probe ion during the iontophoretic pulse as a function of time according to Equation 13 (254, 257), which is the solution to Equation 9 in a spherically symmetric coordinate system:

$$C\left(t\right)=\frac{Q{\lambda }^2}{8\pi D\alpha r}\left[\text{erfc}\left(\frac{r\lambda }{2\sqrt{Dt}}+\sqrt{k^{\prime }t}\right)\text{exp}\left(r\lambda \sqrt{\frac{k^{\prime }}{D}}\right)+\text{erfc}\left(\frac{r\lambda }{2\sqrt{Dt}}-\sqrt{k^{\prime }t}\right)\text{exp}\left(-r\lambda \sqrt{\frac{k^{\prime }}{D}}\right)\right].$$ (13)

Here the concentration C is recorded at distance r from the origin (r = 0) where the source Q is located. Loss of probe ions from the ECS is represented by a first order kinetic constant, k′; this may include entry into cells (164) or loss across the blood-brain barrier (288). When the loss of probe ion is negligible (k′ = 0), Equation 13 reduces to

$$C\left(t\right)=\frac{Q{\lambda }^2}{4\pi D\alpha r}\text{erfc}\left(\frac{r\lambda }{2\sqrt{Dt}}\right).$$ (14)

Other variables are as defined previously.

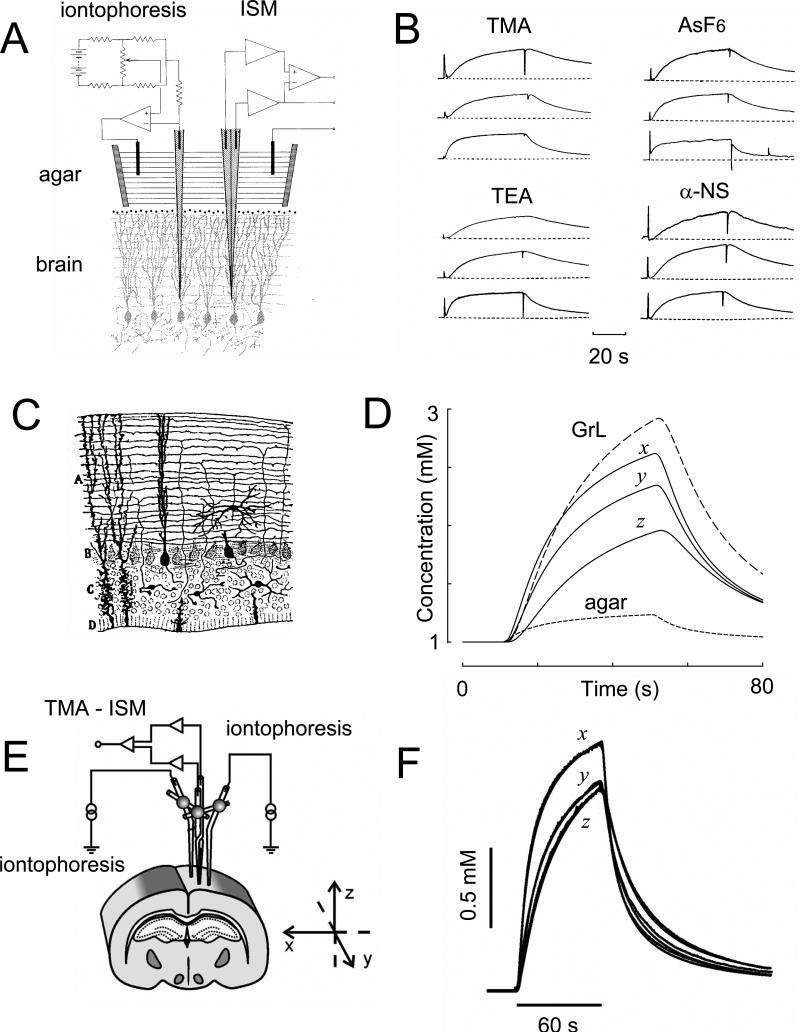
Fig. 4.

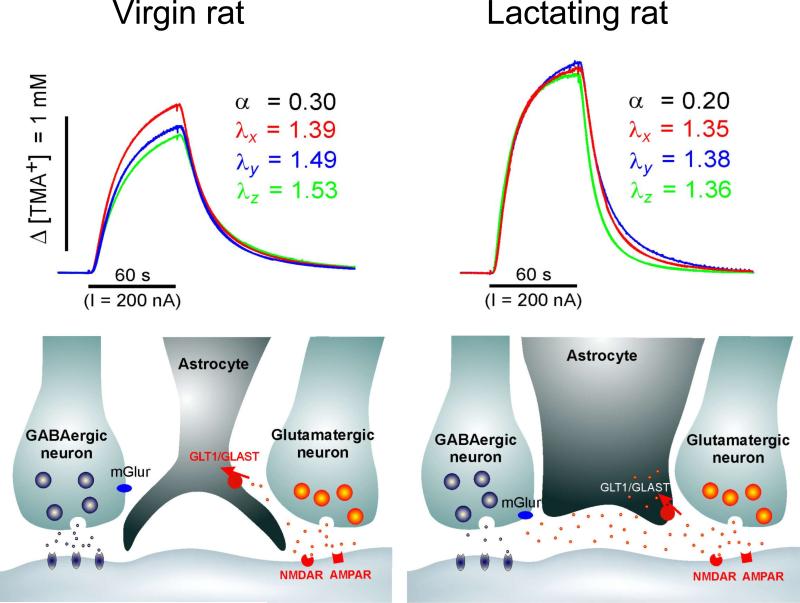
The RTI method. A. Original setup. Paired iontophoretic and ion-selective microelectrodes (ISM) are glued together and lowered into rat cerebellum in vivo. The iontophoretic microelectrode passes a current pulse controlled by a constant current circuit. The signals from the ion-sensing and reference barrels of the ISM are impedance-buffered and subtracted to remove contribution of local potential in brain. This results in an output that is proportional to the logarithm of the local ion concentration. Electrode array is withdrawn into agar for control measurements. (Modified from Ref. 257). B. Examples of RTI records using four different ions. All records taken in rat cerebellum in vivo. Each record in each set was taken at a different spacing between source electrode and ISM. Ordinate is concentration, abscissa is time. See original paper for details. (Modified from Ref. 257). C. Part of a frontal section through the cerebellum of a lizard. This cerebellum is very similar to that of the turtle. A, Molecular layer; B, Purkinje cells; C, granular layer; D, ependyma (Modified from Ref. 56). D. Diffusion anisotropy demonstrated by theoretical concentration-time profiles derived from average diffusion parameters measured in the turtle cerebellum and control medium. Theoretical records illustrate the relative concentration reached during the iontophoresis of TMA⁺ in the x-, y- and z-axes of the molecular layer, the granular layer (GrL) and agar gel. Diffusion distance used to calculate the curves was 120 μm. The tortuosity values were: molecular layer, λ_x = 1.44, λ_y = 1.95, λ_z = 1.58, α = 0.31 and granular layer, λ = 1.77, α = 0.22. (Modified from Ref. 314). E. Setup used to measure anisotropy in rat corpus callosum in vivo with the RTI-TMA method. The design is similar to that shown in panel A except that two iontophoresis microelectrodes are used to allow simultaneous measurements in the x- and y- or x- and z-axes (Modified from Ref. 410). F. Example of measurements in rat corpus callosum with the RTI-TMA method. In this record, λ_x = 1.44, λ_y = 1.70, λ_z = 1.72, α = 0.24. Ordinate is TMA⁺ concentration, abscissa is time. (Modified from Ref. 358).

In order to represent the falling phase of the concentration curve after the iontophoresis ceases following a pulse of duration t_p, a delayed version of Equation 13 or 14 is subtracted from the original function

$$C=C\left(t\right)-C(t-t_{\mathrm{p}}),t>t_{\mathrm{p}}.$$ (15)

Equation 15 is equivalent to switching on an equal and opposite hypothetical ‘sink’ of ions at the end of the required pulse to cancel it out and is valid because of the linear nature of the diffusion equation and its solutions. The RTI-TMA method can also be used with a continuous sinusoidal source (62) instead of a pulse but this method has not been tested extensively. Note that the substitution of a more complex loss term (e.g. Michaelis-Menten kinetics) in the diffusion equation can make the whole equation non-linear and requires a more sophisticated treatment (251).

Equations 13 – 15 may be extended to include anisotropy (Figs. 4C-F), (for details see Refs. 254, 257, 314). Assuming that the so-called principal axes of the diffusion tensor are coincident with the x, y and z axes of the tissue, the equation is:

$$C\left(t\right)=\frac{Q{\lambda }_x{\lambda }_y{\lambda }_z}{8\pi D\alpha R}\left[\text{erfc}\left(\frac{R}{2\sqrt{Dt}}+\sqrt{k^{\prime }t}\right)\text{exp}\left(R\sqrt{\frac{k^{\prime }}{D}}\right)+\text{erfc}\left(\frac{R}{2\sqrt{Dt}}-\sqrt{k^{\prime }t}\right)\text{exp}\left(-R\sqrt{\frac{k^{\prime }}{D}}\right)\right]$$ (16)

where $R=\sqrt{x^2{\lambda }_x^2+y^2{\lambda }_y^2+z^2{\lambda }_z^2}$. In an isotropic medium λ = λ_x = λ_y = λ_z, R = rλ, $r=\sqrt{x^2+y^2+z^2}$ and Equation 16 then reduces to Equation 13. The concentration in the period after the iontophoresis pulse is again given by Equation 15.

When iontophoresis is employed, the source is defined by Q = In_t/zF, where I is the current applied to the iontophoresis micropipette, n_t is the transport number for the ion and electrode, F is Faraday's Electrochemical Equivalent, and z is the ion valency. The transport number n_t represents the fraction of the applied current that actually expels the ion and it is determined from iontophoretic measurements in dilute agar or agarose gel, where by definition λ = 1, α = 1 and k′ = 0 in Equation 13 so Equation 14 is valid. A value for D is also determined in agarose, although it is usually taken as a known constant for a given temperature. An important aspect of the method is that a small forward bias current is applied continually to the iontophoresis electrode to expel the ion at all times and maintain both a constant value of n_t and a finite baseline concentration value. This eliminates dilution of ions in the iontophoretic microelectrode tip between pulses which otherwise is difficult to account for (88). The current is stepped to a higher value for a period of about a minute (typically t_p = 50 – 100 s) for diffusion measurements. Appropriate electronic circuitry ensures that I is maintained constant during the pulse (262).

The ion is sensed with an appropriate ISM, fabricated and calibrated using a suitable paradigm (150, 177, 250, 262, 353). Note that conventional ISMs have response times of a few hundred ms to a few seconds, which is usually adequate but it is possible to make much faster ISMs (98). The iontophoresis microelectrode and the ISM are glued into an array with fixed spacing and this is typically used in studies on the brain of anesthetized animals (Fig. 4E). When brain slices are employed, the microelectrodes can be moved independently using two micromanipulators and the location confirmed by IR-DIC optics (150) (Fig. 5A). The signals from the ISM are impedance-buffered and low-pass filtered with suitable amplifiers, then digitized and sent to a PC for curve fitting of Equation 13 under control of custom software enabling α, λ, and k′ to be extracted. The current software is a package of two MATLAB-based programs (Wanda and Walter) that replace an older program called VOLTORO (see Ref. 150 for more details).

Fig. 5.

A. Setup for integrative optical imaging (IOI) method and RTI-TMA in brain slices. A brain slice or dilute agarose (or agar) gel is placed into a chamber on a stage of a compound microscope equipped with epifluorescent optics. For IOI, a fluorescent molecule is pressure injected from a micropipette and a time series of images captured using a charge-couple device (CCD) camera. The images are processed with a PC to fit Equation 20 to the intensity profiles measured along selected image axes. Diffusion coefficients, D and D*, are extracted in agarose gel and brain slice, respectively. As shown in this figure, RTI-TMA measurements can also be made in this setup with the advantage that the iontophoresis microelectrode and the ISM can be positioned independently under visual control. Both IOI and RTI measurements can be performed simultaneously. (Modified from Ref. 149). B₁-B₂. Diffusion profiles for 70 kDa fluorescent dextran. B₁. Profiles measured at 20, 40, 60, 80, 120 and 160 s after pressure injection in agarose gel as a function of distance in object space (slice). Profiles have characteristic shape of a Gaussian curve. B₂. Similar profiles measured in slices of rat cortex. Note that the profiles collapse much more slowly in brain than in agarose as a consequence of the tortuosity in the slice (λ = 2.25 for 70 kDa dextran). (Modified from Ref. 265). C₁-C₂. Diffusion profiles for 66 kDa fluorescent bovine serum albumin (BSA). C₁. Profiles measured at 4, 8, 12, 16, 24 and 32 s after pressure injection in agarose gel as a function of distance in object space (slice). C₂. Similar profiles measured in slices of rat cortex. Profiles measured at 20, 40, 60, 80, 120 and 160 s after pressure injection; again the profiles collapse much more slowly in brain than in agarose (λ = 2.26 for 66 kDa BSA). (Modified from Ref. 379).

2. Real-time pressure ejection technique

In some situations, iontophoresis may be inappropriate and then the probe ions can be introduced into the brain tissue by pressure ejection from a micropipette (248, 250, 254). This is the real-time pressure (RTP) ejection method. This method allows D* and λ to be measured but because the volume ejected varies with the medium into which the ejection is made, this method does not allow the reliable determination of α. When relatively large volumes are ejected it may be possible to calibrate the volume ejected (400).

When the ejected volume is small (radius less than half the distance to the measuring ISM) it may be considered as a point-source in both space and time, then a simple impulse function (delta function) solution to Equation 9 is appropriate:

$$C(r,t)=\frac{U{C}_{\mathrm{f}}}{\alpha }\frac{{\lambda }^3}{{\left(4Dt\pi \right)}^{\frac{3}{2}}}\text{exp}\left(-\frac{{\lambda }^2{r}^2}{4Dt}-k^{\prime }t\right).$$ (17)

where a volume U, of an ionic solution or other substance at concentration C_f is ejected. It is assumed that ejected volume, although finite, is still a point source. A more complicated analytical expression for an ejected volume with a finite initial volume, which may even exceed the distance to the measuring ISM, while still retaining an impulse function in time (instantaneous delivery) has been provided by Nicholson (248, 250, 254).

In an anisotropic medium Equation 17 would become:

$$C(r,t)=\frac{U{C}_{\mathrm{f}}}{\alpha }\frac{{\lambda }_x{\lambda }_y{\lambda }_z}{{\left(4Dt\pi \right)}^{\frac{3}{2}}}\text{exp}\left(-\frac{R^2}{4Dt}-k^{\prime }t\right)$$ (18)

where the variables have the same meaning as those associated with Equation 16.

The analytical solutions represented by Equations 17 and 18 all assume that the ejected substance infiltrates the ECS. If the substance forms a large cavity, a numerical solution is required (248) but experimental work is more consistent with the infiltration assumption. There is a brief interstitial pressure pulse that accompanies the ejection (27) but this appears to die away quickly and has not been taken into account.

The major advantages of RTI and RTP methods are that they can make real-time measurements in very small volumes of living tissue enabling changes in diffusion parameters to be followed in specific brain regions during drug application or other intervention. The disadvantages are that the method can only be used with a small set of probe substances for which ISMs can be made. The method can be extended to look at the diffusion of K⁺, Ca²⁺ or a few other ions, including the exogenous anions AsF₆⁻ and α-naphthalenesulfonate (see below). ISMs can also be made that sense Na⁺ or Cl⁻ but the high extracellular concentration of these ions combined with the logarithmic response of an ISM prevents the RTI method being used effectively. If the ISM is substituted with a carbon fiber microelectrode and voltammetric methods employed, the diffusion of dopamine, and potentially other electroactive compounds, can also be measured (71, 150, 316, 318). Overall, the range of substances that can be used with RTI and RTP remains small and the method also necessitates the fabrication of microelectrodes and use of electrophysiological recording equipment.

3. Tetraethylammonium

To validate the approach, the original study by Nicholson and Phillips (257) went beyond TMA⁺ to employ another cation, tetraethylammonium (TEA⁺) along with two anions that will be discussed below (Fig. 4B). TEA is closely related to TMA and is an effective blocker of the voltage-gated potassium channels associated with the action potential, but only when applied to the intracellular aspect of the channel. Although TEA is an effective probe of the ECS, TMA has been preferred because it is less potent in blocking K⁺ channels and slightly smaller than TEA. TEA was used in the first RTI study that correctly identified α and λ (258) and more extensively by Nicholson & Phillips (257) (Table 2) where it gave almost identical results to TMA in the rat cerebellum. Note that the TMA results from Nicholson and Phillips (257) are shown in Table 2 for comparison but the main TMA data are presented in Sections IV and V.

Table 2.

Substances other than TMA⁺: Diffusion measured with RTI or RTP method

Molecule	Mr	D × 106	Technique	Species	Region	Prep.	°C	λ	α	Refs.
		cm2 s−1
TMA+,a	74	11.1	RTI-ISM	rat	cereb. mlb	in vivo	37	1.49	0.18	257
TEA+	130	7.90	RTI-ISM	rat	cereb. mlb	in vivo	37	1.48	0.21	257
AsF6−	189	14.0	RTI-ISM	rat	cereb. mlb	in vivo	37	1.68	0.26	257
α-NS−	174	7.60	RTI-ISM	rat	cereb. mlb	in vivo	37	1.54	0.18	257
Ca2+	40	9.90c	RTP-ISM	rat	cortex	in vivo	35	1.82d	n/a	261
Dopamine	153	6.90	RTP-CFM	gp	SNc	slice	32	1.68	n/a	71
Dopamine	153	6.90	RTP-CFM	gp	SNr	slice	32	1.80	n/a	71
Dopamine	153	6.90	RTP-CFM	gp	VTA	slice	32	1.72	n/a	71
Penicillin	356	3.52	RTP-ISM	rat	cortex	in vivo	37	1.62	n/a	191
PTZ	138	8.50	RTP-ISM	rat	cortex	in vivo	37	1.63	n/a	336
T-valproate	142	5.25	RTP-ISM	rat	cortex	in vivo	37	1.67	n/a	209
Valproate	144	6.25	RTP-ISM	rat	cortex	in vivo	37	1.92	n/a	209
Verapamil	455	5.08	RTP-ISM	rat	cortex	in vivo	37	1.51	n/a	171

Footnotes

Penicillin = Na-penicillin-G

PTZ = Pentylenetetrazol

T-valproate = Trans-2-en-valproate

ISM = Ion-selective microelectrode

CFM = Carbon-fiber microelctrode

gp = Guinea Pig

cereb. ml = Cerebellum, molecular layer

SNc = Substantia nigra, pars compacta

SNr = Substantia nigra, pars reticulate

VTA = Ventral tegmental area

^aThis TMA⁺ result included for comparison. Main TMA⁺ results in Tables 4A, 4B – 7

^banisotropy not taken into account

^cD for Ca²⁺ based on unpublished experiments and analysis by Hrabětová, Masri, Tao and Nicholson

^dbased on D* = 3.0 × 10⁻⁶ cm² s⁻¹, Ref (261)

n/a = not available

4. Hexafluoroarsenate and α-naphthalenesulfonate

The anions used by Nicholson & Phillips (257), hexafluoroarsenate (AsF₆⁻) and α-naphthalenesulfonate (α-NS⁻) provided values of λ (Table 2) that were not statistically significantly different from those obtained with the cations TEA⁺ and TMA⁺. Note that the measured free diffusion coefficient for AsF₆⁻ was almost twice the value measured for TEA⁺ and α-NS⁻ even though the molecular weights do not differ by a factor of two and the value of D for AsF₆⁻ is even higher that that obtained for TMA⁺ (257) (Table 2). Similar variations have been noted among the free diffusion coefficients of other small ions and may reflect differing hydration shells (Chapter 10 in Ref. 132). All the D-values presented in Table 2 were measured with a background of 150 mM NaCl to mimic the major constituent of the interstitial fluid of the brain. An important conclusion from the Nicholson and Phillips (257) study was that the ECS failed to discriminate between small monovalent cations and anions in its diffusion properties. This was a disappointment because there had been some expectation that the negatively charged extracellular matrix would discriminate, however, as noted in Section II.B, the fixed charges are probably screened by the relatively high concentration of ions in the interstitial fluid.

5. Calcium

It might be hypothesized that diffusing Ca²⁺ would behave differently from singly charged species because the increased positive charge density would interact with the fixed negative charges on the extracellular matrix. This conjecture appeared to be born out in an early RTI diffusion study (234) where Ca²⁺-ISMs were used in the rat hippocampus to determine a value of D* that was 100 times less than D for this ion. However, a later study (261) using RTP and a Ca²⁺-ISM found a fairly typical value for λ in rat cortex (Table 2; note the original values of λ have been revised upwards using a better estimate of D; the slightly elevated λ may indicate some additional hindrance) and this result is reinforced by the more recent radiotracer study of Patlak et al. (289) where a value of λ = 1.52 was estimated in 450 μm hippocampal slices using the tracer ⁴⁵Ca²⁺ (see also Section V.A.2). Nicholson & Rice (261) attributed the very slow diffusion seen by Morris and Krnjević (234) to ‘warm up’ of the Ca²⁺ iontophoretic microelectrode because it is known that this ion is difficult to iontophorese from a micropipette and the original study used a holding (reverse polarity) current that would compound the problem by reducing the Ca²⁺ content in the tip the iontophoresis micropipette between ion ejections (see also Ref. 88). There remains some uncertainty about D* for calcium in different brain regions and further work is warranted for this physiologically important ion.

6. Dopamine and other electroactive substances

These measurements usually employ a carbon-fiber microelectrode (CFM) that detects dopamine (DA) by measuring the oxidation or reduction of this electroactive molecule using voltammetry or amperometry (262, 318). The most recent measurements were made in the guinea pig substantia nigra pars reticulata (SNr) and pars compacta (SNc) and the ventral tegmental area (VTA) by Cragg et al. (71) (Table 2). This study used RTP and detected DA with carbon fiber microelectrodes and fast-scan cyclic voltammetry based on previously established diffusion paradigms (316). Values of λ measured with DA ranged from 1.68 – 1.80 and were slightly higher than those measured with TMA in the same regions (see Section IV.A.4). In this set of experiments, 3 kDa fluorescent dextran was included with the DA to enable the ejected volume to be controlled and the actual volume was estimated from the voltammetric data using the value of λ obtained from the TMA⁺ measurements in each region (see (71) for details of the method); the ejected volume was maintained in the range 25-50 pL.

Cragg et al. (71) also showed that, in the midbrain, simple clearance kinetics proportional to extracellular DA concentration were adequate to describe the data (i.e. the results were described by Equation 17) but the value of k′ was 0.085 s⁻¹ in SNc and 0.093 s⁻¹ in VTA, in marked contrast to the value of 0.006 s⁻¹ in SNr. The latter value was comparable to the typical non-specific loss measured for TMA⁺ (see Section IV.A). This clearance behavior differs from that in the rat striatum where pressure-injected DA is rapidly removed (400) and Michaelis-Menten kinetics dominate (251).

Early studies of the diffusion of electroactive compounds with point-source paradigms gave more ambiguous results. Dayton et al. (82) pressure ejected ascorbic acid (AA), dihydroxyphenylacetic acid (DOPAC) and α-methyldopamine (α-MeDA) in the rat cortex. The resulting signals were analyzed by chronoamperometry but the investigators relied on the time of the peak of the diffusion curve to estimate D*. For these three substances, the reported values of D* would lead to an estimate of λ ~ 1.8. Rice et al. (313) used a more extensive range of electroactive molecules applying similar methodology in the rat striatum; when diffusion of DA or α-MeDA was to be measured, the investigators blocked cellular uptake pharmacologically. Rice et al. (313) found that they obtained results similar to those of Dayton et al. (82) for anionic electroactive compounds, including AA and DOPAC, but D* was about three times less for cationic compounds, including DA and α-MeDA. The investigators hypothesized that the slow diffusion of the positively charged compounds was caused by interaction with the negatively charged extracellular matrix but this interpretation remains controversial and other factors, such as incomplete pharmacological blockage of substance uptake may have affected the results. Another interesting result of this study was that diffusion measurements with ferrocyanide, $\mathrm{Fe}{\left(\mathrm{CN}\right)}_6^{4\text{-}}$, a small anion with four negative charges, yielded λ = 1.61, suggesting that, at least for anions, charge density has little effect on the diffusion properties in the ECS.

The electroactive substance 5-hydroxytryptamine (5-HT, serotonin) can also be measured with carbon fiber microelectrodes, although a brief study (315) of this neuroactive substance used ISMs and RTI to determine α = 0.17 and λ = 1.65 in the isolated turtle cerebellum. Another study (418) used enzyme-modified carbon fiber microelectrodes and RTP to measure choline diffusion in the rat caudate (striatum) and hypothalamus, obtaining λ ~ 1.8; however, this slice study suffered from technical limitations (see 150). Finally, we note that Meulemans (227, 228) used voltammetric methods to attempt to measure concentration profiles for an antibiotic and for nitric oxide (NO) in rat brain tissue and estimate effective diffusion coefficients. Quantitative measurements of NO are difficult but Zacharia and Deen (424) have established values for D in water and saline solutions.

7. Epileptogenic agents

The final group of substances detailed in Table 2 are agents that either cause seizure activity (penicillin and pentylenetrazol) or suppress it (valproate and verapamil) when introduced into the cortex. Penicillin and pentylenetrazol are important in generating seizure models for drug tests and other purposes and diffusion studies were undertaken to determine the critical mass of agent required to generate a seizure. The actual method of determining the mass relied on co-ejecting TMA with the agent and is detailed in Lehmenkühler et al. (192) and Schwindt et al. (336) but the analysis necessitated diffusion data for the agents themselves. The diffusion measurements were made in rat cortex and made use of the property that some conventional ISMs can also measure these agents, although the ISM behavior is far from ideal. The values of λ obtained by RTP and ISMs for penicillin, pentylenetrazol and verapamil ranged from 1.51 – 1.67 but valproate gave a higher value of λ.

8. Conclusions

It is reassuring that measurements of a variety of small ions and molecules other than TMA, using RTI and RTP methods combined with ISMs or carbon fiber microelectrodes, yield values of λ that are quite similar to those obtained with TMA (detailed later in this review). These measurements with other substances are not as comprehensive as the TMA measurements and the substances often were not ideal probes. These studies suggest at least two lines of further inquiry: first, the need for further comparison of cation and anion diffusion, especially multivalent ions and, second, a requirement for more extensive investigation of the diffusion of dopamine, and possibly serotonin, in different brain regions with different uptake mechanisms and capacities.

C. Integrative optical imaging

A limitation of the RTI method is that it can only be used with a restricted set of small ions and among these the vast majority of measurements have been made with TMA⁺. While the small size of such probes is advantageous for exploring the geometrical structure of the ECS, and possibly the local charge density, the use of much larger molecules opens the way to new classes of investigation. Proteins and various macromolecules form part of the traffic within the ECS and are increasingly candidates for new drug vectors, so their diffusion behavior is important. Beyond that, a sequence of molecules of increasing size can probe the actual dimensions of the interstitial spaces. To provide a tool to study the diffusion of large molecules in brain, the method of integrative optical imaging (IOI) was introduced by Nicholson and Tao (265).

1. Integrative optical imaging technique

The method is conceptually simple but became feasible only with the ready availability of a combination of technical advances: high resolution CCD (charge-coupled device) cameras with a stable linear response to intensity, epifluorescence microscopes using dichroic mirrors, long working distance water-immersion microscope objectives in a variety of magnifications and an ever increasing selection of macromolecules labeled with fluorophores. In the IOI method, macromolecules carrying a fluorescent label are released from a micropipette by a pressure pulse, as in the RTP method. If the pulse is very brief compared to the duration of the subsequent diffusion processes, then the concentration is described by Equation 19, a slightly modified version of Equation 17 (254, 265, 300). Usually it is assumed that the macromolecules stay in the ECS for the duration of the measurements so k′ = 0 in Equation 17. Then the spatial distributions of the concentration, C, of the diffusing molecules at a discrete sequence of times t_i are described by:

$$C(r,t_i)=\frac{U{C}_{\mathrm{f}}}{\alpha }\frac{1}{{\left(4D^{\ast }(t_i+t_0)\pi \right)}^{\frac{3}{2}}}\text{exp}\left(-\frac{r^2}{4D^{\ast }(t_i+t_0)}\right),$$ (19)

where a volume U, typically < 1 nL, of the macromolecular solution at concentration C_f is ejected. The variable t₀ represents a virtual time-origin for the source such that the source appears to have been activated at time t₀ before it actually occurred. This allows a point-source formalism to be employed even when a finite initial volume is released (300). If the tissue is locally anisotropic then Equation 18 can be used instead of Equation 17 as a basis for Equation 19.

To make use of this formalism it is necessary to relate Equation 19 to the actual recorded images. In practice, the theory of how the image of the diffusing cloud of molecules maps onto the plane of the CCD is complex (265, 378) but it may be shown that Equation 19 can be reduced to Equation 20 by considering the effect of the microscope optics:

$$I_i(r,{\gamma }_i)=E_i\left({\gamma }_i\right)e^{-{\left(\frac{r}{{\gamma }_i}\right)}^2}\text{and}{\gamma }_i^2=4D^{\ast }(t_i+t_0)$$ (20)

where I_i is the intensity of the fluorescence at discrete time t_i, E_i is an amplitude term embodying the defocussed point-spread function of the objective (but it does not depend on r; see Ref. 375 for details). By fitting the exponential term in Equation 20 to the spatial distribution at a sequence of times t_i, D* can be determined (265, 300). Control diffusion measurements to determine D are made in dilute agarose.

The experimental setup is illustrated in Fig. 5A and is detailed in Nicholson and Tao (265) and in Hrabětová and Nicholson (150). It consists of a fixed-stage upright compound microscope equipped for epi-fluorescence imaging. Typically, a 10× water-immersion objective, a halogen or xenon epi-illuminator and a dichroic mirror system appropriate to the fluorophore are used. The image is recorded by a CCD camera. Image data are transferred directly to a PC and analyzed with custom software (Vida and Ida, described in more detail in Ref. 150). Until recently, IOI was used exclusively with brain slices but now it is possible to apply it in vivo (Fig. 6A, B).

Fig. 6.

IOI measurements in vivo using 3 kDa dextran and quantum dots. A. Experimental setup for IOI diffusion measurements in vivo. Successive images of fluorescent probe diffusion were captured by a cooled charge-coupled device (CCD) camera and epifluorescent microscope with a 10× water-immersion objective (cf. Fig. 5A) after pressure ejection from a micropipette into either dilute agarose or somatosensory cortex, accessed through an open cranial window in rat (scale bar – 500 μm). B. Dextran diffusion in neocortex. Representative images after fluorescent dex3 ejection into agarose or cortex. Fluorescence intensity profiles and theoretical fits for the images shown below images, yielding D = 2.3 × 10⁻⁶ cm² s⁻¹ and D* = 4.5 × 10⁻⁷ cm² s⁻¹. Scale bars – 200 μm. C. Schematic of quantum dot (QD655, Invitrogen). Inner core cadmium and selenium provides characteristic fluorescence. The core is stabilized with a zinc shell which in turn has an organic coating to which are attached numerous PEG molecules to render the quantum dot water soluble. The final diameter of QD655 is 35 nm. D. Quantum dot diffusion in neocortex. Representative images after QD655 ejection into agarose or cortex. Scale bars – 100 μm. Fluorescence intensity profiles and theoretical fits shown below the images, yielding D = 1.9 × 10⁻⁷ cm²s⁻¹ and D* = 1.6 × 10⁻⁹ cm²s⁻¹. Linear regression of cortex data in inset (see Equation 20); ${\gamma }_i^2=4D^{\ast }(t_i+t_0)$, so regression of ${\gamma }_i^2∕4$ upon t_i returns a slope of D*. (Panels A, B and D modified from Ref. 391).

Among the most useful fluorescent macromolecular probes are labeled dextran molecules in a range of relative molecular masses, M_r =3000 – 70,000, and above (Fig. 5B). While dextrans are easy to work with they have the disadvantage that they are polydisperse (contain a range of molecular sizes) and the shape is not well defined. Proteins alleviate both these problems and various fluorescent albumins are available, including bovine serum albumin (M_r = 66,000; Fig. 5C) but proteins can show a tendency to aggregate that must be carefully controlled for. Polyethylene glycol (PEG) coated quantum dots, which are synthetic nanocrystals of precise size and shape with highly stable fluorescent characteristics, have shown some promise as probes of the ECS (391) (Fig. 6C, D).

The advantages of the IOI method are that it permits the study of the diffusion of many different varieties of molecules. In practice, the size of typical fluorescent labels puts a lower limit on the size of the macromolecule to which it may be attached and the dimensions of the ECS impose an upper limit. Disadvantages include the fact that macromolecules are inherently more difficult to characterize and handle than small dissociated ions and many are biologically active and may be captured by receptors. This can be turned to advantage because the biological activity itself may be studied through deviations from ideal diffusion behavior. The IOI method is usually limited to the most superficial 200 μm or so of grey-matter in brain or brain-slice where an epifluorescent image can be obtained without appreciable light-scattering; substantial myelinated white matter tracts generally produce too much light scattering. The method assumes that the spreading cloud of diffusing molecules approximates a sphere (or ellipsoid in the case of an anisotropic brain region) and integrates the light from a projection of this volume onto a plane so the method cannot measure the volume fraction of the brain in which the molecules are dispersing. These limitations might be removed by confocal or multiphoton (two-photon) microscopy and preliminary studies have been made with the latter technique (325, 331, 347, 348).

Macromolecules may be characterized by their approximate shape, molecular mass, usually expressed in kilo Daltons (kDa) and, for approximately spherical molecules, equivalent hydrodynamic diameter d_H (nm), derived from the free diffusion coefficient, D using Equation 6. These parameters hardly do justice to the complexity of macromolecular structure but serve as a rough guide to some of the distinctions between molecules that play a role in diffusion in brain tissue.

All the data described in Table 3 have been obtained with the IOI method described above, except for the data on FITC-labeled 70 kDa dextran and β-NGF (348) which employed a point-source paradigm with multiphoton imaging. A few studies have attempted to use FRAP and these will be discussed in Section III.D, but the method appears so far to have given inconsistent results in brain tissue. It is convenient to divide the studies into two broad classes based on molecular shape: globular and flexible chain. Nanoparticles will be treated separately.

Table 3.

Macromolecules with fluorescent labels: Diffusion measured with IOI method

Molecule	Label	Mr	dH	D × 107	Species	Region	Prep.	°C	λ	Refs.
		× 103	nm	cm2s−1
Globular
AF-488	AF	0.547	1.1	44	turtle	cereb. ml	isolated	25	(1.44, 1.75)b	417
dex3	TMR/TR	3	2.7-3.2	19-23	rat	cortex	slice	34	1.74-1.81	crefs
dex3	TR	3	3.0	22	rat	cortex	in vivo	37	2.04,	391
dex3	TR	3	2.7	23	rat	hippo. CA1	slice	34	1.54,	145
dex3	TR	3	2.1	23	turtle	cereb. ml	isolated	25	(1.63, 2.05)b	417
dex10	TR	10	4.5	14	rat	cortex	slice	34	1.84	265, 379
dex40	TR	40	15	4.2	rat	cortex	slice	34	2.16	265
dex70	TR	70	16	3.8	rat	cortex	slice	34	2.25	265
dex70	TR	70	14	4.7	rat	cortex	in vivo	37	2.69	391
dex70	FITC	70	16	3.8	rat	striatum	slice	34	2.13	348
dex75	FITC	75	12	4.2	turtle	cereb. ml	isolated	25	(1.84, 2.45)b	417
dex282	FITC	282	21	2.3	turtle	cereb. ml	isolated	25	(2.21, 2.97)b	417
dex525	FITC	525	32	1.5	turtle	cereb. ml	isolated	25	(2.63, 3.49)b	417
Lactalbumin	TR	14.5	5.2	12	rat	cortex	slice	34	2.24	379
Ovalbumin	TR	45	6.1	10	rat	cortex	slice	34	2.50	379
BSA	TR	66	7.4	8.3	rat	cortex	slice	34	2.26	379
Lactoferrin	OG514	80	9.3	7.1	rat	cortex	in vivo	37	3.50	390
Transferrin	TR	80	8.8	7.5	rat	cortex	in vivo	37	2.29	390
EGF	OG514	6.6	3.7	17	rat	cortex	slice	34	1.79	388
β-NGFa	TMR	26.5	4.9	13	rat	striatum	slice	34	2.14	348
Flexible Chain
PHPMA	FITC	7.8		9.8	rat	cortex	slice	34	1.51	300
PHPMA	FITC	28		6.3	rat	cortex	slice	34	1.67	300
PHPMA	FITC/TR	47		4.7	rat	cortex	slice	34	1.55	300
PHPMA	FITC	220		2.0	rat	cortex	slice	34	1.65	300
PHPMA	FITC	515		1.2	rat	cortex	slice	34	1.58	300
PHPMA	FITC	1057		0.72	rat	cortex	slice	34	1.46	300
PHPMA-BSA	FITC	176		2.3	rat	cortex	slice	34	2.27	300
PEG	FITC	2		20	rat	cortex	slice	34	1.59	389
PEG	FITC	2		20	rat	striatum	slice	34	1.50	389
Nanoparticles
QD655	QD655	n/a	35	1.9	rat	cortex	in vivo	37	10.6	391

Footnotes

^amultiphoton techniques used in this study (see text)

^banisotropy measured in plane parallel to surface, (λ_x, λ_y)

^crefs = 145, 183, 265, 379, 375, 388

AF = AlexaFluor

FITC = Fluorescein isothiocyanate

TMR = Tetramethylrhodamine

OG515 = Oregon Green 515

TR = Texas Red

QD655 = Quantum Dot 655

hippo. CA1= hippocampus CA1 region. For other abbreviations see previous Tables.

2. Globular macromolecules - dextrans

The globular macromolecules investigated to date can be subdivided further into two classes, dextrans and proteins. Dextrans are flexible, branched polysaccharide random coil structures, formed from chains of glucose molecules, that are very soluble in water and carry no charge other than that on the fluorescent dye used to label them. They tend to form loose spheres (276) and they have been used extensively in diffusion studies in contexts other than the ECS. The only drawbacks to the use of dextrans are that the exact shape is ill-defined and they are polydisperse to varying degrees; the distribution of molecular weights in a given fraction depends on the fractionation procedure so results are not uniform.

Looking at Table 3 it is apparent that the smallest dextran, with a molecular weight of 3 kDa (dex3), has been the most popular; this was one of the four dextrans employed in the original IOI study by Nicholson and Tao (265) in rat cortical slices. That study obtained a value of λ = 1.70 but with further measurements this was refined to λ = 1.77 (379). This latter value was close to that found in later slice studies so the newer λ-value is given in Table 3 for both D and D*. In contrast to previous slice results, Hrabětová et al. (147) found λ = 2.09 for dex3 in rat neocortical slices. Because it is not clear why these results are so much higher than the earlier data (variation in dex3 sample M_r is a possible explanation) they are not included in Table 3. A careful study of dex3 diffusion in vivo in rat cortex (391) also revealed a somewhat higher value of λ compared to the typical slice results. It is clear that all the λ-values with dex3 both in vitro and in vivo are significantly higher than those with TMA for the same brain region under the same conditions (see Section IV for TMA data). This trend for larger values of λ with dex3 compared to TMA is seen also in the CA1 region of the hippocampus slice (145), although, the λ-values for each probe are lower than those seen in cortex. Tao (375) measured the diffusion of dex3 in neocortical slices under osmotic stress and these data were further analyzed by Kume-Kick et al. (183) (see Section IV.D.3). Hrabětová et al. (147) measured the diffusion of dex3 in a thick-slice ischemia model (see Section V.A.2).

The 10 kDa dextran (dex10) was studied by Nicholson & Tao (265) in cortical slices and a λ-value of 1.63 obtained but again this value was refined in later work (379) to λ = 1.84 and this is the value presented in Table 3. Nicholson & Tao (265) also measured the diffusion of 40 kDa dextran (dex40) and obtained a value of λ = 2.16.

The progressive increases in λ with dextran size continued to be seen with 70 kDa dextran (dex70). Here another comparison is possible between diffusion in cortical slices where λ = 2.25 (265) and the in vivo cortex, where λ = 2.69 (391; Figs. 5 B, 6B) and again the value is higher in vivo. A study in the striatal slice, using a similar point-source paradigm but utilizing multiphoton microscopy (248) arrived at λ = 2.13 with dex70. The signal-to-noise ratio was low in the Stroh et al. (248) study leading to a large standard deviation so this result is not incompatible with values reported for the cortical slice.

The IOI method has been extended to encompass regions of anisotropic grey matter (417). Following an earlier study with the RTI-TMA method (314) (Section IV.A.5), the IOI method was used to make measurements in the ECS of the anisotropic molecular layer of the isolated turtle cerebellum using the small fluorophore Alexa Fluor 488 (AF, 0.547 kDa) and fluorophore-labeled dextrans, with molecular mass of 3, 75, 282 and 525 kDa (417) (Table 3). With all these molecules, the 2D IOI images became elliptical with major and minor axes oriented along and across, respectively, the unmyelinated parallel fibers. The effective diffusion coefficients, D*_major and D*_major, decreased with molecular size. The diffusion anisotropy ratio, defined as DAR = D*_major/D*_major, increased for AF through dex75 but then unexpectedly reached a plateau for the larger dex282 and dex525. The authors hypothesized that diffusion behavior of dex282 and dex525 was consistent with the polymers deforming as the molecular size approached the width of the ECS.

For many types of macromolecules, a power-law correlation can be constructed between the free diffusion coefficient and M_r. In a pioneering study of dextran molecules, Granath and Kvist (Table 1 in Ref. 116,) provide a relation between D at 20 °C and M_r for a range of dextrans. This can be translated to a more physiological temperature and described by the relation (265, 270):

$$D=1.11\times {10}^{-4}{M}_r^{-0.48}$$ (21)

where D is measured in cm² s⁻¹ at 34°C. Thus D is approximately proportional to $M_r^{-0.5}$ which is more characteristic of molecules comparable in size to those of the solvent (81, 321) than macromolecules where it is usually expected that $D\propto M_r^{-1∕3}$ (295, 321).

3. Globular macromolecules - proteins

Turning now to proteins; the advantage of these molecules is that they are often compact with a well-defined molecular weight, suggesting they would be useful probes of the ECS. In practice they are more prone to aggregation than are dextrans, frequently carry multiple charges and may bind to specific receptors. Diffusion studies in ECS have employed several proteins: albumins, lactoferrin and transferrin and growth factors.

Three common albumins were explored by Tao and Nicholson (379) using the IOI method in rat cortex: Lactalbumin (14.5 kDa), derived from milk, egg albumin, ovalbumin (45 kDa) and bovine serum albumin (BSA, 66 kDa; Fig. 5C). The lactalbumin, ovalbumin and BSA native proteins carry negative charges of −8, −17 and −33 respectively (158), to which must be added the charge on the fluorescent label. None of these molecules are actually spherical but were long considered to be ellipsoids; they are now thought to have more complex shapes, despite this, the hydrodynamic diameters (d_H, derived from D using Equation 6) are still a useful, if rough, gauge of size. After the usual temperature correction, the values of D given Table 3 are consistent with other determinations, (see Refs. 158, 159, 328 for compilations of other studies). Comparing the d_H values for BSA with dex70 and ovalbumin with dex40 it is apparent that the larger albumins are half the size of dextrans of similar molecular weight. Despite this size difference, the λ-values of all the albumins, including the relatively small lactalbumin, are close to the λ-value obtained with the largest dextran. This paradox might be resolved by noting that albumins are rigid structures while dextrans are pliable, loosely organized molecules; in discussing flexible chain macromolecules below it will become apparent that flexibility may be a factor in reducing tortuosity.

As noted in Section II.B and will be discussed later in Section VI.E, there are few quantitative data on the extracellular matrix. A study employing lactoferrin, an iron-binding protein, provided the first in vivo demonstration of macromolecule sequestration by an ECM component using IOI (390). Diffusion measurements in rat somatosensory cortex revealed that D* for lactoferrin was reduced much more than the value for transferrin, a very similar molecule (390, Table 3). The apparently elevated tortuosity of lactoferrin in brain was attributed to binding by heparan sulfate proteoglycan (HSPG), a prominent component of the extracellular matrix and cell surfaces in brain. This was confirmed by co-infusing heparin with lactoferrin; the heparin bound to the lactoferrin, resulting in a larger molecular complex but the measured tortuosity fell because the lactoferrin was no longer impeded by transient attachment to HSPG in the tissue. Further analysis provided an estimate of the concentration of HSPG binding sites in the ECS of the somatosensory cortex. This work also indicated why heparin co-infusion might benefit drug delivery strategies for some growth factors and other vectors for drug delivery (122).

Neurotrophic factors are diffusible proteins, mostly 5 – 30 kDa in size, that are capable of regulating development, growth and survival of brain cells (204, 387). Reliable diffusion data for brain tissue are presently available for epidermal growth factor (EGF) and nerve growth factor (NGF) along with some preliminary data for brain-derived neurotrophic factor (BDNF).

Epidermal growth factor is about 6 kDa in molecular mass and negatively charged at physiological pH. Functionally, EGF is capable of stimulating neuron proliferation, outgrowth and survival (420). There are receptors for EGF on neurons in layers IV and V of the rat cortex (114); the diffusion studies of Thorne et al. (388) therefore took care to eject an excess of unlabeled molecule, along with the fluorescent EGF, to saturate any binding sites. The value of λ = 1.79 measured in rat cortical slice (388) (Table 3) was less than that seen for any of the albumins but consistent with the small size of EGF.

Nerve growth factor is composed of three subunits with a total molecular weight of 130 kDa (385). The β-subunit (26.5 kDa) is responsible for the bioactivity of NGF and, among its many functions, it may be potentially therapeutic for Alzheimer's disease (106). The diffusion of the rhodamine-labeled β-subunit of NGF was investigated in slices from rat striatum using multiphoton microscopy by Stroh et al. (348) (Table 3) who found λ = 2.14, similar to the value these same investigators obtained with dex70 (Table 3), although the standard deviation was high for both determinations. These results may be compared with data obtained using radiolabeled NGF (174).

Brain-derived neurotrophic factor (BDNF) (27 kDa), is another neurotrophin very similar to the β-subunit of NGF in size, shape and charge. Stroh et al. (347) again used point-source ejection and multiphoton microscopy to try to analyze the diffusion of rhodamine-labeled BDNF and concluded that it diffused poorly in the rat striatum but the attachment of polyethylene glycol (PEG) to the protein enhanced its diffusion. Unfortunately, these results are questionable because of technical issues (see Refs. 346, 389 for further discussion).

Values of D reported in Table 3 together with additional values from the literature indicate that the following correlation is valid for the free diffusion coefficient of globular proteins (388)

$$D=2.28\times {10}^{-5}{M}_r^{-1∕3}$$ (22)

where D is measured in cm²s⁻¹ at 20 °C. This, or some of the other similar correlations reviewed by Thorne et al. (388), may be useful in predicting D for protein molecules.

4. Flexible chain macromolecules

These macromolecules consist of a chain of repeating groups, with limited or absent side chains, which do not coil into spherical shapes. The diffusion properties of such flexible molecules in a restricted environment may differ from globular molecules of similar molecular weight (294).

The only major study (300) of flexible chain macromolecules in brain tissue employed polymers of PHPMA (poly[N-(2-hydoxypropyl)methacrylamide]). These synthetic, water-soluble, linear macromolecules are formed from repeating subunits with an occasional spacer where a variety of compounds might be attached. An intended therapeutic use of PHPMA is to attach drugs to the spacers so as to deliver them to cells (395) but Prokopová-Kubinová et al. (300) attached fluorescent molecules and explored the diffusion of the PHPMAs in the rat cortical slice. Fluorescent PHPMAs ranging from M_r = 7.8 × 10³ to M_r = 1057 × 10³ were used, along with a branched or bulky fluorescent polymer structure with BSA at the center and several chains of PHPMA attached.

The free diffusion coefficients for the range of linear PHPMAs investigated by Prokopová-Kubinová et al. (300) were commensurate with their molecular weights (Table 3) and could be represented by the correlation

$$D=14.6\times {10}^{-5}{M}_r^{-0.54}$$ (23)

where D is measured in cm²s⁻¹ at 34°C. Thus D is approximately proportional to $M_r^{-0.5}$, a relation that has been derived from the Zimm model for polymer diffusion under some conditions (page 80 in Ref. 89 and Ref. 294). Equation 23 also exhibits a similar type of power law exponent as seen in Equation 21 for dextrans, which are also deformable macromolecules.

In rat cerebral cortex, the behavior of the PHPMA polymers differed markedly from that seen for large globular macromolecules because the tortuosity remained approximately constant in the range 1.46 – 1.67, regardless of molecular weight (300) (Table 3) and surprisingly similar to the values obtained with TMA. This anomaly was further highlighted when the diffusion of BSA-conjugated PHPMA was measured and its λ-value was almost identical to that obtained with BSA alone and significantly larger than that obtained with any of the flexible-chain PHPMAs alone, including ones more than five times greater in molecular weight. At this time no explanation can be provided for the small value of λ for the PHPMA molecules except to note the flexibility of the molecules. If the results can be replicated with other flexible polymers, they may imply unusual structural properties in the ECS.

The only other data on linear molecule diffusion in brain comes from a preliminary study with the IOI method by Thorne et al. (389) of 2 kDa fluorescent PEG that yielded tortuosities of 1.5-1.6 in rat cortical and striatal slices (Table 3) and a determination of ¹⁴C-PEG (3.3 kDa) diffusion using a multi-compartment kinetic model in incubated slices (289) that produced λ = 1.88. The Patlak et al. experiments (289) are considered also in Section V.A.2.

5. Nanoparticles

The advent of quantum dot (QD) synthetic nanocrystals presents new opportunities to probe the ECS. Quantum dots consist of a core that is tuned to fluoresce at a wavelength determined by the semiconductor composition and core size. The core is enclosed in a protective shell that, in turn, is coated with molecules that give the QD biocompatibility or added functionality. To render these nanocrystals water soluble, the outer coating must be a substance such as PEG and this coating process considerably increases the overall size. In the first study to employ QDs to explore the ECS, Thorne & Nicholson (391) (Fig. 6 C, D) used Invitrogen Qtracker® 655 (QD655), a pegylated QD with overall d_H = 35 nm, to make diffusion measurements in rat cortex in vivo. It had long been thought that the width of the ECS was about 20 nm (see Section II.A) so it was a surprise that QD655 actually diffused in the ECS, albeit with a very high tortuosity represented by λ = 10.6. The greatly hindered diffusion of QD655 suggested that the diameter of the nanoparticle was close to the actual width of the ECS and that very local interaction with the ECS boundaries was the main determinant of the diffusion behavior of such large particles. This led Thorne and Nicholson (391) to apply theories of restricted diffusion in fluid-filled pores to estimate the actual ECS width as 38-64 nm (see also Section II.H).

6. Conclusions

The capability to measure the diffusion of macromolecules in ‘real time’ in small brain regions has considerably extended our knowledge of the ECS revealing hitherto unsuspected properties but also raising new questions. We note that most of the work with the IOI technique has been carried out in brain slices but two recent studies (390, 391) extended this work to the in vivo rat brain and allowed a direct comparison with the slice data. This confirms that the values of λ obtained with IOI in vivo are slightly larger than those in slices for dex3 and dex70 but both in vitro and in vivo preparations show a significant increase in λ over the value obtained with TMA and also confirm that λ measured with dex70 is larger than that found with dex3.

All the globular molecules show an increasing tortuosity with molecular size and the effect may be more pronounced with the rigid proteins compared to the more amorphous and flexible dextrans. This raises the question of what is the largest molecule that can diffuse through the ECS and a preliminary answer has been obtained with a QD nanocrystal as a surrogate macromolecule. QDs have well-defined sizes and geometries and a QD with a hydrodynamic diameter of 35 nm is able to slowly diffuse in the ECS. This suggests that drug molecules or vectors up to this size should be able to migrate through the brain but the spread may be limited by other factors; it may be better to conclude that substances larger than this are unlikely to move effectively.

When the substance takes the form of a long, flexible, linear structure, the constraints to movement in the brain apparently are quite different. The synthetic polymer PHPMA with molecular mass up to 1000 kDa can diffuse with a similar hindrance to TMA, although the effective diffusion coefficient of the macromolecule is small. At this time there is no ready explanation for these results but, taken together with the ability of QD655 to move in spaces that were formerly regarded as too narrow to allow such movement, these findings hint that the structural constraints of the ECS may differ from a classical porous medium or even a dense polymer network. A similar paradox has arisen in studies of the diffusion characteristics of cytoplasm using fluorescent dextrans as probes. Luby-Phelps et al. (205) found that dextrans as large as 28 nm in diameter were able to move through the dense intracellular matrix. Those authors considered that the flexible random coils of the dextran molecule might migrate by reptation (83) through pores that would not admit more rigid molecules. A related argument was invoked in the study of large dextrans in the cerebellar ECS (417) (see above). Luby-Phelps et al. (83) also entertained the novel possibility that the size and position of pores in the cytoplasm could fluctuate on a sufficiently rapid timescale to allow passage of molecules considerably greater in diameter than the average mesh size of the cytoplasm. A similar idea of fluctuating polymeric structures had been mooted earlier by Ogsten (274). The ceaseless ionic and water fluxes across glial, and possibly, neuronal membranes in the CNS conceivably might lead to similar fluctuations.

D. Other methods

1. Magnetic resonance (MR)

Magnetic resonance spectroscopy is widely used in analytical chemistry to identify compounds and MR techniques can be extended to measure diffusion coefficients in solution and in tissues (344). Magnetic resonance imaging (MRI) is derived from basic MR concepts to provide a non-invasive technique in wide clinical use to visualize internal structures in body and brain based on the MR signature of water. Magnetic resonance imaging can also be ‘diffusion weighted’ (DW-MRI) to measure the apparent diffusion coefficient of water (ADC_W) and some other molecules in vivo (187). The use of the specific nomenclature ‘apparent diffusion coefficient’ in both imaging and non-imaging contexts indicates that the value of this parameter may be influenced by the method of measurement (188, 267).

To measure an ADC, a pulsed magnetic field gradient is used to determine the mean-square displacement, 〈r²〉, of an ensemble of a selected molecular species over a diffusion time Δ (180). Then, by analogy with Equation 8, in a free medium of dimension d,

$$\langle r^2\rangle =2d\times ADC\times \Delta .$$ (24)

The theoretical and experimental basis of the measurement is complex and will not be described in much detail here. In essence the technique relies on applying the magnetic field gradients as a pair of pulses separated by an interval Δ so that the first pulse encodes the positions of the probe molecules into the phase of the nuclear spin magnetization and the second, later, pulse reverses the effect of the first to re-phase the magnetization. When molecules are diffusing, the re-phasing is imperfect and this phenomenon enables the average molecular displacement during the interval Δ to be measured. In a free medium, MR used in this way leads to good estimates of the diffusion coefficient, however in the complex medium of the brain it is difficult to relate the ADC to the local structure, although there have been several attempts (e.g. Refs. 185, 372). One source of this difficulty is that the interval Δ is very short compared to the typical observation times used in the RTI method (179) so that, under the MRI paradigm, the diffusing molecules are only able to explore a very small region of the tissue, often only a few micrometers in extent, and consequently smaller than the overall dimensions of a typical nerve cell. For this reason the ADC measured with MR shows a dependence on Δ that in turn is related to the available field strength of the magnet in use (267).

Another important issue that enters into MR measurements of diffusion is that of finding a suitable probe molecule. By far the most abundant molecule in tissue is water, which, at a concentration of about 80M (113), greatly exceeds any other substance. All routine MRI measurements image water distribution in the brain, although the images may be enhanced with contrast agents. Water, however, is found in both the intracellular and extracellular spaces and can move between them so any MR measurement based on water is some type of weighted averaged of two compartments and it is a matter of continuing debate about how to interpret such data (113, 267, 302). Regardless of the eventual interpretation of the MR-derived ADC_W, it is well established that the value decreases immediately in brain regions undergoing ischemia (236) and this observation has motivated much of the clinical use of DW-MRI. The consensus hypothesis (267) about the cause of the fall in ADC_W in ischemia is that it is attributable to a combination of a shift in water from extra- to intracellular compartments (i.e. cellular swelling) and an increase in extracellular tortuosity (which may be over and above that resulting from a reduction in the volume fraction of the ECS). Both these phenomena have been well established by conventional diffusion measurements based on radiotracers or the RTI-TMA method (See Section V.A). Some MR results do not fit the consensus hypothesis (267) and recent work (e.g. Ref. 113) suggests that it may be necessary to assume that the ADC_W associated with the intracellular compartment is lower than previously thought and decreases further during ischemia.

Attempts have been made to introduce probe compounds into the brain that were expected to remain extracellular and use MR to probe the ECS by measuring the ADC of the probes. These compounds included phenylphosphonate (PPA, M_r = 158), mannitol (M_r = 182) and polyethylene glycols (PEGs) ranging in M_r from 200 to 4600 (90). After infusion into the lateral ventricles of rats for about 1 hr, to allow diffusion into surrounding brain tissue, the smaller molecules (PPA, mannitol, PEG-200 and PEG-1000) all appeared to diffuse in the ECS with λ-values between 1.75 and 1.83, which are only slightly more than values obtained with radiotracer, RTI-TMA and IOI methods for molecules of roughly similar size. Curiously, PEG-2000 and PEG-4600 both diffused with lower tortuosities of 1.26 and 1.34 respectively, which remains unexplained. Actually, higher tortuosities were measured in the experiments (90) but the authors believed that significant amounts of the probe molecules had both entered intracellular compartments and bound to membranes and consequently they corrected the final λ-values for this. The correction of λ was based on separate assay experiments using tissue culture and also involved additional assumptions. Thus, these results are promising but must be interpreted with caution until further work has been carried out with similar paradigms.

In the context of this review, Kroenke et al. (179) made an important investigation when they used MR methods to study the ADC of TMA⁺ (ADC_TMA) in the rat brain. They first established theoretically that the MR and RTI methods were, in principle, measuring the same parameter. However, the ADC_TMA was typically 3.6 fold lower than that measured with the RTI method. To account for this discrepancy, it was hypothesized that different subpopulations of TMA⁺ molecules diffused different distances during the MR measurement. For those molecules that traveled a distance of 15 μm or more, the ADC_TMA approached that obtained with the RTI method, where the measurement distance is typically ≥ 100 μm while for displacements shorter that 15 μm the ADC_TMA was smaller. As noted by Kroenke et al. (179), the short diffusion paths may represent an intracellular fraction of the TMA⁺ population because the investigators exposed the brain to the ion for two hours prior to measurements and this almost certainly allowed TMA⁺ to enter cells and that intracellular fraction would be measured by the MR procedure. This interpretation was strengthened by recent experiments measuring the entry over time of TMA⁺ into the cells of rat cortical slices (164). In contrast, the RTI method only measures diffusion of the TMA⁺ that resides in the ECS and, through application of the kinetic constant k′, is able to factor out any TMA⁺ that is lost from this compartment. Unfortunately, an attempt by Kaur et al. (164) to use ${\mathrm{SbF}}_6^{\text{-}}$, which is readily detected by both MR and ISMs, to repeat and extend the TMA paradigm, failed because ${\mathrm{SbF}}_6^{\text{-}}$ was not sufficiently chemically stable in solution.

Measurements with both the RTI-TMA⁺ method and conventional (i.e. water imaging) DW-MRI under similar, though not simultaneous, conditions have been made in several experiments (397, 408, 370, 371). These studies will be reviewed in later Sections (IV.D.3, IV.E.3, V.A.1, V.B.1, V.C.1, V.C.5).

Another important development in MR has been the introduction of diffusion tensor imaging (DTI) to resolve diffusion anisotropy of water molecules in single voxels (the basic volume element resolved by MRI) (28, 189, 233). Diffusion tensor imaging enables the major fiber tracts of the brain to be followed in 3D in both normal and pathological tissue in humans and even in small animals (e.g. Ref. 428). The method also has promise in guiding convection-enhanced delivery (CED) of drugs along fiber tracts in the CNS (330) because the diffusion tensor can be applied to other physical modalities such as hydraulic (330) and electrical conductivity (394). As with conventional MRI, the precise origin of the enhanced image contrast in white matter tracts is not fully understood although experiments (29) and modeling (338) are clarifying the issues. Comparison with the anisotropy data obtained from IOI (Section III.C.2) and RTI-TMA (Section IV.A.5) studies may be useful also.

In conclusion, most diffusion-oriented MR methods measure diffusion of water in the brain but this determination is dominated to an ill-defined extent by the intracellular compartment so the results are not directly relevant to this review. Some MR studies are beginning to use specific probe substances targeted at the ECS and these approaches may offer considerable promise in the future.

2 Light scattering and light transmission

It has long been known that changes in axon volume (131) or cell volume in nervous tissue (14, 198) lead to changes in optical properties. These changes may either be observed in the light scattered from the tissue or in changes in the amount of light transmitted through the tissue (173, 376). Various forms of stimulation or pathophysiology also produce optical changes, perhaps the most spectacular being the changes in the appearance of the retina during spreading depression that are visible to the naked eye (216, 217). Evoked optical changes arising in tissue are now known collectively as intrinsic optical signals (IOS). Because a swelling cell would be expected to reduce the volume of the ECS and because of the association of cell volume changes with optical signals, some investigators have suggested that the observation of this modality might lead to estimates of changes in α (135, 138). If proven this would be a useful adjunct to diffusion measurements. Unfortunately, while there is little doubt that IOS are correlated with physiological changes in many experiments, several groups (6, 377, 368) have shown that the changes in transmission or scattering can show both increases and decreases when it is known that the changes in α are occurring in one direction only. The major problem at this time is that the biophysical mechanisms responsible for the optical changes are poorly understood, although a number of candidates have been proposed (6, 13). It is likely that several mechanisms are in play and different ones dominate under different conditions. Thus optical measurements cannot be relied upon for quantitative measurements of changes in α.

3. Fluorescence Recovery after Photobleaching (FRAP)

Fluorescence recovery after photobleaching (FRAP) involves bathing a region of tissue with fluorescent molecules, bleaching the molecules in a small subregion using a powerful light source, typically a laser, and then quantifying the re-establishment of the concentration as unbleached molecules diffuse in from the periphery of the bleached subregion (21). This is an excellent method for measuring the free or effective diffusion coefficient and other transport properties, such as flow or binding, in a two dimensional region such as a cell membrane, where the bleached region is a well-defined circular spot. When applied in three dimensions the method suffers from two fundamental challenges. The first is that it is difficult to bleach a spherical volume because the bleaching beam must travel through the tissue. The second problem is that a measurement of the repopulation of the bleached volume with new molecules requires imaging through a layer of fluorescent molecules. Most of the early attempts to apply FRAP in tissues were made by Jain and collaborators (34, 35, 59, 153, 163, 293) in a variety of non-nervous tissues and tumors. These studies relied on thin preparations, surface measurements or computational methods to alleviate the problems mentioned above. The problems can in principle be removed by multiphoton techniques and Brown et al. (50) demonstrated that this was indeed possible for small 3D volumes ~ 1 μm in diameter, such as the cytoplasm of a cell. If this approach were extended to much larger volumes it might be an excellent way to measure the diffusion properties of the ECS.

Recently Verkman and associates applied a novel FRAP method to the superficial regions of the mouse cortex in vivo (39). They reported that λ ~ 1.7 for three FITC-labeled dextrans with molecular masses of 4 kDa, 70 kDa and 500 kDa. Both the low value of λ and apparent lack of correlation with molecular size are puzzling; the authors explained their conflict with published IOI data, where a larger λ has been reported for dextrans that increases with M_r (see Table 3), by suggesting that the IOI data was obtained in brain slices that had suffered damage or swelling. This explanation can now be dismissed in the light of measurements with the IOI method in vivo (390, 391) (Table 3). The surface-FRAP method was applied to mouse models of edema (282) to show that 70 kDa dextran diffused more readily in vasogenic edema than in controls while the situation was reversed in cytotoxic edema. The explanation proposed (282) was that vasogenic edema increased the fluid content of the ECS while cytotoxic edema caused cell swelling that reduced the ECS, however there was no actual measurement of ECS volume fraction.

The surface photobleaching method was modified to use an elliptical bleach area with the goal of measuring diffusion anisotropy and applied to the dorsal white matter tracts of the mouse spinal cord (283). It was estimated that the effective diffusion coefficient in the direction of the fiber tracts was reduced by a factor of 1.8 while the diffusion across the fibers was reduced by a factor of five. The investigators (283) claimed that diffusion along the fibers would only be impeded by the effect of the extracellular matrix and so directly measured the hindrance of this component. Measurements were also made in the isotropic cortex. Putting both sets of measurements together it was concluded that the extracellular matrix reduces the diffusion coefficient by 1.8 and the geometrical factors contributed a similar amount of hindrance. These are interesting results but major assumptions were invoked (e.g. that the spaces between fibers contain only matrix and the composition of the matrix in spinal cord fiber tracts is identical to that found in cortical grey matter).

Verkman and co-workers addressed the limitation that their FRAP method could only be applied at the brain surface by introducing a microfiberoptic epifluorescence FRAP technique (384) that used a single fiber a few micrometers in diameter to both bleach and measure recovery several hundred micrometers into brain tumors in mice. A range of fluorescent dextran molecules were introduced by microinjection. This method has similarities to the TMA method insofar as it introduces cylindrical microprobes into the brain and does not produce an image but only a measurement at a single location. This study indicated that diffusion of 10 kDa and 500 kDa dextrans was substantially slowed deep within solid brain tumors in mice. A further tumor study with the same dextrans showed that the local injection of enzymes to digest collagen or decorin increased diffusion of the dextrans (211). A third study with the fiber optic probe method used calcein (0.623 kDa), 70 kDa and 500 kDa dextran and showed that there was size-dependent slowing of diffusion in cortex and hippocampus that increased when the fiber optic was pushed deeper into the caudate nucleus and thalamus (425).

The FRAP techniques implemented by the Verkman laboratory may be potentially useful but many of the results obtained to date appear preliminary and sometimes contradictory. These implementations of the FRAP method were unable to directly measure diffusion coefficients (although other approaches do so); instead the implementation relied on an indirect calibration procedure, therefore there was no direct test of the validity of the results. Several of the papers (39, 282, 284, 425) also imply that changes in volume fraction of the ECS can be inferred from changes in the measured λ, however, with the definition of tortuosity employed, λ and α are independent parameters (183, 193, 257). To establish a relation between these parameters it is necessary to postulate a simplified and constrained model of the ECS (see Section II.H) and no such universal model exists for actual brain tissue.

4. Microdialysis

Although early studies using in vivo microdialysis did not acknowledge tissue diffusion properties, it is now recognized that the diffusion characteristics of the brain must be taken into account to realize a meaningful quantitative interpretation of microdialysis data. This is because the measuring microdialysis probe removes significant amounts of the substance under study, creating a concentration gradient in its vicinity leading to diffusion-limited access of molecules to the probe (7, 30, 54, 91, 235). This means that the recovery characteristics of the microdialysis probe measured in a free solution will not be directly applicable for estimating recovery in brain tissue.

A less recognized aspect of in vivo microdialysis is that, because it is capable of both introducing substances into the ECS and also removing material for quantitative analysis, it is potentially suitable for the measurement of diffusion properties of brain tissue. This potential for using microdialysis to determine diffusion characteristics has been explored in one set of studies. Using [³H]mannitol and two cylindrical microdialysis probes 4 mm in length, 0.24 mm in outer diameter separated by 1 mm, detailed experiments were carried out in agar gel and in the rat striatum (136). The finite cylindrical geometry of the probes, combined with the induced concentration gradient, led to significant theoretical issues in the interpretation of the experiments (60). The diffusion profile of [³H]mannitol approached quasi steady-state levels within one hour, at which time the delivery of tracer was counteracted by its loss from the ECS by passive uptake into cells and by clearance across the BBB. The measured effective diffusion coefficient was D* = 3.6 × 10⁻⁶ cm² s⁻¹, leading to λ = 1.44, with α = 0.36; the clearance rate constant was 2.2 × 10⁻⁵ s⁻¹. The values of λ and α differ somewhat from those obtained with the radiotracer method (Table 1) but both estimates are probably affected by the non-ideal behavior of mannitol, by different experimental paradigms and by species differences. The dual-probe microdialysis method may have further utility for radiolabeled drugs and other substances.

5. Impedance

The currents generated by synaptic and action potentials across cell membranes loop through the ECS of the brain and generate potential differences across the effective impedance of the interstitial space. These potential differences or extracellular field potentials have long been used to analyze the activity of single cells and neuronal populations (e.g. Refs. 201, 202, 246). It follows that, if a known source of current were introduced into the ECS and the current spread remained confined to this compartment, an analysis of the resulting potential distribution might yield information that could be directly related to the diffusion parameters. Indeed, potential distribution in brain tissue is governed by Poisson's equation (246) which is formally identical to the steady-state diffusion equation. This correspondence was recognized by Gardner-Medwin (110) who pointed out that under the assumption that all current was confined to the ECS, the resistivity, ρ of the brain (the reciprocal of the conductivity σ) would be proportional to λ²/α. The relation between volume fraction, tortuosity and impedance was explored from another perspective by Mathias (218) and Tuch et al. (394) has derived tissue impedance properties from MR diffusion tensor imaging.

A relation between impedance and ECS volume has been acknowledged in many studies (e.g. 102, 141, 266, 304, 393) although frequently there was an implicit assumption that tortuosity remained unchanged during any alteration in volume fraction. In order to arrive at an absolute rather than a relative value for volume fraction from measurements of the electrical properties it is necessary to employ a model of the resistance properties of the ECS and these have almost all been based upon Maxwell's equation (Section II.H) even though this was developed for a dilute suspension of spheres. As the work of Tao and Nicholson (380) and Hrabe et al. (144) suggests, and more detailed analysis confirms, in an electrical context (69, 223), Maxwell's relation now appears to be valid for closely packed convex cells, which may explain the successful use of this relation in earlier work. Two problems remain however. The first is that a certain proportion of any applied current will travel through cells and the amount of this will be a complex function of the cable properties and orientation of the cells (279). The second problem is that resistance will be a function of both λ and α. In many instances changes in λ will be small so changes in ρ will predominantly reflect changes in α and the correspondence might be increased by measuring the complex impedance (frequency-dependent resistance) albeit at the cost of significantly greater technical requirements. Thus resistance measurements may reveal some of the structural information that would be obtained with an ideal point molecule and offer a virtually instantaneous measurement. Resistance measurements will not reveal, however, how different species of molecule will move in the ECS.

IV. TMA-DIFFUSION MEASUREMENTS IN CNS TISSUE

This and subsequent sections are based on results obtained with the RTI-TMA method using the small cation, TMA⁺, which has a diameter of about 0.6 nm and no hydration shell (343). A large body of data has been gathered from adult healthy brains in different regions and several species, both in vivo and in vitro and these data form a critical reference set for all discussions of diffusion in the brain. After reviewing the normal brain, the developing and aging brain will be considered. Finally this section will review a variety of wide-ranging interventions that may change the values of α and λ.

A. Adult healthy brain

In healthy CNS tissue the ECS volume fraction α is about 0.20, so it amounts to 20% of the total tissue volume, while tortuosity is about 1.6, meaning that the effective diffusion coefficient (D*) is about two and a half times less than in a free medium. These are, however, average numbers. Table 4A, 4B shows that ECS diffusion parameters vary in different parts of the CNS as well as during maturation and aging.

Table 4A.

Part 1. Normal tissue: Diffusion measured with RTI-TMA method

Region	Species	Age	Prep.	°C	α	λ	Refs.
Cortex
temporal lobe III, IV	human	10-26 yr	slice	22-24	0.24	1.55	402
	rat	P4-7	in vivo	37	0.30-0.43	1.50-1.68	193, 409
	rat	P8-11	in vivo	37	0.25-0.32	1.49-1.61	193, 397, 409, 410
	rat	P20-23	in vivo	37	0.22-0.23	1.50-1.63	193, 220, 409
	rat	adult	in vivo	37	0.18-0.22	1.54-1.65	drefs
	rat	aged	in vivo	37	0.18-0.19	1.55-1.59	362, 363
auditory cortex	rat	adult	in vivo	37	0.21	(1.51, 1.66, 1.83)a	408
	rat	adult	slice	30-34	0.18-0.25	1.49-1.69	145, 148, 183, 290, 292
somatosensory	mouse	3-6 mo	in vivo	37	0.23	1.67	11
somatosensory	mouse	5-9 mo	in vivo	37	0.17-0.20	1.46-1.57	370, 371
	mouse	17-25mo	in vivo	37	0.13-0.16	1.46-1.49	370
	gp	adult	slice	32	0.22	1.59	71
Corpus callosum
	rat	P4-7	in vivo	37	0.42-0.45	1.48-1.64	193, 409
	rat	P8-12	in vivo	37	0.36-0.40	1.49-1.53	193, 409, 410
	rat	P21-23	in vivo	37	0.19-0.23	1.42-1.52c	193, 409
	rat	P21-23	in vivo	37	0.25-0.26	(1.46, 1.70, 1.72)a	410
	rat	adult	in vivo	37	0.2	1.55c	193
	rat	adult	in vivo	37	0.21	(1.47, 1.68, 1.68)a, b	362, 363
	rat	aged	in vivo	37	0.19-0.20	(1.48, 1.71, 1.71)a, b	362, 363
Hippocampus
CA1	rat	adult	in vivo	37	0.21-0.22	(1.46, 1.61, 1.76)a, b	221, 363
CA1, str. pyr.	rat	adult	slice	31-35	0.12-0.14	1.50-1.67	222, 290
CA1, str. rad.	rat	adult	slice	31-35	0.13	1.71	222
CA1, str. rad.	rat	adult	slice	34	0.24	(1.47, 1.44, 1.46)a	145
CA3	rat	P5	slice	31	0.41	1.39	166
CA3	rat	adult	in vivo	37	0.20-0.22	(1.52, 1.60, 1.70)a, b	221, 363
CA3, str. pyr.	rat	adult	slice	31-35	0.18-0.2	1.57-1.83	222, 290
CA3, str. rad.	rat	adult	slice	31-35	0.16	1.71	222
DG	rat	adult	in vivo	37	0.20-0.22	(1.50, 1.62, 1.71)a, b	221, 363
CA1, CA3, DG	rat	aged	in vivo	37	0.18-0.20	(1.52, 1.56, 1.69)a, b	362, 363
CA1	mouse	5-9 mo	in vivo	37	0.17	1.57	371

Footnotes

str. pyr = stratum pyrimidale

str. rad = stratum radiale

DG = dentate gyrus

^atortuosity is anisotropic, (λ_x, λ_y, λ_z)

^baveraged tensor values

^canisotropy not measured

^drefs: 75, 139, 220, 221, 340, 360, 362, 363, 408, 431

Table 4B.

Part 2. Normal tissue: Diffusion measured with RTI-TMA method

Region	Species	Age	Prep.	°C	α	λ	Refs.
Striatum
	rat	adult	in vivo	37	0.19-0.22	1.59-1.60	154, 311
	rat	adult	slice	31-33	0.21	1.54	317
Cerebellum
molecular layer	rat	adult	in vivo	37	0.18	1.49c	257
molecular layer	gp	adult	slice	37	0.28	1.84c	142
molecular layer	turtle	n/a	isolated	21-23	0.31	(1.44, 1.95, 1.58)a	314
granular layer	turtle	n/a	isolated	21-23	0.21-0.22	1.70-1.77	178, 314
molecular layer	skate	n/a	in vivo	15	0.24	1.62c	259
Midbrain
SNc	gp	adult	slice	32	0.3	1.58	71
SNr	gp	adult	slice	32	0.29	1.69	71
VTA	gp	adult	slice	32	0.3	1.62	71
Supraoptic nucleus
	rat, virgin	adult	slice	30-34	0.32	(1.39, 1.48, 1.50)a	292
Spinal cord
dorsal horn gm	rat	adult	in vivo	37	0.20-0.24	1.54-1.62	339, 350, 366
dorsal horn gm	rat	P4-13	isolated	20-22	0.22-0.25	1.52-1.63	298, 369, 403
dorsal horn gm	rat	P19-21	isolated	20-22	0.21-0.22	1.62-1.65	298, 369
wm	rat	adult	in vivo	37	0.18	1.56	339
dorsal horn wm	rat	P7-8	isolated	20-22	0.27	(1.33, 1.52)a	298
dorsal horn wm	rat	P13-14	isolated	20-22	0.23	(1.38, 1.80, 1.78)a	298, 369
dorsal horn gm	rat	P8-11	slice	21-22	0.21-0.25	1.52-1.54	368, 401
ventral horn	rat	adult	in vivo	37	0.23	1.46	339
dorsal horn gm	mouse	P8-10	slice	22	0.27	1.54	11
dorsal horn gm	frog	adult	isolated	17-19	0.19,	1.59	299
filum terminale	frog	adult	isolated	17-19	0.31-0.32	1.40-1.43	299
Invertebrate
vertical lobe	cuttlefish	n/a	in vivo	8	0.09	1.68	256
vertical lobe	cuttlefish	n/a	slice	14	0.12	1.54	256
optical lobe	cuttlefish	n/a	slice	14	0.29	1.86	256
vertical lobe	octopus	n/a	in vivo	8	0.13	1.75	256

Footnotes

gm = grey matter

wm = white matter

See Part 1 and earlier Tables

There is increasing evidence that diffusion in brain tissue is not only heterogeneous but also anisotropic in several regions (see Section II.D and Equations 16 and 18). Anisotropic diffusion might preferentially channel the movement of neuroactive substances in the ECS, e.g. along axon bundles or glial processes and therefore it may be responsible for some specificity in extrasynaptic volume transmission. Indeed, using the RTI-TMA method, anisotropic diffusion has been established (Table 4A, 4B) in the white matter of the corpus callosum and spinal cord, the gray matter of the molecular layer of the cerebellum, in some regions of the hippocampus and in the supraoptic nucleus of the hypothalamus. Anisotropy has been reported in the auditory and somatosensory cortex but the evidence for this is less convincing.

Some of the RTI-TMA studies have been accompanied by DW-MRI measurements. As discussed in Section III.D.1, DW-MRI methods provide information about the apparent diffusion coefficient of water (ADC_W). The relationship between water movement, ADC_W maps and changes in cell volume and ECS diffusion parameters (α and λ) is not well understood yet because changes in both α and λ are accompanied by changes in ADC_W. Consequently it may be most useful to regard ADC_W maps as simply providing anatomical data in living animals. Changes in ADC_W, however, are valuable for diagnosis during pathological states.

Most of the diffusion studies in the normal CNS have been made with TMA using the RTI method and are summarized in Table 4A, 4B. The extent of the data makes it appropriate to break it down by brain region. Only the most important or controversial contributions will be discussed; for other studies the detail in the table will suffice. These data provide an extensive database of measurements with which to define ‘normal’ diffusion parameters. The material reviewed was mostly based on the rat as a representative mammal with a few measurements in mice, guinea pigs and humans. Other vertebrate orders where some measurements have been made include reptiles (turtle), amphibians (frog) and fish (elasmobranch). Finally, a few data are available from invertebrates (cephalopods). The relative constancy of values for λ and α across all regions and species is striking and suggests that these parameter values represent an optimum both for allowing movement of substances in the interstitial space and for providing a reservoir of water, ions and other molecules essential to physiological function.

Values of loss or clearance (also referred to as non-specific uptake) of TMA⁺, characterized by the parameter k′, have been omitted because generally they do not vary much. Specifically, the values of k′ in normal in vivo rat brain are usually in the range 3.3 – 6.3 × 10⁻³ s⁻¹ (75, 193, 409). Where there is a substantial deviation from these values it is noted in the text. In brain slices, the value of k′ may reflect the way in which the slice environment is controlled especially how molecules are lost at the surfaces of the slices (150). The nomenclature for the effective diffusion coefficient, D*, for TMA⁺, varies in different papers. Sometimes it is referred to as the ‘apparent diffusion coefficient’ denoted by ADC or ADC_TMA but this nomenclature is increasingly associated with DW-MRI measurements so in this review we use ‘effective diffusion coefficient’ and D* for the value measured with the RTI-TMA method.

1. Neocortex

The cortex is a convenient region to study because it is predominantly isotropic, meaning that tortuosity is characterized by a single value of λ. The most extensive study was by Lehmenkühler et al. (193) (Fig. 7) covering the postnatal rat neocortex in vivo from P2 – P23 on a layer-by-layer basis. At P20 – P23 the rat brain has the diffusion characteristics of the adult. The developmental implications (P4 – P11) will be discussed in Section IV.B. As for the different layers of the neocortex, some small differences were measured (averaged over in Table 4A, 4B, see original papers for details) but the uniformity is much more striking than the differences. The studies employing adult rats in vivo are in agreement that α is in the range 0.18 – 0.22 and λ in the range 1.56-1.65. Studies in the adult mouse cortex in vivo (370, 371) show that values of α and λ are similar to those in the adult rat. An early in vivo study in rat cortex by Lundbæk & Hansen (207) found λ = 1.4 but the curve-fitting procedure was poor and these data are omitted from Table 4A, 4B. Voříšek et al. (408) produced evidence for cortical anisotropy in the auditory cortex, which has different organization and structure to the rest of the neocortex and it is intriguing to wonder if there is a correlation with function here. This same study (408) also claimed, however, a small degree of anisotropy in the somatosensory cortex, in contrast to all previous studies from the same laboratory which had found the somatosensory cortex to be isotropic.

Fig. 7.

Changes in diffusion parameters during development. A. Three-dimensional bar chart depicting the distribution of volume fraction as a function of age in postnatal days and cortical layer. Layers II and III were too small to make measurements at some early ages. B. Comparison of theoretical diffusion curves for layers IV, V, VI of the cortex and for the subcortical white matter (WM) at different postnatal days. Each curve was computed using Equation 13 and Equation 15 and the mean values for diffusion parameters α, λ, k′ given in Lehmenkühler et al. (193) (also summarized in Table 4A, 4B). To compute the curves a spacing between iontophoresis microelectrode and ISM of r = 175 μm, a value of D = 1.26 × 10⁻⁵ cm² s⁻¹ and n_t = 0.5 were used. Note that the curves with lowest amplitude occur at the earliest age caused primarily by the large volume fraction at that time. (Panels A and B modified from Ref. 193).

The rat neocortical brain slice has been employed in four RTI-TMA studies and three of them (145, 148, 183) have given α-values between 0.24 and 0.25 along with λ-values between 1.65 and 1.69. A fourth slice study (290) found α = 0.18 and λ = 1.62 and in a study (292), primarily on the supraoptic nucleus (see below), the investigators obtained control values of α = 0.23 and λ = 1.49 in the cortex. One reason for the variation among slice results may be variable gain of water by slices (146), which, in turn, may be related to different slice preparation paradigms. Nonetheless, these studies show that the diffusion properties of the ECS in slices largely replicate those of the intact animal.

Interestingly, studies on slices of human cortex (402, 427) show that here α is about the same as in rat (α = 0.24) and λ = 1.50-1.65. A study of the cortex in the guinea pig slice (71) shows similar values of α and λ to those of the rat.

2. Corpus callosum

There have been three in vivo studies of this massive white matter tract that lies beneath the cortex. It is to be expected that this oriented bundle of fibers would generate anisotropy in α but the first investigation, part of the extensive cortical study by Lehmenkühler et al. (193) (Fig. 7), did not attempt to measure anisotropy. This was remedied in two subsequent studies (362, 363) (Table 4A, 4B) where it was found that the component of λ measured along the fibers (x-axis) was 1.47 and that across the fibers (y- and z-axes) averaged 1.68 while α was 0.21 (Fig. 4F). Importantly, anisotropy was absent during early postnatal days (P4 – P10 in rat), i.e. before myelination.

3. Hippocampus

There have been two studies of the adult rat hippocampus in vivo (221, 363). Both recorded anisotropy in the CA1, CA3 and the dentate gyrus regions and similar α-values of 0.20-0.22. Earlier slice studies (222, 290) on CA1 and CA3 did not attempt to measure anisotropy and recorded an unusually small α of 0.13-0.14, possibly caused by the failure to account for the anisotropy (for details see Table 4A, 4B). Hrabětová, (145), however, failed to find anisotropy in CA1 stratum radiatum and recorded a λ -value of about 1.45 and an α-value of 0.24. This investigator also hypothesized that the low value of λ in this region of the hippocampus, compared to that in the cortex, reflected the relative prevalence of dead-space microdomains in the two brain areas. A single study (371) on the CA1 region of the mouse hippocampus confirmed similar values of α and λ to the average values seen in rat CA1 (Table 4A, 4B).

4. Striatum

While the caudate nucleus was a favored target for radiotracer measurements (Table 1) there have been only three studies on the rat striatum with the RTI-TMA method (Table 4A, 4B). The measured diffusion parameters are similar to those of the cortex, moreover, both the in vivo (154, 311) and slice measurements (317) are in agreement.

Jansson et al. (154) also looked at the effect of systemic NO synthase inhibition (which would reduce endogenous NO) on diffusion parameters and found a very small increase in α and λ after administration of 50 mg kg⁻¹ of N^G-nitro-l-arginine methyl ester (l-NAME) but a more substantial increase in non-specific clearance (k′) of TMA⁺. The spread of biotinylated 3 kDa dextran, assessed from histological data, was also reduced by NO synthase inhibition.

5. Cerebellum

The first application of the RTI-TMA method was in the cerebellar molecular layer in vivo (257) (Table 4A, 4B; Fig 4B), although a preliminary study with TEA had been published earlier (258). The Nicholson & Phillips study (257) looked for anisotropy but the results for the different axes were not statistically significant, possibly because the data analysis techniques did not have adequate resolution (k′, the loss term in Equation 13, could not be extracted by curve-fitting at that time).

Anisotropy was first convincingly detected in the isolated turtle cerebellar molecular layer (314) (Fig 4C, D; Table 4A, 4B). The turtle study established that the component of λ at right angles to the parallel fibers but in the plane of the cerebellar surface (λ_y = 1.95) was considerably larger than the component along the parallel fibers (λ_x = 1.44) or the component perpendicular to the surface (λ_z = 1.58). The turtle study also confirmed that, while volume fraction was not anisotropic, the anisotropy in tortuosity had to be measured in order to estimate α accurately. When this was done it was discovered that α = 0.31 in the turtle molecular layer, substantially higher than that in the mammalian cortex. In contrast, the granular layer of the turtle cerebellum was isotropic with a value of α similar to mammalian cortex but with an elevated λ (Table 4A, 4B); these results for the granular layer of the turtle were confirmed by Križaj et al. (178). The anisotropy in the molecular layer of the turtle cerebellum has been confirmed and the results extended using IOI with dextran molecules (417) and are detailed in Section III.C.2 and Table 3.

The first TMA diffusion measurements in a brain slice were made in the molecular layer of the guinea pig cerebellum (142). Although no attempt was made to look for anisotropy, the study did open the way to the use of the slice for future diffusion measurements. Finally, a brief in vivo study on the skate (259), a marine elasmobranch fish, established that the molecular layer had similar diffusion parameter values to those in other species, even though the osmolality of interstitial fluid in elasmobranchs is three times greater that that in most other fish and mammals; again anisotropy was neglected.

6. Midbrain

One study (71; Table 4A, 4B), directed primarily toward understanding dopamine diffusion (see Section III.B.6), also made measurements of RTI-TMA in the midbrain of the guinea pig slice. Values of λ in substantia nigra pars compacta (SNc) and ventral tegmental area (VTA) were in the range 1.59-1.62 but in the substantia nigra pars reticulata (SNr) the value was 1.69. More unexpected, the values of α in all three regions were about 0.30, some 50% larger than the predominant value for many other brain regions. The authors of the study (71) speculated that the increased volume fraction might facilitate extrasynaptic volume transmission.

7. Supraoptic nucleus of the hypothalamus

The glial cells that cover the magnocellular neurons in this brain region are known to retract when female rats enter a period of lactation (383). This preparation therefore provides a model to examine the possible role of glial morphology in determining diffusion parameters. Piet et al. (292) found that the tortuosity in brain slices from virgin rats exhibited anisotropy (with the x-axis defined as the ventro-dorsal direction, the y-axis as mediolateral and the z-axis as rostrocaudal) but the anisotropy disappeared in lactating animals (Tables 4A, 4B, 6). Perhaps more surprising, α significantly decreased in lactating compared to virgin animals, possibly reflecting an increase in direct neuronal surface membrane juxtapositions made possible after the glial retraction. This study will be reviewed in more detail in Section IV.E.6.

Table 6.

Systemic intervention: Diffusion measured with RTI-TMA method

Intervention	Region	Species	Age	Prep.	°C	α	Δα	λ	Δλ	Ref
water compartmentalization
Hypernatremia	cortex	rat	adult	in vivo	37	0.12a	−	1.65	+	75
X-irradiation
40 Gy	ipsilat cortex IV/V	rat	P4-5	in vivo	37	0.48-0.51	+	1.49-1.55	−	367
40 Gy	ipsilat cortex IV/V	rat	P8-11	in vivo	37	0.34-0.47	+	1.58-1.68	+	367
40 Gy	ipsilat cortex IV/V	rat	P18-21	in vivo	37	0.49-0.55	+	1.79-1.81	+	367
40 Gy	ipsilat cortex wm	rat	P4-5	in vivo	37	0.48	+	1.38	−	367
40 Gy	ipsilat cortex wm	rat	P8-11	in vivo	37	0.50-0.61	+	1.45-1.60	~	367
40 Gy	ipsilat cortex wm	rat	P18-21	in vivo	37	0.29	+	1.47	~	367
matrix knockout
TN-R−/−	cortex, somatosen	mouse	5-9 mo	in vivo	37	0.15	−	1.49	−	371
TN-R−/−	hippocampus CA1	mouse	5-9 mo	in vivo	37	0.13	−	1.48	−	371
ST−/−	cortex, somatosen	mouse	5-9 mo	in vivo	37	0.17	−	1.46	−	371
ST−/−	hippocampus CA1	mouse	5-9 mo	in vivo	37	0.14	−	1.49	−	371
GFAP knockout
GFAP−/−	spinal cord, dh	mouse	P8-10	slice	22	0.28	~	1.55	~	11
GFAP−/−, 50 mM K+	spinal cord, dh	mouse	P8-10	slice	22	0.12	−	1.72	+	11
GFAP−/−, 200
mosmol/kg	spinal cord, dh	mouse	P8-10	slice	22	0.16	−	1.66	+	11
GFAP−/−	cortex	mouse	3-6 mo	in vivo	37	0.23	~	1.62	−	11
plasticity
lactation	supraoptic nuclei	rat	3-5 mo	slice	32	0.2	−	(1.34,1.39,1.36)a	−	292

Footnotes

Control values in Table 4A, 4B

See Table 5 and earlier Tables

^aanisotropy tensor (λ_x, λ_y, λ_z)

8. Spinal cord

Three studies looked at diffusion in the grey matter of the dorsal horn in adult rats in vivo (339, 350, 366; Table 4A, 4B) and found values for λ and α that were very similar to those for the in vivo cortex. Two studies (298, 369) on the isolated rat cord in the same region taken from animals at P19 – P21 showed similar volume fractions to the in vivo preparation but a slightly elevated tortuosity. Unfortunately, the spinal cord slice from older animals has not proved a viable physiological preparation. Anisotropic diffusion in the white matter of the myelinated spinal cord has been confirmed (298).

The frog spinal cord ends in a filum terminale that was thought at one time to be entirely composed of astrocytic glial cells (111). Subsequently, however, it was demonstrated (63) that a neuronal network is present; nevertheless this remains a predominantly glial region, which makes it especially interesting for diffusion studies. Prokopová-Kubinová and Syková (299) showed that in the dorsal horn of the isolated frog spinal cord, λ and α were similar to those in the same region of the in vivo rat but in the frog filum terminale, λ was reduced (1.40-1.43) and α elevated (0.31-0.32). This suggests that in a predominantly glial (but not gliotic) region, diffusion is facilitated and this may reflect the morphology of the glial cells and alterations in the extracellular matrix (see Section VI.E). Some aspects of diffusion in the spinal cord have been reviewed by Nicholson (252).

9. Invertebrate brain

Most invertebrates present too small a mass of neural tissue to allow meaningful diffusion measurements with the RTI-TMA method. The cephalopods, i.e. octopus, cuttlefish and squid, provide an exception. In octopus, the brain is comparable in size to that of a rat, although very different in regional organization (423) and the brains of squid and cuttlefish are similar. This has allowed both in vivo and slice studies on the vertical and optical lobes of the cuttlefish and octopus (256) (Table 4A, 4B). Tortuosities ranged from 1.54-1.75 while volume fractions ranged from 0.09-0.29. The variation was probably caused both by the lack of established protocols for dealing with these preparations and an apparent sensitivity to ischemia. Nevertheless, these studies suggest that the values of α and λ are comparable to those found in vertebrates.

B. Development

Early electron microscopy, using freeze substitution fixation in an attempt to preserve the ECS, indicated that the volume fraction of the cortex in P10 rats was 41% and decreased in size with maturity, becoming 22% in adults (46). Conventional fixation in the rat inferior colliculus revealed a volume fraction of 15% at P1 diminishing to 8% in the adult (301). The diminished and artifactual ECS reported in this study (301) is routinely observed with conventional electron microscopy techniques (Section II.A) but the overall trend of a diminishing size with maturation remains apparent. Both these studies (46, 301) noted that most of the ECS they saw was accounted for by large ‘lakes’ between cells, although this too may have been a fixation artifact. Because it is so difficult to preserve the ECS in electron microscopy, it became important to employ diffusion methods to revisit the size, and particularly the evidence of a 50% reduction with maturation.

Consequently, Lehmenkühler et al. (193) (Fig. 7) carried out an extensive study with the RTI-TMA method in rat cortex (Table 4A, 4B) and confirmed that α was about 40% at P2-P4 but by P10 – P11 the value of α was about 27%, in contrast to the value found by Bondareff and Pysh (46) and then steadily diminished to the adult value of around 20% by P23, in concert with expansion of the cortical layers and gliogenesis. On the other hand, λ remained in the range 1.5-1.6 from P2-P4 to the adult, again showing that λ is not a simple function of α. These results were confirmed in later studies, not only in cortex (409, 410), but also in hippocampus (166). A similar pattern of changes in diffusion parameters during development was seen in the corpus callosum (410) (Table 4A, 4B) with the added and important observation that this region remained isotropic until about P12 but then from P13 to P17, which is a period of extensive gliogenesis in the rat, anisotropy gradually increased. At P21 – P23 and subsequently, values of α and λ remained constant (410) (Table 4A, 4B). The development of anisotropy was correlated also with myelination of the axons of the corpus callosum (410). The trends seen in the corpus callosum occur in the rat spinal cord but are less marked (298) (Table 4A, 4B).

The large ECS volume seen during development may facilitate the movement of molecules involved in development and provide better conditions for cell migration through larger intercellular channels. On the other hand, the large ECS in the neonatal brain could dilute ions, metabolites and neuroactive substances released from cells, relative to release in adults, and may be a factor in the delay or prevention of anoxic injury (409), seizure (166) or spreading depression in young individuals (220). These issues will be addressed also in Section V.

It would be rewarding to attempt to estimate the width of the ECS in the immature brain. Indeed, it must be supposed that the large volume fraction of ECS early in development implies that the spaces are wider than in the adult and may contain more extracellular matrix for structural integrity. This supposition is bolstered by the constancy of the tortuosity in the adult and neonate brain suggesting that something in the enlarged ECS is responsible for sustaining the hindrance in the latter. Another possibility, consistent with the observations of Bondareff and Pysh (46), assuming they are not artifacts, is that there is an increased number or size of distended spaces or ‘lakes’ in the immature ECS that could increase tortuosity by increasing local molecular retention time (61, 183, 381; see Section II.G). Finally, a large ECS in neonates may reflect a lack of full dendritic arborizations or fewer glial processes that later come to intercalate themselves between neurons.

C. Aging

Aging is accompanied by serious cognitive deficits, especially loss of memory and impaired learning. Nervous tissue, particularly in the hippocampus and cortex, is subject to various degenerative processes, including a decreased number and efficacy of synapses, neuronal loss, astrogliosis, demyelination, deposits of beta amyloid and changes in extracellular matrix proteins (115).

An early electron microscopic study using freeze-substitution fixation in rat cortex (45) reported that α diminished from 21% at three months of age (i.e. adult) to a value of 10% at two years and two months (i.e. an aged rat). The dramatic reduction in α was questioned by Rees et al. (306), who used a technique based on both sucrose perfusion and electron microscopy, and not entirely confirmed by more recent RTI-TMA studies but the diffusion studies did show a reduction in α from 0.21 – 0.22 in the young adult to 0.17 – 0.19 in aged rats (362, 363) in the three regions studied: cortex, corpus callosum and hippocampus and from 0.17 – 0.20 to 0.13 – 0.16 in the mouse somatosensory cortex and CA1 region of the hippocampus (371). Interestingly, significant differences in α were found in aged female mice compared to age-matched males (370). An even more pronounced difference was found in ADC_w (370). This was the first observation of a gender difference in α and ADC_w. A possible contributing factor, although it was only reported in the hippocampus, is that female mice have higher numbers of astrocytes and microglia than males and this difference increases with age (239).

The average tortuosity was either unchanged or decreased slightly with age in all these RTI-TMA studies. There was a loss of anisotropy in the aging hippocampus, particularly in the CA3 region and the dentate gyrus in rats (363). Clearance or loss of TMA, represented by k′, was also significantly lower in aged rats than in normal adults.

One of the studies on aging in rats also correlated learning deficits with altered diffusion parameters (362). The rats were divided into ‘good’ (superior) and ‘bad’ (inferior) learners, based on performance in a water maze, and it was found that the degree of impaired performance in aged rats correlated with the extent of the decrease in α and loss of anisotropy in the hippocampus. Concomitantly, the value of α in the dentate gyrus of bad learners was significantly smaller than in good learners. In addition, anisotropy in λ in the hippocampus of bad learners, particularly in the dentate gyrus, was reduced, while a substantial degree of anisotropy was still present in aged rats with good learning performance.

In the CA1 and CA3 regions, as well as the dentate gyrus, changes in the arrangement of fine astrocytic processes were found regularly in aged animals (362, 363) along with a decreased staining for chondroitin sulfate proteoglycans and for fibronectin, both of which are predominant in perineuronal nets. This loss of extracellular matrix macromolecules may partly account for the reduction in ECS volume (see also Section VI.E).

These results on aged animals, together with the data on the developing brain, support the conclusion that α is decreasing during the entire postnatal life. The changes in diffusion parameters seen in the aging brain again might be ascribed to changes in glial architecture or extracellular matrix. However it seems likely that the large decrease in volume fraction reported by Bondareff and Narotsky (45) was mainly artifactual. The learning studies along with the measured changes in glia morphology and extracellular matrix point to considerable reorganization of the ECS with age and this could affect many things including the ability of neurons to maintain communication through extrasynaptic volume transmission and even the migration of neural precursor cells, assuming there is lifelong neurogenesis.

There have been no studies in either the developing or the aged brain with IOI methods. It would surely be informative to determine if large macromolecules moved more readily in the 40% volume fraction of the neonatal brain than in the 20% space of the adult and less readily in the ECS of the aging brain.

D. Local intervention

The term ‘local intervention’ is used to indicate a procedure that is only applied to a small region of the tissue and is limited in duration. Three examples are discussed: electrical stimulation and injury, direct application of substances and osmotic challenge.

1. Electrical stimulation and injury

The electrical activity of the CNS, consisting primarily of action potentials and synaptic activation, is mediated by ionic shifts across cell membranes that are accompanied by water movement and, because the net flux is usually into the cell, the cell swells.

In the spinal cord of the rat, repetitive electrical stimulation causes an increase in extracellular K⁺ concentration, [K⁺]_e, by 1 – 2 mM (on a resting baseline of 3 mM) accompanied by a small increase in α during the stimulation followed by a more prolonged decrease in α to 0.19 - 0.13 (from a resting baseline value of 0.24), i.e. the ECS volume decreases by as much as 20-45% (350) (Table 5). A decrease of 20-50% occurs after injury of the ipsilateral hind paw evoked by subcutaneous injection of turpentine or after thermal injury (350) (Table 5). The changes in ECS diffusion parameters persist after stimulation ends (30 min after 1 min of electrical stimulation or even 120 min after peripheral injury). The relatively long time course of recovery is correlated with an extracellular acidification, as measured with a pH-sensitive microelectrode (350, 365).

Table 5.

Local intervention: Diffusion measured with RTI-TMA method

Intervention	Region	Species	Age	Prep.	°C	α	Δα	λ	Δλ	Refs.
stimulation
electrical	spinal cord, dh	rat	adult	in vivo	37-38	0.13-0.19	−	1.54	~	350
chemical injury	spinal cord, dh	rat	adult	in vivo	37-38	0.13-0.16	−	1.54	~	350
electrical	spinal cord, dh	frog	adult	isolated	17-19	0.13	−	1.60	~	299
electrical	filum terminale	frog	adult	isolated	17-19	0.28	−	1.60	+	299
K+, EAA
50 mM K+	spinal cord, dh	rat	P4-13	isolated	21-22	0.07-0.09	−	2.06-2.16	+	369
50 mM K+	spinal cord, dh	rat	P20-21	isolated	21-22	0.17	−	1.93	+	369
50 mM K+	spinal cord, wm	rat	P13-14	isolated	21-22	0.12	−	1.92,2.42	+	369
50 mM K+	spinal cord, dh	mouse	P8-10	slice	22	0.07	−	1.92	+	11
50 mM K+	spinal cord	frog	n/a	isolated	17-19	0.09	−	1.70	+	299
50 mM K+	filum terminale	frog	n/a	isolated	17-19	0.20	−	1.68	+	299
GLU 10−2 mM	spinal cord	rat	P4-12	isolated	21-22	0.09	−	1.79	+	403
NMDA 10−4 mM	spinal cord	rat	P4-12	isolated	21-22	0.09	−	1.83	+	403
AMPA 10−5 mM	spinal cord	rat	P4-12	isolated	21-22	0.12	−	1.79	+	403
osmotic challengea
238 mosmol/kg	cereb. grl	turtle	n/a	isolated	21-23	0.12	−	1.79	+	178
461 mosmol/kg	cereb. grl	turtle	n/a	isolated	21-23	0.45	+	1.50	−	178
668 mosmol/kg	cereb. grl	turtle	n/a	isolated	21-23	0.6	+	1.50	−	178
150 mosmol/kg	cortex	rat	adult	slice	34	0.14	−	1.86	+	147
200 mosmol/kg	cortex	rat	adult	slice	34	0.12	−	1.82	+	183
400 mosmol/kg	cortex	rat	adult	slice	34	0.29	+	1.67	~	183
500 mosmol/kg	cortex	rat	adult	slice	34	0.42	+	1.68	~	183
215 mosmol/kg	hippo. CA3	rat	P5	slice	31	0.17	−	1.49	+	166
235 mosmol/kg	spinal cord, dh	rat	P4-13	isolated	21-22	0.13-0.15	−	1.62-1.83	+	369
235 mosmol/kg	spinal cord, dh	rat	P20-21	isolated	21-22	0.14	−	1.79	+	369
235 mosmol/kg	spinal cord, wm	rat	P13-14	isolated	21-22	0.10	−	1.83, 2.00	+	369
200 mosmol/kg	spinal cord	rat	P8-10	slice	22	0.15	−	1.62	+	401
400 mosmol/kg	spinal cord	rat	P8-10	slice	22	0.30	+	1.54	~	401
200 mosmol/kg	spinal cord, dh	mouse	P8-10	slice	22	0.12	−	1.63	+	11
175 mosmol/kg	spinal cord	frog	n/a	isolated	17-19	0.11	−	1.6	~	299
175 mosmol/kg	filum terminale	frog	n/a	isolated	17-19	0.22	−	1.39	~	299

Footnotes

Δα, Δλ Change in volume fraction or tortuosity relative to control values (see Table 4A, 4B)

+ = increase; − = decrease, ~ = no change

cereb. grl = cerebellum granule cell layer

^anormal osmolality ~ 300 mosmol/kg

Electrical stimulation of the VIII or IX dorsal root at 30 Hz in the frog spinal cord proper evokes an increase in [K⁺]_e from 3 mM to 11-12 mM in spinal cord, but to only 4-5 mM in filum terminale (FT) (299) (see Section IV.A). In the spinal cord this stimulation led to a 30% decrease in α and a small increase in λ while in the FT the decrease in α was only about 10% and there was no increase in λ (299). Comparable changes were reported in a preliminary study using the RTI method with TEA in the frog spinal cord after repetitive electrical stimulation (352).

2. Direct application of K⁺ or excitatory amino acids

Neuronal activity following electrical stimulation or injury is always accompanied by a substantial rise in [K⁺]_e and this prompts the question of whether direct application of potassium itself leads to changes in diffusion parameters. Because glutamate is the predominant excitatory neurotransmitter of the CNS, application of this substance or related excitatory amino acids is likely to also alter diffusion parameters.

Isolated rat spinal cords of P4 – P21 rats were exposed to 50 mM K⁺ (369) (Table 5) or hypotonic solution (discussed in next section). The application of K⁺ resulted at first in a decrease in α and an increase in λ in spinal gray matter and white matter. These changes were attributed to cell swelling because the total water content of the spinal cord was unchanged and the changes were blocked when Cl⁻ was absent from the bathing solution. Diffusion in white matter was anisotropic and the K⁺-induced increase of λ across the fiber bundles was greater than that along them, reaching values as high as 2.4. Interestingly, application of 50 mM K⁺ for 45 min induced astrogliosis (revealed by an increase in glial fibrillary acidic protein (GFAP) staining), which persisted after the removal of the K⁺. During astrogliosis, λ increased to as high as 2.0 in grey matter, while α either returned to or increased above control values. Syková et al. (368) also found changes in λ after application of 10 mM K⁺, and both λ and α were altered in 20 mM K⁺. The results of these two studies (368, 369) show that glial swelling and astrogliosis are associated with a persistent increase in ECS diffusion barriers manifested as an increase in λ (see Section VI.B).

The extent of glial involvement in the changes in diffusion parameters evoked by K⁺ application was further explored in two more studies. In the first study (11), astrocyte membrane properties and swelling in mouse spinal cord slices at P8 – P10 were compared in wild-type control (GFAP+/+) and GFAP-knockout (GFAP−/−) mice. These experiments will be discussed in detail in Section IV.E.4; here we note only the results in the wild-type animals where application of either 50 mM K⁺ or hypotonic solution (200 mosmol kg⁻¹) produced large decreases in α and an increase in λ (Table 5). The size of the changes apparently was exaggerated by the immaturity of the animals, as also seen in the rat (369).

The second study that focused on glia employed the spinal cord and FT in the frog (299). Histological analysis revealed that in the central region of the FT, the cell density was lower than in the spinal cord, neurons and oligodendrocytes were scarce and GFAP-positive astrocytes were abundant (299) (Table 4A, 4B). In 50 mM K⁺, α in the spinal cord decreased from about 0.19 to 0.09, i.e. by 53%, while in FT it decreased from about 0.32 to 0.20, i.e. by only 38%. However, λ increased significantly more in FT than in spinal cord (299; Table 5). Hypotonic solution resulted in similar decreases in α, and there were no changes in λ in either spinal cord or FT. In summary, the application of 50 mM K⁺, hypotonic stress and dorsal root stimulation all evoke a greater decrease in ECS volume in the spinal cord than in the FT. In contrast, the K⁺-induced increase in λ was higher in the FT, suggesting the generalization that a substantial part of the K⁺-evoked increase in λ may be attributed to astrocytic swelling (299).

Glutamate release, particularly in pathologic conditions, may result in cellular swelling (368), although the studies just discussed indicate that some, or even all, of this swelling may be induced by the K⁺ release that usually accompanies glutamate elevation. Nevertheless it has been useful to explore the direct effects of excitatory amino acids (EAAs) and one study (403) (Table 5) explored the effects of glutamate, N-methyl-D-aspartate (NMDA), and alpha-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid (AMPA) on extracellular pH, [K⁺]_e and changes in ECS diffusion parameters in the isolated spinal cord of P4 – to P12 rats. The application of these EAAs increased [K⁺]_e and caused a substantial decrease in α, and an increase in λ. Pre-treatment with compounds that blocked EAA-mediated channels prevented the changes in [K⁺]_e and in the diffusion parameters caused by NMDA or AMPA application. The changes in diffusion parameters also were blocked when Ca²⁺ was absent from the bathing solution but there was no effect on the [K⁺]_e. These results suggest that sufficiently increased glutamate release may produce a large [Ca²⁺]_e - dependent decrease in α and increase in λ.

3. Osmotic challenge

The hypothesis underlying the stimulation results, as well as the application of potassium and EAAs, is that they all cause cells of the brain, particularly glia, to swell at the expense of the ECS thereby reducing the volume fraction. This may also increase the tortuosity slightly but it is likely that major increases in λ are brought about by other mechanisms such as gliosis. The volume of cells also can be directly manipulated by applying solutions of different osmolality and some of the experiments described in the last section also featured osmotic challenges over a limited range. Two sets of experiments (178, 183) systematically explored osmotic challenge over an extensive range of values (Table 5). These studies also combined diffusion measurements with wet-weight dry-weight determinations to arrive at a detailed description of water compartmentalization; this approach had been pioneered in a study of hypernatremia (75) that will be described in Section IV.E.1.

The first detailed osmotic challenge study was carried out in the isolated turtle brain because of the outstanding ability of this preparation to retain physiological viability (143). Križaj et al. (178; Table 5) used isolated cerebella from the pond turtle and immersed them in normal physiological saline (302 mosmol kg⁻¹), hypotonic saline (238 mosmol kg⁻¹) and a series of hypertonic salines (up to 668 mosmol kg⁻¹). The osmolality was varied by altering the NaCl content. Using the RTI-TMA method in the granular layer of the cerebellum (to avoid the anisotropy in the molecular layer), an α-value of 0.22 was obtained in normal saline, 0.12 in hypotonic medium and 0.60 in the most hypertonic medium. The corresponding values of λ were 1.70, 1.79 and 1.50. Raising the osmolality above 500 mosmol kg⁻¹ caused no significant change in λ although α continued to fall. The water content, defined as (wet weight - dry weight)/wet weight, of a whole isolated cerebellum was 82.9% and increased to 85.2% in hypotonic saline and decreased to 80.1% in the most hypertonic saline. Combining these data showed that hypotonic solutions caused water to move from the extracellular to the intracellular compartment while hypertonic solutions caused water to move from the intracellular to extracellular compartment, with only small changes in total tissue water in both cases. Building on this work, O'Shea et al. (271) used the isolated turtle cerebellar preparation combined with osmotic challenge and MR to establish that the hypotonic solutions caused a reduction in ADC_w and increase of the T-2 MR signal, while the hypertonic solutions had the opposite effect. This lent support to the concept that ADC_w varies with the volume fraction of the ECS. The results were consistent also with fast or slow transmembrane water exchange models with effective diffusion coefficients for water that are approximately 1.7 times lower in intracellular than in extracellular compartment (271).

Obviously the work on the turtle needed to be replicated in a mammalian preparation and this was done by Kume-Kick et al. (183) (Table 5) in rat cortical slices, again varying osmolality by altering NaCl content of the physiological saline bathing the preparation (Fig. 8A). Slices or isolated preparations are preferred for this type of study because they allow complete control of the external environment. In normal medium (305 mosmol kg⁻¹), α was 0.24 and λ was 1.69. Reducing osmolality to 150 mosmol kg⁻¹, decreased α to 0.12 and increased λ to 1.86. Increasing osmolality to 350 mosmol kg⁻¹, reduced λ to 1.67 where it stayed constant as osmolality increased further to 500 mosmol kg⁻¹. In contrast, α increased steadily to reach 0.42 at the highest osmolality (Fig. 8B). Comparison with the study of Tao (375) using IOI and 3kDa dextran to measure λ, showed the same behavior as for TMA⁺, including the same plateau value for λ in hypertonic media but with a steeper slope in the hypotonic solutions (Fig. 8B). These data show that λ and α behave differently as the ECS geometry changes. When α decreases, λ increases but when α increases, λ rapidly attains a constant value. A model based on changes in cell shape (Fig. 2B), leading to the creation of residual ECS (i.e. a local void space), was proposed by Chen and Nicholson (61) to account for the results of Kume-Kick et al. (183).

Fig. 8.

Effects of osmotic challenges on diffusion curves in rat cortical slices. A. Challenge with 150 mosmole kg⁻¹ ACSF. Sequence of four control diffusion records in 305 mosmole kg⁻¹ medium followed by four in 150 mosmole kg⁻¹ medium and finally four more records after return to 305 mosmole kg⁻¹ medium. The interval between records was longer than that illustrated to permit baseline concentration to stabilize. For all records in Panel A, r = 106 μm, n_t = 0.44. Average results for initial four control records were, λ = 1.67, α = 0.27; for the curves in hypotonic medium, λ = 1.80, α = 0.10; for the four records on return to control medium, λ = 1.57, α = 0.34. B. Effect of challenge with 500 mosmole kg⁻¹ ACSF. The experiment was similar to that illustrated in Panel A, except that hypertonic medium 500 mosmole kg⁻¹ medium was used. For all records in Panel B, r = 132 μm, n_t = 0.29. Average results for initial four control records were, λ = 1.77, α = 0.20; for the four curves in hypertonic medium, λ = 1.72, α = 0.37; the four records on return to control medium, λ = 1.88, α = 0.13. C. Comparison of behavior of λ measured with RTI-TMA method and 3 kDa dextran measured with IOI with behavior of α (measured with RTI-TMA). Dextran data calculated from Ref.375. Tortuosity measured with both molecules increases linearly as osmolality decreases below control value (305 mosmoles kg⁻¹), but the slope measured with the larger molecule (dextran) is greater than that measured with the smaller (TMA⁺). In hypertonic ACSF, the value of λ measured with both molecules quickly reaches a constant value, λ₀ = 1.67. In contrast, α varies smoothly and monotonically with osmolality, decreasing in hypotonic ACSF and increasing in hypertonic medium. (All panels modified from Ref. 183).

These detailed results have been supported by several studies that used a more limited range of osmotic variation (11, 147, 299, 369, 401) (Table 5). A study (166) on the CA3 region of the rat hippocampus at age P5 noted that α changed from 0.41 to 0.17 while λ increased from 1.38 to 1.49 after exposure to 215 mosmol kg⁻¹ solution (Table 5).

Also related to these osmotic studies was an investigation of the relationship of changes in light scattering to changes in diffusion parameters (368). As noted in Section III.D.2, it has been proposed that variations in intrinsic optical signals could be related to cell swelling but the evidence is ambiguous. Syková et al. (368) measured light transmittance, α, and [K⁺]_e in rat spinal cord slices during electrical stimulation, application of elevated potassium, NMDA, or solutions of different osmolality using similar paradigms to those described above. After this careful study, the investigators concluded that light transmittance changes do not correlate with changes in α but may be associated with neuronal activity and morphological changes in astrocytes.

E. Systemic intervention

The term ‘systemic intervention’ is used to imply a treatment or condition applied to the whole animal and which is usually irreversible within a practical time frame. The examples include: hypernatremia, X-irradiation, knockouts for extracellular matrix components and GFAP, and lactation.

1. Regulation of water content – Hypernatremia

The main purpose of the study by Cserr et al. (75) was to examine regulation of brain extracellular and intracellular water content and electrolytes in response to 90 min of hypernatremia in the cerebral cortex of rats in vivo. The partitioning of tissue Na⁺, K⁺ and Cl⁻ and water between extracellular and intracellular compartments was assessed in two sets of experiments. In the first set, electrolytes and water were measured in tissue samples. In the second set of experiments, α and λ were measured in ECS in vivo using RTI-TMA methods (Tables 4A, 4B, 6), along with [Na⁺]_e and [K⁺]_e measured with ion-selective microelectrodes. The study found that the induced water loss from cerebral cortex was less than that predicted for ideal osmotic behavior, demonstrating a selective regulation of cell volume, which was associated with net tissue uptake of Na⁺, Cl⁻ and K⁺. In control animals, the value of α averaged 0.18 and λ averaged 1.57 while α dropped to about 0.12 and λ increased to 1.65 with hypernatremia. The study concluded that during acute hypernatremia the ECS decreases in volume through the loss of water and electrolytes while the intracellular compartment maintains its water content and gains electrolytes in the form of Na⁺, Cl⁻ and K⁺.

2. X-irradiation

During the early postnatal period, the CNS is more sensitive to X-irradiation than the adult nervous system, apparently because of the proliferative potential and increased radiation sensitivity of glial and vascular endothelial cells in the immature nervous system (see Ref. 367 for references).

Diffusion parameters have been studied in the somatosensory neocortex and subcortical white matter of the rat during P2 – P21 after X-irradiation at P0 – P1 (367). X-irradiation with a single dose of 40 Gy resulted in extensive neuronal loss, blood-brain barrier damage, activated macrophages, astrogliosis, increased extracellular fibronectin and concomitant changes in the diffusion parameters (Table 6). The changes were observed as early as 48 h post-irradiation and still persisted at P21. Lehmenkühler et al. (193) (Table 4A, 4B) had already established that α in the non-irradiated cortex is large in newborn rats and diminishes with age. A single dose of 40 or 20 Gy radiation changed the normal decrease in α during postnatal development into an increase throughout the grey and white matter (Table 6) and the change persisted three weeks after irradiation. Tortuosity and non-specific loss (k′) of TMA decreased significantly at P2 – P5; at P8 – P9 they were not significantly different from those of control animals, while they increased at P10 – P21. It was noteworthy that changes in diffusion parameters also occurred in the contralateral hemisphere (367). It was concluded that X-irradiation of the brain in the early postnatal period, even when it results in only light damage (20 Gy), blocks gliogenesis and therefore produces changes in diffusion parameters, most demonstrably a large increase in α in all cortical layers and in subcortical white matter; these effects are accompanied eventually by an increase of λ in the grey matter.

3. Extracellular matrix knockout

In addition to interstitial fluid, the ECS contains many long-chain polyelectrolytes, such as glycosaminoglycans (e.g. hyaluronate), glycoproteins (e.g. tenascins) and proteoglycans (e.g. chondroitin sulfate and heparin sulfate) either attached or unattached to cellular membranes that collectively form the extracellular matrix (269, 322) (see Section VI.E for more discussion). Additionally, various adhesion molecules have been described, e.g. fibronectin, tenascin and laminin (58, 386), and their expression can change during development, aging, wound healing and pathological processes. Molecules of the extracellular matrix are produced by both neurons and glia and may segregate groups of neurons, axon tracts, and nuclei of the brain into distinct functional units.

The RTI-TMA method was used to assess the changes in ECS diffusion parameters in mice lacking tenascin-R (TN-R −/−) and tenascin-C (TN-C −/−) along with mice deficient in human natural killer 1 sulfotransferase (ST−/−) (371). Human natural killer 1 (HNK-1) is a carbohydrate structure, a sulfated glucuronyl-lactosaminyl residue, that attaches to many cell adhesion molecules in brain, including TN-R and TN-C (26) and mediates neuron-astrocyte and astrocyte-astrocyte adhesion (165). Tenascin-R is a large extracellular glycoprotein and an important component of the extracellular matrix that persists in the adult brain in some species, including mice, while TN-C is expressed mainly during early development (26, 157). In adulthood, TN-C expression only persists in areas with functional plasticity, such as the hippocampus or hypothalamus (240, 382). Together with chondroitin sulfate proteoglycans, TN-R is a critical component of the perineuronal nets that surround some interneurons in the cerebral cortex and hippocampus (52, 126).

Syková et al. (371) investigated the effect on the ECS of the absence of these matrix molecules in adult mouse knockouts. This was assessed in vivo with the RTI-TMA and DW-MRI methods in the somatosensory cortex and CA1 region of the hippocampus and the sites of the measurements were verified histologically. Differences between knockout and wild-type mice were found in all anatomical layers of the brain cortex and hippocampus (Table 6). In TN-R −/− mice, α decreased by 22% and λ decreased to about 1.49, while in the hippocampus α decreased by 26% and λ decreased to about 1.48. Compared to controls, α in ST −/− mice decreased by 9-15%. No significant changes were found in adult TN-C −/− animals, consistent with the adult status of the animals. The DW-MRI measurements showed a reduction in ADC_W in cortex, hippocampus and thalamus in the knockouts. This correlated with the reduction in α rather than the decrease in λ suggesting again that, in this example, ADC_W might be dominated by the size of the ECS.

This study shows that in TN-R−/− and ST−/− mice, which show morphological, electrophysiological and, importantly, behavioral abnormalities, the ECS is reduced and its geometry altered. The behavioral abnormalities revealed themselves as a decreased learning ability in an open water maze and were correlated, just as seen in studies on aging mice, with a reduced volume of the ECS. This role of these molecules in determining the volume fraction is likely played in concert with other matrix elements but note that tenacins are largely absent in the adult brain of many species (157), including the human brain (427). Tenascin molecules become more abundant in the injured brain and in brain tumors (see section V).

4. GFAP knockout

Glial fibrillary acidic protein (GFAP) is the main component of intermediate filaments in astrocytes (95). Surprisingly, knocking out GFAP does not produce any obvious anatomical or behavioral abnormalities but it may affect astrocyte-neuronal interactions (196). Astrocyte membrane properties and swelling in spinal cord slices at P8 – P10 were compared in wild-type control (GFAP+/+) and GFAP-knockout (GFAP−/−) mice (11). The whole-cell patch-clamp technique revealed that K⁺ accumulation evoked by membrane depolarization was lower in the vicinity of GFAP−/− astrocytes than GFAP+/+ astrocytes, suggesting the possible presence of a larger ECS around GFAP−/− astrocytes. Nonetheless, no differences in control values of α and λ in the spinal cord of GFAP+/+ and GFAP−/− mice were found. A difference was seen, however, when either 50 mM K⁺ or hypotonic solution (200 mosmol kg⁻¹) was applied; both solutions produced larger decreases in α and an increase in λ in GFAP+/+ mice compared to the GFAP−/− preparation. Anděrová et al. (11) also looked at spreading depression in the cortex of GFAP−/− mice (see Section V.A.3). This work suggests a role for intermediate filaments in astrocytic swelling during pathological states.

5. Plasticity – lactation

A reduction in the astrocytic coverage of hypothalamic magnocellular neurons in the supraoptic nucleus of the rat takes place during lactation or dehydration (128, 383). These modifications are reflected in changes in ECS diffusion parameters measured in slices from virgin and lactating rats (292) (Table 6; Fig. 9). Because the supraoptic nucleus is anisotropic, the diffusion measurements were performed along three perpendicular axes (with the x-axis defined as the ventro-dorsal direction, the y-axis as mediolateral and the z-axis as rostrocaudal). The values of both α and λ were reduced in lactating animals, and the anisotropy present in λ measured in the virgin animals disappeared during lactation (292). The reduction in λ in lactating animals may reflect the relative absence of astrocytic processes around neurons and the diminished α also could result from the retraction of astrocytic processes together with an enhanced proportion of direct neuronal membrane juxtapositions. These conditions greatly enhanced glutamate spillover, which was monitored through the metabotropic glutamate receptor-mediated depression of GABAergic transmission (long-term depression, LTD) (292). Because glial cells in the supraoptic nucleus in virgin rats constitute a physical barrier to diffusion and are essential for glutamate uptake, the retraction of their processes in lactating animals should result in glutamate-mediated cross-talk between synapses. This hypothesis was supported in additional experiments where this form of synaptic cross-talk was prevented by reducing diffusion through the introduction of 5% 40 kDa dextran into the ECS (292), which increases ECS viscosity (331). Taken together, these experiments indicate that the astrocytic environment of neurons can be a critical regulator of communication between neighboring synapses and possibly of more widespread extrasynaptic volume transmission in the CNS.

Fig. 9.

Retraction of glial processes in rat supraoptic nucleus (SON) and consequences for diffusion and synaptic crosstalk. Upper row: Examples of diffusion curves in virgin and lactating rats. SON is anisotropic so three values of λ together with one value of α extracted from these curves are indicated on the figure. Lower row: The values shown in the upper row and electron micrographic evidence (383) indicate that reduced astrocytic coverage of SON neurons in lactating rats leads to deficient glutamate clearance, resulting in increased glutamate concentration in the ECS, increased crosstalk between synapses and increased activation of either presynaptic or postsynaptic receptors. (Adapted from Refs. 292, 359).

V. TMA-DIFFUSION PARAMETERS IN PATHOLOGICAL STATES

Changes in diffusion parameters may serve both as an important indicator of pathological processes and also offer insights into their underlying mechanisms. Consequently, diffusion changes have been studied in several experimental pathological preparations and model states using the RTI-TMA method together with DW-MRI in some instances. Correlations between the results of the two techniques may be useful for diagnostic purposes.

A. Anoxia, ischemia and spreading depression

Hypoxia, anoxia, partial and global ischemia usually are accompanied by large ionic shifts in the ECS. There is a dramatic rise in [K⁺]_e to about 50-70 mM, decreases in [Na⁺]_e to 48-59 mM, [Cl⁻]_e to 70-75 mM, [Ca²⁺]_e to 0.06-0.08 mM and a pH_e decrease to 6.4-6.6 (i.e. extracellular acid shift). These ionic changes are accompanied by an extracellular accumulation of excitatory amino acids, particularly glutamate, and a slow negative potential shift measured in the ECS (for reviews see Refs. 123, 342, 351, 354, 358). The transmembrane ionic shifts are paralleled by the redistribution of water from extracellular to intracellular compartments, and both neurons and glia swell.

1. In vivo studies of anoxia/ischemia

During severe anoxia or ischemia, the value of α in rat spinal cord or cortex decreases precipitously from about 0.20 to as low as 0.05, while tortuosity increases from 1.5 to about 2.1 (366, 409) (Table 7; Fig. 10). A smaller increase in cortical λ was seen by Lundbaek & Hansen (207) but there were technical shortcomings with that study.

Table 7.

Pathological tissue: Diffusion measured with RTI-TMA method

Pathology	Region	Species	Age	Prep.	°C	α	λ	Refs.
A. Ischemia/anoxia/SD
ischemia	cortex	rat	P4-P12	in vivo	37	0.05-0.06	2.04-2.12	397, 409
ischemia	cortex	rat	P20-P23	in vivo	37	0.06	2.00	409
hypoxia/ischemia 30 min	cortex	rat	adult	in vivo	37	0.07	1.88	139
hypoxia 30 min	cortex	rat	adult	in vivo	37	0.14	1.69	431
ischemia	corpus cal.	rat	P4-P12	in vivo	37	0.04	2.08-2.10	397, 409
ischemia	corpus cal.	rat	P20-P23	in vivo	37	0.05	2.10	409
ischemia/anoxia	spinal cord, dh	rat	adult	in vivo	37	0.07	2.20	366
ischemia	cortex	rat	adult	slice	34	0.09	1.74	290
ischemia	hippo. CA1	rat	adult	slice	34	0.05	1.73	290
ischemia	hippo. CA3	rat	adult	slice	34	0.13	1.73	290
hypoxia, 8min	neostriatum	rat	adult	slice	32	0.15	1.53	317
hypoxia, 15min	neostriatum	rat	adult	slice	32	0.12	1.53	317
ischemia	cortex	rat	adult	thick slice	34	0.1-0.15	1.79-1.99	146, 147, 148
SD	cortex	rat	P13-P15	in vivo	37	0.05	1.95	220
SD	cortex	rat	P21	in vivo	37	0.07	2.07	220
SD	cortex	rat	adult	in vivo	37	0.09	1.99	220
SD	cortex GFA+/+	mouse	3-6 mo	in vivo	37	0.05	2.29	11
SD	cortex GFA−/−	mouse	3-6 mo	in vivo	37	0.08	1.97	11
B. Mechanical injury
stab wound	cortex	rat	adult	in vivo	37	0.25-0.26	1.67-1.77	319, 408
grafts	cortex, midbrain	rat	adult	in vivo	37	0.24-0.29	1.66-1.85	364
C. Disease models
Alzheimer's disease
APP23	cortex	mouse	adult	in vivo	37	0.19	1.48-1.49	370
APP23	cortex	mouse	aged	in vivo	37	0.22-0.23	1.51-1.53	370
Parkinson's disease
6-OHDA lesion	striatum	rat	adult	in vivo	37	0.14	1.50	311
6-OHDA lesion, in graft	striatum	rat	adult	in vivo	37	0.24	1.80	311
Epilepsy
Pilocarpine-induced	cortex	rat	adult	in vivo	37	0.13	1.58	340
Multiple sclerosis & inflammation.
EAE (14-17dpi)	spinal cord gm	rat	adult	in vivo	37	0.28-0.47	1.40-1.48	339
EAE (14-17dpi)	spinal cord wm	rat	adult	in vivo	37	0.3	1.48	339
Hydrocephalus
HTX-rat	cortex	rat	P21	in vivo	37	0.16	1.54	360
kaolin	cortex	rat	adult	in vivo	37	0.14-0.11	1.47	360
D. Gliomas
pilocytic astrocyt. GR I	cortex	human	2.5-17 yr	slice	22-24	0.37	1.50	402
diffuse astrocyt. GR II	cortex	human	9-28 yr	slice	22-24	0.29	1.67	427
anaplastic astrocyt. GR III	cortex	human	8-47 yr	slice	22-24	0.49	1.77	402
glioblastoma GR IV	cortex	human	43-75 yr	slice	22-24	0.47	1.67	427
oligodendrogliomas GR II	cortex	human	46-50 yr	slice	22-24	0.23	1.50	402
ependymomas GR II	cortex	human	2.5-39 yr	slice	22-24	0.39	1.55	402
medulloblastomas	cortex	human	1.5-17 yr	slice	22-24	0.38	1.57	402

Footnotes astrocyt. = astrocytoma. corpus cal. = corpus callosum. For other abbreviations see previous Tables.

Fig. 10.

Effects of anoxia and ischemia on cortical diffusion parameters in vivo and in brain slices. A. Sequences of RTI-TMA measurements in the young adult and an aged (28-months) rats after cardiac arrest. Diffusion curves were recorded in cortical layer V before and after cardiac arrest and are superimposed on the increasing TMA⁺ baseline caused by ECS volume shrinkage. Diffusion parameters indicated on the figure (Modified from Ref. 363). B. detailed curves from rat cortex in vivo during anoxia showing the large changes in diffusion curves compared to normoxia caused by the drastic reduction in α and a more modest but still significant increase in λ (Syková et al., unpublished). C. Cortical slice before and after exposure to hypoxic medium and gas. Note that the changes are not as large as those encountered in vivo. (Modified from Ref. 290). D. DW-MRI measurements in control rat cortex and ischemic cortex. Measurements were also made with RTI-TMA and the parameters are indicated below the DW-MRI images (Syková et al., unpublished).

In the dorsal horn of rat spinal cord in vivo, progressive ischemia evoked by exsanguination or anoxia following respiratory or cardiac arrest, produced large changes in [K⁺]_e and diffusion parameters (366) (Table 7). As the blood pressure (BP) fell to 50-60 mm Hg, [K⁺]_e rose to 6-12 mM and α decreased, to 0.16 while λ remained constant. With continued fall of BP to 20-30 mm Hg, [K⁺]_e reached 60-70 mM while α dropped to 0.05 and λ increased to 2.0. No further increase in [K⁺]_e or changes in α were found, even up to 120 min after the death of the animal but λ increased to 2.20. In experiments where death did not occur, full recovery to ‘normoxic’ diffusion parameters could be obtained after re-injection of the blood or after an injection of noradrenaline during experiments involving severe ischemia, so long as BP rose above 80 mm Hg and [K⁺]_e fell below 12 mM. At 10-30 min after such recovery, α increased above normoxic values, to reach 0.25 – 0.30 but λ did not change.

The effects of anoxia on diffusion parameters, measured with either TMA⁺ or TEA⁺ using the RTI method, were also studied in cortex and corpus callosum (i.e. subcortical white matter, WM) of the developing rat (409) (Table 7; Fig. 10A). In the cortex and WM of animals at P4 – P12, α is larger than that found in animals at P20 – P21 or older (Table 4A, 4B) and anoxia evoked by cardiac arrest caused a typical rise in [K⁺]_e to 60 – 70 mM accompanied by a decrease in α and increase in λ. At P4 – P6, α decreased to 0.05 in both cortical layer V and in corpus callosum while λ increased in the cortex to 2.12 and in corpus callosum to 2.08. At P10 – P12 and at P21 – P23, when α in normoxic rats is smaller than at P4 – P6 (Table 4A, 4B), the final changes in values of α and λ evoked by anoxia were not significantly different from those in P4 – P6. However, the younger the animal, the slower was the time course of the changes. This time course was longer in WM than in cortex, particularly during the first postnatal days, when the WM is largely unmyelinated, and there was a positive correlation between the normoxic size of the ECS volume fraction and the time course (409). These findings are consistent with the well-known resistance of the immature CNS, and the greater susceptibility of the aged brain, to anoxia (123, 206). Slower changes in α and λ could lessen accumulation of ions and neuroactive substances released from cells in the immature brain and facilitate their diffusion away from hypoxic areas.

Two studies combined RTI-TMA measurements with microdialysis to look at changes in brain metabolites during transient hypoxia/ischemia and transient global ischemia. In the first study (139) (Table 7), oxygen was reduced to 10% for 30 min in rats combined with a simultaneous unilateral clamping of the carotid artery. The diffusion parameters showed similar changes to those seen in previous cortical ischemia studies (Table 6). After release of the carotid artery occlusion, both α and λ returned to normal values (α = 0.19, λ = 1.57) within 20 minutes but subsequently α increased to 0.23 and λ fell to 1.53. The microdialysis measurements showed that lactate and glutamate increased in the ECS during the hypoxia/ischemia while glucose fell. After reperfusion, the metabolites trended towards normal values.

In a similar study to that described above, Zoremba et al. (431) (Table 7) used global hypoxia with oxygen content reduced to 6% for 30 min. There was no ischemia in this study and consequently the changes in α and λ were not as large as those seen by Homola et al. (139) and the values after restoration of oxygen attained levels very similar to the control values. Lactate and glutamate again increased during the hypoxia while glucose fell. In common with previous studies of hypoxia, the changes in diffusion parameters were delayed for some time after the breathing mixture was changed.

Both the above-mentioned studies (139, 431) recognized, but were not able to fully take into account, the effects of the changing diffusion parameters on the microdialysis recovery (c.f. Refs. 30, 31) (see Section III.D.4) and therefore the absolute levels of the metabolite changes are unknown.

Finally, it is noteworthy that the time course of the changes in ECS diffusion parameters during anoxia and ischemia measured by the RTI-TMA method strongly correlate with the time course of a decrease in ADC_W determined by DW-MRI (397) (Fig. 10B, D). Similar decreases in α and increases in λ are evoked also by the application of high concentrations of glutamate, NMDA or 50-80 mM K⁺ to brain slices (403) (see Section IV.D.2).

2. In vitro studies of anoxia/ischemia

Slices have been used to study hypoxia, anoxia and some aspects of global ischemia, although the use of such models has been criticized, primarily because all slices undergo an initial phase of global ischemia during their preparation. Rice and Nicholson (317) bathed submerged rat striatal slices in physiological saline gassed with 95% N₂/ 5% CO₂ for 10-30 min and obtained a 38% decrease in α to 0.13, while λ remained unchanged. The atmosphere above the slice bathing solution was not controlled and glucose in the bathing medium was normal so the effects of the hypoxia would be attenuated in these experiments.

The experiments of Pérez-Pinzón et al. (290) (Table 7; Fig. 10C) on stratum pyramidale of CA1 and CA3 regions of the hippocampus and on the cortex of the rat used physiological saline gassed with the same gas mixture used by Rice & Nicholson (317) but in addition the atmosphere above the bath was maintained with the anoxic gas mixture and glucose was removed from the bathing media to better simulate anoxia. During the anoxia, α decreased to 0.05, 0.17, and 0.09 in CA1, CA3, and cortex, respectively (Table 7), from normoxic values of 0.14, 0.20, and 0.18 (Table 4A, 4B). Only in CA3 did λ change significantly, increasing to 1.75 from the normoxic value of 1.62. These data support the idea that initial volume fraction of a region is a predictor of the rise of extracellular K⁺ during ischemia; later work, however, on normoxic tissue where anisotropy was encountered cast doubt on the true hippocampal volume fractions (see Section IV.A.3).

The two studies of hypoxia discussed above used slices of normal thickness (~ 400 μm) but Newman and co-workers (245) proposed that slices cut at 1000 μm, so-called ‘thick slices’, provided a ready model of global ischemia. Diffusion studies in this model have led to unexpected results and the concept of dead-space microdomains or dead-end pores.

The key discovery was made by Patlak et al. (289) using radiotracers to show that thick slices had a lower value of λ compared to normal slices, whereas, as detailed in this review, all the prior data both in vivo and in vitro showed the opposite effect. This paradox was resolved by Hrabětová and Nicholson (148). Using the RTI-TMA method, these investigators (148) found that λ did indeed increase from a normoxic value of 1.66 to 1.99 in thick slices. However, λ dropped to 1.54 when 70 kDa dextran (dex70) was added to the bathing medium (Fig. 11, A₁-A₃, B) while α was consistently diminished to approximately 10% in all thick slices, with or without dextran. In the original radiotracer study of Patlak et al. (289), the investigators had routinely used dextran as a component of their physiological saline (244) without realizing the anomalous effect it was having on the diffusion properties of the thick slices. Hrabětová et al. (146) went on to analyze water compartmentalization in thick slices and to show that, although there was a continuous loss of [K⁺]_e from the tissue, ischemic conditions remained pervasive throughout the slice.

Fig. 11.

Combined use of RTI-TMA and IOI methods to investigate dead-space microdomains. A₁-A₃. RTI-TMA studies. A₁. Schematic of independent iontophoresis microelectrode and ISM placement in a normal 400 μm slice and a 1000 μm ‘thick’ slice. The thick slice represents a model of ischemic tissue. A₂. TMA⁺ diffusion curves in brain slices. TMA⁺ pulse applied for 50 s (horizontal bar) and detected by a TMA⁺-ISM 100 μm away. Diffusion curves are superimposed with theoretical curve (Equations 13 and 15). Representative recordings from 400 (blue curve) and 1000 μm neocortical ‘thick’ slices (red curve). As expected, the tortuosity is higher and volume fraction is lower in the ischemic slice. A₃. Representative recording from 1000 μm slice incubated with 70 kDa dextran in the bath (black curve); this brings about a paradoxical fall in tortuosity. For comparison, the diffusion curve from 1000 μm slices incubated without dextran (red curve) shown in A₂ is superimposed (Modified from Ref. 148). B. Use of IOI to study effect of added background molecules (70 kDa dextran without fluorescent label) on diffusion of 3 kDa dextran fluorescent molecules (fdex3). Top image row: Images of fdex3 taken immediately after the pressure injection (labeled as 0 s) and at 60, 120, and 180 s later in neocortical thick slices. The intensity shown in pseudo color (red highest, blue lowest) represents the concentration of the fdex3 in the tissue. The images in the upper row were taken in the absence of background macromolecules (no macro.). The images in the lower row were in the presence of non-fluorescent dex70. The intensity profiles of data (bottom), obtained along the horizontal line running through the center of the image. In the presence of dex70, the image intensity dissipated faster and therefore the collapse of the curve (blue) is more pronounced. Tortuosities were 3.66 and 2.37 in the absence and presence of dex70, respectively. (Modified from Ref. 147). C. It is hypothesized that during ischemia and other pathological conditions, cellular elements expand their volume as water moves from the extracellular to the cellular compartment and blockages are formed in some interstitial planes. Diffusing molecules that enter these pocket-like regions are delayed and tortuosity increases (left schematic). When background macromolecules, such as dex70, are added to this tissue, they become trapped in the dead-spaces. By excluding the dead-space volume, dex70 prevents marker molecules from being delayed there and tortuosity decreases (right schematic). (Modified from Ref. 147).

These diffusion studies led to the hypothesis that the increase in λ in a thick-slice model of ischemia may arise from diffusion delays in newly formed dead-space microdomains of the ECS (Fig. 11C; Section II.H) and the delays may be eliminated by trapping exogenous high molecular weight dextran molecules so that they fill in these microdomains. Hrabětová et al. (147) showed that the diffusion of fluorescent dex70 in thick slices declined over time, indicating the entrapment of such background macromolecules. Using the RTI-TMA method, it was established (147) that the reduction of λ depended on the size of the background macromolecule. Non fluorescent 70 kDa dextran was also effective in reducing λ in normal normoxic slices (400 μm thick) after hypoosmotic stress had reduced the volume of the ECS. The effect of 70 kDa dextarn was confirmed independently by measuring the diffusion of the smaller 3 kDa fluorescent dextran with the IOI method: λ decreased from 3.29 to 2.44 (147) (Fig. 11B).

3. Spreading depression

Spreading depression (SD) shares many of the characteristic changes in ECS ionic and diffusion properties associated with anoxia and ischemia but there is the important distinction that SD is a transient event that lasts for a minute or so and the affected region of tissue then returns to apparently normal conditions. This transient event typically propagates through susceptible tissue with a velocity of about 3 mm min⁻¹ (55, 342). Two early studies of changes in ECS volume fraction used ISMs and a variety of cations and anions that were concentrated in the ECS as water left the space (124, 291).

Changes in ECS diffusion parameters were studied during cortical SDs in P13 – P15, P21 and adult rats (220). During SD in all age groups, α decreased to 0.05 – 0.09 while λ increased to 1.95 – 2.07 (Table 7). After SD, both α and λ remained elevated in adults, compared to controls, and this increase persisted for more than an hour.

A study comparing diffusion parameters in cortical SD in wild type and GFAP−/− mice (11) (Table 7) revealed only small differences between the two types and overall the changes resembled those encountered in the rat. In summary, the changes in α and λ during SD in vivo are quite similar to those seen during global ischemia in vivo.

B. Mechanical injury and brain grafts

Brain injury of many kinds elicits reactive gliosis, involving both hyperplasia and hypertrophy of astrocytes, which show intense staining for GFAP (268). Such trauma may be expected to alter the ECS and these alterations may need to be taken into account during therapeutic intervention. The injuries also provide insight into the origin of some of the diffusion properties of the ECS.

1. Stab wounds

In rodents, cortical stab wounds provide a ready model to study mechanical injury. The lesion is accompanied by substantial increases in both α and λ along with increased staining for GFAP and chondroitin-sulfate proteoglycans (CSPGs) (319) (Table 7). A further study (408) of this type of injury employed both the RTI-TMA method to measure α and D* (denoted by ADC_TMA in the study) and DW-MRI to measure ADC_W in the cortex of adult rats from the third to the 35th day after a unilateral sterile cut through the cortex. Severe astrogliosis was found up to 1 mm from the injury site and mild astrogliosis up to 2 mm away in the ipsilateral cortex, but no astrogliosis was found in the ipsilateral auditory cortex or contralateral hemisphere. In contrast to GFAP staining, immunostaining for CSPGs showed increases in the whole ipsilateral hemisphere (319, 408). The mean values of α, D* and ADC_W in the contralateral hemisphere were not significantly different from those in non-lesioned, control animals. In the astrogliotic cortex, less than 1 mm distant from the wound, the mean values of α were significantly higher (α = 0.26), while the mean values of D* were lower: (4.2 × 10⁻⁶ cm² s⁻¹, λ = 1.76). Further from the wound, values of α differed less from control values. In contrast, D*, as well as ADC_W, were significantly lower throughout the whole ipsilateral hemisphere, particularly in the auditory cortex where ADC_W = 5.5 × 10⁻⁶ cm² s⁻¹; λ = 1.53. The results indicate that an increase in diffusion barriers, manifested by a decrease of D* (increased λ) and correlated with a decrease in ADC_W, occurs throughout the entire cortex of the wounded hemisphere without significant changes in ECS volume fraction, consistent with a build-up of extracellular matrix macromolecules such as CSPG.

2. Grafts

Grafts of one brain region into another often produce tissue with some of the same characteristics as those induced by stab wounds. In a study in the rat brain (364) both α and, surprisingly, λ, were significantly higher in fetal cortical grafts to midbrain than in host cortex, α = 0.34 and λ = 1.78, and in tectal grafts to the midbrain, α = 0.29 and λ = 1.85, where severe gliosis occurred (Table 7). This did not happen in fetal cortical grafts placed into a cavity in the cortex, where only mild astrogliosis was seen (364). Another characteristic feature of cortical grafts into the midbrain is the variability of α and λ, although these parameters did correlate with the morphological heterogeneity of the graft neuropil. Compared to host cortex, immunohistochemistry showed myelinated patches and a larger number of hypertrophic astrocytes in areas with high λ values, suggesting a glial origin for the increased tortuosity. The results of dopaminergic grafts are discussed below in Section V.C.2.

C. Disease models

It is very likely that the ECS, through a change in size or an impaired ability of substances to move in this domain, contributes to a number of diseases of the brain. Investigations of diffusion properties have been carried out in animal models of Alzheimer's and Parkinson's disease and in models of epilepsy, multiple sclerosis and hydrocephalus.

1. Mouse model of Alzheimer's disease

ECS diffusion parameters have been studied in the cortex of a mouse model of Alzheimer's disease. The model utilized transgenic APP23 mice in which overproduction of mutated human amyloid precursor protein (APP) leads to amyloid plaque formation (229, 349). Diffusion parameters were measured in vivo in hemizygous APP23 mice aged 6 – 8 and 17 – 25 months and in age-matched controls (Table 7). Results were compared with data obtained in the same animals using DW-MRI to measure the ADC_w (370). In APP23 mice aged 6 – 8 months α, λ and ADC_w were not significantly different from age-matched controls (for both groups, α = 0.19 – 0.20; λ = 1.47 – 1.50; ADC_w = 5.91 – 6.02 × 10⁻⁶ cm² s⁻¹). Mice at 17 – 25 months are regarded as aged and controls at this age showed decreases in α (0.13 – 0.16), which was significantly greater in females than in males. These results confirm that in mice as in rats, aging leads to a decrease in α (see Section IV.C). There was also a reduction in ADC_w in females (5.47 × 10⁻⁶ cm² s⁻¹), but no change in λ. In contrast, in aged, 17-25-month-old, APP23 mice, α was increased to 0.22 – 0.23, while λ values were increased compared to age-matched controls.

In contrast to the results just described, the deposition of beta-amyloid is associated with an increase in α, λ (Table 7) and ADC_w (370). Based on immunohistochemistry, the amyloid plaque load in the older APP23 transgenic mice was 20% in females compared to 10% in males and this gender difference correlated with impaired navigation in a Morris water maze, though not in the diffusion parameters (370). It is reasonable to assume that the volume fraction occupied by the amyloid plaques, which are located extracellularly, is not included in the value of α determined by the RTI-TMA method. If α is about 20% and the amyloid plaque load in the old female transgenic mice used by Syková et al. (370) was also about 20%, then the true ECS volume fraction would be about 40% of total tissue volume, although only 20% would be accessible to diffusing molecules.

2. Rat model of Parkinson's disease and dopaminergic grafts

Injection of 6-hydroxydopamine (6-OHDA) at any point along the nigrostriatal pathway or within the striatum results in destruction of the dopaminergic input to the striatum and is a widely used animal model of Parkinson's disease (396, 429). The model has been employed extensively to show that grafting fetal dopaminergic cells into the 6-OHDA-lesioned striatum can lead to functional recovery (40).

After transplantation of dopaminergic cells into the lesioned striatum, functional recovery appears to depend on widespread diffusion of the dopamine transmitter released by the graft and this fact led to a study with the RTI-TMA method of the diffusion properties of the ECS in the striatum of control, 6-OHDA-lesioned, intrastriatally grafted, and sham-grafted rats in vivo (311) (Table 6). Control experiments in striatum measured α = 0.19 and λ = 1.59; both these parameters were reduced in lesioned animals to α = 0.14 and λ = 1.50 but increased within single macrografts and multiple micrografts to values of α = 0.24 and λ = 1.80. Similar increases in λ were seen in sham-grafted areas, (α = 0.24, λ = 1.72). Compared with controls therefore, α and λ were reduced in dopamine-depleted regions and increased in striatal areas with grafts. It was also noted that multiple, small grafts, in contrast to their enhanced capability for dopaminergic re-innervation, impaired diffusion in a larger volume of the striatum to a greater extent than did single macrografts, presumably because of more extensive tissue damage and astrogliosis, as reported in other graft studies (see Section V.B.2).

3. Epileptic models

Seizure can be reliably induced in cortical tissue by the application of penicillin (137) or pentylenetetrazol (PTZ) (203). When applied focally, a critical tissue volume must be infiltrated with a concentration of the drug that is above a threshold concentration. These volume and threshold parameters have been established using a novel application of diffusion paradigms. First, the effective diffusion coefficients for penicillin (191) or PTZ (336) were measured using the RTP method (see Section II.B.2 and Table 2) then the drugs were pressure injected into the cortex in vivo along with TMA as a ‘reporter substance’ and the known diffusion characteristics of TMA used to estimate the critical volumes and concentrations of the drug required to induce seizure (192, 336). Direct measurements of the diffusion of the drugs in the epileptic model were not practical because the appropriate ISMs were not reliable at low concentrations. It was established that the critical parameters for penicillin to induce epileptic discharge were a spherical tissue volume of about 150 μm in radius and a concentration of 1 mM (192). For PTZ the parameters were a volume of radius 220 μm and a concentration of 1.8 mM (336).

In another set of epilepsy-related studies, the diffusion properties of the anti-epileptic drugs valproate and trans-2-en valproate (209) and verapamil (171) were measured. All three compounds diffused in the ECS with tortuosity values in the range 1.51-1.92 (see Table 2) but verapamil apparently failed to penetrate when administered to the cortical surface (171).

Frequency of epileptic seizures is higher in children than in adults (237, 329). Several factors may contribute to the higher susceptibility of the immature brain tissue to excitatory stimuli (for a review see Ref. 70). ECS volume fraction is an additional factor in seizures (12, 166, 393); though perhaps acting to reduce neonatal seizure susceptibility. As already noted, α is almost doubled in the rat cortex or hippocampus just after birth in comparison with the adult values (166, 193) (see Section IV.C). The increased volume fraction of the immature ECS is therefore expected to attenuate the concentration of released neuroactive substances, especially K⁺ and glutamate (358, 393) and might actually increase the threshold, as has been postulated for aquaporin-4 knockout mice (9, 38). Indeed, reduction of the ECS volume in the hippocampus under hypoosmolar conditions (a reduction of the osmolality of normal bathing medium by 90 mOsm) in P5 rats evokes a decrease in α to values similar to those in adults, along with an increase in λ, and is accompanied by an increase in the frequency of epileptiform discharges, while hyperosmolar conditions reduce neuronal excitability (166). Reduction in extracellular space and impaired diffusion thus may contribute to the greater local accumulation of neuroactive substances and facilitate the development of epileptic seizures.

A comprehensive study in the in vivo adult rat somatosensory cortex during pilocarpine-induced epilepsy showed that α dropped from 0.19 to 0.134 during seizure but λ remained unchanged at 1.58 (340) (Table 7). Measurement of ADC_W using DW-MRI under similar conditions showed that this parameter was significantly reduced during seizure. The study (340) also measured changes in extracellular K⁺ with ion-selective microelectrodes and extracellular lactate, glucose and glutamate as well as the lactate/pyruvate ratio using microdialysis.

4. Rat model of multiple sclerosis and inflammation

Experimental autoimmune encephalomyelitis (EAE) is a commonly used animal model of multiple sclerosis (184). Dramatic changes in the ECS diffusion parameters occurred in the spinal cord of rats during EAE (339). Induction of EAE by the injection of guinea-pig myelin basic protein caused characteristic morphological changes 17-24 days later, namely demyelination, an inflammatory reaction, astrogliosis and damage to the BBB as well as paraparesis. Paraparesis (partial paralysis of the lower extremities) was accompanied by increases in α in the dorsal horn, in the intermediate region, in the ventral horn and in white matter (Table 7). The value of λ decreased significantly in the dorsal horn and in the intermediate region while non-specific loss of TMA, as measured by k', decreased in the intermediate region and the ventral horn (339). There was a close correlation between the changes in ECS diffusion parameters and the manifestation of neurological signs.

Changes in ECS diffusion parameters can be expected during inflammation, which is often accompanied by brain edema. In another experimental model where diffusion parameters were measured, inflammation was brought about by an intracerebral inoculation of a weakly pathogenic strain of Staphylococcus aureus (199). This caused acute inflammation and an increase in BBB permeability in the abscess region but only resulted in a small increase in α and a small decrease in λ.

5. Kaolin and H-Tx rat models of hydrocephalus

The effects on diffusion of the tissue compression that typically accompanies hydrocephalus have been investigated (360) in two rat models: kaolin-induced hydrocephalus, and in the hydrocephalus Texas (H-Tx) strain of rats in which many pups manifest obstruction of the cerebral aqueduct in late gestation (161, 170). Results obtained with the RTI-TMA method were compared with those of DW-MRI performed in the same group of animals (360). In both hydrocephalus models, the thickness of the cortex was diminished and volume fraction decreased (Table 7). In the cortices of adult rats with kaolin-induced hydrocephalus, α decreased from control values of about 0.20 to 0.14, 24 h after the injection of a kaolin suspension into the cisterna magna, and to 0.11 seven days post-injection. In 21-day-old animals with inborn hydrocephalus, α measured in the cortex decreased from 0.23 to 0.16. In animals that later developed an edema of the corpus callosum, however, α values went on to increase to 0.24. In contrast to these results, ADC_w was unchanged 24 hours after the onset of kaolin-induced hydrocephalus, but it increased after seven days so there was no simple correlation between α and ADC_w.

D. Human gliomas

Brain tumors, particularly the gliomas, are among the deadliest of tumors and many patients, including children, die within 2 years (402). One aspect of brain tumors is the marked presence of CNS-specific extracellular matrix proteins, e.g. brain-enriched hyaluronan binding proteins (BEHAB) and brevican, which are expressed at high levels during initial gliogenesis and also in all types and grades of human gliomas (155). Hyaluronan binding proteins help cells to move through tissue during development and have been associated with invasive cancers. It is plausible, therefore, that the migration of cells could be critically dependent on the size and geometry of the ECS. Another issue is that the delivery of drugs to tumors, as well as their side-effects, is affected by the permeability of the BBB and by how the drug distributes in both normal and malignant tissues, which will be a function of the diffusion properties of the ECS.

Older studies, using electron microscopy (22) and sucrose space estimation (23) indicated that the ECS is larger in human gliomas than in normal brain tissue. However, in common with other conventional electron microscopy studies (see Section II.A) these investigations resulted in small control values for the size of the ECS (22) and the sucrose distribution space showed great variation (23), in part because of the difficulty of working with human tissue. The potential importance of the ECS in tumor development and treatment prompted a re-investigation of their diffusion properties with modern methods.

ECS geometry and diffusion properties in tumors, particularly malignant gliomas, were quantified with RTI-TMA measurements in slices of tissue removed from the brains of patients undergoing surgery (402, 427) (Table 7; Fig. 12). Subsequently the tumor slices were histopathologically graded according to the World Health Organization (WHO) system and proliferative activity was assessed. The average values of α and λ in control human cortex were 0.24 and 1.55, respectively (Table 4A, 4B). In anaplastic astrocytomas and glioblastomas, the average α was as large as 47-49% (Table 7). There was also an increase in λ to 1.67-1.77, which could be attributed to either astrogliosis, commonly observed in tumor tissue, or to changes in the extracellular matrix. Indeed, the increase in tortuosity in high-grade tumors correlated with an increased accumulation of matrix molecules, particularly tenascin-R (427). Tenascin is largely absent in the normal human adult brain (157, 427) (see Section IV.E.3). In pilocytic astrogliomas and ependymomas, α was significantly higher while λ was unchanged. Somewhat elevated values of α as well as λ were also found in low-grade diffuse astrocytomas. In the cellular region of high-grade astrocytomas (WHO grade III and IV), α and λ were further increased (402). Classic meduloblastomas had increased α but λ remained unchanged. In contrast, values of α and λ in oligodendrogliomas were similar to controls.

Fig. 12.

Left: Hematoxylin and eosin staining of the studied brain tumor tissues and the corresponding immunolabeling shown in insets (see Ref. 402 for details). Right: Representative TMA-diffusion curves recorded in each distinct type of tumor with the corresponding values of the ECS diffusion parameters α and λ. A: Pilocytic astrocytoma (WHO grade I). B: Diffuse fibrillary astrocytoma (WHO grade II). C: Anaplastic astrocytoma (WHO grade III). D: Glioblastoma (WHO grade IV). Scale bar = 50μm applies to each photomicrograph. (Modified from Ref. 402).

In summary, the increased malignancy of astrocytic tumors generally correlates with increases in α, λ and deposition of extracellular matrix; recent work has been reviewed by Zámečník (426). The excess matrix may contribute to the increased tortuosity. The geometry and composition of the ECS may play an important role in cancer malignancy and invasiveness. This conjecture is strengthened by the resemblance of the diffusion parameters in tumors to those encountered during development (Section IV.B; Table 4A, 4B) and such data might be used for diagnostic purposes before extensive tumor removal and, perhaps more importantly, should be considered when therapeutic drug delivery paradigms are being formulated.

VI THE BRAIN CELL MICROENVIRONMENT

A. Diffusion parameters and ECS geometry

Given the value of the free diffusion coefficient for a chosen molecule, it is the structure and contents of the ECS that most determine how the molecule actually migrates through the brain. As this review shows, a major outcome of diffusion measurements, using appropriate ‘probe’ molecules, has been to reveal some of the structural properties of the ECS.

Our present understanding of the ECS volume fraction, α, and how this was arrived at has been outlined in Section II.A. In summary, early ideas based primarily on electron microscopy suggested there was little or no ECS but later work with microscopy that better preserved the water content and diffusion studies with radiotracers indicated that the ECS occupied at least 15% of brain tissue. The work reviewed here with the RTI-TMA technique raises that estimate to about 20%. This still left open the question of the average width of the space, i.e. the distance between cells. Again, electron microscopy provided an estimate, which is widely quoted as 20 nm but this is not entirely consistent with a 20% volume fraction. This paradox now may have been resolved by a recent estimate (391) of an actual ECS width of 38-64 nm.

Kuffler and Potter (page 316 in Ref. 181) provided an elegant depiction of the topology of the ECS: “the system of spaces ... in three dimensions ... resemble the water phase of a foam.” This description implies that cellular structures of the brain – the voids of the foam – are convex and the water phase – the ECS – is highly connected so that from any given point in the ECS, another location may be reached by multiple pathways. This simple picture has been challenged by the hypothesis that the ECS may harbor dead-space microdomains (147). These microdomains have not been identified anatomically but, if they are formed by cellular invaginations or local constrictions of the ECS, they would constitute a concave region. Any molecule entering such a dead-space microdomain would have to retrace its path in order to leave so these regions at least would not be multiply connected. Dead-space microdomains might equally well be formed by glial wrappings and this too could lead to regions that were not multiply connected; Hrabětová (145) noted that regions of the brain with different glial content had different tortuosities. Whether there are more severe violations of connectivity, such as volumes of the ECS that are isolated and unreachable by molecules in adjacent regions, remains unknown. Such isolated regions are found in other porous media as the so-called critical percolation threshold is approached (pages 83-88 in Ref. 327).

B. Diffusion parameters and glial cells

It is likely that glial cells play an important role in modulating ECS diffusion parameters. Several anatomical observations support this conclusion. As described in Section IV.B, during development, gliogenesis is accompanied by a dramatic reduction in α. Furthermore, the diffusion parameters are substantially different in myelinated and unmyelinated fiber tracts (298, 409). Diffusion is isotropic in the corpus callosum and spinal cord tracts of young rats with incomplete myelination. In contrast, after myelination, diffusion in these regions is largely anisotropic. Turning to pathology, the common occurrence of astrogliosis is correlated with a substantial decrease in diffusibility.

From a physiological perspective, it is well established that neuronal activity causes a transient decrease in α (85, 86, 87, 350) and it is suspected that the main cause of this reduction is swelling of astrocytes, possibly in response to the stimulus-induced rise in [K⁺]_e; this conclusion is based partly on evidence that astrocytic swelling is the primary factor in the concomitant decrease in α during pathological states (231) (see below next Section). In such pathological states, cell swelling is usually attributed to cytotoxic or cellular edema, representing a shift of fluid from the extracellular to the intracellular compartment, accompanied by shrinkage of the ECS volume, but without an increase in total brain volume. If the BBB is breached and fluid enters the brain, vasogenic edema may occur along with an overall increase in brain volume, providing that tissue expansion is possible.

There are numerous mechanisms that might be involved in astrocytic swelling and the operation of these mechanisms may further affect the diffusion properties of the ECS. Many of the data related to this have been obtained in primary astrocyte cultures (167, 231, 287) so the applicability in the complex environment of the living brain remains to be established. Swollen astrocytes in hypoosmotic media show a regulatory volume decrease (RVD), re-establishing their normal volume by losing intracellular ions and amino acids (287). The extrusion of excitatory amino acids (e.g. glutamate) could also occur in vivo, activating receptors on neurons. In vivo, however, cell swelling is more likely to be caused by a rise in [K⁺]_e, for example during ischemia, epileptic activity, trauma and excessive stimulation of afferent inputs. Mechanistically, astrocytic swelling is a complex phenomenon. Besides the entry of water after exposure to hypoosmotic medium, other processes are in operation including the simultaneous operation of the Cl⁻/HCO₃⁻ and Na⁺/H⁺ transporters, extracellular acidosis, and uptake of KCl following a rise in extracellular K⁺, a net uptake of glutamate and Na⁺ and the accumulation of free radicals leading to lipid peroxidation and the breakdown of unsaturated fatty acids (for review see Ref. 231). It has been suggested that K⁺ accumulation and extracellular acid shifts can block ion channels in neurons and therefore function as a negative feedback mechanism suppressing neuronal activity (354).

What are the diffusion-related consequences of a decrease in ECS volume after cell swelling? The most obvious will be an increased concentration of neuroactive substances in the ECS as water leaves this compartment. For a given concentration gradient, there may be a reduction in the diffusive flux because of the fall in α and, if there is an increase in λ associated with the reduction in ECS volume, the effective diffusion coefficient for all extracellular molecules will fall, increasing the average time required for them to travel through the ECS.

C. Local glial ECS

The volume of the immediate ECS surrounding glial cells in the CNS affects membrane currents generated in response to voltage steps applied though a patch-clamp because of K⁺ accumulation just outside the cell (33, 66, 67). In the gray matter of rat spinal cord slices at different ages, which contains neurons as well as mature astrocytes and oligodendrocytes and their respective precursors (68), the occurrence of large tail-currents in patch-clamp studies is observed in oligodendrocytes but not in other cell types (66). As calculated from the Nernst equation, changes in the reversal potentials of the tail-currents reveal a significantly larger accumulation of [K⁺]_e around oligodendrocytes than around astrocytes during the depolarization of the cells, apparently caused by a more ‘compact’ ECS surrounding the oligodendrocytes. To study the effects of cell swelling on the [K⁺]_e changes evoked by a depolarizing pulse, 50 mM K⁺ or hypotonic solution was applied. These maneuvers led to an increase in evoked [K⁺]_e that was much greater in the vicinity of astrocytes than near oligodendrocytes (66, 401). These results indicate that swelling is more pronounced in astrocytes than in oligodendrocytes, and suggests that astrocytes are responsible for the majority of the cell volume changes seen in nervous tissue (66). On the other hand, the electrophysiological properties of oligodendrocytes, i.e., the K⁺ movement indicated by the presence of tail-currents, show that this type of cell may more efficiently contribute to the regulation of K⁺ changes arising from neuronal activity. Further confirmation was obtained in studies of the oligodendrocytes that are responsible for myelinating the axons of the corpus callosum in both mice (33) and rats (67). Myelination leads to changes in membrane currents consistent with a reduction in the space around the oligodendrocytes as well as an overall reduction in α (67).

The above-mentioned results prompted a quantitative analysis to determine the actual volumes of local ECS around these respective cell types (65). Based on a model (92, 308) (see Section II.H) incorporating K⁺ fluxes, Chvátal and colleagues estimated that the width of the ECS around the cell bodies of oligodendrocytes was only 0.3 – 10 nm whereas the width around the cell bodies of astrocytes was 4 – 154 nm. It is noteworthy that the latter estimate is consistent with a revised assessment of ECS width as 38 – 64 nm (391) (see Section III.C). The estimates provided by Chvátal and co-workers are only relevant to the environment of the cell body; it remains unknown what the width of ECS is in the vicinity of the fine processes that constitute most of the protoplasmic expansion in astrocytes. These results receive some additional support from several studies on the periaxonal space between the giant axon and the ensheathing Schwann cells of the squid. In a classic paper, Frankenhaeuser and Hodgkin (107) used the changes in spike-train amplitude to estimate that the periaxonal space had a width of about 30 nm. This estimate was revised upwards to a width of as much as 100 nm in a later study where the axons and Schwann cells were likely in better physiological condition (19). Further work suggested that the estimated periaxonal space was probably a ‘virtual’ space because K⁺ actually left the vicinity of the axon membrane by a combination of mesaxonal clefts, tubular systems within the Schwann cells and cellular uptake (49).

D. The tripartite (or quadripartite) synapse and diffusion parameters

Recent studies show that glial cells play several important roles in synaptic transmission. Certain synapses (‘private synapses’), or even whole neurons, are tightly ensheathed by glial processes and by the extracellular matrix; these constituents may combine to form perineuronal nets (58); other synapses are left more ‘open’. The ‘open’ synapses are likely to be easily reached by molecules diffusing in the ECS. One source of these molecules is those transmitters, such as glutamate or GABA, that may escape from nearby synaptic clefts, especially during repetitive activation, and affect extrasynaptic receptors on glia or neurons or reach a neighboring synapse. Such phenomena have been called ‘transmitter spillover’ and ‘synaptic cross-talk’ (20, 182). Cross-talk may be particularly relevant during long-term potentiation (LTP) and long-term depression (LTD) that involves the activation of both ionotropic and metabotropic receptors (152, 182, 292).

Glia themselves are increasingly seen as a source of classical transmitter molecules; when these molecules originate in glia they are known as gliotransmitters (242, 407). The release process is probably vesicular but on a slower time-scale than classical neurotransmitter release and the volume of the ECS accessed by such gliotransmitters is unknown. As demonstrated for the squid giant axon and the enveloping Schwann cells, transmitters released by neurons also act as signals to glia, which have a range of appropriate receptors and glia can release substances that act back on neurons (97). In the vertebrate CNS, glia can respond by generating changes in intracellular Ca²⁺ concentrations that may even become a wave that spreads through a local glial syncytium formed by the tight junctions that occur between many glial cells (15, 407). Such waves also may spread by the extracellular diffusion of ATP released by glial cells (17, 120, 243); a hypothesis that hints at the possibility of new forms of glial – ECS interactions, yet to be elucidated.

Improved anatomical visualization techniques (64, 121) are revealing the complex structure and huge surface-to-volume ratio of astrocytes and suggesting that each cell may occupy a distinct territory (273). There is also evidence that astrocytic extensions form local microdomains that might restrict transmitter spillover in the ECS to one or a few synapses (119).

At the level of a single synapse, three elements, the presynaptic and postsynaptic terminals and adjacent glial processes, form a unique and plastic entity that has been called a ‘tripartite’ synapse (15, 130). Indeed, if we include the ECS and its constituent matrix as a separate entity, even a ‘quadripartite’ synapse (359) (Fig. 13). Glial cells maintain not only ECS ionic homeostasis, but also ECS volume homeostasis by swelling and shrinking as a result of ionic shifts, as described above. In addition, glia produce extracellular matrix molecules (see below) and, when hypertrophied and proliferating, may form additional diffusion barriers (355, 356). Glial structures around synapses are increasingly seen as quite labile and both lamellipodal gliding as well as filopodial extension have been directly observed in brain slices (133); extensive glial remodeling also takes place during lactation in the hypothalamic supraoptic nucleus (292) (see Section IV.E.6).

Fig. 13.

Extracellular microenvironment and volume transmission. Upper panel. Synapses and the entire ECS are embedded in an extracellular matrix of unknown density. The extracellular matrix has several components, including lecticans, tenascin-R (TN-R), as well as tenascin-C in the developing brain, and hyaluronan (HA). G, glia; N, neuron. (Modified from Ref. 421). Lower panels. Extracellular communication. Short distance communication. This occurs via closed synapses that are typical of synaptic transmission. These synapses are often ensheathed by glial processes and by the extracellular matrix, forming perineuronal or perisynaptic nets. The ECS changes its diffusion parameters in response to neuronal activity and glial cell re-arrangement. In short-distance communication by diffusion, presynaptic terminals, postsynaptic terminals, glial cell processes and the ECS form a ‘plastic’ quadripartite synapse. Long-distance communication. The CNS architecture is composed of neurons, axons, glia, cellular processes, molecules of the extracellular matrix and intercellular channels between the cells. This architecture slows down the movement (diffusion) of substances in the brain, which is critically dependent on the ECS diffusion parameters volume fraction (α), tortuosity (λ) and in some situations, loss or uptake (k′). (Modified from Ref. 358).

E. Extracellular matrix

It has long been recognized that the extracellular matrix is a potentially important component of the brain cell microenvironment (335). In addition, it is well established that the extracellular matrix plays a major role in orchestrating the development of the CNS (341) and is almost certainly involved in remodeling the adult CNS after injury (232) and perhaps in some of the plastic events that are thought to underlie aspects of memory (312, 415). These important topics are outside the scope of this review, however, and we shall confine discussion to those aspects of the extracellular matrix that might affect diffusion.

The ECM is composed of negatively charged glycosaminoglycans and proteoglycans (156, 212, 269, 322, 421). From a diffusion perspective, the elements of the extracellular matrix that are most likely to be involved are the glycosaminoglycans (GAGs). A GAG is defined as a highly polymerized, unbranched polysaccharide chain composed of repeating disaccharide units (269). One of the sugar residues is always an amino sugar, which is often sulfated and the GAG is frequently attached to a protein core to form a proteoglycan. One major exception from this characterization is hyaluronan (also known as hyaluronate or hyaluronic acid), which is neither sulfated nor attached to a protein. Hyaluronan is a polymeric molecule of varying length that may exceed 1000 kDa that is synthesized by cells and extruded before being cleaved off at some point to reside wholly and freely in the ECS (269). Hyaluronan is an extremely hydrated, coiled, polymer where there may be as much as 1000-fold more associated water than polymer (186). Among the many proteoglycans are a number that have chondroitin sulfate groups and consequently are referred to as chondroitin sulfate proteoglycans (CSPGs) and another set featuring heparin – heparin sulfate proteoglycans (HSPGs) (24, 269). Within the CSPGs are a family known as lecticans that comprises aggrican, versican, neurocan and brevican. These lecticans appear to combine with hyaluronan and tenascin-R to structure the extracellular matrix (421) (Fig. 13). Tenascin itself is an oligomeric glycoprotein (96). GAGs have many carboxyl groups, and most have sulfate groups; both these endow GAGs with numerous fixed negative charges (269). Hyaluronan and CSPGs are essential components of the so-called perineuronal nets surrounding neurons in the cortex and hippocampus (37, 57, 58, 172). Härtig et al. (127) proposed that perineuronal nets act as rapid local buffers of excess cation changes in ECS and that the effectiveness of this buffering is dependent on the diffusion parameters in the local extracellular matrix in the vicinity of these nets. Extracellular matrix molecules show diverse patterns of expression (e.g. in different regions of the hippocampus, see Ref. 51).

There are several conceivable ways the extracellular matrix could change the diffusion parameters of the ECS. First, the presence of extracellular matrix molecules might increase the interstitial viscosity of the ECS so that it no longer approximated a free medium. Second, the abundance of negative changes on some extracellular matrix molecules might differentially affect the diffusion of cations and anions. Third, the extracellular matrix might regulate the width of the ECS, perhaps through the hydration of hyaluronan. The evidence for all of these roles for the extracellular matrix in the CNS will now be reviewed but note that none can yet be conclusively established.

An increased ECS viscosity has been postulated in models (324) and experiments where 40 kDa dextran was added to normal brain slices showed that an increased ECS viscosity might affect synaptic signaling (230, 331), though these results should be distinguished from a different effect when larger macromolecules were applied to a thick-slice ischemic model (148). Some fraction of the tortuosity may indeed be attributable to enhanced ECS viscosity arising from the extracellular matrix but we do not know how much.

Charge discrimination by the extracellular matrix has been established in specialized tissues like cartilage and in solutions of hyaluronan and chondroitin sulfate (215, 286) where the fixed negative charges tend to partition mobile ions in accord with Donnan equilibrium. It is unlikely that the charge density will be as high in the CNS as in cartilage, however; in addition, the presence of significant concentrations of Na⁺, Ca²⁺ and Mg²⁺ in the interstitial fluid may tend to neutralize fixed negative charges (see Section II.B). Early experiments using the RTI method (257) failed to reveal discrimination between the diffusion of small monovalent cations and anions.

The ECS might be kept patent by the presence of the massively hydrated hyaluronan, especially in the developing brain, where the width almost certainly exceeds that in the adult and where an abundance of hyaluronan has been reported (36). In cultured cellular ensembles there is evidence also that the polysialic acid content of neural adhesion molecules (NCAM) may participate in maintaining the intercellular spaces (422). Further evidence for the role of the extracellular matrix in maintaining ECS width comes from the studies on tenascin-R knockout mice where α is reduced by 22 – 26% (371). It is noteworthy that, even under extreme global ischemia where ions and water leaves the ECS, α never falls below 5% (see Section V.A.1), which may represent the extent to which the extracellular matrix can be compacted. Interestingly, under global ischemic conditions the ECS width has been estimated to be less than 10 nm, based on diffusion of 3 kDa dextran and TMA⁺ (391). Preliminary experiments (356, 357) suggest that the injection of the enzymes chondroitinase and endoneurominidase, which disrupt the extracellular matrix, have the potential to facilitate diffusion, while the addition of hyaluronic acid may retard diffusion.

F. Blood-brain-barrier (BBB) and the neurovascular unit

The journey of many substances through the ECS begins when they cross the BBB. This is the tightly-controlled interface between the blood vessels and the brain. After many years of uncertainty, the barrier in mammals is now thought to reside primarily in the thin endothelial cells that surround the blood vessels of the brain where the enclosure of the cells is completed by tight junctions (47, 129, 307). Recently, this concept has been extended to include not only the microvascular endothelium but also the adjacent astrocytes, pericytes, neurons and extracellular matrix in the form of the basement membrane with the idea that all these components are involved in forming, maintaining and controlling the BBB. This new community of elements has been called the ‘neurovascular unit’ (2, 129) and provides a complex interface for substances entering, or leaving the ECS (226).

Studies of brain vascularization indicate that most brain cells are within 8 – 20 μm of a capillary (333) so that the diffusion distance for a substance entering the brain by that route may be quite short. This has to be qualified by noting that the movement of most substances across the BBB is regulated by specific transporters and these may not always be present in the capillary that is nearest to the target cell. Finally, we note that, despite the proximity of capillaries to cells, the brain volume occupied by vessels is no more than 3% (Chapter 15 in Ref. 42).

G. Ionic transients in the ECS

Ever since the first measurements of K⁺ transients in the brain it was recognized that the restricted volume of the ECS and the relatively low value of [K⁺]_e would amplify and channel changes in this ion and others and these might act as diffusible signals between cells (247, 342). While there is no question that the resting potential of neurons and especially glia are sensitive to extracellular K⁺, the lack of specificity of this signal probably makes it less useful than that of a substance for which specific receptors exist. The resting level of [Ca²⁺]_e is also low and arguments have been advanced, based both on models and measurements, that transient extracellular Ca²⁺ depletion and local diffusion in the ECS do have functional roles (93, 323). Such extracellular ionic fluctuations may be very localized and act primarily on the cells that generate them or they may be more widespread and influence populations of cells, in which case they may be encompassed under the topic of volume transmission.

H. Extrasynaptic volume transmission

Volume transmission (VT) is defined as a signaling modality that involves the exchange of information between cells of the brain by means other than the conventional ‘wiring transmission’ mediated by neuronal circuitry and synaptic transmission (4, 109, 406, 430) (Fig. 13). In many contexts, ‘volume transmission’ is synonymous with ‘extrasynaptic’ or ‘nonsynaptic’ transmission and occasionally ‘paracrine’ transmission, although there are nuances of difference in these terminologies (253). The VT signal could be an electric field, a change in temperature or even pressure (5) but it is most commonly conceived of as being a molecule or ‘informational substance’ (334). Consequently the diffusion properties of the ECS are thought to play an essential role in VT. The notion that VT is pervasive in the CNS is widely accepted and the concept has been evoked to interpret observations that range from the spillover of neurotransmitter at a synapse to reach receptors outside the immediate postsynaptic site (168, 337, 405) to the distribution of neuroactive compounds in the cerebrospinal fluid (190, 297). It is likely also that glia play an important role in VT (e.g. Refs. 120, 243, 292). Nevertheless, relatively few definitive examples of VT have been characterized in detail, and VT has not always been explicitly identified, even when the mechanism under study meets appropriate criteria (e.g. Ref. 414). So VT remains an elusive concept that on occasion has prompted fanciful hypotheses about intercellular communication in the CNS. For all these reasons, VT would necessitate an entire critical review to do justice to the topic, which we cannot provide here.

VII. CONCLUSIONS

Molecules or particles dissolved in an aqueous medium undergo ceaseless random motion as they collide with the much more numerous water molecules. This fundamental process is sufficient to account for the aggregate movement of molecules from regions of high concentration to regions of lower concentration with a flux that is proportional to the concentration gradient. The process is diffusion and the constant of proportionality is the diffusion coefficient. The process is formalized in the diffusion equation.

It is a remarkable finding, based on more than 50 years of work with several techniques, that the diffusion equation can be applied to the behavior of molecules in the ensemble of narrow labyrinthine interstitial spaces that constitute the ECS. To correctly apply the diffusion equation, however, it must be recognized that the molecules are moving in a limited space, the ECS, and make occasional collisions with cell membranes as well as the vastly more frequent encounters with the solvent molecules. These insights enable the process of diffusion in the ECS to be characterized by the volume fraction α and the tortuosity λ. The parameters α and λ are structural descriptors of the ECS. From a theoretical perspective, once these parameters are introduced into the diffusion equation one may ignore the anatomical complexity of real tissue and just imagine it is a free medium with a new effective diffusion coefficient and a reduced distribution space for the molecules.

Using this theoretical basis, it is now clear from many experiments that α is approximately 0.2 for most regions of most brains studied. This means that 20% of the brain is located in the narrow spaces between cells. There is good reason to think that brain cells require an ‘atmosphere’ of salt solution, closely resembling the CSF. One reason is that the ion fluxes which are involved in signaling and transport require a reservoir of ions on the outside of the cell. The value of α is as large as 0.4 in the neonatal rat cortex (we do not know the magnitude in the pre-natal brain) and this may reflect a requirement for a permissive environment for cellular migration and remodeling during development. With aging, α diminishes. Volume fraction diminishes locally during intense neuronal activity and this almost certainly reflects the swelling of glia and to a lesser extent, neurons. The most dramatic changes in α are seen, however, during pathological events such as ischemia, when α drops to about 0.05. An important and unanswered question is how the normal value of α is maintained. It is likely that the extracellular matrix plays a role here, perhaps especially the extremely hydrated hyaluronan component.

Another reason for the existence of the ECS is to allow the ready movement of small molecules and this requirement necessitates an extensive interconnection of the spaces around cells. This connectedness is in part measured by the tortuosity, which, like volume fraction, is also surprisingly constant with λ approximately 1.6. This means that a small molecule will have its diffusion coefficient reduced by a factor of about 2.6 compared to that in a free solution. It was thought for a long time that the value of λ was determined entirely by the geometrical requirement that diffusing particles had to go around the cellular obstacles in the brain and this delayed them relative to the paths they would take if not hindered in this way. In reality, calculating the tortuosity is more complicated because it requires a weighted average over all possible paths between two points. Even when the calculation is carried out properly, however, it turns out that, for packed ensembles of convex cells, the tortuosity estimated in theory is always less than 1.6. This led to a search for more sophisticated concepts of the ECS and two possibilities have emerged to date. The first is that the ECS harbors dead-space microdomains and second is that the extracellular matrix is sufficiently dense so as to increase the effective viscosity of the ECS.

The discussion so far in this section has been based on the concept that a small molecule approximating an ideal point particle is diffusing in the ECS so the molecular probe is much smaller than the local width of the ECS;.this is likely to be true for the small cation TMA⁺ with which most recent data have been obtained. When much larger, globular, macromolecules are used, such as dextrans or proteins, a new behavior appears and it is seen that λ increases with hydrodynamic diameter of the molecule. This may reflect increasing interaction with the ‘walls’ of the ECS and this may be partially explained by pore models of the ECS. There is also the unresolved issue of how much the extracellular matrix might affect macromolecules. Another issue concerning macromolecules is the behavior of flexible long-chain molecules that apparently have an anomalously low tortuosity in the ECS. We still have a limited understanding of how different types of large molecule move in the ECS.

Neither the importance of dead-space microdomains nor that of the matrix have been established conclusively at this time and they remain an exciting topic for further research, while the pore model for large molecules needs further testing. In all of this work, however, models are playing an increasingly important role and as the data improve it should be possible to apply more sophisticated concepts culled from other disciplines where porous media theory has been developed and applied.

The conclusions discussed above are predicated on the assumption that the diffusion equation accurately describes the experimental data. When this is not so and deviations occur, they indicate the presence of a new property. For example, in order to fit a TMA⁺ diffusion curve accurately, a term for loss of molecules from the ECS must be present and this tells us that even these nearly ideal probes exhibit some membrane or BBB permeability. Deviations can be much more marked when the diffusing molecules are actively transported into cells or bound to receptors on membranes or the extracellular matrix. One unresolved issue here is if and when the numerous fixed negative charges on the extracellular matrix interact with charged mobile molecules. Careful experiments exploring and manipulating the deviations from ideal behavior for specific molecules may reveal the nature of the underlying kinetic process.

By manipulating the brain, for example by applying osmotic stress or by knocking out components of the extracellular matrix, or by studying specific behaviors like learning and correlating them with differences in the diffusion properties, we are acquiring evidence that the ECS may play an essential role in many brain functions. Furthermore, basic diffusion concepts have great importance for understanding and treating many pathologies. We now know how diffusion characteristics of brain tissue change in a variety of disease models and we know the free diffusion characteristics of a vast number of molecules and the behavior of a small but representative sample of those molecules in normal brain tissue. From these data we can make some useful predictions about how to deliver drugs into the brain; this is likely to be of especial relevance for the diffusion phase of convection-enhanced delivery of drugs. Diffusion measurements may also aid in diagnostic procedures by helping to define some of the diffusion properties of tissue underlying the DW-MRI and DTI magnetic resonance techniques.

The diffusion properties of the brain may be said to be controlled by the cellular populations, the neurons and the glia, through the influences they exert on their local microenvironment. The glia cells, many with vast sheet like extensions, are especially relevant here. These cells can retract and extend processes, swell and shrink to alter the ECS volume fraction and proliferate in response to injury.

This review has a avoided a detailed evaluation of the complex subject of extrasynaptic volume transmission – the idea that cells use the ECS as a communication channel for chemical, and possibly other types of signal. Mechanisms of this sort operate over a vast range of time scales and a vast range of distances. There is much evidence to be gleaned from the literature but the studies were not always designed to investigate volume transmission and there are few if any definitive investigations of this topic. Extrasynaptic volume transmission offers rich possibilities for future research and almost certainly many types of these signals are mediated by diffusion. It may well be that specific molecules are channeled to specific targets by the anisotropic structure of brain tissue or by local geometry, charge discrimination or molecular size. Whatever the mechanisms, the results reviewed here are likely to be useful in coming to understand them.