Stomatal Crypts Have Small Effects on Transpiration: A Numerical Model Analysis

Abstract

Stomata arranged in crypts with trichomes are commonly considered to be adaptations to aridity due to the additional diffusion resistance associated with this arrangement; however, information on the effect of crypts on gas exchange, relative to stomata, is sparse. In this study, three-dimensional Finite Element models of encrypted stomata were generated using commercial Computational Fluid Dynamics software. The models were based on crypt and stomatal architectural characteristics of the species Banksia ilicifolia, examined microscopically, and variations thereof. In leaves with open or partially closed stomata, crypts reduced transpiration by less than 15% compared with nonencrypted, superficially positioned stomata. A larger effect of crypts was found only in models with unrealistically high stomatal conductances. Trichomes inside the crypt had virtually no influence on transpiration. Crypt conductance varied with stomatal conductance, boundary layer conductance, and ambient relative humidity, as these factors modified the three-dimensional diffusion patterns inside crypts. It was concluded that it is unlikely that the primary function of crypts and crypt trichomes is to reduce transpiration.

Stomatal structure varies widely among plant taxa (Meidner and Mansfield, 1968). Since stomata represent the main interface for gas exchange between the leaf interior and the atmosphere, it is generally believed that their morphological and architectural features represent adaptations to environmental factors that affect transpiration and photosynthesis. In many xeromorphic or sclerophyllous species, stomata are clustered in depressed epidermal areas called “stomatal crypts” (Napp-Zinn, 1973; Metcalfe and Chalk, 1979). These invaginations of the leaf epidermis represent a prominent structural feature that is usually considered to be an adaptation to drought (Lösch et al., 1982; Larcher, 2003), under the assumption that the total leaf resistance to diffusion is increased by adding a crypt component to the stomatal component, referred to in this paper as crypt resistance or crypt conductance (resistance = 1/conductance). Moreover, trichomes that are often present inside the crypts may further increase crypt resistance.

Studies concerning the significance of the impact of the recession of stomata on leaf transpiration are sparse considering the general acceptance of this idea. Lösch et al. (1982) studied transpiration and stomatal resistance of various Mediterranean perennials, including Nerium oleander, representing a classic example of stomatal crypts filled with trichomes. The transpiration rate of N. oleander was among the highest values in the examined species, which suggests that stomatal crypts are not necessarily associated with high leaf resistances.

Recent evidence indicates that the evolution and presence of sunken and encrypted stomata are not restricted to dry habitats. Conifers with sunken stomata (which often have stomatal plugs), for example, occupy a range of habitats (Brodribb and Hill, 1997). Moreover, in a study of the gas exchange of the cloud forest species Drimys winteri, there was no evidence for a significant increase in resistance caused by sunken stomata (Feild et al., 1998). In a recent study, the association of sunken stomata with drought was investigated by analyzing the evolutionary history of Proteaceae (Jordan et al., 2008). No straightforward coupling of stomatal architecture to climate was found, but a more complex form-function relationship emerged. Only very pronounced encryption was associated with drought, whereas many other sunken or encrypted stomatal types did not appear to be drought-related (Jordan et al., 2008).

Early models of leaf diffusive resistance demonstrated the importance of stomatal dimensions and architectural variations of the leaf epidermis. A well-established mathematical model for the interrelationship between stomatal structure and resistance by Parlange and Waggoner (1970) calculates the resistance based on the number of stomata per unit leaf area and the stomatal pore area, length and depth, and takes into account that the gradient of humidity (or CO₂) “bulges out” from the stomatal pore. This effect results in a virtual prolongation of the pore channel. In a single sunken stoma, the resistances of the stoma and the stomatal antechamber are additive (Lee and Gates, 1964). If the stoma is deeply sunken and the cross-sectional area of the antechamber is similar to the area of the open pore, then the additional resistance of the antechamber will be significant. Treating a catena of resistances as additive, however, is only appropriate if (1) the architecture can be considered as being composed of connected ducts of simple architecture (e.g. cylinders) and (2) the single channel components are “tight” (i.e. there is no gas exchange across the channel walls). Gas-exchanging pores are distributed all over the walls of crypts; thus, proper assessment of diffusion resistance in such spaces requires a three-dimensional (3D) modeling approach.

Further complexity of gas diffusion through crypts arises from the presence of trichomes within these structures. Ignoring the trichomes may lead to serious errors with respect to resistance, since their presence turns the space from a simple cavity into a fibrous porous medium. Extensive research in certain technical disciplines, such as filter or textile technology, has documented the importance of fiber density, diameter, and arrangement for the permeability of fibrous materials (Tomadakis and Sotirchos, 1993; Lawrence and Liu, 2006; Shen and Chen, 2007).

In this study, transpiration through stomatal crypts was examined using a computer simulation approach. Banksia ilicifolia (Proteaceae), representing a typical example of stomatal encryption, was chosen as a case study. Microscopic analyses of the crypt architecture as well as the stomatal and crypt/trichome characteristics led to the generation of a 3D Finite Element model of a B. ilicifolia crypt. In this model, the effect of the crypt and crypt trichomes on transpiration was examined. Subsequently, model variations that considered a range of crypt architectures and stomatal characteristics were generated, with the aim of investigating the partitioning between the stomatal and the crypt resistance in situations of differing crypt and stomatal arrangement, similar to those found in nature.

RESULTS

Spatial Pattern of the Humidity Gradient

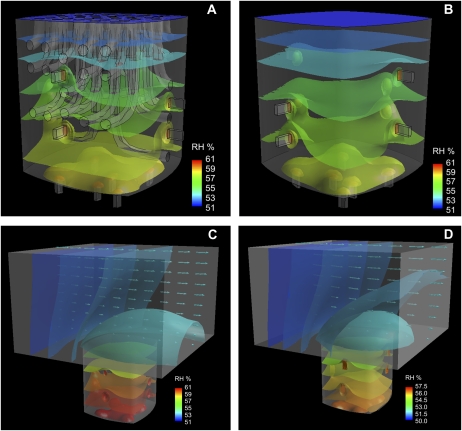
The 3D spatial humidity distribution in steady-state conditions is presented in Figure 1 for four models, namely with/without trichomes, with/without boundary layer, with standard stomata, and with narrow stomata. For all models, the distinct “vapor concentration shells” around the stomata are visible. This is true for the stomata located at the crypt bottom as well as for the stomata seated at the crypt side walls. Farther away from the stomata, the humidity contours at the stomatal pores merge with the humidity contours of the crypt. This results in vapor shells that are bulged toward the crypt bottom with a shape similar to a “hanging cloth.” For the models including a boundary layer (Fig. 1, C and D), the development of a vapor shell around the crypt aperture is clearly visible. The similarity of the humidity patterns in models that differ only with respect to the absence/presence of trichomes (Fig. 1, A versus B) indicates that trichomes do not significantly influence transpiration. The differences between the models shown in Figure 1, C and D, with respect to the humidity gradient are due to their different stomatal sizes.

Figure 1.

Humidity patterns inside four crypt models. A, CS₅₀A: standard stomata, ascending trichomes. B, CS₅₀: standard stomata, no trichomes. C, CSB₅₀: standard stomata, no trichomes, boundary layer present. D, CNB₅₀: narrow stomata, no trichomes, boundary layer present. The scales provide the color code for relative humidity (%).

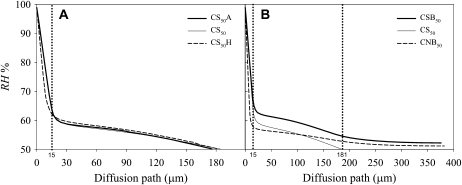
Gradients of relative humidity (RH) within stomatal pores, crypts, and the leaf boundary layer varied considerably among models. The steepest gradient was always located along the stomatal channel. Directly above the stomatal pores, the gradients became much flatter, and they became even flatter in the boundary layer (Fig. 2; for model parameters, see Table I). The steepness of the stomatal gradient increased with decreasing stomatal pore size, as expected. For the models with standard and narrow stomata, the stomatal gradients (reflecting the stomatal conductances) led to low average crypt humidity, particularly in the absence of a boundary layer (Fig. 2A). The presence of trichomes in the crypts (model CS₅₀A and CS₅₀H versus model CS₅₀) modified the humidity gradient only slightly (Fig. 2A). The addition of a boundary layer did not have a large effect on total conductance and transpiration: transpiration dropped by 10% in CSB₅₀ compared with CS₅₀ (Table I). The presence of a boundary layer also reduced the crypt gradient. Crypt conductance was 34% lower in CSB₅₀ compared with CS₅₀ (Table I).

Figure 2.

Gradient of RH along a line of transect from an internal stomatal pore (at 0 μm) to the crypt opening for CS₅₀A (standard stomata, ascending trichomes), CS₅₀ (standard stomata, no trichomes), and CS₅₀H (standard stomata, horizontal trichomes; A) and from an internal stomatal pore (at 0 μm) to the top of the boundary layer for CSB₅₀ (standard stomata, no trichomes, boundary layer present) and CNB₅₀ (narrow stomata, no trichomes, boundary layer present; B). The transition from the external stomatal pore into the crypt is indicated by a dotted line at 15 μm (=stomatal depth), and the transition from the crypt to the boundary layer is indicated by a dotted line at 181 μm.

Table I.

Summary of all Finite Element crypt models listing the parameters that were varied and the results

Models with crypts carry code C, while models with stomata on the leaf surface have code S. Model 1 is the basic model and best representation of B. ilicifolia crypts with fully open stomata. Models 1 to 3 explore the effect of crypt trichomes, where code A represents trichomes that are ascending toward the crypt aperture and code H represents trichomes that are horizontally oriented. Models 4 to 12 explore the effect of stomatal conductance at ambient relative humidities of 50%, 65%, and 80% (indicated as subscripts in the model code). Stomatal size codes are N (narrow), S (standard), and L (large). Stomatal dimensions are given in Table II. Model 13 explores the effect of reduced crypt depth, indicated by the code R replacing the C.

Parameter	Model 1	Model 2	Model 3	Model 4	Model 5	Model 6	Model 7	Model 8	Model 9	Model 10	Model 11	Model 12	Model 13
Crypt models	CS50A	CS50H	CS50	CNB50	CNB65	CNB80	CSB50	CSB65	CSB80	CLB50	CLB65	CLB80	RSB50
Stomatal size	S	S	S	N	N	N	S	S	S	L	L	L	S
Trichomes	A	H	–	–	–	–	–	–	–	–	–	–	–
Boundary layer	No	No	No	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes
RH (%)	50	50	50	50	65	80	50	65	80	50	65	80	50
Crypt depth	166	166	166	166	166	166	166	166	166	166	166	166	138.5
Transpiration rate (mmol m−2 s−1)	3.91	3.89	3.97	2.05	1.35	0.67	3.58	2.31	1.15	11.7	7.47	3.74	3.74
Stomatal conductance (mol m−2 s−1)	0.37	0.35	0.37	0.17	0.17	0.17	0.37	0.37	0.37	3.30	3.30	3.30	0.37
Crypt conductance (mol m−2 s−1)	1.66	1.62	1.78	1.52	1.25	1.07	1.17	1.02	0.93	1.51	1.41	1.36	1.37
Crypt effect (%)							15.1	14.8	14.9	48.4	48.5	48.5	11.3
Analogs with stomata on surface							SSB50	SSB65	SSB80	SLB50	SLB65	SNB80
Transpiration rate (mmol m−2 s−1)							4.22	2.71	1.35	22.6	14.5	7.26
Stomatal conductance (mol m−2 s−1)							0.39	0.39	0.39	2.26	2.26	2.26

Stomatal and Crypt Conductance and Transpiration

To check the model approach, the conductances of the models with superficial stomata were compared with estimates obtained by applying the equation of Parlange and Waggoner (1970). For example, the model with superficial stomata of standard size (for model parameters, see Tables I and II) had a stomatal conductance of 0.39 mol m⁻² s⁻¹, which compared favorably with a stomatal conductance of 0.35 mol m⁻² s⁻¹ resulting from applying the equation of Parlange and Waggoner (1970).

Table II.

Crypt and stomatal parameters of the Finite Element model variations

For explanations of the model names, see Table I. na, Not applicable.

Crypt Parameters								Stomatal Parameters
Model	Diameter	Depth	No. of Trichomes	Trichome Diameter	Trichome Orientation	Porosity	No. of Stomata	Pore Width	Pore Length	Pore Depth
	μm	μm		μm		%		μm	μm	μm
CS50A	140	166	36	9	Ascending	94	14	4 (standard)	9	15
CS50H	140	166	37	6 and 8	Horizontal	94	14	4 (standard)	9	15
CS50, CSB50, CSB65, CSB80	140	166	No trichomes	–	–	100	14	4 (standard)	9	15
RSB50	140	138.5	No trichomes	–	–	100	14	4 (standard)	9	15
CNB50, CNB65, CNB80	140	166	No trichomes	–	–	100	14	1.8 (narrow)	9	15
CLB50, CLB65, CLB80	140	166	No trichomes	–	–	100	14	10 (large)	20	10
SSB50, SSB65, SSB80	na	na	na	na	na	na	na	4 (standard)	9	15
SLB50, SLB65, SLB80	na	na	na	na	na	na	na	10 (large)	20	10

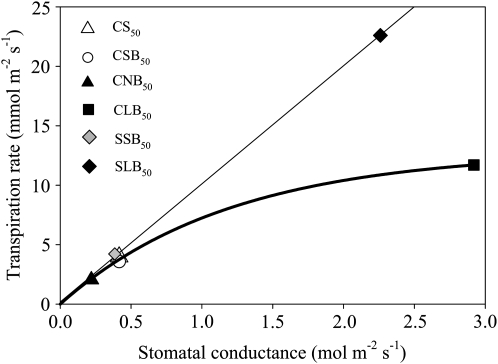
The stomatal conductance values were different for the models with different stomatal sizes, but they were hardly affected by crypt or boundary layer properties, as expected (Table I). The dominant role of the stomata is evident in Figure 3, showing a strong relationship between stomatal conductance and transpiration rate, with minor effects of trichomes and boundary layers. In models with standard stomata, the presence of a boundary layer decreased transpiration by 10% and the presence of trichomes decreased transpiration by 2% (Table I). Only in models with “large” stomata, which had unrealistically high stomatal conductances, did crypts have substantial effects on transpiration. Changes in ambient RH affected transpiration rate but not the relative magnitude of the effect that crypts have on transpiration rate (“crypt effect” in Table I; compare models CSB₅₀, CSB₆₅, and CSB₈₀).

Figure 3.

Transpiration rate against stomatal conductance of crypt models CS₅₀A (standard stomata, vertical trichomes), CS₅₀ (standard stomata, no trichomes), CS₅₀H (standard stomata, horizontal trichomes), CSB₅₀ (standard stomata, no trichomes, presence of boundary layer), CNB₅₀ (narrow stomata, no trichomes, presence of boundary layer), CLB₅₀ (large stomata, no trichomes, presence of boundary layer), SSB₅₀ (superficial standard stomata), and SLB₅₀ (superficial large stomata). White symbols represent the models without a boundary layer, whereas shaded symbols represent the models including a boundary layer (black, crypt stomata; gray, superficial stomata).

Crypts with the same dimensions showed, contrary to stomatal conductances, significant variation in conductance, depending on stomatal dimensions and whether a boundary layer was present or not (Table I). The presence of trichomes decreased crypt conductance by only 5% to 9% (compare models CS₅₀A, CS₅₀H, and CS₅₀; Table I). Decreasing crypt depth by 16% led to an approximately proportional increase of crypt conductance of 15% (model RSB₅₀), as expected. Interestingly, factors that also showed a large influence on crypt conductance were stomatal conductance, boundary layer conductance, and RH. At all RHs, crypt conductances were lowest in models with intermediate stomatal conductances. Crypt conductances were 13% to 23% higher for models with narrow compared with standard stomata, corresponding to a 50% decrease in stomatal conductance (Table I). When RH was raised from 50% to 80%, crypt conductances decreased by 30%, 21%, and 10% for narrow, standard, and large stomatal models, respectively (Table I). The presence of a boundary layer decreased crypt conductance by 34% (models CS₅₀ and CSB₅₀), although it is worth noting that transpiration rate and the RH gradient in the crypt decreased by only 10%. Crypt conductance thus depended not only on the structure of the crypt but also on the water vapor sources (stomata) and on the environmental conditions.

DISCUSSION

The results of this numerical study provide detailed accounts of the effects of stomatal encryption and crypt trichomes on the humidity profile, total leaf conductance, and transpiration. Of course, crypts and trichomes will also affect overall conductances to CO₂, but the analysis of these effects involves further complexities (see below). The models demonstrate that, at realistic stomatal conductances, stomatal encryption causes only minor reductions in leaf transpiration. This small effect occurs despite a near doubling of the epidermal surface area and very strong clustering of stomata in the crypts. Internal crypt surface area in B. ilicifolia is about five times larger than the crypt pore area, and crypt openings occupy about one-fifth of the area of the abaxial side of the leaf. The very high density of stomata at the bottom of the crypts represents a very moderate stomatal density when expressed per leaf surface area (190 mm⁻²). In fact, species in the Banksia genus that have stomata on the surface tend to have more stomata per unit leaf surface area than species with crypts (Hassiotou et al., 2009a).

Conductances estimated by the model are in reasonable agreement with empirical values for B. ilicifolia. Maximum measured stomatal conductance of well-watered plants of the species is 0.36 mol m⁻² s⁻¹ (F. Hassiotou, unpublished data), which is very close to the value of 0.37 mol m⁻² s⁻¹ in the models with open stomata of standard size (e.g. CS₅₀A). Crypt conductances cannot be measured in leaves, but the values obtained here are consistent with estimations using validated simpler equations (discussed below).

In the models with standard stomata, which represent B. ilicifolia leaves with open stomata (models CSB₅₀–CSB₈₀), the crypt effect on transpiration was only 15%. As stomata close, the stomatal contribution to total resistance increases and crypt effects become even smaller. Jordan et al. (2008) found that in the Proteaceae, deep stomatal crypts evolved preferably in dry climates. Those authors defined deep crypts as having a depth that is at least twice the diameter of the crypt opening. According to this criterion, the B. ilicifolia crypts do not fall in the deep crypt category and thus may not have evolved as an adaptation to dry environments. If increased crypt depth results in a roughly proportional decrease of crypt conductance, as suggested by model RSB₅₀, increasing the depth of the basic model CS₅₀A to a value equaling twice the diameter would yield a crypt conductance of approximately 1.15 mol m⁻² s⁻¹, which is still almost three times as high as the maximum stomatal conductance measured for this species.

While the contribution of crypts to total leaf conductance is generally small, their influence is maximized at high stomatal conductance (i.e. when stomata are large and numerous within crypts). Interestingly, stomatal densities at the crypt bottom, which are up to 900 mm⁻² in Banksia species, are positively correlated with crypt depth (Hassiotou et al., 2009a). Therefore, crypt effects are largest in the species with deep crypts that are known to have evolved in dry environments (Jordan et al., 2008), supporting the idea that there may be a water-saving advantage in these more extreme forms of crypts, perhaps when such species respond to temporarily enhanced water availability by fully opening their stomata. It is to be expected that the spatial distribution of stomata inside a crypt has some influence on the effect of crypts on transpiration. For example, if stomata are located more closely to the crypt aperture, transpiration is somewhat higher (with all other parameters constant).

An important and novel outcome of the models is that crypt conductance is quite dependent on stomatal conductance and the external environment (i.e. on the factors that define the rates at which water vapor can enter and leave the crypt). Changes in crypt conductance without changes in crypt structure are caused by complex changes in humidity gradients at different transpiration rates. Crypt conductance decreased when transpiration rates decreased due to a higher atmospheric humidity or due to the presence of a boundary layer, whereas the change in crypt conductance with increasing stomatal conductance was more complex. It should be reiterated at this point that the composite stomata-crypt diffusion pathway is not a simple resistance-in-series duct. Changing the stomatal pore area, with all other parameters remaining constant, will change not only stomatal conductance but also the spatial humidity distribution inside the crypt, affecting crypt conductance. An impact of boundary layer thickness on crypt conductance is to be expected, since the development of a boundary layer above the crypt allows for the development of water vapor shells above the crypt apertures. The presence of a boundary layer decreases the transpiration rate and increases the influence of the crypt on diffusion. With a thick boundary layer, a crypt will impede transpiration more strongly than under conditions that favor a thin boundary layer (e.g. with high wind velocities). It must be noted, however, that better quantitative assessment of the influence of boundary layers on crypt conductance will require the modeling of populations of crypts on leaf surfaces to properly describe the RH surfaces. Such a model would also allow the definition of vapor cups around crypts and a clear delimitation between crypt resistance and boundary layer resistance, which was not possible in the single crypt model.

A decrease in stomatal conductance, shown in models with narrow stomata, caused an increase in crypt conductance, whereas a decrease in boundary layer conductance (model CSB₅₀ compared with CS₅₀) caused a decrease in crypt conductance. This means that under conditions that are usually associated with aridity, partial stomatal closure and high boundary layer conductance, crypts appear to offer no great advantage with respect to water conservation. The limited impact of crypts on total leaf resistance is consistent with the observation that species with crypts can actually have high rates of transpiration (Lösch et al., 1982; Mohammadian, 2005) and therefore that crypts are not adaptations for inherently low rates of transpiration. In environments where constitutively low rates of transpiration have adaptive value, plants can achieve that with low stomatal density and smaller stomata or by stomatal regulation that is sensitive to environmental and plant signals, a more flexible way to control transpiration than through a fixed resistance component.

Ignoring the presence of crypts in measurements of gas exchange will overestimate the stomatal component of leaf resistance and underestimate the magnitude of stomatal responses to environmental conditions or physiological status. However, given the relatively minor influence of crypts on gas diffusion, it could be argued that for some applications an approximate value of crypt resistance is sufficient, rather than an elaborate model-derived value. One possible approach is to use the Parlange and Waggoner (1970) equation that is commonly used for stomata. In the case of a crypt with the standard dimensions (Table II), this equation yields a crypt conductance of 0.9 mol m⁻² s⁻¹, which is somewhat lower than most models in Table I. An even simpler approach that considers diffusion through an impermeable layer perforated with pores having the dimensions and density of the crypts in the leaves (Hassiotou et al., 2009a) yields a crypt conductance of 1.5 mol m⁻² s⁻¹. Such deviations from the values obtained by detailed 3D modeling are probably similar to the inaccuracy associated with boundary layer conductance estimates. When greater accuracy is required, 3D modeling is recommended.

A clearly counterintuitive result of this study was the small influence of crypt trichomes on transpiration. Neither their presence nor their spatial arrangement had a substantial influence on crypt resistance. A crypt with trichomes represents a fibrous porous material. Of fundamental importance for the diffusion through a porous material is its porosity. Obviously, diffusion of a gas can only occur in the void space of a porous material, and the restriction of the gas movement increases with decreasing void space. Furthermore, the presence of solid material leads to a deviation of the diffusion paths from straight lines; in other words, the molecules are forced to travel around the solid elements. This average increase of the diffusion path length is termed “tortuosity” (τ; Shen and Chen, 2007):

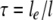(l)

with l_e = path length in the porous material and l = shortest path length.

The usual practice of considering the impeded diffusion in porous materials is to scale the diffusion coefficient of a gas with τ. The actual value of τ depends on porosity (P), which is defined as the fractional value of the air with respect to the entire crypt volume, and on the structure of the porous material. A collection of different approaches to τ = f(P) can be found in Shen and Chen (2007). One suitable approach for fibrous materials is provided by the numerical treatment of Tomadakis and Sotirchos (1993), which gives the tortuosity for random arrays of freely overlapping cylinders:

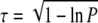(2)

The scaling of the diffusion coefficient reads as:

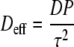(3)

with D_eff = the effective diffusivity.

If we use the approach of Tomadakis and Sotirchos (1993) for freely overlapping cylinders for models CS₅₀A and CS₅₀H, then D_eff = D × 0.94 = 2.28 × 10⁻⁵. If we now compare this result with the simulated effects of the trichomes on crypt conductance, then we find the values 0.93 and 0.91 for the ratios of crypt conductances between CS₅₀A and CS₅₀ and between CS₅₀H and CS₅₀, respectively. Thus, the simulation results agree well with the technical literature on gas diffusion through fibrous materials.

In the Proteaceae, Jordan et al. (2008) found no correlation between the presence of trichomes and aridity, suggesting that crypt trichomes are not primarily an adaptation related to plant water use. If dense trichome fillings occur in crypts, only a detailed study of the crypt porosity will provide a realistic estimation of the effective diffusivity of these structures. Any increase of the diffusion resistance for water vapor out of the leaf will also hinder CO₂ diffusion into the leaf. If structures like crypts have evolved as adaptations to optimize plant water use, it must be through a greater effect on water loss than on CO₂ uptake. For simple structures like stomata, the relationship between resistances for water vapor and CO₂ is given by the relative values of their diffusivities. For a complex structure like a stomatal crypt, it may not be appropriate to directly calculate resistance to the inward flux for CO₂ from the resistance to the outward flux of water, because the 3D diffusion space of the crypt may cause larger differences in the pathways of water vapor and CO₂ compared with superficial stomata.

For example, for the model CS₅₀, RH at the external stomatal pores varied between 56.9% and 61.1%, despite the fact that all internal pores had identical RH (internal pore = stomatal pore leading into the leaf interior). In this context, it is important to consider that CO₂, compared with water vapor, experiences additional resistances in the mesophyll before reaching the chloroplasts. Therefore, it is to be expected that these additional resistances and the local concentration gradients inside the crypt caused by the 3D diffusion space would lead to substantial differences at the internal stomatal pores with respect to CO₂ concentration. It is thus not possible at the moment to estimate the effects of crypts on CO₂ diffusion.

Mesophyll resistance is increasingly being recognized as a significant factor in photosynthesis (Flexas et al., 2008) and has been shown to be relatively high in thick Banksia leaves (Hassiotou et al., 2009b). The diffusion of CO₂ through the tortuous mesophyll air spaces is a component of mesophyll resistance. In leaves with crypts, this pathway is considerably shortened, because stomata in crypt walls are much closer to the palisade mesophyll than stomata that would be positioned on the abaxial leaf surface. In this context, deep crypts with high porosity may actually facilitate diffusion of CO₂ to palisade cells. Evidence supportive of this was presented by Hassiotou et al. (2009a), who showed that in the genus Banksia, encryption increases with increasing leaf lamina thickness. Whether or not the diffusion resistance within the intercellular air spaces affects photosynthesis is dependent on the leaf anatomy and porosity, the cell shape and packing, and the pattern of stomatal openings (Morison et al., 2005). Facilitated diffusion by crypts may be particularly beneficial for thick leaves with densely packed mesophyll cells. Expansion of the crypt models to include substomatal cavities and mesophyll air spaces will give new insight into the potential benefits of these anatomical traits for the diffusion of CO₂ and water vapor and their impact on photosynthesis and water use efficiency.

Stomatal crypts and crypt trichomes may have adaptive value unrelated to their effects on gas diffusion. Alternative roles of stomatal encryption are discussed in Hassiotou et al. (2009a) and include stomatal protection from mechanical damage (Haworth and McElwain, 2008) and from harsh climatic conditions. Trichomes may provide a barrier to invasion by pathogens and blockage by dust or liquid water (Levin, 1973; Brewer et al., 1991; Paling et al., 2001).

In future studies, it may be worthwhile to examine the possible consequences of temperature gradients across the transpiration path in crypts. Our models assumed isothermal conditions. Banksia species are sclerophyllous and frequently exposed to intense insolation. Such conditions may cause temperature gradients in these thick and dense leaves, because heat conductivity of leaves is small (Vogel, 2009). Stomata placed at the bottom of crypts may be less exposed to the extreme temperatures of the leaf surface, particularly in dynamic conditions such as fluctuating insolation. Leaf-to-air temperature gradients strongly affect evaporation and are themselves affected by evaporative cooling. This feedback behavior may be influenced by crypts, which cause spatial separation of the surfaces that exchange heat and water vapor.

CONCLUSION

This study shows that under conditions of limited soil moisture when stomata will tend to close, crypts do not contribute much to water conservation. In contrast, when plants have higher stomatal conductances, the influence of crypts on water loss might be more significant. Such situations would be expected in arid-zone plants that respond to rainfall pulses or perhaps during periods of high early morning stomatal conductances after overnight rehydration. Trichomes had only minor effects on diffusion in the modeled crypts and thus do not appear to have a water-saving function. Thus, there is limited justification for interpreting the presence of crypts and, in particular, crypts with trichomes, as indicators of aridity in palaeobotanical and palaeoclimatological investigations. Future studies must focus on the effects of crypts with different characteristics (architecture, stomatal density and distribution, as well as trichome density) on diffusion of water vapor and CO₂, and explicitly include mesophyll diffusion of CO₂. Deep invaginations into the mesophyll may facilitate diffusion of CO₂ to the sites of assimilation, especially in thick leaves with densely packed mesophyll cells.

The influence of crypts on total leaf resistance depends on the detailed anatomy and on stomatal and boundary layer resistances. The question of the actual benefits of encrypted stomata is not fully resolved. Model simulations are useful in exploring diffusion processes within complex 3D leaf structures where approximations based on electrical resistivity networks are potentially flawed.

MATERIALS AND METHODS

Study Species

Initial model parameters were based on a species of the genus Banksia (Proteaceae), which is an excellent example of stomatal encryption, with the majority of its species possessing crypts (Mast and Givnish, 2002). The species Banksia ilicifolia has a crypt architecture that is representative for the genus. Diffusion was first modeled for a typical crypt, after which morphological variations both at the crypt and stomatal levels were introduced, and their effects on transpiration were examined.

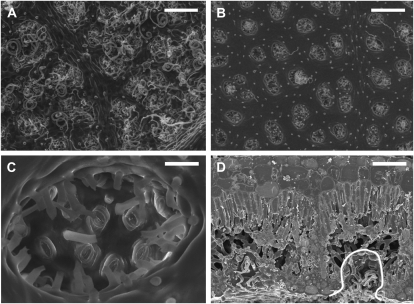
B. ilicifolia is a shrub or tree (up to 10 m high) that is relatively common in the southwest part of Australia and occurs within 70 km of the coast in open woodlands on sandy soils and low-lying flats (George, 1996). Its leaves have serrated edges and nonrecurved margins. Crypt and stomatal traits were measured on young fully mature leaves of 4-year-old plants. The plants were grown from seed in 10-L pots containing a mixture of river sand and potting mix in Perth (Australia) and were maintained outdoors. Microscopic examination confirmed that stomata were exclusively situated in crypts on the abaxial leaf surface, as was reported previously by Mast and Givnish (2002). In mature leaves, trichomes were almost absent from the adaxial surface, where trichome bases indicated that trichomes fell off during leaf development; however, the abaxial leaf surface was pubescent, with trichomes mainly situated inside the crypts and often extending outside the crypts covering part of the surface (Fig. 4).

Figure 4.

Leaf and stomatal crypt anatomy of B. ilicifolia. A and B, Scanning electron micrographs of the abaxial leaf surface before (A) and after (B) partial removal of trichomes. Bars = 250 μm. C, Scanning electron micrograph showing a single crypt after removal of trichomes. Trichome bases and stomata are clearly visible. Bar = 35 μm. D, Cryoscanning electron micrograph of a leaf transverse section. A crypt is highlighted. Bar = 92 μm.

Microscopy

Optical, scanning, and cryoscanning electron micrographs were used to analyze 100 crypts of young, fully mature leaves of B. ilicifolia using ImageJ software (Abramoff et al., 2004). The following parameters were determined: crypt diameter, crypt depth, number of stomata, trichome diameter, trichome number, and stomatal dimensions. Crypt diameter was calculated from the measured crypt area assuming a circular shape for all crypts. Crypt area was measured in variable-pressure scanning electron micrographs (Philips XL30) of the abaxial leaf surface after partial removal of surface trichomes by applying wood glue that was peeled off once hardened. Crypt depth was measured in optical transverse sections obtained using fluorescence microscopy (Zeiss Axioplan 2). The number of stomata per crypt, trichome diameter, trichome number, and stomatal dimensions were measured using both scanning (Philips XL30) and cryoscanning (Cambridge S360, Cryo-system Oxford CT1500) electron microscopy, capturing top and side views of crypts. The leaf and crypt anatomies of B. ilicifolia are shown in Figure 4.

Simulation Method

For diffusion in a complex structure comprising sources and/or sinks, Fick's law in its general form must be used:

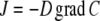(4)

with J = diffusional flux, D = diffusion coefficient, C = concentration of diffusing substance, and grad = the differential operator (∂/∂x, ∂/∂y, ∂/∂z), with grad C representing the concentration gradient in all three spatial directions.

The mathematical description of the diffusion process is complete if the principle of mass conservation is included. Then the diffusion equation reads as (∑ = ∑(x, y, z, t, C), t \,= time, div = divergence):

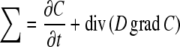(5)

It is usually impossible to solve Equation 5 analytically for complex structures containing sources or sinks. This problem can be assessed by numerical methods, such as the Finite Element method. This mathematical scheme converts the partial differential equation into a set of algebraic equations (Zienkiewicz and Taylor, 1989). Application of this method requires the subdivision of the structure considered into a mesh consisting of elements with a simple geometry, such as triangles for two-dimensional problems or tetrahedrons for 3D problems. The calculation is then performed for each element. Since the elements making up the considered structure are connected at their nodes, an approximate solution is achieved for the entire structure. The degree of exactness increases with the number of elements and converges to the exact value. In practice, the number of elements is increased until the solution does not change significantly.

3D Finite Element models with a high spatial resolution can now be run on common personal computers. In this study, the commercial Finite Element-based program FIDAP (version 8.7; ANSYS) was applied. FIDAP is a Computational Fluid Dynamics program that includes a diffusion module. The meshes were generated using the mesh generator GAMBIT (2.1; ANSYS). The results were calculated for the steady state.

Model Setup

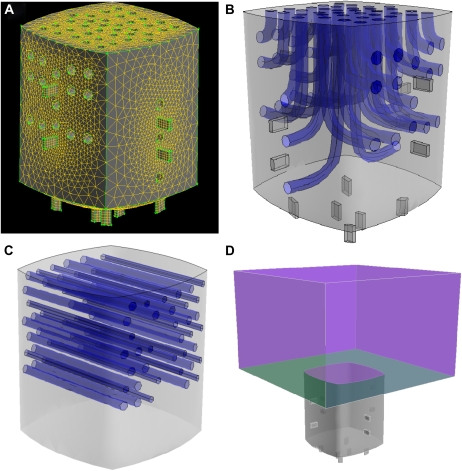
For the first model (CS₅₀A) representing the typical morphology of a B. ilicifolia crypt, the parameters are shown in Table II. The real dimensions of B. ilicifolia stomata are 24 μm and 3 to 6 μm for average guard cell length and width, respectively. The typical depth of a stomatal pore is 6 to 10 μm (measured for B. littoralis). The crypt was modeled as a cubic shape with slightly curved walls and bottom (Fig. 5A). Crypt depth was defined as the maximum extension from the crypt aperture to the crypt bottom, and crypt diameter was defined as the maximum distance between opposite side walls. Generation of a Finite Element mesh required a slight simplification of the trichomes, which were modeled as growing out of the crypt walls and turning toward the crypt aperture (Fig. 5B). In accordance with the scanning electron microscopy studies (Fig. 4), 14 stomata were positioned inside the crypt with two stomata being placed at each side wall and six stomata located at the bottom of the cavity (Fig. 5B).

Figure 5.

Graphical representations of some Finite Element models. A, 3D representation of the Finite Element mesh of the B. ilicifolia model CS₅₀A. The holes in the outer walls show the positions of trichomes. The “boxes” on the crypt wall are the stomata. B, Transparent representation of the model showing the trichome architecture of model CS₅₀A. C, Transparent representation of the model showing the trichome architecture of model CS₅₀H. Here, the trichomes are arranged parallel to the stomatal aperture (stomata not shown). D, Model CSB₅₀ as an example of a model with a boundary layer. The boundary layer is represented by an air space above the leaf surface (green).

Temperature for all simulations was set at 20°C, and the model was devised to be isothermal. External concentration of water vapor was set at a RH of 50%, and that at the internal stomatal pore was set at 99%. This corresponds to vapor pressure deficits of 1.17 and 0.02, respectively. The internal pore is defined here as the plane where the stoma leads into the leaf interior. The plane where the stoma leads into the crypt or the external environment (in leaves without crypts) is termed the external stomatal pore. The stomata of these basic models are modeled as rectangular pores with length of 9 μm, width of 4 μm, and depth of 15 μm.

Variations of the basic model included models without trichomes, with trichomes in different orientations (Fig. 5C), with narrower and larger stomata, and with reduced crypt depth. Moreover, the effects of different ambient RH and the addition of a leaf boundary layer (Fig. 5D) were examined for crypts with different stomatal sizes. For a description of the parameters of the different models, see Table II.

In all models with trichomes, porosity was kept constant despite the difference in trichome arrangement. Porosity (P) is defined as the fractional value of the air with respect to the entire crypt volume:

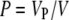(6)

with V_p = volume occupied by air and V = entire crypt volume.

A local boundary layer was constructed assuming a leaf of 0.02 m width and a distance from the leading edge of 0.01 m, at a moderate wind velocity of 0.32 m s⁻¹. For these conditions, the local wind velocity close to the leaf surface can be calculated according to the following equation (Vogel, 1996):

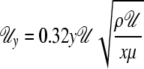(7)

with U_y = wind velocity at a perpendicular distance y from the surface, U = ambient velocity, x = distance from the leading edge in the wind direction, ρ = air density, and μ = viscosity of air. The oncoming wind carried the ambient humidity of 50%.

In the models to which no boundary layer was added, the crypt aperture was directly exposed to ambient humidity. This corresponds to conditions of high wind velocity and turbulence intensity that prevent the development of a significant boundary layer. General theory suggests that at the leaf surface the wind velocity will be close to zero (Eq. 7). This is also expected for higher wind velocities, leading to a turbulent boundary layer, since in these cases a laminar sublayer close to the leaf surface will develop (Vogel, 1996). To evaluate the impact of the crypts on transpiration, models were devised in which stomata were not encrypted but located on the leaf surface. Stomatal density per unit leaf area corresponded to the mean stomatal density per unit leaf area of B. ilicifolia leaves (190 mm⁻²). In these models, stomata were of standard or large size (dimensions listed in Table II), a boundary layer was present, and ambient RH was 50%, 65%, or 80%, as in the corresponding variants of the crypt model.

The program calculates RH at each mesh element for the steady-state situation. From this humidity matrix, the diffusion through a single stoma, and therefore transpiration rate for each stoma of the crypt, can be calculated using Fick's law (Eq. 4). Transpiration rate per crypt was computed by summing the transpiration rates of all individual stomata. Transpiration per leaf area (J_leaf) was obtained by multiplication of the transpiration rate per crypt with the crypt density (n_crypt = number of crypts per unit leaf area; Eq. 8):

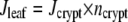(8)

Stomatal and crypt conductances were derived by dividing the transpiration rate by the corresponding humidity gradients. For the stomatal conductance (g_s) of the superficial stomata, the humidity gradient included the superstomatal air layer but not the boundary layer (Parlange and Waggoner, 1970; Vesala, 1998):

(9)

The height of the air layer (H_{air layer}) was calculated according to Vesala (1998), with n_stomata = stomatal density and r = radius of stomatal pore:

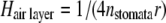(10)

The conductance of the stomata situated in the crypt was calculated based on the humidity gradient between the internal and external pore. A superstomatal air layer was not considered, because the crypt stomata, unlike those of the superficial stomata models, were part of a composite duct (stoma-crypt); therefore, the gradient outside a stoma represented the gradient inside the subsequent duct section “crypt.”

Crypt conductance (g_c) was calculated by dividing the transpiration rate per leaf area by the average difference between water vapor concentration at the external stomatal pores and the ambient water vapor concentration; that is, the humidity in the outer atmosphere:

(11)

Using ambient air is appropriate for a single pore (stoma or crypt), since the superstomatal air layer is undefined in this case (Parlange and Waggoner, 1970; Vesala, 1998; see Eq. 10).

To check the model, the conductances of the superficial stomata models were compared with estimates obtained with the equation of Parlange and Waggoner (1970). To this end, the width of the stomatal rectangle was multiplied by 4/π to correct for the area difference between a rectangular and an elliptical pore (Parlange and Waggoner, 1970).

The quantitative influence of the crypts on transpiration rate, termed “crypt effect,” was calculated by relating the transpiration rate of the crypt models to the transpiration rates of the models with superficial stomata at the same ambient RH and stomatal size:

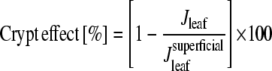(12)