Supporting the Process of Exploring and Interpreting Space–Time Multivariate Patterns: The Visual Inquiry Toolkit

Abstract

While many data sets carry geographic and temporal references, our ability to analyze these datasets lags behind our ability to collect them because of the challenges posed by both data complexity and tool scalability issues. This study develops a visual analytics approach that leverages human expertise with visual, computational, and cartographic methods to support the application of visual analytics to relatively large spatio-temporal, multivariate data sets. We develop and apply a variety of methods for data clustering, pattern searching, information visualization, and synthesis. By combining both human and machine strengths, this approach has a better chance to discover novel, relevant, and potentially useful information that is difficult to detect by any of the methods used in isolation. We demonstrate the effectiveness of the approach by applying the Visual Inquiry Toolkit we developed to analyze a data set containing geographically referenced, time-varying and multivariate data for U.S. technology industries.

Introduction

Exploring and analyzing large space– time–attribute data sets is challenging due to data complexity (i.e., potential interactions among space, time, and attributes) and tool scalability issues (i.e., the challenge of coping with both data volume and high dimension). In this paper, space–time–attribute refers to geographically referenced, time-varying data involving multiple thematic attributes; the focus of methods and tools described is on identifying and interpreting spatio-temporal, multivariate patterns in these data. Existing approaches to pattern identification and interpretation, from entirely computational to visually led methods, are limited in analyzing complex patterns that include space, time, and attribute components together. Moreover, traditional information visualization methods do not support analysis of large data sets. Pattern recognition, machine learning, and other computational methods have been developed explicitly to deal with large and high-dimensional data sets, but typically do not provide ways to incorporate both space and time, nor do they leverage the power of human vision and cognition to help analysts notice and quickly interpret patterns in complex data. The goal of this research is to bridge this gap by developing analytic methods that couple visual, computational methods and human expertise in productive ways. The approach presented here was developed within the broad research framework provided by visual analytics, defined as “the science of analytical reasoning facilitated by interactive visual interfaces” (Thomas and Cook 2005, p. 4).

This research introduces a Visual Inquiry Toolkit (VIT) which provides information analysts with a flexible interface to integrated visual, computational, and cartographic methods that support an overview+detail strategy for identifying and interpreting patterns in space–time–attribute datasets of relatively large size. Overview+detail describes a strategy for supporting multiple levels of detail in an interactive visual display (Plaisant et al. 1995). This strategy is best known through Shneiderman’s (1996) information-seeking mantra: overview first, zoom and filter, with details on demand. We propose adding a step to Shneiderman’s mantra—information synthesis, which refers to capturing novel, relevant patterns and reorganize them to yield more useful information. Beyond support for the extended visual overview+detail strategy, the VIT also emphasizes flexible interaction strategies designed to enable human knowledge and judgment to be coupled productively with computational pattern-finding methods to support an iterative analysis process.

The remainder of the paper is organized as follows. In the next section, we review related literature. Following that, we discuss our strategy and methodologies, with a focus on representation issues; then, we demonstrate an interactive visual analytics approach for identifying and interpreting spatio-temporal multivariate patterns. Finally, the advantages and limitations of the approach and possible further work are discussed.

Related Work

A starting point for our approach is past work on visualizing multivariate data. The commonly used data representations for multivariate visualization include tables and scatter plots; more sophisticated methods include scatterplot matrices (Andrews 1972), parallel coordinate plots (Inselberg 1985), matrix permutation (Mäkinen and Siirtola 2000; Bertin 1981), and multivariate glyphs (Pickett et al. 1995). A comprehensive review of the methods can be found in a paper by Keim et al. (2005). All of these methods, however, have difficulty representing large data sets. As the number of data items/variables goes up, the potential for over-plotting on displays goes up as well. Two major solutions have been proposed to address this problem. One is to reduce the data size being displayed by grouping individual data records into subsets (e.g., aggregation or clustering); in this case, collective characteristics of the grouped data are visualized and investigated (Guo et al. 2005; Johansson et al. 2004; Ward 2004). The other solution is data selection, which allows zooming, filtering, and focusing on a subset of data (Keim et al. 2005). This research takes a combination of both approaches.

Visualization of space–time–attribute data are challenging because traditional single 2D or 3D views do not provide enough dimensional space to display all space, time, and multiple attribute components simultaneously. A widely adopted method for space–time data is to represent these data in a three-dimensional view where time data are visualized in the third dimension over a two-dimensional map (Kwan 2000; Lodha and Verma 2000; Kapler and Wright 2004). This method, however, has severe limitations for visualizing multivariate data of even modest size (e.g., hundreds of data records for more than two or three variables). Some other systems use animation to display time, presenting sequential representations of spatial information at a moment of time (Slocum et al. 2000; Oberholzer and Hurni 2000; Stojanovic et al. 1991). However, this technique imposes burdens on human short-term memory to retain temporal changes, thus it is not suitable for complex, large data sets. Two approaches that show some potential to address these issues are: (1) small multiple adjacent views (MacEachren et al. 2003) and (2) linked views (MacEachren et al. 1999; Andrienko and Andrienko 2001; Robinson et al. 2005). We extend both approaches, combining them with computational clustering methods.

Successful analysis of large, space–time–attribute datasets requires more than advances in visual representation or computational methods. Human interaction also plays important roles in identifying and interpreting complex patterns. Considerable effort has been directed toward methods for interactively detecting multivariate patterns (Harri 2004; Seo and Shneiderman 2002) and temporal patterns (Buono et al. 2005; Carlis and Konstan 1998). While several studies have focused on spatio-temporal data (Gatalsky et al. 2004; Kwan 2000), few approaches have been developed to interactively search for patterns using strategies that consider all aspects of space, time, and attribute components.

Most of the research within the geovisualization and information visualization communities on interaction has been focused primarily on developing methods and mechanisms to support real-time interaction with individual and linked views, using brushing, linking, focusing, and other direct manipulation methods (Shneiderman 1997; Andrienko and Andrienko 1999; Dykes 2005). As has been outlined from the perspective of both science (Gahegan 2005) and intelligence analysis (Pirolli and Card 2005), however, a goal of both exploratory geovisualization and visual analytics, generally, is to support an analytical process that is often complex, iterative, and carried out over an extended period of time. Thus, approaches to support interaction need to move beyond interaction as an action to interaction as a process. A key component in supporting an analytic process is provision of interaction methods that allow analysts to create, save, retrieve, and share analytic artifacts (Pike et al. 2007). The concept of a pattern basket, detailed below, is a step in this direction intended specifically to support saving, comparing, revising, and sharing patterns identified in complex space–time–attribute data sets.

Our own previous work (Guo et al. 2006) specifically addresses space, time, and multiple attributes. In that complementary work, the computational and visual methods are integrated and applied to single session analysis (e.g., an exploration session intended to uncover hidden patterns and/or generate hypotheses about multivariate relationships). The visual-computational tools described in the paper cited above, while interactive, put the emphasis on computational methods and offered relatively limited human interaction support and no explicit support for a sequential knowledge building process. The work introduced in this paper emphasizes support for a spiral multi-session analysis process with a systematic overview+detail strategy, allowing human judgment to steer the analysis process, refine the computational outcomes, and synthesize relevant, potentially useful information. Specifically, our methods and tools incorporate flexible human interaction focused on process, including: a highly manipulable, parallel coordinate plot that supports overview plus detail analysis; a dynamic dendrogram integrated with a reorderable matrix; and pattern baskets as a mechanism for supporting a multi-step analytical process of pattern identification and interpretation.

This paper expands in several ways upon a preliminary report on the above extensions presented in (Chen et al. 2006). For example, we detail the complementary roles played by various visual and interactive methods. We also clarify the way in which a Self-Organizing Map (SOM) can facilitate multivariate analysis and provide details on the color encoding applied to the multivariate clusters generated. Another instance of expansion is the provision of details on how to construct an holistic overview and detailed views for visualizing spatio-temporal, multivariate patterns, and how the techniques of static link and dynamic link, combined with the color scheme generated by the SOM, facilitates the construction of the overview. And, we formally introduce and illustrate application of the Pattern Basket concept—a reasoning artifact to facilitate externalizing cognition (for discussion of reasoning artifacts in visual analytics, see chapter 2 in Thomas and Cook, 2005); and clarify the concept of information synthesis and the way pattern baskets supports it.

Visual Inquiry Toolkit: An Integrated Approach

In this section, we provide a detailed, six-part introduction to the components of the Visual Inquiry Toolkit. First, we outline the tasks for which the toolkit is designed and the strategies for supporting those tasks. Second, we introduce the approach for applying visual-computational methods to multivariate data analysis. Third, we focus on how support for overview+detail is implemented for the space-time component of the data. Fourth, we outline the strategy for linking among toolkit components. Fifth, we detail how hierarchical clustering and ordering tools are integrated with interactive visualization tools. Finally, we introduce the concept of pattern baskets for supporting an analytical process.

Tasks and Strategy

Our approach to conceptualizing tasks and the strategy for supporting them builds on past research, particularly that by Peuquet (2002), Andrienko and Andrienko (2005b), MacEachren (1995) and Bertin (1983). As detailed in that research, questions posed by space-time-attribute data analysis usually involve three components: where (space), when (time), and what (attribute/thematic objects) (Peuquet 1994). Drawing upon Peuquet’s ideas, Andrienko et al. (2003) discussed three basic analysis tasks in detail as they relate to exploratory visualization: when + where → what; when + what → where; where + what → when. The tasks follow a general question scheme A+B→X, where A and B denote known information and X stands for unknown information. Based on Bertin’s concept of levels of reading (elementary, intermediate, and overall), Andrienko et al. (2003) introduced two “search levels” to the analysis tasks: (1) an elementary level in which a task deals with individual objects (such as a time, a place or a characteristic); and (2) a general level in which a task considers a set of objects as general situations.

A sample elementary level task related to the U.S. industry analysis presented below is: What were the industry sales in the 2001 for the Kansas? A question of this style can easily be answered by a database query. The more challenging questions are the general level ones such as: What changes in industry composition have occurred in the U.S. during the past decade? What geographical areas have similar or unusual composition, and what characterizes them?

The general questions are hard to answer through database queries alone because exploratory goals are initially vague and we do not know which data components (what, when, where) to query; thus, formal queries are difficult or impossible to construct. Furthermore, a system that forces users to query data iteratively, and view and act on a partial result at each iteration, is time-consuming, error-prone, and often does not produce the desired results (Kapler and Wright 2004). Hence, analysts working with large and complex data sets need to first gain an overview of the entire data set to quickly understand the scope and structure of the data set and discriminate between interesting and uninteresting content (Greene et al. 2000), then focus on a subset of data with more viable patterns in detail views.

To support the approach suggested above, this research employs the overview+detail strategy, which follows the three steps in Shneiderman’s (1996) “information-seeking mantra” as interpreted by Keim et al. (2004). Step one is Overview—examine the representation of a summary of the entire data, which presents a context from all space, time, and attribute perspectives. Step two is Zoom and filter—select interesting patterns or data subsets revealed by the holistic view or by previous processes. The third step is Details on demand—focus on the patterns identified in the previous step, inspecting details from various perspectives to form or valid hypotheses. This mantra has been adopted widely as a framework for exploratory tool development in Information Visualization (Keim et al. 2004). Here, we propose one more step in the process, directed explicitly toward supporting an extended analytical process: information synthesis—capture novel, relevant patterns and reorganize them to yield more useful information. The four steps form a spiral process to incrementally search, identify, and analyze patterns and, eventually, to synthesize useful information out of the patterns for knowledge construction and decision-making.

Initially introduced by DiBiase (1990), the concept of information synthesis has been discussed repeatedly as a core stage in the geovisualization process by MacEachren and colleagues (1994; 2004; 1997) and Gahegan and Brodaric (2002). The concept has also been considered in the Information Visualization community by Spence and Tweedie (1998), who focus particularly on the role of synthesis in the task of information retrieval, specifically on integration of insights from multiple information retrieval actions that leads gradually to refined problem formulation. Synthesis has also been recently highlighted by the visual analytics community (Thomas and Cook 2006; Keim et al. 2006). In spite of attention to the concept, limited progress has been made toward tools that support synthesis (for one recent effort targeted at support of intelligence analysis focused on heterogeneous and unstructured information, see Wright et al. (2006)). The research presented here addresses this partially by a specific focus on a method of information synthesis focused on identifying and interpreting patterns and relationships within numerical data sets that include space, time, and multiple attribute components.

The proposed strategy and methods are implemented in the Visual Inquiry Toolkit. Specifically, the toolkit employs a Self-Organizing Map (SOM) (Kohonen 1997) to cluster multivariate data, then encodes the clusters with a 2D diverging-diverging cartographic color scheme (Guo et al. 2005). The colored clusters are visualized in a space–time matrix—a re-orderable, graphical tabular view in which cells represent categories (or multivariate clusters) rather than individual values. Supported by hierarchical clustering methods, the matrix orders and reorders the layout of the rows, thus presenting an overview of coarse-grained patterns and exposing major explicit patterns by grouping similar entities. A parallel coordinate plot, linked to the matrix, serves as a legend for interpreting the multivariate patterns in a detail view. A matrix of small multiple geographic maps supports the examination of both the spatial distribution of multivariate patterns and changes in that distribution over time (Chen et al. 2006; Guo et al. 2006). Finally, a Pattern Basket (a place in which an analyst can store interesting fragments of information during an extended analysis process) supports pattern synthesis. We demonstrate our research and the Visual Inquiry Toolkit through an application to a benchmark data set, provided for the IEEE InfoVis 2005 contest (Grinstein et al. 2005), analyzing the changing characteristics of U.S. technology industries and companies over time. These data are described below, briefly, and used to exemplify aspects of the toolkit discussed in subsequent sections.

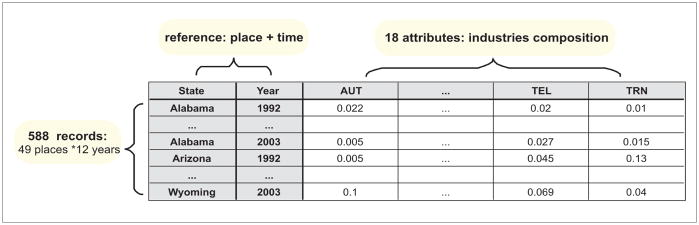
The full dataset used here to demonstrate the Visual Inquiry Toolkit capabilities has approximately 563,000 records, involving 87,659 companies over 15 years. The focus of the analysis is geographic pattern change for national industry composition over time. Hence, the data are aggregated by state and year as shown in Figure 1. The 18 industries to be analyzed are: factory automation (AUT), biotechnology (BIO), chemicals (CHE), computer hardware (COM), defense (DEF), energy (ENR), environmental (ENV), manufacturing equipment (MAN), advanced materials (MAT), medical (MED), not-primarily-high-tech (NON), pharmaceuticals (PHA), Photonics (PHO), computer software (SOF), Test & Measurement (TAM), telecommunications and Internet (TEL), transportation (TRN) and subassemblies and components (SUB).

Figure 1.

Aggregated data model in a tabular view. It has 588 records (49 places * 12 yr) and 20 columns. The state and year columns constitute a “reference column,” and 18 attribute columns represent 18 industries, respectively. Hence, each record has a state–year as reference and 18 attribute values, each of which is an industry’s percentage of total sales. For each record, the 18 attribute values depict the industry composition for a given state in a given year; the sum of the 18 values is equal to 1; hence, 100 percent for this set of industries.

Visualization of Multivariate Patterns

The parallel coordinate plot (PCP) method (Inselberg 1985) is a widely used technique for visualizing multivariate data. We have extended the method in several ways to facilitate its use as a multivariate “legend” for interpreting the multivariate patterns (i.e., generated by the Self-Organizing Map) within a multi-view application that combines visual and computational methods.

A well known problem with PCPs is overplot-ting—data patterns become illegible as the number of data entities displayed increases. This problem has been addressed primarily from two directions (Andrienko and Andrienko 2005a; Edsall 2003; Ward 2004; Guo et al. 2005; Novotny and Hauser 2006): (1) computationally grouping the data (e.g., aggregating or clustering) to achieve an overview with fewer data groups displayed; and (2) data selection (zooming, focusing, filtering) to investigate individual data records or a subset of data in a detail view. Both methods are adopted in our research.

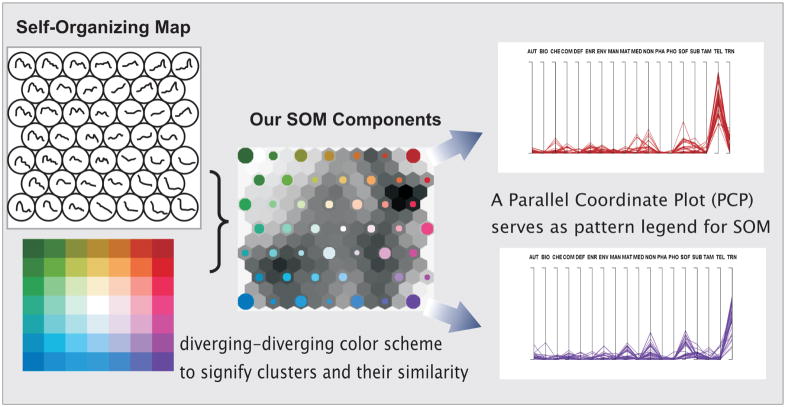
Grouping of data can be achieved by a wide array of computational clustering methods (Hastie et al. 2001). Among them, the Self-Organizing Map (SOM) has proved to be an effective method for multivariate clustering (Vesanto and Alhoniemi 2000; Kohonen 1997); in addition, the SOM preserves inter-cluster relations with a 2D layout. Basically, a SOM clusters a set of n-dimensional data vectors, dividing the entire dataset into a group of non-overlapping subsets, each of which is a cluster that contains similar multivariate vectors. The SOM projects the clusters to an array of circular nodes on a 2D space (as shown in the diagram at the left-top corner of Figure 2), where a string in a node depicts a multivariate profile (e.g., industry composition). More importantly, the SOM places similar clusters in neighboring nodes, while distinct clusters are placed at the four corners. Johansson et al. (2004) demonstrated an integration of a SOM with a PCP for the exploration of large multivariate data. Guo et al. (2005) also adopt the similar approach, enhancing interpretation of clusters by applying a 2D cartographic color scheme (left bottom graph in Figure 2) to the SOM to highlight similarities and differences of clusters. Specifically, a color is used to encode a multivariate pattern uniquely, and similar clusters are assigned similar colors and different clusters are assigned distinct colors (Figure 2). This approach is adopted in our research and is demonstrated next.

Figure 2.

A 2-D cartographic color scheme is applied to a Self-Organizing Map (after Kohonen (2001)), the result is displayed in the SOM component (middle). A circular node in the SOM component represents a cluster, the multivariate characteristics of which are depicted in a PCP (i.e., the red node is depicted by the PCP at right-upper corner). Similar clusters (thus the nodes) are assigned similar colors and different clusters are assigned distinct colors. A node’s size is proportional to the amount of data items contained in the cluster.

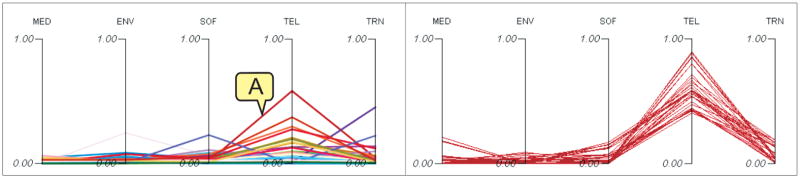
In the example shown in Figure 3, percentage data for 18 industries (as explained in Figure 1) are clustered by our SOM component. To illustrate, the figure shows five of the industries displayed in the PCP. Each industry is treated as a variable and represented by a vertical axis in the PCP. All axes in the PCP are scaled to the same maximum and minimum value (from a proportion of zero to a proportion of one, representing that industry’s contribution to the total); thus, the value of a string at each axis is directly comparable, and the slope of line segments between strings is meaningful. A string in the PCP depicts the industry composition for an observation (i.e., a state/year combination). The strings are assigned different colors by the SOM to represent different industry compositions. For example in the right plot of Figure 3, a red string represents an industry composition dominated by Telecom (TEL) industry with small amounts of Transportation (TRN), some Software (SOF) and Medical (MED) industries, while the purple string represents an industry mix dominated by Transportation (TRN) industry.

Figure 3.

The PCP displays five industries, each represented by an axis. We select the salient red string marked as A in the overview, and switch the PCP to the detail view mode to display the data items belonging to the cluster. The outline of the strings depicts a pattern of the cluster; it has a high percentage of Telecom (TEL) industry, a percentage of Transportation (TRN) industry, and some percentages of Software (SOF) and Medical (MED) industries.

Our PCP implementation supports switching between overview mode (to display data groups) and detail view mode (to display individual data items). This method is useful for visualizing relatively large datasets (Robinson et al. 2005; Andrienko and Andrienko 2005a; Guo et al. 2006). In the overview mode (Figure 3, left plot), a string represents a cluster (by displaying the median value of the cluster’s data items for each attribute) and depicts a multivariate pattern for the cluster. In the detail view mode (Figure 3, right plot), a single string represents an individual data item (in this case, the industry composition for a specific state in a specific year); the red strings together represent a cluster of related data items. The outline of the red strings depicts the pattern of the cluster. The overview implementation in the PCP alleviates the overplotting problem while also reducing the “noise” generated by individual variations, exposing multivariate patterns in a more legible manner.

Visualization of Space–Time–Attribute Patterns

In order to support the proposed overview+detail strategy, space–time–attribute data need to be visualized in a holistic overview and detail views. The toolkit follows the common multiple-view strategy of breaking the complex information into manageable pieces and displaying each piece in multiple-linked views. Specifically, spatio-temporal, multivariate data are broken into a spatio-temporal and a multivariate component; the former is visualized in a space–time matrix and a map matrix, and the latter is visualized in the PCP and the SOM. All the views are linked; in this section, we focus on the link between the space–time matrix and the PCP.

Matrix-based representations of data are a common way to depict tabular data graphically (as shown in Figure 1). Bertin (1981) was perhaps the first to highlight the analytical power achieved when users are given the ability to order the rows and columns of a matrix to search for patterns. Several others have built upon this idea by proposing dynamic linking between a re-orderable matrix and a map (Gluck 2001). Here, we extend and apply the re-orderable matrix method to space–time–attribute analysis.

Specifically, we develop a space–time matrix (Figure 4, left) in which (for data used here) rows represent places (states) and columns represent times (years). A cell reflects a coarse-grained multivariate pattern of the 18 attributes via its color. The detail of a multivariate pattern is depicted by the PCP that is linked to the space–time matrix. The link is achieved on two levels: a dynamic link and a static link. In this research, the former is to link the information for a single (or a subset of) data item(s) via human interaction, while the latter is to link the information for all the data items without human interaction.

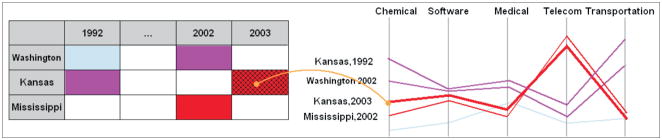
Figure 4.

A dynamic link between the space–time matrix and the PCP. The matrix cell highlighted with a texture is linked to the red string highlighted with bold in the PCP; the link is shown as a virtual curve in orange. Through the dynamic link, we know that in 2003, Kansas had an industry mix depicted by the highlighted red string: high percentage in Telecom; some amount of Software; and a smaller amount of Transportation, Chemical, and Medical industries.

We first briefly describe the dynamic link and then focus on the static link. A dynamic link (Becker and Cleveland 1987; Buja et al. 1991) typically means simultaneously highlighting of one-to-one, one-to-many, or many-to-many visual elements across views so that various aspects of the data can be investigated concurrently. In this research, a data item is referenced by place and time represented as a matrix cell, and its attributes are displayed in the PCP. The dynamic link is achieved by the mouse-over operation—when a mouse is moved over a matrix cell, the corresponding string in the PCP is highlighted, or vice versa (Figure 4); or by brushing—selecting multiple data records in a view, causing them to be highlighted in all the views.

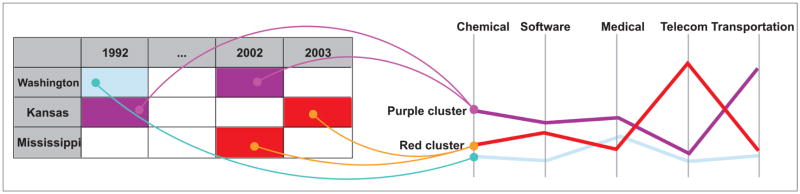
Static link, as described by Andrienko and Andrienko (2005b), refers to applying the same visual expressive means to the pieces of related information so that they are known as “linked” to visualize the same “thing” or related things in the multiple views even without human interaction. In this research, static link is achieved by applying consistent color scheme generated by the SOM to represent the multivariate clusters, across all the views. Static link is not a new concept. Cartographers (Olson 1981; Brewer 1994), since the 1970s, have used logical color-coding strategies to depict individual categories, and the relationships among categories, for map depiction. An example is a legend for a bivariate map as illustrated by Andrienko and Andrienko (1999; Figure 8, p. 370). Here, we use the term to emphasize linkages across views in a static (thus symbolic) manner. Static links are essential for constructing a holistic overview of spatio-temporal and multivariate patterns because they allow visually distinguishing multiple data clusters from all spatial, temporal, and multivariate perspectives simultaneously, thus exposing major patterns in the overview without human interaction. Establishing the links without human interaction is important at the initial stage of data exploration, when little is known about the data or with which data items one wishes to interact.

Figure 8.

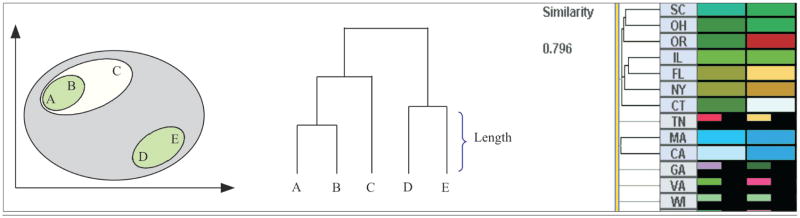
A data set {A, B, C, D, and E} is agglomeratively clustered and visualized in a dendrogram (middle). In this research, a dendrogram (oriented vertically) is attached to the matrix (right), with similarity value ranging from 0 (meaning not similar) to 1 (meaning identical). States with similarity values less than the user-controlled threshold value (currently 0.796 as specified by the vertical bar) are filtered out (e.g., Tennessee, Georgia, Virginia, Wisconsin).

The implementation of static link is as described below. A cluster of data carrying a multivariate pattern is assigned a unique color generated by the SOM. The multivariate pattern of the cluster is displayed in the PCP, and the spatio-temporal reference of each data item is represented as a matrix cell in the same color as the cluster. The result is a static link between the matrix cells and a string in an overview-mode PCP established via the unique color as shown in Figure 5. A typical analysis case in Figure 6 illustrates how a temporally varying pattern within a single state is visualized via a static link. We will demonstrate the benefits of static links and the holistic overview in later sections, when they work together with human interactions.

Figure 5.

Static link. A space–time matrix is statically linked to an overview-mode PCP via colors, as illustrated by the virtual curves. The interpretation is: Kansas–2003 and Mississippi–2002 had a similar industry mix (shown by the red string in the PCP). Similarly, Washington–2002 and Mississippi–1992 had a similar industry mix (purple string).

Figure 6.

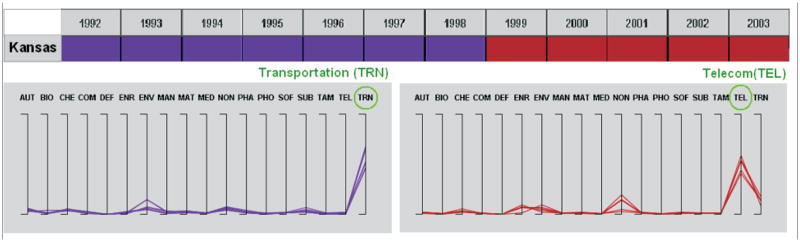
The matrix row representing Kansas has two distinct colors—purple and red—during the period 1992– 2003. Each snapshot of the PCP (in detail-view mode) depicts a pattern: purple strings depict an industry mix for Kansas in 1992–98 dominated by Transportation, while red strings depict a Kansas industry mix in 1999–03 dominated by the Telecom industry. Kansas had some Environmental industry during both periods. The state switched focus from Transportation (purple) to Telecom (red) in 1999; while maintaining a focus on Environmental through the period 1992 to 2003.

Complementary Linked Views

To expose spatial patterns more effectively, a map matrix is coupled to the space–time matrix and PCP via the static and dynamic link. The map matrix is composed of small multiple geographic map views ordered by years (Figure 7, top-right). These maps each depict the multivariate cluster results derived by the SOM, using the same color scheme as in the space–time matrix and PCP. While each individual map is useful for displaying multivariate patterns across space, the multiple yearly ordered maps are particularly useful for uncovering how geographic patterns change over time.

Figure 7.

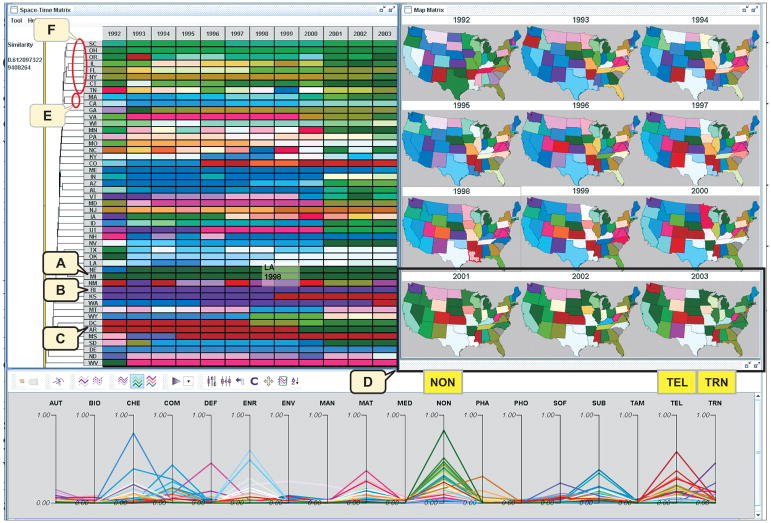
An overall view of spatio-temporal multivariate patterns. The PCP is in overview mode showing clusters rather than individual state–year composition. (A) Green clusters: Nevada and Michigan have NON as the dominant industry in all the years. (B) Purple clusters: Rhode Island, Kansas, and Washington have TRN as the dominant industry in most years. (C) Red clusters: Washington, DC, Arkansas, Mississippi, and Kansas have TEL as the dominant industry in some periods. (D) In the last row of the map matrix (2001–2003), many states change to green, indicating a shift in relative importance of non-primary high tech industry.

The space–time matrix, map matrix, and PCP complement each other to construct a holistic overview of complex patterns from spatial, temporal, and thematic perspectives. The space–time matrix and map matrix display the salient, multivariate, spatio-temporal patterns as distinct color regions (e.g., (A), (B), (C), and (D) in Figure 7), while the PCP depicts the multivariate component of the patterns for either a group of space–time entities (in overview mode) or an individual state–time entity (in detail view mode). For example, the green region (A) in the space–time matrix indicates that some constant multivariate pattern occurred in Michigan and Nebraska for all the years. The pattern is interpreted in the PCP as an industry composition dominated by non-primary-high-tech (NON). In addition, we notice that many the matrix rows are ordered to group states with similar industry composition over time together. The matrix allows columns (years) to be ordered as well. However, because a relatively short run of yearly data is available for this application, we fix the order of columns in calendar order and focus on the patterns uncovered by re-ordering the places (rows).

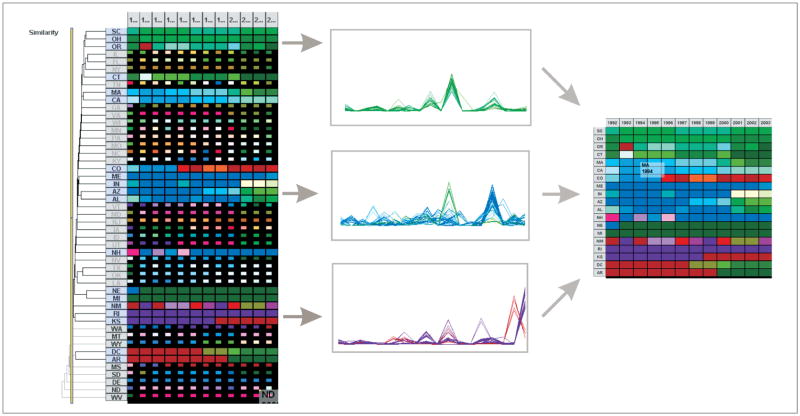
While the space–time matrix can be used with any ordering method, the Visual Inquiry Toolkit employs agglomerative hierarchical clustering methods to derive 1D ordering of the matrix rows. The general approach has been found to be effective for pattern identification (Seo and Shneiderman 2002; Bar-Joseph et al. 2001). We first discuss the hierarchical clustering methods. An agglomerative clustering method typically includes three basic steps: (1) initially treat each data item as its own leaf cluster, (2) find and merge the most “similar” pair of clusters (e.g., (A) and (B) in Figure 8); and (3) repeat step one and two until all the clusters are agglomerated in one root cluster, forming a cells are shrunken to a quarter of their original size). The remaining rows (in full size) are those rows where attention should be focused on at the moment. A detailed application of the dendrogram is illustrated in the section entitled Exploratory Pattern Analysis.

The entire hierarchical cluster solution is used to derive 1D ordering of the matrix rows. A simple and fast ordering mechanism could be merging two clusters, always putting the cluster containing more leaf clusters on one side (e.g., top), and the other cluster opposite it. When applied to the single-link algorithm, this ordering approach results in ordering from clusters that are more similar (i.e., with short branches) to those that are less similar (i.e., with long branches). For example, as shown on top of the dendrogram in Figure 7, when cluster E (contains two states: California, Massachusetts) and cluster F (contains eight states from South Carolina to Tennessee) are merged, cluster F is put on the top. Ordering algorithms is beyond the scope of the discussion in this paper, hence readers are directed to Bar-Joseph et al. (2003), Bar-Joseph et al. (2001) and Guo and Gahegan (2006) for advanced information. In order to overcome limitations (or biases) of computational ordering methods, our space–time matrix also supports manual matrix ordering; this is particularly useful for identifying hidden and complex patterns and for synthesizing information, as demonstrated below.

Pattern Basket

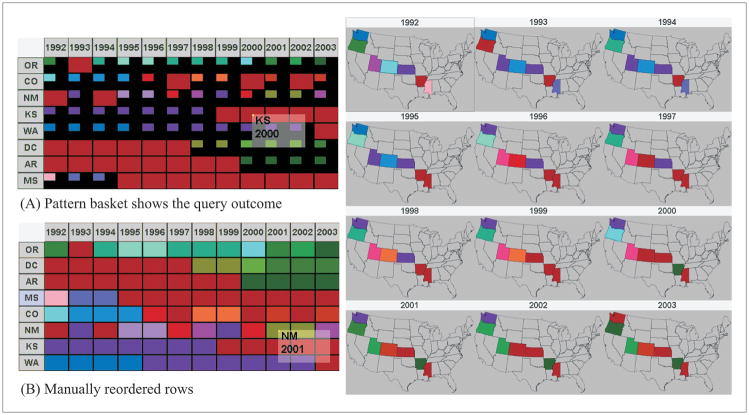
To support identification of complex, implicit spatio-temporal patterns in a multiple session data analysis process, a new concept—a Pattern Basket—is introduced. A Pattern Basket provides a way of externalizing cognition through external representation (Scaife and Rogers 1996; Zhang 1997; Reisberg 1987), helping human cognition to identify complex and implicit patterns that may be missed by computational methods and/or may not become apparent until multiple steps in a spiral analytical process have been carried out. In this paper, the term externalizing refers to “the act of creating and modifying an external representation” (Nakakoji and Yamamoto 2003). Graphical representation plays important roles in helping human cognition because appropriate external representations are critical in conveying information correctly and more efficiently (Scaife and Rogers 1996; Zhang 1997). In the Visual Inquiry Toolkit, a Pattern Basket is a variation of the space–time matrix where some discovered patterns are stored, and where an analyst can manually readjust the representations of patterns as part of the interpretation process—specifically, change the sequence of rows in the matrix to highlight specific space–time–attribute features of interest. By manually adjusting representations generated by computational methods, analysts can incorporate their expertise and domain knowledge. This increases the opportunity to expose and interpret complex, implicit, and relevant patterns that computational methods are unable to extract (as shown in Figure 13). In addition, while focusing on the patterns exported to the Pattern Basket, the analyst can still view the space–time matrix, map matrix, and PCP, thus having access to the contextual information in the overview. By comparing the focus and the context, insights are often derived.

Figure 13.

States previously focused on TEL industry are exported into the Pattern Basket (snapshot A on the left). A state–year that focused on TEL is represented by a red matrix cell (or a geographic unit in a map). Those states (Oregon, Washington) having few red cells are unimportant and are therefore removed. Then the matrix rows in the Pattern Basket are manually reordered as shown in the snapshot B. Previously hidden spatio-temporal patterns are exposed: Washington, D.C. and Arkansas changed color from red to green in the late 1990s, indicating a switch in focus from TEL to NON industry during the time. Mississippi, Colorado, and Kansas switched to TEL in later years.

In addition to a role in enabling cognition, external representations provide a memory aid for complex, multi-step tasks (Zhang 1997). The Pattern Basket also serves this role. When analyzing a large data set carrying complex spatio-temporal patterns, pattern identification often requires repeated processes carried out by an analyst over hours or even multiple days. It is unlikely that human memory can hold all the discovered patterns (explicit or implicit), along with other potentially useful information, during an extended exploratory analysis process. A visual analytical tool must allow analysts to off-load the discovered patterns and to retrieve, later, what was found when it is thought to be relevant. The pattern basket component enables an analyst to expand the capacity of human memory to an external memory—the basket. Specifically, interesting and potentially useful regions/rows discovered in the main space–time matrix are exported (copied) to one or multiple baskets for temporal storage for further investigation.

Exploratory Pattern Analysis

In this section, we illustrate an application of the proposed overview+detail strategy for analyzing a complex industry dataset. This case study application highlights three processes: (1) interactive pattern detection and filtering; (2) interactive pattern examination; and (3) identification of implicit patterns and information synthesis. They are described in the following three subsections

Interactive Pattern Detection and Filtering

The goal of the interactive pattern detection and filtering is to select interesting and relevant patterns. Initially, the space–time matrix displays an overview of patterns in which matrix rows are ordered by a computational method alone (Figure 7). Patterns seen in this overview are not fully satisfying because all kinds of patterns—relevant/irrelevant, explicit/implicit—are put together in the matrix view. The mixture of patterns can distract human attention and hinder an analyst in identifying the most important patterns, as well as any hidden ones. Hence, we need to go through step 2 (Zoom and filter) to find the most interesting and relevant patterns. To support this process, we designed and implemented an interactive dendro-gram which is attached to the space–time matrix. The two components work together with the PCP to support human judgments about the novelty, relevance, and importance of patterns.

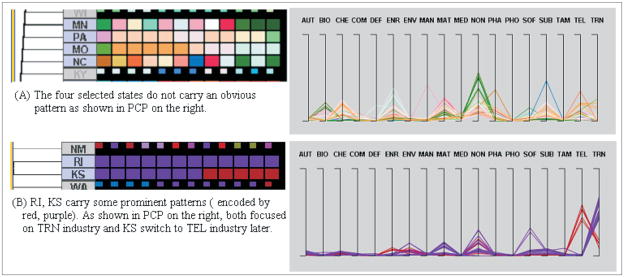
Analysts can gradually adjust the threshold value for the cluster similarity (by dragging the vertical bar on the dendrogram), and clusters with high similarity are highlighted. However, clusters with high similarity values do not necessarily mean relevant or potentially useful patterns. Analysts are often interested in patterns with some constant characteristics over time or with an abrupt change (as demonstrated in Figure 9); hence, an analyst must investigate the patterns in detail in the PCP and apply domain knowledge to determine which patterns are novel, relevant, and important. Rows that carry irrelevant, known, or unimportant patterns can be manually disabled (thus filtered out). The rows with interesting patterns can then be exported for later use. By “export” we mean copy the selected rows from the space–time matrix to the Pattern Basket (Figure 10, right) so that the patterns thought to be relevant can be saved for further analysis.

Figure 9.

The states in group A (Minnesota, Pennsylvania, Missouri, North Carolina) are identified by computational methods as being more similar to each other than states in group B (Rhode Island, Kansas). The group A states are “similar” in sharing the absence of an obvious pattern in industry composition; this kind of “similarity” is less interesting than many that are computationally less strong. In contrast, Rhode Island and Kansas carry a prominent pattern that is interesting.

Figure 10.

Interesting patterns are found in the space–time matrix (on the left) as sub-areas with relatively constant colors; they are investigated in the PCP. Novel, relevant, and important patterns are identified and exported to a Pattern Basket (on the right). Well known, irrelevant, and unimportant rows are filtered out.

Interactive Pattern Examination

Having found some interesting patterns via step 2 (filtering), we can go to step 3, i.e., examine the patterns in detail. We demonstrate the process via an analysis case. We select the blue region (Figure 10, in the middle of the matrix). It contains four states—Maine (ME), Indiana (IN), Arizona (AZ), and Alabama (AL). The strings in the PCP depict an industry composition pattern that is dominated largely by SUB industry (Figure 11, left). This exploration follows a where+when→ what model in which where and when are identified in the space–time matrix (through common colors that suggest a pattern) and what is found in the PCP (where the industry composition is indicated by color, as can the specific extent to which each state–time entity fits the pattern). To investigate the pattern, we do an incremental brushing along the SUB axis. It is a what → where+when process, and two more states—New Hampshire (NH) and Washington (WA)—are found to focus on the SUB industry. The six rows are exported into a Pattern Basket and manually re-ordered for better interpretation (Figure 11, right).

Figure 11.

Left: PCP (in detail view mode) shows the industry mix for four states: Maine, Indiana, Arizona, and Alabama. All axes are scaled from 0 as the minimum value to 1 as the maximum value, to express the proportion of all technology industry at a given place and time represented by the specific industry. The industry mix is dominated by SUB industry with a considerable amount of NON industry. Right: Six states were found to focus/had focused on an industry mix dominated by SUB industry (shown in blue).

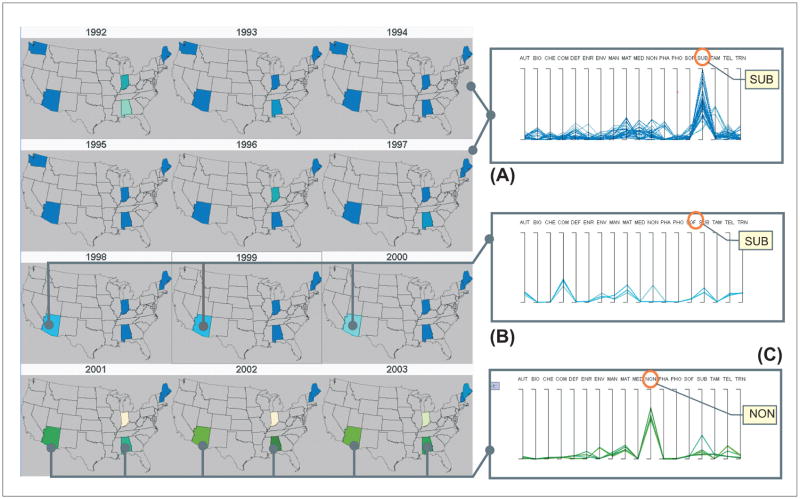
In the map matrix (Figure 12, top left plot), we notice that most of the states were in blues in the early years from 1992 to 1997; more recently, Arizona changed to bright blue from 1998 to 2000, then dramatically changed to green from 2001 to 2003. To determine what this means, we make three drill-down selections on the space–time matrix (see Figure 12(A), (B), and (C)). Our complementary, linked views effectively visualize how multivariate patterns (industry mix) changed across geographic space and over time. As shown in Figure 12(A, B, C), an industry composition dominated by SUB was seen in the six states except NH from 1992 to 1997; SUB expanded from ME to NH, while significantly decreasing in the other states after 2001; and AZ switched focus from SUB to NON eventually.

Figure 12.

A map matrix screen shot (left) displays how industry mix (a multivariate pattern) changes across the six states over twelve years. Three PCP displays outcomes of three selection operations, respectively, each of which was visible separately at different points in the interactive analysis sequence (A, B, and C). The three selection are: (A) Select six states from 1992 to 1997: five states except New Hampshire are in blue (an industry mix dominated by SUB, indicating the five states focused on SUB; (B) Select Arizona from 1998 to 2000: Arizona switched focus to COM, NON, MAT, but still kept some SUB. (C) Select Arizona and Alabama from 2001 to 2003; they switched focus to NON. Because only Maine and New Hampshire remain in blue (an industry mix dominated by SUB), we can conclude that SUB expanded from Maine to New Hampshire, while decreasing significantly in the other states after 2001.

The views allow interactive exploration from all space, time, and attribute perspectives; compound selection operations can be made to achieve any combination of where, when, and what for a query schema of either A+B→ C or A→ B+C. The queries can be made on a group of entities to address general level questions or on an individual entity to address elementary level questions. In summary, being coupled together, the space–time matrix, map matrix, and PCP, with their underlying computational clustering and ordering methods, complement each other to support the overview+detail strategy for an exploratory data analysis process.

Identification of Implicit Patterns and Information Synthesis

In this section, we discuss how the Pattern Basket facilitates the identification of hidden, implicit patterns that are initially not obvious. Computational methods are limited in identifying complex patterns (including spatial patterns), especially those that are hard to define formally. They typically must impose predetermined assumptions prior to having detailed knowledge of the data. In addition, it is hard for computational methods to figure out whether the patterns they detect are relevant or not. Figure 9(A) shows data items considered by computational methods to be highly similar to each other but they may not be of interest because no dominant industries are found. Hence, the analyst must be involved to detect implicit, complex patterns and judge their relevance.

As described previously, a Pattern Basket provides a way of externalizing cognition through external representation (Scaife and Rogers 1996; Zhang 1997; Reisberg 1987), allowing readjustment of the representation to support identification of complex, implicit patterns via human vision. For example, we query what states had focused on the TEL industry and in what years by brushing red strings in the PCP, which represents states and times with an industry composition dominated by TEL industry, as illustrated in the right plot of Figure 3. The red cells in the space–time matrix (those indicating the TEL-dominated cluster) are selected, then they are exported into the Pattern Basket for further analysis (Figure 13(A)). The sequence of the rows remains the same as that exported from the main space–time matrix, reflecting overall similarity between the rows (as computed by the hierarchical clustering method).

Because we are interested only in TEL industry, the rows in the Pattern Basket are manually adjusted (Figure 13(B)) to exposed hidden spatio-temporal patterns: in the early years, Washington D.C. (DC) and Arkansas (AR) had focused on TEL industry and then switched to NON industry in the late 1990s. While decreasingly important in DC and AR, TEL was dominant in Kansas, Colorado, Mississippi, and eventually in Washington. Of course, Telecom industry also exists in many other states (e.g., in California and Virginia), but it has never been a dominant industry in those states, when compared to all technology industries. Interestingly, most of the states involved in the transition of TEL form a geographically contiguous region (i.e., Colorado, Kansas, Arkansas, Mississippi) (Figure 13, right). In early years, these states had a diversified industry mix; eventually, we see two thematic groups with one focused on TEL industry and the other on NON industry.

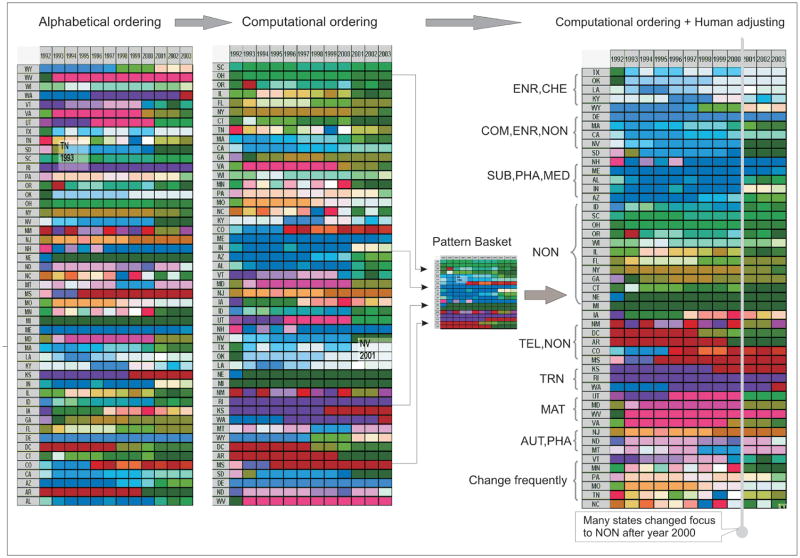
Eventually, the combined application of computational methods and human interaction can produce a refined overview of patterns for the entire data. Compared to the view obtained from computational methods alone, the refined overview thematically organizes all patterns (Figure 14, right), exposing insights that were hidden before by presenting them in a more legible manner (e.g., a new insight exposed is that many states switched focus to non-primary-high-tech (NON) industry after 2000, indicating, in a way, the economic recession of 2001–2003). In this way, the synthesis process facilitates effective extraction of unknown, relevant, and potentially useful information from a relatively large data set, often by revealing implicit patterns leading to insights and presenting the complex insights derived in a more illustrative manner.

Figure 14.

Overview of patterns achieved through different approaches. Left: alphabetical ordering, patterns are barely exposed. Middle: computational clustering method is applied and some salient patterns (i.e., red, purple, and blue regions) are exposed. Right: by combining strengths of computational methods and human vision and judgment, the patterns are in a thematic ordering.

Conclusion and Future Research

The exploratory analysis approach for space–time–attribute data presented here provides two major advantages. First, by integrating visual, computational, and cartographic methods, the approach effectively supports the application of overview+detail exploratory analysis to relatively large volumes of space–time–attribute data, achieving a holistic overview of the entire data set as well as detailed views on particular themes and/or subsets of data. Second, by productively coupling visual representation, flexible interaction, and computational methods, our toolkit aids analysts in a process of incremental pattern searching, filtering, and synthesizing; it, thus, has a better chance to find novel, relevant, and potentially useful information.

One of the future efforts of this research will be to address the challenge of scaling the methods for application to massive data sets. Currently, our methods work well for high-dimensional data, with modest numbers of places and times (data aggregated to states and to years). Additional insights are likely to be obtained if methods can be extended to deal effectively with multiple levels of drill down—in the case of this study to monthly data by zip code. In general, the goal is to support visual analytical activities that move smoothly across scales of analysis as suggested by uncovered patterns and relationships.

Another direction of future study will be to focus on developing, implementing, and testing a more systematic approach to interaction that supports a discontinuous (and potentially collaborative) process of sense-making carried out over an extended period of time (as typical for most real-world information analysis, whether in science, business, defense, public health, or other domains). As outlined in the recent visual analytical research agenda, meeting the goal of enhancing analytical reasoning requires that we move beyond the now traditional ideas of direct manipulation interfaces and linked brushing (which focus on interacting with the data) to “support a true human–information discourse in which the mechanics of interaction vanish into a seamless flow of problem solving” (Thomas and Cook 2005). Thus, a specific goal for the future is to develop a conceptual and technical framework to support analytical reasoning and problem solving with large, complex, space–time-attribute data sets. The specific objectives related to this research include developing mechanisms to help users find previously generated patterns that are relevant to a current task; and to allow users to compare, contrast, and link sets of pattern baskets that carry complementary information, and eventually synthesize some novel insights. This is a challenge which will require integration of multiple perspectives.