Exploring pathways from gene coexpression to network dynamics

Abstract

One of major challenges in post genomic research is to understand how physiological and pathological phenotypes arise from the networks or connectivity of expressed genes. In addressing this issue, we have developed two computational algorithms, CoExMiner and PathwayPro, to explore static features of gene coexpression and dynamic behaviors of gene networks. CoExMiner is based on B-spline approximation followed by coefficient of determination (CoD) estimation for modeling gene coexpression patterns. The algorithm allows exploration of transcriptional responses that involve coordinated expression of genes encoding proteins that work in concert in the cell. PathwayPro is based on a finite-state Markov chain model for mimicking dynamic behaviors of a transcriptional network. The algorithm allows quantitative assessment of a wide range of network responses, including susceptibility to disease, potential usefulness of a given drug, and consequences of such external stimuli as pharmacological interventions or caloric restriction. We demonstrated the applications of CoExMiner and PathwayPro by examining gene expression profiles of ligands and receptors in cancerous and non-cancerous cells and network dynamics of the leukemia-associated BCR-ABL pathway. The examinations disclosed both linear and nonlinear relationships of ligand-receptor interactions associated with cancer development, identified disease and drug targets of leukemia, and provided new insights into biology of the diseases. The analysis using these newly developed algorithms show the great usefulness of computational systems biology approaches for biological and medical research.

1. Introduction

One of major challenges in post genomic research and in computational systems biology is to understand how physiological and pathological phenotypes arise from the networks or connectivity of expressed genes [1, 2]. The utilization of high-throughput data generated by microarrays and other methodologies provides scientists with a first step towards the goal of system-level analyses of biological networks [3]. Systems biology has shown promise in many areas of biology, particularly for identifying diagnostic biomarkers and drug-affected genes or drug targets [4, 5]. In this chapter, we identify two cruxes in the study of biological networks, i.e. static features of gene coexpression and dynamic behaviors of networks, and describe how to decipher network or pathway information using computational systems biology approaches based on gene expression data.

1.1. Gene Coexpression

The study of gene coexpression allows the discovery of transcriptional responses that involve coordinated expression of genes that likely work in concert in the cell. With recent interest in biological networks, the use of gene coexpression measured across large number of experiments has emerged as a novel holistic approach for microarray data analysis [6–9]. Typically, the metric of co-expression that has been used is Pearson's correlation coefficient [6, 7, 10, 11]. This linear-model-based correlation coefficient provides a good first approximation of co-expression, but is also associated with certain pitfalls. When the relationship between log-expression levels of two genes is nonlinear, the degree of co-expression is underestimated [12]. Since the correlation coefficient is a symmetrical measurement, it cannot provide evidence of a directional relationship in which one gene is upstream of another [13]. Similarly, mutual information is also not suitable for modeling directional relationship, although it has been applied in various coexpression studies [11, 14].

Recently, we proposed a new algorithm, CoExMiner, which provides a more biologically meaningful and comprehensive model for gene coexpression, functional relationships, and network structure [15]. The new algorithm is based on B-spline approximation followed by CoD estimation. The algorithm is capable of uncovering both linear and nonlinear relationships of coexpression and suggesting the directionality. It is thus particularly useful in prediction analysis of gene expression, the determination of connectivity in a pathway, and network inference. The computation by the new algorithm requires no quantization of microarray data, thus avoiding significant loss or misrepresentation of biological information, which would otherwise occur in the conventional application of CoD [16, 17]. In this chapter, we describe the basics of the CoExMiner algorithm. We also show the application of the algorithm to modeling the co-expression patterns and exploring biological information from microarray data of different cancers. The algorithm allowed the correct identification of coexpressed ligand-receptor pairs specific to cancerous tissues and provided new insight into the understanding of cancer development.

1.2. Network Dynamics

Biological networks or pathways behave only under controlled manners in response to disease development, changing cellular conditions, or external stimuli [18]. By characterizing the dynamic behavior of biological pathways, we aim to identify how disease or cellular phenotypes arise from the connectivity or networks of genes and their products. Various algorithms have been employed in examining dynamic behaviors of biological networks in silico, including the Markov chain [19] and probabilistic Boolean network [20]. In silico simulation has been particularly important in network analysis since network activity is constrained by the various complex forms of interactions [21, 22].

Recently, we developed a new algorithm, PathwayPro, to mimic the complex behavior of a biological pathway through a series of perturbations made in silico to each gene or gene combination [23]. The inputs to the algorithm are the topologies of pathways and gene expression data. The outputs are the estimated probabilities of network transition across different cellular conditions under each transcriptional perturbation. The algorithm can provide answers to two questions. First, whether or how much a gene or external perturbation contributes to the dynamic behavior of a pathway in instances such as disease development or recovery, aging processes, and cell differentiation. Second, in what specific ways is this contribution manifested. PathwayPro analysis is particularly valuable in its ability to simulate in silico pathway behaviors that may not be easy to create in vitro. The hypotheses subsequently derived can then be tested via independent experiments. The analysis thus facilitates the development of systematic approaches to effective preventive and therapeutic intervention in disease. The potential clinical impact of such analysis is tremendous as the type of intervention analysis can not only open up a window on the biological behavior of an organism and the disease progression, but can also translate into accurate diagnosis, target identification, drug development, and treatment. We demonstrate the application of PathwayPro by analyzing the leukemia-related BCR-ABL proteins and the pathway. The analysis correctly identified drug targets for leukemia and shed light on the understanding of the disease.

2. Basics of Algorithms

2.1. Computational Model for Gene Coexpression of Mixed Patterns

The algorithm we present here is based on CoExMiner [15]. The algorithm uses a B-spline approximation to predict the expression value of the target gene g_y using the predictor gene g_x, followed by CoD estimation of coexpression of g_x and g_y. The algorithm allows measurement of both linear and nonlinear patterns and directionality of coexpression.

2.1.1. B-spline Approximation

The B-spline is a set of piecewise polynomial functions [24]. It can be defined as follows:

$$\stackrel{\rightharpoonup }{\mathbf{P}}\left(t\right)=\sum _{j=1}^{n+1}{B}_{j,k}\left(t\right){\stackrel{\rightharpoonup }{\mathbf{P}}}_j,t_{\min }\le t<t_{\max }$$ (1)

In Eq. (1), ${\stackrel{\rightharpoonup }{\mathbf{P}}}_1$, ${\stackrel{\rightharpoonup }{\mathbf{P}}}_2$,…,${\stackrel{\rightharpoonup }{\mathbf{P}}}_{n+1}$ are n+1 control points. The B_j,k basis function is of order k . k must be at least 2, and can be no more than n+1. Eq. (1) defines a piecewise continuous function. A knot vector, t₁,t₂,…,t_k+(n+1), must be specified for a given number of control points n+1 and B-spline order k. It is necessary that: t_j ≤ t_j+1, ∀j. The basis function B_j,k depends only on the value of k and the values in the knot vector. B_j,k is defined recursively as:

$$\begin{array}{cc}\hfill B_{j,1}\left(t\right)& =\{\begin{array}{cc}1,\hfill & t_j\le t<t_{j+1}\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\phantom{\}}\hfill \\ \hfill B_{j,k}\left(t\right)& =\frac{t-t_j}{t_{j+k-1}-t_j}{B}_{j,k-1}\left(t\right)+\frac{t_{j+k}-t}{t_{j+k}-t_{j+1}}{B}_{j+1,k-1}\left(t\right)\hfill \end{array}$$ (2)

By viewing the coexpression pattern as a two-dimensional scatter plot for a given pair of genes g_x and g_y with expression values{(x_i,y_i),i = 1,…,N}, the plot pattern can be modeled by Eq. (1). To construct a 2D B-spline curve requires that $\stackrel{\rightharpoonup }{\mathbf{P}}\left(t\right)$ and ${\stackrel{\rightharpoonup }{\mathbf{P}}}_j$ in Eq. (1) are written as $\stackrel{\rightharpoonup }{\mathbf{P}}\left(t\right)=\left(\begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \end{array}\right)=\left(\begin{array}{c}\hfill f\left(t\right)\hfill \\ \hfill g\left(t\right)\hfill \end{array}\right)$ and ${\stackrel{\rightharpoonup }{\mathbf{P}}}_j=\left(\begin{array}{c}\hfill {\tilde{x}}_j\hfill \\ \hfill {\tilde{y}}_j\hfill \end{array}\right)$. Here f(t) and g(t) are the x and y components of a point on the curve. {(x̃_j,ỹ_j),j = 1,…,n + 1} are the control points selected from {(x_i,y_i),i = 1,…,N}where n + 1 ≤ N.

2.1.2. CoD Estimation

CoD is the ratio of the explained variation to the total variation and denotes the strength of the association between predictor genes and target gene. Specifically, for any feature set X, CoD relative to the target variable Y is defined as ${\mathrm{CoD}}_{X\to Y}=\frac{{\epsilon }_0-{\epsilon }_X}{{\epsilon }_0}$ where ε₀ is the prediction error in the absence of predictor and ε_X is the error for the optimal predictors [16]. For the purpose of exploring a co-expression patterns, we only consider a pair of genes g_x and g_y, where g_y is the target gene that is predicted by the predictor gene g_x. The errors are estimated based on available samples for simplicity.

In specific, given a pair of genes g_x and g_y with expression values x_i and y_i, i = 1,…,N, where N is the number of samples, CoD can be computed according to the definition.

$${\mathrm{CoD}}_{g_x\to g_y}=\frac{{\epsilon }_0-{\epsilon }_X}{{\epsilon }_0}=\frac{{\Sigma }_{i=1}^N{(y_i-\stackrel{‒}{y})}^2-{\Sigma }_{i=1}^N{(y_i-{\widehat{y}}_i)}^2}{{\Sigma }_{i=1}^N{(y_i-\stackrel{‒}{y})}^2}$$ (3)

The key point for computing CoD from Eq. (3) is to find the optimal estimator ŷ_i from continuous data samples (x_i,y_i). Motivated by the spirit of B-spline, an algorithm is formulated to estimate the CoD from continuous data of gene expression. The proposed algorithm is summarized as follows.

Input

• A pair of genes g_x and g_y with expression values x_i and y_i, i = 1,…N . N is the number of samples.

• M intervals of control points. By given N and M, the number of control points (n+1) is determined as $n=\lfloor \frac{N}{M}\rfloor$, where ⌊·⌋ is the floor function.

• Spline order k.

Output

• CoD of gene g_y predicted by gene g_x.

Algorithm

• Fit B-spline curve $\stackrel{\rightharpoonup }{\mathbf{P}}\left(t\right)=\left(\begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \end{array}\right)=\left(\begin{array}{c}\hfill f\left(t\right)\hfill \\ \hfill g\left(t\right)\hfill \end{array}\right)$ based on control points ${\stackrel{\rightharpoonup }{\mathbf{P}}}_1$,${\stackrel{\rightharpoonup }{\mathbf{P}}}_2$,⋯,${\stackrel{\rightharpoonup }{\mathbf{P}}}_{n+1}$ a knot vector, t₁,t₂,…,t_k+(n+1), and the order of k.

  • Find indices of $\left\{\left(\begin{array}{c}\hfill x_i^{\prime }\hfill \\ \hfill y_i^{\prime }\hfill \end{array}\right),i=1,\cdots ,N\right\}$ where $(x_1^{\prime }\le x_2^{\prime }\le \cdots \le x_N^{\prime })$ are ordered as monotonic increasing based on (x₁,x₂,…,x_N), $y_i^{\prime }$ is the value with the same index as $x_i^{\prime }$.

  • Assign (n+1) control points as: ${\stackrel{\rightharpoonup }{\mathbf{P}}}_j=\left\{\left(\begin{array}{c}\hfill {\tilde{x}}_j\hfill \\ \hfill {\tilde{y}}_j\hfill \end{array}\right)=\left(\begin{array}{c}\hfill x_{1+(j-1)\times M}^{\prime }\hfill \\ \hfill y_{1+(j-1)\times M}^{\prime }\hfill \end{array}\right),j=1,\cdots ,n\right\}$ and ${\stackrel{\rightharpoonup }{\mathbf{P}}}_{n+1}=\left\{\left(\begin{array}{c}\hfill {\tilde{x}}_{n+1}\hfill \\ \hfill {\tilde{y}}_{n+1}\hfill \end{array}\right)=\left(\begin{array}{c}\hfill x_N^{\prime }\hfill \\ \hfill y_N^{\prime }\hfill \end{array}\right)\right\}$.

  • Compute the B_j,k(t) basis functions recursively from Eq. (2).

  • Formulate $\stackrel{\rightharpoonup }{\mathbf{P}}\left(t\right)={\sum }_{j=1}^{n+1}{B}_{j,k}\left(t\right)\left(\begin{array}{c}\hfill {\tilde{x}}_j\hfill \\ \hfill {\tilde{y}}_j\hfill \end{array}\right)$ based on Eq. (1).

• Calculate CoD of gene g_y predicted by gene g_x

  • Compute mean expression value of g_y without predictors according to $\stackrel{‒}{y}=\frac{{\sum }_{i=1}^N{y}_i}{N}$

  • For i = 1,…,N, find ${\widehat{y}}_i^{\prime }=\mathcal{f}\left(x_i^{\prime }\right)$ by eliminating t between x = f(t) and y = g(t). First find $t_i=\arg \left\{\underset{t}{\min }\mid f\left(t\right)-x_i^{\prime }\mid \right\}$. Then compute ${\widehat{y}}_i^{\prime }=g\left(t_i\right)$ >.

  • Calculate CoD from Eq. (3) based on the ordered $\left\{\left(\begin{array}{c}\hfill x_i^{\prime }\hfill \\ \hfill y_i^{\prime }\hfill \end{array}\right),i=1,\cdots ,N\right\}$. Refer to Eq. (3), CoD value is the same as calculated based on $\left\{\left(\begin{array}{c}\hfill x_i\hfill \\ \hfill y_i\hfill \end{array}\right),i=1,\cdots ,N\right\}$. Including the special cases, we have (i)ε₀>0, ifε₀≥ε_X, compute CoD from Eq. (3); else set CoD to 0. (ii)ε₀ = 0, ifε_X = 0, set CoD to 1; else set CoD to 0.

2.1.3. Statistical Significance

For a given CoD value estimated on the basis of B-spline approximation (referred as CoD-B in the following), the probability of obtaining a larger CoD-B by randomly shuffling one of the expression profiles (P_shuffle) is calculated by Monte Carlo simulation. In the simulation, random datasets can be created by shuffling the expression profiles of the predictor gene A and the target gene B, and then CoD-B is determined based on the random dataset. P_shuffle of CoD-B from the real data could be determined according to the derived probability distribution of CoD-B from the simulation.

2.2. Computational Model for Pathway Dynamics

The algorithm we present here is based on PathwayPro [23]. In this algorithm, a finite-state Markov chain model is constructed with the gene expression profile and network topology. The probability of network transition is determined based on state-dependent multivariate conditional probabilities between gene expression levels.

2.2.1. Model Construction

The proposed computational model contains n selected genes. Each gene has a ternary expression value, which is assigned as either over-expressed (1), equivalently-expressed (0), or under-expressed (−1), depending whether the expression level is significantly lower than, similar to, or greater than the respective control threshold. For capturing the dynamics of the network, we use the state of predictor genes at step t and the corresponding conditional probabilities, which are estimated from observed data, to derive the state of the target gene at step t + 1. Eq. (4) shows the definition of transition between gene states at step t and the state at step t + 1, which can be represented as a Markov chain [19].

$$S^{\left(t\right)}≕(g_1^{\left(t\right)}{g}_2^{\left(t\right)}...g_n^{\left(t\right)})\to S^{(t+1)}≕(g_1^{(t+1)}{g}_2^{(t+1)}...g_n^{(t+1)})$$ (4)

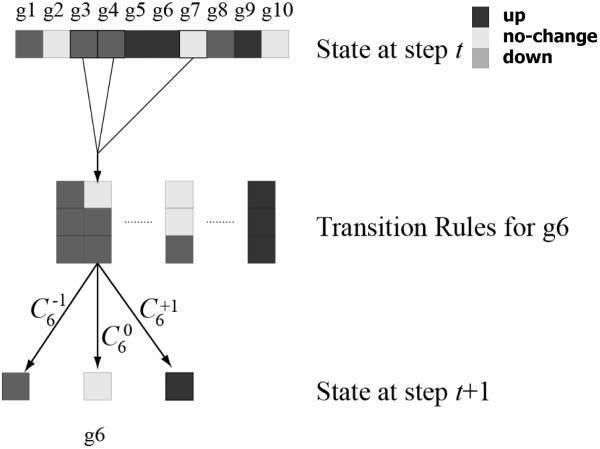
Here, we generalize the model which allows any number of predictor genes for each target gene based on the topology of the network. If the network topology shows there are no predictors as inputs to predict a gene in the next step, the current gene value is kept. The transition rule for S^(t)→S^(t+1) is depicted in Figure 1 and characterized by Eq. (5).

$$g_l^{(t+1)}=\{\begin{array}{c}-1:\mathrm{with}{C}_l^{-1}(g_{i_1}^{\left(t\right)}{g}_{i_2}^{\left(t\right)}\cdots g_{i_k}^{\left(t\right)})=p(g_l^{(t+1)}=-1\mid g_{i_1}^{\left(t\right)}{g}_{i_1}^{\left(t\right)}\cdots g_{i_k}^{\left(t\right)})\hfill \\ 0:\mathrm{with}{C}_l^0(g_{i_1}^{\left(t\right)}{g}_{i_2}^{\left(t\right)}\cdots g_{i_k}^{\left(t\right)})=p(g_l^{(t+1)}=0\mid g_{i_1}^{\left(t\right)}{g}_{i_1}^{\left(t\right)}\cdots g_{i_k}^{\left(t\right)})\hfill \\ 1:\mathrm{with}{C}_l^1(g_{i_1}^{\left(t\right)}{g}_{i_2}^{\left(t\right)}\cdots g_{i_k}^{\left(t\right)})=p(g_l^{(t+1)}=1\mid g_{i_1}^{\left(t\right)}{g}_{i_1}^{\left(t\right)}\cdots g_{i_k}^{\left(t\right)})\hfill \end{array}\phantom{\}}$$ (5)

where i₁,i₂,…i_k,l ∈{1,2,…,n}and k is the number of predictor genes. $C_l^{-1}$,$C_l^0$, and $C_l^1$ are conditional probabilities that depend on the states of the predictor genes and satisfy $C_l^{-1}+C_l^0+C_l^1=1$ 1 in Eq. (5). For example, if there are three predictor genes for a target gene with a ternary value, there are 3³ = 27 possible states observable. The conditional probabilities $C_l^{-1}$,$C_l^0$ and $C_l^1$ are estimated from the data. Since the number of experiments (data) in microarray studies is often limited, there may be some states not observed in the data. In such case, we assign Pr(g_l = −1), Pr(g_l = 0) , and Pr(g_l = 1) for $C_l^{-1}$,$C_l^0$ and $C_l^1$, respectively. Based on the transition rule, we can compute the transition probability between any two arbitrary states of the Markov chain as follows:

$$\mathbf{Pr}\{S^{\left(t\right)}\to S^{(t+1)}\}=\prod _{l=1}^n{C}_l^{g_l^{(t+1)}}$$ (6)

In the simulation, a small but sufficient perturbation is added to guarantee a steady state distribution exists and the chain converges to the steady-state distribution. With a perturbation, the entire Markov chain is ergodic and every state will eventually be visited. Considering gene perturbation, the transition probability Eq. (6) can be generalized as [19] Eq. (7):

$$\mathrm{Pr}\{S^{\left(t\right)}\to S^{(t+1)}\}=\left(\prod _{l=1}^n{C}_l^{g_l^{(t+1)}}\right)\times {(1-p)}^n+p^{n_0}{(1-p)}^{n-n_0}{p_0}^{n_0}\times 1_{[S^{\left(t\right)}\ne S^{(t+1)}]}$$ (7)

where p is the perturbation probability for each gene, $n_0={\sum }_{l=1}^n{1}_{[g_l^{\left(t\right)}\ne g_l^{(t+1)}]}$ is the number of genes to be perturbed, and p₀ = 1/(q−1). In the ternary case, q = 3, so p₀ is equal to 0.5. The simulation algorithm used in this study is summarized in Figure 2.

Figure 1.

Illustration of transition rules for target genes in the Markov chain model. In this example, target gene g6 has three predictor genes g3, g4, and g7. The value of g6 at step (t+1) is determined by the conditional probabilities under the condition g3 = 0, g4 = −1, and g7 = −1 at step (t).

Figure 2.

Simulation algorithm for steady-state analysis. The algorithm starts from a random initial state and repeats R times before collecting samples from steady-state distribution. In the simulation, a small but measurable perturbation is added to guarantee a steady state distribution exists and the chain converges to the steady-state distribution.

2.2.2. Intervention Analysis by Markov Chain Model

The ability of the current model to enhance our understanding of biological systems should be further investigated by exploring another common biological system feature, the ability to readily switch from one relatively stable state to another in response to a simple stimulus. To a certain extent, this study can also verify how well the model mimics biological systems. Basically, one question may be interesting to ask: Given a desired target state and an initial state, with which genes in network should we intervene by simultaneously flipping their status so that the probability that the network will reach the desired target state is greatest? We could address this question by finding the best candidate genes for intervention based on first-passage time [20, 25]. The first-passage time provides a natural way to capture the goals of intervention in the sense that we wish to transit to certain states (or avoid certain states) as quickly as possible, or, alternatively, by maximizing the probability of reaching such states before a certain time. So it can be used as a tool for deciding which genes are the best candidates for intervention. The first passage time from state x to state y can be defined as follows: with the probability F_k (x,y) that, starting in state x, the first time the network reach a given state y will be at step k. It is easy to see that for k = 1, F₁(x,y) = A(x, y), which is just the transition probability from x to y. For k ≥ 2, F_k (x, y) satisfies [25]

$$F_k(x,y)=\sum _{Z\in {[-1,0,1]}^n-\left\{y\right\}}A(x,z)F_{k-1}(z,y)$$ (8)

In Eq. (8), each element A(x, y) of the transition matrix A can be computed using Eq. (7). For a fixed K, a 3ⁿ ×, K matrix F can be created in which each column contains the probability F_k (x, y) from all possible starting states x to a given target state y at k steps. We can then use $H_k(x,y)={\sum }_{k=1}^K{F}_k(x,y)$ as a measurement index. Because the events that the first passage time from x to y will be at step k are disjoint for different k, the sum of their probabilities for k = 1,…,K is equal to the probability that the network, starting in state x, will visit state y before step K. Since the chain is ergodic with perturbation probability p, when K = ∞, H_∞ (x, y) is equal to the probability that the chain ever visits the state y, which is equal to 1.

Using the above measurement tool, we construct the intervention information matrix H at a fixed K = 3. In this matrix, each row H₃ (x,:) represents the probability that the network, from a starting state x, will visit all desired ending states before step K = 3. Each column H₃ (:, y) represents the probability that the network, starting in all possible intervened states, will visit state y before step K = 3. For simulating simple stimuli, we mathematically change the expression level of one gene, two genes, and three genes each time and keep the rest of the genes unchanged for a starting state x. For a ternary expression, that will generate $C_n^3\times 3^3$ intervened states for changing one, two, and three genes which include the original state x.

3. Biological Applications

We implemented both CoExMiner and PathwayPro algorithms in Java-based interactive computational tools [15, 23]. With the software tools, we analyzed ligand and receptor expression profiles in cancerous and normal tissues, and examined the leukemia-related ABL-BCR pathway.

3.1. Coexpression of Ligand-Receptor Pairs

In this study, we used CoExMiner to analyze the co-expression of ligands and their corresponding receptors in dissected tissues of lung cancer, prostate cancer, acute myeloid leukemia (AML), and their normal tissue counterparts. The ligand-receptor cognate pair data were obtained from the Database of Ligand-Receptor Partners (DLRP) [10]. The gene expression data are downloaded from the GEO database (accession numbers GSE 1987, GSE 1431, and GSE 995, respectively). The array data, initially obtained using Affymetrix microarrays, were normalized by the Robust Multi-Array Analysis (RMA) method [26].

Significantly co-expressed ligand and receptor pairs were identified in the cancer and normal tissue groups at thresholds of R² and CoD-B of 0.50 and P_shuffle of 0.05. From these, differentially coexpressed pairs between cancerous and normal tissues were selected. Table 1 lists the differentially coexpressed genes between cancerous and normal tissues. 12 ligand-receptor pairs were differentially coexpressed between lung cancer and normal tissues (CoD-B difference > 0.40, Table 1A). The ligand BMP7 (bone morphogenetic protein 7), related to cancer development [27, 28], was one of the differentially co-expressed genes. For BMP7 and its receptor ACVR2B (activin receptor IIB), the CoD-B was 0.76 (P_shuffle < 0.028) in the lung cancer and 0.00 (P_shuffle < 0.58) in the normal tissue, and the R² value was 0.042 (cancer) or 0.0012 (normal tissue) (Table 1A). Therefore BMP7 and ACVR2B show a nonlinear coexpression in the lung cancer but no coexpression in the normal tissue. The coexpression profile (Figure 3A) further showed that the two genes displayed approximately the nonlinear pattern (piecewise pattern) of coexpression, and BMP7 was over-expressed in the lung cancer as compared with the normal tissue. These results are suggestive of a certain level of negative feedback involved in the interaction between BMP7 and ACVR2B.

Table 1.

List of ligand-receptor pairs which showed differential coexpression between cancers and normal tissue. (A) Lung cancer; (B) Prostate cancer; (C) Acute myeloid leukemia (AML).

Ligand	Receptor	CoD-B		Pshuffle
		Cancer	Normal	Cancer	Normal
(A) Lung cancer
BMP7	ACVR2B	0.76	0.00	0.028	0.58
EFNA3	EPHA5	0.84	0.00	6.7E-06	0.69
FGF8	FGFR2	0.55	0.00	1.5E-07	0.66
IL16	CD4	0.62	0.031	2.7E-06	0.68
CCL23	CCR1	0.00	0.85	0.73	2.1E-09
IL1RN	IL1R1	0.23	0.83	0.077	8.4E-07
IL18	IL18R1	0.18	0.71	0.097	4.5E-06
IL13	IL13RA2	0.00	0.69	0.62	1.5E-04
BMP5	BMPR2	0.00	0.61	0.69	1.7E-04
(B) Prostate cancer
BMP6	ACVR2B	0.63	0.081	0.0011	0.44
BTC	EGFR	0.75	0.00	1.7E-11	0.28
TGFB2	TGFBR2	0.79	0.00	3.5E-04	0.49
INHA	ACVR2A	0.59	0.019	1.1E-06	0.45
CCL23	CCR1	0.00	0.85	0.43	3.2E-09
IL1RN	IL1R1	0.00	0.82	0.32	3.1E-07
TNFSF8	TNFRSF8	0.00	0.76	0.36	1.5E-06
IL18	IL18R1	0.00	0.70	0.39	2.1E-07
FIGF	KDR	0.00	0.57	0.26	0.0023
CXCL5	IL8RB	0.00	0.58	0.41	1.1E-04
(C) Acute myeloid leukemia
FASLG	FAS	0.90	0.14	3.6E-05	0.34
BMP7	BMPR1B	0.82	0.00	7.7E-04	0.59
EFNA5	EPHA1	0.85	0.00	2.5E-04	0.71
FGF3	FGFR2	0.81	0.00	7.4E-06	0.66
FGF13	FGFR4	075	0.059	0.0097	0.47
NRG1	ERBB3	0.95	0.00	1.7E-05	0.28
CCL4	CCBP2	0.99	0.24	9.6E-06	0.062
CCL7	CCR5	0.97	0.29	0.00476	0.41
IFNA8	IFNAR2	0.88	0.00	2.9E-05	0.70
IFNG	IFNGR1	0.87	0.00	3.4E-04	0.68
IL13	IL4R	0.82	0.00	0.0041	0.70
INHBB	ACVR2B	0.82	0.23	1.5E-04	0.11
AMH	AMHR2	0.00	0.78	0.63	4.7E-05
CD40LG	CD40	0.00	0.97	0.33	8.6E-05
TNFSF7	TNFRSF7	0.39	0.97	0.043	8.2E-05
EFNA1	EPHA4	0.065	0.86	0.59	1.6E-06
FGF1	FGFR4	0.00	0.93	0.32	1.6E-06
CXCL2	IL8RB	0.25	0.84	0.33	3.3E-06
FGF17	FGFR3	0.17	0.70	0.17	3.0E-04
DLK1	NOTCH4	0.00	0.89	0.55	2.5E-07
TNFSF4	TNFRSF4	0.00	0.92	0.67	3.3E-04
CXCL9	CXCR3	0.30	0.98	0.054	1.5E-04
TGFB1	TGFBR1	0.00	0.71	0.62	6.8E-05

Figure 3.

Coexpression profiles of two representative ligand-receptor pairs in lung cancer cells and normal cells. (A) BMP7 and ACVR2B in lung cancer samples (P_shuffle < 0.028) and normal samples (P_shuffle < 0.58); (B) CCL23 and CCR1 in lung cancer samples (P_shuffle < 0.73) and normal samples (P_shuffle < 2.1E–09).

The ligand CCL23 (chemokine ligand 23) and its receptor CCR1 (chemokine receptor 1), on the other hand, exhibited a high linear co-expression in the normal lung tissue but no co-expression in cancerous lung samples. As shown in Table 1A, the CoD-B value of the gene pair was 0.85 in the normal tissue while 0.00 in the lung cancer, and the R² value was 0.91 in the normal tissue and 0.054 in the lung cancer, suggesting a linear co-expression between the genes. The linear coexpression pattern is further profiled in Figure 3B. Similarly, CCL23 and CCR1 were also highly coexpressed in the normal prostate samples (CoD-B = 0.85) but not coexpressed in the cancerous prostate samples (CoD-B = 0.0) (Table 1B). However, CCL23 and CCR1 were not coexpressed in either normal (CoD-B = 0.0) or AML samples (CoD-B = 0.0). The results suggest that CCL23 and CCR1 show differential coexpression not only between cancerous and normal tissues, but also among different cancers. It has been reported that chemokine members and their receptors contribute to tumor proliferation, mobility, and invasiveness [29]. Some chemokines help to enhance immunity against tumor implantation, while others promote tumor proliferation [30]. Our results suggest that a tight interaction between CCL23 and CCR1 is absent in lung and prostate cancer samples but present in AML samples.

Many ligands and receptors showed different patterns of coexpression in cancer and normal tissues. In the lung cancer, for example, 11 ligand-receptor pairs showed a linear coexpression pattern, which were significant in both CoD-B and R², while 28 pairs showed a nonlinear pattern, which were significant only in CoD-B. In the counterpart normal tissue, however, 35 ligand-receptor pairs showed a linear coexpression pattern, while 6 pairs showed a nonlinear pattern. Such differences in the coexpression pattern were not identified in previous coexpression studies based on the correlation coefficient [10]. The findings of nonlinear co-expressed pairs of ligand-receptor by CoExMiner provide novel candidates for further study in cancer biology.

3.2. Identification of Disease Genes and Drug Targets of Leukemia

We conducted an analysis of the leukemia-related BCR-ABL pathway using PathwayPro. The analysis profiled the dynamic behavior of the pathway in response to leukemia development and identified possible disease genes and drug targets. Affymetrix array data from chronic myeloid leukemia (CML) and normal white blood cells [31, 32] were downloaded from the GEO database (accession numbers GSE2535 and GSE 995). We discretized gene expression values into three categories: over-expressed (1), equivalently-expressed (0), and under-expressed (–1), depending whether the expression level is significantly lower than, similar to, or greater than the respective control threshold. Since some genes have small natural ranges of variation, we used z-transformation to normalize expression levels of genes across experiments, so that relative expression levels of all genes have the same mean and standard derivation. We then conducted data quantization with the control threshold set to be one standard derivation.

Figure 4 shows the network topology of the ABL-BCR pathway [33–35]. BCR and ABL are linked to the cytoplasm as a part of a large signaling complex with a variety of cellular substrates, related to the development of chronic myeloid leukemia (CML) [33–35]. In silico simulation was conducted by mathematically perturbation on the expression value of each gene (referred to as single-gene intervention), each combination of two genes (double-gene intervention), and each combination of three genes (triple-gene intervention). In each perturbation, the observed expression of a gene was altered to the opposite direction or remained unchanged. We measured the transition probability of the ABL-BCR pathway between the normal condition and leukemia state under a series of transcriptional interventions. The probability of the network transitioning from normal to leukemia states reveals disease susceptibility of genes involved. The higher the probability is, the more likely a gene or gene combination under a certain intervention is responsible for the development of the disease. On the other hand, the probability of the transition from leukemia to normal states is a measure of the potential usefulness of a drug or therapeutic intervention.

Figure 4.

The topology of leukemia-related BCR-ABL pathway. The arrows represent the directions of the causal relationships among genes. BCR are ABL are linked to the cytoplasm as a part of a large signaling complex with a variety of cellular substrates, related to the development of leukemia. The drug Gleevec is a selective BCR-ABL inhibitor in this pathway.

Our analysis first showed that more genes and gene combinations had higher probabilities to contribute to network transitions from normal to leukemia states than from leukemia to normal states (Table 2). The result suggests that the chance is higher for a human to develop leukemia than to recover from the disease. As illustrated in Table 2, in the double-gene intervention, changes directly involving the genes BCR and ABL yielded the highest probability (0.01) for a normal-to-leukemia transition. The interventions on ABL/AKT1 and BCR/ABL led to the highest transition probabilities (0.002 and 0.001 respectively) for a leukemia-to-normal transition, although they remained nearly 100 times lower than those for normal-to-leukemia transitions. In the triple-gene intervention (Table 2), the triplets BCR/ABL/BAD and BCR/ABL/MYC showed a highest probability (0.01) for normal-to-leukemia transition, while the BCR/ABL/AKT combination appeared to have the highest probability (0.007) for leukemia-to-normal transitions. The importance of BCR and ABL to the network transition was further illustrated by the single-gene intervention, where both BCR and ABL were associated with the highest transition probability (Table 2). Moreover, BCR and ABL showed high frequencies in all of their partnerships with other genes in the double or triple interventions positive for network transition. As illustrated in Figure 5, BCR and ABL were on the top by the frequency of partnership with other genes in the normal to leukemia transition, while BCR and ABL, along with AKT and CRKL, were on the top in the leukemia to normal transition in the triple-gene invention. These results suggest that BCR and ABL are the most contributive to the network behavior transition between the normal condition and the leukemia state, and therefore the most susceptible for the development of CML leukemia as well as the recovery of the disease to a normal condition. The two genes can thus serve as good drug targets for the treatment of the CML leukemia. This result, reached independently by the computational analysis, is in agreement with the conclusion by previous laboratory-based studies. It has been shown that CML is associated in most cases with the fusion of the genes ABL and BCR, and the activation of BCR-ABL represses apoptosis and allows transformed cells to divide, resulting in the development of CML [33–35]. The drug Gleevec is a selective BCR-ABL inhibitor, effective in the treatment of CML [36]. The PathwayPro analysis not only correctly identified the drug targets, but further indicated that BAD and MYC played critical roles in the leukemia development while AKT appeared important in the leukemia recovery to normal. The results provide new insights into our understanding of the leukemia disease.

Table 2.

Probabilities of network transition by serial interventions on genes in the ABL-BCR pathway of human.

Gene	Transcriptional Intervention	Transition Probability
(A) Transition from normal to CML states by single-gene interventiona
BCR	0 => −1 => 1	0.00639
(B) Transition from CML to normal states by single-gene interventionb
ABL1	1 => 0 => −1	0.000299
(C) Transition from the normal to CML states by double-gene interventionc
BCR ABL1	0 −1 => 1 1 => 1 1	0.0109
BCR BAD	0 1 => −1 0 => 1 0	0.00639
BCR MYC	0 −1 => −1 0 => 1 0	0.00639
BCR BAD	0 1 => −1 −1 => 1 0	0.00639
BCR MYC	0 −1 => −1 1 => 1 0	0.00639
BCR STAT5A	0 1 => −1 −1 => 1 1	0.00639
BCR STAT5A	0 1 => −1 0 => 1 1	0.00639
BCR STAT1	0 0 => −1 1 => 1 0	0.00639
BCR STAT1	0 0 => −1 −1 => 1 0	0.00639
BCR CRKL	0 −1 => −1 1 => 1 0	0.00539
BCR CRKL	0 −1 => −1 0 => 1 0	0.00399
BCR PIK3CG	0 −1 => −1 0 => 1 −1	0.00384
BCR JAK2	0 0 => −1 1 => 1 0	0.00224
BCR AKT1	0 0 => −1 −1 => 1 0	0.00107
(D) Transition from the CML to normal states by double-gene interventiond
ABL1 AKT1	1 0 => 0 1 => −1 0	0.00185
ABL1 AKT1	1 0 => 0 −1 => −1 0	0.00179
BCR ABL1	1 1 => 0 −1 => 0 −1	0.00111
(E) Transition from normal to CML states by triple-gene interventione
BCR ABL1 BAD	0 −1 1 => 1 1 0 => 1 1 0	0.010936
BCR ABL1 MYC	0 −1 −1 => 1 1 0 => 1 1 0	0.010936
BCR ABL1 BAD	0 −1 1 => 1 1 −1 => 1 1 0	0.010933
BCR ABL1 MYC	0 −1 −1 => 1 1 1 => 1 1 0	0.010933
BCR ABL1 STAT5A	0 −1 1 => 1 1 0 => 1 1 1	0.010933
BCR ABL1 STAT5A	0 −1 1 => 1 1 −1 => 1 1 1	0.010933
BCR ABL1 STAT1	0 −1 0 => 1 1 −1 => 1 1 0	0.010933
BCR ABL1 STAT1	0 −1 0 => 1 1 1 => 1 1 0	0.010933
(F) Transition from CML to normal states by triple-gene interventionf
BCR ABL1 AKT1	1 1 0 => 0 −1 1 => 0 −1 0	0.00684
BCR ABL1 AKT1	1 1 0 => 0 −1 −1 => 0 −1 0	0.00662
ABL1 CRKL AKT1	1 0 0 => 0 −1 1 => −1 −1 0	0.00297
ABL1 CRKL AKT1	1 0 0 => 0 −1 −1 => −1 −1 0	0.00288
BCR ABL1 AKT1	1 1 0 => −1 −1 1 => 0 −1 0	0.00274
BCR ABL1 AKT1	1 1 0 => −1 −1 −1 => 0 −1 0	0.00265
ABL1 CRKL AKT1	1 0 0 => 0 1 1 => −1 −1 0	0.00250
ABL1 CRKL AKT1	1 0 0 => 0 1 −1 => −1 −1 0	0.00242

The gene expression profile of each state is presented as: initial state (e.g. normal state) => state after intervened => end state (e.g. disease state). Transcriptional intervention is presented as: initial state (e.g. normal state) => state after intervened => end state (e.g. disease state). In each state, expression levels of each gene are presented by ternary values.

^aProbability cutoff 1E-4.

^bProbability cutoff 1E-4.

^cProbability cutoff 1E-3.

^dProbability cutoff 1E-3.

^eProbability cutoff 1E-2.

^fProbability cutoff 2E-3.

Figure 5.

Frequency of partnership of each gene with other genes in the triple-gene interventions on the ABL-BCR associated pathway. The frequency is calculated as the number of occurrence of each gene above a certain transition probability cutoff, after ranking the transition probabilities under the triple-gene interventions. (A) Transition from normal to CML states (transition probability cutoff: 0.01); (B) Transition from CML to normal states (transition probability cutoff: 0.001). BCR and ABL are the most contributive to the network behavior transition from the normal condition to the leukemia state.

4. Notes

1. We have implemented Java-based interactive computational tools for the CoExMiner and PathwayPro algorithms that we have developed. The software tools are available upon request to the authors.

2. The current version of CoExMiner deals with a pair of genes g_x and g_y, where g_y is the target gene that is predicted by the predictor gene g_x. In the future, we would extend our algorithm to explore multivariate gene relations as well.

3. The current version of PathwayPro allows self-regulation and feedback loops exist in the topologies of pathways. Due to the limitation of computational power, it is feasible for PathwayPro to tackle with the network with 10 to 20 nodes.

5. Conclusions

The two algorithms described in this chapter, CoExMiner and PathwayPro, help to decipher biological information from static features of gene coexpression and dynamic behaviors of gene networks. The systems biology analyses allow one to determine how genes interact with each other to perform specific biological processes or functions, and how disease or cellular phenotypes arise from the connectivity or network of genes and their products. The algorithms and software developed for computational systems biology greatly facilitate drug discovery, sensitive diagnostic biomarker identification, and basic investigations in many aspects of biology.