Multivariate Analysis and Geovisualization with an Integrated Geographic Knowledge Discovery Approach

Abstract

The discovery, interpretation, and presentation of multivariate spatial patterns are important for scientific understanding of complex geographic problems. This research integrates computational, visual, and cartographic methods together to detect and visualize multivariate spatial patterns. The integrated approach is able to: (1) perform multivariate analysis, dimensional reduction, and data reduction (summarizing a large number of input data items in a moderate number of clusters) with the Self-Organizing Map (SOM); (2) encode the SOM result with a systematically designed color scheme; (3) visualize the multivariate patterns with a modified Parallel Coordinate Plot (PCP) display and a geographic map (GeoMap); and (4) support human interactions to explore and examine patterns. The research shows that such “mixed initiative” methods (computational and visual) can mitigate each other’s weakness and collaboratively discover complex patterns in large geographic datasets, in an effective and efficient way.

Introduction

Scientific understanding of complex geographic problems often depends on the discovery, interpretation, and presentation of multivariate spatial patterns, e.g., detection of unknown multivariate spatial patterns or relationships between the incidence of various cancers and socioeconomic, demographic, and/or environmental factors can lead to important hypotheses about unexpected cancer risk factors. However, identifying such patterns becomes ever more challenging, as powerful data collection and distribution techniques produce geographic datasets of unprecedented size in many application and research areas. These datasets are not only large in data volume (i.e., number of observations) but also characterized by a high number of attributes or dimensions (Guo et al. 2003a; National Research Council 2003). It is an extremely challenging and yet urgent research problem to effectively and efficiently detect and understand relationships and patterns in such voluminous and high-dimensional data (Fayyad et al. 1996; Miller and Han 2001; Guo 2003; Guo et al. 2003b; National Research Council 2003).

There are several major challenges that are associated with multivariate spatial analysis in large and high-dimensional geographic datasets. First, the high dimensionality of a dataset can cause serious problems for most analysis methods. One typical problem to address is that it is unlikely for all variables to interrelate meaningfully. Analysts need to find interesting subspaces (subsets of variables) out of a combinatorially explosive number of possible subspaces in a high-dimensional dataset. Second, even when a selected multivariate data space is given as the starting point for analysis (which may be a subspace from a higher-dimensional dataset), it is still a challenging problem to discover the hidden relationships among those variables, as potential patterns may take various forms, linear or non-linear, spatial or non-spatial. Third, attribution of meaning to discovered patterns typically requires input from experts who have domain knowledge and the subsequent presentation of the patterns identified to a broader audience (e.g., other experts who will try to replicate the results, or policy makers who need to act on the results). Fourth, large and high-dimensional datasets demand that all analysis methods are computationally efficient in terms of execution time.

Existing methods for multivariate spatial analysis span a continuum between computational and visual approaches. At the computational end, methods typically exploit the computational power and the formalisms of statistical inference to search for patterns. The more visually based methods capitalize instead on the ability of human vision to identify patterns and facilitate this process by presenting the data from different perspectives. Although computational methods can search large volumes of data for a specific type of pattern very quickly, they have very limited pattern interpretation ability. In contrast, visualization methods can help analysts to visually pick out complex patterns, propose explanations and generate hypotheses for further analysis, and present patterns in an easy-to-understand form. Historically, the development of computational and visual methods for multivariate spatial analysis has proceeded independently. When development has considered both computational and visual methods, the focus has been on sequential application of largely independent methods rather than on developing methods that are integrated from the ground up.

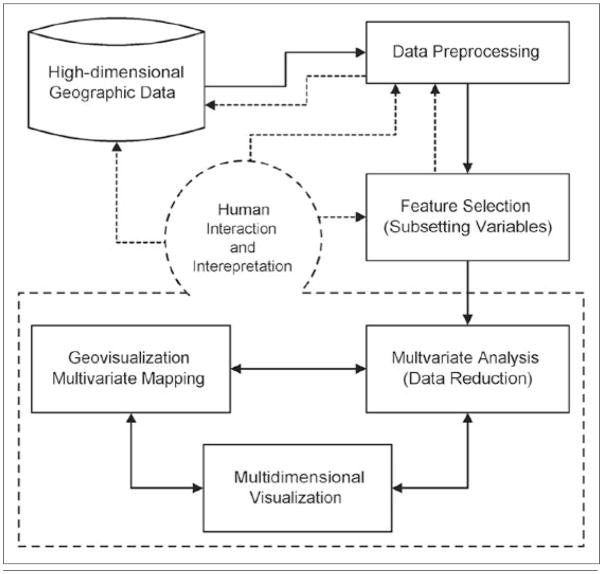
This paper introduces an integrated geographic knowledge discovery environment that is able to detect multivariate spatial patterns within high-dimensional geographic data, visualize the patterns in both the geographic space and the multidimensional attribute space, and support human interactions to examine and explain the patterns. The environment consists of several major components or modules, each of which performs a specific task and can coordinate with other components to facilitate the overall knowledge discovery/construction process. These major components support (a) data preprocessing, (b) unsupervised feature selection, (c) multivariate analysis with the SOM (Self-Organizing Map), (d) multidimensional visualization with PCP (Parallel Coordinate Plot), and (e) multivariate geographic mapping/visualization. This paper focuses primarily on the last three components (c, d, and e) and their coordination with each other.

The paper is organized as follows. In the following section, we introduce the major challenges and related research in the analysis of high-dimensional geographic data. The next section provides an overview of the research presented. This is followed by a section on multivariate analysis with SOM and the design of a cartographically plausible color scheme to encode the SOM result. The next section presents multidimensional visualization, multivariate geographic mapping, and types of interactions that we have implemented. The last but one section provides a case study on cancer data analysis with the integrated approach. Finally, there is discussion and conclusions. The integrated geographic knowledge discovery environment, together with a tutorial and a sample dataset, can be downloaded from http://www.geovistastudio.psu.edu/jsp/tutorial.jsp. Updates and related material are available at http://people.cas.sc.edu/guod/research/.

Challenges and Related Research

A spatial dataset consists of a set of cases, and each case has a spatial location and a set of variables (Haining 2003). Such a data matrix can be decomposed into two parts: the attribute space X and the geographic space S (consisting of spatial locations), which are shown in Figure 1 with two rectangles. In the discussion below, the number of cases is referred to as the dataset size (n) and the number of variables is referred to as the dataset dimensionality (d). When we say a dataset is large, it means that the dataset has a large number of cases. When we say a dataset is high dimensional, it means that the dataset has a large number of variables.

Figure 1.

The spatial data matrix. [After Haining (2003)].

The potential patterns or relationships lurking in the above data matrix can be hard to discover due to at least three major factors: (i) high dimensionality of datasets; (ii) constraints on, or assumptions about, the form that patterns may take; and (iii) lack of visualization methods that support multivariate analysis of geospatial data (in contrast to univariate or bivariate). We discuss each of these factors in the subsections below, briefly.

Combination of Variables

Geographic datasets often have a high dimensionality (National Research Council 2003). When the analysis goal is to search for unknown (and unexpected) multivariate relationships or patterns across different domains, datasets are often compiled from multiple data sources. Compilation of such datasets requires attention to competing goals. On one hand, we need more variables in the dataset since we do not know which variables are interrelated. On the other hand, we know that not all variables are relevant to a specific relationship or pattern.

A dataset may also contain several patterns, and each pattern can involve a different subset of variables. It is important to find the right subset of variables before proceeding to apply a specific pattern analysis method. Otherwise, irrelevant variables may hide or dilute patterns between or among relevant variables. To address these issues, we apply feature (dimension) selection strategies to select a useful subset of variables. Feature selection methods are traditionally used to select a subset of variables for supervised classification problems (Liu and Motoda 1998). Since here we are focusing on exploratory analysis problems rather than classification problems, the feature selection strategy is unsupervised.

Recently new methods have been developed to help identify interesting subsets of variables in a high-dimensional dataset (Agrawal et al. 1998; Procopiuc et al. 2002; Guo 2003; Guo et al. 2003a). Due to space limitation, this paper does not elaborate on this topic. Readers may wish to consult the above references for further details. For the remainder of this paper, we assume that the variables in the input data are meaningful and relevant to each other (namely, that a feature selection step has been executed effectively).

Letting the Data Speak for Themselves

The second difficulty in detecting patterns concerns the various forms that potential patterns may take. The possible patterns (relationships) in a dataset form a hypothesis space. Most analysis methods limit or compress the potential hypothesis space by assuming a simple form of pattern, which can be configured with several parameters. For example, a regression analysis assumes a form of pattern (normally a linear form) and uses data to configure its parameters (e.g., coefficients) in relation to this form.

However, the number of possible patterns, which can be of various forms, is practically infinite in a multivariate spatial dataset. Patterns can be linear or non-linear, spatial or non-spatial, with different configurations. In exploratory analysis, it is important to avoid imposing an a-priori hypothesis and instead to let the data speak for themselves (Gould 1981; Gahegan 2003). In this regard, exploratory visualization approaches stand out since they can present data from multiple perspectives and guide the user through the mining process to draw conclusions (Wong 1999). Visualization approaches include both commonly used information graphics––e.g., tables, maps, histograms, scatter plots, and charts (Harris 1999)––and sophisticated multidimensional visualization techniques (Keim and Kreigel 1996). However, such visual approaches can become impractical or ineffective/inefficient with a large data size and high dimensionality (National Research Council 2003). We elaborate on this point later in this section.

Unlike visual approaches, efficient computational methods are able to handle large datasets and automatically search for patterns, comprehensively and consistently. Computational methods have been traditionally developed in the areas of machine learning, pattern recognition, statistics, and computer science (Fayyad et al. 1996). Clustering analysis, in its broad definition, has been one of the most widely used computational approaches. Clustering methods organize a set of objects into groups (or clusters) such that objects in the same group are similar to each other and different from those in other groups (Jain and Dubes 1988; Gordon 1996; Jain et al. 1999; Everitt et al. 2001). However, although cluster analysis is an efficient method for extracting patterns from data, caution must be exercised in accepting the discovered clusters. Different clustering methods, or the same method with a different parameter configuration, can generate quite different clusters. Thus, a “careful and patient exploration of structure is a far cry from the mechanistic bludgeoning of data then forced through the standard computerized algorithms of cluster and taxonomic analysis” (Gould 1982). One strategy for addressing these problems is to develop visualization methods that support flexible human interaction to examine and verify clustering results (Guo et al. 2003b).

Compared to the two extremes (visual methods and automatic computational methods), the Self-Organizing Map (SOM) provides an intermediate approach. The SOM is capable of projecting high-dimensional data to a low-dimensional space while preserving nonlinear relationships by producing a similarity graph of the input data (Kohonen 2001). Self-Organizing Maps carry out a many-to-one projection, i.e., more than one data item in the input data can be projected to the same node if they are similar enough. Thus, SOMs can also be used as a method of abstraction or summarization since they can compress information while preserving the strongest patterns. Self-Organizing Maps are widely used in various research fields and application areas. Readers are referred to Kaski et al. (1998) and Oja et al. (2003) for a comprehensive reference list.

There are also numerous applications of SOMs in geographic analysis, e.g., visualization of patterns in census data (Skupin and Hagelman 2003), spatialization of non-spatial information (Skupin and Fabrikant 2003), and exploration of health survey data (Koua and Kraak 2004). However, the SOM on its own cannot help much in interpreting the meaning of discovered patterns because it does not have a connection back to the original multivariate data space and the geographic space. We elaborate on this later on when we introduce our integrated approach.

Visualizing Multivariate Geographic Patterns

The third difficulty in detecting patterns is related to the visualization of multivariate geographic patterns. Mapping is essential in visualizing geographic patterns. However, most exploratory spatial analysis methods and associated mapping focus on univariate or bivariate patterns. Multivariate mapping has long been a challenging and interesting research problem. Efforts have focused on a range of methods including composite glyphs (applied to point data and to fields), strategies for overlay of multiple layers, and linked views.

In relation to composite glyphs, one of the best known approaches that has been applied to mapped data are the Chernoff faces (Chernoff and Rizvi 1975). These glyphs visualize multivariate data by relating different variables to different facial features to form a face icon for each data object and then draw each face icon on a map (Dorling 1994). In related work, an icon-based approach has been introduced to visualize multiple variables (layers) for each location in a raster display using a multivariate icon (Zhang and Pazner 2004). Patterns in icon-based maps may be easiest to interpret if the appearance of icons has direct meaning (e.g., smiling faces representing a good socioeconomic situation). However, symbols with clear meaning are often too large to work for large data sets and may not take good advantage of human visual pattern identification capabilities. Symbols that are perceptually based typically require the user to interpret each icon by memorizing its configuration and constructing its meaning on the fly.

There are also many developed visual data mining methods for visualizing multidimensional data (no spatial component), e.g., scatterplot matrices (Andrews 1972), pixel-oriented approaches (Keim and Kreigel 1996), and parallel coordinate plots (PCP) (Inselberg 1985). Several authors have proposed the use of dynamic linking between one or more of these non-spatial multivariate representations and a geographic map (Monmonier 1989; Dykes 1998; MacEachren et al. 1999; Andrienko and Andrienko 2001). It has been demonstrated that users are able to understand this form of linked representation and to use it effectively to construct complex and comprehensive commentaries about spatial and spatio-temporal patterns (Edsall 2003). However, it remains difficult to present a holistic view of multivariate spatial patterns (e.g., generate a single map that shows the distribution of multivariate patterns visible in the multidimensional view).

Large data size and high dimensionality can cause problems for most visualization methods (not just for icon-based symbols). If a dataset is too large, data items overlap in the visual display (e.g., points overlap in scatter plots or line segments overlap in PCP), thus making patterns hard to perceive. For example, with a PCP, the number of the data items that can be visualized on the screen at the same time is limited to about 1000 (Keim and Kreigel 1996). Several research efforts have been directed to address the problem of visualizing very large datasets (Fekete and Plaisant 2002; Keim et al. 2004), resolving the overlap either in the attribute space or in the geographic space. If a dataset has too many variables, it is also difficult for human vision to recognized patterns across many dimensions.

Research Overview

To detect and visualize multivariate spatial patterns, this research integrates computational, visual, and cartographic methods into an environment that collectively addresses the challenges identified above. Similar to data mining in other scientific and applied research fields, geographic knowledge discovery is also by nature an iterative exploration process (Fayyad et al. 1996; MacEachren et al. 1999; Gahegan and Brodaric 2002). With the integrated approach presented here, a normal cycle within the iterative exploration process consists of several steps. These steps include data loading and cleaning; data transformation and preprocessing; selection of an interesting subspace for subsequent analysis; detection of multivariate patterns in the data (using selected variables); visualization of multivariate patterns, multivariate mapping to examine the spatial distribution of the discovered multivariate patterns, and interactive exploration and interpretation by expert users (see Figure 2).

Figure 2.

An integrated geographic knowledge discovery framework.

As mentioned above, this paper focuses primarily on four components in the framework, namely, multivariate analysis (dimension reduction, data reduction and pattern preservation), multidimensional visualization, multivariate mapping, and human interaction. An assumption was made that the input variables were selected based on either domain knowledge or using a formal feature selection method and that they are meaningfully related to each other (i.e., no variable is irrelevant to other variables).

We have adopted and extended the Self-Organizing Map for multivariate analysis. The research exploits two important aspects of SOM, i.e., pattern preservation and abstraction, which make it an important component in the overall process of analysis and exploration. Our implementation of the SOM assigns a color to each node based on a systematically designed color scheme so that nearby (and therefore similar) nodes have similar colors. The SOM outputs to other methods (components) a set of non-empty nodes, each of which contains four pieces of information, namely, the set of data items contained in the node, the total number of data items in the node, the mean vector of the node (i.e., the mean values of all data items contained in it), and the color of the node. These pieces of information are utilized in subsequent multidimensional visualization and mapping components.

To color the SOM map, we integrated a color design component that was developed to support interactive construction of a cartographically plausible 2D color scheme. Our color scheme exploits the 3D CIELAB color space, which was standardized and recommended in 1976 by the CIE (The International Commission on Illumination), to derive a diverging–diverging array of colors with continuous variances in both hue and lightness (i.e., a color scheme uses light colors for data values that are intermediate on both data dimensions and dark colors of different hues for data values that are low on both dimensions, high on both dimensions, low on one dimension and high on the other, or the reverse.

We adopted the parallel coordinate plot (PCP) as the multidimensional visualization method. As noted above, PCPs have been shown to be an understandable device for exploring multivariate data and, when linked to a map, for exploring the relations between geographic and attribute spaces (Edsall, 2003). However, we use the PCP differently in several ways, which greatly enhances the usefulness of a PCP in revealing multivariate patterns in large datasets.

The output of the SOM was linked to a geographic mapping component (GeoMap) in which each data item (not each node) is mapped, geographically, with the color inherited from the node that contains this item. The mapping component itself is rather simple and straightforward as it relies on the SOM to provide the colors and the PCP to provide the meanings of those colors. From a thematic mapping perspective, the SOM component thus serves as a classification method (a multivariate one) and the PCP component serves as the legend. The resulting map is a holistic view of the spatial distribution of discovered multivariate patterns.

This research shows that different methods (computational, visualization, and mapping), if integrated, can mitigate each other’s weakness while leveraging each other’s strengths to collectively address complex problems in an effective and efficient way. The integrated approach was designed and implemented within a component-oriented framework where different components (or a suite of components) focus on different parts of an analysis problem. These components all comply with the JAVA Bean specification and therefore can be easily integrated in GeoVISTA Studio (Gahegan et al. 2001) or other Java development platforms. Below we present details for each component introduced above and for the overall human-centered geographic knowledge discovery process.

Multivariate Analysis and Abstraction

Pattern Preservation with SOM

The input data for the SOM component is the attribute space X At the data preprocessing step, we implemented two normalization methods: (i) normalization using the minimum and maximum values; and (ii) normalization with the mean and standard deviation, which ensures the mean value of the output is zero and the standard deviation is one. The user can also assign a weight to each variable so that each has a specified level of impact on the similarity measure. The Euclidean distance was adopted as the similarity measure. To simplify the presentation, from now on we use the min-max normalization and assume that all variables have equal weights.

We adopted the commonly used two-dimensional, hexagonal layout of SOM nodes. The size of the SOM in this research is no larger than 13×13 nodes as it is difficult to construct a 2D color scheme with more than 13×13 colors. From a data analysis perspective, such a size is sufficient, because 169 (or fewer) nodes (clusters) can adequately approximate major patterns in the data. The user can change the size of the SOM map on the fly (and compare the results). The construction (or “learning”) of a SOM is an iterative process, and the number of iterations needed depends on the size of the SOM (and also the complexity of the data) (Kohonen 2001). A rule of thumb suggested by Kohonen is that the number of iterations must be at least 500 times the number of SOM nodes. Readers are referred to the book (Kohonen 2001) for methodological details about SOM. Below we give a brief introduction of our configuration and visualization of SOM.

Each SOM node is associated with a vector (a.k.a. codebook vector), which represents the position of this node in the input attribute space. The SOM first initializes each node by assigning its codebook vector randomly (or using a specific initialization method) (Kohonen 2001). During the iterative learning process, each codebook vector is adjusted according to the data items falling inside and the codebook vectors of its neighboring nodes are adjusted accordingly. After the learning process is complete, each node has a new position in the input attribute space. With their new positions and topologic relationships in the 2D layout, the SOM nodes form a nonlinear, smooth surface in the input attribute space, which can be regarded as the result of a nonlinear regression. The nodes are not equally spaced on the regression surface, rather, the positions of the nodes in the input data space tend to approximate the density function of the input data items (i.e., dense areas tend to have more nodes).

The SOM result can be visualized as depicted in Figure 3, which uses two different types of hexagons:

Figure 3.

Visualization of the SOM.

• Node hexagons, each of which contains a circle that is scaled to depict the number of data items in the node; and

• Distance hexagons, each of which is shaded to represent the multivariate dissimilarity between two neighboring node hexagons (i.e., two codebook vectors).

This kind of graphic display of the SOM result is called the U-matrix (Kohonen 2001). A data item is assigned to a node if that node’s codebook vector is the closest to the data item. A node can have more than one data item assigned or it may have no data item assigned (in which case it is an empty node). The area of the circles inside node hexagons represents the number of items contained in each node. Since the area of each circle cannot be larger than the hexagon, we linearly scale the size of each circle so that the largest circle touches the border of the hexagon. Each circle is filled with a color (which is discussed in the next subsection).

The SOM preserves patterns during the projection by ensuring that similar data items either are in the same node or are close in the 2D space. This, of course, cannot be done perfectly as a projection from a multidimensional space to a two dimensional space inevitably introduces some distortions. One example of such distortions is that the distance in the 2D space cannot faithfully represent the distance (proportionally) in the multivariate space. This type of distortion can be observed in the U-Matrix shown in Figure 3, where darker areas represent larger multivariate dissimilarity between neighboring nodes.

The right half of Figure 3 shows the SOM result of a cancer dataset (see case study for details), which consists of five variables for 156 counties in Pennsylvania, West Virginia, and Kentucky. From the area of each circle, we can see the data distribution among those nodes. However, this SOM map by itself can only offer limited insights about the data because two critical pieces of the information are not available. First, we cannot see how those nearby nodes are similar to each other since the SOM does not show the original data values. Second, we cannot see where those nearby nodes are in the geographic space. A common SOM (applied to geographic data) labels each node by the names of those counties that fall in that node. However, if the user has very limited knowledge about the geographic locations of those counties, labeling would not provide much helpful information in interpreting the spatial distribution of the discovered patterns.

Encoding Patterns with Colors

Given the fact that the projected 2D space is a similarity graph of the input data, it would be very useful to assign a color to each SOM node so that nearby (and therefore similar) nodes have similar colors. As noted above, distance in the 2D SOM space cannot faithfully represent the distance (proportionally) in the multivariate space. There are recent research efforts that attempt to preserve both the pattern structure and the distances among SOM nodes as faithfully as possible (Kaski et al. 2000; Yin 2002). Kaski and others presented research on coloring a SOM map by first transforming codebook vectors of SOM nodes to reflect true distances among nodes as much as possible and then folding the transformed nodes onto a perceptually uniform color scheme (2D) to assign each node a color.

However, their 2D color scheme is constructed by cutting through the 3D CIELAB color space with a horizontal 2D plane. As a result, the colors covered by such a scheme have the same lightness. This greatly reduces the richness of patterns that this color scheme can represent and that human vision can perceive. Moreover, it is not always a desirable choice to transform the position of SOM nodes to reflect their true mutual distances when the distribution of the data is skewed. It is similar to the situation in choropleth mapping where we prefer (for some applications) using a natural breaks classification rather than an equal interval method when the data are skewed or have extreme values. Because SOM approximates the data distribution by having more nodes in dense areas, it potentially can serve as a useful multivariate classification method.

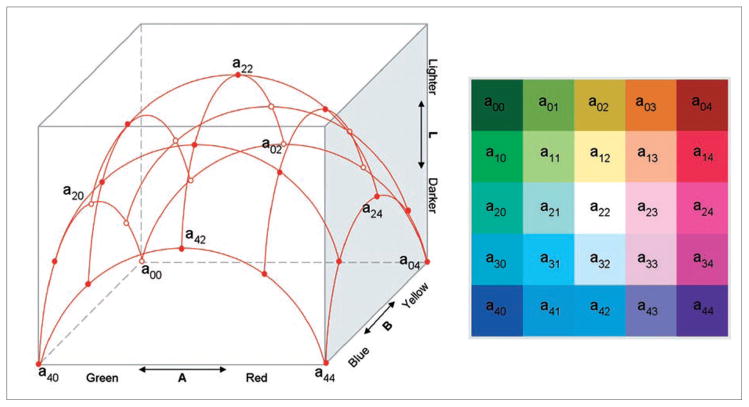
The research reported in this paper does not transform the SOM output space. Rather, we focus our efforts on the design of a cartographically plausible/acceptable 2D color scheme to better present the discovered patterns in the SOM. Building on suggested guidelines for bivariate color schemes (Brewer 1994), our approach utilizes systematic variation in both hue and lightness to construct a 2D array of logically ordered but discriminable colors. First, a square grid net is placed on the CIELAB AB plane, with its center on the origin of the CIELAB color space. Then the grid net is vertically elevated to a surface of a geometric object, and colors are sampled at the grid intersections. The elevation at which the grid intersection meets the surface of the geometric model decides the lightness of the color in the corresponding legend. Together with the coordinates of the grid intersection on the CIELAB AB plane, a color is defined (Figures 4 and 5). The color schemes shown in Figures 4 and 5 are different only in that they used different geometric object models. Figure 4 used an ellipsoid surface and Figure 5 used a bell-shaped surface. The color scheme generated with the bell-shaped model has more lightness variations among colors. The color scheme generated with an ellipsoid model has more bright colors in the center region.

Figure 4.

A 3D structure of a diverging–diverging color scheme from an ellipsoid model. The horizontal dimensions are A (green-red) and B (blue-yellow). The vertical dimension is the L (lightness).

Figure 5.

A 3D structure of a diverging–diverging scheme from a bell-shaped model. The horizontal dimensions are A (green-red) and B (blue-yellow). The vertical dimension is the L (lightness).

We implemented a Color Design component in which the user can interactively design a 2D color scheme (Figure 6). Here we focus on diverging–diverging color schemes. The main control parameters in the design process were:

Figure 6.

The color scheme design interface. The color scheme on the left was derived using a bell-shaped model with the parameters shown. The color scheme on the right was derived using an ellipsoidal model with slightly modified parameters (which are not shown).

• Geometric shape (bell, ellipsoid, etc.);

• Horizontal ranges (the range on A axis and the range on B axis) centered at the origin;

• Vertical range (lightness range);

• Vertical shift (moving the curved surface up or down);

• Horizontal rotation (which can change the colors on four corners); and

• The number of colors (e.g., 5×5, 13×13);

The user can compare the results of different color schemes by dynamically changing the color scheme and see the result in the SOM and other visualization components introduced in the next section.

Multidimensional and Geographic Visualization

At this point, the SOM nodes have assigned colors that collectively represent the patterns in the data. How can we explore and interpret the patterns? What are the multivariate meanings of each SOM node? What is the spatial distribution of these patterns? Where is this group of nodes in the geographic map? In this section, we present approaches that can help the user answer these questions. We describe a component to visualize the multivariate space and a component to visualize the geographic space, with colors representing the same meaning in all components.

Multidimensional Visualization

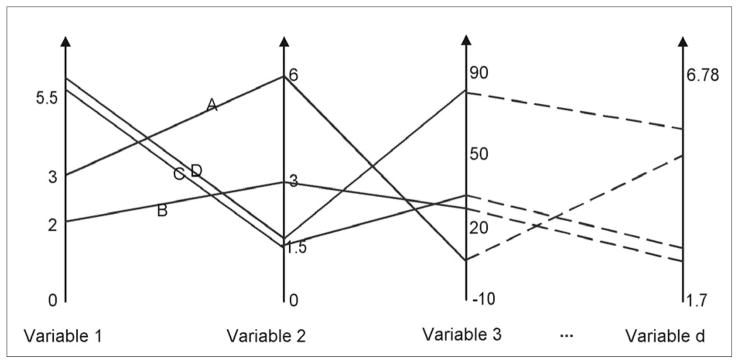
This research adopted the parallel coordinate plot (PCP) as the multidimensional visualization method (Inselberg 1985) because it is simple to understand and yet powerful in revealing data characteristics (Keim and Kreigel 1996) and it is understandable when linked to a map (Edsall 2003). The PCP maps a multidimensional space onto a two-dimensional display by using parallel axes to represent variables. The axes corresponding to each variable are usually scaled linearly from the minimum to the maximum value of that variable. Each data item is presented as a polyline that intersects each axis at the corresponding value. A major advantage of the PCP over the scatter plot is that the PCP can visualize multiple variables at the same time (Figure 7). However, the PCP has limited ability in visualizing datasets of a large or even moderate size (e.g., n>1000) because the polylines may overlap, which makes patterns hard to perceive (Keim and Kreigel 1996).

Figure 7.

A PCP can visualize multiple variables.

Our implementation of the PCP is unique in several ways. First, our PCP component visualizes the summarized data (non-empty SOM nodes) instead of the original data items. Given the SOM size (e.g., 11×11 or smaller), the total number of nodes is very small compared to the number of data items and thus effectively avoids the over-plotting problem mentioned previously. Second, the PCP component configures the thickness of each string (representing a node) according to the total number of data items contained in that node. Third, the color of each string is the same as the SOM node it represents. Thus, similar colors in the PCP represent similarities in terms of all input variables (rather than being colored based on one variable, or not at all). Fourth, in addition to linear scaling, we also implemented a nested-means scaling (which is introduced below) on each axis to avoid the “line over-plotting” problem.

As shown in Figure 7, a normal PCP linearly scales each axis (variable) with its minimum and maximum values. In other words, the minimum value is at the bottom of the axis and the maximum value at the top. The positions of other values on the axis are linearly positioned between the maximum and minimum values. While such a linear scaling can faithfully present the data with no distortion, it may produce a PCP with highly overlapped lines in a small part of the axis, while elsewhere the display remains blank (unused) if the data distribution on a variable is skewed. This situation is similar to that of equal-interval classification in choropleth mapping and can greatly limit the ability of the PCP in presenting patterns in details. To improve this aspect and make the PCP more readable for various data distributions, our version of the PCP uses nested-means scaling on each axis, as an alternative to a linear scaling.

To construct the nested-means intervals, a set of mean values are calculated for each variable. We first calculate the mean value of that variable for the whole dataset, then separate the data into two halves with the mean value, then calculate the mean value for each half, and so on. This recursive process stops when the desired number of intervals is obtained. Normally eight intervals are sufficient (Figure 8). These intervals are equally spaced on the axis although the variable value ranges for different intervals are different. Within each interval, the values are linearly scaled. This nested means approach has two advantages: (1) it can reduce the overlapping problem, and (2) the mean value of each variable is always at the midpoint on each axis. However, such an irregular scaling approach does not faithfully represent the data distribution and can make it very difficult to estimate values at a glance. Therefore, we give the user both options (linear and irregular scaling), which can be switched on the fly as needed. To simplify (and improve) the presentation, only the nested-means intervals are used from now on.

Figure 8.

The PCP visualizes the SOM result in Figure 3. With the nested-mean intervals, the midpoint of each axis is the mean value of that variable for all counties. The color scheme was constructed using the bell-shaped model (see Figure 5). With the colors, we can see not only several major clusters, but also the transition between clusters.

Stabilizing the Meaning of Colors

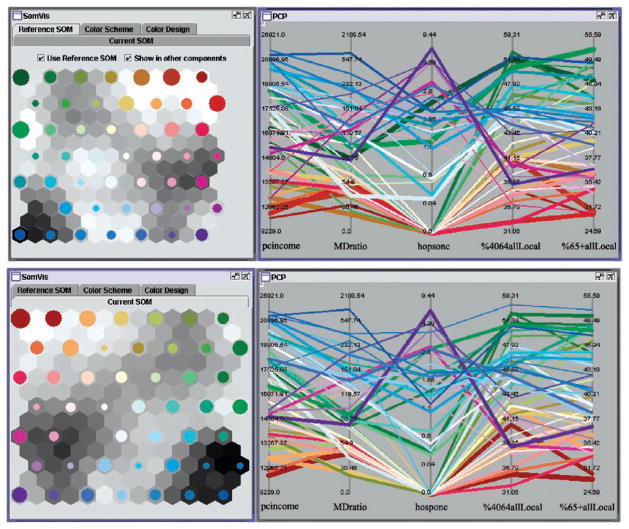
So far, colors have been assigned to SOM nodes by overlaying the 2D color scheme and the 2D layout of SOM nodes. Because the SOM result only preserves the topology (similarity) among data items, several runs of the SOM on the same data may produce different sets of ordered nodes, even though neighboring nodes may remain similar (and therefore patterns are preserved). This variation is due to the random initialization of SOM node vectors before processing the data. To assign meaningful colors to the data, we take two steps to stabilize the meaning of color for different runs. The first step was to match colors with the meaning of data groups, e.g., to use a red hue to represent those counties with serious cancer problems. Our solution is to allow various operations on the 2D color scheme or in the color scheme design process, e.g., rotation, mirroring, transposition of the color matrix. With a combination of these operations, we can achieve a satisfactory result (see Figure 9a).

Figure 9.

(a––top) The color scheme was made to match the meaning of the data. Then this SOM map was set as the reference map. (b––bottom) Another run of the SOM produced a different set of nodes and a different U-matrix. This new map was then colored with the reference SOM map. The patterns in the PCP remained the same in both snapshots, while colors in the two SOMs were different.

The second step was to keep the meaning of colors (after the first step), i.e., when we run the data again, we want the same color to represent the same meaning. To address this problem, our implementation allows the user to set a “reference” map. When a useful SOM map with meaningful colors has been achieved after the first step, we set this as the reference map (Figure 9a). When we run the SOM on the same data (and the same set of variables) again, we may get a different set of data point groupings. Therefore, rather than using a new color scheme, we used the reference map to color the new SOM map. Specifically, for each non-empty node in the new SOM map, we found the most similar node (including empty nodes––empty nodes also have colors based on their positions in the SOM map) in the reference map, and then used the color of that reference node to color the new node. In other words, we folded (or imposed) the new map over the reference map. The colors thus have similar meanings although groupings or the topology may be different from one SOM map to another (Figure 9).

Multivariate Mapping and Its Interpretation

To examine multivariate spatial patterns in the geographic context, mapping is indispensable. We output the SOM result to a mapping component, where each data item (not each SOM node) is represented, geographically, with color assigned based on the node that contains this item. The resulting map is a holistic view of the spatial distribution of discovered multivariate patterns by SOM (Figures 10–14).

Figure 10.

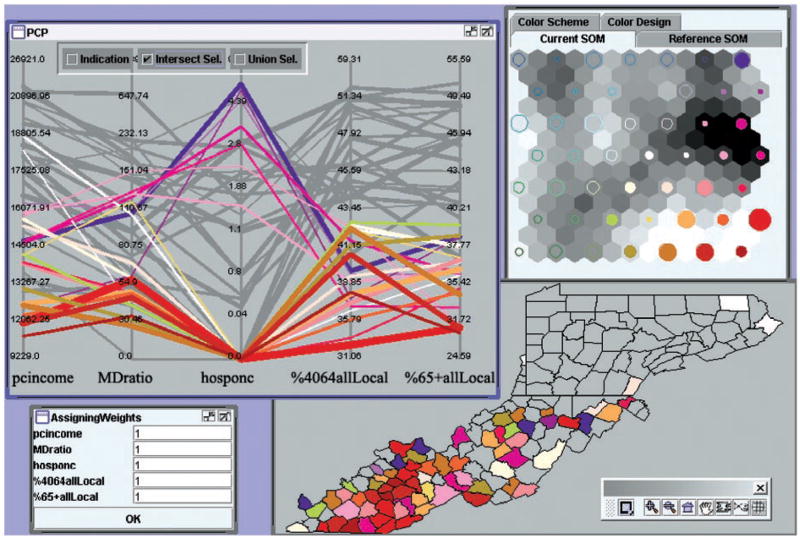
The visualization of the SOM result for subspace {pcincome, MDratio, hosponc, %4064allLocal, %65+allLocal}. The color scheme was constructed with the bell-shaped model and was made to best match the meaning of the data items they represent, e.g., red color represents counties with undesirable situations (low percentage of local stage).

Figure 14.

. A selection of counties in West Virginia, where the geographic pattern is not as clear as in Pennsylvania and Kentucky. However, in the attribute space (in PCP) the pattern remains clear.

An advantage of our integrated approach is that, even without human interaction (e.g., brushing and focusing), we can still perceive a holistic view of the multivariate spatial patterns by looking at only three displays (Figure 10). Our approach is different from the approaches taken by Skupin and Hagelman (2003), and Koua and Kraak (2004), both of which visually compare multiple SOM views (each for one variable) to reveal the relationships between variables.

Human-Centered Exploration

The implementation of each component supports user selection and brushing across components. There are two types of selection: data-item-based and SOM-node-based. As noted earlier, SOM and PCP both show the aggregated data (i.e., SOM nodes) instead of the original data items, while in the GeoMap, each data item (county) is shown. When the user makes a selection by dragging the mouse to draw a rectangle in the SOM or to run across strings in the PCP, nodes are selected and the GeoMap highlights all those data items that fall in those selected nodes (see Figures 11–14). When the user makes a selection by dragging the mouse in the GeoMap, data items (rather than nodes) are selected. While it is easy to map a node-based selection to item-based selection, translating an item-based selection (in GeoMap) to a node-based selection (in PCP and SOM) is more complicated, as it is possible that only a subset of the data items in a node is selected.

Figure 11.

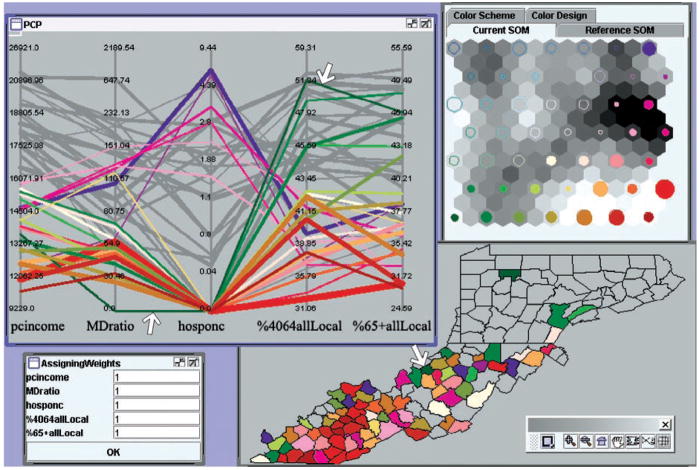
. A selection of those counties that have below-average rates for both cancer variables (%4064allLocal and %65+allLocal).

It takes three steps to translate an item-based selection made in the GeoMap to a node-based selection in the SOM and PCP. The first step is to find the nodes that contain those selected data items. Then calculate the percentage of data items in each node that have been selected. The third step is to adjust the visualization in the SOM and PCP according to the above information. In the SOM, each node is represented by a wedge of a pie, proportional to the percentage selected (see Figure 14). In the PCP, the thickness of the selected string is adjusted by the number of items selected (a subset of the items it contains), the mean vector of this string is recalculated using selected items only, thus the position of this string in the PCP is adjusted according to the new mean vector. Those strings that have no item selected are shown in a gray color. Please see next section for the usage and advantage of these selection and brushing operations.

Cancer Data Analysis: A Case Study

We applied the developed approach to cancer data analysis in order to support public health research and policy-making. Research in this domain often involves many variables, such as variables related to cancer mortality, incidence, screening rates, and accessibility to medical facilities. In this case study, we used our approach specifically to explore, identify, and investigate multivariate spatial patterns of cancer incidence and their relationship to socioeconomic factors. The geographic study region included 156 counties in Pennsylvania, West Virginia, and Kentucky, which are part of the Appalachia Cancer Network (ACN). Although the data set we used was small (156 counties), our approach can analyze very large datasets (e.g., n>10,000) efficiently.

Data Compilation and Preprocessing

Cancer incidence data (directly from CAN) contain count data of incidences for a five-year period (1994–1998, all races/all sexes) for several cancers and for different categories, e.g., a combination of an age group (40–64, 65+, or all ages) and a diagnosis stage (local stage, regional stage, distant stage, or missing stage). Local stage means that the cancer was diagnosed early in its development and is restricted to the organ of origin. Regional stage means that at diagnosis, the cancer has invaded beyond the organ of origin by direct extension to adjacent organs/tissues and/or regional lymph nodes. Distant stage represents the most serious situation where the cancer has extended beyond adjacent organs or tissues (thus, metastases to distant site(s) or distant lymph nodes). Missing stage means that the stage information for that diagnosis is missing.

Data that we analyzed included all four stages and three age ranges (producing 12 dimensions of data). Here, we focus on data for “all cancers” (the total incidence for cancer regardless of type). Using the above 12 dimensions of data, we derived 12 new dimensions by calculating the percentage rate for each stage in each age category for each county. For example, the percentage of all cancer incidences for the 65 + age group that was diagnosed at the local stage. To study possible relationships between cancer incidence and socioeconomic, demographic, and policy-related data, we joined the cancer data with a set of socioeconomic, population, and employment variables. The dataset comprised about 30 variables. We used both domain knowledge and a formal feature selection method to select meaningful and interesting subspaces from the dataset. To simplify the presentation, below we only introduce the analysis of one such subspace. This subspace involves five variables (see Table 1): two are outcome variables (%4064allLocal and %65+allLocal) and three are potential covariates (pcincome, MDratio, and hosponc).

Table 1.

A subspace of five variables.

Variables	Description	Source
pcincome	per capita income	Census 1990
MDratio	# physicians per 100,000 population	ARF* 1997
hosponc	# hospitals with oncology service per 100,000 pop	ARF 1995
%4064allLocal	% cancer incidences for 40–64 age group that were diagnosed at local stage	ACN 1994–98
%65 + allLocal	% cancer incidences for 65 + age group that were diagnosed at local stage	ACN 1994–98

^*Area Resource File (ARF), February 1999, U.S. Department of Health and Human Services, Health Resources and Services Administration, Bureau of Health Professions, Rockville, MD. The original source of MDratio and hosponc are: (a) Number of physicians, from the American Medical Association Physician Master File, 1997; and (b) Number of hospitals with oncology service, from the American Hospital Association Annual Survey, 1995.

Multivariate Analysis and Geovisualization

Since cancer diagnosed at its local stage is easier to cure and contain, high values on the outcome variables (%4064allLocal and %65+allLocal) represent a good cancer control situation in that county. Colors were assigned to match the meaning of the data they represent, e.g., a red hue for bad situations (low values on %4064allLocal and %65+allLocal) and blue/green for good situations (high values on %4064allLocal and %65+allLocal). The integrated components presented a holistic view of the multivariate and spatial patterns in this five-dimensional space (Figure 10). As mentioned above, with our nested-means intervals, the mean value for each variable is always at the midpoint on each axis, which is important in interpreting the patterns visualized in the PCP component.

Associations can be visually recognized in the snapshot shown in Figure 10. One association (represented with red/brown colors) is between very low pcincome, very low MDratio, zero hosponc, and low values for both %4064allLocal, and low %65+allLocal. Moreover, the counties with a relatively undesirable cancer control situation concentrate geographically in eastern Kentucky and part of West Virginia. Another association (represented with a blue hue) is between high pcincome, high MDratio, average hosponc, and high values on both %4064allLocal and %65+allLocal. These counties with a relatively desirable cancer control situation geographically concentrate in Pennsylvania and part of West Virginia. The other two interesting associations are:

• The association (represented with a green hue) between around-average pcincome, low/very low MDratio, very low hosponc, and high values on %4064allLocal and %65+allLocal; and

• The association (represented with a purple hue) between average/below average pcincome, average MDratio, very high hosponc, and low values on %4064allLocal and %65+allLocal (scattered in counties of Kentucky and West Virginia).

Below we discuss how we interacted with the result to gain better understanding of the observed patterns.

To examine the patterns related to relatively undesirable cancer control situations, we made a selection in the PCP of SOM nodes with below-average values for both %4064allLocal and %65+allLocal (Figure 11). Our implementation of the PCP supports intersect selections (i.e., selection within a previous selection) as well as union selections (i.e., adding consecutive selections together). Clearly, we can see that the selected counties (with low percentages of local stage for both age groups) are those in which below-average values for pcincome and MDratio predominate. Very interestingly, their values for hosponc are at the two extremes, either zero or very high.

To examine the reversed relationship, i.e., does below-average pcincome always lead to a relatively undesirable cancer control situation, we made another selection (based on pcincome only) of counties with below average pcincome values (Figure 12). The results showed patterns similar to Figure 11––except that a third group emerged (represented with a green hue)––which have low (not very low) pcincome, low MDratio, and zero hosponc but have very high values on both local-stage percentages (a very good situation). These “outlier” counties scatter around in all three states and are on the periphery, geographically, of the selected counties. There is even a county (shown in Figure 12 with white arrows) with zero MDratio, zero hosponc, below-average (not very low) pcincome, and a very high local-stage percentage. We selected this county (Wirt, WV) and its neighbors in the GeoMap (this selection is not shown in the figure) and found that the neighboring county to its northwest (Wood, WV) has a high MDratio value (151.0), high hosponc (2.0), and high pcincome (20896). It is likely that residents in Wirt County primarily rely on the medical facilities in Wood County or other nearby counties.

Figure 12.

A selection of counties that have below-average pcincome.

To examine the two extremes regarding the hosponc variable shown in Figures 11 and 12, we made a selection (based on hosponc only) of those counties that have non-zero hosponc values (Figure 13). This part of the data clearly showed two distinctive associations. The first association (colored in purple/pink) is between low pcincome, average MDratio, high hosponc and low values for %4064allLocal and %65+allLocal. This association possibly indicates that for counties with proper health facilities (e.g., hospitals with oncology service), poor economic status can still limit the usefulness of these facilities in detecting and controlling cancers. This group of counties is distributed across West Virginia and Eastern Kentucky. The second association (colored with a blue hue) is between high pcincome, high MDratio, average hosponc and high values for %4064allLocal and %65+allLocal. This association supports, from the other side, the hypothesis generated from the first association that economic status is an important factor (in addition to health facilities) in detecting and controlling cancers. This group of counties is located primarily in Pennsylvania.

Figure 13.

A selection of counties that have non-zero hosponc values, i.e., these counties have at least one hospital with oncology service.

From the above analysis, it appears that residents in Pennsylvania have better access to health care, better economic status, and the outcome values (percentages of local stage diagnosis for age groups 40–64 and 65+) are higher. In Kentucky there is some evidence to suggest that access to health care is more limited, which may correspond with lower local-stage diagnoses. However, the situation in West Virginia is more diverse. We made a geographic selection (by drawing a rectangle) of most counties in West Virginia (see Figure 14). As noted earlier, this is an item-based selection. The mean vectors for each SOM node were automatically adjusted based on the data items selected in each node. The visualization of the SOM was also adjusted to show the partial selection in each node. The result of this geographically based selection shows that all of the four major associations discovered in Figure 10 (represented by blue, purple, green, and red hues) exist in West Virginia. It supports the hypothesis that there is a relationship between economic status, oncology service, and early detection of cancers and that this relationship is not of a simple linear form.

To sum up, the exploratory spatial analysis and geographic knowledge discovery environment we developed facilitates an interactive and iterative analysis process that can lead to important hypotheses about cancer risk factors, thereby helping to reveal the form of the relationship. As a critical step prior to formal hypothesis tests or modeling, such exploratory analysis offers valuable insights about the existence and form of unknown patterns, in an efficient way. Domain expertise is incorporated into the exploratory analysis with human interactions and an iterative discovery/refining process. The patterns discovered and the hypotheses generated from the discovery are then subject to formal tests and validation.

Conclusions

This paper introduces an integrated geographic knowledge discovery environment that is able to detect and visualize multivariate spatial patterns within high-dimensional geographic data, while also supporting human interactions to examine the patterns. The environment consists of several major components, each of which performs a specific task and can coordinate with others to facilitate the overall knowledge discovery process. Within the integrated environment, this paper focused on four components, which include a self-organizing map (SOM), a parallel coordinate plot (PCP), a geographic mapping component (GeoMap), and a 2D color design tool. By coordinating among these components and exercising domain expertise via interactive exploration, the developed environment can produce insights into multivariate spatial patterns and let the data speak for themselves prior to developing hypotheses.

Formal usability tests are needed for further development of the knowledge discovery environment described here. As noted in this paper, human interaction and expertise are indispensable in using exploratory analysis tools. The developed environment can only achieve its ultimate goal in supporting hypothesis generation and geographic knowledge discovery if it is designed and implemented with a proper user interface and a suitable set of functions for domain experts (e.g., epidemiologists). We have begun working with our users in epidemiology to customize the interface, incorporate new functions (e.g., provide statistical measures in the visualization component), and develop applications.

Designed with a component-based framework, the developed environment is open to additions of new components. The integration of new components to extend the capability of the current system is relatively easy. For example, other clustering methods, temporal analysis components, analysis methods that can process categorical data (the current system can only accommodate numerical data), or new visualization components can be added. However, the coordination among components can become complicated as different components may require a different set of inputs and are likely to produce a different set of outputs.